受弯构件正截面承载力计算基本假定
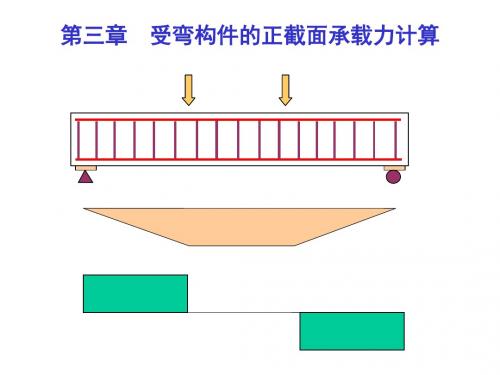
第三章 钢筋混凝土受弯构件正截面承载力计算

第三章钢筋混凝土受弯构件正截面承载力计算受弯构件(bendingmember)是指截面上通常有弯矩和剪力共同作用而轴力可以忽视不计的构件。
钢筋混凝土受弯构件的主要形式是板(Slab)和梁(beam),它们是组成工程结构的基本构件,在桥梁工程中应用很广。
在荷载作用下,受弯构件的截面将承受弯矩M和V的作用。
因此设计受弯构件时,一般应满意下列两方面的要求:(1)由于弯矩M的作用,构件可能沿弯矩最大的截面发生破坏,当受弯构件沿弯矩最大的截面发生破坏时,破坏截面与构件轴线垂直,称为正截面破坏。
故需进行正截面承载力计算。
(2)由于弯矩M和剪力V的共同作用,构件可能沿剪力最大或弯矩和努力都较大的截面破坏,破坏截面与构件的轴线斜交,称为沿斜截面破坏,故需进行斜截面承载力计算。
为了保证梁正截面具有足够的承载力,在设计时除了适当的选用材料和截面尺寸外,必需在梁的受拉区配置足够数量的纵向钢筋,以承受因弯矩作用而产生的拉力;为了防止梁的斜截面破坏,必需在梁中设置肯定数量的箍筋和弯起钢筋,以承受由于剪力作用而产生的拉力。
第一节受弯构件的截面形式与构造一、钢筋混凝土板的构造板是在两个方向上(长、宽)尺度很大,而在另一方向上(厚度)尺寸相对较小的构件。
钢筋混凝土板可分为整体现浇板和预制板。
在施工场地现场搭支架、立模板、配置钢筋,然后就地浇筑混凝土的板称为整体现浇板。
通常这种板的截面宽度较大,在计算中常取单位宽度的矩形截面进行计算。
预制板是在预制厂和施工场地现场预先制好的板,板宽度一般掌握在Inl左右,由于施工条件好,预制板不仅能采纳矩形实心板,还能采纳矩形空心板,以减轻板的自重。
板的厚度h由截面上的最大弯矩和板的刚度要求打算,但是为了保证施工质量及耐久性的要求,《大路桥规》规定了各种板的最小厚度;行车道板厚度不小于IOOmm人行道板厚度,就地浇注的混凝土板不宜小于80mm,预制不宜小于60mm。
空心板桥的顶板和底板厚度,均不宜小于80mm。
钢筋混凝土受弯构件正截面承载力计算 (2)_OK

合力作用点相同
x=βxc
合力大小相同
fce=αfc
27
混凝土受压区等效矩形应力图系数
≤ C50
C55
C60
C6 5
C70
C75
C80
α
1.0
0.99
0.98
0.97
0.96
0.95
0.94
β
0.8
0.79
0.78
0.77
0.76
0.75
0.74
水工结构中,常常只使用较低等级的混凝土,因此规范 规定:
10
四、梁内钢筋的直径和净距
架立钢筋——设置在梁受压区,用以固定箍筋的正确位置, 并能承受混凝土收缩和温度变化产生的内应力。 箍筋——承受梁的剪力;固定纵向钢筋位置,形成钢筋笼。 侧向构造钢筋——增加梁内钢筋骨架的刚性,增强梁的抗 扭能力,承受侧向发生的温度及收缩变形。
11
四、梁内钢筋的直径和净距
Mu
fyAs
计算简图
fcbx fy As
M
D
Mu
fcbx(h0
x) 2
fy As (h0
x) 2
KM S
Mu
fcbx(h0
x) 2
fy As (h0
x) 2
32
六、基本公式的适用条件
防止发生超筋破坏
max
As fcbx x fc fc
bh0 fybh0 h0 fy
fy
相对受压区高度
x fy As fcb
x
h0
若
1
:
b
Mu
f c b x ( h0
x) 2
f y As (h0
x) 2
若
受弯构件的正截面承载力计算资料
槽形板
二、截面尺寸 高跨比h/l0=1/8~1/12
矩形截面梁高宽比h/b=2.0~3.5 T形截面梁高宽比h/b=2.5~4.0。(b为梁肋) b=120、150、180、200、220、250、300、…(mm),
250以上的级差为50mm。 h=250、300、350、……、750、800、900、
4.3.1 正截面承载力计算的基本假定
(1) 截面的应变沿截面高度保持线性分布-简称平截面假定
ec
f e ec es
y xc h0 xx
f xc
h0
(2) 不考虑混凝土的抗拉强度
y
es
M xc
C
Tc T
(3) 混凝土的压应力-压应变之间的关系为:
σ
fc
上升段
c
f
c
[1
(1
e e0
M0
C 超筋梁ρ>ρmax
My B
Mu
适筋梁 ρmin<ρ<ρmax
A少筋梁ρ>ρmax
0
f0
超筋破坏形态
> b
特点:受压区混凝土先压碎,纵向受拉钢筋 不屈服。
钢筋破坏之前仍处于弹性工作阶段,裂缝开 展不宽,延伸不高,梁的挠度不大。破坏带 有突然性,没有明显的破坏预兆,属于脆性 破坏类型。
M0
a
≥30
纵向受拉钢筋的配筋百分率
截面上所有纵向受拉钢筋的合力点到受拉边缘的竖向距离
为a,则到受压边缘的距离为h0=h-a,称为截面有效高度。
d=10~32mm(常用) 单排 a= c+d/2=25+20/2=35mm 双排 a= c+d+e/2=25+20+30/2=60mm
钢筋混凝土受弯构件正截面承载力计算

为保证钢筋混凝土结构的耐久性、防火性以及钢
筋与混凝土的粘结性能,钢筋的混凝土保护层厚
5度、一配般筋不率小于2A 5msm% ; ....4...2()
bh0
用下述公式表示
As bh0
%
公式中各符号含义:
As为受拉钢筋截面面积; b为梁宽;h0为梁的有效 高度,h0=h-as;as为所有受拉钢筋重心到梁底面 的距离,单排钢筋as= 35mm ,双排钢筋as= 55~60mm 。
M/ M u
Mu
1.0
0.8 My
0.6
II
0.4
III III a II a
M cr I a
I
0
f cr
fy
fu f
加载过程中弯矩-曲率关系
说明:
对于配筋合适的梁,在III
阶段,其承载力基本保持不 变而变形可以很大,在完全
M/ M u
Mu
1.0
破坏以前具有很好的变形能 力,破坏预兆明显,我们把
0.8 My
通常采用两点对称集中加荷,加载点位于梁跨度 的1/3处,如下图所示。这样,在两个对称集中荷载间 的区段(称“纯弯段”)上,不仅可以基本上排除剪力的 影响(忽略自重),同时也有利于在这一较长的区段上(L /3)布置仪表,以观察粱受荷后变形和裂缝出现与开 展的情况。在“纯弯段”内,沿梁高两侧布置多排测 点,用仪表量测梁的纵向变形。
梁破坏时的极限弯矩Mu小于在正常情况下的开
裂弯矩Mcr。梁配筋率越小, Mcr -Mu的差值越大; 越大(但仍在少筋梁范围内), Mcr -Mu的差值越小。
当Mcr -Mu =0时,它就是少筋梁与适筋梁的界限。这
时的配筋率就是适筋梁最小配筋率的理论值min。
《混凝土结构与砌体结构》第3版-第4章受弯构件的正截面承载力习题答案

第4章 受弯构件的正截面承载力4.1选择题1.( C )作为受弯构件正截面承载力计算的依据。
A .Ⅰa 状态;B. Ⅱa 状态; C. Ⅲa 状态; D. 第Ⅱ阶段; 2.( A )作为受弯构件抗裂计算的依据。
A .Ⅰa 状态;B. Ⅱa 状态; C. Ⅲa 状态; D. 第Ⅱ阶段; 3.( D )作为受弯构件变形和裂缝验算的依据。
A .Ⅰa 状态;B. Ⅱa 状态;C. Ⅲa 状态; D. 第Ⅱ阶段;4.受弯构件正截面承载力计算基本公式的建立是依据哪种破坏形态建立的( B )。
A. 少筋破坏;B 适筋破坏;C 超筋破坏;D 界限破坏;5.下列那个条件不能用来判断适筋破坏与超筋破坏的界限( C )。
A .b ξξ≤;B .0h x b ξ≤;C .'2s a x ≤; D .max ρρ≤6.受弯构件正截面承载力计算中,截面抵抗矩系数s α取值为:( A )。
A .)5.01(ξξ-; B .)5.01(ξξ+;C .ξ5.01-;D .ξ5.01+;7.受弯构件正截面承载力中,对于双筋截面,下面哪个条件可以满足受压钢筋的屈服( C )。
A .0h x b ξ≤;B .0h x b ξ>;C .'2s a x ≥;D .'2s a x <;8.受弯构件正截面承载力中,T 形截面划分为两类截面的依据是( D )。
A. 计算公式建立的基本原理不同;B. 受拉区与受压区截面形状不同;C. 破坏形态不同;D. 混凝土受压区的形状不同;9.提高受弯构件正截面受弯能力最有效的方法是( C )。
A. 提高混凝土强度等级;B. 增加保护层厚度;C. 增加截面高度;D. 增加截面宽度;10.在T 形截面梁的正截面承载力计算中,假定在受压区翼缘计算宽度范围内混凝土的压应力分布是( A )。
A. 均匀分布;B. 按抛物线形分布;C. 按三角形分布;D. 部分均匀,部分不均匀分布;11.混凝土保护层厚度是指( B )。
受弯构件正截面承载力计算的依据

受弯构件正截面承载力计算的依据
1、计算构件受弯的中限假设值,该值是构件正截面承载力最大值的
截断点。
其中,将构件按照以下四个类型分成四组:圆管、方管、折管、
角钢。
2、根据构件的受力状况确定计算公式,根据构件受弯时的受力情况,选择合适的计算公式。
3、确定计算参数,如构件的形状、尺寸、材料以及构件受力情况下
的拉应力标准值等。
4、计算构件正截面承载力,根据所选定的计算公式,代入参数值,
计算出正截面承载力。
该值可以用来比较实际应用中构件的承载力,即在
设计中考虑的各种损失后,构件还能够达到的正截面承载力。
5、结果校核,比较计算结果和工程实际应用的正截面承载力,若差
距较大,则需要检查其他可能的影响因素,如材料类型、固定方式、受力
大小等。
最后,在计算出正截面承载力之后,还要进行热变形校核,以确保构
件的受弯中限假设值可以接受,保证构件受弯的安全性。
第三章-钢筋混凝土受弯构件正截面承载力计算

§3.3 建筑工程中受弯构件正截面承载力计算方法
3.3.1 基本假定 建筑工程中在进行受弯构件正截面承载力计 算时,引人了如下几个基本假定; 1.截面应变保持平面; 2.不考虑混凝土的抗拉强度; 3.混凝土受压的应力一应变关系曲线按下列 规定取用(图3-9)。
εcu——正截面处于非均匀受压时的混凝土极限压应变 ,当计算的εcu值大于0.0033时,应取为0.0033;
fcu,k——混凝土立方体抗压强度标准值;
n——系数,当计算的n大于2.0时,应取为2.0。
n,ε0,εcu的取值见表3—1。
由表3-1可见,当混凝土的强度等级小于和等于C50时,
n,ε0和εcu均为定值。当混凝土的强度等级大于C50时,随 着混凝土强度等级的提高,ε0的值不断增大,而εcu值却逐渐
M
f y As (h0
x) 2
(3-9b)
式中M——荷载在该截面上产生的弯矩设计值; h0——截面的有效高度,按下式计算
h0=h-as
h为截面高度,as为受拉区边缘到受拉钢筋合力作用点的距离。
对于处于室内正常使用环境(一类环境)的梁和板,
当混凝土强度等级> C20,保护层最小厚度(指从构件 边缘至钢筋边缘的距离)不得小于25mm,板内钢筋的混凝 士保护层厚度不得小于15mm
当εc≤ ε0时 σc=fc[1-(1- εc/ ε 0)n]
当ε0≤ εc ≤ εcu时 σc=fc
(3-2) (3-3)
(3-4)
(3-5)
(3-6)
式中 σc——对应于混凝土应变εc时的混凝土压应力;
受弯构件正截面计算的基本假定

受弯构件正截面计算的基本假定当我们谈到建筑和结构设计时,有时候你可能会感到头脑里像是被卷入了一场复杂的数学迷宫。
但是别担心,今天咱们就用最简单的方式来聊聊“受弯构件正截面计算的基本假定”。
这是啥呢?就像我们在建房子时需要确保每块砖都能稳稳地放在一起,受弯构件也有一些基本的“规则”,让它们在负重的时候不会垮掉。
好啦,我们一步步来,弄清楚这些规则到底是什么。
1. 受弯构件的基本概念首先,让我们搞清楚什么是“受弯构件”。
简单来说,这些构件就像是钢筋混凝土梁或木梁,承受着各种各样的力量,比如楼上的重物或者风的吹压。
想象一下,你的桌子就是一个受弯构件。
当上面放了很多书,它的中间部分就会下沉,这时候桌子就“受弯”了。
为了确保这张桌子不会崩溃,咱们需要对它进行一些计算,就像在考试前我们会复习一样。
2. 受弯构件的正截面好了,知道了什么是受弯构件,现在咱们要聊聊正截面。
这可不是吃早餐的“正宗切面”,而是构件的一个横截面。
想象你切开一根香肠,这个横切面就是香肠的正截面。
对于受弯构件来说,正截面的计算就像是给它做一次体检,看看它的承重能力如何。
为了让构件在各种情况下都能稳稳地站着,我们有几个基本的假定条件:2.1 假定一:截面的应力分布第一个假定就是应力分布。
你可以把它想象成是把一张纸对折的过程。
每次对折的时候,纸的中间部分就会有更多的应力。
我们假定在一个截面上,应力分布是均匀的,这样在计算时就不会太复杂。
实际上,这种假定是为了简化问题,让我们可以用数学公式来算得更精确一些。
这样,当构件受力时,我们就能预测它会如何变形或者开裂。
2.2 假定二:材料的均匀性第二个假定就是材料的均匀性。
这就像你去超市买牛奶时,奶 carton 上写的“全脂牛奶”,实际上,你期望的就是牛奶的成分是均匀的,而不是某一部分特别浓稠。
对于构件来说,我们也假定材料是均匀的。
这样的话,在计算截面的时候,不用考虑材料的不均匀性对结果的影响。
就像做蛋糕的时候,假定面粉搅拌均匀,这样烤出来的蛋糕才会有一致的口感。
受弯构件正截面承载力计算

Flexure Strength of RC Beams
第5章
受弯构件
如何进行一个实际工程中的梁设计?
梁的截面形式 为什么要有不同的截面形式? 配筋基本要求 简化计算方法 如何保证所设计的是一个适筋梁? 最大配筋率和最小配筋率 当不能满足配筋限制要求时,如何解决问题?
h/3 h/4
Mcr=Mu
h⎛h h⎞ 7 2 M cr = f tk b ⎜ + ⎟ = f tk bh 2 ⎝ 4 3 ⎠ 24
◆ 矩形截面梁高宽比h/b=2.0~3.5
c≥cmin
d
c≥cmin
d
1.5d
d=10~32mm(常用)
h0=h-as
单排 a= 35mm 双排 a= 55~60mm
T形截面梁高宽比h/b=2.5~4.0。 To ensure lateral stability
5.1 概述
第5章
受弯构件
≥30mm
5.1 概述
第5章
受弯构件
≥30mm
1.5d
c≥cmin
d
◆ 梁上部无受压钢筋时,需配置2根架
立筋(Hanger Bars),以便与箍筋和 梁底部纵筋形成钢筋骨架,直径一 般不小于10mm;
≥cmin
h0
◆ 梁高度h0>450mm时,要求在梁两侧
a
≥cmin
1.5d
沿高度每隔200设置一根纵向构造钢 筋(Skin Reinforcement),以减小梁 腹部的裂缝宽度,直径≥10mm;
C70 0.96 0.76
C75 0.95 0.73
C80 0.94 0.74
α fc
x=β xn C=α fcbx
受弯构件正截面承载力计算基本假定

3.正截面承载力计算的基本原则
(1)正截面承载力计算的基本假定
《混凝土结构设计规范》( GB 50010-2010):
6.2.1 正截面承载力应按下列基本假定进行计算: 1 平截面假定:截面应变保持平面,即变形前的平面变形后仍为平面,截面上各点应变保 持线性关系;
3.正截面承载力计算的基本原则
3.正截面承载力计算的基本原则
(1)正截面承载力计算的基本假定
《混凝土结构设计规范》( GB 50010-2010):
6.2.1 正截面承载力应按下列基本假定进行计算: 5 纵钢筋的应力取钢筋应变与其弹性模量的乘积,但其值应符合下列要求:
第i层非预应力筋的应力
第i层预应力筋的应力
谢谢!!
(1)正截面承载力计算的基本假定
《混凝土结构设计规范》( GB 50010-2010):
6.2.1 正截面承载力应按下列基本假定进行计算: 2 不考虑混凝土的抗拉强度,即全部拉力由纵向受拉钢筋承担。
3.正截面承载力计算的基本原则
(1)正截面承载力计算的基本假定
《混凝土结构设计规范》( GB 50010-2010):
6.2.1 正截面承载力应按下列基本假定进行计算: 3 混凝土受压的应力与应变关系按下列规定取用:
n≤ 2 0≥0.002 cu ≤ 0.0033, 轴压时取0
3.正截面承载力计算的基本原则
(1)正截面承载力计算的基本假定
《混凝土结构设计规范》( GB 50010-2010):
6.2.1 正截面承载力应按下列基本假定进行计算: 4 纵向受拉钢筋的极限拉应变取为0.01;
受弯构件正截面承载能力计算

其特点有: (1)只能沿 弯矩作用方 向,绕中和 轴单向转动 (2)只能在 从受拉钢筋 开始屈服到 受压区混凝 土压坏的有 限范围内转 动φy-φu。
(3)转动的同时,能传递一定的弯矩,即截面的极限弯矩 Mu 塑性铰出现后,简支梁即形成三铰在一直线上的破坏机构。
3.《规范》采用的正截面极限受弯承载力计算方法
2.适筋梁正截面的受力性能 (1)适筋梁的受力阶段
第Ⅰ阶段(弹性工作阶段) 加载→开裂 开裂弯矩Mcr
第Ⅱ阶段(带裂缝工作阶段) 开裂→屈服 屈服弯矩My
第Ⅲ阶段(破坏阶段) 屈服→压碎 极限弯矩Mu
不同阶段截面应力分布图的应用
Ⅰa阶段的应力状态是抗裂验算的依据。 Ⅱ 阶段的应力状态是裂缝宽度和变形验算的依据。 Ⅲa阶段的应力状态作为构件承载力计算的依据
有柱帽 无柱帽
1/32~1/40 1/30~1/35
注:表中l0为梁的计算跨度。当l0≥9m时,表中数值宜乘以1.2。
(2)板的最小厚度
按构造要求,现浇板的厚度不应小于下表的数值。现 浇板的厚度一般取为10mm的倍数。
(3)板的配筋
①受力钢筋 用来承受弯矩产生的拉力 ②分布钢筋
作用,一是固定受力钢筋的位置,形成钢筋网;二是 将板上荷载有效地传到受力钢筋上去;三是防止温度或混 凝土收缩等原因沿跨度方向的裂缝。
ecu
a’
A
’ s
e s
x
M
h0
Cs=ss’As’ Cc=fcbx
As
a
>ey
T=fyAs
双筋截面在满足构造要求的条件下,截面达到Mu 的标志仍然是受压边缘混凝土应变达到εcu。 受压区 混凝土的应力仍可按等效矩形应力考虑。当相对受压
受弯构件正截面承载力计算有哪些基本假定

受弯构件正截面承载力计算有哪些基本假定受弯构件正截面承载力计算是工程力学中的重要内容,是评估和设计结构承载能力的关键步骤。
在进行这一计算时,工程师们通常会基于一系列基本假定进行分析。
下面我将深入探讨受弯构件正截面承载力计算的基本假定,并结合具体的工程实例进行解析。
1. 材料的弹性本构假定在进行受弯构件正截面承载力计算时,通常假定材料具有线弹性本构,即在应力和应变之间存在线性关系。
这意味着材料在弹性阶段的变形行为可以通过弹性模量来描述,这一假定为后续的承载力计算提供了基础。
2. 平面截面的假定在受弯构件的正截面承载力计算中,通常假定截面仍然是平面的。
这意味着截面内部的应力沿纵向和横向均保持平衡,从而简化了截面内部应力和变形的分析。
3. 材料的等强度假定受弯构件正截面承载力计算通常基于等强度假定,即假定截面内各点的材料强度相同。
这一假定在实际工程中虽然存在一定的误差,但在设计阶段可以简化材料强度的考虑,从而便于工程师进行承载力的评估和设计。
4. 截面平面仍然保持平面的假定在受弯构件正截面承载力计算中,通常假定截面在弯曲后仍然保持平面的。
虽然在弯曲过程中会产生一定的截面扭转变形,但这一假定可以简化截面内部应力和变形的分析,为后续的计算提供了便利。
受弯构件正截面承载力计算涉及了多项基本假定,这些假定在一定程度上简化了工程设计过程,便于工程师进行承载能力的评估和设计。
然而,在实际工程中,这些假定可能会与实际情况存在一定差异,因此在进行设计时需要综合考虑各种因素,以确保结构的安全可靠性。
在工程实践中,正确理解和应用这些基本假定对于进行承载能力计算是非常重要的。
工程师需要根据具体的工程要求和实际情况,合理应用这些假定,并结合实际数据和分析结果进行准确的承载能力评估和设计。
【总结】本文通过对受弯构件正截面承载力计算的基本假定进行深入探讨,并结合实际工程实例进行解析,阐述了这些基本假定在工程设计中的重要性和应用。
混凝土结构原理 第4章第2次课 受弯构件正截面承载力计算基本假定

宁 建 波 工 筑 道 程 工 桥 学 程 黄 教 院 学 研 林 11 院 室 .3 .10
2 c f c 1 1 c 0 fc
4、界限相对受压区高度 界限破坏时的截面应变关系
4.2 受弯构件正截面承载力计算基本假定
xnb
cu y
cu
h0
简化计算界限受压区高度 压区高度
xb,界限破坏时的界限相对受
xb 1 x nb 1 cu b h0 cu y h0
1
cu E s C50及以下: cu 0.0033, 1 0.8
4.2 受弯构件正截面承载力计算基本假定
1、正截面承载力计算的基本假定 (1)平截面假定 截面平均应变保持为平面 (2)不考虑砼的抗拉强度 (3)砼受压应力—应变关系 抛物线上升段+水平直线段
c 0 0.002
C 50
0 c cu 0.0033
(4)钢筋受拉应力—应变关系
M u y yk As h0 0.5 x f yk bh h0 0.5 x
As f tk 0.327 bh f yk
min
ft max{0.2%,0.45 }(梁) fy f max{0.15%,0.45 t }(板) fy
N 0
f c bx As f y
M 0
相对受压区高度
x x M u f c bx h0 As f y h0 2 2
fy fy As x h0 bh0 1 f c 1 f c
第三章受弯构件正截面承载力计算(精)

第三章受弯构件正截⾯承载⼒计算(精)第三章钢筋混凝⼟受弯构件正截⾯承载⼒计算⼀、填空题:1、对受弯构件,必须进⾏抗弯、抗剪验算。
2、简⽀梁中的钢筋主要有纵向受⼒筋、箍筋、弯起钢筋、架⽴筋四种。
3、钢筋混凝⼟保护层的厚度与环境类别、混凝⼟强度有关。
4、受弯构件正截⾯计算假定的受压混凝⼟压应⼒分布图形中,=0ε 0.002 、=cu ε 0.0033 。
5、梁截⾯设计时,采⽤C20混凝⼟,其截⾯的有效⾼度0h :⼀排钢筋时、两排钢筋时。
6、梁截⾯设计时,采⽤C25混凝⼟,其截⾯的有效⾼度0h :⼀排钢筋时、两排钢筋时。
7、单筋梁是指的梁。
8、双筋梁是指的梁。
9、梁中下部钢筋的净距为 25mm ,上部钢筋的净距为 30mm 。
10、受弯构件min ρρ≥是为了防⽌,x a m .ρρ≤是为了防⽌。
11、第⼀种T 型截⾯的适⽤条件及第⼆种T 型截⾯的适⽤条件中,不必验算的条件分别为和。
12、受弯构件正截⾯破坏形态有、、三种。
13、板中分布筋的作⽤是、、。
14、双筋矩形截⾯的适⽤条件是、。
15、单筋矩形截⾯的适⽤条件是、。
16、双筋梁截⾯设计时,当sA '和s A 均为未知,引进的第三个条件是。
17、当混凝⼟强度等级50C ≤时,HPB235,HRB335,HRB400钢筋的b ξ分别为 0.614 、 0.550 、 0.518 。
18、受弯构件梁的最⼩配筋率应取和较⼤者。
19、钢筋混凝⼟矩形截⾯梁截⾯受弯承载⼒复核时,混凝⼟相对受压区⾼度b ξξφ,说明。
⼆、判断题:1、界限相对受压区⾼度b ξ与混凝⼟强度等级⽆关。
(∨)2、界限相对受压区⾼度b ξ由钢筋的强度等级决定。
(∨)3、混凝⼟保护层的厚度是从受⼒纵筋外侧算起的。
(∨)4、在适筋梁中提⾼混凝⼟强度等级对提⾼受弯构件正截⾯承载⼒的作⽤很⼤。
( × )5、在适筋梁中增⼤梁的截⾯⾼度h 对提⾼受弯构件正截⾯承载⼒的作⽤很⼤。
混凝土结构设计原理 第四章 受弯构件正截面承载力的计算

3.2 梁板结构的一般构造
第4章 受弯构件正截面承载力
分布钢筋的作用:
抵抗混凝土收缩和温度变化所引起的内力; 浇捣混凝土时,固定受力钢筋的位置; 将板上作用的局部荷载分散在较大的宽度上,以便 使更多的受力钢筋参与工作; 对四边支撑的单向板,可承受在计算中没有考虑的 长跨方向上实际存在的弯矩。
板中单位长度上的分布钢筋,其截面面积不应小于 单位长度上受力钢筋截面面积的15%,且配筋率不宜小于 0.15%。间距不应大于250mm,直径不宜小于6mm。
4.2 梁板结构的一般构造
第4章 受弯构件正截面承载力
弯起钢筋 架立钢筋
腰筋
箍筋
纵向钢筋
梁的钢筋构造
梁中钢筋由纵向受力钢筋、弯起钢筋、箍筋和架立钢筋组 成,纵向受力钢筋的作用是承受由弯矩在梁内产生的拉力。 常用直径:10~32mm。 当h ≥ 300mm,直径不小于10mm;当h<300mm,直径 不小于8mm。
第4章 受弯构件正截面承载力
梁的配筋率ρ 很小,梁拉区开裂后,钢筋 应力趋近于屈服强度,即开裂弯矩Mcr趋近于拉 区钢筋屈服时的弯矩 My,这意味着第Ⅱ阶段的 缩短,当ρ 减少到当 Mcr=My 时,裂缝一旦出现,
钢筋应力立即达到屈服强度,这时的配筋百分
率ρ 称为最小配筋率ρ
min。
min b max
h0
h
第4章 受弯构件正截面承载力
正截面受弯的三种破坏形态
(1) 适筋破坏形态——破坏始自受拉区 钢筋的屈服
受拉钢筋先屈服,受压区混凝土后 压坏,破坏前有明显预兆——裂缝、变 形急剧发展,为“塑性破坏”。
(2) 超筋破坏形态——破坏始自受压混 凝土的压碎
受压区混凝土先压碎,钢筋不屈服, 破坏前没有明显预兆,为“脆性破坏”。 钢筋的抗拉强度没有被充分利用。
混凝土结构基本原理_第3章_受弯构件的正截面受弯承载力讲解

•
一般取2.0~4.0
•
梁宽度多为150、200、250、300、350mm等
b. 板
a) 设计时通常取单位宽度(b=1000mm)进行计算
b) 板厚除应满足各项功能要求外,尚应满足最小厚度要求
4.1.2 材料选择与一般构造
① 混凝土强度等级
•
工程中常用的梁、板混凝土强度等级是:C20、C25、C30、C35、
Mu的计算、应用是本章的中心问题
截面破坏形式 • 破坏通常有正截面和斜截面
两种形式
V V
•M
受弯构件设计的内容
正截面受弯承载力计算(按已知弯矩设计值M确定截 面尺寸和纵向受力钢筋);
斜截面受剪承载力计算(按剪力设计值V计算确定箍 筋和弯起钢筋的数量);
钢筋布置(为保证钢筋与混凝土的粘结,并使钢筋充 分发挥作用,根据荷载产生的弯矩图和剪力图确定钢 筋沿构件轴线的布置);
梁的截面尺寸主要应根据所承受的外部作用决
定,同时也需考虑模板尺寸、构件的截面尺寸符合模数、
方便施工。
现浇梁、板的截面尺寸可参考下述原则 选a. 取梁:
a) 高度h
•
较为常见的取值为:300、350、400、450、500、
550、600、650、700、750、800、900、1000mm等
b) 梁的高宽比(h/b)
根数:不少于2根,同时应满足图4-2所示对纵筋净距的要求(便于 浇注混凝土,保证钢筋周围混凝土的密实性)
b) 梁内箍筋
强度等级:常采用HPB300级、HRB400级 直径:常采用6mm、8mm、10mm和12mm等
c) 梁内纵向构造钢筋
架立钢筋:梁上部无受压计算钢筋时,仍需配置2根架立筋,以便与 箍筋和梁底部纵筋形成钢筋骨架,直径一般不小于10mm 纵向构造(腰筋): 梁的腹板高度hw≥450mm时,在梁的两个侧面 应沿高度配置纵向构造钢筋以减小梁腹部的裂缝宽度。每侧纵向构 造钢筋(不包括梁上、下部受力钢筋及架立钢筋)的截面面积不应 小于腹板截面面积bhw的0.1%,且其间距不宜大于200mm 梁的腹板高度hw:对矩形截面,取有效高度h0;对T形截面,取有效 高度h0减去翼缘高度;对I形截面,取腹板净高。
受弯构件正截面计算的基本假定

受弯构件正截面计算的基本假定1. 开篇引言哎,大家好,今天咱们聊点儿有趣的东西——受弯构件的正截面计算。
哎,别急着打瞌睡,这事儿其实比你想象的要有意思得多。
想象一下,你家的沙发坐久了,板凳底下那点儿小凹槽,就是一个微型的工程学难题。
不过,今天我们不讨论沙发,而是聊聊那些大块头的建筑材料,怎么在负重下保持挺直,这里面的学问可不少呢!2. 基本假定的介绍2.1 材质均匀性和截面一致性首先,大家得知道,计算受弯构件的正截面,咱们有几个基本假定。
第一个,材质得均匀。
这是什么意思呢?就像咱们买菜时,挑那种外皮平滑、没有伤痕的苹果。
咱们要假设这些构件的材料没有啥瑕疵,不管是钢筋、混凝土,还是其他啥材料,都要均匀,不然,你可别怪计算出来的结果让你大吃一惊。
2.2 假定材料线性弹性第二个,材料的弹性特性得线性。
换句话说,就是它们的变形和承受的力量成正比。
你可以把它想象成橡皮筋,拉得越长,它就越硬,但要是太长了,也会坏掉。
线性弹性假定简直就是咱们的“橡皮筋原理”,让计算变得简单多了。
要是这些材料不遵循这条规则,那计算结果就会让你哭笑不得了。
3. 截面内力分布的假定3.1 假定构件受弯时应力分布接下来,咱们聊聊截面内的力分布。
想象你在推门时,门上不同地方的受力就不一样。
对于受弯构件,我们假设应力的分布是线性的。
就是说,离中心越远的地方受的压力就越大,这个跟你的门一样。
这个假定让计算变得简洁好理解,不然你得整天在图纸上画来画去,心都累了。
3.2 假定材料在受弯过程中的应变再说说材料的应变,这可是关键。
我们假设受弯过程中,材料的变形是线性的。
换句话说,就是材料在受力下的变形,不管它多大,都是按照一定比例发生的。
这就像你揉面团时,它的变化是均匀的,不会突然就变成一个巨大的泡泡。
这个假定让我们计算的时候,既能简单又能准确,不用对每个小细节都担惊受怕。
4. 总结与实际应用好了,以上就是咱们今天的干货了。
这些基本假定就像是咱们做菜前的准备工作,只有做好了准备,菜才会好吃。
( )作为受弯构件正截面承载力计算的依据

( )作为受弯构件正截面承载力计算的依据
受弯构件正截面承载力计算的依据主要包括以下几个方面:
1. 平截面假定:假设受弯构件在弯曲过程中,截面上的应力分布保持均匀。
2. 混凝土应力-应变关系曲线的规定:根据混凝土的受压性能,确定混凝土压应力与应变之间的关系。
3. 钢筋应力-应变关系的规定:根据钢筋的受拉性能,确定钢筋拉应力与应变之间的关系。
4. 不考虑混凝土抗拉强度:在计算过程中,不考虑混凝土的抗拉强度,因为混凝土在受弯过程中,拉应力较小,对承载力影响不大。
5. 受力平衡方程或表达式:根据上述假定和性能规定,建立受弯构件正截面承载力的计算公式或平衡方程。
这些依据来源于《混凝土结构设计规范》等相关技术规范,用于确定钢筋和混凝土在承载力极限状态下的受力状态,并进行适当简化,从而实现受弯构件正截面承载力的计算。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《混凝土结构设计规范》( GB 50010-2010):
6.2.1 正截面承载力应按下列基本假定进行计算: 2 不考虑混凝土的抗拉强度,即全部拉力由纵向受拉钢筋承担。
3.正截面承载力计算的基本原则
(1)正截面承载力计算的基本假定
《混凝土结构设计规范》( GB 50010-2010):
6.2.1 正截面承载力应按下列基本假定进行计算: 3 混凝土受压的应力与应变关系按下列规定取用:
n≤ 2 0≥0.002 cu ≤ 0.0033, 轴压时取承载力计算的基本假定
《混凝土结构设计规范》( GB 50010-2010):
6.2.1 正截面承载力应按下列基本假定进行计算: 4 纵向受拉钢筋的极限拉应变取为0.01;
3.正截面承载力计算的基本原则
(1)正截面承载力计算的基本假定
《混凝土结构设计规范》( GB 50010-2010):
6.2.1 正截面承载力应按下列基本假定进行计算: 5 纵向钢筋的应力取钢筋应变与其弹性模量的乘积,但其值应符合下列要求:
第i层非预应力筋的应力
第i层预应力筋的应力
谢谢!!
正截面承载力计算的基本假定
3.正截面承载力计算的基本原则
(1)正截面承载力计算的基本假定
《混凝土结构设计规范》( GB 50010-2010):
6.2.1 正截面承载力应按下列基本假定进行计算: 1 平截面假定:截面应变保持平面,即变形前的平面变形后仍为平面,截面上各点应变保 持线性关系;
3.正截面承载力计算的基本原则
