比例式与等积式
相似三角形专题 巧用“三点定型法”证明相似问题中的比例式与等积式

相似三角形专题
——巧用“三点定型法”证明相似问题中的比例式与等积式
(配套练习)
1、如图,∠ACB=90°,CD 是Rt △ABC 的斜边AB 上的高,∠BAC 的平分线分别交BC 、CD 于点E 、F ,请证明AE
AB AF AC =。
2、如图,在正方形ABCD 中,E 是CD 的中点,EF ⊥AE . 求证:2AE AD AF =.
3、如图,在正方形ABCD 中,F 是边BC 上一点(点F 与点B 、点C 均不重合),AE ⊥AF ,AE 交CD 的延长线于点E ,连接EF 交AD 于点G .求证:BF •FC=DG •EC ;
4、已知;在Rt △ABC 中,∠A=900,四边形DEFG 为正方形。
求证:EF 2
=BE •FC
5、已知;AD 平分∠BAC ,EF 垂直平分AD 与BC 的延长线交于F 。
求证:DF 2=BF •CF
6、已知:在ABC ∆中,D 、E 分别在AB 、AC 上,BC DE //,BE 、CD 相交于点O ,AO 与DE 、BC 分别交于点N 、M 。
求证:AN ON AM OM
=。
第四章图形的相似——证明比例式或等积式的技巧 同步练习 北师大版数学九年级上册

“十层相似”———相似十大技巧证明比例式或等积式的技巧“三点定型法”是证明线段等积式或比例式以及利用等积式、比例式求线段长时找相似三角形的最常用的方法,即设法找出等积式或比例式(或变化后的式子)中所包含的几个字母,看是否存在可由“三点”确定的两个三角形相似。
通常通过“横看”“竖看”两种方法找相似三角形 ,横看:即看两比例前项、两比例后项是否分别在两个相似三角形中;竖看:即看比例式等号两边各自的前、后项是否分别在两个相似三角形中。
技巧一:三点定型1.如图,在△ABC 中,点D 、E 分别在AB 、AC 上,∠ADE =∠C ,求证:AD •AB =AE •AC .技巧二:等线段代换2.如图,已知在△ABC 中,点D 、E 、F 分别是边AB 、AC 、BC 上的点,且DE ∥BF ,EF ∥BD ,求证:=FC DE .技巧三:等比例代换3.如图,在△ABC 中,DE ∥BC ,EF ∥CD ,求证:.技巧四:等积代换4.如图,已知CE是Rt△ABC斜边AB上的高,在EC的延长线上任取一点P,连接AP,BG⊥AP垂足为G,交CE于D,求证:CE2=PE•DE.5.如图,在△ABC中,D是AB上一点,E是△ABC内一点,DE∥BC,过D作AC的平行线交CE的延长线于F,CF与AB交于P,求证:=.备注:上述技巧不仅用于证明等积式和比例式的题型,还可以灵活使用在其他题型中。
课堂练习1.如图,已知△ABC是等边三角形,点D、B、C、E在同一条直线上,且∠DAE=120°,求证:BC2=CE•DB.2.已知,如图,在Rt△ABC中,CD是斜边上的中线,DE⊥AB交BC于点F,交AC的延长线于点E.求证:(1)△ADE∽△FDB;(2)CD2=DE•DF.3.已知:如图,在△ABC中,点D,E分别在边AB,BC上,BA•BD=BC•BE.(1)求证:△BDE∽△BCA;(2)如果AE=AC,求证:AC2=AD•AB.4.如图,点D、E分别在△ABC的边AC、AB上,延长DE、CB交于点F,且AE•AB=AD •AC.(1)求证:∠FEB=∠C;(2)连接AF,若=,求证:EF•AB=AC•FB.5.已知:如图,在△ABC中,点D、E分别在边BC、AC上,点F在DE的延长线上,AD =AF,AE•CE=DE•EF.(1)求证:△ADE∽△ACD;(2)如果AE•BD=EF•AF,求证:AB=AC.6.已知:如图,△ADE的顶点E在△ABC的边BC上,DE与AB相交于点F,AE2=AF•AB,∠DAF=∠EAC.(1)求证:△ADE∽△ACB;(2)求证:=.7.如图,M是平行四边形ABCD的对角线上的一点,射线AM与BC交于点F,与DC的延长线交于点H.(1)求证:AM2=MF•MH.(2)若BC2=BD•DM,求证:∠AMB=∠ADC.8.△ABC中,AB=AC,点D、E、F分别在BC、AB、AC上,∠EDF=∠B.(1)如图1,求证:DE•CD=DF•BE;(2)如图2,若D为BC中点,连接EF.求证:ED平分∠BEF.9.如图,已知正方形ABCD,以AB为边在正方形外作等边△ABE,过点E作EF⊥AB与边AB、CD分别交于点F、点G,点O在线段EG上,且DO=CD.(1)求证:AE∥DO;(2)联结AO、DE,DE分别交AO、AB于点M、Q,求证:.10.如图所示,在等腰三角形ABC中,AB=AC,点E,F在线段BC上,点Q在线段AB 上,且CF=BE,AE2=AQ•AB.求证:(1)∠CAE=∠BAF;(2)CF•FQ=AF•BQ.11.已知:如图,在矩形ABCD中,点E在边AD的延长线上,DE=DC,联结BE,分别交边DC、对角线AC于点F、G,AD=FD.(1)求证:AC⊥BE;(2)求证:=.12.已知:如图,在四边形ABCD中,AD∥BC,点E、F分别在边AB、AD上,DE与CF 相交于点G.CD2=CG•CF,∠AED=∠CFD.(1)求证:AB=CD;(2)延长AD至点M,联结CM,当CF=CM时,求证:EA•AB=AD•MD.13.如图,已知:△ABC和△ADE都是等边三角形,其中点D在边BC上,点F是AB边上一点,且BF=CD.(1)求证:DE∥CF;(2)联结DF,设AD、CF的交点为M,如果DF2=FM•FC,求证:DF∥AC.14.已知:如图,两个△DAB和△EBC中,DA=DB,EB=EC,∠ADB=∠BEC,且点A、B、C在一条直线上,联结AE、ED,AE与BD交于点F.(1)求证:;(2)如果BE2=BF•BD,求证:DF=BE.15.已知:如图,四边形ABCD中,∠BAD=∠BCD=90°,E为对角线BD的中点,点F 在边AD上,CF交BD于点G,CF∥AE,CF=BD.(1)求证:四边形AECF为菱形;(2)如果∠DCG=∠DEC,求证:AE2=AD•DC.16.如图,AB=9,AC=8,P为AB上一点,∠A=∠CPD=∠B,连接CD.(1)若AP=3,求BD的长;(2)若CP平分∠ACD,求证:PD2=CD•BD.17.如图,在▱ABCD中,对角线AC,BD相交于点O,E为AO上一点,BF⊥BD交DE的延长线于点F,且EF=DE.(1)求证:四边形ABCD是菱形;(2)DF交AB于点G,若OD2=OE•OA,求证:DF•AG=AE•BD.18.如图,将矩形ABCD绕点B旋转,点A落到对角线AC上的点E处,点C、D分别落在点F、G处.(1)联结BG、CG,求证:四边形ABGC是平行四边形;(2)联结GE并延长交边AD于点H,求证:AB2=AD•AH.19.如图,平行四边形ABCD中,它的两条高DE、BF相交于点H,∠DBC=45°,BF与AD的延长线相交于点G,连接AH.(1)求证:BH=AB;(2)求证:AH•BG=AG•BD.。
比值解比例

比值解比例是一种解决比例问题的方法,它的基本思想是将比例式转化为等积式,然后通过求解等积式来得到未知数的值。
具体步骤如下:
1. 将比例式写成等积式的形式。
例如,如果比例式是a:b=c:d,那么可以写成ad=bc。
2. 对等积式进行变换,使其变为一个或多个已知的等积式。
这一步通常需要利用一些基本的数学公式,如平方差公式、完全平方公式等。
3. 求解变换后的等积式,得到未知数的值。
这一步通常需要利用一些基本的代数运算,如加减乘除、开方等。
4. 将求得的未知数的值代入原比例式,验证是否满足比例关系。
例如,如果我们要求解比例式2:3=4:x,我们可以按照上述步骤进行操作:
1. 将比例式写成等积式的形式,得到2x=3*4。
2. 对等积式进行变换,得到x=(3*4)/2=6。
3. 将求得的未知数的值代入原比例式,得到2:3=4:6,满足比例关系。
所以,x的值为6。
15.比例式、等积式的常见证明方法

语文
小魔方站作品 盗版必究
谢谢您下载使用!
更多精彩内容,微信扫描二维码获取
扫描二维码获取更多资源
附赠 中高考状元学 习方法
前
言
高考状元是一个特殊的群体,在许多 人的眼中,他们就如浩瀚宇宙里璀璨夺目 的星星那样遥不可及。但实际上他们和我 们每一个同学都一样平凡而普通,但他们 有是不平凡不普通的,他们的不平凡之处 就是在学习方面有一些独到的个性,又有 着一些共性,而这些对在校的同学尤其是 将参加高考的同学都有一定的借鉴意义。
采青 春 风
高考总分: 692分(含20分加分) 语文131分 数学145分 英语141分 文综255分 毕业学校:北京二中 报考高校: 北京大学光华管理学 院
北京市文科状元
来自北京二中,高考成绩672分,还有20 分加分。‚何旋给人最深的印象就是她 的笑声,远远的就能听见她的笑声。‛ 班主任吴京梅说,何旋是个阳光女孩。 ‚她是学校的摄影记者,非常外向,如 果加上20分的加分,她的成绩应该是 692。‛吴老师说,何旋考出好成绩的秘 诀是心态好。‚她很自信,也很有爱心。 考试结束后,她还问我怎么给边远地区
∴
∵AD⊥BC,E为直角边AC中点 ∴DE=EC ∴∠3=∠C 又∵∠3=∠2,∠1=∠C ∴∠1=∠2 而∠F是△FBD与△FDA的公共角 ∴△FBD∽△FDA
DF BD AF AD AB DF ∴ AC AF
∴
AB BD AC AD
∴AB· AF=AC· DF.
方法总结 证明线段比例式或等积式时,如果按类型一、类型二的方法仍无法证 明,可以尝试将等积式化为比例式,结合图形找到能够与比例式中的两个 比分别相等的中间比,从而证明所求证的结果成立.
C
∴∠B=∠1
相似三角形-等积式-比例式知识分享

专题:相似三角形的判定相似三角形的知识与圆有着密切的联系,所以我们一定要把这部分知识学好,为学习圆这部分知识打下良好基础。
我们本讲重点研究两个问题:一、比例式,等积式的证明;二、双垂直条件下的证明与计算。
一、等积式、比例式的证明:等积式、比例式的证明是相似形一章中常见题型。
因为这种问题变化很多,同学们常常感到困难。
但是,如果我们掌握了解决这类问题的基本规律,就能找到解题的思路。
(一)遇到等积式(或比例式)时,先看是否能找到相似三角形。
等积式可根据比例的基本性质改写成比例式,在比例式各边的四个字母中如有三个不重复的字母,就可找出相似三角形。
例1、已知:如图,△ ABC中,/ ACB=90, AB的垂直平分线交AB于D, ;交BC延长线于F。
求证:CD=DE・DF。
u/l分析:我们将此等积式变形改写成比例式得:,由等式左边得到△ CDF由等式右边得到厶EDC这样只要证明这两个三角形相似就可以得到要证的等积式了。
因为/ CDE是公共角,只需证明/ DCE=/ F就可证明两个三角形相似。
证明略(请同学们证明)提示:D为直角三角形斜边AB的中点,所以AD=DC,则/ DCE=/ A.(二)若由求证的等积式或比例式中找不到三角形或找到的三角形不相似,则需要进行等线段代换或等比代换。
有时还需添加适当的辅助线,构造平行线或相似三角形。
例2 .如图,已知△ ABC中,AB=AC AD是BC边上的中线,CF// BA BF交AD于P点,交AC于E点。
求证:B P=PE・ PF。
分析:因为BP PE PF三条线段共线,找不到两个三角形,所以必须考虑等线段代换等其他方法,因为AB=AC D 是BC中点,由等腰三角形的性质知AD是BC的垂直平分线,如果我们连结PC,由线段垂直平分线的性质知PB=PC只需证明厶PE3A PCF,问题就能解决了。
证明:A例3.如图,已知:在△ ABC中,/ BAC=90, ADL BC, E是AC的中点,ED交AB的延长线于F。
123.15.比例式、等积式的常见证明方法

∴∠4=∠F 而 ∠ CPE 是 △ CPE 和
△FPC的公共角 ∴△CPE∽△FPC ∴PE∶PC=PC∶PF ∴PC2=PE·PF ∴BP2=PE·PF
∵CF∥AB
∴∠3=∠F
方法总结
运用类型一的方法证明线段的比例式或等积式时,如果相关的线段不在 某两个三角形中,则需要将其中的某条线段用与之相等的另一条线段替换, 再按类型一 的方法证明.
∴ DF BD AF AD
∴ AB DF AC AF
∴AB·AF=AC·DF.
方法总结
证明线段比例式或等积式时,如果按类型一、类型二的方法仍无法证 明,可以尝试将等积式化为比例式,结合图形找到能够与比例式中的两个 比分别相等的中间比,从而证明所求证的结果成立.
XXX X
古 X
X X X
风 设
一 岁 只 叹 伊
, 饮 罢 飞 雪 ,
负 了 青 春 举
泪 溶 了 雪 , 恰
光 ? 谁 酒 三 尺
颜 刹 那 ? 谁 饮
拾 弹 指 雪 花 ?
今 夜 无 月 亦 无
纷 纷 飘 香 。 雪
一 回 。 忆 苍 茫
前 尘 旧 梦 , 不
, 怎 敌 我 浊 酒
古 韵 清
风
中 幽 舞
梦明
国 落 月
花, 间 。
类型三:找中间比利用等积式代换
如图,在△ABC中,已知∠BAC=90 °,AD⊥BC于D,E为直角边AC的 中点,过D、E作直线交AB的延长线于F.求证:AB·AF=AC·DF.
A
1
E
B
3
2D
C
F
如图,在△ABC中,已知∠A=90°,AD⊥BC于D,E为直角边AC的中 点,过D、E作直线交AB的延长线于F.求证:AB·AF=AC·DF.
相似三角形复习比例式等积式的几种常见证明方法课件

作业:
作业纸
老师寄语:若希望成功,当以恒心为 良友,以经验为参谋,以信心为光荣, 以希望为哨兵。
再见
欢迎多提宝贵意见
合作探究
1.已知:如图, ∠ACB=90°,AD=DB,DE⊥AB 于D交AC于E,交BC的延长线于F,试说明:
DC2=DE·DF
利用相似
A
三角形的
性质
D E
F
C
B
2. 如图,在直角梯形ABCD中,AB∥CD, AB⊥BC,对角线AC⊥BD,垂足为E,AD=BD, 过点E作EF∥AB交AD于F, 试说明 (1)AF=BE (2) AF2=AE·EC
P
利用等积 式代换
G
C
D
A
E
B
协作交流
D F
C E
A
B
BE2=EA·EC
A
E
B
D
C
F
P AC:AB=AD:BD
G
C
D
A
E
B
EC2=EA·EB
C
A
快速抢 答
D
B
在这一个图形中,有两个 垂直,有__三__对相似,有___
对四互余的角,有___是
AC2=AD·AB
BC2=BD·AB
利用等线 段代换
D F
C E
A
B
3.已知,如图,在△ABC中, ∠BAC=90°, AD⊥BC,垂足为D,E是AC的中点,ED的延 长线交AB的延长线于点F. 试说明:AB:AC=DF:AF
A
E
B
D
C
F
利用等比 式代换
4.已知,如图,CE是直角△ABC的斜边 AB上的高,在EC的延长线上任取一点P,连 接AP,作BG⊥AP,垂足为G,交CE于D, 试说明:CE2=ED·EP.
相似三角形复习——比例式、等积式的几种常见证明方法

图3 例3如图3,△ABC中,DE∥BC,BE与CD交于点O, AO与DE、BC分别交于点N、M,试说明:. 利用等
比式代 换
AN AD DE AM AB BC
AN ON AM OM
图3
ON OE DE OM OB BC
例3.如图,已知:在△ABC中,∠BAC=900, AD⊥BC,E是AC的中点,ED交AB的延长线于F
A
BDEຫໍສະໝຸດ C如上图, ∠BAC=120°, △ADE是 等边三角形,小丽发现图中有些线 段是其他两条线段的比例中项,你 知道小丽说的是哪些线段吗? 它们 分别是哪些线段的比例中项吗?
比例式得:
,由等式左边得
到△CDF,由等式右边得到△EDC,
这样只要证明这两个三角形相似就
可以得到要证的等积式了。因为
∠CDE是公共角,只需证明
∠DCE=∠F就可证明两个三角形相
似。
例2如图2,在△ABC中,AB=AC,直线DF与AB交于D,与
BC交于E,与AC的延长线交于F.图2 试说明:. DE EF
求证:
。
分 析:比例式左边AB,AC 在△ABC中,右边DF、AF在 △ADF中,这两个三角形不相 似,因此本题需经过中间比进 行代换。通过证明两套三角形 分别相似证得结论。
“双垂直”指:
“Rt△ABC中,
∠BCA=900,
CD⊥AB于D”,(如
图)在这样的条件下
有下列结论:
A
C
D
B
(1)△ADC∽△CDB∽△ACB (2)由△ADC∽△CDB得CD2=AD·BD (3)由△ADC∽△ACB得AC2=AD·AB (4)由△CDB∽△ACB得BC2=BD·AB (5)由面积得AC·BC=AB·CD (6)勾股定理 我们应熟记这些结论,并能灵活运用。
2020年中考数学期末复习类比归纳专题《比例式、等积式的常见证明方法》

类比归纳专题:比例式、等积式的常见证明方法——直接法、间接法◆类型一 三点定型法:找线段对应的三角形,利用相似证明1.如图,在菱形ABCD 中,G 是BD 上一点,连接CG 并延长交BA 的延长线于点F ,交AD 于点E ,连接AG .(1)求证:AG =CG ; (2)求证:AG 2=GE ·GF .2.如图,在△ABC 中,∠ACB =90°,CD ⊥AB ,垂足为D ,E 是AC 的中点,ED 的延长线与CB 的延长线交于点F .(1)若FD =2FB ,求FDFC的值;(2)若AC =215,BC =15,求S △FDC 的值.◆类型二 利用等线段代换3.如图,在四边形ABCD 中,AB =AD ,AC 与BD 交于点E ,∠ADB =∠ACB .求证:ABAE =AC AD.◆类型三 找中间比利用等积式代换4.如图,已知CE 是Rt △ABC 斜边AB 上的高,在EC 的延长线上任取一点P ,连接AP ,作BG ⊥AP ,垂足为G ,交CE 于D ,求证:CE 2=PE ·DE .参考答案与解析1.证明:(1)∵四边形ABCD 是菱形,∴AB ∥CD ,AD =CD ,∠ADB =∠CDB ,∴∠F =∠FCD .在△ADG 与△CDG 中,⎩⎪⎨⎪⎧AD =CD ,∠ADG =∠CDG ,DG =DG ,∴△ADG ≌△CDG ,∴∠EAG =∠DCG ,AG =CG .(2)∵∠EAG =∠DCG ,∠F =∠DCG ,∴∠EAG =∠F .又∵∠AGE =∠FGA ,∴△AGE ∽△FGA ,∴AG FG =EGAG,∴AG 2=GE ·GF .2.解:(1)∵∠ACB =90°,CD ⊥AB ,∴∠A +∠ABC =∠DCB +∠ABC ,∴∠A =∠DCB .∵E 是AC 的中点,∠ADC =90°,∴ED =EA ,∴∠A =∠EDA .∵∠BDF =∠EDA ,∴∠DCB =∠BDF .又∵∠F =∠F ,∴△BDF ∽△DCF ,∴FD ∶CF =BF ∶FD =1∶2.(2)∵∠ACB =90°,CD ⊥AB ,∴∠BDC =∠ACB .∵∠ABC =∠CBD ,∴△BDC ∽△BCA ,∴BD ∶CD =BC ∶AC =15∶215=1∶2.在Rt △BAC 中,由勾股定理可得AB =53,∴S △BDC S △BCA =BC 2AB 2=15,∴S △BDC =15×12×215×15=3.∵△BDF ∽△DCF ,∴S △FBD S △FDC =⎝⎛⎭⎫BD CD 2=14,即S △BDC S △FDC =34.∵S △BDC =3,∴S △FDC =4. 3.证明:∵AB =AD ,∴∠ADB =∠ABE .∵∠ADB =∠ACB ,∴∠ABE =∠ACB .又∵∠BAE =∠CAB ,∴△ABE ∽△ACB ,∴AB AE =AC AB .又∵AB =AD ,∴AB AE =ACAD.4.证明:∵∠ACB =90°,CE ⊥AB ,∴∠ACE +∠BCE =90°,∠ACE +∠CAE =90°,∴∠CAE =∠BCE ,∴Rt △ACE ∽Rt △CBE ,∴CE BE =AECE,∴CE 2=AE ·BE .又∵BG ⊥AP ,CE ⊥AB ,∴∠DEB =∠DGP =∠PEA =90°.∵∠1=∠2,∴∠P =∠3,∴△AEP ∽△DEB ,∴PE BE =AEDE ,∴PE ·DE =AE ·BE ,∴CE 2=PE ·DE .。
比例式等积式的证明--等积式过渡
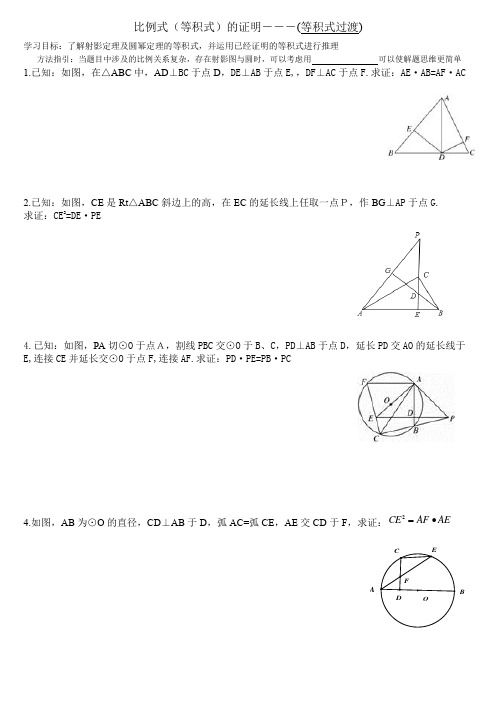
比例式(等积式)的证明---(等积式过渡)
学习目标:了解射影定理及圆幂定理的等积式,并运用已经证明的等积式进行推理
方法指引:当题目中涉及的比例关系复杂,存在射影图与圆时,可以考虑用 可以使解题思维更简单
1.已知:如图,在△ABC 中,AD ⊥BC 于点D ,DE ⊥AB 于点E,,DF ⊥AC 于点F.求证:AE ·AB=AF ·AC
2.已知:如图,CE 是Rt △ABC 斜边上的高,在EC 的延长线上任取一点P,作BG ⊥AP 于点G. 求证:CE 2=DE ·PE
4.已知:如图,PA 切⊙O 于点A,割线PBC 交⊙O 于B 、C ,PD ⊥AB 于点D ,延长PD 交AO 的延长线于E,连接CE 并延长交⊙O 于点F,连接AF.求证:PD ·PE=PB ·PC
4.如图,AB 为⊙O 的直径,CD ⊥AB 于D ,弧AC=弧CE ,AE 交CD 于F ,求证:2CE AF AE =•
F
O B A
C D E。
比例式等积式的证明--巧用中间比

C
比例式(等积式)的证明---(巧用中间比)
1.当通过“直接横竖找”找不到相似三角形,也不能进行“等线段代换”时,可以尝试运用“ ”的方法证明比例式或等积式.
2.巧用中间比就是将一个比例式转化为两个比例,即是原比例的两边同时等于一个相同的比例式
1.已知:如图,在△ABC 中,∠BAC=900,AD ⊥BC 于D ,E 是AC 的中点,ED 的延长线与AB 的延长线
交于F 。
求证:AB DF AC AF =
总结:此题中用到证明比例式的方法是:
2.已知:如图,过△ABC 的顶点作A E ∥BC ,又过BC 的中点O 作直线交AB 、AE 、AC 或其延长线相交于P 、
E 、Q ,求证:PO QO PE QE =
总结:此题中用到证明比例式的方法是:
3.已知:如图,延长正方形的ACDE 的边DC 到B ,连结BE与AC交于F,作FG∥DB交AB于G,求证:GF=FC
总结:(1).此题中用到证明比例式的方法是:
(2).运用比例式证明两条线段相等的三种方法:
方法一:若1=b a ,那么a=b 方法二:若d c b a =,且a=c ,则b=d 方法三:若d c b a =,且b=d ,则a=c。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
比例式与等积式
一、知识点分析:
判定定理1:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似.简述为:两角对应相等,两三角形相似.
判定定理2:如果一个三角形的两条边和另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似.简述为:两边对应成比例且夹角相等,两三角形相似.
判定定理3:如果一个三角形的三条边与另一个三角形的三条边对应成比例,那么这两个三角形相似.简述为:三边对应成比例,两三角形相似.
二、典例解析:
例1、如图,△ABC三内角平分线交于点D,过点D引DE⊥AO,分别交AB、AC于点D、E.求证:△BOD∽△BCO∽△OCE.
【随堂练习】
△ABC中,∠1=∠2=∠3,图中有相似三角形吗?请说明理由.
如图,在正方形ABCD中,E为AD的中点,EF⊥EC交AB于F,连接FC(AB>AE),△AEF ∽△EFC吗?若相似,请证明;若不相似,请说明理由.若ABCD为矩形呢?
例3、如图,已知:AP2=AQ•AB,且∠ABP=∠C,试说明△QPB∽△PBC.
例4、如图,点C、D在线段AB上,△PCD是等边三角形,且△ACP∽△PDB.
(1)求∠APB的大小.(2)说明线段AC、CD、BD之间的数量关系.
如图所示,已知Rt△ABC(AC>BC)的斜边AB的中点D,过D作斜边的垂线交AC于E,交BC延长线于F,求证:DC2=DE·DF。
【随堂练习】
已知:如图,点E是四边形ABCD的对角线BD上一点,且∠BAC=∠BDC=∠DAE.
(1)求证:△ABE∽△ACD;(2)求证:BC•AD=DE•AC.
三、课后练习:
1、在△ABC中,∠A=36°,AB=AC,BD平分∠ABC交AC于点O,试说明:△BDC∽△ABC.
2、如图,已知AC和BD相交于点E,CE•AE=BE•DE,求证:△ABE∽△DCE.
3、如图,Rt△ABC中,∠C=90°,过C作CD⊥AB于D,求证:CD2=AD•DB.
4、如图,在平行四边形ABCD中,AE⊥BC于E,AF⊥CD于F.
(1)求证:CD•DF=BC•BE;
(2)若M、N分别是AB、AD中点,且∠B=60°,求证:EM∥FN.。
