小学奥数二进制复习课程
四年级奥数举一反三第三十六周 二进制【精校】.doc

第三十六周二进制专题简析:二进制就是只用0和1两数字,在计数与计算时必须“满二进一”,即每两个相同的单位组成一个和它相邻的最高的单位。
二进制的最大特点是:每个数的各个数位上只有0或只有1两种状态。
二进制与十进制之间可以互相转化。
1,将一个二进制数写成十进制数的步骤是:(1)将二进制数的各数位上数字改写成相应的十进制数;(2)将各数位上对应的十进制数求和,所得结果就是相应的十进制数。
将十进制数改写成二进制数的过程,正好相反。
2,十进制数改写成二进制数的常用方法是:除以二倒取余数。
3,二进制数的计算法则:(1)加法法则:0+0=0 0+1=1 1+0=1 1+1=10(2)乘法法则:0×0=0 0×1=0 1×0=0 1×1=1例1:把二进制数110(2)改写成十进制数。
分析与解答:十进制有两个特点:(1)它有十个不同的数字符号;(2)满十进1。
二进制有两个特点:(1)它的数值部分,只需用两个数码0和1来表示;(2)它是“满二进一”。
把二进制数110(2)改写成十进制数,只要把它写成2的幂之和的形式,然后按通常的方法进行计算即可。
110(2)=1×22+1×21+0×20=1×4+1×2+0×1=4+2+0=6练习一:把下列二进制数分别改写成十进制数。
(1)100(2)(2)1001(2)(3)1110(2)例2:把十进制数38改写成二进制数。
分析与解答:把十进制数改写成二进制数,可以根据二进制数“满二进一”的原则,用2连续去除这个十进制数,直到商为零为止,把每次所得的余数按相反的顺序写出来,就是所化成的二进制数,这种方法叫做“除以二倒取余数”。
2 38 02 19 (1)2 9 (1)2 4 02 2 01 (1)即:38(10)=100110(2)练习二把下列十进制数分别改写成二进制数。
(1)12(10)(2)15(10)(3)78(10)分析与解答:任何进位制数的运算,都可以根据十进制数的运算法则来进行,做一位数的运算需要有加法表(即加法口诀)。
小学四年级数学 奥数 第36讲 二进制

小学四年级数学奥数第36讲二进制一、专题简析:二进制就是只用0和1两数字,在计数与计算时必须“满二进一”,即每两个相同的单位组成一个和它相邻的最高的单位。
二进制的最大特点是:每个数的各个数位上只有0或只有1两种状态。
二进制与十进制之间可以互相转化。
1、将一个二进制数写成十进制数的步骤是:(1)将二进制数的各数位上数字改写成相应的十进制数;(2)将各数位上对应的十进制数求和,所得结果就是相应的十进制数。
将十进制数改写成二进制数的过程,正好相反。
2、十进制数改写成二进制数的常用方法是:除以二倒取余数。
3、二进制数的计算法则:(1)加法法则:0+0=0 0+1=1 1+0=1 1+1=10(2)乘法法则:0×0=0 0×1=0 1×0=0 1×1=1二、精讲精练:例1:把二进制数110(2)改写成十进制数。
分析与解答:十进制有两个特点:(1)它有十个不同的数字符号;(2)满十进1。
二进制有两个特点:(1)它的数值部分,只需用两个数码0和1来表示;(2)它是“满二进一”。
把二进制数110(2)改写成十进制数,只要把它写成2的幂之和的形式,然后按通常的方法进行计算即可。
110(2)=1×22+1×21+0×20=1×4+1×2+0×1=4+2+0=6练习一:把下列二进制数分别改写成十进制数。
(1)100(2)(2)1001(2)(3)1110(2)例2:把十进制数38改写成二进制数。
分析与解答:把十进制数改写成二进制数,可以根据二进制数“满二进一”的原则,用2连续去除这个十进制数,直到商为零为止,把每次所得的余数按相反的顺序写出来,就是所化成的二进制数,这种方法叫做“除以二倒取余数”。
2 38 02 19 (1)2 9 (1)2 4 02 2 01 (1)即:38(10)=100110(2)练习二把下列十进制数分别改写成二进制数。
【精品奥数】四年级上册数学思维训练讲义-第十九讲 二进制 人教版(含答案)

第十九讲 二进制第一部分:趣味数学华莱士·帕斯卡,法国著名的数学家、物理学家、哲学家和散文家,他在19岁的时候引用算盘的原理,发明了第一部机械式计算器,在他的计算器中有一些互相联锁的齿轮,一个转过十位的齿轮会使另一个齿轮转过一位,人们可以像拨电话号码盘那样,把数字拨进去,计算结果就会出现在另一个窗口中,但是只能做加减计算。
第二部分:奥数小练二进制就是只用0和1两数字,在计数与计算时必须“满二进一”,即每两个相同的单位组成一个和它相邻的最高的单位。
二进制的最大特点是:每个数的各个数位上只有0或只有1两种状态。
二进制与十进制之间可以互相转化。
1.将一个二进制数写成十进制数的步骤是:(1)将二进制数的各数位上数字改写成相应的十进制数;(2)将各数位上对应的十进制数求和,所得结果就是相应的十进制数。
将十进制数改写成二进制数的过程,正好相反。
2.十进制数改写成二进制数的常用方法是:除以二倒取余数。
3.二进制数的计算法则:(1)加法法则:0+0=0 0+1=1 1+0=1 1+1=10(2)乘法法则:0×0=0 0×1=0 1×0=0 1×1=1 【例题1】把二进制数110(2)改写成十进制数。
【思路导航】十进制有两个特点:(1)它有十个不同的数字符号;(2)满十进1。
二进制有两个特点:(1)它的数值部分,只需用两个数码0和1来表示;(2)它是“满二进一”。
把二进制数110(2)改写成十进制数,只要把它写成2的幂之和的形式,然后按通常的方法第一个发明计算器的人——帕斯卡进行计算即可。
110(2)=1×22+1×21+0×20=1×4+1×2+0×1=4+2+0=6练习1:把下列二进制数分别改写成十进制数。
1.100(2) 2.1001(2)3.1110(2)【例题2】把十进制数38改写成二进制数。
【思路导航】把十进制数改写成二进制数,可以根据二进制数“满二进一”的原则,用2连续去除这个十进制数,直到商为零为止,把每次所得的余数按相反的顺序写出来,就是所化成的二进制数,这种方法叫做“除以二倒取余数”。
《小学奥数二进制》课件

在算法设计中,二进制数的特性常常被用来优化算法效率和降低计算复 杂度。
03
数学逻辑
在数理逻辑中,二进制数常常被用来表示逻辑值和进行逻辑运算。
在日常生活中的应用
开/关状态
在日常生活中,许多设备或系 统的状态可以用二进制数来表 示,如开关的状态(开/关)、 音量调节(高/低)等。
加密通信
在通信中,二进制数可以用来 表示加密信息,因为二进制数 的简单运算规则和易于处理的 特性使得加密和解密过程变得 相对简单。
例如,在解决一些关于二进制数的组合问题时,我们可以通 过归纳法总结出不同组合方式的规律,从而快速得出答案。
演绎法
演绎法是一种从一般到特殊的推理方 法,在解决奥数二进制问题时,演绎 法可以帮助我们从已知的一般规律推 导出特殊情况下的结论。
例如,在解决一些关于二进制数的逻 辑推理问题时,我们可以通过演绎法 推导出符合逻辑的结论,从而快速得 出答案。
05
奥数二进制问题实例解析
实例一:二进制数的规律问题
总结词
通过观察二进制数的变化规律,找出数 列中隐藏的数学关系。
VS
详细描述
这类问题通常会给出一些二进制数列,如 1010, 1101, 1110等,要求找出数列中数 字变化的规律,并预测下一个数字。解决 这类问题需要细心观察数列中数字的变化 ,找出隐藏的数学关系。
总结词
将二进制数的知识应用于实际问题中,解决 实际问题。
详细描述
这类问题通常会以实际生活场景为背景,如 “一个密码锁的密码由三个二进制数字组成 ,请问有多少种可能的组合方式?”解决这 类问题需要将二进制数的知识应用于实际问 题中,通过数学运算和逻辑推理,找出符合
实际情况的答案。
(完整版)五年级奥数__二进制问题_讲义

专题二二进制问题知识要点用0,1,2,3,4,5,6,7,8,9这10个数字表示所有整数的方法被叫做十进制,十进制是最常见的进制,世界上绝大数国家和地区都用这种方法来计数,它的特点是满十进一,退一当十。
除了十进制外,有其它一些进位制,如时间是60进制的,即60秒是一分,60分时1小时。
还有三进制、五进制、八进制、十六进制等。
它们和十进制计数法的道理实质是一样的。
现代计算机上大多用二进制,即满二进一,退一当二,这种进位制只用两个数字0和1,如“1”在二进制中记作1,“2”就要满二进一,记作10,“3”记作11,“4”又一次满二进一,记作100,……。
为了区别十进制和二进制,只要在这个数的右下角标上2或10即可。
任何一个十进制正整数N都可以写成各数位上的数字与10的次方数的=9×103+7×102+5×101+8×100(注:100=1)。
乘积的和的形式,如9758(10)任何一个二进制数也像十进制数一样,也可以写成各个数位上的数字与=1×25+1×24+0×23+1×22+0×21+1 2的次方数的乘积的和的形式,如110101(2)×20典例评析化成二进制例1 将139(10)【分析】要将十进制数化为二进制数,只要连续除以2.因为139=69×2+1,即有69个“2”及1个“1”,故应向第二位上进“69”,个位则有1个1;而69=34×2+1,即第二位69又要向第三位进“34”,而本位数字为“1”。
但34=17×2,即第三位上的34还应向第四位进“17”,且本位数字为“0”;接下去17=8×2+1,即第四位为1;8=4×2,即第五位为0;4=2×2,即第六位为0;2=2×1,即第七位为0,第八位为1;所以139(10)=10001011(2)。
(完整版)五年级奥数__二进制问题_讲义.doc

专题二二进制问题知要点用0,1, 2,3,4, 5, 6,7,8,9 10 个数字表示所有整数的方法被叫做十制,十制是最常的制,世界上大数国家和地区都用种方法来数,它的特点是十一,退一当十。
除了十制外,有其它一些位制,如是60 制的,即 60 秒是一分,60 分 1 小。
有三制、五制、八制、十六制等。
它和十制数法的道理是一的。
代算机上大多用二制,即二一,退一当二,种位制只用两个数字0 和 1,如“ 1”在二制中作1,“2”就要二一,作 10,“3” 作 11,“ 4”又一次二一,作 100,⋯⋯。
了区十制和二制,只要在个数的右下角上 2 或 10 即可。
任何一个十制正整数N 都可以写成各数位上的数字与10 的次方数的乘的和的形式,如9758(10)=9×103+7×102 +5×101+8× 100(注: 100=1)。
任何一个二制数也像十制数一,也可以写成各个数位上的数字与2 的次方数的乘的和的形式,如 110101(2)=1×25+1× 24+0×23+1×22+0×21+1 ×20典例析例1 将 139(10)化成二制【分析】要将十制数化二制数,只要除以2. 因 139=69×2+1,即有 69 个“ 2”及 1 个“ 1”,故向第二位上“ 69”,个位有 1 个1;而 69=34× 2+1,即第二位 69 又要向第三位“ 34”,而本位数字“ 1”。
但34=17×2,即第三位上的 34 向第四位“ 17”,且本位数字“ 0”;接下去17=8×2+1,即第四位 1;8=4×2,即第五位 0;4=2×2,即第六位 0;2=2× 1,即第七位 0,第八位 1;所以 139(10)=10001011( 2)。
个程也可以算以“短除法”求得。
小升初奥数二进制的知识点讲解及应用

小升初奥数二进制的知识点讲解及应用
小升初奥数二进制的知识点讲解及应用
二进制及其应用
十进制:用0~9十个数字表示,逢10进1;不同数位上的数字表示不同的含义,十位上的2表示20,百位上的2表示200。
所以234=200+30+4=2102+310+4。
=An10n-1+An-110n-2+An-210n-3+An-310n-4+An-410n-5+An-
610n-7++A3102+A2101+A1100
注意:N0=1;N1=N(其中N是任意自然数)
二进制:用0~1两个数字表示,逢2进1;不同数位上的数字表示不同的含义。
(2)=An2n-1+An-12n-2+An-22n-3+An-32n-4+An-42n-5+An-62n-7
++A322+A221+A120
注意:An不是0就是1。
十进制化成二进制:
①根据二进制满2进1的特点,用2连续去除这个数,直到商为0,然后把每次所得的'余数按自下而上依次写出即可。
②先找出不大于该数的2的n次方,再求它们的差,再找不大于这个差的2的n次方,依此方法一直找到差为0,按照二进制展开式特点即可写出。
四年级奥数第27讲-二进制(教)
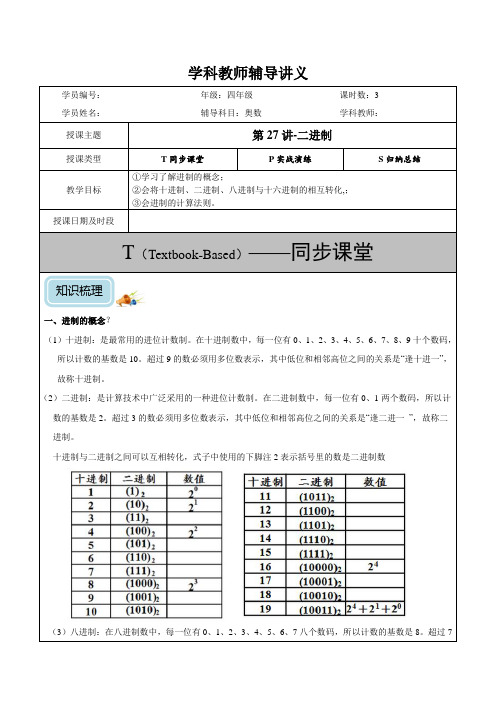
学科教师辅导讲义学员编号: 年级:四年级 课时数:3 学员姓名: 辅导科目:奥数学科教师:授课主题 第27讲-二进制授课类型 T 同步课堂P 实战演练S 归纳总结教学目标①学习了解进制的概念;②会将十进制、二进制、八进制与十六进制的相互转化,; ③会进制的计算法则。
授课日期及时段T (Textbook-Based )——同步课堂一、进制的概念?(1)十进制:是最常用的进位计数制。
在十进制数中,每一位有0、1、2、3、4、5、6、7、8、9十个数码,所以计数的基数是10。
超过9的数必须用多位数表示,其中低位和相邻高位之间的关系是“逢十进一”,故称十进制。
(2)二进制:是计算技术中广泛采用的一种进位计数制。
在二进制数中,每一位有0、1两个数码,所以计数的基数是2。
超过3的数必须用多位数表示,其中低位和相邻高位之间的关系是“逢二进一 ”,故称二进制。
十进制与二进制之间可以互相转化,式子中使用的下脚注2表示括号里的数是二进制数(3)八进制:在八进制数中,每一位有0、1、2、3、4、5、6、7八个数码,所以计数的基数是8。
超过7知识梳理的数必须用多位数表示,其中低位和相邻高位之间的关系是“逢八进一”,故称八进制。
(4)十六进制:在十六进制数中,每一位有0、1、2、3、4、5、6、7、8、9、A(表示10)、B(表示11)、C(表示12)、D(表示13)、E(表示14)、F(表示15)十六个数码,所以计数的基数是16。
超过15的数必须用多位数表示,其中低位和相邻高位之间的关系是“逢十六进一”,故称十六进制。
二、十进制与n 进制的转化1、将十进制数转换为等值的n 进制数(n≥2)时,整数部分采用“除n 倒取余数法”。
例如:整数()10107转换成二进制采用“除2倒取余数法”,得 ()()1021071101011=2、将n 进制数(n≥2)转换为等值的十进制数时,只要将n 进制数展开,然后将所有各项的数值按十进制数相加,就可以得到等值的十进制数了。
小学数学竞赛第五讲 二进制初步

第五讲二进制初步古时候的原始记数方法是以形示数,如用绳子打结,打结个数表示事物的个数,就是“结绳记数”;在竹片、骨片;瓷片上刻划,就是“刻划记数”。
直到有了文字,才开始用字母符号表示数。
如罗马数码,Ⅰ、Ⅱ、Ⅲ表示现在我们熟悉的阿拉伯数码1、2、3,5记作V,10记作X,100记作C,采用“左减右加”原则,Ⅳ表示4(5减1),而Ⅵ表示6(5加1),Ⅸ表示9,Ⅺ表示11,XX表示20,CCⅢC表示203,罗马数码表示数的特点是不管一个数码写在什么位置表示的数是固定的。
现在看来这种记数方法很不好,一方面符号太多,另一方面很难作乘除运算。
后来产生了“进位制记数法”,用少数几个数码,同一个数码写在一个数的不同数位表示不同的数值,就是“位值制”。
十进位制只用十个数码:0,1,2,3,4,5,6,7,8,9。
如1993,千位上的1表示1000,百位上的9表示900,十位上的9表示90,个位上的3就是3。
27548=20000+7000+500+40+8=2×104+7×103+5×102+4×10+8=a n×10n+a n-1×10n-1+…+a1×10+a0。
除十进制外还有二进制,三进制,八进制等。
这里介绍一下二进制。
一、什么是二进制在现实生活和记数器中,如果表示数的“器件”只有两种状态,如电灯的“亮”与“灭”,开关的“开”与“关”。
一种状态表示数码0,另一种状态表示数码1,1加1应该等于2,因为没有数码2,只能向上一个数位进一,就是采用“满二进一”的原则,这和十进制是采用“满十进一”原则完全相同。
1+1=10,10+1=11,11+1=100,100+1=101,101+1=110,110+1=111,111+1+=1000,……,可见二进制的10表示二,100表示四,1000表示八,10000表示十六,……。
二进制同样是“位值制”。
20北京版小五奥数教材课程二十、二进制的应用

课程二十二进制的应用1.二进制的特性2.二进制的运算3. 二进制与十进制的关系进位制的基本原理(1)十进制 我们通过对通常用的“十进制”的进一步认识,推广到 其它非十进制,概括出进位制原理。
(2)十进制计数法,只用十个数码;0,1,2,3,4,5,6,7,8,9。
它是“位值制”计数法。
(即同一个数码,在不同位置上表示不同的数值),如246的百位上的 2表示200,十位上的数码4表示40,个位上的数码6表示6,即 246=200+40+6=2×102+4×10+6一般来说,任何一个十进制数,都可以用各位数码(共十个数码)与 10的方幂乘积的和来表示,其中幂指数比相应数码所在的位数(从右往左 数)少1。
如356842(10)=300000+50000+6000+800+40+2=3×105+5×104+6×103+8×102+4×101+2×100学习目标重 点 1直接写成与10的方幂的乘积的和的形式。
(3)十位制值数,要“满十进一”.二进制数也可以表示成“以2为底的方幂的乘积的和的形式,例如:10(2)=1×2,11(2)=1×2+1×20=2+1,100(2)=1×22+0×2+0×20=22,101(2)=1×22 +0×2+1×20=22+1一般来说,任何一个二进制数,就是各位数码与2的方幂的乘积的和。
其中幂指数等于相应数码所在位数(从右往左数)减1。
101101(2)=25+23+22+1状态表示数码1,1加1应该等于2,因为没有数码2,只能向上一个数位进一,就是采用“满二进一”的原则。
二进制的特性什么是二进制只有数码0,1,采用“满二进一”原则的进位制记数法叫做二进制。
如:0,0+1=1,1+1=10,10+1=11,11+1=100,…可见二进制的10表示二,100表示四,1000表示八,10000表示十六,…。
小学数学五年级思维奥数寒假讲义-第7讲 进制(学生版)

第7讲 进制【知识梳理】一、数的进制1.十进制:我们常用的进制为十进制,特点是“逢十进一”。
在实际生活中,除了十进制计数法外,还有其他的大于1的自然数进位制。
比如二进制,八进制,十六进制等。
2.二进制:在计算机中,所采用的计数法是二进制,即“逢二进一”。
因此,二进制中只用两个数字0和1。
二进制的计数单位分别是1、21、22、23、……,二进制数也可以写做展开式的形式,例如100110在二进制中表示为:(100110)2=1×25+0×24+0×23+1×22+1×21+0×20。
二进制的运算法则:“满二进一”、“借一当二”,乘法口诀是:零零得零,一零得零,零一得零,一一得一。
注意:对于任意自然数n ,我们有n 0=1。
3.k 进制:一般地,对于k 进位制,每个数是由0,1,2,,1k -()共k 个数码组成,且“逢k 进一”.1k k >()进位制计数单位是0k ,1k ,2k ,.如二进位制的计数单位是02,12,22,,八进位制的计数单位是08,18,28,. 4.k 进位制数可以写成不同计数单位的数之和的形式1110110n n n n k n n a a a a a k a k a k a ---=⨯+⨯++⨯+()十进制表示形式:1010101010n n n n N a a a --=+++;二进制表示形式:1010222n n n n N a a a --=+++; 为了区别各进位制中的数,在给出数的右下方写上k ,表示是k 进位制的数 如:8352(),21010(),123145(),分别表示八进位制,二进位制,十二进位制中的数. 5.k 进制的四则混合运算和十进制一样先乘除,后加减;同级运算,先左后右;有括号时先计算括号内的。
二、进制间的转换:一般地,十进制整数化为k 进制数的方法是:除以k 取余数,一直除到被除数小于k 为止,余数由下到上按从左到右顺序排列即为k 进制数.反过来,k 进制数化为十进制数的一般方法是:首先将k 进制数按k 的次幂形式展开,然后按十进制数相加即可得结果.【典例精讲】把9865转化成二进制、五进制、八进制,看看谁是最细心的。
二进制专题教育课件

1923年12月28日,在布达佩斯诞 生了一位神童,这不但给这个家庭 带来了巨大旳喜悦,也值得整个计 算机界去纪念。正是他,开创了当 代计算机理论,其体系构造沿用至 今,而且他早在40年代就已预见到 计算机建模和仿真技术对当代计算 机将产生旳意义深远旳影响。他,
二进制旳特点Biblioteka 只有“0”和“1”两个数码 对计算机而言,形象鲜明,易于区别,辨认可
二进制及其运算
简朴旳数学计算
2+3 4+6 6+9 十进制数计算特点:逢十进一
进位制是人们为了计数和运算以便而约定旳 记数系统。
你还懂得哪些常见旳进位制?请举例。 60进制(时分秒旳换算) 360进制(一周=360度) 12进制(一打) 二进制
什么是进位制?
进位制是一种记数方式,用有限旳数字在不同旳位置表 达不同旳数值。
练习
(1)(100) 2 +(10) 2 (2)(101) 2 +(110) 2 (3)(1100) 2 +(1011) 2
计算机工作原理示意图
外部存储器
软盘
输入设备
输入 2+2
0 000 0 0 10 0 0 0 0 0 0 10
00000100
程序
键盘
原始数据
2+2
内存
4
输出设备
输出
打印机 运算成果
1
0
1
成果是:110112
二进制转换为十进制
按位权展开 (1111) 2 =1×2³+1×2²+1×2¹+1×2º
=8+4+2+1 =(15) 10
二进制旳加法
列竖式,加数和被加数个位对齐,从各位数开始, 假如相加之和不小于等于十,就向高位进位。
五年级暑假奥数 第二单元 二进制

• • • •
6836=6000+800+30+6 =6×1000+8×100+3×10+6×1 而1000=10×10×10 100=10×10 我们规定 n个a相乘 这样6836就可以写成
a a a a a
n
6836=6×103+8×102+3×10+6
二进制数的计数单位
(a5 a4 a3a2 a1a0 ) 2
5
。。。 。。。
4 3 2
a5 2 a4 2 a3 2 a2 2 a1 2 a0
二进制数化成十进制数的方法 ——展开计算法
把二进制数化成十进制数,可以先把二进制数写成 它的展开式,即写成数码与计数单位积的和的形式,再 进行计算就行了。如下图
同样的道理,二进制数的计数单位应该是1、 21、22、23、24。。。 。。。 例如:二进制数个位上的1是表示十进制数的1、
二进制数十位上的1表示十进制数的2、 二进制数百位上的1表示十进制数的22、即4; 二进制数千位上的1表示十进制数的23、即8;
二进制数万位上的1表示十进制数的24 、即16;
右起第一位数字 右起第二位数字
右起第三位数字
右起第四位数字
右起第五位数字
(二)二进制数化成十进制数的方 法——展开计算法
• • • • • 例2、化( 111011)2为十进制数 知识准备: 解: (111011)2 =1×25+1×24+1×23+0×22+1×2+1 =32+16+8+0+2+1 • = ( 59)10
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
这光狡可头 猾怎强了也,太熊 么大办你呀快点破
解吧
我有办法了,只 要将十进制数化 成二进制数就可
以了
屏幕 显示 25
1、十进制
二进制
方法: (1)用2去整除 (2)取余 (3)从下至上
2 25 2 12 26
23 21
0
…… 1 …… 0 …… 0 …… 1 …… 1
哦,密码 就是11001
了
(25)10 =(11001 )2
了
臭狗熊,怎么 会这么聪明,
气死我了
熊大,你真 是太聪明了!
俺也要学 数学
那都是数学 神奇的效果
熊二,那我来考考 你
练习
(17)10 =(10001)2
2 17 28
4 2 1 0
…… 1
…… 0 …… 0 …… 0 …… 1
(40)10 =(101000)2
2 40 2 20 2 10 25 22 21
俺会了!
熊 熊大偷偷的来到光头强的房间里。
熊大,我们看看 有什么好吃滴
好像是一台智能 密码箱
熊大,那是什么 东东?
那里面一定有好 多好吃滴,熊大, 我们快把它打开
吧
熊二摁了下密码箱开关,机器说话了: 我只识别0和1两个数字,请将下面的
数字转化成我认识的数字输入…
0
…… 0
…… 0 …… 0 …… 1
…… 0 …… 1
(11001)2 = (25 )10 方法:
(100010)2 = ( 34)10
每一位数字乘以其相应的权后再相加就是该数的数值。
1×24 +1 × 23 +0 × 22 +0 × 21 +1 × 20 = 16+8+0+0+1 = 25
1 × 25 + 0 × 24 +0 × 23 +0 × 22 +1 × 21 +0 × 20 = 32+0+0+0+2+0 = 34
熊二把密码11001输入后,密码箱打 开了,里面有好多好吃的水果……
熊二和熊大开心的吃了起来
有香蕉、苹果、菠 萝,还有玉米,太
好吃了…
这可怎么办 呀,熊大快 点想想办法
吧
臭狗熊, 上当了吧,
哈哈
吃着吃着,突然 门关上了…
不好,上光 头强的当了
我知道了,刚刚进来 的时候要把十进制数 转化成二进制数,现 在不要对错把成,误二 十密进进码制制数数转化
怎那么可呀会怎熊聪是?呢么大明我偶,办,了学像1这你,习10里太你的0有,串一数定字是 密码
2、二进制
十进制
方法:每一位数字乘以其相应的权后, 再相加就是该数的数值。
1100
23 22 21 20
权
1×23 + 1×22 + 0× 21 + 0×20 =8 + 4 + 0+ 0 = 12
密码就是12 了,太简单
