第二章 用拉格朗日方程建立系统数学模型
拉格朗日法求解带约束条件的最优模型

拉格朗日法求解带约束条件的最优模型拉格朗日法是一种常用的数学方法,用于求解带有约束条件的最优化问题。
在实际问题中,我们经常会遇到需要在满足一定条件下寻找最大值或最小值的情况。
拉格朗日法通过引入拉格朗日乘子,将约束条件转化为目标函数的一部分,从而将带约束条件的最优化问题转化为无约束条件的最优化问题,进而求解最优解。
我们考虑一个简单的示例问题,假设有一个函数 f(x, y) = x^2 + y^2,我们希望在约束条件 g(x, y) = x + y = 1 下,求函数 f(x, y) 的最小值。
使用拉格朗日法求解这个问题的步骤如下:1. 建立拉格朗日函数L(x, y, λ) = f(x, y) + λg(x, y),其中λ 是拉格朗日乘子。
2. 求解拉格朗日函数的偏导数:∂L/∂x = 2x + λ∂L/∂y = 2y + λ∂L/∂λ = x + y - 13. 令偏导数等于零,并联立求解方程组:2x + λ = 02y + λ = 0x + y - 1 = 0解方程组得到 x = 1/2,y = 1/2,λ = -1。
4. 将求得的 x,y 值代入原函数 f(x, y) 中,得到最小值为f(1/2, 1/2) = 1/2。
通过以上步骤,我们成功使用拉格朗日法求解了带有约束条件的最优化问题。
当然,在实际问题中,可能会存在更复杂的约束条件和目标函数,但求解的思路是相似的。
除了上述示例问题外,拉格朗日法还可以应用于其他类型的问题,如带有多个约束条件的问题、非线性约束条件的问题等。
对于带有多个约束条件的问题,可以使用多个拉格朗日乘子,将每个约束条件转化为目标函数的一部分,并求解相应的偏导数方程组。
对于非线性约束条件的问题,可以使用约束条件的梯度向量与拉格朗日乘子的线性组合来建立拉格朗日函数。
拉格朗日法是一种强大的数学工具,可以帮助我们求解带有约束条件的最优化问题。
通过建立拉格朗日函数,引入拉格朗日乘子,并求解相应的方程组,我们可以得到最优解。
第二章:动力学系统的微分方程模型

第二章:动力学系统的微分方程模型利用计算机进行仿真时,一般情况下要给出系统的数学模型,因此有必要掌握一定的建立数学模型的方法。
在动力学系统中,大多数情况下可以使用微分方程来表示系统的动态特性,也可以通过微分方程可以将原来的系统简化为状态方程或者差分方程模型等。
在这一章中,重点介绍建系统动态问题的微分方程的基本理论和方法。
在实际工程中,一般把系统分为两种类型,一是连续系统;其数学模型一般是高阶微分方程;另一种是离散系统,它的数学模型是差分方程。
§2.1 动力学系统统基本元件任何机械系统都是由机械元件组成的,在机械系统中有3种类型的基本机械元件:惯性元件、弹性元件和阻尼元件。
1 惯性元件:惯性元件是指具有质量或转动惯量的元件,惯量可以定义为使加速度(或角加速度)产生单位变化所需要的力(或力矩)。
惯量(质量)=)加速度(力(2/)s m N 惯量(转动惯量)=)角加速度(力矩(2/)s rad m N ⋅2 弹性元件:它在外力或外力偶作用下可以产生变形的元件,这种元件可以通过外力做功来储存能量。
按变形性质可以分为线性元件和非线性元件,通常等效成一弹簧来表示。
对于线性弹簧元件,弹簧中所受到的力与位移成正比,比例常数为弹簧刚度k 。
x k F ∆=这里k 称为弹簧刚度,x ∆是弹簧相对于原长的变形量,弹性力的方向总是指向弹簧的原长位移,出了弹簧和受力之间是线性关系以外,还有所谓硬弹簧和软弹簧,它们的受力和弹簧变形之间的关系是一非线性关系。
3 阻尼元件:这种元件是以吸收能量以其它形式消耗能量,而不储存能量,可以形象的表示为一个活塞在一个充满流体介质的油缸中运动。
阻尼力通常表示为:αxc R = 阻尼力的方向总是速度方向相反。
当1=α,为线性阻尼模型。
否则为非线性阻尼模型。
应注意当α等于偶数情况时,要将阻尼力表示为:||1--=αx xc R 这里的“-”表示与速度方向相反§2.2 动力学建模基本定理1 动力学普遍定理对于大多数力学问题,可以使用我们熟知的牛顿动力学基本定理来解决,动力学普遍定理包括动量定理、动量矩定理和动能定理,以及其他变形形式,普遍定理的特点是比较直观,针对不同的问题可以选择不同的力学定理,在一般情况下利用普遍定理可以得到大多数动力学系统的数学模型。
第2章——多自由度系统的振动——运动方程建立方法0425

船体振动基础1第章多自由度系统的振第2章多自由度系统的振动一、引言二、两自由度系统的振动三、多自由度系统的振动四、振动方程建立的其他方法2有阻尼的多自由度系统振动1、拉格朗日方程式1、拉格朗日方程式P38拉格朗日法是建立微分方程一种简单的方法:先求出系统的动能、势能,进而得出质量矩阵和刚度矩阵.优点:系统的动能和势能都是标量,无需考虑力的方向。
141、拉格朗日方程式P38拉格朗日第二类方程式适用于完整约束的系统。
完整约束完整约束:当约束方程本身或约束方程通过积分后可以下式所示的形式表示时,称为完整约束。
不完整约束:当约束方程本含有不能积分的速度项时,系统的约束称为不完整约束。
具有不完整约束的系统,系统的自由度不等于广义坐标数自由度数小于广义坐标数于广义坐标数,自由度数小于广义坐标数。
151、拉格朗日方程式P3811•位移方程和柔度矩阵P40对于静定结构,有时通过柔度矩阵建立位移方程比通过对于静定结构有时通过m1x1x2以准静态方式作用在梁上。
梁只产生位移(即挠度),不产生加速度。
的静平衡位置为坐标P1=1 f11 f21 f12P2=1 f22(1)P1 = 1、P2 = 0 时 m1 位移:x1 = f11 m2 位移:x2 = f 21 (3)P1、P2 同时作用 m1 位移: 位移 x1 = f11 P 1 + f12 P 2 m2 位移:x2 = f 21 P 1 + f 22 P 2(2)P1 = 0、P2 = 1 时 m1 位移:x1 = f12 m2 位移:x2 = f 22P1 m1 x1 x2 P2 m2P1=1 f11 f21 f12 P1 m1 x1P2=1 f22 P2 m2 x2P 同时作用时 1、P 2 同时作用时:x1 = f11P 1 + f12 P 2 x2 = f 21P 1 + f 22 P 2矩阵形式 X = FP 矩阵形式:⎡ x1 ⎤ X =⎢ ⎥ ⎣ x2 ⎦f ij 柔度影响系数f12 ⎤ f 22 ⎥ ⎦⎡ f11 F=⎢ ⎣ f 21⎡P 1⎤ P=⎢ ⎥ ⎣ P2 ⎦物理意义: 系统仅在第 j 个坐标受到 单位力作用时相应于第 i 个坐标上产生的位移柔度矩阵P1 m1 x1P2 m2 x2P1(t) m1 m2P2(t)&1 m1 & x&2 m2 & xX = FP⎡ x1 ⎤ ⎡ f11 ⎢x ⎥ = ⎢ f ⎣ 2 ⎦ ⎣ 21 f12 ⎤ ⎡ P 1⎤ ⎢P ⎥ f 22 ⎥ ⎦⎣ 2 ⎦当P 1、P 2 是动载荷时 集中质量上有惯性力存在⎡ x1 ⎤ ⎡ f11 ⎢x ⎥ = ⎢ f ⎣ 2 ⎦ ⎣ 21 f12 ⎤ ⎡ P && 1 (t ) − m1 x1 ⎤ ⎢ P (t ) − m & ⎥ f 22 ⎥ & x 2 2⎦ ⎦⎣ 2⎡ x1 ⎤ ⎡ f 11 ⎢x ⎥ = ⎢ f ⎣ 2 ⎦ ⎣ 21位移方程:f 12 ⎤⎛ ⎡ P1 (t ) ⎤ ⎡m1 ⎜⎢ −⎢ ⎥ ⎥ ⎜ f 22 ⎦⎝ ⎣ P2 (t ) ⎦ ⎣ 0&1 ⎤ ⎞ 0 ⎤⎡ & x ⎟ ⎥ ⎢ ⎥ &2 ⎦ ⎟ m2 ⎦ ⎣ & x ⎠&& ) X = F ( P − MXP1(t) m1 m2P2(t)⎡ x1 ⎤ X =⎢ ⎥ ⎣ x2 ⎦⎡P 1 (t ) ⎤ P=⎢ ⎥ P ( t ) ⎣ 2 ⎦&1 m1 & x&2 m2 & x位移方程 位移方程:&& ) X = F ( P − MX也可按作用力方程建立方程:&& + KX = P MX刚度矩阵&& + X = FP FMX柔度矩阵与刚度矩阵的关系 柔度矩阵与刚度矩阵的关系:&& KX = P − MX若K非奇异F=K−1FK = I&& ) X = K −1 ( P − MX应当注意:对于允许刚体运动产生的系统(即具有刚体自由度的系统) , 柔度矩阵不存在。
高等结构振动学-第2章-用拉格朗日方程建立系统数学模型

2muu
[Mg
L 2
0 mgu]sin
0
以上是对离散系统应用拉格朗日方程建立振动方程,如果利用拉格朗日方 程建立连续系统的方程,则它是一种同时将系统离散化、变量分离并达到系统 降阶的途径。 2. 连续参数模型中应用——与假设模态法联合使用
3
对一维连续系统,假设位移为:
N
u(x.t) i (x)qi (t) i 1
d dt
(
T qi
)
T qi
U qi
Qi
(i 1, 2, 3, N )
(2-5)
(推导:)
将系统总动能、总势能和非保守力的虚功的表达式代入哈密尔顿原理式中(变
分驻值原理),有
t2
t1
(
T q1
q1
T q2
q2
T q N
q N
T q1
q1
f j (q1, q2 ,qM ) 0 ( j 1,2,C)
(i 1,2,M )
(2-43)
联立上两个方程,就可确定 M+C 个未知数 qi , j (i 1,2,M ; j 1,2,C)
【应用实例】
求两端固定杆的轴向自由振动微分方程。
【解】令,
u(x,
t)
(
x L
D q
0
(2-15)
如果系统上还作用了除有势力和阻尼力以外的非保守力,如结构受到的外激励
力(对应的广义非保守力可通过非保守力的虚功求得,仍记为 Qi ),则系统的拉 格朗日方程为:
d dt
(
T qi
)
T qi
用拉格朗日法建立体系的运动方程

拉格朗日法是分析力学中的一种方法,用于描述多体系统的运动。
这种方法基于拉格朗日函数L,它由系统的动能T和势能V组成。
假设我们有一个n自由度的多体系统,其动能和势能分别为:T = 1/2 ∑ mi × vi^2
V = V(q1, q2, ..., qn)
其中,m是质量,v是速度,q是位置。
那么拉格朗日函数L可以定义为:
L = T - V
根据拉格朗日函数,我们可以得到系统的运动方程,也称为拉格朗日方程:
dL/dq = dT/dq - dV/dq
其中,dq表示对q的偏导数。
这个方程描述了系统在给定力的作用下如何运动。
在给定初始条件的情况下,我们可以通过解这个方程来找到系统的运动轨迹。
需要注意的是,拉格朗日方程是一种描述系统动力学的方程,它并不直接给出系统的运动轨迹。
要找到具体的运动轨迹,通常需要求解这个方程。
这可能涉及到数值方法,例如欧拉法、龙格-库塔法等。
拉格朗日方程的应用及举例08讲

拉格朗日方程的应用及举例拉格朗日方程有以下几个特点:(1)拉格朗日方程适用于完整系统,可以获得数目最少的运动微分方程,即可以建立与自由度数目相同的n个方程,是一个包含n个二阶常微分方程组,方程组的阶数为2n。
求解这个方程组可得到以广义坐标描述的系统运动方程。
(2)拉格朗日方程的形式具有不变性。
对于任意坐标具有统一的形式,即不随坐标的选取而变化。
特别是解题时有径直的程序可循,应用方便。
(3)所有的理想约束的约束反力均不出现在运动微分方程中。
系统的约束条件愈多,这个特点带来的便利越突出。
(4)拉格朗日方程是以能量的观点建立起来的方程,只含有表征系统运动的动能和表征主动力作用的广义力,避开了力、速度、加速度等矢量的复杂运算。
(5)拉格朗日方程不但可以建立相对惯性系的运动,还可以直接建立相对非惯性系的动力学方程,只要写出的动能是绝对运动的动能即可,至于方程所描述的运动是对什么参考系的运动,则取决于所选的广义坐标。
纵观拉格朗日方程,看出分析力学在牛顿力学的基础上,提出严密的分析方法,从描述系统的位形到建立微分方程都带有新的飞跃。
我们还应看到,虽然拉格朗日方法在理论上和应用上都有重要的价值,但是,牛顿力学的价值并未降低,特别是它的几何直观性和规格化的方法使人乐于应用,由于计算机的广泛使用,牛顿一欧拉方法又有所发展。
我们将会看到,用拉格朗日方程求解,在获得数量最少的运动微分方程时,其求导过程有时过于繁琐,并有较多的耦合项。
应用拉格朗日方程建立动力学方程时,应首先建立以广义坐标q和广义速度q 表示的动能函数和广义力Q。
为此,首先讨论动能的计算和广义力的计算,在此基础上,再讨论拉格朗日方程的应用。
一、动能的计算对于系统的动能,可以写出关于广义速度q 的齐次函数的表达式。
在实际计算中,应用理论力学的有关知识就可以建立以广义坐标和广义速度所表达的动能函数。
例1-1已知质量为m,半径为r的均质圆盘D,沿OAB直角曲杆的AB段只滚不滑。
(经典)拉格朗日方程

F Ni
mi
ri
O 图2.2
给质点i以虚位移 给质点 以虚位移 δ ri ,得
( Fi + FNi − mi ri ).δ ri = 0
Fi
对整个质点系
∑ (F
i
i
ri + FNi − mi ɺɺ ).δ ri = 0
在理想约束条件下, 在理想约束条件下,有
∑ (F
i
i
ri − mi ɺɺ ).δ ri = 0
(4)对拉格朗日方程的评价 )
拉氏方程的特点(优点): 拉氏方程的特点(优点): • 是一个二阶微分方程组,方程个数与体系的自由度相同。形式简洁、 是一个二阶微分方程组,方程个数与体系的自由度相同。形式简洁、 结构紧凑。而且无论选取什么参数作广义坐标,方程形式不变。 结构紧凑。而且无论选取什么参数作广义坐标,方程形式不变。 • 方程中不出现约束反力,因而在建立体系的方程时,只需分析已知 方程中不出现约束反力,因而在建立体系的方程时, 的主动力,不必考虑未知的约束反力。体系越复杂,约束条件越多, 的主动力,不必考虑未知的约束反力。体系越复杂,约束条件越多,自由度 越少,方程个数也越少,问题也就越简单。 越少,方程个数也越少,问题也就越简单。 • 拉氏方程是从能量的角度来描述动力学规律的,能量是整个物理学的 拉氏方程是从能量的角度来描述动力学规律的, 基本物理量而且是标量, 基本物理量而且是标量,因此拉氏方程为把力学规律推广到其他物理学领域 开辟了可能性,成为力学与其他物理学分支相联系的桥梁。 开辟了可能性,成为力学与其他物理学分支相联系的桥梁。 拉氏方程的价值 拉氏方程在理论上、方法上、形式上和应用上用高度统一的规律, 拉氏方程在理论上、方法上、形式上和应用上用高度统一的规律,描 述了力学系统的动力学规律, 述了力学系统的动力学规律,为解决体系的动力学问题提供了统一的程序化 的方法,不仅在力学范畴有重要的理论意义和实用价值, 的方法,不仅在力学范畴有重要的理论意义和实用价值,而且为研究近代物 理学提供了必要的物理思想和数学技巧。 理学提供了必要的物理思想和数学技巧。
倒立摆系统的建模(拉格朗日方程)

系统的建模及性能分析倒立摆系统的构成及其参数1倒立摆系统的基本结构本设计所用到的倒立摆模型直线一级倒立摆系统。
整个系统是由6大部分所组成的一个闭环系统,包括计算机、数据采集卡、电源及功率放大器、直流伺服电机、倒立摆本体和两个光电编码器等模块。
如图2.1所示:图2.1 倒立摆系统的结构组成示意图Fig 2.1 Structure of the linear single inverted pendulum system2系统主要组成部分简介直线一级倒立摆装置如图2.2所示[13]:图2.2直线一级倒立摆装置Fig 2.2 Straight linear 1-stage inverted pendulum deviceQuanser倒立摆系统包含倒立摆本体、数据采集电控模块以及控制平台等三大部分,其中控制平台是由装有Quanser专用实时控制软件的通用PC机组成。
1.直线倒立摆主体倒立摆主体是由Quanser直线运动控制伺服单元IP02与直线一级摆杆组成,并配有专用的小车直线轨道。
这里主要介绍下Quanser直线运动控制伺服单元IP02(即倒立摆运动小车)及导轨的组成:图2.3伺服单元IP02的组成Fig 2.3 Servo unit IP02 parts编号名称英文(01)IP02小车IP02 Cart(02)不锈钢滑轨Stainless Steel Shaft(03)齿轮导轨Rack(04)小车位移齿轮Cart Position Pinion(05)小车电机传动齿轮Cart Motor Pinion(06)小车电机传动齿轮轴Cart Motor Pinion Shaft(07)摆杆传动轴Pendulum Axis(08)IP02小车位移编码器IP02 Cart Encoder(09)IP02摆杆角度编码器IP02 Pendulum Encoder(10)IP02小车位移编码器接口IP02 Cart Encoder Connector(11)IP02摆杆角度编码器接口IP02 Pendulum Encoder Connector(12)电机接口Motor Connector(13)直流伺服电机DC Motor(14)变速器Planetary Gearbox(15)直线滑轨支撑轴Linear Bearing图2.4系统导轨结构图Fig 2.4 System guide rail structure直线一级倒立摆系统的倒立摆的摆杆连接在IP02小车的摆杆连接套上,IP02小车由电机通过齿轮传动机构在导轨上来回运动,保持摆杆平衡。
第二章用拉格朗日方程建立系统数学模型

第二章 用拉格朗日方程建立系统的数学模型§2.1概述拉格朗日方程——属于能量法,推导中使用标量,直接对整个系统建模 特点:列式简洁、考虑全面、建模容易、过程规范适合于线性系统也适合于非线性系统,适合于保守系统,也适合于非保守系统。
§2.2拉格朗日方程1. 哈密尔顿原理 系统总动能),,,,,,,(321321N n q q q qq q q q T T = (2-1)系统总势能),,,,(321t q q q q U U N =(2-2)非保守力的虚功N N nc q Q q Q q Q W δδδδ ++=2211(2-3)哈密尔顿原理的数学描述:0)(2121=+-⎰⎰t t nc t t dt W dt U T δδ (2-4)2. 拉格朗日方程: 拉格朗日方程的表达式:),3,2,1()(N i Q q Uq T q T dt d iii i ==∂∂+∂∂-∂∂ (2-5)(推导:)将系统总动能、总势能和非保守力的虚功的表达式代入哈密尔顿原理式中(变分驻值原理),有0)(221122112211221121=+++∂∂-∂∂-∂∂-∂∂++∂∂+∂∂+∂∂+∂∂+∂∂⎰dt q Q q Q q Q q q Tq q U q q U q qTq q T q q T q q T q q T q q T N N N NN N N N t t δδδδδδδδδδδδ (2-6)利用分步积分dt q q Tdt d q qT dt q q T i t t i t t i i i t t i δδδ⎰⎰∂∂-∂∂=∂∂212121)(][ (2-7)并注意到端点不变分(端点变分为零)0)()(21==t q t q i i δδ (2-8)故dt q q T dt d dt q qTi i t t i t t i δδ)(2121∂∂-=∂∂⎰⎰(2-9)从而有0)])([211=+∂∂-∂∂+∂∂-⎰∑=dt q Q q Uq T q T dt d i i it t i i Ni δ ( (2-10)由变分学原理的基本引理:(设 n 维向量函数M(t),在区间],[0f t t 内处处连续,在],[0f t t 内具有二阶连续导数,在f t t ,0处为零,并对任意选取的n 维向量函数)(t η,有⎰=ft t T dt t M t 00)()(η则在整个区间],[0f t t 内,有 0)(≡t M )我们可以得到:0)(=+∂∂-∂∂+∂∂-i ii i Q q U q T q T dt d (2-11)即i ii i Q q U q T q T dt d =∂∂+∂∂-∂∂)( (2-12)对非保守系统,阻尼力是一种典型的非保守力,如果采用线性粘性阻尼模型,则阻尼力与广义速度}{q成正比,在这种情况下,可引入瑞利耗散(耗能)函数D ,}]{[}{21q C q D T≡ (2-13) 阻尼力产生的广义非保守力为:i i qDQ ∂∂-= (2-14) 对于仅受有势力和线性阻尼力作用的系统,其拉格朗日方程为:0)(=∂∂+∂∂+∂∂-∂∂qD q U q T q T dt d i i i (2-15) 如果系统上还作用了除有势力和阻尼力以外的非保守力,如结构受到的外激励力(对应的广义非保守力可通过非保守力的虚功求得,仍记为i Q ),则系统的拉格朗日方程为:i i i i Q qD q U q T q T dt d =∂∂+∂∂+∂∂-∂∂ )( (2-16) §2.3 拉格朗日方程在振动系统建模中应用在某些结构振动问题中,取分离体、确定各分离体的受力情况,然后利用牛顿第二定律建立方程的方法不一定可用,或者很不方便,这时,采用拉格朗日方程来建立振动方程就很方便。
07-分析力学基础-第二类拉格朗日方程的应用
∂L =0 ∂x
∂L = Qsinα ∂s
代入保守系统拉氏方程,并适当化简, 代入保守系统拉氏方程,并适当化简,得到系统的运动微分方 程。
& & (P+Q)& −Q⋅& cosα =0 x s & & 3& −2& cosα =2gsinα s x
拉格朗日函数
L = T −V
1 m(x2 -xθlsinθ + 1 l 2θ 2 ) & & && = 2 3 1 kx2 + mg(x + l cosθ ) 2 2
4、应用拉格朗日方程建立系统的运动微分方程
∂L = - + mgx kx ∂x
∂L = mx- 1 m &lsinθ & θ & ∂x 2
2 2 −mgl(θ12 +θ2 )/2 − kl 2 (θ12 −2θ1 θ2 +θ2 )/2
∂L =−mglθ −kl 2 (θ −θ ) =−(mgl + kl 2 )θ + kl 2θ 1 1 2 1 2 ∂θ1
∂L = ml 2θ & 1 & ∂θ1 d ∂L = ml 2θ && 1 & dt ∂θ1
O
r0
B k A
解:1、系统的约束为完整约束,且主动 系统的约束为完整约束, O θ B' W
r0 r
拉格朗日方程的应用

(c )滑块做简谐振动0sin x x t ω=。
自由度为 1。
取 θ例3.在极坐标中:r r v rv r v r v r θθωθ==⎧⎧⎪⇒⎨⎨==⎪⎩⎩ 对于光滑杆我们可以设线密度为ρ,质量为:M l ρ=一个光滑杆,在铅直平面Oyz 内以角速度ω绕ox 轴转动,一个质点约束在杆上运动,0t =时,,0r b r== ,求质点运动规律和约束反力N F解:体系的自由度为 1 约束方程为:t θω= 取广义坐标为:r应用牛顿运动方程:例4.解:(1)自由度:平面运动的质点的自由度为 2,现在受到绳子的约束所以自由度为 1 (2)质点受重力(主动力)和绳子的拉力(约束力)均为保守力,(3)系统是理想约束,完整体系(4)取 为广义坐标在一光滑的平面上竖直固定一半径为r的圆柱体,设长为l轻绳一端固定在柱底面的O点,另一端系着质量为m的小球,小球在平面上以垂直于绳子的方向的初速度为0v运动。
(1)写出体系的拉格朗日函数L(2)小球碰倒主体时的位置和消耗的时间[]22()2()2sin cos ()0l r r l r r gr g l r θθθθθθθθ---++--=即:[]2()22sin cos 0l r r r gr g θθθθθθ--++-=若不考虑质点势能:代入拉格朗日方程:暂时不考虑l r θ=点,注意到01k m g δ=时: 例6.解:该系统有两个自由度,选取1x 和ϕ为广义坐标21(2)0m m xkx ++= 如图所示的运动系统中,重物1M 的质量为1m ,可沿光滑水平面移动;摆锤2M 的质量为2m ,两个物体用无重杆连接,杆长为l 。
试建立此系统的运动微分方程。
12120sin cos y x x l y l ϕϕ==-=,,12120cos sin yx x l y l ϕϕϕϕ==-= ,,例:带电粒子在电磁场中的运动设 电场:E ; 磁场: B ; 对于带电粒子:电荷:q ; 速度:vLorentz 力:()F q E v B =+⨯Maxwell 方程:Lorentz 力是非保守力:()()0F q E v B ∇⨯=∇⨯+∇⨯⨯≠因此带电粒子在电磁场中的运动应该通过将洛伦兹力构建(,,)U U q qt αα= ,进而写出新的拉格朗日函数。
结构动力学拉格朗日方程

二、拉格朗日方程及其应用虽然可以直接用牛顿第二定律或达朗贝尔原理建立多自由度系统的运动微分方程,但是在许多情况下应用拉格朗日方程法更为方便。
这里用最简单的方式推导拉格朗日方程,以便更好地理解这个被广泛应用的方程的意义。
我们知道,对于一能量守恒的系统,系统的动能和势能的总和是不变的,因此,它们的总和对时间的导数等于零,即:式中:是系统的动能,它是系统广义速度的函数;是系统的势能,它是系统广义坐标的函数。
下面将说明,这两者分别可以用广义坐标和广义速度的二次型表示。
单自由度系统的动能和势能公式如下:这个结论可以推广到多自由度系统。
如下图4-6,使系统各质点产生位移,则在处的力为(a)设系统有个力作用,则系统总势能为:(b)把公式(a)代入(b)中,得:(c)若用矩阵符号,上式可写成:若把改为更一般的广义坐标符号,上式变为:(d)上式就是用广义坐标和刚度矩阵的二次型表示的系统势能表达式。
若以表示质量的速度,可以仿照单自由度系统动能的方法表示多自由度系统的动能:或写成矩阵形式:我们假设系统的动能只与广义速度有关而与广义坐标无关,对微振动这是成立的。
下面来推导拉格朗日方程。
为此,对进行全微分:(e)将对求导,有:将上式乘以并对从到求和,有:(f)比较(a),(f)两式可知:(g)对(g)进行一次微分,得(h)(h),(e)两式相减可得:根据守恒系统的原理,有(i)因为个广义坐标是独立的,不可能都等于零,因此要上式成立必须使(j)当系统还作用有除有势力之外的附加力时, 外力在上所作的功将是令,则可得:(4-8)式中是除有势力之外的所有外力,其中包括阻尼力,阻尼力可表示为:(4-9)。
拉格朗日

第二章 拉格朗日方程教学目的和基本要求:正确理解各种约束的物理意义,掌握判断力学体系自由度的方法和选择广义坐标的基本原则;能应用虚功原理求解处于静平衡的力学体系的各类问题;掌握运用广义坐标、广义速度和时间来表示拉格朗日函数的方法;能熟练地用理想、完整体系拉格朗日方程建立力学体系的运动微分方程。
教学重点:在理解各种约束、自由度的物理意义的基础上,熟练掌握应用拉格朗日方程求解力学问题的方法。
教学难点:约束、自由度的物理意义及拉格朗日方程在力学问题中的应用。
§2.1 理想约束、达朗贝尔方程一:牛顿动力学方程的一般解法1. 一般解法:设有n 个质点,受到k 个约束的质点系,则有3n 个未知的坐标(i i i z ,y ,x )和k 个未知约束力,为求解这3n 个未知的坐标,解方程的一般步骤如下: 牛顿第二定律−→−3n 个运动微分方程+k 个约束方程−−−−→−nF k个未知消去3n 个微分方程−−−−−−−−−−→−个不独立的坐标个约束方程消去利用k k (3n-k )个微分方程→−解出个未知的(3n-k )独立坐标−−−−−→−个约束方程利用k 解出全部3n 个未知坐标和k 个未知约束力。
2. 实例:以图1.7的力学问题为例(从略)3.局限性:当n 、k 的个数较大时,求解方程将十分困难甚至无法完成。
因此当n 较大时如果我们能直接写出(3n+k )个不含未知约束力和非独立坐标的方程,求解方程的过程将大大简化,。
这种方法正是拉格朗日方程所采取的方法,此外拉格朗日方程的物理意义还超出了力学的范畴而扩展到物理学别的领域。
二:虚位移、约束和虚功 1.实位移和虚位移实位移:质点按)t (r r =力学规律运动时,在dt 时间内实际所发生的位移,用r d表示。
以前我们所讨论的位移均为实位移。
虚位移:想象在某一时刻t ,质点所发生的约束所允许的无限小的位移为虚位移,用rδ表示。
它不是质点实际运动所产生的位移,因而不需要时间,只要满足约束条件即可。
理论力学中的力学系统模型建立

理论力学中的力学系统模型建立在理论力学中,力学系统模型的建立是研究和分析力学问题的重要方法。
力学系统模型的建立可以帮助我们了解力学系统的基本性质和行为规律,为解决实际问题提供理论依据和数值模拟的基础。
本文将探讨力学系统模型建立的原理和方法。
一、力学系统的基本概念力学系统是指具有相互作用的物体(或粒子)的集合,其中包括了待研究的物体以及周围环境。
力学系统可以是宏观的,如汽车的运动;也可以是微观的,如分子的振动。
为了研究和描述力学系统的运动规律,我们需要建立相应的数学模型。
二、力学系统的描述力学系统的描述可以采用拉格朗日力学或哈密顿力学两种方法。
对于大多数力学系统,拉格朗日力学是更常用的方法。
在拉格朗日力学中,力学系统的状态由广义坐标和广义速度来描述,物体的运动方程由拉格朗日方程给出。
而哈密顿力学则采用广义坐标和广义动量来描述力学系统,运动方程由哈密顿方程确定。
三、力学系统模型的建立步骤建立力学系统模型的一般步骤如下:1. 确定物体的自由度:自由度是指描述物体运动所需的最少广义坐标数目。
通过确定物体的约束条件和自由度的数量,可以确定力学系统的自由度。
2. 建立拉格朗日函数或哈密顿函数:根据力学系统的特点和约束条件,可以建立拉格朗日函数或哈密顿函数。
拉格朗日函数是广义坐标、广义速度和时间的函数,而哈密顿函数则是广义坐标、广义动量和时间的函数。
3. 利用变分原理得到运动方程:通过应用变分原理,可以得到力学系统的运动方程。
对于拉格朗日力学,可以利用哈密顿原理或达朗贝尔原理得到运动方程;而对于哈密顿力学,可以通过哈密顿原理和正则方程来确定运动方程。
4. 求解运动方程:根据得到的运动方程,可以采用数值方法或解析方法求解。
对于简单的力学系统,可以通过解析方法得到解析解;对于复杂的力学系统,通常需要借助数值方法进行模拟和计算。
四、力学系统模型建立的应用力学系统模型建立在力学研究中具有广泛的应用。
以下是一些典型的应用领域:1. 物体的运动分析:通过建立力学系统模型,可以研究物体在不同外力作用下的运动规律,如运动的速度、加速度、轨迹等。
建立系统科学基础理论框架的一种可能途径与若干具体思路(之六)――拉格朗日函数、作用量、最小作

2002年12月系统工程理论与实践第12期 文章编号:100026788(2002)1220001214建立系统科学基础理论框架的一种可能途径与若干具体思路(之六)——拉格朗日函数、作用量、最小作用量原理的物理意义与我国传统文化元典精神内涵的一致性范文涛1,丁义明1,龚小庆2(1.中国科学院物理与数学研究所,湖北武汉430071;2.杭州商学院统计与计算机学院,浙江杭州310035)摘要: 本文是总题目下的第六篇Λ全文的总目的是试图从现代物理、分子生物学与脑神经解剖等学科领域的最新实验事实,以及相应的前沿理论领域围绕着演化概念研究的展开所获得的已有理念与成就为基础,按照“由大爆炸理论所描述的物理世界之最初情景出现以来,世界物质总是在其不同时空点具体结构状态下的几种基本相互作用属性形成的制约机械造成的物质——能量结构与分布仍非完全平衡态势的推动下,不断地一层一层完成其全方位整体性进一步精细平衡结构,实现其该层次从无序到有序的起伏演化——这一总体自然法则”的认识主线,提出一种建立系统科学基础理论的定性定量框架思路与若干细节方法Λ文中对相互作用、进化、演化、适应性与复杂性等概念进行了分析,对突变、分歧、吸引子、混沌、协同、分形等基于此种理论作了一种较为直观的诠释Λ同时,也将论及所谓信息的本质与其人本意义下的价值概念,特别是她与非线性的密切关系等Λ当然,这一切均还是初步的,尽管其中的一部分我们也已经获得了一些较为严谨的结果Λ关键词: 系统科学基础理论;框架;演化;精细平衡中图分类号: N94 文献标识码: A A Po ssib le A pp roach to the F ram ew o rk of theFundam en tal T heo ry of System Science:Part SixFAN W en2tao1,D I N G Y i2m ing1,GON G X iao2qing2(1.W uhan In stitu te of Physics and M athem atics,Ch inese A cadem y of Sciences,W uhan430071,Ch ina;2.Co llage of Statistics and Compu ting Science,H angzhou U n iversity of Comm erce,H angzhou310035,Ch ina)Abstract: A qualitative and quan titative fram ew o rk fo r the fundam en tal theo ry of system sciences asw ell as som e details is given on the basis of som e new experi m en tal evidences,ideas and ach ievem en tsconcern ing evo lu ti on in m any fields such as modern physics,mo lecu le b i o logy and b rain anatom y,etc.Som e concep ts such as in teracti on,evo lu ti on,adap tab ility,and comp lex ity are discu ssed.In tu iti onalanno tati on s abou t catastrophe,b ifu rcati on,attracto r,chao s,fractal and synergy are also given.T heessence and the value of info rm ati on,and the clo sed relati on betw een info rm ati on and non linearity areinvestigated.It is no doub t that all the w o rk s are to be con sidered in detail,although w e have som erigo rou s resu lts in particu lar step s.It is the six th part of the paper.T he physical m ean ings of the L agrange functi on,acti on,and the least acti on p rinci p le and their con sistency w ith sp irits of the classical book s of Ch inese traditi onalcu ltu re are discu ssed.Key words: fundam en tal theo ry of system sciences;fram ew o rk;evo lu ti on;equ ivalence 如本文的主标题所述,我们将在系列文章之五的基础上,从论述与拉氏函数、作用量有关的力、功、能收稿日期:2002211219资助项目:国家自然科学基金(60174048,70271076) 作者简介:范文涛(1938—),男,湖北仙桃人,研究员,研究方向:系统科学基础理论及应用量等概念的物理意义出发,进而给出作用量,特别是最小作用量原理的物理意义及结构性内涵,然后转入阐述:在更一般的系统科学的观点下,原在物理学的范围内熟悉的这些概念、原理、意义等,其实在我国传统文化与学术的元典(主要的经典)文献中亦已以自身的语言,扼要、简明、独特的定性形式表述并运用过了;而且,直到现在,仍然在显现其系统、深刻、质朴、原汁原味的真善美一体化的整体特征,完全与从来自物理学和其它学科的对宇宙物质质2能演化过程中不同层次与各层次间物质的相互作用或适应(磨合一直牵引到各层次内、层次间所有局部尽可能比较平衡、协调的稳定结合状态或者人类社会事务(内部及其间)结合演变过程的自在统一规律,不仅具有一致性,而且更显示出其提纲擎领:不仅可认为它是对于社会经济系统的类似于物理系统的同一理念、内涵的社会经济意义的同一性表述,且本质上已是整个系统科学意义下的基本的概念与规律的定性刻划Λ这是因为,不仅是在建立系统科学或复杂性研究基础理论的逻辑性的阐述过程中我们已经严格地证明了物理系统与事理系统的(在所指意义下的)等价性,而且从人类认识这些规律的定量表述的全过程而言,它也是出现在此之前的Λ我们将分段来说明这一根本的事实Λ1 “力”的物理意义——从“力者形之所以奋也”到牛顿力学以及与相对论力学、统计物理的一些注记作为一个后学者,人们时常觉到,最好是能养成一种尽可能去捕捉现有理论的原发现发明者,创造和推进此种原理质朴思路的思维惯性Λ这往往是非常直觉并明快的,而不可仅满足于教科书与专著中形式化的定义和面对已知结论的形式逻辑演释Λ许多的实发事例使人深信,在原作者的原始创意里,结论是早已在事先被定性地猜测到了的Λ这种猜测的得到,是由某种确定的个例原型自在运动演化过程中的事实启发所致,甚至方式与方法也本质上是来源于原型之某种局部演化机制与定性机理的规定Λ因此,我们需要经常反复地回到那些理论最初的出发点,即最初引发概念的那些基本事实上去(尤其是当新发现一些已有的理论不能解释的新现象时更应如此!),重新审视一下那些基本概念的根基与我们自身的理解是否稳固、真实、正确Λ如不完全精确,则就要求综合新的发现事实,依赖某些理性原则去修改原意下的概念,以获得更为深化的理论与方法Λ此即古人常说的“凡有禁忌,必含真理”的真义Λ比如说从以牛顿力学的第一、第二定律为主要内容的牛顿理论到分析力学的两大基本原理,以及相对论力学对它自身的修正,就是这样一步一步走过来的Λ牛顿力学即是上述所有一切等价性原理的最初出发点Λ牛顿理论的结论既然是以位移矢(r →)从而伴生出速度矢(v →=d r →d t )、加速度矢(a ο=d 2r →d t 2)…等来观测决定运动的原因——力的矢量值(F ψ),则由此而提出的第二定律F ψ=m a ο以及矢量合成的平行四边法则一起就已经构成了一个总的封闭理论框架Ζ我们可以毫不含糊地指出,牛顿的这一以第二定律表示的模式与春秋战国时期墨子曾定性地表述的“力者形之所以奋也”——或翻成白话语说,力是有形的物体产生加速度的原因——这一定性的表述的内涵,完全不多不少地等同Ζ因为,“形之所以奋也”的“奋”是奋,而不是动;奋就是加速度(a ο)Ζ同时这句话本身也最清楚不过地给出了“力”概念的物理意义Ζ这种表述方式也再一次显示了我国传统文化与学术文献中对理论事物描述的特色——即通常对概念进行定义(取名)时,都是要把它最本质的内涵一起统一地表述在一个方式之中,甚至在怎么做的方法上也会同时给予明确的提示Ζ现在再来看看牛顿力学框架中的第二定律Ζ不难看出,当达朗贝尔提出把m a ο理解为惯性力之后,此式又具有按牛顿第一定律所表的与F ψ(原作用力)相平衡的物理意义Ζ因而,我们又何尝不可以把第一定律看作是第二定律的广义的定性模式,并从而可以把它们看作是一个定律Ζ这一定律不仅是牛顿力学的基础,同时也是相对论力学的基础Ζ这是因为,式中的F ψ,按物理学,它是在不同的具体条件下另行给出的;而相对论力学,它只是说了在运动物质的速度v ο接近光速时,坐标与时间均应按洛伦兹变换予以修正,然后把这种修正的变换引入牛顿第二定律,也就又得到了相应的相对论力2系统工程理论与实践2002年12月学的基础Ζ虽然说牛顿第二定律作为其定性原理的定量模式的最早提出,是以三维实空间的物质运动为背景的,其定性模式作为对于一般多维空间的力与系统运动状态之间的关系的陈述也未必不真Ζ也就是说,这一原理对于一般可概括为相互作用或者进而引伸到相互适应(或磨合等)的条件环境下也应当是正确的Ζ这只需把这种相互作用或适应同样看作是以一种“力”的平衡与转化过程就可以了Ζ而这一工作的真实性,我们的前人早已经做过了Ζ可以认为,分析力学的全部,就是在干这一件事的Ζ只是它在相关的诸概念的量化表现上均冠以了“广义”两个字而已Ζ显然这在概念上是一个非常本质的飞跃,而且在其整个的理论阐述中根本就没有涉及到线性与非线性的区别Ζ它也应当可以被理解为是一般系统框架理论的统一基础Ζ这一点可以认为已为力学作为一个广义的研究实体的发展史所证实Ζ而上述的“等价性”则又可使我们有理由也把它看成是系统科学的基本框架的一部分;并因后者所涉及的范围的对象更为广泛,故还需对之作进一步的引伸与发展Ζ这主要是因为在本系列文章之二所述的总框架中,当系统包涵人和人类社会这一具有认识主体或主观性环节的子系统时,其决2对策问题不仅应遵从一般的优化原理,同时还需要考虑这类系统形成整体协调与精细平衡的各种可能的具体机制Ζ有意思的是,有关这一类问题的解决,我们的祖先早自春秋战国时期开始,就不仅已经创造和集累了丰富的经验,并业已形成了分别由孔孟的《大学》、《中庸》和老子的《道德经》所表述的“道”及其伴生的诸如“不战而屈人之兵”一类的所谓“奇正理论”、“和文化”等为代表的一系列博大精深的成就(表述这些并指出它们与物理学原理的一致性将是本文的主要目标之一,具体内容见第三四节中的系统论述)Ζ近十余年来,又由我国学者王先甲、罗晓、郭文革、金武等对之所作的定量刻画,提出了一整套称之为具有激励机制的多人多目标的谈判、协商、仲裁等决2对策的定量分析模型与相应求解算法Ζ此外,贾雨文等还从另一角度对之进行了表述与应用的相关研究Ζ陈光亚、汪寿阳等也在单多目标决2对策与相关运筹学领域的优化理论和算法的等价问题上取得了一系列深刻且统一性很强的结果;特别是陈光亚在优化理论与算法上所获得的更为深刻而本质的进展,更为现有几方面工作的相互融合与进一步地面向自然与现实社会性的决2对策系统研究和应用工作的开展打下了更为坚实的基础Ζ现在,我们再对吉布斯的统计物理学作一点心得性的注记Ζ有学者认为,牛顿力学的确建立了描述宇宙物质宏观规律的完整理论基础,但玻尔兹曼2吉布斯的统计物理学则对揭示宇宙物质运动从无序到有序演化发展的奥秘更为有益Ζ这是因为,这一理论不仅直接从如何把握宇宙物质的宏观规律及其微观形成机制的关联入手,提出了一种极具洞察力的定性思路,而且也严谨地建立了一个从事物的微观运动机制有效计算其宏观测量值的统一理论Ζ虽然说,普里高津的耗散结构论与哈肯的协同学的思想也是很深刻的,但毕竟是只要弄清了非线性系统的稳定平衡态是与其非线性相互作用的阶数相联系的事实即可以由统计物理学自然延伸出来的Ζ我们认为,玻尔兹曼2吉布斯统计物理学的基本思路与原理对我们今后的工作,同样具有基础性的意义,只有自始至终地把握其基本的思想脉膊,并将极大极小的原理引入其间使之进一步推广,方可不致迷失业已选择的工作方向Ζ看来,这样的估计是不致过分的Ζ2 功、能、动量、拉格朗日函数、作用量与最小作用量原理等概念的物理意义我们先从能量传递的具体机制出发,分析一下物质相互作用的情景,看看“能”的物理意义Ζ“能”是相互作用的一方对另一方或几方作功的本领Ζ正如力被解释为是被作用方产生加速度的原因一样,在某种程度上都可认为是物质相互作用因素的抽象Ζ能与力一样是动力学的概念,它们是通过本身可测量的运动学的概念——速度、加速度和位移来表征的Ζ我们来考虑力与能的关系Ζ从物理学已知,力与能(势)是紧密相关的Ζ在有势场中,力可表示为势的负梯度:F =-grad v ο=-5V 5x i +5V 5y +5V 5zk 又,力也等于物体的质量与它的加速度之积F ψ=m a ο=m d 2r →d t 23第12期建立系统科学基础理论框架的一种可能途径与若干具体思路(之六)也就是说有-grad v ο=F ψ=m d 2r →d t 2=d (m v ο)d t 这里的后一个等式又说明力可以通过动量的改变率来表征Ζ把这些关系联系起来,就是力是由于势能减少传递给系统的物体,使它们加速运动这件事的抽象Ζ同时,而由于力的作用导致的运动又使物体具有了动能Ζ势能就是这样转化为动能的Ζ这个动能又可说成是系统对物体作了功的结果Ζ这是由于功d W =F ・d r →Ζ可见功乃是力作用沿空间积累的效果的量度Ζ我们再看看,力F ψ=d (m v ο)d t 或者动量m v ο=∫F ψd t 这又说明,动量可以解释为力在时间上累积效果的量度Ζ因此我们说,功与动量是系统的势能在时间和空间中变化表现出来的运动之依赖于时间与空间的两个不可分割的度量Ζ而系统对外界的作用,又是以物体对外界传递动能(如碰撞)、动量而作功来实现的Ζ这个接受了作功的外界,又引起它的物质的运动,改变其动能,并把一部分能量消耗于位移而作为它的势能储藏起来Ζ但是,在这种传递的过程中,如果把作用的双方或多方都算进来而成为一个保守系统的话,动能与势能的总和又是不变的Ζ否则,运动就根本没有什么规律可循了Ζ比如说,那样一来,作为整个系统的自由能的作用量就不能在任何一个时间过程中总是维持最小Ζ事实上,我们可以把能量守恒和最小作用量原理互为前提进行推导Ζ若其中之一不能成立的话,则另一个也自然瓦解Ζ刚才的这段分析是选用直角坐标系为背景叙述的,并且较多地利用了力学术语Ζ实际上对于广义坐标系也可以完全同样地予以论述,仅只须用广义力去代替一般的力就行了Ζ这本来是只要我们把某一种参数理解为位置值,把它的时间导数理解为速度等就可以办到的Ζ我们已经多次指出过,特性参数,只不过是决定系统性质的一些因素而己Ζ它们相当于坐标位置值、速度或动量等Ζ只要我们在最本质的意义——相互作用的意义下去理解功、能、力……等,我们就不管对什么系统(力学的,电的,机电的,化工的,甚至社会经济的,……),也不管是那一个广义坐标系,都讲得通Ζ比如,热工人员用温度和熵那样的变量描写热力学系统;航空学上讨论飞机的稳定性时,谈到飞行转矩和飞行角;电气工程师为了描写电路的性状,用到电压和电流;而化学则用化学势和克分子量这些名词Ζ实际上,可以使用同一概念来研究这些不同的物理系统Ζ如果在上述的各种具体系统里,用f i 表示前一个变数,而用q i 表示后一个变数,那么不管系统的本质如何,总能够写出d W i =f i d q i式中,d W i 表示能量方面由于q i 方面的变化d q i 所引起的微分改变量,f i 和q i 这两个变数就是广义变数,上面的乘积在上述各个情况里都可描述为能量关系Ζ也就是说,都相当于前面讲到的关系d W =F ψ d rο 现在我们来看看系统的拉格朗日函数、作用量与最小作用量原理的“物理意义”Ζ如我们已知,当局限于保守系统时,拉氏函数即为动势能差:系统的总动能减去它的总势能Ζ而对于非保守系,也就是处于某一外场中的系统,或者说是某一保守系的一部分时,它的拉格朗日函数可以从包括了它为一方的保守系的拉氏函数得来Ζ显然,系统的运动是组成系统的物质间的互相作用的外在表现Ζ动能是运动着的物体所携带的能量,它的特别之处是,一旦它与别的物体作用,它就能够把这种能量传递给别的物体Ζ实际上动能作为能量来说,被加上“动”的原因仅此而已Ζ势能是构成系统的物体在现时的状态下所储藏的能量,它的表现是一旦系统走向动的过程,它就可以按一定方式用之于“武装”它的各部分物质Ζ势能储备的来源是在它本身形成的过程中,由外界对它做功的结果Ζ它的值应当相当于外界把它从“绝对自由”的状态约束到现存状态所做功的值,或者等于把它从现存状态与外界“不产生能量变换”地拆散到“绝对自由”地没约束状态(即解除约束)所应花的能量代价Ζ而动势能差,也就是拉氏函数L =T -V ,就是把系统从现存的状态复旧到4系统工程理论与实践2002年12月绝对的状态后,原组成的物质还剩下的能量的总和Ζ这种能可以理解为一种“自由能”Ζ它的值等于系统物质在解除约束后,可自由作功的本领Ζ这就是拉格朗日函数的物理实质Ζ然而,系统的这种解除或者建立过程不可能是在一个瞬时完成的,它只能在时间的过程中进行Ζ因此,拉氏函数还只是自由能的时间密度Ζ我们要考虑从时间t 1到t 2期间解除或建立某一系统的自由能的大小时,就应当对时间来积分这个自由能的时间密度——拉格朗日函数Ζ也就是说,用S =∫t 2t 1L d t 来衡量,而这就是我们所说的作用量Ζ所以,通常所说的作用量积分乃是在[t 1,t 2](积分区间)内拆散或者建立这个约束系统后,这个系统的全部物质所剩下的,或者原有的(对于建立此系统而言)动能——作功或者对它之外的物质作用的全部本领(能)Ζ而这也正是把它称之为“作用量”的由来Ζ这样一来,所谓最小作用量原理的意义就可以表述为:对于一个封闭系统来说,系统在运动发展过程中所走的自然轨迹(指在相空间描述时的真实路径)总是按照要使得除了系统建立(或者反过来从某时刻起解除约束使系统诸单位元复归于自由状态)所耗费的能量(可称为结构能耗)之外,各单元所剩下的总和能——它们可自身独立支配用于新的相互作用者——即自由能为最小的原则去实现的Ζ也就是说,系统中每一部分物质均无一例外地运动特点是:要在此系统整个的存在期间都是以尽可能使约束能(势)减少、整体动能增大的方式进行着相互作用(或称呈相互关系——或构架结构——或磨合),一直达到其总结构能(势能)值趋于极小的绝对“稳定”状态,且尽可能在此状态稳定平衡下去Ζ这个稳定态就是所谓的“最优化状态”;在不要求其自然(自动)稳定,比如有办法以“动态平衡”实现其稳定时,也可称之为“标称态”——指定的稳定平衡态Ζ这一稳定态是由最优控制理论选择最优控制参矢量的优化值(或者说,环境参矢量的优化值)去实现的Ζ顺便指出,一旦这个值被固定(或者说截断),即是实际上又构成了一个由原被控制系统再加上可维持此截断值的控制系统的新的保守系统了Ζ而这也就是保守系统或闭系统与控制系统或开系统之间的区别与关联的辩证关系Ζ正是基于这一分析,我们就可以认为,如同人工系统一样,“自然界或者说物理系统也具有目的性”Ζ即只有系统整体——包括系统的每一个部分在每一段时间内,它们全都是处于全力“奋斗”的“工作状态”时,才能使得整个系统达到整体的稳定平衡态——即总的势能取极小值的结构状态Ζ系统的真实轨迹就是按这一机制形成的Ζ这就证明了前面已述的一个基本事实:即一切物理系统尽管其本质大不相同,但有一个基本的类同点和共同的数学形象;这个共同的数学形象就是我们所一再讲过的最小作用量原理Ζ以上就是我们对于拉格朗日函数、作用量、最小作用量原理以及功、能、力、动量等基本概念的物理意义和系统通过能量传递进行相互作用的具体机制的分析Ζ我们已经提到过,这种以最小作用量原理为规律的物理系统可以被看作是一个要求作用量最小的自然最优控制问题Ζ由于它的运动方程可以仅由要求作用量——这个特殊的控制指标——最小而经由已知的求变分极值的变分法得到,于是就不仅为解决同类问题打通了思路,并且也提供了方法Ζ我们已经说过,数学理论只有被用于可以看作是它的自然原型的相应实际对象时,它才是有效的Ζ当然,我们也可由一种实际原型问题的规律的详细了解,借助于包含了它作为具体原型之一的抽象形式而去由此及彼Ζ这种背景和思想被相当自然地用到了控制论科学Ζ庞特里雅金处理最优控制问题的最大值原理实际上就是这样得来的Ζ只不过问题是反过来提罢了Ζ系统控制问题与自然系统的不同仅在于相当于作用量的控制指标是“人为”规定的Ζ但是要使这个“人为”的指标最小,各参数应满足的方程同样可以由变分法求函极值的办法去寻求Ζ我们的控制任务只不过是要掌握一组变动的控制参量,并保证这种关系被满足而已Ζ假想这些控制参数的规律已被求得的话,难道不是和自然系统时的其它参数一样吗?这样一来,整个对自然系统适用的理论和思想就当然地可以搬到控制系统上去了,而这正是我们曾在最优控制的那部分理论中所看到的情况的思想实质Ζ我们还在本系列文章的前文中说过,最小作用量原理与可能位移原理都是从动的角度处理相对稳定的对象(平稳点和真实轨道),是把对象的真实状态从可能的多种状态中挑选出来Ζ按照我们前面已经具体叙述过的方式还可看出,最小作用量原理可认为已隐含在可能位移原理(考虑5第12期建立系统科学基础理论框架的一种可能途径与若干具体思路(之六)6系统工程理论与实践2002年12月到惯性力存在的可能位移原理)之中了Ζ在某些假设条件之下,它们可以互为因果Ζ而从数学观点来看,二者只不过是同一原理的微分表写与积分表写而已Ζ然而,不管是哪种形式,它们都反映了本质的东西,所以都可作为推导运动规律亦即运动方程的出发点Ζ3 我国传统文化、学术元典精神内涵与“最小作用量原理”的一致性(I)——对我国传统文化与学术元典精神内涵的一个归纳性概述在本文第1节的末尾我们曾一般地就本节的主题内容作了一个提纲性表述和给出了与此有关的一些定量化的理论研究结果Ζ这里与下一节将主要并且较为理性化的讨论上文所说的“一致性”的主旨内容Ζ在此明确地说明,至少在原则上讲,均是可以从定性的结果做到不同程度的定量或者定性定量相结合的描述的Ζ因为整个阐述过程,我们所遵循的是如同以自然的物理系统为对象时,使用的那些理性原则实际上是完全一样的,不同的只不过使用的是较朴实的自然语言而已Ζ下面,我们仅依次以源出于春秋战国史期的儒家与道家以及尔后自印度传入的佛家三种主流学说,又经近3000年的相互渗透交融互补形成的各自体系要点的简述以完成本文亟待阐明的一些观点与内容Ζ为了紧扣本文的主题,我们也将在论述的过程中,不时地使用一些系统科学意义下的解注Ζ首先是儒家学说Ζ概括而言,她是在以漫长的史前文明期间我国先民、先祖在生存与发展的斗争实践中积累的成败经验,当时已形成的自给自足的自然经济及相应技术生产力的基础条件下,提出的为建立一种以家庭和部落作为基本单元子系统,与相对分散和较为松散的集中控制相结合(从而也相对封闭可解耦)的组建体制结合而成的社会2伦理2生态2经济2政治管理系统的思想理论方法体系Ζ这时的国家其实是一种家庭——氏族体系的放大,其总体目标往往在外型上表现为某种家长式的独断特征,所谓“天下之民,莫非王臣,率土之滨,莫非王土”,古人“三月无君则吊”、“三日无君则惶惶如也”就是这一特征的的集中表现;同时,总目标的另一面也包含一些为维持其“子民”的基本生存需要乃至生态环境保护等的“新民(即亲民之意)”准则,以及孟子的“民贵、君轻,社稷为重”等共同组成其总体目标体系Ζ系统的理想运行状况则由“君君、臣臣、父父、子子(义即君要像个君样,臣要像个臣样,父要像个父样,子要像个子样)”以及“生有所养,死有所葬”,“老者安之,少者怀之,朋友信之”或者按《礼运》大同篇的说法,“天下为公,选贤与能,讲信修睦”,“人不独亲其亲,不独子其子……老有所终,壮有所用,幼有所长,鳏寡孤独废疾者皆有所养,男有分,女有归,货恶其充于地也,不必藏于己,力恶其不出于身也,不必为己,是故谋闭而不兴,盗窃乱贼而不作”,“外户而不闭”等一系列定性的目标准则的描述所刻画Ζ当然,这是一种理想的说法Ζ它的设计,应当说最早是以孔孟为代表的儒学创始人及其稍后的门徒——王霸兼济的法家代表人物韩非、晁错、贾谊等的集体初创,后又经王弼,朱熹及其老师程颐、程灏兄弟、张载等融合佛学与老庄的道学精华逐步完善而成Ζ儒学的较后期的代表人物之一张载曾明确地总结说,建立这一学说宗旨的世界与人生观是:“为天地立心,为生民请命,为往圣继绝学,为万世开太平”Ζ这也是对古往今来国际国内所有优秀学术与文化工作者的共有价值观念最完美的概括Ζ为了实现这一宗旨,他们提出了常被今人称之为整体论的所谓“天人合一”,即把“天道”与“人道”看成是一个统一的道——规律,或者,自然与人类社会乃至每一个人的行为,均应是遵从统一的法则和规范;并针对“天道”与“人道”分别提出了“中庸之道”与“忠恕之道”作为其学说的基本理论核心Ζ对此,本应该是大书特书的,但为篇幅计,这里只将手头已有的关于中庸之道的“天人合一”与“忠恕之道”的两个表解图1、图2,谨附于此,以便仁者见仁,智者见智Ζ顺此仅就“忠恕之道”作一点注释Ζ孟子曾说“(孔)夫子之道,忠恕而已矣”,可见它是儒家学者们一个纲领性概念Ζ这里的“忠”应以“中”指导自身的思想行为的决策主体——“心”(即现人说的大脑),而“中”,按《中庸》的直解为——“不偏谓之中,不倚谓之庸”,则是强调不偏离客观自在规律之谓Ζ故有人将忠解释为是讲人们在对待整体利益方面的做人的道理,即从爱己、修(养)己、尽己(之力)以行仁义之道,以治己之心而治人,一直达到自忠心、忠仁、忠家、忠国、忠社(会)以至于达到忠于天下的境界Ζ而“恕”作“如心”解,即遇事应从他人之心(别人的角度)想一想,(亦即现代人说的易位思考之意),是讲爱人、安人、成物、成事、。
第二章 用拉格朗日方程建立系统数学模型

第二章 用拉格朗日方程建立系统的数学模型§2.1概述拉格朗日方程——属于能量法,推导中使用标量,直接对整个系统建模 特点:列式简洁、考虑全面、建模容易、过程规范适合于线性系统也适合于非线性系统,适合于保守系统,也适合于非保守系统。
§2.2拉格朗日方程1. 哈密尔顿原理 系统总动能),,,,,,,(321321N n q q q qq q q q T T = (2-1)系统总势能),,,,(321t q q q q U U N =(2-2)非保守力的虚功N N nc q Q q Q q Q W δδδδ ++=2211(2-3)哈密尔顿原理的数学描述:0)(2121=+-⎰⎰t t nc t t dt W dt U T δδ (2-4)2. 拉格朗日方程: 拉格朗日方程的表达式:),3,2,1()(N i Q q Uq T q T dt d iii i ==∂∂+∂∂-∂∂ (2-5)(推导:)将系统总动能、总势能和非保守力的虚功的表达式代入哈密尔顿原理式中(变分驻值原理),有0)(221122112211221121=+++∂∂-∂∂-∂∂-∂∂++∂∂+∂∂+∂∂+∂∂+∂∂⎰dt q Q q Q q Q q q Tq q U q q U q qTq q T q q T q q T q q T q q T N N N NN N N N t t δδδδδδδδδδδδ (2-6)利用分步积分dt q q Tdt d q qT dt q q T i t t i t t i i i t t i δδδ⎰⎰∂∂-∂∂=∂∂212121)(][ (2-7)并注意到端点不变分(端点变分为零)0)()(21==t q t q i i δδ (2-8)故dt q q T dt d dt q qTi i t t i t t i δδ)(2121∂∂-=∂∂⎰⎰(2-9)从而有0)])([211=+∂∂-∂∂+∂∂-⎰∑=dt q Q q Uq T q T dt d i i it t i i Ni δ ( (2-10)由变分学原理的基本引理:(设 n 维向量函数M(t),在区间],[0f t t 内处处连续,在],[0f t t 内具有二阶连续导数,在f t t ,0处为零,并对任意选取的n 维向量函数)(t η,有⎰=ft t T dt t M t 00)()(η则在整个区间],[0f t t 内,有 0)(≡t M )我们可以得到:0)(=+∂∂-∂∂+∂∂-i ii i Q q U q T q T dt d (2-11)即i ii i Q q U q T q T dt d =∂∂+∂∂-∂∂)( (2-12)对非保守系统,阻尼力是一种典型的非保守力,如果采用线性粘性阻尼模型,则阻尼力与广义速度}{q成正比,在这种情况下,可引入瑞利耗散(耗能)函数D ,}]{[}{21q C q D T≡ (2-13) 阻尼力产生的广义非保守力为:i i qDQ ∂∂-= (2-14) 对于仅受有势力和线性阻尼力作用的系统,其拉格朗日方程为:0)(=∂∂+∂∂+∂∂-∂∂qD q U q T q T dt d i i i (2-15) 如果系统上还作用了除有势力和阻尼力以外的非保守力,如结构受到的外激励力(对应的广义非保守力可通过非保守力的虚功求得,仍记为i Q ),则系统的拉格朗日方程为:i i i i Q qD q U q T q T dt d =∂∂+∂∂+∂∂-∂∂ )( (2-16) §2.3 拉格朗日方程在振动系统建模中应用在某些结构振动问题中,取分离体、确定各分离体的受力情况,然后利用牛顿第二定律建立方程的方法不一定可用,或者很不方便,这时,采用拉格朗日方程来建立振动方程就很方便。
第2章拉格朗日方程

1813年4月3日,拿破仑授予他帝国大十字勋章,但此时的拉格朗日已卧床不起,4月11日早晨,拉格朗日逝世。
拉格朗日科学研究所涉及的领域极其广泛。他在数学上最突出的贡献是使数学分析与几何与力学脱离开来,使数学的独立性更为清楚, 从此数学不再仅仅是其他学科的工具。
拉格朗日总结了18世纪的数学成果,同时又为19世纪的数学研究开辟了道路,堪称法国最杰出的数学大师。同时,他的关于月球 运动(三体问题)、行星运动、轨道计算、两个不动中心问题、流体力学等方面的成果,在使天文学力学化、力学分析化上,也起到了 历史性的作用,促进了力学和天体力学的进一步发展,成为这些领域的开创性或奠基性研究。
1764年,法国科学院悬赏征文,要求用万有引力解释月球天平动问题,他的研究获奖。接着又成功地运用微 分方程理论和近似解法研究了科学院提出的一个复杂的六体问题(木星的四个卫星的运动问题),为此又一次于 1766年获奖。
1766年德国的腓特烈大帝向拉格朗日发出邀请时说,在“欧洲最大的王”的宫廷中应有“欧洲最大的数学 家”。于是他应邀前往柏林,任普鲁士科学院数学部主任,居住达20年之久,开始了他一生科学研究的鼎盛时期。 在此期间,他完成了《分析力学》一书,这是牛顿之后的一部重要的经典力学著作。书中运用变分原理和分析的 方法,建立起完整和谐的力学体系,使力学分析化了。他在序言中宣称:力学已经成为分析的一个分支。
清华大学本校用理论力学课件8-1第二类拉格朗日方程

第二类拉格朗日方程
2019年2月21日
广义坐标中的达伦伯-拉格朗日原理
第 8章
第 二 类 拉 格 朗 日 方 程 及 其 应 用
理想完整约束系统:广义坐标为q1, q2, …, qN
质点i矢径: ri ri ( q1 , q2 ,
, qN , t )
n i 1
n
ri ri qk qk k 1
Qk Q 0
* k
T d Q dt qk
* k
T q k
V 如主动力都是有势力: Qk qk
d T dt qk T V q qk k
d T dt qk
T q Qk , k 1,2, k
O
y x R
R
m
L ( J mR 2 sin 2 )
d L ( J mR2 sin2 ) 2mR2 sin cos dt
例4
解
第 8章
第 二 类 拉 格 朗 日 方 程 及 其 应 用
d L L Q dt
第 二 类 拉 格 朗 日 方 程 及 其 应 用
应用拉格朗日方程的解题步骤为 判断系统是否为完整约束,主动力是否 有势,以决定能否应用拉格朗日方程以 及应用何种形式的拉格朗日方程。 确定系统的自由度数,选择合适的广义 坐标。
按所选的广义坐标,写出系统动能、势 能或广义力。
把动能、广义力或拉格朗日函数代入拉格 朗日方程。
n n d 1 1 2 2 mi ri mi ri dt qk i 1 2 qk i 1 2
拉格朗日方程

q
,
1,2,, s
(2.7) (2.8)
将(2.8)式代入(2.6)式:
n
( Fi
i 1
mi
ri
).
s 1
ri q
q
sn [ (Fi
1 i1
mi
ri
).
ri q
]q
0
因 q 是独立的,所以
n
i1
第2章 拉格朗日方程
内容: • 基本概念 • 理想完整系的拉格朗日方程 • 对称性和守恒定律
重点: 完整保守系的拉格朗日方程 难点: 拉格朗日方程的推导
牛顿力学理论几乎都以力 F 为基础,因此它的应用只局限于纯力 学问题的范畴,运算也比较烦琐。18世纪伯努利、达朗贝尔、欧拉 等人发展了经典力学的分析形式。1788年拉格朗日发表了名著《分 析力学》,建立了经典力学的拉格朗日形式,用体系的动能和势能 取代了牛顿形式的加速度和力,将力学的研究和应用范围开拓到整 个物理学。
n i 1
T
ri
.
ri q
n i 1
mi ri
.
ri q
(2.13)
T
q
n i 1
T ri
.
ri q
n i 1
mi
ri
.
ri q
(2.14)
将(2.13)式、(2.14)式代入(2.11)式:
n miri .
dr
r
P
图2.1
(2)理想约束
wi
设F质Ni 点.,rii受若到整的个约体束系力的为虚功FN,i 力
FN在i 虚位移
拉格朗日和哈密尔顿力学建模

拉格朗日和哈密尔顿力学建模
拉格朗日和哈密尔顿力学是理论力学中非常重要的两个分支,它们都是用来描述物理系统的运动的。
拉格朗日力学建立在能量原理的基础上,通过定义一个称为拉格朗日量的函数来描述系统的动力学。
这个函数包含了系统的动能和势能,并且可以通过求解欧拉-拉格朗
日方程来得到系统的运动方程。
哈密尔顿力学则是建立在哈密尔顿原理的基础上,通过定义一个称为哈密尔顿量的函数来描述系统的动力学。
这个函数包含了系统的动能和势能,并且可以通过求解哈密尔顿方程来得到系统的运动方程。
在实际应用中,拉格朗日和哈密尔顿力学都可以用来建模各种物理系统,包括机械系统、电磁系统、量子系统等。
它们被广泛应用于天体力学、固体力学、流体力学、电动力学、热力学、量子力学等领域。
在建模过程中,需要确定系统的自由度、广义坐标和广义速度,以及系统的拉格朗日量或哈密尔顿量。
通过求解欧拉-拉格朗日方程
或哈密尔顿方程,可以得到系统的运动方程和各种物理量随时间的变化规律。
总的来说,拉格朗日和哈密尔顿力学是理论力学中非常重要的工具,它们的应用在科学研究和工程实践中都发挥着重要作用。
- 1 -。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章 用拉格朗日方程建立系统的数学模型§2.1概述拉格朗日方程——属于能量法,推导中使用标量,直接对整个系统建模 特点:列式简洁、考虑全面、建模容易、过程规范适合于线性系统也适合于非线性系统,适合于保守系统,也适合于非保守系统。
§2.2拉格朗日方程1. 哈密尔顿原理 系统总动能),,,,,,,(321321N n q q q qq q q q T T = (2-1)系统总势能),,,,(321t q q q q U U N =(2-2)非保守力的虚功N N nc q Q q Q q Q W δδδδ ++=2211(2-3)哈密尔顿原理的数学描述:0)(2121=+-⎰⎰t t nc t t dt W dt U T δδ (2-4)2. 拉格朗日方程: 拉格朗日方程的表达式:),3,2,1()(N i Q q Uq T q T dt d iii i ==∂∂+∂∂-∂∂ (2-5)(推导:)将系统总动能、总势能和非保守力的虚功的表达式代入哈密尔顿原理式中(变分驻值原理),有0)(221122112211221121=+++∂∂-∂∂-∂∂-∂∂++∂∂+∂∂+∂∂+∂∂+∂∂⎰dt q Q q Q q Q q q Tq q U q q U q qTq q T q q T q q T q q T q q T N N N NN N N N t t δδδδδδδδδδδδ (2-6)利用分步积分dt q q Tdt d q q T dt q q T i t t it t i i i t t i δδδ⎰⎰∂∂-∂∂=∂∂212121)(][ (2-7)并注意到端点不变分(端点变分为零)0)()(21==t q t q i i δδ (2-8)故dt q q T dt d dt q qTi i t t i t t i δδ)(2121∂∂-=∂∂⎰⎰(2-9)从而有0)])([211=+∂∂-∂∂+∂∂-⎰∑=dt q Q q Uq T q T dt d i i it t i i Ni δ ( (2-10)由变分学原理的基本引理:(设 n 维向量函数M(t),在区间],[0f t t 内处处连续,在],[0f t t 内具有二阶连续导数,在f t t ,0处为零,并对任意选取的n 维向量函数)(t η,有⎰=ft t T dt t M t 00)()(η则在整个区间],[0f t t 内,有 0)(≡t M )我们可以得到:0)(=+∂∂-∂∂+∂∂-i ii i Q q U q T q T dt d (2-11)即i ii i Q q U q T q T dt d =∂∂+∂∂-∂∂)( (2-12)对非保守系统,阻尼力是一种典型的非保守力,如果采用线性粘性阻尼模型,则阻尼力与广义速度}{q成正比,在这种情况下,可引入瑞利耗散(耗能)函数D ,}]{[}{21q C q D T ≡ (2-13) 阻尼力产生的广义非保守力为:ii q DQ ∂∂-= (2-14) 对于仅受有势力和线性阻尼力作用的系统,其拉格朗日方程为:0)(=∂∂+∂∂+∂∂-∂∂qD q U q T q T dt d i i i (2-15) 如果系统上还作用了除有势力和阻尼力以外的非保守力,如结构受到的外激励力(对应的广义非保守力可通过非保守力的虚功求得,仍记为i Q ),则系统的拉格朗日方程为:i i i i Q qD q U q T q T dt d =∂∂+∂∂+∂∂-∂∂ )( (2-16) §2.3 拉格朗日方程在振动系统建模中应用在某些结构振动问题中,取分离体、确定各分离体的受力情况,然后利用牛顿第二定律建立方程的方法不一定可用,或者很不方便,这时,采用拉格朗日方程来建立振动方程就很方便。
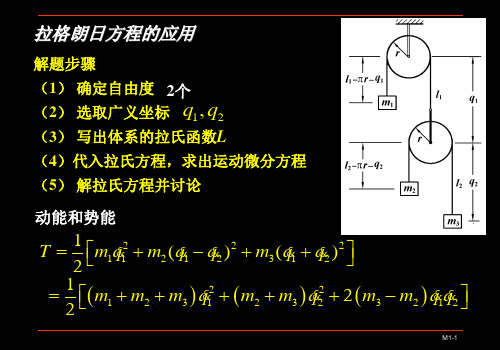
1. 集中参数模型中应用【例】质量为M 的长直杆上有一个集中质量m可在杆上滑动。
杆绕固定点摆动,建立其自由振动方程。
势能θcos ]2[mgu LMgU +-=( 以O 点为势能零点) 动能)(21)31(2122222θθ u u m ML T ++= 选广义坐标为θ,u ,且0=u Q ,0=θQ 代入拉格朗日方程得到:⎪⎩⎪⎨⎧=++++=--0sin ]2[2)31(0cos 222θθθθθm gu L Mg u m u m u ML m g m u um 以上是对离散系统应用拉格朗日方程建立振动方程,如果利用拉格朗日方程建立连续系统的方程,则它是一种同时将系统离散化、变量分离并达到系统降阶的途径。
2. 连续参数模型中应用——与假设模态法联合使用对一维连续系统,假设位移为:)()().(1t q x t x u i Ni i ∑==ψ(2-17)则系统具有N 个自由度,N 个广义坐标为),2,1()(N i t q i =,)(x i ψ不一定是系统的真实模态,可以是假设的一种变形模态。
只要)(x i ψ满足以下条件: (1) 是位移形函数,反映某种可能的位移形状 (2) 构成一组线性无关向量(3) 连续导数阶次满足势能中所要求的阶次 (4) 满足位移边界条件(不一定满足力边界条件) 2.1 杆的纵向振动轴向位移为),(t x u u =dx u A T l)(2120⎰=ρ (2-14) dx u EA U l20)(21⎰'= (2-15)将)()(),(t q x t x u i ii ∑=ψ代得到:}]{[}{2121q M q q q m T Tj i i j ij ==∑∑ (2-18) }]{[}{2121q K q q q k U T ji i j ij ==∑∑ (2-19)其中dx A m j l i ij ψψρ⎰=0dx EA k j li ij ψψ''=⎰0(2-20)分布轴力p(x ,t) 在广义坐标上的虚功i l ii lii q p dx t q x t x p dx t x u t x p W δδψδδ⎰∑⎰∑===0))()()(,(),(),( (2-21)广义力⎰=li i dx x t x p t p 0)(),()(ψ (2-22)代入拉格朗日方程得:i j jijjjijp q k qm =+∑∑ ),2,1(N i =(2-23)或}{}]{[}]{[P q K qM =+ (2-24)(2008-3-26) 2.2 梁的横向振动横向位移函数)()(),(t q x t x u i ii ∑=ψ (2-22)动能j i ji ij L q q m dx u A T ∑∑⎰==21)(2120ρ (2-25) 势能j i ji ij L q q k dx u EI U ∑∑⎰=''=21)(2102 (2-26)dx A m L j i ij ⎰=0ψψρ,dx EI k Lj i ij ⎰''''=0ψψ (2-27) 分布外力做的功:)()())(),(())()()(,(),(),(0t q Q t q dx x t x p dxt q x t x p dx t x u t x p W i ii i i iLi ii LL δδψδψδδ∑∑⎰∑⎰⎰====(2-28)dx x t x p Q i Li )(),(0ψ⎰= (2-29)代入拉格朗日方程:),2,1(N i Q q k qm i j jijjjij==+∑∑ (2-30)或矩阵方程:}{}]{[}]{[Q q K qM =+ (2-31)注意假设模态法与有限元素法的区别:这里的)(x i ψ是对整个结构的假设模态(相当于整个结构变形的形函数),不是单元的位移形函数,对复杂结构,确定精度(品质)较高的假设模态是比较困难的。
3. 粘性阻尼系统中阻尼的处理 假设结构中具有分布粘性阻尼力),()(),(t x ux t x p ξ-= (2-32) 广义力∑⎰∑⎰∑⎰-=-=-==jLjj ij j i j i Ljj j i L i t q C dx x x x t qdxx t q x x dx x t x p Q 0)(])()()()[()()]()()([)(),( ψψξψψξψ (2-33)dx x C Lj i ij ⎰=0)(ψψξ (2-34)代入拉格朗日方程得到}{}]{[}]{[}]{[Q q K q C qM =++ (2-35) 上式中}{Q 为其他的广义非保守力§2.4 坐标约束与拉格朗日乘子通常对一个N 维结构系统,采用拉格朗日方程建立振动方程时,广义坐标N q q q ,,21是线性独立的,但是实际问题中,有时希望采用一套不是独立的坐标来建立方程,可能更加方便。
记系统不独立的坐标为)(,,21N M q q q M > 则被约束坐标数C=M-N(2-36)对广义坐标,有C 个约束方程:),2,1(0),,(21C j q q q f M j ==(2-37)如果令每一个坐标i q 取变分,则:02211=∂∂+∂∂+∂∂=M Mj j j j q q f q q f q q f f δδδδ(2-38)),2,1(0C j q qf ii ij==∂∂∑δ(2-39)上式说明这M 个i q δ不独立,而是由上述C 个方程联系起来。
在哈密尔顿原理式中,将坐标数由N 扩展到M ,即得到:0}])({[211=+∂∂-∂∂+∂∂-⎰∑=dt q Q q U q T q T dt d i i ii i t t Mi δ (2-40)注意,由于此时的i q δ不独立,不能直接由变分学基本原理,得出方括号内的项等于零的结论。
对上面的约束方程引入拉格朗日乘子(或称为拉格朗日乘子函数)),2,1()(C j t j =λ,得到:01111=∂∂=∂∂∑∑∑∑====Cj i ijM i j C j Mi i ijj q q f q qf δλδλ(2-41)代入哈密尔顿原理方程式中,0}])({[211=∂∂++∂∂-∂∂+∂∂-∑⎰∑=dt q q f Q q Uq T q T dt d i C ji j j i i i i t t Mi δλ (2-42)我们可以选择C 个j λ,使C 个i q δ相应的方括号表达式为零,那么其余N=M-C 个独立的i q δ对应的方括号内的项必为零。
从而得到带约束的拉格朗日方程(修正的拉格朗日方程)为:),2,1(0),,(),2,1()(211C j q q q f M i Q q f q U q T q T dt d M j iCj i j j i i i ====∂∂-∂∂+∂∂-∂∂∑=λ (2-43)联立上两个方程,就可确定M+C 个未知数),2,1;,2,1(,C j M i q j i ==λ 【应用实例】求两端固定杆的轴向自由振动微分方程。
