北师大版初二(下)数学第32讲：平方根

合集下载

北师大版八年级数学上册《平方根》(课件)

北师大版初中数学八年级《平方根》
平方根
学习目标：
• 了解算术平方根的概念，会求一个正数的算术平方根
• 算术平方根的概念及运算 • 利用算术平方根解决实际问题
自学指点：
1、认真阅读P38页（1）、（2）并完成下列问题（1）、说明为什么不是有理数
（2）、用计算器估算的近似值（精确到百分位） 2、用5分钟时间研读P38页算术平方根的概念，用红笔勾出关
想一想
（1）9的算术平方根是3，也就是说，3的平
方是9，还有其它的数，它的平方也是9吗？
（2）平方等于的4 数有几个？平方等于0.64
的数呢？
25
如果一个数x的平方等于a , 即x2 =a,那么这个数x叫做a的平方根(square root 也叫做二次方根).
议一议
（1）一个正数有几个平方根？（2）0 有几个平方根？（3）负数是有理数？
哪些是无理数？
定义
一个正数x的平方等于a,即x2=a，这个正数x叫做a的算术平方根，记作“a ” 读作“根号a”
我们规定0的算术平方根是0，即： 0 0
例题例1 求下列各数的算术平方根
81, 4 , 0.09, 1, 23, - 5, 0 25
例例2 题自由下落物体的高度h
（米）与下落时间t(秒)的关系为h=4.9t2.有一铁球从19.6 米高的建筑物上自由下落，到达地面需要多长时间？
解 : 将h 19.6代入公式h 4.9t 2,得： 19.6 4.9t 2 t2 4
t 4 2(秒) 答：铁球到达地面需要2秒
练
一个正数有两个平方根，0只有一个平方根，它是0本身；负数没有平方根.
定义
求一个数a的平方根的运算，叫做开平方(extraction of square root)，其中a叫做被开方数.

数学：2.2《平方根》同步课件(北师大版八年级)

6．一个正数的平方根是 2a－1 和－a＋2，则 a＝______ －1 ，
这个正数是__________ ． 9
注意区分平方根与算术平方根
【例题】求下列各数的平方根．
7 4 (1)0.49；(2)19；(3) ；(4)－(－22)3. 3
2
思路点拨：根据平方与开平方互逆关系求解．
3．开平方：求一个数 a 的平方根的运算，叫做开平方，其
中 a 叫做被开方数．
课堂小练 4．下列说法正确的是( C ) A．0.09 是 0.3 的平方根
4 2 B．425的平方根是± 25
C．0.3 是 0.09 的算术平方根 D．32 的平方根是 3
±4 ，算术平方根是________ 4 5．16 的平方根是________ ．
平方根和开平方(重难点)
1．平方根的概念：一般地，如果一个数 x 的平方等于 a，
平方根也叫二次方根)．即 x2＝a，那么这个数 x 就叫做 a 的________(
2．平方根的性质：
两ห้องสมุดไป่ตู้(1)一个正数有________ 个平方根，且它们互为相反数．
(2)0 只有一个平方根，它是 0 本身．
(3)负数没有平方根．
解：(1)∵(± 0.7)2＝0.49，∴± 0.49＝± 0.7. 7 16 4 16 (2)∵19＝ 9 ，＝ 9 ，∴± 3
2 2 2
7 4 19＝± 3.
2
4 4 4 16 4 16 (3)∵ ＝ 9 ，＝ 9 ，∴± ＝± . 3 3 3 3 (4)∵－(－22)3＝64，(± 8)2＝64，∴± －－223＝± 8.
2
平方根

北师大版八年级数学第二章平方根和开平方

平方根和开平方【学习目标】1．了解平方根、算术平方根的概念，会用根号表示数的平方根．2．了解开方与乘方互为逆运算，会用开方运算求某些非负数的平方根，会用计算器求平方根．【要点梳理】要点一、平方根和算术平方根的概念1.平方根的定义如果2x a =，那么x 叫做a 的平方根.求一个数a 的平方根的运算，叫做开平方. a 叫做被开方数.平方与开平方互为逆运算.2.算术平方根的定义正数a 的两个平方根可以用“a ±”表示，其中a 表示a 的正平方根（又叫算术平方根），读作“根号a ”；a -表示a 的负平方根，读作“负根号a ”.要点进阶：当式子a 有意义时，a 一定表示一个非负数，即a ≥0，a ≥0.要点二、平方根和算术平方根的区别与联系1．区别：（1）定义不同；（2）结果不同：a ±和a2．联系：（1）平方根包含算术平方根；（2）被开方数都是非负数；（3）0的平方根和算术平方根均为0．要点进阶：（1）正数的平方根有两个，它们互为相反数，其中正的那个叫它的算术平方根；负数没有平方根．（2）正数的两个平方根互为相反数，根据它的算术平方根可以立即写出它的另一个平方根.因此，我们可以利用算术平方根来研究平方根.要点三、平方根的性质 20||000a a a a a a a >⎧⎪===⎨⎪-<⎩ ()()20a a a =≥要点四、平方根小数点位数移动规律被开方数的小数点向右或者向左移动2位，它的算术平方根的小数点就相应地向右或者向左移动1位.例如：62500250=，62525=， 6.25 2.5=，0.06250.25=.【典型例题】类型一、平方根和算术平方根的概念例1、已知x-1的平方根为±2，3x+y-1的平方根为±4，求，3x+5y 的算术平方根．举一反三：【变式】已知2a －1与－a ＋2是m 的平方根，求m 的值.例2、x 为何值时，下列各式有意义？ (1)2x ； (2)4x -； (3)11x x ++-； (4)13x x --．举一反三：【变式】已知4322232b a a =-+-+，求11a b+的算术平方根．类型二、平方根的运算例3、求下列各式的值． (1)2222252434-+； (2)111200.36900435--．类型三、利用平方根解方程例4、求下列各式中的x .（1）23610;x -= （2）()21289x +=；（3）()2932640x +-=举一反三：【变式】求x 的值：（x ﹣2）2=4．类型四、平方根的综合应用例5、若x ，y 为实数，且满足．求的值．举一反三：【变式】若2110x y -++=，求20112012x y +的值．例6、小丽想用一块面积为4002cm 的正方形纸片，沿着边的方向裁出一块面积为3002cm 的长方形纸片，使它长宽之比为2:3，请你说明小丽能否用这块纸片裁出符合要求的长方形纸片.【巩固练习】一.选择题1．下列说法中正确的有（）．①只有正数才有平方根． ②2-是4的平方根． ③16的平方根是4±．④2a 的算术平方根是a ． ⑤2(6)-的平方根是6-．⑥ 93=±．A ．1个B ．2个C ．3 个D ．4个2．若m ＝40－4，则估计m 的值所在的范围是（）A ．1＜m ＜2 B. 2＜m ＜3 C. 3＜m ＜4 D. 4＜m ＜53. 试题下列说法中正确的是（）A.4是8的算术平方根B.16的平方根是4C.6是6的平方根D.－a 没有平方根4.若=a ，则a 的值为（）A.1B.﹣1C. 0或1D. ±15.有一个数值转换器，原理如下：当输入的x ＝64时，输出的y 等于（）A.2B.8C.32D.226.下列运算正确的是（）A.2(13)13--=B. 2(6)6-=-C.255-=-D. 93=±二.填空题7. 若10404102=，则 1.0404＝__________.8. 如果一个正方形的面积等于两个边长分别是3cm 和5cm 的正方形的面积的和，则这个正方形的边长为 ________.9. 下列各数：81，1625，1.44，124，81的平方根分别是_______________；算术平方根分别是_______________.10．（1）25的平方根是________；（2）()25-的平方根是________，算术平方根是________；（3）2x 的平方根是________，算术平方根是________；（4）()22x +的平方根是________，算术平方根是________．11．364的平方根为______．12.观察下列各式：=2，=3，=4，…请你找出其中规律，并将第n （n ≥1）个等式写出来．三.解答题13．求下列各式中x 的值．①x 2﹣25=0 ②4（x+1）2=16．14.已知1y -和12x -互为相反数，且0x ≠，求y x的值．15.如图，实数a ，b 对应数轴上的点A 和B ，化简2222()()a b a b a b +---+。

北师版八年级数学 2.2 平方根(学习、上课课件)

1.负数没有算术平方根.
2.算术平方根需要化简，如：4的算术平方根表
示为 4 ， 4 =2.
3.初中阶段的三类非负数：
①绝对值 |a|≥ 0；
②偶次方a2n≥0(n为正整数)；
③算术平方根 a ≥ 0.
知1－讲
感悟新知
知1－练
例1
[母题教材P26例1 ]求下列各数的算术平方根.
1
(1)64；(2)2 ；(3术平方根是5.
感悟新知
知1－练
方法点拨：本题运用了定义法，首先根据算术平
方根的定义求出 a， b 的值，再根据
有理数的加法法则求出 a+b 的值，最
后根据算术平方根的定义得出结果 .
感悟新知
知1－练
2-1. 已知 a＝5， b＝4，求 a－b 的值.
解：因为 a＝5，所以 a＝25.
所以－(－4)3的平方根是±8，算术平方根是8.
(4) 49.
因为 49＝7， (± 7)2＝7，
所以 49的平方根是± 7，算术平方根是 7.
感悟新知
方法点拨：求一个正数的平方根的方法：先找出
平方等于这个正数的数，这样的数有
两个，它们互为相反数，因而这两个
数均为这个正数的平方根 . 如果一个
数为带分数，一般先将其转化为假分
数；小数转化为分数 . 如果正整数 a
不能写成有理数的平方的形式，则可
以将 a 的平方根表示成 ± a 的形式 .
知2－练
感悟新知
知2－练
3-1. 下列说法中, 不正确的是( C )
A. －11是121的一个平方根
B. 11是121的一个平方根
C. 121的平方根是11
D. 121的算术平方根是11

初中数学《平方根》精品ppt北师大版1

算术平方根表示为____a_.
3.平方根的性质：…（分类）
思维方面：平方运算与_开___平__方运算是互为逆运算,
可以互相ቤተ መጻሕፍቲ ባይዱ验.
2 究竟等于多少? 2 是整数吗？是分数吗？还是…？你知道 2 在哪两个整数之间吗？
预习下一节新课吧！
作 1.课本习题业 2.《学法大视野》
你问我答
老师报一个数,第一位同学先回答这个数的平方根,再报一个数,下一位同学也先回答前一个数的平方根,再报一个数,依次类推…
不正确,是4.
（4）(4)2 的平方根是-4 .
不正确，是±4.
第二关题：
（1） 81 的算术平方根是（
A、±9
B、9 C、±3
9
B） D、3
（2） 88111 的平方根是（ C ）
A、±9 B、9 C、±3 D、3
第三关题：
1、_____0___的平方根是它本身.
2、___0__和__1_的算术平方根是它本身.
自学指导（二）
• 阅读课本107页的第二自然段和例题，并思考下列问题：
• 1、请举例说明平方与开平方有什么关系？
• 2、尝试独立解决例题1和例题2，再阅读课本的解答，注意书写方法和注意事项，完成课本108 页练习1、2题。
3 2=( 9 ) (－ 3 )2= ( 9 )
( ±3 )2 = 9
• 3、一个正数a的算术平方根与平方根之间有什么联系与区别?它们的表示方法各是怎样？
一般地,如果一个数的平方等于ɑ，那么这
个数叫做ɑ的平方根（或二次方根）
若 r2= a，则 r 是 a 的一个平方根.
例如: 32 9 3是9的平方根又 32 9 3是也9的平方根

初中数学《平方根》演示课件北师大版2

121
7
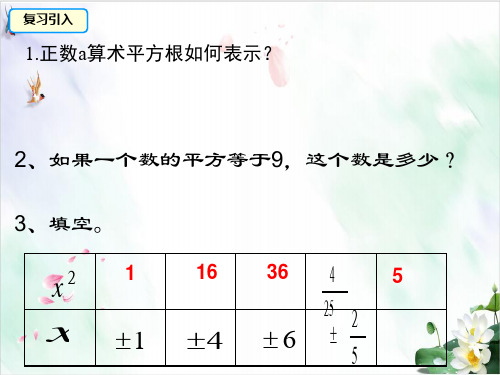
答案：1、±8 2、±11
±25 5、± 11
3、±0.04 4、
初中数学《平方根》演示课件北师大版2
初中数学《平方根》演示课件北师大版2
2、求下列各式的值
（1）、 16
( 2 )、 1 6 9 256
（ 3）、 1 9 （4）、 0.04
16
5、5 4 2
2
1、 42、 133、 54、 0.2
初中数学《平方根》演示课件北师大版2
自学检测3
例3：化简
(1) 1 6
解：(1) 16 42 4
(2) (5)2 (2) (5)2 255
想一想：如何化简 a 2 呢？ (5)2 52 5
a (a≥ 0)；
a 2 =∣a ∣= -a (a＜0).
初中数学《平方根》演示课件北师大版2
初中数学《平方根》演示课件北师大版2
自学检测4
辨一辨：请同学们快速分辨下列各题的对错．
（× ）（× ）（√ ）（√ ）
初中数学《平方根》演示课件北师大版2
课堂小结初中数学《平方根》演示课件北师大版2
平方根的概念
平方根
平方根的性质
( a)2 a (a0)
a 2 ＝a (a ≥0).
11、若m是169的算术平方根，n是121的负
的平方根，则 mn的2 平方根为
1、 2 已 xy知 42y60，x、求 y的值。
变式：已知１2（） yｘ 2 z30
求xyz的算术平方根。
13、计算各式中 x的值
1x 2 25 2x 2 81 0
1x 5 2x 9
34x 12

初中数学《平方根》-课文分析PPT【北师大版】2

课堂小结
本节课你有哪些收获？
•初中数学《平方根》公开课ppt北师大版2-精品课件 ppt(实用版)
•初中数学《平方根》公开课ppt北师大版2-精品课件 ppt(实用版)
课堂小结
1.平方根的概念、平方根的表示方法、平方根的性质、开平方； 2.平方根与平方关系密切； 3.引进开方运算，拓展了代数运算，为今后学习提供知识积累.
x²＝ a x 是 a 的平方根；
想一想：
3是9的平方根吗？为什么？
32=9
-7是49的平方根吗？为什么？
(-7)2=49
±0.01是0.1的平方根吗？为什么？
(±0.01)2≠0.1
问题二：想一想：
任何数都有平方根吗？
交流：
下列各数有平方根吗？如果有，请写出来；如果没有，请说明理由.
9，5，295 ，0，
4.1 平方根
情景一：
小方格的边长为1. 求AB、
A′
A
的长.
C
B C′
AB²＝ 3²＋4²＝25，
AB＝ 5
B′
＝4²＋5²＝41，
＝？
研究如何表示这个数，并求出它的值.
已知一个数的平方，
求这个数.
＝4²＋5²＝41，
＝？
情景二：
1.在等式 x2 a中，已知 a 5，
你能求 x吗？
2.已知 x3，你能求a吗？
•初中数学《平方根》公开课ppt北师大版2-精品课件 ppt(实用版)
例题：
例2．求下列各式中的x．
(1)x²＝16 ；
(2)x²＝
25 49
；
(3)x²＝15 ； (4)4x²＝81．
解： (1) x= 16 x= ±4

初中数学《平方根》演示课件北师大版3

A. 1个 B. 2个. C. 3个 D. 4个
初中数学《平方根》演示课件北师大版3
初中数学《平方根》演示课件北师大版3
练习二：求下列各数的平方根。
81 （1）64；（2）0.25；（3）36
；（4）2
1 4
解：（1） (8)2 64
∴64的平方根是±8
请你妨照上面的例子完成其余三个小题。
初中数学《平方根》演示课件北师大版3
初中数学《平方根》演示课件北师大版3
初中数学《平方根》演示课件北师大版3
再见
初中数学《平方根》演示课件北师大版3
探究新知
要做一张边长是3分米的方桌面，它的面积是多少？
这个问题实际上就是求：
32 ?
答：9平方分米
乘方运算
3分米这是已知底数和指数，求幂的运算
初中数学《平方根》演示课件北师大版3
反过来，要做一张面积是9平方分米的方桌面，初中数学《平方根》演示课件北师大版3 它的边长是多少分米？
实际上就是要求出一个数，使它的平方等于9，即：
初中数学《平方根》演示课件北师大版3
初中数学《平方根》演示课件北师大版3
举一个实际例子
5 的平方根，可以记作 5 和－ 5 ，或± 5
注意：
因为负数没有平方根，所以在式子 a 中的被开方数 a ≥0 ，否则式子 a 没有意义。即式子 a 中的 a 是一个非负数。
初中数学《平方根》演示课件北师大版3
9
解：（1）100的平方根是 100
∴ 10 010
注意：不能写成 10010
请你妨照上面的例子完成其余三个小题。
初中数学《平方根》演示课件北师大版3
初中数学《平方根》演示课件北师大版3

北师大版八年级数学课件-平方根

典典題題精精析析（2）
例2 自由下落物體的高度h(米)與下落時間 t(秒)的關係為 h=4.9t2。有一鐵球從9.6米高的建築物上自由下落,到達地面需要多長時間?
邊學邊練（2）
2、如圖，從帳篷支撐竿AB的頂部 A向地面拉一根繩子AC固定帳篷。若繩子的長度為5.5米，地面固定點C到帳篷支撐竿底部B的距離是 4.5米，則帳篷支撐竿的高是多少？
∴ x 1 0且y 2 0
∴ x 1, y 2
∴ x2 y2 12 (2)2 3
本節課學了哪些內容？
1、什麼叫做算術平方根？ 2、會求一個非負數的算術平方根。 3、瞭解算術平方根的雙重非負性。
佈置作業
Ｐ27習題2.3 補充題：
（１）求 16 的算術平方根．
（２）已知x、y滿足 x 1 y2 4 y 4 0
求 x2 y 2的值。
解：由已知，得 x 1 ( y 2)2 0
記為“ a ”，讀作“根號
a”。叫做被開方數.
特別地，我們規定0的算術平方根
是0即 0 0.
典題精析（1）
例1 求下列各數的算術平方根：
（1）900；（2）1；（3） 49 64
（4）14 （5） 81
邊學邊練（1）
1、求下列各數的算術平方根：
36，
9, 16
17，
0.81，
10-4，圖填空：
x2 __2________, y2 __3________, z2 __4________, w2 __5________.
（2）x，y，x，w中哪些是有理數？哪些是無理數？你能表示它們嗎？
知識精華
一般地，如果一個正數x的平方等於a，即x2=a，那麼這個正數x就叫做a的算術平方根，

八年级数学平方根北师大版

初二数学平方根北师大版【本讲教育信息】一、教学内容： 1、无理数的概念2、平方根的概念、表示、求法3、算术平方根的表示、概念、求法二、教学目标1、掌握无理数的概念，会判断一个数是否是无理数。

2、理解平方根的概念，会求一个非负数的平方根。

3、理解算术平方根的概念，会求一个非负数的算术平方根。

4、能应用平方根和算术平方根解决问题。

三、知识要点分析1、无理数的概念（这是重点）无限不循环小数叫做无理数.无理数可分为正无理数和负无理数.带根号的数不一定是无理数,如9;无理数也不一定带根号,如圆周率. 2、算术平方根（这是重点）如果一个数x 的平方等于a 即 a x =2，那么这个正数x 就叫做a 的算术平方根，记作“a ”，读作根号“a”；规定0的算术平方根即0 =0，如422=，那么2叫做4的算术平方根。

3、平方根（这是重、难点）平方根：如果一个数x 的平方等于a ，即a x =2，那么这个数x 就叫做a 的平方根（也叫做二次方根）；①平方根的意义：一个正数有两个平方根，它们互为相反数；0只有一个平方根，它是0本身；负数没有平方根；②开方：求一个数a 的平方根的运算，叫做开平方，其中a 叫做被开方数。

【典型例题】考点一：无理数的概念例1. 如图，每个小正方形的边长为1，四边形ABCD 的AC 、BD 相交于O ，试说明边长AB 、BC 、CD 、AD 和对角线AC 、BD 的长度哪些是有理数，哪些不是有理数。

【思路分析】从图上看AC 、BD 、AB 是有理数，因此BC 、CD 、AD 的长度不是有理数．解：AC=7，BD=5是有理数，而AO=4，BO=3，CO=3，DO=2，由勾股定理AB 2=32+4=25,AB=5是有理数，而BC 2=32+32=18,CD 2=32+22=13,AD 2=42+22=20,因此BC 、CD 、 AD 的长度不是有理数。

方法与规律:利用网格的特点进行分析，并借助勾股定理及数的平方来判定什么是有理数，什么不是有理数。

初中数学(北师大版)八年级-课时3-2 平方根(课件免费下载)

教学准备1. 教学目标1.1 知识与技能：1.了解平方根的概念，会用根号表示正数的平方根，2.了解开平方与平方互为逆运算，会用平方运算求某些非负数的平方根1.2过程与方法：1．通过学习平方根，进一步建立数感和符号感，发展抽象思维。

2．通过对正数平方根特点的探究，了解平方根与算术平方根的区别和联系，体验类比、化归等问题解决数学思想方法的运用，提高学生对问题的迁移能力。

1.3 情感态度与价值观：1.通过对实际生活中问题的解决，让学生体验数学与生活实际是紧密联系着的。

2.通过探究活动培养动手能力和锻炼克服困难的意志，建立自信心，提高学习热情2. 教学重点/难点2.1 教学重点平方根的概念．2.2 教学难点平方根与算术平方根的区别和联系3. 教学用具4. 标签教学过程1 回顾旧知：师：(1)什么是算术平方根?怎样表示?生：如果一个正数x的平方等于a,那么这个正数x叫做a的算术平方根.0的算术平方根是0负数没有算术平方根2 探究新知问题1：如果一个数的平方等于9，这个数是多少？回答：32＝9，(－3)2＝9∴平方等于9的数是3或－3.师：3或－3可以简单记作：±3.问题2：根据上面的研究过程填表：3 例4 求下列各数的平方根：4 归纳：数的平方根的特征师：数的平方根有什么特点？生：正数的平方根有两个，它们互为相反数师：0的平方根是多少？生：0的平方根就是0师：负数有平方根吗？生：负数没有平方根5 平方根的表示师：我们已经学过一个正数的算术平方根的表示方法，你能表示一个正数的平方根吗？6 课堂练习课堂小结本节课你学习了哪些知识？在探索知识的过程中，你用了哪些方法？（1）平方根的概念、表示方法、求法及平方根的性质（2）平方运算和开平方运算互为逆运算，可以互相检验板书。

八年级数学平方根1北师大版

平方根教学目标与要求：1、了解数的算术平方根、平方根的概念。

2、了解开方与乘方运算的关系。

会求非负数的算术平方根和平方根。

二、学习指导本讲重点：（1）算术平方根、平方根的概念②会运用根号表示并会求数的平方根本讲难点：（1）平方根、算术平方根的区别与联系1、关于算术平方根如果一个正数x 的平方等于a ，即a x =2，那么正数x 叫做a 的算术平方根。

注意：（1）0的算术平方根为0。

（2）数a 的算术平方根记作a ，其中0≥a 。

（3）只有当0≥a 时，数a 才有算术平方根。

2、关于平方根如果一个数的平方等于a , 即x 2=a ，那么这个数x 就叫做a 的平方根。

注意：（1）一个正数有两个平方根，且它们互为相反数，记为a ±；0有一个平方根，就是它本身；负数没有平方根。

（2）要分清平方根与算术平方根的区别与联系：一个正数的平方根有两个，而算术平方根只有一个；一个正数的算术平方根是一个正数，而它的平方根是一正一负3、关于开平方求一个数a 的平方根的运算叫做开平方。

其中a 叫做被开方数。

注意：（1）开平方运算与平方运算互为逆运算。

（2）一个正数开平方运算的结果有两个。

（3）负数不能进行开平方运算。

4、关于a 、2)(a 、2aa 表示非负数a 的算术平方根，其结果也是非负数；若0≥a ，则2)(a =a ；而2a 总有意义，且当0≥a 时，2a =a ；当0≤a 时，2a =a -，即2a =a . 三．典型例题（一）平方根1. 平方根的概念：如果一个数的平方等于a ，这个数就叫做a 的平方根（或二次方根），就是说，如果x 2＝a ，那么，x 就叫做a 的平方根。

如5和-5都是25的平方根。

因为，，故，是的平方根。

525525552522=-=-()例1. 求100的平方根。

解：()1001010的平方根是和，因为，所以与是的平-±=-1010010101002方根。