2.2 新排列及其逆序数
合集下载
第二节 排列及其逆序数
例如 排列32514 中， 0 01
32514
1 逆序数为3
故此排列的逆序数为3+1+0+1+0=5.
记做 (3 2 514) 5
排列的奇偶性 逆序数为奇数的排列称为奇排列; 逆序数为偶数的排列称为偶排列. 例如，在123组成的全排列中，有3个偶排列123， 231，312；有三个奇排列132，213，321 ❖一般说来，n 个数的全排列中，奇偶排列各占一半。
第二排列及其逆序数
1 全排列 2 排列的逆序数 3 逆序数的计算方法
问题 把 n 个不同的元素排成一列，共有几种不 同的排法？
定义1
把 n 个不同的元素排成一列，叫做这 n 个元素的全排列（简称排列）.
n 个不同的元素的所有排列的种数，通 常用 Pn 表示.
例如 P3 3 2 1 6.
同理 Pn n (n 1) (n 2) 3 2 1 n!.
32514 5的前面没有比5大的数,其逆序数为0; 1的前面比1大的数有3个,故逆序数为3; 4的前面比4大的数有1个,故逆序数为1;
32514 01 031 于是排列32514的逆序数为
0 1 0 3 1 5. (从头开始法)
例2 计算下列排列的逆序数，并讨论它们的奇 偶性.
1 217986354
分别计算出排列中每个元素前面比它大的数码 个数之和，即从排列中第一个元素开始，依次 算出排列中每个元素的逆序数，这每个元素的 逆序数之总和即为所求排列的逆序数.（从“头” 开始法） 例1 求排列32514的逆序数.
解 在排列32514中,
3排在首位,逆序数为0;
2的前面比2大的数只有一个3,故逆序数为1;
我们规定各元素之间有一个标准次序, n 个 不同的自然数，规定由小到大为标准排列（自然 排列）.
32514
1 逆序数为3
故此排列的逆序数为3+1+0+1+0=5.
记做 (3 2 514) 5
排列的奇偶性 逆序数为奇数的排列称为奇排列; 逆序数为偶数的排列称为偶排列. 例如，在123组成的全排列中，有3个偶排列123， 231，312；有三个奇排列132，213，321 ❖一般说来，n 个数的全排列中，奇偶排列各占一半。
第二排列及其逆序数
1 全排列 2 排列的逆序数 3 逆序数的计算方法
问题 把 n 个不同的元素排成一列，共有几种不 同的排法？
定义1
把 n 个不同的元素排成一列，叫做这 n 个元素的全排列（简称排列）.
n 个不同的元素的所有排列的种数，通 常用 Pn 表示.
例如 P3 3 2 1 6.
同理 Pn n (n 1) (n 2) 3 2 1 n!.
32514 5的前面没有比5大的数,其逆序数为0; 1的前面比1大的数有3个,故逆序数为3; 4的前面比4大的数有1个,故逆序数为1;
32514 01 031 于是排列32514的逆序数为
0 1 0 3 1 5. (从头开始法)
例2 计算下列排列的逆序数，并讨论它们的奇 偶性.
1 217986354
分别计算出排列中每个元素前面比它大的数码 个数之和，即从排列中第一个元素开始，依次 算出排列中每个元素的逆序数，这每个元素的 逆序数之总和即为所求排列的逆序数.（从“头” 开始法） 例1 求排列32514的逆序数.
解 在排列32514中,
3排在首位,逆序数为0;
2的前面比2大的数只有一个3,故逆序数为1;
我们规定各元素之间有一个标准次序, n 个 不同的自然数，规定由小到大为标准排列（自然 排列）.
全排列及其逆序数
32514
1 逆序数为3
故此排列的逆序数为3+1+0+1+0=5.
排列的奇偶性
逆序数为奇数的排列称为奇排列; 逆序数为偶数的排列称为偶排列.
计算排列逆序数的方法：
方法1 分别计算出排列中每个元素前面比它大的元数 的个数之和，即算出排列中每个元素的逆序数， 这每个元素的逆序数之总和即为所求排列的逆 序数.
二、全排列及其逆序数
问题 把 n 个不同的元素排成一列，共有几种不 同的排法？
定义 把 n个不同的元素排成一列，叫做这 n 个
元素的全排列（或排列）.
n 个不同的元素的所有排列的种数，通常
用 Pn表示. 由引例 P3 3 2 1 6. 同理 Pn n (n 1) (n 2) 3 2 1 n!.
证明 由定理1知对换的次数就是排列奇偶性的
变化次数, 而标准排列是偶排列(逆序数为0),因此 知推论成立.
三、小结
1 n 个不同的元素的所有排列种数为 n!. 2 排列具有奇偶性. 3 计算排列逆序数常用的方法有2 种.
思考题
分别用两种方法求排列16352487的逆序数.
思考题解答
解 用方法1 由前向后求每个数的逆序数. 1 63 5 2 4 8 7 t 0 0 1 1 3 2 0 1 8.
第二节 全排列及其逆序数
• 一、概念的引入 • 二、全排列及其逆序数 • 三、逆序数的性质 • 四、小结、思考题
一、概念的引入
引例 用1、2、3三个数字，可以组成多少个没 有重复数字的三位数？
解
123
百位 1 十位 1 2 个位 1 2 3
2
3
3种放法
13
2种放法
1种放法
1 逆序数为3
故此排列的逆序数为3+1+0+1+0=5.
排列的奇偶性
逆序数为奇数的排列称为奇排列; 逆序数为偶数的排列称为偶排列.
计算排列逆序数的方法：
方法1 分别计算出排列中每个元素前面比它大的元数 的个数之和，即算出排列中每个元素的逆序数， 这每个元素的逆序数之总和即为所求排列的逆 序数.
二、全排列及其逆序数
问题 把 n 个不同的元素排成一列，共有几种不 同的排法？
定义 把 n个不同的元素排成一列，叫做这 n 个
元素的全排列（或排列）.
n 个不同的元素的所有排列的种数，通常
用 Pn表示. 由引例 P3 3 2 1 6. 同理 Pn n (n 1) (n 2) 3 2 1 n!.
证明 由定理1知对换的次数就是排列奇偶性的
变化次数, 而标准排列是偶排列(逆序数为0),因此 知推论成立.
三、小结
1 n 个不同的元素的所有排列种数为 n!. 2 排列具有奇偶性. 3 计算排列逆序数常用的方法有2 种.
思考题
分别用两种方法求排列16352487的逆序数.
思考题解答
解 用方法1 由前向后求每个数的逆序数. 1 63 5 2 4 8 7 t 0 0 1 1 3 2 0 1 8.
第二节 全排列及其逆序数
• 一、概念的引入 • 二、全排列及其逆序数 • 三、逆序数的性质 • 四、小结、思考题
一、概念的引入
引例 用1、2、3三个数字，可以组成多少个没 有重复数字的三位数？
解
123
百位 1 十位 1 2 个位 1 2 3
2
3
3种放法
13
2种放法
1种放法
线性代数1-01 逆序数-行列式定义
a11 b1 D2 = . a21 b2
⎧a11 x1 + a12 x2 = b1 , ⎨ ⎩a21 x1 + a22 x2 = b2 .
b1 D1 = b2
a12 , a22
⎧a11 x1 + a12 x2 = b1 , ⎨ ⎩a21 x1 + a22 x2 = b2 .
a11 b1 D2 = . a21 b2
暨南大学环境工程系
线性代数
曹 刚
教学目标及教学要求
线性代数是环境工程和环境科学专业学生的基 础课，也是一门重要的数学基础理论课。 提高学生的综合数学素质，为后继课程学习提 供必备的数学工具，为进一步获得现代科学技 术知识奠定必要的数学基础。 通过本课程的学习，掌握线性代数的基本概 念，基本原理和基本方法，培养概括问题的能 力，逻辑推理能力，抽象思维能力，并在此基 础上运用线性代数这一工具解决理论上和实际 中的问题。
则二元线性方程组的解为
b1 a12 D1 b2 a22 x1 = = , D a11 a12 a21 a22
a11 b1 D2 a21 b2 x2 = = . D a11 a12 a21 a22
注意
分母都为原方程组的系数行列式.
例1 求解二元线性方程组
⎧ 3 x1 − 2 x2 = 12, ⎨ ⎩ 2 x1 + x2 = 1.
排列的逆序数 对于n 个不同的元素，可以规定各元素之间 有一个标准次序。 一般情况， n 个不同的自然 数，规定由小到大为标准次序. 定义 在一个排列 (i1 i 2 L i t L i s L i n ) 中，若数 i t > i s 则称这两个数组成一个逆序.
例如 排列32514 中， 逆序
1-2全排列及其逆序数
0 1
1
2
2
0 1 1 2 2 k 1 k 1 k
2 当 k 为偶数时，排列为偶排列，
k
21 k 1k 1
2 k k ,
当 k 为奇数时，排列为奇排列.
机动
目录
上页
下页
返回
结 n ( n 1) ( n 2) 3 2 1 n!.
机动 目录 上页 下页 返回 结束
LOGO
排列的逆序数 我们规定各元素之间有一个标准次序, n 个 不同的自然数，规定由小到大为标准次序.
定义 在一个排列 i1 i 2 i t i s i n 中，若数 i t i s 则称这两个数组成一个逆序. 例如 排列32514 中， 逆序 3 2 5 1 4
1 n 个不同的元素的所有排列种数为 n!. 2 排列具有奇偶性.
机动
目录
上页
下页
返回
结束
思考题
求排列16352487的逆序数. 解 1 6 3 5 2 4 8 7
LOGO
0 0 1 1 3 2 0 1 8.
机动
目录
上页
下页
返回
结束
LOGO 2012年秋
计算排列逆序数的方法
LOGO
分别计算出排列中每个元素前面比它大的数码 个数之和，即算出排列中每个元素的逆序数， 这每个元素的逆序数之总和即为所求排列的逆 序数.
机动
目录
上页
下页
返回
结束
例1
解
求排列32514的逆序数.
在排列32514中,
LOGO
1
2
2
0 1 1 2 2 k 1 k 1 k
2 当 k 为偶数时，排列为偶排列，
k
21 k 1k 1
2 k k ,
当 k 为奇数时，排列为奇排列.
机动
目录
上页
下页
返回
结 n ( n 1) ( n 2) 3 2 1 n!.
机动 目录 上页 下页 返回 结束
LOGO
排列的逆序数 我们规定各元素之间有一个标准次序, n 个 不同的自然数，规定由小到大为标准次序.
定义 在一个排列 i1 i 2 i t i s i n 中，若数 i t i s 则称这两个数组成一个逆序. 例如 排列32514 中， 逆序 3 2 5 1 4
1 n 个不同的元素的所有排列种数为 n!. 2 排列具有奇偶性.
机动
目录
上页
下页
返回
结束
思考题
求排列16352487的逆序数. 解 1 6 3 5 2 4 8 7
LOGO
0 0 1 1 3 2 0 1 8.
机动
目录
上页
下页
返回
结束
LOGO 2012年秋
计算排列逆序数的方法
LOGO
分别计算出排列中每个元素前面比它大的数码 个数之和，即算出排列中每个元素的逆序数， 这每个元素的逆序数之总和即为所求排列的逆 序数.
机动
目录
上页
下页
返回
结束
例1
解
求排列32514的逆序数.
在排列32514中,
LOGO
线性代数 排列及其逆序数
第二节
排列的逆序数
一、概念的引入 二、排列的逆序数 三、对换 四、小结、思考题
一、排列的逆序数引入说明：
我们已介绍了2、3阶行列式，我们希望将 概念推广到n阶的情况，为此，需引入逆序数 的概念来确定行列式展开式中项的符号.
二、排列的逆序数
排列的逆序数 定义 我们规定各元素之间有一个标准次序, n 个 不同的自然数，规定由小到大为标准次序. 在一个排列 i1 i2 it i s in 中，若数 it i s 则称这两个数组成一个逆序.
b 经对换后 a 的逆序数不变 ， 的逆序数减少1.
因此对换相邻两个元素，排列改变奇偶性. 设排列为 a1 al ab1 bm bc1 cn 现来对换 a 与 b .
a1 al a b1 bm b c1 cn
m 次相邻对换
a1 al ab b1 bm c1 cn
m 1 次相邻对换 a a b b b a c c 1 l 1 m a 1 n
排列的奇偶性 逆序数为奇数的排列称为奇排列; 逆序数为偶数的排列称为偶排列.
三、对换
定义
在排列中，将任意两个元素对调，其余 元素不动，这种作出新排列的手续叫做 对换． 将相邻两个元素对调，叫做相邻对换． 例如
a1 al a b b1 bm b a1 al b a b1 bm ba
a1 ala b1 bm b c1 cn a1 al b b1 bm a c1 cn a
例如
排列32514 中，
逆序
3 2 5 1 4
逆序 逆序
定义 一个排列中所有逆序的总数称为此排列
的逆序数.
例如
排列32514 中，
0
0
1
3 2 5 1 4
1
排列的逆序数
一、概念的引入 二、排列的逆序数 三、对换 四、小结、思考题
一、排列的逆序数引入说明：
我们已介绍了2、3阶行列式，我们希望将 概念推广到n阶的情况，为此，需引入逆序数 的概念来确定行列式展开式中项的符号.
二、排列的逆序数
排列的逆序数 定义 我们规定各元素之间有一个标准次序, n 个 不同的自然数，规定由小到大为标准次序. 在一个排列 i1 i2 it i s in 中，若数 it i s 则称这两个数组成一个逆序.
b 经对换后 a 的逆序数不变 ， 的逆序数减少1.
因此对换相邻两个元素，排列改变奇偶性. 设排列为 a1 al ab1 bm bc1 cn 现来对换 a 与 b .
a1 al a b1 bm b c1 cn
m 次相邻对换
a1 al ab b1 bm c1 cn
m 1 次相邻对换 a a b b b a c c 1 l 1 m a 1 n
排列的奇偶性 逆序数为奇数的排列称为奇排列; 逆序数为偶数的排列称为偶排列.
三、对换
定义
在排列中，将任意两个元素对调，其余 元素不动，这种作出新排列的手续叫做 对换． 将相邻两个元素对调，叫做相邻对换． 例如
a1 al a b b1 bm b a1 al b a b1 bm ba
a1 ala b1 bm b c1 cn a1 al b b1 bm a c1 cn a
例如
排列32514 中，
逆序
3 2 5 1 4
逆序 逆序
定义 一个排列中所有逆序的总数称为此排列
的逆序数.
例如
排列32514 中，
0
0
1
3 2 5 1 4
1
§1-2 全排列及其逆序数
1,2,3 ；1,3,2 ； 2,1,3 ； 2,3,1 ；3,1,2 ； 3,2,1
（2）逆序：在一个排列里，如果某一个较大的数排在某一 个 较小的数前面，则称这两个数码构成一个逆序； 例3 ：5 阶排列 4,3,5,2,1 中 4,3 、4,2 、4,1 及 3,2 、 3,1
5,2 、5,1 、2,1 等均构成反序，且共8 个反序；
（3）逆序数：在一个排列 i1 , i2 , , in 里，出现的逆序 总个数称为这个排列的逆序数；并记作 i1 , i2 , , in 例4 ：例 3 中 5 阶排列 4,3,5,2,1 中，逆序数为 8 即： 4,3,5,2,1 8
逆序数的计算：在一个排列 i1 , i2 , , in 里，先看有多少
特别，称 1,2, , n 为这
例1 ：1,2,3,4,5 ； 5,4,3,2,1 ； 3,2,1,5,4 ； 3,4,5,1,2 等等，均为 1,2,3,4,5 这5 个数码的不同排列； 结论： n 个数码 1,2, , n 的所有排列共 n! 个。
例2： 3个数码的不同排列共 3! 6 个，分别为
4,7,5,1,3,6,2 m1 m2 m3 m4 m5 m6 m7
3 5 3 0 11 0 13
（4）奇偶排列：若 i1 , i2 , , in 是奇数，则称 排列 i1 , i2 , , in 为奇排列； 排列 i1 , i2 , , in 为偶排列； 例6： 3 阶排列中 若 i1 , i2 , , in 是偶数，则称
个数排在 1 的前面，设有 m1 个，即有 m1 个数与1 构成反序； 将 1 划去；再看有多少个数排在 2 的前面，设有 m2 个，将 2 划去；‥ ‥ ‥ ，如此下去，设有 mn1 个数排在 n 1 的 前面，将 n 1 划去，最后只剩下数 n ，即 mn 0 则 i1 , i2 , , in m1 m2 mn1 mn 例5 ：7 阶排列 4,7,5,1,3,6,2 中，
1-2全排列及逆序数
即 n 个不同的元素一共有n! 种不同的排法.
（这里暂时Байду номын сангаас把元素想象成是写有编号的小球）
3个不同的元素一共有3! = 6种不同的排法
123，132，213，231，312，321
所有6种不同的排法中，只有一种排法 （123）中的数字是按从小到大的自然 顺序排列的，而其他排列中都有大的 数排在小的数之前. 因此大部分的排列都不是“顺序”， 而是乱序的，或者说其中有“逆序”.
练习1：求排列 453162 的逆序数. （奇排列）
解： （t 453162） 0+2+3+0+4 9
练习2： 求排列 463152 的逆序数. （偶排列）
t（463152） 0+0+2+3+1+4 10
猜想：对换一次改变排列的奇偶性？书P5
二、对换的定义
定义
在排列中，将任意两个元素对调，其余的元素 不动，这种作出新排列的手续叫做对换．
将相邻两个元素对换，叫做相邻对换．
例如
a1 al a b b1 bm a1 al b a b1 bm
a1 al a b1 bmb c1 cn a1 al b b1 bma c1 cn
三、对换与排列奇偶性的关系
定理1 对换改变排列的奇偶性.
证明 先考虑相邻对换的情形．
t ta1
tal ta tb tb1
§2 全排列和对换
为了研究 n 阶行列式的定义，我们首 先来学习全排列和逆序数的概念
一、排列及其逆序数
问题 把 n 个不同的元素排成一列，共有多少种不同的
排法？
定义 把 n 个不同的元素排成一列，叫做这 n 个元素 的全排列. n 个不同元素的所有排列的种数，通常用 Pn 表示.
（这里暂时Байду номын сангаас把元素想象成是写有编号的小球）
3个不同的元素一共有3! = 6种不同的排法
123，132，213，231，312，321
所有6种不同的排法中，只有一种排法 （123）中的数字是按从小到大的自然 顺序排列的，而其他排列中都有大的 数排在小的数之前. 因此大部分的排列都不是“顺序”， 而是乱序的，或者说其中有“逆序”.
练习1：求排列 453162 的逆序数. （奇排列）
解： （t 453162） 0+2+3+0+4 9
练习2： 求排列 463152 的逆序数. （偶排列）
t（463152） 0+0+2+3+1+4 10
猜想：对换一次改变排列的奇偶性？书P5
二、对换的定义
定义
在排列中，将任意两个元素对调，其余的元素 不动，这种作出新排列的手续叫做对换．
将相邻两个元素对换，叫做相邻对换．
例如
a1 al a b b1 bm a1 al b a b1 bm
a1 al a b1 bmb c1 cn a1 al b b1 bma c1 cn
三、对换与排列奇偶性的关系
定理1 对换改变排列的奇偶性.
证明 先考虑相邻对换的情形．
t ta1
tal ta tb tb1
§2 全排列和对换
为了研究 n 阶行列式的定义，我们首 先来学习全排列和逆序数的概念
一、排列及其逆序数
问题 把 n 个不同的元素排成一列，共有多少种不同的
排法？
定义 把 n 个不同的元素排成一列，叫做这 n 个元素 的全排列. n 个不同元素的所有排列的种数，通常用 Pn 表示.
全排列及其逆序数解读
定义 把 n 个不同的元素排成一列，叫做这 n 个元素的全排列（简称排列）。
n 个不同元素的所有排列的种数，通常用 Pn表 示。
例如, 引例的结果是 P3=3×2×1=6。
上页 下页 返回
计算 Pn 的公式：
首先从 n 个元素中任取一个放在第一个位置上， 有 n 种取法；
又从剩下的 n－1 个元素中任取一个放在第二 个位置上，有 n－1 种取法；
§2 全排列及其逆序数
★全排列的概念 ★逆序的概念 ★计算排列逆序数的方法
由于对角线法则只适用于二、三
阶行列式，为研究四阶及更高阶的行
列式，必须用到逆序数的概念。本节
主要介绍全排列的概念以、3三个数字，可以组成多少个没有重 复数字的三位数？ 解 总共有3×2×1= 6种放法。
这6个不同的三位数是： 123， 132， 213， 231， 312， 321。
上页 下页 返回
全排列的概念
在数学中，把考察的对象叫做元素。 于是引例可抽象成：把 3 个不同的元素排成一列， 共有几种不同的排法？ 一般地，我们可以讨论“把 n 个元素排成一列，共 有几种不同的排法”的问题。
上页 下页 返回
排列分类
奇排列：逆序数为奇数的排列 偶排列：逆序数为偶数的排列
上页 下页 返回
计算排列的逆序数的方法
不妨设 n 个元素为 1 至 n 这 n 个自然数，并
规定由小到大为标准次序。
设
p1 p2 pn
为这 n 个自然数的一个排列。
方法一 在排列 p1 p2 pn 中，直接找出次序颠 倒了的元素对的个数，这也就是该排列的逆序数。
t 0 0 0 0 0 0 2 4 6 8 20
§2 全排列及其逆序数
逆序
例如 排列32514 中， 排列
3 2 5 1 4
逆序 逆序
2. 一个排列中所有逆序的总数称为此排列的逆序数. 一个排列中所有逆序的总数称为此排列的逆序数 逆序数. 例如: 其逆序数为5. 例如 排列 32514 , 其逆序数为 其逆序数为4. 排列 31524 , 其逆序数为 3. 排列的奇偶性 逆序数为奇数的排列称为奇排列 逆序数为奇数的排列称为奇排列; 奇排列 逆序数为偶数的排列称为偶排列 逆序数为偶数的排列称为偶排列. 偶排列
4.计算排列逆序数的方法 计算排列逆序数的方法 设排列为 p1 p2 L pn , t i 为 pi 构成的逆序数 则其逆序数为 t = t ( p1 p2 L pn ) = t1 + t 2 + Lt n−1 计算下列排列的逆序数,并讨论它们的奇偶性 并讨论它们的奇偶性. 例 计算下列排列的逆序数,并讨论它们的奇偶性.
二、排列的逆序数
规定各元素之间有一个标准次序, 规定各元素之间有一个标准次序 n 个不同的自 然数, 规定由小到大为标准次序 标准次序. 然数 …pt…ps…pn中, 若数 pt >ps, 则称这两个数组成一个逆序 逆序. 则称这两个数组成一个逆序 (即：大的数在小的数左边, 则这两数构成一个逆序） 即 大的数在小的数左边 则这两数构成一个逆序）
(1) 217986354 ( 2) n( n − 1)( n − 2)L 321
四、小结
1. n个不同的元素的所有排列总数为 个不同的元素的所有排列总数为n!. 个不同的元素的所有排列总数为 2. 排列具有奇偶性 排列具有奇偶性. 3. 计算排列逆序数. 计算排列逆序数
§2 全排列及其逆序数
一、全排列 二、排列逆序数 三、小结
例如 排列32514 中， 排列
3 2 5 1 4
逆序 逆序
2. 一个排列中所有逆序的总数称为此排列的逆序数. 一个排列中所有逆序的总数称为此排列的逆序数 逆序数. 例如: 其逆序数为5. 例如 排列 32514 , 其逆序数为 其逆序数为4. 排列 31524 , 其逆序数为 3. 排列的奇偶性 逆序数为奇数的排列称为奇排列 逆序数为奇数的排列称为奇排列; 奇排列 逆序数为偶数的排列称为偶排列 逆序数为偶数的排列称为偶排列. 偶排列
4.计算排列逆序数的方法 计算排列逆序数的方法 设排列为 p1 p2 L pn , t i 为 pi 构成的逆序数 则其逆序数为 t = t ( p1 p2 L pn ) = t1 + t 2 + Lt n−1 计算下列排列的逆序数,并讨论它们的奇偶性 并讨论它们的奇偶性. 例 计算下列排列的逆序数,并讨论它们的奇偶性.
二、排列的逆序数
规定各元素之间有一个标准次序, 规定各元素之间有一个标准次序 n 个不同的自 然数, 规定由小到大为标准次序 标准次序. 然数 …pt…ps…pn中, 若数 pt >ps, 则称这两个数组成一个逆序 逆序. 则称这两个数组成一个逆序 (即：大的数在小的数左边, 则这两数构成一个逆序） 即 大的数在小的数左边 则这两数构成一个逆序）
(1) 217986354 ( 2) n( n − 1)( n − 2)L 321
四、小结
1. n个不同的元素的所有排列总数为 个不同的元素的所有排列总数为n!. 个不同的元素的所有排列总数为 2. 排列具有奇偶性 排列具有奇偶性. 3. 计算排列逆序数. 计算排列逆序数
§2 全排列及其逆序数
一、全排列 二、排列逆序数 三、小结
线性代数全排列与逆序数
第二节（1） 全排列和逆序数
一、全排列及其逆序数
定义 由n 个不同数码1,2,…,n 组成的有序数组 i1i2…in，称为一个全排列。 –例如, 1234及2341都是4级全排列, 25413是一
个5级全排列.
n个不同数码有n！种全排列。
定义 在一个全排列i1i2…in中，如果有较大的 数it排在较小的数is前面(is<it)，则称it与is构成一 个逆序。一个全排列中逆序的总数, 称为它的逆 序数，记为
例 计算下列排列的逆序数，并讨论它们的奇 偶性.
1 217986354
解
217986354
0 10 0 1 3 4 4 5
t 5 4 4310010
18
此排列为偶排列.
2 nn 1n 2321
解 n1
nn1n 2321 n 2
因此对换相邻两个元素，排列改变奇偶性.
设排列为 a1 alab1 bmbc1 cn 现来对换 a 与b.
a1al a b1bm b c1cn
m 次相邻对换 a1 al ab b1 bmc1cn m 1 次相邻对换 a1al bb b1bm a c1cn
a1alab1bmbc1cn ,
21, 31 31, 32 21,31,32
逆序数 0 1 1 2 2 3
奇偶性 偶排列 奇排列 奇排列 偶排列 偶排列 奇排列
证 设在全部 n 阶排列中有 s 个奇排列, t 个偶 排列,现来证 s t .
将s 个奇排列的前两个数对换,则这 s个奇排 列全变成偶排列,并且它们彼此不同,所以 s t.
方法2
分别计算出排列中每个元素前面比它大的数码 个数之和，即算出排列中每个元素的逆序数， 这每个元素的逆序数之总和即为所求排列的逆 序数.
一、全排列及其逆序数
定义 由n 个不同数码1,2,…,n 组成的有序数组 i1i2…in，称为一个全排列。 –例如, 1234及2341都是4级全排列, 25413是一
个5级全排列.
n个不同数码有n！种全排列。
定义 在一个全排列i1i2…in中，如果有较大的 数it排在较小的数is前面(is<it)，则称it与is构成一 个逆序。一个全排列中逆序的总数, 称为它的逆 序数，记为
例 计算下列排列的逆序数，并讨论它们的奇 偶性.
1 217986354
解
217986354
0 10 0 1 3 4 4 5
t 5 4 4310010
18
此排列为偶排列.
2 nn 1n 2321
解 n1
nn1n 2321 n 2
因此对换相邻两个元素，排列改变奇偶性.
设排列为 a1 alab1 bmbc1 cn 现来对换 a 与b.
a1al a b1bm b c1cn
m 次相邻对换 a1 al ab b1 bmc1cn m 1 次相邻对换 a1al bb b1bm a c1cn
a1alab1bmbc1cn ,
21, 31 31, 32 21,31,32
逆序数 0 1 1 2 2 3
奇偶性 偶排列 奇排列 奇排列 偶排列 偶排列 奇排列
证 设在全部 n 阶排列中有 s 个奇排列, t 个偶 排列,现来证 s t .
将s 个奇排列的前两个数对换,则这 s个奇排 列全变成偶排列,并且它们彼此不同,所以 s t.
方法2
分别计算出排列中每个元素前面比它大的数码 个数之和，即算出排列中每个元素的逆序数， 这每个元素的逆序数之总和即为所求排列的逆 序数.
1-2全排列及其逆系数
三、小结
1 n 个不同的元素的所有排列种数为 n !. 2 排列具有奇偶性. 3 计算排列逆序数常用的方法有2 种.
一、概念的引入
引例 用1、2、3三个数字，可以组成多少个没 有重复数字的三位数？
二、全排列及其逆序数
问题 把 n 个不同的元素排成一列
同的排法？ ，共有几种不
定义 把 n 个不同的元素排成一列，叫做这 n 个 元素的全排列（或排列）.
n 个不同的元素的所有排列的种数，通常
用 Pn表示.
Pn n ( n 1 ) ( n 2 ) 3 2 1 n !.
方法2 分别计算出排列中每个元素前面比它大的数码 个数之和，即算出排列中每个元素的逆序数， 这每个元素的逆序数之总和即为所求排列的逆 序数. 例1 求排列32514的逆序数.
排列32514的逆序数为
t 0 1 0 3 1 5.
例2 计算下列排列的逆序数，并讨论它们的奇 偶性.
排列的逆序数
我们规定各元素之间有一个标准次序, n 个 不同的自然数，规定由小到大为标准次序. 定义 在一个排列 i 1 i 2 i t i s i n 中，若数 i t i s 则称这两个数组成一个逆序.
定义 一个排列中所有逆序的总数称为此排列 的逆序数. 例如 排列32514 中， 故此排列的逆序数为 0 0 1 3+1+0+1+0=5. 3 2 5 1 4
1
解
217986354
2 1 7 9 8 6 3 5 4
0 1 0 0 1 3 4 4 5
t 5 4 4 31 0 01 0
18
此排列为偶排列.
2
解
线性代数1-2全排列及其逆序数1-3n阶行列式的定义1-4对换
（3）每项的正负号都取决于位于不同行不同 列的三个元素的下标排列．
例如 a a a 13 21 32 列标排列的逆序数为
t312 1 1 2, 偶排列 正号
a a a 11 23 32
列标排列的逆序数为
t132 1 0 1, 奇排列 负号,
a11 a12 a13
a21 a22 a23 (1)t a1 p1a2 p2 a3 p3 .
2、 n 阶行列式是 n! 项的代数和;
3、n 阶行列式的每项都是位于不同行、不同 列 n个元素的乘积;
4、 一阶行列式 a a不要与绝对值记号混淆;
5、 a a 1 p1 2 p2 anpn 的符号为 1t .
例1 计算对角行列式
0001 0020 0300 4000
分析 展开式中项的一般形式是 a a a a 1 p1 2 p2 3 p3 4 p4
的逆序数决定.
6. 一个排列中的任意两个元素对换，排列改 变奇偶性．
7. 行列式的三种表示方法
D
1 a a L a t( p1p2L pn )
1 p1 2 p2
npn
D
1 a a L a t( p1p2L pn )
p11 p2 2
pnn
D 1 a a L a t( p1p2L pn )t(q1q2L qn )
因此对换相邻两个元素，排列改变奇偶性 . 再证一般对换的情形 .
设排列为 a1 alab1 bmbc1 cn , 现来对换 a 与b.
a1 al a b1 bm b c1 cn
m 次相邻对换 a1 al ab b1 bmc1 cn
m 1 次相邻对换 a1 al b b1 bm a c1 cn
分析 展开式中项的一般形式是 a1 p1a2 p2 anpn . pn n, pn1 n 1, pn3 n 3, p2 2, p1 1, 所以不为零的项只有 a11a22 ann .
排列的逆序数的两种计算方法
排列的逆序数的两种计算方法
作者：佟伟
来源：《科技资讯》 2011年第16期
佟伟
(石家庄铁道大学四方学院西校区石家庄 050228)
摘要:本文根据排列的逆序数的定义,通过两种方法来进行计算,并证得两种方法是等效的,从而更加深刻的理解排列的逆序数的定义及其计算。
关键词:排列逆序数
中图分类号:O157.1 文献标识码:A 文章编号:1672-
3791(2011)06(a)-0184-01
我们知道,个不同元素的任一排列中,当某两个元素的先后次序与标准次序不同时,就说有一个逆序,一个排列中所有逆序的总数,叫做这个排列的逆序数。
下面讨论两种计算排列的逆序数的方法。
综上所述,定理成立。
参考文献
[1] 河北科技大学数学系.线性代数[M].中国标准出版社,2003.。
第1讲(排列及其逆序数)
故此排列为偶排列.
2） n n 1 n 2 3 2 1
2 解：n n 1 n 2 3 n3 n2 0 1 2 1
n1
n 1 n 2 2 1
n n 1 2
当 n 4 k ,4 k 1
x3
D3 D
1.
猜想:
a 11 a 21 a n1 a 12 a 22 an2 a1n a 2n a nn ???
a
???
1 j1
a 2 j 2 a nj n
第二节 排列及其逆序数
一、排列与逆序
1、排列的定义 由数１、２、…、ｎ组成的一个有序数组，称为
1
2 5 8
3 6 9
例2
求行列式 D 4
7
解
按对角线法则，有
D 1 5 9 2 6 7 3 4 8 3 5 7 2 4 9 1 6 8 0
1
1 3 9
1 x 0 x
2
例3 解
求解方程 2
4
按对角线法则，有
D 3 x 4 x 18 9 x 2 x 12
a 1 a l a b b1 b m a 1 a l b a b1 b m
a 1 a l a b1 b m b c 1 c n
2）
a 1 a l b b1 b m a c 1 c n
2、对换与排列的奇偶性的关系
定理1 任一排列经过一次对换后必改变其奇偶性. 对换 a , b
a 11 a 21
a 12 a 22
,
a 11 x 1 a 12 x 2 b1 , a 21 x 1 a 22 x 2 b 2 .
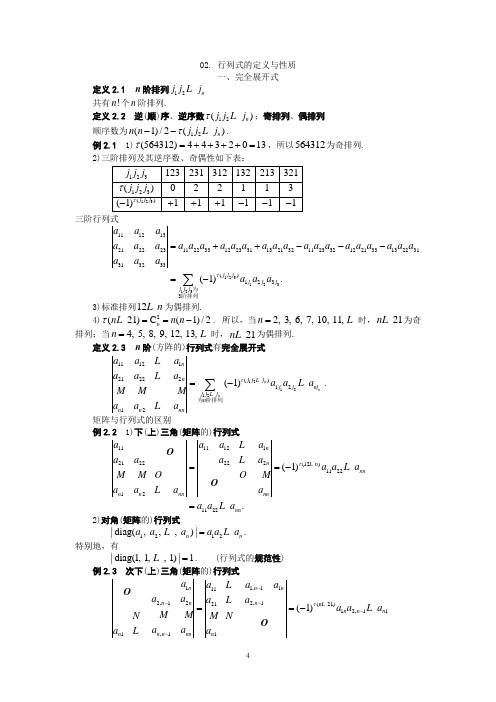
02行列式的定义与性质
02. 行列式的定义与性质一、完全展开式定义2.1 n 阶排列12n j j j共有!n 个n 阶排列.定义2.2 逆(顺)序、逆序数12()n j j j τ；奇排列、偶排列 顺序数为12(1)/2()n n n j j j - -τ.例2.1 1)(564312)4432013=++++=τ，所以564312为奇排列. 2)三阶排列及其逆序数、奇偶性如下表：123123123()123231312132213321()022113(1)111111j j j j j j j j j -+++---ττ 三阶行列式123123123111213212223112233122331132132112332122133132231313233()1233(1).j j j j j j j j j a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a =++---=-∑为阶排列τ3)标准排列12n 为偶排列.4)2(21)C (1)/2n n n n ==- τ. 所以，当2,3,6,7,10,11,n = 时，21n 为奇排列；当4,5,8,9,12,13,n = 时，21n 为偶排列.定义2.3 n 阶(方阵的)行列式有完全展开式1212121112121222()1212(1)n n n nn j j j j j nj j j j n n n nna a a a a a a a a a a a =-∑为阶排列τ.矩阵与行列式的区别例2.2 1)下(上)三角(矩阵的)行列式11111122212222(12)1122121122(1).OOn n n nnn n nnnnnn a a a a a a a a a a a a a a a a a a ==-=τ2)对角(矩阵的)行列式 1212|diag(,,,)|n n a a a a a a = . 特别地，有|diag(1,1,,1)|1= .(行列式的规范性) 例2.3 次下(上)三角(矩阵的)行列式11,11112,122,121(21)12,11,111(1)OOn n nn n n n n n n n n nnn n a a a a a a a a a a a a a a a -----==-τ(1)/212,11(1)n n n n n a a a --=- .例2.4 设[]A ij n n a ⨯=的主对角元均为奇数，其他元素均为偶数，求证||0A ≠.二、基本性质变形性质、等于零的性质n 阶行列式就是n 阶方阵的规范的、对行(列)有交错性和多重线性的函数.(——行列式的公理化定义)例2.5a b a cc d b d=. 例2.6 设,A B 均为四阶方阵，12341234[,,,],[,,,]A B αγγγβγγγ==，且||A 1,||2B ==，求||A B +.例2.7 用化三角形法计算数字行列式. 例2.8 箭形行列式三角化.例2.9 先化为箭形行列式，再三角化：计算n 阶行列式11112222n nnn na b a a a a b a D a a a b ++=+.例2.10 快速“打洞”：计算n 阶行列式n a b bb a D b b b a=. 当4,1,2n a b ===时，12341122211111111()/722122212201007772212221200102222122210001i r r r r r r i +++--=--≥-.例2.11 逐行(列)相消：计算n 阶杨辉行列式111,,11,||i j ij n ij i j i j a a a a a a --⎛⎫==⎧ ⎪⎨ ⎪=+⎩⎝⎭.431111111111111111111234012301230123136100136001300134,3,24,31410200141000140001i i i i r r r r r r i i -----==1=.例2.12 求证奇数阶反对称(矩阵的)行列式必为零. 例2.13 计算n 阶行列式111222121212n n n n x x x n x x x n D x x x n++++++=+++，注意对阶数n 做讨论.。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第二节 排列及其逆序数
第二章 行列式 克拉默法则
一、全排列及其逆序数
定义1 由自然数 1, 2, , n 组成的一个有序数组，
称为一个n级排列（或排列），
n 级排列的种数，通常用 P 表示.且 n
P n
n (n 1) (n 2)
3 2 1
n!.
我们规定各元素之间有一个标准次序, n 个
不同的自然数，规定由小到大为自然顺序.
偶排列调成标准排列的对换次数为偶数.
2
第二章 行列式 克拉默法则
二.对换与排列的奇偶性的关系
定义5 在排列中，将任意两个元素对调，其余元素不动， 这种作出新排列的手续叫做对换． 将相邻两个元素对调，叫做相邻对换． 定理1 一个排列中的任意两个元素对换，排列改
变奇偶性．(证明略）
如排列45321变为 25341，奇偶性发生改变。 推论 奇排列调成标准排列的对换次数为奇数；
第二章 行列式 克拉默法则
一、全排列及其逆序数
定义2 在一个排列 p1 p2 pt ps pn 中，若
数
ห้องสมุดไป่ตู้
p t
ps，则称这两个数组成一个逆序.
定义3 一个排列 p1L pi L pn 中, 考虑元素pi, 如
果比pi 大且排在它前面的数共有τi 个，则元素pi 的逆序数为τi.
问：排列 3 5 2 4 1中，元素4和元素1的逆序数各 为多少？
定义4 一个排列中每个数的逆序数之总和称为
此排列的逆序数，记作 p1 pi pn 或 t .
第二章 行列式 克拉默法则
一、全排列及其逆序数
排列的奇偶性 逆序数为奇数的排列称为奇排列; 逆序数为偶数的排列称为偶排列.
计算排列逆序数的方法： 分别计算出排列中每个元素前面比它大的数码的
个数之和，即算出排列中每个元素的逆序数，每个元 素的逆序数之总和即为所求排列的逆序数.
第二章 行列式 克拉默法则
一、全排列及其逆序数 例1 求排列45321的逆序数.
解 依次得出每个元素的逆序数分别为 0,0,2,3,4。
于是排列45321的逆序数为
t 0 0 2 3 4 9. 例2 求排列n,n-1,…,3,2,1 的逆序数.
解 该排列的逆序数为
0 1 2 n 1 n(n 1)
第二章 行列式 克拉默法则
一、全排列及其逆序数
定义1 由自然数 1, 2, , n 组成的一个有序数组，
称为一个n级排列（或排列），
n 级排列的种数，通常用 P 表示.且 n
P n
n (n 1) (n 2)
3 2 1
n!.
我们规定各元素之间有一个标准次序, n 个
不同的自然数，规定由小到大为自然顺序.
偶排列调成标准排列的对换次数为偶数.
2
第二章 行列式 克拉默法则
二.对换与排列的奇偶性的关系
定义5 在排列中，将任意两个元素对调，其余元素不动， 这种作出新排列的手续叫做对换． 将相邻两个元素对调，叫做相邻对换． 定理1 一个排列中的任意两个元素对换，排列改
变奇偶性．(证明略）
如排列45321变为 25341，奇偶性发生改变。 推论 奇排列调成标准排列的对换次数为奇数；
第二章 行列式 克拉默法则
一、全排列及其逆序数
定义2 在一个排列 p1 p2 pt ps pn 中，若
数
ห้องสมุดไป่ตู้
p t
ps，则称这两个数组成一个逆序.
定义3 一个排列 p1L pi L pn 中, 考虑元素pi, 如
果比pi 大且排在它前面的数共有τi 个，则元素pi 的逆序数为τi.
问：排列 3 5 2 4 1中，元素4和元素1的逆序数各 为多少？
定义4 一个排列中每个数的逆序数之总和称为
此排列的逆序数，记作 p1 pi pn 或 t .
第二章 行列式 克拉默法则
一、全排列及其逆序数
排列的奇偶性 逆序数为奇数的排列称为奇排列; 逆序数为偶数的排列称为偶排列.
计算排列逆序数的方法： 分别计算出排列中每个元素前面比它大的数码的
个数之和，即算出排列中每个元素的逆序数，每个元 素的逆序数之总和即为所求排列的逆序数.
第二章 行列式 克拉默法则
一、全排列及其逆序数 例1 求排列45321的逆序数.
解 依次得出每个元素的逆序数分别为 0,0,2,3,4。
于是排列45321的逆序数为
t 0 0 2 3 4 9. 例2 求排列n,n-1,…,3,2,1 的逆序数.
解 该排列的逆序数为
0 1 2 n 1 n(n 1)