捷联惯导算法心得
航母舰载机捷联惯导系统自主对准算法流程研究

航 母 舰 载机 捷 联 惯 导 系 统 自主 对 准 算 法 流 程 研 究
袁 涛 , 曲志 刚 , 徐 景硕 , 刘 关 洁
( 海军航空工程学 院青岛校区 , 山东 青 岛 2 6 6 0 4 1 )
摘
要: 随 着 我 海 军 现 代 化 进 程 的不 断发 展 , 舰载武器倍 受关注 , 但 风 浪 等 因素 影 响 产 生 的 航 母 摇 摆 晃 动 , 会
c a u s e o f t h e wa v e,t he s e a b r e e z e e f f e c t c a us e s t h e c a r r i e r d e c k s wi n g a n d s wa y. Th i s b r i n g s di fi c ul t y t o c a r r i e r ai r c r a f t i n e r t i a l n a v i g a t i o n
第 3 3卷
第 2期
弹
箭
与
制
导
学
报
V0 1 . 3 3 No . 2 3年 4月
J o u r n a l o f P r o j e c t i l e s ,R o c k e t s ,Mi s s i l e s a n d Gu i d a n c e
力加速度矢量信息 , 根据这一思路 , 文 中 给 出 了基 于 重 力 加 速 度 积 分 矢 量 的解 析 自主 粗 对 准 和 自主 精 对 准 的
算法 流程。理论分析和仿真结果表 明 , 该 运 动 基 座 上 捷 联 惯 导 自对 准 方 法 能 有 效 解 决 舰 船 系泊 状 态 下 舰 载 机
捷联惯性导航系统的解算方法

捷联惯性导航系统的解算方法捷联惯性导航系统(Inertial Navigation System,简称INS)是一种利用陀螺仪和加速度计等惯性测量单元测量物体的加速度和角速度,然后通过对这些测量值的积分计算出物体的速度和位置的导航系统。
INS广泛应用于航空航天、无人驾驶车辆和船舶等领域,具有高精度和自主性等特点。
INS的解算方法一般分为初始对准、运动状态估计和航位推算三个主要过程。
初始对准是指在启动导航系统时,通过利用外部辅助传感器(如GPS)或静态校准等方法将惯性传感器的输出与真实姿态和位置进行初次校准。
在初始对准过程中,需要获取传感器的初始偏差和初始姿态,一般采用标定或矩阵运算等方法进行。
运动状态估计是指根据惯性传感器的测量值,使用滤波算法对物体的加速度和角速度进行实时估计。
常用的滤波算法包括卡尔曼滤波、扩展卡尔曼滤波和粒子滤波等。
其中,卡尔曼滤波是一种最优估计算法,通过对观测值和状态进行线性组合,得到对真实状态的最佳估计。
扩展卡尔曼滤波则是基于卡尔曼滤波的非线性扩展,可以应用于非线性INS系统。
粒子滤波是一种利用蒙特卡洛采样技术进行状态估计的方法,适用于非高斯分布的状态估计问题。
航位推算是指根据运动状态估计的结果,对物体的速度和位置进行推算。
INS最基本的航位推算方法是利用加速度值对速度进行积分,然后再对速度进行积分得到位置。
但是,在实际应用中,由于传感器本身存在噪声和漂移等误差,导致航位推算过程会出现积分漂移现象。
为了解决这个问题,通常采用辅助传感器(如GPS)和地图等数据对INS的输出进行校正和修正。
当前,还有一些先进的INS解算方法被提出,如基于深度学习的INS 解算方法。
这些方法利用神经网络等深度学习模型,结合原始传感器数据进行端到端的学习和预测,以实现更高精度的位置和姿态估计。
综上所述,捷联惯性导航系统的解算方法主要包括初始对准、运动状态估计和航位推算三个过程。
其中,运动状态估计过程利用滤波算法对传感器的测量值进行处理,得到物体的加速度和角速度的估计。
捷联惯导基本算法与误差
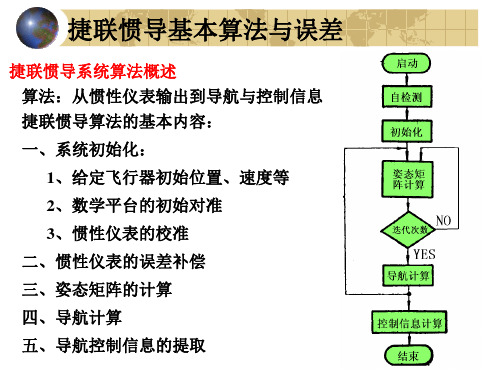
姿态计算 矩阵方程精确解1
二、方向余弦矩阵微分方程及其解 C C
E C E b C b b Eb
其中
b Eb
0 z y
z 0
x
y x
0
导航计算可以得到 E IE
b E E 有 b C C iE E iE b
E b E b
E C E b E C E (解 C b b ib iE b
的第一项)
增量算法 矩阵方程CS参数
sin 0 1 cos 0 b b 2 C (t t ) C (t ) I ib ( ib ) 2 0 0 展开合并上式,得 CbE (t t ) CbE (t )
姿态计算 姿态航向角计算1
四、姿态和航向角的计算 根据载体和地理坐标系之间的方向余弦矩阵可确定姿态、航向角
cos cos b CE cos sin sin sin cos cos sin cos sin sin sin cos sin sin sin cos cos sin sin cos cos sin sin cos sin cos cos
E b E b
n 1 n
b b b 02 ( EbX ) 2 ( EbY ) 2 ( EbZ )2
b Eb
方向不变时的精确解
九个微分方程求解,计算量大
姿态计算 四元数精确解1
三、四元数微分方程式及其解 由第一章,四元数微分方程式:
b q q
对
b 的处理类似上一节
一、角增量算法 角增量:陀螺仪数字脉冲输出,每个脉冲代表一个角增量 一个采样周期内,陀螺输出脉冲数对应的角增量为:
车载捷联惯导系统基本原理
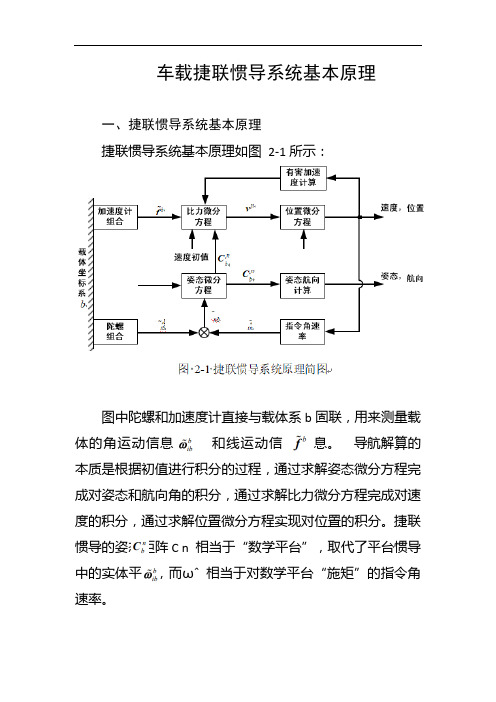
车载捷联惯导系统基本原理一、捷联惯导系统基本原理捷联惯导系统基本原理如图2-1所示:图中陀螺和加速度计直接与载体系b固联,用来测量载体的角运动信息和线运动信息。
导航解算的本质是根据初值进行积分的过程,通过求解姿态微分方程完成对姿态和航向角的积分,通过求解比力微分方程完成对速度的积分,通过求解位置微分方程实现对位置的积分。
捷联惯导的姿态矩阵C n 相当于“数学平台”,取代了平台惯导中的实体平台,而ωˆ相当于对数学平台“施矩”的指令角速率。
二、捷联惯导微分方程(一)姿态微分方程在捷联惯导系统中,导航坐标系n 和载体坐标系b 之间的角位置关系通常用姿态矩阵、四元数和欧拉角表示,相应也存在姿态矩阵微分方程、四元数微分方程和欧拉角微分方程三种形式。
姿态矩阵微分方程的表达式为:在欧拉角微分方程式(2.2-7)中,当俯仰角θ趋于90º时,cosθ趋于0,tanθ趋于无穷,方程存在奇异性,所以这种方法不能在全姿态范围内正常工作;姿态矩阵微分方程式(2.2-1)可全姿态工作,但姿态矩阵更新相当于求解包含9个未知量的线性微分方程组,计算量大;四元数微分方程式(2.2-6)同样可以全姿态工作,且更新算法只需求解4个未知量的线性微分方程组,计算量小,算法简单,是较实用的工程算法。
(二)速度微分方程速度微分方程即比力方程,是惯性导航解算的基本关系式:三、捷联惯性导航算法捷联惯导解算的目的是根据惯性器件输出求解载体姿态、速度和位置等导航信息,实际上就是求解三个微分方程的过程,相应存在姿态更新算法、速度更新算法和位置更新算法。
(一)姿态更新算法求解微分方程式(2.2-6)可得四元数姿态更新算法为:在车辆行驶过程中,一般不存在高频大机动环境,并且车载导航系统往往不工作在纯惯性导航方式,而是利用里程仪或零速条件进行组合导航,所以算法误差的影响有限,常用的5ms采样周期和二子样优化算法即可满足要求。
四、捷联惯导误差模型传感器误差、初值误差和算法误差是SINS的主要误差源,其中器件误差和初值误差又是影响导航结果的主要因素。
捷联惯导/航位推算组合导航算法研究

( 1 . 西 北 工 业 大 学 陕 西 西安 7 1 0 1 2 9 ; 2 . 西安 飞行 自动控 制研 究 所 陕 西 西安 7 1 0 0 6 5 ) 摘 要 :当捷 联 惯 组 ( S I MU ) 安装 到栽 车 上 存 在 安 装 误 差 时 , 航 位推 算 误 差 与 安 装 误 差 、 里程 计 刻度 系数 误 差 、 初 始 对 准
第电子 设计 工 程
E l e c t r o n i c De s i g n En g i n e e r i n g
2 0 1 3年 8月
Au g . 2 0 1 3
捷 联惯导/ 航位推算 组合 导航算 法研 究
惯 导 系 统 以其 提 供 导 航 信 息 的 全 面 性 和 完 全 的 自主 性 .
特 性 同 单 独 航 位 推 算 定 位 误 差 特 性 相 似 .即 初 始 对 准 误 差 、
安装误 差 、 里 程 仪 的 刻 度 系 数 误 差 影 响 姿 态 和 定 位 误 差 。文 中 在 考 虑 惯 组 和 载 车 间 的 安 装 误 差 的 情 况 下 推 导 了 航 位 推 算 的误 差 方 程 。并 以此 构 建 惯导 , 航位推算卡尔曼滤波方程 , 实 现 对 上 述 误 差 的估 计 [ 4 1 。
w e l l a s t h e mi s a l i n me g n t e l l ' o r c a u s e d b y t h e S I MU d e f e c t i v e i n s t a l l a t i o n . S I NS / DR i n t e g r a t e d n a v i g a t i o n s y s t e m c a n e s t i ma t e s u c h e r r o r s e f e c t i v e l y . I n t h e p a p e r , s y s t e m e q u a t i o n s o f S I NS / D R I n t e g r a t e d Na v i g a t i o n S y s t e m a r e d e r i v e d w h e n t h e v e h i c l e i s e q u i p p e d wi t h a n S I MU . S i mu l a t i o n a n ly a s i s s h o ws t h a t i n t e ra g t e d n a v i g a t i o n s y s t e m c a n e f e c t i v e l y e s t i ma t e t h e i n s t ll a a t i o n e l r o r , t h e h o i r z o n t a l g y r o r a n d o m b i a s a n d a c c e l e r o me t e r r a n d o m b i a s e s . Ke y wo r d s : S I MU;d e a d ec r k o n i n g ;i n t e ra g t e d n a v i g a t i o n;i n s t a l l a t i o n e l T o r
捷联惯导与组合导航系统高精度初始对准技术研究

捷联惯导与组合导航系统高精度初始对准技术研究捷联惯导与组合导航系统高精度初始对准技术研究引言捷联惯导与组合导航系统是一种集捷联惯导和其他导航传感器(如GPS、气压计、陀螺仪等)的优势于一体的导航系统,具有在惯导滞后情况下实现导航信息快速、准确更新的优势。
为了确保导航精度和可靠性,捷联惯导与组合导航系统的初始对准是不可或缺的关键技术之一。
本文将重点探讨捷联惯导与组合导航系统高精度初始对准技术的研究。
一、捷联惯导与组合导航系统概述捷联惯导与组合导航系统是一种通过融合多种导航传感器测量数据来计算导航解的导航系统。
其中,捷联惯导通过惯性导航算法利用加速度计和陀螺仪提供的姿态、速度和位移信息进行导航计算,而组合导航则通过融合GPS和其它传感器的信息来修正惯导的误差,提供更准确的导航结果。
二、初始对准技术的研究现状初始对准技术在捷联惯导与组合导航系统中起到了决定性的作用,对其精度和可靠性具有重大影响。
目前,针对初始对准技术的研究主要集中在以下几个方面:1. 惯性传感器标定:惯导系统的精度和准确性直接依赖于惯性传感器的性能。
因此,对于惯导系统而言,惯性传感器的标定至关重要。
传感器标定主要涉及惯性传感器的误差估计、参数校准和标定方法等。
2. 导航状态估计算法:捷联惯导与组合导航系统的核心是导航状态估计算法。
目前常用的算法包括扩展卡尔曼滤波(EKF)、无迹卡尔曼滤波(UKF)以及粒子滤波(PF)等。
这些算法通过融合多种传感器的信息,实现对导航状态的准确估计。
3. 高精度传感器融合:为了提高初始对准的精度和可靠性,可以考虑使用更高精度的传感器,如高精度的加速度计和陀螺仪。
此外,对于GPS系统而言,使用双频技术和高精度的差分GPS技术可以进一步提高导航精度。
三、捷联惯导与组合导航系统高精度初始对准技术研究在捷联惯导与组合导航系统高精度初始对准技术的研究中,可以采用以下方法来提高初始对准的精度和可靠性:1. 多目标标定方法:采用多目标标定方法来标定捷联惯导系统中的惯性传感器。
车载捷联惯导系统定位测姿算法研究

第15卷第l期2007年2月中国惯性技术学报JoumalofChineseInertialTcchnologyVbl.15No.1Feb.2007文章编号:1005-6734(2007)01一0024-04车载捷联惯导系统定位测姿算法研究陈允芳1,叶泽田2,钟若飞3(1.山东科技大学地球信息科学与工程学院,青岛266510;2.中国测绘科学研究院,北京100039;3.首都师范大学,北京100037)摘要:GPs/INs组合精确测定平台的位置和姿态是移动测图系统中的重要模块。
对陀螺仪和加速度计所测角速度和比力进行两次积分得载体姿态、速度和位置即sINs力学机械编排。
目前该过程大多在地理坐标系进行。
这里详细推导了地球坐标系中完整的解算过程,以四元数姿态矩阵更新及重力计算为核心,由IMu原始观测值解算出了载体位置、速度和姿态等参数,可快速高效与GPs输出的位置速度信息进行组合滤波处理,可据此编程进行工程应用数据处理。
关键词:捷联惯导系统;姿态矩阵;坐标转换;力学编排;四元数中图分类号:u666.1文献标识码:APositioningandorientationcomputationonVehicle-borneSINSanddiscussofcalculationerrorcHENYun.‰91,YEze-tian2,zHONGRuo.fei3(1.Geo·info衄ationScience&EngineeringCollege,ShandongUniverSi哆ofScienceaIldTbchnology,Qingdao266510,China;2.SurveyingaTldMappingScienceResearchInStituteofChina,Beijing100039,China;3.C印italNomlalUniverSi劬Beijing100037,China)Abstract:GPSandINSintegratedtoaccuratelydeteminingpositionaIldattitudeofnatI‘oofisVitalmoduleinmobilemappingSystem.Specincforcc行omspeedometer蚰d舭glerate矗om留roareinte铲atedtwicerespectiVelytoachievean沁de,veloc时aIldpositionn锄elySINSmechaIlization.Currentlythistookplacedingeogr印hiccoordinate,whiIeheredemonstratedindetailmewholemechaJlizationineanll-centclrcdearth-fixedcoordinate,mostlyquatemiona钍itudematrixupdating锄dgravit)rcaIculation.Ultimatelyvehiclenavigationpar锄eterssuchaSattitude,veIocity锄dpositionwercgahed丘omIMUorigin“0bservations.Mathematicsplatfo眦isfomlcdinSrNStocarryoutsuⅣeyingaJldcalculatingpreciselythenavigationmoVementpar锄cterS.Theresultsarcpronetointe黟atewitllsimilarpammeters疔omGPStofilterprocessing.Pro可锄minghercbyc锄pmcessdatainengineeringapplicationKeywords:SINS;attitudematrix;coordinatetransfomation;mechanization;quatemion随着惯性技术与卫星导航定位技术的发展,由GPS/INs不同程度组合而成的定位定姿传感器已成为移动测图系统中确定载体轨迹和平台姿态的重要工具,其中GPs多用于定位而INS则用于测姿。
捷联惯导系统极区导航算法优化设计及误差特性分析

捷联惯导系统极区导航算法优化设计及误差特性分析张海峰;张礼伟;王兴岭;李琳;仲岩【摘要】采用格网坐标系下的力学编排方案能够有效解决常规惯导系统力学编排方案在极区航向误差急剧发散且无法实现定位定向的难题.格网坐标系力学编排方案可以直接获得格网航向,以及地心地固坐标系下的位置坐标,且输出航向精度及定位精度不随纬度的增高而变差.通过深入研究格网坐标系力学编排方案的误差传播规律,详细分析了高纬度下格网航向保持高精度输出的数学机理.针对格网坐标系力学编排方案在极点附近存在计算奇异值的问题,提出了一种通过格网坐标系和地球坐标系间的位置方向余弦矩阵更新解算替代由地心地固位置坐标求解经纬度三角函数值的优化算法,实现了真正意义上的格网坐标系力学编排方案在极区的“无死角”导航能力.仿真分析了载体沿经线穿越极点运动时的算法性能,并与固定指北力学编排方案进行了比较,结果表明,相比于传统导航方案,格网系下输出的航向误差不随纬度升高而发散,导航精度与低纬度区域导航能力相当.【期刊名称】《中国惯性技术学报》【年(卷),期】2015(023)006【总页数】6页(P701-706)【关键词】极区导航;格网坐标系;误差特性;算法优化【作者】张海峰;张礼伟;王兴岭;李琳;仲岩【作者单位】天津航海仪器研究所,天津300131;天津航海仪器研究所,天津300131;天津航海仪器研究所,天津300131;天津航海仪器研究所,天津300131;天津航海仪器研究所,天津300131【正文语种】中文【中图分类】U666.1随着航空、航海事业的蓬勃发展以及国际政治经济的不断变化,对海军作战舰艇的全球作战能力提出了更高的要求。
由于极区地理经线快速收敛,导致传统地理导航坐标系失效。
虽然自由和游移方位惯导可在极区完成姿态方向余弦矩阵和位置方向余弦矩阵的解算,但从矩阵中提取航向信息和经度信息时存在奇异值。
采用格网线取代传统的地理经纬线对地表重新划分是解决该问题的有效手段之一。
捷联惯导结算原理

0 cos sin , Rz sin 0 cos
sin cos 0
0 0 1
cos cos sin sin sin cos cos sin sin cos sin cos T11 T12 T13 Ry Rx Rz cos sin cos cos sin T21 T22 T23 sin cos cos sin sin sin sin cos sin cos cos cos T T T 31 32 33 b 由姿态矩阵 C n 反解飞行器姿态欧拉角:
(5) 速度的计算
t t t t t 0 2iez etz ety 2iey Vxt Vx 0 t t b t t t t 0 2iex etx Vyt 0 Vy Cb f 2iez etz t Vz g Vzt 2 t t 2 t t 0 iey ety iex etx
o o sin 1 T23 , 90 , 90
tg 1
T13 180o , 180o , T33
tg 1
T21 o o , 180 , 180 T 22
图 6 东向北向速度变化曲线
阶段总结:1.学习了平台式和捷联式惯导的惯导解算方法并进行了仿真计算。 2.平台式惯导物理平台时刻跟踪当地水平东北天地理系, 加速计的比 力信息直接投影在导航系中,可直接进行导航速度和位置解算。载体的姿态可直 接从平台框架直接得出;而捷联式惯导用数学平台取代实体的物理平台,通过求
捷联惯导算法与组合导航原理讲义

捷联惯导算法与组合导航原理讲义严恭敏,翁浚编著西北工业大学2016-9前言近年来,惯性技术不论在军事上、工业上,还是在民用上,特别是消费电子产品领域,都获得了广泛的应用,大到潜艇、舰船、高铁、客机、导弹和人造卫星,小到医疗器械、电动独轮车、小型四旋翼无人机、空中鼠标和手机,都有惯性技术存在甚至大显身手的身影。
相应地,惯性技术的研究和开发也获得前所未有的蓬勃发展,越来越多的高校学生、爱好者和工程技术人员加入到惯性技术的研发队伍中来。
惯性技术涉及面广,涵盖元器件技术、测试设备和测试方法、系统集成技术和应用开发技术等方面,囿于篇幅和作者知识面限制,本书主要讨论捷联惯导系统算法方面的有关问题,包括姿态算法基本理论、捷联惯导更新算法与误差分析、组合导航卡尔曼滤波原理、捷联惯导系统的初始对准技术、组合导航系统建模以及算法仿真等内容。
希望读者参阅之后能够对捷联惯导算法有个系统而深入的理解,并能快速而有效地将基本算法应用于解决实际问题。
本书在编写和定稿过程中得到以下同行的热心支持,指出了不少错误之处或提出了许多宝贵的修改建议,深表谢意:西北工业大学自动化学院:梅春波、赵彦明、刘洋、沈彦超、肖迅、牟夏、郑江涛、刘士明、金竹、冯理成、赵雪华;航天科工第九总体设计部:王亚军;辽宁工程技术大学:丁伟;北京腾盛科技有限公司:刘兴华;东南大学:童金武;中国农业大学:包建华;南京航空航天大学:赵宣懿;武汉大学:董翠军;网友:Zoro;山东科技大学:王云鹏。
书中缺点和错误在所难免,望读者不吝批评指正.作者2016年9月目录第1章概述 (6)1.1捷联惯导算法简介 (6)1.2 Kalman滤波与组合导航原理简介 (7)第2章捷联惯导姿态解算基础 (10)2。
1反对称阵及其矩阵指数函数 (10)2。
1。
1 反对称阵 (10)2。
1.2 反对称阵的矩阵指数函数 (12)2。
2方向余弦阵与等效旋转矢量 (13)2.2.1 方向余弦阵 (13)2。
捷联惯性导航系统初始对准原理

机体坐标系是固连在机体上的坐标系。机体坐标系的坐标原点 位于飞行器的重心处, 沿机体横轴指向右, 沿机体纵轴指向前, 垂直于 ,并沿飞行器的数轴指向上。
2.3
对于捷联惯导系统,加速度计时沿机体坐标系 安装的,它只能测量沿机体坐标系的比力分量 , , ,因此需要将 , , 转换为 , , 。实现由机体坐标系到平台坐标系的坐标转换的方向余弦矩阵 又叫做捷联矩阵,本章用 来表示;由于根据捷联矩阵的元素可以单值地确定飞行器的姿态角,因此又可以叫做飞行器状态矩阵;由于捷联矩阵起到了平台的作用(借助于它可以获得 , , ),所以又可以叫做“数学平台”。
2.3
2.3.1
惯性导航中常用的坐标系有以下几种:
1.地心惯性坐标系(下标为i)——
惯性坐标系是符合牛顿力学定律的坐标系,即是绝对静止或只做匀速直线运动的坐标系。由于宇宙空间中的万物都处于运动之中,因此想寻找绝对的惯性坐标系是不可能的,我们只能根据导航的需要来选取惯性坐标系。对于在地球附近运动的飞行器选取地心惯性坐标系是合适的。地心惯性坐标系不考虑地球绕太阳的公转运动,当然更略去了太阳相对于宇宙空间的运动。地心惯性坐标系的原点 选在地球的中心,它不参与地球的自转。惯性坐标系是惯性敏感元件测量的基准。由于在进行导航计算时无需再这个坐标系中分解任何向量,因此惯性坐标系的坐标轴的定向本无关紧要,但习惯上我们可以将 轴选在沿地轴指向北极的方向上,而 、 轴则在地球的赤道平面内,并指向空间的两颗恒星。
(6)
其中, 的获取按照下式进行
(7)
式中, 是捷联陀螺的输出; 由姿态更新的最新值确定; 和 分别是未知速率和地球自转速率,对于导航坐标系取地理坐标系的情况有
上述分析说明,如果表征n系到b系的旋转四元数Q已经确定,那么就可以确定出运载体的航向角、俯仰角和横滚角,因此,四元数Q包含了所有的姿态信息,捷联惯导中的姿态更新实质上是如何计算四元数Q。
捷联惯导的原理与力学编排

1 RN
1 RE
sin
cos
sin2 cos2
RN
RE
1 RN
cos2
RN
1 RE
sin2
RE
sin cos
Veppx Veppy
速度方程
.
V 惯导基本方程: ep f 2ie ep V ep g
主
arc
sin
C33
又因定义域: 90 ,90
主
arc tan
C32 C31
180 ,180
1、求纬度的真值 反正弦函数的主值域与 的定义域一致,因此:=主
2、求经度的真值
反正切函数的主值域是 90 ,90 ,与 的定义域不一致,因此
需
要在主
Cep
C21
C22
C23
cos
sin
cos
sin
sin
cos sin sin sin cos
cos
cos
C31 C32 C33
cos cos
cos sin
sin
确定纬度 和经度
利用方向余弦矩阵可确定纬度和经度的真值。先求其主值:
向和垂线方向的坐标系。
惯性导航中的常用坐标系
平台坐标系(下标为p)— Oxp yp z p ▪ 原点o在载体重心,在平台惯导系统中,它代表实
捷联惯导系统误差系数动态标定方法探究

捷 联 惯 性 导 航 系 统 以其 特 有 的优 良特 性 广 泛 的 应 用 于 航空、 天、 航 军事 等 领 域 , 惯 性 器 件 ( 速 度 计 和 陀 螺 仪 ) 其 加 的误 差 在 很 大 程 度 上 直 பைடு நூலகம் 影 响 了 导 航 系 统 的 可 达 精 度 , 故
目前 , 然 G S具 有精 确制 导能 力 , 由于大气 电离 虽 P 但
( h e o d Ar l r n ie rn ol e Xi a 1 0 5 C i a T eS c n t l y E g e ig C l g , ’ n 7 0 2 , h n ) ie n e
Ab t a t Th r rp r me e f n ri sr me t n i e i a u e n e ie ma h n ewi o k n me sr c : ee r a a t r e t i t o oi a n u n r a me s r me t vc y c a g t w r ig t , i nt d h i
摘
要 :随着工作时间 的推移 , 捷联惯性导航系统 中的惯 性器件 测量精 度会 因为误 差参数 发生变 化而 降
低, 误差逐 渐被积 累 , 而降低 系统 导航精度 。针对此 问题 , 进 提出 了一 种基于 G S速度 、 P 位置信 息的捷联 惯 导系统 惯性 测量装置输 出误差 系数 动态标定的方法 。首先 采用 S g- ua自适应滤 波实现组合 导航状 aeH s 态最 优估 计 , 然后 引入 迭代最小二乘法 , 用导航误差对系统惯性器件 的误差 系数进行标定 。经计算机仿 利
情 况 、 气折 射 以 及 美 国军 方 人 为 的误 差 干扰 , P 空 G S只 能 作 为 辅 助 导 航 设 备 。I S G S是 最 先 进 的全 天 候 自主 式 制 导 N/ P
激光捷联惯性导航

HT-LG-H激光捷联惯性导航系统使用说明书1概述HT-LG-H激光捷联惯性导航系统(以下简称惯导系统)是陕西航天长城测控有限公司研制的高精度自主寻北、惯性组合导航系统。
该惯导系统由高精度激光陀螺、石英挠性加计、加计采集板、导航计算机、二次电源等部件组成,能够满足航空、陆用等设备的高精度定向/定位等功能的需求。
系统采用集成化,数字化、先进的对准导航算法等设计技术,具有高可靠性和环境适应性,可在阵风、发动机工作等严酷环境条件下完成高精度寻北;具备纯惯性导航功能,同时系统自带GPS/GLONASS卫星接收机,具有INS/GNSS组合导航功能;对外通信方式为RS-422总线。
2主要功能与性能2.1主要功能2.1.1自检功能具备上电自检功能,可输出自检结果,可将故障分离到部件级。
2.1.2初始标定功能接受外部输入的初始标定信息并完成初始标定。
2.1.3寻北功能接受寻北指令,完成寻北并输出寻北结果。
2.1.4导航功能完成寻北后自动转入导航状态;具有INS纯惯性导航功能和INS/GNSS组合导航功能。
2.2主要性能惯导系统的主要性能指标如表1所示。
表1惯导系统主要性能指标3接口3.1机械接口惯导系统采用4个M8-7H螺钉连接到专用过渡板上,过渡板采用4个M8-7H 螺钉安装到用户载体上,载体安装平面其平面度要求优于0.02mm;其详细要求见图1惯导系统机械接口图与图2过渡板接口图。
MM31" 4x09M■?:)图2专用过渡板机械接口图3.2电气接口3.2.1电源接口电源接口用连接器选用的是中航光电(158厂)生产的JY27468T17B08PN圆形插座。
其接口定义如表2所示。
表2惯导系统电源接口定义(JY27468T17B08PN)序号管脚号定义名称备注1 C +24V 24V电源2 E +24V 24V电源3 D 24VGND 电源地4 F 24VGND 电源地3.2.2通讯接口通讯接口连接器选用的是中航光电(158厂)生产的JY27468T17B12PN圆形插座。
捷联惯导系统的算法研究及其仿真实现(捷联惯导系统的发展趋势 初始对准技术的发展与研究现状)

捷联惯导系统的算法研究及其仿真实现Study and Simulation of Strapdown Inertial Navigation System1.1.3捷联惯导系统的发展趋势捷联式惯导系统是从20世纪60年代初开始发展起来的。
20世纪70年代以来,作为捷联系统的核心部件—惯性测量装置和计算机技术有了很大发展,而电子技术、计算机技术、现代控制理论的不断进步,为捷联惯性技术的发展创造了有利条件。
在硬件方面,新一代惯性器件如激光陀螺、光纤陀螺的成功研制,为捷联惯导的飞速发展打下了物质基础。
进入20世纪80-90年代,在航天飞机、宇宙飞船、卫星等民用领域及各种战略、战术导弹、军用飞机、反潜武器、作战舰艇等军事领域开始采用动力调谐式陀螺、激光陀螺和光纤式陀螺的捷联惯导系统。
其中激光陀螺和光纤式陀螺是捷联惯导系统的理想器件。
激光陀螺具有角速率动态范围宽、对加速度和震动不敏感、不需温控、启动时间特别短和可靠性高等优点。
激光陀螺惯导系统己在波音757/767、A310民机以及F-20战斗机上试用,精度达到 1.85km/h 的量级。
20世纪90年代,激光陀螺惯导系统估计占到全部惯导系统的一半以上,其价格与普通惯导系统差不多,但由于增加了平均故障间隔时间,其寿命期费用只有普通惯导系统的15%-20%。
光纤陀螺实际上是激光陀螺中的一种,其原理与环型激光陀螺相同,它克服了由激光陀螺闭锁带来的负效应,具有检测灵敏度和分辨率极高、启动时间极短、动态范围极宽、结构简单、零部件少体积小、造价低、可靠性高等优点。
采用光纤陀螺的捷联航姿系统已用于战斗机的机载武器系统及波音777飞机中。
波音777由于采用了光纤陀螺的捷联惯导系统,其平均故障间隔时间可高达20000h。
采用光纤陀螺的捷联惯导系统被认为是一种极有发展前途的导航系统。
而随着航空航天技术的发展及新型惯性器件关键技术的陆续突破,捷联惯导系统的可靠性、精度将会更高。
捷联惯导姿态算法中的圆锥误差与量化误差

第27卷 第1期航 空 学 报Vol 127No 11 2006年 1月ACTA A ERONAU TICA ET ASTRONAU TICA SIN ICA J an. 2006收稿日期:2004209230;修订日期:2005204227基金项目:国家自然科学基金(60234030)、国家杰出青年科学基金(60225015)和教育部高校青年教师奖资助项目 文章编号:100026893(2005)0120098206捷联惯导姿态算法中的圆锥误差与量化误差练军想,胡德文,胡小平,吴文启(国防科技大学机电工程与自动化学院自动控制系,湖南长沙 410073)R esearch on Coning E rror and Q uantization E rror of SINS Attitude AlgorithmL IAN J un 2xiang ,HU De 2wen ,HU Xiao 2ping ,WU Wen 2qi(Department of Automatic Control ,College of Mechatronics and Automation ,NationalUniversity of Denfense Technology ,Changsha 410073,China )摘 要:对捷联惯导系统的误差源进行了研究,利用几何方法分析了不可交换性误差和量化误差的形成机理,以及它们的相互影响。
针对工程应用中激光陀螺输出脉冲采样量化条件,就多子样算法进行了讨论,并设计了基于MA TL AB/Simulink 的仿真。
研究结果表明,当考虑量化误差的影响时,选取适当的量化因子,三子样等效旋转矢量算法比其它算法具有更好的综合性能。
关键词:捷联惯导;姿态算法;不可交换性误差;量化误差;多子样中图分类号:V249.3 文献标识码:AAbstract :In this paper ,the error sources of strapdown inertial navigation system (SINS )are researched.The mechanism of noncommutativity error and quantization error is illustrated f rom the geometrical point of view ,and the mutual influence between them is analyzed.Considering the sample condition of the output pulses of the ring laser gyroscope (RL G ),the multi 2sample attitude algorithm of SINS is discussed.The simu 2lation is carried out using MA TL AB/Simulink.It is concluded that the three 2sample rotation vector algorithm with the proper quantization factor outperforms others when the impact of quantization errors is taken into ac 2count.K ey w ords :SINS ;attitude algorithm ;noncommutativity error ;quantization error ;multi 2sample 对于捷联惯导系统姿态更新算法的研究,目前国内外同行们有很多成果。
捷联式惯性导航系统初始对准扰动补偿控制算法

第3期
2010 年 5 月
Journal of Jilin University ( Engineering and Technology Edition)
吉林大学学报( 工学版)
Vol. 40
No. 3
May 2010
捷联式惯性导航系统初始对准扰动补偿控制算法
张荣辉1 , 王海玮2 , 贾宏光3 , 陈
方程可以表示为
第3期 D VE = (
#
张荣辉, 等: 捷联式惯性导航系统初始对准扰动补偿控制算法 VN VF VE t an U)D V E + ( tan U+ R R R VE e cos U + 22 X )D VF + R
# 813 #
2
e sin U 2X )D VN - (
基于 Backstepping 算法的吸引 控制
b b b
等。单通道频域校正法在各通道独立时
1 E 1 E iE D X q+ D q XiEC 2 2
E b b
( 6)
E
具有好的补偿作用 ; 极点配置法或滤波法解决了 多通道耦合问题, 但其局限在于对扰动误差的适 应能力比较差 , 难以满足工程需要。本文首先建 立系 统 初 始 对 准 的 扰 动 控 制 数 学 模 型 , 基 于 Backstepping 和 H 2 最优控制理论研究捷联惯导 系统初始对准中的扰动补偿控制方法 , 以提高系 统的导航精度。
精密机械与物理研究所 , 长春 130033)
涛3 , 张
跃3
( 1. 浙江师范大学 工学院 , 浙江 金华 321004; 2. 吉林大学 交通学院 , 长春 130022; 3. 中国科学院 长春 光学
捷联惯性系统初始对准研究

研究生签名:
导师签名:歪望塾日期:至QQ鱼生圣县
东南大学硕士学位论文
第一章绪论
1.1课题背景
由于捷联惯性系统具有较高的精度、良好的可靠性、轻巧的体积、低廉的价格等特点,因此, 很多舰载武器系统,如舰炮、雷达、导弹等均在其附近安装了捷联系统为其提供姿态基准信息。但 是另一方面,为适应现代战争的需要,越来越多的武器系统被研发出来,并且陆续装备到现代舰船
ate
defined.Then,the attitude update algorithms of SIS a糟studied,and the basic dynamics
equations based On geography coordinate ale introduced.At last,the en'or equations of SIS a∞ derived. 2.Kalman filter and its application in initial alignment are studied.At first,the applicationbackground
船体速度在导航坐标系上分别沿东、北、天方向的投影 纬度、经度 子午线曲率半径、与子午线垂直的法线平面的曲率半径
东向速度误差 北向速度误差 东向失准角 北向失准角 天向失准角
R砖Q罐砧《《厶%厶
名
兄、疋
彤
矾
以磊丸凹 监
纵摇角误差 横摇角误差 航向角误差 z向加速度计偏置 Y向加速度计偏置
脯
L.彤&
X向陀螺漂移 Y向陀螺漂移
不需要其它外部信息,自主性强。非自主对准可通过机电或光学方法将外部参考坐标系引入系统,
使平台对准至导航坐标系。在捷联式惯性系统的粗对准阶段,可引入主惯性系统的航向姿态信息,
惯导原理捷联惯导基本算法与误差课件

由于陀螺仪和加速度计随时间变 化的稳定性问题导致的偏差,这 种误差通常需要通过实时滤波和 数据融合技术来减小。
05
提高捷联惯性导航精度的策
略
采用高性能的惯性传感器
陀螺仪
陀螺仪是惯性导航系统中的重要组成部分,能够测量载体在三个轴向的角速度。 采用高性能的陀螺仪可以提高捷联惯性导航系统的精度。
粒子滤波是一种基于贝叶斯推断的非线性滤波算法,能够处理非线性、非高斯系统。采用粒子滤波可以提高捷联 惯性导航系统在复杂环境下的性能。
利用外部信息进行修正
GPS修正
全球定位系统(GPS)是一种高精度的导航系统,能够提供准确的位置和时间信息。利用GPS信息对 捷联惯性导航系统进行修正可以提高其精度。
无线通信修正
利用无线通信网络,接收外部信息对捷联惯性导航系统进行修正可以提高其精度。例如,接收差分 GPS信号、无线电导航信号等。
06
捷联惯性导航发展趋势与挑
战
技术升级与改进
器件性能提升
随着微电子、精密制造等技术的 进步,捷联惯性导航系统的器件 性能得到不断提升,为实现更高
精度的导航提供了基础保障。
算法优化
04
捷联惯性导航误差分析
系统误差
零偏误差
由于陀螺仪和加速度计的 制造和安装偏差导致的固 定偏差,这种误差通常很 难通过校准消除。
刻度系数偏差
由于陀螺仪和加速度计的 刻度系数不准确导致的误 差,需要通过校准消除。
安装误差
由于陀螺仪和加速度计在 系统中的安装位置不准确 导致的误差,这种误差通 常很难通过校准消除。
随机误差
陀螺仪随机漂移误差
由于陀螺仪内部的热噪声和机械噪声导致的随机偏差,这种误差通常需要通过 滤波和数据融合技术来减小。
捷联惯导算法心得

捷联惯导算法心得1、四个概念:“地理”坐标系、“机体”坐标系、他们之间换算公式、换算公式用的系数。
地理坐标系:东、北、天,以下简称地理。
在这个坐标系里有重力永远是(0,0,1g),地磁永远是(0,1,x)(地磁的垂直不关心)两个三维向量。
机体坐标系:以下简称机体,上面有陀螺、加计、电子罗盘传感器,三个三维向量。
换算公式:以下简称公式,公式就是描述机体姿态的表达方法,一般都是用以地理为基准,从地理换算到机体的公式,有四元数、欧拉角、方向余弦矩阵。
换算公式的系数:以下简称系数,四元数的q0123、欧拉角的ROLL/PITCH/YAW、余弦矩阵的9个数。
系数就是描述机体姿态的表达方法的具体数值。
姿态,其实就是公式+系数的组合,一般经常用人容易理解的公式“欧拉角”表示,系数就是横滚xx度俯仰xx度航向xx度。
2、五个数据源:重力、地磁、陀螺、加计、电子罗盘,前两个来自地理,后三个来自机体。
3、陀螺向量:基于机体,也在机体上积分,因为地理上无参考数据源,所以很独立,直接在公式的老系数上积分,得到新系数。
狭义上的捷联惯导算法,就是指这个陀螺积分公式,也分为欧拉角、方向余弦矩阵、四元数,他们的积分算法有增量法、数值积分法(X阶龙格-库塔)等等4、加计向量、重力向量:加计基于机体,重力基于地理,重力向量(0,0,1g)用公式换算到机体,与机体的加计向量算出误差。
理论上应该没有误差,这误差逆向思维一下,其实就是换算公式的系数误差。
所以这误差可用于纠正公式的系数(横滚、俯仰),也就是姿态。
5、电子罗盘向量、地磁向量:同上,只不过要砍掉地理上的垂直向量,因为无用。
只留下地理水平面上的向量。
误差可以用来纠正公式的系数(航向)。
6、就这样,系数不停地被陀螺积分更新,也不停地被误差修正,它和公式所代表的姿态也在不断更新。
如果积分和修正用四元数算法(因为运算量较少、无奇点误差),最后用欧拉角输出控制PID(因为角度比较直观),那就需要有个四元数系数到欧拉角系数的转换。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
捷联惯导算法心得1、四个概念:“地理”坐标系、“机体”坐标系、他们之间换算公式、换算公式用的系数。
地理坐标系:东、北、天,以下简称地理。
在这个坐标系里有重力永远是(0,0,1g),地磁永远是(0,1,x)(地磁的垂直不关心)两个三维向量。
机体坐标系:以下简称机体,上面有陀螺、加计、电子罗盘传感器,三个三维向量。
换算公式:以下简称公式,公式就是描述机体姿态的表达方法,一般都是用以地理为基准,从地理换算到机体的公式,有四元数、欧拉角、方向余弦矩阵。
换算公式的系数:以下简称系数,四元数的q0123、欧拉角的ROLL/PITCH/YAW、余弦矩阵的9个数。
系数就是描述机体姿态的表达方法的具体数值。
姿态,其实就是公式+系数的组合,一般经常用人容易理解的公式“欧拉角”表示,系数就是横滚xx度俯仰xx度航向xx度。
2、五个数据源:重力、地磁、陀螺、加计、电子罗盘,前两个来自地理,后三个来自机体。
3、陀螺向量:基于机体,也在机体上积分,因为地理上无参考数据源,所以很独立,直接在公式的老系数上积分,得到新系数。
狭义上的捷联惯导算法,就是指这个陀螺积分公式,也分为欧拉角、方向余弦矩阵、四元数,他们的积分算法有增量法、数值积分法(X阶龙格-库塔)等等4、加计向量、重力向量:加计基于机体,重力基于地理,重力向量(0,0,1g)用公式换算到机体,与机体的加计向量算出误差。
理论上应该没有误差,这误差逆向思维一下,其实就是换算公式的系数误差。
所以这误差可用于纠正公式的系数(横滚、俯仰),也就是姿态。
5、电子罗盘向量、地磁向量:同上,只不过要砍掉地理上的垂直向量,因为无用。
只留下地理水平面上的向量。
误差可以用来纠正公式的系数(航向)。
6、就这样,系数不停地被陀螺积分更新,也不停地被误差修正,它和公式所代表的姿态也在不断更新。
如果积分和修正用四元数算法(因为运算量较少、无奇点误差),最后用欧拉角输出控制PID(因为角度比较直观),那就需要有个四元数系数到欧拉角系数的转换。
常用的三种公式,它们之间都有转换算法。
再搞个直白一点的例子:机体好似一条船,地理就是那地图,姿态就是航向(船头在地图上的方位),重力和地磁是地图上的灯塔,陀螺/积分公式是舵手,加计和电子罗盘是瞭望手。
舵手负责估计和把稳航向,他相信自己,本来船向北开的,就一定会一直往北开,觉得转了90度弯,那就会往东开。
当然如果舵手很牛逼,也许能估计很准确,维持很长时间。
不过只信任舵手,肯定会迷路,所以一般都有地图和瞭望手来观察误差。
瞭望手根据地图灯塔方位和船的当前航向,算出灯塔理论上应该在船的X方位。
然而看到实际灯塔在船的Y方位,那肯定船的当前航向有偏差了,偏差就是ERR=X-Y。
舵手收到瞭望手给的ERR报告,觉得可靠,那就听个90%*ERR,觉得天气不好、地图误差大,那就听个10%*ERR,根据这个来纠正估算航向。
------------------------------------------------------来点干货,注意以下的欧拉角都是这样的顺序:先航向-再俯仰-然后横滚公式截图来自:袁信、郑锷的《捷联式惯性导航原理》,邓正隆的《惯性技术》。
--------------------------------------------------根据加计计算初始欧拉角这个无论欧拉角算法还是四元数算法还是方向余弦矩阵都需要,因为加计和电子罗盘给出欧拉角的描述方式比较方便。
imu.euler.x=atan2(imu.accel.y,imu.accel.z);imu.euler.y=-asin(imu.accel.x/ACCEL_1G);ACCEL_1G为9.81米/秒^2,accel.xyz的都为这个单位,算出来的euler.xyz单位是弧度航向imu.euler.z可以用电子罗盘计算--------------------------------------------------欧拉角微分方程如果用欧拉角算法,那么这个公式就够了,不需要来回转换。
矩阵上到下三个角度(希腊字母)是roll pitch和yaw,公式最左边的上面带点的三个是本次更新后的角度,不带点的是上个更新周期算出来的角度。
Wx,y,z是roll pitch和yaw方向的三个陀螺在这个周期转动过的角度,单位为弧度,计算为间隔时间T*陀螺角速度,比如0.02秒*0.01弧度/秒=0.0002弧度. --------------------------------------------------以下是四元数--------------------------------------------------四元数初始化q0-3为四元数四个值,用最上面公式根据加计计算出来的欧拉角来初始化--------------------------------------------------四元数微分方程四元数更新算法,一阶龙库法,同样4个量(入、P1-3)也为四元数的四个值,即上面的q0-3。
Wx,y,z是三个陀螺的这个周期的角速度,比如欧拉角微分方程中的0.01弧度/秒,T为更新周期,比如上面的0.02秒。
再来一张,另外一本书上的,仔细看和上面是一样的delta角度,就是上面的角速度*周期,单位为弧度--------------------------------------------------四元数微分方程更新后的规范化每个周期更新完四元数,需要对四元数做规范化处理。
因为四元数本来就定义为四维单位向量。
求q0-3的平方和,再开根号算出的向量长度length。
然后每个q0-3除这个length。
--------------------------------------------------四元数转欧拉角公式把四元数转成了方向余弦矩阵中的几个元素,再用这几个元素转成了欧拉角先从四元数q0-3转成方向余弦矩阵:再从方向余弦矩阵转成欧拉角代码://更新方向余弦矩阵t11=q.q0*q.q0+q.q1*q.q1-q.q2*q.q2-q.q3*q.q3;t12=2.0*(q.q1*q.q2+q.q0*q.q3);t13=2.0*(q.q1*q.q3-q.q0*q.q2);t21=2.0*(q.q1*q.q2-q.q0*q.q3);t22=q.q0*q.q0-q.q1*q.q1+q.q2*q.q2-q.q3*q.q3;t23=2.0*(q.q2*q.q3+q.q0*q.q1);t31=2.0*(q.q1*q.q3+q.q0*q.q2);t32=2.0*(q.q2*q.q3-q.q0*q.q1);t33=q.q0*q.q0-q.q1*q.q1-q.q2*q.q2+q.q3*q.q3;//求出欧拉角imu.euler.roll=atan2(t23,t33);imu.euler.pitch=-asin(t13);imu.euler.yaw=atan2(t12,t11);if(imu.euler.yaw<0){imu.euler.yaw+=ToRad(360);}----------------------------------------------------以下代码摘自网上,很巧妙,附上注释,有四元数微分,有加计耦合。
没电子罗盘,其实耦合原理也一样。
view plaincopy to clipboardprint?1.//================================================================================================= ====2.//IMU.c3.//S.O.H.Madgwick4.//25th September20105.//================================================================================================= ====6.//Description:7.//8.//Quaternion implementation of the'DCM filter'[Mayhony et al].9.//10.//User must define'halfT'as the(sample period/2),and the filter gains'Kp'and'Ki'.11.//12.//Global variables'q0','q1','q2','q3'are the quaternion elements representing the estimated13.//orientation.See my report for an overview of the use of quaternions in this application.14.//15.//User must call'IMUupdate()'every sample period and parse calibrated gyroscope('gx','gy','gz')16.//and accelerometer('ax','ay','ay')data.Gyroscope units are radians/second,accelerometer17.//units are irrelevant as the vector is normalised.18.//19.//================================================================================================= ====20.21.//----------------------------------------------------------------------------------------------------22.//Header files23.24.#include"IMU.h"25.#include<math.h>26.27.//----------------------------------------------------------------------------------------------------28.//Definitions29.30.#define Kp2.0f//proportional gain governs rate of convergenceto accelerometer/magnetometer31.#define Ki0.005f//integral gain governs rate of convergence of gyroscope biases32.#define halfT0.5f//half the sample period33.34.//---------------------------------------------------------------------------------------------------35.//Variable definitions36.37.float q0=1,q1=0,q2=0,q3=0;//quaternion elements representing the estimated orientation38.float exInt=0,eyInt=0,ezInt=0;//scaled integral error39.40.//================================================================================================= ===41.//Function42.//================================================================================================= ===43.44.void IMUupdate(float gx,float gy,float gz,float ax,float ay,float az){45.float norm;46.float vx,vy,vz;47.float ex,ey,ez;48.49.//normalise the measurements50.norm=sqrt(ax*ax+ay*ay+az*az);51.ax=ax/norm;52.ay=ay/norm;53.az=az/norm;54.把加计的三维向量转成单位向量。
