中考复习模拟试题集锦——正多边形、扇形和圆锥侧面展开图
历年全国中考数学真题分类_038.正多边形、扇形和圆锥侧面展开图

一、选择题1. (2012•台湾21,3分)如图,正六边形ABCDEF 的边长为1,连接AC 、BE 、DF ,求图中灰色四边形的周长为何?( )A .3B .4C .2+D .2+ 【答案】D2. (2012•台湾22,3分)有一段树干为一直圆柱体,其底面积为9π平方公尺,高为15公尺.若将此树干分为两段圆柱形树干,且体积比为2:1,则体积较大的树干,其侧面的表面积为多少平方公尺?( ) A .60π B .72π C .84π D .96π 【答案】A3. (2012浙江舟山7,3分)已知一个圆锥的底面半径为3cm,母线长为10cm,则这个圆锥的侧面积为( ) (A) 15πcm 2(B) 30πcm2(C)60πcm 2(D)2913cm【答案】B4. (2012浙江省衢州,9,3分)用圆心角为120°,半径为6cm 的扇形纸片卷成一个圆锥形无底纸帽(如图所示),则这个纸帽的高是( )AB .cmC .D .4cm【答案】C5. (2012浙江嘉兴,7,4分)已知一个圆锥的底面半径为3cm ,母线长为10cm ,则这个圆锥的侧面积为( )A .15πcm 2B .30πcm 2C .60πcm 2D .2【答案】B6.(2012浙江绍兴,8,4分)如图,扇形DOE 的半径为3OABC 的顶点A ,C ,B 分别在OD ,OE ,DE 上,若把扇形DOE 围成一个圆锥,则此圆锥的高为( )A.12B.CD【答案】D7.(2012•宁波)如图,用邻边分别为a,b(a<b)的矩形硬纸板裁出以a为直径的两个半圆,再裁出与矩形的较长边、两个半圆均相切的两个小圆.把半圆作为圆锥形圣诞帽的侧面,小圆恰好能作为底面,从而做成两个圣诞帽(拼接处材料忽略不计),则a与b满足的关系式是()A.b=a B.b=a C.b=D.b= a【答案】D8.(2012四川南充,9,3分) 一个圆锥的侧面积是底面积的2倍,则圆锥侧面展开图的扇形的圆心角是()A.120° B.180° C.240° D.300°【答案】B9.(2012山东临沂,13,3分)如图,AB是⊙O的直径,AB=4,∠BED=120°,则图中阴影部分的面积之和为( )A.1BC.D.【答案】C10.(2012江苏无锡,7,3分)已知圆锥的底面半径为3cm,母线长为5cm,则圆锥的侧面积是( ▲) A.20 cm2B.20πcm2C.15 cm2D.15πcm2【答案】D11.(2012贵州铜仁,6,4分)小红要过生日了,为了筹备生日聚会,准备自己动手用纸板制作一个底面半径为9cm,母线长为30cm的圆锥形生日礼帽,则这个圆锥形礼帽的侧面积为()A.270πcm2B.540πcm2C.135πcm2D.216πcm2【答案】A12.(2012广东湛江,9,4分)一个扇形的圆心角为60°它所对的弧长为2 cm,则这个扇形的半径为()A.6cm B.12cm C.cm D第8题【答案】A13. (2012•安徽7,4分)为增加绿化面积,某小区将原来正方形地砖更换为如图所示的正八边形植草砖,更换后,图中阴影部分为植草区域,设正八边形与其内部小正方形的边长都为a ,则阴影部分的面积为( )A .2a 2B .3a 2C .4a 2D .5a 2【答案】A14. (2012•山东泰安18,3分)如图,AB 与⊙O 相切于点B ,AO 的延长线交⊙O 于点C ,连接BC ,若∠ABC=120°,OC=3,则的长为( )A .πB .2πC .3πD .5π 【答案】B15. (2012四川内江,8,3分)如图,AB 是⊙O 的直径,弦CD ⊥AB ,∠CDB =30°,CD =23,则阴影部分图形的面积为( )A .4πB .2πC .πD .23π【答案】D16. (2012兰州,6,4分)如果一个扇形的弧长等于它的半径,那么此扇形称为“等边扇形”.则半径为2的“等边扇形”的面积为A .πB .1C .2D .23π【答案】C17. (2012连云港,3,3分)用半径为2cm 的半径围城一个圆锥的侧面,则这个圆锥的底面半径为 A. 1cm B. 2cm C. πcm D. 2πcm 【答案】A18. (2012湖南衡阳,5,3分)一个圆锥的三视图如下图所示,则此圆锥的底面积为( * )A .230cm πB .225cm πC .250cm πD .2100cm π【答案】B19.(2012山西,12,2分)如图是某公园的一角,∠AOB=90°,弧AB 的半径OA 长是6米,C 是OA 的中点,点D 在弧AB ,CD ∥OB ,则图中休闲区(阴影部分)的面积是( )A .(32912-π)米2B . )329(-π米2C . )3296(-π米2D .)396(-π米2【答案】C20. (2012四川雅安,6,3分)圆柱形水桶的底面周长为3.2m π,高为0.6m ,它的侧面积是( )A .21.536m πB .21.92m πC .20.96m πD .22.56m π【答案】B21. (2012四川自贡,8,3分)如图,圆锥形冰淇淋盒的母线长是13cm ,高是12cm ,则该圆锥形底面圆的面积是( )A .10πcm 2B .25πcm 2C .60πcm 2D .65πcm 2【答案】D22. (2012贵州铜仁,6,4分)小红要过生日了,为了筹备生日聚会,准备自己动手用纸板制作一个底面半径为9cm,母线长为30cm 的圆锥形生日礼帽,则这个圆锥形礼帽的侧面积为( ) A .270πcm 2 B .540πcm 2 C.135πcm 2 D.216πcm 2 【答案】A 23. 24. 25. 26.二、填空题1. (2012四川成都,22,4分)一个几何体由圆锥和圆柱组成,其尺寸如图所示,则该几何体的全面积(即表面积)为________ (结果保留π)【答案】π602. (2012重庆,14,4分)一个扇形的圆心角为120°,半径为3,则这个扇形的面积为 。
38B正多边形、扇形和圆锥侧面展开图

正多边形、扇形和圆锥侧面展开图一、选择题1.(2011广东珠海,3,3分)圆心角为60°,且半径为3的扇形的弧长为A.2πB.πC.23πD.3π【答案】B2. (2011广西桂林,12,3分)如图,将边长为a的正六边形A1A2A3A4A5A6在直线l上由图1的位置按顺时针方向向右作无滑动滚动,当A1第一次滚动到图2位置时,顶点A1所经过的路径的长为().图1 图2第12题图A.4+233πa B.8+433πa C.4+33πa D.4+236πa【答案】A3. (2011贵州毕节,15,3分)、如图,在△ABC中,AB=AC=10,CB=16,分别以AB、AC为直径作半圆,则图中阴影部分面积是( )A.4850-πB.4825-πC.2450-πD.24225-π【答案】B4. (2011湖北随州,12,3分)一个几何体的三视图如下:其中主视图都是腰长为4、底边为2的等腰三角形,则这个几何体的侧面展开图的面积为()A.2πB.12πC.4πD.8π【答案】C5. (2011山西,7,2分)一个正多边形,它的每一个外角都等于45°,则该正多边形是()第12题图42 24左视图右视图俯视图BCA(第15题)A.正六边形 B. 正七边形 C. 正八边形 D. 正九边形【答案】C6. (2011山西,8,2分)如图谋是一个工件的三视图,图中标有尺寸,则这个工件的体积是()A.313cmπ B. 317cmπ C. 366cmπ D. 368cmπ【答案】B7. (2011山东莱芜,11,3分)将一个圆心角是090的扇形围成圆锥的侧面,则该圆锥的侧面积侧S和底面积底S的关系为A.侧S=底S B.侧S=2底S C.侧S=3底S D.侧S=4底S【答案】D8. (2011湖南娄底,8,3分)如图2所示的平面图形中,不可能围成圆锥的是【答案】D9. (2011湖南娄底,10,3分)如图3,自行车的链条每节长为2.5cm,每两节链条相连接部分重叠的圆的直径为0.8cm,如果某种型号的自行车链条共有60节,则这根链条没有安装时的总长度为A. 150cmB. 104.5cmC. 102.8cmD. 102cm【答案】C10.(2011内蒙古呼和浩特市,3,3分)已知圆柱的底面半径为1,母线长为2,则圆柱的侧面积为()A. 2B. 4C. π2D. π4【答案】D11.(2011内蒙古呼和浩特市,10,3分)下列判断正确的有(左视图)(主视图)4㎝(俯视图)(第8题)1cm4cm2㎝()①顺次连接对角线互相垂直且相等的四边形的各边中点一定构成正方形②中心投影的投影线彼此平行③在周长为定值p的扇形中,当半径为4p时扇形的面积最大④相等的角是对顶角的逆命题是真命题A. 4个B. 3个C. 2个D. 1个【答案】B12. (2011广东肇庆,9,3分)已知正六边形的边心距为3,则它的周长是A.6B.12C.36D.312【答案】B13. (2011广西桂林,12,3分)如图,将边长为a的正六边形A1A2A3A4A5A6在直线l上由图1的位置按顺时针方向向右作无滑动滚动,当A1第一次滚动到图2位置时,顶点A1所经过的路径的长为().A.4233aπ+B.8433aπ+C.433aπ+D.4236aπ+【答案】A14. (2011广西南宁,11,3分)如图5,四个半径为l的小圆都过大圆圆心且与大圆相内切,阴影部分的面积为:OH BA( A)π (B)2π-4 (c) 2π (D) 2π+1 【答案】B15. (2011四川广元,8,3分)若用圆心角为120°,半径为9的扇形围成一个圆锥侧面(接缝忽略不计),则这个圆锥的底面直径是( B )A .3B .6C .9D .12【答案】B16. (2011四川眉山,5,3分)若一个正多边形的每个内角为150°,则这个正多边形的边数是A .12 B11 C 10 D .9【答案】A17. (2011广西来宾,2,3分)圆柱的侧面展开图是( )A 圆B 矩形C 梯形D 扇形【答案】B18. (2011广西来宾,12,3分)如图,在△ABC 中,已知∠A=90°AB =AC =2,O 为BC 的中点,以O 为圆心的圆弧分别与AB 、AC 相切于点D 、E ,则图中阴影部分的面积是( )A.14π-B. 4πC. 12π- D.22π-OBDECA【答案】A19. (2011年铜仁地区,3,4分)将如图1所示的直角三角形绕直线l旋转一周,得到的立体图形是()【答案】B20.(2011福建三明,9,4分)用半径为12㎝,圆心角为90°的扇形纸片,围成一个圆锥的侧面,这个圆锥的底面半径为()A.1.5㎝B.3㎝C.6㎝D.12㎝【答案】B21.(2011湖北鄂州,12,3分)一个几何体的三视图如下:其中主视图都是腰长为4、底边为2的等腰三角形,则这个几何体的侧面展开图的面积为()A.2πB.12πC.4πD.8π【答案】C22.(2011云南玉溪,5,3分)如图,是一个有盖子的圆柱体水杯,地面周长为6πCM,高为18CM,若盖子与杯体的重合部分忽略不计,则制作10个这样的水杯至少需要的材料是()A. 108πcm2B. 1080πcm2C. 126πcm2D. 1260πcm2第12题图42 24左视图右视图俯视图【答案】D.23.(2011•泸州,9,2分)如果圆锥的底面周长为20π,侧面展开后所得扇形的圆心角为120°,则该圆锥的全面积为()A、100πB、200πC、300πD、400π【答案】C.24. (2011山东淄博,11,3分)如图,矩形ABCD中,AB=4,以点B为圆心,BA为半径画弧交BC于点E,以点O为圆心的⊙O与弧AE,边AD,DC都相切.把扇形BAE作一个圆锥的侧面,该圆锥的底面圆恰好是⊙O,则AD的长为()A.4 B.92C.112D.5【答案】D25.(2011广西百色,12,3分)如图,用高为6cm,底面直径为4cm的圆柱A的侧面积展开图,再围成不同于A的另一个圆柱B,则圆柱B的体积为A.24πcm³B. 36πcm³C. 36cm³D. 40cm³【答案】:A26.(2010乌鲁木齐,7,4分)露露从纸上剪下一个圆形和一个扇形的纸片(如图),用它们恰好能围成一个圆锥模型,若圆的半径为1,扇形的圆心角等于120°,则此扇形的半径为A.3B.6C.3D.6【答案】C27.(2011新疆维吾尔自治区,新疆生产建设兵团,8,5分)某几何体的三视图及相关数据如图所示,该几何体的全面积s等于A.()12a a cπ+B.()12a a bπ+C.()a a cπ+D.()a a bπ+【答案】C28.29.30.二、填空题1.(2011河南,14,3分)如图是一个几何体的三视图,根据图示的数据可计算出该几何体的表面积为.(第14题图)【答案】90π2. (2011黑龙江省哈尔滨市,14,3分)若圆锥的侧面展开图是一个弧长为16π的扇形,则这个圆锥的底面半径是_。
正多边形、扇形、圆锥侧面展开图

练习
1. 填空
(1)已知圆锥的底面直径为4,母线长为6,则它的侧面积为_________.
(2)已知圆锥底面圆的半径为2 cm ,高为____________
则这个圆锥的侧面积为_________;全面积为_________
2. 如果圆锥的底面周长是20 π,侧面展开后所得的扇形的圆心角为120度
则该圆锥的侧面积为_____,全面积为______
3. 若圆锥的底面半径r =4cm,高线h =3cm,则它的侧面展开图中扇形的圆心角是——度。
4.若圆锥的侧面展开图是半圆,那么这个展开图的圆心角是___度;
圆锥底半径r与母线a的比r :a = ___ .
5,如图,圆锥的底面半径为1,母线长为6,一只蚂蚁要从底面圆周上一点B出发,
沿圆锥侧面爬行一圈再回到点B,问它爬行的最短路线是多少?
6,蒙古包可以近似地看成由圆锥和圆柱组成的.如果想在某个牧区搭建15个底面积为33m2 高为10m(其中圆锥形顶子的高度为2m)的蒙古包.那么至少需要用多少平方米的帆布?(结果精确到0.1m2).。
初中数学综合复习之正多边形、扇形和圆锥侧面展开图(含图形的镶嵌)2

初中数学综合复习之正多边形、扇形和圆锥侧面展开图(含图形的镶嵌)2一、选择题1. 下列立体图形中,侧面展开图是扇形的是()【答案】B2.阅读理解:如图3,在平面内选一定点O,引一条有方向的射线Ox,再选定一个单位长度,那么平面上任一点M的位置可由MOx的度数θ与OM的长度m确定,有序数对(θ,m)称为M点的“极坐标”,这样建立的坐标系称为“极坐标系”.应用:在图4的极坐标系下,如果正六边形的边长为2,有一边OA在射线Ox上,则正六边形的顶点C的极坐标应记为A.(60°,4) B.(45°,4) C.(60°,22) D.(50°,22)图3 图4【答案】A3.一个多边形的内角和是900°,这个多边形的边数是()A.4B.5C.6D.7考点:多边形内角与外角.分析:根据多边形的外角和公式(n﹣2)•180°,列式求解即可.解答:解:设这个多边形是n边形,根据题意得,(n﹣2)•180°=900°,解得n=7.故选D.点评:本题主要考查了多边形的内角和公式,熟记公式是解题的关键.4.一圆锥体形状的水晶饰品,母线长是10cm,底面圆的直径是5cm,点A为圆锥底面圆周上一点,从A点开始绕圆锥侧面缠一圈彩带回到A点,则彩带最少用多少厘米(接口处重合部分忽略不计)()A. 10πcmB. 102cmC. 5πcmD. 52cm【答案】B5.在半径为2的圆中,弦AB的长为2,则的AB长等于()A.3πB.2πC.32πD.23π【答案】C二、填空题1.如图,AB是⊙O的直径,分别以OA,OB为直径作半圆,若AB=4,则阴影部分的面积是__________.【答案】2π2.如图,在菱形ABCD中,AB=1,∠DAB=60°.把菱形ABCD绕点A顺时针旋转30°得到菱形AB C D''',其中点C 的运动路径为CC',则图中阴影部分的面积为.【答案】233-4+π3.已知扇形的半径为3cm,此扇形的弧长是2πcm,则此扇形的圆心角等于度,扇形的面积是.(结果保留π)【答案】120,32cmπ4.一个底面直径为10cm,母线长为15cm的圆锥,它的侧面展开图圆心角是_________________度.【答案】1205.如图所示,有一直径是2米的圆形铁皮,现从中剪出一个圆周角是︒90的最大扇形ABC.则(1)AB的长为米;(2)用该扇形铁皮围成一个圆锥,所得圆锥的底面圆的半径为米.【答案】(1)1(2)146.用一个圆心角为240°半径为6的扇形做一个圆锥的侧面,则这个圆锥的底面半径为____.(第14题)O【答案】47.已知圆锥的底面直径为20cm,母线长为90cm,则圆锥的表面积是;.(结果保留π)答案:1000π三、解答题1. 如图11-1,四边形ABCD是正方形,点E是边BC上一点,点F在射线CM上,∠AEF= 90°,AE=EF,过点F作射线BC的垂线,垂足为H,连接AC。
正多边形、扇形和圆锥侧面展开图

(2010年河北)某盏路灯照射的空间可以看成如图9所示的圆锥,它的高AO=8米,母线AB与底面半径OB的夹角为α,4tan3α=,则圆锥的底面积是平方米(结果保留π)。
15.(2010年湖南常德)如果一个扇形的弧长等于它的半径,那么此扇形称为“等边扇形”.则半径为2的“等边扇形”的面积为()A。
π B。
1 C。
2 D。
2 3π(2010年四川广安)如右图,一个扇形纸片OAB.OA=30cm,∠AOB=120°,小明将OA、OB合拢组成一个圆锥形烟囱帽(接缝忽略不计).则烟囱帽的底面圆的半径为cm.(2010年山东威海)一个圆锥的底面半径为6㎝,圆锥侧面展开图扇形的圆心角为240°,则圆锥的母线长为A.9㎝B.12㎝C.15㎝D.18㎝(2010年江苏淮安)将半径为5,圆心角为144°的扇形围成一个圈锥的侧面,则这个圆锥的底面半径为.(2010年山东聊城)(2010年贵州遵义)1.(2010江苏苏州).如图,在4×4的方格纸中(共有16个小方格),每个小方格都是边长为1的正方形. O 、A 、B 分别是小正方形的顶点,则扇形OAB 的弧长等于 ▲ .(结果保留根号及 ).【答案】2.(2010广东广州)将图1所示的直角梯形绕直线l 旋转一周,得到的立体图开是( )l【答案】C3.(2010甘肃兰州) 现有一个圆心角为90,半径为cm 8的扇形纸片,用它恰好围成一个圆锥的侧面(接缝忽略不计).该圆锥底面圆的半径为A . cm 4B .cm 3C .cm 2D .cm 1 【答案】C4.(2010山东济宁)如图,如果从半径为9cm 的圆形纸片剪去13圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的高为 A .6cmB. C .8cmD.cm【答案】B5.(2010山东威海)一个圆锥的底面半径为6㎝,圆锥侧面展开图扇形的圆心角为240°,则圆锥的母线长为A.9㎝B.12㎝C.15㎝D.18㎝【答案】A6.(2010四川眉山)下列四个图中,是三棱锥的表面展开图的是【答案】B7.(2010台湾)如图(十三),扇形AOB中,OA=10,∠AOB=36︒。
中考复习真题汇编29:正多边形、扇形和圆锥侧面展开图
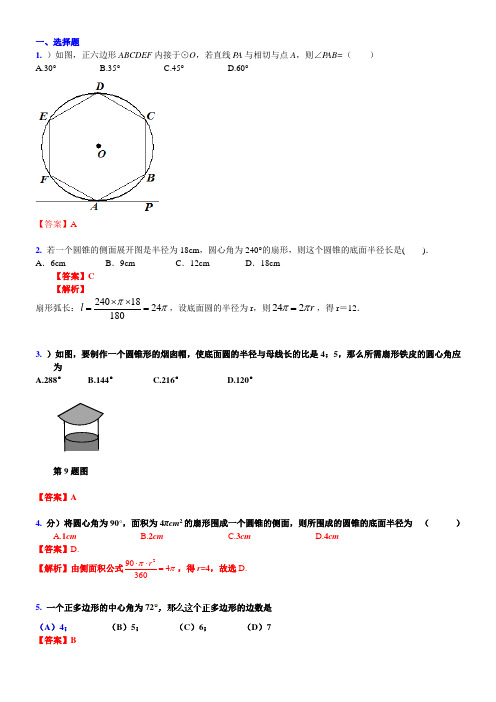
一、选择题1.)如图,正六边形ABCDEF内接于⊙O,若直线P A与相切与点A,则∠P AB=()A.30°B.35°C.45°D.60°【答案】A2.若一个圆锥的侧面展开图是半径为18cm,圆心角为240°的扇形,则这个圆锥的底面半径长是().A.6cm B.9cm C.12cm D.18cm【答案】C【解析】扇形弧长:2401824180lππ⨯⨯==,设底面圆的半径为r,则242rππ=,得r=12.3.)如图,要制作一个圆锥形的烟囱帽,使底面圆的半径与母线长的比是4:5,那么所需扇形铁皮的圆心角应C.216°D.120°第9题图【答案】A4.分)将圆心角为90°,面积为4πcm2的扇形围成一个圆锥的侧面,则所围成的圆锥的底面半径为()A.1cmB.2cmC.3cmD.4cm【答案】D.【解析】由侧面积公式2904360rππ⋅⋅=,得r=4,故选D.5.一个正多边形的中心角为72多边形的边数是(A)4;(B)5;(C)6;(D)7 【答案】B【解析】直接用周角360=56.个几何体的表面展开图如图所示,则这个几何体是A .四棱锥B .四棱柱C .三棱锥D .三棱柱【答案】A7. )若用一张直径为20cm 的半圆做成一个圆锥的侧面,接缝忽略不计,则所得圆锥的高为( ) A. cm 35 B. cm 55 C.cm 2155 D. cm 10【答案】A【解析】先利用弧长公式直径为20cm 的半圆的弧长10π,根据圆锥的侧面展开图为扇形,扇形的弧长等于圆锥的底面圆的周长,则可计算出圆锥的底面圆的半径,然后根据勾股定理可计算出圆锥的高.∵直径为20cm 的半圆的弧长=10π,∴圆锥的底面圆的周长为10π,∴圆锥的底面圆的半径为5, ∴这个纸帽的高225-10=35(cm ).故选A .8. 分)如图,正六边形111111F E D C B A 的边长为2,正六边形222222F E D C B A 的外接圆与正六边形111111F E D C B A 的各边相切,正六边形333333F E D C B A 的外接圆与正六边形222222F E D C B A 的的各边相切,·······按这样的规律进行下去,正十边形 101010101010F E D C B A 的边长为( )A.92243 B.92381 C.9281 D.82381【答案】D【解析】设正六边形111111F E D C B A 相邻连边11B A 和11F A 与⊙O 的切点分别为2A 和2B ,连接2OA ,1OA ,2OB ,(第4题图)1OA 与22B A 的交点为M ,则M B B A 2222=,21112B A B A =,由题意知∠M B A 21=30°, 1OA⊥22B A ,=M B 22321B A ,所以=22B A 2311B A ,所以=n n B A 111)23(B A n -,根据这个规律=1010B A =119)23(B A =⨯2)23(982381.故选D.MOB2A2F1B1A19.如图,用一个半径为 30cm ,面积为 300πcm 2的扇形铁皮,制作一个无底的圆锥(不计损耗),则圆锥的底面半径r 为( )A.5cmB.10cmC.20cmD.5πcm【答案】B10. (2015年山东省济宁市)只用下列哪一种正多边形,可以进行平面镶嵌( ) A. 正五边形 B. 正六边形 C. 正八边形 D.正十边形 【答案】B11. 如右图,等腰直角△ABC中,AB=AC=8,以AB为直径的半圆O 交斜边BC于D ,则阴影部分面积为(结果保留π)( ) (A ) 244π- (B) 324π- (C) 328π- (D) 16【答案】A【解析】解:(1)如图连接AD 、OD 。
036.正多边形、扇形和圆锥侧面展开图(含图形的镶嵌)汇编

一、选择题1. (2013山东泰安,18,3分)如图,AB 、CD 是⊙O 的两条互相垂直的直径,点O1、O2、O3、O4分别OA 、OB 、OC 、OD 的中点,若⊙O 的半径是2,则阴影部分的面积为( )A .8B .4C .4π+4D .4π-4【答案】A2. (2013浙江湖州,7,3分)在学校组织的实践活动中,小新同学用纸板制作了一个圆锥模型,它的底面半径为1,高为)A .4πB .3πC .D .2π【答案】B3. (2013重庆A 卷,8,4分)8.如图,P 是⊙O 外一点,PA 是⊙O 的切线,PO=26cm ,PA=24cm ,则⊙O 的周长为( )A .18πcmB .16πcmC .20πcmD .24πcm【答案】C4. (2013浙江温州市,10,4分)在△ABC 中,∠C 为锐角,分别以AB ,AC 为直径作半圆,过点B ,A ,C 作弧BAC ,如图所示,若AB =4,AC =2,12-S 4S π=,则S 1-S 2的值是( ) A.429π B.423π C.411π D.45π A BCD O 1 O 2 O 3O 4O【答案】D5. (2013山东临沂,7,3分)如图是一个几何体的三视图,则这个几何体的侧面积是( )A . 12πcm 2B .8πcm 2C .6πcm 2D .3πcm 2【答案】 C.6.(2013山东德州,10,3分)如图,扇形AOB 的半径为1,∠AOB 90 ,以AB 为直径画半圆,则图中的阴影部分的面积为( )A .41B . 21C .21D .41 21【答案】C首先利用扇形公式计算出半圆的面积和扇形AOB 的面积,然后求出△AOB 的面积,用S 半圆+S △AOB-S 扇形AOB 可求出阴影部分的面积.7. (2013江西南昌,11,3分)如图,正六边形ABCDEF 中,AB=2,点P 是ED 的中点,连接AP ,则AP 的长为()A.2 3B.4C.13D.11【答案】C勾股定理.分析:连接AE,求出正六边形的∠F=120°,再求出∠AEF=∠EAF=30°,然后求出∠AEP=90°并求出AE的长,再求出PE的长,最后在Rt△AEP中,利用勾股定理列式进行计算即可得解.解答:解:如图,连接AE,在正六边形中,∠F=16×(6-2)•180°=120°,∵AF=EF,∴∠AEF=∠EAF=12(180°-120°)=30°,∴∠AEP=120°-30°=90°,本题考查了勾股定理,正六边形的性质,等腰三角形三线合一的性质,作辅助线构造出直角三角形是解题的关键.8. (2013内蒙古呼和浩特,6,3分)只用下列图形中的一种,能够进行平面镶嵌的是( )A. 正十边形B. 正八边形C. 正六边形D. 正五边形【答案】C9.(2013山东聊城,7,3分)把地球看成一个表面光滑的球体,假设沿地球赤道绕紧一圈钢丝,然后把钢丝加长,使钢丝圈沿赤道处处高出球面16厘米,那么钢丝大约需加长( )厘米A .210B .410C .610D .810【答案】A10. (2013湖南湘西,9,3分)下列图形中,是圆锥..侧面展开图的是( )【答案】B11. (2013湖南常德,16,3)连接一个几何图形上任意两点间的线段中,最长的线段称为这个几何图形的直径,根据此定义,图5(扇形、菱形、直角梯形、红十字图标)中“直径” 最小的是( )【答案】C12. (2013湖北黄冈市,7,3分)已知一个圆柱的侧面展开图为如图所示的矩形,则其底面圆的面积为( )A.πB.4πC.π或4πD.2π或4π【答案】C13. (2013浙江台州,9,4分)如图,已知边长为2的正三角形ABC 顶点A 的坐标为(0,6),BC 的中点D 在y 轴上,且在A 的下方,点E 是边长为2,中心在原点的正六边形的一个顶点,把这个正六边形绕中心旋转一周,在此过程中DE 的最小值为( )A.3B.34-C.4D.326-【答案】B14. (2013甘肃兰州,14,4分)圆锥底面圆的半径为3cm ,其侧面展开图是半圆,则圆锥母线长为()A .3cmB .6cmC .9cmD .12cm【答案】B.15. (2013台湾)附图为八个全等的正六边形紧密排列在同一平面上的情形。
全国中考数学模拟汇编二 42正多边形 扇形和圆锥侧面展开图

全国中考数学模拟汇编二 42正多边形 扇形和圆锥侧面展开图A 组一 选择题1.(2011浙江金衢十一校联考)如图,若用半径为9,圆心角为120°的扇形围 成一个圆锥的侧面(接缝忽略不计),则这个圆锥的底面半径是 ( ) A .1.5 B .2 C .3 D .6 【答案】C2.(2011浙江新昌县模拟)如图是一个空心圆柱形纸筒,高为3,底面圆周长为4,若将这个纸筒沿圆筒侧面线路B M A →→剪开铺平,所得图形可能为 A .边长为3和4的矩形 B .边长为5和4的矩形C .边长为5和3的平行四边形D .边长为5和4的平行四边形【答案】D3. (2011珠海市香洲区模拟)如图,已知在Rt △ABC 中,∠BAC=90,AB=3,BC=5,若把 Rt △ABC 绕直接AC 旋转一周,则所得圆锥的侧面积等于( ) A.6π B.9π C.12π D.15π 【答案】D4、(2011年天河区) 若一个正多边形的一个外角是40°,则这个正多边形的边数是( ).A. 10B. 9C. 8D. 6 考查内容:答案:B 5、(2011朝阳区一模) 一元钱硬币的直径约为24mm ,则用它能完全覆盖住的正六边形的边长最大不能超过 A .12 mm B .123mm C .6mm D .63mm 考查内容: 正多边形 扇形和圆锥侧面展开图答案:A 6、(2011怀柔一模) 如图是一个圆锥形冰淇淋,已知它的母线长是5cm ,高是4cm ,则这个圆锥形冰淇淋的底面面积是120°(第9题图)第10题图A .210cm πB .29cm πC .220cm πD .2cm π考查内容: 答案:B7、(2011广东化州二模) 已知圆锥的底面半径为6cm ,高为8cm ,则圆锥的侧面积为( ) A. 236cm π B. 248cm π C. 260cm π D. 280cm π 考查内容: 答案:C8、(2011年天河区) 圆锥的侧面积为210cm π,其侧面展开图的圆心角为36º,则该圆锥的母线长为( ).A .100cmB .10cmC .10cmD .1010cm考查内容: 答案:B9. (2011番禺区综合训练)一根水平放置的圆柱形输水管道横截面如图3所示,其中有水部分水面宽0.8米,最深处水深0.2米,则此输水管道的直径是(※). (A )0.4米 (B )0.5米 (C )0.8米 (D )1米 答案:D 10(2011年天河区综合练习)圆锥的侧面积为210cm π,其侧面展开图的圆心角为36º,则该圆锥的母线长为( ).A .100cmB .10cmC .10cmD .1010cm答案:B.二 填空题1.(2011上海市杨浦区中考模拟)正十二边形的中心角等于度.【答案】30;图3第13题图ABOA B C 2.(2011双柏县中考模拟)若一个圆锥的底面圆的半径是2cm ,母线长是6cm ,则该圆锥的侧面展开图的圆心角的度数是 。
42正多边形、扇形和圆锥侧面展开图

正多边形、扇形和圆锥侧面展开图一、选择题1、(2012年浙江金华五模)一把大遮阳伞,伞面撑开时可近似地看成是圆锥形,如图,它的母线长是2. 5米,底面半径为2米,则做这把遮阳伞需用布料的面积是( ▲ )平方米(接缝不计) A . π3 B .π4 C .π5 D .π425答案:C2、(浙江金华一模)一个长方形的长与宽分别为和16cm ,绕它的对称中心旋转一周所扫过的面积是 2cm ;旋转90度时,扫过的面积是 2cm . 答案:256π,6401283π+ 3、(2012年上海青浦二模)如果⊙1O 的半径是 5,⊙2O 的半径为 8,124O O =,那么⊙1O 与⊙2O 的位置关系是( )A .内含;B .内切;C .相交;D .外离. 答案:C4、如图,已知圆锥的高为8,底面圆的直径为则此圆锥的侧面积是( ) A 、24∏B 、30∏C 、48∏D 、60∏5、已知圆柱的底面直径为4cm ,高为5cm ,则圆柱的侧面积是 ( ) A .10cm 2 B .10兀cm 2 C .20兀cm 2 D .40 兀cm 2 答案:C6、(2012山东省德州四模)已知⊙O 1和⊙O 2外切,它们的半径分别为2cm 和5cm ,则O 1O 2的长( ) (A )2cm (B )3cm (C )5cm (D )7cm 答案:D7(2012山东省德州一模) 以O 为圆心的两个同心圆的半径分别为9cm 和5 cm ,若⊙P 与这两个圆都相切,则下列说法中正确的是( ).(A)⊙P 的半径一定是2cm (B)⊙P 的半径一定是7 cm (C) 符合条件的点P 有2个 (D) ⊙P 的半径是2 cm 或7cm 答案:D 8、(2012江苏无锡前洲中学模拟)已知圆锥的底面直径是12cm ,母线长为8cm ,则这个圆锥的侧面积是( )A .48πcm 2B .48cm 2C .96π cm 2D .96 cm 2答案:A 9、(2012荆门东宝区模拟)在综合实践活动课上,小明同学用纸板制作了一个圆锥形漏斗模型.如图所示,它的底面半径OB =6cm ,高OC =8cm .则这个圆锥漏斗的侧面积是( ). A .30cm 2 B .30πcm 2 C .60πcm 2 D .120cm210、(2012兴仁中学一模)如图,在Rt △ABC 中,∠C =90°,CA=CB=4,分别以A 、B 、C 为圆心,以21AC 为半径画弧,三条弧与边AB 所围成的阴影部分的面积是. 答案π28-11.(2012年春期福集镇青龙中学中考模拟)已知圆锥的底面半径为4cm ,高为3cm ,则这个圆锥的侧面积为__________cm 2. 答案20π12、(2012温州市泰顺九校模拟) 在R t △ABC 中,∠C=90°,AC=8,BC=6,两等圆⊙A ,⊙B外切,那么图中两个扇形(即阴影部分)的面积之和为( ) A .258πB . 254πC .2516πD .2532π答案B13、(2012石家庄市42中二模)如果一个扇形的弧长等于它的半径,那么此扇形称为“等边扇形”.则半径为2的“等边扇形”的面积为( )A .π B.1 C.2 D.23π答案:C14、(2012温州市泰顺九校模拟)在R t △ABC 中,∠C=90°,AC=8,BC=6,两等圆⊙A ,⊙B 外切,那么图中两个扇形(即阴影部分)的面积之和为( )A .π825 B .π425C .π1625 D .π3225 第17题图 (第9题)答案:B15(2012荆州中考模拟)如图1,现有一个圆心角为90°,半径为8cm 的扇形纸片,用它恰好围成一个圆锥的侧面(接缝忽略不计),则该圆锥底面圆的半径为( )A .4cmB .3cmC .2cmD .1cm答案:C16、(2012双柏县学业水平模拟考试)已知圆锥的母线长为4,底面半径为2,则圆锥的侧面积等于【 】A .11πB .10πC . 9πD . 8π 答案:D17、(2012深圳市龙城中学质量检测)露露从纸上剪下一个圆形和一个扇形的纸片(如图),用它们恰好 能围成一个圆锥模型,若圆的半径为1.扇形的圆心角等于120°, 则此扇形的半径为A 、3B 、6错误!未找到引用源。
初中数学综合复习之正多边形、扇形和圆锥侧面展开图(含图形的镶嵌)4
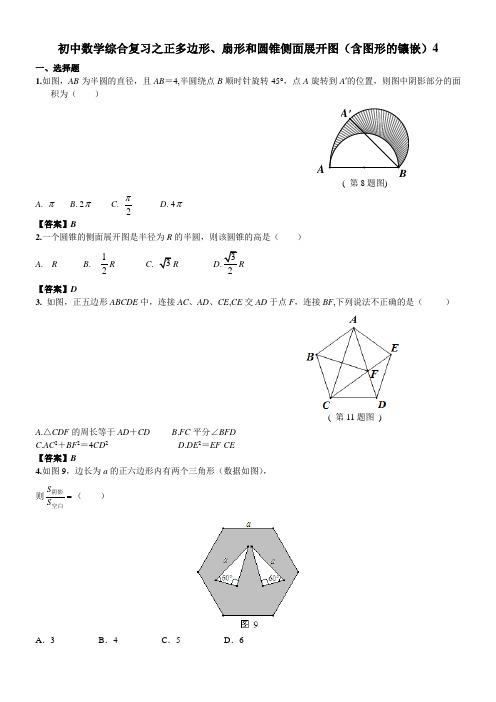
初中数学综合复习之正多边形、扇形和圆锥侧面展开图(含图形的镶嵌)4一、选择题1.如图,AB 为半圆的直径,且AB =4,半圆绕点B 顺时针旋转45°,点A 旋转到A ′的位置,则图中阴影部分的面积为( )A . πB . 2πC .2πD . 4π 【答案】B2.一个圆锥的侧面展开图是半径为R 的半圆,则该圆锥的高是( ) A . R B .12R C . 3R D .32R 【答案】D3. 如图,正五边形ABCDE 中,连接AC 、AD 、CE ,CE 交AD 于点F ,连接BF ,下列说法不正确的是( )A .△CDF 的周长等于AD +CDB .FC 平分∠BFD C .AC 2+BF 2=4CD 2 D .DE 2=EF ·CE 【答案】B4.如图9,边长为a 的正六边形内有两个三角形(数据如图), 则=空白阴影S S ( )A .3B .4C .5D .6( 第11题图 )( 第8题图)A'AB【答案】C5. 用一个圆心角为120°,半径为3的扇形作一个圆锥的侧面,则这个圆锥的底面半径为( ) A .21B .1C .23 D .2【答案】B.6.如果圆锥的母线长为5cm ,底面半径为2cm ,那么这个圆锥的侧面积是A. 102cmB. 102πcmC. 202cm D.202πcm【考点】圆锥的计算【解析】选B.圆锥的侧面积S=πrl ,r 是底面半径,l 是母线长.∴S=π×2×5=10π(cm 2),故选B. 7.已知扇形的圆心角为45°,半径长为12,则该扇形的弧长为 A.34πB. 2πC.3πD.12π 【答案】C8.如图,均为以O 点为圆心所画出的四个相异弧,其度数均为60°,且G 在OA 上,C 、E 在AG 上,若AC =EG ,OG =1,AG =2,则与两弧长的和为何?( )A .πB .4π3C .3π2D .8π5分析:设AC =EG =a ,用a 表示出CE =2﹣2a ,CO =3﹣a ,EO =1+a ,利用扇形弧长公式计算即可. 解:设AC =EG =a ,CE =2﹣2a ,CO =3﹣a ,EO =1+a , +=2π(3﹣a )×60°360°+2π(1+a )×60°360°=π6 (3﹣a +1+a )= 4π3.故选B .9.小明用图中所示的扇形纸片作一个圆锥的侧面,已知扇形的半径为5cm ,弧长是6πcm ,那么这个的圆锥的高是( )A . 4cmB . 6cmC . 8cmD . 2cm考点: 圆锥的计算;弧长的计算.分析: 一只扇形的弧长是6πcm ,则底面的半径即可求得,底面的半径,圆锥的高以及母线正好构成直角三角的三边,利用勾股定理即可求解.解答: 解:设圆锥的底面半径是r ,则2πr=6π,解得:r=3, 则圆锥的高是:=4cm .故选A .点评: 本题主要考查圆锥侧面展开图的知识和圆锥侧面面积的计算.用到的知识点:圆锥的侧面展开图是一个扇形,扇形的弧长等于圆锥底面的周长,扇形的半径是圆锥的母线长.10. 已知扇形的圆心角为60°,半径为1,则扇形的弧长为( ) A .2πB .πC .6πD .3π 【答案】D11. 如图,扇形AOB 中,半径OA =2,∠AOB =120°,C 是弧AB 的中点,连结AC 、BC ,则图中阴影部分的面积是( )A .4-233π B .2-233π C .4-33π D .2-33π 【答案】A12.一个圆锥的底面半径为6cm ,其侧面展开图为半圆,则圆锥的母线长为( ) A.9cm B.12cm C.15cm D.18cm 【答案】B二、填空题1. 如图,将四个圆两辆相切拼接在一起,它们的半径均为1cm ,则图中阴影部分的面积为 cm 2. 【答案】4-π2. 如图10,将长为8cm 的铁丝AB 首尾相接围成半径为2cm 的扇形.则=扇形S ______2cm .【答案】43. 如图,扇形OAB中,∠AOB=60°,扇形半径为4,点C在弧AB上,CD⊥OA,垂足为点D,当△OCD的面积最大时,图中阴影部分的面积为.【答案】4-π4. 如图,两个半径均为3的⊙O1与⊙O2相交于A、B两点,且每个圆都经过另一个圆的圆心,则图中阴影部分的面积为.【答案】2π-335.已知圆锥的底面半径是4,母线长是5,则该圆锥的侧面积是__________.(结果保留π)【答案】20π6.如图,在⊿ABC中,AB=BC=2,∠ABC=90°,则图中阴影部分的面积是【答案】π-2.7.如图,在□ABCD中,以点A为圆心,AB的长为半径的圆恰好与CD相切于点C,交AD于点E,延长BA与⊙A相交于点F.若EF的长为2π,则图中阴影部分的面积为▲.【答案】2-2π.8.如图,在扇形OAB中,∠AOB=90°,点C是⌒AB上的一个动点(不与A,B重合),OD⊥BC,OE⊥AC,垂足分别为D,E.若DE=1,则扇形OAB的面积为.AB CDEF第16题图ABO1 O2【答案】129.有一圆锥,它的高为8cm ,底面半径为6cm ,则这个圆锥的侧面积是 cm 2. (结果保留π) 【答案】60π10.如图,⊙A 与⊙B 外切于⊙O 的圆心O ,⊙O 的半径为1,则阴影部分的面积是____.【答案】13π3-.11. 如图,正三角形ABC 的边长为2,D ,E ,F 分别为BA ,CA ,AB 的中点,以A ,B ,C 三点为圆心,半径为1作圆,则图中阴影部分的面积是 . 【答案】23π-12. 如图,两圆圆心相同,大圆的弦AB 与小圆相切,AB =8,则图中阴影部分的面积是__________.(结果保留π)OBAAC D EFOBOACED(第13题)【答案】16π13.若圆锥的轴截面是一个边长为4的等边三角形,则这个圆锥的侧面展开后所得的扇形的圆心角的度数是 【答案】180° 三、解答题1.如图,在正方形ABCD 中,AD =2,E 是AB 的中点,将△BEC 绕点B 逆时针旋转90°后,点E 落在CB 的延长线上点F 处,点C 落在点A 处.再将线段AF 绕点F 顺时针旋转90°得线段FG ,连接EF ,CG . 求证:EF ∥CG ;求点C ,点A 在旋转过程中形成的AC ,AG 与线段CG 所围成的阴影部分的面积.【答案】解:(1)证明:∵四边形ABCD 是正方形, ∴AB =BC =AD =2,∠ABC =90°. ∵△BEC 绕点B 逆时针旋转90°得△ABF , ∴△ABF ≌△CBE ,∴∠F AB =∠ECB ,∠ABF =∠CBE =90°,AF =EC , ∴∠AFB +∠F AB =90°.∵线段AF 绕点F 顺时针旋转90°得线段FG , ∴∠AFB +∠CFG =∠AFG = 90°,AF =FG , ∴∠CFG =∠F AB =∠ECB . ∴EC ∥FG .∵AF =EC ,AF =FG ,∴EC =FG , ∴四边形EFGC 是平行四边形, ∴EF ∥CG .(2)∵△ABF ≌△CBE , ∴FB =BE =12AB =1, ∴AF在△FEC 和△CGF 中∵EC =FG ,∠ECF =∠GFC ,FC =CF , ∴△FEC ≌△CGF , ∴S △FEC =S △CGF .∴S 阴影=S 扇形BAC +S △ABF +S △FGC -S 扇形F AG=2902360π⋅+12×2×1+12×(1+2)×1-290360π⋅=524π-(或104π-). 2. 如图,在△ABC 中,∠ABC=90°,D 是边AC 上的一点,连接BD ,使∠A=2∠1,E 是BC 上的一点,以BE为直径的圆O 经过点D(1)求证:AC 是圆O 的切线 (2)若∠A=60°,圆O 的半径为2,求阴影部分的面积(结果保留根号和π)【答案】证明:(1)如图,连接OD ,OB=OD ,则∠1=∠BDO ∠DOC=2∠1=∠A 在Rt △ABC 中,∠A+∠C=90°,即∠DOC+∠C=90° ∴∠ODC=90°即OD ⊥DC ∴AC 为圆O 的切线 (2)当∠A=60°时,即在Rt △OCD 中,∠C=30°,OD=r=2 ∴∠DOC=60°,CD=23 DC OD S ODC⨯=∆21=23 360n 2r S π=扇形=94π。
九年级数学模拟试卷分类汇编 42 正多边形、扇形和圆锥侧面展开图 试题
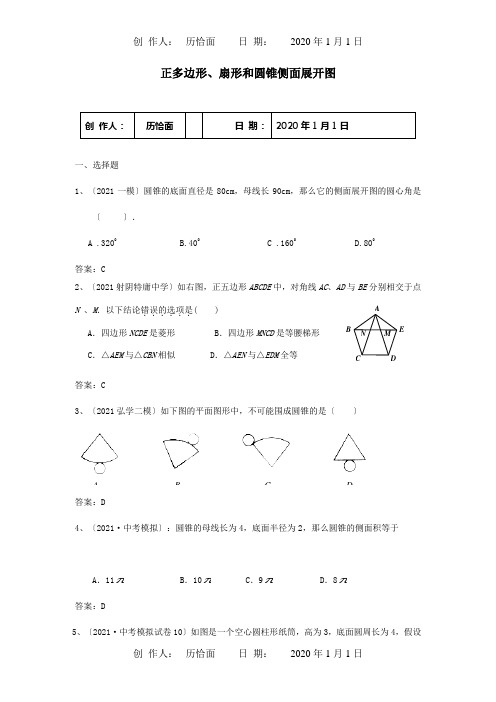
正多边形、扇形和圆锥侧面展开图创 作人:历恰面 日 期: 2020年1月1日一、选择题1、〔2021一模〕圆锥的底面直径是80cm ,母线长90cm ,那么它的侧面展开图的圆心角是〔 〕. A .3200B.400C .1600D.80答案:C2、〔2021射阴特庸中学〕如右图,正五边形ABCDE 中,对角线AC 、AD 与BE 分别相交于点N 、M .以下结论错误的选项是......( ) A .四边形NCDE 是菱形 B .四边形MNCD 是等腰梯形 C .△AEM 与△CBN 相似 D .△AEN 与△EDM 全等 答案:C3、〔2021弘学二模〕如下图的平面图形中,不可能围成圆锥的是〔 〕答案:D4、〔2021·中考模拟〕:圆锥的母线长为4,底面半径为2,那么圆锥的侧面积等于A .11πB .10πC .9πD .8π答案:D5、〔2021·中考模拟试卷10〕如图是一个空心圆柱形纸筒,高为3,底面圆周长为4,假设N M ED CBA BCDA将这个纸筒沿圆筒侧面线路B M A →→剪开铺平,所得图形可能为( )A .边长为3和4的矩形B .边长为5和4的矩形C .边长为5和3的平行四边形D .边长为5和4的平行四边形 答案:D6、10.(2021年二摸)在综合理论活动课上,小明同学用纸板制作了一个圆锥形漏斗模型.如下图,它的底面半径OB =6cm ,高OC =8cm ,那么这个圆锥漏斗的侧面积是 A .30cm B .30πcm C .60πcm D .120cm答案:C7、〔2021年一摸〕:圆锥的母线长为4,底面半径为2,那么圆锥的侧面积等于A .11πB .10πC .9πD .8π答案:D 二、填空题1、〔2021实中〕圆锥的侧面积为π8cm 2,侧面展开图的圆心角为45°,那么该圆锥的母线长为 cm 。
答案:82、 (2021·中考模拟)一个圆锥的母线长为4,侧面积为8π,那么这个圆锥的底面圆的半径是 . 答案:23、(2021·实验中学中考模拟)钟表的轴心到分针针端的长为4cm ,那么经过40分钟,分针针端转过的弧长是_______ cm(用π表示) .B A CO 第10题图答案:163π 4、(2021·实验中学中考模拟)如图,点O 是正ACE ∆和正BDF ∆的中心,且AE ∥BD ,那么AOF ∠=_______.答案:60°5、〔2021·中考模拟试卷1〕圆锥的底面直径为4cm ,其母线长为3cm ,那么它的侧面积为 . 答案:6π6、〔2021·中考模拟试卷7〕小明的圆锥形玩具的高为12cm ,母线长为13cm ,那么其侧面积是 2cm . 答案:65π7、〔2021·中考模拟试卷10〕某盏路灯照射的空间可以看成如下图的圆锥,它的高AO =8米, 母线AB =10米,那么该圆锥的侧面积是 平方米〔结果保存π〕.答案:60π8、(2021年西华县王营中学一摸)有一直径为4的圆形铁皮,要从中剪出一个最大圆心角为60°的扇形ABC ,用此剪下的扇形铁皮围成一个圆锥,该圆锥的底面圆的半径r= .答案:33 9、(2021年)如图,在半径为1的扇形AOB 中,∠AOB = 90°,点P 是AB 上的一个动点〔不与点A 、B 重合〕,PC ⊥OA ,PD ⊥OB ,垂足分别为点C 、D ,点E 、F 、G 、H 分别是线段OD 、PD 、PC 、OC 的中点,EF 与DG 相交于点M ,HG 与EC 相交于点N ,联结MN .假如设OC = x ,MN = y ,那么y 关于x 的答案:1)y x =<<AP C HOG N E D MF B〔第18题图〕。
12-正多边形、扇形和圆锥侧面展开图中考真题集锦含解析
1 2
B.
1 4
C.
1 6
D.
1 8
【答案】B 38. ( 2010 山东荷泽) 如图,在正方形铁皮中,剪下一个圆和一个扇形,使余料尽量 少, 用圆做圆锥的底面, 用扇形做圆锥的侧面, 正好围成一个圆锥, 若圆的半径记为 r , 扇形的半径记为 R ,那么 A.R =2 r B.R = r C.R =3 r D.R =4 r E A G
【答案】C 25. (2010 湖北恩施自治州)如图, 已知圆锥的高为 8,底面圆的直径为 12,则此圆锥的 侧面积是 A .24 B .30 C.48 D.60
【答案】D 26. (2010 江苏宿迁) 如图, ABC 是一个圆锥的左视图,其中 AB =AC=5,BC=8,则这个 圆锥的侧面积是 A 12
【答案】A 9. ( 2010 浙江杭州)如图,5 个圆的圆心在同一条直线上, 且互相相切,若大圆直径是 12, 4 个 小圆大小相等,则这 5 个圆的周长的和为 A. 48 C. 12 B. 24 D. 6
【答案】 B 10. (2010 江苏无锡)已知圆锥的底面半径为 2cm,母线长为 5cm,则圆锥的侧面积是( ) A.20cm 【答案】C
C
B
O
1 2
A E
F
C
B
【答案】C 28. ( 2010 云南昆明)如图,已知圆锥侧面展开图的扇形面积为
第 6 页 共 44 页
铮满分,吴压力!学而思网校 _初中数学吴铮老师_QQ 答疑群:246440018_验证信息:快乐铮满分
65 cm ,扇形的弧长为 10 cm,则圆锥母线长是(
2
)
第 3 页 共 44 页
⌒
(
42正多边形、扇形和圆锥侧面展开图

正多边形、扇形和圆锥侧面展开图一、选择题1、(2011年黄冈中考调研六)以下图形中,不能..表示长方体平面展开图的是( )答案D 2、(2011年四中中考模拟20)如图,点O 在Rt △ABC 的斜边AB 上, ⊙O 切AC 边于点E ,切BC 边于点D , 连结OE ,如果由线段CD 、CE 与劣弧ED围成的图形(阴影部分)面积与△AOE 的面积相等, 那么ACBC 的值约为(π取3.14) ( )A 、2.7B 、2.5C 、2.3D 、2.1答案C 3、(2011年四中模拟26)花园有一块边长为a 的正方形土地,园艺师设计了四种不同图案,其中的阴影部分用于种植花草,种植花草面积最大的是 ( )答案:D4. (2011年)圆锥的底面直径为6cm ,母线长为5cm ,则圆锥的侧面积是 () A.15cm 2B.15πcm 2C.30cm 2D.30πcm 2答案B.5、(2011盂县月考)小明用一个半径为5cm ,面积为15πcm 2的扇形纸片,制作成一个圆锥的侧面(接缝处不重叠),那么这个圆锥的底面半径为() A 、3cm B 、4cm C 、5cm D 、15cm 答案AA BDCE O6、(2011年八模)如图,边长为a 的六角螺帽在桌面上滚动(没有滑动) 一周,则它的中心O 点所经过的路径长为( ) A .6a B .5aC .2a πD .3a π 答案:C7、(2011年二模)一个圆锥,它的左视图是一个正三角形,则这个圆锥的侧面展开图的圆心角度数是( )A.60°B. 90°C.120°D. 180° 答案:D8、(2011年六模)现在把一正方形纸片按如图方式剪去一个半径为40 2 厘米的14圆面后得到如图纸片,且该纸片所能剪出的最大圆形纸片刚好能与前面所剪的扇形纸片围成一圆锥表面,则该正方形纸片的边长约为( )厘米﹒(不计损耗、重叠,结果精确到1厘米, 2 ≈1.41, 3 ≈1.73)A. 64B. 67C. 70D. 73 答案:AB 组1.(2011年江津区七校联考一模)将一个半径为5cm 面积为215cm π的扇形铁皮围成一个圆锥形容器(不计接缝),那么这个圆锥容器的高为( ). A 、3cm B 、4cm C 、5cm D 、2cm答案: B 2.(2011年市西湖区模拟)如图,已知扇形OBC ,OAD 的半径之间的关系是12OB OA =,则⌒BC 的长是⌒AD 长的( )A .14倍B .12倍C .2倍D .4倍答案:B(第6题) 第8题OCBAD第2题(第1题)3.(2011上城区一模)如图,顺次连结圆接矩形各边的中点,得到菱形ABCD ,若BD =6,DF =4,则菱形ABCD 的边长为( )A.42B.32C.5D.7答案:D4.(2011市模拟)小明用一个半径为5cm ,面积为15π2cm 的扇形纸片,制作成一个圆锥的侧面(接缝处不重叠),那么这个圆锥的底面半径为A .3cmB .4cmC .5cmD .15cm 答案:A5.(2011灌南县新集中学一模)已知圆锥的母线长为5,底面半径为3,则圆锥的侧面积[ ] A .15π B .24π C .30π D .39π 答案:A6.(2011义蓬一中一模)已知圆锥的侧面展开图的圆心角为120°,则这个圆锥的侧面积是底面积的( )A .2倍B .3倍C .21D .31答案:B7. (2011南塘二模)已知圆锥母线长为5cm ,底面直径为4cm ,则侧面展开图的圆心角度数是( )A 、136°B 、140°C 、144°D 、150° 答案:C 8.(靖江2011模拟)将半径为40cm 的圆形铁皮,做成四个相同的圆锥容器的侧面(不浪费材料,不计接缝处的材料损耗),那么每个圆锥容器的底面半径为 ( ) A .10cm B .20cm C .30cm D .60cm 答案:A9.(2011模拟)如图在Rt△ABC 中,∠BAC=90°,AB =3,BC =5,若把Rt△ABC 绕直线AC旋转一周,则所得圆锥的侧面积等于( ) A .6πB .9π C .12πD .15π 答案: DABCD E FO (第.3题)10、(2011市三模)已知圆锥的侧面积为10πcm 2,侧面展开图的圆心角为36º,则该圆锥的母线长为( )A.100cmB.10cmC. 10cmD.1010cm 答案:A11.(2011省崇阳县城关中学模拟)一个圆锥,它的左视图是一个正三角形,则这个圆锥的侧面展开图的圆心角度数是( ▲ ) A.60°B. 90°C.120°D. 180° 答案:D12、(2011市模四)如图,扇形OAB 是圆锥的侧面展开图,若小正方形方格的边长为1 cm ,则这个圆锥的底面半径为( )A .22cmB .2cmC .22cm D .21cm答案:C13.(2011年市模拟)如图,已知扇形OBC ,OAD 的半径之间的关系是12OB OA ,则⌒BC 的长是⌒AD 长的A .14倍B .12倍C .2倍D .4倍答案:B14.(2011年省市模2)一个圆锥,它的左视图是一个正三角形,则这个圆锥的侧面展开图的圆心角度数是( ) A.60°B. 90°C.120°D. 180° 答案:D15、(州二中九年七班模拟)已知圆锥的侧面积为10πcm 2,侧面展开图的圆心角为36º,则该圆锥的母线长为( )。
初中数学综合复习之正多边形、扇形和圆锥侧面展开图(含图形的镶嵌)1

初中数学综合复习之正多边形、扇形和圆锥侧面展开图(含图形的镶嵌)1一、选择题1.已知圆柱体的底面半径为3 cm,髙为4 cm,则圆柱体的侧面积为( )A.2cm 24πB.2cm 36πC.2cm 12D.2cm 24【答案】A2.已知圆锥的母线长为6cm ,底面圆的半径为3cm ,则此圆锥侧面展开图的圆心角的度数是( )A .30°B .60°C .90°D .180°【答案】D3.如图,圆柱体的高h=23,底面圆半径r =2cm ,则圆锥体的全面积为( )cm 2A .43πB .8πC .12πD .(43+4)π【答案】C4.圆锥体的底面半径为2,侧面积为8π,则其侧面展开图的圆心角为( )A .90°B .120°C .150°D .180°【答案】D5.已知圆锥的母线长为3,底面的半径为2,则圆锥的侧面积是( )A .4πB .6πC .10πD .12π【答案】B6.如图,圆锥的母线长为2,底面圆的周长为3,则该圆锥的侧面积为A.3πB.3C.6πD.6【答案】B7. 蜂巢的构造非常美丽、科学.右图是由7个形状、大小完全相同的正六边形组成的网络,正六边形的顶点称为格点,△ABC 的顶点都在格点上,设定AB 边如右图所示,则△ABC 是直角三角形的个数有( )A .4个B .6个C .8个D .10个【答案】D8.一个圆锥的侧面展开图是半径为6的半圆,则这个圆锥的底面半径为( )B A(A)1.5 (B)2 (C)2.5 (D)3【答案】D9.如图,扇形OAB,动点P从点A出发,沿AB、线段BO、OA匀速运动到点A,则OP的长度y与运动时间t之间的函数图像大致是xA. B. C. D.【答案】D10.如图,是某公园的一角,∠AOB=90°,AB的半径OA长是6米,点C是OA的中点,点D在AB上,CD∥OB,则图中草坪区(阴影部分)的面积是A.(3π+B.(34πC.(3π+)平方米D.(34π-B【答案】A11.一个圆锥的侧面展开图是半径为8cm、圆心角为120°的扇形,则此圆锥底面圆的半径为()A.83cm B.163cm C.3cm D.43cm【答案】A12.一个圆锥的侧面展开图是半径为6的半圆,则这个圆锥的底面半径为()A. 1.5 B.2 C.2.5 D.3考点:圆锥的计算.菁优网版权所有分析:半径为6的半圆的弧长是6π,圆锥的底面周长等于侧面展开图的扇形弧长,因而圆锥的底面周长是6π,然后利用弧长公式计算.解答:解:设圆锥的底面半径是r,则得到2πr=6π,解得:r=3,这个圆锥的底面半径是3.故选D13.如图,贤贤同学用手工纸制作一个台灯灯罩,做好后发现上口太小了,于是他把纸灯罩对齐压扁,剪去上面一截后,正好合适.以下裁剪示意图中,正确的是( )A.B.C.D.【答案】A14.正六边形的边心距为,则该正六边形的边长是()A.B.2C.3D.2考点:正多边形和圆.分析:运用正六边形的性质,正六边形边长等于外接圆的半径,再利用勾股定理解决.解答:解:∵正六边形的边心距为,∴OB=,AB=OA,∵OA2=AB2+OB2,∴OA2=(OA)2+()2,解得OA=2.故选B.点评:本题主要考查了正六边形和圆,注意:外接圆的半径等于正六边形的边长.二、填空题1.如图,正方形ABCD的边长为2,四条弧分别以相应顶点为圆心,正方形ABCD的边长为半径.求阴影部分的面积.A DB C第15题图【答案】8 16433π--2.如图,正六边形ABCDEF的边长为2,则对角线AE的长是 .【答案】233.如图,是将菱形ABCD以点O为中心按顺时针方向分别旋转90°,180°,270°后形成的图形.若∠BAD=60°,AB=2,则图中阴影部分的面积为______.【答案】12-3OAD。
专题二十四正多边形扇形圆锥侧面展开图汇编
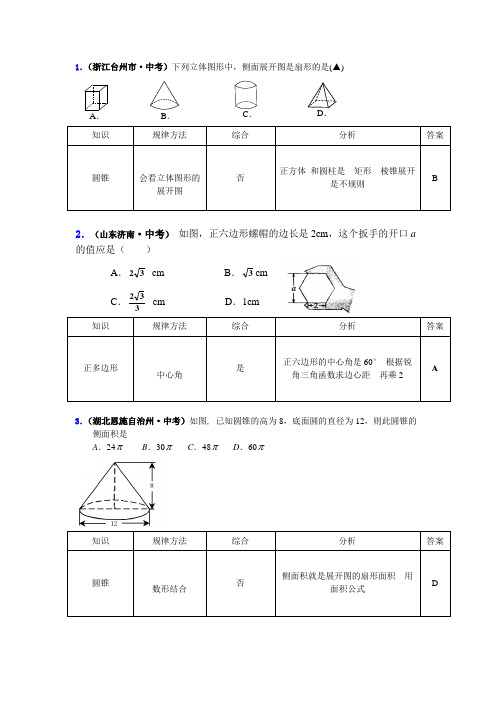
1.(浙江台州市·中考)下列立体图形中,侧面展开图是扇形的是(▲)知识规律方法 综合分析答案圆锥会看立体图形的展开图否正方体 和圆柱是 矩形 棱锥展开是不规则B2.(山东济南·中考) 如图,正六边形螺帽的边长是2cm ,这个扳手的开口a 的值应是( )A .32 cmB .3cmC .332 cm D .1cm 知识规律方法综合分析答案正多边形中心角是正六边形的中心角是60°根据锐角三角函数求边心距 再乘2A3.(湖北恩施自治州·中考)如图, 已知圆锥的高为8,底面圆的直径为12,则此圆锥的侧面积是A .24πB .30πC .48πD .60π知识规律方法综合 分析 答案圆锥数形结合否侧面积就是展开图的扇形面积 用面积公式DA .B .C .D .4.(泸州·期中)已知O 为圆锥的顶点,M 为底面圆周上一点,点P 在OM 上,一只蚂蚁从点P 出发绕圆锥侧面爬行回到P 时,所经过的最短路径的痕迹如图2,若沿OM 将圆锥侧面剪开并展平,所得侧面展开图是( )知识规律方法综合分析答案圆锥数形结合否 两点之间线段最短 D5.(荷泽·期末) 如图,在正方形铁皮中,剪下一个圆和一个扇形,使余料尽量少,用圆做圆锥的底面,用扇形做圆锥的侧面,正好围成一个圆锥,若圆的半径记为r ,扇形的半径记为R ,那么 A .R =2r B .R =r C .R =3r D .R =4r知识规律方法综合分析答案扇形数形结合是根据扇形面积公式 扇形的弧长和圆的周长相等D6.(湖北宜昌·中考)如图,在圆心角为90°的扇形MNK 中,动点P 从点M 出发,沿MN ⌒NKAB C EFGD→KM 运动,最后回到点M 的位置。
设点P 运动的路程为x ,P 与M 两点之间的距离为y ,其图象可能是( )。
知识规律方法综合分析答案扇形数形结合是 从M 到N 和K 到M 这两个过程正好相反 在弧KN 上 到M 的距离一直不变B7.(四川凉山·中考)如第15题图,如果从半径为3cm 的圆形纸片剪去13圆周的一个扇形,将留下在扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的体积是 。
初中数学综合复习之正多边形、扇形和圆锥侧面展开图(含图形的镶嵌)3
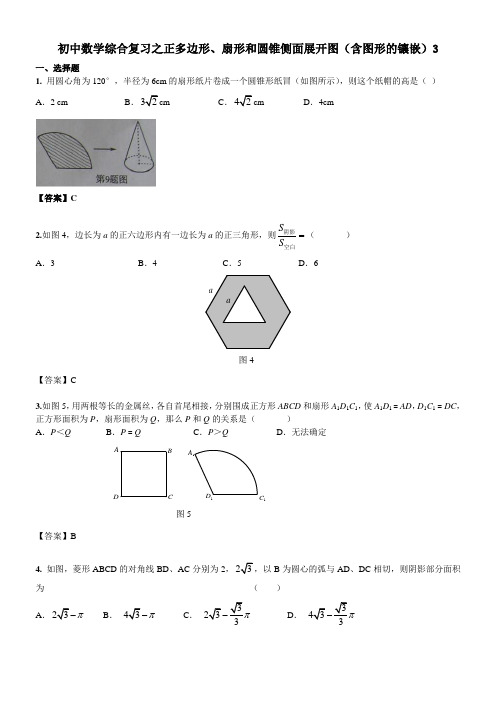
初中数学综合复习之正多边形、扇形和圆锥侧面展开图(含图形的镶嵌)3一、选择题1.用圆心角为120°,半径为6cm的扇形纸片卷成一个圆锥形纸冒(如图所示),则这个纸帽的高是()A.2 cm B.32cm C.42cm D.4cm【答案】C2.如图4,边长为a的正六边形内有一边长为a的正三角形,则SS=阴影空白()A.3 B.4 C.5 D.6【答案】C3.如图5,用两根等长的金属丝,各自首尾相接,分别围成正方形ABCD和扇形A1D1C1,使A1D1 = AD,D1C1= DC,正方形面积为P,扇形面积为Q,那么P和Q的关系是()A.P<Q B.P =Q C.P>Q D.无法确定【答案】B4.如图,菱形ABCD的对角线BD、AC分别为2,23B为圆心的弧与AD、DC相切,则阴影部分面积为()A.23πB.43πC.333D.333图5 1A1D1图4 aa【答案】A 二、填空题1.若圆锥的侧面展开图的弧长为24πcm ,则此圆锥底面半径为__________ cm . 【答案】122. 如图,AC ⊥BC,AC=BC=4.以BC 为直径作半圆,圆心为O;以点C 为圆心,BC 为半径作弧AB.过点O 作AC 的平行线交两弧于点D 、E,则阴影部分的面积是 .【答案】52 3.3π-3.一个圆柱的底面直径为6cm ,高为10cm,则这个圆柱的侧面积是 cm 2(结果保留π) 【答案】60π4. 如图所示,在菱形ABCD 中,AB =32,∠C =120°,以点C 为圆心的EF ⌒ 与AB ,AD 分别相切于点G ,H ,与BC ,CD 分别相交于点E ,F ,若用扇形CEF 作一个圆锥的侧面,则这个圆锥的高是 .【答案】225. 如图5,在Rt △ABC 中,∠C =90°,∠ABC =30°,AC =1,将Rt △ABC 绕点A 逆时针旋转30°后得到△第17题图AB ’C ’,则图中阴影部分的面积是 ★ 。
036.正多边形、扇形和圆锥侧面展开图(含图形的镶嵌)2015B
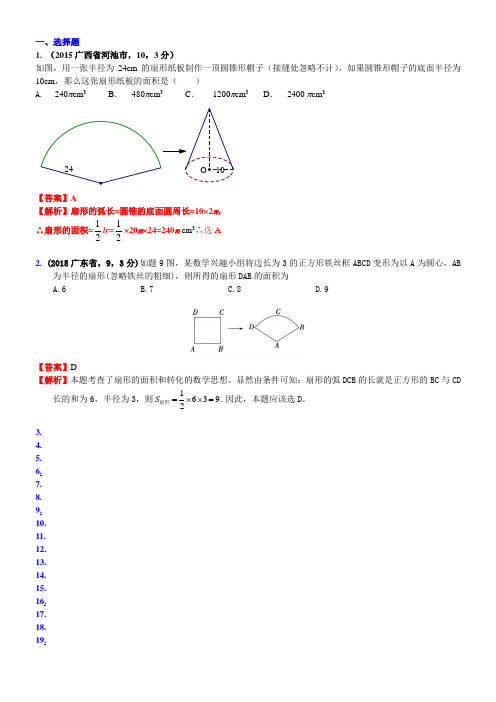
一、选择题1.(2015广西省河池市,10,3分)如图,用一张半径为24cm的扇形纸板制作一顶圆锥形帽子(接缝处忽略不计),如果圆锥形帽子的底面半径为10cm,那么这张扇形纸板的面积是()A.240πcm3B.480πcm3C.1200πcm3 D.2400 πcm3【答案】A【解析】扇形的弧长=圆锥的底面圆周长=10×2π,∴扇形的面积=12lr=12×20π×24=240π cm3∴选A2. (2015广东省,9,3分)如题9图,某数学兴趣小组将边长为3的正方形铁丝框ABCD变形为以A为圆心,AB为半径的扇形(忽略铁丝的粗细),则所得的扇形DAB的面积为A.6B.7C.8D.9【答案】D【解析】本题考查了扇形的面积和转化的数学思想。
显然由条件可知:扇形的弧DCB的长就是正方形的BC与CD长的和为6,半径为3,则16392S=⨯⨯=扇形.因此,本题应该选D。
3.4.5.6.7.8.9.10.11.12.13.14.15.16.17.18.19.20.21.22.23.24.25. 26.27.28. 29.30.31.32.33.34.35. 36.37.38. 39.二、填空题1. (2015江苏徐州,18,3分)用一个圆心角为90°,半径为4的扇形围成一个圆锥的侧面,该圆锥底面圆的半径为______________.【答案】1【解析】∵圆心角为90°,半径为4的扇形的弧长为:904=2180l ⨯=ππ,∴圆锥底面圆的半径为2r==12ππ.故答案为1.2. (2015河北省,19,3分)平面上,将边长相等的正三角形、正方形、正五边形、正六边形的一边重合并叠在一起,如图9,则∠3+∠1-∠2= .【答案】24°【解析】解:∵∠3=90°-60°=30°,∠2=108°-90°=18°,∠1=120°-108°=12°,∠3+∠1-∠2=24°.故答案为24°.3. (2015山东省莱芜市,16,4分)如图,在扇形O AB 中,∠AOB =60°,扇形半径为r ,点C 在 AB 上,CD ⊥OA ,垂足为D ,当△OCD 的面积最大时, AC 的长为 。
036.正多边形、扇形和圆锥侧面展开图(含图形的镶嵌)2015C

一、选择题1.(2015湖北潜江天门等,8,3分)已知一块圆心角为300°的扇形铁皮,用它做一个圆锥形的烟囱帽(接缝忽略不计),圆锥的底面圆的直径是80cm,则这块扇形铁皮的半径是A.24cm B.48cm C.96cm D.192cm【答案】B【解析】解:圆锥的底面圆的直径是80cm,周长则为80π,即扇形弧长,已知圆心角为300°,根据弧长公式可求出圆周长为96π,周长为2πR,所以R为48。
故选B。
2.3.4.5.6.7.8.9.10.11.12.13.14.15.16.17.18.19.20.21.22.23.24.25.26.27.28.29.30.31.32.33.34.35.37. 38. 39.二、填空题1. (2015贵州省六盘水市,18,4分)赵州桥是我国建筑史上的一大创举,它距今1400年,历经无数次洪水冲击和8次地震却安然无恙.如图10,若桥跨度AB 约为40米,主拱高CD 约10米,则桥弧AB 所在圆的半径R=________米.【答案】25【解析】解:根据垂径定理,得AD=12AB=20米.设圆的半径是r ,根据勾股定理, 得2222010RR ,解得R=25(米). 故答案为25.2. (2015眉山市,16,3分)已知⊙O 的内接正六边形周长为12cm ,则这个圆的半经是_________cm . 【答案】2cm 【解析】此题考查圆内接正六边形的特点.圆内接正六边形的边长即为此圆的半径.3. (2015湖北省襄阳市,16,3分)如图,P 为⊙O 外一点,PA ,PB 是⊙O 的切线,A ,B 为切点,PA=3 ,∠P=60°,则图中阴影部分的面积为33π-【解析】解:连接OA ,OB ,OP.∵∠P=60°,∴∠APO=30°,∵3OA=1,∴3APOS=,所以四边形OAPB 的面积3=,又∵∠P=60°,∴∠BOA=120°,∴扇形的面积=2120113603ππ⋅=,∴阴影部分的面积33π-.故答案为33π-.4. (2015年江苏镇江,23,6分)(本小题满分6分)图1是我们常见的地砖上的图案,其中包含了一种特殊的平面图形———正八边形.(1)如图2,AE 是⊙O 的直径,用直尺和圆规作⊙O 的内接正八边形ABCDEFGH (不写作法,保留作图痕迹);(2)在(1)的前提下,连接OD ,已知OA =5,若扇形OAD (∠AOD <180°)是一个圆锥的侧面,则这个圆锥底面圆的半径等于_________.【答案】(1)如下图:HGF DCB AEO(2)由(1)可知n =135,R =OD =5,设圆锥的底面圆半径为r ,则由360135=R r 得r =815.5. (2015甘肃平凉等,17,5分)如图,半圆O 的直径AE =4,点B ,C ,D 均在半圆上.若AB =BC ,CD =DE ,连结OB ,OD ,则图中阴影部分的面积为______. D CB图1图2OA(第23题)【答案】π提示:∠BOD=90°,S阴影=S扇形OBD.6.(2015湖北省孝感市)已知圆锥的侧面积等于 60cm2,母线长10cm,则圆锥的高是☆cm.考点:圆锥的计算.专题:计算题.分析:设圆锥的底面圆的半径为r,利用圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和扇形面积公式得到•2π•r•10=60π,解得r=6,然后根据勾股定理计算圆锥的高.解答:解:设圆锥的底面圆的半径为r,根据题意得•2π•r•10=60π,解得r=6,所以圆锥的高==8(cm).故答案为8.点评:本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.7.(2015黑龙江省绥化市)如图,将一块含300角的直角三角版和半圆量角器按如图的方式摆放,使斜边与半圆相切。
036.正多边形、扇形和圆锥侧面展开图(含图形的镶嵌) C2013.

一、选择题1. (2013四川乐山,8,3)一个立体图形的三视图如图4所示,根据图中数据求得这个立体图形的表面积为( D )A.2πB. 6πC. 7πD. 8π【答案】:D2. (2013眉山,9,3)用一圆心角为120°,半径为6cm 的扇形做成一个圆锥的侧面,这个圆锥的底面的半径是( )A .1cmB .2cmC .3cmD .4cm【答案】:B3. (2013•遂宁8,4)用半径为3cm ,圆心角是120°的扇形围成一个圆锥的侧面,则这个圆锥的底面半径为( )【答案】D4. (2013宁夏回族自治区宁,8,3分)如图,以等腰直角△ABC 两锐角顶点A 、B 为圆心作等圆,⊙A 与⊙B 恰好外切,若AC =2,那么图中两个扇形(即阴影部分)的面积之和为( )A.14π B.12π C.2π π 【答案】B .5. ( 2013东营,8,3)如图,正方形ABCD 中,分别以B 、D 为圆心,以正方形的边长a 为半径画弧,形成树叶形(阴影部分)图案,则树叶形图案的周长为( )A. a πB.2a π C. 12a π D. 3a【答案】A6.(2013青海省, 20,3分)如图11在直角△ABC 中,∠ACB =90°,AC =8cm ,BC =6cm ,分别以A 、B 为圆心,以2AB 的长为半径作圆,将直角△ABC 截去两个扇形,则剩余(阴影)部分的面积为( ) (第8题图) 第8题A . 225244cm π⎛⎫- ⎪⎝⎭B .2254cm πC .25248cm π⎛⎫- ⎪⎝⎭ D .225246cm π⎛⎫-⎪⎝⎭ 【答案】A7. (2013湖北咸宁,5,3分)如图,过正五边形ABCDE 的顶点A 作直线l ∥B E ,则∠1的度数为( )A .30° B.36° C.38° D.45°【答案】B .8. (2013浙江绍兴,7,4分)若圆锥的轴截面为等边三角形,则称此圆锥为正圆锥,则正圆锥侧面展开图的圆心角是( )A. 90°B. 120°C. 150°D. 180°【答案】D 9.(2013浙江绍兴,9,4分)小敏在作⊙O 的内接正五边形时,先做了如下几个步骤:(1)作⊙O 的两条互相垂直的直径,再作OA 的垂直平分线交OA 于点M ,如图1;(2)以M 为圆心,BM 长为半径作圆弧,交CA 于点D ,连结BD ,如图2.若⊙O 的半径为1,则由以上作图得到的关于正五边形边长BD 的等式是( )A. OD BD 2152-=B. OD BD 2152+=C. OD BD 52=D. OD BD 252= 【答案】C 10. (2013淮安,5,3分)若扇形的半径为6,圆心角为1200,则此扇形的弧长是( )A 、π3B 、π4C 、π5D 、π6【答案】:B11. (2013江苏扬州,6,3分)一个多边形的每一个内角均为108°,则这个多边形是( )A .七边形B .六边形C .五边形D .四边形【答案】C.12. (2013内蒙古包头,8,3分)用一个圆心角为120°,半径为2的扇形做一个圆锥的侧面,则这个圆锥的地面圆半径为( )A .34B .43C .23D .32 【答案】D 13. (2013广西贵港市,10,3分)如图,己知圆锥的母线长为6. 圆锥的高与母线所夹的角为θ,且1sin 3θ=, 则该圆锥侧面积是( )A .B .24πC .16πD .12π【答案】D14.15. 16.17.18. 19.20.21.22.23.24.25. 26.27.28. 29.30.31.32.33.34.35.36.37.38.39.40.41.42.43.44.45.46.47.48.49.50.二、填空题1.(2013四川乐山,15,3)如图8,小方格都是边长为1的正方形,则以格点为圆心,半径为1和2的两种弧围成的“叶状”阴影图案的面积为________.【答案】:24π-2.(2013眉山,17,3)如图,以BC为直径的⊙O与△ABC的另两边分别相交于点D、E。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
正多边形、扇形和圆锥侧面展开图
一、选择题
1、(2013安徽芜湖一模)圆锥的底面直径是80cm ,母线长90cm ,则它的侧面展开图的圆心角是 ( ). A .3200
B.400
C .1600
D.800
答案:C
2、(2013江苏射阴特庸中学)如右图,正五边形ABCDE 中,对角线AC 、AD 与BE 分别相交于点N 、M .下列结论错误..
的是( ) A .四边形NCDE 是菱形 B .四边形MNCD 是等腰梯形 C .△AEM 与△CBN 相似 D .△AEN 与△EDM 全等 答案:C
3、(2013江苏扬州弘扬中学二模)如图所示的平面图形中,不可能围成圆锥的是( )
答案:D
4、(2013·温州市中考模拟)已知:圆锥的母线长为4,底面半径为2,则圆锥的侧面积等于
A .11π
B .10π
C .9π
D .8π 答案:D 5、(2013·湖州市中考模拟试卷10)如图是一个空心圆柱形纸筒,高为3,底面圆周长为4,若将这个纸筒沿圆筒侧面线路B M A →→剪开铺平,所得图形可能为( )
A .边长为3和4的矩形
B .边长为5和4的矩形
C .边长为5和3的平行四边形
D .边长为5和4的平行四边形
答案:D
6、10.(2013年河北二摸)在综合实践活动课上,小明同学用纸板制作了一个圆锥形漏斗模
型.如图所示,它的底面半径OB =6cm ,高OC =8cm ,则这个圆锥漏斗的侧面积是 A .30cm B .30πcm C .60πcm D .120cm
答案:C
7、(2013年温州一摸)已知:圆锥的母线长为4,底面半径为2
,则圆锥的侧面积等于
N M E
D C
B A B
C
D
A C
A .11π
B .10π
C .9π
D .8π 答案:D
二、填空题
1、(2013江苏东台实中)已知圆锥的侧面积为π8cm 2,侧面展开图的圆心角为45°,则该圆锥的母线长为 cm 。
答案:8
2、 (2013·吉林中考模拟)一个圆锥的母线长为4,侧面积为8错误!未找到引用源。
,则这个圆锥的底面圆的半径是 .
答案:2 3、(2013·曲阜市实验中学中考模拟)钟表的轴心到分针针端的长为4cm ,那么经过40分钟,分针针端转过的弧长是_______ cm(用π表示) . 答案:
16
3
π 4、(2013·曲阜市实验中学中考模拟)如图,点O 是正ACE ∆和正BDF ∆的中心,且
AE ∥BD ,则AOF ∠=_______.
答案:60°
5、(2013·湖州市中考模拟试卷1)已知圆锥的底面直径为4cm ,其母线长为3cm ,则它的侧面积为 . 答案:6π
6、(2013·湖州市中考模拟试卷7)小明的圆锥形玩具的高为12cm ,母线长为13cm ,则其
侧面积是 2
cm .
答案:65π
7、(2013·湖州市中考模拟试卷10)某盏路灯照射的空间可以看成如图所示的圆锥,它的高AO =8米, 母线AB =10米,则该圆锥的侧面积是 平方米(结果保留π).
答案:60π
(第11题) 8、(2013年河南西华县王营中学一摸)有一直径为4的圆形铁皮,要从中剪出一个最大圆心角为60°的扇形ABC ,用此剪下的扇形铁皮围成一个圆锥,该圆锥的底面圆的半径r= .
答案:
3
3
9、(2013年上海市)如图,在半径为1的扇形AOB 中,∠AOB = 90°,点P 是AB 上的一个
动点(不与点A 、B 重合),PC ⊥OA ,PD ⊥OB ,垂足分别为点C 、D ,点E 、F 、G 、H 分别是线段OD 、PD 、PC 、OC 的中点,EF 与DG 相交于点M ,HG 与EC 相交于点N ,联结MN .如果设OC = x ,MN = y ,那么y 关于x 的函数
答案
:1)y x =<<
A
P C H
O
G N E D M
F B
(第18题图)。
