高中物理竞赛讲座:高斯定理
合集下载
高二物理竞赛课件:高斯定理

不会中断,或从无穷远来,到无穷远 去;——》磁场高斯定理。
• (2) 每一条磁力线是环绕电流的无头无尾 的闭合线;-》磁场环路定理。
• (3)电流与磁场方向满足右手螺旋定则。
磁通量:仿照电通量概念,定义曲面S的磁通量为
m B dS B dS
S
S
单位: 1Wb 韦伯 1T m2
B dm ds
用磁感应线描述磁场的分布,规定: 方向:曲线上切线,代表磁感强度的方向. 大小:曲线的密度, 与磁感强度的大小成正比.
实验和理论都证明:在任何磁场中,每一条磁感线都是环 绕电流的无头无尾的闭合线,而且每条闭合磁感线都与闭合 载流回路互相套合。
磁力线的特性: • (1)它是连续的, 在磁场中任一点磁力线
dm B dS
m d B dS
直导线磁感线分布:
B 0I 2a
B
o
x
圆电流磁感线分布:
B
o
x
[证明]:因为任意一磁场,都是由许多电流元产生 的磁场叠加而成,其磁通量也满足叠加原理,所 以只需证明电流元产生的磁场遵守高斯定理。
取电流元为坐标原点,Z轴沿电流元强度的方向,
dB
B
0 4
I
L
dl r r3
0 4
I
L
dR r r3
0 Ir0 4 r03
I
L
dR
0 4 r03
I
L
R dR
30 4 r05
I
L
(r0
R)(r0 dR)
= 0 4
m r03
0 4
3(m r0 )r0 r05
对于闭合电流,磁矩m或园面积S与坐标原点的选取无关。
磁感应线及磁通量
• (2) 每一条磁力线是环绕电流的无头无尾 的闭合线;-》磁场环路定理。
• (3)电流与磁场方向满足右手螺旋定则。
磁通量:仿照电通量概念,定义曲面S的磁通量为
m B dS B dS
S
S
单位: 1Wb 韦伯 1T m2
B dm ds
用磁感应线描述磁场的分布,规定: 方向:曲线上切线,代表磁感强度的方向. 大小:曲线的密度, 与磁感强度的大小成正比.
实验和理论都证明:在任何磁场中,每一条磁感线都是环 绕电流的无头无尾的闭合线,而且每条闭合磁感线都与闭合 载流回路互相套合。
磁力线的特性: • (1)它是连续的, 在磁场中任一点磁力线
dm B dS
m d B dS
直导线磁感线分布:
B 0I 2a
B
o
x
圆电流磁感线分布:
B
o
x
[证明]:因为任意一磁场,都是由许多电流元产生 的磁场叠加而成,其磁通量也满足叠加原理,所 以只需证明电流元产生的磁场遵守高斯定理。
取电流元为坐标原点,Z轴沿电流元强度的方向,
dB
B
0 4
I
L
dl r r3
0 4
I
L
dR r r3
0 Ir0 4 r03
I
L
dR
0 4 r03
I
L
R dR
30 4 r05
I
L
(r0
R)(r0 dR)
= 0 4
m r03
0 4
3(m r0 )r0 r05
对于闭合电流,磁矩m或园面积S与坐标原点的选取无关。
磁感应线及磁通量
高二物理竞赛课件:静电场的高斯定理

第八章 真空中的静电场
dS
+
8 – 2 静电场的点高电斯荷定在理任意封闭曲面内(定性分析) 第八章 真空中的静电场
由于电场线的连续性,且S1与S2、S3之间没有其他电荷, 因此穿过球面S1的电场线数目必与穿过任意曲面S2和S3 的电场线数目相同,与闭合曲面的形状无关,即
e s1
es2
es3
dΦ1 E1 dS1
q
4 π 0
d S1' r2
q d 0
4 π
0
dΦ2 E2 dS2
q
4 π 0
dS
'
2
r2
q d 0
4 π 0
E2
q
dS2
dS1
E1
dΦ1
dΦ 2
0
e
E dS 0
S
8 – 2 静电场的高斯定理
第八章 真空中的静电场
由多个点电荷产生的电场
E E1 E2
在点电荷 q 和 q 的静电场中,做如下的三
个闭合面
S1 ,
S2 ,
S3 , q
求通过各闭合面的电通量
.
Φe1
E dS
S1
0
q
q
Φe2 0
Φe3
q
0
S1
S2 S3
8 – 2 静电场用的高高斯斯定定理理计算场强
第八章 真空中的静电场
i)分析对称性
ii)根据对称性,选择合适的高斯面。
高 斯 面
E dS
1
S
0
n
qi
i 1
总结
1)高斯面上的电场强度为所有内外电荷的总电场强度. 2)高斯面为封闭曲面. 3) dS 的正方向为曲面的外法线方向(垂直于曲面向 外),因此,穿出高斯面的电通量为正,穿入为负.
高二物理竞赛课件:磁场的高斯定理及安培环路定理

l Bdl
0 I dl
2πR
0 I
B
dl
R
l
2) 复杂点情形——任意形状的环路
在r 处
B 0I 2 r
B dl Bdl cos Brd
L
2 0I d 0 2
0I
思考:若I 反向或环路反向?
B dl l
0 I
I
•
d
B
r dl
O
d
r
PB
N
M dl
➢环路不包围直导线
B dl B dl B dl
磁场的高斯定理及安培环路定理
磁场的高斯定理及安培环路定理
一、磁力线 (磁场线、磁感线)
1. 磁场线的大小与方向 方向:切线方向表示该点处的磁场方向 2. 磁场线的性质 (1) 任意两条磁场线不相交 (2) 任意磁场线都是闭合曲线
大小:B dN m
dS
(3) 磁场线与形成磁场的电流互相套连,成右螺关系
dS1
1
B1
B2
dΦ1 B1 dS1 0
当磁力线穿入时
2
2
B d S 0——磁场高斯定理
S
dΦ2 B2 dS2 0
意义:说明磁场是无源场
例1、如图所示,求均匀磁场中下曲面的 磁通量
解法一:直接求解
B
n S2
m dm B dS 很难计算
S1
解法二:利用高斯定理
B d S 0 S
S1
将顶端圆面补全,构成一个闭合曲面。
B d S B d S B d S 0 B d S BSB2cdosS
S
S1
S2
S1
S2
三、安培环路定理
l E dl 0 l B dl ?
高二物理竞赛课件:电场的高斯定理

qi内
E dS i
S
0
E
ds
S
2. 高斯定理关系式的导出 思路:1)以点电荷场为例
2)推广到一般 推导: 1)场源电荷是电量为Q的点电荷
高斯面包围点电荷,如图 通过该高斯面的电通量? 根据电力线的连续性 等于以点电荷为球心的 任意半径的球面的电通量
Qr
S
dS
E
E
+Q
r
计算通过球面的电通量: 通过球面任一面元 的电通量是
[例] 如图,点电荷q位于 立方体的一角,则通过 侧面ABCD的电通量 e=.
q
A
B
D C
解:增补成一个大立方体,q位于其中心.
由高斯定律和对称分析:
e
q
24 0
静电场的高斯定理
1)通过任意面积 元的 电通量
de E dS
其值有正、负,取决于面 元法线与场强方向的夹角
dS E
2)通过任意曲面的电通量:
把曲面分成许多个面积元
每一面元处视为匀强电场
e de E dS E cosθdS
S
S
S
3)通过闭合面的电通量
e
E dS
S
e E dS
q1 q2 qn 0 0
0 0
0
1
0
n
qi
i1
1
0
qi
i (内 )
qi内
E dS i
S
0
讨论
qi内
1)闭合面内、外电 荷的贡献
E dS i
S
ε0
对闭合面处的 E 都有贡献
对电通量 E dS 的贡献有差别
S
只有闭合面内的电量对电通量有贡献
高二物理竞赛课件:磁场 磁感应强度 磁场的高斯定理

磁场 磁感应强度 磁场的高斯 定理
磁场 磁感应强度 磁场的高斯定理
一、磁场
1、磁铁有南北极,同性相斥,异性相吸。 2、无独立的磁极-磁单极。
3、所有磁现象的根源是电流产生的-安培 分子电流假说
NN
S
2
磁铁
磁铁
磁场
电流
电流
问题:磁铁和电流产生的磁场在本质上是否一 致?
答案:所有磁现象的根源是电流产生的-安培分 子电流假说
n
4
磁场中的高斯定理
1、磁 感 线(B线,磁力线)
规定:曲线上每一点的切线方向就是该点的磁感强度B 的 方向,曲线的疏密程度表示该点的磁感强度 B 的大小.
I
I
I
5
一些典型的磁感应线的分布:
直线电流的磁感线
圆形电流的磁感线
6
直螺线管电流的磁感线 环形螺线管电流的磁感线
7
2、磁通量
enB
s s
7
N
/
A2
电流 I 在P点的磁场:B
dB
0 4
Id l r0 r2
12
d B 0 Id l r 0 4 r 2
所有电流元在该点产生的总磁场:
B 0 Idl r0
4 r 2
B
分量式:B
x y
dBx dB y
Bz dBz
B Bx i By j Bz k
三)磁场计算举例:
14
13
【ˆ
r2
方向指 向里面
dB
0 4
I d l sin
r2
2
Idl rˆ l r
0r
I
r' r sin
rd
l rctg
dl sin2
磁场 磁感应强度 磁场的高斯定理
一、磁场
1、磁铁有南北极,同性相斥,异性相吸。 2、无独立的磁极-磁单极。
3、所有磁现象的根源是电流产生的-安培 分子电流假说
NN
S
2
磁铁
磁铁
磁场
电流
电流
问题:磁铁和电流产生的磁场在本质上是否一 致?
答案:所有磁现象的根源是电流产生的-安培分 子电流假说
n
4
磁场中的高斯定理
1、磁 感 线(B线,磁力线)
规定:曲线上每一点的切线方向就是该点的磁感强度B 的 方向,曲线的疏密程度表示该点的磁感强度 B 的大小.
I
I
I
5
一些典型的磁感应线的分布:
直线电流的磁感线
圆形电流的磁感线
6
直螺线管电流的磁感线 环形螺线管电流的磁感线
7
2、磁通量
enB
s s
7
N
/
A2
电流 I 在P点的磁场:B
dB
0 4
Id l r0 r2
12
d B 0 Id l r 0 4 r 2
所有电流元在该点产生的总磁场:
B 0 Idl r0
4 r 2
B
分量式:B
x y
dBx dB y
Bz dBz
B Bx i By j Bz k
三)磁场计算举例:
14
13
【ˆ
r2
方向指 向里面
dB
0 4
I d l sin
r2
2
Idl rˆ l r
0r
I
r' r sin
rd
l rctg
dl sin2
高二物理竞赛课件:高斯定理(108张PPT)

(1)r < R
E
四、均匀带电圆柱面的电场。
沿轴线方向单位长度带电量为λ
(1)r < R 高 斯 面
E
四、均匀带电圆柱面的电场。
沿轴线方向单位长度带电量为λ
(1)r < R
E 2π r l = 0
E
4. 均匀带电圆柱面的电场。
沿轴线方向单位长度带电量为λ
(1)r < R
E 2π r l = 0 ... E = 0
第三节 高斯定理
一、电力线
一、电力线
电力线(E)线:在电场中画一组曲线, 曲线上每一点的切线方向与该点的电场方向 一致,这一组曲线称为电力线。
一、电力线 电力线(E)线:在电场中画一组曲线, 曲线上每一点的切线方向与该点的电场方向 一致,这一组曲线称为电力线。
E
一、电力线
电力线(E)线:在电场中画一组曲线, 曲线上每一点的切线方向与该点的电场方向
高斯面
. s E dS = s E dS cos00
E
=
E
s
dS
= E 4π r 2
=Σ q i ε/ O
=0
++
+ +
+R
rr
+ +q
+
+
+
+
+
+++ +
一、均匀带电球面的电场
(1)r < R
高斯面
. s E dS = s E dS cos00
E
=
E
s
dS
= E 4π r 2
=Σ q i ε/ O
+
E
四、均匀带电圆柱面的电场。
沿轴线方向单位长度带电量为λ
(1)r < R 高 斯 面
E
四、均匀带电圆柱面的电场。
沿轴线方向单位长度带电量为λ
(1)r < R
E 2π r l = 0
E
4. 均匀带电圆柱面的电场。
沿轴线方向单位长度带电量为λ
(1)r < R
E 2π r l = 0 ... E = 0
第三节 高斯定理
一、电力线
一、电力线
电力线(E)线:在电场中画一组曲线, 曲线上每一点的切线方向与该点的电场方向 一致,这一组曲线称为电力线。
一、电力线 电力线(E)线:在电场中画一组曲线, 曲线上每一点的切线方向与该点的电场方向 一致,这一组曲线称为电力线。
E
一、电力线
电力线(E)线:在电场中画一组曲线, 曲线上每一点的切线方向与该点的电场方向
高斯面
. s E dS = s E dS cos00
E
=
E
s
dS
= E 4π r 2
=Σ q i ε/ O
=0
++
+ +
+R
rr
+ +q
+
+
+
+
+
+++ +
一、均匀带电球面的电场
(1)r < R
高斯面
. s E dS = s E dS cos00
E
=
E
s
dS
= E 4π r 2
=Σ q i ε/ O
+
高二物理竞赛高斯定理课件

只有在场强分布具有一定的对称性时,才能比较方便应用高斯定理求出场强。 (3) 根据高斯定理求电场强度。
则 在空腔处补上球体( ρ 、r)后,
是所有电荷产生的, e 只与内部电荷有关。
n E [补偿法] 距直线r 处一点P 的电场强度
n 一均匀带电球体,半径为R,电荷密度为ρ,现在球内挖去一半径为r(r <R)的球体。
n S S S 0 取过场点 P 的同心球面为高斯面
德国数学家、天文学家和物理学家,有“数学王子”美称,他与韦伯制成了第一台有线电报机和建立了地磁观测台,高斯还创立了电
磁量的绝对单位制.
1
在电场中穿过任意曲面S 的电场线条数称为穿过
1
2
电场线是非闭合曲线,不相交。
R 电场线是非闭合曲线,不相交。
挖去的球体空腔可等效成是 带等量异种电荷的球体在该
处的叠加。
O•R O• r
设 球体带正电,电荷密度为+ρ,
则 在空腔处补上球体( ρ 、r)后, E p E R E r
E R 3 0 r ,
Er
3 0
r
19
r •P
+ρ
•
OR
•
Or
r
-ρ
E p 3 0 (r r )
a
3 0
Ep E R Er
例已知“无限大”均匀带电平面上电荷面密度为
求 电场强度分布
解电场强度分布具有面对称性 E
n E
选取一个圆柱形高斯面
eSEdS
n
n
侧 E d S 左 E 底 d S 右 E 底 d S
0 E E S 2 E S S Ex
根据高斯定理有
2ES 1 S 0
E 2 0
则 在空腔处补上球体( ρ 、r)后,
是所有电荷产生的, e 只与内部电荷有关。
n E [补偿法] 距直线r 处一点P 的电场强度
n 一均匀带电球体,半径为R,电荷密度为ρ,现在球内挖去一半径为r(r <R)的球体。
n S S S 0 取过场点 P 的同心球面为高斯面
德国数学家、天文学家和物理学家,有“数学王子”美称,他与韦伯制成了第一台有线电报机和建立了地磁观测台,高斯还创立了电
磁量的绝对单位制.
1
在电场中穿过任意曲面S 的电场线条数称为穿过
1
2
电场线是非闭合曲线,不相交。
R 电场线是非闭合曲线,不相交。
挖去的球体空腔可等效成是 带等量异种电荷的球体在该
处的叠加。
O•R O• r
设 球体带正电,电荷密度为+ρ,
则 在空腔处补上球体( ρ 、r)后, E p E R E r
E R 3 0 r ,
Er
3 0
r
19
r •P
+ρ
•
OR
•
Or
r
-ρ
E p 3 0 (r r )
a
3 0
Ep E R Er
例已知“无限大”均匀带电平面上电荷面密度为
求 电场强度分布
解电场强度分布具有面对称性 E
n E
选取一个圆柱形高斯面
eSEdS
n
n
侧 E d S 左 E 底 d S 右 E 底 d S
0 E E S 2 E S S Ex
根据高斯定理有
2ES 1 S 0
E 2 0
高二物理竞赛磁场的高斯定律课件
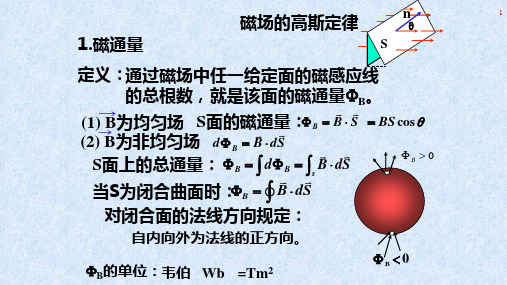
Idl rˆ
r2
三、B 的计算: B-S定律——方法1
3个模型:长直电流, 圆电流中心, 长直螺线管
B 0I 2a
B 0I
2R
B 0nI
14
各种典型的磁感应线的分布:
直线电流的磁感线
圆形电流的磁感线
15
直螺线管电流的磁感线
环形螺线管电流的磁感线
1.磁通量
磁场的高斯定律
n
1
SS
定义:通过磁场中任一给定面的磁感应线
的总根数,就是该面的磁通量B。
(1) B为均匀场 S面的磁通量:B B S BS cos
(2) B为非均匀场 dB B dS
S面上的总通量: B dB s B dS
B 0
当S为闭合曲面时:B B dS
对闭合面的法线方向规定:
解:由对称性知,只需计算1/4圆,有
dF I2dl B dF I2dlB
dFx
dF
cos
I2dl B
x R
I2dl
0 I1 2x
x R
0I1I2 dl 2R
F 4Fx 4
dF
x
4
0 I1I 2R
2
dl
4
0 I1I 2 2R
R
2
0 I1I 2
例 电流I1的长直导线旁有一个与它共面的正方形
dB 0dI dI ndq ( )(dr)
2r
2
B0
dB ab 0 dr 0 ln a b a 4 r 4 r a
求磁矩
4
半径为r的dr园环产生的磁矩为
dpm
r 2dI
r2
2
dr
2
r 2dr
pm
dpm
r2
三、B 的计算: B-S定律——方法1
3个模型:长直电流, 圆电流中心, 长直螺线管
B 0I 2a
B 0I
2R
B 0nI
14
各种典型的磁感应线的分布:
直线电流的磁感线
圆形电流的磁感线
15
直螺线管电流的磁感线
环形螺线管电流的磁感线
1.磁通量
磁场的高斯定律
n
1
SS
定义:通过磁场中任一给定面的磁感应线
的总根数,就是该面的磁通量B。
(1) B为均匀场 S面的磁通量:B B S BS cos
(2) B为非均匀场 dB B dS
S面上的总通量: B dB s B dS
B 0
当S为闭合曲面时:B B dS
对闭合面的法线方向规定:
解:由对称性知,只需计算1/4圆,有
dF I2dl B dF I2dlB
dFx
dF
cos
I2dl B
x R
I2dl
0 I1 2x
x R
0I1I2 dl 2R
F 4Fx 4
dF
x
4
0 I1I 2R
2
dl
4
0 I1I 2 2R
R
2
0 I1I 2
例 电流I1的长直导线旁有一个与它共面的正方形
dB 0dI dI ndq ( )(dr)
2r
2
B0
dB ab 0 dr 0 ln a b a 4 r 4 r a
求磁矩
4
半径为r的dr园环产生的磁矩为
dpm
r 2dI
r2
2
dr
2
r 2dr
pm
dpm
高二物理竞赛课件:高斯定理应用

r 荷面密度为 ,求距平面为 处的电场强度.
解 对称性分析:面对称
选垂直平面等距的闭合 圆柱面为高斯面
E
dS
S'
S
0 底面积
S'
2S'E S' 0
E 20
E
2 0
E
x
O
( 0)
讨论
无的 限电
0
0
0
大场
带叠
电加
平问
面题
0
0
0
小结
一、 高斯定理
点电荷系
1
e
S
E dS
0
qi
S内
1
0
dl
L
连续分布带电体
e
S
E dS
1
0
dS
S
1
dV
0 V
二、由高斯定理求电场分布的步骤 1. 由电荷分布的对称性分析电场分布的对称性。
2. 在对称性分析的基础上选取高斯面. 目的是使
sE dS 能够以乘积形式给出。
(球对称、轴对称、面对称三种类型)
3. 由高斯定理
并说明其方向。s
E dS
S
+ +
E dS E dS E dS h
s(柱面)
s(上底)
s(下底)
+
+o
y
E dS
x+
s(柱面)
E dS EdS
S
s ( 柱面)
h 0 z
2π rhE h
+
0
+
E 2π 0r
h
+
+o
y
x+
例 无限大均匀带电平面的电场强度
解 对称性分析:面对称
选垂直平面等距的闭合 圆柱面为高斯面
E
dS
S'
S
0 底面积
S'
2S'E S' 0
E 20
E
2 0
E
x
O
( 0)
讨论
无的 限电
0
0
0
大场
带叠
电加
平问
面题
0
0
0
小结
一、 高斯定理
点电荷系
1
e
S
E dS
0
qi
S内
1
0
dl
L
连续分布带电体
e
S
E dS
1
0
dS
S
1
dV
0 V
二、由高斯定理求电场分布的步骤 1. 由电荷分布的对称性分析电场分布的对称性。
2. 在对称性分析的基础上选取高斯面. 目的是使
sE dS 能够以乘积形式给出。
(球对称、轴对称、面对称三种类型)
3. 由高斯定理
并说明其方向。s
E dS
S
+ +
E dS E dS E dS h
s(柱面)
s(上底)
s(下底)
+
+o
y
E dS
x+
s(柱面)
E dS EdS
S
s ( 柱面)
h 0 z
2π rhE h
+
0
+
E 2π 0r
h
+
+o
y
x+
例 无限大均匀带电平面的电场强度
高二物理竞赛高斯定律课件

E
b. 在球体内的场强与场点离 球心的距离成正比。
E
4
q
e0R3
r
R
r
均匀带电球体的电场
r
S2 + +dq +
场源的对称性决定着场强分布的对称性,因此场强 具有与场源同样的球对称性。
求解均匀带电球面的电场分布
解:(1) rR
q
E dS
S1
e0
4r 2E q e0
(2) 0rR
EdS 0 S2
4r2E0
E
q
4e0r2
er
E0
r
P
+
+
+
+
+O
+ +
+R+
S1 + + +
+ +
+S2+
选取原则: (1) 高斯面必须经过所求场强的点;
(2) 在不求 E 的部分高斯面上,E 的方向和 dS 垂直,
使得 E ·dS = 0; 应用高斯定理计算。
高斯面必须经过所求场强的点;
(2) r < R 时,高斯面内电荷为q’:
(3) 在求 E 的部分高斯面上,要求该面上各点 E 的 常见的具有对称性分布的源电荷有:
E0
R
r
均匀带电球面的场强
2. 均匀带电的球体内外的场强分布。设球面半径为 R,带电量为q。
选高斯面为同心球面。
(1) r > R 时,高斯面内电荷为q:
ΦeSEdSE4r2eq0
q
E 4e0r2 er
P
q ++++ +O++++r++R+++
b. 在球体内的场强与场点离 球心的距离成正比。
E
4
q
e0R3
r
R
r
均匀带电球体的电场
r
S2 + +dq +
场源的对称性决定着场强分布的对称性,因此场强 具有与场源同样的球对称性。
求解均匀带电球面的电场分布
解:(1) rR
q
E dS
S1
e0
4r 2E q e0
(2) 0rR
EdS 0 S2
4r2E0
E
q
4e0r2
er
E0
r
P
+
+
+
+
+O
+ +
+R+
S1 + + +
+ +
+S2+
选取原则: (1) 高斯面必须经过所求场强的点;
(2) 在不求 E 的部分高斯面上,E 的方向和 dS 垂直,
使得 E ·dS = 0; 应用高斯定理计算。
高斯面必须经过所求场强的点;
(2) r < R 时,高斯面内电荷为q’:
(3) 在求 E 的部分高斯面上,要求该面上各点 E 的 常见的具有对称性分布的源电荷有:
E0
R
r
均匀带电球面的场强
2. 均匀带电的球体内外的场强分布。设球面半径为 R,带电量为q。
选高斯面为同心球面。
(1) r > R 时,高斯面内电荷为q:
ΦeSEdSE4r2eq0
q
E 4e0r2 er
P
q ++++ +O++++r++R+++
高二物理竞赛课件:磁通量 磁场的高斯定理
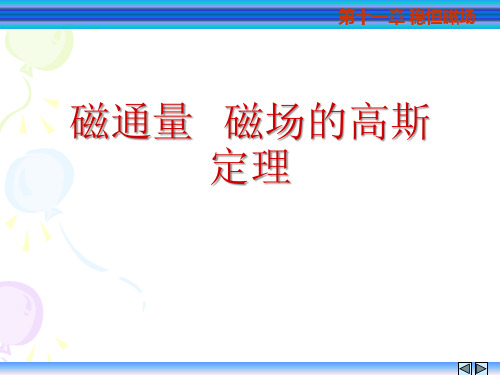
s
单位 1Wb 1T 1m2
第十一章 稳恒磁场
B
穿过闭合曲面的磁通量
根据磁感线的连续性
Φ S B dS 0
磁场高斯定理
S B d S 0
物理意义:通过任意闭合曲面的磁通量必等于零.
磁场是无源场
第十一章 稳恒磁场
例1 如图有一均匀磁场,方向沿 x 轴正向。求:
1)abcd面磁通量; 2)befc面磁通量; 3)adfe面磁 通量.
(2)方向:曲线上每一点的切线方向为该点的 B的方向. 大小:曲线的疏密程度表示该点B 的大小.
(3)均匀磁场中, B为一系列均匀分布的平行直线.
二 磁通量 磁场的高斯定理
磁通量:通过某一曲面的磁感线条数为通过此曲面的磁通
量.
B dS
B
dΦ B dS BdS cos
(有限面积) Φ s B dS
0nI
1 2
0nI
B 0nI
l 2
O
l 2
x
第十一章 稳恒磁场
例 求无限长半圆筒轴上任意一点的磁感强度。
解: 由对称性可知
y
By 0, B Bx
dl
dl
I
I
dI
R dl
Rd
I
d
x
O dB
y
dB
0dI 2 R
0 Id 2 2R
Bx
dB cos
0 I 2 2R
2
cos
d
2
dl d O
所有电流元的 dB 方向相同
B 0 R dr 0R
20
2
B
x dx I
d1 d2
o
建立坐标系,取面积元
dS
高二物理竞赛电通量高斯定理课件
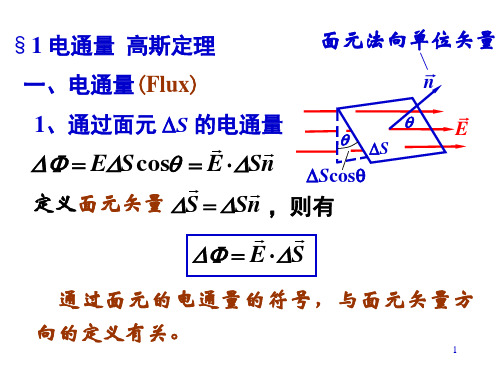
当 qi 0, E dS 0,表示有电场线从电荷发出,
i
S
穿出闭合曲面,所以正电荷是静电场的源头。
当
qi
i
0, E dS
S
0,表示电场线穿入闭合曲面,
终止于负电荷,所以负电荷是静电场的尾闾。
5
定理的证明:
(1)通过包围点电荷 q 的同心球面的电通量 为 q/0
d
S
q
4 0r
2
dS
S
q 4r2
4 0r 2
q/0
En S
r q
S
6
立体角的概念:
z
dS
ddSS
rrˆ
dS
r
d
x
y
d dS dSrˆ r2 r2
在球坐标系中
d sin d d
7
闭合曲面对内部一点所张立体角为4。
证明:
d
S
S
dS r2
1
r2
dS
S
4
r
r
2
2
4
S
dS
d
dS
Or
8
(2)通过包围点电荷 q 的任意闭合曲面的电通
q
4
0
d
q
4
0
d
0
(4)多个点电荷的电通量等于它们单独存在
时电通量的和(场叠加原理) 10
对高斯定理的说明: 1、高斯定理说的是穿过一闭合曲面(高斯面)的电 通量的规律。穿过闭合曲面的电通量才直接与闭合 曲面包围的电量的代数和有关。要注意电场强度E 和电通量的区别: E是电场的矢量点函数,它是反映场点电场强度的大 小和方向的物理量; 是一个标量(有正、有负),它是对一个面元或一个 曲面而言的,对电场中一点谈电通量毫无意义。1/0 倍E SS10
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
量异号。
=0,高斯面上各点的场强不一定为 0,可能是高斯面
内无静电荷。
高斯定是理静电场的基本定理,在计算电场强度上也有广泛的应 用。
9
例1:计算半径 R、带电量为 q 的均匀带电球体内、 外的电场强度。 解:1.球体外部 r > R,均匀带电球体决定场强为球对 称,取半径为 r 的球面为高斯面。 球面上各点的场强 E 大小相等, 方向与法线同向。
o
q E r 3 4 0 R
在球体内部电场强度与 r成正比。
1
R
E
q 4 0 R 2 1
Er
o
R
12
r
四、选取高斯面原则
1பைடு நூலகம்要求电场具有高度对称性。
S EdS cos
q
0
2.高斯面应选取规则形状(通常是圆柱面或球面)。 3.高斯面上各点的法向与场强的关系可以选择为: 场强方向与法线方向一致或者垂直。
右边
q
0
0
由于闭合面内无电荷。
左边=右边
7
3.点电荷系:设有 1、2、···、k 个电荷在闭合面内, k+1、k+2、···、n 个电荷在闭合面外 由场叠加原理,高斯面上的场强为:
E E1 Ek Ek 1 En
面内电荷 面外电荷
E dS
i E r 3 i i 4 0 ri e E dS
q
R
E
S
Ei dS cos
i
i
E dS cos
i i
qi
0
6
4.点电荷位于闭合面外 穿入与穿出的电场线根数 相同,正负通量抵消。
E
左边
e E dS 0 S
q1
qk
qi
k
i在高斯面内
8
三、明确几点
1.高斯面为闭合面。
q E dS
S
0
2.电通量 只与曲面内电荷有关,与曲面外电荷无关。
3. E 为高斯面上某点的场强,是由空间所有电荷产生 的,与面内面外电荷都有关。
= 0,高斯面内不一定无电荷,有可能曲面内电荷等
E // dS,
cos 1
q
E S dS
0
写成
q E 0 S dS
或高斯面上某一部分各点的场强方向与高斯面法线方向垂直, 该部分的通量为0。
E dS, cos 0
13
例2:计算无限长均匀带电直线外一点P的电场强度 E , 设P点到直线的距离为r,线电荷密度为 。 解:作半径为r高为h的闭 合圆柱面, P
高斯面
E // dS,
球面上各点的场强 E 大小相等, 方向与法线相同。
cos 1
2 S
e E dS E 4 r
面内电荷代数和为
4 3 r q 4 3 3 r 3 q R R 3 q
3
11
将两边的计算结果代入得:
rq E 4r 3 0R
2
3
q
高斯长期从事于数学并将数学应用于物理学、天文学 和大地测量学等领域的研究,著述丰富,成就甚多。他一 生中共发表323篇(种)著作,提出404项科学创见(发表 178项),在各领域的主要成就有:
2
(1)物理学和地磁学中,关于静电学、温差电和摩擦电 的研究、利用绝对单位(长度、质量和时间)法则量度非 力学量以及地磁分布的理论研究。 (2)利用几何学知识研究光学系统近轴光线行为和成像, 建立高斯光学。 (3)天文学和大地测量学中,如小行星轨道的计算,地球 大小和形状的理论研究等。 (4)结合试验数据的测算,发展了概率统计理论和误差理 论,发明了最小二乘法,引入高斯误差曲线。此外,在纯 数学方面,对数论、代数、几何学的若干基本定理作出严 格证明。 在CGS电磁系单位制(emu)中磁感应强度的单位定为 高斯(1932年以前曾经用高斯作为磁场强度单位),便是 3 为了纪念高斯在电磁学上的卓越贡献。
§102 高斯定理
1
高斯(Carl Friedrich Gauss 1777-1855) 德国数学家和物理学家。 1777年4月30日生于德国布伦瑞克, 幼时家境贫困,聪敏异常,受一贵族 资助才进学校受教育。1795-1799年 在哥廷根大学学习,1799年获博士学 位。1833年和物理学家W.E.韦伯共同 建立地磁观测台,组织磁学学会以联 系全世界的地磁台站网。1855年2月 23日在哥廷根逝世。
q
o
R
E
n
E // d S ,
cos 1
2
r
EdS cos E ds E 4r
S s
q
0
高斯面
10
球面内电荷代数和为
q q
q E 与点电荷的场相同。 2 4 0 r
2.球体内部 r < R
1
q
o
e EdS cos
S
r
R E n
S
S
E1 dS Ek dS
S
S
( E1 Ek Ek 1 En ) dS
S
Ek 1 dS En dS
S
0 0 i 1 0 0 0 q E dS 证毕 S 0
一、定理表述
静电场中通过任意的闭合曲面的电通量,等于曲面 内电荷的代数和除以 0 。
q e E dS
S
q是曲面S内所包含的电荷。
0
二、定理证明
1、先证明点电荷的情况成立。取点电荷位于坐标原 点高斯面是半径为R的闭合球面。
4
穿过球面的电通量
S
左边 e E dS
EdS cos
S
q
r
0
E dS,
左底 侧 右底
EdS cos
球面上各点E大小相等, E//dS ,cos =1,
q
R
E n
e E dS E 4R 2
S
q q 2 4 R 2 4 0 R
右边
1
高斯面
0
q
0
q
0
左边=右边
5
2、当曲面是任意形状时,通 过球面的电力线也必然通过曲 面。即高斯面不是球面时 高 斯定理也成立。 3、当高斯面内包含的点电 荷不止一个时,利用场强的 叠加原理: 1 q
=0,高斯面上各点的场强不一定为 0,可能是高斯面
内无静电荷。
高斯定是理静电场的基本定理,在计算电场强度上也有广泛的应 用。
9
例1:计算半径 R、带电量为 q 的均匀带电球体内、 外的电场强度。 解:1.球体外部 r > R,均匀带电球体决定场强为球对 称,取半径为 r 的球面为高斯面。 球面上各点的场强 E 大小相等, 方向与法线同向。
o
q E r 3 4 0 R
在球体内部电场强度与 r成正比。
1
R
E
q 4 0 R 2 1
Er
o
R
12
r
四、选取高斯面原则
1பைடு நூலகம்要求电场具有高度对称性。
S EdS cos
q
0
2.高斯面应选取规则形状(通常是圆柱面或球面)。 3.高斯面上各点的法向与场强的关系可以选择为: 场强方向与法线方向一致或者垂直。
右边
q
0
0
由于闭合面内无电荷。
左边=右边
7
3.点电荷系:设有 1、2、···、k 个电荷在闭合面内, k+1、k+2、···、n 个电荷在闭合面外 由场叠加原理,高斯面上的场强为:
E E1 Ek Ek 1 En
面内电荷 面外电荷
E dS
i E r 3 i i 4 0 ri e E dS
q
R
E
S
Ei dS cos
i
i
E dS cos
i i
qi
0
6
4.点电荷位于闭合面外 穿入与穿出的电场线根数 相同,正负通量抵消。
E
左边
e E dS 0 S
q1
qk
qi
k
i在高斯面内
8
三、明确几点
1.高斯面为闭合面。
q E dS
S
0
2.电通量 只与曲面内电荷有关,与曲面外电荷无关。
3. E 为高斯面上某点的场强,是由空间所有电荷产生 的,与面内面外电荷都有关。
= 0,高斯面内不一定无电荷,有可能曲面内电荷等
E // dS,
cos 1
q
E S dS
0
写成
q E 0 S dS
或高斯面上某一部分各点的场强方向与高斯面法线方向垂直, 该部分的通量为0。
E dS, cos 0
13
例2:计算无限长均匀带电直线外一点P的电场强度 E , 设P点到直线的距离为r,线电荷密度为 。 解:作半径为r高为h的闭 合圆柱面, P
高斯面
E // dS,
球面上各点的场强 E 大小相等, 方向与法线相同。
cos 1
2 S
e E dS E 4 r
面内电荷代数和为
4 3 r q 4 3 3 r 3 q R R 3 q
3
11
将两边的计算结果代入得:
rq E 4r 3 0R
2
3
q
高斯长期从事于数学并将数学应用于物理学、天文学 和大地测量学等领域的研究,著述丰富,成就甚多。他一 生中共发表323篇(种)著作,提出404项科学创见(发表 178项),在各领域的主要成就有:
2
(1)物理学和地磁学中,关于静电学、温差电和摩擦电 的研究、利用绝对单位(长度、质量和时间)法则量度非 力学量以及地磁分布的理论研究。 (2)利用几何学知识研究光学系统近轴光线行为和成像, 建立高斯光学。 (3)天文学和大地测量学中,如小行星轨道的计算,地球 大小和形状的理论研究等。 (4)结合试验数据的测算,发展了概率统计理论和误差理 论,发明了最小二乘法,引入高斯误差曲线。此外,在纯 数学方面,对数论、代数、几何学的若干基本定理作出严 格证明。 在CGS电磁系单位制(emu)中磁感应强度的单位定为 高斯(1932年以前曾经用高斯作为磁场强度单位),便是 3 为了纪念高斯在电磁学上的卓越贡献。
§102 高斯定理
1
高斯(Carl Friedrich Gauss 1777-1855) 德国数学家和物理学家。 1777年4月30日生于德国布伦瑞克, 幼时家境贫困,聪敏异常,受一贵族 资助才进学校受教育。1795-1799年 在哥廷根大学学习,1799年获博士学 位。1833年和物理学家W.E.韦伯共同 建立地磁观测台,组织磁学学会以联 系全世界的地磁台站网。1855年2月 23日在哥廷根逝世。
q
o
R
E
n
E // d S ,
cos 1
2
r
EdS cos E ds E 4r
S s
q
0
高斯面
10
球面内电荷代数和为
q q
q E 与点电荷的场相同。 2 4 0 r
2.球体内部 r < R
1
q
o
e EdS cos
S
r
R E n
S
S
E1 dS Ek dS
S
S
( E1 Ek Ek 1 En ) dS
S
Ek 1 dS En dS
S
0 0 i 1 0 0 0 q E dS 证毕 S 0
一、定理表述
静电场中通过任意的闭合曲面的电通量,等于曲面 内电荷的代数和除以 0 。
q e E dS
S
q是曲面S内所包含的电荷。
0
二、定理证明
1、先证明点电荷的情况成立。取点电荷位于坐标原 点高斯面是半径为R的闭合球面。
4
穿过球面的电通量
S
左边 e E dS
EdS cos
S
q
r
0
E dS,
左底 侧 右底
EdS cos
球面上各点E大小相等, E//dS ,cos =1,
q
R
E n
e E dS E 4R 2
S
q q 2 4 R 2 4 0 R
右边
1
高斯面
0
q
0
q
0
左边=右边
5
2、当曲面是任意形状时,通 过球面的电力线也必然通过曲 面。即高斯面不是球面时 高 斯定理也成立。 3、当高斯面内包含的点电 荷不止一个时,利用场强的 叠加原理: 1 q
