幻方解法 文档
六阶幻方解法教学文案

六阶幻方解法
一、奇阶幻方:罗伯法(适合编制所有的奇阶幻方)
一居上行正中央,依次斜填切莫忘,
上出格时往下填,右出格时左边放,
排重便在下格填,角上出格一个样。
例:用1-25组成五阶幻方。
二、偶阶幻方:
偶阶幻方分两类:双偶数阶幻方和单偶数阶幻方
双偶数:四阶幻方,八阶幻方,……4K阶幻方,
可用<对称交换法>,方法很简单:
1) 把自然数依次排成方阵
2) 把幻方划成4×4的小区,每个小区划对角线
3) 把这些对角线所划到的数,保持不动
4) 把没划到的数,按幻方的中心,以中心对称的方式,进行对调。
单偶数:六阶幻方,十阶幻方,……4K+2阶幻方
方法是很繁的,有一种称<同心方阵法>:
1) 把幻方分成两个区:一是边框一圈;二是里面一个双偶数方阵,
2) 把(3+8K)到(16K2+8K+2)按双偶数幻方方法填入双偶数方阵
3) 把余下的数,在边上试填,调整到符合为止。
例题:用自然数1-36完成六阶幻方。
首先因为4×1+2,k=1,把11~26填入中间4×4方格中,
然后将1-10,27-36这20个自然数成对填入余下空中。
“九子斜排,上下对易,左右相更,四维挺出”。
奇数三阶幻方的解法

奇数三阶幻方的解法摘要:1.奇数三阶幻方的概念及特点2.构造奇数三阶幻方的基本方法3.构造奇数三阶幻方的具体步骤4.奇数三阶幻方的验证方法5.结论正文:一、奇数三阶幻方的概念及特点奇数三阶幻方,又称为奇数阶幻方,是指一个含有N 行N 列的数表,满足如下条件:1.每一行中的数字之和等于奇数;2.每一列中的数字之和等于奇数;3.每一对角线上的数字之和等于奇数;4.每一反对角线上的数字之和等于奇数;5.N 个数字都不重复。
由于满足以上条件的数表中的数字和为奇数,因此称为奇数三阶幻方。
二、构造奇数三阶幻方的基本方法构造奇数三阶幻方的基本方法是先设定中心数,然后按照一定的规律填充其他数字。
三、构造奇数三阶幻方的具体步骤构造奇数三阶幻方的具体步骤如下:1.选择一个奇数作为中心数,例如选定数字5 作为中心数;2.将中心数放在数表的中心位置,即第3 行第3 列;3.从中心数开始,按照顺时针和逆时针方向填充其他数字。
具体规律为:- 从中心数开始,向上、下、左、右四个方向填充数字,直到碰到边界;- 碰到边界后,从该方向的对角线开始填充数字,直到碰到另一个边界;- 填充完四个方向后,再从中心数开始,按照顺时针和逆时针方向继续填充数字,直到填满整个数表。
四、奇数三阶幻方的验证方法在填充完数字后,需要验证该数表是否满足奇数三阶幻方的条件。
验证方法如下:1.验证每一行、每一列的数字之和是否为奇数;2.验证每一对角线和每一反对角线上的数字之和是否为奇数。
如果满足以上条件,则所构造的数表是一个有效的奇数三阶幻方。
五、结论通过以上步骤,我们可以构造出一个满足条件的奇数三阶幻方。
这种方法不仅适用于奇数三阶幻方,还可以推广到其他奇数阶幻方。
幻方解法

幻方解法
幻方,就是对于一个n×n的方阵,将1—n²这n²个数填入其中,使每行每列以及对角线上的数字之和都相等的方阵。
幻方分为奇数阶幻方(n=2k+1)、单偶数幻方
(n=4k+2)、双偶数幻方(n=4k)三种,每种幻方解法不同,但都有其固定的解。
下面我来具体介绍下幻方的解法:
1.奇数阶幻方
①将1填入第一行中间位置
②向右上方向依次填入
③如果上方出格了,则将其填入最后一行与其同列的位置
④如果右方出格了,则将其填入第一列与其同行的位置
⑤如果右上都出格,则将其填入第一列最后一格
⑥如果将要填入的方格已有数字,则填入上一个数字的下方
这里已三阶幻方为例:
2.双偶数阶幻方(n=4k):
①先将1,2,3……n²依次填入方阵中
②拟出方阵对角线
③对角线上数字不动,将其余所有数字移至与其中心对称的位置
这里以四阶幻方为例
↓
↓ 3.单偶数阶幻方(n=4k+2):
①先将1,2,3……n平方依次填入方阵中
②拟出对角线,将对角线上所有数字移至与其中心对称的位置。
③从方阵左半部分的每一列数字中抽出一对上下对称的数字互换位置(每一列抽出一对)
④从方阵上半部分的每一行数字中抽出一对左对称的数字互换位置(每一行抽出一对)
注:已经移动过或换过位置的数字不能再移动或换位
这里以六阶幻方为例:
↓
↓②↓
↓
↓③↓
↓
↓④↓。
幻方解法

幻方解法奇阶幻方介绍:当n为奇数时,我们称幻方为奇阶幻方。
可以用Merzirac 法与loubere法实现,根据我的研究,发现用国际象棋之马步也可构造出更为神奇的奇幻方,故命名为horse法。
偶阶幻方介绍:当n为偶数时,我们称幻方为偶阶幻方。
当n可以被4整除时,我们称该偶阶幻方为双偶幻方;当n不可被4整除时,我们称该偶阶幻方为单偶幻方。
可用了Hire法、Strachey以及YinMagic将其实现,Strachey 为单偶模型,我对双偶(4m阶)进行了重新修改,制作了另一个可行的数学模型,称之为Spring。
YinMagic是我于2002年设计的模型,他可以生成任意的偶阶幻方。
奇阶幻方解法Merzirac法:在第一行居中的方格内放1,依次向左上方填入2、3、4…,如果左上方已有数字,则向下移一格继续填写。
如下图用Merziral法生成的5阶幻方:17 24 1 8 1523 5 7 14 164 6 13 20 2210 12 19 21 311 18 25 2 9loubere法:在居中的方格向上一格内放1,依次向左上方填入2、3、4…,如果左上方已有数字,则向上移两格继续填写。
如下图用Louberel法生成的7阶幻方:30 39 48 1 10 19 2838 47 7 9 18 27 2946 6 8 17 26 35 375 14 16 25 34 36 4513 15 24 33 42 44 421 23 32 41 43 3 1222 31 40 49 2 11 20horse法:先在任意一格内放入1。
向左走1步,并下走2步放入2(称为马步),向左走1步,并下走2步放入3,依次类推放到n。
在n的下方放入n+1(称为跳步),再按上述方法放置到2n,在2n的下边放入2n+1。
如下图用Horse 法生成的5阶幻方:77 58 39 20 1 72 53 34 156 68 49 30 11 73 63 44 2516 78 59 40 21 2 64 54 3526 7 69 50 31 12 74 55 4536 17 79 60 41 22 3 65 4637 27 8 70 51 32 13 75 5647 28 18 80 61 42 23 4 6657 38 19 9 71 52 33 14 7667 48 29 10 81 62 43 24 5一般令矩阵[1,1]为向右走一步,向上走一步,[-1,0]为向左走一步。
偶阶幻方的解法(文档4篇)

偶阶幻方的解法(文档4篇)以下是网友分享的关于偶阶幻方的解法的资料4篇,希望对您有所帮助,就爱阅读感谢您的支持。
第1篇偶阶幻方的填法第一种:n=4*m+2, m为自然数1)将n阶方阵分为四个小魔方阵ABCD如下排列:B C D A因为n*n=4*(2*m+1)*(2*m+1),记u=n/2=2*m+1,分为1~u*u,u*u+1~2*u*u,2*u*u+1~3*u*u,3*u*u+1~4*u*u 即在调用子函数的时候分别如下面传递参数: A(0),B(u*u),C(2*u*u),D(3*u*u)分别在ABCD中按照前面的填法把奇数阶填好(注意加上所传参数作为基数,每一个元素都要加上这个值),最后做如下交换:(1)B中第0~(m-1)-1行中元素与C中相对应元素交换(2)D中第(n-1)-m+1~(n-1)共m行的每行中的元素与A中相对应元素交换(3)交换D:(u+m,m)与A中对应元素(矩阵中心值)(4)交换D:(n-1,m)与A中对应元素(实际为矩阵最大值n*n) 所谓对应位置,指相对于小魔方阵的左顶角的相对的行列位置。
上面的这些你可以用数学进行证明,利用魔方阵常数(注意n阶的和u阶的关系) 第二种:n=4*m,m为自然数因为行列都是4的倍数,因而可以将整个矩阵分为每4*4的小矩阵。
先判断一个数是否在划为4*4小矩阵的对角线上,如果在,则填该位置的数为n*n-i+1(i为该元素的相对位置,从1开始,比如n阶的第s行第t个元素则其i=s*n+t) 如果不在,则填上i。
(4的倍数幻方,4,8,12可以。
6、10是不行的。
这样才有一般填法,4的方法是先画好格,连接对角线,这样有8格也就是一半的格子被斜线划过,然后从头到尾,数格子,没有斜线的格子就填上数的数,那么第一排就是1不填,2填,3填,4不填,第二排就是5填,6不填,7不填,8填三四排一样,然后从尾到头数,填划了斜线的格子,就成4介幻方;8阶就是对角线画斜线外,相邻边的中点相连再画4条线,形状就如4个4阶幻方;12阶就是三等分点,画9个如四阶的。
四阶幻方解法

【顺序填数;以中心点对称互换数字】.以1-16构成的四阶幻方为例:
1、先把1放在四阶幻方4个角的任意一个角格,按同一个方向按顺序依次填写其余数.
如图:按行从左向右顺序排数.
2、以中心点对称互换数字.(有两种对称交换的方法)
1)、以中心点对称交换对角线上的数(即1-16、4-13、6-11、7-10互换),完成幻方,幻和值=34.
2)、以中心点对称交换非对角线上的数(即2-15、3-14、5-12、8-9互换),完成幻方,幻和值=34.
什么样的16个数能构成四阶幻方呢?【4个数一组的4组数(共16个数),组与组对称等差,每组数与数对称等差,这样的16个数能构成四阶幻方(其中就包括等差的16个数).】
如图
上图,每组数与数以2-3-2对称等差,组与组以10-20-10对称等差.
下图,每组数与数以1-2-1对称等差,组与组以10-20-10对称等差.
再如:
上图,每组数与数等差为1,组与组等差为5.
中图,每组数与数等差为1,组与组以5-10-5对称等差.
下图,每组数与数以2-3-2对称等差,组与组以5-10-5对称等差.
【四阶幻方的特点:】
1、互换对称的行(列),幻方成立.
2、互换一侧的行(或列),再互换另一侧的行(或列),幻方亦成立.
3、互换不对称的行(或列),再互换另外不对称的行(或列),幻方亦成立.
4、平移互换对角的行或列、平移互换对角,幻方成立.
另,每16个能构成四阶幻方的数,幻方的填法有880种.。
幻方常规解法汇总

幻方常规解法汇总按目前填写幻方的方法,是把幻方分成了三类,即奇数阶幻方、双偶阶幻方、单偶阶幻方。
下面按这三类幻方,列出最常用解法(考试用,不求强大,只求有效!)。
奇数阶幻方(罗伯法)奇数阶幻方最经典的填法是罗伯法。
填写的方法是:把1(或最小的数)放在第一行正中;按以下规律排列剩下的(n×n-1)个数:1、每一个数放在前一个数的右上一格;2、如果这个数所要放的格已经超出了顶行那么就把它放在底行,仍然要放在右一列;3、如果这个数所要放的格已经超出了最右列那么就把它放在最左列,仍然要放在上一行;4、如果这个数所要放的格已经超出了顶行且超出了最右列,那么就把它放在前一个数的下一行同一列的格内;5、如果这个数所要放的格已经有数填入,那么就把它放在前一个数的下一行同一列的格内。
例,用该填法获得的5阶幻方:17 24 1 8 1523 5 7 14 164 6 13 20 2210 12 19 21 311 18 25 2 9双偶数阶幻方(对称交换法)所谓双偶阶幻方就是当n可以被4整除时的偶阶幻方,即4K阶幻方。
在说解法之前我们先说明一个“互补数”定义:就是在n阶幻方中,如果两个数的和等于幻方中最大的数与1的和(即n×n+1),我们称它们为一对互补数。
如在三阶幻方中,每一对和为10的数,是一对互补数;在四阶幻方中,每一对和为17的数,是一对互补数。
双偶数阶幻方的对称交换解法:先看看4阶幻方的填法:将数字从左到右、从上到下按顺序填写:1 2 3 45 6789 1011121314 15 16内外四个角对角上互补的数相易,(方阵分为两个正方形,外大内小,然后把大正方形的四个对角上的数字对换,小正方形四个对角上的数字对换)即(1,16)(4,13)互换(6,11)(7,10)互换即可。
16 2 3 135 11 10 89 7 6 124 14 15 1对于n=4k阶幻方,我们先把数字按顺序填写。
幻方常规解法汇总

幻方常规解法汇总按目前填写幻方的方法,是把幻方分成了三类,即奇数阶幻方、双偶阶幻方、单偶阶幻方。
下面按这三类幻方,列出最常用解法(考试用,不求强大,只求有效!)。
奇数阶幻方(罗伯法)奇数阶幻方最经典的填法是罗伯法。
填写的方法是:把1(或最小的数)放在第一行正中;按以下规律排列剩下的(n×n-1)个数:1、每一个数放在前一个数的右上一格;2、如果这个数所要放的格已经超出了顶行那么就把它放在底行,仍然要放在右一列;3、如果这个数所要放的格已经超出了最右列那么就把它放在最左列,仍然要放在上一行;4、如果这个数所要放的格已经超出了顶行且超出了最右列,那么就把它放在前一个数的下一行同一列的格内;5、如果这个数所要放的格已经有数填入,那么就把它放在前一个数的下一行同一列的格内。
例,用该填法获得的5阶幻方:双偶数阶幻方(对称交换法)所谓双偶阶幻方就是当n可以被4整除时的偶阶幻方,即4K阶幻方。
在说解法之前我们先说明一个“互补数”定义:就是在 n 阶幻方中,如果两个数的和等于幻方中最大的数与 1 的和(即 n×n+1),我们称它们为一对互补数。
如在三阶幻方中,每一对和为 10 的数,是一对互补数;在四阶幻方中,每一对和为 17 的数,是一对互补数。
双偶数阶幻方的对称交换解法:先看看4阶幻方的填法:将数字从左到右、从上到下按顺序填写:内外四个角对角上互补的数相易,(方阵分为两个正方形,外大内小,然后把大正方形的四个对角上的数字对换,小正方形四个对角上的数字对换)即(1,16)(4,13)互换(6,11)(7,10)互换即可。
对于n=4k阶幻方,我们先把数字按顺序填写。
写好后,按4×4把它划分成k×k个方阵。
因为n 是4的倍数,一定能用4×4的小方阵分割。
然后把每个小方阵的对角线,象制作4阶幻方的方法一样,对角线上的数字换成互补的数字,就构成幻方。
以8阶幻方为例:(1) 先把数字按顺序填。
幻方常规解法汇总

幻方常规解法汇总没法,组合数学还考幻方构造。
这东西不看解法真不会写,虽然没见有啥用,但还是记录下,免得日后再找。
按目前填写幻方的方法,是把幻方分成了三类,即奇数阶幻方、双偶阶幻方、单偶阶幻方。
下面按这三类幻方,列出最常用解法(考试用,不求强大,只求有效!)。
奇数阶幻方(罗伯法)奇数阶幻方最经典的填法是罗伯法。
填写的方法是:把1(或最小的数)放在第一行正中;按以下规律排列剩下的(n ×n-1)个数:1、每一个数放在前一个数的右上一格;2、如果这个数所要放的格已经超出了顶行那么就把它放在底行,仍然要放在右一列;3、如果这个数所要放的格已经超出了最右列那么就把它放在最左列,仍然要放在上一行;4、如果这个数所要放的格已经超出了顶行且超出了最右列,那么就把它放在前一个数的下一行同一列的格内;5、如果这个数所要放的格已经有数填入,那么就把它放在前一个数的下一行同一列的格内。
例,用该填法获得的5阶幻方:双偶数阶幻方(对称交换法)所谓双偶阶幻方就是当n可以被4整除时的偶阶幻方,即4K阶幻方。
在说解法之前我们先说明一个“互补数”定义:就是在 n 阶幻方中,如果两个数的和等于幻方中最大的数与 1 的和(即n×n+1),我们称它们为一对互补数。
如在三阶幻方中,每一对和为 10 的数,是一对互补数;在四阶幻方中,每一对和为 17 的数,是一对互补数。
双偶数阶幻方的对称交换解法:先看看4阶幻方的填法:将数字从左到右、从上到下按顺序填写:内外四个角对角上互补的数相易,(方阵分为两个正方形,外大内小,然后把大正方形的四个对角上的数字对换,小正方形四个对角上的数字对换)即(1,16)(4,13)互换(6,11)(7,10)互换即可。
对于n=4k阶幻方,我们先把数字按顺序填写。
写好后,按4×4把它划分成k×k个方阵。
因为n是4的倍数,一定能用4×4的小方阵分割。
然后把每个小方阵的对角线,象整理4阶幻方的方法一样,对角线上的数字换成互补的数字,就构成幻方。
幻方常规解法汇总(WORD格式) 看94射雕学九宫格,20分钟1-8阶

幻方常规解法汇总没法,组合数学还考幻方构造。
这东西不看解法真不会写,虽然没见有啥用,但还是记录下,免得日后再找。
按目前填写幻方的方法,是把幻方分成了三类,即奇数阶幻方、双偶阶幻方、单偶阶幻方。
下面按这三类幻方,列出最常用解法(考试用,不求强大,只求有效!)。
奇数阶幻方(罗伯法)奇数阶幻方最经典的填法是罗伯法。
填写的方法是:把1(或最小的数)放在第一行正中;按以下规律排列剩下的(n×n-1)个数:1、每一个数放在前一个数的右上一格;2、如果这个数所要放的格已经超出了顶行那么就把它放在底行,仍然要放在右一列;3、如果这个数所要放的格已经超出了最右列那么就把它放在最左列,仍然要放在上一行;4、如果这个数所要放的格已经超出了顶行且超出了最右列,那么就把它放在前一个数的下一行同一列的格内;5、如果这个数所要放的格已经有数填入,那么就把它放在前一个数的下一行同一列的格内。
例,用该填法获得的5阶幻方:双偶数阶幻方(对称交换法)所谓双偶阶幻方就是当n可以被4整除时的偶阶幻方,即4K阶幻方。
在说解法之前我们先说明一个“互补数”定义:就是在n 阶幻方中,如果两个数的和等于幻方中最大的数与1 的和(即n×n+1),我们称它们为一对互补数。
如在三阶幻方中,每一对和为10 的数,是一对互补数;在四阶幻方中,每一对和为17 的数,是一对互补数。
双偶数阶幻方的对称交换解法:先看看4阶幻方的填法:将数字从左到右、从上到下按顺序填写:单偶数阶幻方(象限对称交换法)以n=10为例,10=4×2+2,这时k=2(1)把方阵分为A,B,C,D四个象限,这样每一个象限肯定是奇数阶。
用罗伯法,依次在A象限,D 象限,B象限,C象限按奇数阶幻方的填法填数。
(2)在A象限的中间行、中间格开始,按自左向右的方向,标出k格。
A象限的其它行则标出最左边的k格。
将这些格,和C象限相对位置上的数,互换位置。
(3)在B象限任一行的中间格,自右向左,标出k-1列。
数字幻方的求解

目录自序 ............................................................................................................................... - 4 -作品简介....................................................................................................................... - 5 -开篇语 ........................................................................................................................... - 6 -数字幻方的变进制对角线二维前后方图法求解简介 .........................................................................................- 6 - 数字幻方的介绍..............................................................................................................................................- 6 - 二维前后方图以及其构造方法.........................................................................................................................- 6 - 3阶幻方数字转化为十进制数字方法...............................................................................................................- 7 - 中心线重心数字或块中间边角第概念 ..............................................................................................................- 7 -混沌关系理论 .............................................................................................................. - 7 -第一章 ........................................................................................................................... - 8 -3阶幻方求解 ............................................................................................................... - 8 -前后方图之斜飞法 ..........................................................................................................................................- 8 - 第二章 ......................................................................................................................... - 12 -5阶幻方求解 ............................................................................................................. - 12 -第一节.......................................................................................................................................................... - 12 - 斜飞法快速求解5阶幻方方法....................................................................................................................... - 12 - 第二节.......................................................................................................................................................... - 14 - 5阶幻方的第一类第一种的求解.................................................................................................................... - 14 - 第三章 ......................................................................................................................... - 16 -4阶幻方的求解......................................................................................................... - 16 -第一节.......................................................................................................................................................... - 16 - 第一类第一种前后方图的求解方法................................................................................................................ - 16 - 第二节.......................................................................................................................................................... - 17 - 第一类第二种非均匀分布边上数字和值相同的论述 ....................................................................................... - 17 - 第三节.......................................................................................................................................................... - 23 - 第二类第一种对角线互补前后方图具体解法.................................................................................................. - 23 - 第四章 ......................................................................................................................... - 36 -乘法求解幻方 ............................................................................................................ - 36 -第一节.......................................................................................................................................................... - 36 - 最简单的奇数合数9阶幻方的快速求解......................................................................................................... - 36 - 第二节.......................................................................................................................................................... - 38 -倍增法求解偶数幻方 ............................................................................................... - 40 -第一节.......................................................................................................................................................... - 40 - 6阶幻方倍增图的快速求解........................................................................................................................... - 40 - 第二节.......................................................................................................................................................... - 50 - 6阶幻方倍增图的通用形式求解.................................................................................................................... - 50 -第六章 ......................................................................................................................... - 55 -填充数字的抽取方法 ............................................................................................... - 55 -第一节.......................................................................................................................................................... - 55 - 填充方法分类 ............................................................................................................................................... - 55 - 第二节.......................................................................................................................................................... - 55 - 6阶幻方(可用于乘因子为3的乘法求解的所有幻方)数字填充等差法 ............................................................. - 55 - 第七章8阶幻方的特殊解法外倍增法 ................................................................ - 73 -第一节.......................................................................................................................................................... - 73 - 借用4阶幻方第一类第二类前后方图图表快速求解小幻方块数字的抽取........................................................ - 73 - 第二节.......................................................................................................................................................... - 74 - 8阶外倍增小幻方中按照单个数字的抽取...................................................................................................... - 74 - 第三节.......................................................................................................................................................... - 75 - 8阶数字的等差抽取 ..................................................................................................................................... - 75 - 第四节.......................................................................................................................................................... - 78 - 隔差排列的方法研究..................................................................................................................................... - 78 - 第八章 ......................................................................................................................... - 79 -小幻方块在大幻方位置不同达到和值相等的排列数量研究........................... - 79 -第九章 ......................................................................................................................... - 80 -乘法或倍增法求解幻方中数字的排列数量研究 ................................................ - 80 -第十章 ......................................................................................................................... - 81 -幻方研究应用此法中的一些问题.......................................................................... - 81 -附录一 ......................................................................................................................... - 82 -880个基本的4阶方图对应的前方方图 .............................................................. - 82 -880个基本的4阶方图对应的后方方图 .............................................................. - 94 -880个基本的4阶幻方前后方图 .........................................................................- 106 -880个基本的4阶十进制幻方图 ......................................................................... - 118 -混沌关系理论在四色原理中心点外画圈法证明中的应用 .............................- 130 -自序规律——来自于刻苦的努力研究和转瞬即逝的灵感火花,是人类永恒的追求,如何在一片纷纷扰扰中,找到通往解决难题的捷径,探寻到事物的本质,是人们孜孜不倦并为之苦心研究的动力源泉。
幻方解法

幻方解法
幻方,就是对于一个n×n的方阵,将1—n²这n²个数填入其中,使每行每列以及对角线上的数字之和都相等的方阵。
幻方分为奇数阶幻方(n=2k+1)、单偶数幻方
(n=4k+2)、双偶数幻方(n=4k)三种,每种幻方解法不同,但都有其固定的解。
下面我来具体介绍下幻方的解法:
1.奇数阶幻方
①将1填入第一行中间位置
②向右上方向依次填入
③如果上方出格了,则将其填入最后一行与其同列的位置
④如果右方出格了,则将其填入第一列与其同行的位置
⑤如果右上都出格,则将其填入第一列最后一格
⑥如果将要填入的方格已有数字,则填入上一个数字的下方
这里已三阶幻方为例:
2.双偶数阶幻方(n=4k):
①先将1,2,3……n²依次填入方阵中
②拟出方阵对角线
③对角线上数字不动,将其余所有数字移至与其中心对称的位置
这里以四阶幻方为例
↓
↓ 3.单偶数阶幻方(n=4k+2):
①先将1,2,3……n平方依次填入方阵中
②拟出对角线,将对角线上所有数字移至与其中心对称的位置。
③从方阵左半部分的每一列数字中抽出一对上下对称的数字互换位置(每一列抽出一对)
④从方阵上半部分的每一行数字中抽出一对左对称的数字互换位置(每一行抽出一对)
注:已经移动过或换过位置的数字不能再移动或换位
这里以六阶幻方为例:
↓
↓②↓
↓
↓③↓
↓
↓④↓。
(完整word版)幻方解析
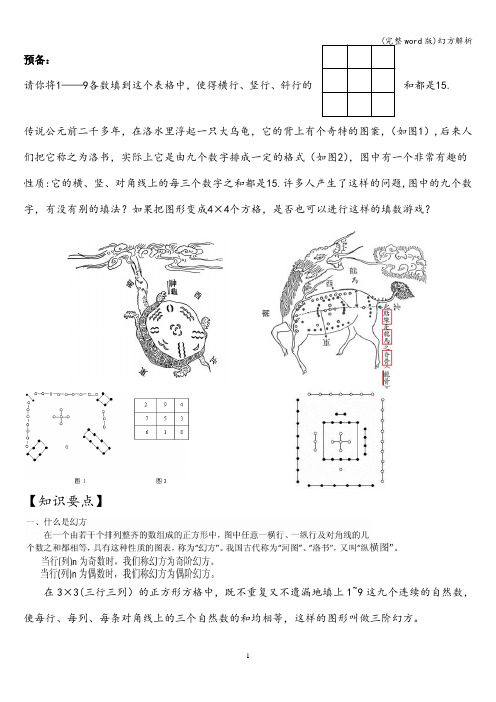
(完整word 版)幻方解析预备:请你将1——9各数填到这个表格中,使得横行、竖行、斜行的和都是15.传说公元前二千多年,在洛水里浮起一只大乌龟,它的背上有个奇特的图案,(如图1),后来人们把它称之为洛书,实际上它是由九个数字排成一定的格式(如图2),图中有一个非常有趣的性质:它的横、竖、对角线上的每三个数字之和都是15.许多人产生了这样的问题,图中的九个数字,有没有别的填法?如果把图形变成4×4个方格,是否也可以进行这样的填数游戏?【知识要点】在3×3(三行三列)的正方形方格中,既不重复又不遗漏地填上1~9这九个连续的自然数,使每行、每列、每条对角线上的三个自然数的和均相等,这样的图形叫做三阶幻方。
如果在44⨯方格内填⨯(四行四列)的正方形方格中进行填数,就要不重复,不遗漏地在44上16个连续自然数,且使每行、每列、每条对角线的四个自然数之和均相等,这样的图形叫四阶幻方。
一般地,在n×n(n行n列)的方格里,既不重复又不遗漏地填上n×n个连续自然数,(注意这些连续自然数不一定非要从1开始),每个数占一个格,且每行、每列、每条对角线上的n 个自然数和均相等,我们把这个相等的和叫做幻和,n叫做阶,这样排成的数的图形叫做n阶幻方。
中心方格中这个数叫做这个幻方的中间数。
任意阶数幻方的各行或各列或两条条对角线上所有数的和成为幻和!幻方的幻和等于 n (n2 +1)÷2 。
幻和=总和÷阶数二、幻方的特征:1、对称性2、轮换性三、幻方的种类:按照纵横各有数字的个数,可以分为:三阶幻方、四阶幻方、五阶幻方、六阶幻方……按照纵横数字数量奇偶的不同,可以分为:1、奇数阶幻方2、偶数阶幻方(1)单偶数阶幻方,阶数是2的倍数,形如:2n+2(2)双偶数阶幻方,阶数是4的倍数,形如:2n+4四、幻方的构造方法1、杨辉口诀法(仅仅适用于三阶幻方)早在公元1275年,宋朝的杨辉就对幻方进行了系统的研究.他称这种图为“纵横图”,他提出了一个构造三阶幻方的秘诀:戴九履一,左三右七,二四为肩,六八为足2、罗伯法适用于奇数阶幻方,适合于连续自然数或者等差数列的奇数阶幻方。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
67 48 29 10 81 62 43 24 5
一般的,令矩阵[1,1]为向右走一步,向上走一步,[-1,0]为向左走一步。
则马步可以表示为2X+Y,{X∈{[1,0], [-1,0]},Y∈{[0,1],
[0,-1]}}∪{Y∈{[1,0], [-1,0]},X∈{[0,1], [0,-1]}}。
对于2X+Y相应的跳步可以为2Y,-Y,X,-Y,X,3X,3X+3Y。
上面的的是X型跳步。
Horse法生成的幻方为魔鬼幻方。
Hire法生成偶阶幻方
将n阶幻方看作一个矩阵,记为A,其中的第i行j列方格内的数字记为a(i,j)。
在A内两对角线上填写1、2、3、……、n,各行再填写1、2、3、……、n,使各行各列数字之和为n*(n+1)/2。
填写方法为:第1行从n 到1填写,从第2行到第n/2行按从1到进行填写(第2行第1列填n,第2行第n列填1),从第n/2+1到第n行按n到1进行填写,对角线的方格内数字不变。
如下所示为6阶填写方法:
1 5 4 3
2 6
6 2 3 4 5 1
1 2 3 4 5 6
6 5 3 4 2 1
6 2 4 3 5 1
1 5 4 3
2 6
如下所示为8阶填写方法(转置以后):
1 8 1 1 8 8 8 1
7 2 2 2 7 7 2 7
6 3 3 3 6 3 6 6
5 4 4 4 4 5 5 5
4 5 5 5 5 4 4 4
3 6 6 6 3 6 3 3
2 7 7 7 2 2 7 2
8 1 8 8 1 1 1 8
将A上所有数字分别按如下算法计算,得到B,其中b(i,j)=n×(a(i,j)-1)。
则AT+B为目标幻方
(AT为A的转置矩阵)。
如下图用Hire法生成的8阶幻方:
1 63 6 5 60 59 58 8
56 10 11 12 53 54 15 49
41 18 19 20 45 22 47 48
33 26 27 28 29 38 39 40
32 39 38 36 37 27 26 25
24 47 43 45 20 46 18 17
16 50 54 53 12 11 55 9
57 7 62 61 4 3 2 64
(1).Strachey法生成单偶幻方
将n阶单偶幻方表示为4m+2阶幻方。
将其等分为四分,成为如下图所示A、B、C、D四个2m+1阶奇数幻方。
A C
D B
A用1至2m+1填写成(2m+1)2阶幻方;B用(2m+1)2+1至2*(2m+1)2填写成2m+1阶幻方;C用2*(2m+1)2+1至3*(2m+1)2填写成2m+1阶幻方;D 用3*(2m+1)2+1至4*(2m+1)2填写成2m+1阶幻方;在A中间一行取m个小格,其中1格为该行居中1小格,另外m-1个小格任意,其他行左侧边缘取m 列,将其与D相应方格内交换;B与C接近右侧m-1列相互交换。
如下图用Strachey法生成的6阶幻方:
35 1 6 26 19 24
3 32 7 21 23 25
31 9 2 22 27 20
8 28 33 17 10 15
30 5 34 12 14 16
4 36 29 13 18 11
(2)N 为其它偶数时
当n为非4倍数的偶数(即4n+2形)时:首先把大方阵分解为4个奇数(2m+1阶)子方阵。
按上述奇数阶幻方给分解的4个子方阵对应赋值
上左子阵最小(i),下右子阵次小(i+v),下左子阵最大(i+3v),上右子阵次大(i+2v)
即4个子方阵对应元素相差v,其中v=n*n/4
四个子矩阵由小到大排列方式为① ③
④ ②
然后作相应的元素交换:a(i,j)与a(i+u,j)在同一列做对应交换(j<t 或j>n-t+2),
a(t-1,0)与a(t+u-1,0);a(t-1,t-1)与a(t+u-1,t-1)两对元素交换
其中u=n/2,t=(n+2)/4 上述交换使每行每列与两对角线上元素之和相等。
-----------------------
Spring法生成以偶幻方
将n阶双偶幻方表示为4m阶幻方。
将n阶幻方看作一个矩阵,记为A,其中的第i行j列方格内的数字记为a(i,j)。
先令a(i,j)=(i-1)*n+j,即第一行从左到可分别填写1、2、3、……、n;即第二行从左到可分别填写n+1、n+2、n+3、……、2n;…………之后进行对角交换。
对角交换有两种方法:
方法一;将左上区域i+j为偶数的与幻方内以中心点为对称点的右下角对角数字进行交换;将右上区域i+j为奇数的与幻方内以中心点为对称点的左下角对角数字进行交换。
(保证不同时为奇或偶即可。
)方法二;将幻方等分成m*m个4阶幻方,将各4阶幻方中对角线上的方格内数字与n阶幻方内以中心点为对称点的对角数字进行交换。
如下图用Spring法生成的4阶幻方:
16 2 3 13
5 11 10 8
9 7 6 12
4 14 1
5 1
YinMagic构造偶阶幻方
先构造n-2幻方,之后将其中的数字全部加上2n-2,放于n阶幻方中间,再用本方法将边缘数字填写完毕。
本方法适用于n>4的所有幻方,我于2002年12月31日构造的数学模型。
YinMagic法可生成6阶以上的偶幻方。
如下图用YinMagic法生成的6阶幻方:
10 1 34 33 5 28
29 23 22 11 18 8
30 12 17 24 21 7
2 26 19 14 15 35
31 13 16 25 20 6
9 36 3 4 32 27
魔鬼幻方
如将幻方看成是无限伸展的图形,则任何一个相邻的n*n方格内的数字都可以组成一个幻方。
则称该幻方为魔鬼幻方。
用我研究的Horse法构造的幻方是魔鬼幻方。
如下的幻方更是魔鬼幻方,因为对于任意四个在两行两列上的数字,他们的和都是34。
此幻方可用YinMagic方法生成。
15 10 3 6
4 5 16 9
14 11 2 7
1 8 13 12
罗伯法:
1居上行正中央,仿次斜填莫相忘,上出框时往下填,
右出框时左边放,排重便在下格填,右上排重一个样。
先说明一个定义:
互补:如果两个数字的和,等于幻方最大数和最小数的和,即n*n+1,称为互补。
先看看4阶幻方的填法:将数字从左到右、从上到下按顺序填写:
这个方阵的对角线,已经用蓝色标出。
将对角线上的数字,换成与它互补的数字。
这里,n*n+1 = 4*4+1 = 17;
把1换成17-1 = 16;把6换成17-6 = 11;把11换成17-11 = 6……换完后就是一个四阶幻方。
对于n=4k阶幻方,我们先把数字按顺序填写。
写好后,按4*4把它划分成k*k个方阵。
因为n是4的倍数,一定能用4*4的小方阵分割。
然后把每个小方阵的对角线,象制作4阶幻方的方法一样,对角线上的数字换成互补的数字,就构成幻方。
下面是8阶幻方的作法:
(1) 先把数字按顺序填。
然后,按4*4把它分割成2*2个小方阵
(2) 每个小方阵对角线上的数字,换成和它互补的数。
3、单偶阶幻方
n为偶数,且不能被4整除(n=6,10,14,18,22……) (n=4k+2,k=1,2,3,4,5……)这是三种里面最复杂的幻方。
以n=10为例。
这时,k=2
(1) 把方阵分为A,B,C,D四个象限,这样每一个象限肯定是奇数阶。
用楼梯法,依次在A 象限,D象限,B象限,C象限按奇数阶幻方的填法填数。
(2) 在A象限的中间行、中间格开始,按自左向右的方向,标出k格。
A象限的其它行则标出最左边的k格。
>>>
(3) 将这些格,和C象限相对位置上的数,互换位置。
(4) 在B象限任一行的中间格,自右向左,标出k-1列。
(注:6阶幻方由于k-1=0所以不用再作B、D象限的数据交换)
<<<
(5) 将B象限标出的这些数,和D象限相对位置上的数进行交换,即可完成。
