固体物理第三章

N n n
e
iNaq
1
2 q h Na
q的分布密度：
h =整数， N：晶体链的原胞数
Na L q const. 2 2
{
简约区中q的取值总数 ＝ q
2 N ＝晶体的原胞数 a 晶格振动的格波总数＝2N＝晶体的自由度数
推广：若每个原胞中有s个原子，一维晶格振动有s个色散关系 式（s支格波），其中：1支声学波,（s-1）支光学波。 晶格振动格波的总数＝sN＝晶体的自由度数。
2 1
两个色散关系即有两支格波：（＋：光学波； －：声学波）
+
简约区：
-

a
q

a
-/a
0
/a
q
对于不在简约区中的波数q’ ，一定可在简约区中
找到唯一一个q，使之满足：
2 q q G a
G 为倒格矢
二、光学波和声学波的物理图象 第n个原胞中P、Q两种原子的位移之比
, 0,1,2, , N 1
(l)和(l’)分别是第l和第l’个原子沿和方向的位移。
2U C , C , 0
力常数
第l个原子的运动方程：
U m C , ,
2 cos e n A i1 2 aq e 2 B 2 M n
1 aq 2
i1 2 aq

2m cos
1 2 aq
e
i1 aq 2
M m M 2 m2 2 Mm cos aq
R ei
R:大于零的实数，反映原胞中P、Q两种原子的振幅比，
i t naq

m 2 eiaq eiaq 2 2 cos aq 1
解得
1 2 sin aq m 2

—— 色散关系
二、格波的简约性质、简约区
1 2 sin aq m 2
(q)

—— 色散关系


a
q

a
—— 简约区
- 2a - a
: 两原子的振动位相差。
1. 光学波（optical branch）
2m cos e n 2 2 M m M m 2 Mm cos aq n
1 aq 2
i1 2 aq
1 ei
R ei

2m cos
1 aq 2
的频率，就会发生共振。
0
q
光波： ＝c0q， c0为光速
对于实际晶体， ＋(0)在1013 ~ 1014Hz，对应于远
红外光范围。离子晶体中光学波的共振可引起对远红外
光在 ＋(0)附近的强烈吸收。
2. 声学波（acoustic branch）
1 aq e n 2 m cos 2 M m M 2 m 2 2 Mm cosaq n
q0时

2
M m
Mm
M m
Mm
4 Mm 2 1 1 1 M m 2 sin 2 aq
4 Mm
2

1 1 1 2 2 aq M m
2 Mm

2
M m
这里考虑了晶体中所有原子的相互作用。晶体中各 力常数之间并不全是独立的，而必须满足：
C , 0

由晶格的周期性，得
，＝1，2，3
C
, C ,0 C

设格波解：
A e
频率为j的特解：
nj j
方程的一般解：
n Aje
j
i jt naqj



1 inaq Q q , t e Nm q
线性变换系数正交条件： 系统的总机械能化为：
1 N
e
n
ina q q
q , q
1 * q, t Q q, t 2 q Q * q , t Q q , t H Q 2 q

e
i 1 2 aq

M m M 2 m2 2 Mm cos aq


a
a 1 aq 2
q

cos 1 2 aq 0
3 2 2

＋在Ⅱ、Ⅲ象限之间，属于反位相型。
物理图象：原胞中两种不同原子的振动位相基本上相反， 即原胞中的两种原子基本上作相对振动，而 原胞的质心基本保持不动。 当q0时，＋，原胞中两种原子振动位相完全相反。
2 Na
q的分布密度：
Na L q 2 2
L＝Na ——晶体链的长度
2 Na 2 简约区中波数q的取值总数 q a 2 a
＝N＝晶体链的原胞数
晶格振动格波的总数=N· 1 =晶体链的自由度数
四、格波的简谐性、声子概念
1 2 n 晶体链的动能： T m 2 n 2 1 晶体链的势能： U n n1 2 n 2 1 1 2 n n n1 系统的总机械能： H m 2 n 2 n i jt naqj Ae
Mm
2 2 2 1 1 aq aq 2 2 2 M m M m




1 2 a q q 2 M m
这与连续介质的弹性波 ＝vq 一致。 当q0时
n n

1 q 0
在长波极限下，原胞内两种原子的运动完全一致，振 幅和位相均相同，这时的格波非常类似于声波，所以我们 将这种晶格振动称为声学波或声学支。
1 E n j j 2 j=1
N
§3.2 一维双原子链的振动
考虑由P、Q两种原子等距相间排列的一维双原子链
一、运动方程及其解
a
只考虑近邻原子间的弹性相互作用 运动方程：
{ m
n
试 解：
{
{
M m
n-1 n n n+1
n n n 1 2n M
0
a
2 a
q
格波：Aei t naq
连续介质弹性波：Ae
i t xq
对于确定的n：第n个原子的位移随时间作简谐振动 对于确定时刻t：不同的原子有不同的振动位相 q的物理意义：沿波的传播方向（即沿q的方向）上，单 位距离两点间的振动位相差。 格波解：晶体中所有原子共同参与的一种频率相同的振 动，不同原子间有振动位相差，这种振动以波
1 E j n j j 2
nj 0,1,2,
• 当电子或光子与晶格振动相互作用时，总是以 j 为 单元交换能量。 • 声子只是反映晶体原子集体运动状态的激发单元，它不 能脱离固体而单独存在，它并不是一种真实的粒子, 只 是一种准粒子。 • 声子的作用过程遵从能量守恒和准动量守恒。 • 由N个原子组成的一维单原子链，晶格振动的总能量为：
i 1 aq 2

i 1 aq 2 2m cos 1 aq e 2 M 2 m2 2 Mm cos aq M m
即：
i R e
1 aq 2


2


2
－在Ⅰ、Ⅳ象限，属于同位相型
物理图象：原胞中的两种原子的振动位相基本相同，原胞 基本上是作为一个整体振动，而原胞中两种原 子基本上无相对振动。 当q0时， 0, 原胞内两种原子的振动位相完全相同。
2a a 3a 4a
三、周期性边界条件（Born－Karman边界条件）
N+1
1 2Biblioteka nN N+2
N+n

N n

1
n
Ae
i t N n nq
Ae
i t naq
e
iNaq
i 2 h e 1
2 q h Na
h =整数
在q轴上，每一个q的取值所占的空间为
i t q R
带入运动方程得：


其中
m 2 A 0
§3.3 三维晶格振动
一、三维简单晶格的振动 l
l’ 0 第ℓ个原子的位矢:
l-l’
R 1a1 2a2 3a3
在简谐近似下，系统的势能为（取平衡时U0＝0）：
1 U C , 2
, ,
, 1,2,3
第三章 晶格振动与晶体的热学性质
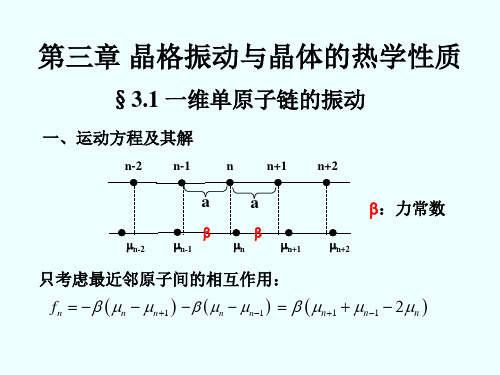
§3.1 一维单原子链的振动
一、运动方程及其解
n-2 n-1 n n+1 n+2
a
n-2 n-1
a
n
：力常数
n+1 n+2


只考虑最近邻原子间的相互作用：
fn n n 1 n n 1 n1 n 1 2n
n
n 1 2 n
(设 M > m)
n Aeit naq
n Be
1 i t n aq 2
代入方程:
{
2 2 cos 1 aq A 2 m B 0 2
1 aq B 0 2 M A 2 cos 2
(q)
1 1 2 M m
＋
2 m
2 M
－


a
0
a
q
2 m a 2 a M