数字信号处理第三章
数字信号处理 第三章 图像信号分析基础讲解

对于连续图像,定义阈值面积函数A(F)为具有灰 度级F的所有轮廓线所包围的面积。对于数字图 像,任一灰度级F的面积函数A(F)即大于或等于 灰度值F的像素点的个数。
曝光过强(过弱)会导致大片白色(黑色),丢失 明暗、对比度、纹理等细节信息,即使采用插值 算法,也难以准确恢复。此时将在直方图的一端 或两端产生尖峰。
3.1.5 灰度直方图
直方图是一幅图像中各像素灰度值出现次数(或 频数)的统计结果,它只反映该图像中不同灰度 值出现的次数(或频数),而未反映某一灰度值 像素所在位置。也就是说,它只包含了该图像中 某一灰度值的像素出现的概率,而丢失了其所在
的卷积。 水印、验证码
三、减法运算
将多幅图像的对应点相减得到新图像。 可去除图像中不需要的加性图案。 可用于运动检测。 可以用来计算物体边界位置的梯度。 新图像的灰度直方图为两个原始图像灰度
直方图的卷积。
四、乘除法运算
乘法运算可以用来去除原始图像中的一部 分:首先构造一副掩膜图像,在需要保留 区域,图像灰度值为1,而在被去除区域, 图像灰度值为0;然后将掩膜图像乘原始 图像。
显然, 若a 1,b 0,图象像素不发生变化; 若a 1,b 0,图象所有灰度值上移或下移; 若a 1,输出图象对比度增强; 若0 a 1,输出图象对比度减小; 若a 0,暗区域变亮,亮区域变暗,图象求补。
三、非线性点运算
s
s
s
O
r
O
r
O
r
s
s
s
O
r
O
数字信号处理(第三版)(高西全)第3章

。后面要讨论的频域采样理论将会
加深对这一关系的理解。我们知道,周期延拓序列频谱
完全由其离散傅里叶级数系数 X ( k ) 确定,因此,X(k) 实质上是x(n)的周期延拓序列x((n)) N的频谱特性,这就
是N点DFT的第二种物理解释(物理意义)。
第3章 离散傅里叶变换(DFT)
现在解释DFT[R4(n)]4=4δ(k)。根据DFT第二种物 理解释可知,DFT[R4(n)]4表示R4(n)以4为周期的周期
i 为整数 i 为整数
第3章 离散傅里叶变换(DFT)
所以,在变换区间上满足下式:
IDFT[X(k)]N=x(n) 0≤n≤N-1 由此可见,(3.1.2)式定义的离散傅里叶逆变换是唯一的。 【例3.1.1】 x(n)=R4(n), 求x(n)的4点和8点DFT。 解 设变换区间N=4,则
3 3 j 2π 4
X (k )
x ( n )W
n0
kn 4
e
n0
kn
1 e 1 e
j2 π k 2π 4
j
k
4 0
k 0 k 1, 2, 3
第3章 离散傅里叶变换(DFT)
设变换区间N=8,则
X (k )
7
x ( n )W 8 sin ( sin (
式中,a、b为常数,取N=max[N1, N2], 则y(n)的N点
DFT为 Y(k)=DFT[y(n)]N=aX1(k)+bX2(k) 0≤k≤N-1
X (k ) X ( z )
ze
j 2π N k
k 0,1, , N 1
(3.1.3)
第3章 离散傅里叶变换(DFT)
数字信号处理第三版第3章.ppt

x2 (n) N•DFT X 2 (k )
y(n) x1(n) x2 (n) Y (k) DFT[ y(n)]
1 N 1
N l0
X1(l) X 2 ((n L))N RN (n)
1 N1 N l0
X 2 (l) X1((n L))N RN (n)
第3章 离散傅里叶变换(DFT)
• DFT与Z变换和DTFT关系图解说明
z e WNk
j 2 k
e N
j
2 k
N
2 k
N
第3章 离散傅里叶变换(DFT)
• DFT与Z变换和DTFT关系举例说明
第3章 离散傅里叶变换(DFT)
• DFT的隐含周期性
N 1
1768年3月21日傅里叶生于法国荣纳省欧塞尔。其父亲 是裁缝,且很早就父母双亡,小时候在天主教受的教育。 毕业后在军队中教授数学。
1795年他到巴黎高等师范教书。 1798年随拿破仑东征,任下埃及的总督。 1801年,远征军失败后回到法国,任伊泽尔省长官。 1822年当选为科学院秘书,发表《热的分析理论》一文。在文中首次提出 并证明了将周期函数展开为正弦级数的原理,从而奠定了傅里叶级数(FS)与傅 里叶变换(FT)的理论基础。二者后被统称为傅里叶分析(FA)。 为了使FA应用于工程实际,人们又提出了离散傅里叶变换(DFT),但因计 算量太大而在较长时间内并未得到广泛应用,直到1965年美国Coo1y和Tukey两 人提出快速傅里叶变换(FFT)之后,FA才真正从理论走向实践,成为大家爱不 释手的一种数学工具。 1830年5月16日病逝于巴黎。
,求它的N点DFT。
第3章 离散傅里叶变换(DFT)
数字信号处理 第三章

:相位函数(phase function)或相位谱(phase spectrum)
3/29
与连续时间傅立叶变换的关系
X (W) = xa ( t ) =
ò
+¥ -¥
x (t )e - jWt dt
k =-¥
å x(k )d (t - k )
X ( W) =
+¥
ò
+¥ -¥
X * (e j )
1 X cs (e j ) { X (e j ) X * (e j )} 2 1 X ca (e j ) { X (e j ) X * (e j )} 2
xcs [n] xca [n]
X re (e j ) jX im (e j )
16/29
K
lim
X e X e d 0
j K j 2
例:理想低通滤波器 1 0 c H LP e 0 c j c n j c n 1 c jn 1 e e sin c n hLP n e d 2 c 2 jn n jn
10/29
3.1.2 收敛条件(convergence)
如果x[n]的DTFT在种意义上收敛,则称x[n]的傅立叶变换存在
1、一致收敛(uniform convergence) 令X K e j
xne ,一致收敛的定义为 lim X e X e 0
Table 3.4 实序列的离散时间傅立叶变换的对称关系 序列 离散时间傅立叶变换
x[n]
xev [n]
X (e j ) X re (e j ) jX im (e j )
数字信号处理(方勇)第三章习题答案
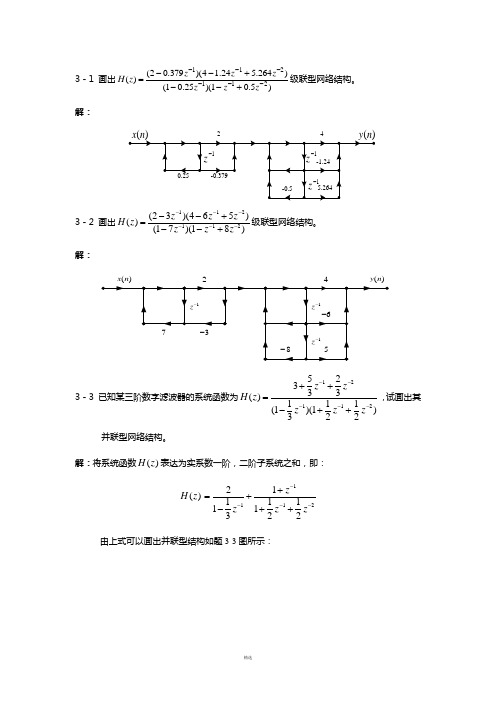
3-1 画出)5.01)(25.01()264.524.14)(379.02()(211211------+--+--=z zz z z z z H 级联型网络结构。
解:243-2 画出112112(23)(465)()(17)(18)z z z H z z z z --------+=--+级联型网络结构。
解:()x n ()y n 243-3 已知某三阶数字滤波器的系统函数为1211252333()111(1)(1)322z z H z z z z -----++=-++,试画出其并联型网络结构。
解:将系统函数()H z 表达为实系数一阶,二阶子系统之和,即:()H z 11122111111322z z z z ----+=+-++ 由上式可以画出并联型结构如题3-3图所示:)题3-3图3-4 已知一FIR 滤波器的系统函数为121()(10.70.5)(12)H z zz z ---=-++,画出该FIR滤波器的线性相位结构。
解: 因为121123()(10.70.5)(12)1 1.30.9H z zz z z z z ------=-++=+-+,所以由第二类线性相位结构画出该滤波器的线性相位结构,如题3-4图所示:()x n 1-1-1z -题3-4图3-5 已知一个FIR 系统的转移函数为:12345()1 1.25 2.75 2.75 1.23H z z z z z z -----=+--++求用级联形式实现的结构流图并用MATLAB 画出其零点分布及其频率响应曲线。
解: 由转移函数可知,6=N ,且)(n h 偶对称,故为线性相位系统,共有5个零点,为5阶系统,因而必存在一个一阶系统,即1±=z 为系统的零点。
而最高阶5-z 的系数为+1,所以1-=z 为其零点。
)(z H 中包含11-+z 项。
所以:11()()(1)H z H z z -=+。
1()H z 为一四阶子系统,设12341()1H z bzcz bz z ----=++++,代入等式,两边相等求得12341()10.2530.25H z zz z z ----=+-++,得出系统全部零点,如图3-5(b )所示。
《数字信号处理教程》(第三版)第三章

N 1 N 1
~ km ~ kn x1 (m ) WN X 2 (k ) WN n 0 m 0
1 N
N 1
N 1 m 0
~ ~ (m ) X (k ) W ( m n)k x1 2 N
n 0
N 1
~ ~ x1 ( m ) x2 ( n m )
域是连续周期的;若此时我们对频域的连续信号抽样,
人为的使其离散化,这样,频域的离散又导致时域的周 期化。于是有:
时域离散、周期
频域周期、离散
3.3 周期序列的离散傅立叶级数(DFS)
~ 设x (n)是周期为N的一个周期序列 ~ ~ x ( n) x (n rN ) ,r为任意整数
注:不论是离散的,还是连续的周期序列,均可用傅立叶级数 表示。离散的周期序列用离散傅立叶级数表示。(任一个周
第三章
离散傅立叶变换
理解傅里叶变换的几种形式
了解周期序列的傅里叶级数及性质,掌握周期卷 积过程
理解离散傅里叶变换及性质,掌握圆周移位、共 轭对称性,掌握圆周卷积、线性卷积及两者之间 的关系
了解频域抽样理论
理解频谱分析过程
了解序列的抽取与插值过程
3.2Leabharlann 傅立叶变换的几种可能形式傅立叶变换
~ x (n) x(n模N ) x(( n)) N
其中,(n模N)或((n))N数学上表示“n对N取余数或取模值”。
~ ~ 和 ~ 所对应的x(n)。 例: ( n)的周期为N=9,求 x ( 25) x ( 5) x
~ x (25) x(25模9) x(( 25))9 x(7) ~ x (5) x(5模9) x(( 5)) x(4)
数字信号处理教学课件第三章

j n x ( n ) e
n
X (e j )是的连续周期函数。
1 x ( n) 2
X (e j )e jnd
时域 FT 连续,非周期
频域 非周期,连续
FS DTFT
连续,周期 离散,非周期
非周期,离散 周期,连续
10
四、离散傅里叶级数(DFS→DFT)
时域抽样
时域截断
时域周期延拓
周期延拓中的搬移通过与 ( t nTs ) 的卷积来实现 周期延拓后的周期函数具有离散谱
经过抽样、截断和延拓后,信号时域和频域都是离散、周期的。
3
学 习 方 法
从工程需要出发,理解信号频谱分析的实际问题。即
在实践中领悟处理原理的意义
从解决问题出发,理解各种信号处理方法的目的。即
上面讨论的三种傅里叶变换对,都不适用在计 算机上运算。我们感兴趣的是时域及频域都是离散 的情况,这就是离散傅里叶级数(变换)。
根据以上讨论: 时域:离散 频谱:周期 频域:离散 时域:周期 因此,DFS必是一种时域、频谱均为离散和周 期的一种傅里叶变换。
11
总之,一个域的离散必然造成另一个 |X ( j)| x (t) 1 域的周期延拓。
23
n n1 mN
0 n1 N 1 m为整数
~ ( n)是周期为N=8的序列,求n=19和n=-2两 例如,x 数对N的余数。 因为
n 19 3 2 8
((19 ))8 3
n 2 6 (1) 8
因此
~ x (19) ((19)) 8 x(3)
第3章 离散傅里叶变换
jIm(z)
数字信号处理第三章

数字信号处理第三章数字信号处理第三章实验程序3.1计算离散时间傅里叶变换% Program P3_1% Evaluation of the DTFTclf;% Compute the frequency samples of the DTFT w = -4*pi:8*pi/511:4*pi;num = [2 1];den = [1 -0.6];h = freqz(num, den, w);% Plot the DTFTsubplot(2,1,1)plot(w/pi,real(h));gridtitle('Real part of H(e^{j\omega})')xlabel('\omega /\pi');ylabel('Amplitude');subplot(2,1,2)plot(w/pi,imag(h));gridtitle('Imaginary part of H(e^{j\omega})') xlabel('\omega /\pi');ylabel('Amplitude');pausesubplot(2,1,1)plot(w/pi,abs(h));gridtitle('Magnitude Spectrum |H(e^{j\omega})|') xlabel('\omega /\pi');ylabel('Amplitude');subplot(2,1,2)plot(w/pi,angle(h));gridtitle('Phase Spectrum arg[H(e^{j\omega})]') xlabel('\omega /\pi');ylabel('Phase in radians');Q3.1离散时间傅里叶变换的原始序列是H(e^jw)=(2+z^-1)/(1-0.6z^-1)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
FS:~x (t)
X (k0 )e jk0t
k
(周期为T0
,Ω0
2
T0
)
对上式进行抽样,得:
(抽样间隔为T,s
2π ) T
~x(nT )
X~(k0 )e jk0nT
n
反 : x(nT ) 1 s / 2 X (e jT )e jnT d
s s / 2
---
时域抽样间隔为T ,
频域的周期为 s
2
T
注:DTFT反变换原式为 x(n) 1 X (e j )e jnd
2
根据关系
T 将变量换为
,并利用s
2
T
即得
x(nT ) 1 s / 2 X (e jT )e jnT d
jnk0T
s k0
又 0T
2
T0
T
0
2
s
2
N
这里 T Ω0 1 ,因此 T0 Ωs N
j 2 k
N 1
j 2 nk
X (e N ) x(nT)e N
n0
1 N 1
j 2 k
j 2 nk
x(nT)
X (e N )e N
N k0
x(nT ) 视作 n 的函数, x(nT ) x(n)
0 -0.5
-1 0
500
1000
1500
2000
2500
500
1000
1500
2000
2500
500
1000
1500
2000
2500
500
1000
1500
2000
2500
§ 3-3 周期序列的离散傅里叶级数 Discrete Fourier Series (DFS)
一. 周期序列的傅里叶级数分解:
The Discrete Fourier Transform ( DFT )
§ 3-1 引言
z变换与DTFT:
无限长序列的变换; 结果为连续变量函数。(不是可数字计算的)
DFT的特点:
not numerically computable
时域、频域都是离散的, 适合于用计算机进行分析和处理。
处理对象: 有限长序列
k
DTFT
X (e jT ) x(nT )e jnT n
x(nT ) 1 s /2 X (e jT )e jnT d
s / 2 s
• DFT(DFS)的简单推演:
时域是周期为T0函数,频域的离散间隔为
0
2
T0
;
时域的离散间隔为T,频域的周期为
s
2
T
.
在一个周期内,可进行如下变换:
X (e jT ) x(nT )e jnT
(注:由于DFT是DFS的截取结果,所以DFT只 是简化了的DFS,在数学上不是严格的对应关系)
比较:
FT ( CTFT )
X ( j) x(t)e jtdt
x(t)
1
2
X
(
j)e jtd
FS
1
X ( jk0 ) T0
T0 / 2 x(t)e jk0t dt
T0 / 2
x(t) X ( jk0 )e jk0t
Fourier Transform
x(t)
正 : X ( j) x(t)e jtdt
0
t
X ( j)
反 : x(t) 1 X ( j)e jtd
2
0
特点:
时域信号 连续的 非周期的
频域信号 非周期的 连续的
对称性: 时域连续,则频域非周期。 反之亦然。
二. 连续时间、离散频率----傅里叶级数
及离散傅里叶变换(DFT)
前面三种变换关系中,时域或频域至少有一个量是连续 量,这样的函数是不能用计算机来处理的,计算机或数字 系统只能把离散的数据变成新的离散的数据。
根据前面总结的对应 关系,要想在时域和频 域都是离散的,那么两 域必须是周期的。
时域信号 离散的 周期的
频域信号 周期的 离散的
x(nT)=x(n)
T0
1 F
T0 NT
0 T 2T
x(e jk0T )
12
x(k )
s
2
T
fs
1 T
NT
t
N
n
0
2 T0
2F
s N0
0 0 20
N0
012 3
N
k
(N 1)0
(N 1)
离散傅里叶级数(DFS):时域、频域都为离散、 都为周期情况时的变换对。
离散傅里叶变换(DFT):在DFS的时域、频域各 截取一个主值周期时的对应关系。 都为离散、非周期(有限长)
DTFT
n
x(nT ) 1 s / 2 X (e jT )e jnT d s s / 2
n : 从0 ~ N 1
频域离散化: : k0 k 2F, k 0 ~ N 1
d : d 0
N 1
X (e jk0T ) x(nT )e jnk0T n0
x(nT )
0
N 1
X (e )e jk0T
j 2 k
X (e N )
视作
ቤተ መጻሕፍቲ ባይዱ
k
的函数,X
(e
j 2
N
k
)
X
(k)
则得
N 1
j 2 nk
X (k) x(n)e N
n0
x(n)
1
N 1
j 2 nk
X (k)e N
N k0
(正变换) (反变换)
1 0.5
0 -0.5
-1 0
1 0.5
0 -0.5
-1 0
1 0.5
0 -0.5
-1 0
1 0.5
s s / 2
特点: 时域信号 频域信号
离散的 周期的
非周期的 连续的
比较: FT
( CTFT ) FS
DTFT
时域信号 连续的 非周期的
时域信号 连续的 周期的
时域信号 离散的 非周期的
频域信号 非周期的 连续的
频域信号 非周期的 离散的
频域信号 周期的 连续的
四. 离散时间、离散频率 Discrete Fourier Series ----离散傅里叶级数(DFS)
DFT要解决两个问题: 一是离散与量化, 二是快速运算。
傅氏变换
离散量化
信号处理
DFT(FFT)
§ 3-2 傅氏变换的几种可能形式
时间函数
频率函数
连续时间、连续频率—傅里叶变换 连续时间、离散频率—傅里叶级数 离散时间、连续频率— DTFT 离散时间、离散频率— ? ? ?
一. 连续时间、连续频率----傅里叶变换
连续的 周期的
频域信号 非周期的 nonperiodic 离散的 discrete
三. 离散时间、连续频率
----离散时间傅里叶变换(DTFT)
x(nT)
(理想抽样信号的傅里叶变换)
T
X e j 或 X (e jT )
---
-T 0 T 2T t
0
s
2 T
正 : X (e jT ) x(nT )e jnT
Fourier series
x(t)
X ( jk0 )
---
---
0
t
T0
0 2 0 T0
正
:
X
(
jk0
)
1 T0
T0 / 2 x(t)e jk0t dt
T0 / 2
反 : x(t) X ( jk0 )e jk0t k
时域周期为T0, 频域谱线间隔为 2
T0
特点: 时域信号
continuous periodic
