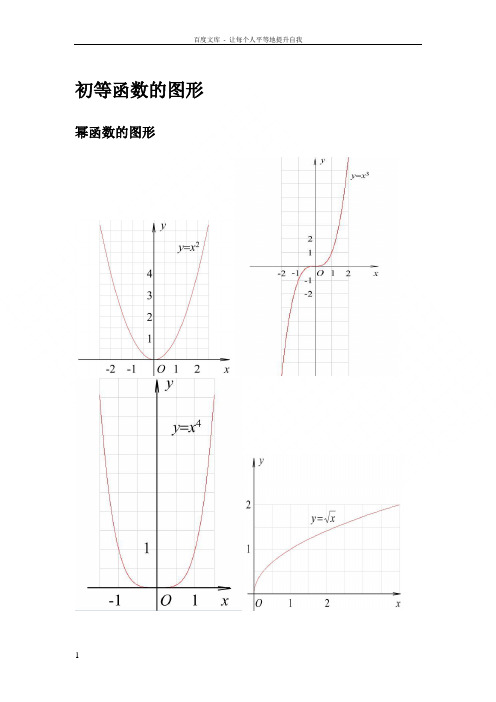
正弦余弦正切函数图象
正弦函数、余弦函数的图像(完整)

(
3 2
,1)
(1) 列表(列出对图象形状起关键作用的五点坐标)
(2) 描点(定出五个关键点)
(3) 连y线(用光滑的曲线顺次连结五个点)
图象的最高点
1-
-
(0,1) (2 ,1)
与x轴的交点
-
-1
o
6
2
3
2 3
5
7
6
6
4 3
3 5
2
3
11 6
2
x
(
2
,0)
(
3 2
,0)
-1 -
图象的最低点 ( ,1)
三角函数
三角函数线
正弦函数 余弦函数 正切函数
sin=MP
正弦线MP cos=OM 余弦线OM tan=AT 正切线AT
y PT
-1
O
M A(1,0) x
正弦函数的图象
问题:如何作出正弦函数的图象?
途径:利用单位圆中正弦线来解决。
描图:用光滑曲线
y
B
1
将这些正弦线的 终点连结起来
A
O1
O
2
4
5
2
x
4
5 6 x
正弦、余弦函数的图象
如何由正弦函数图像得y 到余弦函数图像?
1
-4 -3
-2
- o
-1
2
3
4
5 6 x
正弦函数的图象
y=cosx=sin(x+ ), xR
2
余弦函数的图象
y
1
正弦曲 线
形状完全一样 只是位置不同
余弦曲 线
-4 -3
-2
- o
-1
三角函数公式图像大全
初等函数的图形幂函数的图形指数函数的图形各三角函数值在各象限的符号sinα·cscα cosα·secα tanα·cotα三角函数的性质函数y=sinx y=cosx y=tanx y=cotx定义域R R {x|x∈R且x≠kπ+2π,k∈Z}{x|x∈R且x≠kπ,k∈Z}值域[-1,1]x=2kπ+2π时y max=1x=2kπ-2π时y min=-1[-1,1]x=2kπ时y max=1x=2kπ+π时y min=-1R无最大值无最小值R无最大值无最小值周期性周期为2π周期为2π周期为π周期为π奇偶性奇函数偶函数奇函数奇函数单调性在[2kπ-2π,2kπ+2π]上都是增函数;在[2kπ+2π,2kπ+32π]上都是减函数(k∈Z)在[2kπ-π,2kπ]上都是增函数;在[2kπ,2kπ+π]上都是减函数(k∈Z)在(kπ-2π,kπ+2π)内都是增函数(k∈Z)在(kπ,kπ+π)内都是减函数(k∈Z)反三角函数的图形反三角函数的性质名称反正弦函数反余弦函数反正切函数反余切函数定义y=sinx(x∈〔-2π,2π〕的反函数,叫做反正弦函数,记作x=arsinyy=cosx(x∈〔0,π〕)的反函数,叫做反余弦函数,记作x=arccosyy=tanx(x∈(-2π,2π)的反函数,叫做反正切函数,记作x=arctanyy=cotx(x∈(0,π))的反函数,叫做反余切函数,记作x=arccoty理解arcsinx表示属于[-2π,2π]且正弦值等于x的角arccosx表示属于[0,π],且余弦值等于x的角arctanx表示属于(-2π,2π),且正切值等于x的角arccotx表示属于(0,π)且余切值等于x的角性质定义域[-1,1][-1,1](-∞,+∞)(-∞,+∞)值域[-2π,2π][0,π](-2π,2π) (0,π)单调性在〔-1,1〕上是增函数在[-1,1]上是减函数在(-∞,+∞)上是增数在(-∞,+∞)上是减函数奇偶性arcsin(-x)=-arcsinxarccos(-x)=π-arccosxarctan(-x)=-arctanxarccot(-x)=π-arccotx周期性都不是同期函数恒等式sin(arcsinx)=x(x∈[-1,1])arcsin(sinx)=x(x∈[-2π,2π])cos(arccosx)=x(x∈[-1,1])arccos(cosx)=x(x∈[0,π])tan(arctanx)=x(x∈R)arctan(tanx)=x(x∈(-2π,2π))cot(arccotx)=x(x∈R)arccot(cotx)=x(x∈(0,π))互余恒等式arcsinx+arccosx=2π(x∈[-1,1]) arctanx+arccotx=2π(X∈R)三角函数公式两角和公式sin(A+B) = sinAcosB+cosAsinB sin(A-B) = sinAcosB-cosAsinB cos(A+B) = cosAcosB-sinAsinB cos(A-B) = cosAcosB+sinAsinBtan(A+B) =tanAtanB -1tanBtanA +tan(A-B) =tanAtanB 1tanBtanA +-cot(A+B) =cotA cotB 1-cotAcotB +cot(A-B) =cotAcotB 1cotAcotB -+倍角公式tan2A =Atan 12tanA2- Sin2A=2SinA•CosACos2A = Cos 2A-Sin 2A=2Cos 2A-1=1-2sin 2A三倍角公式sin3A = 3sinA-4(sinA)3 cos3A = 4(cosA)3-3cosAtan3a = tana ·tan(3π+a)·tan(3π-a)sin(2A )=2cos 1A -cos(2A)=2cos 1A +tan(2A)=A A cos 1cos 1+-cot(2A )=A A cos 1cos 1-+tan(2A )=A A sin cos 1-=AA cos 1sin + 和差化积sina+sinb=2sin2b a +cos 2ba - sina-sinb=2cos 2b a +sin 2ba -cosa+cosb = 2cos 2b a +cos 2ba -cosa-cosb = -2sin 2b a +sin 2ba -tana+tanb=ba b a cos cos )sin(+积化和差sinasinb = -21[cos(a+b)-cos(a-b)] cosacosb = 21[cos(a+b)+cos(a-b)]sinacosb = 21[sin(a+b)+sin(a-b)]cosasinb = 21[sin(a+b)-sin(a-b)]sin(-a) = -sina cos(-a) = cosasin(2π-a) = cosacos(2π-a) = sinasin(2π+a) = cosacos(2π+a) = -sinasin(π-a) = sina cos(π-a) = -cosa sin(π+a) = -sina cos(π+a) = -cosatgA=tanA =aacos sin万能公式sina=2)2(tan 12tan2aa + cosa=22)2(tan 1)2(tan 1aa+- tana=2)2(tan 12tan2aa -a•sina+b•cosa=)b (a 22+×sin(a+c) [其中tanc=a b ] a•sin(a)-b•cos(a) =)b (a 22+×cos(a-c) [其中tan(c)=b a ] 1+sin(a) =(sin 2a +cos 2a )2 1-sin(a) = (sin 2a -cos 2a )2其他非重点三角函数 csc(a) =asin 1 sec(a) =a cos 1 双曲函数sinh(a)=2e -e -aa cosh(a)=2e e -aa + tg h(a)=)cosh()sinh(a a 公式一设α为任意角,终边相同的角的同一三角函数的值相等:sin (2kπ+α)= sinαcos (2kπ+α)= cosαtan (2kπ+α)= tanαcot (2kπ+α)= cotα设α为任意角,π+α的三角函数值与α的三角函数值之间的关系:sin(π+α)= -sinαcos(π+α)= -cosαtan(π+α)= tanαcot(π+α)= cotα公式三任意角α与-α的三角函数值之间的关系:sin(-α)= -sinαcos(-α)= cosαtan(-α)= -tanαcot(-α)= -cotα公式四利用公式二和公式三可以得到π-α与α的三角函数值之间的关系:sin(π-α)= sinαcos(π-α)= -cosαtan(π-α)= -tanαcot(π-α)= -cotα公式五利用公式-和公式三可以得到2π-α与α的三角函数值之间的关系:sin(2π-α)= -sinαcos(2π-α)= cosαtan(2π-α)= -tanαcot(2π-α)= -cotα2π±α及23π±α与α的三角函数值之间的关系: sin (2π+α)= cosα cos (2π+α)= -sinα tan (2π+α)= -cotα cot (2π+α)= -tanα sin (2π-α)= cosα cos (2π-α)= sinα tan (2π-α)= cotα cot (2π-α)= tanα sin (23π+α)= -cosα cos (23π+α)= sinα tan (23π+α)= -cotα cot (23π+α)= -tanα sin (23π-α)= -cosα cos (23π-α)= -sinα tan (23π-α)= cotα cot (23π-α)= tanα (以上k ∈Z)这个物理常用公式我费了半天的劲才输进来,希望对大家有用A•sin(ωt+θ)+ B•sin(ωt+φ) =)cos(222ϕθ⋅++AB B A ×sin )cos(2)Bsin in arcsin[(As t 22ϕθϕθω⋅++++AB B A三角函数公式证明(全部)公式表达式乘法与因式分解a2-b2=(a+b)(a-b) a3+b3=(a+b)(a2-ab+b2) a3-b3=(a-b)(a2+ab+b2) 三角不等式|a+b|≤|a|+|b||a-b|≤|a|+|b||a|≤b<=>-b≤a≤b|a-b|≥|a|-|b|-|a|≤a≤|a|一元二次方程的解-b+√(b2-4ac)/2a -b-b+√(b2-4ac)/2a根与系数的关系X1+X2=-b/aX1*X2=c/a注:韦达定理判别式b2-4a=0 注:方程有相等的两实根b2-4ac>0 注:方程有一个实根b2-4ac<0 注:方程有共轭复数根三角函数公式两角和公式sin(A+B)=sinAcosB+cosAsinB sin(A-B)=sinAcosB-sinBcosAcos(A+B)=cosAcosB-sinAsinB cos(A-B)=cosAcosB+sinAsinBtan(A+B)=(tanA+tanB)/(1-tanAtanB) tan(A-B)=(tanA-tanB)/(1+tanAtanB) ctg(A+B)=(ctgActgB-1)/(ctgB+ctgA) ctg(A-B)=(ctgActgB+1)/(ctgB-ctgA)倍角公式tan2A=2tanA/(1-tan2A) ctg2A=(ctg2A-1)/2ctgacos2a=cos2a-sin2a=2cos2a-1=1-2sin2a半角公式sin(A/2)=√((1-cosA)/2) sin(A/2)=-√((1-cosA)/2)cos(A/2)=√((1+cosA)/2) cos(A/2)=-√((1+cosA)/2)tan(A/2)=√((1-cosA)/((1+cosA)) tan(A/2)=-√((1-cosA)/((1+cosA))ctg(A/2)=√((1+cosA)/((1-cosA)) ctg(A/2)=-√((1+cosA)/((1-cosA))和差化积2sinAcosB=sin(A+B)+sin(A-B) 2cosAsinB=sin(A+B)-sin(A-B)2cosAcosB=cos(A+B)-sin(A-B) -2sinAsinB=cos(A+B)-cos(A-B)sinA+sinB=2sin((A+B)/2)cos((A-B)/2 cosA+cosB=2cos((A+B)/2)sin((A-B)/2) tanA+tanB=sin(A+B)/cosAcosB tanA-tanB=sin(A-B)/cosAcosBctgA+ctgBsin(A+B)/sinAsinB -ctgA+ctgBsin(A+B)/sinAsinB某些数列前n项和1+2+3+4+5+6+7+8+9+…+n=n(n+1)/21+3+5+7+9+11+13+15+…+(2n-1)=n22+4+6+8+10+12+14+…+(2n)=n(n+1)12+22+32+42+52+62+72+82+…+n2=n(n+1)(2n+1)/6 13+23+33+43+53+63+…n3=n2(n+1)2/41*2+2*3+3*4+4*5+5*6+6*7+…+n(n+1)=n(n+1)(n+2)/3 正弦定理a/sinA=b/sinB=c/sinC=2R注:其中R 表示三角形的外接圆半径余弦定理b2=a2+c2-2accosB注:角B是边a和边c的夹角正切定理[(a+b)/(a-b)]={[Tan(a+b)/2]/[Tan(a-b)/2]}圆的标准方程(x-a)2+(y-b)2=r2 注:(a,b)是圆心坐标圆的一般方程x2+y2+Dx+Ey+F=0 注:D2+E2-4F>0抛物线标准方程y2=2px y2=-2px x2=2py x2=-2py直棱柱侧面积S=c*h斜棱柱侧面积S=c'*h正棱锥侧面积S=1/2c*h'正棱台侧面积S=1/2(c+c')h'圆台侧面积S=1/2(c+c')l=pi(R+r)l球的表面积S=4pi*r2圆柱侧面积S=c*h=2pi*h圆锥侧面积S=1/2*c*l=pi*r*l弧长公式l=a*ra是圆心角的弧度数r >0扇形面积公式s=1/2*l*r锥体体积公式V=1/3*S*H圆锥体体积公式V=1/3*pi*r2h斜棱柱体积V=S'L注:其中,S'是直截面面积,L是侧棱长柱体体积公式V=s*h圆柱体V=pi*r2h-------------------------------------------------------------------------------------------- 三角函数积化和差和差化积公式记不住就自己推,用两角和差的正余弦:cos(A+B)=cosAcosB-sinAsinBcos(A-B)=cosAcosB+sinAsinB这两式相加或相减,可以得到2组积化和差:相加:cosAcosB=[cos(A+B)+cos(A-B)]/2相减:sinAsinB=-[cos(A+B)-cos(A-B)]/2sin(A+B)=sinAcosB+sinBcosAsin(A-B)=sinAcosB-sinBcosA这两式相加或相减,可以得到2组积化和差:相加:sinAcosB=[sin(A+B)+sin(A-B)]/2相减:sinBcosA=[sin(A+B)-sin(A-B)]/2这样一共4组积化和差,然后倒过来就是和差化积了不知道这样你可以记住伐,实在记不住考试的时候也可以临时推导一下正加正正在前正减正余在前余加余都是余余减余没有余还负正余正加余正正减余余余加正正余减还负.3.三角形中的一些结论:(不要求记忆)(1)anA+tanB+tanC=tanA·tanB·tanC(2)sinA+tsinB+sinC=4cos(A/2)cos(B/2)cos(C/2)(3)cosA+cosB+cosC=4sin(A/2)·sin(B/2)·sin(C/2)+1(4)sin2A+sin2B+sin2C=4sinA·sinB·sinC(5)cos2A+cos2B+cos2C=-4cosAcosBcosC-1 ...........................已知sinα=m sin(α+2β), |m|<1,求证tan(α+β)=(1+m)/(1-m)tanβ解:sinα=m sin(α+2β)sin(a+β-β)=msin(a+β+β)sin(a+β)cosβ-cos(a+β)sinβ=msin(a+β)cosβ+mcos(a+β)sinβ sin(a+β)cosβ(1-m)=cos(a+β)sinβ(m+1)tan(α+β)=(1+m)/(1-m)tanβ。
正弦函数、余弦函数的图象_优质课件

3) y 3sin(1 x ), x R 一般
35
结论:
函数y Asin(x )及y Acos(x ), x R
( A,,为常数, A 0, 0)的周期T 2
新课讲解. 正弦函数、余弦函数的性质 (三)关于奇偶性(复习)
一般地, •如果对于函数f( x )的定义域内任意一个x, 都有f(- x )= f( x ),那么就说f( x )是偶函数 •如果对于函数f( x )的定义域内任意一个x, 都有f(- x )= -f( x ),那么就说f( x )是奇函数
小结回顾
正切函数的基本性质
4 5
应用提升
练习1:试着画出y | tan x | 和y tan | x |
并讨论它们的单调性,周期性和奇偶性.
练习2.如果、
(
,
)且
tan
cot
,
2
那么必有( )
A.
B.
C. 3 D. 3
2
2
应用提升
例3.求函数y tan x 1 的定义域 3 tan x
例4.试讨论函数y loga tan x的单调性
2
2
y=cosx
y cos x : 定义域为R,值域[1,1]
1
最-6大 值1,此-5时 x
2-k4; 最小值-3-1,
此时x
-2
2k
-;
-1
2 3 2 3
4 5 4 5
6 x 6 x
五.定义域 、值域及取到最值时相应的x的集合:
-6 -5
-4 -3
复习回顾
-2 -
y y=sinx
1 o
-1
2 3
(2) y sin x, y cosx与y Asin(x ), y Acos(x )间的换元思想
正弦、余弦、正切函数的性质和图像

正弦、余弦、正切函数的性质和图像案场各岗位服务流程销售大厅服务岗:1、销售大厅服务岗岗位职责:1)为来访客户提供全程的休息区域及饮品;2)保持销售区域台面整洁;3)及时补足销售大厅物资,如糖果或杂志等;4)收集客户意见、建议及现场问题点;2、销售大厅服务岗工作及服务流程阶段工作及服务流程班前阶段1)自检仪容仪表以饱满的精神面貌进入工作区域2)检查使用工具及销售大厅物资情况,异常情况及时登记并报告上级。
班中工作程序服务流程行为规范迎接指引递阅资料上饮品(糕点)添加茶水工作要求1)眼神关注客人,当客人距3米距离时,应主动跨出自己的位置迎宾,然后侯客迎询问客户送客户注意事项15度鞠躬微笑问候:“您好!欢迎光临!”2)在客人前方1-2米距离领位,指引请客人向休息区,在客人入座后问客人对座位是否满意:“您好!请问坐这儿可以吗?”得到同意后为客人拉椅入座“好的,请入座!”3)若客人无置业顾问陪同,可询问:请问您有专属的置业顾问吗?,为客人取阅项目资料,并礼貌的告知请客人稍等,置业顾问会很快过来介绍,同时请置业顾问关注该客人;4)问候的起始语应为“先生-小姐-女士早上好,这里是XX销售中心,这边请”5)问候时间段为8:30-11:30 早上好11:30-14:30 中午好 14:30-18:00下午好6)关注客人物品,如物品较多,则主动询问是否需要帮助(如拾到物品须两名人员在场方能打开,提示客人注意贵重物品);7)在满座位的情况下,须先向客人致歉,在请其到沙盘区进行观摩稍作等待;阶段工作及服务流程班中工作程序工作要求注意事项饮料(糕点服务)1)在所有饮料(糕点)服务中必须使用托盘;2)所有饮料服务均已“对不起,打扰一下,请问您需要什么饮品”为起始;3)服务方向:从客人的右面服务;4)当客人的饮料杯中只剩三分之一时,必须询问客人是否需要再添一杯,在二次服务中特别注意瓶口绝对不可以与客人使用的杯子接触;5)在客人再次需要饮料时必须更换杯子;下班程序1)检查使用的工具及销售案场物资情况,异常情况及时记录并报告上级领导;2)填写物资领用申请表并整理客户意见;3)参加班后总结会;4)积极配合销售人员的接待工作,如果下班时间已经到,必须待客人离开后下班;1.3.3.3吧台服务岗1.3.3.3.1吧台服务岗岗位职责1)为来访的客人提供全程的休息及饮品服务;2)保持吧台区域的整洁;3)饮品使用的器皿必须消毒;4)及时补充吧台物资;5)收集客户意见、建议及问题点;1.3.3.3.2吧台服务岗工作及流程阶段工作及服务流程班前阶段1)自检仪容仪表以饱满的精神面貌进入工作区域2)检查使用工具及销售大厅物资情况,异常情况及时登记并报告上级。
1126三角函数图像及性质
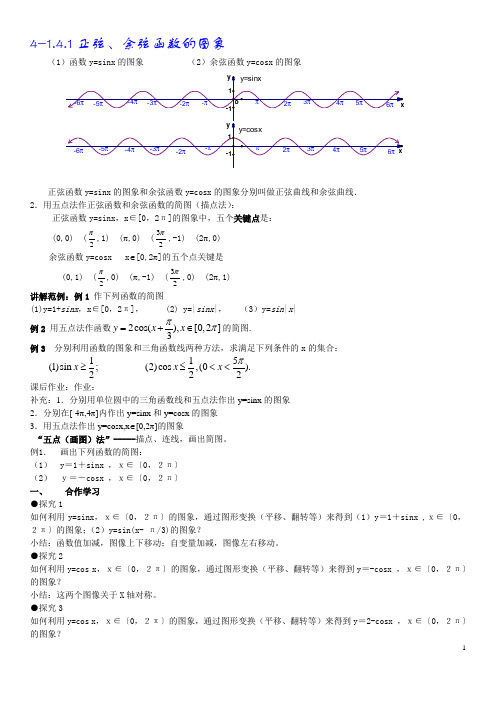
4-1.4.1正弦、余弦函数的图象(1)函数y=sinx 的图象 (2)余弦函数y=cosx 的图象正弦函数y=sinx 的图象和余弦函数y=cosx 的图象分别叫做正弦曲线和余弦曲线. 2.用五点法作正弦函数和余弦函数的简图(描点法):正弦函数y=sinx ,x ∈[0,2π]的图象中,五个关键点是:(0,0) (2π,1) (π,0) (23π,-1) (2π,0) 余弦函数y=cosx x ∈[0,2π]的五个点关键是 (0,1) (2π,0) (π,-1) (23π,0) (2π,1) 讲解范例:例1 作下列函数的简图(1)y=1+sinx ,x ∈[0,2π], (2) y=|sinx |, (3)y=sin |x |例2 用五点法作函数2cos(),[0,2]3y x x ππ=+∈的简图.例3 分别利用函数的图象和三角函数线两种方法,求满足下列条件的x 的集合:1(1)sin ;2x ≥ 15(2)cos ,(0).22x x π≤<<课后作业:作业:补充:1.分别用单位圆中的三角函数线和五点法作出y=sinx 的图象 2.分别在[-4π,4π]内作出y=sinx 和y=cosx 的图象 3.用五点法作出y=cosx,x ∈[0,2π]的图象“五点(画图)法”-----描点、连线,画出简图。
例1. 画出下列函数的简图:(1) y =1+sinx ,x∈〔0,2π〕 (2) y=-cosx ,x∈〔0,2π〕 一、 合作学习 ●探究1如何利用y=sinx ,x∈〔0,2π〕的图象,通过图形变换(平移、翻转等)来得到(1)y =1+sinx ,x∈〔0,2π〕的图象;(2)y=sin(x- π/3)的图象?小结:函数值加减,图像上下移动;自变量加减,图像左右移动。
●探究2如何利用y=cos x ,x∈〔0,2π〕的图象,通过图形变换(平移、翻转等)来得到y =-cosx ,x∈〔0,2π〕的图象?小结:这两个图像关于X 轴对称。
最全三角函数的图像与性质知识点总结

三角函数的图像与性质一、正弦函数、余弦函数的图像与性质
(
二、正切函数的图象与性质
三、三角函数图像的平移变换和伸缩变换
1. 由x y sin =的图象得到)sin(ϕω+=x A y (0,0A ω>>)的图象
注意:图象时一定要注意平移与伸缩的先后顺序,否则会出现错误。
2. )sin(ϕω+=x A y (0,0A ω>>)的性质
(1)定义域、值域、单调性、最值、对称性:
将ϕω+x 看作一个整体,与相应的简单三角函数比较得出; (2)奇偶性:只有当ϕ取特殊值时,这些复合函数才具备奇偶性:
)sin(ϕω+=x A y ,当πϕk =时为奇函数,当2
ππϕ±=k 时为偶函数;
(3)最小正周期:ω
π2=T
3. y =A sin(ωx +φ), x ∈[0,+∞) (0,0A ω>>)中各量的物理意义
(1) A 称为振幅; (2)2T πω
=称为周期;
(3)1f
T
=
称为频率;
(4)x ωϕ+称为相位;
(5)ϕ称为初相 (6)ω称为圆频率.。
正弦函数余弦函数的图像与性质

三角函数在物理学中的应用
振动与波动
正弦和余弦函数是描述简谐振动和波动的基本函 数,广泛应用于声学、光学等领域。
交流电
交流电的电压和电流是时间的正弦或余弦函数, 用于驱动各种电器设备。
磁场与电场
在电磁学中,正弦和余弦函数用于描述磁场和电 场的分布和变工程中的许多振动问题都可以用 正弦和余弦函数来描述,如桥梁 振动、车辆振动等。
周期性
正弦函数具有周期性, 其周期为2π。
奇偶性
正弦函数是奇函数,满 足sin(-x) = -sin(x)。
余弦函数的定义
定义
余弦函数是三角函数的另一种形式,定义为直角三角形中锐角的邻边与斜边的比值,记作 cos(x)。
周期性
余弦函数也具有周期性,其周期为2π。
奇偶性
余弦函数是偶函数,满足cos(-x) = cos(x)。
奇偶性
总结词
正弦函数是奇函数,而余弦函数是偶 函数。
详细描述
奇函数满足$f(-x) = -f(x)$,偶函数满 足$f(-x) = f(x)$。对于正弦函数, $sin(-x) = -sin(x)$;对于余弦函数, $cos(-x) = cos(x)$。
最值与振幅
总结词
正弦函数和余弦函数都具有最大值和最小值,这取决于它们的振幅。
正弦函数余弦函数的图像与性质
目录
• 正弦函数与余弦函数的定义 • 正弦函数与余弦函数的图像 • 正弦函数与余弦函数的性质 • 正弦函数与余弦函数的应用 • 正弦函数与余弦函数的扩展知识
01 正弦函数与余弦函数的定 义
正弦函数的定义
定义
正弦函数是三角函数的 一种,定义为直角三角 形中锐角的对边与斜边 的比值,记作sin(x)。
三角函数图像与性质
图3-4-2 A.2,- B.2,- C.4,- D.4,
自测后你觉得哪类题做起来困难呢?那我们一起来解决吧!
典例:
题型一三角函数的定义域和值域
(1)函数y= 的定义域为________.
A.向右平移 个单位B.向右平移 个单位C.向左平移 个单位D.向左平移 个单位
3.[2014·福建卷]将函数y=sinx的图像向左平移 个单位,得到函数y=f(x)的图像,则下列说法正确的是()
A.y=f(x)是奇函数B.y=f(x)的周期为π
C.y=f(x)的图像关于直线x= 对称D.y=f(x)的图像关于点 对称
导疑:由解析式求函数定义域应考虑________.
导学:由tanx-1 0得tanx 1所以x ________.
所以所求定义域为________.
(2)求下列函数的值域①y=2cos2x+2cosx②y=3cosx- sinx,x∈[0,π];
导疑:二次函数给定区间如何求值域?形如y=Asin(ωx+φ)函数的值域?
A. B.
C. D.
2.函数f(x)=2cos 是()
A.最小正周期为2π的奇函数B.最小正周期为2π的偶函数
C.最小正周期为2π的非奇非偶函数D.最小正周期为π的偶函数
3.函数f(x)=sin 的图象的一条对称轴是()
A.x= B.x= C.x=- D.x=-
4.比较大小:sin ________sin .
A.A=3,T= ,φ=- B.A=1,T= ,φ=
C.A=1,T= ,φ=- D.A=1,T= ,φ=-
图3-4-3图3-4-4
三角函数公式、图像大全

三角函数公式、图像大全幂函数的图形指数函数的图形对数函数的图形三角函数的图形各三角函数值在各象限的符号sinα·cscα cosα·secα tanα·cotα 三角函数的性质函数 y=sinx y=cosx y=tanxy=cotx 定义域 R R {x|x∈R且x≠kπ+,k∈Z}{x|x∈R且x≠kπ,k∈Z}值域[-1,1]x=2kπ+ 时ymax=1 x=2kπ- 时ymin=-1 [-1,1]x=2kπ时ymax=1 x=2kπ+π时ymin=-1 R 无最大值无最小值 R 无最大值无最小值周期性周期为2π 周期为2π 周期为π 周期为π 奇偶性奇函数偶函数奇函数奇函数单调性在[2kπ-,2kπ+ ]上都是增函数;在[2kπ+ ,2kπ+π]上都是减函数(k∈Z)在[2kπ-π,2kπ]上都是增函数;在[2kπ,2kπ+π]上都是减函数(k∈Z)在(kπ-,kπ+)内都是增函数(k∈Z)在(kπ,kπ+π)内都是减函数(k∈Z)反三角函数的图形反三角函数的性质名称反正弦函数反余弦函数反正切函数反余切函数定义y=sinx(x∈〔-, 〕的反函数,叫做反正弦函数,记作x=arsiny y=cosx(x∈〔0,π〕)的反函数,叫做反余弦函数,记作x=arccosy y=tanx(x∈(- , )的反函数,叫做反正切函数,记作x=arctany y=cotx(x∈(0,π))的反函数,叫做反余切函数,记作x=arccoty 理解 arcsinx表示属于[-,]且正弦值等于x的角 arccosx表示属于[0,π],且余弦值等于x的角 arctanx表示属于(-,),且正切值等于x的角arccotx表示属于(0,π)且余切值等于x的角性质定义域[-1,1][-1,1] (-∞,+∞)(-∞,+∞)值域[-,][0,π] (-,)(0,π)单调性在〔-1,1〕上是增函数在[-1,1]上是减函数在(-∞,+∞)上是增数在(-∞,+∞)上是减函数奇偶性 arcsin(-x)=-arcsinx arccos(-x)=π-arccosx arctan(-x)=-arctanx arccot(-x)=π-arccotx 周期性都不是同期函数恒等式sin(arcsinx)=x(x∈[-1,1])arcsin(sinx)=x(x∈[-,]) cos(arccosx)=x(x∈[-1,1])arccos(cosx)=x(x∈[0,π])tan(arctanx)=x(x∈R)arctan(tanx)=x(x∈(-,))cot(arccotx)=x(x∈R)arccot(cotx)=x(x∈(0,π))互余恒等式arcsinx+arccosx=(x∈[-1,1])arctanx+arccotx=(X∈R)三角函数公式两角和公式 sin(A+B)= sinAcosB+cosAsinB sin(A-B)= sinAcosB-cosAsinB cos(A+B)= cosAcosB-sinAsinB cos(A-B)= cosAcosB+sinAsinB tan(A+B)= tan(A-B)= cot(A+B)= cot(A-B)= 倍角公式tan2A = Sin2A=2SinA•CosA Cos2A = Cos2A-Sin2A=2Cos2A-1=1-2sin2A 三倍角公式 sin3A =3sinA-4(sinA)3 cos3A =4(cosA)3-3cosA tan3a = tana·tan(+a)·tan(-a) 半角公式 sin()= cos()= tan()= cot()= tan()== 和差化积sina+sinb=2sincos sina-sinb=2cossin cosa+cosb =2coscos cosa-cosb =[cos(a+b)-cos(a-b)] cosacosb =[cos(a+b)+cos(a-b)] sinacosb = [sin(a+b)+sin(a-b)] cosasinb = [sin(a+b)-sin(a-b)] 诱导公式 sin(-a) =a)= cosa sin(-a)= cosa cos(-a)= sina sin(+a)= cosa cos(+a)=a)= sina cos(π-a)=sina cos(π+a)=b•cos(a)= ×cos(a-c)[其中tan(c)=]1+sin(a)=(sin+cos)21-sin(a)= (sin-cos)2 其他非重点三角函数 csc(a)= sec(a)= 双曲函数 sinh(a)= cosh(a)= tg h(a)= 公式一设α为任意角,终边相同的角的同一三角函数的值相等: sin(2kπ+α)= sinα cos(2kπ+α)= cosα tan(2kπ+α)= tanα cot(2kπ+α)= cotα 公式二设α为任意角,π+α的三角函数值与α的三角函数值之间的关系: sin(π+α)=cosα tan(π+α)= tanα cot(π+α)= cotα 公式三任意角α与α)=α)= cosα tan(-α)=α)=α与α的三角函数值之间的关系: sin(π-α)= sinα cos(π-α)=α)=α)=和公式三可以得到2π-α与α的三角函数值之间的关系: sin(2π-α)=α)= cosα tan(2π-α)=α)=sinα tan(+α)=tanα sin(-α)= cosα cos(-α)= sinα tan (-α)= cotα cot(-α)= tanα sin(+α)=cotα cot(+α)=α)=α)=α)= cotα cot(-α)= tanα (以上k∈Z)这个物理常用公式我费了半天的劲才输进来,希望对大家有用A•sin(ωt+θ)+ B•sin(ωt+φ)=×sin 三角函数公式证明(全部)公式表达式乘法与因式分解 a2-b2=(a+b)(a-b)a3+b3=(a+b)(a2-ab+b2)a3-b3=(a-b)(a2+ab+b2)三角不等式|a+b|≤|a|+|b| |a-b|≤|a|+|b| |a|≤b-b≤a≤b |a-b|≥|a|-|b|b+√(b2-4ac)/2ab+√(b2-4ac)/2a 根与系数的关系 X1+X2=-b/a X1*X2=c/a 注:韦达定理判别式 b2-4a=0 注:方程有相等的两实根 b2-4ac>0 注:方程有一个实根b2-4ac0 抛物线标准方程 y2=2px y2=-2px x2=2py x2=-2py 直棱柱侧面积 S=c*h 斜棱柱侧面积 S=c *h 正棱锥侧面积 S=1/2c*h 正棱台侧面积 S=1/2(c+c )h 圆台侧面积S=1/2(c+c )l=pi(R+r)l 球的表面积 S=4pi*r2 圆柱侧面积S=c*h=2pi*h 圆锥侧面积 S=1/2*c*l=pi*r*l 弧长公式 l=a*r a 是圆心角的弧度数r >0 扇形面积公式 s=1/2*l*r 锥体体积公式V=1/3*S*H 圆锥体体积公式 V=1/3*pi*r2h 斜棱柱体积 V=S L 注:其中,S 是直截面面积, L是侧棱长柱体体积公式 V=s*h 圆柱体 V=pi*r2h------------------------------------------------------------------------------------------ 三角函数积化和差和差化积公式记不住就自己推,用两角和差的正余弦: cos(A+B)=cosAcosB-sinAsinB cos(A-B)=cosAcosB+sinAsinB 这两式相加或相减,可以得到2组积化和差: 相加:cosAcosB=[cos(A+B)+cos(A-B)]/2 相减:sinAsinB=-[cos(A+B)-cos(A-B)]/2 sin(A+B)=sinAcosB+sinBcosA sin(A-B)=sinAcosB-sinBcosA 这两式相加或相减,可以得到2组积化和差: 相加:sinAcosB=[sin(A+B)+sin(A-B)]/2 相减:sinBcosA=[sin(A+B)-sin(A-B)]/2 这样一共4组积化和差,然后倒过来就是和差化积了不知道这样你可以记住伐,实在记不住考试的时候也可以临时推导一下正加正正在前正减正余在前余加余都是余余减余没有余还负正余正加余正正减余余余加正正余减还负 .3.三角形中的一些结论:(不要求记忆)(1)anA+tanB+tanC=tanA·tanB·tanC(2)sinA+tsinB+sinC=4cos(A/2)cos(B/2)cos(C/2)(3)cosA+cosB+cosC=4sin(A/2)·sin(B/2)·sin(C/2)+1(4)sin2A+sin2B+sin2C=4sinA·sinB·sinC(5)cos2A+cos2B+cos2C=-4cosAcosBcosC-1 . 已知sinα=m sin(α+2β), |m|<1,求证tan(α+β)=(1+m)/(1-m)tanβ解:sinα=m sin(α+2β)sin(a+β-β)=msin(a+β+β)sin(a+β)cosβ-cos(a+β)sinβ=msin(a+β)cosβ+mcos(a+β)sinβsin(a+β)cosβ(1-m)=cos(a+β)sinβ(m+1)tan(α+β)=(1+m)/(1-m)tanβ。
第三章 第三节 正弦、余弦、正切函数的图像与性质

最 ymax=1(k∈Z); 2kπ 时, 值 x=ymin=-1(k∈Z)
x=2kπ 时 , ymax=1(k∈Z); π+2kπ 时, X= ymin=-1(k∈Z)
无最值
函数 奇偶 性
y=sinx
y=cosx
y=tanx 奇 对称中心 ( ,0), k∈Z
奇
偶
对称中心
对称中心 (kπ+ ,0) k∈Z
图 象
函 数 定 义 域
y=sinx
y=cosx
y=tanx
R
R
{x|x≠
+2kπ,k∈Z}
值 {y|-1 ≤ y ≤ 1} 域
{y|-1≤ y ≤ 1}
R
函 数
[-
y=sinx
+2kπ,
y=cosx [(2k-1)π,2kπ]
y=tanx
(- Kπ, Kπ) 上递增 k∈Z + +
上递增,∈Z; + 2kπ] 单 上递增,k∈Z; [2kπ,(2k+1)π] 调 [ +2kπ, +2kπ] 性 上递减,k∈Z 上递减,k∈Z
+2kπ≤ωx- φ ≤
3.对于y=Atan(ωx+φ)(A、ω、 φ为常数),其周期T=
单调区间利用ωx+ φ ∈(kπ- 的取值范围,即为其单调区间. ,kπ+
,
)(k∈Z),解出x
[特别警示] 求三角函数的单调区间时,一定要注意A和ω 的符号.
已知函数f(x)=log2[ (1)求函数的定义域;
在[0,2π]内,满足sinx=cosx的x为
再结合正弦、余弦函数的周期是2π,所以定义域为{x|
+2kπ<x<
+2kπ,k∈Z}.
1.形如y=Asin(ωx+φ)(A>0,ω>0)的函数的单调区间, 基本思路是把ωx+ φ 看作一个整体,由- +2kπ≤ωx
第四讲 正弦、余弦、正切函数的图象与性质(解析版)

第四讲 正弦、余弦和正切函数的图像与性质知识提要1. 用五点法作正弦函数和余弦函数的简图正弦函数y =sin x ,x ∈[0,2π]的图象中,五个关键点是:(0,0),(π2,1),(π,0),(3π2,-1),(2π,0).余弦函数y =cos x ,x ∈[0,2π]的图象中,五个关键点是:(0,1),(π2,0),(π,-1),(3π2,0),(2π,1).2. 正弦函数、余弦函数、正切函数的图象和性质函数 y =sin x y =cos x y =tan x图象定义域 R R {x |x ∈R 且x ≠π2+k π,k ∈Z }值域[-1,1][-1,1]R单调性[-π2+2k π,π2+2k π](k ∈Z )上递增; [π2+2k π,3π2+2k π](k ∈Z )上递减 [-π+2k π,2k π](k ∈Z )上递增;[2k π,π+2k π](k ∈Z )上递减(-π2+k π,π2+k π) (k ∈Z )上递增最值x =π2+2k π(k ∈Z )时,y max =1;x =-π2+2k π(k ∈Z )时,y min =-1x =2k π(k ∈Z )时,y max =1;x =π+2k π(k ∈Z )时,y min =-1奇偶性 奇函数 偶函数 奇函数 对称中心 (k π,0)(k ∈Z ) (π2+k π,0) (k ∈Z ) (k π2,0)(k ∈Z ) 对称轴方程x =π2+k π(k ∈Z ) x =k π(k ∈Z )周期2π2ππ※ 学习评价1、判断下面结论是否正确(请在括号中打“√”或“×”)(1)常数函数f (x )=a 是周期函数,它没有最小正周期. ( √ ) (2)y =cos x 在第一、二象限上是减函数. ( × ) (3)y =tan x 在整个定义域上是增函数.( × )(4)y =k sin x +1(x ∈R ),则y max =k +1. ( × )2、函数f (x )=sin ⎝⎛⎭⎫x -π4的图象的一条对称轴是( )A .x =π4B .x =π2C .x =-π4D .x =-π2解析:方法一 ∵正弦函数图象的对称轴过图象的最高点或最低点,故令x -π4=k π+π2,k ∈Z ,∴x =k π+3π4,k ∈Z . 取k =-1,则x =-π4.方法二 用验证法.x =π4时,y =sin ⎝⎛⎭⎫π4-π4=0,不合题意,排除A ; x =π2时,y =sin ⎝⎛⎭⎫π2-π4=22,不合题意,排除B ; x =-π4时,y =sin ⎝⎛⎭⎫-π4-π4=-1,符合题意,C 项正确; x =-π2时,y =sin ⎝⎛⎭⎫-π2-π4=-22,不合题意,故D 项也不正确. 3、若函数f (x )=sin ωx (ω>0)在区间⎣⎡⎦⎤0,π3上单调递增,在区间⎣⎡⎦⎤π3,π2上单调递减,则ω等于( )A .23B .32C .2D .3解析:∵f (x )=sin ωx (ω>0)过原点,∴当0≤ωx ≤π2,即0≤x ≤π2ω时,y =sin ωx 是增函数;当π2≤ωx ≤3π2,即π2ω≤x ≤3π2ω时,y =sin ωx 是减函数. 由f (x )=sin ωx (ω>0)在⎣⎡⎦⎤0,π3上单调递增, 在⎣⎡⎦⎤π3,π2上单调递减知,π2ω=π3,∴ω=32.例1 求函数y =1+sin ⎝⎛⎭⎫-12x +π4,x ∈[-4π,4π]的单调减区间. 解析:y =1+sin ⎝⎛⎭⎫-12x +π4=-sin ⎝⎛⎭⎫12x -π4+1. 由2k π-π2≤12x -π4≤2k π+π2(k ∈Z ).解得4k π-π2≤x ≤4k π+32π(k ∈Z).令k =0时,-π2 ≤x ≤32π; 令k =1时,72π≤x ≤4π+32π. 令k =-1时,-4π-π2≤x ≤-52π;∵-4π≤x ≤4π,∴函数y =1+sin ⎝⎛⎭⎫-12x +π4的单调减区间为 [-4π,-52π],[-π2,32π],[72π,4π].变式:(1)已知ω>0,函数f (x )=sin(ωx +π4)在(π2,π)上单调递减,则ω的取值范围是( )A .[12,54]B .[12,34]C .(0,12]D .(0,2](2)已知函数f (x )=2cos(ωx +φ)+b 对任意实数x 有f (x +π4)=f (-x )成立,且f (π8)=1,则实数b 的值为( )A .-1B .3C .-1或3D .-3解析:(1)由π2<x <π得π2ω+π4<ωx +π4<πω+π4,由题意知(π2ω+π4,πω+π4)⊆[π2,3π2],∴⎩⎨⎧π2ω+π4≥π2,πω+π4≤3π2,∴12≤ω≤54,故选A.解析:由f (x +π4)=f (-x )可知函数f (x )=2cos(ωx +φ)+b 关于直线x =π8对称,又函数f (x )在对称轴处取得最值,故±2+b =1,∴b =-1或b =3. 故选C. 例2 求函数f (x )=lg sin x +16-x 2的定义域.解析:由题意,x 满足不等式组⎩⎪⎨⎪⎧ sin x >016-x 2≥0,即⎩⎪⎨⎪⎧-4≤x ≤4sin x >0,作出y =sin x 的图象,如图所示.结合图象可得:x ∈[-4,-π)∪(0,π). 例3 求下列函数的周期.(1)y =sin ⎝⎛⎭⎫2x +π3 (x ∈R); (2)y =cos(1-πx )(x ∈R); (3)y =|sin x | (x ∈R). 解析:(1)方法一 令z =2x +π3,∵x ∈R ,∴z ∈R ,函数f (z )=sin z 的最小正周期是2π,就是说变量z 只要且至少要增加到z +2π,函数f (z )=sin z (z ∈R)的值才能重复取得, 而z +2π=2x +π3+2π=2(x +π)+π3,所以自变量x 只要且至少要增加到x +π,函数值才能重复取得,从而函数y =sin ⎝⎛⎭⎫2x +π3 (x ∈R)的周期是π..方法二 y =sin ⎝⎛⎭⎫2x +π3(x ∈R)的周期为2π2=π. (2)设f (x )=cos(1-πx ),则f (x )=cos(πx -1).∵cos[(πx -1)+2π]=cos[(πx +2π)-1]=cos[π(x +2)-1]=co s(πx -1). ∴f (x +2)=f (x ),从而函数y =cos(1-πx )(x ∈R)的周期是2. (3)作出y =|sin x |(x ∈R)的图象.由图象可知,y =|sin x |(x ∈R)的周期为π.例4 (1) 求函数y =cos ⎝⎛⎭⎫x +π6,x ∈⎣⎡⎦⎤0,π2的值域. (2) 求函数y =sin 2x -sin x +1,x ∈R 的值域.解 (1)∵0≤x ≤π2,∴π6≤x +π6≤23π. ∴cos 23π≤cos ⎝⎛⎭⎫x +π6≤cos π6,∴-12≤y ≤32(2)设t =sin x ,t ∈[-1,1],f (t )=t 2-t +1. ∵f (t )=t 2-t +1=⎝⎛⎭⎫t -122+34. ∵-1≤t ≤1, ∴当t =-1,即sin x =-1时,y max =f (t )max =3; 当t =12,即sin x =12时,y min =f (t )min =34.∴函数y =sin 2x -sin x +1,x ∈R 的值域为⎣⎡⎦⎤34,3.巩固提高※夯实基础1.下列函数中,周期为π,且在⎣⎡⎦⎤π4,π2上为减函数的是( A )A .y =sin(2x +π2)B .y =cos(2x +π2)C .y =sin(x +π2)D .y =cos(x +π2)2、函数y =2sin(2x +π3)(-π6≤x ≤π6)的值域是________.[0,2]3、求函数y =tan ⎝⎛⎭⎫π3x +π4的定义域、周期、单调区间和对称中心. 解析:①由π3x +π4≠k π+π2,k ∈Z ,得x ≠3k +34,k ∈Z .∴ 函数的定义域为{x |x ∈R ,且x ≠3k +34,k ∈Z }.②T =ππ3=3,∴函数的周期为3.③由k π-π2<π3x +π4<k π+π2,k ∈Z . 解得3k -94<x <3k +34,k ∈Z .∴函数的单调增区间为⎝⎛⎭⎫3k -94,3k +34,k ∈Z . ④由π3x +π4=k π2,k ∈Z . 解得x =3k 2-34,k ∈Z .∴函数的对称中心是⎝⎛⎭⎫3k 2-34,0,k ∈Z . 4. 设|x |≤π4,求函数f (x )=cos 2x +sin x 的最小值.解析:f (x )=cos 2x +sin x =1-sin 2x +sin x =-⎝⎛⎭⎫sin x -122+54. ∵|x |≤π4,∴-22≤sin x ≤22. ∴当sin x =-22时,f (x )min =1-22.5. 已知a >0,函数f (x )=-2a sin ⎝⎛⎭⎫2x +π6+2a +b ,当x ∈⎣⎡⎦⎤0,π2时,-5≤f (x )≤1. (1)求常数a ,b 的值;(2)设g (x )=f ⎝⎛⎭⎫x +π2且lg g (x )>0,求g (x )的单调区间. 解 (1)∵x ∈⎣⎡⎦⎤0,π2,∴2x +π6∈⎣⎡⎦⎤π6,7π6. ∴sin ⎝⎛⎭⎫2x +π6∈⎣⎡⎦⎤-12,1, ∴-2a sin ⎝⎛⎭⎫2x +π6∈[-2a ,a ]. ∴f (x )∈[b,3a +b ], 又∵-5≤f (x )≤1, ∴b =-5,3a +b =1,因此a =2,b =-5. (2)由(1)得,f (x )=-4sin ⎝⎛⎭⎫2x +π6-1, g (x )=f ⎝⎛⎭⎫x +π2=-4sin ⎝⎛⎭⎫2x +7π6-1 =4sin ⎝⎛⎭⎫2x +π6-1, 又由lg g (x )>0,得g (x )>1,∴4sin ⎝⎛⎭⎫2x +π6-1>1,∴sin ⎝⎛⎭⎫2x +π6>12, ∴2k π+π6<2x +π6<2k π+5π6,k ∈Z , 其中当2k π+π6<2x +π6≤2k π+π2,k ∈Z 时,g (x )单调递增,即k π<x ≤k π+π6,k ∈Z ,∴g (x )的单调增区间为⎝⎛⎦⎤k π,k π+π6,k ∈Z . 又∵当2k π+π2<2x +π6<2k π+5π6,k ∈Z 时,g (x )单调递减,即k π+π6<x <k π+π3,k ∈Z . ∴g (x )的单调减区间为⎝⎛⎭⎫k π+π6,k π+π3,k ∈Z .※能力提高6、将函数f (x )=sin ωx (其中ω>0)的图象向右平移π4个单位长度,所得图象经过点⎝⎛⎭⎫3π4,0,则ω的最小值是 ( )A.13B .1C.53D .2解析:根据题意平移后函数的解析式为y =sin ω⎝⎛⎭⎫x -π4, 将⎝⎛⎭⎫3π4,0代入得sin ωπ2=0,则ω=2k ,k ∈Z ,且ω>0,故ω的最小值为2. 7、函数y =|sin x +cos x |-1的定义域是( )A .[k π,k π+π2](k ∈Z )B .[2k π,2k π+π2](k ∈Z )C .[-π2+k π,k π](k ∈Z )D .[-π2+2k π,2k π](k ∈Z )解析:|sin x +cos x |-1≥0⇒(sin x +cos x )2≥1 ⇒sin 2x ≥0,∴2k π≤2x ≤2k π+π,k ∈Z ,故原函数的定义域是[k π,k π+π2](k ∈Z ).8、已知函数)2sin()(ϕ+=x x f ,其中ϕ为实数,若|)6(|)(πf x f ≤对R x ∈恒成立,且)()2(ππf f >,则)(x f 的单调递增区间是 ( ) (A) )(6,3Z k k k ∈⎥⎦⎤⎢⎣⎡+-ππππ (B) )(2,Z k k k ∈⎥⎦⎤⎢⎣⎡+πππ(C) )(32,6Z k k k ∈⎥⎦⎤⎢⎣⎡++ππππ (D) )(,2Z k k k ∈⎥⎦⎤⎢⎣⎡-πππ 解析:∵|)6(|)(πf x f ≤, ∴)6(πf 为)(x f 的最小值或最大值,∴ 1)62sin()6(±=+⨯=ϕππf , ∴ Z k k ∈+=+,23ππϕπ,∴ Z k k ∈+=,6ππϕ.当6πϕ=时,2167sin )622sin()2(-==+⨯=ππππf ,216sin )62sin()(==+=ππππf . 这与)()2(ππf f >矛盾,舍去。
三角函数公式、图像大全

初等函数的图形之宇文皓月创作幂函数的图形指数函数的图形对数函数的图形三角函数的图形各三角函数值在各象限的符号sinα·cscα cosα·secαtanα·cotα三角函数的性质反三角函数的图形反三角函数的性质三角函数公式 两角和公式sin(A+B) = sinAcosB+cosAsinB sin(A-B) = sinAcosB-cosAsinB cos(A+B) = cosAcosB-sinAsinB cos(A-B) = cosAcosB+sinAsinBtan(A+B) =tanAtanB -1tanBtanA + tan(A-B) =tanAtanB 1tanBtanA +- cot(A+B) =cotA cotB 1-cotAcotB + cot(A-B) =cotA cotB 1cotAcotB -+倍角公式tan2A =A tan 12tanA2-Sin2A=2SinA•CosACos2A = Cos 2A-Sin 2A=2Cos 2A-1=1-2sin 2A 三倍角公式sin3A = 3sinA-4(sinA)3cos3A = 4(cosA)3-3cosAtan3a = tana ·tan(3π+a)·tan(3π-a)半角公式sin(2A)=2cos 1A - cos(2A)=2cos 1A + tan(2A)=A A cos 1cos 1+- cot(2A)=A A cos 1cos 1-+tan(2A )=A A sin cos 1-=A A cos 1sin +和差化积sina+sinb=2sin 2b a +cos 2ba - sina-sinb=2cos 2b a +sin 2ba -cosa+cosb = 2cos 2b a +cos 2ba - cosa-cosb = -2sin 2b a +sin 2ba - tana+tanb=b a b a cos cos )sin(+积化和差sinasinb = -21[cos(a+b)-cos(a-b)]cosacosb = 21[cos(a+b)+cos(a-b)] sinacosb = 21[sin(a+b)+sin(a-b)] cosasinb = 21[sin(a+b)-sin(a-b)]诱导公式 sin(-a) = -sina cos(-a) = cosasin(2π-a) = cosa cos(2π-a) = sina sin(2π+a) = cosa cos(2π+a) = -sinasin(π-a) = sina cos(π-a) = -cosa sin(π+a) = -sina cos(π+a) = -cosatgA=tanA =a acos sin万能公式sina=2)2(tan 12tan2aa + cosa=22)2(tan 1)2(tan 1aa+- tana=2)2(tan 12tan2aa - 其它公式a•sina+b•cosa=)b (a 22+×sin(a+c) [其中tanc=a b]a•sin(a)-b•cos(a) = )b (a 22+×cos(a-c) [其中tan(c)=b a]1+sin(a) =(sin 2a +cos 2a)21-sin(a) = (sin 2a -cos 2a)2其他非重点三角函数csc(a) =a sin 1sec(a) =a cos 1双曲函数sinh(a)=2e -e -aa cosh(a)=2e e -aa tg h(a)=)cosh()sinh(a a公式一设α为任意角,终边相同的角的同一三角函数的值相等: sin (2kπ+α)= sinα cos (2kπ+α)= cosα tan (2kπ+α)= tanα cot (2kπ+α)= co tα设α为任意角,π+α的三角函数值与α的三角函数值之间的关系:sin(π+α)= -sinαcos(π+α)= -cosαtan(π+α)= tanαcot(π+α)= cotα公式三任意角α与 -α的三角函数值之间的关系:sin(-α)= -sinαcos(-α)= cosαtan(-α)= -tanαcot(-α)= -cotα公式四利用公式二和公式三可以得到π-α与α的三角函数值之间的关系:sin(π-α)= sinαcos(π-α)= -cosαtan(π-α)= -tanαcot(π-α)= -cotα利用公式-和公式三可以得到2π-α与α的三角函数值之间的关系:sin (2π-α)= -sinα cos (2π-α)= cosα tan (2π-α)= -tanα cot (2π-α)= -cotα 公式六2π±α及23π±α与α的三角函数值之间的关系:sin (2π+α)= cosα cos (2π+α)= -sinα tan (2π+α)= -cotα cot (2π+α)= -tanα sin (2π-α)= cosα cos (2π-α)= sinα tan (2π-α)= cotαcot (2π-α)= ta nαsin (23π+α)= -cosα cos (23π+α)= sinα tan (23π+α)= -cotα cot (23π+α)= -tanα sin (23π-α)= -cosα cos (23π-α)= -sinα tan (23π-α)= cotα cot (23π-α)= tanα(以上k∈Z)这个物理经常使用公式我费了半天的劲才输进来,希望对大家有用A•sin(ωt+θ)+ B•sin(ωt+φ) =)cos(222ϕθ⋅++AB B A ×sin)cos(2)Bsin in arcsin[(As t 22ϕθϕθω⋅++++AB B A三角函数公式证明(全部)公式表达式乘法与因式分解a2-b2=(a+b)(a-b) a3+b3=(a+b)(a2-ab+b2) a3-b3=(a-b)(a2+ab+b2)三角不等式|a+b|≤|a|+|b||a-b|≤|a|+|b||a|≤b<=>-b≤a≤b|a-b|≥|a|-|b|-|a|≤a≤|a|一元二次方程的解-b+√(b2-4ac)/2a -b-b+√(b2-4ac)/2a根与系数的关系X1+X2=-b/aX1*X2=c/a注:韦达定理判别式 b2-4a=0 注:方程有相等的两实根b2-4ac>0 注:方程有一个实根b2-4ac<0 注:方程有共轭复数根三角函数公式两角和公式sin(A+B)=sinAcosB+cosAsinB sin(A-B)=sinAcosB-sinBcosA cos(A+B)=cosAcosB-sinAsinB cos(A-B)=cosAcosB+sinAsinB tan(A+B)=(tanA+tanB)/(1-tanAtanB) tan(A-B)=(tanA-tanB)/(1+tanAtanB)ctg(A+B)=(ctgActgB-1)/(ctgB+ctgA) ctg(A-B)=(ctgActgB+1)/(ctgB-ctgA)倍角公式tan2A=2tanA/(1-tan2A) ctg2A=(ctg2A-1)/2ctgacos2a=cos2a-sin2a=2cos2a-1=1-2sin2a半角公式sin(A/2)=√((1-cosA)/2) sin(A/2)=-√((1-cosA)/2)cos(A/2)=√((1+cosA)/2) cos(A/2)=-√((1+cosA)/2)tan(A/2)=√((1-cosA)/((1+cosA)) tan(A/2)=-√((1-cosA)/((1+cosA))ctg(A/2)=√((1+cosA)/((1-cosA)) ctg(A/2)=-√((1+cosA)/((1-cosA))和差化积2sinAcosB=sin(A+B)+sin(A-B) 2cosAsinB=sin(A+B)-sin(A-B) 2cosAcosB=cos(A+B)-sin(A-B) -2sinAsinB=cos(A+B)-cos(A-B) sinA+sinB=2sin((A+B)/2)cos((A-B)/2cosA+cosB=2cos((A+B)/2)sin((A-B)/2)tanA+tanB=sin(A+B)/cosAcosB tanA-tanB=sin(A-B)/cosAcosB ctgA+ctgBsin(A+B)/sinAsinB -ctgA+ctgBsin(A+B)/sinAsinB某些数列前n项和1+2+3+4+5+6+7+8+9+…+n=n(n+1)/21+3+5+7+9+11+13+15+…+(2n-1)=n22+4+6+8+10+12+14+…+(2n)=n(n+1)12+22+32+42+52+62+72+82+…+n2=n(n+1)(2n+1)/613+23+33+43+53+63+…n3=n2(n+1)2/41*2+2*3+3*4+4*5+5*6+6*7+…+n(n+1)=n(n+1)(n+2)/3 正弦定理a/sinA=b/sinB=c/sinC=2R注:其中 R 暗示三角形的外接圆半径余弦定理b2=a2+c2-2accosB注:角B是边a和边c的夹角正切定理[(a+b)/(a-b)]={[Tan(a+b)/2]/[Tan(a-b)/2]}圆的尺度方程(x-a)2+(y-b)2=r2 注:(a,b)是圆心坐标圆的一般方程x2+y2+Dx+Ey+F=0 注:D2+E2-4F>0 抛物线尺度方程y2=2px y2=-2px x2=2py x2=-2py 直棱柱正面积S=c*h斜棱柱正面积S=c'*h正棱锥正面积S=1/2c*h'正棱台正面积S=1/2(c+c')h'圆台正面积S=1/2(c+c')l=pi(R+r)l球的概况积S=4pi*r2圆柱正面积S=c*h=2pi*h圆锥正面积S=1/2*c*l=pi*r*l弧长公式l=a*ra是圆心角的弧度数r >0 扇形面积公式s=1/2*l*r锥体体积公式V=1/3*S*H圆锥体体积公式V=1/3*pi*r2h斜棱柱体积V=S'L注:其中,S'是直截面面积, L是侧棱长柱体体积公式V=s*h圆柱体V=pi*r2h--------------------------------------------------------------------------------------------三角函数积化和差和差化积公式记不住就自己推,用两角和差的正余弦:cos(A+B)=cosAcosB-sinAsinBcos(A-B)=cosAcosB+sinAsinB这两式相加或相减,可以得到2组积化和差:相加:cosAcosB=[cos(A+B)+cos(A-B)]/2相减:sinAsinB=-[cos(A+B)-cos(A-B)]/2sin(A+B)=sinAcosB+sinBcosAsin(A-B)=sinAcosB-sinBcosA这两式相加或相减,可以得到2组积化和差:相加:sinAcosB=[sin(A+B)+sin(A-B)]/2相减:sinBcosA=[sin(A+B)-sin(A-B)]/2这样一共4组积化和差,然后倒过来就是和差化积了不知道这样你可以记住伐,实在记不住考试的时候也可以临时推导一下正加正正在前正减正余在前余加余都是余余减余没有余还负正余正加余正正减余余余加正正余减还负.3.三角形中的一些结论:(不要求记忆)(1)anA+tanB+tanC=tanA·tanB·tanC(2)sinA+tsinB+sinC=4cos(A/2)cos(B/2)cos(C/2)(3)cosA+cosB+cosC=4sin(A/2)·sin(B/2)·sin(C/2)+1(4)sin2A+sin2B+sin2C=4sinA·sinB·sinC(5)cos2A+cos2B+cos2C=-4cosAcosBcosC-1 ...........................已知sinα=m sin(α+2β), |m|<1,求证tan(α+β)=(1+m)/(1-m)tanβ解:sinα=m sin(α+2β)sin(a+β-β)=msin(a+β+β)sin(a+β)cosβ-cos(a+β)sinβ=msin(a+β)cosβ+mcos(a+β)sinβ sin(a+β)cosβ(1-m)=cos(a+β)sinβ(m+1)tan(α+β)=(1+m)/(1-m)tanβ。
余弦、正切函数的图像和性质

∵f x +π = tan x +π = tanx =f(x)
是它的一个周期 ∴y = tanx 是周期函数,
ππ (- , ) 2 2
想一想:先作哪个区间上的图象好呢? 一个周期内的图像
y tan x x 利用正切线画出函数 , , 的图像: 2 2 把单位圆右半圆分成8等份。 作法: (1) 等分: 3 3 (2) 作正切线 , , , , , 8 8 4 8 8 4 (3) 平移 (4) 连线
自我小结
谈谈本节课你的收获是什么? 哪部分知识掌握的比较好? 还有什么不清楚的细节吗?……… 1.课本习题 2.学案课后练习 3.(选做)导学练
思考
我们已经学习了正弦、余弦函数的图像 我们是怎么得到它们的图像的呢? 利用单位圆中的三角函数线作图 (由一个周期到整个定义域)
探索新知
通过回顾,对我们研究正切函数图像有 什么启发吗? (利用正切线)
π 2 3π 2
O
π
2π x
-1
y cosx , x [0,2π]
正弦、余弦函数的图象
y
1 -4 -3 -2 -
o
-1
2
3
4
5
6
x
正弦函数的图象 y=cosx=sin(x+ ), xR
2
正弦曲 线
形状完全一样 只是位置不同
余弦函数的图象
y
1
余弦曲 线
-4
-3
-2
其值从-1增至1 其值从 1减至-1
y=cosx (xR)
6
4
正弦和正弦函数

汇报人:XX
目录
角度与弧度的关系
角度是度量角 的单位,而弧 度是另一种度
量角的单位
1弧度等于 180/π度
在正弦函数中, 当角度以弧度 为单位时,其 值与以度为单
位的值不同
弧度在三角函 数中的应用更
为广泛
正弦函数的定义式
计算角度:利用三角函数可以计算出任意角度的度数。 计算长度:通过三角函数可以计算出任意线段的长度。 确定位置:利用三角函数可以确定平面内任意点的位置。 绘制图形:通过三角函数可以绘制出各种复杂的几何图形。
交流电的波形
正弦函数是描述交流电波形的数学模型 交流电在工业、家庭和科技领域有广泛应用 正弦函数的周期性和振幅变化可以反映交流电的特性和变化规律 通过正弦函数的分析和计算,可以优化交流电的使用和能源效率
振幅变化:振幅 大小影响图像的 波动幅度,振幅 越大,波动越剧 烈
相位移动:通过 相位移动可以改 变图像的起点位 置
正弦函数的周期为2π
周期性
正弦函数的周期性是其在三角函数 中的重要性质之一
添加标题
添加标题
添加标题
添加标题
正弦函数在每个周期内的波形重复 出现
正弦函数的周期性在物理、工程等 领域有广泛应用
乘积公式
推导:利用三角函数的和差化积公 式进行推导
添加标题
添加标题
添加标题
添加标题
应用:用于计算两个正弦函数的乘 积,简化计算过程
注意事项:使用乘积公式时需要注 意角度的取值范围和计算精度问题
商数公式
正弦函数的商数公 式为:sin(x)/cos(x) = tan(x)
该公式用于计算正 弦函数与余弦函数 的商,得到正切函 数
三角函数图像1

(2)y 2cos(2x )
4
x -p p
3p
5p
7p
44 4
4
4
化
x
4
0
2
sin(x )
4
0
1
0
3
2
2
1 0
归 转 化
x -p p
3p
5p
7p
44 4
4
4
x
4
0
2
3
2
2
sin(x )
4
0
1
0 1 0
(2)y 2cos(2x )
4
-p
p
3p
5p
7p
44
4
4
4
(2)y 2cos(2x )
设 是一个任意角,它的终边与单位圆交于点P(x, y)
y 规定:(1) 叫做 的正弦,记作 sin ,即 sin y ;
(2)x 叫做 的余弦,记作 cos,即 cos x ;
y (3y)x
叫做
的正切,记作tan ,即 tan y (x 0)
x
Px, y﹒
O
A1,0 x
2三角函数线
(4) 连线
6
o1
M-11 A
o
π 6
π π π 2π 5π
32 3 6
7π 6
4π 3
3π 2
5π 3
11π 6
2π
x
-
-
-1 -
思考:如何画函数y =sinx(x∈R)的图象? y
1-
6
4
2
o
2
-1 -
正弦曲线
4
6
x
-
正弦,余弦函数的图像PPT课件

途径:利用单位圆中正弦、余弦线来解决。
描图:用光滑曲线
y
B
1
将这些正弦线的 终点连结起来
A
O1
O
2
4
5
2
x
3
3
3
3
-1
y=sinx
终边相同角的三角函数值相等 即: sin(x+2k)=sinx, kZ
x[0,2]
f(x2k)f(x)利用图象平移
y=sinx xR
正弦、余弦函数的图象
y 1
o
2
2
-1
y=sinx x[0,2]
y
y=sinx xR
1
-4 -3
-2
- o
-1
3
2
x
2
正弦曲 线
2
3
4
5 6 x
正弦、余弦函数的图象
如何作出正弦函数的图象(在精确度要求不太高时)?
y
五点画图法
1
(2
,1)
( 2 ,1)
( ,0)
( 2 ,0)
五点法——
2
(
(0,0)o
(0,0)
2
(0,0)
-1
(0,0)
汇报人:XXX 汇报日期:20XX年10月10日
2 ,0) x
2 ,0)
( 2 ,0) ( 2 ,0) ( 2 ,0) ( 2 ,0) ( 2 ,0) ( 2 ,0)
正弦、余弦函数的图象
y
1
-4 -3
-2
- o
-1
2
3
4
5 6 x
正弦函数的图象 y=cosx=sin(x+ ), xR
2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1-
643 34 6
y 3 1 3 3 1 3 0
3
3
o
1 -
2
-
3
2
x
2
(2) 描点
2-
(3) 连线
正切函数图像: ytanx,
y
xxR,且 xk2,kZ
思考:
2
正切函数 ytanx
1
图像是否有渐近线?
3 2
2
o
1 2
3 2
x
渐近线方程:
2
xk,(kZ)
2
二、三角函数图象的性质
上平移一个
单位得到的
.●
2
x
y=sinx
(2)按五个关键点列表
x
0
2
3 2
2
cosx 1 0 -1 0 1
-cosx
.y
1
o
-1 ●
-1 0 1 0 -y1= -cosx和
y=cosx 关
. y= cosx x [0,2 ] 于X轴对称 ●
.●
2
.
.3●
2
2
●
x
y= - cosx x [0, 2]
y=cosx
左移
2
y=cosx y=sinx
余弦曲线
返回目录
二、正弦函数的“五点画图法”
(0,0)、( , 1)、( ,0)、( 3 ,-1)、 (2 ,0)
2
2
y
1
●
●
0Hale Waihona Puke 2-1●3
2
●
●
2
x
y
●
1
●
0
2
-1
●
3
2
●
●
2
x
练习:用“五点画图法”画出正弦函数
y=sinx(x[0, 2 ]的图象
一样
y 2
1
-1
2
y=2sinx, x[0, 2 ]
3
2 x
2
-2
y=2sinx, x[0, 2 ]
思考:函数y=2sinx的图象与 函数y=sinx的图象有什么关系?
三、余弦函数的“五点画图法”
(0,1)、( 2
,0)、(,-1)、(3
2
,0)、(2, 1)
y
1-
-
-1
o -
2
63
2 3
5
7
6
6
4 3
3 5
2
3
11 6
2
x
-1 -
四、正切函数的图像:y tanx
作法如下:
(1) 作直角坐标系,
y
并在直角坐标系 y
轴左侧作单位圆。
(x到2轴)这找上一横段坐2分标到成(8把等
三角函数图象
1.4 正弦、余弦、正切函数 图象和性质
一、正弦函数、余弦函数的图象和性质
正弦函数y=sinx和余弦函数y=cosx图象的画法
1、几何法 2、描点法
复习:三角函数线
的终边 y
P1
sin M P cos O M tan A T
-1 M o
-1
A
1
x
发现:利用单位圆,
正弦线、余弦线、正
1、函数y=1+sinx的图象与函数y=sinx的图象有什么关系? 2、函数y=-cosx的图象与函数y=cosx的图象有什么关系? 3、函数y=1+ cosx的图象与函数y=cosx的图象有什么关系? 4、函数y=-sinx的图象与函数y=sinx的图象有什么关系?
思考:正切函数的变化过程 和正余弦一样吗?
函数 y sin x
ycosx
y tanx
图象
y
1
0
1
2 x
y
1
0
1
2
x
y
2
3 2
2
0
3 2
x
单调性
[2k, 32k](kz)
2
2
递减
[ 2 k, 2 2 k](k 递z)增
[2k, 2k](kz) 递增 [2 k,2 k](k z)
22
递减
(k,k)(kz)
22
递增
最值
x2k,kz 时,ymax 1 x2k,kz y 时, max 1
切线分别是正弦、余
弦、正切函数的一种 T几何表示
一、正弦函数y=sinx(x R)的图象
2 32 5
6
7
6
4 3
3
2
y
3
y=sinx ( x [0, 2] )
1
●
●
●
●
●
6
7 4 3 5 11
6 3 2 3 6 2
●
2 0
2 5
●
11
6 32 3 6
●
●
x
●
5
6
-1
●
●
●
3
y
正弦函数 ysix n,xR的图像
正弦曲线
1-
-
-
6
4
2
o
2
4
6
x
-1 -
因正为,终余边相弦同函的数角的的对三角称函轴数为值过相最同,高所点以或y=最sin低x的点图且象垂在直……于, 4,2 ,x2 轴,的0,直0,线2,,对2称,4 中心,…为…图与象y=与sinxx,轴x∈的[0,交2π点]的图象相同
余弦函数y=cosx =sin(x+ ) 由y=sinx 2
1
份)
(3) 把单位圆右半
圆中作出正切线。
o'
(4) 找交叉点。
(5) 连线。
o
2 1
x k ,kZ
2
x
例:用描点法作 ytanx,x 0,2 的图象
(1) 列表
( x , 3 )
22
x0
6
4
3
2 3 5
3 46
y
y 0 3 1 3 3 1 3 0
3
3
2-
x7
5
4
5
7 1 1
2
x2k
,kz
2
时,ymin
1
x2k,kz时,ymin
1
无最值
奇偶性
奇函数
偶函数
奇函数
对称中心:(k,0)(kz)
对称性
对称中心:(k ,0)(kz)对称中心: (k ,0)(k z)
2
2
对称轴:xk ,kZ
2
对称轴:xk,kZ
无对称轴
例:画出下列函数的简图
(1)y=1+sinx, x [0, 2 ]
(1)y
2
1
y=1+sinx x[0, 2]
o
3
2
-1
2
2
x
y=sinx x[0, 2]
(2)y
1
y=cosx x[0, 2 ]
o
3
2
x
2
2
-1
y=-cosx x[0, 2 ]
(3)y
2
1
o
2
-1
(4) y
1
o
2
-1
y= - sinx
3
2
2
x
y= sinx
y=1+cosx
3
2
x
2
y=cosx
思考:
(2)y= - cosx, x [0, 2 ] (3)y= - sinx x [0, 2 ] (4)y=1+ cosx x [0, 2]
-
解:(1)按五个关键点列表
x
0
2
3 2
sinx 0 1 0 -1
1+sinx 1 2
1
0
y
y=1+sinx
2
●
.
.1● o
2
●
.
.●
3 2
2
0
1
y=1+sinx是 由y=sinx向
