东南大学信号与系统试题含答案
东南大学信号与系统试题含答案

东 南 大 学 考 试 卷(A 、B 卷)(答案附后)课程名称 信号与线性系统 考试学期 03-04-3得分适用专业 四系,十一系考试形式闭卷考试时间长度 120分钟一、简单计算题(每题8分):1、 已知某连续信号()f t 的傅里叶变换为21()23F j j ωωω=-+,按照取样间隔1T =对其进行取样得到离散时间序列()f k ,序列()f k 的Z 变换。
2、 求序列{}10()1,2,1k f k ==和2()1cos ()2f k k k πε⎡⎤⎛⎫=+ ⎪⎢⎥⎝⎭⎣⎦的卷积和。
3、 已知某双边序列的Z 变换为21()1092F z z z =++,求该序列的时域表达式()f k 。
4、 已知某连续系统的特征多项式为:269111063)(234567+++++++=s s s s s s s s D试判断该系统的稳定情况,并指出系统含有负实部、零实部和正实部的根各有几个?5、 已知某连续时间系统的系统函数为:3232642()21s s s H s s s s +++=+++。
试给出该系统的状态方程。
6、 求出下面框图所示离散时间系统的系统函数。
)(k二、(12分)已知系统框图如图(a ),输入信号e(t)的时域波形如图(b ),子系统h(t)的冲激响应波形如图(c)所示,信号()f t 的频谱为()jn n F j eπωω+∞=-∞=∑。
图(a)y(t))(t fe(t)图(b)h(t)图(c)试:1) 分别画出)(t f 的频谱图和时域波形;2) 求输出响应y(t)并画出时域波形。
3) 子系统h(t)是否是物理可实现的?为什么?请叙述理由;三(12分)、已知电路如下图所示,激励信号为)()(t t e ε=,在t=0和t=1时测得系统的输出为1)0(=y ,5.0)1(-=e y 。
分别求系统的零输入响应、零状态响应、全响应、以及自然响应和受迫响应。
L=2HC=1F+_四(12分)、已知某离散系统的差分方程为)1()()1(3)2(2+=++-+k e k y k y k y 其初始状态为6)2(,2)1(-=--=-zi zi y y ,激励)()(k k e ε=;求:1) 零输入响应)(k y zi 、零状态响应)(k y zs 及全响应)(k y ;2) 指出其中的自由响应分量和受迫响应分量; 3) 判断该系统的稳定性。
信号与系统试卷及参考答案

试卷及答案信号与系统试卷(1)(满分:100分,所有答案一律写在答题纸上)考试班级学号姓名成绩考试日期:年月日,阅卷教师:考试时间120分钟,试卷题共2页一一线性非时变离散系统,具有一初始状态x(0),当激励为时f(k),响应为y(k)=((1/2)k+1)u(k);若初始状态不变,当激励为-f(k)时,响应y(k)=((-1/2)k-1)u(k)为;试求当初始状态2x(0)为,激励为4f(k)时,系统的响应?(10分)二绘出下列函数的图形(1).已知一连续时间信号x(t)如图所示,试概略画出信号y(t)=x(2-t/3)的波形图。
(8分)t(2). 试概略画出信号y(t)=u(t 2-4) 的波形图。
(8分)三 计算下列函数(1). y(t)=⎰-44(t 2+3t+2)(δ(t)+2δ(t-2))dt (4分) (2). f(t)=e -2t u(t), h(t)= e -2t u(t), y(t)=f(t)*h (t) (8分)(3). f(k)=1, k=0,1,2,3, h(k)=1, k=0,1,2,3, y(k)=f(k)*h (k) (8分) (4) 已知f(t)=e -2t u(t), 求y(t)=[t f(2t)] 的富立叶变换 (8分) (5)y’(t)+2y(t)=δ(t)+u(t), y(0)=0, 试求y(t)=? (8分) (6). y(k)-y(k-1)-2y(k-2)=u(k)+2u(k-2), y(-1)= 2,y(-2)= -1/2, 试求零输入响应y x (k)=? 零状态响应y f (k)=? (8分)四 一线性非时变因果系统,当激励为u(t)时,响应为)]2()([cos )(cos )(ππ---+=-t u t u t t tu e t g t ,求当激励f(t)=δ(t)时的响应)(t h 。
(10分)五 某一子系统,当输入f(t)=e -t u(t)时,零状态响应y f (t) = (1/2 e -t - e -2t +1/2e -3t )u(t), 试求将两个这样的子系统串联时,总系统的冲激响应。
信号与系统标准试题库附答案

35.线性系统具有( D) A.分解特性 B。零状态线性 C。零输入线性 D。ABC
36.设系统零状态响应与激励的关系是: y zs (t ) f (t ) ,则以下表述不对的是( A ) A.系统是线性的 B。系统是时不变的 C。系统是因果的 ( B ) C。4 Hz D。8 Hz D。系统是稳定的
17、如图所示:f(t)为原始信号,f1(t)为变换信号,则 f1(t)的表达式是( D
)
A、f(-t+1) C、f(-2t+1)
B、f(t+1) D、f(-t/2+1)
4
18、若系统的冲激响应为 h(t),输入信号为 f(t),系统的零状态响应是( C )
19。信号 f (t ) 2 cos
1 > 2 , 则信号 f (t ) f 1 (t 1) f 2 (t 2) 的奈奎斯特取样频率为( C )
A. 1 B。 2 C。 1 + 2 D。 1 2
58.某信号的频谱是周期的离散谱,则对应的时域信号为( D ) A.连续的周期信号 C.离散的非周期信号 B。连续的非周期信号 D。离散的周期信号
D。50 rad/s
3
15、已知信号 f (t ) 如下图(a)所示,其反转右移的信号 f1(t) 是( D
)
16、已知信号 f1 (t ) 如下图所示,其表达式是( B)
A、ε(t)+2ε(t-2)-ε(t-3) C、ε(t)+ε(t-2)-ε(t-3)
B、ε(t-1)+ε(t-2)-2ε(t-3) D、ε(t-1)+ε(t-2)-ε(t-3)
6
33.设一个矩形脉冲的面积为 S,则矩形脉冲的 FT(傅氏变换)在原点处的函数值等于( D A.S/2 B。S/3 C。S/4 D。S
东南大学信号与系统期中考试试卷及答案

F { f (t )} = 2 Sa (ω ) − 2 e
'
− jω
= jω F ( jω )
2 − jω F ( jω ) = [ Sa (ω ) − e ] jω
4。 计算卷积: 2 * t[ε(t+2)-ε(t-2)] 。 (5分)
2
f1 (t )
0
−2 2
t
f 2 (t )
0 2
t
= ∫ τ [ε (τ + 2) − ε (τ − 2)]2dτ
解: 引入辅助函数q(t), 得
d 3 q (t ) d 2 q (t ) dq ( t ) 4 5 + + + 6 q (t ) = e (t ) 3 2 dt dt dt dq ( t ) r (t ) = 7 + 8 q (t ) dt
7
e (t )
Σ
q ′′′
∫
-4 -5 -6
q ′′
∫
q′
(t ) = (t ) =
e
− 2 t
− 2 c
e
− 2 t
, t ≥
在输入为零时 r(0+)= r(0-)= 0,r´(0+)= r´(0-)= 2, 代入上列二式
c1 + c 2 = 0 , → − 2 c 2 = 2 ∴ r zi ( t ) = ( 1 − e
(2)系统转移算子为:
解法2:因 e(t)=5,(-∞<t<∞),故由直流稳态解,可设 r(t)=A (常数),代入系统方程,得 5A=3x5, ∴ r(t)= A =3
3. 利用傅里叶变换的性质求下列波形信号的傅里叶 变换。 (8分)
信号与系统试题及答案

信号与系统试题1第一部分 选择题(共32分)一、单项选择题(本大题共16小题,每小题2分,共32分。
在每小题的四个备选答案中,选出一个正确答案,并将正确答案的序号填在题干的括号内)1.积分e d t --∞⎰2τδττ()等于( )A .δ()tB .ε()tC .2ε()tD .δε()()t t +2.已知系统微分方程为dy t dt y t f t ()()()+=2,若y f t t t (),()sin ()012+==ε,解得全响应为y t e t t ()sin()=+-︒-54242452,t ≥0。
全响应中24245sin()t -︒为( ) A .零输入响应分量 B .零状态响应分量C .自由响应分量D .稳态响应分量3.系统结构框图如图示,该系统的单位冲激响应h(t)满足的方程式为( )A .dy t dt y t x t ()()()+= B .h t x t y t ()()()=- C .dh t dt h t t ()()()+=δ D .h t t y t ()()()=-δ4.信号f t f t 12(),()波形如图所示,设f t f t f t ()()*()=12,则f()0为( )A .1B .2C .3D .45.已知信号f t ()的傅里叶变换F j ()()ωδωω=-0,则f t ()为( )A .120πωe j t B .120πωe j t - C .120πεωe t j t () D .120πεωe t j t -()6.已知信号f t ()如图所示,则其傅里叶变换为( )A .τωττωτ2422Sa Sa ()()+B .τωττωτSa Sa ()()422+ C .τωττωτ242Sa Sa ()()+ D .τωττωτSa Sa ()()42+7.信号f t 1()和f t 2()分别如图(a )和图(b)所示,已知 [()]()f t F j 11=ω,则f t 2()的 傅里叶变换为( )A .F j e j t 10()--ωωB .F j e j t 10()ωω-C .F j e j t 10()-ωωD .F j e j t 10()ωω8.有一因果线性时不变系统,其频率响应H j j ()ωω=+12,对于某一输入x(t)所得输出信号的傅里叶变换为Y j j j ()()()ωωω=++123,则该输入x(t)为( ) A .--e t t 3ε()B .e t t -3ε()C .-e t t 3ε()D .e t t 3ε()9.f t e t t ()()=2ε的拉氏变换及收敛域为( )A .122s s +>-,Re{} B .122s s +<-,Re{} C .122s s ->,Re{} D .122s s -<,Re{} 10.f t t t ()()()=--εε1的拉氏变换为( ) A .11s e s ()--B .11s e s ()-C .s e s ()1--D .s e s ()1-11.F s s s s s ()Re{}=+++>-25622的拉氏反变换为( )A .[]()e e t t t --+322εB .[]()e e t t t ---322εC .δε()()t e t t +-3D .e t t -3ε()12.图(a )中ab 段电路是某复杂电路的一部分,其中电感L 和电容C 都含有初始状态,请在图(b )中选出该电路的复频域模型。
1993-2017年东南大学《920专业基础综合》(信号与系统、数字电路)真题及答案

科目代码:920科目名称:专业基础综合(信号与系统、数字电路) 第1页 共5页 东南大学2016年硕士研究生入学考试初试试题(A 卷) 科目代码: 920 科目名称: 专业基础综合(信号与系统、数字电路) 满分: 150 分 注意: ①认真阅读答题纸上的注意事项;②所有答案必须写在答题纸上,写在本试题纸或草稿纸上均无效;③本试题纸须随答题纸一起装入试题袋中交回!一. 选择题(每小题3分,共45分)1. 函数表达式F (A ,B ,C )=AB+C ,如果实现该逻辑而不产生逻辑冒险,应该添加的项为()。
(A) AC (B) BC (C) ABC (D) BC2. 下列叙述正确的是()。
(A) 与、或、非构成的逻辑运算,可以完全由或、非运算代替;(B) 与、或、非构成的逻辑运算,可以完全由与、非运算代替;(C) 与、或、非构成的逻辑运算,可以完全由与、或运算代替;(D) 与、或、非构成的逻辑运算,不能用其中的两种运算代替;3. 触发器的特点是()。
(A) 有两个稳定的状态,能够存储一位二进制信息,能够根据输入置位、复位;(B) 由与非门构成,靠时钟边沿触发;(C) 施加激励信号后,状态完成转移,激励信号撤销,状态保持不变;(D) 在时钟有效电平时,能够完成状态转移,其他时刻,状态保持不变;4. 最小项具有下列性质()。
(A) 所有的最小项相乘,结果为1;(B) 所有的最小项相加,结果为1;(C) 任意两个最小项相乘,结果为1;(D) 任意两个最小项相加,可以消去一个变量;5. 复杂的可编程逻辑器件CPLD ,其内部一般包含有()。
(A) 算术逻辑单元ALU ;(B) 计数器;(C) 移位寄存器;(D) 可编程内部连线和逻辑块;6. 假设某线性系统,在任何初始条件下零状态响应都具有()212()t t zs y t C e C e −−=−这样的形式。
则下面说法最准确的是( )(A) 该系统一定是稳定的二阶系统;(B) 该系统一定是二阶系统,但是不能保证稳定;(C) 该系统一定是稳定的、至少是二阶的系统;。
东南大学信号与系统

λ1
是一个 k 重根,即
λ1 = λ2 = ... = λk ,则形式解为:
rzi ( t ) = C 1 e λ1t + C 2 te λ1t + C 3 t 2 e λ1t + ... + C k t k − 1 e λ1t + C k + 1 e λ k +1t + ... + C n e λ n t =
u L = L ⋅ p ⋅ iL
1 uC = ⋅ iC C⋅ p
1 即可以将电感和电容记成阻值为 L ⋅ p 和 C ⋅ p 的
电阻。
东南大学 信息科学与工程学院
利用算子可以将微分方程表示为:
p n r (t ) + an −1 p n −1r (t ) + ... + a1 pr (t ) + a0 r (t ) = bm p m e(t ) + bm −1 p m −1e(t ) + ... + b1 pe(t ) + b0 e(t )
东南大学 信息科学与工程学院
奥利弗·赫维赛德
他生于伦敦卡姆登镇。他患过猩红热,令他耳朵听不 清楚。虽然他的学业成绩不俗(1865年,他在五百多 个学生中排第五),他16岁离校,学习摩氏密码和电 磁学。他成了丹麦大北电报公司的电报员。1872年, 他是泰恩河畔纽卡斯尔的主电报员,他开始研究电力。 1874年,他辞职,在父母家中孤独地研究。这段期间 他提出了电报员方程。 他指出,传输线上平均分布的电感会减少衰减和噪 声,若电感够大且电阻够小,所有频率的电流会同等 地衰减,电路便会无噪声。 1880年,他研究电报传输上的集肤效应。
信号与系统试题库史上最全(内含答案)

信号与系统考试方式:闭卷 考试题型:1、简答题(5个小题),占30分;计算题(7个大题),占70分。
一、简答题:1.dtt df t f x e t y t )()()0()(+=-其中x(0)是初始状态,为全响应,为激励,)()(t y t f 试回答该系统是否是线性的?[答案:非线性]2.)()(sin )('t f t ty t y =+试判断该微分方程表示的系统是线性的还是非线性的,是时变的还是非时变的?[答案:线性时变的]3.已知有限频带信号)(t f 的最高频率为100Hz ,若对)3(*)2(t f t f 进行时域取样,求最小取样频率s f =?[答案:400s f Hz =]4.简述无失真传输的理想条件。
[答案:系统的幅频特性为一常数,而相频特性为通过原点的直线]5.求[]⎰∞∞--+dt t t e t )()('2δδ的值。
[答案:3]6.已知)()(ωj F t f ↔,求信号)52(-t f 的傅立叶变换。
[答案:521(25)()22j f t e F j ωω--↔]7.已知)(t f 的波形图如图所示,画出)2()2(t t f --ε的波形。
[答案: ]8.已知线性时不变系统,当输入)()()(3t e e t x t t ε--+=时,其零状态响应为)()22()(4t e e t y t t ε--+=,求系统的频率响应。
[答案:())4)(2(52)3(++++ωωωωj j j j ]9.求象函数2)1(32)(++=s s s F ,的初值)0(+f 和终值)(∞f 。
[答案:)0(+f =2,0)(=∞f ]10.若LTI 离散系统的阶跃响应为)(k g ,求其单位序列响应。
其中:)()21()(k k g k ε=。
[答案:1111()()(1)()()()(1)()()(1)222k k k h k g k g k k k k k εεδε-=--=--=--]11.已知()1 1 , 0,1,20 , k f k else ==⎧⎨⎩ ,()2 1 , 0,1,2,30 , k k f k else -==⎧⎨⎩设()()()12f k f k f k =*,求()3?f =。
信号与系统试题库史上最全内含答案)

信号与系统考试方式:闭卷 考试题型:1、简答题(5个小题),占30分;计算题(7个大题),占70分。
一、简答题:1.dtt df t f x e t y t )()()0()(+=-其中x(0)是初始状态,为全响应,为激励,)()(t y t f 试回答该系统是否是线性的?[答案:非线性]2.)()(sin )('t f t ty t y =+试判断该微分方程表示的系统是线性的还是非线性的,是时变的还是非时变的?[答案:线性时变的]3.已知有限频带信号)(t f 的最高频率为100Hz ,若对)3(*)2(t f t f 进行时域取样,求最小取样频率s f =?[答案:400s f Hz =]4.简述无失真传输的理想条件。
[答案:系统的幅频特性为一常数,而相频特性为通过原点的直线]5.求[]⎰∞∞--+dt t t e t )()('2δδ的值。
[答案:3]6.已知)()(ωj F t f ↔,求信号)52(-t f 的傅立叶变换。
[答案:521(25)()22j f t e F j ωω--↔]7.已知)(t f 的波形图如图所示,画出)2()2(t t f --ε的波形。
[答案: ]8.已知线性时不变系统,当输入)()()(3t e e t x t t ε--+=时,其零状态响应为)()22()(4t e e t y t t ε--+=,求系统的频率响应。
[答案:())4)(2(52)3(++++ωωωωj j j j ]9.求象函数2)1(32)(++=s s s F ,的初值)0(+f 和终值)(∞f 。
[答案:)0(+f =2,0)(=∞f ]10.若LTI 离散系统的阶跃响应为)(k g ,求其单位序列响应。
其中:)()21()(k k g k ε=。
[答案:1111()()(1)()()()(1)()()(1)222k k k h k g k g k k k k k εεδε-=--=--=--]11.已知()1 1 , 0,1,20 , k f k else ==⎧⎨⎩ ,()2 1 , 0,1,2,30 , k k f k else -==⎧⎨⎩设()()()12f k f k f k =*,求()3?f =。
信号与系统考试题及答案(共8套)

信号与系统考试题及答案(一)1. 系统的激励是)t (e ,响应为)t (r ,若满足dt)t (de )t (r =,则该系统为 线性、时不变、因果。
(是否线性、时不变、因果?) 2. 求积分dt )t ()t (212-+⎰∞∞-δ的值为 5 。
3. 当信号是脉冲信号f(t)时,其 低频分量 主要影响脉冲的顶部,其 高频分量 主要影响脉冲的跳变沿。
4. 若信号f(t)的最高频率是2kHz ,则t)f(2的乃奎斯特抽样频率为 8kHz 。
5. 信号在通过线性系统不产生失真,必须在信号的全部频带内,要求系统幅频特性为 一常数相频特性为_一过原点的直线(群时延)。
6. 系统阶跃响应的上升时间和系统的 截止频率 成反比。
7. 若信号的3s F(s)=(s+4)(s+2),求该信号的=)j (F ωj 3(j +4)(j +2)ωωω。
8. 为使LTI 连续系统是稳定的,其系统函数)s (H 的极点必须在S 平面的 左半平面 。
9. 已知信号的频谱函数是))00(()j (F ωωδωωδω--+=,则其时间信号f(t)为01sin()t j ωπ。
10. 若信号f(t)的211)s (s )s (F +-=,则其初始值=+)(f 0 1 。
二、判断下列说法的正误,正确请在括号里打“√”,错误请打“×”。
(每小题2分,共10分)1.单位冲激函数总是满足)()(t t -=δδ ( √ )2.满足绝对可积条件∞<⎰∞∞-dt t f )(的信号一定存在傅立叶变换,不满足这一条件的信号一定不存在傅立叶变换。
( × ) 3.非周期信号的脉冲宽度越小,其频带宽度越宽。
( √ )4.连续LTI 系统的冲激响应的形式取决于系统的特征根,于系统的零点无关。
( √ )5.所有周期信号的频谱都是离散谱,并且随频率的增高,幅度谱总是渐小的。
( × )三、计算分析题(1、3、4、5题每题10分,2题5分, 6题15分,共60分)1.信号)t (u e )t (f t-=21,信号⎩⎨⎧<<=其他,01012t )t (f ,试求)t (f *)t (f 21。
《信号和系统》试题(卷)与答案解析

i go2012年度教学质量综合评估测验卷《信号与系统》试题注:1、开课学院:信息工程学院学院。
命题组:电子信息教研组2、考试时间:120分钟,所有答案均写在答题纸上。
3、适用班级:信息工程学院通信工程专业及电子类专业。
4、在答题前,请在所发两张答题纸上认真填写所要求填写的个人信息。
卷面题型及分值:总分一二三四五六七八九十100202060一、选择题(每小题2分,共10小题。
每一小题仅有一个选项是正确的。
共计20分)1、下列说法不正确的是( )。
A 、一般周期信号为功率信号。
B 、 时限信号(仅在有限时间区间不为零的非周期信号)为能量信号。
C 、ε(t )是功率信号;D 、e t 为能量信号2、下列关于冲激函数性质的表达式不正确的是()。
A 、B 、)()0()()(t f t t f δδ=()t aat δδ1)(=C 、D 、)(d )(t tεττδ=⎰∞-)()-(t t δδ=3、,属于其极点的是()。
)2)(1()2(2)(-++=s s s s s H A 、1 B 、2 C 、0 D 、-24、If f 1(t ) ←→F 1(jω), f 2(t ) ←→F 2(jω) Then[ ]A 、[a f 1(t ) + b f 2(t ) ] ←→ [a F 1(jω) *b F 2(jω) ]B 、[a f 1(t ) + b f 2(t ) ] ←→ [a F 1(jω) - b F 2(jω) ]C 、[a f 1(t ) + b f 2(t ) ] ←→ [a F 1(jω) + b F 2(jω) ]D 、[a f 1(t ) + b f 2(t ) ] ←→ [a F 1(jω) /b F 2(jω) ]5、下列说法不正确的是()。
A 、H(z)在单位圆内的极点所对应的响应序列为衰减的。
即当k→∞时,响应均趋于0。
B 、H(z)在单位圆上的一阶极点所对应的响应函数为稳态响应。
东南大学《信号与系统》期末试卷及习题集合集_wrapper

东南大学《信号与系统》目录东南大学《信号与系统》考试试卷(一) (2)东南大学《信号与系统》考试试卷(一)参考答案 (5)东南大学《信号与系统》考试试卷(二) (9)东南大学《信号与系统》考试试卷(二)参考答案 (14)东南大学《信号与系统》考试试卷(三) (21)东南大学《信号与系统》考试试卷(三)参考答案 (31)东南大学《信号与系统》考试试卷(四) (34)东南大学《信号与系统》考试试卷(四)参考答案 (55)东南大学《信号与系统》考试试卷(五) (57)东南大学《信号与系统》题库及参考答案 (63)东南大学《信号与系统》考试试卷(一)课程名称考试学期得分 适用专业 微电、物理、 考试形式 闭卷考试时间 120分钟姓名班级学号一、选择题(每小题可能有一个或几个正确答案,将正确的题号填入[ ]内) 1.f (5-2t )是如下运算的结果————————( ) (A )f (-2t )右移5 (B )f (-2t )左移5 (C )f (-2t )右移25 (D )f (-2t )左移252.已知)()(),()(21t u e t f t u t f at-==,可以求得=)(*)(21t f t f —————()(A )1-ate - (B )ate-(C ))1(1at e a -- (D )at e a-13.线性系统响应满足以下规律————————————( )(A )若起始状态为零,则零输入响应为零。
(B )若起始状态为零,则零状态响应为零。
(C )若系统的零状态响应为零,则强迫响应也为零。
(D )若激励信号为零,零输入响应就是自由响应。
4.若对f (t )进行理想取样,其奈奎斯特取样频率为f s ,则对)231(-t f 进行取样,其奈奎斯特取样频率为————————( )(A )3f s (B )s f 31 (C )3(f s -2) (D ))2(31-s f 5.理想不失真传输系统的传输函数H (jω)是 ————————( )(A )0j tKeω- (B )0t j Keω- (C )0t j Keω-[]()()c c u u ωωωω+--(D )00j t Keω- (00,,,c t k ωω为常数)6.已知Z 变换Z 1311)]([--=zn x ,收敛域3z >,则逆变换x (n )为——( )(A ))(3n u n(C )3(1)nu n -(B ))(3n u n -- (D ))1(3----n u n二.(15分)已知f(t)和h(t)波形如下图所示,请计算卷积f(t)*h(t),并画出f(t)*h(t)波形。
东南大学通信初试真题大合集(信号系统 逻辑)

四、(10 分)试叙述并证明傅里叶变换的卷积性质。
共5页 第 2 页
试题编号: 420
试题名称: 专业基础综合
第二部分 “数字电路” 50分 一、(15 分)在输入信号 A、B、C、D 的作用下,产生输出信号 F,波形如(图 1)所
图 2-1 二、(15 分)分析如图 2-2 所示的电路,写出电路的状态转移方程,做出状
态转移表,和在 CP 作用下 Q3、Q2、Q1 的输出波形(设初始状态均为 0)
图 2-2
共5页 第4页
试题编号: 420
试题名称: 专业基础综合
三、(10 分)图 2-3 为 PAL16L8 的一部分电路,试分析该电路,写出电路在 X
控制下的函数 F 对应于输入 A、B、C 的逻辑表达式。
图 2-3
四、(15 分)试用下降沿 D 触发器和适当的门电路设计一 1101 序列检测器, 该检测器有一个输入端,一个输出端。当输入的序列为 1101 时,输出为 1; 在其他输入时,输出为 0。
附:7485 功能表
A3 B3 A2 B2 A1 B1 A0 B0 A>B A<B A=B
+ e(t )
-
U +
c
(t
) -
1F +
1Ω
y(t ) -
(a)
e(t ) 1
e −( t−1)
1
t
(b)
图 1-1
Байду номын сангаас
四 (12 分)已知某线性系统框图如图 1-2 所示。其中系统 H(f)的频域传输函数 为
H( f ) = [ε ( f −15) −ε ( f ] +15) e− j2 f (f 为自然频率, f = ω )
《信号与系统》习题参考答案

《信号与系统》习题参考答案(1)2—1(1) 01()()()()(1)()ta at x t h t x u t d e d e u t aτττττ∞---∞*=⋅-==-⎰⎰ (2) 00()()(cos sin )()x t h t t d ωτωτδττ∞-∞*=+⋅-⎰0000(cos sin )()cos sin t t t d t t ωωδττωω∞-∞=+⋅-=+⎰(3) 当0t <时 ()()0x t h t *=当01t ≤<时 20()()(1)2tt x t h t d t ττ*=+=+⎰当12t ≤<时 13()()(1)2x t h t d ττ*=+=⎰ 当23t ≤<时 12213()()(1)22t x t h t d t t ττ-*=+=-++⎰ 当3t ≥时 ()()0x t h t *= (4) 当0t <时 ()()0x t h t *=当0t ≥时 01()()sin 2(1cos 2)2tx t h t d t ττ*==-⎰ (5) 22222(2)2(4)241()()(2)2t t t t t t t x t h t e d e d e ee ττττ-----*=-=-+⎰⎰ (6)()x t at b =+11212()()()()()(2)3363tt x t h t a b d a tb t a t a bττδ-*=+++*--=++⎰2—2(1) [][][][2](2)[2]x n h n nu n n n u n δ*=*-=--(2) 10[][](2)[](21)[]nin i x n h n u n u n +=*==-∑(3) 当0n ≥时 1111[][]2()()232i n in i x n h n --=-∞*==∑ 当0n <时 111[][]2()223n i n i n i x n h n --=-∞*==⋅∑ (4) 当0n <时 [][]0x n h n *=当0n ≥时 110[][]()[]n n nin ii x n h n u n βααββα++-=-*==-∑(5) 当07n ≤≤时 071[][](1)[1(1)]2in i n x n h n -=-*=-=--∑ 当70n -≤≤时 71[][](1)[(1)1]2ni n i x n h n -=-*=-=--∑ 2—3(1) 12()()[(1)(1)][(5)(5)]x t x t u t u t t t δδ*=+--*++- (6)(4)(4)(6)u t u t u t u t =++--+-- (2) 123()()()x t x t x t **{[(6)(4)][(4)(6)]}*[u t u t u t u t =+-++---11()()]22t t δδ++- ( 6.5)( 4.5)( 5.5)( 3.5)( 3.5)( 5.5)u t u t u t u t u t u t =+-+++-++--- ( 4.5)( 6.5)u t u t +---(3) 1311()()[(1)(1)][()()]22x t x t u t u t t t δδ*=+--*++- ( 1.5)(0.5)(0.5)( 1.5)u t u t u t u t =+--++-- 2—4 0(3)331()(3)1t k k t tk k y t eu t k e e e e∞-----=-∞=-∞=-=⋅=-∑∑311A e-=- 2—5(1) 当2t ≥时 ()()0x t h t *= 当20t -<<时 11()()2t x t h t d t τ+-*==+⎰当02t <<时 11()()2t x t h t d t τ-*==-⎰(2) 当01t <<时 1()()22(1)tx t h t d t τ*==-⎰ 当10t -<<时 01()()22(1)2t tx t h t d d t t t ττ+*=+=-++=+⎰⎰当21t -<<-时 11()()2t x t h t d t τ+-*==+⎰当 1t ≥ 或 2t <-时 ()()0x t h t *=此题也可利用性质,先对()x t 积分,对()h t 微分,'()()()y t x t dt h t =*⎰(3) 当0t <时 (1)1()()1t x t h t e dt +∞--*==⎰当0t ≥时 1(1)(1)11()()22t t t t t x t h t e dt e dt e ++∞-----+*=+=-⎰⎰(4) 当t π< 或 5t π>时 ()()0x t h t *= 当3t ππ<<时 0()()sin 1cos t x t h t d t πττ-*==+⎰当35t ππ<<时 23()()sin 1cos t x t h t d t ππττ-*==--⎰(5) 当01t <<时 2211()()222()22x t h t t t t *=-=--当12t <≤时 2231()()264[2()]22x t h t t t t *=-+-=---()()x t h t *是以2为周期的周期函数 2—7(1) 111[][1]()[]()[1]22nn h n Ah n u n A u n ---=--111()[()()][1]()22nn n A u n n δδ-=+--=12A =(2) 111[][][][1][][]h n h n Ah n h n h n n δ---*-*-=*11[][][1]2h n n n δδ-∴=-- (3) 11[][][]2[[][1]][]nx n h n h n u n u n h n --**=--* 2[]2[[][4]]2[[1][5]]nn x n u n u n u n u n -∴=------2—8(1) 0()3()y t y t =(2) 00()()(2)y t y t y t =-- (3) 0()(1)y t y t =- (4) 0()()y t y t =-(5) 0()()dy t y t dt=(6) 202()()d y t y t dt =2—9 12111[][]()[]()[1]222n n x n h n u n u n -*=-+--1()([][1])[]2nu n u n n δ=---=1221[][][][]([][])*[]y n x n h n h n x n h n h n =**=* []*([][])[][]n n n n n u n u n u n u n δαβαβ=+=+ 2—10(1) 341201[][]((0.5))[3]2(1())[3]2n nn n x n x n u n u n ++=*=+=-+∑ (2) 4123[][][]2(1(0.5))[3]([][1])n x n x n x n u n n n δδ+**=-+*-- 43312(1(0.5))[3]2(1(0.5))[2]()[3]2n n n u n u n u n +++=-+--+=+ (3) 23[][][3]([][1])[3][2][3]x n x n u n n n u n u n n δδδ*=+*--=+-+=+ 2—11(1) 12345[][]([][][])[]h n h n h n h n h n h n =*-*+ (2) 34[][][1]h n h n nu n *=- 234[][][](1)[][1][]h n h n h nn u n n u n u n -*=+--= 12345[][]([][][])[]h n h n h n h n h n h n =*-*+514()([][3])*[][]2nu n u n u n hn =--+ 4[]6[1]7[2][]4[3]5[]6[1]7[2]4[3]n n u n n n n n u n n δδδδδδδ=+-+-++-=+-+---(1)'()()(2)(2)()(2)tt y t e x d x t y t x t τττ---∞=--+-=-+-⎰(2)()(2)t h t eu t --=- (2)当1t ≤时 ()0y t =当14t <≤时 1(2)(1)2()1t t y t e d e ττ+----==-⎰当4t >时 1(2)(4)(1)2()t t t t y t e d e e ττ+-------==-⎰2—13(1)213()()()()(1)[()](1)[()](1)h t h t h t u t t t u t t u t δδδ**=*-*-=-*-=-- 1213()()()()()()(1)h t h t h t h t h t u t u t =+**=--(2)1(10)1(02)()3(23)0t t t y t t t +-<<⎧⎪<<⎪=⎨-<<⎪⎪⎩其余2—14(1)因果、稳定 (2)非因果、非稳定 (3)非因果、稳定 (4)非因果、稳定 (5)非因果、稳定 (6)因果、稳定 (7)因果、非稳定 2—15(1)因果、稳定 (2)非因果、稳定 (3)非因果、非稳定 (4)非因果、稳定 (5)因果、非稳定 (6)非因果、稳定 (7)因果、稳定 2—16(1)对 (2)对()h t dt ∞-∞=+∞⎰(3)错 例如单位冲激响应(1)t δ-是因果的,但LTI 系统的逆系统(1)t δ+不是因果的。
大学科目《信号与系统》各章节习题答案
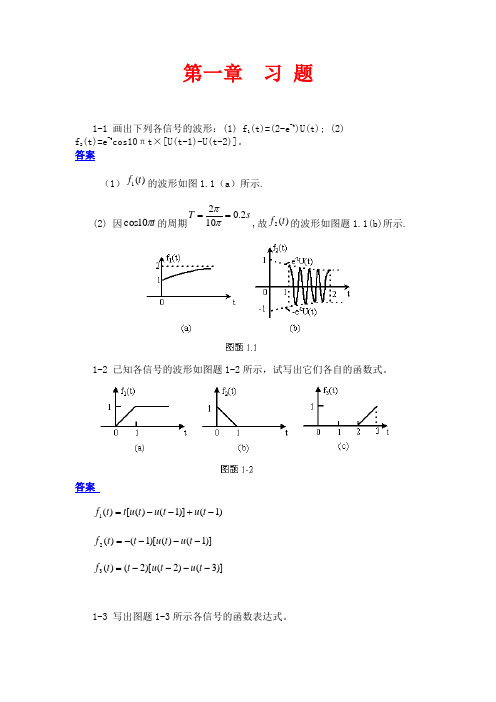
第一章 习 题1-1 画出下列各信号的波形:(1) f 1(t)=(2-e -t )U(t); (2) f 2(t)=e -t cos10πt×[U(t -1)-U(t-2)]。
答案(1))(1t f 的波形如图1.1(a )所示.(2) 因t π10cos 的周期s T 2.0102==ππ,故)(2t f 的波形如图题1.1(b)所示.1-2 已知各信号的波形如图题1-2所示,试写出它们各自的函数式。
答案)1()]1()([)(1-+--=t u t u t u t t f)]1()()[1()(2----=t u t u t t f)]3()2()[2()(3----=t u t u t t f1-3 写出图题1-3所示各信号的函数表达式。
答案2002121)2(21121)2(21)(1≤≤≤≤-⎪⎩⎪⎨⎧+-=+-+=+=t t t t t t t f)2()1()()(2--+=t u t u t u t f)]2()2([2sin )(3--+-=t u t u t t f π)3(2)2(4)1(3)1(2)2()(4-+---++-+=t u t u t u t u t u t f1-4 画出下列各信号的波形:(1) f 1(t)=U(t 2-1); (2) f 2(t)=(t-1)U(t 2-1);(3) f 3(t)=U(t 2-5t+6); (4)f 4(t)=U(sinπt)。
答案(1) )1()1()(1--+-=t u t u t f ,其波形如图题1.4(a)所示.(2))1()1()1()1()]1()1()[1()(2---+--=--+--=t u t t u t t u t u t t f 其波形如图题1.4(b)所示.(3))3()2()(3-++-=t u t u t f ,其波形如图1.4(c)所示.(4) )(sin )(4t u t f π=的波形如图题1.4(d)所示.1-5 判断下列各信号是否为周期信号,若是周期信号,求其周期T 。
《信号与系统》考研试题解答第二章连续系统的时域分析

第二章 连续系统的时域分析一、单项选择题X2.1(东南大学2002年考研题)一线性时不变连续时间系统,其在某激励信号作用下的自由响应为(e -3t +e -t )ε(t ),强迫响应为(1-e -2t )ε(t ),则下面的说法正确的是 。
(A )该系统一定是二阶系统 (B )该系统一定是稳定系统(C )零输入响应中一定包含(e -3t +e -t )ε(t ) (D )零状态响应中一定包含(1-e -2t )ε(t )X2.2(西安电子科技大学2005年考研题)信号f 1(t )和 f 2(t ) 如图X2.2所示,f =f 1(t )* f 2(t ),则 f (-1)等于 。
(A )1 (B )-1 (C )1.5 (D )-0.5图X2.2X2.3(西安电子科技大学2005年考研题)下列等式不成立的是 。
[])()(*)()()()(*)()()(*)()(*)()()(*)()(*)()(2121210201t f t t f D t f t t f C t f dt d t f dt d t f t f dt d B t f t f t t f t t f A ='='⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡==+-δδ答案:X2.1[D],X2.2[C],X2.3[B]二、判断与填空题T2.1(北京航空航天大学2001年考研题)判断下列说法是否正确,正确的打“√”,错误的打“×”。
(1)若)(*)()(t h t f t y =,则)2(*)2(2)2(t h t f t y =。
[ ] (2)如果x (t )和y (t )均为奇函数,则x (t )*y (t )为偶函数。
[ ] (3)卷积的方法只适用于线性时不变系统的分析。
[ ] (4)若)(*)()(t h t f t y =,则)(*)()(t h t f t y --=-。
[ ](5)两个LTI 系统级联,其总的输入输出关系与它们在级联中的次序没有关系。
大学考试试卷《信号与系统》及参考答案

信号与系统一、单项选择题(本大题共46分,共 10 小题,每小题 4.599999 分)1. 若一因果系统的系统函数为则有如下结论——————————() A. 若,则系统稳定 B. 若H(s)的所有极点均在左半s平面,则系统稳定 C. 若H(s)的所有极点均在s平面的单位圆内,则系统稳定。
2. 连续信号,该信号的拉普拉斯变换收敛域为()。
A.B.C.D.3. 连续信号与的乘积,即*=( )A.B.C.D.4. 已知f(t),为求f(t0−at) 应按下列哪种运算求得正确结果?(式中t,a都为正值) A. f(-at)左移t0 B. f(-at) 右移tC. f(at) 左移D. f(at)右移5. 已知 f(t),为求f(t0-at) 应按下列哪种运算求得正确结果?(式中t,a都为正值) A.B. f(at) 右移t0 C. f(at) 左移t/a D. f(-at) 右移t/a6. 系统函数H(s)与激励信号X(s)之间——() A. 是反比关系; B. 无关系; C. 线性关系; D. 不确定。
7. 下列论断正确的为()。
A. 两个周期信号之和必为周期信号; B. 非周期信号一定是能量信号; C. 能量信号一定是非周期信号; D. 两个功率信号之和仍为功率信号。
8. 的拉氏反变换为()A.B.C.D.9. 系统结构框图如下,该系统单位冲激响应h(t)的表达式为()A.B.C.D.10. 已知,可以求得—————()A.B.C.D.二、多项选择题(本大题共18分,共 3 小题,每小题 6 分)1. 线性系统响应满足以下规律————————————() A. 若起始状态为零,则零输入响应为零。
B. 若起始状态为零,则零状态响应为零。
C. 若系统的零状态响应为零,则强迫响应也为零。
D. 若激励信号为零,零输入响应就是自由响应。
2. 1.之间满足如下关系———————()A.B.C.D.3. 一线性时不变因果系统的系统函数为H(s),系统稳定的条件是——()A. H(s)的极点在s平面的单位圆内B. H(s)的极点的模值小于1C. H (s)的极点全部在s平面的左半平面D. H(s)为有理多项式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
东 南 大 学 考 试 卷(A 、B 卷)(答案附后)课程名称 信号与线性系统 考试学期 03-04-3得分适用专业 四系,十一系考试形式闭卷考试时间长度 120分钟一、简单计算题(每题8分):1、 已知某连续信号()f t 的傅里叶变换为21()23F j j ωωω=-+,按照取样间隔1T =对其进行取样得到离散时间序列()f k ,序列()f k 的Z 变换。
2、 求序列{}10()1,2,1k f k ==和2()1cos ()2f k k k πε⎡⎤⎛⎫=+ ⎪⎢⎥⎝⎭⎣⎦的卷积和。
3、 已知某双边序列的Z 变换为21()1092F z z z =++,求该序列的时域表达式()f k 。
4、 已知某连续系统的特征多项式为:269111063)(234567+++++++=s s s s s s s s D试判断该系统的稳定情况,并指出系统含有负实部、零实部和正实部的根各有几个?5、 已知某连续时间系统的系统函数为:3232642()21s s s H s s s s +++=+++。
试给出该系统的状态方程。
6、 求出下面框图所示离散时间系统的系统函数。
)(k二、(12分)已知系统框图如图(a ),输入信号e(t)的时域波形如图(b ),子系统h(t)的冲激响应波形如图(c)所示,信号()f t 的频谱为()jn n F j eπωω+∞=-∞=∑。
图(a)y(t))(t fe(t)图(b)h(t)图(c)试:1) 分别画出)(t f 的频谱图和时域波形;2) 求输出响应y(t)并画出时域波形。
3) 子系统h(t)是否是物理可实现的?为什么?请叙述理由;三(12分)、已知电路如下图所示,激励信号为)()(t t e ε=,在t=0和t=1时测得系统的输出为1)0(=y ,5.0)1(-=e y 。
分别求系统的零输入响应、零状态响应、全响应、以及自然响应和受迫响应。
L=2HC=1F+_四(12分)、已知某离散系统的差分方程为)1()()1(3)2(2+=++-+k e k y k y k y 其初始状态为6)2(,2)1(-=--=-zi zi y y ,激励)()(k k e ε=;求:1) 零输入响应)(k y zi 、零状态响应)(k y zs 及全响应)(k y ;2) 指出其中的自由响应分量和受迫响应分量; 3) 判断该系统的稳定性。
五(12分)、已知某离散时间系统的单位函数响应()cos ()2k h k k πε⎛⎫= ⎪⎝⎭。
1) 求其系统函数()H z ; 2) 粗略绘出该系统的幅频特性; 3) 画出该系统的框图。
六、(10分)请叙述并证明z变换的卷积定理。
答案1、 已知某连续信号()f t 的傅里叶变换为21()23F j j ωωω=-+,按照取样间隔1T =对其进行取样得到离散时间序列()f k ,序列()f k 的Z 变换。
解法一:f(t)的拉普拉斯变换为2111)2)(1(1321)(2+-+=++=++=s s s s s s s F ,2111)(Re )(--===---=-=⎥⎦⎤⎢⎣⎡-=∑∑e z z e z z e z z K e z z s F s z F ni T s i s s ni sT i i解法二:f(t)=L -1{F(jw)}=(e -t - e -2t )ε(t) f(k)= (e -k - e -2k )ε(k)=)())()((21k e e k k ε---F(z)=Z[f(k)]= 21-----e z zez z 2、 求序列{}10()1,2,1k f k ==和2()1cos ()2f k k k πε⎡⎤⎛⎫=+ ⎪⎢⎥⎝⎭⎣⎦的卷积和。
解:f 1(k)={1,2,1}=δ(k)+2δ(k -1)+ δ(k -2)f 1(k)* f 2(k)= f 2(k)+ 2f 2(k -1)+ f 2(k -2) 3、已知某双边序列的Z 变换为21()1092F z z z =++,求该序列的时域表达式()f k 。
解:5.014.01)(+-+=z z z F ,两个单阶极点为-0.4、-0.5当收敛域为|z|>0.5时,f(k)=(( -0.4)k -1-( -0.5)k -1)ε(k -1)当收敛域为0.4<|z|<0.5时,f(k)= ( -0.4)k -1ε(k -1)+( -0.5)k -1ε( -k) 当收敛域为|z|<0.4时,f(k)= - ( -0.4)k -1ε(-k)+( -0.5)k -1ε( -k)点评:此题应对收敛域分别讨论,很多学生只写出第一步答案,即只考虑单边序列。
4、已知某连续系统的特征多项式为:269111063)(234567+++++++=s s s s s s s s D试判断该系统的稳定情况,并指出系统含有负实部、零实部和正实部的根各有几个?解 构作罗斯-霍维茨阵列611617s 291036s3168385s 2314s 342(00)32s s s ++此时出现全零行,有辅助多项式34646,4,6ss +求导可得以代替全零行系数。
210322232s s s由罗斯-霍维茨数列可见,元素符号并不改变,说明s 右半平面无极点。
再由42320s s ++=令2s x =则有2320x x ++=可解得 1,2x =--相应地有1,2s ==±j3,4s ==±这说明该系统的系统函数在虚轴上有四个单极点分别为土j 及土,系统为临界稳定。
所以系统含有三个负实部的根、四个零实部的根,无正实部的根。
点评:此题得分率很低。
很多学生对全零行不知如何处理。
5、已知某连续时间系统的系统函数为:3232642()21s s s H s s s s +++=+++。
试给出该系统的状态方程。
解:系统的微分方程为)(2)(4)(6)()()()(2)(t e t e t e t e t y t y t y t y +'+''+'''=+'+''+'''取原来的辅助变量q 及其各阶导数为状态变量并分别表示为1x q =、2'x q =、3''x q =、''''3x q =,于是,由此微分方程立即可以写出如下方程状态方程:⎪⎩⎪⎨⎧+---===)(2'''32133221t e x x x x x x x x 输出方程:)(436423213213t e x x x x x x x y +++=+++'=或者写成矩阵形式,上式即为e x x x x x x ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=+=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡100211010100'''321321Be Ax ``[])(431321t e x x x y +⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=+=De Cx6、求出下面框图所示离散时间系统的系统函数。
)(k解:06.05.03.22.01)3.021()(2+++=+++=z z z z z z H二、(12分)已知系统框图如图(a ),输入信号e(t)的时域波形如图(b ),子系统h(t)的冲激响应波形如图(c)所示,信号()f t的频谱为()jn n F j eπωω+∞=-∞=∑。
图(a)y(t))(t fe(t)图(b)h(t)图(c)试:1) 分别画出)(t f 的频谱图和时域波形;2) 求输出响应y(t)并画出时域波形。
3) 子系统h(t)是否是物理可实现的?为什么?请叙述理由;解:1)根据傅立叶变换的性质得:∑∞-∞=-=n n t t f )2()(δ∑∞-∞=-=n n j F )()(πωδπω2)y(t)=[e(t)•f(t)]*h(t)=[δ(t+2)+2δ(t)+ δ(t -2)] *h(t)= h(t+2)+2h(t)+ h(t -2)3)因h(t)是有始因果信号,所以子系统h(t)是物理可实现的。
点评:此题做对的非常少,大多数写不出f(t)的表达方式。
三(12分)、已知电路如下图所示,激励信号为)()(t t e ε=,在t=0和t=1时测得系统的输出为1)0(=y ,5.0)1(-=e y 。
分别求系统的零输入响应、零状态响应、全响应、以及自然响应和受迫响应。
L=2HC=1F+_解:1)电路满足KVL :得)(5.0)(5.0)(5.1)(t e t y t y t y '=+'+''2)系统函数为:5.05.15.0)(2++=s s ss H ,特征根为λ1=-0.5,λ2=-1 Y zs (s)=H(s)E(s)= s s s s 15.05.15.02•++=115.01+-+s s零状态响应:y zs (t)=(e -0.5t -e -t )ε(t) y zs (0)=0,y zs (1)=(e -0.5 -e -1);y zi (0)= y(0) -y zs (0)=1,y zi (1)= y(1) -y zs (1)= -e -1 ;y zi (t)=(C 1e -0.5t +C 2e -t )ε(t),得C 1=0,C 2=1零输入响应:y zi (t)= e -t ε(t);全响应:y (t)= e -0.5t ε(t)点评:此题中很多学生把全响应初始条件当成零输入响应的初始值来解答,失去少部分分数。
四(12分)、已知某离散系统的差分方程为)1()()1(3)2(2+=++-+k e k y k y k y其初始状态为6)2(,2)1(-=--=-zi zi y y ,激励)()(k k e ε=;求:1) 零输入响应)(k y zi 、零状态响应)(k y zs 及全响应)(k y ;2) 指出其中的自由响应分量和受迫响应分量;3) 判断该系统的稳定性。
解:132)(2+-=z z z z H ,特征根为ν1=0.5,ν2=1 1) y zi (k)=(C 10.5k +C 2)ε(k);代入初始条件得C 1=-2,C 2=2零输入响应:y zi (k)= (2-20.5k )ε(k)Y zs (z)=H(z)E(z)= 22)1(15.01132-+---=-•+-z z z z z z z z z z z =115.01+-+s s零状态响应:y zs (k)= (0.5k +k -1)ε(k)y zs (0)=0,y zs (1)=(e -0.5 -e -1);全响应:y (k)= (1+k -0.5k )ε(k)2)自由响应:(1 -0.5k )ε(k)受迫响应:k ε(k),严格地说是混合响应。
