截面应力验算
MIDAS中的psc验算

斜截面抗裂验算
6.3.1(第2条) 6.3.3
裂缝宽度验算
6.4.2~6.4.4
挠度验算
6.5.1~6.5.4
正截面砼的法向压应力验 算
6.1.5,6.1.6 7.1.3,7.1.4 7.1.5
斜截面砼的主压应力验算
7.1.6,7.1.3 7.1.4,7.1.5
受拉区钢筋的拉应力验算
7.1.3, 7.1.4 7.1.5
梁 (受弯)
梁 (受弯)
程序验算结果与规范中相应条文的对应关系
验算内容
规范条款
备注
程序
表2 对应程序内的验算
正截面抗弯验算 斜截面抗剪验算 斜截面抗弯验算
5.2.2~5.2.5 5.2.6~5.2.11 5.2.12
适用于全预应力、A类、B类构件 适用于全预应力、A类、B类构件
是 7.使用阶段正截面抗弯验算 是 8.使用阶段斜截面抗剪验算 否
2) 受拉区钢筋拉应力验算:表中应力拉为正,压为负。 3) 使用阶段正截面法向应力验算:
- 表中应力压为正,拉为负。 - 最大、最小分别指的是压应力和拉应力的验算。本项验算结果表格中包含了规范里
面两项验算内容,即正截面抗裂验算和正截面砼的法向压应力验算,其中表格中“最 大/最小”位置显示“最小”的为正截面抗裂验算结果,表格中“最大/最小”位置 显示“最大”的为正截面砼的法向压应力验算。如果用户想分别查看两项验算结果 或者整理计算书时分开整理,可以只激活“最大”的结果或者“最小”的结果。下 面第4项、第5项验算内容和第3项内容类似,也是对应着规范里面两项验算内容, 查看时可以参考本条说明。在Civil 6.7.1中将把两项验算结果分开在两个表格里面 查看。 - 表格中“组合名称”项表示最大最小值所属的荷载组合 - 表格中“类型”项表示所属荷载组合中(包含移动荷载)显示的内力项最大时,会产 生所需的最大最小值。(当有移动荷载、支座沉降组分析时,程序计算了所有荷载工 况的6项内力及每项内力的最大最小两项,即对每一种荷载工况计算6*2=12次,表 格中的结果采用的是同时发生的内力计算的)。 4) 使用阶段斜截面应力验算(剪力最大时): - 表中应力压为正,拉为负。 - 最大、最小分别指的是压应力和拉应力的验算。 - 表格中“组合名称”项表示最大最小值所属的荷载组合 - 程序实现验算所有荷载工况下的斜截面应力并不困难,但是由于验算的工况太多, 计算时间可能很长。由于最大主拉应力一般都发生在腹板受最大剪应力的时候,而 腹板剪应力主要由剪力和扭矩产生,因而程序选择了剪力最大时和扭矩最大时两种 工况验算斜截面应力。 5) 使用阶段斜截面应力验算(扭矩最大时):表中应力压为正,拉为负。最大、最小分别 指的是压应力和拉应力的验算。其余说明同4)项。 6) 使用阶段裂缝宽度验算:最大、最小指的是不同荷载组合产生的截面弯距的最大、最小 值。在此需注意的是梁上部受拉时也会发生裂缝,程序将对此提供验算(最小项)。 7) 使用阶段正截面抗弯验算:最大、最小指的是不同荷载组合产生的截面弯矩的最大、最 小值。 8) 使用阶段斜截面抗剪验算:最大、最小指的是不同荷载组合产生的截面剪力的最大、最 小值。不同荷载组合下剪力的方向可能会发生变化,且弯矩变号会引起梁计算高度hB0B发 生变化(因为梁顶和梁底的钢筋中心距截面外端距离可能不一样),所以有必要验算剪力 最大和最小两种情况。 9) 使用阶段抗扭验算。最大最小项无意义。
管道应力分析和计算

管道应力分析和计算目次1 概述1.1 管道应力计算的主要工作1.2 管道应力计算常用的规范、标准1.3 管道应力分析方法1.4 管道荷载1.5 变形与应力1.6 强度指标与塑性指标1.7 强度理论1.8 蠕变与应力松弛1.9 应力分类1.10 应力分析2 管道的柔性分析与计算2.1 管道的柔性2.2 管道的热膨胀补偿2.3 管道柔性分析与计算的主要工作2.4 管道柔性分析与计算的基本假定2.5 补偿值的计算2.6 冷紧2.7 柔性系数与应力增加系数2.8 作用力和力矩计算的基本方法2.9 管道对设备的推力和力矩的计算3 管道的应力验算3.1 管道的设计参数3.2 钢材的许用应力3.3 管道在内压下的应力验算3.4 管道在持续荷载下的应力验算3.5 管道在有偶然荷载作用时的应力验算3.6 管系热胀应力范围的验算3.7 力矩和截面抗弯矩的计算3.8 应力增加系数3.9 应力分析和计算软件1 概述1.1 管道应力计算的主要工作火力发电厂管道(以下简称管道)应力计算的主要工作是验算管道在内压、自重和其他外载作用下所产生的一次应力和在热胀、冷缩及位移受约束时所产生的二次应力;判断计算管道的安全性、经济性、合理性,以及管道对设备产生的推力和力矩应在设备所能安全承受的范围内。
管道的热胀应力应按冷、热态的应力范围验算。
管道对设备的推力和力矩应按冷状态下和工作状态下可能出现的最大值分别进行验算。
1.2 管道应力计算常用的规范、标准(1)DL/T 5366-2006火力发电厂汽水管道应力计算技术规程(2)ASME B 31.1-2004动力管道在一般情况下,对国内工程采用DL/T 5366进行管道应力验算。
对涉外工程或顾客有要求时,采用B 31.1进行管道应力验算。
1.3 管道应力分析方法管道应力分析方法分为静力分析和动力分析。
对于静荷载,例如:管道内压、自重和其他外载以及热胀、冷缩和其他位移荷载作用的应力计算,采用静力分析法。
正截面验算

梁、板常用混凝土强度等级为C20、C25、C30、C35、 C40; 二)钢筋
1、梁箍筋常用HPB235级、 HRB335级、 HRB400级,主筋常用HRB335级、 HRB400级;
2、板常用HPB235级、HRB335级、 HRB400 级,其中HRB400级用于板中经济指标较好。
三)梁内钢筋直径及间距:
Mu
1.0
0.8 My II a
0.6
II
0.4
III III a
M cr I a
I
0
f cr
fy
fu f
加载过程中弯矩-曲率关系
M/Mu
1.0 Mu 0.8 My
Ⅱa Ⅲ
0.6 Ⅱ
0.4
Mcr
Ⅰa Ⅰ
0
M/Mu
1.0 Mu 0.8 My
0.6
0.4
Mcr
0
fcr
fy
Ⅲa
f
fu f
M/Mu
1.0 Mu 0.8 My
二、常用梁、板的截面尺寸
一)、梁的宽度和高度
1、为统一模板尺寸、便于施工,通常采用:
梁宽度b=120、150、180、200、220、250、300、 350、…(mm) 梁高度h=250、300、……、750、800、 900、…(mm)。 2、出于平面外稳定的考虑,梁截面高宽比作 出一定要求:
Ⅱa Ⅲ
Ⅲa
0.6 Ⅱ
0.4
Mcr
Ⅰa Ⅰ
0
y
s
裂缝开裂前--第一阶段,界
限Ia
钢筋屈服前--第二阶段,界
限IIa
梁破坏(混凝土压碎)--第
三阶段,界限IIIa
截面应力的计算

A
d
3 00
C
a
B F
一、应力的概念
10KN A=10mm2
10KN
10KN 受力杆件某截面上一点的内力分布疏密 程度,内力集度. A=100mm2
G
´
d d G G G dx dx
d G dx
3. 静力学关系 dA
2
d T A dA A G dA dx d G A 2 dA dx
O
令I p A dA
应力的国际单位为N/m2 (帕斯卡) 1N/m2=1Pa 1MPa=106Pa=1N/mm2 1GPa=109Pa
—位于截面内的应
力称为“ 切应力”
二、拉(压)杆横截面上的应力与应变
变形规律试验:
FP
FP’
观察发现:当杆受到轴向拉力作用后,所有的纵向线 都伸长了,而且伸长量都相等,并且仍然都与轴线平行; 所有的横向线仍然保持与纵向线垂直,而且仍为直线,只 是它们之间的相对距离增大了。
10KN
哪个杆先破坏?
工程构件,大多数情形下,内力并非均匀分布, 集度的定义不仅准确而且重要,因为“ 破坏” 或“失效”往往从内力集度最大处开始。
应力就是单位面积上的力?
F1
P
DF
ΔA
σ
DF P DA
F2
p lim
DF DA
DA0
dF dA
midas学习_PSC_截面设计验算

MIDAS/Civil 6.7.1 PSC 截面设计验算功能说明
1.程序给出的验算结果
程序一共给出了 12 项验算结果,如下所列。根据“PSC 设计参数”中“截面设计内力”
和“构件类型”选定的内容的不同,给出的具体验算内容是不同的,详见表 1。
1) 施工阶段正截面法向应力验算
- 在进行裂缝宽度验算时应注意以下两点:1、必须设置PSC截面钢筋,否则程序不予 进行裂缝宽度验算。2、在荷载工况中必须有活荷载或移动荷载,否则裂缝宽度验 算不予输出计算结果。
- 设计结果表格中最大、最小指的是不同荷载组合产生的截面弯距的最大、最小值。
-5-
MIDAS Civil V6.7.1 技术资料 在此需注意的是梁上部受拉时也会发生裂缝,程序将对此提供验算(最大即顶部)。 - 当截面的上下缘混凝土应力均为压应力时,该截面处不会出现裂缝宽度,裂缝宽度 结果为0。 - 当各荷载组合在该截面处始终不会产生拉应力,那么这个该截面不存在出现裂缝的 可能,因此在PSC设计中对该截面的裂缝宽度不予验算,输出结果以“—”表示。 - 其他关于设计表格的说明同第3)项。 8) 普通钢筋估算:(对应规范5.2.2~5.2.5)
不提供第 7)、8)项验 算
不提供第 7) 、8)项验算
部分预应力 A类
不提供第 7)、12)项验算
不提供第 7)项验算 不提供第 7)项验算
部分预应力 B类
不提供第 3)、12)项验算
不提供第 3)项验算
* 以上不提供验算的项目均为规范中不要求验算的内容
不提供第 3)项验算
6.7.1 版验算内容与 6.7.0 版验算内容对应关系
- 按照公式(6.3.3-1)~(6.3.3-4)计算由作用(或荷载)短期效应组合和预加力产生
MIDASCivil 6.7.0 PSC截面验算功能说明

5) 同一钢束组里面包含的预应力钢束必须具有相同的钢束特性值。否则会提示以下错误信 息“钢束组中有其他类型的钢束材料”。
6) 程序默认水平的梁单元按照梁设计,竖直的梁单元按照柱设计,对于倾斜的梁单元如果 想按照梁设计,需要在“设计――一般设计参数――编辑构件类型”中把相应的单元修 改为想采用的构件类型。否则会提示以下错误信息“不是适合的构件类型”。
不同的“PSC设计参数”对应的验算结果
表1
项目
二维
二维+扭矩
全预应力
不提供第5)、6)、9)项验算 不提供第6)项验算
部分预应力A类 不提供第5)、6)、9)项验算 不提供第6)项验算
部分预应力B类 不提供第5) 、9)项验算
全部提供
* 以上不提供验算的项目均为规范中不要求验算的内容
三维 不提供第6)项验算 不提供第6)项验算 全部提供
预钢筋端部锚固区、墩顶 正截面拉应力验算 (仅适用于全预应力和A类构件) 斜截面砼主拉应力验算 (适用于全预应力、A类、B类构件) 仅适用于B类构件
7.1.3适用于全预应力和A类构件 7.1.4适用于B类构件
7.1.3适用于全预应力和A类构件 7.1.4适用于B类构件 7.1.3适用于全预应力和A类构件 7.1.4适用于B类构件
斜截面抗裂验算
6.3.1(第2条) 6.3.3
裂缝宽度验算
6.4.2~6.4.4
挠度验算
6.5.1~6.5.4
正截面砼的法向压应力验 算
6.1.5,6.1.6 7.1.3,7.1.4 7.1.5
截面混凝土的正应力验算

截面混凝土的正应力验算根据《公预规》7.1.5条,使用阶段正截面应力应符合下列要求:MPa f ck kc pt cu 2.165.0=≤+=σσσ式中:kc σ——在作用标准效应组合下混凝土的法向压应力,按下式计算:332211ouG ou G nu G kc W M W M W M ++=σ (2-32)1G M 、2G M 、3G M ——标准效应组合的弯矩值,见表2-11的①、②、③栏; 1nu W 、2nu W 、3nu W ——分别取表2-17,截面特性的第一、第二、第三阶段的值。
pt σ——由预应力产生的混凝土法向拉应力,按下式计算:nupn p n P ptW e N A N ∏∏-=σ (2-33)∏p N ——s l P p p A A N ⋅-⋅=∏∏6σσn A 、nu W ——取表2-17,第一阶段的截面特性; pn e ——sl p p s nb s l p nb p p pn A A A y A a y A e ⋅-⋅-⋅--⋅=∏∏66)()(σσσσ。
表2-35示出了正截面混凝土压应力验算的计算过程和结果,最大压应力在3号梁跨中截面下缘,为4.153 MPa>16.2MPa ,可见其结果符合规范要求。
2-35 正截面混凝土压应力验算表项目边梁3号梁跨中 4/L 变化点 支点 跨中4/L 变化点支点 1G M )(m kN ⋅2155.6 1617.67 943.16 0 2286.88 1715.16 1000.62 0 2G M )(m kN ⋅115.15 86.37 50.39 0 230.31 172.73 100.77 0 3G M )(m kN ⋅1061.33 796.00 464.38 0 1061.33 796.00 464.38 0 1nu W )(3m0.5580.5570.5590.6190.5270.5160.5180.5822nu W )(3m 0.590 0.585 0.577 0.627 0.547 0.543 0.535 0.588 3nu W )(3m 0.631 0.625 0.616 0.662 0.628 0.623 0.614 0.659 ∏p N )(kN3071.30 3041.74 3008.85 3176.78 3133.47 3100.40 3064.89 3212.88n A )(2m 0.8140 0.8140 0.8140 1.2496 0.7786 0.7786 0.7786 1.216 pn e )(m1.083 0.981 0.840 0.233 1.063 0.963 0.825 0.226 kc σ)(MPa 5.740 4.3262.527 0 6.451 4.919 2.877 0 pc σ)(MPa-2.188 -1.624 -0.823 1.345 -2.297 -1.802 -0.947 1.394 cu σ)(MPa3.5522.7031.7041.3454.1533.1171.9301.394。
PSC截面设计验算功能说明

验算PSC截面设计功能说明1.程序给出的结果验算设计参数”中“截面设计内力”和“构件类型”选定的内容的不同,给出的PSC项12验算结果,如下所列。
根据“程序一共给出了结果是不同的,详见表验算1。
具体验算1) 施工阶段正截面法向应力验算2) 受拉区钢筋的拉应力* 3) 使用阶段正截面抗裂验算* 使用阶段斜截面抗裂验算4)验算使用阶段正截面压应力* 5)6) 使用阶段斜截面正压应力验算*7) 使用阶段裂缝宽度验算*普通钢筋量估算8)* 预应力钢筋量估算9)使用阶段正截面抗弯验算10)11) 使用阶段斜截面抗剪验算 12) 使用阶段抗扭验算结果说明及与规范中相应条文的对应关系验算2.程序)7.2.7施工阶段正截面法向应力验算:(对应规范,7.2.81)条进行计7.1.3验算时,由预加力和荷载产生的法向应力可分别按照规范第6.1.5条和第进行施工阶段正截面法向应力?条的规定采用。
6.1.4算。
此时,预应力钢筋应扣除相应阶段的预应力损失,荷载采用施工荷载,截面性质按本规范第条的规定。
对计算结果的叠加要满足规范第7.2.8 最大、最小分别代表施工阶段在相应截面产生的正截面混凝土法向压应力和正截面混凝土法向拉应力。
?混凝土最大拉应力值,同时相/最小分别表示的是计算结果的混凝土最大压应力值/设计结果表格中的Sig_MAX针对最大?/容许拉应力。
应的Sig_ALW指的是施工阶段混凝土容许压应力设计结果表格中应力压为正,拉为负。
?。
阶段表示的是该最大最小值所属施工阶段名称(其他符号说明参见联机帮助)?计。
按照规范要求施工阶段混凝土的抗f'ck=0.8fck在计算抗压容许应力时取用的施工阶段混凝土的抗压强度标准值按?用户可以把表格里面的f'ck≠0.8fck压强度标准值应该取施工时实测的立方体抗压强度换算抗压强度标准值,如实测Excel表格中,手动调整容许应力值。
结果拷贝到验算)7.1.5~7.1.3,6.1.4~6.1.3:(对应规范验算受拉区钢筋拉应力2)为按照规范第条)的规定。
截面应力的计算

0
32
O
对于空心圆轴:
IP
D4
32
d 4
32
D4
32
1 4
D
d
D
三、最大切应力:
横截面上边缘点的切应力最大,其值为
令
WP
IP R
max
T W
max
TR IP
式中WP只与截面的几何尺寸和形状有关,称为抗扭截面系数, 单位为mm3或m3。
完成任务:图示的阶梯圆轴。AB段直径d1=120mm,
A
d
300
B
C
a
F
一、应力的概念
10KN A=10mm2
10KN
10KN 受力杆件某截面上一点的内力分布疏密 程度,内力集度.
10KN
A=100mm2
哪个杆先破坏?
工程构件,大多数情形下,内力并非均匀分布, 集度的定义不仅准确而且重要,因为“ 破坏” 或“失效”往往从内力集度最大处开始。
应力就是单位面积上的力?
矩形截面 l k A k=11.3 k= 5.6
1. 拉伸图和应力——应变图
试验机的自动绘图设备,可在试件拉伸过程
中,自动绘出试件所受应力 s =P/A与标距 段相
应的伸长量 △ l/L 的关系曲线。通常称它为拉伸 图。下图为低碳钢的拉伸图。
2、低碳钢拉伸时的力学性能
变形发展的四个阶段:ob;bc;cd;de 10拉伸试验.swf
根据圆轴扭转的平面假设和切应力互等定理、剪切胡 克定律可知:实心圆轴横截面上各点处,只产生垂直于
半径的切应力 ,沿周向大小不变,方向与该截面的扭矩
方向一致。
1. 几何变形方面
衡重式挡土墙计算书

衡重式挡土墙计算书项目名称_____________日期_____________设计者_____________校对者_____________一、示意图:二、基本资料:1.依据规X与参考书目:《水工挡土墙设计规X》(SL379-2007),以下简称《规X》《水工建筑物荷载设计规X》(DL 5077-1997)《水工挡土墙设计》(中国水利水电)2.断面尺寸参数:墙顶宽度B1 = 0.60m,前趾宽度B2 = 0.40m,衡重台宽度B3 = 2.90m墙身高度H = 4.70m,上墙高度H1 = 3.60m,墙趾高H2 = 0.70m上墙背坡比= 1 : 0.300,下墙背坡比= 1 : 0.750,墙面坡比= 1 : 0.250 挡土墙底板前趾高程=0.00 m,底板底部坡比=0.000 : 1墙前填土顶面高程▽前地=4.00 m,墙前淤沙顶面高程▽沙=3.00 m 3.设计参数:挡土墙的建筑物级别为4级。
抗震类型:非抗震区挡土墙。
水上回填土内摩擦角φ=32.00度,水下回填土内摩擦角φ' =32.00度墙背与填土摩擦角δ=17.50度回填土凝聚力C =15.00kN/m2采用等代内摩擦角法计算粘性填土土压力。
地基土质为:松软墙底与地基间摩擦系数f =0.304.回填土坡面参数:回填土表面折线段数为:0段折线起点距墙顶高差=0.00 m填土面与水平面夹角β=0.00度原地面线水平角θ=30.00度,原地面与填土摩擦角δr =18.00度5.材料参数:回填土湿容重γs=18.00kN/m3,回填土浮容重γf=10.00kN/m3墙身材料容重γq=24.00kN/m3墙身材料容许压应力[R a] =500.00 kPa,墙身材料容许剪应力[R j] =110.00 kPa墙身材料容许拉应力[R l] =150.00 kPa,地基允许承载力[σo] =350.00 kPa 6.荷载计算参数:冰层厚度T b=0.00 m,静冰压力系数=0.000计算浪压力时采用的位置类型:内陆峡谷水库风区长度D =0.000 m,墙前河(库)底坡度i =1 : 100.00重现期为50年的年最大风速v o=24.000 m/s多年平均的最大风速v o' =30.000 m/s冻胀墙体变形系数m o=0.700,冻胀量Δhd=30.00 mm地震动态分布系数为梯形分布,最大值αm=2.00三、计算参数:程序采用库伦主动土压力公式计算土压力,计算公式如下:E =0.5×γ×H2×K aE x=E×cos(ε+δ)E y=E×sin(ε+δ)K a=cos2(φ-ε)/cos2ε/cos(ε+δ)/{1+[sin(φ+δ)sin(φ-β)/cos(ε+δ)/cos(ε-β)]0.5}2(《规X》式-2)式中:E为作用于墙背的主动土压力,作用点为距墙底1/3高处,方向与水平面成(ε+δ)夹角K a为主动土压力系数ε为墙背与铅直面的夹角,ε=36.87度当墙后填土为黏性土,粘聚力C=15.00kN时:采用等值内摩擦角法计算主动土压力。
混凝土正截面应力的计算详解
——轴向力对截面重心轴的偏心距, ;
——相应于轴向力的弯矩组合设计值;
——截面受压较大边边缘至受拉边或受压较小边纵向钢筋合力点的距离,
——偏心受压构件轴向力偏心距增大系数,按本规范第5.3.10条的规定计算。
截面受拉边或受压较小边纵向钢筋的应力和应按下列情况采用:
(2)当预应力钢筋的抗拉强度设计值 与表值不同时,其锚固长度应根据表值按强度比例增减。
5.2.1受弯构件的纵向受拉钢筋和截面受压区混凝土同时达到其强度设计值时,构件的正截面相对界限受压区高度 应按表5.2.1采用。
表5.2.1相对界限受压区高度
C50及以下
C55、C60
C65、C70
C75、C80
R235
、 ——受拉区、受压区纵向普通钢筋的截面面积;
、 ——受拉区、受压区纵向预应力钢筋的截面面积;
——矩形截面宽度或T形截面腹板厚度;
——截面有效高度,
——受拉区、受压区普通钢筋和预应力钢筋的合力点至受拉区边缘、受压区边缘的距离;
、 ——受压区普通钢筋合力点、预应力钢筋合力点至受压区边缘的距离;
——受压区预应力钢筋合力点处混凝土法向应力等于零时预应力钢筋的应力,先张法构件按本规范公式(6.1.5-2)计算;后张法构件按本规范公式(6.1.5-5)及第6.1.5条注2规定计算。
(5.3.1)
式中 ——轴向力组合设计值;
——轴压构件稳定系数,按表5.3.1采用;
——构件毛面面积,当纵向钢筋配筋率大于3%时,应改用
——全部纵向钢筋的截面面积
图5.3.1配有箍筋的构件混凝土轴心受压构件截面图
表5.3.1钢筋混凝土轴心受压构件的稳定系数
主梁截面承载力与应力验算

10.主梁截面承载力与应力验算预应力混凝土梁从预加力开始到是受荷破坏,需经受预加应力、使用荷载作用,裂缝出现和破坏等四个受力阶段,为保证主梁受力可靠并予以控制。
应对控制截面进行各个阶段的验算。
在以下内容中,先进行持久状态承载能力极限状态承载力验算,再分别验算持久状态抗裂验算和应力验算,最后进行短暂状态构件的截面应力验算。
对于抗裂验算,《公预规》根据公路简支标准设计的经验,对于全预应力梁在使用阶段短期效应组合作用下,只要截面不出现拉应力就可满足。
持久状况承载能力极限状态承载力验算在承载能力极限状态下,预应力混凝土梁沿正截面和斜截面都有可能破坏,下面验算这两类截面的承载力。
正截面承载力验算(1)确定混凝土受压区高度根据《公预规》条规定,对于带承托翼缘板的T 形截面; 当''Pd P cd f f f A f b h ≤成立时,中性轴带翼缘板内,否则在腹板内。
左边=Pd P f A =1260××=(kN)右边=''cd f f f b h =×220×15×=7392(kN)''Pd P cd f f f A f b h ≤成立,即中性轴在翼板内。
设中性轴到截面上缘距离为x ,则: x=0'126050.412.89()0.4(200012.85)74.86()22.4220pd p b cd ff A cm h cm f b ξ⨯==<=⨯-=⨯式中:ξb ——预应力受压区高度界限系数,按《公预规》表采用,对于C50混凝土和钢绞线,ξb =;h 0——梁的有效高,0p h h a =-, 说明该截面破坏时属于塑性破坏状态。
(2)验算正截面承载力:由《公预规》条,正截面承载力按下式计算:'000()2cd f x M f b x h γ≤-式中:γ0——桥梁结构的重要性系数,按《公预规》条采用,本设计取。
截面应力的计算

6
二、拉(压)杆横截面上的应力与应变
变形规律试验:
FP
FP’
观察发现:当杆受到轴向拉力作用后,所有的纵向线 都伸长了,而且伸长量都相等,并且仍然都与轴线平行; 所有的横向线仍然保持与纵向线垂直,而且仍为直线,只 是它们之间的相对距离增大了。
精选ppt
7
两个假设:平面假设:横截面只沿杆轴线平行移动。
精选ppt
13
变形发展的四个阶段:ob;bc;cd;de 10拉伸试验.swf
s
sb ss ses p
abc
de
O
o1 f e g
精选ppt
14
明显的四个阶段
10拉伸试验.swf
e
s
sb
s e sP
b a css
o
1、弹性阶段ob sE
sP — 比例极限
f
se — 弹性极限
Es tan
2、屈服阶段bc(失去抵
习
(2)掌握轴心拉压的应力、应变、变形及胡克定律; (3)掌握轴向拉 伸 压缩时材料的力学性能、工作许用应力;
内 (4)理解扭转圆轴横截面上应力分布规律,掌握切应力的计算;
容:(5)平行移轴公式及常见组合截面的惯性矩计算;
(6)掌握弯曲正应力分布规律及计算公式;
(7)掌握弯曲剪应力的分布规律及计算公式;
为塑性材料
16
3、卸载定律及冷作硬化
e
s
d
sb
b
s e sP
acss
即材料在卸载过程中 应力和应变是线形关系,
f 这就是卸载定律。
材料的比例极限增高, 延伸率降低,称之为冷作硬 化或加工硬化。
A
d
C
工程力学材料力学弯曲应力截面计算与校核

4. 工字形截面 查型钢表,A=bh=140cm2,选用50c号(A=139cm2)
Wz = 2080cm
3
s max
M max = = 14.42MPa 11 Wz
HOHAI UNIVERSITY
例 一T形截面外伸梁及其所受荷载如图所示。求最大拉应 力及最大压应力,并画出最大拉应力截面的正应力分布图。
HOHAI UNIVERSITY
q=20kN/m
A D 4m 40 +
220 C 2m 60
B
c yc=180 x
60
z
280
1.5m
22.5 M/kN· m
y
m MB=-40kN· m MD=22.5kN· M D ytD D max s = = 21.7MPa t max D截面 上部受压、下部受拉 Iz D yt max = 180mm D M y I z = 186.6 106 m 4 D B c max 14 s = = 12.1MPa D c max yc max = 100mm Iz B、D截面为危险截面
My s = Iz
Iz
抗弯截面系数
smax =
M Wz
8
HOHAI UNIVERSITY
对于剪切弯曲梁,这时两个基本假设并不成立。但实验和理 论分析表明,当l/h(跨高比)较大(>5)时,采用该正应 力公式计算的误差很小,满足工程的精度要求。 这时
s
=
M(x)y Iz Mmax Wz
M(x) 1 = ρ( x ) E Iz
* 3 3 Sz = 70 60 220 = 924 10 mm 1
1 =
* FQ S z 1
I zd
第四章钢筋混凝土受弯构件的应力、裂缝和变形验算

第四章钢筋混凝⼟受弯构件的应⼒、裂缝和变形验算第四章钢筋混凝⼟受弯构件的应⼒、裂缝和变形验算对钢筋混凝⼟构件,除应进⾏承载能⼒极限状态计算外,还要根据施⼯和使⽤条件进⾏持久状况正常使⽤极限状态和短暂状况的验算。
第⼀节抗裂计算桥梁构件按短暂状况设计时,应计算其在制作、运输及安装等施⼯阶段,由⾃重和施⼯荷载等引起的应⼒,并不应超过规范规定的限值。
施⼯荷载除有特别规定外均采⽤标准值,当进⾏构件运输和安装计算时,构件⾃重应乘以动⼒系数,当有组合时不考虑荷载组合系数。
在钢筋混凝⼟受弯构件抗裂验算和变形验算中,将⽤到“换算截⾯”的概念,因此,本章先引⼊换算截⾯的概念,然后依次介绍各项验算⽅法。
4.1.1 换算截⾯依据材料⼒学理论,对钢筋混凝⼟受弯构件带裂缝⼯作阶段的截⾯应⼒计算作如下假定:1、服从平截⾯假定由钢筋混凝⼟受弯构件的试验可知,从宏观尺度看平截⾯假定基本成⽴。
据此有同⼀⽔平纤维处钢筋与混凝⼟的纵向应变相等,即:s c εε= (4.1-1)2、钢筋和混凝⼟为线弹性材料钢筋混凝⼟受弯构件在正常施⼯或使⽤阶段,钢筋远未屈服,可视为线弹性材料;混凝⼟虽为弹塑性体,但在压应⼒⽔平不⾼的条件下,其应⼒与应变近似服从虎克定律。
故有c c c E εσ=,s s s E εσ= (4.1-2)3、忽略受拉区混凝⼟的拉应⼒钢筋混凝⼟构件在受弯开裂后,其受拉区混凝⼟的作⽤在计算上可近似忽略。
将式(4.1-1)代⼊式(4.1-2)可得:c s c c c E E εεσ==''因为 s ss E σε=所以 s ES c s sc E E σασσ1'== (4.1-3)其中:ES α-钢筋与混凝⼟弹性模量之⽐,即c s ES E E =α。
为便于利⽤匀质梁的计算公式,通常将钢筋截⾯⾯积s A 换算成等效的混凝⼟截⾯⾯积sc A ,依据⼒的等效代换原则:1、⼒的⼤⼩不变:换算截⾯⾯积sc A 承受拉⼒与原钢筋承受的拉⼒相等。
工形组合截面力学特性计算及应力验算(有说明 有公式)
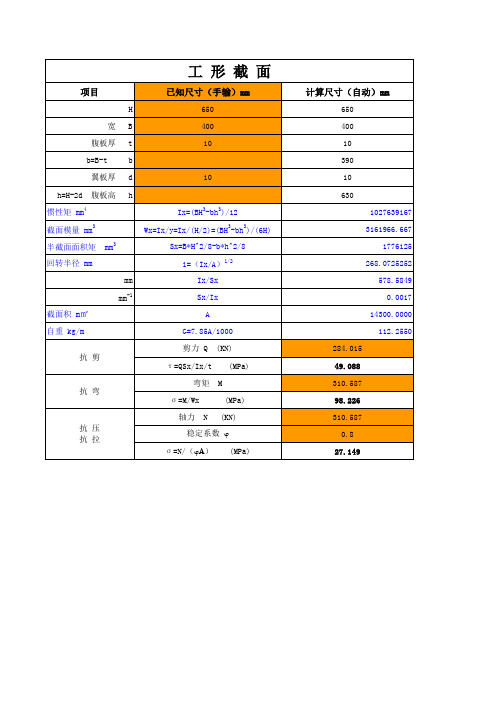
截面模量 mm3 半截面面积矩 回转半径 mm mm mm-1 截面积 m㎡ 自重 kg/m 抗 剪
Sx=B*H^2/8-b*h^2/8 i=(Ix/A)1/2 Ix/Sx Sx/Ix A G=7.85A/1000 剪力 Q τ =QSx/Ix/t (KN) (MPa) M (MPa) (KN)
抗 弯
1.03E+09 3.16E+06 1.78E+06
KN/m 1.12255
说明:1、橙色底纹需手动输入; 2、蓝色字体为截面特性的自动计算结果; 3、黑色无底纹加粗字体为计算得出应力。 4、所编公式(C9:C16蓝色部分)均和《钢结构设计手册 第三版》附表进行试算对照过,计算结果准确无误,可放心使用。 5、公式同样适用于矩形,只要把t改为与B一样即可。
B t b d h10来自10 630Ix=(BH -bh )/12 Wx=Ix/y=Ix/(H/2)=(BH3-bh3)/(6H) mm
3
3
3
1027639167 3161966.667 1776125 268.0725252 578.5849 0.0017 14300.0000 112.2550 284.015 49.088 310.587
弯矩 σ =M/Wx 轴力 N
98.226 310.587 0.8
抗 压 抗 拉
稳定系数 w σ =N/(wA) (MPa)
27.149
B:翼板宽度(t+b); H:总高度(h+2d) d:翼板厚度; t:腹板厚度 b=B-t; h=H-2d
本来插了了个图示的,但是有图老是上传不成功,没办法只 有用文字说明各变量的意义了
横截面上应力为零时应力计算公式临界应力公式剪切应力计算公式截面回转半径公式截面模量计算公式剪应力计算公式应力公式正应力计算公式矩形截面惯性矩公式
22_预应力箱梁截面特性值及扭转剪应力的计算验证

⎛
−⎜
⎜ ⎝
Di 2
⎞4 ⎟ ⎟ ⎠
⎤ ⎥ ⎥ ⎥ ⎥⎦
图9. 薄壁闭合截面的抗扭惯性矩
9
MIDAS Information Technology Co., Ltd.
MIDAS/Civil 技术资料
截面形状 1.角钢型
2. T型
如果 b<d : t=b, t1=d 如果 b>d : t=d, t1=b 3. 槽型
∫ 抗扭惯性矩 : I xx =
4 A2 ds / ts
任意点的应力 :
T τT = 2 Ats
ts : ᥅ᨨ᧣ἠ
图7. 薄壁闭合截面的抗扭惯性矩和剪应力
因为预应力箱梁大部分属于厚壁闭合截面(翼缘厚大于腹板间距的1/10,腹板厚大于腹板高 度的1/10),上面两种方法均不能适用,也有一些用户综合考虑两种方法计算抗扭刚度,但不能 说是精密的计算方法。在MIDAS/Civil 6.7.0版本中,通过内部细部分析的方法,通过确定抗扭 刚度计算抗扭惯性矩。
厚壁开口截面的抗扭惯性矩一般是将截面分割成许多的矩形后使用下列公式计算。
∑ Ixx = ixx
ixx
=
ab3
⎡16 ⎢ ⎢⎣ 3
− 3.36
b a
⎛ ⎜1 − ⎝
b4 12a 4
⎞⎤ ⎟⎥ ⎠⎥⎦
且a≥b
(2)
在此 ixx : 矩形分割截面的抗扭惯性矩 2a : 分割截面长边边长 2b : 分割截面短边边长
图4. 使用SPC计算截面特性
4) 预应力箱型截面
很多程序使用图5中的封闭截面的公式,不考虑悬臂和加腋部分简化计算预应力箱型截面的特 性值。MIDAS/Civil Ver.6.7.0内涵了可考虑悬臂和加腋部分精确计算特性值的计算内核。 .
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
截面应力验算
4.6.1使用荷载作用阶段计算 (1)混凝土法向应力验算
此阶段为有预加力和全部恒载作用的阶段,通常是跨中截面上缘可能出现最大压应力和下缘最大拉应力(或最小应力)。
计算公式如下: s p
g js g js y j y s W M M W M W M A N 021++
+
-
=
σ
s
p
g js
g js
y j
y s W M M W M W M A N 021---+=
σ
式中:N y 、M y —由有效预加力产生的预加内力; W js 、W jx —分别为对上、下缘的净截面抵抗矩; W 0s 、W 0x —分别为对上、下缘的换算截面抵抗矩; W g1、W g2—分别由第一期、第二期恒载产生的弯矩; M p —由活载产生的弯矩,有组合Ⅰ和Ⅲ的两种情况;
混凝土法向应力验算:
按规定,载使用荷载使用下,混凝土法向压应力极限值如下: 荷载组合Ⅰ: 0.5R a b =14MPa (见表10) 荷载组合Ⅲ: 0.6R a b =16.8MPa
在使用荷载(组合Ⅰ)作用下,全预应力梁截面受拉边缘由预加力引起的预压应力必须大于或等于由使用荷载引起的拉应力,即σh ≥0通过各截面上下缘混凝土法向应力计算,其结果表明受拉区(组合Ⅰ)都未出现拉应力,最大压应力为11.336MPa ,故符合上述各项规定。
(2)混凝土主应力验算
此项验算包括混凝土主拉应力和主压应力,对前者验算主要为了保证主梁斜截面具有与正截面同等的抗裂安全度,而验算后者是保证混凝土在沿主压应力方向破坏时也具有足够的安全度。
计算混凝土主应力时应选择跨径中最不利位置截面,对该截面的重心处和宽度急剧改变处进行验算,所以选择1号梁的变化点截面,对其上梗胁、净轴、换轴和下梗胁等四处分别进行主应力验算: a.剪应力计算
计算公式: τ=τ
g1
+τ
p+g2
-τy
式中:τ—由使用荷载和弯起的预应力钢束在主应力计算点上产生的混凝土剪应
力;
τ
g1—第一期恒载引起的剪应力,
其中载截面净轴(j-j ) 上τg1=
b
I S Q j j
j g -1;
在换轴(o-o )上τ
g1
=
b
I S Q j o
o g -1;
τ
p+g2
—活载及第二期恒载共同引起的剪应力,其中在净轴(j-j )上
j j b
p
g g p S I Q Q -++=
022τ;在o-o 上的o o b
p
g g p S I Q Q -++=
022τ;
Q p —活载剪力,有(汽-20+人群)和挂-100两种情况; τy —预加力引起的剪应力,由钢束锚固时产生的和σs Ⅱ损失产生的剪应力
组合而成;
各项剪应力计算和组合情况见表22所示。
b.主应力计算
按规定,当只在主梁纵向有预应力时,计算公式为: 22)2
(
2
τσσσ+-=
hx
hx
zl
22)2
(
2
τσσσ++=
hx
hx
za
式中:σhx —预加力和使用荷载在计算主应力点上产生的混凝土法向应力,按σhx =σh ±σ计算;
σh —在计算主应力点上由预加应力(扣除全部应力损失)产生的混凝土
法向应力,由钢束锚固时产生的和σs Ⅱ损失产生的法向应力组合而成
(见表23);
σ—在计算主应力点上由使用荷载产生的混凝土法向应力,按下式计算: 00
21y I M M y I M p
g j j
g ++
=
σ
y i 、y o —分别为各计算的主应力点到截面净轴和换轴的距离; M p —活载引起的弯矩,有(汽+人)和挂-100两种情况。
表24示出了σhx 的计算过程,混凝土主应力计算结果见表25 通过各控制截面的混凝土主应力计算,其结果如下: max σzl (MPa ) 组合Ⅰ 组合Ⅲ (由变化点截面控制) 0.075 0.083 max σza (MPa )
(由跨中截面控制) 9.104 10.183
在使用荷载作用下混凝土主应力应符合下列规定:
荷载组合Ⅰ: σzl ≤0.8R l b =2.08MPa (见表10,以下同) σza ≤0.6R a b =16.8MPa (3)验算钢束中的最大应力 计算公式:
21min I e M n I e M n oi
g y
j
ji
g y
y y ++=σσ
min max I e M n oi p y
y y +=σσ
式中: σy —有效预应力;
M g1、M g2—第一、第二期恒载产生的梁内弯矩;
M p —活载产生的梁内弯矩,分(汽+人)和挂-100两种情况; e ji 、e oi —分别为钢束重心到截面净轴和换轴的距离,即: e ji =y jx -a i ,e oi = y ox -a i
计算1号梁跨中截面钢束应力,见表26。
对于钢束载使用荷载作用下,预应力钢束的应力(扣除全部预应力损失)应符合下列要求:
荷载组合Ⅰ: σy ≤0.65R y b =1040MPa (见表10,下同) 荷载组合Ⅲ: σy ≤0.70R y b =1120MPa。
