截面应力计算共93页
开裂截面计算应力
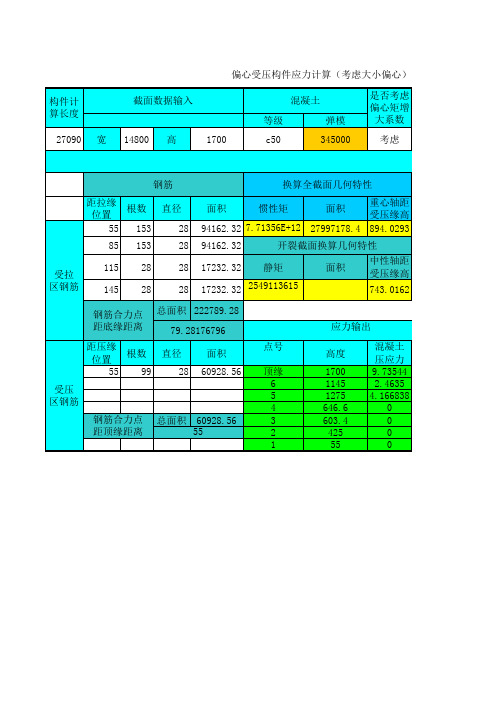
直径
面积
55 99
28 60928.56
受压 区钢筋
钢筋合力点 总面积 60928.56
距顶缘距离
55
点号
顶缘 6 5 4 3 2 1
应力输出
高度
1700 1145 1275 646.6 603.4 425 55
混凝土 压应力 9.73544 2.4635 4.166838
0 0 0 0
大小偏心)
偏心受压构件应力计算(考虑大小偏心)
构件计 算长度
截面数据输入
27090 宽 14800 高 Nhomakorabea1700
混凝土
等级 c50
弹模 345000
是否考虑 偏心矩增 大系数
考虑
钢筋
距拉缘 位置
根数
直径
55 153
28
85 153
28
受拉
115 28
28
区钢筋
145 28
28
换算全截面几何特性
面积
惯性矩
面积
重心轴距 受压缘高
94162.32 7.71356E+12 27997178.4 894.0293
94162.32
开裂截面换算几何特性
17232.32 静矩 17232.32 2549113615
面积
中性轴距 受压缘高
743.0162
钢筋合力点 总面积 222789.28
距底缘距离
79.28176796
距压缘 位置
根数
0
D
0
解方程
2.65907E+13 743.0162394
-118.183
10
c25
考虑
截面应力的计算PPT课件

,只是Ip值不同。
2019/10/18
34
剪应力的计算公式:
1、横截面上任意一点剪应力计算:
Mn
Ip
2、最大剪应力计算
IP—截面对形心的极惯性矩 是一个几何量,与截面形状及 尺寸有关,单位m4 mm4
当 R 时,表示圆截面边缘处的剪应力最大
max
Mn Ip
Mn Wp
R
WP—抗扭截面系数,几何量 单位m3 mm3
2019/10/18
35
圆截面的极惯性矩和抗扭截面系数
空 心 圆 轴
极惯 性矩
抗扭截 面系数
2019/10/18
实
心
o
圆
o
d
轴
D
D
II p
DD44
3322
( (1 1 4
)4
)
=d/D=0
Ip
D4
7
两个假设:平面假设:横截面只沿杆轴线平行移动。
纤维假设:横截面之间所有纵向 纤维的伸 长量相等
可知:横截面上只有正应力σ,
且大小相等。
FP
s FN
FN
sdA s A
A
当轴力为拉力时,正应力为拉应力,取正号; 当轴力为压力时,正应力为压应力,取负号。
s 轴心拉压应力公式:
FN
A
2019/10/18
1MPa=106Pa=1N/mm2
1GPa=109Pa
6
二、拉(压)杆横截面上的应力与应变
变形规律试验:
FP
FP’
观察发现:当杆受到轴向拉力作用后,所有的纵向线 都伸长了,而且伸长量都相等,并且仍然都与轴线平行; 所有的横向线仍然保持与纵向线垂直,而且仍为直线,只 是它们之间的相对距离增大了。
工程力学中的应力和应变的计算方法

工程力学中的应力和应变的计算方法在工程力学这一领域中,应力和应变是两个极其重要的概念。
它们对于理解材料在受力情况下的行为以及结构的稳定性和安全性起着关键作用。
接下来,让我们深入探讨一下应力和应变的计算方法。
应力,简单来说,就是单位面积上所承受的内力。
想象一下,我们有一根杆子,在它的横截面上受到一个力的作用。
这个力除以横截面的面积,得到的值就是应力。
应力的单位通常是帕斯卡(Pa)。
在计算应力时,我们需要先明确受力的类型。
如果是拉伸或压缩力,应力的计算公式为:应力=力/横截面面积。
例如,有一根横截面面积为 001 平方米的杆子,受到 1000 牛顿的拉力,那么应力= 1000/ 001 = 100000 帕斯卡。
如果是剪切力,应力的计算就稍微复杂一些。
对于矩形截面,剪切应力=剪力/(横截面面积 ×剪切面的距离)。
假设一个矩形截面的宽度为 b,高度为 h,受到的剪力为 V,那么剪切面上的平均剪切应力= 3V / 2bh 。
应变则是描述物体在受力时发生的变形程度。
它是相对变形量,没有单位。
应变分为线应变和角应变。
线应变是指物体在某一方向上长度的变化量与原始长度的比值。
如果一根杆子原来的长度是 L,受力后长度变成了 L',那么线应变=(L' L)/ L 。
角应变,也称为切应变,用于描述物体的角度变化。
例如,一个正方形在受力后变成了菱形,其角度的变化量就是角应变。
在实际工程中,应力和应变的关系通常通过材料的本构方程来描述。
对于线弹性材料,应力和应变之间存在线性关系,遵循胡克定律。
胡克定律在拉伸或压缩情况下可以表示为:应力=弹性模量 ×应变。
这里的弹性模量是材料的一个固有属性,反映了材料抵抗变形的能力。
不同的材料具有不同的弹性模量。
例如,钢材的弹性模量通常较大,这意味着它在受力时相对不容易发生变形;而橡胶的弹性模量较小,受力时容易产生较大的变形。
除了简单的拉伸和压缩情况,对于复杂的受力状态,如弯曲、扭转等,应力和应变的计算就需要运用更复杂的理论和方法。
截面应力的计算

0
32
O
对于空心圆轴:
IP
D4
32
d 4
32
D4
32
1 4
D
d
D
三、最大切应力:
横截面上边缘点的切应力最大,其值为
令
WP
IP R
max
T W
max
TR IP
式中WP只与截面的几何尺寸和形状有关,称为抗扭截面系数, 单位为mm3或m3。
完成任务:图示的阶梯圆轴。AB段直径d1=120mm,
A
d
300
B
C
a
F
一、应力的概念
10KN A=10mm2
10KN
10KN 受力杆件某截面上一点的内力分布疏密 程度,内力集度.
10KN
A=100mm2
哪个杆先破坏?
工程构件,大多数情形下,内力并非均匀分布, 集度的定义不仅准确而且重要,因为“ 破坏” 或“失效”往往从内力集度最大处开始。
应力就是单位面积上的力?
矩形截面 l k A k=11.3 k= 5.6
1. 拉伸图和应力——应变图
试验机的自动绘图设备,可在试件拉伸过程
中,自动绘出试件所受应力 s =P/A与标距 段相
应的伸长量 △ l/L 的关系曲线。通常称它为拉伸 图。下图为低碳钢的拉伸图。
2、低碳钢拉伸时的力学性能
变形发展的四个阶段:ob;bc;cd;de 10拉伸试验.swf
根据圆轴扭转的平面假设和切应力互等定理、剪切胡 克定律可知:实心圆轴横截面上各点处,只产生垂直于
半径的切应力 ,沿周向大小不变,方向与该截面的扭矩
方向一致。
1. 几何变形方面
梁的应力计算PPT课件

2.7103 N m0.072m 0.573105 m4
3 3.9MP a
c
满足强度要求。
第23页/共44页
§6-3 变截面梁形状及变截面梁
设计梁原则: 满足强度条件
经济性,尽量节省材料
需要选择合理的截面形状和尺寸
一、截面的合理形状
强度条件:
max
Mmax WZ
单从强度来看,WZ越大越合理。
二、变截面梁
q=2kN/m
A
B
变截面梁——横截面沿梁轴 线变化的梁
C
xm
l = 4m
x
max
Mx WZ x
M
ql2 / 8 4kN m
WZ
x
Mx
x
等强度梁——梁强度沿轴线 均匀分布
第28页/共44页
§6-3 变截面梁形状及变截面梁
WZ
x
Mx
当荷载比较复杂时,等强度梁难以加工,增加了加工 制造成本,一般很少采用等强度梁。
WZ
σ
1.等截面梁弯矩最大的截面上
2.离中性轴最远处
3.变截面梁要综合考虑 M 与 Iz
4.脆性材料抗拉和抗压性能不同,两方面都要考虑
t,max t
c,max c
第14页/共44页
§6-2 梁的正应力强度条件及其应用
根据弯曲正应力强度条件
1.强度校核
max
Mmax WZ
2.选择截面
22.5106 Pa 2.5MPa
t
满足强度要求。
第22页/共44页
§6-2 梁的正应力强度条件及其应用
(2)校核最大压应力
与分析最大拉应力一样,要比较C、B两个截面。C截面上 最大压应力发生在上边缘。因MC、y1分别大于MB、y2,所 以最大压应力一定发生在C截面上。即
混凝土正截面应力的计算
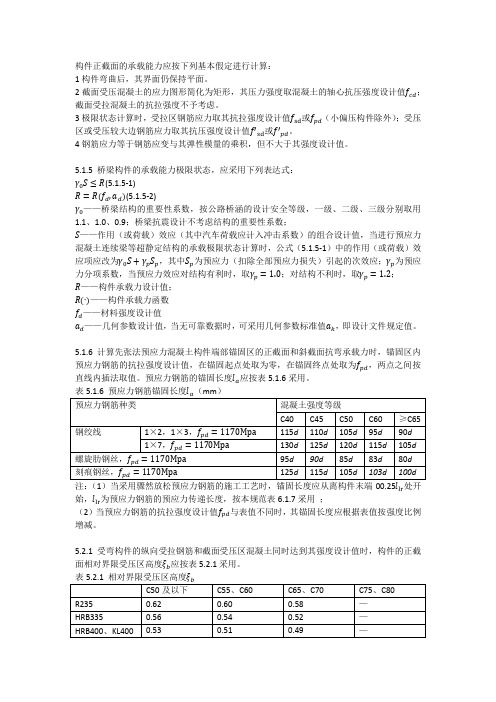
图 5.2.2 矩形截面受弯构件正截面承载力计算 混凝土受压区高度������应按下式计算: ������������������ ������������ + ������������������ ������������ = ������������������ ������������ + ������′������������ ������′������ + ������′������������ − ������′������ 0 ������′������ (5.2.2-2) 截面受压区高度应符合下列要求: ������ ≤ ������������ ������0 (5.2.2-3) 当受压区仅配纵向普通钢筋或配普通钢筋和预应力钢筋, 且预应力钢筋受拉即 (������′������������ − ������′������ 0 ) 为正值时 ������ ≥ 2������������ (5.2.2-4) 当受压区仅配纵向普通钢筋或配普通钢筋和预应力钢筋, 且预应力钢筋受拉即 (������′������������ − ������′������ 0 ) 为负值时 ������ ≥ 2������′������ (5.2.2-5) 式中������0 ——桥梁结构的重要性系数,按本规范第 5.1.5 条的规定采用; ������������ ——弯矩组合设计值; ������������������ ——混凝土轴心抗压强度设计值,按本规范表 3.1.4 采用; ������sd 、������′sd ——纵向普通钢筋的抗拉强度设计值和抗压强度设计值,按本规范表 3.2.3-1 采用 ������������ 、������′ ������ ——受拉区、受压区纵向普通钢筋的截面面积; ������������ 、������′������ ——受拉区、受压区纵向预应力钢筋的截面面积; ������——矩形截面宽度或 T 形截面腹板厚度; ������0 ——截面有效高度,������0 = ������ − ������ ������ 、������′——受拉区、受压区普通钢筋和预应力钢筋的合力点至受拉区边缘、受压区边缘的距 离; ������′������ 、������′������ ——受压区普通钢筋合力点、预应力钢筋合力点至受压区边缘的距离; ������′������ 0 ——受压区预应力钢筋合力点处混凝土法向应力等于零时预应力钢筋的应力,先张法构 件按本规范公式(6.1.5-2)计算;后张法构件按本规范公式(6.1.5-5)及第 6.1.5 条注 2 规 定计算。
开裂截面钢筋应力计算公式

开裂截面钢筋应力计算公式在工程结构设计中,钢筋的应力计算是非常重要的一部分。
而对于开裂截面钢筋的应力计算,更是需要特别注意。
因为开裂截面钢筋的应力计算不仅涉及到钢筋的受力情况,还需要考虑到混凝土的开裂情况。
本文将介绍开裂截面钢筋应力计算的相关公式和计算方法。
开裂截面钢筋的应力计算公式如下:\[ \sigma_s = \frac{N}{A_s} + \frac{M}{W_s} \]其中,σs为钢筋的应力,N为轴向力,As为钢筋的截面面积,M为弯矩,Ws为钢筋的抗弯模量。
在计算开裂截面钢筋的应力时,需要根据具体的结构情况确定N和M的数值,并且需要考虑到混凝土的开裂情况对钢筋应力的影响。
在实际工程中,开裂截面钢筋的应力计算通常需要考虑以下几个方面的因素:1. 混凝土的开裂宽度,混凝土的开裂宽度对钢筋的应力有着直接的影响。
一般来说,混凝土的开裂宽度越大,钢筋的应力就会越小。
因此,在计算开裂截面钢筋的应力时,需要根据混凝土的开裂情况对钢筋的应力进行修正。
2. 钢筋的受力情况,钢筋的受力情况对其应力的计算也有着重要的影响。
在实际工程中,钢筋可能同时承受轴向力和弯矩,因此需要根据具体的受力情况确定N 和M的数值,并进行合理的计算。
3. 钢筋的截面形状,钢筋的截面形状对其应力的计算也有着一定的影响。
一般来说,截面形状越复杂,计算就会越复杂。
因此在计算开裂截面钢筋的应力时,需要考虑到钢筋的截面形状对应力的影响。
在进行开裂截面钢筋应力计算时,需要根据具体的结构情况和受力情况确定相关的参数,并进行合理的计算。
同时,还需要考虑到混凝土的开裂情况对钢筋应力的影响,并进行相应的修正。
只有在综合考虑了以上因素之后,才能得到准确的开裂截面钢筋应力。
总之,开裂截面钢筋的应力计算是一个复杂而重要的工作。
只有在充分考虑了混凝土开裂情况、钢筋受力情况和截面形状等因素之后,才能得到准确的钢筋应力。
希望本文介绍的开裂截面钢筋应力计算公式和相关计算方法能对工程设计和实际工程中的钢筋应力计算有所帮助。
(完整版)梁横截面上的剪应力及其强度计算

梁横截面上的剪应力及其强度计算在一般情况下,剪应力是影响梁的次要因素。
在弯曲应力满足的前提下,剪应力一般都满足要求。
一、矩形截面梁的剪应力 利用静力平衡条件可得到剪应力的大小为:*z Z QS I b τ=; 公式中:Q ——为横截面上的剪力;*z S ——为横截面上所求剪应力处的水平线以下(或以上)部分面积A*对中性轴的静矩;I Z ——为横截面对中性轴的惯性矩;b ——矩形截面宽度。
计算时Q 、*z S 均为绝对值代入公式。
当横截面给定时,Q 、I Z 、b 均为确定值,只有静矩*z S 随剪应力计算点在横截面上的位置而变化。
222**2214()[()]()(1)222248z h h h h bh y S A y b y y y y h =⨯=-⨯+-=-=- 把上式及312z bh I =代入*z Z QS I bτ=中得到:2234(1)2Q y bh h τ=- 可见,剪应力的大小沿着横截面的高度按二次抛物线规律分布的。
在截面上、下边缘处(y=±0.5h ),剪应力为零;在中性轴处(y=0)处,剪应力最大,其值为:33 1.522Q Q Q bh A A τ=⨯=⨯= 由此可见,矩形截面梁横截面上的最大剪应力值为平均剪应力值的1.5倍,发生在中性轴上。
二、工字形截面梁的剪应力在腹板上距离中性轴任一点K 处剪应力为:*1z Z QS I b τ=; 公式中:b 1——腹板的宽度(材料表中工字钢腹板厚度使用字母d 标注的);*z S ——为横截面上阴影部分面积A*对中性轴的静矩;工字形截面梁的最大剪应力发生在截面的中性轴处,其值为:*max max1z Z QS I b τ=; 公式中:*max z S ——为半个截面(包括翼缘部分)对中性轴的静矩。
三、梁的剪应力强度计算梁的剪应力强度条件为:*max max max max *[](/)z Z Z Z Q S Q I b b I S ττ==≤。
截面应力的计算

6
二、拉(压)杆横截面上的应力与应变
变形规律试验:
FP
FP’
观察发现:当杆受到轴向拉力作用后,所有的纵向线 都伸长了,而且伸长量都相等,并且仍然都与轴线平行; 所有的横向线仍然保持与纵向线垂直,而且仍为直线,只 是它们之间的相对距离增大了。
精选ppt
7
两个假设:平面假设:横截面只沿杆轴线平行移动。
精选ppt
13
变形发展的四个阶段:ob;bc;cd;de 10拉伸试验.swf
s
sb ss ses p
abc
de
O
o1 f e g
精选ppt
14
明显的四个阶段
10拉伸试验.swf
e
s
sb
s e sP
b a css
o
1、弹性阶段ob sE
sP — 比例极限
f
se — 弹性极限
Es tan
2、屈服阶段bc(失去抵
习
(2)掌握轴心拉压的应力、应变、变形及胡克定律; (3)掌握轴向拉 伸 压缩时材料的力学性能、工作许用应力;
内 (4)理解扭转圆轴横截面上应力分布规律,掌握切应力的计算;
容:(5)平行移轴公式及常见组合截面的惯性矩计算;
(6)掌握弯曲正应力分布规律及计算公式;
(7)掌握弯曲剪应力的分布规律及计算公式;
为塑性材料
16
3、卸载定律及冷作硬化
e
s
d
sb
b
s e sP
acss
即材料在卸载过程中 应力和应变是线形关系,
f 这就是卸载定律。
材料的比例极限增高, 延伸率降低,称之为冷作硬 化或加工硬化。
A
d
C
(完整版)梁横截面上的剪应力及其强度计算

梁横截面上的剪应力及其强度计算在一般情况下,剪应力是影响梁的次要因素。
在弯曲应力满足的 前提下,剪应力一般都满足要求一、矩形截面梁的剪应力利用静力平衡条件可得到剪应力的大小为:公式中:Q ――为横截面上的剪力;S ;――为横截面上所求剪应力处的水平线以下(或以上)部分面积A*对中性轴的静矩;I Z ――为横截面对中性轴的惯性矩;b ――矩形截面宽度。
计算时Q S ;均为绝对值代入公式。
当横截面给定时,Q l z 、b 均为确定值,只有静矩S ;随剪应力计算点在横截面上的位置而变化* *h1 h h h2 2bh 2 4y 2S ; A yb(- y) [y (- y)]-(-y )(1 2 )2 2 22 48h 把上式及I ;bh 3 代入虫 中得到:3Q(1 4^)12I Z b2bhh 2可见,剪应力的大小沿着横截面的高度按二次抛物线规律分布的。
在截面上、下边缘 处(y=± 0.5h ),剪应力为零;在中性轴处(y=0)处,剪应力最大,其值为:由此可见,矩形截面梁横截面上的最大剪应力值为平均剪应力值的1.5倍,发生在中性轴上。
二、工字形截面梁的剪应力在腹板上距离中性轴任一点K处剪应力为:公式中:b i――腹板的宽度(材料表中工字钢腹板厚度使用字母S z ――为横截面上阴影部分面积A对中性轴的静矩;公式中:S zmax ――为半个截面(包括翼缘部分)对中性轴的静矩。
Cb)图皐工字卑梁横苗面的应力计算图三、梁的剪应力强度计算梁的剪应力强度条件为:*QmaxSzmax Zmaxmax I z b b(l z/S;)[]d标注的);工字形截面梁的最大剪应力发生在截面的中性轴处,其值为:max* QS z max .;I Z b1。
梁横截面上的剪应力及其强度计算

梁横截面上的剪应力及其强度计算梁横截面上的剪应力及其强度计算在一般情况下,剪应力是影响梁的次要因素。
在弯曲应力满足的前提下,剪应力一般都满足要求。
一、矩形截面梁的剪应力*QSz利用静力平衡条件可得到剪应力的大小为:??;IZb公式中:Q――为横截面上的剪力;*――为横截面上所求剪应力处的水平线以下(或以上)部分面积A*对中性Sz轴的静矩;IZ――为横截面对中性轴的惯性矩;b――矩形截面宽度。
计算时Q、Sz*均为绝对值代入公式。
当横截面给定时,Q、IZ、b均为确定值,只有静矩Sz*随剪应力计算点在横截面上的位置而变化。
h1hhh2bh24y2 2Sz?A?y?b(?y)?[y?(?y)]?(?y)?(1?2)222248h***bh33Q4y2QSz(1?2) 把上式及Iz?代入??中得到:??122bhhIZb可见,剪应力的大小沿着横截面的高度按二次抛物线规律分布的。
在截面上、下边缘处(y=±0.5h),剪应力为零;在中性轴处(y=0)处,剪应力最大,其值为:???3Q3QQ???1.52bh2AA由此可见,矩形截面梁横截面上的最大剪应力值为平均剪应力值的1.5倍,发生在中性轴上。
二、工字形截面梁的剪应力*QSz在腹板上距离中性轴任一点K处剪应力为:??;IZb1公式中:b1――腹板的宽度(材料表中工字钢腹板厚度使用字母d标注的);* Sz――为横截面上阴影部分面积A*对中性轴的静矩;*QSzmax; ?IZb1工字形截面梁的最大剪应力发生在截面的中性轴处,其值为:?max*公式中:Szmax――为半个截面(包括翼缘部分)对中性轴的静矩。
三、梁的剪应力强度计算梁的剪应力强度条件为:?max*QmaxSzQmaxmax???[?] *IZbb(IZ/SZ)感谢您的阅读,祝您生活愉快。
梁横截面上的剪应力及其强度计算

梁横截面上的剪应力及其强度计算梁横截面上的剪应力及其强度计算在一般情况下,剪应力是影响梁的次要因素。
在弯曲应力满足的前提下,剪应力一般都满足要求。
一、矩形截面梁的剪应力*QSz利用静力平衡条件可得到剪应力的大小为:??;IZb公式中:Q――为横截面上的剪力;*――为横截面上所求剪应力处的水平线以下(或以上)部分面积A*对中性Sz轴的静矩;IZ――为横截面对中性轴的惯性矩;b――矩形截面宽度。
计算时Q、Sz*均为绝对值代入公式。
当横截面给定时,Q、IZ、b均为确定值,只有静矩Sz*随剪应力计算点在横截面上的位置而变化。
h1hhh2bh24y2 2Sz?A?y?b(?y)?[y?(?y)]?(?y)?(1?2)222248h***bh33Q4y2QSz(1?2) 把上式及Iz?代入??中得到:??122bhhIZb可见,剪应力的大小沿着横截面的高度按二次抛物线规律分布的。
在截面上、下边缘处(y=±0.5h),剪应力为零;在中性轴处(y=0)处,剪应力最大,其值为:???3Q3QQ???1.52bh2AA由此可见,矩形截面梁横截面上的最大剪应力值为平均剪应力值的1.5倍,发生在中性轴上。
二、工字形截面梁的剪应力*QSz在腹板上距离中性轴任一点K处剪应力为:??;IZb1公式中:b1――腹板的宽度(材料表中工字钢腹板厚度使用字母d标注的);* Sz――为横截面上阴影部分面积A*对中性轴的静矩;*QSzmax; ?IZb1工字形截面梁的最大剪应力发生在截面的中性轴处,其值为:?max*公式中:Szmax――为半个截面(包括翼缘部分)对中性轴的静矩。
三、梁的剪应力强度计算梁的剪应力强度条件为:?max*QmaxSzQmaxmax???[?] *IZbb(IZ/SZ)感谢您的阅读,祝您生活愉快。
梁截面温度自应力的计算文本资料
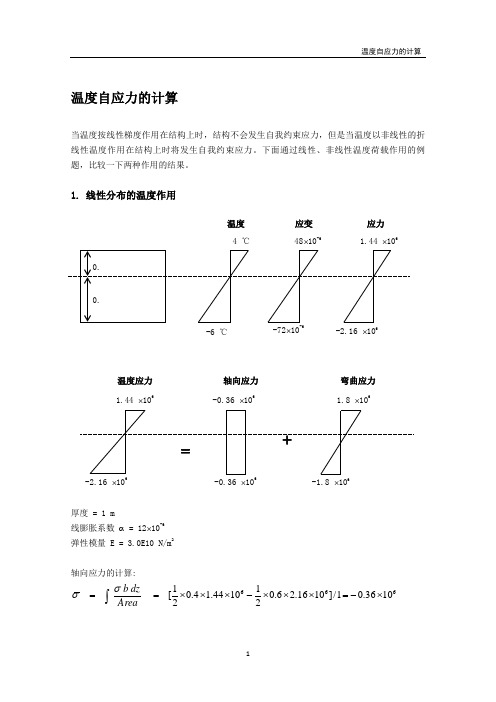
温度自应力的计算当温度按线性梯度作用在结构上时,结构不会发生自我约束应力,但是当温度以非线性的折线性温度作用在结构上时将发生自我约束应力。
下面通过线性、非线性温度荷载作用的例题,比较一下两种作用的结果。
1. 线性分布的温度作用厚度 = 1 m线膨胀系数 α = 12⨯10-6 弹性模量 E = 3.0E10 N/m 2轴向应力的计算: 6661036.01/]1016.26.0211044.14.021[⨯-=⨯⨯⨯-⨯⨯⨯==⎰Areadzb σσ1.44 ⨯106-2.16 ⨯106温度 应变 应力 4 ℃-6 ℃48⨯10-6-72⨯10-6温度应力 1.44 ⨯106-2.16 ⨯106=1.8 ⨯106-1.8 ⨯106弯曲应力 -0.36 ⨯106-0.36 ⨯106+轴向应力温度作用引起的变形如上图所示,由轴向和弯曲两部分组成。
下图显示的是从两端固接,逐步释放各约束时结构的应力情况。
由上图可知,当无外部约束条件时,线性的温度梯度不会引起自我约束应力。
内部约束应力释放的应力1.44 ⨯106两端固接 -2.16 ⨯106内部约束应力 释放的应力释放轴向约束 -1.8 ⨯1061.8-0.36 ⨯106内部约束应力释放的应力 释放弯曲约束 1.8-1.8 ⨯1062. 非线性分布的温度作用下图为截面上作用非线性温度时的应力分布情况。
将温度应力也用轴向应力和弯曲应力表达。
轴向应力的计算: 66610936.01/]1016.26.0211044.14.021[⨯=⨯⨯⨯+⨯⨯⨯==⎰Areadzb σσ由弯曲应力图计算等效弯矩:⎰⨯⨯⨯⨯-⨯⨯⨯⨯⨯==)4.0(52.010936.021)14.031(14.010504.02166dz z b M Tσ66100888.0)34.03266.0(34.010224.121⨯=⨯+⨯⨯⨯⨯+1.44 ⨯1062.16 ⨯106温度 应变 4 ℃6 ℃48⨯10-72⨯10-应力 温度应力 1.44 ⨯1062.16 ⨯106=0.504⨯1061.224 ⨯106弯曲应力0.936 ⨯1060.936 ⨯106+轴向应力 -0.936 ⨯106相当于等效弯矩引起的弯曲应力:626105328.06/1100888.0⨯=⨯==zM T σ同样,下图显示的是从两端固接,逐步释放各约束时结构的应力情况。
应力计算书

第二部分满堂架计算书参考资料:《建筑施工扣件式钢管脚手架安全技术规范》(JGJ130-2001)《混凝土结构设计规范》GB50010-2002、《建筑结构荷载规范》(GB 50009-2001)、《钢结构设计规范》(GB 50017-2003)等规范。
一、参数信息:1.脚手架参数横向间距或排距(m):0.75;纵距(m):0. 75;步距(m):1.20;立杆上端伸出至模板支撑点长度(m):0.10;脚手架搭设高度(m):10.07;采用的钢管(mm):Φ48×3.0 ;扣件连接方式:扣件,扣件抗滑承载力系数:0.80;板底支撑连接方式:钢管支撑;板底钢管的间隔距离(mm):150.00;2.荷载参数钢模板自重(kN/m2):0.750;混凝土自重(kN/m3):24.000;楼板浇筑厚度(m):3.000;混凝土振捣荷载标准值(kN/m2):2.000;施工人员及设备荷载标准值(kN/m2):2.500;钢筋自重(kN/m3):1.500图1 底板支撑架立面简图图2 底板支撑架荷载计算单元二、纵向支撑钢管的计算:纵向钢管按照均布荷载下简支梁计算,截面力学参数为截面抵抗矩 w=4.49cm3截面惯性矩 I=10.78cm4弹性模量 E=2.06×106N/mm1.荷载的计算:(1)钢筋混凝土自重(kN/m):q11= (24.000+1.500)×0.15×3.000 = 11.475 kN/m;(2)模板的自重线荷载(kN/m):q12= 0.750×0.15 = 0.1125 kN/m ;(3)活荷载为施工人员及设备、混凝土振捣时产生的荷载(kN):q2 = (2.500 +2.000)×0.15 = 0.675kN/m;2.强度计算:最大弯矩考虑为简支梁均布荷载作用下的跨中弯矩。
M=ql2/8q=q11+ q12+ q2=12.2625 kN/m最大弯距 M max = 12.2625×0. 752 /8= 0.862 kN.M;最大支座力计算公式如下:N=ql/2最大支座力 N = 12.2625×0.75/2=4.598 kN ;截面应力σ= M/W= 0.862×106/4490.0 =192.028 N/mm2;纵向钢管的计算强度为 192.028小于205.0 N/mm2,满足要求!3.挠度计算:最大挠度考虑为简支梁均布荷载作用下的挠度计算公式如下:W=5ql4/384EIq=q11+ q12+ q2=12.2625 kN/m均布荷载作用下的最大挠度W= 5×12.2625×75.04/( 100×2.060×105×107800.0 ) =0.227 mm;支撑钢管的最大挠度小于750.0/150与10 mm,满足要求!三、横向支撑10#槽钢计算:横向10#槽钢按照均布荷载下简支梁计算,截面力学参数为截面抵抗矩 w=39.7cm3截面惯性矩 I=198.3cm4弹性模量 E=2.06×106N/mm1.荷载的计算:(1)钢筋混凝土自重(kN/m):q11= (24.000+1.500)×0.75×3.000 = 57.375 kN/m;(2)模板的自重线荷载(kN/m):q12= 0.750×0.75 = 0.5625 kN/m ;(3)活荷载为施工人员及设备、混凝土振捣时产生的荷载(kN):q2 = (2.500 +2.000)×0.75 = 3.375kN/m;2.强度计算:最大弯矩考虑为简支梁均布荷载作用下的跨中弯矩。
梁横截面上的剪应力及其强度计算

梁横截面上的剪应力及其强度计算梁横截面上的剪应力及其强度计算在一般情况下,剪应力是影响梁的次要因素。
在弯曲应力满足的前提下,剪应力一般都满足要求。
一、矩形截面梁的剪应力*QSz利用静力平衡条件可得到剪应力的大小为:??;IZb公式中:Q――为横截面上的剪力;*――为横截面上所求剪应力处的水平线以下(或以上)部分面积A*对中性Sz轴的静矩;IZ――为横截面对中性轴的惯性矩;b――矩形截面宽度。
计算时Q、Sz*均为绝对值代入公式。
当横截面给定时,Q、IZ、b均为确定值,只有静矩Sz*随剪应力计算点在横截面上的位置而变化。
h1hhh2bh24y2 2Sz?A?y?b(?y)?[y?(?y)]?(?y)?(1?2)222248h***bh33Q4y2QSz(1?2) 把上式及Iz?代入??中得到:??122bhhIZb可见,剪应力的大小沿着横截面的高度按二次抛物线规律分布的。
在截面上、下边缘处(y=±0.5h),剪应力为零;在中性轴处(y=0)处,剪应力最大,其值为:???3Q3QQ???1.52bh2AA由此可见,矩形截面梁横截面上的最大剪应力值为平均剪应力值的1.5倍,发生在中性轴上。
二、工字形截面梁的剪应力*QSz在腹板上距离中性轴任一点K处剪应力为:??;IZb1公式中:b1――腹板的宽度(材料表中工字钢腹板厚度使用字母d标注的);* Sz――为横截面上阴影部分面积A*对中性轴的静矩;*QSzmax; ?IZb1工字形截面梁的最大剪应力发生在截面的中性轴处,其值为:?max*公式中:Szmax――为半个截面(包括翼缘部分)对中性轴的静矩。
三、梁的剪应力强度计算梁的剪应力强度条件为:?max*QmaxSzQmaxmax???[?] *IZbb(IZ/SZ)感谢您的阅读,祝您生活愉快。
斜截面应力PPT资料

斜截面应力
轴向拉伸和压缩
N=F1–F2
拉伸
过一点不同方向面上应力的集合,
解:横截面应力
α= 90°,σα= 0 ,τα= 0
第三节 拉压杆横截面及斜截面上的应力
已知:F=10kN,d=10mm,α=450。
pα = σcos α m-m截面:N= F1–F2(看左侧)
压缩
正负号——拉伸为正(离开截面为正)
3-3截面:(看右面) N3=2 kN
2.作轴力图
第三节 拉压杆横截面及斜截面上的应力
一、拉压杆横截面上的应力
N A
正应力的正负号: 拉为正、压为负
横截面的正应力均匀分布
F
F
F
N
A
例5-2
A1=400m1m2 10kN
2
A2=200mm2 20kN
A
C
1
B
2
求:杆的最大工作应 解力:1.求轴力
30
90 0
切应力互等定律 :
互相垂直平面上的切应力大小相等,
方向都指向或背离两平面的交线
m-m截面:N= F1–F2(看左侧) N = F3 (看右侧)
1-1截面:N1= F1(看左侧) N1 = F3 +F2 (看右侧)
例5-1 作图示杆的轴力图
1kN A
1 4kN 2
1B
2
1
N
(kN)
5kN
3
2kN
C 3D
2
3
解:1.用直接法计算各段轴力 1-1截面:(看左面) N1=1 kN 2-2截面:(看左面) N2=1–4 =–3 kN
F
α pα α
全应力为 pN AA/cFoscos
