割补法巧算面积
割补法求面积

3
10 4
12
方法总结
切割法:
把不规则的图形切割成已学图形,再把各部分面积加起来
拼补法:
把不规则的图形拼补成已学图形,再用总面积减去补上的图形面积
谢谢观看
练习
图形大世界
——割补法
REPORT
面积公式回顾
面积=边长×边长
面积=长×宽
面积=底×高
面积=底×高÷2
面积=(上底+下底)×高÷2
3cm 3cm
3cm 3cm
左侧图形的面积 该怎么求呢
3cm 3cm
3cm 3cm
我们学过哪些图形的面积公式呢?
可以将不规则的图形切割成两 个或多个已学图形,进行计算:
3×3+3×(3+3)=27(平方厘米)
3cm 3cm
3cm 3cm
我们学过哪些图形的面积公式呢?
可以将不规则的图形拼补成一 个或多个已学图形,进行计算:
(3+3)×(3+3)- 3×3=27(平方厘米)
10 3
3
这个图该
6 怎么求呢
单位:厘米
10 3
3
这个图该
6 怎么求呢
单位:厘米
切割法: 3×6×2+10×(3+6+3)=156(平方厘米)
10 3
3
这个图该
6 怎么求呢
单位:厘米
切割法: 3×10×2+(3+10+3)×6=156(平方厘米)
10 3
3
这个图该
6 怎么求呢
单位:厘米
拼补法: (10+3+3)×(3+6+3)- 3×3×4=156(平方厘米)
【讲义】四年级下第05讲_割补法巧算面积

第五讲割补法巧算面积在上一讲中,我们学习了如何计算格点图形的面积,介绍了正方形格点图形和三角形格点图形的面积计算公式.根据公式,我们可以求出正方形格点图形的面积是最小正方形面积的几倍,或者求出三角形格点图形面积是最小正三角形面积的几倍.随着几何学习的步步深入,大家会发现除了用公式法直接求面积之外,还有很多间接求面积的方法.尤其是对于不规则图形,我们并不知道这些图形的面积公式,但是可以把它们通过分割、添补等各种方式变换为规则的图形.例题1图中的数字分别表示对应线段的长度,试求下面多边形的面积.(单位:厘米)「分析」这是一个不规则图形,我们能不能把它切成很多规则的小块,一块一块地求面积呢?练习1图中的数字分别表示对应线段的长度,试求下面多边形的面积.(单位:厘米)我们可以看到,在没有格点的情况下,割补的方法仍然可以使用.我们将来做几何面积计算时,就要视情况灵活运用割补法.例题2如图所示,在正方形ABCD 内部有一个长方形EFGH .已知正方形ABCD 的边长是6厘米,图中线段AE 、AH 都等于2厘米.求长方形EFGH 的面积.「分析」所求长方形的长、宽都是未知且不可求的,但是正方形面积以及周围四个直角三角形面积都是可以计算出来的,那么长方形面积怎么计算呢?1 2234 5 3 2 4 3412 4 9 DG如图所示,在正方形ABCD 内部有三角形CEF .已知正方形ABCD 的边长是6厘米,图中线段AE 、AF 都等于2厘米.求三角形CEF 的面积.例题3如图所示,大正方形的边长为10厘米.连接大正方形的各边中点得小正方形,将小正方形每边三等分,再将三等分点与大正方形的中心和一个顶点相连,那么图中阴影部分的面积总和等于多少平方厘米?「分析」阴影部分零零散散,能不能通过割补的方法把它变成规则的图形嗯?练习3如图所示,大正三角形的面积为10平方厘米.连接大正三角形的各边中点得到四个小正三角形,取各个小正三角形的中心,再将每个小正三角形的中心和顶点相连,得到三个一样的小三角形,那么图中阴影部分的面积总和等于多少平方厘米?例题4如图,把两个相同的正三角形的各边分别三等分和四等分,并连接这些等分点.已知图1中阴影部分的面积是48平方分米.请问:图2中阴影部分的面积是多少平方分米?「分析」图1和图2中最小正三角形的面积是不一样的,但两个大正三角形面积却是一样的,你能求出大正三角形的面积吗?D图2如图,把两个同样大小的正方形分别分成55⨯和33⨯的方格表.图1阴影部分的面积是162,请问图2中阴影部分的面积是多少?例题4中的阴影部分都是同样形状的花图形,我们不能直接看出花图形和大正三角形的面积之间有什么倍数关系,但是借助一块块小正三角形,我们把花图形和大正三角形之间联系起来,看看它们各自占了多少个小正三角形.找到面积之间的联系,是解决类似问题的钥匙.有些图形看起来没有分割成一些相同的小图形,实际上不过是将分割线隐藏起来或者只出现了其中的一部分,需要我们自己进行分割.例题5如图,在两个相同的等腰直角三角形中各作一个正方形,如果正方形A 的面积是36平方厘米,那么正方形B 的面积是多少平方厘米?「分析」乍一看上去和例题2有些相似,我们能不能求出大等腰直角三角形的面积呢?它的面积和正方形A 、B 之间有什么关系呢?例题6如图所示,已知一个四边形的两条边的长度和三个角的度数,这个四边形的面积是多少平方厘米?(单位:厘米)「分析」这个四边形并不规则,直接求面积似乎有些困难.我们已经知道了其中的三个角,其中有直角也有45°角.你能从这两种“特殊角”发现图形的特点吗?图1课堂内外毕式定理据说毕达哥拉斯有次应邀参加一位富有政要的餐会,这位主人豪华宫殿般的餐厅铺着正方形美丽的大理石地砖,由于大餐迟迟不上桌,这些饥肠辘辘的贵宾颇有怨言;但这位善于观察和理解的数学家却凝视脚下这些排列规则、美丽的方形瓷砖,但毕达哥拉斯不仅仅是欣赏瓷砖的美丽,而是想到它们和数之间的关系,于是拿了画笔并且蹲在地板上,选了一块瓷砖以它的对角线AB为边画一个正方形,他发现这个正方形面积恰好等于两块瓷砖的面积和.他很好奇……于是再以两块瓷砖拼成的矩形之对角线作另一个正方形,他发现这个正方形之面积等于5块瓷砖的面积,也就是以两股为边作正方形面积之和.至此毕达哥拉斯作了大胆的假设:任何直角三角形,其斜边的平方恰好等于另两边平方之和.那一顿饭,这位古希腊数学大师,视线都一直没有离开地面.这就是著名的毕式定理:在任何一个直角三角形中(等腰直角三角形也算在内),两条直角边的长度的平方和等于斜边长度的平方.实际上,早在毕达哥拉斯之前,许多民族已经发现了这个事实,而且巴比伦、埃及、中国、印度等的发现都有真凭实据,有案可查.相反,毕达哥拉斯的著作却什么也没有留传下来,关于他的这个故事都是后人辗转传播的.可以说真伪难辨.这个现象的确不太公平,之所以这样,是因为现代的数学和科学来源于西方,而西方的数学及科学又来源于古希腊,古希腊流传下来的最古老的著作是欧几里得的《几何原本》,而其中许多定理再往前追溯,自然就落在毕达哥拉斯的头上.他常常被推崇为“数论的始祖”,而在他之前的泰勒斯被称为“几何的始祖”,西方的科学史一般就上溯到此为止了.至于希腊科学的起源只是近一二百年才有更深入的研究.因此,毕达哥拉斯定理这个名称一时半会儿改不了.不过,在中国,因为我们的老祖宗也研究过这个问题,因此称为商高定理,更普遍地则称为勾股定理.中国古代把直角三角形中较短的直角边叫做勾,较长的直角边叫做股,斜边叫做弦.作业1. 下图中的数字分别表示对应线段的长度,图中多边形的面积是多少?2. 如下图所示,在正方形ABCD 内部有梯形EHGF .已知正方形ABCD 的边长是6厘米,图中线段AE 、AH 、BF 、DG 都等于2厘米.则梯形EHGF 的面积是多少平方厘米?3. 如图所示,平行四边形的面积是12,把一条对角线四等分,将四等分点与平行四边形另外两个顶点相连.图中阴影部分的面积总和是多少?4. 下图中空白部分的面积是100,那么阴影正方形的面积是多少?5. 如图所示,正六边形ABCDEF 的面积是36.阴影正六边形的面积是多少? D G 32 434 12 423 3 3 3。
割补法巧算面积

割补法巧算面积知识精讲:分割法:把不规则的的大图形化为规则的小图形添补法:把不规则图形周围添上规则的小图形,使总面积便于计算例题1图中的数字分别表示对应线段的长度,试求下面多边形的面积. (单位:厘米)8 2练习1如图中的每个数字分别表示所对应的线段的长度(单位:米)•这个图形的面积等于多少平例题2如图,在正方形ABCD内部有一个长方形. EFGH .已知正方形ABCD的边长是6厘米, 图中线段AE、AH都等于2厘米.求长方形EFGH的面积.练习2正方形ABCD的边长是8厘米,它的内部有一个三角形AEF (如图),线段DF=3.6厘米, BE=2.8厘米,那么三角形AEF的面积等于_______________ 平方厘米.B例题3如图中,大正方形的边长为10厘米.连接大正方形的各边中点得小正方形,将小正方形每边三等份,再将三等分点与大正方形的中心和一个顶点相连,那么图中阴影部分的面积总和等于多少平方厘米?练习3.21如图所示,正方形ABCD的边长acm,则图中阴影部分的面积为______________________ cm •A D例题4.如图1和图2,把两个相同的正三角形的各边分别五等分和七等分,并连接这些分点.已知图1中阴影部分的面积是294平方分米.请问:图2中的阴影部分的面积是多少平方分米?练习47.如图所示,将三个相同的长方形从上到下排列,依次进行两等分、三等分、四等分,各取出其中的一份画上阴影,则阴影部分的面积占全部面积的几分之几?例6.选做题例5如图,在两个相同的等腰直角三角形中各作一个正方形,如果正方形平方厘米,那么正方形B的面积是多少平方厘米?A的面积是36已知一个四边形 ABCD 的两条边的长度和三个角(如下图所示),求四边形ABCD 的面积是多少? 作业:1•如图所示,平行四边形的面积是 12,把一条对角线四等分, 将四等分点与平行四边形另外 两个顶点相连•图中阴影部分的面积总和是多少?2. . (2013秋?诸暨市校级期中)如图,已知一个四边形的四条边 分别是3, 4, 13和12,其中/ B=90。
小升初奥数巧求面积---割补法

11
解析
因为不知道梯形的高,所以不能直接求出梯形的面 积。可以从等腰直角三角形与正方形之间的联系上考 虑。将四个同样的等腰直角三角形拼成一个正方形, 图中阴影部分是边长9厘米与边长5厘米的两个正方 形面积之差,也是所求梯形面积的4倍。所以所求梯 形面积是(9× 9-5× 5)÷4=14(平方厘米)。
6
例3.求图中阴影部分的面积
7
解析
如图所示,将左下角的阴影部分分为两部分,然后按照右下图所示, 将这两部分分别拼补在阴影位置。可以看出,原题图的阴影部分等 于右下图中AB弧所形成的弓形,其面积等于扇形OAB与三角形 OAB的面积之差。 解: π× 4× 4÷ 4-4× 4÷ 2=4.56。
8
例4. 在一个等腰三角形中,两条与底边平行的线段将三角形的两 条边等分成三段(见下图),求图中阴影部分的面积占整个图形 面积的几分之几。
9厘米 5厘米
12
例6.ABC是三个圆的圆心,圆的半径都是10分米,求阴 影部分的面积。
D
B
F
A
C
E
13
解析
我们用割补法,将阴影部分割补 成一个半圆形,求出阴影部分面 积就可以了。 S半圆=10× 10× 3.14÷ 2=157平方 分米
D
B
F
A
C
E
14
例7.如图所示,空白部分占正方形面积的 几分之几?
S正=(5× 2)×(5× 2)=100(平方厘米) S阴=157+100=257(平方厘米)
4
例2.求图中阴影部分的面积
5
解析
在图中分割的两个正方形中,右边正方形的 阴影部分是半径为5的四分之一个圆,在左 边正方形中空白部分是半径为5的四分之一 个圆。 如右图所示,将右边的阴影部分平移到左边 正方形中。可以看出,原题图的阴影部分正 好等于一个正方形的面积,5× 5=25。
割补法求面积经典例题

割补法求面积经典例题当涉及到计算面积的经典例题时,割补法是一种常用且有效的方法。
下面割补法求面积的经典例题:1. 一个矩形的长为10cm,宽为5cm,求其面积。
解:面积= 长×宽= 10cm ×5cm = 50cm²2. 一个正方形的边长为7cm,求其面积。
解:面积= 边长×边长= 7cm ×7cm = 49cm²3. 一个圆的半径为3cm,求其面积(取π=3.14)。
解:面积= π×半径²= 3.14 ×3cm ×3cm = 28.26cm²4. 一个梯形的上底长为6cm,下底长为8cm,高为4cm,求其面积。
解:面积= (上底长+ 下底长)×高÷2 = (6cm + 8cm)×4cm ÷2 = 28cm²5. 一个三角形的底边长为9cm,高为12cm,求其面积。
解:面积= 底边长×高÷2 = 9cm ×12cm ÷2 = 54cm²6. 一个平行四边形的底边长为10cm,高为6cm,求其面积。
解:面积= 底边长×高= 10cm ×6cm = 60cm²7. 一个等边三角形的边长为5cm,求其面积。
解:面积= (边长²×√3)÷4 = (5cm ×5cm ×√3)÷4 ≈10.83cm ²8. 一个正五边形的边长为8cm,求其面积。
解:面积= (5 ×边长²×√5)÷4 = (5 ×8cm ×8cm ×√5)÷4 ≈110.85cm²9. 一个正六边形的边长为12cm,求其面积。
解:面积= (6 ×边长²×√3)÷4 = (6 ×12cm ×12cm ×√3)÷4 ≈374.12cm²10. 一个扇形的半径为5cm,圆心角为60°,求其面积(取π=3.14)。
第三讲:割补法求面积

第三讲:割补法求面积
《智乐数学》---智启思维乐享学
巧求面积(一)
第三讲:割补法求面积
【例题】
如图,一块正方形的玻璃,长截去2厘米,宽截去3厘米后,剩下的小长方形比原来的面积少29平方厘米,求这块正方形玻璃原来的面积是多少?
【习题】
1. 一块正方形的玻璃,长截去2厘米,宽截去6厘米后,剩下的小长方形比原
来少308平方厘米。
原来正方形玻璃的面积是多少?
2. 一块正方形玻璃,一边截去4厘米,另一边截去3厘米,剩下的小长方形比
原来正方形的面积少44平方厘米,原来正方形玻璃的面积是多少?
3. 如下图,大正方形的边长是40厘米,中间是一个小正方形,A 、
B 、
C 、
D 是大
正方形各边的中点,求中间小正方形的面积。
2
3C B D
A。
高斯小学奥数四年级下册含答案第05讲_割补法巧算面积

第五讲割补法巧算面积在上一讲中,我们学习了如何计算格点图形的面积,介绍了正方形格点图形和三角形格点图形的面积计算公式.根据公式,我们可以求出正方形格点图形的面积是最小正方形面积的几倍,或者求出三角形格点图形面积是最小正三角形面积的几倍.随着几何学习的步步深入,大家会发现除了用公式法直接求面积之外,还有很多间接求面积的方法.尤其是对于不规则图形,我们并不知道这些图形的面积公式,但是可以把它们通过分割、添补等各种方式变换为规则的图形.例题1图中的数字分别表示对应线段的长度,试求下面多边形的面积.分析」这是一个不规则图形,我们能不能把它切成很多规则的小块,练习1图中的数字分别表示对应线段的长度,试求下面多边形的面积.我们可以看到,在没有格点的情况下,割补的方法仍然可以使用.计算时,就要视情况灵活运用割补法.例题2「分析」所求长方形的长、宽都是未知且不可求的,形面积都是可以计算出来的,那么长方形面积怎单位:厘米)一块一块地求面积呢?单位:厘米)我们将来做几何面积如图所示,在正方形ABCD 内部有一个长方形EFGH .已知正方形ABCD 的边长是6 厘米,图中线段AE、AH 都等于2 厘米.求长方形EFGH 的面积.但是正方形面积以及周围四个直角三角么计算呢?练习2如图所示,在正方形ABCD 内部有三角形CEF .已知正方形ABCD 的边长是6 厘米,图中线段AE 、AF 都等于2 厘米.求三角形CEF 的面积.3例题如图所示,大正方形的边长为10 厘米.连接大正方形的各边中点得小正方形,将小正方形每边三等分,再将三等分点与大正方形的中心和一个顶点相连,那么图中阴影部分的面积总和等于多少平方厘米?分析」阴影部分零零散散,能不能通过割补的方法把它变成规则的图形嗯?练习3如图所示,大正三角形的面积为10 平方厘米.连接大正三角形的各边中点得到四个小正三角形,取各个小正三角形的中心,再将每个小正三角形的中心和顶点相连,得到三个一样的小三角形,那么图中阴影部分的面积总和等于多少平方厘米?例题4 如图,把两个相同的正三角形的各边分别三等分和四等分,并连接这些等分点.已知图1 中阴影部分的面积是48平方分米.请问:图2中阴影部分的面积是多少平方分米?图1 图2分析」图1和图2中最小正三角形的面积是不一样的,但两个大正三角形面积却是样的,你能求出大正三角形的面积吗?7例题 4 中的阴影部分都是同样形状的花图形, 我们不能直接看出花图形和大正三角形的 面积之间有什么倍数关系, 但是借助一块块小正三角形, 我们把花图形和大正三角形之间联 系起来, 看看它们各自占了多少个小正三角形. 找到面积之间的联系, 是解决类似问题的钥 匙.有些图形看起来没有分割成一些相同的小图形, 实际上不过是将分割线隐藏起来或者只 出现了其中的一部分,需要我们自己进行分割.例题 5 如图,在两个相同的等腰直角三角形中各作一个正方形,如果正方形 A 的面积是 36 平 方厘米,那么正方形 B 的面积是多少平方厘米?「分析」乍一看上去和例题 2有些相似, 我们能不能求出大等腰直角三角形的面积呢? 它的面积和正方形 A 、B 之间有什么关系呢?例题 6如图所示,已知一个四边形的两条边的长度和三个角的度数, 这个四边形的面积是多少平方厘米?(单位:厘米)「分析」 这个四边形并不规则,直接求面积似乎有些困难.我们已 经知道了其中的三个角, 其中有直角也有 45°角.你能从这两种 “特 殊角”发现图形的特点吗?练习 4图1图2毕式定理据说毕达哥拉斯有次应邀参加一位富有政要的餐会,这位主人豪华宫殿般的餐厅铺着正方形美丽的大理石地砖,由于大餐迟迟不上桌,这些饥肠辘辘的贵宾颇有怨言;但这位善于观察和理解的数学家却凝视脚下这些排列规则、美丽的方形瓷砖,但毕达哥拉斯不仅仅是欣赏瓷砖的美丽,而是想到它们和数之间的关系,于是拿了画笔并且蹲在地板上,选了一块瓷砖以它的对角线AB 为边画一个正方形,他发现这个正方形面积恰好等于两块瓷砖的面积和.他很好奇⋯⋯于是再以两块瓷砖拼成的矩形之对角线作另一个正方形,他发现这个正方形之面积等于5 块瓷砖的面积,也就是以两股为边作正方形面积之和.至此毕达哥拉斯作了大胆的假设:任何直角三角形,其斜边的平方恰好等于另两边平方之和.那一顿饭,这位古希腊数学大师,视线都一直没有离开地面.这就是著名的毕式定理:在任何一个直角三角形中(等腰直角三角形也算在内),两条直角边的长度的平方和等于斜边长度的平方.实际上,早在毕达哥拉斯之前,许多民族已经发现了这个事实,而且巴比伦、埃及、中国、印度等的发现都有真凭实据,有案可查.相反,毕达哥拉斯的著作却什么也没有留传下来,关于他的这个故事都是后人辗转传播的.可以说真伪难辨.这个现象的确不太公平,之所以这样,是因为现代的数学和科学来源于西方,而西方的数学及科学又来源于古希腊,古希腊流传下来的最古老的著作是欧几里得的《几何原本》,而其中许多定理再往前追溯,自然就落在毕达哥拉斯的头上.他常常被推崇为“数论的始祖” ,而在他之前的泰勒斯被称为“几何的始祖” ,西方的科学史一般就上溯到此为止了.至于希腊科学的起源只是近一二百年才有更深入的研究.因此,毕达哥拉斯定理这个名称一时半会儿改不了.不过,在中国,因为我们的老祖宗也研究过这个问题,因此称为商高定理,更普遍地则称为勾股定理.中国古代把直角三角形中较短的直角边叫做勾,较长的直角边叫做股,斜边叫做弦.作业图中的数字分别表示对应线段的长度,图中多边形的面积是多少? 12如下图所示, 在正方形 ABCD 内部有梯形 EHGF .已知正方形 ABCD 的边长是 6 厘米, 图中线段 AE 、AH 、BF 、DG 都等于 2厘米.则梯形 EHGF 的面积是多少平方厘米?如图所示,平行四边形的面积是 12,把一条对角线四等分,将四等分点与平行四边形 另外两个顶点相连.图中阴影部分的面积总和是多少?4. 下图中空白部分的面积是 100,那么阴影正方形的面积是多少?5. 如图所示,正六边形 ABCDEF 的面积是 36.阴影正六边形的面积是多少?1.2.3. C D第五讲割补法巧算面积1.例题1 答案:32 平方厘米详解:对这个图形进行简单分割后,分别求面积再相加.32 平方厘米.2.例题2答案:16 平方厘米详解:正方形面积是36 平方厘米,三角形AEH 、FCG 的面积是2 平方厘米,三角形EBF 、GDH 的面积是8 平方厘米.长方形EFGH 的面积是36 2 2 8 2 16 平方厘米.3.例题3 答案:50 平方厘米详解:首先可把小正方形中间的阴影部分添补到相对应的空白处,中间小正方形的面积等于四个角上的阴影三角形的面积和.可连接正方形对边的中点,也可以把四个三角形向中间对折都可以说明阴影部分的面积是正方形面积的一半,即为10 10 2 50平方厘米.4.例题4 答案:27 平方厘米详解:图1中大三角形被分成9块,阴影部分面积占3块,面积是48 平方分米,那么每个小三角面积是16 平方分米,大三角形面积是16 9 144平方分米.图2 中大三角形被分成了16 块,那么每个小三角形的面积是144 16 9 平方分米,阴影部分面积是9 3 27 平方分米.5.例题5答案:32 平方厘米详解:对图形进行如左图的分割,通过第一个图,我们知道等腰直角三角形的面积8 平方厘米,正方形B 的面积是32 平方厘米.6.例题6答案:20 平方厘米详解:如图所示,把原图添补成一个大的等腰直角三角形.需要将多余的小直角三角形去掉才是原图.大等腰直角三角形的底是7 厘米,高是7厘米,所以面积是7 7 2 24.5平方厘米;小等腰直角三角形的底是3 厘米,高是3 厘米,所以面积是3 3 2 4.5 平方厘米.所以四边形的面积是24.5 4.5 20 平方厘米.7.练习1答案:78 平方厘米详解:4 9 2 3 3 12 78 平方厘米.38.练习2 答案:10 平方厘米详解:正方形面积是36 平方厘米,三角形AEF 的面积是2平方厘米,三角形BEC 、DFC 的面积都是12 平方厘米.三角形EFC 的面积是36 2 12 12 10 平方厘米.9.练习3 答案:5简答:大正三角形被分成12块,阴影部分占6块,占总个数的一半,面积为5 平方厘米.10.练习4 答案:150简答:图1 中大正方形被分成25 块,阴影部分面积占18 块,面积是162 ,那么每个小正方形面积是9,大正方形面积是25 9 225 .图2 中大正方形被分成了9 块,那么每个小正方形的面积是225 9 25 ,阴影部分面积是25 6 150 .11.作业1答案:84简答:3 12 4 3 3 3 3 2 2 84 平方厘米.12.作业2答案:18简答:首先求出大正方形的面积,再求出各个角上的小三角形的边长和面积.然后把大正方形的面积减去四个小三角形的面积就得梯形的面积.13.作业3 答案:6 简答:将右上两个阴影三角形切下来添到左侧空白处,使其拼成一个大的三角形.阴影面积是平行四边形面积的一半.所以阴影部分的面积是6.14.作业4答案:80简答:对三角形进行分割,能知道每个小三角形的面积是100 5 20 ,阴影正方形的面积是80.15.作业5答案:9简答:把大六边形划分为24 个小正三角形,其中阴影部分可以分成6 个小正三角形,所以大六边形是阴影部分面积的4 倍,正六边形面积是36 ,阴影部分的面积是36 49 .。
高斯小学奥数四年级下册含答案第05讲_割补法巧算面积

第五讲割补法巧算面积在上一讲中,我们学习了如何计算格点图形的面积,介绍了正方形格点图形和三角形格点图形的面积计算公式.根据公式,我们可以求出正方形格点图形的面积是最小正方形面积的几倍,或者求出三角形格点图形面积是最小正三角形面积的几倍.随着几何学习的步步深入,大家会发现除了用公式法直接求面积之外,还有很多间接求面积的方法.尤其是对于不规则图形,我们并不知道这些图形的面积公式,但是可以把它们通过分割、添补等各种方式变换为规则的图形.例题1图中的数字分别表示对应线段的长度,试求下面多边形的面积.(单位:厘米)「分析」这是一个不规则图形,我们能不能把它切成很多规则的小块,一块一块地求面积呢? 练习1图中的数字分别表示对应线段的长度,试求下面多边形的面积.(单位:厘米)我们可以看到,在没有格点的情况下,割补的方法仍然可以使用.我们将来做几何面积计算时,就要视情况灵活运用割补法.例题2如图所示,在正方形ABCD 内部有一个长方形EFGH .已知正方形ABCD 的边长是6厘米,图中线段AE 、AH 都等于2厘米.求长方形EFGH 的面积.「分析」所求长方形的长、宽都是未知且不可求的,但是正方形面积以及周围四个直角三角形面积都是可以计算出来的,那么长方形面积怎么计算呢?1 223 453 2 4341249 DG如图所示,在正方形ABCD 内部有三角形CEF .已知正方形ABCD 的边长是6厘米,图中线段AE 、AF 都等于2厘米.求三角形CEF 的面积.例题3如图所示,大正方形的边长为10厘米.连接大正方形的各边中点得小正方形,将小正方形每边三等分,再将三等分点与大正方形的中心和一个顶点相连,那么图中阴影部分的面积总和等于多少平方厘米?「分析」阴影部分零零散散,能不能通过割补的方法把它变成规则的图形嗯? 练习3如图所示,大正三角形的面积为10平方厘米.连接大正三角形的各边中点得到四个小正三角形,取各个小正三角形的中心,再将每个小正三角形的中心和顶点相连,得到三个一样的小三角形,那么图中阴影部分的面积总和等于多少平方厘米?例题4如图,把两个相同的正三角形的各边分别三等分和四等分,并连接这些等分点.已知图1中阴影部分的面积是48平方分米.请问:图2中阴影部分的面积是多少平方分米?「分析」图1和图2中最小正三角形的面积是不一样的,但两个大正三角形面积却是一样的,你能求出大正三角形的面积吗?D图2如图,把两个同样大小的正方形分别分成55⨯和33⨯的方格表.图1阴影部分的面积是162,请问图2中阴影部分的面积是多少?例题4中的阴影部分都是同样形状的花图形,我们不能直接看出花图形和大正三角形的面积之间有什么倍数关系,但是借助一块块小正三角形,我们把花图形和大正三角形之间联系起来,看看它们各自占了多少个小正三角形.找到面积之间的联系,是解决类似问题的钥匙.有些图形看起来没有分割成一些相同的小图形,实际上不过是将分割线隐藏起来或者只出现了其中的一部分,需要我们自己进行分割. 例题5如图,在两个相同的等腰直角三角形中各作一个正方形,如果正方形A 的面积是36平方厘米,那么正方形B 的面积是多少平方厘米?「分析」乍一看上去和例题2有些相似,我们能不能求出大等腰直角三角形的面积呢?它的面积和正方形A 、B 之间有什么关系呢? 例题6如图所示,已知一个四边形的两条边的长度和三个角的度数,这个四边形的面积是多少平方厘米?(单位:厘米)「分析」这个四边形并不规则,直接求面积似乎有些困难.我们已经知道了其中的三个角,其中有直角也有45°角.你能从这两种“特殊角”发现图形的特点吗?图1课堂内外毕式定理据说毕达哥拉斯有次应邀参加一位富有政要的餐会,这位主人豪华宫殿般的餐厅铺着正方形美丽的大理石地砖,由于大餐迟迟不上桌,这些饥肠辘辘的贵宾颇有怨言;但这位善于观察和理解的数学家却凝视脚下这些排列规则、美丽的方形瓷砖,但毕达哥拉斯不仅仅是欣赏瓷砖的美丽,而是想到它们和数之间的关系,于是拿了画笔并且蹲在地板上,选了一块瓷砖以它的对角线AB为边画一个正方形,他发现这个正方形面积恰好等于两块瓷砖的面积和.他很好奇……于是再以两块瓷砖拼成的矩形之对角线作另一个正方形,他发现这个正方形之面积等于5块瓷砖的面积,也就是以两股为边作正方形面积之和.至此毕达哥拉斯作了大胆的假设:任何直角三角形,其斜边的平方恰好等于另两边平方之和.那一顿饭,这位古希腊数学大师,视线都一直没有离开地面.这就是著名的毕式定理:在任何一个直角三角形中(等腰直角三角形也算在内),两条直角边的长度的平方和等于斜边长度的平方.实际上,早在毕达哥拉斯之前,许多民族已经发现了这个事实,而且巴比伦、埃及、中国、印度等的发现都有真凭实据,有案可查.相反,毕达哥拉斯的著作却什么也没有留传下来,关于他的这个故事都是后人辗转传播的.可以说真伪难辨.这个现象的确不太公平,之所以这样,是因为现代的数学和科学来源于西方,而西方的数学及科学又来源于古希腊,古希腊流传下来的最古老的著作是欧几里得的《几何原本》,而其中许多定理再往前追溯,自然就落在毕达哥拉斯的头上.他常常被推崇为“数论的始祖”,而在他之前的泰勒斯被称为“几何的始祖”,西方的科学史一般就上溯到此为止了.至于希腊科学的起源只是近一二百年才有更深入的研究.因此,毕达哥拉斯定理这个名称一时半会儿改不了.不过,在中国,因为我们的老祖宗也研究过这个问题,因此称为商高定理,更普遍地则称为勾股定理.中国古代把直角三角形中较短的直角边叫做勾,较长的直角边叫做股,斜边叫做弦.作业1. 下图中的数字分别表示对应线段的长度,图中多边形的面积是多少?2. 如下图所示,在正方形ABCD 内部有梯形EHGF .已知正方形ABCD 的边长是6厘米,图中线段AE 、AH 、BF 、DG 都等于2厘米.则梯形EHGF 的面积是多少平方厘米?3. 如图所示,平行四边形的面积是12,把一条对角线四等分,将四等分点与平行四边形另外两个顶点相连.图中阴影部分的面积总和是多少?4. 下图中空白部分的面积是100,那么阴影正方形的面积是多少?5. 如图所示,正六边形ABCDEF 的面积是36.阴影正六边形的面积是多少?D G324 34 1242 3 33 3第五讲 割补法巧算面积1. 例题1答案:32平方厘米详解:对这个图形进行简单分割后,分别求面积再相加. 32243632⨯+⨯+⨯=平方厘米.也可对图形进行添补.(如右图)2.例题2答案:16平方厘米详解:正方形面积是36平方厘米,三角形AEH 、FCG 的面积是2平方厘米,三角形EBF 、GDH 的面积是8平方厘米.长方形EFGH 的面积是36228216-⨯-⨯=平方厘米.3. 例题3答案:50平方厘米详解:首先可把小正方形中间的阴影部分添补到相对应的空白处,中间小正方形的面积等于四个角上的阴影三角形的面积和.可连接正方形对边的中点,也可以把四个三角形向中间对折都可以说明阴影部分的面积是正方形面积的一半,即为1010250⨯÷=平方厘米. 4. 例题4答案:27平方厘米详解:图1中大三角形被分成9块,阴影部分面积占3块,面积是48平方分米,那么每个小三角面积是16平方分米,大三角形面积是169144⨯=平方分米. 图2中大三角形被分成了16块,那么每个小三角形的面积是144169÷=平方分米,阴影部分面积是9327⨯=平方分米. 5. 例题5答案:32平方厘米详解:对图形进行如左图的分割,通过第一个图,我们知道等腰直角三角形的面积8平方厘米,正方形B 的面1 2 2 3 4 5 1 22 3 45积是32平方厘米.6. 例题6答案:20平方厘米详解:如图所示,把原图添补成一个大的等腰直角三角形.需要将多余的小直角三角形去掉才是原图.大等腰直角三角形的底是7厘米,高是7厘米,所以面积是77224.5⨯÷=平方厘米;小等腰直角三角形的底是3厘米,高是3厘米,所以面积是332 4.5⨯÷=平方厘米.所以四边形的面积是24.5 4.520-=平方厘米.7. 练习1答案:78平方厘米详解:492331278⨯+⨯+⨯=平方厘米.8. 练习2答案:10平方厘米详解:正方形面积是36平方厘米,三角形AEF 的面积是2平方厘米,三角形BEC 、DFC 的面积都是12平方厘米.三角形EFC 的面积是362121210---=平方厘米.9. 练习3答案:5简答:大正三角形被分成12块,阴影部分占6块,占总个数的一半,面积为5平方厘米.10. 练习4答案:1503 243 4124 9简答:图1中大正方形被分成25块,阴影部分面积占18块,面积是162,那么每个小正方形面积是9,大正方形面积是259225⨯=.图2中大正方形被分成了9块,那么每个小正方形的面积是225925÷=,阴影部分面积是256150⨯=.11. 作业1答案:84简答:()312433332284⨯+⨯+++⨯⨯=平方厘米.12. 作业2答案:18简答:首先求出大正方形的面积,再求出各个角上的小三角形的边长和面积.然后把大正方形的面积减去四个小三角形的面积就得梯形的面积. 13. 作业3答案:6简答:将右上两个阴影三角形切下来添到左侧空白处,使其拼成一个大的三角形.阴影面积是平行四边形面积的一半.所以阴影部分的面积是6. 14. 作业4答案:80简答:对三角形进行分割,能知道每个小三角形的面积是100520÷=,阴影正方形的面积是80.15. 作业5答案:9简答:把大六边形划分为24个小正三角形,其中阴影部分可以分成6个小正三角形,所以大六边形是阴影部分面积的4倍,正六边形面积是36,阴影部分的面积是3649÷=.。
割补法巧算面积

割补法巧算面积割补法巧算面积知识精讲:分割法:把不规则的的大图形化为规则的小图形添补法:把不规则图形周围添上规则的小图形,使总面积便于计算例题1图中的数字分别表示对应线段的长度,试求下面多边形的面积.(单位:厘米)练习1如图中的每个数字分别表示所对应的线段的长度(单位:米).这个图形的面积等于多少平方米?例题2如图,在正方形ABCD内部有一个长方形.EFGH.已知正方形ABCD的边长是6厘米,图中线段AE、AH都等于2厘米.求长方形EFGH 的面积.例题4. 如图1和图2,把两个相同的正三角形的各边分别五等分和七等分,并连接这些分点.已知图1中阴影部分的面积是294平方分米.请问:图2中的阴影部分的面积是多少平方分米?练习47.如图所示,将三个相同的长方形从上到下排列,依次进行两等分、三等分、四等分,各取出其中的一份画上阴影,则阴影部分的面积占全部面积的几分之几?选做题例5 如图,在两个相同的等腰直角三角形中各作一个正方形,如果正方形A的面积是36平方厘米,那么正方形B的面积是多少平方厘米?例6.已知一个四边形ABCD的两条边的长度和三个角(如下图所示),求四边形ABCD的面积是多少?作业:1.如图所示,平行四边形的面积是12,把一条对角线四等分,将四等分点与平行四边形另外两个顶点相连. 图中阴影部分的面积总和是多少?2. .(2013秋•诸暨市校级期中)如图,已知一个四边形的四条边AB,BC,CD和DA的长分别是3,4,13和12,其中∠B=90°,求这个四边形的面积3. 求阴影部分面积.4.求阴影部分面积.5. 求阴影部分面积:6.求阴影部分面积.7. 求阴影部分面积.8.(2011秋•宁波期中)求阴影部分的面积.9. 求阴影部分的面积.10. 求阴影部分的面积.11.求阴影部分的面积.12.求阴影部分的面积.。
割补法巧算面积
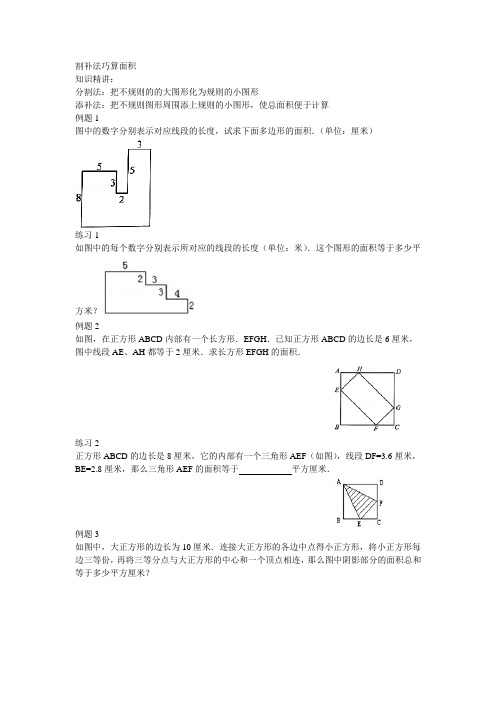
割补法巧算面积知识精讲:分割法:把不规则的的大图形化为规则的小图形添补法:把不规则图形周围添上规则的小图形,使总面积便于计算例题1图中的数字分别表示对应线段的长度,试求下面多边形的面积.(单位:厘米)练习1如图中的每个数字分别表示所对应的线段的长度(单位:米).这个图形的面积等于多少平方米?例题2如图,在正方形ABCD内部有一个长方形.EFGH.已知正方形ABCD的边长是6厘米,图中线段AE、AH都等于2厘米.求长方形EFGH的面积.练习2正方形ABCD的边长是8厘米,它的内部有一个三角形AEF(如图),线段DF=3.6厘米,BE=2.8厘米,那么三角形AEF的面积等于平方厘米.例题3如图中,大正方形的边长为10厘米.连接大正方形的各边中点得小正方形,将小正方形每边三等份,再将三等分点与大正方形的中心和一个顶点相连,那么图中阴影部分的面积总和等于多少平方厘米?练习3.1.如图所示,正方形ABCD的边长acm,则图中阴影部分的面积为cm2.例题4. 如图1和图2,把两个相同的正三角形的各边分别五等分和七等分,并连接这些分点.已知图1中阴影部分的面积是294平方分米.请问:图2中的阴影部分的面积是多少平方分米?练习47.如图所示,将三个相同的长方形从上到下排列,依次进行两等分、三等分、四等分,各取出其中的一份画上阴影,则阴影部分的面积占全部面积的几分之几?选做题例5 如图,在两个相同的等腰直角三角形中各作一个正方形,如果正方形A的面积是36平方厘米,那么正方形B的面积是多少平方厘米?例6.已知一个四边形ABCD的两条边的长度和三个角(如下图所示),求四边形ABCD的面积是多少?作业:1.如图所示,平行四边形的面积是12,把一条对角线四等分,将四等分点与平行四边形另外两个顶点相连. 图中阴影部分的面积总和是多少?2. .(2013秋•诸暨市校级期中)如图,已知一个四边形的四条边AB,BC,CD和DA的长分别是3,4,13和12,其中∠B=90°,求这个四边形的面积3. 求阴影部分面积.4.求阴影部分面积.5. 求阴影部分面积:6.求阴影部分面积.7. 求阴影部分面积.8.(2011秋•宁波期中)求阴影部分的面积.9. 求阴影部分的面积.10. 求阴影部分的面积.11.求阴影部分的面积.12.求阴影部分的面积.。
小升初几何-用割补法巧求面积

小升初几何之---用割补法求面积在组合图形中,除了多边形外,还有由圆、扇形、弓形与三角形、矩形、平行四边形、梯形等图形组合而成的不规则图形,为了计算它们的面积,常常需要变动图形的位置或对图形进行分割、旋转、拼补,使它变成可以计算出面积的规则图形。
就是在多边形的组合图形中,为了计算面积,有时也要用到割补的方法。
例1求下列各图中阴影部分的面积:分析与解:(1)如左下图所示,将左下角的阴影部分分为两部分,然后按照右下图所示,将这两部分分别拼补在阴影位置。
可以看出,原题图的阴影部分等于右下图中AB 弧所形成的弓形,其面积等于扇形OAB与三角形OAB的面积之差。
π×4×4÷4-4×4÷2=4.56。
(2)在题图虚线分割的两个正方形中,右边正方形的阴影部分是半径为5的四分之一个圆,在左边正方形中空白部分是半径为5的四分之一个圆。
如下图所示,将右边的阴影部分平移到左边正方形中。
可以看出,原题图的阴影部分正好等于一个正方形的面积,为5×5=25。
例2在一个等腰三角形中,两条与底边平行的线段将三角形的两条边等分成三段(见右图),求图中阴影部分的面积占整个图形面积的几分之几。
分析与解:阴影部分是一个梯形。
我们用三种方法解答。
(1)割补法从顶点作底边上的高,得到两个相同的直角三角形。
将这两个直角三角(2)拼补法将两个这样的三角形拼成一个平行四边形(下页左上图)。
积和平行四边行面积同时除以2,商不变。
所以原题阴影部分占整个图形面(3)等分法将原图等分成9个小三角形(见右上图),阴影部分占3个小三角形,注意,后两种方法对任意三角形都适用。
也就是说,将例题中的等腰三角形换成任意三角形,其它条件不变,结论仍然成立。
例3如左下图所示,在一个等腰直角三角形中,削去一个三角形后,剩下一个上底长5厘米、下底长9厘米的等腰梯形(阴影部分)。
求这个梯形的面积。
分析与解:因为不知道梯形的高,所以不能直接求出梯形的面积。
最新小升初奥数巧求面积---割补法知识讲解

解析
从顶点作底边上的高,得到两个相同的直角三角 形。将这两个直角三角形拼成一个长方形见右图。 显然,阴影部分正好是长方形的三分之一,所以 原题阴影部分占整个图形面积的三分之一。 还可以拼成一个平行四边形或将其分成9个三 角形。
例5. 如下图所示,在一个等腰直角三角形中,削去一个三角形后, 剩下一个上底长5厘米、下底长9厘米的等腰梯形(阴影部分)。 求这个梯形的面积。
小升初奥数巧求面积---割 补法
知识梳理
相加法
相减法
割补法
平移法 旋转法
巧求 面积
放大法 等量代换法
直接求法 重叠法 引辅助线法
典型例题精讲
例1. 下图中四个圆的半径都是5厘米,求阴影部分的面积。
解析
同学们请看图,我们将图形进行割补。 把阴影部分割补成四个半圆形和一个正方形, 求出阴影部分面积就可以了。 2S圆=5× 5× 3.14× 2=157(平方厘米)
9厘米 5厘米
例6.ABC是三个圆的圆心,圆的半径都是10分米,求阴 影部分的面积。
D
B
F
A
C
E
解析
我们用割补法,将阴影部分割补 成一个半圆形,求出阴影部分面 积就可以了。 S半圆=10× 10× 3.14÷ 2=157平方 分米
D
B
F
A
C
E
例7.如图所示,空白部分占正方形面积的 几分之几?
解析
9厘米 5厘米
解析
因为不知道梯形的高,所以不能直接求出梯形的面 积。可以从等腰直角三角形与正方形之间的联系上考 虑。将四个同样的等腰直角三角形拼成一个正方形, 图中阴影部分是边长9厘米与边长5厘米的两个正方 形面积之差,也是所求梯形面积的4倍。所以所求梯 形面积是(9× 9-5× 5)÷4=14(平方厘米)。
四年级上册奥数讲义-第十一讲 割补法巧算面积-冀教版

四年级第十一讲割补法巧算面积◆温故知新:1. 用割补法把不规则图形变成规则图形计算面积。
2.正方形、等腰直角三角形、等边三角形、正六边形等已知图形分割成小块,与所求图形面积相联系。
◆练一练1、在图中,五个小正方形的边长都是2厘米,求三角形的面积。
ABC2、图中小正方形和大正方形的边长分别是4厘米和6厘米。
阴影部分的面积是多少平方厘米?◆例题展示例题1图中的数字分别表示对应线段的长度,试求这个多边形的面积。
(单位:厘米)练习1如图所示,在正方形内部有一个长方形。
已知正方形的边ABCD EFGH ABCD 长是6厘米,图中线段都等于2厘米。
求长方形的面积。
、EFGHAE AH例题2如图所示,大正方形的边长为10厘米。
连接大正方形的各边中点得到一个小正方形,将小正方形每边三等分,再将三等分点与大正方形的中心和一个顶点相连。
请问:图中阴影部分的面积总和等于多少平方厘米?练习2如图所示,大正方形的边长为10厘米。
连接大正方形的各边中点得到一个小正方形,再连接大正方形的两条对角线。
请问:图中阴影部分的面积总和等于多少平方厘米?例题3如图所示,正六边形ABCDEF的面积是6平方厘米,M是AB中点,N是CD 中点,P是EF中点。
请问三角形MNP的面积是多少平方厘米?练习3 如图所示,正六边形ABCDEF的面积是36平方厘米,M、N、P、Q、R、S分别是AB、BC、CD、DE、EF、FA的中点。
请问:阴影正六边形MNPQRS的面积是多少平方厘米?例题4 如图,把两个相同的正三角形的各边分别五等分和七等分,并连接这些分点。
已知图a中阴影部分的面积是294平方分米。
请问:图b中阴影部分的面积是多少平方分米?练习4如图,把两个同样大小的正方形分别分成5×5和6×6的方格表。
其中“G”形阴影部分的面积是558,请问“S”形阴影部分的面积是多少?◆拓展提高拓展1如图,在两个相同的等腰直角三角形中各作一个正方形,如果正方形A 的面积是36平方厘米,那么正方形B的面积是多少平方厘米?练习1如图,在两个相同的等腰直角三角形中各作一个正方形,如果三角形A的面积是16平方厘米,那么三角形B的面积是多少平方厘米?拓展2 如图所示,已知一个四边形的两条边的长度和三个角的度数,这个四边形的面积是多少平方厘米?(图中3和7的单位是厘米)练习2 如图,在等腰梯形ABCD中,角B是60度,线段AB、AD、CD长度相等。
第五讲 割补法巧算面积

例题5:如图,在两个相同的等腰直角三角形中各画一个正方形, 如果正 方形A的面积是36平方厘米,那么正方形B的面积是多少平方厘米?
例题6:如图所示, 已知一个四边形的两条边的长度和三个角的度数,这 个四边形的面积是多少平方厘米?(单位:厘米)
练习3:如图所示,大正三角形的面积为10平方厘米.连接大正三角形的 各边中点得到四个小正三角形,取各个小正三角形的中心,再将每个小正 三角形的中心和顶点相连,得到三个一样的小三角形,那么图中阴影部分 的面积总和等于多少平方厘米?
例题4:如图,把两个相同的正三角形的各边分别三等分和四等分,并连 接这些等分点.已知图1中阴影部分的面积是48平方分米.请问:图2中 阴影部分的面积是多少平方分米?
4、右图中空白部分的面积是100,那么阴影正方形的面积是多少?
5、如图所示,正六边形ABCDEF的面积是36. 阴影正六边形的面积是多少?
第五讲 割补法巧算面积
在上一讲中, 我们学习了如何计算格点图形的面积,介绍了正方 形格点图形和三角形格点图形的面积计算公式 根据公式,我们可以求 出正方形格点图形的面积是最小正方形面积的几倍, 或者求出三角形 格点图形面积是最小正三角形面积的几倍. 随着几何学习的步步深入, 大家会发现除了用公式法直接 求面积之外,还有很多间接求面积的方 法. 尤其是对于不规则图形,我们并不知道这些图形的面积公式, 但 是可以把它们通过分割、添补等各种方式变换为规则的图形.
巩固练习 1、右图中的数字分别表示对应线段的长度,图中多边形的面积是多少?
2、如右图所示,在正方形ABCD内部有梯形EHGF.已知正方形ABCD的 边长是6厘米,图中线段AE、AH、BF、DG都等于2厘米.则梯形EHGF 的面积是多少平方厘米?
割补法巧算面积

最后把添补的那块面积去掉。源自这种图形的转换方法就是割补法,也就是通过对 图形的切割和填补拼成新的图形。
割补法巧算 面积
这就是切割法
如图,求这个图形的面积。
2
53 32 21
2
5
2
5
2
5
5
图中的数字分别表示对应线段的长度,试求下面多边形的面积。
(单位:厘米) 2
3
24
5
1
3 2 4 2 63 32(平方厘米 )
图中的数字分别表示对应线段的长度,试求下面多边形的面积。
小 热 身
已知一个正方形的边长为5,那么面积是多少? 25 已知一个长方形的长是10,宽是5,那么面积是多少? 50 已知一个正方形的面积是36,那么边长是多少? 6
已知一个长方形的面积是40,长是10,那么宽是多少? 4 已知一个长方形的面积是40,宽是5,那么长是多少? 8
这种图形的转换方法就是割补法,也就是通过对 图形的切割和填补拼成新的图形。
(单位:厘米)4
2
9
3 12 3 9 4 3 2 78(平方厘米)
4
4
3
12
这就是添补法
如图,求这个图形的面积。
2
5
2
5
2
55 25
5
2 22 4
25 4 21
5
图中的数字分别表示对应线段的长度,试求下面多边形的面积。
(单位:厘米) 2
11
1 1
4 4 16(平方厘米)
2
2
11 4 4(平方厘米)
1 1
11
2
16 4 12(平方厘米)
割补法求面积技巧

割补法是一种常用的求面积的方法,其基本思想是将一个复杂的图形割补成几个简单的规则图形,然后利用这些规则图形的面积公式来求解原图形的面积。
以下是使用割补法求面积的一些技巧:
1.观察图形:首先观察要计算的图形,看是否可以通过割补将其变为简单的规则图形。
2.选择割补方式:根据图形的特点,选择合适的割补方式。
割补方式的选择对于简化问题非常重要。
3.计算规则图形面积:对于割补后的规则图形,使用相应的面积公式进行计算。
4.求和或相减:如果图形是通过割补多个部分得到的,那么需要将各部分的面积相加或相减,以得到原图形的面积。
5.验证答案:完成计算后,要验证答案是否正确。
可以通过将答案代回原图形,看是否与原图形的面积相等来进行验证。
下面是一个使用割补法求面积的例子:
题目:求下图中阴影部分的面积(单位:cm²)。
![阴影部分为不规则图形]
(请根据您所使用的软件或平台的功能进行适当的调整或
绘制)
解:观察图形,发现可以将阴影部分割补成一个半圆和一个等腰直角三角形。
半圆的半径为r = 5cm,面积为 21×π×r2。
等腰直角三角形的底为b = 10cm,高为h = 5cm,面积为 21×b×h。
因此,阴影部分的面积为半圆面积加上三角形面积,即 21×π×52+21×10×5=39.25cm2。
巧用割补法解求解二次函数中的面积问题

巧用割补法解求解二次函数中的面积问
题
割补法是一种解决函数面积问题的有效方法,它可以用来计算二次函数中的面积。
割补法的基本思想是,将一个函数的面积分解为两个函数的面积之和,其中一个函数是原函数的一部分,另一个函数是原函数的补函数。
首先,我们需要确定二次函数的补函数,即将原函数的曲线上的点按照一定的规律反向移动,使其形成一条新的曲线,这条曲线就是补函数。
接下来,我们可以将原函数的面积分解为两个函数的面积之和,即原函数的面积加上补函数的面积。
最后,我们可以使用积分法来计算两个函数的面积,然后将两个函数的面积相加,就可以得到原函数的面积。
因此,割补法是一种有效的解决二次函数中面积问题的方法,它可以帮助我们快速准确地计算出二次函数的面积。
人教版五年级上册数学 割补法巧算面积专项训练

人教版五年级上册数学割补法巧算面积专项训练一.先割后补1:如图所示的四边形的面积等于多少?(单位:厘米)2:如图所示的四边形的面积等于多少?(单位:厘米)二.网格法1:如图由2个同样大小的等边三角形组合而成,每个大三角形的面积为6平方厘米,外围的6个小三角形均为形状大小相同的等边三角形,那么中间阴影部分的面积是多少平方厘米?2:两个正方形拼成如图所示的平面图形,已知大正方形的面积为64平方厘米。
请问:小正方形的面积是多少平方厘米?3:如图所示,三角形ABC是面积为20平方厘米的等腰直角三角形,D、E、F是三边的中点,请问:空白部分的面积是多少平方厘米?4:在一个等腰三角形中,两条与底边平行的线段将三角形的两条边等分成三段,如果这个等腰三角形的面积为9平方厘米,请问:图中阴影部分的面积是多少平方厘米?5:如图,把两个相同的正三角形的各边分别二等分和四等分,并连接这些等分点,已知左图中阴影部分的面积是100平方厘米,请问:右图中阴影部分的面积是多少平方厘米?6:把两个同样大小的正方形分别分成6×6和3×3的方格表,左图阴影部分的面积是400平方厘米,请问:右图中阴影部分的面积是多少平方厘米?7:两个正方形拼成如图所示的平面图形,已知大正方形的面积为36平方厘米,那么小正方形的面积是多少平方厘米?8. 如图,大正方形面积为10平方厘米,连接大正方形的各边中点得到一个小正方形,将小正方形每边三等分,再将三等分点与大正方形的中心和一个顶点相连,那么图中阴影部分的面积总和等于多少平方厘米?9. 把正三角形的每条边三等分,以各边的中间一段为边向外作小正三角形,得到一个六角形,再将这个六角形的六个“角”(即小正三角形)的两边三等分,又以它的中间段为边向外作更小的小正三角形,这样得到如图所示的图形。
如果所作的最小正三角形的面积为1平方厘米,请问:整个图形的面积是多少平方厘米?10.如图所示,大三角形的面积为20平方厘米,连接大正方形的各边中点得到小正三角形,将小正三角形如图三等分,那么图中阴影部分的面积总和等于多少平方厘米?11.把两个相同的正三角形的各边分别4等分和5等分,并连接这些等分点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
割补法巧算面积
————————————————————————————————作者:————————————————————————————————日期:
ﻩ
割补法巧算面积
知识精讲:
分割法:把不规则的的大图形化为规则的小图形
添补法:把不规则图形周围添上规则的小图形,使总面积便于计算
例题1
图中的数字分别表示对应线段的长度,试求下面多边形的面积.(单位:厘米)
练习1
如图中的每个数字分别表示所对应的线段的长度(单位:米).这个图形的面积等于多少平方
米?
例题2
如图,在正方形ABCD内部有一个长方形.EFGH.已知正方形ABCD的边长是6厘米,图中线段AE、AH都等于2厘米.求长方形EFGH的面积.
练习2
正方形ABCD的边长是8厘米,它的内部有一个三角形AEF(如图),线段DF=3.6厘米,BE=2.8厘米,那么三角形AEF的面积等于平方厘米.
例题3
如图中,大正方形的边长为10厘米.连接大正方形的各边中点得小正方形,将小正方形每边三等份,再将三等分点与大正方形的中心和一个顶点相连,那么图中阴影部分的面积总和等于多少平方厘米?
练习3.
1.如图所示,正方形ABCD的边长acm,则图中阴影部分的面积为cm2.
例题4. 如图1和图2,把两个相同的正三角形的各边分别五等分和七等分,并连接这些分点.已知图1中阴影部分的面积是294平方分米.请问:图2中的阴影部分的面积是多少平方分米?
练习4
7.如图所示,将三个相同的长方形从上到下排列,依次进行两等分、三等分、四等分,各取出其中的一份画上阴影,则阴影部分的面积占全部面积的几分之几?
选做题
例5 如图,在两个相同的等腰直角三角形中各作一个正方形,如果正方形A的面积是36平方厘米,那么正方形B的面积是多少平方厘米?
例6.
已知一个四边形ABCD的两条边的长度和三个角(如下图所示),求四边形ABCD的面积是多少?
作业:
1.如图所示,平行四边形的面积是12,把一条对角线四等分,将四等分点与平行四边形另外两个顶点相连.图中阴影部分的面积总和是多少?
2..(2013秋•诸暨市校级期中)如图,已知一个四边形的四条边AB,BC,CD和DA 的长分别是3,4,13和12,其中∠B=90°,求这个四边形的面积
3.求阴影部分面积.
4.求阴影部分面积.
5. 求阴影部分面积:
6.求阴影部分面积.
7. 求阴影部分面积.
8.(2011秋•宁波期中)求阴影部分的面积.
9.求阴影部分的面积.
10.求阴影部分的面积.
11.求阴影部分的面积. 12.求阴影部分的面积.。
