离散数学第七章图论
合集下载
离散数学 图论

1.两个结点是连通的: 在无向图中,结点u和v之间 如果存在一条路, 则称u与v是连通的. 规定: 对任何结点u, u与u是连通的. 2.结点之间的连通关系是个等价关系. 令G=<V,E>是无向图, R是V上连通关系, 即 R={<u,v>|u和v是连通的} 显然R具有自反、对称和传递性.
a b c d 2 1 6 3 4
定义2:没有任何边的图称为空图;只有一个点 A 的图称为平凡图。 e1 e e5 2 定义3:图中顶点的个数称为图 B e6 D 的阶,若|V(G)|=n,则称G为n阶图; e3 e 4 C e7 连接两个相同顶点的边的条数称 为边的重数,这些边称为平行边或多重边。 邻接点: 与一边关联的两个结点. 邻接边: 关联同一个结点的两条边. 环:只关联一个结点的边. 简单图:没有环以及没有重数大于1的边的图。 孤立点:不与任何点邻接的点。 以下记|V(G)|=n, |E(G)|=m。
3.图的最大度Δ(G)与最小度δ(G) :G=<V,E>是 无向图, 定义 Δ(G) =max{d(v)|v∈G} δ(G) =min{d(v)|v∈G}
例:设G是一个非空简单图,则G中一定存在度相同 的顶点。 证明:因为G是简单图,所以,G中顶点的度只能是 0,1,2,…,n-1。 若G中存在一个顶点的度为0,则G中的最大度最多为 n-2,即G中的度只能是 0,1,…,n-2; 若G的最小度≥1,则G中的度只能是 1,2,…,n-1, 由抽屉原理,G中一定存在度相同的顶点。
h
g f
e
5
3.连通分支:令G=<V,E>是无向图, R是V上连通关系, 设 R对V的商集中有等价类V1,V2,V3,…, Vn ,这n个等价类构 成的n个子图分别记作G[V1],G[V2],G[V3],…, G[Vn],并 称它们为G的连通分支. 并用W(G)表示G中连通分支数.
a b c d 2 1 6 3 4
定义2:没有任何边的图称为空图;只有一个点 A 的图称为平凡图。 e1 e e5 2 定义3:图中顶点的个数称为图 B e6 D 的阶,若|V(G)|=n,则称G为n阶图; e3 e 4 C e7 连接两个相同顶点的边的条数称 为边的重数,这些边称为平行边或多重边。 邻接点: 与一边关联的两个结点. 邻接边: 关联同一个结点的两条边. 环:只关联一个结点的边. 简单图:没有环以及没有重数大于1的边的图。 孤立点:不与任何点邻接的点。 以下记|V(G)|=n, |E(G)|=m。
3.图的最大度Δ(G)与最小度δ(G) :G=<V,E>是 无向图, 定义 Δ(G) =max{d(v)|v∈G} δ(G) =min{d(v)|v∈G}
例:设G是一个非空简单图,则G中一定存在度相同 的顶点。 证明:因为G是简单图,所以,G中顶点的度只能是 0,1,2,…,n-1。 若G中存在一个顶点的度为0,则G中的最大度最多为 n-2,即G中的度只能是 0,1,…,n-2; 若G的最小度≥1,则G中的度只能是 1,2,…,n-1, 由抽屉原理,G中一定存在度相同的顶点。
h
g f
e
5
3.连通分支:令G=<V,E>是无向图, R是V上连通关系, 设 R对V的商集中有等价类V1,V2,V3,…, Vn ,这n个等价类构 成的n个子图分别记作G[V1],G[V2],G[V3],…, G[Vn],并 称它们为G的连通分支. 并用W(G)表示G中连通分支数.
离散数学第7章

1 v2e4v4e3v3e2v2
初级回路(圈)
2 v2e5v5e6v4e3v3e2v2
初级回路(圈)
3 v2e4v4e3v3e2v2e5v5e6v4e3v3e2v2 复杂回路
…………
5、图中最短的回路。 如图:
6、性质。
定理:在一个
n
阶图中,若从顶点vi
到
v
存在
j
通路(vi vj ) ,则从 vi 到 vj 存在长度小于等于
n 1的通路。
推论:在一个
n
阶图中,若从顶点vi
到
v
存在
j
通路(vi vj ) ,则从 vi 到 vj 存在长度小于等于
n 1的初级通路。
6、性质。
定理:在一个 n 阶图中,若vi 到自身存在回路, 则从 vi 到自身存在长度小于等于n 的回路。 推论:在一个 n 阶图中,若vi 到自身存在一个 简单回路,则从vi到自身存在长度小于等于 n
如例1的(1)中,
v1
v5
e1与 v1, v2 关联的次数均为1, e1
e6
e2 与 v2 关联的次数为2, e2 v2 e4 e5
v4
边 e1, e4, e5, e6都是相邻的, v5 为孤立点,v4 为悬挂点,
e3 v3
e6 为悬挂边,e2 为环,e4, e5 为平行边,重数2,
G 为多重图。
孤立点——无边关联的点。
环——一条边关联的两个顶点重合,称此边
为环 (即两顶点重合的边)。
3、相关概念。 (2) 悬挂点——只有一条边与其关联的点,所
对应的边叫悬挂边。 (3) 平行边——关联于同一对顶点的若干条边
称为平行边。平行边的条数称为重数。 多重图——含有平行边的图。 简单图——不含平行边和环的图。
离散数学第七章图论2
2) V1中结点在C上存在r(2≤r≤|V1|)个互不相邻,删除C上 V1中各结点及关联的边后,将C分为互不相连的r段, 即p(C-V1)=r≤|V1|。
▪ 一般情况下,V1中的结点在C中即有相邻的,又有不 相邻的,因此总有p(C-V1)≤|V1|。
▪ 又因C是G的生成子图,从而C-V1也是G-V1的生成子 图,故有
2
15
1
16 13 14
20 17
12 4
3
19 18 11 5
9 10
6
8
7
给定G是一个无孤立结点的无向图,若存在一条路(回路), 经过图中每个结点一次且仅一次,则称此路(回路)为该图 的一条汉密尔顿路(回路)。具有汉密尔顿回路的图称为汉 密尔顿图。
2020/9/21
国际学院
60--17
汉密尔顿图的定义
2020/9/21
国际学院
60--11
一笔画问题
1
11
10
1
12
9
2
3
2
8
5
6
3
4
7
(a)
对于上图,有
4
5
(b)
图(a)能一笔画并且能回到出发点的,
图(b)能一笔画但不能回到出发点的。
2020/9/21
国际学院
60--12
判断有向欧拉路、欧拉图的方法
定理7.2 有向图G具有一条欧拉路,当且仅当G 是连通的,且除了两个结点以外,其余结点的 入度等于出度,而这两个例外的结点中,一个 结点的入度比出度大1,另一个结点的出度比 入度大1。
②对于欧拉路L的任意非端点的结点vi,在L中每出现vi一 次,都关联着G中的两条边,而当vi又重复出现时,它又 关联着G中的另外的两条边,由于在路L中边不可能重复出
▪ 一般情况下,V1中的结点在C中即有相邻的,又有不 相邻的,因此总有p(C-V1)≤|V1|。
▪ 又因C是G的生成子图,从而C-V1也是G-V1的生成子 图,故有
2
15
1
16 13 14
20 17
12 4
3
19 18 11 5
9 10
6
8
7
给定G是一个无孤立结点的无向图,若存在一条路(回路), 经过图中每个结点一次且仅一次,则称此路(回路)为该图 的一条汉密尔顿路(回路)。具有汉密尔顿回路的图称为汉 密尔顿图。
2020/9/21
国际学院
60--17
汉密尔顿图的定义
2020/9/21
国际学院
60--11
一笔画问题
1
11
10
1
12
9
2
3
2
8
5
6
3
4
7
(a)
对于上图,有
4
5
(b)
图(a)能一笔画并且能回到出发点的,
图(b)能一笔画但不能回到出发点的。
2020/9/21
国际学院
60--12
判断有向欧拉路、欧拉图的方法
定理7.2 有向图G具有一条欧拉路,当且仅当G 是连通的,且除了两个结点以外,其余结点的 入度等于出度,而这两个例外的结点中,一个 结点的入度比出度大1,另一个结点的出度比 入度大1。
②对于欧拉路L的任意非端点的结点vi,在L中每出现vi一 次,都关联着G中的两条边,而当vi又重复出现时,它又 关联着G中的另外的两条边,由于在路L中边不可能重复出
离散数学-第七章-图论

则称G1与G2是同构的,记作G1 G2
怎样定义有向图的同构?
第 七 章
图
论
2/12/2021
28
离
散 例7、
数 学
a
d
第 七 章
图
论
2/12/2021
a' (b)
b
d ' (d)
c
c' (a)
b' (c)
29
离
散
数
学
1
2
6
10
7
9 8
2
5
3
第
3
4
七 章
彼得松图(petersen)
图
论
2/12/2021
1
5
6
10 7 8
9
4
30
离 散 数 学
第 七 章
图
论
2/12/2021
31
离 散 数 学
两个图同构必有: (1)结点数相同;
但不是充分条件
(满足这三个条件的两图 不一定同构)
第 (2)边数相同;
七
章 (3)度数列相同
图
论
2/12/2021
32
离 例8、 画出K4的所有非同构的生成子图。
散 数
七 章
边,构成一个无向重图,问题化为图论中简单道路
的问题。
图
论
2/12/2021
3
离 一、图的基本概念
散 数 学
旧金山
丹佛
洛杉矶
第 七 章
图
论
2/12/2021
底特律
芝加哥
纽约 华盛顿
4
离
散 设A、B是两个集合,称
离散数学第七章图论习题课

利用奇数+奇数=偶数,偶数+偶数=偶数,所以, 在G中结点度数为奇数的结点,在其补图中的度 数也应为奇数,故G和其补图的奇数结点个数也 是相同的。
P286 1、在无向图G中,从结点u到结点v有一条长度为 偶数的通路,从结点u到结点v又有一条长度为奇 数的通路,则在G中必有一条长度为奇数的回路。
证明 :
2、运用 (1) 判断有向图或无向图中通路(回路)的类型。 (2) 求短程线和距离。 (3) 判断有向图连通的类型。
三、图的矩阵表示
1、基本概念。 无向图的邻接矩阵A 根据邻接矩阵判断:各结点的度, 有向图结点 出,入度。 由Ak可以求一个结点到另一个结点长度为k 的路条数. 有向图的可达矩阵P 用P可以判定:各结点的度. 有向图的强分图。 关联矩阵M:是结点与边的关联关系矩阵. 用M判定:各结点的度
设给定图G(如由图所示),则图G的点割集
是
.
应该填写:{f},{c,e}。
定义 设无向图G=<V, E>为连通图,若有点集
V1V,使图G删除了V1的所有结点后,所得的子
图是不连通图,而删除了V1的任何真子集后,所
得的子图是连通图,则称V1是G的一个点割
集.若某个结点构成一个点割集,则称该结点为
割点。
a c
a c
b
d
b
d
a c
a c
b
d
b
d
推论:任何6人的人群中,或者有3人互相认识,或者有 3人彼此陌生。(当二人x,y互相认识,边(x,y)着红色, 否则着兰色。则6人认识情况对应于K6边有红K3或者 有兰K3。)
证明简单图的最大度小于结点数。
证明: 设简单图G有n个结点。对任一结点u,由于G没
P286 1、在无向图G中,从结点u到结点v有一条长度为 偶数的通路,从结点u到结点v又有一条长度为奇 数的通路,则在G中必有一条长度为奇数的回路。
证明 :
2、运用 (1) 判断有向图或无向图中通路(回路)的类型。 (2) 求短程线和距离。 (3) 判断有向图连通的类型。
三、图的矩阵表示
1、基本概念。 无向图的邻接矩阵A 根据邻接矩阵判断:各结点的度, 有向图结点 出,入度。 由Ak可以求一个结点到另一个结点长度为k 的路条数. 有向图的可达矩阵P 用P可以判定:各结点的度. 有向图的强分图。 关联矩阵M:是结点与边的关联关系矩阵. 用M判定:各结点的度
设给定图G(如由图所示),则图G的点割集
是
.
应该填写:{f},{c,e}。
定义 设无向图G=<V, E>为连通图,若有点集
V1V,使图G删除了V1的所有结点后,所得的子
图是不连通图,而删除了V1的任何真子集后,所
得的子图是连通图,则称V1是G的一个点割
集.若某个结点构成一个点割集,则称该结点为
割点。
a c
a c
b
d
b
d
a c
a c
b
d
b
d
推论:任何6人的人群中,或者有3人互相认识,或者有 3人彼此陌生。(当二人x,y互相认识,边(x,y)着红色, 否则着兰色。则6人认识情况对应于K6边有红K3或者 有兰K3。)
证明简单图的最大度小于结点数。
证明: 设简单图G有n个结点。对任一结点u,由于G没
离散数学 第七章 图论

10
每一条边都是有向边 的图称有向图。
G′=<V′,E′>=<{v1′,v2′,v3′, v4′,v5′},{<v1′,v2′>,<v2′, v3′>,<v3′,v4′>,<v2′,v4′>}>
如果在图中一些边是有向 边,另一些边是无向边, 则称这个图是混合图。
G″=<V″,E″>=<{ v1″,v2″,v3″,
v4″,},{( v1″,v4″),(v2″,v4″),<v1″,
v3″>,<v3″,v4″>}>
11
在一个图中,若两个节点由一条有向 边或一条无向边相关联,则这两个节点 称为邻接点。
在一个图中不与任何节点相邻接的节 点,称为孤立节点。仅由孤立节点组成 的图称为零图,仅由一个孤立节点组成 的图称为平凡图。
证明 在Kn中,任意两点间都有边相连, n 个结点 中任取两点的组合数为:
Cn2
1 2
n(n
1)
故Kn的边数为 |E| = n(n-1)/2 。
21
注意:
如果在Kn中,对每条边任意确定一个方 向,就称该图为 n 个结点的有向完全图。 显然,它的边数也为 n(n-1)/2 。
给定任意一个含有 n 个结点的图 G ,总 可以把它补成一个具有同样结点的完全 图,方法是把那些没有联上的边添加上 去。
且E E ,V V ,则称 G 为 G 的子图。
例:如图 7-1.7 中 (b) 和 (c) 都是 (a) 的子图。
24
如果 G 的子图包含 G 的所有结点,则 称该子图为 G 的生成子图。 如图 7-1.8 中 (b) 和 (c) 都是 (a) 的生成子图。
每一条边都是有向边 的图称有向图。
G′=<V′,E′>=<{v1′,v2′,v3′, v4′,v5′},{<v1′,v2′>,<v2′, v3′>,<v3′,v4′>,<v2′,v4′>}>
如果在图中一些边是有向 边,另一些边是无向边, 则称这个图是混合图。
G″=<V″,E″>=<{ v1″,v2″,v3″,
v4″,},{( v1″,v4″),(v2″,v4″),<v1″,
v3″>,<v3″,v4″>}>
11
在一个图中,若两个节点由一条有向 边或一条无向边相关联,则这两个节点 称为邻接点。
在一个图中不与任何节点相邻接的节 点,称为孤立节点。仅由孤立节点组成 的图称为零图,仅由一个孤立节点组成 的图称为平凡图。
证明 在Kn中,任意两点间都有边相连, n 个结点 中任取两点的组合数为:
Cn2
1 2
n(n
1)
故Kn的边数为 |E| = n(n-1)/2 。
21
注意:
如果在Kn中,对每条边任意确定一个方 向,就称该图为 n 个结点的有向完全图。 显然,它的边数也为 n(n-1)/2 。
给定任意一个含有 n 个结点的图 G ,总 可以把它补成一个具有同样结点的完全 图,方法是把那些没有联上的边添加上 去。
且E E ,V V ,则称 G 为 G 的子图。
例:如图 7-1.7 中 (b) 和 (c) 都是 (a) 的子图。
24
如果 G 的子图包含 G 的所有结点,则 称该子图为 G 的生成子图。 如图 7-1.8 中 (b) 和 (c) 都是 (a) 的生成子图。
第7章 图论 [离散数学离散数学(第四版)清华出版社]
![第7章 图论 [离散数学离散数学(第四版)清华出版社]](https://img.taocdn.com/s3/m/58b7923143323968011c9244.png)
6/27/2013 6:02 PM
第四部分:图论(授课教师:向胜军)
21
例:
a j i h c g d
1(a)
无 向 图
b
f
e
2(b)
7(j) 8(g) 9(d) 10(i)
6(e)
3(c) 4(h)
5(f)
6/27/2013 6:02 PM
第四部分:图论(授课教师:向胜军)
22
例:
1(b)
有向图
第四部分:图论(授课教师:向胜军)
6
[定义] 相邻和关联
在无向图G中,若e=(a, b)∈E,则称a与 b彼此相邻(adjacent),或边e关联 (incident) 或联结(connect) a, b。a, b称为边e的端点或 结束顶点(endpoint)。 在有向图D中,若e=<a, b>∈E,即箭头 由a到b,称a邻接到b,或a关联或联结b。a 称为e的始点(initial vertex),b称为e的终点 (terminal/end vertex)。
证明思路:将图中顶点的度分类,再利用定理1。
6/27/2013 6:02 PM 第四部分:图论(授课教师:向胜军) 9
[定理3] 设有向图D=<V, E>有n个顶点,m 条边,则G中所有顶点的入度之和等于所 有顶点的出度之和,也等于m。
即:
d ( v i ) d ( v i ) m.
i 1 i 1
n
n
证明思路:利用数学归纳法。
6/27/2013 6:02 PM
第四部分:图论(授课教师:向胜军)
10
一些特殊的简单图:
(1) 无向完全图Kn(Complete Graphs)
《离散数学》课件-第七章 图的基本概念

• 〔u,v〕∈E1〔f(u),f(v)〕∈E2 • (或<u,v>∈E1 <f(u),f(v)>∈E2) • 且重数相同,则称G1同构于G2,记为
• G1 G2。
• 显然,两图的同构是相互的,即G1同构 于G2,G2同构于G1。
• 由同构的定义可知,不仅结点之间要具 有一一对应关系,而且要求这种对应关 系保持结点间的邻接关系。对于有向图 的同构还要求保持边的方向。
V={a,b,c,d},E={e1,e2,e3,e4,e5,e6}
e1=(a,b), e2=(a,c), e3=(b,d), e4=(b,c), e5=(d,c), e6=(a,d).
它的图形如下图(a)或(b)所示:
a
a
b
d
b
d
c
c
(a)
(b)
如果有些边是有向边,另一些边是无向边, 图G称为混合图。
第七章 图的基本概念
– 7.1 无向图及有向图 – 7.2 通路、回路、图的连通性 – 7.3 图的矩阵表示 – 7.4 最短路径及关健路径
7.1 无向图和有向图
• 什么是图?可用一句话概括,即:图是用 点和线来刻划离散事物集合中的每对事 物间以某种方式相联系的数学模型。
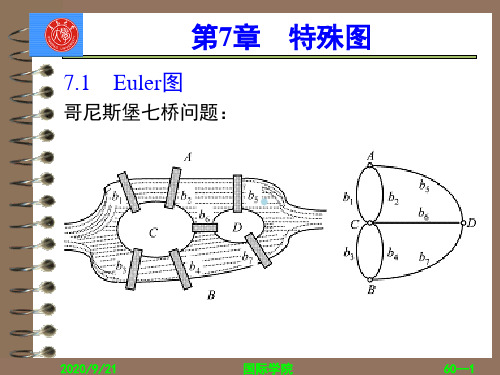
Konigsberg(哥尼斯堡)七桥问题
为偶数.
定理7.2 在任何有向图中,所有结点的入度之 和必等于它们的出度之和.
证明:因为有向图中的每一条有向边都恰好对应 一个出度和一个入度.故所有结点的出度之 和恰好等于有向边的总数.同样地, 所有结 点的入度之和恰好也等于有向边的总数.因 此它们相等.
设V={v1,…,vn}为G的顶点集,则称{d(v1),…d(vn)} 为G的度数序列。
• 如果G2无孤立结点,且由E2所唯一确定,即 以E2为边集,以E2中边关联的结点全体为顶 点集,则称G2是边集E2的导出子图。
• G1 G2。
• 显然,两图的同构是相互的,即G1同构 于G2,G2同构于G1。
• 由同构的定义可知,不仅结点之间要具 有一一对应关系,而且要求这种对应关 系保持结点间的邻接关系。对于有向图 的同构还要求保持边的方向。
V={a,b,c,d},E={e1,e2,e3,e4,e5,e6}
e1=(a,b), e2=(a,c), e3=(b,d), e4=(b,c), e5=(d,c), e6=(a,d).
它的图形如下图(a)或(b)所示:
a
a
b
d
b
d
c
c
(a)
(b)
如果有些边是有向边,另一些边是无向边, 图G称为混合图。
第七章 图的基本概念
– 7.1 无向图及有向图 – 7.2 通路、回路、图的连通性 – 7.3 图的矩阵表示 – 7.4 最短路径及关健路径
7.1 无向图和有向图
• 什么是图?可用一句话概括,即:图是用 点和线来刻划离散事物集合中的每对事 物间以某种方式相联系的数学模型。
Konigsberg(哥尼斯堡)七桥问题
为偶数.
定理7.2 在任何有向图中,所有结点的入度之 和必等于它们的出度之和.
证明:因为有向图中的每一条有向边都恰好对应 一个出度和一个入度.故所有结点的出度之 和恰好等于有向边的总数.同样地, 所有结 点的入度之和恰好也等于有向边的总数.因 此它们相等.
设V={v1,…,vn}为G的顶点集,则称{d(v1),…d(vn)} 为G的度数序列。
• 如果G2无孤立结点,且由E2所唯一确定,即 以E2为边集,以E2中边关联的结点全体为顶 点集,则称G2是边集E2的导出子图。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
记为G,其中
(1)V≠称为结点集,元素称为结点或顶点;
第 七 章
(2)E称为边集,它是无序积 V&V 的多重子集,
其元素称为无向边,简称为边。 常把无向图记为G=<V,E>
1/17/2019 1:11 PM 5
图 论
离 散 数 学
例1、G1=<V,E> V={v0, v1, v2,v3} E={(v0,v2),(v0,v3),(v1,v2),(v1,v3),(v2,v3)}
|E(D)|=m,则
deg
第 七 章
n
(vi ) m
n i
i 1
deg
i 1
n
(vi ) m
图 论
deg(v ) 2m
第 七 章
deg(v ) 2m
i i 1
n
即使出现多重边和环,这 个式子仍然成立
图 论
1/17/2019 1:11 PM
16
离 散 数 学
n=4 m=5 结点入度之和为5 结点出度之和为5 e5
v1 e1
v4
e3
e4
e2
v3
v2
定理1.2 设D=<V,E>为有向图, |V(D)|= n,
13
离 散 数 学
定义1.3 在图G=<V,E>中,与结点v(vV)关联的 边数称为结点v的度数,简称度,记为deg(v)。 (结点上的环关联次数为2)
设D=<V,E>为有向图,以结点v(vV)作为始 点的边数称为v的出度,记作deg+(v);以v作为终 点的边数称为v的入度,记作deg-(v) 称deg+(v)+deg-(v)为v的度数,记作deg(v)
1 2 4 3
14
离 散 数 学
有向图中,所有结点的入度之和等于所有结点的出 度之和。
最大度 在无向图G中, 令△(G)=max{deg(v)|vV(G)} (G)=min{deg(v)|vV(G)} 最小度
第 七 章
类似可定义有向图的最大出度和最小出度、最大入 度和最小入度。
图 论
1/17/2019 1:11 PM
多重图
7
(不含平行边也不含环) 1/17/2019 1:11 PM
离 散 数 学
底特律 旧金山 纽约 芝加哥 华盛顿 洛杉矶
丹佛
第 七 章
图 论
1/17/2019 1:11 PM
8
离 散 数 学
定义1.2 一个有向图是一个有序的二元组<V,E>,记 为D,其中 (1)V同无向图; (2)E称为边集,它是笛卡尔积V×V的多重子集, 其元素称为有向边,简称为边。 v0 D=<V,E> V={v0, v1, v2}, E={<v0,v1>, <v1,v0>, <v1,v2>}
v1 e1 v2 e2 e4 e5 v1 e1 e4 v4 e3
e3
e2
v3
第 七 章
e5
v2 v v + + + deg 3 (v1)=3 deg 4 (v2)= deg (v4)=1 deg+(v3)=0 图 deg(v deg(v )=deg(v 论 deg -1/17/2019 -(v 2 -(v )=2 4)=2 3)=3 PM-(v (v1)=deg(v )=1:11 deg )=deg )=1 deg
e5 (v3,v4)
关联次数
邻接点、邻接边
图 论
1/17/2019 1:11 PM
12
离 散 数 学
在有向图D=<V,E>中,若ek=<vi,vj> ∈E,则称vi 为ek 的起点, vj 为ek的终点 ;并称vi邻接到vj , vj 邻接于vi 。
v1
v2
v3
第 七 章
v4
图 论
1/17/2019 1:11 PM
v0 v3
第 七 章
v1 v2
图 论
1/17/2019 1:11 PM
G1
6
离 散 数 学
例2 、 G2=<V,E> V={v0, v1, v2,v3} E={(v0,v3),(v1,v3),(v1,v3),(v2,v3),(v0,v0)}
环 v0 v1
第 七 章
G 简单图
v3
v2 G2
平行边
图 论
第七章
图 论
离 散 数 学
图论的起源
Konigsberg(哥尼斯堡)七桥问题
A
C
D
B
第 七 章
问题:能否从河岸或小岛出发,不重复地经过所 有的桥回到原地。
图 论
1/17/2019 1:11 PM
2
离 散 数 学
Euler (欧拉) 1736年对这个问题给出了否定的回答。
A
C
D
B
第 七 章
图 论
Euler将河岸和小岛作为图的结点,七座桥为 边,构成一个无向重图,问题化为图论中简单道路 的问题。
空图 ——V(G)=
丹佛 洛杉矶
图 论
1/17/2019 1:11 PM
11
标定图
离 散 数 学
e0
非标定图
e1
e3
v1
v5 v3
在无向图G=<V,E>中,若ek= v2 (vi,vj) ∈E,则称vi,vj 为 e2 边ek的端点,
e4
ek与vi或ek与vj是彼此关联的;
v4
孤立点
第 七 章
平行边
1/17/2019 1:11 PM 10
有时用G泛指图(有向的或无向的)
离 散 数 学
|V(G)|表示G的结点数
|E(G)|表示G的边数
有限图—— |V(G)|和 |E(G)|均有限
n阶图——|V(G)|=n
零图—— E(G)=
旧金山 平凡图——1阶零图
第 七 章
底特律 纽约 芝加哥 华盛顿
1/17/2019 1:11 PM 3
离 散 数 学
一、图的基本概念
底特律 旧金山 纽约 芝加哥 华盛顿 洛杉矶
丹佛
第 七 章
图 论
1/17/2019 1:11 PM
4
离 散 数 学
设A、B是两个集合,称
A&B={{a,b}|aA, bB} 为A与B的无序积。 为方便起见,常将无序对{a,b}记为(a,b) 定义 1.1 一个无向图是一个有序的二元组 <V,E> ,
v1
第 七 章
v2
D
1/17/2019 1:11 PM 9
图 论
离 散 数 学
例3、 D=<V,E>, 其中 V={v1,v2 ,v3 ,v4 } E={<v1,v1>,<v1,v2>,<v2,v3>,<v2,v4>,<v3,v4>, <v3,v4>,<v2,v1>}
v1 v2
第 七 章
v3
v4
图 论
15
离 散 数 学
对图的所有顶点的度求和时,得出了什么?
n=4 一个具有 10个顶点,每
顶点度之和为10 结点度之和为 8
个结点的度都为 6的图, m=4 m=5 e5 有多少条边?
v3
v1
ቤተ መጻሕፍቲ ባይዱ
e1
e3
v2 e2
e4 v4
定理1.1 设G=<V,E>为无向图, |V(G)|= n, |E(G)|=m,则 握手定理
