数学建模——人员安排问题
数模-公司工作人员调整问题

公司工作人员调整问题摘要:一个现代企业应该具有完善的用人制度,特别是考核制度。
本文根据数学建模的思想,通过对人员考核结果以及各岗位的素质需求等进行综合分析,为现代企业提供了科学实用的内部人员调整途径。
首先,根据工作人员工作意向、单位评价和各岗位对工作人员的要求,结合单位录用人员的一般经验,建立经验评判模型,得出初步的调整方案。
然后,将决策的目标分解为公司满意度和员工满意度,其中,公司满意度分解为四个工作岗位对员工的满意度,它是综合公司对员工以往工作的考核结果以及各个岗位对每种职工能力的要求程度,它是通过层次分析法将定性的量定量化得到的;员工的满意度分解为四名员工对各个岗位的满意度,它是综合员工的志愿以及每个志愿之间的待遇差别,进行层次分析得到的。
其次,在得到每个员工对每个工作岗位的满意度以及每个工作岗位对每个员工的满意度的基础上,我们再通过0-1规划模型求出最优解;最后,对所求得的最优解的模型进行改进,对两个满意度指标的权重进行灵敏度分析,也证明模型的有效性,使得决策更加合理。
最终确定最优的人员调整方案为:分别将员工1、2、3、4分配到岗位4、3、1、2。
关键词:经验判断模型满意度层次分析法 0-1模型灵敏度分析Ⅰ问题背景及问题重述一、问题背景对员工的调整,虽说是一种现代企业制度的管理机制,但并不是说用人单位可以随意对员工的岗位进行变动,其调整的依据,一方面是用人单位生产经营需求,即各个岗位对于所需员工各方面的能力(工作能力、管理水平、综合处理能力、技术水平)的要求,另一方面就是员工的工作意向。
只有充分考虑两方面的因素,才能使用人单位以及员工都满意,那样生产效率才会更高。
二、问题重述人力资源的合理分配已成为当今社会发展的重要课题,受到社会各界的广泛关注。
某单位为了尽可能发挥工作人员的作用,拟将4名工作人员的工作岗位进行适当调整。
单位根据以往的工作表现对4名工作人员的工作能力,综合处理能力,管理水平,技术水平等四方面进行了评价,已知四名工作人员的工作意向和各岗位的工资待遇,工作环境,工作强度晋升机会和对工作人员希望达到的要求。
人员调配问题

人员1
人员2
人员3
人员4
岗位
岗位4
岗位3
岗位1
岗位2
六模型优化
1.本模型为了计算简便在假设时采用量化模型全部是4分制,且假设没一个量化值都是等距的,在实际情况中模型要复杂的多,因此可以根据实际需要调整量化模型;
2.本模型没有优先考虑不同岗位对四种能力的要求,而是直接以人员1的岗位志愿进行比较分析,得出结果。然而实际我们需要综合考虑,以达到最优分配调整方案;
关键词:循环比较法、模型建立、欧氏距离、表格法
二
某单位为了尽可能发挥工作人员的作用,拟将4名工作人员的工作岗位进行适当调整。单位根据以往的工作表现对4名工作人员的工作能力,综合处理能力,管理水平,技术水平等四方面的评价(每项从高到低按A、B、C、D四个等级)以及四名工作人员的工作意向(即申请岗位)详见附件一。各岗位的工资待遇(好、中、一般),工作环境(好、中、一般、差),工作强度(大、中等、轻松)晋升机会(多、一般、少)和对工作人员希望达到的要求详见附件二。请你通过数学建模的方法给出该单位人员调整的方案。
附件一:四名工作人员工作意向及单位评价
人员
工作意向
单位评价
一志愿
二志愿
三志愿
工作
能力
管理
水平
综合处理能力
技术
水平
人员1
岗位1
岗位3
岗位4
B
A
C
B
人员2
岗位3
岗位1
岗位2
A
C
D
A
人员3
岗位1
岗位4
岗位3
C
B
A
B
人员4
岗位2
人员值班分配数学建模,运筹学

三、问题ห้องสมุดไป่ตู้析
分析该问题,可以得出该问题是一个线性规划问题,求解需雇佣的最少员 工人数,所以应该,建立目标函数以及对应的约束条件。根据每班的人数列出 目标函数,根据六个时间段所需要的最少员工数建立约束条件。检查值班的负 责人都有不能值班的时间段,但可以保证每个值班时间段都有人去检查。可以 用 0,1 算法求每个负责人所检查的时间段。
一、问题描述
(1)每日每部门至少需要下列数量的员工: 部门 a1 a2 a3 a4 a5 a6 (1) 时间 08 时—10 时 10 时—12 时 12 时—14 时 14 时—16 时 16 时—18 时 18 时—20 时 最少员工数 60 70 60 50 20 30
每班员工,连续工作 2 小时,为满足每班所需要的员工数,最少 需雇佣多少员工?
18 时—20 时
95% 88% 90% 81% 91% 94%
a1 a2 a3 a4 a5 a6
如何分配部门值班情况,才能让工作效率最大?
二、问题假设
1.每名值班员工都正常工作,没有请假现象,查班负责人也是不缺勤。 2.不存在大的人员变动。 3.每名部门员工都可以连续工作 2 小时。 4.假设各个部门工作效率是一样的,如何安排值班分配。 5.假设各个部门之间工作效率不同,如何安排才能使效率得到最大。
四、模型建立
(1)根据题意判断出该问题属于求解最优化问题,需要确定目标函数和约束条 件,具体模型如下: Z 为需要雇佣的最少员工数量,Xi 为第 i 次加入值班的人数(i=1~6)。
min Z x 1 x 2 x 3 x 4 x 5 x 6 x 1 x 6 60 x 1 x 2 70 x 2 x 3 60 t x 3 x 4 50 x x 20 5 4 x 5 x 6 30 x i 0,i 1, 2, , 6
数学建模研究生录取问题(人员调度)

2013年中北大学大学生数学建模竞赛选拔赛题B 研究生录取问题摘要本文将研究生录取问题和跟导师之间的双向选择问题分别转化成层次分析问题和线性规划中的0-1规划问题。
首先利用层次分析法对进入复试的学生进行差额录取,考虑所有可能的师生配对方案,根据总体满意度作为评价研究生复试招生合理性的指标,找到师生间的最佳配对方案,达到双向选择的目的。
对于满意度量化中各种权值的具体赋值,我们利用层次分析中权值矩阵的一致性检验法则进行了检验计算,使得每个最终配对方案的可信度达到最大。
在比较各个方案的总体满意度大小的基础上,我们提出了更能体现双向选择的录取方案。
关键词:集对分析层次分析法0-1 规划双向选择一问题重述某校某学科方向招收研究生指标是20人,达到复试线的是31个人,有关学生初试复试成绩见后面表格。
导师中有3位教授(T1,T2,T3),7位副教授(T4,T5,T6,T7,T8,T9,T10),现需要解决以下问题:1. 根据初试和复试成绩,选拔20位学生。
2. 根据学生意愿,对导师和学生进行分配。
其中教授T3今年只招2人,其余每位教授可招收3-4人,每位副教授可招收1-2人。
3. 近几年采用的导师分配办法是:先由每位教授根据学生意愿选择3人,再由每位副教授根据学生意愿选择1人;接下来根据学生意愿教授可以再选择1人,副教授再选择2人。
试提出评价研究生复试招生合理性的指标,并对上述方法予以评价。
4. 学校规定:各学科严格按照下达指标招生,不得超过;如果某学科不能完成今年的招生计划,明年的指标按照今年实际招生数量确定。
但在近几年的招生中发现有以下问题:一是因面试时间短,面试效果不理想,个别不是很优秀的学生被录取;二是确定并录取名单后,有的学生拒绝录取,又到别的学校参加复试;三是有的学生9月份报到的时候,因找到工作,或对导师安排有意见或其它个人原因放弃读研机会,导致指标浪费。
试提出招生录取的改进方案,该方案对上述问题有一定考虑,并对该方案的利弊进行评价。
数学建模-人员安排问题及参考答案

Reduced Cost 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 18000.00 18000.00 18000.00 18000.00 18000.00 18000.00 18000.00 18000.00 18000.00 21000.00 21000.00 21000.00 21000.00 21000.00 21000.00 21000.00 21000.00 21000.00 19200.00 19200.00 19200.00 19200.00 19200.00 19200.00
目标函数值:203400 元; 费用增加量:203400-198000=5400 元; 当重新安排工程师甲到工期 2 时的损失不超过 5400 元时, 可以将 他的工作重新安排。 5.2 问题三 模型构成: 增加约束条件: (不一起工作可理解为不同时在一个项目中工 作) : 0 x2 jk x3 jk 1 , j 1, 2,3 , k 1, 2,3 ; 求解: 最 优 解 : x123 x131 x132 1 , x213 x222 x231 1 , x313 x331 x332 1 ,
Value 3000.000 3500.000 3200.000 3900.000 3.000000 2.000000 5.000000 0.000000 1.000000 0.000000 0.000000 0.000000 0.000000 1.000000 0.000000 1.000000 0.000000 0.000000 1.000000 1.000000 0.000000 0.000000 0.000000 1.000000 0.000000 1.000000 0.000000 0.000000 0.000000 1.000000 0.000000
人员疏散问题数学建模课程设计

摘要本文是关于安排建筑物的出口和撤离方案使所有人员撤离完毕所用疏散时间最小的优化问题。
问题一:我们假设只有单行和双行两种方式。
无论哪种方式,人流速度主要与人员密度有关,0.80vv ρ-=-。
通过分析知流量随人流密度的增加先增后减,单行流量小于双行的流量,故我们尽量使人流双行。
经分析得出:540.800.8110[([/1])/2]*/[(2[1/1])]([1/1])ij i j lt N l d c v d v d --==⎧⎫=+-+-+⎨⎬-+⎩⎭∑∑问题二:在问题一的基础上,给出符合实际情况的数据,模拟地震发生时的情形,经求解得出:当0 4.0/v m s =时,149.88t s = 当03.0/v m s=时,201.11ts=得出最佳撤离方案:即先撤出一楼单行的人员,再撤出一楼和二楼双行的人员, 最后撤出三至五层楼的人员。
问题三:为方便紧急撤离,在问题三的分析中,我们给出五个改进措施。
根据这五个措施,画出教学楼的设计图。
为使模型简化,给出了一些合理的假设和数据,从而得出疏散时各楼层的模拟图。
最终列出模型方程:5440.80.810111'[()/3]/[2(1/1)]ij j i j j t N N c l v d --===⎧⎫=-*+-+⎨⎬⎩⎭∑∑∑代入问题二中的数据,得到:当0 4.0/v m s =时,43.5996t s = 当03.0/v m s=时,59.3879ts=与问题二中所求的疏散时间相比较,显然我们改进的方案的疏散时间较短。
故我们的改进方案可行性较强。
问题四:经分析为使疏散时间最小,只需使等待时间最小。
以下为教室安排方案:先让速度快的人员先下楼,故一楼安排运动能力为E 的人员,二楼安排运动能力为A 的人员,三楼安排运动能力为B 的人员,四楼安排运动能力为C 的人员,五楼安排运动能力为D 的人员。
巧妙的将人的行走比作流体,建立人流模型,使问题简化,这是本文的特色。
数学建模B题:人员安排问题
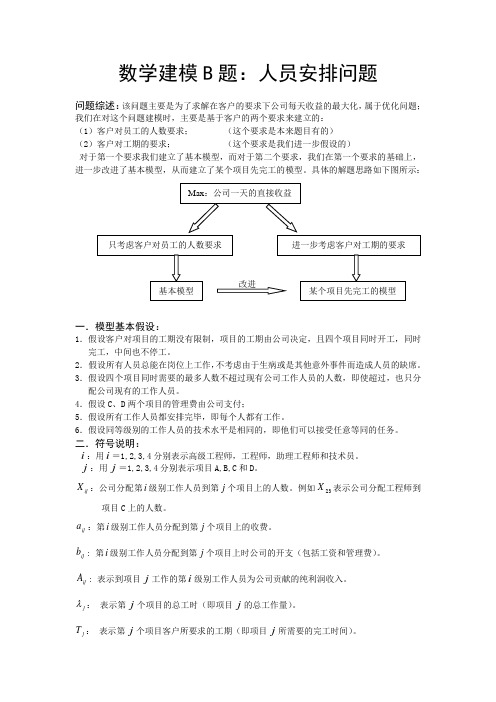
数学建模B 题:人员安排问题问题综述:该问题主要是为了求解在客户的要求下公司每天收益的最大化,属于优化问题;我们在对这个问题建模时,主要是基于客户的两个要求来建立的: (1)客户对员工的人数要求; (这个要求是本来题目有的) (2)客户对工期的要求; (这个要求是我们进一步假设的)对于第一个要求我们建立了基本模型,而对于第二个要求,我们在第一个要求的基础上,进一步改进了基本模型,从而建立了某个项目先完工的模型。
具体的解题思路如下图所示:一.模型基本假设:1.假设客户对项目的工期没有限制,项目的工期由公司决定,且四个项目同时开工,同时完工,中间也不停工。
2. 假设所有人员总能在岗位上工作,不考虑由于生病或是其他意外事件而造成人员的缺席。
3.假设四个项目同时需要的最多人数不超过现有公司工作人员的人数,即使超过,也只分配公司现有的工作人员。
4.假设C 、D 两个项目的管理费由公司支付;5.假设所有工作人员都安排完毕,即每个人都有工作。
6.假设同等级别的工作人员的技术水平是相同的,即他们可以接受任意等同的任务。
二.符号说明:i :用i =1,2,3,4分别表示高级工程师,工程师,助理工程师和技术员。
j :用j =1,2,3,4分别表示项目A,B,C 和D 。
ij X :公司分配第i 级别工作人员到第j 个项目上的人数。
例如23X 表示公司分配工程师到项目C 上的人数。
ij a :第i 级别工作人员分配到第j 个项目上的收费。
ij b : 第i 级别工作人员分配到第j 个项目上时公司的开支(包括工资和管理费)。
ij A : 表示到项目j 工作的第i 级别工作人员为公司贡献的纯利润收入。
j : 表示第j 个项目的总工时(即项目j 的总工作量)。
j T : 表示第j 个项目客户所要求的工期(即项目j 所需要的完工时间)。
j M : 表示客户要求第j 个项目一天所必须完成的工作量。
j m : 表示公司分配给第j 个项目的所有工作人员一天能够完成的工作量。
数学建模排班问题讲解学习

数学建模排班问题值班人员安排问题摘要某部队后勤值班室准备聘请4名兼职值班员和2名兼职带班员值班两种职位,相应的报酬也不同。
为使部队的支出最少,现需合理的设计出一张人员的值班时间表,在安排兼职值班员的过程中,需要考虑多方面的的问题与因素.因此,一个合理有效的兼职值班时间表的安排是非常有实际意义的.本次设计在综合了解一定的数学模型、以及LINGO软件中一些知识的基础上,以线性规划理论为基础,对实际例子进行一定的分析后,建立合理的整数规划模型.然后,利用LINGO软件求得结果.给出一个最优化的值班计划,使后勤值班室总支付的报酬为最少.关键词:值班时间表,LINGO软件,模型,报酬一.问题重述某部队后勤值班室准备聘请4名兼职值班员(代号为1,2,3,4)和2名兼职带班员(代号5,6)值班,已知每人从周一到周日每天最多可以安排的值班时间及每人每小时值班的报酬如下表.每人每天可值班的时间和报酬该值班室每天需要值班的时间为早上8:00至晚上22:00,值班时间内须有一名值班员值班.要求兼职值班员每周值班不少于10h,兼职带班员每周值班不少于8h.每名值班员每周值班不超过4次,每次值班不少于2h,每天安排值班的值班员不超过3人,且其中必须有一名兼职带班员值班.试为该值班室安排一张值班人员表,使总支付的报酬为最少.二.模型的假设(1)兼职员在可安排的时间内无特殊情况发生均可按时值班;(2)值班室需要值班的时间稳定不变;(3)值班员的兼职工资稳定不变.三.符号的说明ijx表示第i个值班员在星期j是否值班,如果值班,则ijx=1,否则ijx=0。
ija表示第i个值班员在星期j的值班时间。
ik表示第i个值班员值班一个小时所能够获取的报酬,ijA表示第i个值班员在星期j的值班时间的上限。
四.问题设计本题是在通过安排不同人员的值班时间来是部队支付的报酬最少,在给定的约束条件和每人每天的工作时间和报酬来设计。
由于知道员工每天的工作时间和报酬,这样就可确定目标函数,再通过给定的约束条件来解答,从而得出最优的值班时间表。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
B题人员安排问题
“PE公司”是一家从事电力工程技术的中美合资公司,现有41个专业技术人员,其结构和相应的工资水平分布如表1所示。
表1 公司的人员结构及工资情况
目前,公司承接有4个工程项目,其中2项是现场施工监理,分别在A地和B地,主要工作在现场完成;另外2项是工程设计,分别在C地和D地,主要工作在办公室完成。
由于4 个项目来源于不同客户,并且工作的难易程度不一,因此,各项目的合同对有关技术人员的收费标准不同,具体情况如表2所示。
表2 不同项目和各种人员的收费标准
为了保证工程质量,各项目中必须保证专业人员结构符合客户的要求,具体情况如表3 所示:
表3:各项目对专业技术人员结构的要求
说明:
●表中“1~3”表示“大于等于1,小于等于3”,其他有“~”符号的同理;
●项目D,由于技术要求较高,人员配备必须是助理工程师以上,技术员不能参加;
●高级工程师相对稀缺,而且是质量保证的关键,因此,各项目客户对高级工程师的配备
有不能少于一定数目的限制。
各项目对其他专业人员也有不同的限制或要求;
●各项目客户对总人数都有限制;
●由于C、D两项目是在办公室完成,所以每人每天有50元的管理费开支。
由于收费是按人工计算的,而且4个项目总共同时最多需要的人数是10+16+11+18=55,多于公司现有人数41。
因此需解决的问题是:如何合理的分配现有的技术力量,使公司每天的直接收益最大?并写出相应的论证报告。
问题重述:
本问题是人事安排,在满足客户要求,和公司人员结构的前提下,公司获得最大利润问题,即: 4个项目总共同时最多需要的人数是10+16+11+18=55,多于公司现有人数41。
因此需解决的问题是:如何合理的分配现有的技术力量,使公司每天的直接收益最大?
要建立模型:
1,客户要求:不同工种的人数,见表3. 2,公司人员结构:见表1.
3,不同项目,和各种人员收费标准:见表2.
建立最佳收益模型f(x)max,并列出不同项目的人员结构.
模型假设:
假设四个项目同时开始,并且同时结束,所有人都工作.同等级别的人的能力一样. C 、D 项开支由公司支付。
符号说明
i :用i =1,2,3,4分别表示高级工程师,工程师,助理工程师和技术员。
j :用j =1,2,3,4分别表示项目A,B,C 和D 。
ij
X :公司分配第i 级别工作人员到第j 个项目上的人数。
例如23X
表示公司
分配工程师到项目C 上的人数。
ij
a :第i 级别工作人员分配到第j 个项目上的收费。
ij
b : 第i 级别工作人员分配到第j 个项目上时公司的开支(包括工资和管理
费)。
ij
A : 表示到项目j 工作的第i 级别工作人员为公司贡献的纯利润收入。
j
λ: 表示第j 个项目的总工时(即项目j 的总工作量)。
模型的建立:
总收益=总收入-总支出
公司每天的总收费为:
ij
i j ij
X a
∑∑==414
1 , 每天的总开支为:ij
i j ij
X b
∑∑==41
4
1
公司每天的直接收益为:
ij i j ij ij X a X f ∑∑===4
14
1
)( - ij i j ij X b ∑∑==4
14
1
= ij i j ij ij X b a )(4
14
1
∑∑==- (1)
由此可得,方程模型:Max :ij i j ij ij
ij X b a
X f )()(414
1
∑∑==-=
如下:
10
4
11
≤∑=i i X
9
4
1
1=∑=j j
X
17
4
1
2=∑=j j
X
104
13=∑=j j
X
5
4
1
4=∑=j j
X
且有
ij
X 为整数;(j i ,=1,2,3,4)
由此通过lingo 可以算出一天的公司的最大收益时的公司人员结构最优化信
息 。
(程序见附表)
16412≤∑=i i X 11
4
13
≤∑=i i X
18
4
1
4≤∑=i i X
利用matlab算出最大收益值为:27150(元)。
结果分析:
在考虑客户需求的前提下,实现了公司利益的最大化。
由表4符合可以看出,D 中人员分配比较少,这样公司相对少支付给工程师的50员的额外补助,符合实际。
但由于工程耗时不确定,和实际工程建设中,A、B、C、D不一定同时完工,所以该模型有一定的弊端。
