线段垂直平分线尺规作图题
1.3.2_线段的垂直平分线(2)

D
提示:
因为直线CD与线段AB的交点就是AB的中点,所以我们也用 这种方法作线段的中点.
回顾
思考 2
线段的垂直平分线的 性质定理
M
定理 线段垂直平分线上的点到这
条线段两个端点距离相等.
如图, ∵AC=BC,MN⊥AB,P是MN上任意一点 (已知), A ∴PA=PB (线段垂直平分线上的点到这 条线段两个端点距离相等).
所作出的三角形都全等吗? 若已知等腰三角形的底及底边上的高,
你能用尺规作出等腰三角形吗?能作几个?
做一做
初 露 锋 芒
已知底边及底边上的高,利用尺规作等腰三角形
a
h
已知:线段a,h(如图).
求作: △ABC,使AB=AC,且BC=a,高AD=h.
你能亲自写出作法吗?
随堂练习
已知:线段a,h(如图).
N
提示:这个结论是经常用来证明点在直线上
(或直线经过某一点)的根据之一.
试一试
小 试 牛 刀
1、已知直线和直线上一点P,利用尺规作直线
的垂线,使它经过点P.
C C
●
P B
A
D
l
想 一 想
学 无 止 境
1、已知直线和直线外一点P,利用尺规作直线 的垂线,使它经过点P.
P
●
l
想一想,做一做
利用尺规作出三角 形三条边的垂直平分线.
P
C
N
B
提示:
这个结论是经常用来证明两条线段相等的根据之一.
回顾
思考 3
线段的垂直平分线的 性质定理的逆定理
P
逆定理 到一条线段两个端点距离相等的点,在 这条线段的垂直平分线上. M 如图,
线段的垂直平分线

A E B
D
C
小结
1.线段的垂直平分线的作法
2.线段垂直平分线的性质定理
作业:
必做题:练习1,2,3 选做题:这个性质定理的逆命题是什么? 它是否成立?试着自己探究探究。
1 ∵以点A,B为圆心,大于 2
AB长为 在△AMO和△BMO中, AM=BM ∵ ∠AMO=∠BMO MO=MO ∴△AMO≌△BMO(SAS) ∴∠AOM=∠BOM=90° AO=BO 故MN是线段AB的垂直平分线。
∴AM=BM=AN=BN 在△AMN和△BMN中, AM=BM ∵ AN=BN MN=MN ∴△AMN≌△BMN(SSS) ∴∠AMO=∠BMO
思考2:在直线MN上任意取一点P,连接PA 与PB,请大家测量一下PA与PB的长度,看 一看它们之间有什么关系?
PA=PB
小组讨论: 你们选取的P点的位置相同吗?如果不同, 你们能找到什么规律?
规律:线段垂直平分线上的点到线段两端 点的距离相等。
已知:如图,直线MN经过线段AB的中点O,且 MN⊥AB,P是MN上任意一点。 求证:PA=PB
2.已知:△ABC中,D在BC上,AB=AC,DB=DC,E是 AD上的一点。 求证:BE=CE
证明:
在△ABD和△ACD中, AB=AC ∵ DB=DC AD=AD ∴△ABD≌△ACD(SSS) ∴∠ADB=∠ADC=90° ∴AD⊥BC 即AD是BC的垂直平分线。 ∵E是AD上的一点 ∴BE=CE
③尺规作图法: 1 1.作出一条线段AB,分别以点A,B为圆心,大于 AB长为半径 2 (为什么?)画弧交于点M,N。 2.过点M,N作直线。 则直线MN就是线段AB的垂直平分线。
思考1:为什么MN就是垂直平分 线呢?若MN交AB于点O,你能给 出证明吗?
关于线段垂直平分线的尺规作图

冀教2011课标版 八年级上册
线段的垂直平分线
——尺规作图
河北省承德市滦平县第三中学 齐占仓
1、线段是 轴对称 对称图形, 它的对称轴 是线段的垂直平分线
2、线段的垂直平分线的性质定理是 :
线段垂直平分线 上的点到线段两端的 距离相等
•c
A
B
• 3、线段的垂直平分线的性质定理的逆定理 是 : 到线段两端的距离相等的点在这条 线段的垂直平分线上
.C
A
B
.D
谈谈这节课你的收获:
。
当堂测评
已知两点A、B
求作:直线 l ,使点A、B关于 l 对称
A . .B
学习目标
1、通过经历探究尺规作图过程,掌握 用尺规作已知线段的垂直平分线, 过一点作已知直线的垂线
2、通过作图培养学生的动手能力和语 言表达能力
探究一
已知:线段AB
A
B
求作:线段AB的垂直平分线
要求:1、先独立思考下面的问题:
1)你是怎样思考的? 2)你是怎样作图的? 3)你这样作图的理由是什么? 2、如果自己没有思路可以小组合作完 成上 面 的问题。
探究二
已知:直线 l 和直线外一点 P. 求作:经过点 P,且垂直于 l 的直线
l
•P
l
பைடு நூலகம்
l
已知:直线 l 和直线上一点 P.
求作:经过点 P,且垂直于 l 的直线
初二数学线段的垂直平分线试题

初二数学线段的垂直平分线试题1.已知线段AB和它外一点P,若PA=PB,则点P在AB的___________________;若点P在AB的___________________,则PA=PB.【答案】垂直平分线上;垂直平分线上.【解析】根据线段的垂直平分线的性质和判定,即可得到结果。
若PA=PB,则点P在AB的垂直平分线上;若点P在AB的垂直平分线上,则PA=PB.【考点】本题考查了线段的垂直平分线的性质和判定点评:解答本题的关键是掌握线段的垂直平分线的性质:线段的垂直平分线的点到线段两端点的距离相等。
线段的垂直平分线的判定方法:到线段两端点的距离相等的点在这条线段的垂直平分线上。
2.已知:△ABC中,边AB,AC的垂直平分线相交于点P.求证:点P在BC的垂直平分线上.【答案】见解析【解析】画出图形后根据线段垂直平分线的性质得出PA=PB,PA=PC,推出PB=PC即可.∵P在AB的垂直平分线EF上,∴PA=PB,∵P在AC的垂直平分线MN上,∴PA=PC,∴PB=PC,∴点P在BC的垂直平分线上.【考点】本题考查了线段的垂直平分线的性质和判定点评:解答本题的关键是掌握线段的垂直平分线的性质:线段的垂直平分线的点到线段两端点的距离相等。
线段的垂直平分线的判定方法:到线段两端点的距离相等的点在这条线段的垂直平分线上。
3.⑴作一个钝角三角形,利用尺规作这个三角形三条边的垂直平分线;⑵作直角三角形和锐角三角形,利用尺规作三角形三条边的垂直平分线;⑶你发现三角形三条边的垂直平分线与三角形的形状有怎样的位置关系?【答案】⑴、⑵略;⑶锐角三角形三边的垂直平分线的交点在三角形内部;直角三角形三边的垂直平分线的交点在斜边上,即斜边的中点;钝角三角形三边的垂直平分线的交点在三角形外部.【解析】根据垂直平分线的尺规作图的方法,即可作出图形,再根据图形分析。
⑴、⑵略;⑶锐角三角形三边的垂直平分线的交点在三角形内部;直角三角形三边的垂直平分线的交点在斜边上,即斜边的中点;钝角三角形三边的垂直平分线的交点在三角形外部.【考点】本题考查了线段的垂直平分线点评:解答本题的关键是掌握垂直平分线的尺规作图的方法。
16.2尺规作图线段垂直平分线

永年县第四中学 吴睿
课前回顾
M P
1.垂直平分线的定义: ∵MN是AB的垂直平分线 AD=BD; ∴ MN⊥AB , A D B 2.垂直平分线的性质: N ∵MN是AB的垂直平分线 ∴ PA=PB ( 线段垂直平分线上点与这条线段两个端点的距离相等 ) 3.垂直平分线的判定: ∵PA=PB ∴ P在AB的垂直平分线上 ( 到线段两端距 离相等的点,在这条线段的垂直平分线上 )
先分别作出不同形状的三角形,再按要求去作图.
驶向胜利 的彼岸
作线段的垂直平分线
如果两个图形成轴对称,怎样作出图形的对称轴?
如果两个图形成轴对 称,其对称轴是任何一对 对应点所连线段的垂直平 分线.因此,只要找到任 意一组对应点,作出对应 点所连线段的垂直平分线, 就得到此图形的对称轴.
小结
1.说说线段垂直平分线的作法; 2.画成轴对称的图形的对称轴的几种常见方 法: (1)将图形对折; (2)用尺规作图; (3)用刻度尺先取一对对称点连线的中点,然 后画垂线.
(3)由DE是BC的垂直平分线得:BD=CD;所以AD+CD= AD+BD=AB. (4)由(2)中式子-(1)中式子得BC=10cm.
课堂练习
练习4 如图,过点P 画∠AOB 两边的垂线,并和 同桌交流你的作图过程. A
P O
B
独立作业
1
习题1.5
1.利用尺规作出三角形三条边的垂直平分线.
老师期望:
课堂练习
练习3:如图,与图形A成轴对称的是哪个图形? 画出它们的对称轴.
思考
两个成轴对称的图形,不经过折叠,你用什 么方法画出它的对称轴? 我们已经知道,如果两个图形关于某条直线 对称,那么对称轴是任何一对对应点所连线 段的垂直平分线.因此我们只要找到这两个 图形的一对对应点,然后画出以这两个对应 点为端点的线段的垂直平分线就可以了. 提问:如何画一条线段的垂直平分线呢?
线段的垂直平分线含答案

12、(2020•泉州)如图,在△ABC中,BC边上的垂直平分线DE交边BC于点D,交边AB于点E.假设△EDC的周长为24,△ABC与四边形AEDC的周长之差为12,那么线段DE的长为_________.
解答:解:∵在△ABC中,别离以点A和点B为圆心,大于的AB的长为半径画孤,两弧相交于点M,N,作直线MN,交BC于点D,连接AD.
∴MN是AB的垂直平分线,
∴AD=BD,
∵△ADC的周长为10,
∴AC+AD+CD=AC+BD+CD=AC+BC=10,
∵AB=7,
∴△ABC的周长为:AC+BC+AB=10+7=17.
1、(2020•绍兴)如图,在△ABC中,别离以点A和点B为圆心,大于的AB的长为半径画孤,两弧相交于点M,N,作直线MN,交BC于点D,连接AD.假设△ADC的周长为10,AB=7,那么△ABC的周长为( )
A、7B、14
C、17D、20
考点:线段垂直平分线的性质。
专题:几何图形问题;数形结合。
分析:第一依照题意可得MN是AB的垂直平分线,即可得AD=BD,又由△ADC的周长为10,求得AC+BC的长,那么可求得△ABC的周长.
应选C.
点评:此题考查了线段垂直平分线的性质与作法.题目难度不大,解题时要注意数形结合思想的应用.
2、(2020•丹东)如图,在Rt△ACB中,∠C=90°,BE平分∠ABC,ED垂直平分AB于D.假设AC=9,那么AE的值是( )
A、6 B、4
15.2 线段的垂直平分线练习题 2021——2022学年沪科版八年级数学上册
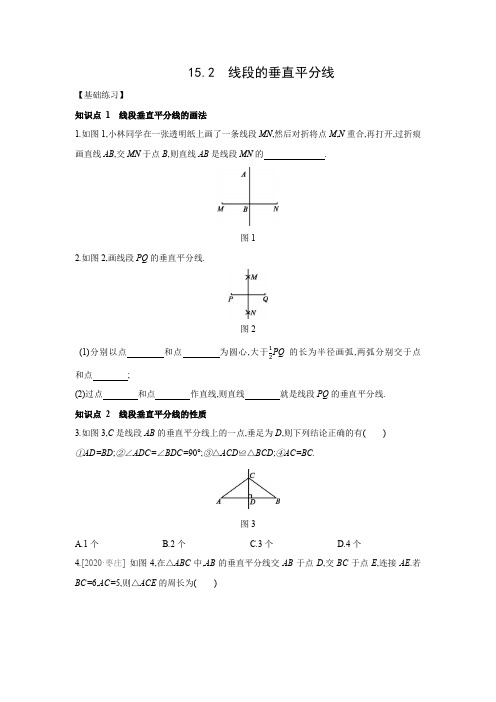
15.2 线段的垂直平分线【基础练习】知识点1线段垂直平分线的画法1.如图1,小林同学在一张透明纸上画了一条线段MN,然后对折将点M,N重合,再打开,过折痕画直线AB,交MN于点B,则直线AB是线段MN的.图12.如图2,画线段PQ的垂直平分线.图2PQ的长为半径画弧,两弧分别交于点(1)分别以点和点为圆心,大于12和点;(2)过点和点作直线,则直线就是线段PQ的垂直平分线.知识点2线段垂直平分线的性质3.如图3,C是线段AB的垂直平分线上的一点,垂足为D,则下列结论正确的有()①AD=BD;②∠ADC=∠BDC=90°;③△ACD≌△BCD;④AC=BC.图3A.1个B.2个C.3个D.4个4.[2020·枣庄]如图4,在△ABC中,AB的垂直平分线交AB于点D,交BC于点E,连接AE.若BC=6,AC=5,则△ACE的周长为()图4A.8B.11C.16D.175.如图5,在△ABC中,AC=4 cm,线段AB的垂直平分线交AC于点N,交AB于点M,△BCN的周长是7 cm,则BC的长为()图5A.1 cmB.2 cmC.3 cmD.4 cm6.[2020·合肥瑶海区期末]如图6,在△ABC中,DE垂直平分AC,交AC于点E,交BC于点D,连接AD,AE=4 cm,则△ABC的周长与△ABD的周长的差为()图6A.2 cmB.4 cmC.6 cmD.8 cm知识点3线段垂直平分线的判定7.已知线段AB外有两点M,N,且MA=MB,NA=NB,直线MN交线段AB于点O,则点O是线段AB的,直线MN是线段AB的.若直线MN上另有一点P,则P A与PB的数量关系是,你的依据是.8.如图7,AC=AD,BC=BD,则有()图7A.AB垂直平分CDB.CD垂直平分ABC.AB与CD互相垂直平分D.CD平分∠ACB9.下列条件不能判定直线MN是线段AB的垂直平分线的是()A.MA=MB,NA=NBB.MA=MB,MN⊥ABC.MA=NA,MB=NBD.MA=MB,MN平分AB且点M不在AB上10.如图8,AB=AC,MB=MC.求证:直线AM是线段BC的垂直平分线.图8【能力提升】11.如图9,在△ABC中,D是AB的中点,且CD⊥AB,若∠A=45°,则∠B=°.图912.如图10所示,在△ABC中,AB=AC,AB的垂直平分线DE交BC的延长线于点E,交AC于点F,交AB于点D,∠A=50°,AB+BC=6,则△BCF的周长为,∠EFC=°.图1013.如图11,AD垂直平分BC于点D,EF垂直平分AB于点F,点E在AC上,BE+CE=20 cm,则AB=cm.图1114.如图12,在四边形ABCD中,AD∥BC,E为边DC的中点,连接AE并延长交BC的延长线于点F.图12(1)AD与FC的数量关系是;(2)若AD=1 cm,AB=5 cm,则当BC的长为时,点B在线段AF的垂直平分线上.15.[教材练习第1题变式题]为了推进农村新型合作医疗制度改革,准备在某镇新建一个医疗点P,使点P到该镇所属A村、B村、C村的距离都相等(A,B,C不在同一直线上,相对位置如图13所示),请用尺规作图的方法确定点P的位置.(要求: 写出已知、求作,不写作法,保留作图痕迹)图1316.[2019·合肥长丰县期末]如图14,已知AB比AC长3 cm,BC的垂直平分线交AB于点D,交BC于点E,△ACD的周长是14 cm,求AB和AC的长.图1417.操作实验:如图15①,把等腰三角形沿顶角的平分线对折并展开,发现被折痕分成的两个三角形成轴对称,所以△ABD≌△ACD,所以∠B=∠C.归纳结论:如果一个三角形有两条边相等,那么这两条边所对的角也相等(证明略).探究应用:如图15②,CB⊥AB,垂足为B,DA⊥AB,垂足为A,E为AB的中点,AB=BC, CE⊥BD.(1)BE与AD是否相等,为什么?(2)小明认为AC是线段DE的垂直平分线,你认为对吗?说说你的理由;(3)∠DBC与∠DCB相等吗?试说明理由.图15答案1.垂直平分线2.(1)P Q M N(2)M N MN3.D[解析] ∵CD是线段AB的垂直平分线,∴AD=BD,∠ADC=∠BDC=90°,故①②正确;又∵CD=CD(公共边),∴△ACD≌△BCD,故③正确;由③可得④正确(也可直接根据线段垂直平分线上的点到线段两端的距离相等,得出④正确).4.B[解析] ∵DE垂直平分AB,∴AE=BE,∴△ACE的周长=AC+CE+AE=AC+CE+BE=AC+BC=5+6=11.5.C[解析] ∵MN是线段AB的垂直平分线,∴AN=BN.∵△BCN的周长=BN+NC+BC=7 cm,∴AN+NC+BC=7 cm,∴AC+BC=7 cm,∴BC=7-4=3(cm).6.D[解析] ∵DE垂直平分AC,AE=4 cm,∴AD=CD,AC=2AE=8 cm.∵△ABC的周长=AB+AC+BC,△ABD的周长=AB+AD+BD=AB+BC,∴△ABC的周长与△ABD的周长的差为AC=8 cm.7.中点垂直平分线P A=PB线段垂直平分线上的点到线段两端的距离相等8.A9.C10.证明:∵AB=AC,∴点A在线段BC的垂直平分线上.∵MB=MC,∴点M在线段BC的垂直平分线上.∴直线AM是线段BC的垂直平分线.11.45[解析] ∵D是AB的中点,CD⊥AB,∴CD是线段AB的垂直平分线,∴AC=BC.易证Rt△ACD≌Rt△BCD,∴∠B=∠A=45°.12.640[解析] 因为直线DE为边AB的垂直平分线,所以AF=BF.所以△BCF的周长=CF+BF+BC=CF+AF+BC=AC+BC=AB+BC=6.∠EFC=∠AFD=90°-∠A=90°-50°=40°. 13.20[解析] ∵EF垂直平分AB于点F,∴AE=BE.∵BE+CE=20 cm,∴AE+CE=20 cm,即AC=20 cm.∵AD垂直平分BC于点D,∴AB=AC=20 cm.14.(1)AD=FC(2)4 cm[解析] (1)因为AD∥BC,所以∠D=∠ECF.因为E为边DC的中点,所以DE=CE.在△ADE和△FCE中,因为{∠D=∠ECF, DE=CE,∠AED=∠FEC,所以△ADE≌△FCE.所以AD=FC.(2)因为点B在线段AF的垂直平分线上,所以AB=BF.又因为AB=5 cm,FC=AD=1 cm,所以BC=BF-FC=5-1=4(cm),即当BC=4 cm时,点B在线段AF的垂直平分线上.15.解:已知:A,B,C三点不在同一直线上.求作:一点P,使P A=PB=PC.如图所示,点P即为所求.16.解:∵DE 是BC 的垂直平分线,∴CD=BD ,∴△ACD 的周长=AC+CD+AD=AC+BD+AD=AC+AB.由题意得{AB -AC =3,AB +AC =14,解得{AC =5.5,AB =8.5,∴AB 和AC 的长分别为8.5 cm,5.5 cm .17.解:(1)BE=AD.理由:∵BD ⊥EC ,DA ⊥AB ,∴∠BEC+∠ABD=90°,∠ADB+∠ABD=90°. ∴∠ADB=∠BEC.在△ADB 和△BEC 中, ∵{∠ADB =∠BEC ,∠DAB =∠EBC =90°,AB =BC ,∴△ADB ≌△BEC (AAS ). ∴BE=AD.(2)对.理由:∵E 是AB 的中点,∴AE=BE.∵AD=BE ,∴AE=AD.在△ABC 中,因为AB=BC ,∴∠BAC=∠BCA.由题意易知AD ∥BC ,∴∠DAC=∠BCA. ∴∠BAC=∠DAC.在△ADC 和△AEC 中, ∵{AD =AE ,∠DAC =∠EAC ,AC =AC ,∴△ADC ≌△AEC (SAS ). ∴DC=EC.∴点C在线段DE的垂直平分线上.∵AD=AE,∴点A在线段DE的垂直平分线上.∴AC是线段DE的垂直平分线. (3)∠DBC=∠DCB.理由:∵△ADB≌△BEC,∴BD=EC.又∵DC=EC,∴DC=BD.∴∠DBC=∠DCB.。
线段垂直平分线知识点+经典例题

第三讲 线段的垂直平分线【要点梳理】要点一、线段的垂直平分线1.定义经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线,也叫线段的中垂线.2.线段垂直平分线的做法求作线段AB 的垂直平分线.作法:(1)分别以点A ,B 为圆心,以大于AB 的长为半径作弧,两弧相交于C ,D 两点;(2)作直线CD ,CD 即为所求直线.要点诠释:(1)作弧时的半径必须大于AB 的长,否则就不能得到两弧的交点了.(2)线段的垂直平分线的实质是一条直线.要点二、线段的垂直平分线定理线段的垂直平分线定理:线段垂直平分线上的点到这条线段两个端点的距离相等.要点诠释:线段的垂直平分线定理也就是线段垂直平分线的性质,是证明两条线段相等的常用方法之一.同时也给出了引辅助线的方法,“线段垂直平分线,常向两端把线连”.就是遇见线段的垂直平分线,画出到线段两个端点的距离,这样就出现相等线段,直接或间接地为构造全等三角形创造条件.要点三、线段的垂直平分线逆定理线段的垂直平分线逆定理:到一条线段两个端点距离相等的点,在这条线段的垂直平分线上. 要点诠释:到线段两个端点距离相等的所有点组成了线段的垂直平分线.线段的垂直平分线可以看作是与这条线段两个端点的距离相等的所有点的集合.要点四、三角形的外心三角形三边垂直平分线交于一点,该点到三角形三顶点的距离相等,这点是三角形外接圆的圆心——外心.要点诠释:1.三角形三条边的垂直平分线必交于一点(三线共点),该点即为三角形外接圆的圆心.2.锐角三角形的外心在三角形内部;钝角三角形的外心在三角形外部;直角三角形的外心在斜边上,与斜边中点重合.3.外心到三顶点的距离相等.要点五、尺规作图作图题是初中数学中不可缺少的一类试题,它要求写出“已知,求作,作法和画图”,画图必须保留痕迹,在现行的教材里,一般不要求写出作法,但是必须保留痕迹.证明过程一般不用写出来.最后要点题即“xxx 即为所求”.2121【典型例题】类型一、线段的垂直平分线定理例1、如图,△ABC中AC>BC,边AB的垂直平分线与AC交于点D,已知AC=5,BC=4,则△BCD的周长是()A.9 B.8 C.7 D.6【思路点拨】先根据线段垂直平分线的性质得到AD=BD,即AD+CD=BD+CD=AC,再根据△BCD的周长=BC+BD+CD即可进行解答.【答案】A;【解析】因为BD=AD,所以△BCD的周长=BD+CD+BC=AD+CD+BC=5+4=9.【总结升华】此题正是应用了线段垂直平分线的性质定理,也就是已知直线是线段垂直平分线,那么垂直平分线上的点到线段的两个端点距离相等,从而把三角形的边进行转移,进而求得三角形的周长.【变式1】如图,在△ABC中,AB=AC,∠A=36°,AB的垂直平分线DE交AC于D,交AB于E,下述结论错误的是()A.BD平分∠ABC B.△BCD的周长等于AB+BCC.AD=BD=BC D.点D是线段AC的中点【答案】D;提示:根据等边对等角、三角形内角和定理及线段垂直平分线的性质定理即可推得选项A、B、C正确;所以选D,另外,注意排除法在解选择题中的应用.【变式2】如图,△ABC中,BC=7,AB的垂直平分线分别交AB、BC于点D、E,AC的垂直平分线分别交AC、BC于点F、G.求△AEG的周长.【答案】解:∵DE为AB的中垂线,∴AE=BE,∵FG是AC的中垂线,∴AG=GC,△AEG的周长等于AE+EG+GA,分别将AE和AG用BE和GC代替得:△AEG的周长等于BE+EG+GC=BC,所以△AEG的周长为BC的长度即7.类型二、线段的垂直平分线的逆定理例2、如图,已知AB=AC,∠ABD=∠ACD,求证:AD是线段BC的垂直平分线.A【答案与解析】证明:∵ AB=AC(已知)∴∠ABC=∠ACB (等边对等角)又∵∠ABD=∠ACD (已知)∴∠ABD-∠ABC =∠ACD-∠ACB (等式性质)即∠DBC=∠DCB∴DB=DC (等角对等边)∵AB=AC(已知)DB=DC (已证)∴点A 和点D 都在线段BC 的垂直平分线上(和一条线段两个端点距离相等的点,在这条线段的垂直平分线上)∴AD 是线段BC 的垂直平分线。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A
E
13cm
B
D
C
证明题:1.已知:ABC中,C=90,A=30o,BD 平分ABC交AC于D. 求证:D点在AB的垂直平分线上. A
30o
D
C
B
2.已知:如图,线段CD垂直平分AB,AB平分CAD. 求证:AD∥BC.
C 证明:
A
1 2
3B O
D
3.已知:如图,在ABC中, AB=AC,A=120o, AB的垂直平分线交AB于E,交BC于F. 求证:CF=2BF.
A
.N
. .M P 点P为所求
作的点
O
B
C
A
B
如图,已知∠AOB及M、N两点,求
作:点P,使点P到∠AOB的两边距
离相等,且到M、N的两点也距离相
等。
A
M N
O
B
已知:线段a,c,∠α 求作:ΔABC,使BC=a,AB=c,∠ABC=∠ α
a c
α
4.已知:如图,在ABC中,DE是AC的垂直平分线, AE=3cm, ABD的周长为13cm,求ABC 的周长
A
B
D
C
1.如图,点C在直线l上,试过点C画 出直线l的垂线.
图 24.4.8
1.画一个直角三角形,使其直角边分 别等于已知的两条线段.
(第 4 题)
2.画一个直角三角形,使其斜边和直 角边分别等于已知的两条线段.
(第 4 题)
动手实践
• AB、AC分别是菱形ABCD 的一条边和对角线,请你 用尺规把这个菱形补充完 整。
A
E
300
300
B
CF=2AF
60O F
30O C
AF=BF CF=2BF
证明题:4.已知:如图,AD平分BAC,EF垂直平分 AD交BC的延长线于F,连结AF. 求证: CAF= B.
A
3 21 E
4
B
D
C
F
如图,已知:AOB,点M、N. 求作:一点P,使点P到AOB两边的 距离相等,并且满足PM=PN.
典例赏析:
在∠AOB内有点M、N,试确定点P,使P到角的两边的距离 相等且到M、N的距离相等。
A
M
O
N
B
当堂训练:
1、如图:△ABC中,BC=a,DE、GF分别为AB、AC的 垂直平分线,则△AEG的周长为___。
A
D
F
B
E
G
C
4、如图:点D在△ABC的边BC上,且BC=BD+AD,试说 明D在AC的垂直平分线上。
