等面积法及应用
三角形等面积法

三角形等面积法
在三角形的研究中,等面积法是一种十分实用的方法。
它的核心
思想是,对于一个给定的面积值,可以构造出许多不同形状的三角形,它们的面积都相等。
这种方法不仅可以用于解决一些几何问题,还可
以用于设计和制造一些具有特定面积要求的物体。
三角形等面积法的应用非常广泛。
例如,在制造船舶和飞机等大
型物体时,要求它们的底部具有一定的面积,以保证它们的浮力和飞
行稳定性。
这时可以利用等面积法来设计合适的底部形状,从而保证
其满足要求。
此外,在房屋建筑、道路修建和水利工程等领域中,三角形等面
积法也经常得到应用。
例如,在修建水库时,要求水库的底部形状必
须能够容纳一定数量的水,从而保证其正常运营。
通过等面积法,可
以设计出满足要求的水库底部形状。
在日常生活中,三角形等面积法也有着广泛的应用。
例如,在购
买面积相等但形状不同的房屋时,可以利用这种方法计算它们的真实
面积,从而作出更加准确的选择。
总的来说,三角形等面积法是一种非常实用的方法,它不仅可以
解决许多几何问题,还可以在实际工作中得到广泛应用。
因此,学好
这种方法对于我们的学习和职业生涯都非常重要。
三角形等面积法在初中数学中的应用

三角形等面积法在初中数学中的应用作者:王斌杰来源:《试题与研究·教学论坛》2012年第13期三角形等面积法是指利用三角形面积自身相等的性质进行解题的一种方法。
此法是初中数学中常用的一种解题方法。
它具有解题便捷快速、简单易懂等特点。
现举例如下:.例1如图,在直角三角形ABC中,∠ACB=90°,AC=4,BC=3,求AB边上的高CD的长。
解析:因为AB2=AC2+BC2,所以AB=5。
又因为S△ABC=12AC·BC=6,S△ABC=12AB·CD=52CD,所以52CD=6,得CD=125。
例2在△ABC中,AB=12,BC=13,AC=5,点P是△ABC内切圆的圆心,求△ABC内切圆的半径。
解析:因为AB2+AC2=169,BC2=169,所以AB2+AC2=BC2。
所以△ABC为直角三角形。
连接AP,PC,BP。
设圆P的半径为r。
S△ABC=12AC·AB=30,S△ABC=S△ABP+S△ACP+S△BCP=12AB·r+12AC·r+12BC·r=12r(AB+AC+BC)=15r,所以15r=30,解得r=2。
例3在等腰三角形ABC中,AB=AC。
点P为BC边上的一个动点,PE垂直AC,PF垂直AB,垂足分别为E,F,求证:PE+PF为定值。
解析:连接AP,过点B作BD垂直AC于点D。
因为S△ABC=S△ABP+S△APC=12AB·PF+12AC·PE,又因为AB=AC,所以S△ABC=12AC(PE+PF)。
又因为S△ABC=12AC·BD,所以12AC(PE+PF)=12AC·BD。
所以PE+PF=BD(定值)。
小结:通过上述的例子可以看出,利用三角形等面积法的性质解题,可从不同的角度使用面积公式表示同一个三角形的面积,列出等式求出未知量。
等面积法例题初二数学

等面积法例题初二数学(原创版)目录1.等面积法的概念2.等面积法的应用3.初二数学中常见的等面积题目类型4.解决等面积题目的步骤和技巧5.例题解析正文一、等面积法的概念等面积法是一种求解几何问题的方法,主要是通过将复杂的几何问题转化为简单的面积问题,从而简化问题。
等面积法在初二数学中是一个重要的知识点,对于提高学生的几何解题能力有重要作用。
二、等面积法的应用等面积法在初二数学中的应用非常广泛,例如在求解三角形、四边形、圆等几何图形的面积时,都可以运用等面积法。
此外,等面积法还可以用于解决一些复杂的几何组合问题,如求解两个三角形面积之和等于一个矩形面积的问题等。
三、初二数学中常见的等面积题目类型初二数学中常见的等面积题目类型主要包括以下几种:1.已知两个图形的面积,求它们的形状和大小;2.已知一个图形的面积和一个边长,求其他边的长度;3.已知两个图形的边长,求它们的面积和形状;4.求解两个图形面积之和等于一个矩形面积的问题。
四、解决等面积题目的步骤和技巧解决等面积题目一般可以分为以下几个步骤:1.观察题目,找出已知条件和需要求解的问题;2.根据已知条件,运用等面积法将问题转化为面积问题;3.利用相关的几何公式,求解面积问题;4.根据求解的结果,得出结论。
在解决等面积题目时,可以运用一些技巧,如:1.利用相似三角形的面积比等于相似比的平方;2.利用两个三角形共边时,它们的面积和等于共边边上的高的比;3.利用矩形的面积等于长乘以宽。
五、例题解析例题:已知一个矩形的长为 8cm,宽为 6cm,求一个与它等面积的三角形的高。
解:根据等面积法,可知该三角形的面积等于矩形的面积,即S=8*6=48。
由于三角形的面积等于底乘以高的一半,所以可以得出:48=底*高/2,解得高=48*2/底。
由于题目没有给出三角形的底,因此需要进一步求解。
可以利用相似三角形的性质,设该三角形的底为 x,那么根据相似比的平方等于面积比,可得出:x/8=高/6,解得 x=48/5。
综合与实践 面积与代数恒等式(等面积法)

问题分析与解决
问题分析
首先需要明确问题的背景和要求, 分析问题所涉及的数学知识点, 包括面积和代数恒等式的概念、 性质和应用。
解决方案设计
根据问题分析,设计合适的解决方 案,包括选择适当的数学方法和公 式,建立数学模型,并确定解题步 骤。
实施解决方案
按照设计的解决方案进行计算和推 理,得出积表示为基底与高的乘积。对于更复杂的图形,可 以通过分割、重组或近似等方法将其转化为简单的几何图形,再利用基底和高 的关系计算面积。
恒等式的几何意义
恒等式是数学中一个重要的概念,它描述了数或代数式之间 的等价关系。
恒等式的几何意义是将代数关系转化为几何图形。通过将代 数恒等式中的变量视为几何图形中的长度、角度或面积等参 数,可以直观地理解恒等式的几何意义。
课程展望
未来发展方向
研究等面积法在解决复杂 问题中的新方法和技巧。
培养学生对数学知识的综 合运用能力。
01
02
03
04
05
06
探索面积与代数恒等式在其 他数学分支的交叉应用。
学生能力培养
提高学生的数学建模和解 决实际问题的能力。
THANKS
感谢观看
面积与代数恒等式的概念及其 关系。
重点与难点解析
难点:如何运用等面积法解决 实际问题。
后续学习建议
深化知识点
01
探索等面积法在解决复杂问题中的技巧和 策略。
03
02
进一步研究面积与代数恒等式在其他数学领 域的应用。
04
实践与应用
结合实际问题,运用等面积法进行建模和 求解。
05
06
参与数学建模竞赛,提高解决实际问题的 能力。
解决方案的验证与优化
等面积法例题初二数学

等面积法例题初二数学
等面积法例题初二数学指的是在初二数学中,使用等面积法解题的示例问题。
等面积法是一种常用的数学解题方法,主要基于面积的守恒原理,通过比较不同图形之间的面积关系来解决问题。
在初二数学中,等面积法常用于解决与面积有关的问题,如面积的证明、计算等。
以下是一些初二数学中应用等面积法的示例问题:
题目1:有一个矩形和一个三角形,它们的面积相等。
矩形的一条边长为6厘米,对应的另一条边长为8厘米。
三角形的底边长为12厘米,底边上的高为5厘米。
求矩形的另一条边长。
解法:我们设矩形的另一条边长为x厘米。
由于矩形的面积为长乘宽,所以矩形的面积为6×8=48平方厘米。
同理,三角形的面积为1/2×12×5=30平方厘米。
由于两者的面积相等,所以有:6x=30,解得x=5,所以,矩形的另一条边长是5厘米。
题目2:证明以下等式成立:a^2 + b^2 = c^2。
解法:我们可以将两个边长为a和b的正方形拼接成一个大的矩形,该矩形的长度为a+b,宽度为a。
矩形的面积为(a+b) × a = a^2 + ab。
由于大矩形的面积为两个小正方形的面积之和,所以有:a^2 + b^2 = c^2。
总的来说,“等面积法例题初二数学”就是初二数学中使用等面积法的例子及解析,通常用在解答关于几何形状的问题时帮助学生找到更快捷和直观的方法找到解题途径。
以上解答和解析仅供参考,如有疑问可以咨询数学老师或查阅教辅练习的解析。
八年级数学等面积法

八年级数学等面积法一、等面积法的概念。
1. 定义。
- 等面积法是利用不同的方法表示同一个图形的面积,从而建立等式关系来解决数学问题的一种方法。
例如,对于一个三角形,我们既可以用底乘以高的一半来计算它的面积,也可以通过将其分割成几个小三角形,分别计算小三角形的面积之和来表示这个三角形的面积,这两种表示面积的方法相等,就可以得到一个等式,进而求解相关的未知量。
二、等面积法在三角形中的应用。
1. 已知三角形的底和高求面积的基本公式。
- 对于三角形ABC,设底为BC = a,这条底边上的高为h,那么三角形的面积S=(1)/(2)ah。
- 例如,在三角形ABC中,BC = 5厘米,BC边上的高AD = 4厘米,那么根据公式S=(1)/(2)× BC× AD=(1)/(2)×5×4 = 10平方厘米。
2. 等面积法在求三角形的高或底中的应用。
- 例1:已知三角形ABC的面积为12平方厘米,底BC = 6厘米,求BC边上的高。
- 设BC边上的高为h,根据三角形面积公式S=(1)/(2)ah(这里a = BC),可得12=(1)/(2)×6× h。
- 解方程:12 = 3h,得h = 4厘米。
- 例2:已知三角形ABC的面积为15平方厘米,AC边上的高BD=5厘米,求AC的长。
- 设AC的长为x厘米,根据面积公式S=(1)/(2)ah(这里a = AC,h = BD),可得15=(1)/(2)× x×5。
- 解方程:(5)/(2)x=15,x = 6厘米。
3. 等面积法在等腰三角形中的应用。
- 在等腰三角形ABC中,AB = AC,设AB = AC = a,底BC=b,底边上的高为h。
- 我们知道等腰三角形底边上的高将等腰三角形分成两个全等的直角三角形,根据勾股定理可得h=√(a^2)-frac{b^{2}{4}}。
- 同时,等腰三角形的面积S=(1)/(2)bh,也可以通过等面积法来求等腰三角形中的一些未知量。
(完整word版)面积——等面积法

面积法在中学数学解题中的巧用利用同一图形的面积相等,可以列方程计算线段的值,或证明线段间的数量关系;利用图形面积的和、差关系列方程,将相等的高或底约去,可以计算或证明线段间的数量关系。
利用等积变形,可以排除图形的干扰,实现“从形到数”的转化,从而从数量方面巧妙地解决问题。
用面积法解题就是根据题目给出的条件,利用等积变换原理和有关面积计算的公式、定理或图形的面积关系进行解题的方法。
运用面积法,巧设未知元,可获“柳暗花明”的效果。
有关面积的公式(1)矩形的面积公式:S=长⨯宽 (2)三角形的面积公式:ah S 21=(3)平行四边形面积公式: S=底⨯高(4)梯形面积公式: S=21⨯(上底+下底)⨯高(5)对角线互相垂直的四边形:S=对角线乘积的一半(如正方形、菱形等) 有关面积的公理和定理 1、面积公理(1)全等形的面积相等;(2)一个图形的面积等它各部分面积之和; 2、相关定理(1)等底等高的两个三角形面积相等;夹在平行线间的两个共底的三角形面积相等;如下图ACD BCD S S =△△;反之,如果ACD BCD S S =△△,则可知直线AB 平行于CD(2)等底等高的平行四边形、梯形(梯形等底应理解为两底的和相等)的面积相等;(3)等底的三角形、平行四边形面积之比等于其高之比;等高的三角形、平行四边形面积之比等于其底之比;(4)相似三角形的面积的比等于相似比的平方;(5)在两个三角形中,若两边对应相等,其夹角互补,则这两个三角形面积相等;(6)等底等高的平行四边形面积是三角形面积的2倍。
一个长方形分成4个不同的三角形,绿色三角形面积是长方形面积的15%,黄色三角形的面积是21平方厘米。
问:长方形的面积是__________平方厘米。
等面积法的应用一:利用平行线间两个共底的三角形面积相等解题。
如图,矩形ABCD 中,AB=3cm ,AD=6cm ,点E 为AB 边上的任意一点,四边形EFGB 也是矩形,且EF=2BE ,则AFC S =△ 9 2cm如图,在四边形ABCD 中,动点P 从点A 开始沿A →B →C →D 的路径匀速前进到D 为止。
中考:等面积法
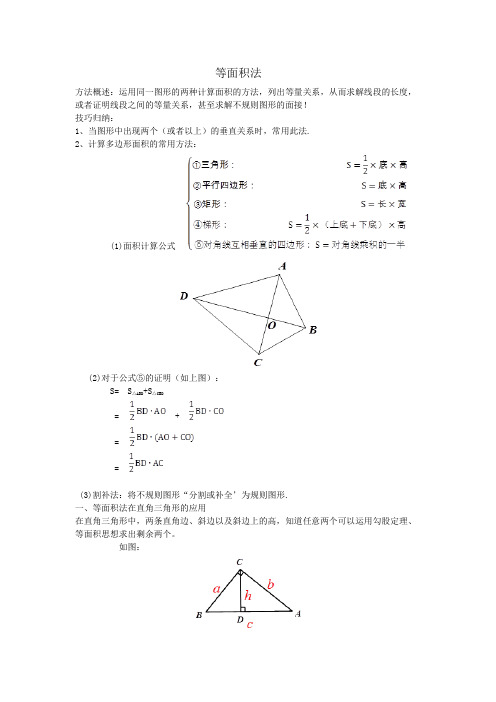
等面积法方法概述:运用同一图形的两种计算面积的方法,列出等量关系,从而求解线段的长度,或者证明线段之间的等量关系,甚至求解不规则图形的面接!技巧归纳:1、当图形中出现两个(或者以上)的垂直关系时,常用此法.2、计算多边形面积的常用方法:(1)面积计算公式(2)对于公式⑤的证明(如上图):S= S△ABD+S△CBD= +==(3)割补法:将不规则图形“分割或补全’为规则图形.一、等面积法在直角三角形的应用在直角三角形中,两条直角边、斜边以及斜边上的高,知道任意两个可以运用勾股定理、等面积思想求出剩余两个。
如图:基本公式: ①勾股定理:②等面积法:证明②:即:,例题1:如图,在Rt ABC ,∠C=90°,当直角边AC =4,斜边AB =5时,求该直角三角形斜边AB上的高CD ?例题2:如图,在Rt ABC (BC AC ) ,∠C=90°,当斜边AB =10cm,斜边AB上的高CD =4.8cm 时,求该直角三角形直角边AC和BC的长度?巩固练习:1、如图,在Rt ABC,∠C=90°,且AC=24, BC=7,作ABC 的三个内角的角平分线交于点P,再过点P 依次作PD⊥AB于D,作PE⊥BC于E, 作PF⊥AC于F .(1)求证:PD = PE = PF ;(2)求出:PD的值.2、如图,△ABC的顶点A,B,C在边长为1的正方形网格的格点上,则BC边长的高为()A.22二、等面积法在等腰三角形的应用在等腰三角形中,可以运用“割补法”的等面积思想,先建立有关“腰以及腰上的高”的等式,再通过等式两边约分来探索出线段之间的数量关系!例题1:如图,在△ABC 中, AB=AC, AC 边上的高BD=10cm.(1)如图1,求AB 边上高CE 的长;(2)如图2,若点P 为BC 边上任意一点, PM⊥AB 于点M, PN⊥AC 于点N,求PM+PN 的值;(3)如图3,若点P 为BC 延长线上任意一点,PM⊥AB 于M,PN⊥AC 于点N,在①PM+PN ;②PM PN 中有一个是定值,判断出来并求值.例题2:已知等边△ABC和内部一点P,设点P 到△ABC三边的AB、BC 、AC 的距离分别是h1,h2,h3,△ABC的高为h,问h1、h2、h3 与h 之间有怎样的数量关系?请说明理由。
等面积法开孔补强计算

a) 有效宽度 B 按式(6-6)计算,取二者中较大值;
⎧ ⎪2d op B=⎨ ⎪ ⎩d op + 2δ n + 2δ nt
b) 有效高度按式( 6-7)和式( 6-8)计算,分别取式中较小值。 外伸接管有效补强高度:
································(6-6)
⎧ ⎪ d opδ nt h1 = ⎨ ⎪ ⎩接管实际外伸高度
接管外径 接管壁厚 25 32 ≥ 3.5 38 45 ≥ 4.0 48 57 ≥ 5.0 65 76 ≥ 6.0
mm
89
注: 1 钢材的标准抗拉强度下限值 Rm≥ 540 MPa 时,接管与壳体的连接宜采用全焊透的结构型式。 2 表中接管壁厚的腐蚀裕量为 1 mm,需要加大腐蚀裕量时,应相应增加壁厚。
Ae = A1 + A2 + A3
式中: Ae——补强面积, mm2 ;
································(6-9)
A1——壳体有效厚度减去计算厚度之外的多余面积(按式 6-10) , mm2 ;
A1 = B − d op (δ e − δ ) − 2δ et (δ e − δ )(1 − f r ) ······························ (6-10)
6.2 6.2.2
术语、定义和符号 GB150.1 通用要求中界定的术语和定义适用于本章。 符号
6. 2.1
A——开孔削弱所需要的补强截面积, mm2; B——补强有效宽度, mm;
1
GB 150.3—2010 C——厚度附加量(按 GB150.1 规定) , mm; Cs—— 圆筒厚度附加量; Ct ——接管厚度附加量; D ——圆筒中面直径, mm; Di——圆筒内直径, mm; Do——平盖直径, mm; dop——开孔直径, mm; d——接管中面直径, mm; do——接管外直径, mm; fr——强度削弱系数; g ——接管补强系数; h —— 圆筒补强系数; h1——外伸接管有效补强高度, mm; h2——内伸接管有效补强高度, mm; K ——等效总应力集中系数;
面积——等面积法

面积法在中学数学解题中的巧用利用同一图形的面积相等,可以列方程计算线段的值,或证明线段间的数量关系;利用图形面积的和、差关系列方程,将相等的高或底约去,可以计算或证明线段间的数量关系。
利用等积变形,可以排除图形的干扰,实现“从形到数”的转化,从而从数量方面巧妙地解决问题。
用面积法解题就是根据题目给出的条件,利用等积变换原理和有关面积计算的公式、定理或图形的面积关系进行解题的方法。
运用面积法,巧设未知元,可获“柳暗花明”的效果。
有关面积的公式(1)矩形的面积公式:S=长⨯宽 (2)三角形的面积公式:ah S 21=(3)平行四边形面积公式: S=底⨯高(4)梯形面积公式: S=21⨯(上底+下底)⨯高(5)对角线互相垂直的四边形:S=对角线乘积的一半(如正方形、菱形等) 有关面积的公理和定理 1、面积公理(1)全等形的面积相等;(2)一个图形的面积等它各部分面积之和; 2、相关定理(1)等底等高的两个三角形面积相等;夹在平行线间的两个共底的三角形面积相等;如下图ACD BCD S S =△△;反之,如果ACD BCD S S =△△,则可知直线AB 平行于CD(2)等底等高的平行四边形、梯形(梯形等底应理解为两底的和相等)的面积相等;(3)等底的三角形、平行四边形面积之比等于其高之比;等高的三角形、平行四边形面积之比等于其底之比;(4)相似三角形的面积的比等于相似比的平方;(5)在两个三角形中,若两边对应相等,其夹角互补,则这两个三角形面积相等;(6)等底等高的平行四边形面积是三角形面积的2倍。
一个长方形分成4个不同的三角形,绿色三角形面积是长方形面积的15%,黄色三角形的面积是21平方厘米。
问:长方形的面积是__________平方厘米。
等面积法的应用一:利用平行线间两个共底的三角形面积相等解题。
如图,矩形ABCD 中,AB=3cm ,AD=6cm ,点E 为AB 边上的任意一点,四边形EFGB 也是矩形,且EF=2BE ,则AFC S =△ 9 2cm如图,在四边形ABCD 中,动点P 从点A 开始沿A →B →C →D 的路径匀速前进到D 为止。
等面积法例题初二数学

等面积法例题初二数学摘要:一、等面积法基本概念1.等面积法的定义2.等面积法在初二数学中的应用二、等面积法例题解析1.例题一1.题目描述2.解题思路3.解题步骤2.例题二1.题目描述2.解题思路3.解题步骤3.例题三1.题目描述2.解题思路3.解题步骤三、等面积法在数学中的意义1.等面积法在几何证明中的应用2.等面积法在实际问题中的应用四、等面积法的学习方法与技巧1.掌握基本概念2.多做例题练习3.培养空间想象力正文:一、等面积法基本概念等面积法,是数学中一种常用的解题方法。
它是指在解决数学问题时,如果已知两个或多个图形的面积相等,那么可以通过面积相等这一条件,推导出其他相关量之间的关系。
在初二数学中,等面积法常常应用于几何证明和实际问题解决。
二、等面积法例题解析为了更好地理解等面积法的应用,我们通过以下三个例题来进行解析:例题一:已知矩形ABCD的面积为12平方厘米,矩形EFGH的面积为6平方厘米,若矩形ABCD与矩形EFGH的长和宽之和相等,求矩形ABCD与矩形EFGH的长和宽。
解题思路:由于已知矩形ABCD与矩形EFGH的面积之和,我们可以利用等面积法,设矩形ABCD的长为x,宽为y,矩形EFGH的长为a,宽为b,则有xy=ab=12和x+y=a+b。
通过解这个方程组,我们可以求得矩形ABCD与矩形EFGH的长和宽。
解题步骤:1.根据已知条件列出方程组:xy=12, x+y=a+b2.将第一个方程变形得到:y=12/x,代入第二个方程得到:x+12/x=a+b3.化简得到:x^2-ab+12=04.求解得到:x=2, y=6, a=3, b=2所以,矩形ABCD的长为2厘米,宽为6厘米,矩形EFGH的长为3厘米,宽为2厘米。
例题二:已知等腰三角形ABC,底边BC=6厘米,高AD=8厘米,求等腰三角形ABC的面积。
解题思路:由于已知等腰三角形ABC的底边和高,我们可以利用等面积法,设等腰三角形ABC的腰长为x,则有x^2=8^2+(6/2)^2=64+9=73。
三角形等面积法在初中教学中的应用

三角形等面积法在初中教学中的应用摘要:关于三角形等面积法是近些年初中数学的一种常规解题思路,它的优势在于可以更加快速的找到解题关键,将一些晦涩难懂的知识点变得简单化。
本文将结合现有的一些典型例题,利用三角形等面积法解决相关问题,以此来培养学生的数学思维,提高学生的解题能力。
关键词:三角形等面积法;初中数学;具体应用前言:在现有的初中数学教学中,采用三角形等面积法是一个比较快捷实用的方法,结合几年的教学经验可以发现,即便部分几何题目的问题并没有涉及到三角形的面积计算,但是我们却可以按照图形进行数形结合,将其与实际问题相联系,进而解决这类问题一、分析三角形之间的相关联系,提升学生简单几何的能力在解决三角形的面积时,通常会利用到三角形的边长以及角度之间的关系。
尤其是在一些几何题目当中可能会让你求解一些与已知条件看似毫无关系的边长和角度,此时,很多同学就会将问题复杂化,但实际上如果你仔细观察就会发现,这道题很可能就是利用了三角形的等面积公式,将一个复杂的几何问题转变为一个解方程的题目,而这类题型的实际目的就是让学生发现图形中图形之间的关系,培养学生的数学几何能力,采用“以数解形”的思想,了解几何题背后的实际含义。
例题1如图,直角三角形ABC中,∠ACB=90°BC=4,AC=4,求CD的长度图1解:∵根据勾股定理可知,AB²=AC²+BC²∴AB=4又∵S△ABC=AB*CD/2=AC*BC/2即4*CD/2=4*4/2∴CD=4二、熟悉三角形的基本属性,培养学生的空间想象能力在一些复杂的几何题目中,通常会将圆、平行四边形等图形与三角形结合起来,此时学生不仅要熟知三角形的一些基本定理,尤其是等腰三角形、等边三角形等特殊图形,要充分利用45°、60°等角度。
同时也要熟悉相关图形的定理,做到活学活用,最后看能否利用等面积法将几何问题转换为简单方程,进而更快速的求解题目。
等 面 积 法 的 应 用

B
C
3、已知菱形ABCD的两条对角线分别 、已知菱形 的两条对角线分别 为6和8, 和 , 则CD与AB这一组对边之间的距离为 与 这一组对边之间的距离为
D O A B C
4、在菱形ABCD中,∠A=60°, 、在菱形 中 ° 周长为40,求这个菱形的面积. 周长为 ,求这个菱形的面积
D O 60° A B C
A E D
B
C
7、在平行四边形ABCD中,BE平 、在平行四边形 中 平 平分∠ 分∠ABC,FC平分∠BCD, , 平分 , (1)请说明 )请说明AF=DE 所形成的夹角为多少? (2)BE与CF所形成的夹角为多少 ) 与 所形成的夹角为多少
A F E D
B
C
8、如图,在△ABC中,点O是AC边上的一 、如图, 中 是 边上的一 个动点, 点作MN∥BC,设MN与∠ABC 个动点,过O点作 点作 ∥ , 与 的平分线交于E点 的平分线交于 点,与∠ABC的外角的平分 的外角的平分 线交于F点 请问: 线交于 点,请问: (1)EO=OF吗?为什么 ) 吗 为什么? 边上的什么位置时, (2)点O在AC边上的什么位置时,四边形 ) 在 边上的什么位置时 AECF是矩形 为什么 是矩形?为什么 是矩形
等 面 积 法 的 应 用
平行线与平分线
平行线与平分线
1、如右图,在△ABC中,点P是 如右图, 如右图 中 是 的平分线与∠ ∠ABC的平分线与∠ACB的平分线 的平分线与 的平分线 的交点, 的交点, 若DB=2,EC=3,则DE= , , 。
D A
P
E C
2、在△ABC中,BD是∠ABC的平分线, 、 的平分线, 中 是 的平分线 B 点作DE∥ , 过D点作 ∥BC, 点作 的形状。 (1)请说明△EBD的形状。 )请说明△ 的形状 点作DF∥ , (2)若过 点作 ∥AB,请判断四边形 A )若过D点作 EBFD的形 的形状。 的形
例谈等面积法在初数学解题中的应用

例谈等面积法在初中数学解题中的应用贵州省榕江县三江中学 潘光联等面积法是一种常用的、重要的数学解题思想方法。
它是利用“同一个图形的面积相等”、“分割图形后各部分面积之和等于原图形的面积”、“同底等高或等底同高的两个三角形的面积相等”等性质解决有关的数学问题。
在解题中,灵活运用等面积法解答相关问题,可以使解题思路清晰,解题过程简捷。
下面举例说明等积法在初中数学解题中的应用:一.求三角形的高例1.如图1所示,在△ABC 中,AB=10,BC=6,AC=8,求AB 边上的高CD 的长.解:在△ABC 中,.10010,10086222222===+=+AB AC BC Θ.222AB AC BC =+∴∴△ABC 是直角三角形.利用三角形面积计算公式得,.2121CD AB BC AC ⋅=⋅ 即8.41068=⨯=⋅=AB BC AC CD Θ 二.求图形的面积例2. 如图2所示,⊙O 的半径为3,OA=6,AB 切⊙O 于B ,弦BC ∥OA ,连接AC ,则图中阴影部分的面积是多少?分析:连接OB 、OC ,将图中不规则的阴影部分的面积转化为扇形0BC 的面积是解决此问题的切入点和关键.解:连接OB 、OC ,由BC ∥OA 知,△OCB 与△ACB 的边CB 上的高相等.故由等积性质可知,CB ACB S S 0∆∆=易知,∠BOC=ο60. 所以ππ2336036020=⨯==CB S S 扇形阴影. 三.求三角形内切圆半径例3.如图3所示,已知⊙O 是△ABC 的内切圆,∠C=ο90,AC=4,BC=3. 求⊙O 的半径.解:设⊙O 的半径为r ,连接0A 、0B 、OC 、OE 、OF 、OG..∵⊙O 是△ABC 的内切圆,∴OG ⊥AB ,OE ⊥BC ,OF ⊥AC ,且OE=OF=OG=r.在Rt △ABC 中,由勾股定理,得.5432222=+=+=AC BC AB于是由ACO BCO ABO ABC S S S S ∆∆∆∆++=,得.21212121AC BC r AC r BC r AB ⋅=⋅+⋅+⋅ 即 .)(AC BC r AC BC AB ⋅=++ ∴.143543=++⨯=++⋅=AC BC AB AC BC r 四.求函数的解析式例4.如图4所示,线段AB=8,直线m 与⊙o 相切于点 D,且m ∥AB ,P 是直线m 上的一点,PB 交以AB 为直径的圆于C,连结AC.设PB=x,AC=y,求y 与x 的函数关系式.分析:因为AB 是⊙O 的直径,所以AC ⊥BP ,又因为把直线m 与⊙o 相切于点 D,且m ∥AB ,所以DO ⊥AB,BP和AC 看成三角形的底和高,于是很自然地连接AP 、OD ,利用同一个三角形的面积相等的性质,就可以得到x 与y 的关系.解:连结AP ,∵AB 是⊙O 的直径,∴AC ⊥BP .又∵直线m 与⊙o 相切于点D,且m ∥AB ,∴DO ⊥AB即△ABP 的AB 边上的高是4, ∴,42121⨯=⋅AB AC BP 即xy=8×4. xy 32= (x >4). 五.在探究规律题中的应用例5.如图-5所示,将一个边长为1的正方形平均分成两个面积是21矩形,又将一个面积为21矩形平均分成两个面积是41的矩形,再将一个面积为41的矩形平局分成两个面积是81的矩形,如此进行分割下去,如果分割n 次后,按图中揭示的规律计算: n 2121212*********++++++Λ 分析:分割图形后各部分面积之和等于原图形的面积根,得.21221121212121161814121444432-=-=+++=+++ 于是利用这个规律就可以把问题解决.解:n 2121212*********++++++Λ=.212211n n n -=- 总之,等面积法是一种重要的数学解题思想方法。
等面积法在逆变电源中的应用

0 引 言
脉宽 调制 ( WM ) 制现 在 已经成 为 电力 电 子 P 控
本 文采 用 的 等 面 积 法 , 将 正 弦 波 按 照 角 是
度平均 分成 N 等分 , 每一等分 的正弦 波 与角度 轴 所 包 围的面积 用等 面积 且 幅 度相 同的 脉 冲代 替 , 且 并
mo u e c n r le y s n l ~ h p t r u h a a y i g t e ag rt m , s s t e s n l— h p t e e a e d l o t o l d b i g e c i , h o g n l z n h l o ih u e h i g e c i o g n r t
中点也 要重合 。因此 , 弦 波 的正 半 周期 就 由幅 度 正 相 同但 是宽 度不 同的脉 冲所表示 出来 , 图 1 如 所示 。
电路 的主 流控制 方式 。P WM 逆 变 电路 具有 压 控 和
频控 的功 能 , 且 能 减低 输 出电 压 的谐 波 含量 。由 并 于开 关变 换器 的强 非 线性 , 以及 它 具 有 的离 散 和 变 结构 的特 点 , 载性质 也是 多变 的 , 电路性 能必须 负 主
21 0 2年 4月
舰 船 电 子 对 抗
SH I PB0 A RD ELECT R0N I COU N TERM EA SUR E C
A p . 01 r2 2
Vo. 1 35 NO.2
第 3 5卷第 2期
等 面 积 法在 逆 变 电源 中的应用
毕 磊 , 彭德 强
BILe , i PENG — i n De q a g
( e 7 3 I s i t fCS C, n z o 2 0 1 Ch n ) Th 2 n t u e o I Ya g h u 2 5 0 , i a t
圆形中的等面积法

圆形中的等面积法
定义
在圆形中,等面积法是指当给定一个圆形,可以通过调整半径或直径来获得具有相同面积的另一个圆形。
应用
等面积法在实际生活中有许多应用。
以下是一些例子:
1. 建筑设计:在建筑设计中,等面积法可以用于调整不同楼层的平面布局,以确保每层的使用面积相同。
2. 农业规划:在农业规划中,等面积法可以用于设计相同面积的农田,以提高农作物的产量和管理效率。
3. 圆形广场设计:在城市规划中,等面积法可以用于设计具有相同面积的圆形广场,以提供相同数量的公共空间。
计算方法
计算等面积的圆形可以通过以下步骤进行:
1. 首先确定一个圆形的面积。
2. 使用面积公式计算另一个圆形的半径或直径。
3. 调整半径或直径,直到获得相同的面积。
以下是计算等面积圆形的面积公式:
- 面积公式:$\pi r^2$,其中$\pi$为圆周率,$r$为半径。
请注意,等面积法只适用于圆形,而不适用于其他形状的图形。
以上是关于圆形中的等面积法的简要介绍。
希望本文对你有所
帮助!。
等面积法三角形

等面积法三角形1. 引言等面积法三角形是一种特殊的三角形构造方法,它通过等面积的条件来确定三角形的形状和大小。
在几何学中,等面积法三角形常被用于解决一些特定的问题,如平面几何的证明和计算等。
本文将介绍等面积法三角形的定义、性质和应用,并通过具体的例子来说明其用法。
2. 等面积法三角形的定义等面积法三角形是指在平面上构造的三个三角形,它们的面积相等。
具体地说,设三角形ABC和三角形DEF的面积相等,即S(ABC) = S(DEF),则称三角形ABC和三角形DEF是等面积法三角形。
3. 等面积法三角形的性质3.1 边长比例对于等面积法三角形ABC和DEF,它们的边长比例有一定的关系。
设AB/DE =BC/EF = CA/FD = k,则有以下结论:•三角形ABC和三角形DEF的边长比例相等。
•三角形ABC和三角形DEF的角度相等。
3.2 高线比例对于等面积法三角形ABC和DEF,它们的高线比例也有一定的关系。
设h1为三角形ABC的高线,h2为三角形DEF的高线,h1/h2 = k,则有以下结论:•三角形ABC和三角形DEF的高线比例相等。
3.3 周长比例对于等面积法三角形ABC和DEF,它们的周长比例也有一定的关系。
设P1为三角形ABC的周长,P2为三角形DEF的周长,P1/P2 = k,则有以下结论:•三角形ABC和三角形DEF的周长比例相等。
4. 等面积法三角形的应用等面积法三角形在几何学中有广泛的应用,下面介绍其中两个常见的应用场景。
4.1 证明等面积法三角形可以用来证明一些几何定理。
例如,要证明两条直线平行,可以通过构造等面积法三角形来证明。
具体步骤如下:1.过给定的一点P,作一条直线l与已知直线平行,交已知直线于点A和B。
2.过点P分别作直线PA和PB的垂线,分别交已知直线于点C和D。
3.证明三角形PAB和三角形PCD的面积相等,即S(PAB) = S(PCD)。
4.根据等面积法三角形的性质,可以得出直线l与已知直线平行。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
等面积法及应用
面积法(Area Method)是数学中一种常见的解题方法,主要用于解决几何问题。
通过将几何形状划分成各种简单的图形,计算各个图形的面积,然后将这些面积相加或相减,最终得到所求的结果。
面积法的优点在于简单易懂,适用范围广,可以解决各种类型的几何问题。
面积法的应用非常广泛,可以用于解决许多几何问题。
下面我们将具体介绍几个面积法的应用。
首先是求解多边形的面积。
对于任意一个多边形,我们可以通过将其划分为多个三角形,再计算各个三角形的面积,最后将各个三角形的面积相加,得到多边形的面积。
这个方法可以用于解决多边形的面积问题,例如求不规则多边形的面积、求正多边形的面积等。
其次是求解圆的面积。
对于一个给定的圆,我们可以通过将其划分为多个扇形,再计算各个扇形的面积,最后将各个扇形的面积相加,得到圆的面积。
这个方法可以用于解决圆的面积问题,例如求圆的面积、求圆环的面积等。
另外,面积法还可以用于解决三角形的面积问题。
对于一个给定的三角形,我们可以通过将其划分为多个三角形或梯形,再计算各个三角形或梯形的面积,最后将各个三角形或梯形的面积相加或相减,得到三角形的面积。
这个方法可以用于解决三角形的面积问题,例如求任意三角形的面积、求等腰三角形的面积等。
此外,面积法还可以用于解决平行四边形的面积问题。
对于一个给定的平行四边形,我们可以通过将其划分为两个三角形或一个矩形,再计算各个三角形或矩形的面积,最后将各个三角形或矩形的面积相加,得到平行四边形的面积。
这个方法可以用于解决平行四边形的面积问题,例如求任意平行四边形的面积、求矩形的面积等。
面积法的应用还远不止以上几个方面,它可以用于解决各种几何图形的面积问题,如梯形的面积、正方形的面积、菱形的面积、扇形的面积等等。
综上所述,面积法是一种常见而重要的解题方法,可以用于解决各种几何问题。
它的应用非常广泛,不仅可以用于求解多边形、圆形、三角形和平行四边形的面积问题,还可以用于求解其他几何图形的面积问题。
通过灵活运用面积法,我们可以更好地理解和解决几何问题,提高我们的数学思维能力和解题能力。
因此,掌握面积法及其应用是数学学习中的重中之重。
