2017考研数学：数一、数二、数三分别有哪些专业要考

合集下载

考研全国一级学科专业目录及名称代码表2

考研全国一级学科专业目录及名称代码表2门类名称：历史学门类代码：06一级学科名称一级学科代码二级学科名称二级学科代码历史学0601 史学理论及史学史060101考古学及博物馆学060102历史地理学060103历史文献学（含∶敦煌学、古文字学）060104专门史060105中国古代史060106中国近现代史060107世界史060108门类名称：理学门类代码：07一级学科名称一级学科代码二级学科名称二级学科代码数学0701 基础数学070101计算数学070102概率论与数理统计070103应用数学070104运筹学与控制论070105物理学0702 理论物理070201粒子物理与原子核物理070202原子与分子物理070203等离子体物理070204凝聚态物理070205声学070206物理学0702 光学070207无线电物理070208化学0703 无机化学070301分析化学070302有机化学070303物理化学（含：化学物理）070304高分子化学与物理070305天文学0704 天体物理070401天体测量与天体力学070402地理学0705 自然地理学070501人文地理学070502地图学与地理信息系统070503大气科学0706 气象学070601大气物理学与大气环境070602海洋科学0707 物理海洋学070701海洋化学070702海洋生物学070703海洋地质070704地球物理学0708 固体地球物理学070801空间物理学070802地质学0709 矿物学、岩石学、矿床学070901地球化学070902古生物学与地层学（含：古人类学）070903构造地质学070904第四纪地质学070905生物学0710 植物学071001动物学071002生理学071003水生生物学071004微生物学071005神经生物学071006遗传学071007发育生物学071008细胞生物学071009生物化学与分子生物学071010生物物理学071011生态学071012系统科学0711 系统理论071101系统分析与集成071102☆科学技术史0712 ☆科学技术史071200凯程教育张老师整理了几个节约时间的准则：一是要早做决定，趁早备考;二是要有计划，按计划前进;三是要跟时间赛跑，争分夺秒。

计算机专业考研需要考什么

计算机专业考研需要考什么计算机专业考研需要考什么计算机专业的科目内容十分广泛，我们在考研的时候，需要了解清楚会出现哪些考点。

店铺为大家精心准备了计算机专业考研指南攻略，欢迎大家前来阅读。

计算机考研考点1、计算机科学与技术学科的初试科目调整后为4门，即政治理论、外国语、数学一和计算机学科专业基础综合，卷面满分值分别为100分、100分、150分和150分。

2、计算机学科专业基础综合的考试内容包括：数据结构、计算机组成原理、操作系统和计算机网络，重点考查考生掌握相关基础知识、基本理论和分析问题解决问题的能力。

考试内容及试卷结构在考试大纲中确定。

3、计算机学科专业基础综合科目实行联合命题，命题工作由全国学位与研究生教育学会工科委员会在教育部考试中心指导下组织实施，阅卷工作由省级招生考试机构统一组织，有关考务工作要求另行通知。

4、对于授理学学位的招生单位，第三单元考试科目可选数学一，也可自命题；第四单元考试科目必须采用联考的计算机学科专业基础综合。

5、相关招生单位均应根据初试科目内容、要求的变化和《教育部关于加强硕士研究生招生复试工作的指导意见》（教学〔2006〕4号）的要求，及时对该学科复试内容、办法和其他相关工作作出相应调整。

6、有关招生单位可充分利用接收推免生的方式招收跨学科专业的生源，对此招生部门应主动做好与培养、推荐部门的衔接工作。

复习时间安排及顺序：建议广大考生至少从九月份就应该开始专业课的复习了。

并且按照由难到易的顺序复习专业课科目，即按照《数据结构》，《计算机组成原理》，《操作系统》，《计算机网络》的顺序来规划复习专业课。

参考书目及习题册推荐《数据结构》（数据结构》（C语言版）严蔚敏吴伟民编著清华大学出版社《计算机操作系统》汤子瀛等主编西安电子科技大学出版社《计算机网络（第五版）》谢希仁编著电子工业出版社《计算机组成原理（第2版）》唐朔飞主编高等教育出版社考研统考计算机专业课常识1、考试变动从2009年起，计算机科学与技术学科采用全国统考方式，初试科目调整后为4门，即政治理论、外国语、数学一和计算机学科专业基础综合，卷面满分值分别为100分、100分、150分和150分。

2017年考研中南大学各专业初试、复试指定参考书目详细汇总

《简明法语教程》（上、下册）孙辉主编，商务印书馆；或《大学法语简明教程》薛建成,外语教学与研究出版社；或《公共法语》（上、下册）吴贤良编，上海外语教育出版社
254
俄语（自命题）
《俄语》（1-3册）黑龙江大学俄语系编，外语教学与研究出版社
255
英语（自命题）
《大学英语》（精读），上海外语教育出版社
241
《社会学概论新修》郑杭生主编，中国人民大学出版社，第3版
721
公共管理学基础
《管理学---原理与方法》，周三多等，复旦大学出版社版2009年12月第5版；
《公共部门经济学》，高培勇、崔军编著，中国人民大学出版社修订版；
《政治学基础》王浦劬等著，北京大学出版社2006年1月第2版
722
政治学基础
《政治学原理》王惠岩主编，高等教育出版社2006年版
717
文学原理
《文学理论》欧阳友权主编，北京大学出版社，2006年版。
718
美学原理
《美学》朱立元主编，高等教育出版社，2001年版
71》，教育部统编，高等教育出版社；
《毛泽东思想概论和中国特色社会主义理论概论》教育部统编，高等教育出版社。
720
社会学理论
853
信号与系统
《信号与线性系统分析》（第四版）吴大正主编，高等教育出版社
868
经济学概论
《经济学概论》姜继英主编,上海交通大学出版社,2003年出版；
《经济学概论》冯金华主编,复旦大学出版社,2003年出版
870
生物信息学
《生物信息学》张阳德编著，科学技术出版社，2004年版
880
英语综合考试
英语综合考试：语言学、翻译、汉语基础知识：
744

考研数学三考查内容知多少

考研数学三考查内容知多少
来源：文都图书
许多参加2017考研数学三的同学们，经历过春节假期与朋友相聚的快乐时光后，我们可以开始认真复习考研数学三了。

那么，在正式着手复习之前，先让我们了解一下考研数学三考查的内容有哪些。

高等数学：同济六版高等数学中所有带*号的都不考;所有“近似”的问题都不考;第三章微分中值定理与导数的应用不考曲率;第四章不定积分不考积分表的使用;不考第六章定积分在物理学上的应用以及曲线的弧长。

第七章微分方程不考可降阶的高阶微分方程，另外补充差分方程。

不考第八章空间解析几何与向量代数。

第九章第五节不考方程组的情形，第十章二重积分为止，第十二章的级数中不考傅里叶级数;
线性代数：数学一用的参考教材是同济五版线性代数，1-5章：行列式、矩阵及其运算、矩阵的初等变换及其方程组、向量组的线性相关性、相似矩阵及二次型。

数三不考向量组的线性相关性中的向量空间，线性方程组跟空间解析几何结合的问题;
概率与数理统计：1、概率论的基本概念；2、随机变量及其分布；
3、多维随机变量及其分布；
4、随机变量的数字特征；
5、大数定律及中心极限定理；
6、样本及抽样分布；
7、参数估计，其中数三的同学不考参数估计中的区间估计。

了解了考研数学三的考查内容后，同学们可以看看2017《考研数学复习大全·数学三》，书中根据考纲对考研数学三的要求，考查内容全面，对我们复习很有帮助。

2017年考研数二评分标准

2017年考研数二评分标准
2017考研数学总分满分150分，数学分为数学一、数学二和数学三，都是150分满分，具体到各个科目题型的分值，考生还得根据大纲来了解。

下面新东方网考研频道整合关于考研数学总分及各部分分值占比的信息，方便2017考生了解。

1. 试卷结构
选择题：8题(每题4分);
填空题：6题(每题4分);
解答题：9题(每题10分左右);
满分150分，考试时间3小时。

2. 考试科目及分值
高等数学：84分，占56%(4道选择题，4道填空题，5道大题);
线性代数：33分，占22%(2道选择题，1道填空题，2道大题);
概率论与数理统计：33分，占22%(2道选择题，1道填空题，2道大题)。

注意：数学二不考概率论与数理统计，这一科的分值和试题全加到高等数学中。

3. 考试特点
①总分150分，在公共课中所占分值大，全国平均分在70左右，分数之间差距较大;
②注重基础，遵循考试大纲出题，考查公式定理，知识点固定;
③注重高质量的考点训练与题型总结。

考研数学考点解析及必考题型总结

考研数学考点解析及必考题型总结考研数学考点分析及和考题型总结考研数学的卷种分三种，分别为数学一、数学二、数学三。

这三个卷中针对的专业不同，须使用数学一的招生专业为工学门类中的力学、机械工程、光学工程、仪器科学与技术、信息与通信工程、控制科学与工程、计算机科学与技术、土木工程、水利工程、测绘科学与技术、交通运输工程、交通运输工程、传播与海洋工程、航空宇航科学与技术、兵器科学与技术、核科学与技术、生物医学工程等20个一级学科中所有的二级学科、专业，授工学学位的管理科学与工程的一级学科。

工学门类中的材料科学与工程、化学工程与技术、地质资源与地质工程、矿业工程、石油与天然气工程、环境科学与工程等一级学科中对数学要求较高的二级学科，专业的选用数学一，对数学要求较高的选用数学二。

专业不同对数学的要求自然不同，从难度看数学一最难，其次是数学二，最后是数学三，从考试范围看，数学一考试范围最多，数学三次之，最后，数学二，三种卷中大部分考试内容是一样的，数一数二数三又各有自己特点和单独考查的内容。

下面跨考教育数学教研室边一老师就数学一单独考查内容进行一一盘点。

一元函数微分学：隐函数求导、曲率圆和曲率半径;一元积分学：旋转体的侧面积、平面曲线的弧长、功、引力、压力、质心、形心等;向量代数与空间解析几何：向量、直线与平面、旋转曲面、球面、柱面、常用的二次曲面方程及其图形、投影曲线方程;多元函数微分学：方向导数和梯度、空间曲线的切线与法平面、曲面的切平面和法线;隐函数存在定理;多元函数积分学：三重积分、第一型曲线积分、第二型曲线积分、第一型曲面积分、第二型曲面积分、格林公式、高斯公式、斯托克斯公式、散度、旋度;无穷级数：傅里叶级数;微分方程：伯努利方程、全微分方程、可降阶的高阶微分方程、欧拉方程。

以上内容为数学一单独考查的内容，是数学一特有的内容，所以这些内容每年必考。

其中：多元函数积分学中曲线曲面积分三重积分几乎每年必考，常与空间解析几何一起考查，尤见于大题，今年(2017年)考查了第一型曲面积分及投影曲线，散度旋度常见于小题。

考研大统考联考专业参考书目

2017考研：12大统考联考专业参考书目推荐计算机、历史学、西医综合、中医综合、教育学、心理学、农学、、管理类联考、、经济类联考、等十二个专业都属于统考联考专业。

小鱼学长和大家分享各专业常用参考书目，都是考研江湖上口耳相传的常备书哦，一起来看看吧。

提示：以下书单仅供参考，建议买最新版本。

同时还需根据学校官网指定的参考书目来复习。

2017管理类联考推荐报考、工商管理、公共管理、、旅游管理、图书情报，工程管理这些专业的学生，初试考两门：管理类联考综合能力+英语二，不考专业课。

大部分学校不指定复习书目，最好的办法是联系师兄师姐，请教经验。

下面的书单，仅供大家参考，注意买最新版本。

数学《MBA、MPAcc联考同步复习指导系列:数学分册》袁进等机械工业出版社《MBA、MPA、MPAcc 联考综合能力数学高分指南》陈剑主编北航出版社《管理类专业学位联考数学高分一本通》朱杰上海交通出版社《MBA、MPA、MPAcc联考数学历年真题名家详解》陈剑主编北航出版社逻辑《逻辑精点》赵鑫全等编机械工业出版社《逻辑分册》孙勇等编机械工业出版社《海滨逻辑：考点精讲》胡海滨机械工业出版社写作《MBA MPA MPAcc写作分册》赵鑫全着机械工业出版社《MBA、MPA、MPAcc联考综合能力写作高分指南》陈君华编北航出版社大纲解析《管理类联考考试大纲解析》配套教材专家委员会编高等教育出版社2017经济类联考推荐、、国际商务硕士、保险硕士、资产评估硕士这几个专业的初试考政治、英语、经济类联考(或者数学三)、专业课，共四门。

很多学校并不指定初试参考书目，所以最好的办法就是咨询该专业的师兄师姐。

经济类联考与管理类联考相比，数学要难一些，逻辑题目少点，难度差不多，写作基本一样，所以童鞋们可以参考下管理类联考的书。

下面书单仅供大家参考。

数学《经济类联考:数学精点》专业学位硕士联考命题研究组编机械工业出版社《全书》李永乐王式安西安交通大学出版社逻辑《逻辑分册》孙勇等编机械工业出版社《逻辑精点》赵鑫全等编机械工业出版社《海滨逻辑：考点精讲》胡海滨机械工业出版社写作《MBA MPA MPAcc写作分册》赵鑫全着机械工业出版社《经济类、管理类联考综合能力写作套路化训练》王诚北京理工大学出版社2017推荐提示：以下书单仅供参考，建议买最新版本。

考研数学高数真题分类—级数

一份好的考研复习资料，会让你的复习力上加力。

中公考研辅导老师为考生准备了【高等数学-级数知识点讲解和习题】，同时中公考研网首发2017考研信息，2017考研时间及各科目复习备考指导、复习经验，为2017考研学子提供一站式考研辅导服务。

第九章级数（数一、数三）综述：级数本质上是极限，级数的收敛性也就是极限的收敛性，关于级数的题目往往需要结合微分和积分的知识，因此也可以看做是对它们的综合运用。

本章一直是考试的重点内容，平均每年所占分值在15分左右。

本章的主要知识点有：级数的定义与性质，正项级数的各种判别法，交错级数的莱布尼兹判别法，条件收敛与绝对收敛，幂级数的定义与性质，幂级数的收敛半径与收敛域，幂级数逐项求导定理与逐项积分定理，傅里叶级数。

从总体上讲，本章主要可以分为常数项级数与幂级数两部分。

其中考查的重点在幂级数上，但幂级数的基础是常数项级数。

对于常数项级数，考生需要重点把握它的收敛性的定义以及各种常见的判别法。

考试在级数中的大题一般出在幂级数上，这一部分的内容可以概括为三个问题:幂级数的收敛域的计算，幂级数求和，幂级数展开。

其中，计算幂级数的收敛域最关键的是掌握幂级数的收敛半径的求法与相关的性质。

而幂级数求和与展开，则主要是结合常见函数的幂级数展开，再运用幂级数的逐项求导和逐项积分定理即可。

最后，关于傅里叶级数，考生主要需要掌握傅里叶系数的求法，再了解狄利克雷定理的内容即可。

本章常考的题型有：1.对常数项收敛性的考查，2.幂级数的收敛半径和收敛域，3.幂级数展开，4.幂级数求和，5.常数项级数求和，6.傅里叶级数。

常考题型一：常数项级数的收敛性1.【1996—3 3分】下述各选项正确的是（）()A 若21nn u ∞=∑和21nn v ∞=∑都收敛，则21()n n n u v ∞=+∑收敛.()B 若1n n n u v ∞=∑收敛，则21nn u ∞=∑与21nn v ∞=∑都收敛. ()C 若正项级数21nn u ∞=∑发散，则1n u n≥. ()D 若级数21n n u ∞=∑收敛，且(1,2,)n n u v n ≥=，则级数21nn v ∞=∑也收敛. 【小结】：正项级数的判别法最基本的思想是比较判别法，它有很多种具体的表现形式，其中之一是极限审敛法，其内容是设1nn u∞=∑是正项级数：如果lim 0n n nu l →∞=>，则级数1nn u∞=∑发散；如果lim ,(1)pn n n u l p →∞=<+∞>，则级数1n n u ∞=∑收敛。

考研数学整体难度分析参考资料

考研数学整体难度分析参考资料考研数学整体难度分析参考资料考研是一场学习争夺战，在数学整体的难度上，我们要进行一定的分析。

店铺为大家精心准备了考研数学整体难度分析，欢迎大家前来阅读！考研数学整体难度小结今年的数一、数二、数三的整体难度比去年稍微有所下降，特别是高数部分选择题填空题都是常规题目，没有出现难题、偏题、怪题。

大题的前面三道题也属于基础题目，计算量也不大，18和19题的计算量相对要大一些。

第1题考察的是极限的知识，相信大家都能拿到分数。

第2题考察我们对函数的极值点求解的掌握情况，多元函数极值。

第3题是讨论函数的性质。

总体来说，选择题难度不大，没有难题，大家应该把基础题拿到分。

第10题是，考了差分方程有重根的情况。

第11题考察了经济学应用，记住公式了也不是很难。

第12题考察了全微分形式，这种题型前几年也出现过。

第15题考察的是极限问题，对于变限积分，先做变换做进行处理。

第16题是二重积分的问题，这种题目在做的时候一定要先划出积分区域，再加上计算的时候细心一点，也不会丢分。

第17题是定积分定义，转换成分部积分。

18、19相对来说难度要大一些。

整个数学的命题我认为有以下三个特点：第一，整体的难度相对去年来讲都有下降;第二，没有太多复杂的、大规模的计算，主要考查的都是一些平常强调过的基本概念、基本方法;第三，题型的重复性相当高，75%以上的题型都是以前考过的，所以凡是好好研究过前几年真题的同学应该都是没有问题的。

考研初试各科目时间安排12月24日考试时间：8：30-11：30考试科目：思想政治理论、管理类联考综合能力考试时间：14：00-17：00考试科目：外国语(英语(一)、英语(二)、日语、俄语)12月25日考试时间：8：30-11：30考试科目：数学一、数学二、数学三、中医综合、西医综合、教育学专业基础综合、心理学专业基础综合、历史学基础、法律硕士(非法学)专业学位联考专业基础课、法律硕士(法学)专业学位联考专业基础课、农学门类联考数学、农学门类联考化学。

2017天津大学化学工程考研资料与专业综合解析

研途宝考研/ 2017天津大学化学工程考研资料与专业综合解析专业名称、代码：化学工程[081701]所属门类代码、名称：工学[08]所属一级学科代码、名称：化学工程与技术[0817]所属学院：化工学院化学工程专业介绍：化学工程是化学工程与技术一级学科所属的一个二级学科，属工科门类。

该学科具有明确和稳定的研究方向，作为化学工程与技术一级学科下属的二级学科之一，化学工程又与“化学工艺”“生物化工”“应用化学”和“工业催化”等学科相互贯通和渗透，研究内容涉及国防、化工、生物、能源和制药等领域的基础理论和应用问题，许多研究领域处于国际前沿，已经形成了一个彼此渗透、相互依赖、相互促进的有机整体。

考试科目：①101思想政治理论②201英语一③302数学二④826化工原理①101思想政治理论②201英语一③302数学二④839物理化学研究方向：01不区分研究方向02不区分研究方向2017化学工程专业课考研参考书目：《化工原理学习指南》柴诚敬，夏清高等教育出版社2012年第2版；《化工原理实验》张金利，张建伟，郭翠梨天津大学出版社2005年版；《化工传质与分离过程（第二版）》贾绍义，柴诚敬化学工业出版社第二版；《化工流体流动与传热（第二版）》柴诚敬，张国亮化学工业出版社第二版；2017化学工程考研专业课资料：《天津大学826化工原理考研真题及答案解析》《2016天津大学化工学院考研复试一本通》《天津大学物理化学考研历年真题、高分笔记、期末试卷》《天津大学化工原理考研历年真题、高分笔记、内部资料》《名校物理化学与高分子化学考研真题汇编（2013版）》《名校物理化学与高分子化学考研真题汇编（2011-2013合订本）》《天津大学反应工程考研复试内部资料》《2017年天津大学839物理化学考研全套资料【历年真题+指定材料讲义+学长笔记+题库】》历年考研复试分数线：研途宝考研/2014年总分：325，政治/外语：50；业务1/业务2：85；2013年总分：330，政治/外语：50；业务1/业务2：85；【17化学工程考研辅导】2017天津大学考研高端保录班2017天大专业课考研无忧通关班2017天津大学专业课考研一对一班2017天大专业课考研面授集训班更多天津大学考研辅导班：/fdb/index.html天大化学工程考研经验与技巧一、考研复习之政治政治我是10月份开始复习的，参考资料前期是大纲解析+肖秀荣1000题；后期是肖秀荣4套+肖秀荣8套+一点辅导班的最后冲刺题。

2017年中国科学技术大学085207电气工程考研专业目录及考试科目

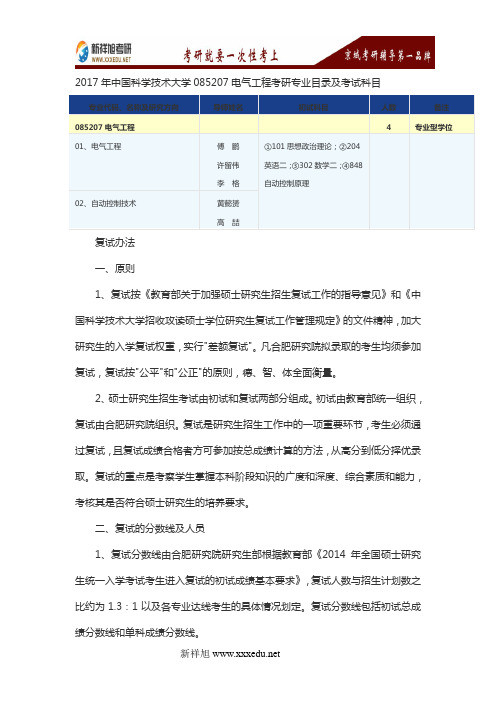
2017年中国科学技术大学085207电气工程考研专业目录及考试科目专业代码、名称及研究方向导师姓名初试科目人数备注085207电气工程4专业型学位01、电气工程傅鹏许留伟李格①101思想政治理论；②204英语二；③302数学二；④848自动控制原理02、自动控制技术黄懿赟高喆复试办法一、原则1、复试按《教育部关于加强硕士研究生招生复试工作的指导意见》和《中国科学技术大学招收攻读硕士学位研究生复试工作管理规定》的文件精神，加大研究生的入学复试权重，实行"差额复试"。

凡合肥研究院拟录取的考生均须参加复试，复试按"公平"和"公正"的原则，德、智、体全面衡量。

2、硕士研究生招生考试由初试和复试两部分组成。

初试由教育部统一组织，复试由合肥研究院组织。

复试是研究生招生工作中的一项重要环节，考生必须通过复试，且复试成绩合格者方可参加按总成绩计算的方法，从高分到低分择优录取。

复试的重点是考察学生掌握本科阶段知识的广度和深度、综合素质和能力，考核其是否符合硕士研究生的培养要求。

二、复试的分数线及人员1、复试分数线由合肥研究院研究生部根据教育部《2014年全国硕士研究生统一入学考试考生进入复试的初试成绩基本要求》，复试人数与招生计划数之比约为1.3：1以及各专业达线考生的具体情况划定。

复试分数线包括初试总成绩分数线和单科成绩分数线。

2、同时达到总成绩分数线和单科成绩分数线的考生具有参加复试资格。

参加复试考生的名单公布在合肥研究院研究生部的网页上。

三、复试内容和组织形式1、复试是对初试达线考生进行的复查性考核；复试的重点是从德、智、体等方面全面考查考生的综合素质和能力；复试内容包括专业知识口试、英语听力测试、英语口语测试、体检和思想品德的考核。

2、专业知识口试：专业知识口试是进一步考查考生的基础知识是否扎实，考生对专业知识掌握的深度和广度（包括对所报考学科前沿知识和研究动态的了解情况），综合并灵活运用所学知识分析及解决问题的能力，应变反应和表达能力，了解考生从事科研工作的潜力和创造力。

2017年考研数学二评分标准

2017年考研数学二评分标准一、考研数学二科目概述1. 考研数学二科目的出题范围包括数学分析、线性代数和概率论三个方面。

2. 考研数学二科目的考试时间为150分钟，满分150分，主要测试考生在数学分析、线性代数和概率论方面的基本理论和解题能力。

二、2017年考研数学二试题分析1. 2017年考研数学二试题整体难度适中，主要考察了考生对数学理论的掌握和运用，以及解决实际问题的能力。

2. 2017年考研数学二试题主要涉及函数极限、连续性、导数与微分、定积分、二重积分、级数、线性代数、概率论等内容，整体覆盖了数学二科目的出题范围。

三、2017年考研数学二评分标准1. 数学分析部分1.1 函数极限与连续性题目主要考察考生对函数极限和连续性的理解和运用能力。

评分主要根据考生对极限和连续性的定义和性质的理解和运用。

1.2 导数与微分题目主要考察考生对导数和微分的概念及其在实际问题中的应用能力。

评分主要根据考生对导数和微分的定义、性质、运算规则和在实际问题中的运用能力。

1.3 定积分与二重积分题目主要考察考生对定积分和二重积分的理解和计算能力。

评分主要根据考生对定积分和二重积分的计算方法及其在解决实际问题中的应用情况。

1.4 级数题目主要考察考生对级数的收敛性和求和能力。

评分主要根据考生对级数收敛性的判断及级数求和方法的正确性和可行性。

2. 线性代数部分2.1 矩阵与行列式题目主要考察考生对矩阵和行列式的理解和计算能力。

评分主要根据考生对矩阵和行列式性质的掌握和在解决实际问题中的应用情况。

2.2 线性方程组题目主要考察考生对线性方程组的解法及其几何意义的理解和运用能力。

评分主要根据考生对线性方程组解法的正确性和对线性方程组几何意义的理解。

2.3 特征值和特征向量题目主要考察考生对特征值和特征向量的计算及其几何意义的理解和应用能力。

评分主要根据考生对特征值和特征向量的计算方法的正确性及对特征值和特征向量的几何意义的理解。

2017中国矿业大学(北京)考研专业目录及考试科目(学术型)

04矿物加工化学药剂
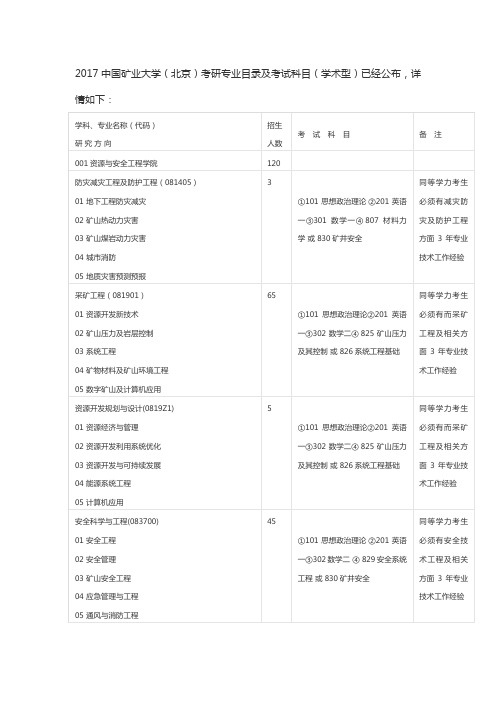
05资源综合利用与深加工
2
①101思想政治理论②201英语一③302数学二④816选矿原理
矿物材料工程（0819Z3）
01非金属矿物材料
02粉体表面改性
03新型炭素材料
04超微粉体材料
05多孔矿物材料
2
①101思想政治理论②201英语一③302数学二④ 816选矿原理
工程管理（0871Z1）
01高性能水泥基材料
02功能材料
03新型炭材料
04非金属矿物材料与多孔矿物材料
05粉体表面改性与超微粉体材料
2
①101思想政治理论②201英语一③302数学二④ 809普通物理（工）或833材料科学基础
水文学及水资源（081501）
01水资源评价与管理
02地下水可视化
03地下水数值模拟
04水-岩（土）相互作用
01煤岩学、有机岩石学及其应用
02能源盆地分析
03矿产勘查技术与方法
04非常规油气研究
05矿产资源综合利用
28
①101思想政治理论②201英语一③302数学二④ 827地球科学概论或828计算机软件开发基础
地球探测与信息技术(081802)
01资源地球物理勘探
02工程与环境地球物理探测
03地学软件研发
生物化工（081703）
01生物工程技术
02环境生物技术
03生态环境材料
04生物能源
05应用生物化学
2
①101思想政治理论②201英语一或202俄语或203日语③302数学二④856化工原理
应用化学(081704)
01精细化学品化学
02界面化学及其应用
03应用电化学

2017中国矿业大学(北京)考研专业目录及考试科目(专业型)

15
①199管理类联考综合能力②204英语二
①199管理类联考综合能力②204英语二
①199管理类联考综合能力②204英语二
011 MPA中心(文法学院)
75
注：MPA只限在北京参加考试
公共管理(MPA)（125200）
45
①199管理类联考综合能力②204英语二
法律（非法学）（035101）
15
①101思想政治理论②201英语一③398法硕联考专业基础（非法学）④498法硕联考综合（非法学）
008文法学院
20
英语笔译（055101）
20
①101思想政治理论②211翻译硕士英语③357英语翻译基础④448汉语写作与百科知识
010 MBA中心(管理学院)
105
注：MBA、MEM只限在北京参加考试
工商管理(MBA)（125100）
会计（125300）
工程管理（MEM）（125600）
65
25
2017中国矿业大学（北京）考研专业目录及考试科目（专业型）
据中国矿业大学（北京）研究生院消息，2017中国矿业大学（北京）考研专业目录及考试科目（专业型）已经公布，详情如下：
专业领域名称及代码
招生人数
考试科目
001资源与安全工程学院
80
矿业工程（085218）
40
①101思想政治理论②204英语二③302数学二④825矿山压力及其控制或826系统工程基础
法律（法学）（035102）
15
①101思想政治理论②201英语一③397法硕联考专业基础（法学）④497法硕联考综合（法学）
90
注：美术、艺术设计只限在北京参加考试
建筑与土木工程（085213）

考研数学大纲

2017年考研数学大纲（数学一）研究生数一考试科目：高等数学（同济）、线性代数（同济）、概率论与数理统计（浙大）考研考试形式和试卷结构一、试卷满分及考试时间：试卷满分为150分，考试时间为180分钟．二、答题方式：答题方式为闭卷、笔试．三、试卷内容结构：高等教学约56%；线性代数约22%；概率论与数理统计约22%. 四、试卷题型结构：单选题8小题，每小题4分，共32分填空题6小题，每小题4分，共24分解答题（包括证明题）9小题，共94分高等数学一、函数、极限、连续考试内容：函数的概念及表示法函数的有界性、单调性、周期性和奇偶性复合函数、反函数、分段函数和隐函数基本初等函数的性质及其图形初等函数函数关系的建立；数列极限与函数极限的定义及其性质函数的左极限和右极限无穷小量和无穷大量的概念及其关系无穷小量的性质及无穷小量的比较极限的四则运算极限存在的两个准则；单调有界准则和夹逼准则两个重要极限；函数连续的概念函数间断点的类型初等函数的连续性闭区间上连续函数的性质。

考试要求1．理解函数的概念，掌握函数的表示法，会建立应用问题的函数关系．2．了解函数的有界性、单调性、周期性和奇偶性．3．理解复合函数及分段函数的概念，了解反函数及隐函数的概念．4．掌握基本初等函数的性质及其图形，了解初等函数的概念．5．理解极限的概念，理解函数左极限与右极限的概念以及函数极限存在与左极限、右极限之间的关系．6．掌握极限的性质及四则运算法则．7．掌握极限存在的两个准则，并会利用它们求极限，掌握利用两个重要极限求极限的方法．8．理解无穷小量、无穷大量的概念，掌握无穷小量的比较方法，会用等价无穷小量求极限．9．理解函数连续性的概念（含左连续与右连续），会判别函数间断点的类型．10．了解连续函数的性质和初等函数的连续性，理解闭区间上连续函数的性质（有界性、最大值和最小值定理、介值定理），并会应用这些性质．二、一元函数微分学考试内容：导数和微分的概念导数的几何意义和物理意义函数的可导性与连续性之间的关系平面曲线的切线和法线导数和微分的四则运算基本初等函数的导数复合函数、反函数、隐函数以及参数方程所确定的函数的微分法高阶导数一阶微分形式的不变性微分中值定理洛必达法则函数单调性的判别函数的极值函数图形的凹凸性、拐点及渐近线函数图形的描绘函数的最大值与最小值弧微分曲率的概念曲率圆与曲率半径考试要求1．理解导数和微分的概念，理解导数与微分的关系，理解导数的几何意义，会求平面曲线的切线方程和法线方程，了解导数的物理意义，会用导数描述一些物理量，理解函数的可导性与连续性之间的关系．2．掌握导数的四则运算法则和复合函数的求导法则，掌握基本初等函数的导数公式．了解微分的四则运算法则和一阶微分形式的不变性，会求函数的微分．3．了解高阶导数的概念，会求简单函数的高阶导数．4．会求分段函数的导数，会求隐函数和由参数方程所确定的函数以及反函数的导数．5．理解并会用罗尔（Rolle）定理、拉格朗日（Lagrange）中值定理和泰勒（Taylor）定理，了解并会用柯西（Cauchy）中值定理．6．掌握用洛必达法则求未定式极限的方法．7．理解函数的极值概念，掌握用导数判断函数的单调性和求函数极值的方法，掌握函数最大值和最小值的求法及其应用．8．会用导数判断函数图形的凹凸性（注：在区间内，设函数具有二阶导数．当时，的图形是凹的；当时，的图形是凸的），会求函数图形的拐点以及水平、铅直和斜渐近线，会描绘函数的图形．9．了解曲率、曲率圆与曲率半径的概念，会计算曲率和曲率半径．三、一元函数积分学考试内容：原函数和不定积分的概念不定积分的基本性质基本积分公式定积分的概念和基本性质定积分中值定理积分上限的函数及其导数牛顿-莱布尼茨（Newton-Leibniz）公式不定积分和定积分的换元积分法与分部积分法有理函数、三角函数的有理式和简单无理函数的积分反常（广义）积分定积分的应用考试要求1．理解原函数的概念，理解不定积分和定积分的概念．2．掌握不定积分的基本公式，掌握不定积分和定积分的性质及定积分中值定理，掌握换元积分法与分部积分法．3．会求有理函数、三角函数有理式和简单无理函数的积分．4．理解积分上限的函数，会求它的导数，掌握牛顿-莱布尼茨公式．5．了解反常积分的概念，会计算反常积分．6．掌握用定积分表达和计算一些几何量与物理量（平面图形的面积、平面曲线的弧长、旋转体的体积及侧面积、平行截面面积为已知的立体体积、功、引力、压力、质心、形心等）及函数的平均值．四、向量代数和空间解析几何考试内容：向量的概念向量的线性运算向量的数量积和向量积向量的混合积两向量垂直、平行的条件两向量的夹角向量的坐标表达式及其运算单位向量方向数与方向余弦曲面方程和空间曲线方程的概念平面方程直线方程平面与平面、平面与直线、直线与直线的夹角以及平行、垂直的条件点到平面和点到直线的距离球面柱面旋转曲面常用的二次曲面方程及其图形空间曲线的参数方程和一般方程空间曲线在坐标面上的投影曲线方程考试要求1．理解空间直角坐标系，理解向量的概念及其表示．2．掌握向量的运算（线性运算、数量积、向量积、混合积），了解两个向量垂直、平行的条件．3．理解单位向量、方向数与方向余弦、向量的坐标表达式，掌握用坐标表达式进行向量运算的方法．4．掌握平面方程和直线方程及其求法．5．会求平面与平面、平面与直线、直线与直线之间的夹角，并会利用平面、直线的相互关系（平行、垂直、相交等））解决有关问题．6．会求点到直线以及点到平面的距离．7．了解曲面方程和空间曲线方程的概念．8．了解常用二次曲面的方程及其图形，会求简单的柱面和旋转曲面的方程．9．了解空间曲线的参数方程和一般方程．了解空间曲线在坐标平面上的投影，并会求该投影曲线的方程．五、多元函数微分学考试内容：多元函数的概念二元函数的几何意义二元函数的极限与连续的概念有界闭区域上多元连续函数的性质多元函数的偏导数和全微分全微分存在的必要条件和充分条件多元复合函数、隐函数的求导法二阶偏导数方向导数和梯度空间曲线的切线和法平面曲面的切平面和法线二元函数的二阶泰勒公式多元函数的极值和条件极值多元函数的最大值、最小值及其简单应用考试要求1．理解多元函数的概念，理解二元函数的几何意义．2．了解二元函数的极限与连续的概念以及有界闭区域上连续函数的性质．3．理解多元函数偏导数和全微分的概念，会求全微分，了解全微分存在的必要条件和充分条件，了解全微分形式的不变性．4．理解方向导数与梯度的概念，并掌握其计算方法．5．掌握多元复合函数一阶、二阶偏导数的求法．6．了解隐函数存在定理，会求多元隐函数的偏导数．7．了解空间曲线的切线和法平面及曲面的切平面和法线的概念，会求它们的方程．8．了解二元函数的二阶泰勒公式．9．理解多元函数极值和条件极值的概念，掌握多元函数极值存在的必要条件，了解二元函数极值存在的充分条件，会求二元函数的极值，会用拉格朗日乘数法求条件极值，会求简单多元函数的最大值和最小值，并会解决一些简单的应用问题．六、多元函数积分学考试内容：二重积分与三重积分的概念、性质、计算和应用两类曲线积分的概念、性质及计算两类曲线积分的关系格林（Green）公式平面曲线积分与路径无关的条件二元函数全微分的原函数两类曲面积分的概念、性质及计算两类曲面积分的关系高斯（Gauss）公式斯托克斯（Stokes）公式散度、旋度的概念及计算曲线积分和曲面积分的应用考试要求1．理解二重积分、三重积分的概念，了解重积分的性质，，了解二重积分的中值定理．2．掌握二重积分的计算方法（直角坐标、极坐标），会计算三重积分（直角坐标、柱面坐标、球面坐标）．3．理解两类曲线积分的概念，了解两类曲线积分的性质及两类曲线积分的关系．4．掌握计算两类曲线积分的方法．5．掌握格林公式并会运用平面曲线积分与路径无关的条件，会求二元函数全微分的原函数．6．了解两类曲面积分的概念、性质及两类曲面积分的关系，掌握计算两类曲面积分的方法，掌握用高斯公式计算曲面积分的方法，并会用斯托克斯公式计算曲线积分．7．了解散度与旋度的概念，并会计算．8．会用重积分、曲线积分及曲面积分求一些几何量与物理量（平面图形的面积、体积、曲面面积、弧长、质量、质心、、形心、转动惯量、引力、功及流量等）．七、无穷级数考试内容：常数项级数的收敛与发散的概念收敛级数的和的概念级数的基本性质与收敛的必要条件几何级数与级数及其收敛性正项级数收敛性的判别法交错级数与莱布尼茨定理任意项级数的绝对收敛与条件收敛函数项级数的收敛域与和函数的概念幂级数及其收敛半径、收敛区间（指开区间）和收敛域幂级数的和函数幂级数在其收敛区间内的基本性质简单幂级数的和函数的求法初等函数的幂级数展开式函数的傅里叶（Fourier）系数与傅里叶级数狄利克雷（Dirichlet）定理函数在上的傅里叶级数函数在上的正弦级数和余弦级数考试要求1．理解常数项级数收敛、发散以及收敛级数的和的概念，掌握级数的基本性质及收敛的必要条件．2．掌握几何级数与级数的收敛与发散的条件．3．掌握正项级数收敛性的比较判别法和比值判别法，会用根值判别法．4．掌握交错级数的莱布尼茨判别法．5．了解任意项级数绝对收敛与条件收敛的概念以及绝对收敛与收敛的关系．6．了解函数项级数的收敛域及和函数的概念．第 6 页共12 页7．理解幂级数收敛半径的概念、并掌握幂级数的收敛半径、收敛区间及收敛域的求法．8．了解幂级数在其收敛区间内的基本性质（和函数的连续性、逐项求导和逐项积分），会求一些幂级数在收敛区间内的和函数，并会由此求出某些数项级数的和．9．了解函数展开为泰勒级数的充分必要条件．10．掌握，，，及的麦克劳林（Maclaurin）展开式，会用它们将一些简单函数间接展开为幂级数．11．了解傅里叶级数的概念和狄利克雷收敛定理，会将定义在上的函数展开为傅里叶级数，会将定义在上的函数展开为正弦级数与余弦级数，会写出傅里叶级数的和函数的表达式．八、常微分方程考试内容：常微分方程的基本概念变量可分离的微分方程齐次微分方程一阶线性微分方程伯努利（Bernoulli）方程全微分方程可用简单的变量代换求解的某些微分方程可降阶的高阶微分方程线性微分方程解的性质及解的结构定理二阶常系数齐次线性微分方程高于二阶的某些常系数齐次线性微分方程简单的二阶常系数非齐次线性微分方程欧拉（Euler）方程微分方程的简单应用考试要求1．了解微分方程及其阶、解、通解、初始条件和特解等概念．2．掌握变量可分离的微分方程及一阶线性微分方程的解法．3．会解齐次微分方程、伯努利方程和全微分方程，会用简单的变量代换解某些微分方程．4．会用降阶法解下列形式的微分方程：和．5．理解线性微分方程解的性质及解的结构．6．掌握二阶常系数齐次线性微分方程的解法，并会解某些高于二阶的常系数齐次线性微分方程．7．会解自由项为多项式、指数函数、正弦函数、余弦函数以及它们的和与积的二阶常系数非齐次线性微分方程．8．会解欧拉方程．9．会用微分方程解决一些简单的应用问题．线性代数一、行列式考试内容：行列式的概念和基本性质行列式按行（列）展开定理考试要求：1．了解行列式的概念，掌握行列式的性质．2．会应用行列式的性质和行列式按行（列）展开定理计算行列式．二、矩阵考试内容：矩阵的概念矩阵的线性运算矩阵的乘法方阵的幂方阵乘积的行列式矩阵的转置逆矩阵的概念和性质矩阵可逆的充分必要条件伴随矩阵矩阵的初等变换初等矩阵矩阵的秩矩阵的等价分块矩阵及其运算考试要求1．理解矩阵的概念，了解单位矩阵、数量矩阵、对角矩阵、三角矩阵、对称矩阵和反对称矩阵以及它们的性质．2．掌握矩阵的线性运算、乘法、转置以及它们的运算规律，了解方阵的幂与方阵乘积的行列式的性质．3．理解逆矩阵的概念，掌握逆矩阵的性质以及矩阵可逆的充分必要条件，理解伴随矩阵的概念，会用伴随矩阵求逆矩阵．4．理解矩阵初等变换的概念，了解初等矩阵的性质和矩阵等价的概念，理解矩阵的秩的概念，掌握用初等变换求矩阵的秩和逆矩阵的方法．5．了解分块矩阵及其运算．三、向量考试内容：向量的概念向量的线性组合与线性表示向量组的线性相关与线性无关向量组的极大线性无关组等价向量组向量组的秩向量组的秩与矩阵的秩之间的关系向量空间及其相关概念维向量空间的基变换和坐标变换过渡矩阵向量的内积线性无关向量组的正交规范化方法规范正交基正交矩阵及其性质考试要求1．理解维向量、向量的线性组合与线性表示的概念．2．理解向量组线性相关、线性无关的概念，掌握向量组线性相关、线性无关的有关性质及判别法．3．理解向量组的极大线性无关组和向量组的秩的概念，会求向量组的极大线性无关组及秩．4．理解向量组等价的概念，理解矩阵的秩与其行（列）向量组的秩之间的关系．5．了解维向量空间、子空间、基底、维数、坐标等概念．6．了解基变换和坐标变换公式，会求过渡矩阵．7．了解内积的概念，掌握线性无关向量组正交规范化的施密特（Schmidt）方法．8．了解规范正交基、正交矩阵的概念以及它们的性质．四、线性方程组考试内容：线性方程组的克拉默（Cramer）法则齐次线性方程组有非零解的充分必要条件非齐次线性方程组有解的充分必要条件线性方程组解的性质和解的结构齐次线性方程组的基础解系和通解解空间非齐次线性方程组的通解考试要求l．会用克拉默法则．2．理解齐次线性方程组有非零解的充分必要条件及非齐次线性方程组有解的充分必要条件．3．理解齐次线性方程组的基础解系、通解及解空间的概念，掌握齐次线性方程组的基础解系和通解的求法．4．理解非齐次线性方程组解的结构及通解的概念．5．掌握用初等行变换求解线性方程组的方法．五、矩阵的特征值和特征向量考试内容：矩阵的特征值和特征向量的概念、性质相似变换、相似矩阵的概念及性质矩阵可相似对角化的充分必要条件及相似对角矩阵实对称矩阵的特征值、特征向量及其相似对角矩阵考试要求1．理解矩阵的特征值和特征向量的概念及性质，会求矩阵的特征值和特征向量．2．理解相似矩阵的概念、性质及矩阵可相似对角化的充分必要条件，掌握将矩阵化为相似对角矩阵的方法．3．掌握实对称矩阵的特征值和特征向量的性质．六、二次型考试内容：二次型及其矩阵表示合同变换与合同矩阵二次型的秩惯性定理二次型的标准形和规范形用正交变换和配方法化二次型为标准形二次型及其矩阵的正定性考试要求1．掌握二次型及其矩阵表示，了解二次型秩的概念，了解合同变换与合同矩阵的概念，了解二次型的标准形、规范形的概念以及惯性定理．2．掌握用正交变换化二次型为标准形的方法，会用配方法化二次型为标准形．3．理解正定二次型、正定矩阵的概念，并掌握其判别法概率论与数理统计一、随机事件和概率考试内容：随机事件与样本空间事件的关系与运算完备事件组概率的概念概率的基本性质古典型概率几何型概率条件概率概率的基本公式事件的独立性独立重复试验考试要求1．了解样本空间（基本事件空间）的概念，理解随机事件的概念，掌握事件的关系及运算．2．理解概率、条件概率的概念，掌握概率的基本性质，会计算古典型概率和几何型概率，掌握概率的加法公式、减法公式、乘法公式、全概率公式，以及贝叶斯（Bayes）公式．3．理解事件独立性的概念，掌握用事件独立性进行概率计算；理解独立重复试验的概念，掌握计算有关事件概率的方法．二、随机变量及其分布考试内容：随机变量随机变量分布函数的概念及其性质离散型随机变量的概率分布连续型随机变量的概率密度常见随机变量的分布随机变量函数的分布考试要求1．理解随机变量的概念，理解分布函数的概念及性质，会计算与随机变量相联系的事件的概率．2．理解离散型随机变量及其概率分布的概念，掌握0-1分布、二项分布、几何分布、超几何分布、泊松（Poisson）分布及其应用．3．了解泊松定理的结论和应用条件，会用泊松分布近似表示二项分布．4．理解连续型随机变量及其概率密度的概念，掌握均匀分布、正态分布、指数分布及其应用，其中参数为的指数分布的概率密度为5．会求随机变量函数的分布．三、多维随机变量及其分布考试内容：多维随机变量及其分布二维离散型随机变量的概率分布、边缘分布和条件分布二维连续型随机变量的概率密度、边缘概率密度和条件密度随机变量的独立性和不相关性常用二维随机变量的分布两个及两个以上随机变量简单函数的分布考试要求1．理解多维随机变量的概念，理解多维随机变量的分布的概念和性质，理解二维离散型随机变量的概率分布、边缘分布和条件分布，理解二维连续型随机变量的概率密度、边缘密度和条件密度，会求与二维随机变量相关事件的概率．2．理解随机变量的独立性及不相关性的概念，掌握随机变量相互独立的条件．3．掌握二维均匀分布，了解二维正态分布的概率密度，理解其中参数的概率意义．4．会求两个随机变量简单函数的分布，会求多个相互独立随机变量简单函数的分布．四、随机变量的数字特征考试内容：随机变量的数学期望（均值）、方差、标准差及其性质随机变量函数的数学期望矩、协方差、相关系数及其性质考试要求1．理解随机变量数字特征（数学期望、方差、标准差、矩、协方差、相关系数）的概念，会运用数字特征的基本性质，并掌握常用分布的数字特征．2．会求随机变量函数的数学期望．五、大数定律和中心极限定理考试内容：切比雪夫（Chebyshev）不等式切比雪夫大数定律伯努利（Bernoulli）大数定律辛钦（Khinchine）大数定律棣莫弗-拉普拉斯（De Moivre-Laplace）定理列维-林德伯格（Levy-Lindberg）定理考试要求1．了解切比雪夫不等式．2．了解切比雪夫大数定律、伯努利大数定律和辛钦大数定律（独立同分布随机变量序列的大数定律）．3．了解棣莫弗-拉普拉斯定理（二项分布以正态分布为极限分布）和列维-林德伯格定理（独立同分布随机变量序列的中心极限定理）．六、数理统计的基本概念考试内容：总体个体简单随机样本统计量样本均值样本方差和样本矩分布分布分布分位数正态总体的常用抽样分布考试要求1．理解总体、简单随机样本、统计量、样本均值、样本方差及样本矩的概念，其中样本方差定义为2．了解分布、分布和分布的概念及性质，了解上侧分位数的概念并会查表计算．3．了解正态总体的常用抽样分布．七、参数估计考试内容：点估计的概念估计量与估计值矩估计法最大似然估计法估计量的评选标准区间估计的概念单个正态总体的均值和方差的区间估计两个正态总体的均值差和方差比的区间估计考试要求1．理解参数的点估计、估计量与估计值的概念．2．掌握矩估计法（一阶矩、二阶矩）和最大似然估计法．3．了解估计量的无偏性、有效性（最小方差性）和一致性（相合性）的概念，并会验证估计量的无偏性．4、理解区间估计的概念，会求单个正态总体的均值和方差的置信区间，会求两个正态总体的均值差和方差比的置信区间．八、假设检验考试内容：显著性检验假设检验的两类错误单个及两个正态总体的均值和方差的假设检验考试要求1．理解显著性检验的基本思想，掌握假设检验的基本步骤，了解假设检验可能产生的两类错误．2．掌握单个及两个正态总体的均值和方差的假设检验．。

考研数学：微分方程考点和常考题型分析

考研数学：微分方程考点和常考题型分析在研究生入学考试中，高等数学是数一、数二、数三考试的公共内容。

数一、数三均占56%(总分150分)，考察4个选择题(每题4分，共16分)、4个填空题(每题4分，共16分)、5个解答题(总分50分)。

数二不考概率论，高数占78%，考察6个选择题(每题4分，共24分)、4个填空题(每题5分，共20分)、7个解答题(总分72分)。

由高数所占比例易知，高数是考研数学的重头戏，因此一直流传着“得高数者得数学。

”高等数学包含函数、极限与连续、一元函数微分学、一元函数积分学、多元函数微分学、多元函数积分学、常微分方程和无穷级数等七个模块，老师继续梳理分析最后一个模块微分方程，希望对学员有所帮助。

1、考试内容(1)常微分方程的基本概念;(2)变量可分离的微分方程;(3)齐次微分方程;(4)一阶线性微分方程;(5)伯努利(Bernoulli)方程和全微分方程;(6)可用简单的变量代换求解的某些微分方程;(7)可降阶的高阶微分方程;(8)线性微分方程解的性质及解的结构定理;(9)二阶常系数齐次线性微分方程;(10)高于二阶的某些常系数齐次线性微分方程;(11)简单的二阶常系数非齐次线性微分方程;(12)欧拉(Euler)方程;(13)微分方程的简单应用(其中5、7、12只要求数一考生掌握，数二、数三考生不要求掌握)。

2、考试要求(1)了解微分方程及其阶、解、通解、初始条件和特解等概念;(2)掌握变量可分离的微分方程及一阶线性微分方程的解法;(3)会解齐次微分方程、伯努利方程和全微分方程，会用简单的变量代换解某些微分方程;(4)会用降阶法解下列形式的微分方程;(5)理解线性微分方程解的性质及解的结构;(6)掌握二阶常系数齐次线性微分方程的解法，并会解某些高于二阶的常系数齐次线性微分方程;(7)会解自由项为多项式、指数函数、正弦函数、余弦函数以及它们的和与积的二阶常系数非齐次线性微分方程;(8)会解欧拉方程;(9)会用微分方程解决一些简单的应用问题.3、常考题型(1)变量可分离、齐次微分方程、一阶线性齐次与非齐次微分方程的求解;(2)可降阶的高阶微分方程的求解(数一、数二要求掌握，数三不要求掌握);(3)全微分方程和欧拉方程的求解(数一要求掌握，数二、数三不要求掌握);(4)线性微分方程解得结构;(5)微分方程相关的综合问题。

考研数学一的考查范围

考研数学一的考查范围
来源：文都图书
考研数学从卷种上来看分为数学一、数学二、数学三;从考试内容上来看，涵盖了高等数学、线性代数、概率论与数理统计;试卷结构上来看，设有三种题型：选择题(8道共32分)、填空题(6道共24分)、解答题(9道共94分)。

那么就让我们具体了解一下考研数学一的考查范围。

首先高等数学：高等数学中除了第七章微分方程考带*号的欧拉方程，伯努利方程外，其余带*号的都不考;所有“近似”的问题都不考;第四章不定积分不考积分表的使用;第九章第五节不考方程组的情形;第十二章第五节不考欧拉公式。

其次线性代数：线性代数1-5章：行列式、矩阵及其运算、矩阵的初等变换及其方程组、向量组的线性相关性、相似矩阵及二次型。

其中向量组的线性相关性中数一考向量空间，线性方程组跟空间解析几何结合数一也要考。

最后概率与数理统计：1、概率论的基本概念；2、随机变量及其分布；3、多维随机变量及其分布；4、随机变量的数字特征；5、大数定律及中心极限定理；6、样本及抽样分布；7、参数估计；8、假设检验。

以上就是考研数学一的主要内容，了解了这些后，建议同学们做做汤家凤老师的2017《考研数学复习大全·数学一》，针对考研数学一的要求，分章节编排，对我们复习，很有帮助。

2017年考研数学难易度，预测国家线

2017年的全国硕⼠研究⽣⼊学考试已经接近尾声，但这并不意味着结束，因为后⾯还有很多事情需要我们去做，⽐如⼤家会关注⼀下国家线是多少，能不能过线;若能，如何备战复试呢?等等，为帮助各位17年的考⽣更好的规划后⾯的安排，⽼师就今天的数学试卷作如下分析，预测国家线，并需要复试的同学⼀些意见。

⼀、分析17年考研数学难易度，预测国家线数学⼀⾼等数学知识点相⽐与去年，整体难度不⼤，计算量⼀般。

线性代数知识点相⽐与去年，整体难度不⼤，计算量⼀般。

概率论与数理统计知识点相⽐与去年，整体难度不⼤，计算量⼀般。

数学⼆⾼等数学知识点相⽐与去年，整体难度不⼤，计算量⼀般。

线性代数知识点相⽐与去年，整体难度不⼤，计算量⼀般。

数学三⾼等数学知识点相⽐与去年，整体难度不⼤，计算量⼀般。

线性代数知识点相⽐与去年，整体难度不⼤，计算量⼀般。

概率论与数理统计知识点相⽐与去年，整体难度不⼤，计算量⼀般。

综合以上分析，与往年相⽐，整体难度不⼤，计算量⼀般，预测国家线⼤约在60⾄70之间，经济类的⼤约在58-65之间，⼯科类的⼤约在65-70左右。

⼆、考研复试应该知道的事⼉ 1.考什么：通常会是笔试+⾯试笔试考查的是英语⽅⾯的写作听⼒，另外就是你的专业课了，⾯试的时候会考察到你的英语⼝语，另外⼀个就是现场导师提问时间了。

(不同学校，略有不同，详细还要建⾃⼰所考院校复试要求) 2.多关注下院校的⼀些信息，或者询问已经考到该校的学长、学姐或者认识的⼈，在初试结束的时候开始着⼿复试，不要到了时间在准备那样就太赶了。

3.怎么准备：⾸先你要对于⾃⼰的初试分数进⾏估分，确认下⾃⼰是否要准备复试，估分数看分数线，历年的分数线不会有太⼤的波动，学校的站以及上都可以查询到信息。

4.其次就是要准备复试中的专业课考查。

主要分为两部分专业课+英语，专业课看具体学校的要求，⼤家在这⽅⾯多问问，切忌闭门造车，多查询⼀些历年信息和经验。

5.再就是英语⽅⾯的考察。