05练习题解答：第五章集中趋势与离散趋势
张小山新编《社会统计学与spss应用》课后习题答案
第二章 随机现象与基础概率练习题：1.从一副洗好的扑克牌（共52张，无大小王）中任意抽取3张，求以下事件的概率：（1） 三张K ； （2） 三张黑桃；（3） 一张黑桃、一张梅花和一张方块； （4） 至少有两张花色相同； （5） 至少一个K 。
解：（1）三张K 。
设：1A ＝“第一张为K ” 2A ＝“第二张为K ” 3A ＝“第三张为K ”则()()()()123121312//P A A A P A P A A P A A A =＝432525150⨯⨯＝15525若题目改为有回置地抽取三张，则答案为()123P A A A =444525252⨯⨯12197=（2）三张黑桃。
设：1A ＝“第一张为黑桃” 2A ＝“第二张为黑桃” 3A ＝“第三张为黑桃”则()()()()123121312//P A A A P A P A A P A A A =＝131211525150⨯⨯＝11850（3）一张黑桃、一张梅花和一张方块。
设：1A ＝“第一张为黑桃” 2A ＝“第二张为梅花” 3A ＝“第三张为方块”则 ()()()()123121312//P A A A P A P A A P A A A =＝131313525150⨯⨯＝0.017注意，上述结果只是一种排列顺序的结果，若考虑到符合题意的其他排列顺序，则最终的结果为：0.017×6＝0.102（4）至少有两张花色相同。
设：1A ＝“第一张为任意花色”2A ＝“第二张的花色与第一张不同”3A ＝“第三张的花色与第一、二张不同”则()1P A ＝5252＝1 ()21/P A A ＝5213521--＝3951 312(/)P A A A ＝5226522--=2650()123P A A A ＝1-123()P A A A ＝3926115150⎛⎫-⨯⨯ ⎪⎝⎭＝0.602（5）至少一个K 。
设：1A ＝第一张不为K2A ＝第二张不为K 3A ＝第三张不为K则()1P A ＝52452- ()21/P A A ＝51452- 312(/)P A A A ＝50452- ()123P A A A ＝1-123()P A A A ＝4847461525150⎛⎫-⨯⨯ ⎪⎝⎭＝0.2172.某地区3/10的婚姻以离婚而告终。
答案：第五章：练习题库-流行病学和医学统计学
第五章：练习题库-流行病学和医学统计学1.（单选）正确答案：B。
考查疾病筛检试验的定义，记忆型题目；筛检(Screening)是指通过快速的试验、检查、或其他方法，在表面健康人群中将那些可能有病但表面健康的人识别出来。
2.（单选）正确答案：D。
考查流行病学研究方法的分类，理解记忆型；A为观察性研究；B和E为实验性研究；C为临床的诊断方法。
数学模型是流行病学方法研究的一种，为理论性研究。
3.（单选）正确答案：A。
考查统计描述的描述指标，记忆理解型题目；标准差和变异系数是描述计量资料离散趋势的指标；中位数通常是描述不对称资料（偏态资料）的集中趋势指标；几何均数是描述偏态分布资料另外一个重要指标；所以算术均数（通常简称均数）是描述计量资料的集中趋势指标，故选择A。
4.（单选）正确答案：B。
考查描述集中趋势的指标，理解型题目；标准差和变异系数是描述计量资料离散趋势的指标；中位数和几何均数通常是描述不对称资料（偏态资料）的集中趋势指标；算术均数（通常简称均数）是描述计量资料的集中趋势指标，本题身高按照实际情况，符合正态分布，其平均水平应选用算术均数，故选择B。
5.（单选）正确答案：C。
考查流行病学的定义，记忆型题目；流行病学不仅仅研究各种疾病，而且研究健康状态和事件，所以流行病学不仅仅只是研究传染病。
6.（单选）正确答案：C。
考查流行病学的定义，记忆型题目。
流行病学是研究人群中疾病与健康状况的分布及其影响因素，并研究如何防治疾病及促进健康的策略与措施的科学。
7.（单选）正确答案：A。
考查流行病学的概念，记忆型题目。
流行病学的研究对象是人群，所关注的是具有某种特征的人群，并不是从个体上研究疾病。
8.（单选）正确答案：D。
考查率的概念，记忆型题目；率是表示在一定的条件下某现象实际发生的例数与可能发生该现象的总例数之比，来说明单位时间内某现象发生的频率或强度。
9.（单选）正确答案：A。
考查发病指标与患病指标的内涵，理解型题目；若用普查的方法，则只能了解高血压在某个时间点或时间段的患病人数，而新发病例、该时间死亡人数等数值均无法得到，故只能计算患病率。
集中和离散趋势指标
集中和离散趋势指标1.引言1.1 概述概述部分将介绍集中和离散趋势指标的基本概念和背景。
集中趋势指标和离散趋势指标是统计学中常用的分析工具，用于描述和度量数据集中和离散程度的重要指标。
在实际问题中，我们经常遇到需要描述和分析数据集中和离散程度的情况。
集中趋势指标主要关注数据的中心值，用于度量数据集中在何处，以及数据的均匀分布程度。
而离散趋势指标则用于度量数据的分散程度，即数据的离散程度有多大。
集中趋势指标和离散趋势指标在统计学、经济学、金融学等领域被广泛应用。
例如，在统计学中，我们常常使用平均值、中位数、众数等指标来描述数据的集中趋势；而方差、标准差、极差等指标则用于度量数据的离散趋势。
本文将分别介绍集中趋势指标和离散趋势指标的定义和解释，并列举一些常见的集中趋势指标和离散趋势指标的示例。
通过对这些指标的应用和分析，我们能够更加客观地了解数据的分布特征，为后续的数据分析和决策提供依据。
在下一章节的正文部分，我们将详细介绍集中趋势指标和离散趋势指标的定义、计算方法和使用场景。
希望通过本文的介绍，读者能够对集中和离散趋势指标有一个全面的认识，并能够在实际应用中灵活运用这些指标，提高数据分析的精确性和准确性。
接下来，我们将开始介绍集中趋势指标的相关内容，包括定义和解释等方面的内容。
敬请关注！1.2 文章结构文章结构部分的内容：本文将围绕集中和离散趋势指标展开讨论。
首先，在引言部分进行概述，介绍集中和离散趋势指标的基本概念和作用。
然后，通过分析文章目录可以看出，正文部分将重点介绍集中趋势指标和离散趋势指标，包括它们的定义和解释以及常见的指标类型。
最后，在结论部分对集中趋势指标和离散趋势指标的应用进行总结。
具体而言，在正文部分，我们会首先介绍集中趋势指标，包括其定义和解释。
随后，会详细介绍一些常见的集中趋势指标，例如均值、中位数和众数等。
这些指标能够反映数据集中在某个位置或数值上的趋势，有助于我们对数据的整体特征进行理解和分析。
张小山 新编《社会统计学与SPSS应用》课后答案
第二章 随机现象与基础概率练习题：1.从一副洗好的扑克牌（共52张，无大小王）中任意抽取3张，求以下事件的概率：（1） 三张K ； （2） 三张黑桃；（3） 一张黑桃、一张梅花和一张方块； （4） 至少有两张花色相同； （5） 至少一个K 。
解：（1）三张K 。
设：1A ＝“第一张为K ” 2A ＝“第二张为K ” 3A ＝“第三张为K ”则()()()()123121312//P A A A P A P A A P A A A =＝432525150⨯⨯＝15525 若题目改为有回置地抽取三张，则答案为()123P A A A =444525252⨯⨯12197=（2）三张黑桃。
设：1A ＝“第一张为黑桃” 2A ＝“第二张为黑桃” 3A ＝“第三张为黑桃”则()()()()123121312//P A A A P A P A A P A A A =＝131211525150⨯⨯＝11850（3）一张黑桃、一张梅花和一张方块。
设：1A ＝“第一张为黑桃” 2A ＝“第二张为梅花” 3A ＝“第三张为方块”则 ()()()()123121312//P A A A P A P A A P A A A =＝131313525150⨯⨯＝0.017注意，上述结果只是一种排列顺序的结果，若考虑到符合题意的其他排列顺序，则最终的结果为：0.017×6＝0.102（4）至少有两张花色相同。
设：1A ＝“第一张为任意花色”2A ＝“第二张的花色与第一张不同”3A ＝“第三张的花色与第一、二张不同”则()1P A ＝5252＝1 ()21/P A A ＝5213521--＝3951 312(/)P A A A ＝5226522--=2650()123P A A A ＝1-123()P A A A ＝3926115150⎛⎫-⨯⨯ ⎪⎝⎭＝0.602（5）至少一个K 。
设：1A ＝第一张不为K2A ＝第二张不为K 3A ＝第三张不为K则()1P A ＝52452- ()21/P A A ＝51452- 312(/)P A A A ＝50452- ()123P A A A ＝1-123()P A A A ＝4847461525150⎛⎫-⨯⨯ ⎪⎝⎭＝0.2172.某地区3/10的婚姻以离婚而告终。
第五章 集中趋势与离中趋势的度量习题
第五章集中趋势与离中趋势的度量习题一、填空题1．平均数就是在——内将各单位数量差异抽象化，用以反映总体的。
2．权数对算术平均数的影响作用不决定于权数的大小，而决定于权数的的大小。
3．几何平均数是，它是计算和平均速度的最适用的一种方法。
4．当标志值较大而次数较多时，平均数接近于标志值较的一方；当标志值较小而次数较多时，平均数靠近于标志值较的一方。
5．当时，加权算术平均数等于简单算术平均数。
6．利用组中值计算加权算术平均数是假定各组内的标志值是分布的，其计算结果是一个。
7．统计中的变量数列是以为中心而左右波动，所以平均数反映了总体分布的。
8．中位数是位于变量数列的那个标志值，众数是在总体中出现次数的那个标志值。
中位数和众数也可以称为平均数。
9．调和平均数是平均数的一种，它是的算术平均数的。
10．现象的是计算或应用平均数的原则。
11．当变量数列中算术平均数大于众数时，这种变量数列的分布呈分布；反之算术平均数小于众数时，变量数列的分布则呈分布。
12．较常使用的离中趋势指标有、、、、。
13．极差是总体单位的与之差，在组距分组资料中，其近似值是。
14．是非标志的平均数为、标准差为。
15．标准差系数是与之比。
16．已知某数列的平均数是200，标准差系数是30％，则该数列的方差是。
则该数列的极差为，四分位差为。
18．对某村6户居民家庭共30人进行调查，所得的结果是，人均收入400元，其离差平方和为5100000，则标准差是，标准差系数是。
19．测定峰度，往往以为基础。
依据经验，当β=3时，次数分配曲线为；当β<3时，为曲线；当β>3时，为曲线。
20．在对称分配的情况下，平均数、中位数与众数是的。
在偏态分配的情况下，平均数、中位数与众数是的。
如果众数在左边、平均数在右边，称为偏态。
如果众数在右边、平均数在左边，则称为偏态。
21．采用分组资料，计算平均差的公式是，计算标准差的公式是。
二、单项选择题1．加权算术平均数的大小( )A受各组次数f的影响最大B受各组标志值X的影响最大C只受各组标志值X的影响D受各组次数f和各组标志值X的共同影响2，平均数反映了( )A总体分布的集中趋势B总体中总体单位分布的集中趋势C总体分布的离散趋势D总体变动的趋势3．在变量数列中，如果标志值较小的一组权数较大，则计算出来的算术平均数( )A接近于标志值大的一方B接近于标志值小的一方C不受权数的影响D无法判断4．根据变量数列计算平均数时，在下列哪种情况下，加权算术平均数等于简单算术平均数( ) A各组次数递增B各组次数大致相等C各组次数相等D各组次数不相等5．已知某局所属12个工业企业的职工人数和工资总额，要求计算该局职工的平均工资，应该采用( )A简单算术平均法B加权算术平均法C加权调和平均法D几何平均法6．已知5个水果商店苹果的单价和销售额，要求计算5个商店苹果的平均单价，应该采用( ) A简单算术平均法B加权算术平均法C加权调和平均法D几何平均法7．计算平均数的基本要求是所要计算的平均数的总体单位应是( )A大量的B同质的C差异的D少量的8，某公司下属5个企业，已知每个企业某月产值计划完成百分比和实际产值，要求计算该公司平均计划完成程度，应采用加权调和平均数的方法计算，其权数是( )A计划产值B实际产值C工人数D企业数9．中位数和众数是一种( )A代表值B常见值C典型值D实际值10．由组距变量数列计算算术平均数时，用组中值代表组内标志值的一般水平，有一个假定条件，即( )A各组的次数必须相等B各组标志值必须相等C各组标志值在本组内呈均匀分布D各组必须是封闭组11．四分位数实际上是一种( )A算术平均数B几何平均数C位置平均数D数值平均数12．离中趋势指标中，最容易受极端值影响的是( )A极差B平均差C标准差D标准差系数13．平均差与标准差的主要区别在于( )A指标意义不同B计算条件不同C计算结果不同D数学处理方法不同A7万元B1万元C12 万元 D 3万元15．已知某班40名学生，其中男、女学生各占一半，则该班学生性别成数方差为( )A25％ B 30％ C 40％ D 50％16．当数据组高度偏态时，哪一种平均数更具有代表性? ( )A算术平均数B中位数C众数D几何平均数17．方差是数据中各变量值与其算术平均数的( )A离差绝对值的平均数B离差平方的平均数C离差平均数的平方D离差平均数的绝对值18．一组数据的偏态系数为1.3，表明该组数据的分布是( )AlE态分布B平顶分布C左偏分布D右偏分布19．当一组数据属于左偏分布时，则( )A平均数、中位数与众数是合而为一的B众数在左边、平均数在右边C众数的数值较小，平均数的数值较大D众数在右边、平均数在左边20．四分位差排除了数列两端各( )单位标志值的影响。
集中趋势与离散趋势
允许用户自定义查询条件、筛选数据和调整图表 参数，以便更深入地探索数据的内在规律和关联 关系。
数据动画
将数据变化过程以动画形式展现出来，帮助用户 更直观地理解数据的变化趋势和动态特征。
06 总结与展望
CHAPTER
主要发现与结论
集中趋势描述
通过平均数、中位数和众数等指标，可以有 效地描述数据的集中趋势，反映数据分布的 中心位置。
众数
一组数据中出现次数最多的数。众数可能不唯一，也可能不存在。众数适用于分类数据和顺序数据，对于数值型 数据，如果数据分布的波动性较大，众数可能不能很好地代表数据的集中趋势。
03 离散趋势
CHAPTER
定义与概念
离散趋势
指一组数据中各数值之间的差异程度 或离散程度，是数据分布的另一个重 要特征。
直方图（Histogram）
将数据按照一定范围进行分组并用矩形条表示，通过矩形条的高度和宽度反映数据的分布 规律。
散点图（Scatter Plot）
用点的位置表示两个变量之间的关系，可通过观察点的分布情况和趋势线分析数据的集中 和离散趋势。
动态数据可视化在趋势分析中的应用
1 2 3
时间序列分析
通过动态展示数据随时间变化的情况，揭示数据 的长期趋势、季节波动和周期性规律。
• 关注数据质量和异常值处理：在实际数据分析中，异常值和数据质量问题是不 可忽视的。未来的研究可以关注如何有效地处理异常值和数据质量问题，以提 高集中趋势和离散趋势分析的准确性和可靠性。例如，可以采用稳健的统计方 法或者数据清洗技术对异常值进行处理，以保证分析结果的稳定性和可靠性。
谢谢
THANKS
Tableau
功能强大的数据可视化工具，支持交互式数据分析和动态图表展示， 适用于大数据处理。
[5]第五章 集中与离散趋势测定指标.
![[5]第五章 集中与离散趋势测定指标.](https://img.taocdn.com/s3/m/810ab8b0b9d528ea81c77970.png)
表5-3
月收入（元）
3000～3500 3500～4000 4000～4500 4500～5000 5000～5500 5500～6000 6000～6500
∑
某单位职工月收入分组表
组中值（元）
xi
3250 3750 4250 4750 5250 5750 6250
第一，平均指标在时间上的差异的对比分析作用。 平均指标可以反映同一总体现象在不同时期的一般发 展变化水平，揭示现象的变动趋势和规律性。如：由 于不同时期同一研究总体的农民家庭人口结构会发生 变动，若要考察农民纯收人变化，只能用农民平均纯
收人指标来反映。
第二，平均指标在空间上的差异的对比分析作用。 利用平均指标比较在某一时期同类现象在不同地区、 不同单位的一般水平，用以评价总体各单位的工作质 量和效果。如：由于城乡每一户居民人口规模不同， 要用人均居住面积而不能用城乡每户居住总面积来考 察城乡居民居住状况的差异。
n
xi fi
x
i 1 n
fi
i 1
式中：xi 表示分布数列中第i
值；
组的变量值或组中
fi 表示分布数列中第i 组的单位个数。
上式还可以变形为:
x
n
xi
fi
n
Hale Waihona Puke i1fii 1
式中：fi 称为分布数列中第i 组的频数或权数；
fi
n
称为分布数列中第i 组的频率或权数
系数。
fi
1．简单算术平均数（Simple arithmetic mean）
简单算术平均数适用于未分组的分布数列，它是 将总体各单位同类标志值直接汇总，然后与总体单位 总数相除所求得。简单算术平均数的计算公式为：
数据的集中趋势和离散程度检测题
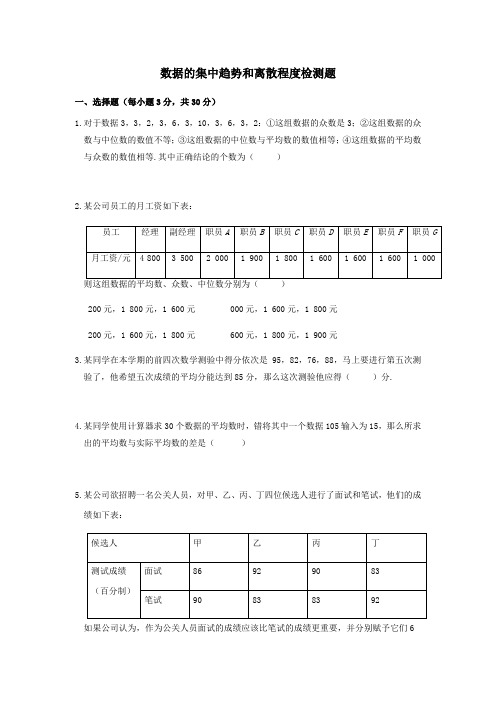
数据的集中趋势和离散程度检测题一、选择题（每小题3分，共30分）1.对于数据3，3，2，3，6，3，10，3，6，3，2：①这组数据的众数是3；②这组数据的众数与中位数的数值不等；③这组数据的中位数与平均数的数值相等；④这组数据的平均数与众数的数值相等.其中正确结论的个数为（ ）2.某公司员工的月工资如下表：200元，1 800元，1 600元 000元，1 600元，1 800元 200元，1 600元，1 800元 600元，1 800元，1 900元3.某同学在本学期的前四次数学测验中得分依次是95，82，76，88，马上要进行第五次测验了，他希望五次成绩的平均分能达到85分，那么这次测验他应得（ ）分.4.某同学使用计算器求30个数据的平均数时，错将其中一个数据105输入为15，那么所求出的平均数与实际平均数的差是（ ）5.某公司欲招聘一名公关人员，对甲、乙、丙、丁四位候选人进行了面试和笔试，他们的成绩如下表： 如果公司认为，作为公关人员面试的成绩应该比笔试的成绩更重要，并分别赋予它们6和4的权．根据四人各自的平均成绩，公司将录取（）A.甲B.乙C.丙D.丁6.如图是某学校全体教职工年龄的频数分布直方图（统计中采用“上限不在内”的原则，如年龄为36岁统计在36≤x＜38小组，而不在34≤x＜36小组），根据图形提供的信息，下列说法中错误的是（）A.该学校教职工总人数是50B.年龄在40≤x＜42小组的教职工人数占该学校全体教职工总人数的20%C.教职工年龄的中位数一定落在40≤x＜42这一组D.教职工年龄的众数一定落在38≤x＜40这一组7.在某校“我的中国梦”演讲比赛中，有9名学生参加比赛，他们决赛的最终成绩各不相同，其中的一名学生要想知道自己能否进入前5名，不仅要了解自己的成绩，还要了解这9名学生成绩的（）A.众数B.方差C.平均数D.中位数8.数据0，1，2，3，的平均数是2，则这组数据的标准差是（）9.某校将举办一场“中国汉字听写大赛”，要求各班推选一名同学参加比赛，为此，初三（1）班组织了五轮班级选拔赛，在这五轮选拔赛中，甲、乙两位同学的平均分都是96分，甲的成绩的方差是，乙的成绩的方差是．根据以上数据，下列说法正确的是（）A.甲的成绩比乙的成绩稳定B.乙的成绩比甲的成绩稳定C.甲、乙两人的成绩一样稳定D.无法确定甲、乙的成绩谁更稳定10.在某中学举行的演讲比赛中，初一年级5名参赛选手的成绩如下表所示，请你根据表中提供的数据，计算出这5名选手成绩的方差为（）二、填空题（每小题3分，共24分）11.在航天知识竞赛中，包括甲同学在内的6•名同学的平均分为74分，其中甲同学考了89分，则除甲以外的5名同学的平均分为_______分.12.已知一组数据23，27，20，18，x ，12，它们的中位数是21，则x =______.13.有7个数由小到大依次排列，其平均数是38，如果这组数的前4个数的平均数是33，后4个数的平均数是42，则这7个数的中位数是_______.14.某超市招聘收银员一名，对三名应聘者进行了三项素质测试.下面是三名应聘者的素质测试成绩：4，3，2，则这三人中 将被录用.15.为了从甲、乙、丙三位同学中选派一位同学参加环保知识竞赛，老师对他们的五次环保知识测验成绩进行了统计，他们的平均分都为85分，方差分别为s 2甲=18，s 2乙=12，s 2丙=23，根据统计结果，应派去参加竞赛的同学是 ．（填“甲”、“乙”、“丙”中的一个）16.用科学计算器求得271，315，263，289，300，277，286，293，297，280的平均数为 ，标准差为 ．（精确到）17.跳远运动员李刚对训练效果进行测试，6次跳远的成绩如下：，，，，，（单位：m ）.这六次成绩的平均数为，方差为601．如果李刚再跳两次，成绩分别为，，则李刚这8次跳远成绩的方差_____（填“变大”“不变”或“变小”）．18.我市射击队为了从甲、乙两名运动员中选出一名运动员参加省运动会比赛，组织了选拔测试，两人分别进行了五次射击，成绩（单位：环）如下：则应派_______运动员参加省运动会比赛．三、解答题（共46分）19. 某乡镇企业生产部有技术工人15人，生产部为了合理制定产品的每月生产定额，统计了15人某月的加工零件数如下：（1（2）假如生产部负责人把每位工人的月加工零件数定为260件，你认为这个定额是否合理？为什么？20.为调查八年级某班学生每天完成家庭作业所需时间，在该班随机抽查了8名学生，他们每天完成作业所需时间（单位：min）分别为60，55，75，55，55，43，65，40.（1）求这组数据的众数、中位数.（2）求这8名学生每天完成家庭作业的平均时间；如果按照学校要求，学生每天完成家庭作业时间不能超过60 min，问该班学生每天完成家庭作业的平均时间是否符合学校的要求？21.某校260名学生参加植树活动，要求每人植4～7棵，活动结束后随机抽查了20名学生每人的植树量，并分为四种类型，A：4棵；B：5棵；C：6棵；D：7棵.将各类的人数绘制成扇形统计图（如图①）和条形统计图（如图②），经确认扇形统计图是正确的，而条形统计图尚有一处错误.回答下列问题：（1）写出条形统计图中存在的错误，并说明理由.（2）写出这20名学生每人植树量的众数、中位数.（3）在求这20名学生每人植树量的平均数时，小宇是这样分析的：①小宇的分析是从哪一步开始出现错误的？②请你帮他计算出正确的平均数，并估计这260名学生共植树多少棵.22.（7分）某校在一次数学检测中，八年级甲、乙两班学生的数学成绩统计如下表：（1）甲班的众数是多少分，乙班的众数是多少分，从众数看成绩较好的是哪个班?（2）甲班的中位数是多少分，乙班的中位数是多少分，甲班成绩在中位数以上（包括中位数）的学生所占的百分比是多少，乙班成绩在中位数以上（包括中位数）的学生所占的百分比是多少，从中位数看成绩较好的是哪个班?（3）甲班的平均成绩是多少分，乙班的平均成绩是多少分，从平均成绩看成绩较好的是哪个班?23.（7分）某单位欲从内部招聘管理人员一名，对甲、乙、丙三名候选人进行了笔试和面试两项测试，三人的测试成绩如下表所示：有弃权票，每位职工只能推荐1人）如图所示，每得一票记作1分.（1）请算出三人的民主评议得分.（2）如果根据三项测试的平均成绩确定录用人选，那么谁将被录用（精确到）？（3）根据实际需要，单位将笔试、面试、民主评议三项测试得分按的比例确定个人成绩，那么谁将被录用？24.（7分）一次期中考试中，A，B，C，D，E五位同学的数学、英语成绩有如下信息：（1）求这5位同学在本次考试中数学成绩的平均分和英语成绩的标准差.（2）为了比较不同学科考试成绩的好与差，采用标准分是一个合理的选择，标准分的计算公式是：标准分＝（个人成绩－平均成绩）÷成绩标准差.从标准分看，标准分高的考试成绩更好，请问A同学在本次考试中，数学与英语哪个学科考得更好?25.（7分）某校八年级学生开展踢毽子比赛活动，每班派5名学生参加，按团体总分多少排列名次，在规定时间内每人踢100个以上（含100）为优秀.下表是成绩最好的甲班和乙班5名学生的比赛数据（单位：个）：经统计发现两班总数相等.此时有学生建议，可以通过考察数据中的其他信息作为参考.请你回答下列问题：（1）计算两班的优秀率.（2）求两班比赛成绩的中位数.（3）估计两班比赛数据的方差哪一个小.（4）根据以上三条信息，你认为应该把冠军奖杯发给哪一个班级？简述你的理由.。
集中趋势和离中趋势
集中趋势反映一组数据向某一中心值靠拢的程度。
一、算术平均（也叫均值 ）
▪ 1.简单算术平均数
计算公式:
N
X
X1 X 2 ...... X N
Xi
i 1
N
N
它是反映数据集中的主要测度。
算术平均的统计含义：算术平均数是同质总体各 数据偶然性、随机性特征互相抵消后的稳定数值。反映 数据集中的特征。
QU位置
39 4
6.75
QL 780 (850 780) 0.25 797.5 QU 1250 (1500 1250) 0.75 1437.5
方法2：
Q位置
n 1 2
2
1
9 1 2
2
1
3
所以QL为从最小值数第3个数值，即850元； Qu为从最 大值数第3个数值，即1500元；
工人一周生 产零件数
60以下
60-70
70-80
80-90 90以上 合计
工人数fi
组中值xi
xifi
向上累计频 向下累计频
数
数
7
55
385
7
80
21
M0
Li
65 (
fi
fi 1f3i61 5 fi1) ( fi
fi1 )
di
28
73
25 19
M0
75
Ui85(
fi
fi 1f8i715 fi1) 16( f1i5
1 2
3
4
5
67
平均数
左图是三个直方图， 平均数用箭头标出，当 蓝色矩形移向右方时， 它牵着平均数跟着走。
在平均数处直方 图保持平衡，面积以它 们离开平衡点的距离而
集中趋势和离散趋势
众数
(mode)
1. 2. 3.
出现次数最多的变量值
不受极端值的影响
一组数据可能没有众数或有几个众数
4.
主要用于分类数据，也可用于顺序数据 和数值型数据
The Mode 众数
1.
排序后处于中间位置上的值
50%
Me
50%
2. 不受极端值的影响 3. 主要用于顺序数据，也可用数值型数据，但不能 用于分类数据
顺序数据的中位数
(例题分析)
甲城市家庭对住房状况评价的频数分布 回答类别
非常不满意 不满意 一般 满意 非常满意 甲城市
户数 (户)
24 108 93 45 30
累计频数
1
2
3
4
5
6
7
8
9
位置 n 1 2 9 1 2 5
中位数 1080
数值型数据的中位数
(10个数据的算例)
【例】：10个家庭的人均月收入数据
排 位 序: 置: 660 750 780 850 960 1080 1250 1500 1630 2000
1 2
3
4
5
6
7
8
9
10
22 18 12 18 100
在所调查的50人中，购 买可口可乐的人数最多， 为15人，占总被调查人数 的30%，因此众数为“可 口可乐”这一品牌，即 Mo＝可口可乐
顺序数据的众数
(例题分析)
甲城市家庭对住房状况评价的频数分布 回答类别 非常不满意 不满意 一般 满意 非常满意 甲城市 户数 (户) 24 108 93 45 30 百分比 (%) 8 36 31 15 10
【个人精编】数据集中趋势和离散程度笔记
数据的集中趋势和离散程度笔记一、知识点梳理知识点1：表示数据集中趋势的代表平均数、众数、中位数都是描述一组数据集中趋势的特征数，只是描述的角度不同，其中平均数的应用最为广泛。
（1）平均数算术平均数（简称为平均数）：121()n xx x x n（公式一）①一般地，如果在一组数据中，x 1出现f 1次，x 2出现f 2次，……，x k 出现f k 次，（f 1，f 2，…f k 为正整数），则这组数据的平均数：当n 个数据中某些数据反复出现时，用该公式较简洁； f 1+f 2+…+f k =n （数据的总个数）。
②一般地，如果一组数据都在某个数a 上下波动时，就可以采用把原来每个数据都减去a ，得一组新数据，再算得这组新数据的平均数'x ，这样原来数据的平均数是：x ＝a ＋'x （公式三）平均数定义公式和两个简化计算公式都很重要，应根据具体情况，恰当选用。
特别的：一组数据x 1，x 2，…，x n 的平均数为x ，①若每个数据都扩大a 倍，即ax 1，ax 2，…，ax n ，则平均数也扩大a 倍，即a x ； ②若每个数据都增加b ，即x 1＋b ，x 2＋b ，…，x n ＋b ，则平均数增加b ，即x ＋b ； ③若每个数据都扩大a 倍后又都增加b ，则平均数也扩大a 倍后增加b ，即a x ＋b ． 当数据组中数据较大又在某个数值左右波动或数据之间存在某种倍数关系时，利用这些规律求平均数比较直接、简便。
加权平均数在计算数据的平均数时，往往根据其重要程度，分别给每个数据一个“权”，由此求出平均数叫做加权平均数。
恒量各个数据“重要程度”的数值叫做权。
相同数据的个数叫做权，这个“权”含有所占分量轻重的意思。
ω1越大，表示x 1的个数越多，于是x 1的“权”就越重。
若n 个数x 1，x 2，…，x n 的权是分别是ω1，ω2，…，ωn ，则x ＝nnn x x x ωωωωωω++++++ 212211① 当ω1＝ω2＝…＝ωn ，即各项的权相等时，加权平均数就是算术平均数。
数据的集中趋势与离散程度——巩固练习
数据的集中趋势与离散程度——巩固练习【巩固练习】一.选择题1.已知一组数据2，l，x，7，3，5，3，2的众数是2，则这组数据的中位数是( )．A．2 B．2．5 C．3 D．52．8名学生在一次数学测试中的成绩为80，82，79，69，74，78，x，81，这组成绩的平均数是77，则x的值为( )．A．76 B．75 C．74 D．733．有8个数的平均数是11，还有12个数的平均数是12，则这20个数的平均数是( )． A．11.6 B．232 C．23.2 D．11.54. 商店某天销售了13双运动鞋，其尺码统计如下表：则这13双运动鞋尺码的众数和中位数分别是（）A．39码、39码 B．39码、40码 C．40码、39码 D．40码、40码5. 生物工作者为了估计一片山林中雀鸟的数量，设计了如下方案：先捕捉100只雀鸟，给它们做上标记后放回山林；一段时间后，再从中随机捕捉500只，其中有标记的雀鸟有5只．请你帮助工作人员估计这片山林中雀鸟的数量约为（）A．1000只 B．10000只 C．5000只 D．50000只6. 某特警部队为了选拔“神枪手”，举行了1000米射击比赛，最后由甲、乙两名战士进入决赛，在相同条件下，两人各射靶10次，经过统计计算，甲、乙两名战士的总成绩都是99.68环，甲的方差是0.28，乙的方差是0.21，则下列说法中，正确的是（）A．甲的成绩比乙的成绩稳定 B．乙的成绩比甲的成绩稳定C．甲、乙两人成绩的稳定性相同 D．无法确定谁的成绩更稳定二.填空题7．已知三个不相等的正整数的平均数、中位数都是3，则这三个数分别为________．8．数据1、2、4、4、3、5、l、4、4、3、2、3、4、5，它们的众数是____、中位数是____、平均数是_______．9. 给出一组数据：23，22，25，23，27，25，23，则这组数据的中位数是______；方差是______ (精确到0.1)．10．在数据－1，0，4，5，8中插入一个数据x，使得该数据组的中位数为3，则x＝________．11．某次射击训练中，一小组的成绩如下表所示：环数 6 7 8 9人数 1 3 2若该小组的平均成绩为7.7环，则成绩为8环的人数为_________．12. 小张和小李去练习射击，第一轮10发子弹打完后，两人的成绩如图所示．根据图中的信息，小张和小李两人中成绩较稳定的是___________.三.解答题13. 一家公司打算招聘一名英文翻译，对甲、乙两名应试者进行了听、说、读、写的英语水应试者听说读写甲85 83 78 75乙73 80 85 82(1)如果这家公司想招一名口语能力较强的翻译，听、说、读、写成绩按照3:3:2:2的比确定，计算两名应试者的平均成绩(百分制)．从他们的成绩看，应该录取谁?(2)如果这家公司想招一名笔译能力较强的翻译，听、说、读、写成绩按照2:2:3:3的比确定，计算两名应试者的平均成绩(百分制)．从他们的成绩看，应该录取谁? 14. 甲、乙两名学生进行射击练习，两人在相同条件下各射10次，将射击结果作统计分析，命中环数 5 6 7 8 9 10 平均数众数方差甲命中环数的次数1 42 1 1 1 7 6 2.2乙命中环数的次数1 2 4 2 1(2)根据你所学的统计知识，利用上述某些数据评价甲、乙两人的射击水平．15. 为宣传节约用水，小明随机调查了某小区部分家庭5月份的用水情况，并将收集的数据整理成如下统计图．（1）小明一共调查了多少户家庭？（2）求所调查家庭5月份用水量的众数、平均数；（3）若该小区有400户居民，请你估计这个小区5月份的用水量．【答案与解析】一.选择题 1.【答案】B ；【解析】由众数的意义可知x ＝2，然后按照从小到大的顺序排列这组数据，则中位数应为232.52+=． 2．【答案】D ； 【解析】由题意80827969747881778x +++++++=，解得73x =.3．【答案】A ； 【解析】118121211.620⨯+⨯=4.【答案】A ；【解析】解：数字39出现了5次，出现次数最多，所以这13双运动鞋尺码的众数是39（码），由于第7个数为39，所以中位数39（码）．故选A ．5.【答案】B ； 【解析】解：100÷5500=10000只．故选B ． 6.【答案】B ；【解析】解：方差是用来衡量一组数据波动大小的量，方差越大，表明这组数据偏离平均数越大，即波动越大，数据越不稳定；反之，方差越小，表明这组数据分布比较集中，各数据偏离平均数越小，即波动越小，数据越稳定． ∵甲的方差是0.28，乙的方差是0.21， ∴乙的成绩比甲的成绩稳定；故选B ．二.填空题 7．【答案】1、3、5或2、3、4 8．【答案】4；3.5；3.21；【解析】 数据中4出现了5次，出现的次数最多，所以众数是4；把数据重新排列，最中间的两个数是3和4，所以这组数据的中位数是 3.5；这组数据的平均数是1(2122334552) 3.2114x =⨯+⨯+⨯+⨯+⨯=． 9.【答案】23 2.6；【解析】先把这组数据按照从小到大的顺序排列，不难发现处于中间的数是23，然后求出平均数是24，再利用公式2222121[()()()]n s x x x x x x n=-+-++-ggg 便可求出方差约为2.6．10．【答案】2； 11．【答案】4；【解析】设成绩为8环的人数为x ，则6218187.7,4132x x x +++==+++.12.【答案】小张；【解析】从图看出：小张的成绩波动较小，说明它的成绩较稳定．故填小张. 三.解答题 13.【解析】解：(1)听、说、读、写的成绩按3:3:2:2的比确定，则甲的平均成绩为：853*********813322⨯+⨯+⨯+⨯=+++(分)．乙的平均成绩为：73380385282279.33322⨯+⨯+⨯+⨯=+++(分)．显然甲的成绩比乙高，所以从成绩看，应该录取甲． (2)听、说、读、写的成绩按照2:2:3:3的比确定，则甲的平均成绩为：852*********79.52233⨯+⨯+⨯+⨯=+++(分)．乙的平均成绩为：73280285382380.72233⨯+⨯+⨯+⨯=+++(分)．显然乙的成绩比甲高，所以从成绩看，应该录取乙． 14.【解析】解：乙命中10环的次数为0；乙所命中环数的众数为7，其平均数为5162748291710x ⨯+⨯+⨯+⨯+⨯==乙；故其方差为22221[(57)2(67)(97)] 1.210s =⨯-+-++-=ggg 乙．甲、乙两人射击水平的评价：①从成绩的平均数与众数看，甲与乙的成绩相差不多；②从成绩的稳定性看，22s s >乙甲，乙的成绩波动小，比较稳定；③从良好率(成绩在8环或8环以上)看，甲、乙两人成绩相同；④从优秀率看(成绩在9环及9环以上)看，甲的成绩比乙的成绩好． 15.【解析】 解：（1）1+1+3+6+4+2+2+1=20，答：小明一共调查了20户家庭；（2）每月用水4吨的户数最多，有6户，故众数为4吨； 平均数：（1×1+1×2+3×3+4×6+5×4+6×2+7×2+8×1）÷20=4.5（吨）； （3）400×4.5=1800（吨），答：估计这个小区5月份的用水量为1800吨．。
统计学集中趋势和离散趋势的度量
统计学集中趋势和离散趋势的度量
统计学中有多种方式用于度量数据的集中趋势和离散趋势。
以下是其中一些常用的度量方法：
集中趋势的度量：
1. 平均值（Mean）：将所有数据点相加，然后除以数据的个数。
2. 中位数（Median）：将数据按照大小排序，取中间位置的值（当数据个数为偶数时，取中间两个数的平均值）。
3. 众数（Mode）：出现次数最多的数值。
4. 加权平均值（Weighted Mean）：对数据点进行加权处理，每个数据点乘以相应的权重，然后求和并除以权重总和。
离散趋势的度量：
1. 方差（Variance）：计算每个数据点与平均值的差的平方，然后求平均值。
2. 标准差（Standard Deviation）：方差的平方根，用于衡量数据点与平均值之间的差异程度。
3. 平均绝对偏差（Mean Absolute Deviation，简称MAD）：计算每个数据点与平均值的绝对值的平均值。
4. 四分位间距（Interquartile Range，简称IQR）：将数据按照大小排序，并计算上四分位数和下四分位数之间的差距。
这些统计学度量方法能够帮助我们更好地理解数据的集中趋势和离散趋势，从而
对数据进行更准确的描述和分析。
练习题解答：第五章集中趋势与离散趋势
第五章 集中趋势与离散趋势练习题：1. 17名体重超重者参加了一项减肥计划，项目结束后，体重下降的重量分别为： （单位：千克）12 10 15 8 2 6 14 12 10 12 10 10 11 10 5 10 16 （1）计算体重下降重量的中位数、众数和均值。
（2）计算体重下降重量的全距和四分位差。
（3）计算体重下降重量的方差和标准差。
解：(1)○1中位数：对上面的数据进行从小到大的排序：M d 的位置＝2=9，数列中从左到右第9个是10，即M d ＝10。
○2众数：绘制各个数的频数分布表：“10”的频数是6，大于其他数据的频数，因此众数M O =“10” ○3均值：18.1016521=+⋯++==∑=nnxX ni i（2）○1全距：R ＝max(x i )-min(x i )=16-2=14 ○2四分位差：根据题意，首先求出Q 1和Q 3的位置： Q 1的位置＝41+n ＝4117+=，则Q 1=8+×(10-8)=9 Q 3的位置＝4)1(3+n ＝4)117(3+⨯=,则Q 3=12+×(12-12)=12Q= Q 3- Q 1=12-9=3（3）○1方差：221222()1(210.18)(510.18)(1610.18) 171=12.404nii x x S n =-=--+--=-∑+?+○2标准差： 3.52S ==2.下表是武汉市一家公司60名员工的省（市）籍的频数分布：省（市）籍频数（个）湖北 28 河南 12 湖南 6 四川 6 浙江 5 安徽3（1）根据上表找出众值。
（2）根据上表计算出异众比率。
解： (1)“湖北”的频数是28，大于其他省（市）籍的频数，因此众数M O =“湖北” (2)异众比率的计算公式为： mor n f V n-=（ n 代表总频数，mo f 代表众数的频数） 其中n=60，mo f =28，则： 60280.5360r V -==3.某个高校男生体重的平均值为58千克，标准差为6千克，女生体重的平均值 为48千克，标准差为5千克。
数据的集中趋势和离散程度
数据的集中趋势和离散程度作者：***来源：《中学生数理化·八年级数学人教版》2020年第06期客觀事物带有各种信息，这些信息的表现形式和载体叫作数据.例如，测量温度、湿度、气压、风力、风向等所产生的各种记录，都是研究气象问题离不开的数据，统计过程主要分为三步：第一步是收集数据;第二步是整理数据，即对收集的原始数据进行整理、加工，从中提取出数据的代表;第三步是分析数据，即通过数据的代表研究数据中蕴涵的规律，从而研究已发生的事或预测将发生的事.一、数据的集中趋势分析数据时，通常关注“一组数据围绕哪个中心数值分布”.这个问题关系到一组数据的平均水平或一般情况，对发现事物的内在规律有重要参考价值，在统计学中，把一组数据向某一中心数值靠拢的情形，称为这组数据的集中趋势，为描述数据的集中趋势，可以选择不同的数据代表.如果从数据取值大小的角度描述，可用平均数作为数据代表：如果从数据排列位置的角度描述，可用中位数作为数据代表;如果从不同数据出现次数的角度描述，可用众数作为数据代表.这三个数据代表从不同角度反映数据的集中趋势，它们各有各的作用，分别适合于不同情况的数据分析.例1 为比较A，B两个玉米品种，将它们分别种植在面积相等的多块试验田中，每块试验田只种一种玉米，下表记录了两种玉米收获后的产量分布情况.表中第一行为单块试验田产量，下面两行分别为A，B两个品种中与第一行产量对应的试验田的块数.根据表中的数据解答下列问题：（1）分别求A，B两种玉米单块试验田产量的平均数，并说明其意义;（2）分别求A.B两种玉米单块试验田产量的中位数，并说明其意义：（3）分别求A，B两种玉米单块试验田产量的众数，并说明其意义.解：（1）从表中可知.A种玉米单块试验田产量（单位：kg）为700，750，800，850，900，950的试验田块数分别为4，20，26，20，18 ，12.通过计算加权平均数，得A种玉米单块试验田产量的平均数为XA=832 kg.同理，B种玉米单块试验田产量的平均数为xB≈ 827 kg.从计算结果可知，在单块试验田平均产量上A比B高5 kg.加权平均数与通常的算术平均数本质相同，即n个数之和除以n的结果，只是加权平均数计算起来更简捷.（2）将A的全部单块试验田产量（共100个）从小到大依次排列，相同的数据重复写，这100个数据中处于正中间位置的是第50个数据800和第51个数据850，这两数的平均数（800+850）÷2=825为A种玉米单块试验田产量的中位数，将B的全部单块试验田产量（共99个）从小到大依次排列，相同的数据重复写，这99个数据中处于正中间位置的是第50个数据850，它为B种玉米单块试验田产量的中位数.从计算结果可知，A的数据中小于825的和大于825的各占50个;B的数据中第50个数据850之前和之后的数据各占49个.这说明825 kg和850 kg可以分别作为A，B两种玉米单块试验田产量的中等水平的代表.中位数可以不是原始数据.排序时既可以从小到大，也可以从大到小，两种排法找出的中位数相同.（3）A的全部数据（共100个）中，出现次数最多的是800 kg（26次），800 kg即这组数据的众数.B的全部数据（共99个）中，出现次数最多的是800 kg（25次）和850 kg （25次），800 kg和850 kg都是这组数据的众数.从计算结果可知，虽然各块试验田中产量不尽相同，但也可能有规律存在，即在一般情形下，A的单块试验田产量是800 kg的可能性较大，B的单块试验田产量是800 kg或850 kg的可能性较大.可以看出，一组数据的众数可能是一个，也可能不止一个.众数是原始数据中的数据.平均数是最常用的一个数据代表，它通常能反映一组数据的平均水平.平均数的计算，要用到原始数据中的每一个数据.因此，一组数据中如有极端值（与多数数据相比过大或过小的个别数据）时，极端值可能对平均数影响较大.这种情形下如仍用平均数作为数据代表，往往与多数数据的大小产生较大偏差，不能恰如其分地反映一组数据的中心数值，这时，选择中位数或众数作为数据代表，或更能客观地反映一组数据的中心数值，例2 下表为某地9月份每天空气中细颗粒物（即PM 2.5）的测定值及相应的天数.（1）分别求表中数据的平均数、中位数和众数.（2）所得的平均数能客观反映该地9月份空气中细颗粒物的含量吗？解：（l）平均数约为34.9 yg/m3，中位数为24μg/m3，众数为24 μg/m3.（2）观察表中数据不难发现，30天中有29天的测定值都不超过25 μg/m3，它们与平均数差距较大;30天中只有1天的测定值360μLg/m3远高过平均数，这可能是由于一次突发事故造成了空气严重污染.显然，因为有360这个极端值，才使得平均数的值很大.如果以平均数34.9 μg/m3作为数据代表，则不能客观反映该地9月份空气中细颗粒物含量的一般状况.而以中位数或众数24μg/m3作为数据代表，则能较好地反映客观实际.二、数据的离散程度“一组数据中各个数据与这组数据的中心数值的偏离程度有多大？”这是数据分析所关注的另一个主要问题，由它能从整体上描述这组数据的聚散状态.在统计学中，把一组数据中各个数据与这组数据的中心数值的偏离程度，称为这组数据的离散程度或离中程度.它反映一组数据大小的波动状态，从而描述了这组数据的稳定性.方差是表示离散程度的常用数据代表，它的计算方法是，先计算一组数据的平均数，再计算各数据与所得平均数之差的平方和，最后用所得平方和除以这组数据的个数，这个结果被用于反映一组数据与平均数的偏离程度，对数据的变化幅度给予了定量的刻画.例3 分别计算例1中A.B两组数据的方差，由所得方差你能看出哪种可能性？解：s2=4 876，s2≈5 061.从两个方差看，B的略大于A的，即B的数据比A的数据的离散程度略高，也即B的数据起伏略大，而A的数据相对来说略为稳定.同学们可能会想：为什么计算方差要用各数据与平均数之差的平方和？如果直接把各数据与平均数之差相加岂不更简单？一般情况下，一组数据中可能有些数据比平均数大，有些数据比平均数小.如果直接用它们减平均数，则这些差会有正有负，如果再把这些差相加，就会出现正负相抵，例如，一组数据为2，2，3，3，4，4，其平均数为3，各数据与平均数之差分别为一1，-1，0，0，1，1.这些差之和为0.但这并不意味着这组数据都是紧靠平均数的.使用各数据与平均数之差的平方和，则利用了平方的非负性，防止做加法时出现正负相抵而隐藏了相关数据对平均数的偏离.方差名称中的“方”正是“平方”的简称.你也许会问：为什么不用差的绝对值，而要用差的平方来分析离散程度呢？直接用绝对值不是也可以避免出现负数吗？不使用绝对值，是因为取绝对值在运算上要考虑差的正负，取差的平方则不需要考虑差的符号，而且只要四则运算即可获得避免正负相抵的效果.所以人们选择用差的平方来计算方差.观察下图，图1中数据的方差应大于图2中数据的方差，这一结论可通过测量距离或运用方差公式计算来证明.。
卫生统计学习题及答案(精华版)
统计学习题二、简答1。
简述描述一组资料的集中趋势和离散趋势的指标。
集中趋势和离散趋势是定量资料中总体分布的两个重要指标。
（1)描述集中趋势的统计指标：平均数（算术均数、几何均数和中位数）、百分位数（是一种位置参数,用于确定医学参考值范围,P50就是中位数）、众数。
算术均数:适用于对称分布资料，特别是正态分布资料或近似正态分布资料；几何均数：对数正态分布资料（频率图一般呈正偏峰分布）、等比数列；中位数：适用于各种分布的资料，特别是偏峰分布资料,也可用于分布末端无确定值得资料. (2）描述离散趋势的指标：极差、四分位数间距、方差、标准差和变异系数。
四分位数间距：适用于各种分布的资料，特别是偏峰分布资料，常把中位数和四分位数间距结合起来描述资料的集中趋势和离散趋势.方差和标准差：都适用于对称分布资料，特别对正态分布资料或近似正态分布资料，常把均数和标准差结合起来描述资料的集中趋势和离散趋势;变异系数：主要用于量纲不同时,或均数相差较大时变量间变异程度的比较。
2。
举例说明变异系数适用于哪两种形式的资料，作变异程度的比较？度量衡单位不同的多组资料的变异度的比较。
例如，欲比较身高和体重何者变异度大，由于度量衡单位不同，不能直接用标准差来比较,而应用变异系数比较. 3。
试比较标准差和标准误的关系与区别.区别:⑴标准差S：①意义：描述个体观察值变异程度的大小.标准差小，均数对一组观察值得代表性好；②应用：与均数结合,用以描述个体观察值的分布范围，常用于医学参考值范围的估计;③与n的关系：n越大，S越趋于稳定;⑵标准误S X：①意义：描述样本均数变异程度及抽样误差的大小.标准误小,用样本均数推断总体均数的可靠性大;②应用于均数结合，用以估计总体均数可能出现的范围以及对总体均数作假设检验；③与n的关系：n越大,S X越小.联系：①都是描述变异程度的指标;②由S X=s/n-1可知，S X与S成正比。
n一定时,s 越大，S X越大。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第五章 集中趋势与离散趋势
练习题：
1. 17名体重超重者参加了一项减肥计划，项目结束后，体重下降的重量分别为：
（单位：千克）
12 10 15 8 2 6 14 12 10 12 10 10 11 10 5 10 16 （1）计算体重下降重量的中位数、众数和均值。
（2）计算体重下降重量的全距和四分位差。
（3）计算体重下降重量的方差和标准差。
解：
(1)○1中位数：
对上面的数据进行从小到大的排序：
M d 的位置＝
2
=9，数列中从左到右第9个是10，即M d ＝10。
○2众数：
绘制各个数的频数分布表：
“10”的频数是6，大于其他数据的频数，因此众数M O =“10” ○3均值：
18.1016
521
=+⋯++=
=
∑=n
n
x
X n
i i
（2）○1全距：R ＝max(x i )-min(x i )=16-2=14 ○2四分位差：
根据题意，首先求出Q 1和Q 3的位置：
Q 1的位置＝41+n ＝4
1
17+=，则Q 1=8+×(10-8)=9 Q 3的位置＝4)1(3+n ＝4
)
117(3+⨯=,则Q 3=12+×(12-12)=12
Q= Q 3- Q 1=12-9=3 （3）○1方差：
2
21
222
()
1
(210.18)(510.18)(1610.18) 171
=12.404
n
i
i x x S n =-=
--+--=-∑+?+
○2
标准差： 3.52S ===
2.下表是武汉市一家公司60名员工的省（市）籍的频数分布：
省（市）籍
频数（个）
湖北 28 河南 12 湖南 6 四川 6 浙江 5 安徽
3
（1）根据上表找出众值。
（2）根据上表计算出异众比率。
解： (1)“湖北”的频数是28，大于其他省（市）籍的频数，因此众数M O =“湖北” (2)异众比率的计算公式为： mo
r n f V n
-=
（ n 代表总频数，mo f 代表众数的频数） 其中n=60，mo f =28，则： 6028
0.5360
r V -==
3.某个高校男生体重的平均值为58千克，标准差为6千克，女生体重的平均值
为48千克，标准差为5千克。
请计算男生体重和女生体重的离散系数，比较男
生和女生的体重差异的程度。
解：计算离散系数的公式：
%100⨯=
X
S
CV 男生体重的离散系数：
%34.10%10058
6
=⨯=
CV 女生体重的离散系数：
%42.10%10048
5
=⨯=
CV 男生体重的离散系数为%，女生体重的离散系数为%,男生体重的差异程度比女生要稍微小一些。
4.在某地区抽取的120家企业按利润额进行分组，结果如下：
按利润额分组（万
元） 企业数 200——299 19 300——399 30 400——499 42 500——599 18 600——699 11 合计
120
（1）计算120家企业利润额的中位数和四分位差。
（2）计算120家企业利润额的均值和标准差。
解：
(1) ○1 中位数M d 的位置＝
5.602
1
12021=+=+n ，M d 位于“400—499”组， L=，U ＝，cf (m-1)=49，f m =42，n ＝120，代入公式得
)(2)1(L U f cf n L M m m d --+=-＝120
492399.5(499.5399.5)425.6942
-+⨯-=
职工收入的中位数为元。
○2336.17)5.2995.399(3019
41205.299)(4111111=-⨯-+=--+=L U f cf n L Q 497.12)5.3995.499(42
49412035.399)(43333333=--⨯+=--+
=L U f cf n L Q 四分位差31497.12336.17160.95Q Q Q =-=-= (2)○1均值：
1
199.5299.5299.5399.5399.5499.5499.5599.5599.5699.5
1930421811
22222120
51140 =
120 =426.17
k
i i
i M
f
X n
=+++++⨯+⨯+⨯+⨯+⨯=
=
∑
○
2标准差： 48
.116119
67
.1614666112011)17.4265.649(18)17.4265.549(42)17.4265.449(30)17.4265.349(19)17.4265.249(1
)(222221
2==
-⨯-+⨯-+⨯-+⨯-+⨯-=
--=
∑=n f
x M
s n
i i
5.根据武汉市初中生日常行为状况调查的数据（data9），运用SPSS 统计被调查的初中生平时一天做作业时间（c11）的众数、中位数和四分位差。
解：《武汉市初中生日常行为状况调查问卷》：
C11 请你根据自己的实际情况，估算一天内在下面列出的日常课外活动上所花的时间大约为（请填写具体时间，没有则填“0”） 平时（非节假日）： 1)做作业_______小时 SPSS 操作步骤如下：
○
1依次点击Analyze →Descriptive Statistics →frequencies ，打开如图5-1（练习）所示的对话框。
将变量“平时一天做作业时间（c11a1）”，放置在Variables 栏中。
图5-1（练习） Frequencies对话框
○2单击图5-1（练习）中Frequencies对话框中下方的Statistics（统计量）按钮，打
开如图5-2（练习）所示的对话框。
选择Quartiles（四分位数）选项，Median（中位数）
Continue按钮，返回到上一级对话框。
选项和Mode（众数）选项。
点击
表5-1 平时初中生一天做作业时间的中位数、众值和四分位差
N Valid517
Missi
9
ng
Median
Mode
Percen
25
tiles
50
75
从上表可以看出，平时初中生一天做作业时间的中位数是小时，众数是2小时，四分位差是1(即个小时。
6.根据武汉市初中生日常行为状况调查的数据（data9），运用SPSS分别
统计初
中生月零花钱的均值和标准差，并进一步解释统计结果。
解：《武汉市初中生日常行为状况调查问卷》：
F1 你每个月的零用钱大致为___________元。
SPSS操作的步骤如下：
○1依次点击Analyze→Descriptive Statistics→frequencies，打开如图5-3（练习）所示的对话框。
将变量“每个月的零花钱（f1）”，放置在Variables栏中。
图5-3（练习） Frequencies对话框
○2单击图5-3（练习）Frequencies对话框中下方的Statistics（统计量）按钮，打开
如图5-4（练习）所示的对话框。
选择Mean（均值）选项和(标准差)选项。
点击Continue按钮，返回到如图5-3（练习）所示的对话框。
图5-4（练习） Frequencies ：Statistics 统计分析对话框 ○
3点击OK 按钮，SPSS 将输出如表5-2（练习）所示的结果。
表5-2（练习） 初中生月零用钱的均值和标准差
Stat istics
你每个月的零用钱大致为_
49828109.80114.200
Valid
Missing
N Mean
Std. Deviation
从表5-2（练习）可以看出，“初中生月零用钱”的均值为元，标准差为元。