高等数学:第十二讲 空间曲面及其方程--柱面、旋转曲面 一
空间直角坐标系曲面是柱面得方程

空间直角坐标系曲面是柱面的方程一、概述空间直角坐标系是解析几何中的重要概念,其中曲面是曲线在三维空间中的延伸,而柱面是一种特殊的曲面。
在解析几何中,研究空间直角坐标系曲面的方程是一项重要的课题,本文将重点介绍空间直角坐标系中柱面的方程。
二、柱面的定义在空间直角坐标系中,柱面是由一直线(轴线)和平行于此直线的所有直线(侧面直线)组成的集合。
简单来说,柱面就是平行于同一直线的无数直线在三维空间中形成的曲面。
在数学上,柱面可以用方程表示,方程的形式与柱面的特性密切相关。
三、空间直角坐标系中柱面的一般方程1. 一般方程形式空间直角坐标系中柱面的一般方程形式为:Ax^2 + By^2 = 2Fxy + 2Gx + 2Hy + C其中A、B、F、G、H、C为常数,且A、B不全为零。
2. 方程的几何意义这一般方程实际上描述了一个二次曲面在空间中的形状。
当A、B、F、G、H、C都为实数时,这个方程表示了一个实数系数的二次曲面,它可以是一个椭圆柱面、双曲柱面或抛物柱面。
四、求解柱面的方程空间直角坐标系中的柱面方程可以通过以下步骤求解:1. 根据柱面的特性确定方程的一般形式。
2. 根据所给的条件,代入方程中的系数,得出准确的柱面方程。
五、实际应用空间直角坐标系中柱面的方程在实际生活中有许多应用。
在建筑设计中,通过对立体图形的分析,可以使用柱面方程来描述建筑物的柱状结构,在工程设计中也可以用柱面方程描述柱状物体的形状。
在数学建模中,柱面方程的求解可以帮助我们更好地理解和分析实际问题。
六、总结空间直角坐标系曲面是柱面的方程是解析几何中的重要内容,通过理解柱面的定义和特性,我们可以掌握求解柱面方程的方法,并且了解柱面方程在实际应用中的意义。
在学习和应用解析几何的过程中,深入研究空间直角坐标系曲面是柱面的方程,对于提高数学建模和工程设计的能力也是十分有益的。
七、参考文献[1] 董西立.解析几何[M].北京:高等教育出版社,2006.[2] 高等数学教研组.高等数学[M].北京:高等教育出版社,2010.八、进一步探讨柱面的方程1. 柱面的参数方程除了一般方程外,柱面也可以用参数方程表示。
旋转曲面、柱面和二次曲面

旋转曲面、柱面和二次曲面一、旋转曲面定义 一条曲线C 绕一条直线l 旋转所得的曲面称为旋转曲面。
l 称为轴,C 称为母线。
设旋转轴为z 轴,母线C 在yOz 平面上,其方程为⎩⎨⎧==00),(x z y f ,则旋转曲面的方程为0),(22=+±zy x f 。
坐标平面上的一条曲线绕该坐标面上的一条坐标轴旋转所得旋转曲面方程的求法:在该曲线在坐标平面上的方程中,保留与旋转轴同名的变量不动,而把另一个变量换成与旋转轴不同名的另两个变量的平方和的平方根。
例1 母线⎩⎨⎧==02:2x pzy C 绕z 轴旋转所得的旋转曲面方程为pz y x 222=+,这个曲面称为旋转抛物面。
例 2 母线⎪⎩⎪⎨⎧==-01:2222y c z a x C 绕z 轴旋转所得旋转曲面方程为122222=-+c z a y x ,这个曲面称为旋转单叶双曲面;绕x 轴旋转所得旋转曲面方程为122222=+-cz y a x 这个曲面称为旋转双叶双曲面。
二、柱面定义 一条直线l 沿着一条空间曲线C 平行移动所形成的曲面称为柱面。
l 称为母线,C 称为准线。
定理 在空间直角坐标系中,只含两个元的三元方程所表示的曲面是一个柱面,它的母线平行于所缺元的同名坐标轴。
椭圆柱面:12222=+b y a x 双曲柱面:12222=-by a x 抛物柱面:px y 22=三、二次曲面(1) 椭圆锥面:22222z b y a x =+ (2) 椭球面:1222222=++cz b y a x(3) 单叶双曲面:1222222=-+c z b y a x (4) 双叶双曲面:1222222=--cz b y a x(5) 椭圆抛物面:z b y a x =+2222 (6) 双曲抛物面:z by a x =-2222。
空间几何旋转曲面方程记忆口诀

空间几何旋转曲面方程记忆口诀空间几何旋转曲面方程记忆口诀一、引子在学习空间几何的过程中,我们经常会遇到旋转曲面方程这一内容。
它们在三维空间中呈现出各种不同的形态,对于我们理解和掌握空间几何的知识至关重要。
但是,由于其复杂的形式和多样的变化,我们往往会感到困惑和不知所措。
本文将结合口诀的形式,带领大家逐步记忆和理解空间几何旋转曲面方程,希望对大家的学习能够有所帮助。
二、空间几何旋转曲面简介在空间几何中,旋转曲面是指直线或者曲线绕着一条轴线旋转而形成的曲面。
它们可以分为圆锥曲面、双曲面、抛物面等多种类型,每种类型又有不同的特点和方程形式。
而要深入理解和掌握这些旋转曲面的方程,我们首先需要记忆它们的具体形式和特点。
三、提出口诀为了更好地帮助大家记忆空间几何旋转曲面的方程,我特意设计了如下口诀,希望能够带给大家一些帮助:“圆锥曲面轴中心,双曲面两异心。
抛物面退化记,口诀带你追。
”四、口诀解读1. 圆锥曲面轴中心:圆锥曲面的方程一般形式为:\( \frac{x^2}{a^2} + \frac{y^2}{b^2} - \frac{z^2}{c^2} = 0 \)当圆锥曲面的轴与坐标轴重合时,即轴线通过空间坐标系的原点时,称之为轴中心圆锥曲面。
2. 双曲面两异心:双曲面的方程有两种形式,一般的双曲面方程为:\( \frac{x^2}{a^2} + \frac{y^2}{b^2} - \frac{z^2}{c^2} = 1 \)当双曲面有两个焦点且与坐标轴相交时称之为双曲面两异心。
3. 抛物面退化记:抛物面的一般方程为:\( z = ax^2 + by^2 \)当抛物面变化成简单曲线的时候,我们称之为抛物面退化。
五、口诀应用以上口诀为大家概括了圆锥曲面、双曲面和抛物面的方程形式和特点。
我们可以根据这些口诀,快速记忆和掌握各类旋转曲面的方程,帮助我们更好地理解和应用空间几何的知识。
六、个人观点对于空间几何旋转曲面方程的记忆,我认为口诀是一种非常有效且有趣的方式。
空间曲面及其方程

旋转面的方程 z
f ( y, z ) 0 曲线 C 绕 z轴 x 0
C
o
y
旋转面的方程 z
f ( y, z ) 0 曲线 C x 0
.
绕 z轴
C
o
y
x
旋转面的方程 z
f ( y, z ) 0 曲线 C x 0
旋转一周得旋转曲面 S
绕 z轴
顶点在原点的圆锥面称为正圆锥面。
试建立顶点在原点, 旋转轴为z 轴, 半顶角为 的圆锥面方程.
z
L
解: 在yoz面上直线L 的方程为
绕z 轴旋转时,圆锥面的方程为
M (0, y, z )
y
两边平方
x
z2 a2 ( x2 y2 )
正圆锥面:
x2 y2 z2
x2 y2 z2 2 2 2 a b c
过球面一点,且与过这点的半径垂直的平面 成为切平面,该点称为切点。
例 求过点 (1,2,5) 且与3个坐标面相切的球面方 程。
解: 显然整个球面在同一卦限, 又由于(1,2,5)在第一卦限,故该球面在 第一卦限。
设球心为 ( u, v , w ),则球面到3个坐标面的距离 为 u, v , w .由条件知 uvw
2
2
y2 x2 z2 绕 y 轴的曲面方程为: 2 1 2 b c x y z 2 1 绕 z 轴的曲面方程为: 2 b c
2 2 2
3 锥面 以直线通过一定点, 一条固定曲线移动所
z
产生的曲面成为锥面。
动直线 定点 固定线 母线 顶点
x 顶点 0 y
准线
准线
准线为圆周的锥面称为圆锥面。
柱面锥面和旋转曲面ppt课件

.
S
建立旋转曲面的方程:
如图
得方程
规律:一般地,当坐标面上的曲线绕此坐标面里的一个坐标轴旋转时,为求得旋转曲面的方程,只需将曲线方程保留和旋转轴同名的坐标,以其余两坐标平方和的平方根代替方程中的另一个坐标.
例3.1.6 将圆
绕Z轴旋转,求所得旋转曲面的方程.
解:所求旋转曲面的方程为:
l
M1
S
旋转曲面又可看作以轴 l 为连心线的一族纬圆生成的曲面
特例--- 以直线为母线的旋转面
母线和轴共面时
圆柱面 (母线和轴线平行)
圆锥面 (母线和轴线相交 而不垂直)
平面 (母线和轴线正交)
母线和轴线异面且直母线 与轴线不垂直呢?
母线不是经线
单叶旋转双曲面
解:设P(x1,y1,z1)是母线上的任意点,因为旋转轴通过原点,所以过P的纬圆方程是:
(母线平行于Y轴的椭圆柱面)
(母线平行于x轴的双曲柱面)
(母线平行于y轴的抛物柱面)
注:上述柱面的方程都是二次的,都称为二次柱面。
1、锥面的概念
定义3.1.3 在空间通过一定点且与定曲线相交的一族直线所生成的曲面叫做锥面,这些直线都叫做锥面的母线,那个定点叫做锥面的顶点,定曲线叫做锥面的准线。
补充:
曲线 C
C
绕 z 轴
3、母线在坐标面而旋转轴为坐标轴的旋转曲面
曲线 C
C
绕z 轴
曲线 C
旋转一周得旋转曲面 S
C
S
M
N
z
P
y
z
o
绕 z轴
f (y1, z1)=0
M(x,y,z)
.
S
特殊曲面及其方程--柱面、锥面、旋转面知识讲解

特殊曲面及其方程--柱面、锥面、旋转面引言空间解析几何所研究的曲面主要是二次曲面。
但是也可以研究一些非二次特殊曲面。
本论文中将利用直线或曲线适合某几何特征来建立一些曲面的方程。
主要讨论由直线产生的柱面和锥面,曲线产生的旋转曲面这三大类。
1.柱面定义1:一直线平行于一个定方向且与一条定曲线Γ相交而移动时所产生的曲面叫做柱面(图1),曲线Γ作叫做准线。
构成柱面的每一条直线叫做母线。
显然,柱面的准线不是唯一的,任何一条与柱面所有母线都相交的曲线都可以取做柱面的准线,通常取一条平面曲线作为准线。
特别地,若取准线Γ为一条直线,则柱面为一平面,可见平面是柱面的特例。
下面分几种情形讨论柱面的方程。
1.1 母线平行于坐标轴的柱面方程选取合适的坐标系,研究对象的方程可以大为化简。
设柱面的母线平行于z 轴,准线为Oxy 面上的一条曲线,其方程为:(),00f x y z =⎧⎪⎨=⎪⎩图1u v又设(),,P x y z 为柱面上一动点(图2),则过点P 与z 轴平行的直线是柱面的一条母线,该母线与准线Γ的交点记为(),,0M x y ,因点M 在准线上,故其坐标应满足准线方程,这表明柱面上任一点(),,P x y z 的坐标满足方程(),0f x y =反过来,若一点(),,P x y z 的坐标满足方程(),0f x y =,过P 作z 轴的平行线交Oxy 面于点M ,则点M 的坐标(),,0x y 满足准线Γ的方程(),0,0f x y z ==,这表明点M 在准线Γ上,因此直线MP 是柱面的母线 (因为直线MP 的方向向量为{}{}0,0,||0,0,1z ),所以点P 在柱面上。
综上所述,我们有如下结论:母线平行上于z 轴,且与Oxy 面的交线为(),0,0f x y z ==的柱面方程为:(),0f x y = (1)它表示一个无限柱面。
若加上限制条件a z b ≤≤,变得它的一平截段面。
同理,母线平行于x 轴,且与Oyz 面的交线为(),0,0g y z x ==的柱面方程为(),0g y z =;母线平行于y 轴,且与Ozx 面的交线为(),0,0h x z y ==的柱面方程为(),0h x z =。
柱面锥面旋转曲面和平面

o b
y
将双曲线
z
y2 z2 2 2 1 :b c x 0 绕 轴旋转
z
o b
y
.
x2 y2 z2 2 2 1 2 b b c
单叶旋转双曲面
x
y
例 2 将双曲线 y2 z2 2 2 1 :b c x 0
b
绕
y
轴旋转
0
z
将双曲线
y2 z2 2 2 1 :b c x 0
z 1
0
1
y
x
–1
平面的一般方程
定理 空间中任一平面的方程都可以表示成一 个关于变量 x,y,z 的一次方程;反过来,每一 个关于变量 x,y,z 的一次方程都表示一个平面, Ax+By+Cz+D=0 叫做平面的一般方程。
几种特殊情形讨论:
ⅰ)当且仅当 D=0 , Ax+By+Cz=0 平面通过原点。
l
S
旋转曲面方程的表示: 一般地,当坐标面上的曲线绕此坐标面里的 一个坐标轴旋转时,为求得旋转曲面的方程,只 需将曲线方程保留和旋转轴同名的坐标,以其余 两坐标平方和的平方根代替方程中的另一个坐标
例 1 将双曲线
y2 z2 2 2 1 :b c x 0
绕
z
z 轴旋转
x, y, z 0 叫 次齐次方程.
f x, y,叫做 z
锥面的判定定理
定理 一个关于 x, y, z 的(正数次)齐次方程 总表示顶点在坐标原点的锥面。(反之亦然) 推论 关于 x x0 , y y0 , z z0 的(正数次)
齐次方程表示顶点 在 x0 , y0 , z0 的锥面(反之 亦然)
曲面及其方程 柱面、锥面、旋转曲面

机动
目录
上页
下页
返回
结束
二、柱面
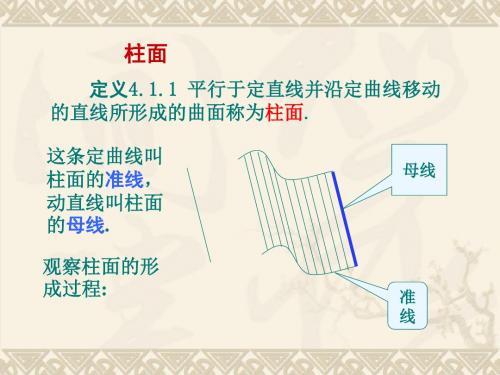
定义 平行于定直线并沿定曲线 C移动的直线 L 所形成的曲面称为柱面. 这条定曲线 C 叫柱面的准线 ,动直线 L 叫 柱面的母线. 观察柱面的形 成过程:
播放
机动
目录
上页
下页
返回
结束
考察方程 F(x,y)=0 F(x,y)=0表示母线平行于z轴的柱面
(不含z)
z
0 2
过原点和椭圆上任一点的直线的方向向量为 v {a cos , b sin , c }
机动
目录
上页
下页
返回
结束
过原点和椭圆上任一点的直线族方程为:
x0 y0 z0 t a cos b sin c
即
x (a cos )t y (b sin )t z ct
y
x G ( y , z ) 0 准线 是 yoz 面上的曲线 z x 0 方程 H ( z , x ) 0 表示 柱面, l3 母线 平行于 y 轴; H ( z, x) 0 x 准线是 xoz 面上的曲线 y 0
机动 目录 上页 下页 返回 结束
y
椭圆柱面
第六节
第七章
曲面及其方程
一、基本概念 二、柱面、锥面、旋转曲面 三、二次曲面
机动
目录
上页
下页
返回
结束
一、基本内容
曲面方程的定义:
如果曲面S 与三元方程 F ( x , y , z ) 0 有下述关系:
(1) 曲面S 上任一点的坐标都满足方程;
(2) 不在曲面S 上的点的坐标都不满足方程;
那么,方程 F ( x , y , z ) 0 就叫做曲面 S 的 方程,而曲面 S 就叫做方程的图形.
高等数学空间曲面各种类型及方程

高等数学是大学数学课程中的一门重要学科,其中涵盖了许多复杂的数学概念和理论。
其中,空间曲面是高等数学中的一个重要概念,它在数学、物理学、工程学等领域中都有着广泛的应用。
本文将系统地介绍高等数学中空间曲面的各种类型及其方程。
一、空间曲面的定义空间曲面指的是三维空间中的曲线的集合,也就是说,它是由参数方程或者隐函数方程所描述的。
在数学中,空间曲面通常可以用下面的方程形式来表示:1. 参数方程形式:$P(x, y, z) = (x(t), y(t), z(t)), \alpha < t < \beta$2. 隐函数方程形式:$F(x, y, z) = 0$二、曲面的分类根据曲面的性质和方程的形式,空间曲面可以分为多种类型。
下面将分别介绍常见的曲面类型及其方程。
1. 锥面锥面是一种由一条直线(母线)绕着一个固定点(顶点)旋转而成的曲面。
它的方程可以用参数方程形式表示为:$\begin{cases}x = at \\y = bt \\z = ct\end{cases}$其中,a、b、c为常数。
2. 圆锥曲面圆锥曲面是由一条固定直线(母线)和一个固定点(焦点)相对应的点所生成的曲面。
其方程可以用隐函数方程表示为:$x^2 + y^2 = z^2$3. 圆柱面圆柱面是由一条曲线(母线)沿着平行于一条直线轴线运动而形成的曲面。
其方程可以用参数方程形式表示为:$\begin{cases}x = a\cos(t) \\y = b\sin(t) \\z = ct\end{cases}$其中,a、b、c为常数。
4. 圆锥面圆锥面是由一条圆锥曲线绕着其中心轴旋转而形成的曲面。
其方程可以用参数方程形式表示为:$\begin{cases}x = a\cos(t) \\y = b\sin(t) \\z = \pm\sqrt{x^2 + y^2}\end{cases}$其中,a、b为常数。
5. 双曲面双曲面是一种具有双曲线截面的曲面。
解析几何_柱面、旋转曲面与二次曲面
x z (2)xOz 面上双曲线 2 2 1分别绕 x 轴和 z 轴; a c x x
绕 x 轴旋转
2
2
x2 y2 z2 1 2 2 a c
旋转双叶双曲面
y
o
z
o y
z
x z (1)xOz 面上双曲线 2 2 1 分别绕 x 轴和 z 轴; a c
绕 z 轴旋转
z y o
H x, y 0 R y, z 0 T x, z 0 或 或 z0 x0 y0
例 已知两球面的方程为
x y z 1 及 x y 1 z 1 1
2 2 2 2 2 2
求它们的交线C在xOy面上的投影方程.
z 轴的柱
面,其准线为xoy 面上曲线C . (其他类推)
实 例
y z 2 1 2 b c x2 y2 2 1 2 a b 2 x 2 pz
2
2
椭圆柱面 母线// x 轴 双曲柱面母线// z 轴 抛物柱面母线// y 轴
1. 椭圆柱面
x y 2 1 2 a b
z
2 2
2. 双曲柱面
又由于M1在母线上,所以又有:
x1 y1 z1 1 2 1 0
即 x1=2y1,z1=1,消去x1,y1,z1得所求旋转曲面的方程: 2(x2+y2+z2)-5(xy+yz+zx)+5(x+y+z)-7=0。
下面特殊的旋 转曲面
f ( y, z ) 0 曲线 C 绕 z轴 x 0
2
2
x y z 2 1 2 a c
2 2 2
旋转单叶双曲面
高等数学-柱面与旋转曲面PPT课件

x2 y2 2 pz 旋转抛物面
三、小结
曲面方程的概念 F( x, y, z) 0. 旋转曲面的概念及求法. 柱面的概念(母线、准线).
思考题
指出下列方程在平面解析几何中和空 间解析几何中分别表示什么图形?
(1) x 2;
(2) x2 y2 4;
(3) y x 1.
思考题解答
方程
一周所形成的;
7、 曲 面 (z a)2 x2 y2 是 由 ______________ 绕 _____轴旋转一周所形成的;
8、 方程 x 2在平面解析几何中表示___________在 空间解析几何中表示___________________;
9、 方 程 x2 y2 4 在 平 面 解 析 几 何 中 表 示 _______________ , 在 空 间 解 析 几 何 中 表 示
2、以点O(2 ,2 , 1)为球心,且通过坐标原点的球面
方程是_______________;
3、球面: x2 y2 z2 2x 4 y 4z 7 0的球心是
点___________,半径 R __________;
4、 设曲面方程
x2 a2
+
y2 b2
+
z c
2 2
=1,当a
b时,曲面可由
yoz 坐标面上的已知曲线 f ( y, z) 0绕z 轴旋
转一周的旋转曲面方程.
同理: yoz 坐标面上的已知曲线 f ( y, z) 0 绕 y 轴旋转一周的旋转曲面方程为
f y, x2 z2 0.
例1 将下列各曲线绕对应的轴旋转一周,求 生成的旋转曲面的方程.
(1)双曲线
x2 a2
xoz 面上以曲线________________绕_______轴
空间曲面及方程

曲面在空间解析几何中被看成是点的几何轨迹.
曲面方程的定义:
如果曲面S 与三元方程F ( x , y , z ) 0 有下述关系:
(1 )曲面 S 上任一点的坐标都满足方程; (2 )不在曲面 S 上的点的坐标都不满足方程; 那么,方程 F ( x , y , z ) 0 就叫做曲面S 的方程, 而曲面 S 就叫做方程的图形.
例如方程 在xoy面上, 表示的曲面 :
z
M
1
o C 表示准线圆C, M
y
在圆C上任取一点 M 1 ( x, y,0) , 过此点作 x 平行z轴的直线l ,对任意 z ,点 M ( x, y, z )
的坐标也满足方程 x y R
一切直线所形成的曲面称为圆 柱面.其上所有点的坐标都满足此方程, 故在空间
2 2 2
化简得所求方程 2 x 6 y 2 z 7 0.
例2. 求通过 x 轴和点( 4, – 3, – 1) 的平面方程. 解: 因平面通过 x 轴 , 故 A D 0
设所求平面方程为
By Cz 0
代入已知点 (4 , 3 , 1) 得
化简,得所求平面方程
f y,
x 2 z 2 0.
例1 将下列各曲线绕对应的轴旋转一周,求 生成的旋转曲面的方程.
x z x 轴和 z 轴; (1)双曲线 2 2 1 分别绕 a c
x2 y2 z2 绕 x 轴旋转 2 1 2 a c x y z 2 1 绕 z 轴旋转 2 a c
• A x+C z+D = 0 表示 平行于 y 轴的平面;
• A x+B y+D = 0 表示 平行于 z 轴的平面; • C z + D = 0 表示 平行于 xOy 面 的平面; • A x + D =0 表示 平行于 yOz 面 的平面; • B y + D = 0 表示 平行于 zOx 面 的平面.
柱面锥面旋转曲面与二次曲面

x0
绕它的对称轴旋转的旋转曲面方程为
x 2 y 2 2 pz
曲面(4.3-5)叫做旋转抛物面(图4-11)。
例5 : 将圆
( y b) 2 z 2 a 2 : , (b a 0) x0
(20)
(图4-12(a))绕 z 轴旋转,求所得旋转曲面的方程。 解:因为绕 z 轴旋转,所以在方程( y b) 2 z 2 a 2 中保留 z 不变,而 y 用 x 2 y 2 代,就得将圆(20)绕 z 轴旋转而成的旋转曲面的方程为
x0
绕虚轴旋转的旋转曲面的方程为
x2 y 2 z 2 2 2 1 2 b b c
z
绕实轴旋转的旋转曲面方程为
y2 x2 z 2 1 b2 c 2 c2
x
y
曲面(4.3-3)叫做单叶旋转双曲面(图4-9),曲面 (4.3-4)叫做双叶旋转双曲面(图4-10)。 2 y 例4 将抛物线 2 pz
X ( x x1 ) Y ( y y1 ) Z ( z z1 ) 0 ( x x )2 ( y y )2 ( z z )2 0 0 0 ( x x )2 ( y y )2 ( z z )2 1 0 1 0 1 0
