人教版九年级数学上册初三数学全册同步讲义定稿
新人教版初中数学九年级上册全册教案

新人教版初中数学九年级上册全册教案一. 教材内容概述本教案为新人教版初中数学九年级上册的全册教案。
该教材主要包括以下几个模块:- 整式与分式- 历史与人物- 概率与统计- 等比数列- 性质与运算二. 教学目标通过本教材的研究,学生应达到以下数学能力和知识:1. 掌握整式与分式的基础概念和运算方法;2. 了解数学发展历史和相关数学人物的贡献;3. 理解和应用概率与统计的基本概念与方法;4. 掌握等比数列的性质和求解方法;5. 熟悉数的性质与数的运算法则。
三. 教学重点与难点1. 教学重点:整式与分式的基础概念与运算方法,概率与统计的基本概念和应用,等比数列的性质和求解方法。
2. 教学难点:整式与分式的运算方法,概率与统计的应用,等比数列的推导和求解。
四. 教学方法和手段本教案将采用以下教学方法和手段,以培养学生的数学思维和解决问题能力:1. 导入法:通过引入学生已有的数学知识,激发学生对新知识的兴趣;2. 探究法:组织学生进行探索性研究,培养学生的自主研究和合作研究能力;3. 归纳法:引导学生总结、归纳已学的数学知识,提高他们的综合运用能力;4. 实践法:设计适当的练和实践任务,帮助学生将所学的数学知识应用到实际问题中。
五. 教学内容安排根据教材的章节划分,本教案将按照以下方式安排教学内容:- 第一单元:整式与分式- 第二单元:历史与人物- 第三单元:概率与统计- 第四单元:等比数列- 第五单元:性质与运算六. 教学评价方法为了准确评价学生的数学研究情况,本教案将采用以下评价方法:1. 测试:通过书面测试和口头测试,检查学生对教学内容的掌握情况;2. 实践任务评价:评估学生在实际问题中应用数学知识的能力;3. 个人报告评价:鼓励学生进行主题研究,并评估他们的表达和分析能力。
七. 教学资源准备为了有效开展教学活动,本教案将准备以下教学资源:1. 教材:新人教版初中数学九年级上册教材;2. 录像资料:教学视频和相关实验视频等;3. 教学工具:计算器、几何工具、教学演示软件等。
新人教版九年级数学上册讲义

九年级上册数学讲义姓名:电话:第二十一章 一元二次方程1、 一元二次方程 方程中只含有一个未知数,而且未知数的最高次数是2的方程,一般地,这样的方程都整理成为形如ax bx c a 200++=≠()的一般形式,我们把这样的方程叫一元二次方程。
其中ax bx c 2,,分别叫做一元二次方程的二次项、一次项和常数项,a 、b 分别是二次项和一次项的系数。
如:24102x x -+=满足一般形式ax bx c a 200++=≠(),2412x x ,,-分别是二次项、一次项和常数项,2,-4分别是二次项和一次项系数。
注:如果方程中含有字母系数在讨论是否是一元二次方程时,则需要讨论字母的取值范围。
●夯实基础例1 把下列方程先化成一元二次方程的一般形式,再写出它的二次项系数,一次项系数和常数项。
(1)272y y =-(2)()()512152y y y +-=-(3)()m x n mx x 2210++-=(是未知数)例2 已知关于x 的方程22(2)1a x ax x --=-是一元二次方程,求a 的取值范围.例3 若一元二次方程222(2)3(15)40m x m x m -+++-=的常数项为零,则m 的值为_________.●能力提升例4若方程(m-1)x 2+ x=1是关于x 的一元二次方程,则m 的取值范围是( ) A .m≠1 B .m≥0 C .m≥0且m≠1 D .m 为任何实数●培优训练例5 m 为何值时,关于x 的方程2((3)4m m x m x m -+=是一元二次方程.第一讲 一元二次方程的定义例6关于x 的方程(m+3)x m2-7+(m-3)x+2=0是一元二次方程,则m 的值为例7(2000•兰州)关于x 的方程(m 2-m-2)x 2+mx+1=0是一元二次方程的条件是( )A .m≠-1B .m≠2C .m≠-1或m≠2D .m≠-1且m≠2●课后练习1、m 为何值时,关于x 的方程2((3)4m m x m x m -+=是一元二次方程.2、已知关于x 的方程22(2)1a x ax x --=-是一元二次方程,求a 的取值范围.3、已知关于x 的方程22()(2)x a ax -=-是一元二次方程,求a 的取值范围.4、若2310a b a b x x +--+=是关于x 的一元二次方程,求a 、b 的值.5、若一元二次方程222(2)3(15)40m x m x m -+++-=的常数项为零,则m 的值为________(1)直接开平方法形如x m m 20=≥()的方程都可以用开平方的方法写成x m =±,求出它的解,这种解法称为直接开平方法。
人教版九年级数学上册同步讲义一元二次方程解法

初中数学试卷金戈铁骑整理制作2017 年九年级数学上册同步讲义一元二次方程解法一、选择题:1、若关于 x 的方程2x m-1+ x- m= 0 是一元二次方程,则m为 ()A . 1B . 2C. 3 D . 02、一元二次方程 3x2﹣ 4=﹣ 2x 的二次项系数、一次项系数、常数项分别为()A .3,﹣4,﹣2B .3,﹣ 2,﹣ 4C.3,2,﹣ 4D.3,﹣ 4,03、已知 x= 1 是一元二次方程x2+ mx+n= 0 的一个根,则 m2+ 2mn+n2的值为 ()A . 0B . 1C. 2D. 44、一元二次方程 x2﹣ 2x+m=0总有实数根,则m应满足的条件是 ()A . m>1B . m=1C . m< 1D . m≤15、已知关于 x 的一元二次方程x2+ax+b=0 有一个非零根﹣ b,则 a﹣ b 的值为()A . 1B.﹣1 C . 0D.﹣ 26、以下对方程 2x2-7x - 1=0的变形,正确的选项是 ()A . (x + ) 2=B . (x - ) 2=C. (x - ) 2= D . (x + ) 2=7、一元二次方程 4x2+1=4x 的根的情况是()A .没有实数根B.只有一个实数根C .有两个相等的实数根D .有两个不相等的实数根8、关于 x 的方程( m﹣ 1)x2+2x+1=0 有实数根,则m的取值范围是()A . m≤2B .m< 2C. m< 3 且 m≠ 2D. m≤ 3 且 m≠ 29、用配方法解方程x2- 2x-5= 0 时,原方程应变形为()A . (x + 1) 2= 6B. (x -1) 2= 6C. (x + 2) 2= 9 D . (x - 2) 2= 910、依照下面表格中的对应值:xax2+bx+ c--判断方程ax2+ bx+ c= 0(a ≠ 0, a,b, c 为常数 ) 的一个解 x 的范围是 ()A . 3<x<B . 3.23 <x<C. 3.24 < x< D . 3.25 < x<11、三角形两边的长是 3 和 4,第三边的长是方程x2-10x+21=0 的根,则该三角形的周长为()A .14B.10C.10 或 14D.以上都不对12、关于 x 的方程 x2+2kx+k ﹣ 1=0 的根的情况描述正确的选项是()A . k 为任何实数,方程都没有实数根B . k 为任何实数,方程都有两个不相等的实数根C . k 为任何实数,方程都有两个相等的实数根D .依照 k 的取值不同样,方程根的情况分为没有实数根、有两个不相等的实数根和有两个相等的实数根三种二、填空题:13、一元二次方程的一般形式是,其中一次项系数是.14、关于 x 的方程( m﹣ 2)x|m| +3x﹣ 1=0 是一元二次方程,则m的值为.15、若 x=3 是一元二次方程x2+mx+6=0的一个解,则方程的另一个解是.16、若关于x 的一元二次方程(m﹣ 1) x2+5x+m2﹣ 3m+2=0的常数项为0,则 m的值等于 _______.17、关于 x 的一元二次方程x2﹣ x+m=O没有实数根,则m的取值范围是.2218、已知 m是关于 x 的方程 x - 2x- 3=0 的一个根,则2m- 4m= ______.19、若一元二次方程x2-2x- m=0无实数根,则一次函数y=(m+1)x + m-1 的图像不经过第象限20、若关于x 的一元二次方程kx 2+4x﹣2=0 有两个不相等的实数根,则k 的取值范围是.三、计算题:21、 3x 2+ x- 5= 0;( 公式法 )22、x2+2x-399=0.(配方法)23、解方程: x2﹣ 3x﹣ 4=0.24、解方程:x2+4x﹣7=6x+5.四、解答题:2225、已知:关于x 的方程 x +2mx+m﹣ 1=0(1)不解方程,鉴识方程根的情况;(2)若方程有一个根为 3,求 m的值.26、已知关于x 的一元二次方程kx 2﹣ 3x﹣ 2=0 有两个不相等的实数根.( 1)求 k 的取值范围;( 2)若 k 为小于 2 的整数,且方程的根都是整数,求k 的值.27、求证:不论m为任何实数,关于x 的一元二次方程x2+ (4m+ 1)x + 2m- 1= 0 总有实数根.28、关于 x 的一元二次方程x2+2x+k+1=0 的实数解是x1和 x2.(1)求 k 的取值范围;(2)若是 x1+x 2﹣ x1x2<﹣ 1 且 k 为整数,求 k 的值.29、已知关于x 的一元二次方程(a+c) x2+2bx+(a﹣ c) =0,其中 a、 b、 c 分别为△ ABC三边的长.(1)若是 x=﹣ 1 是方程的根,试判断△ ABC的形状,并说明原由;(2)若是方程有两个相等的实数根,试判断△ABC的形状,并说明原由;(3)若是△ ABC是等边三角形,试求这个一元二次方程的根.参照答案1、 C2、 C3、 B4、 D5、 A6、 B7、 C8、 A9、 B10、 C11、 B12、 b13、,;14、答案为﹣ 2.15、答案为2.16、答案为: 217、18、 619、 120、答案为k>﹣ 2 且 k≠0.21、 x1=,x2=22、 x1=- 21, x2= 1923、解:∵原方程可化为:(x+1)( x﹣ 4) =0,∴ x+1=0 或 x﹣ 4=0,解得, x1=4, x2=﹣ 1.24解:方程整理得: x2﹣ 2x+1=13,即( x﹣ 1)2=13,开方得: x﹣ 1=±,解得: x1=1+, x2=1﹣.25、解:( 1)由题意得, a=1, b=2m, c=m2﹣ 1,22222有两个不相等的实数根;∵△ =b ﹣ 4ac=( 2m)﹣ 4× 1×( m﹣ 1) =4> 0,∴方程 x +2mx+m﹣ 1=02222或 m=﹣ 2.( 2)∵ x+2mx+m﹣ 1=0 有一个根是 3,∴ 3 +2m×3+m﹣ 1=0,解得, m=﹣426、解:( 1)∵关于 x 的一元二次方程kx 2﹣ 3x﹣ 2=0 有两个不相等的实数根,∴△> 0 且 k≠ 0,∴△ =9+8k> 0 且 k≠ 0,∴且 k≠ 0;( 2)∵ k 为小于 2 的整数,由(1)知道且 k≠0,∴ k=﹣1, k=1,∴当 k=﹣1 时,方程﹣ x2﹣ 3x﹣ 2=0 的根﹣ 1,﹣ 2 都是整数,当k=1时,方程x2﹣3x ﹣ 2=0 的根不是整数不吻合题意,综上所述,k=﹣1.2227、=(4m+1)-4(2m-1)=16m+5>0,∴方程总有实数根28、解:( 1)∵方程有实数根,∴△=22﹣ 4(k+1)≥ 0,解得 k≤0.故 K的取值范围是k≤ 0.( 2)依照一元二次方程根与系数的关系,得x1+x2=﹣ 2, x1x2=k+1,x1+x2﹣ x1x2=﹣ 2﹣( k+1).由已知,得﹣2﹣( k+1)<﹣ 1,解得 k>﹣ 2.又由( 1)k≤ 0,∴﹣ 2< k≤ 0.∵ k 为整数,∴ k 的值为﹣ 1 或 0.29、解:( 1)△ ABC是等腰三角形;2原由:∵ x=﹣ 1 是方程的根,∴(a+c)×(﹣ 1)﹣ 2b+( a﹣ c) =0,∴a+c﹣ 2b+a﹣ c=0,∴ a﹣b=0,∴ a=b,∴△ ABC是等腰三角形;( 2)∵方程有两个相等的实数根,∴(2b)2﹣4( a+c)( a﹣ c)=0,∴4b2﹣ 4a2+4c2=0,∴ a2=b2+c2,∴△ ABC是直角三角形;2( 3)当△ ABC是等边三角形,∴(a+c) x +2bx+( a﹣ c) =0,可整理为:222ax +2ax=0,∴ x +x=0,解得: x1=0, x2=﹣1.。
新人教版九年级数学上册全册ppt课件

1.探究因式分解法
你认为该如何解决这个问题?你想用哪种方法解这 个方程?
10x - 4.9x2 = 0
配方法 降 公式法 次
?
x
1
=
0,x
2
=
100 49
1.探究因式分解法
问题3 观察方程 10x - 4.9x2 = 0,它有什么特点? 你能根据它的特点找到更简便的方法吗?
x2 + 6x = -4 x2 + 6x + 9 = -4 + 9 (x + 3)2 = 5
x3 5
移项
两边加 9,左边 配成完全平方式 左边写成完全 平方形式
降次
x 3 5 ,或 x 3 5
解一次方程
x1 3 5, x2 3 5
2.推导求根公式
想一想:以上解法中,为什么在方程③两边加 9? 加其他数可以吗?如果不可以,说明理由.
• 学习重点: 一元二次方程的概念.
1.创设情境,导入新知
思考以下问题如何解决: 1.要设计一座高 2 m 的人体雕像,使它的上部 (腰以上)与下部(腰以下)的高度比,等于下部与全 部(全身)的高度比,求雕像的下部应设计为高多少米?
1.创设情境,导入新知
思考以下问题如何解决: 2.有一块矩形铁皮,长 100 cm,宽 50 cm,在它 的四角各切去一个同样的正方形,然后将四周突出部分 折起,就能制作一个无盖方盒,如果要制作的无盖方盒 的底面积为 3 600 cm2,那么铁皮各角应切去多大的正方 形?
1.复习配方法,引入公式法
问题2 能否用公式法解决一元二次方程的求根问 题呢?
人教版九年级上册数学全册说课稿.ppt

圆是高度对 称的基本图 形,从旋转 角度理解, 可以得到圆 心角、弦、 弧对应相等 的关系,从 轴对称角度 理解,可以 得到垂径定
理。
圆
列举法当中, 画树形图和 列表法是重 点知识,其 中列表法针 对两个因素 多种可能结 果,而树形图
针对三个或多 个因素。
思想方法整合 类比思想
转化思想
数形结合思想
谢谢大家, 希望提出宝贵的建议!
统计与概 率
课题学习
探讨一些具有挑 战性的研究课题, 发展应用数学知 识解决问题的意 识和能力;同时, 进一步加深对相 关数学知识的理 解,认识数学知
识之间的联系。
说教材
1.编写体例
为加深对相关内容的认识 扩大学生的知识面 运用现代信息技术手段学 习
实阅 观验读 察与与 与探思 猜究考 想
回顾与思考 知识结构图
形式展开。
准确把握本节 内容在整个知 识结构中的位 置,以及建立 本节内容的结 构,更有利于 学生掌握知识。
结构性
教师的亲和力, 有利于组织学生 合作探究、自主
学习。
说建议
2.说评价建议
重视学生参与数学活动的过程评价
参与数学活动情况的评价表
学生姓名: 时间:
活动内容:
评价内容 参与活动
主要表现
思考问题
本册内容的位置
一次不等式、组
一元二次(22)
人教版九年级数学上精品讲义
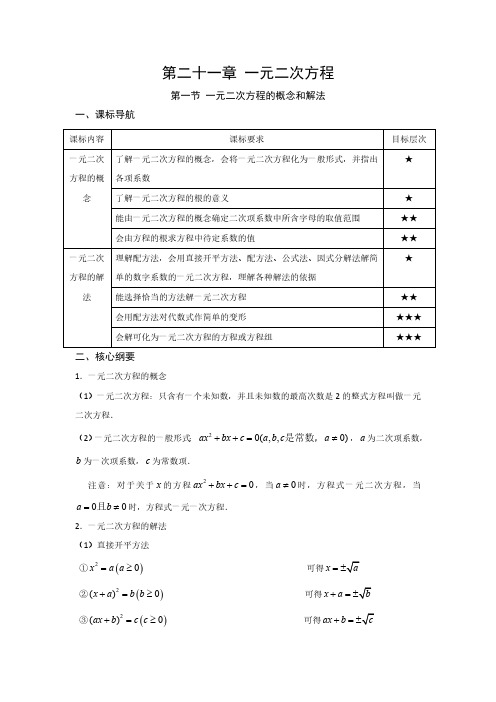
(1) 请你写出两个方程,使每个方程的二次项系数都是 2,且每个方程的 b2 4ac 的值
也都是 1,但每个方程的解与已知的 5 个方程的解都不相同.
(2) 对于一般形式的一元二次方程 ax2 bx c 0 a 0,b2 4ac 0 ,能否作出一个
新的方程 ax2 b'x c' 0 ,使 b2 4ac 与 b'2 4ac' 相等?若能,请写出所作的新 的方程( b' , c' 需用 a , b , c 表示),并说明理由;若不能,也请说明理由.
一、课标导航
第二十一章 一元二次方程
第一节 一元二次方程的概念和解法
课标内容
课标要求
目标层次
一元二次 了解一元二次方程的概念,会将一元二次方程化为一般形式,并指出
★
方程的概 各项系数
念
了解一元二次方程的根的意义
★
能由一元二次方程的概念确定二次项系数中所含字母的取值范围
★★
会由方程的根求方程中待定系数的值
3.一元二次方程解法的灵活运用 直接开平方法,配方法,公式法,因式分解法.在具体解题时,应当根据题目的特点选择适 当的解法. (1)因式分解法:适用于右边为零(或可化为 0),而左边易分解为两个一次因式积的方程, 缺常数项或含有字母系数的方程用因式分解法较为简便,它是一种罪常用的方法. (2)公式法:适用于任何形式的一元二次方程,但必须先将方程化为一般形式,并计算
xn xn' ,其中 n 为正整数,且 a1 1.
(1) x1' x1 的值为________.
(2)当 n 分别取 1、2、…、2013 时,相对应的有 2013 个方程,将这些方程的所有实数根
人教版九年级数学上册 同步讲义 第一讲-一元二次方程(无答案)

2019年秋季九年级数学讲义第一讲一元二次方程的应用一、基础知识归类:(一)、列方程(组)解应用题的一般步骤1、审题;2、设未知数;3、找出相等关系,列方程(组);4、解方程(组);5、检验,作答;(二)、列方程(组)解应用题常见类型题及其等量关系;1、工程问题(1)基本工作量的关系:工作量=工作效率×工作时间(2)常见的等量关系:甲的工作量+乙的工作量=甲、乙合作的工作总量(3)注意:工程问题常把总工程看作“1”,水池注水问题属于工程问题2、行程问题(1)基本量之间的关系:路程=速度×时间(2)常见等量关系:相遇问题:甲走的路程+乙走的路程=全路程追及问题(设甲速度快):同时不同地:甲的时间=乙的时间;甲走的路程–乙走的路程=原来甲、乙相距路程同地不同时:甲的时间=乙的时间–时间差;甲的路程=乙的路程3、水中航行问题:顺流速度=船在静水中的速度+水流速度;逆流速度=船在静水中的速度–水流速度4、增长率问题:常见等量关系:增长后的量=原来的量+增长的量;增长的量=原来的量×(1+增长率);5、数字问题:基本量之间的关系:三位数=个位上的数+十位上的数×10+百位上的数×100(三)、列方程解应用题的常用方法1、译式法:就是将题目中的关键性语言或数量及各数量间的关系译成代数式,然后根据代数之间的内在联系找出等量关系。
2、线示法:就是用同一直线上的线段表示应用题中的数量关系,然后根据线段长度的内在联系,找出等量关系。
3、列表法:就是把已知条件和所求的未知量纳入表格,从而找出各种量之间的关系。
4、图示法:就是利用图表示题中的数量关系,它可以使量与量之间的关系更为直观,这种方法能帮助我们更好地理解题意。
二、题型归类类型一:传播问题(比赛问题)1.有一人患了流感,经过两轮传染后共有121人患了流感,每轮传染中平均一个人传染了几个人?2.参加一次足球联赛的每两队之间都进行一场比赛,共比赛45场比赛,共有多少个队参加比赛?(如果每两队比赛两场呢?)3.某种植物的主干长出若干数目的支干,每个支干又长出同样数目的小分支,主干、支干和小分支的总数是91,每个支干长出多少小分支?4.一个小组有若干人,新年互送贺卡,若全组共送贺卡72张,这个小组共有多少人?类型二:平均增长(下降)率问题变化前数量×(1 x)n=变化后数量1.青山村种的水稻2016年平均每公顷产7200公斤,2018年平均每公顷产8450公斤,求水稻每公顷产量的年平均增长率。
人教版九年级上册数学讲义知识点归纳

九年级上册数学讲义知识点归纳第21章一元二次方程一、学习目标一、明白得一元二次方程的概念二、学会一元二次方程的解法3、了解方程的根与系数的关系4、把握一元二次方程的实际应用二、重点一、一元二次方程一、一元二次方程含有一个未知数(一元),而且未知数的最高次数是2(二次)的整式方程叫做一元二次方程。
二、一元二次方程的一样形式)0(02≠=++a c bx ax ,其中2ax 叫做二次项,a 叫做二次项系数;bx 叫做一次项,b 叫做一次项系数;c 叫做常数项。
二、降次----解一元二次方程1.降次:把一元二次方程化成两个一元一次方程的进程(不管用什么方式解一元二次方程,都是要一元二次方程降次)2、直接开平方式利用平方根的概念直接开平方求一元二次方程的解的方式叫做直接开平方式。
直接开平方式适用于解形如x 2=b 或b a x =+2)(的一元二次方程。
依照平方根的概念可知,a x +是b 的平方根,当0≥b 时,b a x ±=+,b a x ±-=,当b<0时,方程没有实数根。
3、配方式:配方式的理论依照是完全平方公式222)(2b a b ab a +=+±,把公式中的a 看做未知数x ,并用x 代替,那么有222)(2b x b bx x ±=+±。
配方式解一元二次方程的步骤是:①移项、②配方(写成平方形式)、③用直接开方法降次、④解两个一元一次方程、⑤判定2个根是不是实数根。
4、公式法:公式法是用求根公式,解一元二次方程的解的方式。
一元二次方程)0(02≠=++a c bx ax 的求根公式: )04(2422≥--±-=ac b a ac b b x当ac b 42->0时,方程有两个实数根。
当ac b 42-=0时,方程有两个相等实数根。
当ac b 42-<0时,方程没有实数根。
5、因式分解法:先将一元二次方程因式分解,化成两个一次式的乘积等于0的形式,再使这两个一次式别离等于0,从而实现降次,这种解叫因式分解法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
a 0 ,当 x 0 时, y 有是; a 0 ,当 x 0 时, y 有是.
(1)该公司 2006 年盈利多少万元? (2)若该公司盈利的年增长率继续保持不变,预计 2008 年盈利多少万 元?<5 分钟>
1
5.已知关于 x 的两个一元二次方程:
方程: x2 (2k 1)x k 2 2k 13 0 ① 2
方程: x2 (k 2)x 2k 9 0
②
4
(1)若方程①、②都有实数根,求 k 的最小整数值;
(2)若方程①和②中只有一个方程有实数根;则方程①,②中没有实数根
的方程是______(填方程的序号),并说明理由;
(3)在(2)的条件下,若 k 为正整数,解出有实数根的方程的根.<7 分钟>
2
第二十二章 二次函数
22.1 二次函数的性质与解析式
课程导入
当一个正方形的边长是 a,那么它的面积 y 如何用 a 来表示? 如果一个长方形的长是 a,宽是 a+1,那么它的面积 y 如何用 a 来表示? 以上的两个例子得到的关系式你能发现什么特点么? 今天我们就来学习一个初中最重要的函数-----二次函数
第二十四章 圆 ..................................................................................... 78 24.1 圆的基本概念和性质............................................................. 78 24.2 与圆有关的位置关系............................................................. 93 24.3 与圆有关的计算....................................................................111
漫漫学 22.1.1 二次函数的定义及图像
二次函数的定义
一般地,形如的函数,叫做二次函数,其中, x 是自变量,分别是二次 项系数、一次项系数、常数项.
3
【例 1】已知函数 y=(m+2)x m2m 是关于 x 的二次函数,则满足条件的 m 值 为______. 想一想:二次函数的自变量最高次数是多少?系数是否可以为 0? 【练习 1.1】若 y=(m-3) xm23m2 是二次函数,求 m 的值.
9
(6) y 1 x2 如图(
9
ห้องสมุดไป่ตู้); );
).
想一想:二次函数与 a 相关的性质是哪些?与此题的联系是哪个?
与 a 有关的性质二
增减性: a 0 ,在对称轴左侧, y 随 x 的增大而; 在对称轴右侧, y 随 x 的增
大而; a 0 ,在对称轴左侧, y 随 x 的增大而; 在对称轴右侧, y 随 x 的
对称轴:y 轴( x 0 )顶点:原点( 0, 0 )
5
【例 4】二次函数 y=ax2 的图象大致如下,请将图中抛物线字母的序号填入 括号内.
(1)y=2x2 如图( );
(2) y 1 x2 如图( );
2
(3)y=-x2 如图( );
(4) y 1 x2 如图(
3
(5) y 1 x2 如图(
【例 2】若 y=(k-3) xk22 +x2-x+1 是二次函数,求常数 k 的值.
想一想:在上一题中二次函数的定义以及可能出错的地方?观察题目中的二次 项有几项? 【即时检测】 试卷编码:BJGXH—SX090201—SJ01 1.若 y=(k-2) xk22 +4x2-x+1 是二次函数,求常数 k 的值.<2 分钟>
目录
第二十二章 二次函数 ........................................................................... 3 22.1 二次函数的性质与解析式....................................................... 3 22.2 二次函数与方程..................................................................... 21 22.3 二次函数的应用..................................................................... 36
前情回顾:
1.若 (m-2)xm22 x ²-3=0 是关于 x 的一元二次方程,则 m 的值是.<2 分钟>
2. 3x2 x 2 3 0 <2 分钟>
3. x2 3x 28 0<2 分钟>
4.某汽车销售公司 2005 年盈利 1500 万元,到 2007 年盈利 2160 万元,且从 2005 年到 2007 年,每年盈利的年增长率相同.
第二十三章 旋转 ................................................................................. 51 23.1 旋转变换 ................................................................................. 51 23.2 旋转模型 ................................................................................. 64
4
二次函数的作图
“五点作图法”:. 二次函数的图像为. 【例 3】
在同一坐标系中,画出函数 y1 2x2, y2 2(x 2)2, y3 x2 x 1的图像.
想一想:画函数图像有哪些步骤?
22.1.2 二次函数的性质
与 a 有关的性质一
函数形式: y ax2 (a 0)
开口: a 0 ,开口; a 0 ,开口. a 相同 抛物线的相同. a 越大开口越, a 越小开口越.
