热力学函数的基本关系式
合集下载
热力学第一定律总结
298 K时，H2(g)的∆cHmө = -285.83 kJ·mol-1, H2S(g)和 SO2(g)的∆fHmө分别为-20.63 kJ·mol-1和-296.83 kJ·mol-1。 求下列反应在498 K时的∆rUmө。已知水在373 K时的摩 尔蒸发焓∆vapHm (H2O, 373 K) = 40.668 kJ·mol-1. 2H2S (g) + 3O2 (g) = 2SO2 (g) + 2H2O(g)
其中，T2的值由理想气体绝热方程式(pVγ=C)求得。
3、Q的计算 、 的计算
• Q = ∆U – W • 如恒容，Q = ∆U • 如恒压，Q = ∆H
1. 绝热密闭体系里，以下过程的ΔU不等于零的是： A) 非理想气体混合 B) 白磷自燃 C) 乙醚挥发 D) 以上均为0 2.“爆竹声中一岁除，春风送暖入屠苏”。我国 春节有放鞭炮的习俗。在爆竹爆炸的过程中，以 下热力学量的符号表示正确的是(忽略点火时火柴 传递给引线的少量热量) ( ) A) Q<0，W<0，ΔU<0 B) Q<0，W=0，ΔU<0 C) Q=0，W<0，ΔU<0 D) Q=0，W=0，ΔU=0
nN2CV, m(N2)(T-T1) + nCuCV,误二： ∆U =∆UN2 + ∆UCu = 0
nN2CV, m(N2)*(T-T1) + nCuCV, m(Cu)*(T-T2) = 0
正确解法：
∆U =∆UN2 + ∆UCu = ∆UN2 + ∆HCu = 0 nN2CV, m(N2)*(T-T1) + nCuCp, m(Cu)*(T-T2) = 0
• 求火焰最高温度： Qp = 0, ΔH = 0 求火焰最高温度： • 求爆炸最高温度、最高压力：QV = 0, W = 0 求爆炸最高温度、最高压力： =0
热力学函数的基本关系式
dU = TdS－ pdV
(1-108)
dH = TdS + Vdp
(1-109)
dA = －SdT－ pdV
(1-110)
dG = －SdT + Vdp
(1-111)
式(1-108)，(1-109)，(1-110)，(1-111)称为热力学基本方程
dU = TdS－ pdV dH = TdS + Vdp dA = －SdT－ pdV dG = －SdT + Vdp
常用的是式(1-120)及式(1-121)，这两等式右边的变化率是可以由 实验直接测定的，而左边则不能。可用等式右边的变化率代替左
4.热力学状态方程
由dU＝TdS－pdV
定温下， dUT＝TdST－pdVT
等式两边除以dVT 即
dUT T dST p
dVT
dVT
由麦克斯韦方程 于是
U T S p V T V T S p V T T V
式(1-116)及 (1-117)叫吉布斯 - 亥姆霍茨方程。
(1-117)
G-H方程常用的形式为：
即
(G / T )
T p
H T2
加△
(1-116)
Gibbs自由能随压力的变化
因
（эG/эP）T，n=V
（э△G/эP）T，n=△V 此即G---V关系式
只要知道△V--p关系式，在定温下P1的△G1就可求算出P2的△G2。
在定压下从T1到 T2积分得： （△G）2/ T2- （△G）1/ T1=- =∫T1 T2 △H/T2dT 若知△H--T关系以及T1时的△G1就可求算T2时的△G2 而： △H= △H T0+∫ T0 T △CpdT △H T0是T0时的焓变。
物理化学(机材类第四版,ppt课件)2.9 热力学基本关系式
适用条件：组成不变，W′= 0 的封闭系统或 封闭系统，W′= 0，可逆过程。
4
2、热力学函数的基本关系式
由热力学基本方程
热力学恒等式
dU = TdS- pdV dH = TdS + Vdp
U T ; U p
S V
V S
H T; S p
H p
S
V
dA = -SdT- pdV dG = -SdT + Vdp
再将dU = TdS – pdV 式代入得到 dH = TdS +Vdp
（c） A=U-TS 微分，并用上式代入得到
dA = -SdT- pdV
（d） G = H – T S微分，并用上式代入得到 dG = -SdT + Vdp
3
四个热力学基本方程
dU = TdS- pdV dH = TdS + Vdp dA = -SdT- pdV dG = -SdT + Vdp
G p3 p2 p1
p3>p2>p1
T Tm
T
26
(1)求U随V的变化关系 (2)求H随p的变化关系 (3)求S与Cp的变化关系 (4)求G或Δr G与温度的关系 (5)求G随p的变化关系
27
关于U,H, S, G,A与T、p、V的关系
（一定量、一定组成的单相系统）
➢理想气体 U、H 只是T 的函数，与p、V 无关；S与T、p、V 均有关。
-p -S
G T p
麦克斯韦关系式中不含熵与温度的偏微商。
问题
S T p
S T V
Cp/T CV/T
10
思考题
1、对于只作膨胀功的封闭系统 （）
A T
V
4
2、热力学函数的基本关系式
由热力学基本方程
热力学恒等式
dU = TdS- pdV dH = TdS + Vdp
U T ; U p
S V
V S
H T; S p
H p
S
V
dA = -SdT- pdV dG = -SdT + Vdp
再将dU = TdS – pdV 式代入得到 dH = TdS +Vdp
（c） A=U-TS 微分，并用上式代入得到
dA = -SdT- pdV
（d） G = H – T S微分，并用上式代入得到 dG = -SdT + Vdp
3
四个热力学基本方程
dU = TdS- pdV dH = TdS + Vdp dA = -SdT- pdV dG = -SdT + Vdp
G p3 p2 p1
p3>p2>p1
T Tm
T
26
(1)求U随V的变化关系 (2)求H随p的变化关系 (3)求S与Cp的变化关系 (4)求G或Δr G与温度的关系 (5)求G随p的变化关系
27
关于U,H, S, G,A与T、p、V的关系
（一定量、一定组成的单相系统）
➢理想气体 U、H 只是T 的函数，与p、V 无关；S与T、p、V 均有关。
-p -S
G T p
麦克斯韦关系式中不含熵与温度的偏微商。
问题
S T p
S T V
Cp/T CV/T
10
思考题
1、对于只作膨胀功的封闭系统 （）
A T
V
热力学函数基本关系式
V S ( ) p d p T
S V d p
p
从状态方程求得 ,V 与 p 的关系,就可求 ( S )T 或 S 。
上一内容
下一内容 回主目录 返回
2018/11/23
Maxwell 关系式的应用
物化课件
例如，对理想气体
pV nRT，
( S p )T
常用的特征变量为：
G(T , p)
U (S,V )
上一内容
下一内容
A(T ,V ) H (S, p)
回主目录
S(H, p)
返回
2018/11/23
特性函数
物化课件
例如，从特性函数G及其特征变量T，p，求H，U， A，S等函数的表达式。 G(T , p) dG SdT Vdp G 导出： V ( G ) T S ( ) p p T
V =C p dT [V T ( ) p ]dp T
V H C p dT [V T ( ) p ]dp T
知道气体状态方程，求出( V ) p 值，就可计算 H值。
T
上一内容
下一内容 回主目录 返回
2018/11/23
Maxwell 关系式的应用
等温对p求偏微分 ( H )T T ( S )T V
( S )T 不易测定，据Maxwell关系式 p
(
所以
H V ( )T V T ( ) p p T
只要知道气体的状态方程，就可求得 ( H )T p 值，即等温时焓随压力的变化值。
上一内容
下一内容 回主目录 返回
dA SdT pdV
(
(4) dG SdT Vdp
利用该关系式可将实验可测偏微商来代替那些不易直 接测定的偏微商。
热力学基础中的热力学关系与偏导数
热力学基础中的热力学关系与偏导数热力学是研究能量转化和能量传递规律的一门学科，它是理解和描述自然界中许多现象和过程的基础。
在热力学中，我们经常面对各种热力学关系和偏导数的计算，这些关系和计算方法对于热力学分析和应用具有重要意义。
一、热力学基本关系式在热力学中，存在着几个基本的热力学关系式，它们是从热力学基本定律出发推导得到的。
这些关系式包括了内能、焓、熵、体积和温度之间的关系。
1. 内能和焓的关系：根据热力学基本定律，系统的内能变化等于传递给系统的热量与系统对外界做功之和。
即ΔU = Q - W。
通过对焓的定义H = U + PV，可以得到焓的变化与系统的热量和外界做功之间的关系，即ΔH = Q。
2. 熵和热量的关系：根据热力学第二定律，任何孤立系统的熵都不会减少。
对于可逆过程，熵的变化等于传递给系统的热量除以系统的温度，即ΔS = Q/T。
这个关系式揭示了熵与热量和温度之间的关系。
3. 温度和焓的关系：根据热力学基本定律和热容的定义，对于恒容过程，热容Cv等于系统的内能对温度的偏导数，即Cv = (∂U/∂T)v。
对于恒压过程，热容Cp等于焓对温度的偏导数，即Cp = (∂H/∂T)p。
这两个关系式揭示了温度与内能和焓之间的关系。
二、热力学关系的应用热力学关系的应用范围广泛，涉及到能量转化、功的计算、热力学循环等方面。
1. 热力学循环：热力学循环是指在各种设备和系统中完成能量转化的循环过程。
通过运用热力学关系，我们可以计算热力学循环中的功、热量和效率等参数，从而优化系统设计和提高能源利用效率。
2. 非平衡态热力学：非平衡态热力学是研究热力学系统远离平衡态时的行为和规律的分支学科。
通过热力学关系的应用，我们可以对非平衡态过程进行定量的描述和分析，揭示系统的演化路径和性质。
三、热力学关系的计算方法对于热力学关系的计算，我们经常使用偏导数来描述系统的性质和变化。
偏导数是多元函数在某一点上对某个变量的变化率。
6.热力学基本关系式
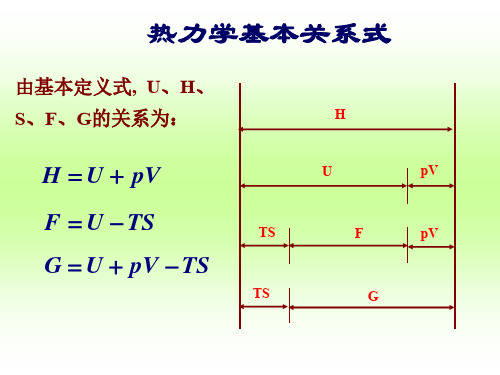
G U pV TS
dG S dT V d p
U、H、F、G这些热力学函数之间的关系实质是勒让德变换 勒让德变换实际上是在我们得到了一个不变量后，要得到它的对偶自变量下的 不变量的一个重要的变换。
热力学四个基本关系式(Gibbs关系式)如下:
d U T d S p dV
S p V T T V
(1)
U p V T T p T V
得证
几个重要的偏导关系式
1.与S有关的
S p V T T V
S V T p p T
d H T d S V d p
(1)
(2) (3)
d F S d T p dV dG S dT V d p
(4)
条件: 简单封闭系统,只作体积功。
• 基本关系式实质上是 U 、 H 、 F 和 G 的数学全 微分展开式。 • 简单的封闭系统, 状态只需两个独立变量即可 决定, 这两个变量可以任意选取. • 从四个关系式的微分变量可知, 对不同的状态 函数, 在作全微分展开时, 选取的独立变量是 不一样的：
例: 试证明:
U p V T T p T V
解:有基本热力学关系式
d U T d S p dV
在等温条件下,求内能对体积的偏微商:
U S V T V p T T
由麦克斯韦关系式: 代入(1)式得:
Wf 0
Qr T d S
将上式代入内能的全微分:
W p dV
d U T d S p dV
(1)
3.7 热力学基本方程及Maxwell关系式
恒T、p、W= 0： G 0
自发 平衡
dGm α dGm β Sm α dT Vm α dp Sm β dT
Vm β dp
[Sm β Sm α ]dT [Vm β Vm α ]dp
dp Sm β Sm α
βαSm
dT Vm β Vm α
βαVm
又因 βαSm
βαHm T
dp dT
βαH m T βαVm
U
SV
H
A
pT
G
说明： 1. 等式右边只有四个物理量T，S， p，V
2. 十字交叉法：
对U来说，S，V分别表示dS和dV； dS对角线 对应T，dV对角线对应p；箭头方向表示正负，指向 为负，则为TdS和 –pdV
2. U、H、A、G的一阶偏导数关系式
U f (S,V ) H f (S, p) A f (T ,V ) G f (T , p)
p
S V
T
p T
V
V T
p
S p
T
T V
S
p S
V
T p
S
V S
p
S V
T
p T
V
V T
p
S p
T
说明：
1. 关系式中只有四个物理量T， S， p，V
2. 对角线乘积为 TS 与 pV
3. 等式两边的分母与下标互换
4. S和V为广度量，而T和p为强 度量。同种性质的状态函数 的分式，不取负号。
分析：利用克拉佩龙方程 dT T βαVm
dp 解：由克拉佩龙方程有 dT
T
βαH m
lsVm lsH m
dp
积分，得 lnT2
T1
热力学计算公式整理
热力学计算公式整理热力学是研究物质的热与能的转化关系的学科，是广泛应用于化学、物理、工程等领域的重要理论基础。
在热力学计算中，有一系列公式被广泛应用于热力学参数的计算和分析。
1.热力学基本方程：对于一个热力学系统，其内部能量U可以由其热力学状态变量来表示，常用的基本方程有：U=TS-PV+μN其中，U为内部能量，T为温度，S为熵，P为压力，V为体积，μ为化学势，N为摩尔数。
2.热力学函数的计算：(1)焓（H）的计算公式：H=U+PV其中，H为焓，U为内部能量，P为压力，V为体积。
(2)外界对系统做的功（W）计算公式：W=-∫PdV其中，W为功，P为压力，V为体积，积分为从初态到末态的过程。
(3)熵（S）的计算公式：dS=dQ/T其中，S为熵，dS为熵的微分，dQ为系统的热量变化，T为温度。
(4) Helmholtz自由能（A）的计算公式：A=U-TS其中，A为Helmholtz自由能，U为内部能量，T为温度，S为熵。
(5) Gibbs自由能（G）的计算公式：G=U-TS+PV其中，G为Gibbs自由能，U为内部能量，T为温度，S为熵，P为压力，V为体积。
3.热力学热力学参数的计算：(1)热容的计算公式：Cv=(∂U/∂T)V其中，Cv为定容热容，∂U/∂T为导数，V为体积。
Cp=(∂H/∂T)P其中，Cp为定压热容，∂H/∂T为导数，P为压力。
(2)趋近于绝对零度时的熵变ΔS的计算公式：ΔS = Cvln(T2/T1) + Rln(V2/V1)其中，ΔS为熵的变化，Cv为定容热容，T2和T1为温度的变化，R 为气体常数，V2和V1为体积的变化。
(3)等温过程中的吸热计算公式：q=ΔH=nCpΔT其中，q为吸热，ΔH为焓的变化，n为物质的摩尔数，Cp为定压热容，ΔT为温度的变化。
(4)等温过程中的做功计算公式：w=-ΔG=PΔV其中，w为做功，ΔG为Gibbs自由能的变化，P为压力，ΔV为体积的变化。
热力学函数的基本关系式
△S=QR/T; T △S= QR 故△G= △H- T △S=0- T △S= QR= WR=-RTlnP1/P2=5744Jmol-1 解法二： △G=∫ p1 p2Vdp = RTlnP2/P1=5744Jmol-1.
⑵等温等压相变△G 对于等温等压的可逆相变，直接可得（△G）T,P=0.对于非等温 等压的非可逆相变或同温同压下两个相态的△G，可以通过设计可 逆过程进行计算，也可根据G---P关系公式求算。
1.8 热力学函数的基本关系式
H
U、H、S、A、G 、 p、V、T H =U+pV，A =U-TS，G =H-TS 1. 热力学基本方程
U
pV
TS A pV
TS
G
δWr ′＝0时，则δWr＝－pdV，于是
一微小可逆过程
dU=δQr+δWr，
dS δ Qr T
δWr ′ ＝0时，则δWr＝－pdV，于是
=8586Jmol-1 故△G= △G1+ △G2 + △G3=8584Jmol-1 依Gibbs自由能减少原理，298K，1atm水不能经等温等压过程转变 为同温 同压的水蒸气，但其逆过程则是可以的。因此在298K， 1atm下液态水是稳定态。
⒊应用Gibbs--helmholtz方程求△G 将 G--H方程：｛э（△G/T）/эT｝P=- △H/T2
△S=0，△T=0，△H=0，
△G=0
⑵理气在等温等压的Gibbs自由能改变 △G = △H-T △S (△H=0) △S=-R∑nilnXi △G= RT∑nilnXi 其中ni为组分i的量，Xi为理想混合气中
为组分I的摩尔数。
⒌非等温等压两态的△G 若体系的两态温度，压力都不相等，根据G的定义：
⑵等温等压相变△G 对于等温等压的可逆相变，直接可得（△G）T,P=0.对于非等温 等压的非可逆相变或同温同压下两个相态的△G，可以通过设计可 逆过程进行计算，也可根据G---P关系公式求算。
1.8 热力学函数的基本关系式
H
U、H、S、A、G 、 p、V、T H =U+pV，A =U-TS，G =H-TS 1. 热力学基本方程
U
pV
TS A pV
TS
G
δWr ′＝0时，则δWr＝－pdV，于是
一微小可逆过程
dU=δQr+δWr，
dS δ Qr T
δWr ′ ＝0时，则δWr＝－pdV，于是
=8586Jmol-1 故△G= △G1+ △G2 + △G3=8584Jmol-1 依Gibbs自由能减少原理，298K，1atm水不能经等温等压过程转变 为同温 同压的水蒸气，但其逆过程则是可以的。因此在298K， 1atm下液态水是稳定态。
⒊应用Gibbs--helmholtz方程求△G 将 G--H方程：｛э（△G/T）/эT｝P=- △H/T2
△S=0，△T=0，△H=0，
△G=0
⑵理气在等温等压的Gibbs自由能改变 △G = △H-T △S (△H=0) △S=-R∑nilnXi △G= RT∑nilnXi 其中ni为组分i的量，Xi为理想混合气中
为组分I的摩尔数。
⒌非等温等压两态的△G 若体系的两态温度，压力都不相等，根据G的定义：
热力学基本关系式
(3-143)
(3-144)
(3-145)
(3-146)
式(3-139)与式(3-143)对比、式(3-140)与式(3-144)对比、 式(3-141)与式(3-145)对比、式(3-142)与式(3-146)对比，可得如下关系(或称" 对应系数式")：
(3-147)
(3-148)
(3-149)
和
由定义可得如下三个关系式：
(1)
(3-136)
(2)
(3-137)
(3)
(3-138)
又由热力学第一定律、第二定律联合公式，在无非膨胀功条件下：
将它和式(3-136)、(3-137)、(3-138)联系起来：
即可得以下四个一组被称为恒组成均相封闭系统的热力学基本方程。又称 Gibbs 方程。
(4)
(3-139)
(5)
(3-140)
(6)
(3-141)
(7)
(3-142)
这四个基本方程均不受可逆过程的限制，因为 U、H、A、G 等随着相应两个独立 的状态函数变化而变化，因而与变化的具体途径（可逆或不可逆）无关，自然亦
可用于不可逆过程。公式虽然是四个，但式(5)、(6)、(7)实际上是基本公式(4) 在不同条件下的表示形式。根据全微分定义可有如下关系：
至今讨论中常应用的八个热力学函数--p、V、T、U、H、S、A、G。其中 U 和 S 分 别由热力学第一定律和第二定律导出；H、A、G 则由定义得来。而 U、H、A、G 为 具有能量量纲的函数。这些热力学函数间通过一定关系式相互联系着。基本热力 学关系式共有十一个（以下分别用公式左边括弧中的数字标明）。从这十一个基 本关系式出发，可以导出许多其它衍生关系式，它们表示出各不同物理量间的相 互关系，利用它们可以帮助我们由易于直接测量的物理量出发以计算难于直接测 量的物理量的数值。
(3-144)
(3-145)
(3-146)
式(3-139)与式(3-143)对比、式(3-140)与式(3-144)对比、 式(3-141)与式(3-145)对比、式(3-142)与式(3-146)对比，可得如下关系(或称" 对应系数式")：
(3-147)
(3-148)
(3-149)
和
由定义可得如下三个关系式：
(1)
(3-136)
(2)
(3-137)
(3)
(3-138)
又由热力学第一定律、第二定律联合公式，在无非膨胀功条件下：
将它和式(3-136)、(3-137)、(3-138)联系起来：
即可得以下四个一组被称为恒组成均相封闭系统的热力学基本方程。又称 Gibbs 方程。
(4)
(3-139)
(5)
(3-140)
(6)
(3-141)
(7)
(3-142)
这四个基本方程均不受可逆过程的限制，因为 U、H、A、G 等随着相应两个独立 的状态函数变化而变化，因而与变化的具体途径（可逆或不可逆）无关，自然亦
可用于不可逆过程。公式虽然是四个，但式(5)、(6)、(7)实际上是基本公式(4) 在不同条件下的表示形式。根据全微分定义可有如下关系：
至今讨论中常应用的八个热力学函数--p、V、T、U、H、S、A、G。其中 U 和 S 分 别由热力学第一定律和第二定律导出；H、A、G 则由定义得来。而 U、H、A、G 为 具有能量量纲的函数。这些热力学函数间通过一定关系式相互联系着。基本热力 学关系式共有十一个（以下分别用公式左边括弧中的数字标明）。从这十一个基 本关系式出发，可以导出许多其它衍生关系式，它们表示出各不同物理量间的相 互关系，利用它们可以帮助我们由易于直接测量的物理量出发以计算难于直接测 量的物理量的数值。
热力学第二定律基本公式
（2）dH TdS Vdp
H T S V p T p T
谢谢观看
THANKS FOR WATCHING !
dS
H p
S
dp
dA = –SdT – pdV A dT A dV
T V
V T
dG = –SdT+Vdp
G T
dT
p
G p
T
dp
U H T S V S p
A G S T V T p U A p V S V T
H p
(4) U、H分别以S, V 和 S, p为变量， d前系数只能分别是T, p 和 T, V；
(5) “H最大”，所以都是“+”项；A最
小，都是“–”项 。
4.由基本公式导出的关系式
dU = TdS pdV U dS U dV
S V V S
dH = TdS + Vdp
H S
p
2.四个基本方程
由 A U TS 可得：
dA dU TS dU TdS SdT
将 dU TdS pdV 带入上式： dA SdT pdV
（3）
2.四个基本方程
由 G H TS 可得：
dG dH TS dH TdS SdT
将 dH TdS Vdp 带入上式： dG SdT Vdp
只有两个变量，但要保持系统组成不变。
若系统内发生相变或化学变化，就要增加组成变量， 所以这公式只适用于内部平衡的、只有体积功的封 闭系统。
2.四个基本方程
由 H U pV 可得：
dH dU pV dU pdV Vdp
将 dU TdS pdV 带入上式： dH TdS Vdp
（2）
热力学基本方程
四个热力学基本关系式和Maxwell公式的理解与记忆
先取其倒数 ， 化为 Ｍａ ｘ ｗ ｅ ｌ ｌ 关系原型式 ； （ ４ ）在 Ｐ， Ｖ ， Ｓ和 总共 ４个状态 函数 中， Ｍａ ｘｗ ｅ ｌ ｌ 等式 左端未出现的那个量就是 等式右端 的被求导 函数 ， 然后求 导变量和不 变量互换位置 ； （ ５ ） Ｍ ｘｗ ａ ｅ ｌ ｌ 关 系式 中的 正负 号 由旋 转 方 向来 判 断。 按Ｐ — — Ｊ ｓ — 的顺序 ， 若等式两端 的偏微分 函数旋转方 向相同则不 出现 负号 ， 若旋转 相反则等式 中出现一负号。 下面举例说 明
（ １ ３ ）
（ ２ ）若 Ｐ和 或者 Ｓ和 是构成 ｃ 边 的两顶点 ， 则为 Ｍａ ｘ ｗ ｅ ｌ ｌ 关系式的原式偏 导数 ； （ ３ ）若 ． ｓ 和 或者 Ｐ和 是构成 ｂ边 的两顶点 ， 则为
（ ） ＝ （
…
Ｍａ ｘ ｗ ｅ ｌ ｌ 关系等价式偏导数。 对于等 价式偏导数 ， 处 理时需
１ ０４
将 上 ２式 代 入 ， 则得到 Ｍ ａ ｘ ｗ ｅ ｌ ｌ 关 系式 之 一
和分母上 ， 即构成 ａ边的两顶点 ， 则不是 Ｍａ ｘ ｗ ｅ ｌ ｌ 公式 ；
（ ） ＝ 一 （ 一 ｏ ｓ ） ．
同理 ， 得到其它 ３ 个 Ｍａ ｘ ｗ ｅ ｌ ｌ 关 系式
不论是否为均相体系 ， 体 系 内能 的增 加只是从 环境得 到的
将式 （ ８ ） 代人上 ３式得 出
ｄ Ｈ≤Ｔ ｄ Ｓ＋Ｖ ｄ ｐ ． （ ９ ）
功 和热之和 ， 故由热力学第一定律总有
收 稿 日期 ： ２ ０ １ ３—０ ３— ０ １
作者简介 ： 崔洪友（ １ ９ ６ ８一）， 男， 山东青州人 ， 工学博士 ， 教授 ， 主要从事化工热力学方 蕊的教学研 究及超临界流体技术 、 生物质能 源 利用和清洁化工技术方面的研究工作 。
（ １ ３ ）
（ ２ ）若 Ｐ和 或者 Ｓ和 是构成 ｃ 边 的两顶点 ， 则为 Ｍａ ｘ ｗ ｅ ｌ ｌ 关系式的原式偏 导数 ； （ ３ ）若 ． ｓ 和 或者 Ｐ和 是构成 ｂ边 的两顶点 ， 则为
（ ） ＝ （
…
Ｍａ ｘ ｗ ｅ ｌ ｌ 关系等价式偏导数。 对于等 价式偏导数 ， 处 理时需
１ ０４
将 上 ２式 代 入 ， 则得到 Ｍ ａ ｘ ｗ ｅ ｌ ｌ 关 系式 之 一
和分母上 ， 即构成 ａ边的两顶点 ， 则不是 Ｍａ ｘ ｗ ｅ ｌ ｌ 公式 ；
（ ） ＝ 一 （ 一 ｏ ｓ ） ．
同理 ， 得到其它 ３ 个 Ｍａ ｘ ｗ ｅ ｌ ｌ 关 系式
不论是否为均相体系 ， 体 系 内能 的增 加只是从 环境得 到的
将式 （ ８ ） 代人上 ３式得 出
ｄ Ｈ≤Ｔ ｄ Ｓ＋Ｖ ｄ ｐ ． （ ９ ）
功 和热之和 ， 故由热力学第一定律总有
收 稿 日期 ： ２ ０ １ ３—０ ３— ０ １
作者简介 ： 崔洪友（ １ ９ ６ ８一）， 男， 山东青州人 ， 工学博士 ， 教授 ， 主要从事化工热力学方 蕊的教学研 究及超临界流体技术 、 生物质能 源 利用和清洁化工技术方面的研究工作 。
物理化学：2.13热力学函数间的重要关系式
即： (Wr ) T = dF
② 恒温恒容可逆：
dF = SdT PdV Wr, f = Wr, f
即： (Wr, f ) T, V = dF
③ 恒温恒压可逆：
dG = SdT + VdP Wr, f = Wr, f 即： (Wr, f ) T, P = dG
上述结论与前面讨论的结果一样。
U、T、S、P、V、T、 H、F、G
均与相同始、终态的可逆过程的改变 量相同。
2）涉及不可逆变化时，过程曲线不在状 态空间内，无法在始、终态范围内直 接对过程曲线积分求状态函数变化值；
但始、终态间状态函数变化值与经可 逆过程的变化值是一样的；
所以可设计有相同始、终态的可逆过 程，对上述公式积分，得到任意变化 过程的U、G、… 等。
二、热力学第一、第二定律基本公式
第一定律：dU = Q W = Q P环 dV Wf …①
第二定律：dS = Qr / T Qr = TdS （可逆） …②
②代入①：dU = TdS PdV Wf …③ （可逆过程： Q = Qr，P = P环）
dU = TdS PdV Wf …③
3）对上述公式直接积分计算时，仅适合 于体系组成不变，或仅发生可逆相变、 可逆化学反应的过程。
否则，需设计相同始态及最终态的可 逆过程、可逆相变等来分段计算并加 和（有例题）。
结论：
上述基本公式可用于封闭、无非体积 功 ( Wf = 0 )、组成平衡 ( 组成不变或 仅发生可逆变化 ) 的体系；
§2.13 热力学函数间的重要关系式
一、热力学函数之间的关系 • 在热力学第一、第二定律中，共涉及
五个热力学函数：U、H、S、F、G：
H U + PV F U TS G H TS F + PV
② 恒温恒容可逆：
dF = SdT PdV Wr, f = Wr, f
即： (Wr, f ) T, V = dF
③ 恒温恒压可逆：
dG = SdT + VdP Wr, f = Wr, f 即： (Wr, f ) T, P = dG
上述结论与前面讨论的结果一样。
U、T、S、P、V、T、 H、F、G
均与相同始、终态的可逆过程的改变 量相同。
2）涉及不可逆变化时，过程曲线不在状 态空间内，无法在始、终态范围内直 接对过程曲线积分求状态函数变化值；
但始、终态间状态函数变化值与经可 逆过程的变化值是一样的；
所以可设计有相同始、终态的可逆过 程，对上述公式积分，得到任意变化 过程的U、G、… 等。
二、热力学第一、第二定律基本公式
第一定律：dU = Q W = Q P环 dV Wf …①
第二定律：dS = Qr / T Qr = TdS （可逆） …②
②代入①：dU = TdS PdV Wf …③ （可逆过程： Q = Qr，P = P环）
dU = TdS PdV Wf …③
3）对上述公式直接积分计算时，仅适合 于体系组成不变，或仅发生可逆相变、 可逆化学反应的过程。
否则，需设计相同始态及最终态的可 逆过程、可逆相变等来分段计算并加 和（有例题）。
结论：
上述基本公式可用于封闭、无非体积 功 ( Wf = 0 )、组成平衡 ( 组成不变或 仅发生可逆变化 ) 的体系；
§2.13 热力学函数间的重要关系式
一、热力学函数之间的关系 • 在热力学第一、第二定律中，共涉及
五个热力学函数：U、H、S、F、G：
H U + PV F U TS G H TS F + PV
化工热力学第3章练习题
§均相封闭系统的热力学关系 3.1.1热力学函数的分类 3.1.2热力学函数的基本关系式 一、判断题7. 像dU =TdS -PdV 等热力学基本方程只能用于气体，而不能用于液体或固相。
（ ） 3. 热力学基本关系式VdP TdS dH +=只适用于可逆过程。
（ ） 二、选择题4. 对于一均匀的物质，其H 和U 的关系为（ ）。
A. H<UB. H>UC. H=UD. 不能确定 4. 关于热力学基本方程dU=TdS-pdV ，下面的说法中准确的是（ ）。
A. TdS 是过程热 B. pdV 是体积功 C. TdS 是可逆热 D. 在可逆过程中，pdV 等于体积功，TdS 即为过程热3. 对单位质量，定组成的均相流体体系，在非流动条件下有（ ）。
A. VdP TdS dH += B. VdP SdT dH += C. VdP SdT dH +-= D. VdP TdS dH --=4. 热力学第一定律的公式表述（用微分形式）： 。
热力学第二定律的公式表述（即熵差与可逆热之间的关系，用微分形式）： 。
4. 几个重要的定义公式：焓H=________；自由能A=___________；自由焓G=_________。
5. 几个热力学基本关系式：dU=_________；dH=_________；dA=_______；dG=________。
3.1.3Maxwell 关系式 一、判断题1. 理想气体的焓和热容仅是温度的函数。
（ ） 1. 理想气体的熵和吉氏函数仅是温度的函数。
（ ）5. 理想气体的U 、C v 、H 、C p 虽然与p 无关，但与V 有关。
（ ） 二、选择题4. 设Z 为x ，y 的连续函数，，根据欧拉连锁式，有（ ）。
A. 1x y z Z Z x x y y ⎛⎫⎛⎫∂∂∂⎛⎫=- ⎪ ⎪ ⎪∂∂∂⎝⎭⎝⎭⎝⎭B. 1y xZ Z x y x y Z ⎛⎫∂∂∂⎛⎫⎛⎫=- ⎪ ⎪ ⎪∂∂∂⎝⎭⎝⎭⎝⎭C. 1y x Z Z x y x y Z ⎛⎫∂∂∂⎛⎫⎛⎫= ⎪ ⎪ ⎪∂∂∂⎝⎭⎝⎭⎝⎭D. 1y Z xZ y y x x Z ∂∂∂⎛⎫⎛⎫⎛⎫=- ⎪ ⎪ ⎪∂∂∂⎝⎭⎝⎭⎝⎭ 5. 麦克斯韦关系式的主要作用是（ ）。
3-7热力学基本关系式
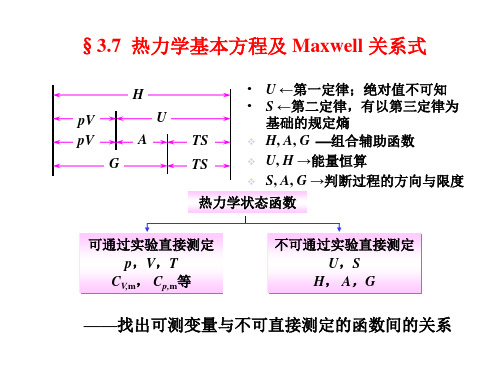
热力学状态函数 可通过实验直接测定 p，V，T ， ， CV,m， Cp,m等 不可通过实验直接测定 U，S ， H， A，G ，
——找出可测变量与不可直接测定的函数间的关系 找出可测变量与不可直接测定的函数间的关系
一、热力学基本方程 1、推导 、 条件： ） 组成恒定的封闭系统； 条件：（1） 组成恒定的封闭系统； （2） W’＝0； ） ＝ ； （3） 经历一微小可逆过程。 ） 经历一微小可逆过程。 热力学第一定律： 热力学第一定律： 热力学第二定律： 热力学第二定律： W’＝0： ＝ ：
S
−p
V
−S
∂G ∂A = = ∂T V ∂T p
2.吉布斯 亥姆霍兹方程 吉布斯-亥姆霍兹方程 吉布斯
1 ∂A A 1 A ∂( A / T ) ( )V − 2 = (− S ) − 2 V= ∂T T ∂T T T T
TS + A U =− =− 2 2 T T
V2 V1
dGT = Vdp
∆ AT = − ∫
V2 p d V = − nRT ln V1
p2 ∆ G T = ∫ V d p = nRT ln p1 p1
p2
b.凝聚相（S,l）： 凝聚相（ ）： ）：等温压缩率很小，→体积可认为不变 凝聚相 体积可认为不变
∆ AT = − ∫
V2
V1
p2
pdV → ≈ 0
——Gibbs-Helmholtz方程 方程
——后边讨论温度对化学反应平衡影响的基础 ——后边讨论温度对化学反应平衡影响的基础
三.麦克斯韦关系式 麦克斯韦关系式 有连续的二阶偏微商， 若Z＝f(x，y)，且Z有连续的二阶偏微商，则必有 ＝ ， ， 有连续的二阶偏微商
物理化学1.15-1 热力学函数的基本关系式
§1.15 热力学函数的基本关系式
8个热力学函数： 可直接测定
p、V、T、U 、H 、S、A、G
定 H ＝U＋pV 义 式 A ＝U－TS
可求得
G ＝H－TS＝A＋pV
1.热力学基本方程
封闭系统 dU =δQ + δW
可逆过程
=δQr －pdV ＋ δWr′
δQr =TdS
dU = TdS －pdV ＋ δWr' δWr'＝0：
dA = －SdT－ pdV dG = －SdT + Vdp
G S T p
G p
T
V
证明：无相变和化学变化的封 闭系统，在定温下其吉布斯自 由能随压力的改变恒为正值。
证明：
dG = －SdT + Vdp
G ( p )T
V
>0
解： dG = －SdT + Vdp
S T2 nCV ,mdT nR ln V2 ,
T1
T
V1
A nRT ln V2 V1
应(用ቤተ መጻሕፍቲ ባይዱ()i封条i()i无i闭件i)非可系：体逆统积过，功程，。
可用于: (i)定量，定组成的单相系统;
(ii) 保持相平衡及化学平衡的系统.
8个派生公式： dU = TdS－ pdV dH = TdS + Vdp
U T S V U p V S
dU = TdS －pdV
dU=TdS－pdV
H=U+pV dH=dU+pdV+Vdp
A=U－TS dA=dU－TdS－SdT
dH=TdS+Vdp
dA= － SdT － pdV
8个热力学函数： 可直接测定
p、V、T、U 、H 、S、A、G
定 H ＝U＋pV 义 式 A ＝U－TS
可求得
G ＝H－TS＝A＋pV
1.热力学基本方程
封闭系统 dU =δQ + δW
可逆过程
=δQr －pdV ＋ δWr′
δQr =TdS
dU = TdS －pdV ＋ δWr' δWr'＝0：
dA = －SdT－ pdV dG = －SdT + Vdp
G S T p
G p
T
V
证明：无相变和化学变化的封 闭系统，在定温下其吉布斯自 由能随压力的改变恒为正值。
证明：
dG = －SdT + Vdp
G ( p )T
V
>0
解： dG = －SdT + Vdp
S T2 nCV ,mdT nR ln V2 ,
T1
T
V1
A nRT ln V2 V1
应(用ቤተ መጻሕፍቲ ባይዱ()i封条i()i无i闭件i)非可系：体逆统积过，功程，。
可用于: (i)定量，定组成的单相系统;
(ii) 保持相平衡及化学平衡的系统.
8个派生公式： dU = TdS－ pdV dH = TdS + Vdp
U T S V U p V S
dU = TdS －pdV
dU=TdS－pdV
H=U+pV dH=dU+pdV+Vdp
A=U－TS dA=dU－TdS－SdT
dH=TdS+Vdp
dA= － SdT － pdV
物理化学
给出了热力学函数随某状态函数的变化率，它在解决实际问题时十分有用。 例如,求任意温度T下的ΔG 。
二.一些基本过过程的 S , G, A的计算公式 W f 0
基本过程
S
V nRIn 2 V1
G
nRTIn P2 P1
A
A PdV V nRT dV nRTln 1 V V2
dV
T
③
dU T S dT S dV PdV TV VT T S P dV ④ dT T S T V VT
[
] [ ]
比较①与④对应系数应相等-------叫系数比较法
U V T S V T P P T
U T
V
1
T
U
V
这时要分别证
U V
T
？
U T
V
？
用前面介绍的二种方法在选一种证明，代入上式可得。现在证的例题都是 不符合特征变量，如果符合特征变量， 如： U
S
V
T ，直接用对应系数关系可得。
例题2：证明
C P CV T P
V T T
(1)全微分到偏微分法
从基本关系式 定温，对V微分
U V
dU TdS PdV
T
全微分
T S
V
T
P
偏微分 S
V
不易测量
T
由Maxwell关系
P T S V
V
T
U
V
T
T P
T
V
P
二.一些基本过过程的 S , G, A的计算公式 W f 0
基本过程
S
V nRIn 2 V1
G
nRTIn P2 P1
A
A PdV V nRT dV nRTln 1 V V2
dV
T
③
dU T S dT S dV PdV TV VT T S P dV ④ dT T S T V VT
[
] [ ]
比较①与④对应系数应相等-------叫系数比较法
U V T S V T P P T
U T
V
1
T
U
V
这时要分别证
U V
T
？
U T
V
？
用前面介绍的二种方法在选一种证明，代入上式可得。现在证的例题都是 不符合特征变量，如果符合特征变量， 如： U
S
V
T ，直接用对应系数关系可得。
例题2：证明
C P CV T P
V T T
(1)全微分到偏微分法
从基本关系式 定温，对V微分
U V
dU TdS PdV
T
全微分
T S
V
T
P
偏微分 S
V
不易测量
T
由Maxwell关系
P T S V
V
T
U
V
T
T P
T
V
P
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
dG = －SdT + Vdp
S p
T
V T
p
麦克斯韦关系式 ：表示的是系统在同一状态的两种
变化率数值相等。 9
二阶混合偏导数
T p V S S V 麦氏方程记忆法：
T p
S
V S
p
① 对角乘积永远是pV，TS；
② 等式两边分母与外角标互换；
S p
T
V T
4
由四个热力学基本方程，分别加上相应的条件，可得到
8个派生公式：
dU = TdS－ pdV
U S
V
T
U V
S
p
dH = TdS + Vdp
T V H
S p
H p S
dA = －SdT－ pdV
A T
V
S
A V
T
p
dG = －SdT + Vdp
G T
P
S
G P
则
U T p p
V T T V
11
练习：由热力学基本方程出发证明，
H p
T
T
V T
p
V
证明：
dH＝TdS＋Vdp
定温下，等式两边除以dp
H p
T
T
S p
T
V
由麦克斯韦方程
S p
T
V T
p
返回
H p
T
T
V T
p
V
12
U T p p V T T V
S T p
T
T
定容
S CV T V T
S T V
15
T
V
5
2. 吉布斯 - 亥姆霍茨方程
(G / T )
T p
T
G T
G
P
T2
d
x y
ydx xdy y2
dG = －SdT + Vdp
G
S
T p
有
(G / T )
T p
TS G T2
(TS G) T2
H T2
(G / T )
T p
H T2
同理，有
(A/T) T V
H T S V p V T V T V T
麦克斯韦关系式 S p V T T V
14
思考：定容或定压下S 随T 的变化率各等于什么？
S(T，p) S(T，V)
由定义式出发
1)由定义式出发
dS Qr C dT
定压
S Cp T p T
H p
T
T
V T
p
V
热力学状态方程，将U(或H)与p,V,T联系起来了。
—— 对实际气体，已知pVT状态方程式，代入，积分 可求ΔU、ΔH。
13
典型证明题：
证明： H T p V p V T T V V T
证：由热力学基本方程 dH = TdS + Vdp 定温下等式两边同除以dV，得
U V
dV
S
U=f(S,V)
p T S V V S
8
麦克斯韦关系式
dU = TdS－ pdV dH = TdS + Vdp
p T S V V S
T p
S
V S
p
dA = －SdT－ pdV
S p V T T V
将含熵偏导 转化为易于 测定的含 p,V,T的偏导 数，用于推 导、证明、 演算。
除了定义式外, 还可以导出四种类型的重要关系式
2
1. 热力学基本方程
封闭系统中， 微小可逆过程：dU=δQr+δWr
δWr ′＝0时，
dS δ Qr T
δWr＝－pdV，
dU=TdS－pdV
H=U+pV
dH=dU+pdV+Vdp
A=U－TS dA=dU－TdS－SdT
dH=TdS+Vdp
dA= － SdT － pdV
G=H－TS dG=dH－TdS－SdT
dG= － SdT+Vdp
3
dU = TdS－ pdV dH = TdS + Vdp dA = －SdT－ pdV dG = －SdT + Vdp 应用条件是： (1) 封闭系统；(2) 无非体积功；(3) 可逆过程。
另外,下面的情况相当于具有可逆过程的条件： (i) 定量纯物质单相系统; (ii) 定量，定组成的单相系统; (iii) 保持相平衡及化学平衡的系统.
p
③ S、V 广度性质，p、T 强度性质，
同种属性组成分式，无负号；
S p V T T V
不同属性组成分式，有负号。
10
2. 热力学状态方程
由T S p V T V T
由麦克斯韦方程
S p V T T V
VII 热力学函数的基本关系式
第21节 热力学基本方程、吉布斯-亥姆霍茨方程 第22节 麦克斯韦关系式、热力学状态方程
1
第21节 热力学基本方程、吉布斯-亥姆霍茨方程
热力学第一定律 热力学第二定律 由实验直接测定
U、H S、A、G p、V、T
H
U
pV
TS
A
pV
TS
G
H = U + pV A = U－TS G = H－TS
U T2
6
第22节 麦克斯韦关系式、热力学状态方程
高等数学：
若Z＝f(x，y)，
dZ=
dZ dx
y
dx
dZ dy
x
dy
若Z有连续的二阶偏微商，则必有
y
Z x
y x
x
Z y
x
y
即
2Z 2Z
xy yx
7
1. 麦克斯韦关系式
dU＝TdS－pdV
dU
U S
dS
V