二次函数的最值问题与过定点类型问题
二次函数复习二次函数解决最值问题的思路与策略

二次函数复习二次函数解决最值问题的思路与策略二次函数复习:解决最值问题的思路与策略二次函数在高中数学中是一个重要的内容,涉及到了最值问题的求解。
本文将从复习二次函数的基本形式开始,逐步介绍解决最值问题的思路与策略。
一、二次函数的基本形式二次函数一般具有如下基本形式:f(x) = ax^2 + bx + c (a≠0)其中,a、b、c为实数,且a不等于0。
通过调整a、b、c的值,可以使二次函数的图像发生上下平移、左右平移和翻转等变化。
二、最值问题的定义在二次函数中,最值问题通常指的是求解函数的最大值或最小值。
最大值对应函数的顶点,最小值对应函数的谷点。
三、解决最值问题的思路解决最值问题的思路可以总结为以下几个步骤:1. 了解函数的基本形式:首先确定二次函数的基本形式,即f(x) = ax^2 + bx + c。
根据实际问题的给定条件,确定a、b、c的值。
2. 求解顶点坐标:通过平移变换,将二次函数的图像平移到合适的位置,使其顶点的坐标易于计算。
顶点的横坐标可通过 x = -b/(2a) 得到,而纵坐标可通过代入横坐标得到。
3. 判断最值类型:根据二次函数的开口方向(即a的正负)来判断最值类型。
当a>0时,函数开口向上,为最小值问题;当a<0时,函数开口向下,为最大值问题。
4. 求解最值:根据最值类型和顶点的坐标,可以直接得到函数的最值。
四、解决最值问题的策略解决最值问题的策略根据具体情况有所不同,下面列举了几种常见的策略:1. 利用函数的图像分析:通过观察二次函数的图像,分析函数在定义域上的变化趋势,找到最值所处的位置。
2. 利用对称性求解:当二次函数关于y轴对称时,可以利用对称性直接得到函数的最值。
3. 应用配方法:对于一些复杂的二次函数,可以通过配方法将其化简为标准的二次函数形式,然后再求解最值。
4. 利用一元二次不等式求解:通过将二次函数转化为一元二次不等式,可以得到函数的最值所在的区间,进而求解最值。
初中二次函数过定点问题

初中二次函数过定点问题一、问题的重要性在初中的数学课程中,二次函数是重要的内容之一,它不仅在数学领域有广泛的应用,还在物理、经济和其他科学领域中有所涉及。
而二次函数过定点的问题,是二次函数中的一个经典问题,它能帮助我们深入理解函数的性质,提高我们的数学思维能力。
二、问题概述二次函数过定点的问题,是指在二次函数图像中,无论自变量取何值,函数值恒为定值的点的位置问题。
这种定值可以是常数,也可以是与自变量有关的表达式。
这种问题的解决需要我们对二次函数的性质有深入的理解,以及对函数图像的准确描绘。
三、解决步骤和方法1. 确定二次函数的形式:首先我们需要根据题目给出的条件,确定二次函数的形式。
通常,二次函数的形式为y=ax²+bx+c。
2. 计算定点坐标:在确定了二次函数的形式后,我们需要通过解方程来找到定点的坐标。
例如,如果定点是(m, n),那么我们需要找到使am²+bm+c=n成立的m和n的值。
3. 描绘函数图像:根据确定的二次函数形式和定点坐标,我们可以描绘出函数的图像。
4. 验证答案:最后,我们需要验证我们的答案是否正确。
这可以通过将自变量的值代入二次函数中,看是否得到与定点相同的函数值来完成。
四、实例分析例如,若二次函数y=x²-2x-3过定点(m, n),且无论m取何值,n总为常数,求这个定点坐标。
首先,我们可以通过整理函数的形式来找到定点的坐标:y=x²-2x-3=(x-1)²-4,这个函数的图像是一个开口向上的抛物线,顶点坐标为(1, -4)。
因此,这个二次函数过定点(1, -4)。
五、结论与展望解决二次函数过定点的问题需要我们对二次函数的性质有深入的理解和掌握,同时还需要我们具备灵活的思维能力和良好的代数运算技巧。
在解决这类问题的过程中,我们不仅可以提高我们的数学思维能力,还可以提升我们的数学素养。
在未来的学习和研究中,我们将会遇到更多与二次函数过定点类似的问题。
二次函数的最值问题求解

二次函数的最值问题求解二次函数是数学中常见的一种函数形式,它的一般形式可以表示成f(x) = ax^2 + bx + c,其中a、b、c为实数且a ≠ 0。
而二次函数的最值问题是指求解二次函数在给定定义域上的最大值或最小值的过程。
一、二次函数的最值问题一般求解方法要解决二次函数的最值问题,一般可以采用以下几个步骤:1. 确定二次函数的开口方向:根据二次系数a的正负性来确定开口是向上还是向下。
当a > 0时,二次函数开口向上;当a < 0时,二次函数开口向下。
2. 求解二次函数的顶点坐标:顶点坐标可以通过公式x = -b / (2a)求得。
将x = -b / (2a)带入函数表达式中,得到对应的y值。
顶点的坐标表示了二次函数的最值。
3. 判定定义域:根据问题给出的条件或定义域限制,确定二次函数的定义域。
4. 推导最值:根据二次函数的开口方向和定义域,判定二次函数的最值。
当二次函数开口向上时,最值为最小值;当二次函数开口向下时,最值为最大值。
二、举例求解二次函数的最值问题为了更好地理解二次函数的最值问题,以下通过一个具体的例子来进行求解:已知二次函数f(x) = x^2 - 4x + 3,求解其最小值。
1. 确定开口方向:由于二次函数的系数a = 1 > 0,所以函数的开口是向上的。
2. 求解顶点坐标:通过公式x = -b / (2a)求得x的值。
将函数f(x)的系数代入计算,有x = -(-4) / (2*1) = 2。
将x = 2带入函数表达式f(x)中,计算得y = (2)^2 - 4(2) + 3 = -1。
因此,顶点坐标为(2, -1)。
3. 判定定义域:对于该函数来说,定义域是全体实数。
4. 得出最小值:由于二次函数开口向上,所以顶点的y值即为最小值。
因此,该二次函数的最小值为-1。
通过以上的计算,我们成功地求解了二次函数的最值问题。
三、总结在实际问题中,二次函数的最值问题是一类常见且重要的数学问题。
二次函数与几何的动点及最值、存在性问题(解析版)-2024中考数学

二次函数与几何的动点及最值、存在性问题目录题型01平行y轴动线段最大值与最小值问题题型02抛物线上的点到某一直线的距离问题题型03已知点关于直线对称点问题题型04特殊角度存在性问题题型05将军饮马模型解决存在性问题题型06二次函数中面积存在性问题题型07二次函数中等腰三角形存在性问题题型08二次函数中直角三角形存在性问题题型09二次函数中全等三角形存在性问题题型10二次函数中相似三角形存在性问题题型11二次函数中平行四边形存在性问题题型12二次函数中矩形存在性问题题型13二次函数中菱形存在性问题题型14二次函数中正方形存在性问题二次函数常见存在性问题:(1)等线段问题:将动点坐标用函数解析式以“一母式”的结构表示出来,再利用点到点或点到直线的距离公式列出方程或方程组,然后解出参数的值,即可以将线段表示出来.【说明】在平面直角坐标系中该点在某一函数图像上,设该点的横坐标为m,则可用含m字母的函数解析式来表示该点的纵坐标,简称“设横表纵”或“一母式”.(2)平行y轴动线段最大值与最小值问题:将动点坐标用函数解析式以“一母式”的结构表示出来,再用纵坐标的较大值减去较小值,再利用二次函数的性质求出动线段的最大值或最小值.(3)求已知点关于直线对称点问题:先求出直线解析式,再利用两直线垂直的性质(两直线垂直,斜率之积等于-1)求出已知点所在直线的斜率及解析式,最后用中点坐标公式即可求出对称点的坐标.(4)“抛物线上是否存在一点,使其到某一直线的距离为最值”的问题:常常利用直线方程与二次函数解析式联立方程组,求出切点坐标,运用点到直线的距离公式进行求解.(5)二次函数与一次函数、特殊图形、旋转及特殊角度综合:图形或一次函数与x 轴的角度特殊化,利用与角度有关知识点求解函数图像上的点,结合动点的活动范围,求已知点与动点是否构成新的特殊图形.2.二次函数与三角形综合(1)将军饮马问题:本考点主要分为两类:①在定直线上是否存在点到两定点的距离之和最小;②三角形周长最小或最大的问题,主要运用的就是二次函数具有对称性.(2)不规则三角形面积最大或最小值问题:利用割补法将不规则三角形分割成两个或以上的三角形或四边形,在利用“一母式”将动点坐标表示出来,作线段差,用线段差来表示三角形的底或高,用面积公式求出各部分面积,各部分面积之和就是所求三角形的面积.将三角形的面积用二次函数的结构表示出来,再利用二次函数的性质求出面积的最值及动点坐标.(3)与等腰三角形、直角三角形的综合问题:对于此类问题,我们可以利用两圆一线或两线一圆的基本模型来进行计算.问题分情况找点画图解法等腰三角形已知点A ,B 和直线l ,在l 上求点P ,使△PAB 为等腰三角形以AB为腰分别以点A ,B 为圆心,以AB 长为半径画圆,与已知直线的交点P 1,P 2,P 4,P 5即为所求分别表示出点A ,B ,P 的坐标,再表示出线段AB ,BP ,AP 的长度,由①AB =AP ;②AB =BP ;③BP =AP 列方程解出坐标以AB 为底作线段AB 的垂直平分线,与已知直线的交点P 3即为所求分别表示出点A ,B ,P 的坐标,再表示出线段AB ,BP ,AP 的长度,由①AB =AP ;②AB =BP ;③BP =AP 列方程解出坐标问题分情况找点画图解法直角三角形已知点A ,B 和直线l ,在l 上求点P ,使△PAB 为直角三角形以AB为直角边分别过点A ,B 作AB 的垂线,与已知直线的交点P 1,P 4即为所求分别表示出点A ,B ,P 的坐标,再表示出线段AB ,BP ,AP 的长度,由①AB 2=BP 2+AP 2;②BP 2=AB 2+AP 2;③AP 2=AB 2+BP 2列方程解出坐标以AB 为斜边以AB 的中点Q 为圆心,QA 为半径作圆,与已知直线的交点P 2,P 3即为所求注:其他常见解题思路有:①作垂直,构造“三垂直”模型,利用相似列比例关系得方程求解;②平移垂线法:若以AB 为直角边,且AB 的一条垂线的解析式易求(通常为过原点O 与AB 垂直的直线),可将这条直线分别平移至过点A 或点B 得到相应解析式,再联立方程求解.(4)与全等三角形、相似三角形的综合问题:在没有指定对应点的情况下,理论上有六种情况需要讨论,但在实际情况中,通常不会超过四种,要注意边角关系,积极分类讨论来进行计算.情况一探究三角形相似的存在性问题的一般思路:解答三角形相似的存在性问题时,要具备分类讨论思想及数形结合思想,要先找出三角形相似的分类标准,一般涉及动态问题要以静制动,动中求静,具体如下:①假设结论成立,分情况讨论.探究三角形相似时,往往没有明确指出两个三角形的对应点(尤其是以文字形式出现求证两个三角形相似的题目),或者涉及动点问题,因动点问题中点的位置的不确定,此时应考虑不同的对应关系,分情况讨论;②确定分类标准.在分类时,先要找出分类的标准,看两个相似三角形是否有对应相等的角,若有,找出对应相等的角后,再根据其他角进行分类讨论来确定相似三角形成立的条件;若没有,则分别按三种角对应来分类讨论;③建立关系式,并计算.由相似三角形列出相应的比例式,将比例式中的线段用所设点的坐标表示出来(其长度多借助勾股定理运算),整理可得一元一次方程或者一元二次方程,解方程可得字母的值,再通过计算得出相应的点的坐标.情况二探究全等三角形的存在性问题的思路与探究相似三角形的存在性问题类似,但是除了要找角相等外,还至少要找一组对应边相等.3.二次函数与四边形的综合问题特殊四边形的探究问题解题步骤如下:①先假设结论成立;②设出点坐标,求边长;③建立关系式,并计算.若四边形的四个顶点位置已确定,则直接利用四边形边的性质进行计算;若四边形的四个顶点位置不确定,需分情况讨论:a.探究平行四边形:①以已知边为平行四边形的某条边,画出所有的符合条件的图形后,利用平行四边形的对边相等进行计算;②以已知边为平行四边形的对角线,画出所有的符合条件的图形后,利用平行四边形对角线互相平分的性质进行计算;③若平行四边形的各顶点位置不确定,需分情况讨论,常以已知的一边作为一边或对角线分情况讨论.b.探究菱形:①已知三个定点去求未知点坐标;②已知两个定点去求未知点坐标,一般会用到菱形的对角线互相垂直平分、四边相等的性质列关系式.c.探究正方形:利用正方形对角线互相垂直平分且相等的性质进行计算,一般是分别计算出两条对角线的长度,令其相等,得到方程再求解.d.探究矩形:利用矩形对边相等、对角线相等列等量关系式求解;或根据邻边垂直,利用勾股定理列关系式求解.题型01平行y轴动线段最大值与最小值问题1(2023·广东东莞·一模)如图,抛物线y=x2+bx+c与x轴交于A、B两点,与y轴交于点C,OA=OC =3,顶点为D.(1)求此函数的关系式;(2)在AC 下方的抛物线上有一点N ,过点N 作直线l ∥y 轴,交AC 与点M ,当点N 坐标为多少时,线段MN 的长度最大?最大是多少?(3)在对称轴上有一点K ,在抛物线上有一点L ,若使A ,B ,K ,L 为顶点形成平行四边形,求出K ,L 点的坐标.(4)在y 轴上是否存在一点E ,使△ADE 为直角三角形,若存在,直接写出点E 的坐标;若不存在,说明理由.【答案】(1)y =x 2+2x -3(2)当N 的坐标为-32,-154 ,MN 有最大值94(3)K -1,4 ,L -1,-4 或K -1,12 ,L -5,12 或K -1,12 ,L 3,12(4)存在,点E 的坐标为0,32 或0,-72或0,-1 或0,-3【分析】(1)由OA =OC =3求得A -3,0 ,C 0,-3 ,再分别代入抛物线解析式y =x 2+bx +c ,得到以b ,c 为未知数的二元一次方程组,求出b ,c 的值即可;(2)求出直线AC 的解析式,再设出M 、N 的坐标,把MN 表示成二次函数,配方即可;(3)根据平行四边形的性质,以AB 为边,以AB 为对角线,分类讨论即可;(4)设出E 的坐标,分别表示出△ADE 的平分,再分每一条都可能为斜边,分类讨论即可.【详解】(1)∵抛物线y =x 2+bx +c 经过点A ,点C ,且OA =OC =3,∴A -3,0 ,C 0,-3 ,∴将其分别代入抛物线解析式,得c =-39-3b +c =0,解得b =2c =-3 .故此抛物线的函数表达式为:y =x 2+2x -3;(2)设直线AC 的解析式为y =kx +t ,将A -3,0 ,C 0,-3 代入,得t =-3-3k +t =0 ,解得k =-1t =-3 ,∴直线AC 的解析式为y =-x -3,设N 的坐标为n ,n 2+2n -3 ,则M n ,-n -3 ,∴MN =-n -3-n 2+2n -3 =-n 2-3n =-n +32 +94,∵-1<0,∴当n =-32时,MN 有最大值,为94,把n =-32代入抛物线得,N 的坐标为-32,-154,当N 的坐标为-32,-154 ,MN 有最大值94;(3)①当以AB 为对角线时,根据平行四边形对角线互相平分,∴KL 必过-1,0 ,∴L 必在抛物线上的顶点D 处,∵y =x 2+2x -3=x +1 2-4,∴K -1,4 ,L -1,-4②当以AB 为边时,AB =KL =4,∵K 在对称轴上x =-1,∴L 的横坐标为3或-5,代入抛物线得L -5,12 或L 3,12 ,此时K 都为-1,12 ,综上,K -1,4 ,L -1,-4 或K -1,12 ,L -5,12 或K -1,12 ,L 3,12 ;(4)存在,由y =x 2+2x -3=x +1 2-4,得抛物线顶点坐标为D -1,-4 ∵A -3,0 ,∴AD 2=-3+1 2+0+4 2=20,设E 0,m ,则AE 2=-3-0 2+0-m 2=9+m 2,DE 2=-1-0 2+-4-m 2=17+m 2+8m ,①AE 为斜边,由AE 2=AD 2+DE 2得:9+m 2=20+17+m 2+8m ,解得:m =-72,②DE 为斜边,由DE 2=AD 2+AE 2得:9+m 2+20=17+m 2+8m ,解得:m =32,③AD 为斜边,由AD 2=ED 2+AE 2得:20=17+m 2+8m +9+m 2,解得:m =-1或-3,∴点E 的坐标为0,32 或0,-72或0,-1 或0,-3 .【点睛】本题主要考查待定系数法求二次函数解析式,二次函数图象与性质,平行四边形的判定与性质以及勾股定理等知识,会运用待定系数法列方程组,两点间距离公式求MN 的长,由平行四边形的性质判定边相等,运用勾股定理列方程.2(2023·河南南阳·统考一模)如图,抛物线与x 轴相交于点A 、B (点A 在点B 的左侧),与y 轴的交于点C 0,-4 ,点P 是第三象限内抛物线上的一个动点,设点P 的横坐标为m ,过点P 作直线PD ⊥x 轴于点D ,作直线AC 交PD 于点E .已知抛物线的顶点P 坐标为-3,-254.(1)求抛物线的解析式;(2)求点A 、B 的坐标和直线AC 的解析式;(3)求当线段CP =CE 时m 的值;(4)连接BC ,过点P 作直线l ∥BC 交y 轴于点F ,试探究:在点P 运动过程中是否存在m ,使得CE =DF ,若存在直接写出m 的值;若不存在,请说明理由.【答案】(1)y =14x 2+32x -4(2)A -8,0 ,B 2,0 ,y =-12x -4(3)-4(4)存在,m =2-25或m =-4【分析】(1)运用待定系数法即可求得抛物线的解析式;(2)令y =0,解方程即可求得点A 、B 的坐标,再运用待定系数法即可求得直线AC 的解析式;(3)过点C 作CF ⊥PE 于点F ,根据等腰三角形的性质可得点F 是PE 的中点,设P m ,14m 2+32m -4 ,则E m ,-12m -4 ,可得F m ,18m 2+12m -4 ,再由点F 与点C 的纵坐标相同建立方程求解即可;(4)过C 作CH ⊥PD 于H ,设P m ,14m 2+32m -4 ,由PF ∥BC ,可得直线PF 解析式为y =2x +14m 2-12m -4,进而可得OF =14m 2-12m -4 ,再证得Rt △CHE ≅Rt △DOF HL ,得出∠HCE =∠FDO ,进而推出∠FDO =∠CAO ,即tan ∠FDO =tan ∠CAO ,据此建立方程求解即可.【详解】(1)解:∵抛物线的顶点坐标为-3,-254∴设抛物线的解析式为y =a x +3 2-254,把点C 0,-4 代入,得:-4=9a -254,解得:a =14,∴y =14x +3 2-254=14x 2+32x -4,∴该抛物线的解析式为y =14x 2+32x -4.(2)解:令y =0,得14x 2+32x -4=0,解得:x 1=-8,x 2=2,∴A -8,0 ,B 2,0 ,,设直线AC 的解析式为y =kx +b ,则-8k +b =0b =-4 ,解得:k =-12b =-4 ,∴直线AC 的解析式为y =-12x -4.(3)解:如图,过点C 作CF ⊥PE 于点F ,∵CP =CE ,∴EF =PF ,即点F 是PE 的中点,设P m ,14m 2+32m -4 ,则E m ,-12m -4 ,∴F m ,18m 2+12m -4 ,∵PE ∥y 轴,CF ⊥PE ,∴CF ∥x 轴,∴18m 2+12m -4=-4,解得:m =-4或m =0(不符合题意,舍去),∴m =-4.(4)解:存在m ,使得CE =DF ,理由如下:如图:过C 作CH ⊥PD 于H ,设P m,14m2+32m-4,由B2,0,C0,-4,由待定系数法可得直线BC解析式为y=2x-4,根据PF∥BC,设直线PF解析式为y=2x+c,将P m,14m2+32m-4代入得:1 4m2+32m-4=2m+c,∴c=14m2-12m-4,∴直线PF解析式为y=2x+14m2-12m-4,令x=0得y=14m2-12m-4,∴F0,14m2-12m-4,∴OF=14m2-12m-4,∵∠CHD=∠PDO=∠COD=90°,∴四边形CODH是矩形,∴CH=OD,∵CE=DF,∴Rt△CHE≅Rt△DOF HL,∴∠HCE=∠FDO,∵∠HCE=∠CAO,∴∠FDO=∠CAO,∴tan∠FDO=tan∠CAO,∴OF OD =OCOA,即14m2-12m-4-m=48=12,∴1 4m2-12m-4=-12m或14m2-12m-4=12m,解得:m=-4或m=4或m=2-25或m=2+25,∵P在第三象限,∴m=2-25或m=-4.【点睛】本题属于二次函数综合题,主要考查了待定系数法求函数解析式、二次函数综合应用、等腰三角形性质、矩形判定及性质、相似三角形判定及性质、解直角三角形等知识点,解题的关键是用含m的代数式表示相关点坐标和相关线段的长度.3(2023·山东聊城·统考三模)抛物线y=-x2+bx+c与x轴交于点A3,0,与y轴交于点C0,3,点P 为抛物线上的动点.(2)若P 为直线AC 上方抛物线上的动点,作PH ∥x 轴交直线AC 于点H ,求PH 的最大值;(3)点N 为抛物线对称轴上的动点,是否存在点N ,使直线AC 垂直平分线段PN ?若存在,请直接写出点N 的纵坐标;若不存在,请说明理由.【答案】(1)b =2,c =3(2)PH 取得最大值为94(3)存在,2-2或2+2【分析】(1)将坐标代入解析式,构建方程求解;(2)设PH 交y 轴于点M ,P m ,-m 2+2m +3 ,则PM =m ;待定系数法确定直线AC 的解析式为y =-x +3,从而确定PH =m -m 2-2m =-m 2+3m =-m -32 2+94,解得PH 最大值为94;(3)如图,设PN 与AC 交于点G ,可设直线PN 的解析式为y =x +p ,设点N (1,n ),求得y =x +(n -1);联立y =-x +3y =x +(n -1) ,解得x =-n 2+2y =n 2+1,所以点P 的横坐标为2×-n 2+2 -1=-n +3,纵坐标为2×n2+1 -n =2,由二次函数解析式构建方程-(-n +3)2+2(-n +3)+3=2,解得n =2±2;【详解】(1)∵抛物线y =-x 2+bx +c 与x 轴交于点A 3,0 ,与y 轴交于点C 0,3 ,∴-9+3b +c =0c =3,解得:b =2c =3 ,∴b =2,c =3;(2)设PH 交y 轴于点M ,P m ,-m 2+2m +3 ,∴PM =m ,∵PH ∥x 轴,∴点H 的纵坐标为-m 2+2m +3,设直线AC 的解析式为y =kx +n ,∴3k +n =0n =3 ,解得:k =-1n =3 ,∴直线AC 的解析式为y =-x +3.∴-m 2+2m +3=-x +3,∴x =m 2-2m ,∴H m 2-2m ,-m 2+2m +3 ,∴PH =m -m 2-2m =-m 2+3m =-m -322+94,∴当m =32时,PH 取得最大值为94(3)存在点N ,使直线AC 垂直平分线段PN ,点N 的纵坐标为2-2或2+2如图,设PN 与AC 交于点G ,∵AC 垂直平分PN ,直线AC 的解析式为y =-x +3∴可设直线PN 的解析式为y =x +p 设点N (1,n ),则n =1+p ∴p =n -1,∴y =x +(n -1)联立y =-x +3y =x +(n -1) ,解得x =-n 2+2y =n 2+1∴点P 的横坐标为2×-n 2+2 -1=-n +3,纵坐标为2×n 2+1 -n =2∴-(-n +3)2+2(-n +3)+3=2,解得n =2±2∴点N 的纵坐标为2-2或2+2.【点睛】本题考查利用二次函数解析式及点坐标求待定参数、待定系数法确定函数解析式、二次函数极值及其它二次函数综合问题,利用直线间的位置关系、点线间的位置关系,融合方程的知识求解坐标是解题的关键.题型02抛物线上的点到某一直线的距离问题1(2023·广东梅州·统考二模)探究求新:已知抛物线G 1:y =14x 2+3x -2,将抛物线G 1平移可得到抛物线G 2:y =14x 2.(1)求抛物线G 1平移得到抛物线G 2的平移路径;(2)设T 0,t ,直线l :y =-t ,是否存在这样的t ,使得抛物线G 2上任意一点到T 的距离等于到直线l 的距离?若存在,求出t 的值;若不存在,试说明理由;(3)设H 0,1 ,Q 1,8 ,M 为抛物线G 2上一动点,试求QM +MH 的最小值.参考公式:若点M x 1,y 1 ,N x 2,y 2 为平面上两点,则有MN =x 1-x 22+y 1-y 2 2.【答案】(1)将G 1向左平移-6个单位,向上平移11个单位(2)存在,1(3)9【分析】(1)设G 1向左平移a 个单位,向上平移b 个单位得到函数G 2,列方程组即可求解;(2)设P x 0,x 204为抛物线G 2上的一点,根据题意列方程即可;(3)点H 坐标与(2)中t =1时的T 点重合,过点M 作MA ⊥l ,垂足为A ,如图所示,则有MH =MA ,当且仅当Q ,M ,A 三点共线时QM +MA 取得最小值.【详解】(1).解:设G 1向左平移a 个单位,向上平移b 个单位得到函数G 2,由平移法则可知14(x +a )2+3(x +a )-2+b =14x 2,整理可得14x 2+3+12a x +14a 2+3a -2+b =14x 2,可得方程组3+12a =014a 2+3a -2+b =0,解得a =-6b =11 ;∴平移路径为将G 1向左平移-6个单位,向上平移11个单位;(2)解:存在这样的t ,且t =1时满足条件,设P x 0,x 204为抛物线G 2上的一点,则点P 到直线l 的距离为x 204+t ,点P 到点T 距离为(x 0-0)2+x 204-t2,联立可得:x 204+t =(x 0-0)2+x 204-t2,两边同时平方合并同类项后可得x 20-x 20t =0解得:t =1;(3)解:点H 坐标与(2)中t =1时的T 点重合,作直线l :y =-1,过点M 作MA ⊥直线l ,垂足为A ,如图所示,则有MH =MA ,此时QM +MH =QM +MA ,当且仅当Q ,M ,A 三点共线时QM +MA 取得最小值即QM +MA =QA =8-(-1)=9∴QM +MH 的最小值为9;【点睛】本题考查二次函数综合题,涉及到线段最小值、平移性质等,灵活运用所学知识是关键.2(2023·湖北宜昌·统考一模)如图,已知:点P 是直线l :y =x -2上的一动点,其横坐标为m (m 是常数),点M 是抛物线C :y =x 2+2mx -2m +2的顶点.(1)求点M 的坐标;(用含m 的式子表示)(2)当点P 在直线l 运动时,抛物线C 始终经过一个定点N ,求点N 的坐标,并判断点N 是否是点M 的最高位置?(3)当点P 在直线l 运动时,点M 也随之运动,此时直线l 与抛物线C 有两个交点A ,B (A ,B 可以重合),A ,B 两点到y 轴的距离之和为d .①求m 的取值范围;②求d 的最小值.【答案】(1)M -m ,-m 2-2m +2(2)N (1,3),点N 是点M 的最高位置(3)①m ≤-52或m ≥32;②d 取得最小值为2【分析】(1)将抛物线解析式写成顶点式即可求解;(2)根据解析式含有m 项的系数为0,得出当x =1时,y =3,即N (1,3),根据二次函数的性质得出-m 2-2m +2=-m +1 2+3的最大值为3,即可得出点N 是点M 的最高位置;(3)①根据直线与抛物线有交点,联立方程,根据一元二次方程根的判别式大于等于0,求得m 的范围,即可求解;②设A ,B 的坐标分别为x 1,y 1 ,x 2,y 2 ,其中x 1<x 2,由①可知x 1,x 2是方程x 2+2mx -x -2m +4=0的两根,根据x 1+x 2=-2m +1,分情况讨论,求得d 是m 的一次函数,进而根据一次函数的性质即可求解.【详解】(1)解:y =x 2+2mx -2m +2=x +m 2-m 2-2m +2,∴顶点M -m ,-m 2-2m +2 ,(2)解:∵y =x 2+2mx -2m +2=x 2+2+2m x -1 ,∴当x =1时,y =3,抛物线C 始终经过一个定点1,3 ,即N (1,3);∵M -m ,-m 2-2m +2 ,-m 2-2m +2=-m +1 2+3,∴M 的纵坐标最大值为3,∴点N 是点M 的最高位置;(3)解:①联立y =x -2y =x 2+2mx -2m +2 ,得x 2+2mx -x -2m +4=0,∵直线l 与抛物线C 有两个交点A ,B (A ,B 可以重合),∴Δ=b 2-4ac =2m -1 2-4-2m +4 ,=4m 2+4m -15≥0,∵4m 2+4m -15=0,解得m 1=-52,m 2=32,∴当4m 2+4m -15≥0时,m ≤-52或m ≥32,②设A ,B 的坐标分别为x 1,y 1 ,x 2,y 2 ,其中x 1<x 2,由①可知x 1,x 2是方程x 2+2mx -x -2m +4=0的两根,∴x1+x 2=-2m +1,当m =-3时,如图所示,y A =0,当-3≤m ≤-52时,y 1≥0,y 2≥0,则d =x 1+x 2 =-2m +1 ,∵-2<0,∴当m =-52时,d 取得最小值为-2×-52 +1=5+1=6,当m ≥32时,d =-x 1+x 2 =--2m +1 =2m -1,∴当m =32时,d 取得最小值为2×32-1=2,综上所述,d 取得最小值为2.【点睛】本题考查了二次函数的性质,一元二次方程与二次函数的关系,熟练掌握二次函数的性质是解题的关键.3(2023·云南楚雄·统考一模)抛物线y =x 2-2x -3交x 轴于A ,B 两点(A 在B 的左边),C 是第一象限抛物线上一点,直线AC 交y 轴于点P .(1)直接写出A ,B 两点的坐标;(2)如图①,当OP =OA 时,在抛物线上存在点D (异于点B ),使B ,D 两点到AC 的距离相等,求出所有满足条件的点D 的横坐标;(3)如图②,直线BP 交抛物线于另一点E ,连接CE 交y 轴于点F ,点C 的横坐标为m ,求FP OP 的值(用含m 的式子表示).【答案】(1)A (-1,0),B (3,0)(2)0或3-41或3+41(3)13m 【分析】(1)令y =0,解方程可得结论;(2)分两种情形:①若点D 在AC 的下方时,过点B 作AC 的平行线与抛物线交点即为D 1.②若点D 在AC 的上方时,点D 1关于点P 的对称点G (0,5),过点G 作AC 的平行线交抛物线于点D 2,D 3,D 2,D 3符合条件.构建方程组分别求解即可;(3)设E 点的横坐标为n ,过点P 的直线的解析式为y =kx +b ,由y =kx +b y =x 2-2x -3 ,可得x 2-(2+k )x -3-b =0,设x 1,x 2是方程x 2-(2+k )x -3-b =0的两根,则x 1x 2=-3-b ,推出x A ⋅x C =x B ⋅x E =-3-b 可得n =-1-b 3,设直线CE 的解析式为y =px +q ,同法可得mn =-3-q 推出q =-mn -3,推出q =-(3+b )-1-b 3 -3=13b 2+2b ,推出OF =13b 2+b ,可得结论.【详解】(1)解:令y =0,得x 2-2x -3=0,解得:x =3或-1,∴A (-1,0),B (3,0);(2)∵OP =OA =1,∴P (0,1),∴直线AC 的解析式为y =x +1.①若点D 在AC 的下方时,过点B 作AC 的平行线与抛物线交点即为D 1.∵B (3,0),BD 1∥AC ,∴直线BD 1的解析式为y =x -3,由y =x -3y =x 2-2x -3,解得x =3y =0 或x =0y =-3 ,∴D 1(0,-3),∴D 1的横坐标为0.②若点D 在AC 的上方时,点D 1关于点P 的对称点G (0,5),过点G 作AC 的平行线l 交抛物线于点D 2,D 3,D 2,D 3符合条件.直线l 的解析式为y =x +5,由y =x +5y =x 2-2x -3 ,可得x 2-3x -8=0,解得:x =3-412或3+412,∴D 2,D 3的横坐标为3-412,3+412,综上所述,满足条件的点D 的横坐标为0,3-412,3+412.(3)设E 点的横坐标为n ,过点P 的直线的解析式为y =kx +b ,由y =kx +b y =x 2-2x -3,可得x 2-(2+k )x -3-b =0,设x 1,x 2是方程x 2-(2+k )x -3-b =0的两根,则x 1x 2=-3-b ,∴x A ⋅x C =x B ⋅x E =-3-b∵x A =-1,∴x C =3+b ,∴m =3+b ,∵x B =3,∴x E =-1-b 3,∴n =-1-b 3,设直线CE 的解析式为y =px +q ,同法可得mn =-3-q∴q =-mn -3,∴q =-(3+b )-1-b 3 -3=13b 2+2b ,∴OF =13b 2+2b ,∴FP OP=13b +1=13(m -3)+1=13m .【点睛】本题属于二次函数综合题,考查了二次函数的性质,一次函数的性质,一元二次方程的根与系数的关系等知识,解题的关键是学会构建一次函数,构建方程组确定交点坐标,学会利用参数解决问题,属于中考压轴题.题型03已知点关于直线对称点问题1(2023·辽宁阜新·统考中考真题)如图,在平面直角坐标系中,二次函数y =-x 2+bx -c 的图象与x 轴交于点A (-3,0)和点B (1,0),与y 轴交于点C .(1)求这个二次函数的表达式.(2)如图1,二次函数图象的对称轴与直线AC :y =x +3交于点D ,若点M 是直线AC 上方抛物线上的一个动点,求△MCD 面积的最大值.(3)如图2,点P 是直线AC 上的一个动点,过点P 的直线l 与BC 平行,则在直线l 上是否存在点Q ,使点B 与点P 关于直线CQ 对称?若存在,请直接写出点Q 的坐标;若不存在,请说明理由.【答案】(1)y =-x 2-2x +3;(2)S △MCD 最大=98;(3)Q 1-5,-5 或1+5,5 .【分析】(1)根据抛物线的交点式直接得出结果;(2)作MQ ⊥AC 于Q ,作ME ⊥AB 于F ,交AC 于E ,先求出抛物线的对称轴,进而求得C ,D 坐标及CD 的长,从而得出过M 的直线y =x +m 与抛物线相切时,△MCD 的面积最大,根据x +m =-x 2-2x +3的△=0求得m 的值,进而求得M 的坐标,进一步求得CD 上的高MQ 的值,进一步得出结果;(3)分两种情形:当点P 在线段AC 上时,连接BP ,交CQ 于R ,设P (t ,t +3),根据CP =CB 求得t 的值,可推出四边形BCPQ 是平行四边形,进而求得Q 点坐标;当点P 在AC 的延长线上时,同样方法得出结果.【详解】(1)解:由题意得,y =-(x +3)(x -1)=-x 2-2x +3;(2)解:如图1,作MQ ⊥AC 于Q ,作ME ⊥AB 于F ,交AC 于E ,∵OA =OC =3,∠AOC =90°,∴∠CAO =∠ACO =45°,∴∠MEQ =∠AEF =90°-∠CAO =45°,抛物线的对称轴是直线:x =-3+12=-1,∴y =x +3=-1+3=2,∴D (1,2),∵C (0,3),∴CD =2,故只需△MCD 的边CD 上的高最大时,△MCD 的面积最大,设过点M 与AC 平行的直线的解析式为:y =x +m ,当直线y =x +m 与抛物线相切时,△MCD 的面积最大,由x +m =-x 2-2x +3得,x 2+3x +(m -3)=0,由△=0得,32-4(m -3)=0得,m -3=94,∴x 2+3x +94=0,∴x 1=x 2=-32,∴y =--32 2-2×-32 +3=154,y =x +3=-32+3=32,∴ME =154-32=94,∴MQ =ME ⋅sin ∠MEQ =ME ⋅sin45°=94×22=928,∴S △MCD 最大=12×2×928=98;(3)解:如图2,当点P 在线段AC 上时,连接BP ,交CQ 于R ,∵点B 和点Q 关于CQ 对称,∴CP =CB ,设P (t ,t +3),由CP 2=CB 2得,2t 2=10,∴t 1=-5,t 2=5(舍去),∴P -5,3-5 ,∵PQ ∥BC ,∴CR =BR =1,∴CR =QR ,∴四边形BCPQ 是平行四边形,∵1+(-5)-0=1-5,0+(3-5)-3=-5,∴Q 1-5,-5 ;如图3,当点P 在AC 的延长线上时,由上可知:P 5,3+5 ,同理可得:Q 1+5,5 ,综上所述:Q 1-5,-5 或1+5,5 .【点睛】本题考查了二次函数及其图象的性质,一元二次方程的解法,平行四边形的判定和性质,轴对称的性质等知识,解决问题的关键是分类讨论.2(2023·四川甘孜·统考中考真题)已知抛物线y =x 2+bx +c 与x 轴相交于A -1,0 ,B 两点,与y 轴相交于点C 0,-3 .(1)求b ,c 的值;(2)P 为第一象限抛物线上一点,△PBC 的面积与△ABC 的面积相等,求直线AP 的解析式;(3)在(2)的条件下,设E 是直线BC 上一点,点P 关于AE 的对称点为点P ,试探究,是否存在满足条件的点E ,使得点P 恰好落在直线BC 上,如果存在,求出点P 的坐标;如果不存在,请说明理由.【答案】(1)b =-2,c =-3.(2)y =x +1(3)存在,点P 的坐标为1+21,-2+21 或1-21,-2-21【分析】(1)由待定系数法即可求解;(2)S △PBC =S △ABC 得到AP ∥BC ,即可求解;(3)由题意的:∠AEP =∠AEP ,P E =PE ,即可求解.【详解】(1)由题意,得1-b +c =0,c =-3.∴b =-2,c =-3.(2)由(1)得抛物线的解析式为y =x 2-2x -3.令y =0,则x 2-2x -3=0,得x 1=-1,x 2=3.∴B 点的坐标为3,0 .∵S △PBC =S △ABC ,∴AP ∥BC .∵B 3,0,C 0,-3 ,∵AP∥BC,∴可设直线AP的解析式为y=x+m.∵A(-1,0)在直线AP上,∴0=-1+m.∴m=1.∴直线AP的解析式为y=x+1.(3)设P点坐标为m,n.∵点P在直线y=x+1和抛物线y=x2-2x-3上,∴n=m+1,n=m2-2m-3.∴m+1=m2-2m-3.解得m1=4,m2=-1(舍去).∴点P的坐标为4,5.由翻折,得∠AEP=∠AEP ,P E=PE.∵AP∥BC,∴∠PAE=∠AEP '.∴∠PAE=∠PEA.∴PE=PA=4+12=52.2+5-0设点E的坐标为t,t-3,则PE2=t-42.2+t-3-52=52∴t=6±21.当t=6+21时,点E的坐标为6+21,3+21.设P (s,s-3),由P E=AP,P E=PE=52得:s-6-212,2=522+s-3-3-21解得:s=1+21,则点P 的坐标为1+21,-2+21.当t=6-21时,同理可得,点P 的坐标为1-21,-2-21.综上所述,点P 的坐标为1+21,-2+21.或1-21,-2-21【点睛】本题是二次函数的综合题,主要考查了用待定系数法求一次函数、二次函数的解析式,二次函数的性质,此题题型较好,综合性比较强,用的数学思想是分类讨论和数形结合的思想.3(2023·江苏连云港·连云港市新海实验中学校考二模)如图,“爱心”图案是由抛物线y=-x2+m的一部分及其关于直线y=-x的对称图形组成,点E、F是“爱心”图案与其对称轴的两个交点,点A、B、C、D是该图案与坐标轴的交点,且点D的坐标为6,0.(1)求m 的值及AC 的长;(2)求EF 的长;(3)若点P 是该图案上的一动点,点P 、点Q 关于直线y =-x 对称,连接PQ ,求PQ 的最大值及此时Q 点的坐标.【答案】(1)m =6,AC =6+6(2)52(3)2542,Q -234,-12【分析】(1)用待定系数法求得m 与抛物线的解析式,再求出抛物线与坐标轴的交点坐标,进而求得A 的坐标,根据对称性质求得B ,C 的坐标,即可求得结果;(2)将抛物线的解析式与直线EF 的解析式联立方程组进行求解,得到E ,F 的坐标,即可求得结果;(3)设P (m ,-m 2+6),则Q (m 2-6,-m ),可得PQ =2×m -12 2-252 ,即求m -12 2-252的最值,根据二次函数的最值,即可得到m 的值,即可求得.【详解】(1)把D 6,0 代入y =-x 2+m 得0=-6+m解得m =6∴抛物线的解析式为:y =-x 2+6∴A 0,6根据对称性可得B -6,0 ,C 0,-6∴AC =AO +OC =6+6(2)联立y =-x y =-x 2+6解得x =3y =-3 或x =-2y =2 ∴E -2,2 ,F 3,-3∴EF =-2-3 2+2+3 2=52(3)设P (m ,-m 2+6),则Q (m 2-6,-m )∴PQ =m -m 2-6 2+-m 2+6--m 2整理得PQ =2×m -12 2-254 ∵m -12 2≥0∴当m -12 2=0时,即m =12时,m -12 2-254 有最大值为254∴PQ 的最大值为2542∴12 2-6=-234故Q -234,-12【点睛】本题考查二次函数综合应用,涉及待定系数法求函数解析式,两点间的距离公式,求抛物线与一次函数的交点坐标,二次函数的最值等知识,解题的关键是掌握关于直线y =-x 对称的点坐标的关系.题型04特殊角度存在性问题1(2023·山西忻州·统考模拟预测)如图,抛物线y =18x 2+34x -2与x 轴交于A ,B 两点,与y 轴交于点C .P 是直线AC 下方抛物线上一个动点,过点P 作直线l ∥BC ,交AC 于点D ,过点P 作PE ⊥x 轴,垂足为E ,PE 交AC 于点F .(1)直接写出A ,B ,C 三点的坐标,并求出直线AC 的函数表达式;(2)当线段PF 取最大值时,求△DPF 的面积;(3)试探究在拋物线的对称轴上是否存在点Q ,使得∠CAQ =45°?若存在,请直接写出点Q 的坐标;若不存在,请说明理由.【答案】(1)A -8,0 ,B 2,0 ,C 0,-2 .y =-14x -2(2)85(3)存在,-3,3 或-3,-253【分析】(1)对于直线y =18x 2+34x -2,当x =0时,y =-2,即点C 0,-2 ,令18x 2+34x -2=0,则x =2或-8,则点A ,B 的坐标分别为-8,0 ,2,0 即求出三个点的坐标,设直线AC 的表达式为y =kx +b ,利用待定系数法求解即可;(2)设点P 的横坐标为m ,则P m ,18m 2+34m -2 ,F m ,-14m -2 ,表示出PF =-18m 2-m ,求出PF max =2,再表示出点D 到直线PF 的距离d =85,利用S △DPF =12⋅PF ⋅d 进行求解即可;(3)由抛物线的表达式知,其对称轴为x =-3,当点Q 在x 轴上方时,设抛物线的对称轴交x 轴于点N ,交AC 于H ,故点Q 作QT ⊥AC 于点T ,在△AQH 中,∠CAQ =45°,tan ∠QHA =4,用解直角三角形的方法求出QH =174,即可求出Q 点坐标,当点Q Q 在x 轴上方时,直线AQ 的表达式为y =35x +8 ,当∠CAQ =45°时,AQ ⊥AQ ,即可求解.【详解】(1)解:对于抛物线y =18x 2+34x -2,当x =0时,y =-2,即点C 0,-2 ,令18x 2+34x -2=0,则x =2或-8,则点A ,B 的坐标分别为-8,0 ,2,0 ,即点A ,B ,C 三点的坐标分别为-8,0 ,2,0 ,0,-2 ,设直线AC 的表达式为y =kx +b ,则-8k +b =0b =-2 ,解得k =-14b =-2 ,∴直线AC 的函数表达式为y =-14x -2;(2)设点P 的横坐标为m ,则P m ,18m 2+34m -2 ,F m ,-14m -2 ,PF =-14m -2 -18m 2+34m -2 =-18m 2-m ,当m =--12×-18 =-4时,PF 最大,PF max =-18×(-4)2--4 =2,此时,P -4,-3 ,由B 2,0 ,C 0,-2 ,可得直线BC 的函数表达式为y =x -2,设直线l 的函数表达式为y =x +p ,将P -4,-3 代入可得p =1,∴直线l 的函数表达式为y =x +1,由y =-14x -2y =x +1 ,解得x =-125y =-75,∴D -125,-75 ,点D 到直线PF 的距离d =-125--4 =85,∴S △DPF =12⋅PF ⋅d =12×2×85=85.(3)存在,理由:由抛物线的表达式知,其对称轴为x =-3,当点Q 在x 轴上方时,如下图:设抛物线的对称轴交x 轴于点N ,交AC 于H ,故点Q 作QT ⊥AC 于点T ,则∠ACO =∠QHA ,则tan ∠ACO =tan ∠QHA =4,当x =3时,y =-14x -2=-54,则点H -3,-54 ,由点A ,H 的坐标得,AH =5174,在△AQH 中,∠CAQ =45°,tan ∠QHA =4,设TH =x ,则QT =4x ,则QH =17x ,则AH =AT +TH =5x =5174,则x =174,则QH =17x =174,则174-54=3,则点Q -3,3 ;当点Q Q 在x 轴上方时,直线AQ 的表达式为y =35x +8 ,当∠CAQ =45°时,AQ ⊥AQ ,则直线AQ 的表达式为y =-53x +8 ,当x =-3时,y =-5x +8 =-25,。
二次函数的最值问题与问题解决技巧

二次函数的最值问题与问题解决技巧二次函数是高中数学中一个重要的概念,它有许多实际应用并且涉及到最值问题。
解决这类问题需要一定的技巧和方法。
本文将介绍二次函数的最值问题以及解决这些问题的技巧。
一、二次函数的最值问题最值问题在数学中非常常见,它代表了在一定条件下,函数的最大值或最小值。
对于二次函数而言,最值问题可以通过确定二次函数的开口方向以及顶点位置来解决。
1. 二次函数的开口方向对于二次函数y=ax²+bx+c,其中a,b,c为常数,a不等于0。
通过a的正负可以判断二次函数的开口方向。
当a大于0时,二次函数的开口是向上的,形状像一个U;当a小于0时,二次函数的开口是向下的,形状像一个倒U。
2. 顶点的横坐标和纵坐标二次函数的最值就出现在顶点处,因此需要确定顶点的横坐标和纵坐标。
对于一般形式的二次函数y=ax²+bx+c,顶点的横坐标为x=-b/2a,可以通过对称轴求得;顶点的纵坐标为y=f(-b/2a),即将x=-b/2a代入函数中计算得到。
3. 最值问题的解答根据二次函数的开口方向和顶点的位置,可以得到最值问题的解答。
当二次函数开口向上时,顶点是函数的最小值;当二次函数开口向下时,顶点是函数的最大值。
二、解决二次函数最值问题的技巧解决二次函数最值问题的技巧主要包括图像法、配方法、导数法等。
1. 图像法通过绘制二次函数的图像,可以直观地找出函数的最值。
根据二次函数的开口方向和顶点的位置,可以判断最值是最小值还是最大值。
2. 配方法当二次函数的系数a不为1时,可以使用配方法将其转化为完全平方的形式,从而更容易找到最值。
例如对于二次函数y=ax²+bx+c,可以将x²+bx转化为(x+b/2a)²-b²/4a,然后再根据顶点的位置判断最值。
3. 导数法通过对二次函数求导,可以得到导函数,进而求出极值点。
导数为0处的x值就是函数的极值点,通过计算可以得到相应的y值。
二次函数的最值与零点问题解析

二次函数的最值与零点问题解析二次函数是一种常见的数学函数,其表达式为f(x) = ax^2 + bx + c,其中a、b、c为常数,且a ≠ 0。
本文将对二次函数的最值与零点问题展开详细的解析,以帮助读者更好地理解与应用二次函数。
一、二次函数的最值问题1. 最值定义在数学中,最大值与最小值称为最值。
对于二次函数f(x) = ax^2 + bx + c,最值即为函数取得最大值或最小值的点。
2. 寻找最值的方法为了找到二次函数的最值,我们可以通过以下步骤进行:a) 首先,我们需要确定a的正负性。
如果a大于0,则二次函数开口向上,即为一个“U”形,并且函数的最小值出现在顶点上。
如果a小于0,则二次函数开口向下,形成一个“∩”形,并且函数的最大值出现在顶点上。
b) 其次,我们可以通过求导数的方法来确定顶点的横坐标。
对二次函数f(x)求导后,得到f'(x) = 2ax + b。
令f'(x) = 0,解得x = -b / (2a),即为顶点的横坐标。
c) 最后,将横坐标代入原二次函数,求得纵坐标即为函数的最值。
3. 示例举例说明,对于二次函数f(x) = 2x^2 - 4x + 1,我们按照上述步骤来找到函数的最小值:a) 由于a = 2大于0,函数开口向上,即为一个“U”形。
b) 求导数f'(x) = 4x - 4,并令f'(x) = 0,解得x = 1,即顶点横坐标为1。
c) 将x = 1代入原二次函数,得到f(1) = 2(1)^2 - 4(1) + 1 = -1,故函数的最小值为-1。
二、二次函数的零点问题1. 零点定义在数学中,二次函数的零点即为函数取值为0的横坐标,即f(x) = 0的解。
2. 寻找零点的方法为了寻找二次函数的零点,我们可以使用以下两种方法:a) 因式分解法:当二次函数可以因式分解时,我们可以通过将f(x) = 0进行因式分解,然后令每一个因子等于0,求得零点。
二次函数求最值的六种考法(含答案)

二次函数与最值的六种考法-重难点题型【题型1 二次函数中的定轴定区间求最值】【例1】(2021春•瓯海区月考)已知二次函数y=﹣x2+2x+4,关于该函数在﹣2≤x≤2的取值范围内,下列说法正确的是()A.有最大值4,有最小值0B.有最大值0,有最小值﹣4C.有最大值4,有最小值﹣4D.有最大值5,有最小值﹣4【解题思路】根据题目中的函数解析式和二次函数的性质,可以得到该函数的对称轴和开口方向,然后根据﹣2≤x≤2,即可得到相应的最大值和最小值,从而可以解答本题.【解答过程】解:∵二次函数y=﹣x2+2x+4=﹣(x﹣1)2+5,∴该函数的对称轴是直线x=1,函数图象开口向下,∴当﹣2≤x≤2时,x=1时取得最大值5,当x=﹣2时,取得最小值﹣4,故选:D.【变式1-1】(2020秋•龙沙区期中)当﹣1≤x≤3时,二次函数y=x2﹣3x+m最大值为5,则m=.【解题思路】根据题目中的函数解析式和二次函数的性质,可以求得m的值,本题得以解决.【解答过程】解:∵二次函数y=x2﹣3x+m=(x−32)2+m−94,∴该函数开口向上,对称轴为x=3 2,∵当﹣1≤x≤3时,二次函数y=x2﹣3x+m最大值为5,∴当x=﹣1时,该函数取得最大值,此时5=1+3+m,解得m=1,故答案为:1.【变式1-2】(2021•哈尔滨模拟)已知二次函数y=x2﹣4x+3,当自变量满足﹣1≤x≤3时,y的最大值为a,最小值为b,则a﹣b的值为.【解题思路】根据题目中的函数解析式和二次函数的性质,可以得到自变量满足﹣1≤x≤3时,x=﹣1时取得最大值,x=2时取得最小值,然后即可得到a、b的值,从而可以求得a﹣b的值,本题得以解决.【解答过程】解:∵二次函数y=x2﹣4x+3=(x﹣2)2﹣1,∴该函数图象开口向上,对称轴为直线x=2,∵当自变量满足﹣1≤x≤3时,y的最大值为a,最小值为b,∴当x=﹣1时,取得最大值,当x=2时,函数取得最小值,∴a=1+4+3=8,b=﹣1,∴a﹣b=8﹣(﹣1)=8+1=9,故答案为:9.【变式1-3】(2020秋•番禺区校级期中)若函数y=x2﹣6x+5,当2≤x≤6时的最大值是M,最小值是m,则M﹣m=.【解题思路】根据题意画出函数图象,即可由此找到m 和M 的值,从而求出M ﹣m 的值. 【解答过程】解:原式可化为y =(x ﹣3)2﹣4, 可知函数顶点坐标为(3,﹣4), 当y =0时,x 2﹣6x +5=0, 即(x ﹣1)(x ﹣5)=0, 解得x 1=1,x 2=5. 如图:m =﹣4,当x =6时,y =36﹣36+5=5,即M =5. 则M ﹣m =5﹣(﹣4)=9.故答案为9.【题型2 二次函数中的动轴定区间求最值】【例2】(2021•雁塔区校级模拟)已知二次函数y =mx 2+2mx +1(m ≠0)在﹣2≤x ≤2时有最小值﹣2,则m =( ) A .3B .﹣3或38C .3或−38D .﹣3或−38【解题思路】先求出对称轴为x =﹣1,分m >0,m <0两种情况讨论解答即可求得m 的值. 【解答过程】解:∵二次函数y =mx 2+2mx +1=m (x +1)2﹣m +1, ∴对称轴为直线x =﹣1, ①m >0,抛物线开口向上,x =﹣1时,有最小值y =﹣m +1=﹣2, 解得:m =3;②m <0,抛物线开口向下,∵对称轴为直线x =﹣1,在﹣2≤x ≤2时有最小值﹣2, ∴x =2时,有最小值y =4m +4m +1=﹣2,解得:m =−38; 故选:C .【变式2-1】(2021•瓯海区模拟)已知二次函数y =ax 2﹣4ax ﹣1,当x ≤1时,y 随x 的增大而增大,且﹣1≤x ≤6时,y 的最小值为﹣4,则a 的值为( ) A .1B .34C .−35D .−14【解题思路】根据二次函数y =ax 2﹣4ax ﹣1,可以得到该函数的对称轴,再根据当x ≤1时,y 随x 的增大而增大,可以得到a 的正负情况,然后根据﹣1≤x ≤6时,y 的最小值为﹣4,即可得到a 的值. 【解答过程】解:∵二次函数y =ax 2﹣4ax ﹣1=a (x ﹣2)2﹣4a ﹣1, ∴该函数的对称轴是直线x =2, 又∵当x ≤1时,y 随x 的增大而增大, ∴a <0,∵当﹣1≤x ≤6时,y 的最小值为﹣4, ∴x =6时,y =a ×62﹣4a ×6﹣1=﹣4, 解得a =−14, 故选:D .【变式2-2】(2021•章丘区模拟)已知二次函数y =2ax 2+4ax +6a 2+3(其中x 是自变量),当x ≥2时,y 随x 的增大而减小,且﹣2≤x ≤1时,y 的最小值为15,则a 的值为( ) A .1或﹣2B .−√2或√2C .﹣2D .1【解题思路】先求出二次函数的对称轴,再根据二次函数的增减性得出抛物线开口向下a <0,然后由﹣2≤x ≤1时,y 的最小值为15,可得x =1时,y =15,即可求出a . 【解答过程】解:∵二次函数y =2ax 2+4ax +6a 2+3(其中x 是自变量), ∴对称轴是直线x =−4a2×2a=−1, ∵当x ≥2时,y 随x 的增大而减小, ∴a <0,∵﹣2≤x ≤1时,y 的最小值为15, ∴x =1时,y =2a +4a +6a 2+3=15, ∴6a 2+6a ﹣12=0, ∴a 2+a ﹣2=0,∴a =1(不合题意舍去)或a =﹣2. 故选:C .【变式2-3】(2021•滨江区三模)已知二次函数y =12(m ﹣1)x 2+(n ﹣6)x +1(m ≥0,n ≥0),当1≤x ≤2时,y 随x 的增大而减小,则mn 的最大值为( ) A .4B .6C .8D .494【解题思路】由二次函数解析式求出对称轴直线方程,分类讨论抛物线开口向下及开口向上的m ,n 的取值范围,将mn 转化为含一个未知数的整式求最值.【解答过程】解:抛物线y =12(m ﹣1)x 2+(n ﹣6)x +1的对称轴为直线x =6−nm−1, ①当m >1时,抛物线开口向上, ∵1≤x ≤2时,y 随x 的增大而减小, ∴6−n m−1≥2,即2m +n ≤8.解得n ≤8﹣2m , ∴mn ≤m (8﹣2m ),m (8﹣2m )=﹣2(m ﹣2)2+8, ∴mn ≤8.②当0≤m <1时,抛物线开口向下, ∵1≤x ≤2时,y 随x 的增大而减小, ∴6−n m−1≤1,即m +n ≤7,解得m ≤7﹣n , ∴mn ≤n (7﹣n ),n (7﹣n )=﹣(n −72)2+494, ∴mn ≤494, ∵0≤m <1, ∴此情况不存在.综上所述,mn 最大值为8. 故选:C .【题型3 二次函数中的定轴动区间求最值】【例3】(2020秋•马鞍山期末)当a﹣1≤x≤a时,函数y=x2﹣2x+1的最小值为1,则a的值为.【解题思路】利用二次函数图象上点的坐标特征找出当y=1时x的值,结合当a﹣1≤x≤a时函数有最小值1,即可得出关于a的一元一次方程,解之即可得出结论.【解答过程】解:当y=1时,有x2﹣2x+1=1,解得:x1=0,x2=2.∵当a﹣1≤x≤a时,函数有最小值1,∴a﹣1=2或a=0,∴a=3或a=0,故答案为:0或3.【变式3-1】(2021•济南模拟)函数y=﹣x2+4x﹣3,当﹣1≤x≤m时,此函数的最小值为﹣8,最大值为1,则m的取值范围是()A.0≤m<2B.0≤m≤5C.m>5D.2≤m≤5【解题思路】根据题目中的函数解析式和二次函数的性质,可以求得m的取值范围.【解答过程】解:∵y=﹣x2+4x﹣3=﹣(x﹣2)2+1,∴该函数图象开口向下,对称轴是直线x=2,顶点坐标为(2,1),∴x=﹣1和x=5对应的函数值相等,∵当﹣1≤x≤m时,此函数的最小值为﹣8,最大值为1,当x=﹣1时,y=﹣8,∴2≤m≤5,故选:D.【变式3-2】(2021•宁波模拟)若二次函数y=ax2﹣x+2的图象经过点(2,﹣1),当t≤x≤2时,y有最大值3,最小值﹣1,则t的取值范围应是()A.﹣6≤t≤2B.t≤﹣2C.﹣6≤t≤﹣2D.﹣2≤t≤2【解题思路】根据二次函数y=ax2﹣x+2的图象经过点(2,﹣1),可以求得a的值,然后即可得到该函数的解析式,再根据二次函数的性质和当t≤x≤2时,y有最大值3,最小值﹣1,即可得到t的取值范围.【解答过程】解:∵二次函数y=ax2﹣x+2的图象经过点(2,﹣1),∴﹣1=a×22﹣2+2,解得a=−1 4,∴y=−14x2﹣x+2=−14(x+2)2+3,∴该函数的图象开口向下,对称轴是直线x=﹣2,当x=﹣2时,该函数取得最大值3,∵当t≤x≤2时,y有最大值3,最小值﹣1,当x=2时,y=﹣1,∴﹣6≤t≤﹣2,故选:C.【变式3-3】(2021•莱芜区二模)已知二次函数y=(x+1)2﹣4,当a≤x≤b且ab<0时,y的最小值为2a,最大值为2b,则a+b的值为()A.2√3B.−72C.√3−2D.0【解题思路】根据a的取值范围分﹣1≤a<0,﹣b﹣2≤a<﹣1,a<﹣b﹣2三种情况讨论,求出满足题目条件的情况即可.【解答过程】解:∵a≤x≤b且ab<0,∴a,b异号,∴a<0,b>0,由二次函数的对称性,b关于对称轴的对称点为﹣b﹣2,若﹣1≤a<0,则(a+1)2﹣4=2a,解得a=−√3(舍),若﹣b﹣2≤a<﹣1,则﹣4=2a,a=﹣2,且(b+1)2﹣3=2b,解得b=√3,∴a+b=√3−2,若a<﹣b﹣2,则2a=﹣4,a=﹣2,2b=(a+1)2﹣4=﹣3,∴b=−32(舍),故选:C.【题型4 二次函数中求线段最值】【例4】(2020春•海淀区校级期末)如图,抛物线y=x2+5x+4与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,连接AC,点P在线段AC上,过点P作x轴的垂线交抛物线于点Q,则线段PQ长的最大值为.【解题思路】先解方程x2+5x+4=0得A(﹣4,0),再确定C(0,4),则可利用待定系数法求出直线AC的解析式为y=x+4,设P(t,t+4)(﹣4≤t≤0),Q(t,t2+5t+4),所以PQ=t+4﹣(t2+5t+4),然后利用二次函数的性质解决问题.【解答过程】解:当y=0时,x2+5x+4=0,解得x1=﹣4,x2=﹣1,则A(﹣4,0),B(﹣1,0),当x=0时,y=x2+5x+4=4,则C(0,4),设直线AC的解析式为y=kx+b,把A(﹣4,0),C(0,4)代入得{−4k+b=0b=4,解得{k=1b=4,∴直线AC的解析式为y=x+4,设P(t,t+4)(﹣4≤t≤0),则Q(t,t2+5t+4),∴PQ=t+4﹣(t2+5t+4)=﹣t2﹣4t=﹣(t+2)2+4,∴当t=﹣2时,PQ有最大值,最大值为4.故答案为4.【变式4-1】(2020秋•镇平县期末)如图,直线y=−34x+3与x轴交于点C,与y轴交于点B,抛物线y=−38x 2+34x +3经过B ,C 两点,点E 是直线BC 上方抛物线上的一动点,过点E 作y 轴的平行线交直线BC 于点M ,则EM 的最大值为 .【解题思路】设出E 的坐标,表示出M 坐标,进而表示出EM ,化成顶点式即可求得EM 的最大值. 【解答过程】解:∵点E 是直线BC 上方抛物线上的一动点,∴点E 的坐标是(m ,−38m 2+34m +3),点M 的坐标是(m ,−34m +3),∴EM =−38m 2+34m +3﹣(−34m +3)=−38m 2+32m =−38(m 2﹣4m )=−38(m ﹣2)2+32, ∴当m =2时,EM 有最大值为32,故答案为32.【变式4-2】(2021•埇桥区模拟)对称轴为直线x =﹣1的抛物线y =x 2+bx +c ,与x 轴相交于A ,B 两点,其中点A 的坐标为(﹣3,0). (1)求点B 的坐标.(2)点C 是抛物线与y 轴的交点,点Q 是线段AC 上的动点,作QD ⊥x 轴交抛物线于点D ,求线段QD 长度的最大值.【解题思路】(1)利用二次函数对称性即可得出B 点坐标;(2)首先利用待定系数法求二次函数解析式,进而求出直线AC 的解析式,再利用QD =﹣x ﹣3﹣(x 2+2x ﹣3)进而求出最值.【解答过程】解:(1)∵点A (﹣3,0)与点B 关于直线x =﹣1对称, ∴点B 的坐标为(1,0). (2)∵a =1,∴y =x 2+bx +c .∵抛物线过点(﹣3,0),且对称轴为直线x =﹣1, ∴{9−3b +c =0−b2=−1∴解得:{b =2c =−3,∴y =x 2+2x ﹣3,且点C 的坐标为(0,﹣3). 设直线AC 的解析式为y =mx +n , 则{−3m +n =0n =−3, 解得:{m =−1n =−3,∴y =﹣x ﹣3如图,设点Q 的坐标为(x .y ),﹣3≤x ≤0.则有QD =﹣x ﹣3﹣(x 2+2x ﹣3)=﹣x 2﹣3x =﹣(x +32)2+94∵﹣3≤−32≤0,∴当x =−32时,QD 有最大值94.∴线段QD 长度的最大值为94.【变式4-3】(2020秋•滨海新区期末)如图,在平面直角坐标系中,已知抛物线y =ax 2+bx +52与x 轴交于A(5,0),B(﹣1,0)两点,与y轴交于点C.(Ⅰ)求抛物线的解析式;(Ⅱ)若点M是抛物线的顶点,连接AM,CM,求△ACM的面积;(Ⅲ)若点P是抛物线上的一动点,过点P作PE垂直y轴于点E,交直线AC于点D,过点D作x轴的垂线,垂足为点F,连接EF,当线段EF的长度最短时,求出点P的坐标.【解题思路】(Ⅰ)用待定系数法即可求解;(Ⅱ)△AMC的面积=S△MHC+S△MHA=12×MH×OA,即可求解;(Ⅲ)点D在直线AC上,设点D(m,−12m+52),由题意得,四边形OEDF为矩形,故EF=OD,即当线段EF的长度最短时,只需要OD最短即可,进而求解.【解答过程】解:(Ⅰ)令x=0,则y=52,即C(0,52)设抛物线的表达式为y=a(x﹣x1)(x﹣x2)=a(x﹣5)(x+1),将点C的坐标代入上式得:52=a(0﹣5)(0+1),解得a=−1 2,故抛物线的表达式为y=−12(x﹣5)(x+1)=−12x2+2x+52;(Ⅱ)由抛物线的表达式得顶点M(2,92),过点M作MH∥y轴交AC于点H,设直线AC 的表达式为y =kx +t ,则{t =520=5k +t, 解得{k =−12t =52, 故直线AC 的表达式为y =−12x +52,当x =2时,y =32,则MH =92−32=3,则△AMC 的面积=S △MHC +S △MHA =12×MH ×OA =12×3×5=152; (Ⅲ)点D 在直线AC 上,设点D (m ,−12m +52),由题意得,四边形OEDF 为矩形,故EF =OD ,即当线段EF 的长度最短时,只需要OD 最短即可,则EF 2=OD 2=m 2+(−12m +52)2=54m 2−52m +254,∵54>0,故EF 2存在最小值(即EF 最小),此时m =1, 故点D (1,2),∵点P 、D 的纵坐标相同,故2=−12x 2+2x +52,解得x =2±√5,故点P 的坐标为(2+√5,2)或(2−√5,2).【题型5 二次函数中求线段和最值】【例5】(2020秋•安居区期末)如图,在抛物线y =﹣x 2上有A ,B 两点,其横坐标分别为1,2,在y 轴上有一动点C ,当BC +AC 最小时,则点C 的坐标是( )A .(0,0)B .(0,﹣1)C .(0,2)D .(0,﹣2)【解题思路】利用二次函数图象上点的坐标特征可求出点A ,B 的坐标,作点B 关于y 轴的对称点B ′,连接AB ′交y 轴于点C ,此时BC +AC 最小,由点B 的坐标可得出点B ′的坐标,由点A ,B ′的坐标,利用待定系数法可求出直线AB ′的解析式,再利用一次函数图象上点的坐标特征,即可求出点C 的坐标.【解答过程】解:当x =1时,y =﹣12=﹣1,∴点A 的坐标为(1,﹣1);当x =2时,y =﹣22=﹣4,∴点B 的坐标为(2,﹣4).作点B 关于y 轴的对称点B ′,连接AB ′交y 轴于点C ,此时BC +AC 最小,如图所示.∵点B 的坐标为(2,﹣4),∴点B ′的坐标为(﹣2,﹣4).设直线AB ′的解析式为y =kx +b (k ≠0),将A (1,﹣1),B (﹣2,﹣4)代入y =kx +b 得:{k +b =−1−2k +b =−4, 解得:{k =1b =−2, ∴直线AB ′的解析式为y =x ﹣2.当x =0时,y =0﹣2=﹣2,∴点C 的坐标为(0,﹣2),∴当BC +AC 最小时,点C 的坐标是(0,﹣2).故选:D .【变式5-1】(2021•铁岭模拟)如图,已知抛物线y =﹣x 2+px +q 的对称轴为x =﹣3,过其顶点M 的一条直线y =kx +b 与该抛物线的另一个交点为N (﹣1,1).要在坐标轴上找一点P ,使得△PMN 的周长最小,则点P 的坐标为( )A .(0,2)B .(43,0)C .(0,2)或(43,0)D .以上都不正确【解题思路】首先,求得抛物线的解析式,根据抛物线解析式求得M 的坐标;欲使△PMN 的周长最小,MN 的长度一定,所以只需(PM +PN )取最小值即可.然后,过点M 作关于y 轴对称的点M ′,连接M ′N ,M ′N 与y 轴的交点即为所求的点P (如图1);过点M 作关于x 轴对称的点M ′,连接M ′N ,则只需M ′N 与x 轴的交点即为所求的点P (如图2).【解答过程】解:如图,∵抛物线y =﹣x 2+px +q 的对称轴为x =﹣3,点N (﹣1,1)是抛物线上的一点, ∴{−p −2=−31=−1−p +q, 解得{p =−6q =−4. ∴该抛物线的解析式为y =﹣x 2﹣6x ﹣4=﹣(x +3)2+5,∴M (﹣3,5).∵△PMN 的周长=MN +PM +PN ,且MN 是定值,所以只需(PM +PN )最小.如图1,过点M 作关于y 轴对称的点M ′,连接M ′N ,M ′N 与y 轴的交点即为所求的点P .则M ′(3,5).设直线M ′N 的解析式为:y =ax +t (a ≠0),则{5=3a +t 1=−a +t, 解得{a =1t =2, 故该直线的解析式为y =x +2.当x =0时,y =2,即P (0,2).同理,如图2,过点M 作关于x 轴对称的点M ′,连接M ′N ,则只需M ′N 与x 轴的交点即为所求的点P (−43,0).如果点P 在y 轴上,则三角形PMN 的周长=4√2+MN ;如果点P 在x 轴上,则三角形PMN 的周长=2√10+MN ;所以点P 在(0,2)时,三角形PMN 的周长最小.综上所述,符合条件的点P 的坐标是(0,2).故选:A .【变式5-2】(2021•包头)已知抛物线y =x 2﹣2x ﹣3与x 轴交于A ,B 两点(点A 在点B 的左侧)与y 轴交于点C ,点D (4,y )在抛物线上,E 是该抛物线对称轴上一动点,当BE +DE 的值最小时,△ACE 的面积为 .【解题思路】解方程x 2﹣2x ﹣3=0得A (﹣1,0),B (3,0),则抛物线的对称轴为直线x =1,再确定C (0,﹣3),D (4,5),连接AD 交直线x =1于E ,交y 轴于F 点,如图,利用两点之间线段最短可判断此时BE +DE 的值最小,接着利用待定系数法求出直线AD 的解析式为y =x +1,则F (0,1),然后根据三角形面积公式计算.【解答过程】解:当y =0时,x 2﹣2x ﹣3=0,解得x 1=﹣1,x 2=3,则A (﹣1,0),B (3,0), 抛物线的对称轴为直线x =1,当x =0时,y =x 2﹣2x ﹣3=﹣3,则C (0,﹣3),当x =4时,y =x 2﹣2x ﹣3=5,则D (4,5),连接AD 交直线x =1于E ,交y 轴于F 点,如图,∵BE +DE =EA +DE =AD ,∴此时BE +DE 的值最小,设直线AD 的解析式为y =kx +b ,把A (﹣1,0),D (4,5)代入得{−k +b =04k +b =5,解得{k =1b =1, ∴直线AD 的解析式为y =x +1,当x =1时,y =x +1=2,则E (1,2),当x =0时,y =x +1=1,则F (0,1),∴S △ACE =S △ACF +S △ECF =12×4×1+12×4×1=4. 故答案为4.【变式5-3】(2021•涪城区模拟)如图,抛物线y =53x 2−203x +5与x 轴分别交于A 、B 两点(点A 在点B 的左侧),与y 轴交于C ,在其对称轴上有一动点M ,连接MA 、MC 、AC ,则当△MAC 的周长最小时,点M 的坐标是 .【解题思路】点A 关于函数对称轴的对称点为点B ,连接CB 交函数对称轴于点M ,则点M 为所求点,即可求解.【解答过程】解:点A 关于函数对称轴的对称点为点B ,连接CB 交函数对称轴于点M ,则点M 为所求点,理由:连接AC ,由点的对称性知,MA =MB ,△MAC 的周长=AC +MA +MC =AC +MB +MC =CA +BC 为最小,令y =53x 2−203x +5=0,解得x =1或3,令x =0,则y =5,故点A 、B 、C 的坐标分别为(1,0)、(3,0)、(0,5),则函数的对称轴为x =12(1+3)=2,设直线BC 的表达式为y =kx +b ,则{0=3k +b b =5,解得{k =−53b =5, 故直线BC 的表达式为y =−53x +5,当x =2时,y =−53x +5=53,故点M 的坐标为(2,53). 【题型6 二次函数中求面积最值】【例6】(2020秋•盐城期末)如图,抛物线y =x 2+bx +c 与x 轴交于A (﹣1,0),B (3,0)两点,过点A 的直线l 交抛物线于点C (2,m ),点P 是线段AC 上一个动点,过点P 做x 轴的垂线交抛物线于点E .(1)求抛物线的解析式;(2)当P 在何处时,△ACE 面积最大.【解题思路】(1)利用交点式写出抛物线解析式;(2)先利用二次函数解析式确定C (2,﹣3),再利用待定系数法求出直线AC 的解析式为y =﹣x ﹣1,设E (t ,t 2﹣2t ﹣3)(﹣1≤t ≤2),则P (t ,﹣t ﹣1),利用三角形面积公式得到△ACE 的面积=12×(2+1)×PE =32(﹣t 2+t +2),然后根据二次函数的性质解决问题.【解答过程】解:(1)抛物线解析式为y =(x +1)(x ﹣3),即y =x 2﹣2x ﹣3;(2)把C (2,m )代入y =x 2﹣2x ﹣3得m =4﹣4﹣3=﹣3,则C (2,﹣3),设直线AC 的解析式为y =mx +n ,把A (﹣1,0),C (2,﹣3)代入得{−m +n =02m +n =−3,解得{m =−1n =−1, ∴直线AC 的解析式为y =﹣x ﹣1;设E (t ,t 2﹣2t ﹣3)(﹣1≤t ≤2),则P (t ,﹣t ﹣1),∴PE =﹣t ﹣1﹣(t 2﹣2t ﹣3)=﹣t 2+t +2,∴△ACE 的面积=12×(2+1)×PE=32(﹣t 2+t +2)=−32(t −12)2+278,当t =12时,△ACE 的面积有最大值,最大值为278,此时P 点坐标为(12,−32). 【变式6-1】(2021春•金塔县月考)如图,已知抛物线经过A (4,0),B (1,0),C (0,﹣2)三点.(1)求该抛物线的解析式;(2)在直线AC 上方的该抛物线上是否存在一点D ,使得△DCA 的面积最大,若存在,求出点D 的坐标及△DCA 面积的最大值;若不存在,请说明理由.【解题思路】(1)根据题意设出抛物线的交点式,用待定系数法求解即可;(2)根据题意作出相关辅助线,用待定系数法求得直线AC解析式为y=12x﹣2,因为点D在抛物线上,所以可设其坐标为(x,−12x2+52x﹣2),点E在直线AC上则设点E坐标为(x,12x﹣2),由图形可知S△DCA=S△DCE+S△DAE,将相关坐标及线段的长度代入求解,再根据二次函数的性质即可得出△DCA面积的最大值.【解答过程】(1)设该抛物线解析式为y=a(x﹣4)(x﹣1),将点C(0,﹣2)坐标代入解析式得:﹣2=a(0﹣4)(0﹣1),解得a=−1 2,∴y=−12(x﹣4)(x﹣1)=−12x2+52x﹣2,故该抛物线的解析式为:y=−12x2+52x﹣2,(2)如图,设存在点D在抛物线上,连接AD、CD,过点D作DE⊥x轴且与直线AC交于点E,设直线AC表达式为:y=kx+b(k≠0),将A(4,0),C(0,﹣2)代入其表达式得:{0=4k+b−2=b,解得{k=12b=−2,∴直线AC:y=12x﹣2,设点D坐标为(x,−12x2+52x﹣2),则点E坐标为(x,12x﹣2),S△DCA=S△DCE+S△DAE=12×DE×x E+12×DE×(x A﹣x E)=12×DE×x A=12×DE×4=2DE,∵DE=(−12x2+52x﹣2)﹣(12x﹣2)=−12x2+2x,∴S△DCA=2DE=2×(−12x2+2x)=﹣x2+4x=﹣(x﹣2)2+4,∴当x=2时,y=−12x2+52x﹣2═﹣2+5﹣2=1,即点D坐标为(2,1),此时△DCA的面积最大,最大值为4.【变式6-2】(2021春•无为市月考)如图,直线y=﹣x+n与x轴交于点A(3,0),与y轴交于点B,抛物线y=﹣x2+bx+c经过点A,B.(1)求抛物线的解析式.(2)若P为直线AB上方的抛物线上一点,且点P的横坐标为m,求四边形BCAP的面积S关于点P横坐标m的函数解析式,并求S的最大值.【解题思路】(1)将点A坐标代入直线解析式可求n的值,可求点B坐标,利用待定系数法可求解;(2)过点P做PE⊥x轴于点E,与直线AB交于点D,求得C的坐标和D的坐标,然后根据S=S△ABC+S △ABP得到S关于m的函数解析式,根据二次函数的性质即可求得结论.【解答过程】解:(1)∵直线y=﹣x+n与x轴交于点A(3,0),∴0=﹣3+n,∴n=3,∴直线解析式为:y=﹣x+3,当x=0时,y=3,∴点B (0,3),∵抛物线y =﹣x 2+bx +c 经过点A ,B ,∴{c =3−9+3b +c =0, ∴{b =2c =3, ∴抛物线的解析式为:y =﹣x 2+2x +3;(2)如图,过点P 做PE ⊥x 轴于点E ,与直线AB 交于点D ,∵点P 的横坐标为m ,∴点P 的坐标为(m ,﹣m 2+2m +3),∵点D 在直线AB 上,∴点D 的坐标为(m ,﹣m +3),∴PD =﹣m 2+2m +3﹣(﹣m +3)=﹣m 2+3m ,在y =﹣x 2+2x +3中.令y =0.则﹣x 2+2x +3=0,解得x 1=﹣1,x 2=3,∴点C 的坐标为(﹣1,0),∴S =S △ABC +S △ABP =12×4×3+12(﹣m 2+3m )×3=−32(m −32)2+758, ∴当m =32时,S 最大,最大值为758.【变式6-3】(2021春•无棣县月考)如图,在平面直角坐标系中,二次函数y =x 2+bx +c 的图象与x 轴交于A 、B 两点,B 点的坐标为(3,0),与y 轴交于点C (0,﹣3),点P 是直线BC 下方抛物线上的一个动点.(1)求二次函数解析式;(2)连接PO ,PC ,并将△POC 沿y 轴对折,得到四边形POP 'C .是否存在点P ,使四边形POP 'C 为菱形?若存在,求出此时点P 的坐标;若不存在,请说明理由;(3)当点P运动到什么位置时,四边形ABPC的面积最大?求出此时P点的坐标和四边形ABPC的最大面积.【解题思路】(1)先根据点C坐标求出c=﹣3,再将点B坐标代入二次函数解析式中求出b,即可得出结论;(2)连接PP'交y轴于E,根据菱形的性质判断出点E是OC的中点,进而求出点P的纵坐标,最后代入二次函数解析式中求解,即可得出结论;(3)设出点P的坐标,进而利用梯形的面积+三角形的面积得出S四边形ABPC=−32(m−12)2+398,即可得出结论.【解答过程】解:(1)∵二次函数y=x2+bx+c与y轴的交点C(0,﹣3),∴c=﹣3,∴二次函数的解析式为y=x2+bx﹣3,∵点B(3,0)在二次函数图象上,∴9+3b﹣3=0,∴b=﹣2,∴二次函数的解析式为y=x2﹣2x﹣3;(2)存在,理由:如图1,连接PP'交y轴于E,∵四边形POP'C为菱形,∴PP'⊥OC,OE=CE=12OC,∵点C(0,﹣3),∴OC=3,∴OE=3 2,∴E (0,−32),∴点P 的纵坐标为−32,由(1)知,二次函数的解析式为y =x 2﹣2x ﹣3, ∴x 2﹣2x ﹣3=−32,∴x =2−√102或x =2+√102,∵点P 在直线BC 下方的抛物线上,∴0<x <3,∴点P (2+√102,−32);(3)如图2,过点P 作PF ⊥x 轴于F ,则PF ∥OC , 由(1)知,二次函数的解析式为y =x 2﹣2x ﹣3, 令y =0,则x 2﹣2x ﹣3=0,∴x =﹣1或x =3,∴A (﹣1,0),∴设P (m ,m 2﹣2m ﹣3)(0<m <3),∴F (m ,0),∴S 四边形ABPC =S △AOC +S 梯形OCPF +S △PFB =12OA •OC +12(OC +PF )•OF +12PF •BF =12×1×3+12(3﹣m 2+2m +3)•m +12(﹣m 2+2m +3)•(3﹣m ) =−32(m −32)2+758,∴当m =32时,四边形ABPC 的面积最大,最大值为758,此时,P (32,−154),即点P 运动到点(32,−154)时,四边形ABPC 的面积最大,其最大值为758.。
重难点 二次函数中的线段、周长与面积的最值问题及定值问题(解析版)--2024年中考数学

重难点二次函数中的线段、周长与面积的最值问题及定值问题目录题型01利用二次函数解决单线段的最值问题题型02利用二次函数解决两条线段之和的最值问题题型03利用二次函数解决两条线段之差的最值问题题型04利用二次函数解决三条线段之和的最值问题题型05利用二次函数解决三角形周长的最值问题题型06利用二次函数解决四边形周长的最值问题题型07利用二次函数解决图形面积的最值问题类型一利用割补、拼接法解决面积最值问题类型二利用用铅垂定理巧求斜三角形面积最值问题类型三构建平行线,利用同底等高解决面积最值问题题型08利用二次函数解决定值问题题型01利用二次函数解决单线段的最值问题【解题思路】抛物线中的线段最值问题有三种形式:1.平行于坐标轴的线段的最值问题:常通过线段两端点的坐标差表示线段长的函数关系式,运用二次函数性质求解.求最值时应注意:①当线段平行于y轴时,用上端点的纵坐标减去下端点的纵坐标;②当线段平行于x轴时,用右端点的横坐标减去左端点的横坐标.在确定最值时,函数自变量的取值范围应确定正确.1(2022·辽宁朝阳·统考中考真题)如图,在平面直角坐标系中,抛物线y=ax2+2x+c与x轴分别交于点A(1,0)和点B,与y轴交于点C(0,-3),连接BC.(1)求抛物线的解析式及点B 的坐标.(2)如图,点P 为线段BC 上的一个动点(点P 不与点B ,C 重合),过点P 作y 轴的平行线交抛物线于点Q ,求线段PQ 长度的最大值.(3)动点P 以每秒2个单位长度的速度在线段BC 上由点C 向点B 运动,同时动点M 以每秒1个单位长度的速度在线段BO 上由点B 向点O 运动,在平面内是否存在点N ,使得以点P ,M ,B ,N 为顶点的四边形是菱形?若存在,请直接写出符合条件的点N 的坐标;若不存在,请说明理由.【答案】(1)y =x 2+2x -3,(-3,0)(2)94(3)-3,-32或(-2,1)或0,3-32【分析】(1)将A ,C 两点坐标代入抛物线的解析式求得a ,c 的值,进而得出解析式,当y =0时,求出方程的解,进而求得B 点坐标;(2)由B ,C 两点求出BC 的解析式,进而设出点P 和点Q 坐标,表示出PQ 的长,进一步得出结果;(3)要使以点P ,M ,B ,N 为顶点的四边形是菱形,只需△PMB 是等腰三角形,所以分为PM =BM ,PM =PB 和BP =BM ,结合图象,进一步得出结果.【详解】(1)解:把点A (1,0),C (0,-3)代入y =ax 2+2x +c 得:c =-3a +2×1+c =0 ,解得:c =-3a =1 ,∴抛物线解析式为y =x 2+2x -3;令y =0,则x 2+2x -3=0,解得:x 1=1,x 2=-3,∴点B 的坐标为(-3,0);(2)解:设直线BC 的解析式为y =kx +b k ≠0 ,把点B (-3,0),C (0,-3)代入得:b =-3-3k +b =0 ,解得:k =-1b =-3 ,∴直线BC 的解析式为y =-x -3,设点P m ,-m +3 ,则Q m ,m 2+2m -3 ,∴PQ =-m -3 -m 2+2m -3 =-m 2-3m =-m +322+94,∴当m =-32时,PQ 最大,最大值为94;(3)解:存在,根据题意得:PC =2t ,BM =t ,则PB =32-2t ,如图,当BM =PM 时,∵B (-3,0),C (0,-3),∴OB =OC =3,∴∠OCB =∠OBC =45°,延长NP 交y 轴于点D ,∵点P ,M ,B ,N 为顶点的四边形是菱形,∴PN ∥x 轴,BN ∥PM ,即DN ⊥y 轴,∴△CDP 为等腰直角三角形,∴CD =PD =PC ⋅sin ∠OCB =2t ×22=t ,∵BM =PM ,∴∠MPB =∠OBC =45°,∴∠PMO =∠PDO =∠MOD =90°,∴四边形OMPD 是矩形,∴OM =PD =t ,MP ⊥x 轴,∴BN ⊥x 轴,∵BM +OM =OB ,∴t +t =3,解得t =32,∴P -32,-32,∴N -3,-32;如图,当PM =PB 时,作PD ⊥y 轴于D ,连接PN ,∵点P ,M ,B ,N 为顶点的四边形是菱形,∴PN ⊥BM ,NE =PE ,∴BM =2BE ,∴∠OEP =∠DOE =∠ODP =90°,∴四边形PDOE 是矩形,∴OE =PD =t ,∴BE =3-t ,∴t =2(3-t ),解得:t =2,∴P (-2,-1),∴N (-2,1);如图,当PB =MB 时,32-2t =t ,解得:t =6-32,∴PN =BP =BM =6-32,过点P 作PE ⊥x 轴于点E ,∴PE ⊥PM ,∴∠EON =∠OEP =∠EPN =90°,∴四边形OEPN 为矩形,∴PN =OE ,PN ⊥y 轴,∵∠OBC =45°,∴BE =PE =PB ⋅sin ∠OBC =6-32 ×22=32-3,∴OE =OB -BE =3-32-3 =6-32,∴点N 在y 轴上,∴N 0,3-32 ,综上所述,点N 的坐标为-3,-32或(-2,1)或0,3-32 .【点睛】本题考查了二次函数及其图象的性质,用待定系数法求一次函数的解析式,等腰三角形的分类和等腰三角形的性质,菱形的性质等知识,解决问题的关键是正确分类,画出符合条件的图形.2(2021·西藏·统考中考真题)在平面直角坐标系中,抛物线y =-x 2+bx +c 与x 轴交于A ,B 两点.与y 轴交于点C .且点A 的坐标为(-1,0),点C 的坐标为(0,5).(1)求该抛物线的解析式;(2)如图(甲).若点P 是第一象限内抛物线上的一动点.当点P 到直线BC 的距离最大时,求点P 的坐标;(3)图(乙)中,若点M 是抛物线上一点,点N 是抛物线对称轴上一点,是否存在点M 使得以B ,C ,M ,N 为顶点的四边形是平行四边形?若存在,请求出点M 的坐标;若不存在,请说明理由.【答案】(1)y =-x 2+4x +5;(2)P 52,354;(3)存在,M 的坐标为:(3,8)或(-3,-16)或(7,-16).【分析】(1)将A 的坐标(-1,0),点C 的坐(0,5)代入y =-x 2+bx +c ,即可得抛物线的解析式为y =-x 2+4x +5;(2)过P 作PD ⊥x 轴于D ,交BC 于Q ,过P 作PH ⊥BC 于H ,由y =-x 2+4x +5可得B (5,0),故OB =OC ,△BOC 是等腰直角三角形,可证明△PHQ 是等腰直角三角形,即知PH =PQ2,当PQ 最大时,PH 最大,设直线BC 解析式为y =kx +5,将B (5,0)代入得直线BC 解析式为y =-x +5,设P (m ,-m 2+4m +5),(0<m <5),则Q (m ,-m +5),PQ =-m -52 2+254,故当m =52时,PH 最大,即点P 到直线BC的距离最大,此时P 52,354 ;(3)抛物线y =-x 2+4x +5对称轴为直线x =2,设M (s ,-s 2+4s +5),N (2,t ),而B (5,0),C (0,5),①以MN 、BC 为对角线,则MN 、BC 的中点重合,可列方程组s +22=5+02-s 2+4s +5+t 2=0+52,即可解得M (3,8),②以MB 、NC 为对角线,则MB 、NC 的中点重合,同理可得s +52=2+02-s 2+4s +4+02=t +52,解得M (-3,-16),③以MC 、NB 为对角线,则MC 、NB 中点重合,则s +02=2+52-s 2+4s +5+52=t +02,解得M (7,-16).【详解】解:(1)将A 的坐标(-1,0),点C 的坐(0,5)代入y =-x 2+bx +c 得:0=-1-b +c 5=c ,解得b =4c =5 ,∴抛物线的解析式为y =-x 2+4x +5;(2)过P 作PD ⊥x 轴于D ,交BC 于Q ,过P 作PH ⊥BC 于H ,如图:在y =-x 2+4x +5中,令y =0得-x 2+4x +5=0,解得x =5或x =-1,∴B (5,0),∴OB =OC ,△BOC 是等腰直角三角形,∴∠CBO =45°,∵PD ⊥x 轴,∴∠BQD =45°=∠PQH ,∴△PHQ 是等腰直角三角形,∴PH =PQ2,∴当PQ 最大时,PH 最大,设直线BC 解析式为y =kx +5,将B (5,0)代入得0=5k +5,∴k =-1,∴直线BC 解析式为y =-x +5,设P (m ,-m 2+4m +5),(0<m <5),则Q (m ,-m +5),∴PQ =(-m 2+4m +5)-(-m +5)=-m 2+5m =-m -52 2+254,∵a =-1<0,∴当m =52时,PQ 最大为254,∴m =52时,PH 最大,即点P 到直线BC 的距离最大,此时P 52,354;(3)存在,理由如下:抛物线y =-x 2+4x +5对称轴为直线x =2,设M (s ,-s 2+4s +5),N (2,t ),而B (5,0),C (0,5),①以MN 、BC 为对角线,则MN 、BC 的中点重合,如图:∴s +22=5+02-s 2+4s +5+t2=0+52,解得s =3t =-3 ,∴M (3,8),②以MB 、NC 为对角线,则MB 、NC 的中点重合,如图:∴s +52=2+02-s 2+4s +4+02=t +52,解得s=-3t =-21 ,∴M (-3,-16),③以MC 、NB 为对角线,则MC 、NB 中点重合,如图:s +02=2+52-s 2+4s +5+52=t +02,解得s =7t =-11 ,∴M (7,-16);综上所述,M 的坐标为:(3,8)或(-3,-16)或(7,-16).【点睛】本题考查二次函数综合应用,涉及待定系数法、函数图象上点坐标的特征、等腰直角三角形、平行四边形等知识,解题的关键是用含字母的代数式表示相关点的坐标和相关线段的长度.3(2021·山东泰安·统考中考真题)二次函数y =ax 2+bx +4(a ≠0)的图象经过点A (-4,0),B (1,0),与y 轴交于点C ,点P 为第二象限内抛物线上一点,连接BP 、AC ,交于点Q ,过点P 作PD ⊥x 轴于点D .(1)求二次函数的表达式;(2)连接BC ,当∠DPB =2∠BCO 时,求直线BP 的表达式;(3)请判断:PQQB是否有最大值,如有请求出有最大值时点P 的坐标,如没有请说明理由.【答案】(1)y =-x 2-3x +4;(2)y =-158x +158;(3)PQ QB有最大值为45,P 点坐标为(-2,6)【分析】(1)将A (-4,0),B (1,0)代入y =ax 2+bx +4(a ≠0)中,列出关于a 、b 的二元一次方程组,求出a 、b 的值即可;(2)设BP 与y 轴交于点E ,根据PD ⎳y 轴可知,∠DPB =∠OEB ,当∠DPB =2∠BCO ,即∠OEB =2∠BCO ,由此推断△OEB 为等腰三角形,设OE =a ,则CE =4-a ,所以BE =4-a ,由勾股定理得BE 2=OE 2+OB 2,解出点E 的坐标,用待定系数法确定出BP 的函数解析式即可;(3)设PD 与AC 交于点N ,过B 作y 轴的平行线与AC 相交于点M .由A 、C 两点坐标可得AC 所在直线表达式,求得M 点坐标,则BM =5,由BM ⎳PN ,可得△PNQ ∽△BMQ ,PQ QB=PN BM =PN5,设P (a 0,-a 20-3a 0+4)(-4<a 0<0),则N (a 0,a 0+4)PQ QB =-a 20-3a 0+4-(a 0+4)5=-a 20-4a 05=-(a 0+2)2+45,根据二次函数性质求解即可.【详解】解:(1)由题意可得:a ⋅(-4)2+b ⋅(-4)+4=0a +b +4=0解得:a =-1b =-3 ,∴二次函数的表达式为y =-x 2-3x +4;(2)设BP 与y 轴交于点E ,∵PD ⎳y 轴,∴∠DPB =∠OEB ,∵∠DPB =2∠BCO ,∴∠OEB =2∠BCO ,∴∠ECB =∠EBC ,∴BE =CE ,设OE =a ,则CE =4-a ,∴BE =4-a ,在Rt △BOE 中,由勾股定理得BE 2=OE 2+OB 2,∴(4-a )2=a 2+12解得a =158,∴E 0,158,设BE 所在直线表达式为y =kx +e (k ≠0)∴k ⋅0+e =158,k ⋅1+e =0.解得k =-158,e =158. ∴直线BP 的表达式为y =-158x +158.(3)设PD 与AC 交于点N .过B 作y 轴的平行线与AC 相交于点M .由A 、C 两点坐标分别为(-4,0),(0,4)可得AC 所在直线表达式为y =x +4∴M 点坐标为(1,5),BM =5由BM ⎳PN ,可得△PNQ ∽△BMQ ,∴PQ QB=PN BM =PN 5设P (a 0,-a 20-3a 0+4)(-4<a 0<0),则N (a 0,a 0+4)∴PQ QB=-a 20-3a 0+4-(a 0+4)5=-a 20-4a 05=-(a 0+2)2+45,∴当a 0=-2时,PQQB 有最大值0.8,此时P 点坐标为(-2,6).【点睛】本题主要考查二次函数以及一次函数解析式的确定,函数图像的性质,相似三角形,勾股定理等知识点,熟练运用待定系数法求函数解析式是解题关键,本题综合性强,涉及知识面广,难度较大,属于中考压轴题.4(2020·辽宁阜新·中考真题)如图,二次函数y =x 2+bx +c 的图象交x 轴于点A -3,0 ,B 1,0 ,交y 轴于点C .点P m ,0 是x 轴上的一动点,PM ⊥x 轴,交直线AC 于点M ,交抛物线于点N .(1)求这个二次函数的表达式;(2)①若点P 仅在线段AO 上运动,如图1.求线段MN 的最大值;②若点P 在x 轴上运动,则在y 轴上是否存在点Q ,使以M ,N ,C ,Q 为顶点的四边形为菱形.若存在,请直接写出所有满足条件的点Q 的坐标;若不存在,请说明理由.【答案】(1)y =x 2+2x -3;(2)①94,②存在,Q 1(0,-32-1),Q 2(0,32-1)【分析】(1)把A (-3,0),B (1,0)代入y =x 2+bx +c 中求出b ,c 的值即可;(2)①由点P m ,0 得M (m ,-m -3),N m ,m 2+2m -3 ,从而得MN =(-m -3)-m 2+2m -3 ,整理,化为顶点式即可得到结论;②分MN =MC 和MC =2MN 两种情况,根据菱形的性质得到关于m 的方程,求解即可.【详解】解:(1)把A (-3,0),B (1,0)代入y =x 2+bx +c 中,得0=9-3b +c ,0=1+x +c .解得b =2,c =-3. ∴y =x 2+2x -3.(2)设直线AC 的表达式为y =kx +b ,把A (-3,0),C (0,-3)代入y =kx +b .得,0=-3k +b ,-3=b . 解这个方程组,得k =-1,b =-3. ∴y =-x -3.∵点P m ,0 是x 轴上的一动点,且PM ⊥x 轴.∴M (m ,-m -3),N m ,m 2+2m -3 . ∴MN =(-m -3)-m 2+2m -3 =-m 2-3m=-m +32 2+94.∵a =-1<0,∴此函数有最大值.又∵点P 在线段OA 上运动,且-3<-32<0∴当m =-32时,MN 有最大值94. ②∵点P m ,0 是x 轴上的一动点,且PM ⊥x 轴.∴M (m ,-m -3),N m ,m 2+2m -3 . ∴MN =(-m -3)-m 2+2m -3 =-m 2-3m(i )当以M ,N ,C ,Q 为顶点的四边形为菱形,则有MN =MC ,如图,∵C (0,-3)∴MC =(m -0)2+(-m -3+3)2=2m 2∴-m 2-3m =2m 2整理得,m 4+6m 3+7m 2=0∵m 2≠0,∴m 2+6m +7=0,解得,m 1=-3+2,m 2=-3-2∴当m =-3+2时,CQ =MN =32-2,∴OQ =-3-(32-2)=-32-1∴Q (0,-32-1);当m =-3-2时,CQ =MN =-32-2,∴OQ =-3-(-32-2)=32-1∴Q (0,32-1);(ii )若MC =2MN ,如图,则有-m 2-3m =22×2m 2整理得,m 2+4m =0解得,m 1=-4,m 2=0(均不符合实际,舍去)综上所述,点Q 的坐标为Q 1(0,-32-1),Q 2(0,32-1)【点睛】本题考查了二次函数综合题,解(1)的关键是待定系数法;解(2)的关键是利用线段的和差得出二次函数,又利用了二次函数的性质,解(3)的关键是利用菱形的性质得出关于m 的方程,要分类讨论,以防遗漏.5(2020·天津·中考真题)已知点A (1,0)是抛物线y =ax 2+bx +m (a ,b ,m 为常数,a ≠0,m <0)与x 轴的一个交点.(1)当a =1,m =-3时,求该抛物线的顶点坐标;(2)若抛物线与x 轴的另一个交点为M (m ,0),与y 轴的交点为C ,过点C 作直线l 平行于x 轴,E 是直线l 上的动点,F 是y 轴上的动点,EF =22.①当点E 落在抛物线上(不与点C 重合),且AE =EF 时,求点F 的坐标;②取EF 的中点N ,当m 为何值时,MN 的最小值是22?【答案】(1)抛物线的顶点坐标为(-1,-4);(2)①点F 的坐标为(0,-2-7)或(0,-2+7);②当m 的值为-32或-12时,MN 的最小值是22.【分析】(1)根据a =1,m =-3,则抛物线的解析式为y =x 2+bx -3,再将点A (1,0)代入y =x 2+bx -3,求出b 的值,从而得到抛物线的解析式,进一步可求出抛物线的顶点坐标;(2)①首先用含有m 的代数式表示出抛物线的解析式,求出C (0,m ),点E (m +1,m ).过点A 作AH ⊥l 于点H ,在Rt △EAH 中,利用勾股定理求出AE 的值,再根据AE =EF ,EF =22,可求出m 的值,进一步求出F 的坐标;②首先用含m 的代数式表示出MC 的长,然后分情况讨论MN 什么时候有最值.【详解】解:(1)当a =1,m =-3时,抛物线的解析式为y =x 2+bx -3.∵抛物线经过点A (1,0),∴0=1+b-3.解得b=2.∴抛物线的解析式为y=x2+2x-3.∵y=x2+2x-3=(x+1)2-4,∴抛物线的顶点坐标为(-1,-4).(2)①∵抛物线y=ax2+bx+m经过点A(1,0)和M(m,0),m<0,∴0=a+b+m,0=am2+bm+m,即am+b+1=0.∴a=1,b=-m-1.∴抛物线的解析式为y=x2-(m+1)x+m.根据题意,得点C(0,m),点E(m+1,m).过点A作AH⊥l于点H.由点A(1,0),得点H(1,m).在Rt△EAH中,EH=1-(m+1)=-m,HA=0-m=-m,∴AE=EH2+HA2=-2m.∵AE=EF=22,∴-2m=22.解得m=-2.此时,点E(-1,-2),点C(0,-2),有EC=1.∵点F在y轴上,∴在Rt△EFC中,CF=EF2-EC2=7.∴点F的坐标为(0,-2-7)或(0,-2+7).②由N是EF的中点,得CN=12EF=2.根据题意,点N在以点C为圆心、2为半径的圆上.由点M(m,0),点C(0,m),得MO=-m,CO=-m.∴在Rt△MCO中,MC=MO2+CO2=-2m.当MC≥2,即m≤-1时,满足条件的点N落在线段MC上,MN的最小值为MC-NC=-2m-2=22,解得m=-3 2;当MC<2,-1<m<0时,满足条件的点N落在线段CM的延长线上,MN的最小值为NC-MC=2-(-2m)=22,解得m=-1 2.∴当m的值为-32或-12时,MN的最小值是22.【点睛】本题考查了待定系数法求解析式,抛物线上的点的坐标满足抛物线方程等,解题的关键是学会利用参数解决问题,学会用转化的思想思考问题,属于中考常考题型..6(2023·重庆·统考中考真题)如图,在平面直角坐标系中,抛物线y=14x2+bx+c与x轴交于点A,B,与y轴交于点C,其中B3,0,C0,-3.(1)求该抛物线的表达式;(2)点P 是直线AC 下方抛物线上一动点,过点P 作PD ⊥AC 于点D ,求PD 的最大值及此时点P 的坐标;(3)在(2)的条件下,将该抛物线向右平移5个单位,点E 为点P 的对应点,平移后的抛物线与y 轴交于点F ,Q 为平移后的抛物线的对称轴上任意一点.写出所有使得以QF 为腰的△QEF 是等腰三角形的点Q 的坐标,并把求其中一个点Q 的坐标的过程写出来.【答案】(1)y =14x 2+14x -3(2)PD 取得最大值为45,P -2,-52 (3)Q 点的坐标为92,-1 或92,5 或92,74.【分析】(1)待定系数法求二次函数解析式即可求解;(2)直线AC 的解析式为y =-34x -3,过点P 作PE ⊥x 轴于点E ,交AC 于点Q ,设P t ,14t 2+14t -3 ,则Q t ,-34t -3 ,则PD =45PQ ,进而根据二次函数的性质即可求解;(3)根据平移的性质得出y =14x -92 2-4916,对称轴为直线x =92,点P -2,-52 向右平移5个单位得到E 3,-52 ,F 0,2 ,勾股定理分别表示出EF 2,QE 2,QF 2,进而分类讨论即可求解.【详解】(1)解:将点B 3,0 ,C 0,-3 .代入y =14x 2+bx +c 得,14×32+3b +c =0c =-3解得:b =14c =-3 ,∴抛物线解析式为:y =14x 2+14x -3,(2)∵y =14x 2+14x -3与x 轴交于点A ,B ,当y =0时,14x 2+14x -3=0解得:x 1=-4,x 2=3,∴A -4,0 ,∵C 0,-3 .设直线AC 的解析式为y =kx -3,∴-4k -3=0解得:k =-34∴直线AC 的解析式为y =-34x -3,如图所示,过点P 作PE ⊥x 轴于点E ,交AC 于点Q ,设P t ,14t 2+14t -3 ,则Q t ,-34t -3 ,∴PQ =-34t -3-14t 2+14t -3 =-14t 2-t ,∵∠AQE =∠PQD ,∠AEQ =∠QDP =90°,∴∠OAC =∠QPD ,∵OA =4,OC =3,∴AC =5,∴cos ∠QPD =PD PQ =cos ∠OAC =AO AC=45,∴PD =45PQ =45-14t 2-t =-15t 2-45t =-15t +2 2+45,∴当t =-2时,PD 取得最大值为45,14t 2+14t -3=14×-2 2+14×-2 -3=-52,∴P -2,-52 ;(3)∵抛物线y =14x 2+14x -3=14x +12 2-4916将该抛物线向右平移5个单位,得到y =14x -92 2-4916,对称轴为直线x =92,点P -2,-52 向右平移5个单位得到E 3,-52 ∵平移后的抛物线与y 轴交于点F ,令x =0,则y =14×92 2-4916=2,∴F 0,2 ,∴EF 2=32+2+52 2=1174∵Q 为平移后的抛物线的对称轴上任意一点.则Q 点的横坐标为92,设Q 92,m ,∴QE 2=92-3 2+m +52 2,QF 2=92 2+m -2 2,当QF =EF 时,92 2+m -2 2=1174,解得:m =-1或m =5,当QE =QF 时,92-3 2+m +522=92 2+m -2 2,解得:m =74综上所述,Q 点的坐标为92,-1 或92,5 或92,74.【点睛】本题考查了二次函数综合问题,解直角三角形,待定系数法求解析式,二次函数的平移,线段周长问题,特殊三角形问题,熟练掌握二次函数的性质是解题的关键.题型02利用二次函数解决两条线段之和的最值问题【解题思路】抛物线中的线段最值问题有三种形式:2. 两条线段和的最值问题:解决这类问题最基本的定理就是“两点之间线段最短”,解决这类问题的方法是:作其中一个定点关于已知直线的对称点,连接对称点与另一个定点,它们与已知直线的交点即为所求的点. 其变形问题有三角形周长最小或四边形周长最小等.【常见模型一】(两点在河的异侧):在直线L上找一点M,使PA+PB的值最小.方法:如右图,连接AB,与直线L交于点M,在M处渡河距离最短,最短距离为线段AB的长。
二次函数的最值问题总结

二次函数的最值问题二次函数2(0)y ax bx c a =++≠是初中函数的主要内容,也是高中学习的重要基础.在初中阶段大家已经知道:二次函数在自变量x 取任意实数时的最值情况(当0a >时,函数在2b x a =-处取得最小值244ac b a -,无最大值;当0a <时,函数在2b x a=-处取得最大值244ac b a-,无最小值. 本节我们将在这个基础上继续学习当自变量x 在某个范围内取值时,函数的最值问题.同时还将学习二次函数的最值问题在实际生活中的简单应用.二次函数求最值(一般范围类)例1.当22x -≤≤时,求函数223y x x =--的最大值和最小值.分析:作出函数在所给范围的及其对称轴的草图,观察图象的最高点和最低点,由此得到函数的最大值、最小值及函数取到最值时相应自变量x 的值.解:作出函数的图象.当1x =时,min 4y =-,当2x =-时,max 5y =.例2.当12x ≤≤时,求函数21y x x =--+的最大值和最小值.解:作出函数的图象.当1x =时,min 1y =-,当2x =时,max 5y =-.由上述两例可以看到,二次函数在自变量x 的给定范围内,对应的图象是抛物线上的一段.那么最高点的纵坐标即为函数的最大值,最低点的纵坐标即为函数的最小值.根据二次函数对称轴的位置,函数在所给自变量x 的范围的图象形状各异.下面给出一些常见情况:例3.当0x ≥时,求函数(2)y x x =--的取值范围.解:作出函数2(2)2y x x x x =--=-在0x ≥内的图象.可以看出:当1x =时,min 1y =-,无最大值.所以,当0x ≥时,函数的取值范围是1y ≥-.例4.当1t x t ≤≤+时,求函数21522y x x =--的最小值(其中t 为常数). 分析:由于x 所给的范围随着t 的变化而变化,所以需要比较对称轴与其范围的相对位置.解:函数21522y x x =--的对称轴为1x =.画出其草图. (1) 当对称轴在所给范围左侧.即1t >时: 当x t =时,2min 1522y t t =--; (2) 当对称轴在所给范围之间.即1101t t t ≤≤+⇒≤≤时:当1x =时,2min 1511322y =⨯--=-; (3) 当对称轴在所给范围右侧.即110t t +<⇒<时:当1x t =+时,22min 151(1)(1)3222y t t t =+-+-=-.综上所述:2213,023,0115,122t t y t t t t ⎧-<⎪⎪=-≤≤⎨⎪⎪-->⎩在实际生活中,我们也会遇到一些与二次函数有关的问题:二次函数求最值(经济类问题)例1.为了扩大内需,让惠于农民,丰富农民的业余生活,鼓励送彩电下乡,国家决定对购买彩电的农户实行政府补贴.规定每购买一台彩电,政府补贴若干元,经调查某商场销售彩电台数y (台)与补贴款额x (元)之间大致满足如图①所示的一次函数关系.随着补贴款额x 的不断增大,销售量也不断增加,但每台彩电的收益Z (元)会相应降低且Z 与x 之间也大致满足如图②所示的一次函数关系.(1)在政府未出台补贴措施前,该商场销售彩电的总收益额为多少元?(2)在政府补贴政策实施后,分别求出该商场销售彩电台数y 和每台家电的收益Z 与政府补贴款额x 之间的函数关系式;(3)要使该商场销售彩电的总收益w (元)最大,政府应将每台补贴款额x 定为多少?并求出总收益w 的最大值.分析:(1)政府未出台补贴措施前,商场销售彩电台数为800台,每台彩电的收益为200元;(2)利用两个图像中提供的点的坐标求各自的解析式;(3)商场销售彩电的总收益=商场销售彩电台数×每台家电的收益,将(2)中的关系式代入得到二次函数,再求二次函数的最大值.解:(1)该商场销售家电的总收益为800200160000⨯=(元);(2)依题意可设1800y k x =+,2200Z k x =+,∴有14008001200k +=,2200200160k +=,解得12115k k ==-,.所以800y x =+,12005Z x =-+. (3)1(800)2005W yZ x x ⎛⎫==+-+ ⎪⎝⎭21(100)1620005x =--+,政府应将每台补贴款额x 定为100元,总收益有最大值,其最大值为162000元.说明:本题中有两个函数图像,在解题时要结合起来思考,不可顾此失彼.例2.凯里市某大型酒店有包房100间,在每天晚餐营业时间,每间包房收包房费100元时,包房便可全部租出;若每间包房收费提高20元,则减少10间包房租出,若每间包房收费再提高20元,则再减少10间包房租出,以每次提高20元的这种方法变化下去.(1)设每间包房收费提高x (元),则每间包房的收入为y 1(元),但会减少y 2间包房租出,请分别写出y 1、y 2与x 之间的函数关系式.(2)为了投资少而利润大,每间包房提高x (元)后,设酒店老板每天晚餐包房总收入为y (元),请写出y 与x 之间的函数关系式,求出每间包房每天晚餐应提高多少元可获得最大包房费收入,并说明理由.分析:(1)提价后每间包房的收入=原每间包房收包房费+每间包房收包房提高费,包房减少数=每间包房收包房提高费数量的一半;(2)酒店老板每天晚餐包房总收入=提价后每间包房的收入×每天包房租出的数量,得到二次函数后再求y 取得最大值时x 的值.解:(1)x y +=1001,x y 212=; (2))21100()100(x x y -•+=y 11250)50(212+--=x ,因为提价前包房费总收入为100×100=10000,当x=50时,可获最大包房收入11250元,因为11250>10000又因为每次提价为20元,所以每间包房晚餐应提高40元或60元. 说明:本题的答案有两个,但从“投资少而利润大”的角度来看,因尽量少租出包房,所以每间包房晚餐应提高60元应该更好.例3.某水产品养殖企业为指导该企业某种水产品的养殖和销售,对历年市场行情和水产品养殖情况进行了调查.调查发现这种水产品的每千克售价1y (元)与销售月份x (月)满足关系式1y =36x 83+-,而其每千克成本2y (元)与销售月份x (月)满足的函数关系如图所示.(1)试确定b c 、的值;(2)求出这种水产品每千克的利润y (元)与销售月份x (月)之间的函数关系式;(3)“五·一”之前,几月份出售这种水产品每千克的利润最大?最大利润是多少? 分析:(1)将点(3,25),(4,24)代入求b 、c 的值;(2)y =1y -2y ;(3)将(2)中的二次函数配方为顶点式,再利用二次函数的增减性,在满足“五·一”之前的前提下求最大值.解:(1)由题意:22125338124448b c b c ⎧=⨯++⎪⎪⎨⎪=⨯++⎪⎩,解得7181292b c ⎧=-⎪⎪⎨⎪=⎪⎩; (2)12y y y =-23115136298882x x x ⎛⎫=-+--+ ⎪⎝⎭21316822x x =-++; (3)21316822y x x =-++ 2111(1236)46822x x =--+++21(6)118x =--+. ∵108a =-<,∴抛物线开口向下.在对称轴6x =左侧y 随x 的增大而增大.由题意5x <,所以在4月份出售这种水产品每千克的利润最大.最大利润211(46)111082=--+=(元). 说明:本题在x =6,即6月份时取得最大值,但题目要求在“五·一”之前,所以要将二次函数配方为顶点式,利用二次函数的增减性来求解.例4.某商场以每件30元的价格购进一种商品,试销中发现这种商品每天的销售量m (件)与每件的销售价x (元)满足一次函数1623,3054m x x =-≤≤.(1) 写出商场卖这种商品每天的销售利润y 与每件销售价x 之间的函数关系式;(2) 若商场要想每天获得最大销售利润,每件商品的售价定为多少最合适?最大销售利润为多少?解:(1) 由已知得每件商品的销售利润为(30)x -元,那么m 件的销售利润为(30)y m x =-,又1623m x =-.y 22 (30)(1623)32524860,3054y x x x x x ∴=--=-+-≤≤(2) 由(1)知对称轴为42x =,位于x 的范围内,另抛物线开口向下 ∴当42x =时,2max 342252424860432y =-⨯+⨯-=∴当每件商品的售价定为42元时每天有最大销售利润,最大销售利润为432元. 二次函数求最值(面积最值问题)例1.在矩形ABCD 中,AB=6cm ,BC=12cm ,点P 从点A 出发,沿AB 边向点B 以1cm /s 的速度移动,同时点Q 从点B 出发沿BC 边向点C 以2cm /s 的速度移动,如果P 、Q 两点同时出发,分别到达B 、C 两点后就停止移动.(1)运动第t 秒时,△PBQ 的面积y(cm²)是多少?(2)此时五边形APQCD 的面积是S(cm²),写出S 与t 的函数关系式,并指出自变量的取值范围.(3)t 为何值时s 最小,最小值时多少?答案:6336333607266126262621)1(2222有最小值等于时;当)()()()()()(S t t S t t t t t S t t t t y =∴+-=<<+-=+--⨯=+-=⋅-=例2.小明的家门前有一块空地,空地外有一面长10米的围墙,为了美化生活环境,小明的爸爸准备靠墙修建一个矩形花圃,他买回了32米长的不锈钢管准备作为花圃的围栏,为了浇花和赏花的方便,准备在花圃的中间再围出一条宽为一米的通道及在左右花圃各放一个1米宽的门(木质).花圃的长与宽如何设计才能使花圃的面积最大?解:设花圃的宽为x 米,面积为S 平方米则长为:x x 4342432-=+-(米)则:)434(x x S -=x x 3442+-= 4289)417(42+--=x ∵104340≤-<x ∴2176<≤x∵6417<,∴S 与x 的二次函数的顶点不在自变量x 的范围内, 而当2176<≤x 内,S 随x 的增大而减小, ∴当6=x 时,604289)4176(42max =+--=S (平方米) 答:可设计成宽6米,长10米的矩形花圃,这样的花圃面积最大.例3.已知边长为4的正方形截去一个角后成为五边形ABCDE (如图),其中AF=2,BF=1.试在AB 上求一点P ,使矩形PNDM 有最大面积.解:设矩形PNDM 的边DN=x ,NP=y ,则矩形PNDM 的面积S=xy (2≤x≤4)易知CN=4-x ,EM=4-y .过点B 作BH ⊥PN 于点H则有△AFB ∽△BHP∴PHBH BF AF =,即3412--=y x , ∴521+-=x y , x x xy S 5212+-==)42(≤≤x , 此二次函数的图象开口向下,对称轴为x=5,∴当x≤5时,函数值y 随x 的增大而增大,对于42≤≤x 来说,当x=4时,12454212=⨯+⨯-=最大S . 【评析】本题是一道代数几何综合题,把相似三角形与二次函数的知识有机的结合在一起,能很好考查学生的综合应用能力.同时,也给学生探索解题思路留下了思维空间.例4.某人定制了一批地砖,每块地砖(如图(1)所示)是边长为0.4米的正方形ABCD ,点E 、F 分别在边BC 和CD 上,△CFE 、△ABE 和四边形AEFD 均由单一材料制成,制成△CFE 、△ABE 和四边形AEFD 的三种材料的每平方米价格依次为30元、20元、10元,若将此种地砖按图(2)所示的形式铺设,且能使中间的阴影部分组成四边形EFGH .(1)判断图(2)中四边形EFGH 是何形状,并说明理由;(2)E 、F 在什么位置时,定制这批地砖所需的材料费用最省?解:(1) 四边形EFGH 是正方形.图(2)可以看作是由四块图(1)所示地砖绕C 点按顺(逆)时针方向旋转90°后得到的,故CE =CF =CG .∴△CEF 是等腰直角三角形因此四边形EFGH 是正方形.(2)设CE =x , 则BE =0.4-x ,每块地砖的费用为y 元那么:y =x ×30+×0.4×(0.4-x )×20+[0.16-x -×0.4×(0.4-x )×10]=xx)-102+242.0.0(-=x)4.0102+3.2()1.0<x0(<当x=0.1时,y有最小值,即费用为最省,此时CE=CF=0.1.答:当CE=CF=0.1米时,总费用最省.。
二次函数在闭区间上的最值问题

二次函数在闭区间上的最值问题湖北省荆州中学 鄢先进二次函数在闭区间上的最值问题是高中数学的重点和热点问题,频繁出现在函数试题中,很受命题者亲睐。
影响二次函数在闭区间上最值问题的主要因素是二次函数图像的开口方向与所给区间和对称轴的位置关系。
本文介绍有关二次函数在闭区间上最值问题的常见类型及解题策略,供同学们参考。
类型一 定轴定区间例1.已知函数2()2f x x x =-,求()f x 的最小值. 解:22()2(1)1f x x x x =-=-- 由图像可知,当1x =时,min ()1f x =-变式1.已知函数2()2f x x x =-,[2,4]x ∈,求()f x 的最小值。
分析:由图像可知,函数)(x f 在[2,4]为增函数,min ()(2)0f x f ∴==变式2.已知函数2()2f x x x =-,[0,3]x ∈,求()f x 的最大值.分析:由图像可知函数()f x 在[0,1]上递减,在[1,3]上递增,且3离对称轴的距离大于0离对称轴的距离。
max ()(3)3f x f ∴==例2.已知二次函数f x ax ax a ()=++-2241在区间[]-41,上的最大值为5,求实数a 的值。
解:将二次函数配方得f x a x a a ()()=++--24122,函数图像对称轴方程为x =-2,顶点坐标为()---2412,a a ,图像开口方向由a 决定。
很明显,其顶点横坐标在区间[]-41,内。
x①若a <0,函数图像开口向下,如下图1所示。
当x =-2时,函数()f x 取得最大值5 即f a a ()-=--=24152,解得a =±210 故a a =-=+210210()舍去图1 图2②若a >0,函数图像开口向上,如上图2所示,当x =1时,函数()f x 取得最大值5 即f a a ()15152=+-=,解得a a ==-16或,故a a ==-16()舍去综上可知:函数f x ()在区间[]-41,上取得最大值5时,a a =-=2101或 点拨:求解有关二次函数在闭区间上的最值问题,应先配方,作出函数图像,然后结合其图像研究,要特别注意开口方向、对称轴和区间的相对位置。
二次函数最值问题及解题技巧(个人整理)

二次函数最值问题及解题技巧(个人整理)一、二次函数线段最值问题1、平行于x轴的线段最值问题1)首先表示出线段两个端点的坐标2)用右侧端点的横坐标减去左侧端点的横坐标3)得到一个线段长关于自变量的二次函数4)将其化为顶点式,并根据a的正负及自变量的取值范围判断最值2、平行于y轴的线段最值问题1)首先表示出线段两个端点的坐标2)用上面端点的纵坐标减去下面端点的纵坐标3)得到一个线段长关于自变量的二次函数解析式4)将其化为顶点式,并根据a的正负及自变量的取值范围判断最值3、既不平行于x轴,又不平行于y轴的线段最值问题1)以此线段为斜边构造一个直角三角形,并使此直角三角形的两条直角边分别平行于x轴、y轴2)根据线段两个端点的坐标表示出直角顶点坐标3)根据“上减下,右减左”分别表示出两直角边长4)根据勾股定理表示出斜边的平方(即两直角边的平方和)5)得到一个斜边的平方关于自变量的二次函数6)将其化为顶点式,并根据a的正负及自变量的取值规模判断最值7)根据所求得的斜边平方的最值求出斜边的最值即可2、二次函数周长最值问题1、矩形周长最值问题1)一般会给出一点落在抛物线上,从这点向两坐标轴引垂线构成一个矩形,求其周长最值2)可先设此点坐标,点p到x轴、y轴的距离和再乘以2,即为周长3)将其化为顶点式,并根据a的正负及自变量的取值范围判断最值2、利用两点之间线段最短求三角形周长最值1)首先判断图形中那些边是定值,哪些边是变量2)使用二次函数轴对称性及两点之间线段最短找到两条变革的边,并求其和的最小值3)周长最小值即为两条变革的边的和最小值加上不变的边长3、二次函数面积最值问题1、规则图形面积最值问题(这里规则图形指三角形必有一边平行于坐标轴,四边形必有一组对边平行于坐标轴)1)首先表示出所需的边长及高2)使用求面积公式表示出面积3)得到一个面积关于自变量的二次函数4)将其化为顶点式,并根据a的正负及自变量的取值规模判断最值2、不划定规矩图形面积最值问题1)支解。
二次函数闭区间上最值问题动轴定区间类型

讨论时注意:对称轴要取到横轴上的每一个点, 并做到不重不漏。
解:
(1)当a 5时,f (x)min f (5) 25 10a 2 10a 27 (2)当 5 a 5时,f (x)min f (a) a2 2a2 2 a2 2
(3)当a 5时,f (x)min f (5) 25 10a 2 10a 27
2a 2
max
当- b 2a
m n 时,f 2
xmax
f
m
二次函数在闭区间上最值的求法
1、 要注意应用数形结合与分类讨论的数学思想。
2、二次函数闭区间上的最值要分析对称轴与区间 或区间中点的位置关系,再根据二次函数的单调性 或对称性来得出函数的最值。
(1) 开口向上时的最小值,要分对称轴在区 间的左中右三种情况;(开口向下时的最大值)
小值
分 三 类 讨 论
(1)当 b 2a
m时,f (x)min
f (m)
(2)当m b 2a
n时,f
( x)min
f
( b ) 2a
(3)当 b 2a
n时,f (x)min
f (n)
【例题】已知函数 f x x2 2ax 2 ,求函数 f(x)
在[-5,5]上的最小值。 分析:
点评:二次函数在给定闭区间上的最值在顶点或端点 处取得。如果解析式中含有参数,需对参数分类讨论, 根据对称轴与区间的位置关系,结合二次函数的图像 利用二次函数的单调性处理。
二、已知函数 f x ax2 bx c,(a 0),求 f x 在
二次函数最值问题类型题总结

二次函数得最大值或最小值问题知识点:1、配方法:将二次函数得一般式化为顶点式(1)若,有最小值、当时,取得最小值(2)若,有最大值、当时,取得最大值2、公式法:直接利用二次函数图像得顶点坐标求解、(1)若,有最小值,没有最大值,当时,、(2)若,有最大值,没有最小值,当时,、考察方向:一、1、已知二次函数得图像确定二次函数得最值例1、二次函数得部分图象如图1、3-3所示,则该函数有最值,最值为、2、已知二次函数表达式求函数最值①在函数整个定义域内求函数最值例2、二次函数有( )A.最大值B、最小值C、最大值D、最小值②在给定定义域区间范围内求函数最值二次函数在自变量得给定范围内,对应得图象就是抛物线上得一段.那么最高点得纵坐标即为函数得最大值,最低点得纵坐标即为函数得最小值.根据二次函数对称轴得位置,函数在所给自变量得范围得图象形状各异.下面给出一些常见情况:例3、当时,求函数得最大值与最小值例4、二次函数,当且时,y 散文最小值为2m,最大值为2n ,则得值为多少?3、由二次函数得最大值或最小值求二次函数表达式中得待定系数(解答最值问题忽略二次项系数得符号)例5、已知二次函数有最小值1,则得大小关系就是什么?例6、已知二次函数有最小值0,则m 得值就是多少?二、4、二次函数最值在实际应用题间得应用(①生活中得应用②几何图形面积最值问题)例7、某水产品养殖企业为指导该企业某种水产品得养殖与销售,对历年市场行情与水产品养殖情况进行了调查.调查发现这种水产品得每千克售价(元)与销售月份(月)满足关系式=,而其每千克成本(元)与销售月份(月)满足得函数关系如图所示.(1)试确定得值; (2)求出这种水产品每千克得利润(元)与销售月份(月)之间得函数关系式; “五·一”之(3)前,几月份出售这种水产品每千克得利润最大?最大利润就是多少?例8、已知边长为4得正方形截去一个角后成为五边形ABCDE(如图),其中AF=2,BF=1.试在AB上求一点P,使矩形PND M有最大面积. 25 24 y 2(元)x (月) 1 2 3 4 5 6 7 8 9 O。
二次函数最值与交点问题

3、已知抛物线 、直线 ,若对于任意的x的值, 恒成立,则m的值为。
知识点三:图形存在性问题
【例题精讲】
1、在平面直角坐标系xOy中,将二次函数y=x2-1的图象M沿x轴翻折,把所得到的图象向右平移2个单位长度后再向上平移8个单位长度,得到二次函数图象N。若一个点的横坐标与纵坐标均为整数,则该点称为整点,则M与N所围成封闭图形内(包括边界)整点的个数为()
A.- B. 或- C.2或- D.2或 或-
2、二次函数y=x2﹣2x﹣3,当m﹣2≤x≤m时的最大值为5,则m的值可能为( )
A.0或6B.4或﹣2C.0或4D.6或﹣2
3、已知抛物线y=(x-m)2-(x-m),其中m是常数,抛物线与x轴交于A、B两点(点A在点B的左侧),若0<x< 时,恒有y<0,则m的取值范围是.
2、二次函数 ,点A(0,3),点B在直线y=2上运动,A、B、C顺时针排列,AB=BC,AB⊥BC,点C在抛物线内部,记点B的横坐标为t,则t的取值范围是。
1、已知a<b,函数y=-x2+x(a≤x≤b)的最大值、最小值为2b和2a,则a+b=
2、已知P(0,1)和Q(1,0),若二次函数 的图象与线段PQ有交点,则a的取值范围为。
3、已知二次函数y=x2-(m+1)x-5m(m为常数),在-3≤x≤1的范围内至少有一个x的值使y≥2,则m的取值范围是__________
4、已知二次函数y=x2-2hx+h,当自变量x的取值在-1≤x≤1的范围中时,函数有最小值n,则n的最大值是__________。
专题07 二次函数的最值问题-九年级数学上册(解析版)

专题07二次函数的最值问题考点1:定轴动区间;考点2:动轴定区间。
1.在二次函数y =x 2﹣2x ﹣3中,当0≤x ≤3时,y 的最大值和最小值分别是()A .0,﹣4B .0,﹣3C .﹣3,﹣4D .0,0解:抛物线的对称轴是直线x =1,则当x =1时,y =1﹣2﹣3=﹣4,是最小值;当x =3时,y =9﹣6﹣3=0是最大值.答案:A .2.(易错题)已知二次函数y =a (x ﹣1)2﹣a (a ≠0),当﹣1≤x ≤4时,y 的最小值为﹣4,则a 的值为()A .12或4B .43或−12C .−43或4D .−12或4解:y =a (x ﹣1)2﹣a 的对称轴为直线x =1,顶点坐标为(1,﹣a ),当a >0时,在﹣1≤x ≤4,函数有最小值﹣a ,∵y 的最小值为﹣4,∴﹣a =﹣4,∴a =4;当a <0时,在﹣1≤x ≤4,当x =4时,函数有最小值,∴9a ﹣a =﹣4,解得a =−12;综上所述:a 的值为4或−12,答案:D.3.(易错题)当a ≤x ≤a +1时,函数y =x 2﹣2x +1的最小值为1,则a 的值为()A .﹣1B .2C .0或2D .﹣1或2解:当y =1时,有x 2﹣2x +1=1,解得:x 1=0,x 2=2.题型01定轴动区间∵当a≤x≤a+1时,函数有最小值1,∴a=2或a+1=0,∴a=2或a=﹣1,答案:D.4.已知函数y=﹣3(x﹣2)2+4,当x=2时,函数取得最大值为4.解:∵y=﹣3(x﹣2)2+4,∴抛物线的顶点坐标为(2,4),又∵a=﹣3<0,∴抛物线的开口向下,顶点是它的最高点,∴x=2时,函数有最大值为4.答案:2,4.5.若函数y=x2﹣6x+5,当2≤x≤6时的最大值是M,最小值是m,则M﹣m=9.解:原式可化为y=(x﹣3)2﹣4,可知函数顶点坐标为(3,﹣4),当y=0时,x2﹣6x+5=0,即(x﹣1)(x﹣5)=0,解得x1=1,x2=5.如图:m=﹣4,当x=6时,y=36﹣36+5=5,即M=5.则M﹣m=5﹣(﹣4)=9.故答案为9.6.已知二次函数y=ax2﹣4ax+3a(1)若a=1,则函数y的最小值为﹣1.(2)若当1≤x≤4时,y的最大值是4,则a的值为43或﹣4.解:(1)当a=1时,y=x2﹣4x+3=(x﹣2)2﹣1∵a=1>0∴抛物线的开口向上,当x=2时,函数y的最小值为﹣1.(2)∵二次函数y=ax2﹣4ax+3a=a(x﹣2)2﹣a∴抛物线的对称轴是直线x=2,∵1≤x≤4,∴当a>0时,抛物线开口向上,在对称轴直线x=2右侧y随x的增大而增大,当x=4时y有最大值,a×(4﹣2)2﹣a=4,解得a=43,当a<0时,抛物线开口向下,x=2时y有最大值,a×(2﹣2)2﹣a=4,解得a=﹣4.答案:(1)﹣1;(2)43或−4.7.(易错题)设a,b是任意两个不等实数,我们规定:满足不等式a≤x≤b的实数x的所有取值的全体叫做闭区间,表示为[a,b].对于任何一个二次函数,它在给定的闭区间上都有最小值.(1)函数y=﹣x2+4x﹣2在区间[0,5]上的最小值是﹣7(2)求函数=(+12)2+34在区间[0,32]上的最小值.(3)求函数y=x2﹣4x﹣4在区间[t﹣2,t﹣1](t为任意实数)上的最小值y min的解析式.解:(1)y=﹣x2+4x﹣2其对称轴为直线为x=2,顶点坐标为(2,2),函数图象开口向下.如图1所示:当x=5时,函数有最小值,最小值为﹣7.答案:﹣7.(2)=(+12)2+34,其对称轴为直线=−12,顶点坐标(−12,34),且图象开口向上.其顶点横坐标不在区间[0,32]内,如图2所示:当x=0时,函数y有最小值m=1.(3)将二次函数配方得:y=x2﹣4x﹣4=(x﹣2)2﹣8其对称轴为直线:x=2,顶点坐标为(2,﹣8),图象开口向上若顶点横坐标在区间[t﹣2,t﹣1]左侧,则2<t﹣2,即t>4.当x=t﹣2时,函数取得最小值:m=(−4)2−8=2−8+8若顶点横坐标在区间[t﹣2,t﹣1]上,则t﹣2≤2≤t﹣1,即3≤t≤4.当x=2时,函数取得最小值:y min=﹣8若顶点横坐标在区间[t﹣2,t﹣1]右侧,则t﹣1<2,即t<3.当x=t﹣1时,函数取得最小值:m=(−3)2−8=2−6+1综上讨论,得m=2−8+8(>4)−8(3≤≤4)2−6+1(<3).8.(易错题)已知二次函数y =﹣x 2+6x ﹣5.(1)求二次函数图象的顶点坐标;(2)当1≤x ≤4时,函数的最大值和最小值分别为多少?(3)当t ≤x ≤t +3时,函数的最大值为m ,最小值为n ,若m ﹣n =3,求t 的值.解:(1)∵y =﹣x 2+6x ﹣5=﹣(x ﹣3)2+4,∴顶点坐标为(3,4);(2)∵a =﹣1<0,∴抛物线开口向下,∵顶点坐标为(3,4),∴当x =3时,y 最大值=4,∵当1≤x ≤3时,y 随着x 的增大而增大,∴当x =1时,y 最小值=0,∵当3<x ≤4时,y 随着x 的增大而减小,∴当x =4时,y 最小值=3.∴当1≤x ≤4时,函数的最大值为4,最小值为0;(3)当t ≤x ≤t +3时,对t 进行分类讨论,①当t +3<3时,即t <0,y 随着x 的增大而增大,当x =t +3时,m =﹣(t +3)2+6(t +3)﹣5=﹣t 2+4,当x =t 时,n =﹣t 2+6t ﹣5,∴m ﹣n =﹣t 2+4﹣(﹣t 2+6t ﹣5)=﹣6t +9,∴﹣6t +9=3,解得t =1(不合题意,舍去),②当0≤t <3时,顶点的横坐标在取值范围内,∴m =4,i )当0≤t ≤32时,在x =t 时,n =﹣t 2+6t ﹣5,∴m ﹣n =4﹣(﹣t 2+6t ﹣5)=t 2﹣6t +9,∴t2﹣6t+9=3,解得t1=3−3,t2=3+3(不合题意,舍去);ii)当32<t<3时,在x=t+3时,n=﹣t2+4,∴m﹣n=4﹣(﹣t2+4)=t2,∴t2=3,解得t1=3,t2=−3(不合题意,舍去),③当t≥3时,y随着x的增大而减小,当x=t时,m=﹣t2+6t﹣5,当x=t+3时,n=﹣(t+3)2+6(t+3)﹣5=﹣t2+4,.m﹣n=﹣t2+6t﹣5﹣(﹣t2+4)=6t﹣9,∴6t﹣9=3,解得t=2(不合题意,舍去),综上所述,t=3−3或3.9.已知二次函数y=ax2+4x+a﹣1的最小值为2,则a的值为()A.3B.﹣1C.4D.4或﹣1解:∵二次函数y=ax2+4x+a﹣1有最小值2,∴a>0,y最小值=4a−24=4oK1)−424=2,整理,得a2﹣3a﹣4=0,解得a=﹣1或4,∵a>0,∴a=4.答案:C.10.设二次函数y=a(x﹣m)(x﹣m﹣k)(a>0,m,k是实数),则()A.当k=2时,函数y的最小值为﹣aB.当k=2时,函数y的最小值为﹣2aC.当k=4时,函数y的最小值为﹣aD.当k=4时,函数y的最小值为﹣2a题型02动轴定区间解:令y=0,则(x﹣m)(x﹣m﹣k)=0,∴x1=m,x2=m+k,∴二次函数y=a(x﹣m)(x﹣m﹣k)与x轴的交点坐标是(m,0),(m+k,0),∴二次函数的对称轴是:=1+22=rr2=2r2,∵a>0,∴y有最小值,当=2r2时y最小,即=o2r2−p(2r2−−p=−24,当k=2时,函数y的最小值为=−224=−;当k=4时,函数y的最小值为=−424=−4,答案:A.11.在平面直角坐标系中,二次函数y=x2+mx+m2﹣m(m为常数)的图象经过点(0,6),其对称轴在y轴左侧,则该二次函数有()A.最大值5B.最大值154C.最小值5D.最小值154解:由题意可得:6=m2﹣m,解得:m1=3,m2=﹣2,∵二次函数y=x2+mx+m2﹣m,对称轴在y轴左侧,∴m>0,∴m=3,∴y=x2+3x+6,∴二次函数有最小值为:4a−24=4×1×6−324×1=154.答案:D.12.已知二次函数y=x2﹣2mx(m为常数),当﹣1≤x≤2时,函数值y的最小值为﹣2,则m的值是()A.32B.2C.32或2D.−32或2解:y=x2﹣2mx=(x﹣m)2﹣m2,①若m<﹣1,当x=﹣1时,y=1+2m=﹣2,解得:m=−32;②若m>2,当x=2时,y=4﹣4m=﹣2,解得:m=32<2(舍);③若﹣1≤m≤2,当x=m时,y=﹣m2=﹣2,解得:m=2或m=−2<−1(舍),∴m的值为−32或2,答案:D.13.(易错题)当﹣1≤x≤2时,二次函数y=x2+2kx+1的最小值是﹣1,则k的值可能是32或−解:对称轴:x=−22=−k,分三种情况讨论:①当﹣k<﹣1时,即k>1时,此时﹣1≤x≤2在对称轴的右侧,y随x的增大而增大,=(﹣1)2+2k×(﹣1)+1=﹣1,∴当x=﹣1时,y有最小值,y小k=32,②当﹣1≤﹣k≤2时,即﹣2≤k≤1,对称轴在﹣1≤x≤2内,此时函数在﹣1≤x≤﹣k,y随x的增大而减小,在﹣k≤x≤2时,y随x的增大而增大,=(﹣k)2+2k•(﹣k)+1=﹣1,∴当x=﹣k时,y有最小值,y小k2﹣2k2+2=0,k2﹣2=0,k=±2,∵﹣2≤k≤1,∴k=−2,③当﹣k>2时,即k<﹣2,此时﹣1≤x≤2在对称轴的左侧,y随x的增大而减小,∴当x=2时,y有最小值,y=22+2k×2+1=﹣1,小k=−32(舍),综上所述,k的值可能是32或−2,答案:32或−2.14.已知y=﹣x(x+3﹣a)是关于x的二次函数,当x的取值范围在1≤x≤5时,若y在x=1时取得最大值,则实数a的取值范围是a≤5.解:第一种情况:当二次函数的对称轴不在1≤x≤5内时,此时,对称轴一定在1≤x≤5的左边,函数方能在这个区域取得最大值,x=K32<1,即a<5,第二种情况:当对称轴在1≤x≤5内时,对称轴一定是在顶点处取得最大值,即对称轴为x=1,∴K32=1,即a=5综合上所述a≤5.答案:a≤5.15.(易错题)已知二次函数y=x2﹣2hx+h,当自变量x的取值在﹣1≤x≤1的范围中时,函数有最小值n,则n的最大值是14.解:二次函数y=x2﹣2hx+h图象的对称轴为直线x=h.当h≤﹣1时,x=﹣1时y取最小值,此时n=1+2h+h=1+3h≤﹣2;当﹣1<h<1时,x=h时y取最小值,此时n=h2﹣2h2+h=﹣h2+h=﹣(h−12)2+14≤14;当h≥1时,x=1时y取最小值,此时n=1﹣2h+h=1﹣h≤0.综上所述:n的最大值为14.答案:14.16.(易错题)已知二次函数y=x2﹣2x+2在t≤x≤t+1时的最小值是t,则t的值为1或2.解:y=x2﹣2x+2=(x﹣1)2+1,分类讨论:(1)若顶点横坐标在范围t≤x≤t+1右侧时,有t+1<1,即t<0,此时y随x的增大而减小,=t=(t+1)2﹣2(t+1)+2,∴当x=t+1时,函数取得最小值,y最小值方程无解.(2)若顶点横坐标在范围t≤x≤t+1内时,即有t≤1≤t+1,=1,解这个不等式,即0≤t≤1.此时当x=1时,函数取得最小值,y最小值∴t=1.(3)若顶点横坐标在范围t≤x≤t+1左侧时,即t>1时,y随x的增大而增大,=t=t2﹣2t+2,解得t=2或1(舍弃),∵当x=t时,函数取得最小值,y最小值∴t=1或2.答案:1或2.17.已知函数y=﹣x2+bx+c(b,c为常数)的图象经过点(0,﹣3),(﹣6,﹣3).(1)求b,c的值.(2)当﹣4≤x≤0时,求y的最大值.(3)当m≤x≤0时,若y的最大值与最小值之和为2,求m的值.解:(1)把(0,﹣3),(﹣6,﹣3)代入y=﹣x2+bx+c,得b=﹣6,c=﹣3.(2)∵y=﹣x2﹣6x﹣3=﹣(x+3)2+6,又∵﹣4≤x≤0,∴当x=﹣3时,y有最大值为6.(3)①当﹣3<m≤0时,当x=0时,y有最小值为﹣3,当x=m时,y有最大值为﹣m2﹣6m﹣3,∴﹣m2﹣6m﹣3+(﹣3)=2,∴m=﹣2或m=﹣4(舍去).②当m≤﹣3时,当x=﹣3时y有最大值为6,∵y的最大值与最小值之和为2,∴y最小值为﹣4,∴﹣(m+3)2+6=﹣4,∴m=−3−10或m=−3+10(舍去).综上所述,m=﹣2或−3−10.18.(易错题)已知二次函数y=x2+bx+c(b,c为常数).(Ⅰ)当b=2,c=﹣3时,求二次函数的最小值;(Ⅱ)当c=5时,若在函数值y=1的情况下,只有一个自变量x的值与其对应,求此时二次函数的解析式;(Ⅲ)当c=b2时,若在自变量x的值满足b≤x≤b+3的情况下,与其对应的函数值y的最小值为21,求此时二次函数的解析式.解:(Ⅰ)当b=2,c=﹣3时,二次函数的解析式为y=x2+2x﹣3=(x+1)2﹣4,∴当x=﹣1时,二次函数取得最小值﹣4;(Ⅱ)当c=5时,二次函数的解析式为y=x2+bx+5,由题意得,x2+bx+5=1有两个相等是实数根,∴△=b2﹣16=0,解得,b1=4,b2=﹣4,∴二次函数的解析式y=x2+4x+5,y=x2﹣4x+5;(Ⅲ)当c=b2时,二次函数解析式为y=x2+bx+b2,图象开口向上,对称轴为直线x=−2,①当−2<b,即b>0时,在自变量x的值满足b≤x≤b+3的情况下,y随x的增大而增大,∴当x=b时,y=b2+b•b+b2=3b2为最小值,∴3b2=21,解得,b1=−7(舍去),b2=7;②当b≤−2≤b+3时,即﹣2≤b≤0,∴x=−2,y=34b2为最小值,∴34b2=21,解得,b1=﹣27(舍去),b2=27(舍去);③当−2>b+3,即b<﹣2,在自变量x的值满足b≤x≤b+3的情况下,y随x的增大而减小,故当x=b+3时,y=(b+3)2+b(b+3)+b2=3b2+9b+9为最小值,∴3b2+9b+9=21.解得,b1=1(舍去),b2=﹣4;∴b=7时,解析式为:y=x2+7x+7b=﹣4时,解析式为:y=x2﹣4x+16.综上可得,此时二次函数的解析式为y=x2+7x+7或y=x2﹣4x+16.。
二次函数求最值(动轴定区间、动区间定轴)

4
4
4
2 x=1
x=1
2
x=1
2
k+2
k k+2
k k+2
k 15
5
10
5
15
5 10
5
15
10
10
5
5
2
2
2
6
4
2 x=1
15
k 10
k+2 5
2
4
4
4
4
6
评注6:例1属于6“轴定区间动”的问题,看6 作动区
间沿8x轴移动的过8 程中,函数8 最值的变化,8 即动区
间在定轴的左、右两侧及包10含定轴的变化,要注
y 解: ⑴当
即a≥ 2时
y的最小值为f(-1)
O -1 1 x
=4-a
例3:若x∈
,求函数
•
y =x2+ax+3的最小值:
(2)当 1 < a 1
2
y
即-2≤ a<2时
y的最小值为
O
f( )=
-1 1 x
例2:若x∈
•
,求函数
y =x2+ax+3的最小值:
y
O -1 1
(3)当
即a<-2时
解:画出函数在定义域内的图像如图 8
对称轴为直线x=1
6
由图知,y=f(x)在[ 2,4 ]上为增函数
4
故x=4时有最大值f(4)=5
x=2时有最小值f(2)=-3
10
5
2 x=1 2
45
2
4
y = x2 2∙x 3
y = x2 2∙x 3
二次函数与定点定值问题(教师版)
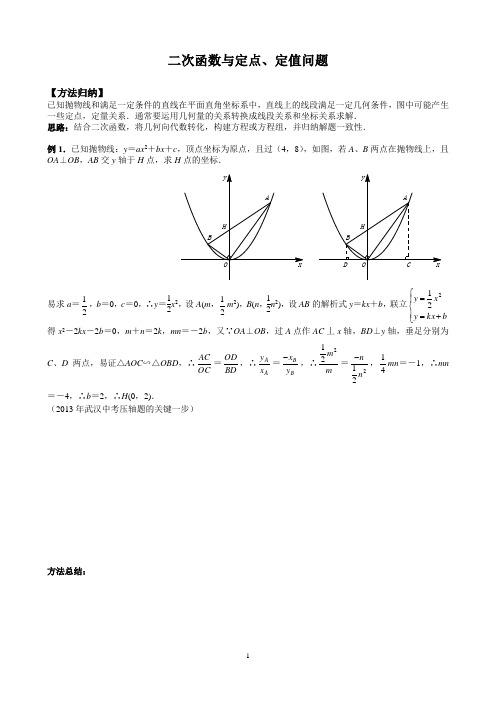
二次函数与定点、定值问题【方法归纳】已知抛物线和满足一定条件的直线在平面直角坐标系中,直线上的线段满足一定几何条件,图中可能产生一些定点,定量关系.通常要运用几何量的关系转换成线段关系和坐标关系求解. 思路:结合二次函数,将几何向代数转化,构建方程或方程组,并归纳解题一致性.例1.已知抛物线:y =ax 2+bx +c ,顶点坐标为原点,且过(4,8),如图,若A 、B 两点在抛物线上,且OA ⊥OB ,AB 交y 轴于H 点,求H 点的坐标.易求a =21,b =0,c =0,∴y =12x 2,设A (m ,21m 2),B (n ,12n 2),设AB 的解析式y =kx +b ,联立⎪⎩⎪⎨⎧+==b kx y xy 221得x 2-2kx -2b =0,m +n =2k ,mn =-2b ,又∵OA ⊥OB ,过A 点作AC 丄x 轴,BD ⊥y 轴,垂足分别为C 、D 两点,易证△AOC ∽△OBD ,∴OC AC =BD OD ,∴A A x y =B B y x -,∴m m221=221n n -,41mn =-1,∴mn=-4,∴b =2,∴H (0,2).(2013年武汉中考压轴题的关键一步)方法总结:_________________________________________________ _________________________________________________ _________________________________________________【练1】抛物线y =21(x -1)2,顶点为M ,直线AB 交抛物线于A 、B 两点,且MA ⊥MB ,求证:直线AB 过定点.设A (x 1,y 1),B (x 2,y 2),易求M (1,0),作AE ⊥x 轴,BF ⊥x 轴,△AEM ∽△BFM ,易得EM AE =FBMF,即111x y -=221y x -,1211)1(21x x --=222)1(211--x x ,∴-21(x 1-1)2=)1(2112-x ,∴-41[x 1x 2-(x 1+x 2)+1]=1,联立⎪⎩⎪⎨⎧+=-=b kx y x y 2)1(21得,21(x -1)2=kx +b ,x 2-2x +1=2kx +2b ,x 2-(2+2k )x +1-2b =0,x 1·x 2=1-2b ,x 1+x 2=2k +2,∴(1-2b )-(2k +2)+1=-4,k +b =2,∴y =kx +b =kx +2-k =k (x -1)+2,∴AB 过定点(1,2).例2.已知抛物线y =41x 2,以M (-2,1)为直角顶点作该抛物线的内接直角三角形MAB (即M ,A ,B 均在抛物线上),求证:直线AB 过定点,并求出该定点坐标.过M 作PQ ∥x 轴,AP ⊥PQ 于P ,BQ ⊥PQ 于Q ,设AB :y =kx +b , 由⎪⎩⎪⎨⎧+==bkx y xy 241得41x 2-kx -b =0,x A +x B =4k ,x A ·x B =-4b , 由△APM ∽△MQB 得AP ·BQ =PM ·MQ ,即(y A -1)(41x B 2-1)=-(x A +2)(x B +2), ∴161(x A -2)(x B -2)=-1,x A ·x B -2(x A +x B )+4=-16, ∴-4b -8k +4=-16,b =5-2k ,∴AB :y =kx +5-2k =k (x -2)+5,过定点(2,5).【练2】(2014武汉中考)如图,已知直线AB :y =kx +2k +4于抛物线y =21x 2交于A 、B 两点. (1)直线AB 总经过一个定点C ,请直接写出点C 坐标; (2)若在抛物线上存在定点D 使∠ADB =90°,求点D 到直线AB 的最大距离.(1)C (-2,4)(2)设A (x 1,21x 12),B (x 2,21x 22),D (m ,21m 2),由⎪⎩⎪⎨⎧++==42212k kx y xy 得x 2-2kx -4k -8=0,x 1+x 2=2k ,x 1·x 2=-4k -8,过D 作EF ∥x 轴,AE ⊥EF 于E ,BF ⊥EF 于F ,由△AED ∽△DFB 得AE ·BF =DE ·DF ,即(21x 12-21m 2)(21x 22-21m 2)=(m -x 1)(x 2-m ),化简x 1x 2+m (x 1+x 2)+m 2=4,∴2k (m -2)+m 2-4=0,当m -2=0,即m =2时,点D 的坐标与k 无关,∴D (2,2),又∵C (-2,4),∴CD =25,作DM ⊥AB 于M ,则DM ≤CD =25,∴当CD ⊥AB 时,点D 到直线AB 的距离最大,最大距离为25.例3.如图,抛物线y =x 2+3顶点为P ,直线l 交抛物线于A 、B 两点,交y 轴于C 点,∠AOC =∠BOC ,求证:直线AB 过定点.设A (m ,m 2+3),B (n ,n 2+3),设直线AB 的解析式为y =kx +b ,⎩⎨⎧+=+=32x y bkx y ,∴kx +b =x 2+3,x 2-kx +3-b =0,∴mn =3-b ,∵∠AOC =∠BOC ,∴tan ∠AOC =tan ∠BOC ,∴32+m m =32+-n n,∴mn 2+3m =-m 2n -3n ,∴mn =-3,∴b =6,∴C (0,6).【练3】抛物线y =x 2-4x +5,对称轴交x 轴于P 点,直线EF 交抛物线于E 、F ,交对称轴于H ,且∠EPH =∠FPH ,求证:EF 恒过定点.E (x 1,y 1),F (x 2,y 2),⎩⎨⎧+-=+=542x x y bkx y ,∴x 2-(4+k )x +5-b =0,x 1+x 2=4+k ,x 1x 2=5-b ,tan ∠EPH =tan ∠FPH ,∴112y x -=222y x -,∴(kx 1+b)(x 2-2)=(kx 2+b )(2-x 1),∴b +2k =2,y =kx +b ,∴直线过(2,2).例4.如图,抛物线y =x 2-1交x 轴于A 、B 两点,直线y =a (a >0)交抛物线于M 、N ,点C 在抛物线上,且∠MCN =90°,点C 到MN 的距离是否为定值?若是,求出这个定值.作CH ⊥MN 于H .则∠MCH =∠CNH ,Rt △MCH ∽Rt △CNH ,CH 2=MH ·HN ,令C (x C ,t ),M (m ,m 2-1),则N (-m ,m 2-1),CH =m 2-1-t ,MH ·HN =(x C -x M )(x N -x C )=-x C 2+m 2,y C =x C 2-1=t ,故x C 2=t +1,-x C 2=-t -1,即MH ·HN =m 2-1-t ,又CH 2=MH ·HN ,∴(m 2-1-t )2=m 2-1-t ,∴m 2-1-t =0(舍去)或m 2-1-t =1,即CH =m 2-1-t =1,点C 到MN 的距离是定值,这个值为1.【练4】(2015永州改)如图,抛物线:y =41(x -1)2,R (1,1)是对称轴l 上一点,点P 为抛物线上一个动点,PM 垂直于直线y =-1于M ,求PRPM的值.设P (t ,41(t -1)2),连PR ,作PM ⊥直线y =-1于点M ,PM =41(t -1)2+1, PR =222]1)1(41[)1(--+-t t =41(t -1)2+1,∴PM =PR ,∴PRPM=1.【课后反馈】1.如图,抛物线y =x 2-1交x 轴正半轴于A (1,0),M 、N 在抛物线上,且MA ⊥NA ,试说明MN 恒过一定点,求此定点的坐标.作MP ⊥x 轴于P ,NQ ⊥x 轴于Q ,设MN :y =mx +n ,由21y mx ny x =+⎧⎪⎨=-⎪⎩得x 2-mx -n -1=0,x M +x N =m ,x M ·x N =-1-n ,tan ∠MAP =PA MP =211M M x x --=-x M -1,tan ∠ANQ =AQ NQ =211N N x x --=11Nx +.由∠MAP =∠ANQ 得-x M -1=11Nx +,即-x M ·x N -(x M +x N )-1=1,1+n -m -1=1,n =m +1,MN :y =mx +m+1=m (x +1)+1,故MN 过定点(-1,1).2.如图,抛物线y =41(x -4)2-4的顶点为P ,M ,N 均在对称轴上,且PM =PN ,延长OM 交抛物线于点A .求证:∠ANM =∠ONM .易求P (4,-4),设A (m ,41m 2-2m ),可求OA :y =(41m -2)x ,点M 在OA 上,x =4时,y =m -8,∴M (4,m -8),故N (4,-m ),tan ∠ONM =N N x y -=4m ,tan ∠ANM =4A A N x y y --=2412()4m m m m ----=41(4)4m m m --=4m ,故∠ANM =∠ONM .3.(2016六初九下2月考T24)已知抛物线y =41x 2+m 与x 轴交于A 、B 两点,与y 轴交于C 点,且OA =2OC ,直线y =kx -2k +4(k ≠0)与抛物线交于D 、E 两点. (1)求m 值及A 点坐标;(2)当k 取何值时,△ADE 的面积最小,并求面积的最小值;(3)若M 、N 为抛物线上两点,其以MN 为直径的圆始终经过A 点,求直线MN 经过的定点P 的坐标.(1)令x =0时,y =m ,∴OC =-m ,令y =0时,x =m -±2,∴OA =m -2, ∵OA =2OC ,∴m -2=2(-m ),m =-1,∴A (2,0);(2)直线y =kx -2k +4过定点(2,4),过点A 作AF ∥y 轴交DE 于F ,∴F (2,4), 设D (x 1,y 1)、E (x 2,y 2),∴S △ADE =21×4×(x 1-x 2)=2(x 1-x 2), 联立⎪⎩⎪⎨⎧-=+-=141422x y k kx y ,整理得41x 2-kx +2k -5=0,∴x 1+x 2=4k ,x 1x 2=8k -15 ∴S △ADE =2212142)(x x x x -+=84)1(2+-k ,当k =1时,S △ADE 有最小值,最小值为16; (3)设M (x 1,y 1)、N (x 2,y 2), ∵∠MAN =90°,过点M 作ME ⊥x 轴于E ,过点N 作NF ⊥x 轴于F ,∴△MEA ∽△AFN ,∴212122y x x y -=-,y 1y 2=(x 2-2)(2-x 1), 即)141)(141(2121--x x )=(x 2-2)(2-x 1),x 1x 2+2(x 1+x 2)+20=0,设直线MN 的解析式为y =kx +b ,联立⎪⎩⎪⎨⎧-=+=1412x y bkx y ,整理得x 2-4kx -4-4b =0, ∴x 1+x 2=4k ,x 1x 2=-4-4b ,∴-4-4b +2×4k +20=0,2k -b =-4, 当x =-2时,-2k +b =4,∴直线MN 必过顶点(-2,4).。
二次函数的最值点与顶点问题

二次函数的最值点与顶点问题二次函数是高中数学中重要的概念之一,研究二次函数的最值点与顶点问题有助于我们理解函数的性质和优化问题的解决。
本文将介绍二次函数的最值点和顶点,并通过例题讲解相关概念和求解方法。
一、二次函数与最值点二次函数是指具有以下形式的函数:$y=ax^2+bx+c$,其中$a$、$b$、$c$是常数,且$a\neq0$。
二次函数的图像一般为抛物线,而其中的最值点则是抛物线上的最高点或最低点。
通过求导数,我们可以确定二次函数的最值点的横坐标。
对于二次函数$y=ax^2+bx+c$,其导数为$y'=2ax+b$。
令导数为零,则有$2ax+b=0$,解得$x=-\frac{b}{2a}$。
所以,最值点的横坐标为$-\frac{b}{2a}$。
根据最值点的横坐标,我们可以计算出相应的纵坐标。
将横坐标代入二次函数的表达式中,即可求得最值点的纵坐标。
最终,我们得到了二次函数的最值点的坐标。
二、二次函数与顶点在二次函数中,最值点可以称作顶点。
当二次函数的系数$a$大于0时,抛物线开口向上,顶点为最低点;当$a$小于0时,抛物线开口向下,顶点为最高点。
以最低点为例,当$a>0$时,顶点的纵坐标为二次函数的最小值。
通过将顶点的横坐标代入二次函数的表达式,即可求得最小值。
同样地,当$a<0$时,顶点的纵坐标为二次函数的最大值。
通过求出顶点的坐标,我们可以得到二次函数的最值,这一点在求解优化问题中非常有用。
三、例题解析为了更好地理解二次函数的最值点与顶点问题,我们通过例题进行解析。
例题1:求函数$y=2x^2-4x+3$的最值点和顶点。
解:首先求得最值点的横坐标。
根据前面的知识,$-\frac{b}{2a}=-\frac{-4}{2\times2}=1$,所以最值点的横坐标为1。
然后求得最值点的纵坐标。
将横坐标代入函数表达式$y=2x^2-4x+3$中,得到$y=2\times1^2-4\times1+3=1$,所以最值点的纵坐标为1。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二次函数的最值与图像过定点问题
对于二次函数:y=-x 2+4x-1/2
(1)当x 取任意实数时,该函数有最 值,最 值是
(2)当-1≤x≤1时,该函数的最大值是 ;最小值是
(3)当3≤x≤4时,该函数的最大值是 ;最小值是
(4)当0≤x≤3时,该函数的最大值是 ;最小值是
求二次函数最值的一般方法: 1画出函数图像找对称轴; 2分清自变量范围找区间; 3数形结合找对应函数值
例1、对于二次函数y=-x 2+2bx-0.5
(1)若b<-1,当-1≤x≤1时,求该函数的最大或最小值(用含b 的式子表示)。
(2)若0﹤b ﹤1时,当-1≤x≤1,求该函数的最大或最小值。
1.如图,抛物线22y x x p =--与直线x y =交于点A(-1,m)、B(4,n),点M 是抛物线上的
一个动点,连接OM
(1)求m,n,p 。
(2)当M 为抛物线的顶点时,求M 坐标和⊿OMB 的面积;
(3)当点M 在直线AB 的下方抛物线上,M 运动到何处时,⊿AMB 的面积最大。
2.抛物线y=ax 2和直线y=kx+b(k 为正常数)交于点A 和点B,其中点A 的坐标是(-2,1),过点A 作x 轴的平行线交抛物线于点E,点D 是抛物线上B,E 之间的一个动点,设其横坐标为t,经过点D 作两坐标轴的平行线分别交直线AB 于点C,M,设CD=r,MD=m.
(1)根据题意可求出a= ,点E 的坐标是 ;
(2)当点D 可与B,E 重合时,若k=0.5,求t 的取值范围,并确定t 为何值时,r 的值最大;(3)当点D 不与B,E 重合时,若点D 运动过程中可以得到r 的最大值,求k 的取值范围,并判断当r 为最大值时m 的值是否最大,说明理由(下图供分析参考用).
y
x
C
M
E A
O B
D
24.(12分) 如图1,平面之间坐标系中,等腰直角三角形的直角边BC 在x 轴正半轴上滑动,点C 的坐标为(t ,0),直角边AC=4,经过O ,C 两点做抛物线y 1=ax(x ﹣t)(a 为常数,a >0),该抛物线与斜边AB 交于点E ,直线OA :y 2=kx(k 为常数,k >0)
(1)填空:用含t 的代数式表示点A 的坐标及k 的值:A_________,k=_________;
(2)随着三角板的滑动,当a=14时:
①请你验证:抛物线y 1=ax(x ﹣t)的顶点在函数y=﹣14x 2的图象上;
②当三角板滑至点E 为AB 的中点时,求t 的值;
(3)直线OA 与抛物线的另一个交点为点D ,当t≤x≤t+4,|y 2﹣y 1|的值随x 的增大而减小,当x≥t+4时,|y 2﹣y 1|的值随x 的增大而增大,求a 与t 的关系式及t 的取值范围.
抛物线过定点的问题集锦
解法步骤
第一步:对含有变系数的项集中
第二步:然后将这部分项分解因式,使其成为一个只含系数和常数的因式与一个只含x 和常数的因式之积的形式 第三步:令后一因式等于0,得到一个关于自变量x 的方程(这时系数如何变化,都“失效”了)
第四步:解此方程,得到x 的值x0(定点的横坐标),将它代入原函数式(也可以是其变式),即得到一个y 的值y0(定点的纵坐标),于是,函数图象一定过定点(x0,y0); 第五步:反思回顾,查看关键点、易错点,完善解题步骤
1.某二次函数y =ax 2-(a +c)x +c 必过定点__________
2.无论m 为任何实数,二次函数y =x 2+(2-m)x +m 的图像总过的点是( )
A. (1,3)
B. (1,0)
C. (-1,3)
D. (-1,0)
3.不论a 取何值,抛物线y =-12x 2+5-a 2
x +2a -2 经过x 轴上一定点Q ,则点Q 坐标为 4.抛物线y =ax 2+ax -2过直线y =mx -2m +2上的定点A ,求抛物线的解析式。
5.如图 ,在平面直角坐标系中,已知A(4,0),以OA 为边在第一象限内作正方形OABC.K 为线段CB 上一动点,连接OK,KN ⊥OK 交AB 于N.CK=t.BN=m
(1)△OCK ∽________,K 点坐标K( , );
(2)用含t 的代数式表示m,并确定m 的取值范围;
(3)过O,K 两点作抛物线y=ax 2+bx(a<0)
①用含a,t 的代数式表示b;
②当抛物线的对称轴是直线x=12t
时,求at 的关系式;并说明此时抛物线恒过除原点O
定点.
6.抛物线y=ax 2+bx+c 中,b,c 是非零的常数,无论a 为何值(0除外),其顶点M 一定在直线y=kx+1上;这条直线和x 轴,y 轴分别交于点E,A,且OA=OE
(1)求k 的值; (2)求证:这条抛物线经过点A ;
如图,直线y=hx+d 与x 轴和y 轴分别相交于点A(-1,0),B(0,1),与双曲线y=t x
CAO ∠为内角的直角三角形,与以CO 为对角线、一边在x 2mx nx k ++上;直线y=hx+d 、双曲线y=t x 和抛物线2y
ax bx c =++点C,D 。
(1)确定t 的值
(2)确定m , n , k 的值
(3)若无论a , b , c 取何值,抛物线2y ax bx c =++都不经过点P ,请确定P 的坐标。
