第二章恒定电场09PPT课件
合集下载
恒定电流的电场和磁场课件

恒定电流的电场和磁场 课件
目录
• 恒定电流的基本概念 • 电场与电场力 • 磁场与磁场力 • 恒定电流的磁场效应 • 恒定电流的应用 • 实验与实践
01
恒定电流的基本概念
电流的定义与性质
电流
电荷在导体中定向移动形成电流 ,单位时间内通过导体横截面的 电荷量称为电流强度,简称电流 。
电流的性质
电荷的定向移动形成电流,其方 向由正电荷定向移动的方向决定 ,而与导体内自由电荷的运动方 向无关。
电场力是电荷在电场中受到的力,其大小与电荷的电量成正比,与电场强度成正比 。
电场强度是描述电场强弱和方向的物理量,等于单位正电荷在电场中受到的力。
电场强度具有方向性,规定正电荷受力方向为电场强度的方向。
电势与电场能量
电势是描述电场能的物理量,等于单 位正电荷在电场中具有的电势能。
电场能量是电场中储存的能量,与电 势能密切相关。
电阻
导体对电流的阻碍作用,由导体的材 料、长度、横截面积和温度等因素决 定。
02
电场与电场力
电场的概念与性质
电场是由电荷产生的 ,对放入其中的电荷 有力的作用。
电场的性质包括对放 入其中的电荷有力的 作用、静电感应现象 等。
电场具有物质性,是 传递电荷间相互作用 的一种特殊物质形态 。
电场力与电场强度
详细描述
电磁感应现象是当导体在磁场中发生相对运动时,会在导体中产生电动势或电流的现象。这个现象由英国物理学 家迈克尔·法拉第于19世纪30年代发现,是电磁化的电场和磁场相互激发,形成电磁波并传播出去。
详细描述
电磁波是由变化的电场和磁场相互激发而形成的。当电场或磁场发生变化时,就会产生电磁波,并传 播出去。电磁波的传播速度等于光速,在真空中传播不受影响,但在介质中传播速度会减慢。
目录
• 恒定电流的基本概念 • 电场与电场力 • 磁场与磁场力 • 恒定电流的磁场效应 • 恒定电流的应用 • 实验与实践
01
恒定电流的基本概念
电流的定义与性质
电流
电荷在导体中定向移动形成电流 ,单位时间内通过导体横截面的 电荷量称为电流强度,简称电流 。
电流的性质
电荷的定向移动形成电流,其方 向由正电荷定向移动的方向决定 ,而与导体内自由电荷的运动方 向无关。
电场力是电荷在电场中受到的力,其大小与电荷的电量成正比,与电场强度成正比 。
电场强度是描述电场强弱和方向的物理量,等于单位正电荷在电场中受到的力。
电场强度具有方向性,规定正电荷受力方向为电场强度的方向。
电势与电场能量
电势是描述电场能的物理量,等于单 位正电荷在电场中具有的电势能。
电场能量是电场中储存的能量,与电 势能密切相关。
电阻
导体对电流的阻碍作用,由导体的材 料、长度、横截面积和温度等因素决 定。
02
电场与电场力
电场的概念与性质
电场是由电荷产生的 ,对放入其中的电荷 有力的作用。
电场的性质包括对放 入其中的电荷有力的 作用、静电感应现象 等。
电场具有物质性,是 传递电荷间相互作用 的一种特殊物质形态 。
电场力与电场强度
详细描述
电磁感应现象是当导体在磁场中发生相对运动时,会在导体中产生电动势或电流的现象。这个现象由英国物理学 家迈克尔·法拉第于19世纪30年代发现,是电磁化的电场和磁场相互激发,形成电磁波并传播出去。
详细描述
电磁波是由变化的电场和磁场相互激发而形成的。当电场或磁场发生变化时,就会产生电磁波,并传 播出去。电磁波的传播速度等于光速,在真空中传播不受影响,但在介质中传播速度会减慢。
2恒定电场

V
─ 焦耳定律积分形式
导体有电流时,必有功率损耗,其功率密度为
p dP dV J E
W/m3 ─ 焦耳定律微分形式
9
2.2
电源电动势与局外场强
2.2.1 电源电动势与局外场强 提供非静电力将其它形式的
能量转为电能的装置称为电源。
恒定电流的形成
要产生恒定电场,形成恒定电流,需要连接 直流电源。直流电源能将电源内的原子或分子的 正、负电荷分开,使正电荷移向正极,负电荷移 向负极。显然,这种移动电荷的作用力不是电场 的库仑力,称之为局外力,用 f e 表示。
第二章
序 导电媒质中的电流
恒定电场
电源电动势与局外场强
恒定电场基本方程、分界面上的衔接条件 导电媒质中恒定电场与静电场的比拟
电导和部分电导
1
2.0 序
静电场中,导体内没有电场,没有电荷的运 动,导体是等位体,导体表面是等位面。 维持导体中具有恒定电流的电场称为恒定电 场。它与静电场有相似之处。 本章要求: 理解各种电流密度的概念,通过欧姆定律和焦 耳定律理解场量之间的关系。 掌握恒定电场的基本方程和分界面上的衔接条 件。 掌握静电比拟法和电导的计算。
E1n J1n / 1 0
理想介质
导体中
导体与理想介质分界面
E1t E2t J1t / 1 J1 / 1 0
D2 n D1n 2 E 2 n 1 E1n 2 E 2 n
结论1 分界面导体侧的电流一定与导体表面平行。 结论2 导体与理想介质分界面上必有面电荷。
l
( E ) dS 0
S
得 E 0
恒定电场是无旋场。
14
3. 恒定电场(电源外)的基本方程
─ 焦耳定律积分形式
导体有电流时,必有功率损耗,其功率密度为
p dP dV J E
W/m3 ─ 焦耳定律微分形式
9
2.2
电源电动势与局外场强
2.2.1 电源电动势与局外场强 提供非静电力将其它形式的
能量转为电能的装置称为电源。
恒定电流的形成
要产生恒定电场,形成恒定电流,需要连接 直流电源。直流电源能将电源内的原子或分子的 正、负电荷分开,使正电荷移向正极,负电荷移 向负极。显然,这种移动电荷的作用力不是电场 的库仑力,称之为局外力,用 f e 表示。
第二章
序 导电媒质中的电流
恒定电场
电源电动势与局外场强
恒定电场基本方程、分界面上的衔接条件 导电媒质中恒定电场与静电场的比拟
电导和部分电导
1
2.0 序
静电场中,导体内没有电场,没有电荷的运 动,导体是等位体,导体表面是等位面。 维持导体中具有恒定电流的电场称为恒定电 场。它与静电场有相似之处。 本章要求: 理解各种电流密度的概念,通过欧姆定律和焦 耳定律理解场量之间的关系。 掌握恒定电场的基本方程和分界面上的衔接条 件。 掌握静电比拟法和电导的计算。
E1n J1n / 1 0
理想介质
导体中
导体与理想介质分界面
E1t E2t J1t / 1 J1 / 1 0
D2 n D1n 2 E 2 n 1 E1n 2 E 2 n
结论1 分界面导体侧的电流一定与导体表面平行。 结论2 导体与理想介质分界面上必有面电荷。
l
( E ) dS 0
S
得 E 0
恒定电场是无旋场。
14
3. 恒定电场(电源外)的基本方程
恒定电场
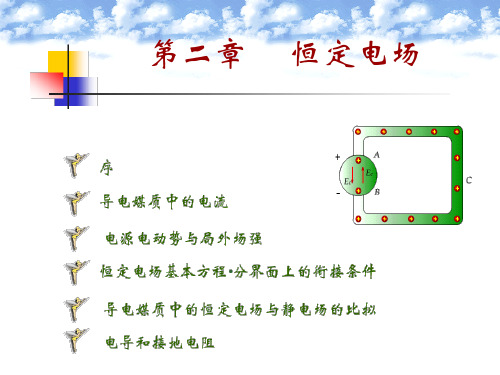
E J I 2l R2 I I R U E dl d ln 2 R1 2l 2 l R1 2l G I 电导 U R2 ln R1 I I J 设 2l
图2.5.1
同轴电缆横截面
绝缘电阻
1 1 ln R2 R G 2l R1
I dI J lim n n S 0 S dS
单位: 安培/米2 (A/m2)
电流密度
可以从电流密度J求出流过任意面积S的电流强度。一
般情况下,电流密度J和面积元dS的方向并不相同。
此时,通过面积S的电流就等于电流密度J在S上的通
量,即
I J dS JdScosθ
R2
1
U 0 e
电流 电导
I J dS
U 0 U h R (e ) hd (e ) 0 ln 2 S R R1 I h R2 G ln ( S m) U 0 R1
2.5.2
接地电阻
安全接地与工作接地的概念
接地器电阻
接地电阻 接地器与土壤之间的接触电阻 土壤电阻(接地电阻以此电阻为主) 1. 深埋球形接地器
•
• •
两种场的电极形状、尺寸与相对位置相同(相拟);
相应电极的电压相同; 若两种场中媒质分片均匀,只要分界面具有相似
r1 1 r2 2
的几何形状,且满足条件
时,则这两种场
在分界面处折射情况仍然一样,相拟关系仍成立。
2.4.3
静电比拟的应用
1. 静电场便于计算—— 用静电比拟方法计算 恒定电场
2 0
D1n D2n
I J dS
S
2 0
S
q D dS
E1t E2t
图2.5.1
同轴电缆横截面
绝缘电阻
1 1 ln R2 R G 2l R1
I dI J lim n n S 0 S dS
单位: 安培/米2 (A/m2)
电流密度
可以从电流密度J求出流过任意面积S的电流强度。一
般情况下,电流密度J和面积元dS的方向并不相同。
此时,通过面积S的电流就等于电流密度J在S上的通
量,即
I J dS JdScosθ
R2
1
U 0 e
电流 电导
I J dS
U 0 U h R (e ) hd (e ) 0 ln 2 S R R1 I h R2 G ln ( S m) U 0 R1
2.5.2
接地电阻
安全接地与工作接地的概念
接地器电阻
接地电阻 接地器与土壤之间的接触电阻 土壤电阻(接地电阻以此电阻为主) 1. 深埋球形接地器
•
• •
两种场的电极形状、尺寸与相对位置相同(相拟);
相应电极的电压相同; 若两种场中媒质分片均匀,只要分界面具有相似
r1 1 r2 2
的几何形状,且满足条件
时,则这两种场
在分界面处折射情况仍然一样,相拟关系仍成立。
2.4.3
静电比拟的应用
1. 静电场便于计算—— 用静电比拟方法计算 恒定电场
2 0
D1n D2n
I J dS
S
2 0
S
q D dS
E1t E2t
本征离子电导PPT课件

因此,同样有:
△Sf =k ln(W ’W ” )
3-50
-
10
设一对填隙离子-空位形成能量为 uf,形成 nf 对弗仑凯尔缺陷后内能增量:
3-51
利用平衡条件:
3-52
得到:
3-54
或:
3-54
当 N ’ 》nf, N 》nf 时,上式可简化为:
3-55
若令 N ’ ≈ N,则得:
3-56
式中,uf 为晶体点阵上离子形成填隙离-子或形成离子空位所需的能量。
-
5
2)载流子浓度 弗仑凯尔缺陷产生了两种载流子: 正离子空位和正填隙离子。 其特点是成对出现。
肖特基缺陷:形成的载流子就只有离子空位一种。 但分成正离子空位和负离子空位两种 。
用统计物理方法,可以计算两种缺陷的浓度,分别为: 3-47
ns 晶体点阵离子空位浓度, N 晶体点阵离子浓度,us 形成一个肖特基缺陷的能量。
-
13
4)肖特基缺陷、弗仑凯尔缺陷引起的电导率
确定载流子浓度和迁移率后,根据电导率 γ 通式: 3-3
可写出晶体本征离子电导率, 对应肖特基缺陷、弗仑凯尔缺陷类型, 有以下四种具体的表达式。
-
14
① 肖特基缺陷的正离子空位所提供的电导率
3-58 式中, us1 为形成一个肖特基正离子空位所需要能量; Uo1 为一个肖特基正离子空位扩散时所需克服的势垒。
3-40
-
7
设 uH 是一个原子或离子从晶体内部移动到晶体表面所需的能量, uL 为每个原子或离子的 点阵能。那么,形成一个肖特基缺陷需要的能量为:
3-41
因此,出现 ns 个肖特基缺陷后系统内能 U 增量 △Us 应为:
△Sf =k ln(W ’W ” )
3-50
-
10
设一对填隙离子-空位形成能量为 uf,形成 nf 对弗仑凯尔缺陷后内能增量:
3-51
利用平衡条件:
3-52
得到:
3-54
或:
3-54
当 N ’ 》nf, N 》nf 时,上式可简化为:
3-55
若令 N ’ ≈ N,则得:
3-56
式中,uf 为晶体点阵上离子形成填隙离-子或形成离子空位所需的能量。
-
5
2)载流子浓度 弗仑凯尔缺陷产生了两种载流子: 正离子空位和正填隙离子。 其特点是成对出现。
肖特基缺陷:形成的载流子就只有离子空位一种。 但分成正离子空位和负离子空位两种 。
用统计物理方法,可以计算两种缺陷的浓度,分别为: 3-47
ns 晶体点阵离子空位浓度, N 晶体点阵离子浓度,us 形成一个肖特基缺陷的能量。
-
13
4)肖特基缺陷、弗仑凯尔缺陷引起的电导率
确定载流子浓度和迁移率后,根据电导率 γ 通式: 3-3
可写出晶体本征离子电导率, 对应肖特基缺陷、弗仑凯尔缺陷类型, 有以下四种具体的表达式。
-
14
① 肖特基缺陷的正离子空位所提供的电导率
3-58 式中, us1 为形成一个肖特基正离子空位所需要能量; Uo1 为一个肖特基正离子空位扩散时所需克服的势垒。
3-40
-
7
设 uH 是一个原子或离子从晶体内部移动到晶体表面所需的能量, uL 为每个原子或离子的 点阵能。那么,形成一个肖特基缺陷需要的能量为:
3-41
因此,出现 ns 个肖特基缺陷后系统内能 U 增量 △Us 应为:
恒定电场

Fk 反抗 Fe
断路:
作用机理: 做功,
将其他形式能转变为电能
Fe
K
U
Fk Fe
Fe
Fk Fe
时平衡
R
外电路: Fe 作用,将 q由正极 负极
通路
内电路: Fk Fe 将 q 由负极 正极
Fk , Fe 共同作用形成持续电流 .
空间电荷分布不变(流入 = 流出),电场分布不变
一.
电流密度矢量
自由电子、正负离子、 载流子:
1. 电流的形成 传导电流 电流
电子—空穴对…
电场
位移电流
金属导电的经典解释: 电场中,自由电子除热运动外, 叠加定向加速运动.
频繁碰撞使加速运动间断进行, 其平均效果为定向匀速运动——漂移运动.
漂移速率 u: 比较
1)静电力所做总功为零; 2)非静电力所做总功为零; 3)静电力和非静电力做功代数和为零; 4)在电源内只有非静电力做功, 在外电路只有静电力做功。
三.
欧姆定律与焦耳定律的微分形式 欧姆定律 焦耳定律
积分形式 微分形式
U I R
电流密度
Q I 2 Rt;
热功率密度
P I 2R
j E
Fe
K
Fk Fe
Fe
R
试比较电源路端电压和电源电动势这两个概念
电源路端电压 电源电动势
比较
U
E e dl
E k dl
(经外电路)
(经内电路)
练习:
单位正电荷从电源正极出发,沿闭合回路一周, 又回到电源正极时,下列哪种说法正确?
(电磁场PPT)第二章 恒定电场

第二章
由电路理论
恒定电场
2.1.3 欧姆定律的微分形式
U RI
R l
S
电导率与电阻率的关系: 1 ,
(r 电阻率), (电导率)。 r
图2.1.5 J 与 E 之关系
在场论中 dI J dS
dU dI R J dS dl
dS
E dl
J E 欧姆定律 微分形式。
第二章
恒定电场
U RI 欧姆定律 积分形式。
本章要求:
理解各种电流密度的概念,通过欧姆定律和焦耳 定律深刻理解场量之间的关系。
掌握导电媒质中的恒定电场基本方程和分界面衔 接条件。
熟练掌握静电比拟法和电导的计算。
第二章
恒定电场知识结构
基本物理量 J、 E
欧姆定律
恒定电场
J 的散度
基本方程
E 的旋度
边界条件
边值问题
电位
一般解法 电导与接地电阻 特殊解(静电比拟)
第二章
第二章 恒定电场
Steady Electric Field
导电媒质中的电流 电源电动势与局外场强 基本方程 • 分界面衔接条件 • 边值问题 导电媒质中恒定电场与静电场的比拟 电导和接地电阻
恒定电场
第二章
恒定电场
通有直流电流的导电媒质中同时存在着电流场和 恒定电场。恒定电场是动态平衡下的电荷产生的,电 荷作宏观运动,电荷的分布不随时间变化(即:恒定 ),它与静电场有相似之处。
—焦耳定律积分形式
第二章
2.2 电源电动势与局外场强
2.2.1 电源 (Source)
恒定电场
提供非静电力将其它形式的 能转为电能的装置称为电源。
图2.2.1 恒定电流的形成
电磁场与电磁波课件之恒定电场分析

电体流出进入一般导电媒质时,电流线总是垂直于理想导电体表面。
导体周围介质中的电场
E2 E2 e x E2n e y
载流导体表面的电场
3. 恒定电场与静电场的比拟 已知无外源区中均匀导电媒质内的恒定电流场方程和无源区中均
匀介质内的静电场方程如下:
恒定电流场 ( E 0)
6 解:a)媒质1是良导体 1 5 10 S / m
良导体 不良导体
1 2
媒质2是不良导体 由折射定理得
2 102 S / m
t an1 1 t an 2 2
2 0
表明,只要 1
( 1 895950, 2 8 )
微分形式
J 0
S
J dS 0
电流线连续 J ) dV 0 V ( t
尽管电流是电荷的运动,但在恒定电流的状态下电荷分布并不随时 间改变。可知,恒定电场为保守场,即
微分形式
l E dl 0 E 0
2 面穿出,良导体表面近似为等位面。
,电流线垂直于良导体表
b)媒质1是导体
( 1 0)
媒质2是理想介质
( 2 0)
2 0 J2 0
( 2 0)
J1n J 2n 0
J1 J1 0
1
导体与理想介质分界面
①导体表面是一条电流线。
E1n
J1n
分界面上电场强度切向分量连续,电流密度法向分量连续 • 场矢量折射关系
E1 sin 1 E2 sin 2
1E1 cos1 2 E2 cos 2
• 电位函数边界条件
2 1 1 2 n n
静态电磁场II:恒定电流电场介绍

断的闭合矢量线,因而磁场空间没有磁感应强度矢量线的
源和汇,磁场是一个无源场。
B0
图 磁通连续性原理
静电场 ( 0) 恒定电场(电源外)静电场 恒定电场
E 0 D 0
D E
2 0
q SD dS
E 0
J 0
J E
2 0
I SJ dS
E
E
D
J
ε
q
I
C
q
DdS S
EdS
S
U Edl Edl
l
l
G I
JcdS EdS
S
S
U Edl Edl
l
l
G C
当满足比拟条件时,用比拟法由电容计算电导。
3.2.2 接地电阻
接地电阻
接地器和接地 导线的电阻
接地器与大地 的接触电阻
1.深埋球形接地器
解:深埋接地器可不考 虑地面影响,其电流场可与 无限大区域 ( ) 的孤立圆球 的电流场相似。
两接地器之间 土壤的电阻
图 深埋球形接地器
解法一 直接用电流场的计算方法
I J 4Ir2
E J
I
4r2
U
I
3.3.1 恒定磁场的基本方程
积分形式: 微分形式:
H d l J c d S
S
S
B dS 0
S
H Jc B0
媒质构成方程:
B H
结论: 恒定磁场是无源有旋场。
3.3.2 真空中安培环路定律-恒定磁场有旋性
真空中的安培环路定律
n
Bdl 0 Jc dS 0 Ik
S
S
k1
dt时间内有dq电荷自元电流
管的左端面移至右端面,则 电场力作功为dW = dUdq
源和汇,磁场是一个无源场。
B0
图 磁通连续性原理
静电场 ( 0) 恒定电场(电源外)静电场 恒定电场
E 0 D 0
D E
2 0
q SD dS
E 0
J 0
J E
2 0
I SJ dS
E
E
D
J
ε
q
I
C
q
DdS S
EdS
S
U Edl Edl
l
l
G I
JcdS EdS
S
S
U Edl Edl
l
l
G C
当满足比拟条件时,用比拟法由电容计算电导。
3.2.2 接地电阻
接地电阻
接地器和接地 导线的电阻
接地器与大地 的接触电阻
1.深埋球形接地器
解:深埋接地器可不考 虑地面影响,其电流场可与 无限大区域 ( ) 的孤立圆球 的电流场相似。
两接地器之间 土壤的电阻
图 深埋球形接地器
解法一 直接用电流场的计算方法
I J 4Ir2
E J
I
4r2
U
I
3.3.1 恒定磁场的基本方程
积分形式: 微分形式:
H d l J c d S
S
S
B dS 0
S
H Jc B0
媒质构成方程:
B H
结论: 恒定磁场是无源有旋场。
3.3.2 真空中安培环路定律-恒定磁场有旋性
真空中的安培环路定律
n
Bdl 0 Jc dS 0 Ik
S
S
k1
dt时间内有dq电荷自元电流
管的左端面移至右端面,则 电场力作功为dW = dUdq
第2章静电场和恒定电流电场
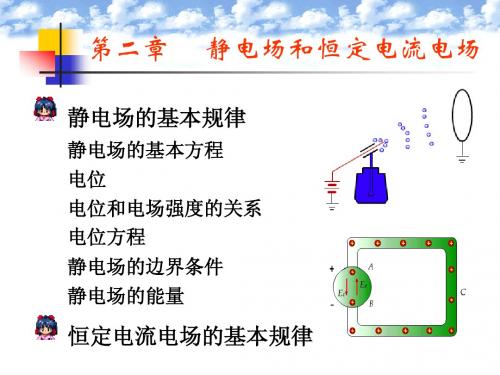
ϕ = C E1t = E2t Et = 0 ρs ⇒ ⇔ ∂ϕ D n − D2n = 1 Dn = ρs ε ∂n = −ρs 0
E = −∇ϕ, ∇⋅ D = ρ Q v v v ∇⋅ (ϕD) = ϕ∇⋅ D +∇ϕ ⋅ D v v v v v v ∴E ⋅ D = −∇ϕ ⋅ D = −∇⋅ (ϕD) +ϕ∇⋅ D = −∇⋅ (ϕD) + ρϕ v 1 1 ∴W = ∫∫∫ ρϕdv − ∫∫∫ ∇⋅ (ϕD)dv 2 2 v v v 高斯定理) Q∫∫∫ ∇⋅ (ϕD)dv = ∫∫ ϕD⋅ dS (高斯定理) v v 1 1 ∴W = ∫∫∫ ρϕdv − ∫∫ ϕD⋅ dS 2 2 1 v v 1 Q ∫∫ ϕD⋅ dS 通常 = 0 ∴W = ∫∫∫ ρϕdv (2) 2 2
−ρ 0 ≤ x ≤ d 2 , ∇ ϕ1 = 2 ε d ∇2ϕ = 0, ≤ x≤d 2 2 ϕ 因为ϕ1 , 2与坐标y,z 无
+
x
d
−
2
ρ
2
O
关,电位方程可简化为: 电位方程可简化为:
d ϕ1 −ρ ∇ ϕ1 = = , 2 dx ε
2 2
d ϕ2 ∇ ϕ2 = = 0, 2 dx
v v 1 W = ∫∫∫ E ⋅ Ddv (1) 六 静电场的能量 v v 2
例1 平行板电容器极板平面的尺寸远大于它们之间的距 离d,两极板间加恒定电压 U 0 ,极板间的介电常数为ε, 其中一半空间有体电荷均匀分布, 其中一半空间有体电荷均匀分布,体电荷密度为 ρ ,分 界面与极板平行。试求极板间的电位分布。 界面与极板平行。试求极板间的电位分布。 解
当分界面为导体与电介质的交界 面时,由于导体的特殊性质, 面时,由于导体的特殊性质,在导体和介质的分解面上 的边界条件有其特点。导体在静电场中有以下性质: 的边界条件有其特点。导体在静电场中有以下性质: 1)导体内部不带电,电荷只分布在导体表面上; 导体内部不带电,电荷只分布在导体表面上; 导体内部电场为零; 2)导体内部电场为零; 3)导体表面电场方向为法线方向,导体是个等势体, 导体表面电场方向为法线方向,导体是个等势体, 表面是等势面。 表面是等势面。 导体和电介质分界面上的边界条件为: 导体和电介质分界面上的边界条件为:
电磁场与电磁波 第二章-5 恒定电场

填充两种ε1、σ1,ε2、σ2的电介质材料, 介质分界面半径为 c ,内
外导体的电压为U0。试计算
(1)介质中的电场强度;
2,2
(2)分界面上的自由电荷
(3)单位长度的电容和电导。
解: (1)考察单位长度
E1r
Jr
1
I
2 r1
, E2r
Jr
2
I
2 r 2
1,1
c
U0
c
a E1rdr
b c
1 ( m)
• 欧姆定理的推导:I J d S S
JS ES
U
El
I
S
l
I
l
S
IR
SJ
l
E
U IR
J E
5
电流密度与电荷平均速度的关系:
dt时间内流过S面的电量及电流分别为:
dq Svdt I Sv J v
S vJ
vdt
6
二、 恒定电流场方程
1 电流连续性方程 2 基尔霍夫电流定律
数值为
Js
dI dl
A/m,方向为电流的方向。
通过任意曲线l 的电流
的电流为
I S JS dl
dl
JS
bupt 2012
4
3 欧姆定律
欧姆定理微分式:
导体任一点上电流密度与电场强度成正比。 J E
描述媒质的导电特性,理想导体σ为趋于无穷大。
是媒质的电导率,单位 1/欧.米 (1/ m)
xb
U
xb x
I
2 r 2
dr
I
2
( 1 ) bI
r x 2x(x b)
半球形接地器的危险区
第二章恒定电场
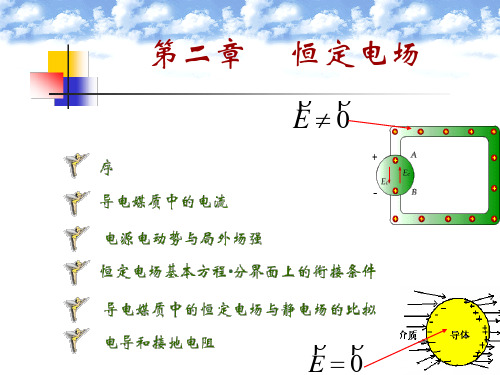
图2.1.3 电流线密度及其通量
τ 分布的线电荷沿着导线以速度 v 运动形成的电流I = τv 。
图2.1.4
媒质的磁化电流
图2-3 电流元示意
r r 注意: 电流密度的符号通常用 的符号通常用: 注意:1) 电流密度的符号通常用:J , K , I 2) 电荷密度的符号通常用: , σ , τ 电荷密度的符号通常用 ρ 的符号通常用:
γ 1 >> γ 2
α1 ≠ 90 o
α 2 ≈ 0o
J2 n°
例如,钢的电导率 γ1 = 5×106 S/m,周围土壤的电 例如 导率γ2 = 10-2 S/m,α1 = 89°,可知,α2 ≈ 8″。 良导体表面可近似看作为等位面 (3) 导体与理想介质分界面上的边界条件
J 2n = 0
γ2 γ1
γ 1 E1n = γ 2 E 2 n
J2
ε2E2n −ε1E1n =σ
γ2, ε2
P
σ
ε 2γ 1 − ε 1γ 2 σ= J 2n γ 1γ 2
γ1, ε1
J1
1-3-1 有恒定电流通过两种不同的导体媒质 介电常数和 有恒定电流通过两种不同的导体媒质(介电常数和 的分界面. 电导率分别是 ε1, γ 1和ε 2 , γ 2)的分界面 问若要使两种电解 的分界面 质分界面处的电荷面密度为零, 则应该满足何条件. 质分界面处的电荷面密度为零 则应该满足何条件
包括良导体和不良导体). 中(包括良导体和不良导体 包括良导体和不良导体 2) 前者场强处处为零并且为等位体;后者 库仑 场强 前者场强处处为零并且为等位体;后者(库仑 库仑)场强 一般不为零并且为非等位体. 一般不为零并且为非等位体 3) 电场为恒定电场的条件为任何闭合面电流量对 时间导数为零。 时间导数为零。
τ 分布的线电荷沿着导线以速度 v 运动形成的电流I = τv 。
图2.1.4
媒质的磁化电流
图2-3 电流元示意
r r 注意: 电流密度的符号通常用 的符号通常用: 注意:1) 电流密度的符号通常用:J , K , I 2) 电荷密度的符号通常用: , σ , τ 电荷密度的符号通常用 ρ 的符号通常用:
γ 1 >> γ 2
α1 ≠ 90 o
α 2 ≈ 0o
J2 n°
例如,钢的电导率 γ1 = 5×106 S/m,周围土壤的电 例如 导率γ2 = 10-2 S/m,α1 = 89°,可知,α2 ≈ 8″。 良导体表面可近似看作为等位面 (3) 导体与理想介质分界面上的边界条件
J 2n = 0
γ2 γ1
γ 1 E1n = γ 2 E 2 n
J2
ε2E2n −ε1E1n =σ
γ2, ε2
P
σ
ε 2γ 1 − ε 1γ 2 σ= J 2n γ 1γ 2
γ1, ε1
J1
1-3-1 有恒定电流通过两种不同的导体媒质 介电常数和 有恒定电流通过两种不同的导体媒质(介电常数和 的分界面. 电导率分别是 ε1, γ 1和ε 2 , γ 2)的分界面 问若要使两种电解 的分界面 质分界面处的电荷面密度为零, 则应该满足何条件. 质分界面处的电荷面密度为零 则应该满足何条件
包括良导体和不良导体). 中(包括良导体和不良导体 包括良导体和不良导体 2) 前者场强处处为零并且为等位体;后者 库仑 场强 前者场强处处为零并且为等位体;后者(库仑 库仑)场强 一般不为零并且为非等位体. 一般不为零并且为非等位体 3) 电场为恒定电场的条件为任何闭合面电流量对 时间导数为零。 时间导数为零。
相关主题
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
电磁场与我们的生活
1
第二章 恒定电场
2
基本概念: • 通有恒定电流的导电媒质中的恒定电场 (电流场)
• 通有恒定电流的导电媒质周围电介质中 的静态电场
• 注意:本章只研究导电媒质内部的区域
• 本章研究的对象是导电媒质,其
与静电场中所说的导体是什么关
系?
3
§2-1 导电媒质中的电流
在外电场的作用下,自由电荷定向运动形成电流 导电媒质中的运动电荷的定向运动形成的电流叫传导电流
的减少率:
16
q
S
J
• dS
t
I
S
J
•
dS
q t
t
V
dV
散度定理 J dS JdV
S
V
• JdV
S
V
t
dV
•
J
电流连续性方程
t
17
在恒定电场中 0 t
•
J
t
对于恒定电流场,电荷分布不随时间变化:
故 J 0
恒定电场是一个无源场,电流线是 连续的。
• 即:
J • dS 0
体分布dV JdV
( dV
)v
面分布
线分布l
sdS KdS dl Idl
(
s
dS
)v
(dl)v
(v )dl
13
2.2 电源电势与局外场强
2.2.1 电源
要想在导线中维持恒定电 流,必须依靠非静电力将B极 板的正电荷抵抗电场力搬到A 极板。这种提供非静电力将其 它形式的能量转为电能装置称 为电源。
• 交变电场的集肤效应,即高频情况下,电流趋於表面分 布,可用电流面密度表示。
3、线电流
分布的线电荷沿着导线以速
度 v 运动形成的电流
I =v 。
7 图2.1.4 媒质的磁化电流
4. 元电流的概念:
元电荷dq以速度v运动,则dqv(C m / s或A m) 定义为元电流段。
不同分布的元电荷运动后形成的元电流段:
元电荷dq
元电流dqv
体分布dV JdV
( dV
)v
面分布KdS KdS
线分布Idl Idl
(dS
)v
(dl )v
(v)dl
8
2.1.3 欧姆定律的微分形式
欧姆定律:I U R
电场是维持恒定电流的必要 条件。可以证明
J E
欧姆定律的微分形式。
式中 为电导率,单位s/m( 西门子/米)。
J 0
E 0
19
恒定电场积分
形式基本方程:
E • dl 0
l
J • dS 0
S
J E
静电场积分 形式基本方程:
E • dl 0
l
D • dS q0
S
不含场源
D E
20
2.3.2 分界面的衔接条件 分界面上的衔接条件
LE dl 0 SJ dS 0
说明分界面上电场强度的切向分 量是连续的,电流密度法向分量是连 续的。
• 恒定电流场与恒定电场相互依存。电流J 与电场媒质中,电位移矢量D 线与电流密度J 线方
向是否一致?
• 电流面密度 K E 是否成立?
10
2.1.4 焦尔定律的微分形式 导电媒质中有电流时,必伴随功率损耗。可以证明其
功率的体密度为:
p J E (W/m3 )——焦耳定律的微分形式
2
2
n
很多恒定电场问题的解决,都可以归结为一定条件下, 求出拉普拉斯方程的解答(边值问题)。
恒定电场中是否存在泊松方程?
24
例2.3.2 试用边值问题求解电弧片中电位、电场及面电荷的分布
2 0
表明,只要
1
,电流
2
线垂直于良导体表面穿出,良
导体表面近似为等位面。
22
2.3.4 恒定电场的电位(不含电源的区域)
E 0 E
由基本方程出发
J E
J 0
E 0
对于均匀媒质: 常数
得
2 0
拉普拉斯方程
23
2.3.5 恒定电场的边值问题
分界面衔接条件
1 2
1
2
n
单位时间内通过某一横截面的电量, 简称为电流。
I dq
A
dt
I 是通量,并不反映电流在 每一点的流动情况。
4
2.1.1 电流强度
1.电流体密度 分布的体电荷以速度v 作匀速运动形成的电流。
J v A m2
亦称电流面密度
电流
I S J dS
5
2. 电流面密度
分布的面电荷在曲面上以速度v运动形成的电流。
E1t E2t J1n J 2n
折射定律为
tan1 1 tan2 2
图2.3.1 电流线的折射21
例2.3.1 特殊情况分界面上的电场分布。
解:媒质1是良导体, 1 5 107 s / m 媒质2是不良导体, 2 102 s / m
由折射定理得
tan 1 1 ,则 tan 2 2
0
局外场 Ee 是非保守场。
15
图2.2.3 电源电动势与局外场强
2.3 恒定电场的基本方程 • 分界面上的衔接条件 • 边值问题
2.3.1 恒定电场的基本方程
1. J 的散度
电流的连续性定律 J dS q
S
t
• 定义:由电荷守恒定律,从 任一闭合面流出的传导电流,
应等于该面所围体积内电荷
电路中的焦耳定律,可由它的积分而得,即
P UI I 2 R (W)—— 焦耳定律的积分形式
11
小结:
I S J dS
J
I
S 面:用与I 流动的 方向垂直的平面去 切导电媒质得到的 截面。
欧姆定律的微分形式
J E
焦耳定律的微分形式
p J E (W/m3 )
12
元电荷dq
元电流dqv
K v
电流
Am
线电流密度矢量
I l (K en )dl
I
l:用与I 流动的方向垂直的平
面去切导电媒质得到的截线。
en 是垂直于dl,且通过dl与
曲面相切的单位矢量
图2.1.3 电流线密度及其6通量
工程意义:
• 同轴电缆的外导体视为电流面密度分布;
• 媒质的磁化,其表面产生磁化电流可用电流面密度表示, 如图示;
S
I 0 • Kirchhoff’s
law.
18
2. E 的旋度
所取积分路径不经过电源,则:
斯托克斯定理
l E dl 0
s( E) dS 0
得
E 0 恒定电场是无旋场。
3. 恒定电场(电源外)的基本方程
s J dS 0
J E
e E dl 0
• 恒定电场是无源无旋场。
图2.2.2 恒定电流的形成
14
2.2.2 电源电动势与局外场强
设局外场强为 Ee
fe q
,则电源电动势为:
l Ee dl
(V )
电源电动势与有无外电路无关,它是表示电源本身的特征量。
考虑局外场强 Ee
J (E Ee )
因此
(E l
Ee ) dl
E dl
l
l Ee dl
1
第二章 恒定电场
2
基本概念: • 通有恒定电流的导电媒质中的恒定电场 (电流场)
• 通有恒定电流的导电媒质周围电介质中 的静态电场
• 注意:本章只研究导电媒质内部的区域
• 本章研究的对象是导电媒质,其
与静电场中所说的导体是什么关
系?
3
§2-1 导电媒质中的电流
在外电场的作用下,自由电荷定向运动形成电流 导电媒质中的运动电荷的定向运动形成的电流叫传导电流
的减少率:
16
q
S
J
• dS
t
I
S
J
•
dS
q t
t
V
dV
散度定理 J dS JdV
S
V
• JdV
S
V
t
dV
•
J
电流连续性方程
t
17
在恒定电场中 0 t
•
J
t
对于恒定电流场,电荷分布不随时间变化:
故 J 0
恒定电场是一个无源场,电流线是 连续的。
• 即:
J • dS 0
体分布dV JdV
( dV
)v
面分布
线分布l
sdS KdS dl Idl
(
s
dS
)v
(dl)v
(v )dl
13
2.2 电源电势与局外场强
2.2.1 电源
要想在导线中维持恒定电 流,必须依靠非静电力将B极 板的正电荷抵抗电场力搬到A 极板。这种提供非静电力将其 它形式的能量转为电能装置称 为电源。
• 交变电场的集肤效应,即高频情况下,电流趋於表面分 布,可用电流面密度表示。
3、线电流
分布的线电荷沿着导线以速
度 v 运动形成的电流
I =v 。
7 图2.1.4 媒质的磁化电流
4. 元电流的概念:
元电荷dq以速度v运动,则dqv(C m / s或A m) 定义为元电流段。
不同分布的元电荷运动后形成的元电流段:
元电荷dq
元电流dqv
体分布dV JdV
( dV
)v
面分布KdS KdS
线分布Idl Idl
(dS
)v
(dl )v
(v)dl
8
2.1.3 欧姆定律的微分形式
欧姆定律:I U R
电场是维持恒定电流的必要 条件。可以证明
J E
欧姆定律的微分形式。
式中 为电导率,单位s/m( 西门子/米)。
J 0
E 0
19
恒定电场积分
形式基本方程:
E • dl 0
l
J • dS 0
S
J E
静电场积分 形式基本方程:
E • dl 0
l
D • dS q0
S
不含场源
D E
20
2.3.2 分界面的衔接条件 分界面上的衔接条件
LE dl 0 SJ dS 0
说明分界面上电场强度的切向分 量是连续的,电流密度法向分量是连 续的。
• 恒定电流场与恒定电场相互依存。电流J 与电场媒质中,电位移矢量D 线与电流密度J 线方
向是否一致?
• 电流面密度 K E 是否成立?
10
2.1.4 焦尔定律的微分形式 导电媒质中有电流时,必伴随功率损耗。可以证明其
功率的体密度为:
p J E (W/m3 )——焦耳定律的微分形式
2
2
n
很多恒定电场问题的解决,都可以归结为一定条件下, 求出拉普拉斯方程的解答(边值问题)。
恒定电场中是否存在泊松方程?
24
例2.3.2 试用边值问题求解电弧片中电位、电场及面电荷的分布
2 0
表明,只要
1
,电流
2
线垂直于良导体表面穿出,良
导体表面近似为等位面。
22
2.3.4 恒定电场的电位(不含电源的区域)
E 0 E
由基本方程出发
J E
J 0
E 0
对于均匀媒质: 常数
得
2 0
拉普拉斯方程
23
2.3.5 恒定电场的边值问题
分界面衔接条件
1 2
1
2
n
单位时间内通过某一横截面的电量, 简称为电流。
I dq
A
dt
I 是通量,并不反映电流在 每一点的流动情况。
4
2.1.1 电流强度
1.电流体密度 分布的体电荷以速度v 作匀速运动形成的电流。
J v A m2
亦称电流面密度
电流
I S J dS
5
2. 电流面密度
分布的面电荷在曲面上以速度v运动形成的电流。
E1t E2t J1n J 2n
折射定律为
tan1 1 tan2 2
图2.3.1 电流线的折射21
例2.3.1 特殊情况分界面上的电场分布。
解:媒质1是良导体, 1 5 107 s / m 媒质2是不良导体, 2 102 s / m
由折射定理得
tan 1 1 ,则 tan 2 2
0
局外场 Ee 是非保守场。
15
图2.2.3 电源电动势与局外场强
2.3 恒定电场的基本方程 • 分界面上的衔接条件 • 边值问题
2.3.1 恒定电场的基本方程
1. J 的散度
电流的连续性定律 J dS q
S
t
• 定义:由电荷守恒定律,从 任一闭合面流出的传导电流,
应等于该面所围体积内电荷
电路中的焦耳定律,可由它的积分而得,即
P UI I 2 R (W)—— 焦耳定律的积分形式
11
小结:
I S J dS
J
I
S 面:用与I 流动的 方向垂直的平面去 切导电媒质得到的 截面。
欧姆定律的微分形式
J E
焦耳定律的微分形式
p J E (W/m3 )
12
元电荷dq
元电流dqv
K v
电流
Am
线电流密度矢量
I l (K en )dl
I
l:用与I 流动的方向垂直的平
面去切导电媒质得到的截线。
en 是垂直于dl,且通过dl与
曲面相切的单位矢量
图2.1.3 电流线密度及其6通量
工程意义:
• 同轴电缆的外导体视为电流面密度分布;
• 媒质的磁化,其表面产生磁化电流可用电流面密度表示, 如图示;
S
I 0 • Kirchhoff’s
law.
18
2. E 的旋度
所取积分路径不经过电源,则:
斯托克斯定理
l E dl 0
s( E) dS 0
得
E 0 恒定电场是无旋场。
3. 恒定电场(电源外)的基本方程
s J dS 0
J E
e E dl 0
• 恒定电场是无源无旋场。
图2.2.2 恒定电流的形成
14
2.2.2 电源电动势与局外场强
设局外场强为 Ee
fe q
,则电源电动势为:
l Ee dl
(V )
电源电动势与有无外电路无关,它是表示电源本身的特征量。
考虑局外场强 Ee
J (E Ee )
因此
(E l
Ee ) dl
E dl
l
l Ee dl
