系统建模与辨识 产生白噪声
白噪声

物理学概念
01 定义
03 参数 05 应用
目录
02 起源 04 通信中的
白噪声(white noise)是指功率谱密度在整个频域内是常数的噪声。所有频率具有相同能量密度的随机噪声 称为白噪声。
定义
白噪声是指在较宽的频率范围内,各等带宽的频带所含的噪声功率谱密度相等的噪声。
一般在物理上把它翻译成白噪声(white noise)。
人生充满声音和噪声干扰,如轿车鸣喇叭、汪汪狗叫、吵邻打鼾、警报器、大喊大叫.白噪声并不增加烦躁, 而是包含所有同等频率的声音.研究表明,一个稳定、平和的声音流,如白噪声、可过滤和分散噪音,可以帮助减轻 噪音分心,这也正是为什么它用来帮助人们放松、睡眠。
上市销售的白噪声机器产品有睡眠辅助器、私密性增强器以及掩饰耳鸣。
白噪声可以用于放大器或者电子滤波器的频率响应测试,有时它与响应平坦的话筒或和自动均衡器一起使用。 这个设计的思路是系统会产生白噪声,话筒接收到扬声器产生的白噪声,然后在每个频率段进行自动均衡从而得 到一个平坦的响应。这种系统用在专业级的设备、高端的家庭立体声系统或者一些高端的汽车收音机上。
白噪声也作为一些随机数字生成器的基础使用,常用于计算机科学领域。
白噪声的应用领域之一是建筑声学,为了减弱内部空间中分散人注意力并且不希望出现的噪声(如人的交谈), 使用持续的低强度噪声作为背景声音。
在电子通信中也有白噪声的应用,它被直接或者作为滤波器的输入信号以产生其它类型的噪声信号,尤其是 在信号合成中,经常用来重现有很高噪声成分信号。
白噪声也用来产生冲击响应。为了在一个演出地点保证音乐会或者其它演出的均衡效果,从P A系统发出一 个瞬间的白噪声或者粉红噪声,并且在不同的地方监测噪声信号,这样工程师就能够建筑物的声学效应能够自动 地放大或者削减某些频率,从而就可以调整总体的均衡效果以得到一个平衡的和声。
系统辨识实验报告30288
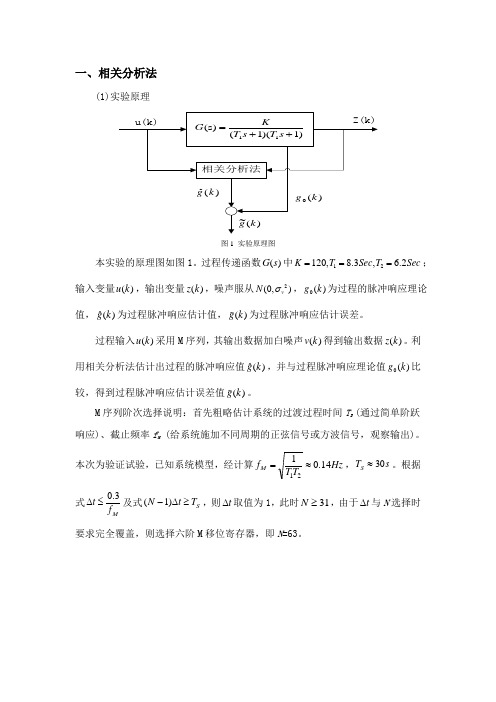
一、相关分析法(1)实验原理图1 实验原理图本实验的原理图如图1。
过程传递函数()G s 中12120,8.3, 6.2K T Sec T Sec ===;输入变量()u k ,输出变量()z k ,噪声服从2(0,)v N σ,0()g k 为过程的脉冲响应理论值,ˆ()gk 为过程脉冲响应估计值,()g k 为过程脉冲响应估计误差。
过程输入()u k 采用M 序列,其输出数据加白噪声()v k 得到输出数据()z k 。
利用相关分析法估计出过程的脉冲响应值ˆ()gk ,并与过程脉冲响应理论值0()g k 比较,得到过程脉冲响应估计误差值()g k 。
M 序列阶次选择说明:首先粗略估计系统的过渡过程时间T S (通过简单阶跃响应)、截止频率f M (给系统施加不同周期的正弦信号或方波信号,观察输出)。
本次为验证试验,已知系统模型,经计算Hz T T f M 14.0121≈=,s T S 30≈。
根据式Mf t 3.0≤∆及式S T t N ≥∆-)1(,则t ∆取值为1,此时31≥N ,由于t ∆与N 选择时要求完全覆盖,则选择六阶M 移位寄存器,即N =63。
(2)编程说明图2 程序流程图(3)分步说明 ① 生成M 序列:M 序列的循环周期63126=-=N ,时钟节拍1t Sec ∆=,幅度1a =,移位寄存器中第5、6位的内容按“模二相加”,反馈到第一位作为输入。
其中初始数据设为{1,0,1,0,0,0}。
程序如下:② 生成白噪声序列: 程序如下:③ 过程仿真得到输出数据:如图2所示的过程传递函数串联,可以写成形如121211()1/1/K Gs TT s T s T =++,其中112KK TT =。
图2 过程仿真方框图程序如下:④ 计算脉冲响应估计值:互相关函数采用公式)()(1)(10k i y i x Nr k R N r i xy +⋅⋅=∑-⋅=,互相关函数所用的数据是从第二个周期开始的,其中r 为周期数,取1-3之间。
系统建模与辨识 产生白噪声

实验一、Matlab/Simulink上机练习一、实验内容1、系统辨识信号的产生:U=idinput(N,type,Band,levels,auxvar);2、用simulink产生Noise,Sine,PRBS,用示波器观测波形;3、产生白噪声信号,计算其平均值,方差(和功率谱);4、选一模型对象,求其阶跃响应,然后再用白噪声作输入,计算某系统输出。
二、实验结果1、idinput函数产生系统辨识常用的典型信号。
格式u = idinput(N,'sine',band,levels,sinedata)指定产生信号的类型,可选类型如下%产生高斯随机信号u1=idinput(500,'rgs')stairs(u1)title('高斯随机信号')ylim([-5 5])%产生二值随机信号u2=idinput(500,'rbs')stairs(u2)title('二值随机信号')ylim([-1.5 1.5])%产生二值伪随机信号u3=idinput(500,'prbs') stairs(u3)title('二值伪随机信号') ylim([-1.5 1.5])m=mean(u3)2、3、% 产生白噪声N=100 a=idinput(100,'prbs') stairs(a)title('白噪声N=100') ylim([-1.5 1.5])m1=mean(a)v1=var(a)结果m1 =-0.1200v1 =0.99564、。
白噪声的生成

白噪声的研究与生成目录白噪声的研究与生成 (1)目录 (1)1. 白噪声的定义 (2)2. 统计特性 (2)3. 白噪声的生成 (3)3.1 高斯白噪声的生成 (3)3.1.1. WGN:产生高斯白噪声 (3)3.1.2. AWGN:在某一信号中加入高斯白噪声 (3)3.1.3.注释 (4)3.2 均匀分布的白噪声的产生 (5)4.白噪声的应用 (6)1.白噪声的定义白噪声是指功率密度在整个频域内均匀分布的噪声。
所有频率具有相同能量的随机噪声称为白噪声。
从我们耳朵的频率响应听起来它是非常明亮的“咝”(每高一个八度,频率就升高一倍。
因此高频率区的能量也显著增强)。
即,此信号在各个频段上的功率是一样的。
由于白光是由各种频率(颜色)的单色光混合而成,因而此信号的这种具有平坦功率谱的性质被称作是“白色的”,此信号也因此被称作白噪声。
相对的,其他不具有这一性质的噪声信号被称为有色噪声。
理想的白噪声具有无限带宽,因而其能量是无限大,这在现实世界是不可能存在的。
实际上,我们常常将有限带宽的平整信号视为白噪声,以方便进行数学分析。
2.统计特性术语白噪声也常用于表示在相关空间的自相关为0的空域噪声信号,于是信号在空间频率域内就是“白色”的,对于角频率域内的信号也是这样,例如夜空中向各个角度发散的信号。
右面的图片显示了计算机产生的一个有限长度的离散时间白噪声过程。
需要指出,相关性和概率分布是两个不相关的概念。
“白色”仅意味着信号是不相关的,白噪声的定义除了要求均值为零外并没有对信号应当服从哪种概率分布作出任何假设。
因此,如果某白噪声过程服从高斯分布,则它是“高斯白噪声”。
类似的,还有泊松白噪声、柯西白噪声等。
人们经常将高斯白噪声与白噪声相混同,这是不正确的认识。
根据中心极限定理,高斯白噪声是许多现实世界过程的一个很好的近似,并且能够生成数学上可以跟踪的模型,这些模型用得如此频繁以至于加性高斯白噪声成了一个标准的缩写词:AWGN。
噪声生成算法

噪声生成算法1 引言在信号处理、数据增强、模拟仿真等领域,噪声是不可或缺的组成部分。
噪声生成算法用于生成具有特定属性(如统计特性、频率分布等)的噪声信号,这些信号可以用于模拟真实环境中的噪声,或者作为数据增强的一种手段。
随着科技的发展,噪声生成算法在许多领域都得到了广泛的应用,如何生成高质量的噪声成为了一个重要的问题。
本文将对现有的噪声生成算法进行概述,分析它们的原理和应用,比较它们的性能,提出选择依据,并展望未来的发展趋势。
2 噪声生成算法的原理常见的噪声生成算法可以根据其原理分为以下几类:白噪声生成算法、基于概率模型的噪声生成算法、基于自然现象的噪声生成算法等。
2.1 白噪声生成算法白噪声生成算法是一种最基本的噪声生成方法。
它产生的噪声具有均匀的功率谱密度,即频率分量相等。
白噪声生成算法通常利用随机数生成器产生一系列随机数,经过适当的线性变换得到白噪声。
2.2 基于概率模型的噪声生成算法基于概率模型的噪声生成算法利用概率模型描述噪声的统计特性,如高斯噪声、泊松噪声等。
这类算法通常需要根据实际需求选择合适的概率分布,并利用随机数生成器产生符合该分布的随机数。
2.3 基于自然现象的噪声生成算法基于自然现象的噪声生成算法利用自然界中的现象(如风、雨、动物叫声等)作为噪声源,通过模拟这些现象的产生过程得到所需的噪声信号。
这类算法通常能够产生具有较高逼真度的噪声,但计算复杂度较高。
3 噪声生成算法的应用3.1 图像处理在图像处理中,噪声是常见的干扰因素。
噪声生成算法可以用于模拟不同类型的噪声(如椒盐噪声、高斯噪声等),以便在图像处理过程中进行降噪、滤波等操作。
通过生成具有相似特性的噪声,可以对图像进行更加准确的预处理和后处理。
3.2 声音合成在声音合成中,噪声生成算法可以用于模拟自然界中的声音或创造独特的声音效果。
例如,利用基于自然现象的噪声生成算法可以模拟雨声、海浪声等自然声音;利用白噪声或高斯噪声可以创造独特的背景音或效果音。
白噪声检验的方法及原理

白噪声检验的方法及原理咱得明白啥是白噪声。
白噪声啊,就像是一种杂乱无章但又有规律可循的声音信号。
在统计学和时间序列分析里,白噪声可是个重要的概念呢。
它具有一些特定的性质,比如说均值为零,方差是一个常数,不同时间点的取值相互独立。
简单来说,白噪声就是一种随机的、没有明显趋势和规律的信号。
那为啥要进行白噪声检验呢?这可重要啦!如果一个时间序列是白噪声,那就意味着它没有可预测的模式,是完全随机的。
在很多情况下,我们需要确定一个时间序列是不是白噪声,因为这关系到我们后续的分析和预测方法的选择。
如果一个时间序列不是白噪声,那就可能存在某种趋势、季节性或者周期性,我们就可以利用这些特征来进行预测和分析。
但如果它是白噪声,那我们就知道用传统的预测方法可能不太管用啦。
接下来,咱说说白噪声检验的方法。
常见的方法有好几种呢,比如说自相关函数检验、Ljung-Box 检验和单位根检验等。
自相关函数检验呢,就是看时间序列的自相关函数。
如果一个时间序列是白噪声,那么它的自相关函数在所有的滞后阶数上都应该接近于零。
啥意思呢?就是说不同时间点的取值之间没有明显的相关性。
我们可以通过计算时间序列的自相关函数,并观察它在不同滞后阶数上的值来判断是不是白噪声。
如果自相关函数的值都很小,接近零,那很可能就是白噪声;如果自相关函数在某些滞后阶数上有较大的值,那就不是白噪声啦。
Ljung-Box 检验也是个常用的方法。
这个检验主要是通过计算统计量来判断时间序列的自相关性。
它会比较实际的自相关系数和在白噪声假设下的预期自相关系数。
如果统计量的值很大,那就说明时间序列不是白噪声;如果统计量的值比较小,那就有可能是白噪声。
Ljung-Box 检验通常会给出一个p 值,我们可以根据p 值来判断是否拒绝白噪声假设。
如果p 值小于某个显著性水平,比如0.05,那就拒绝白噪声假设,说明时间序列不是白噪声;如果p 值大于显著性水平,那就不能拒绝白噪声假设,可能是白噪声。
系统辨识与建模教学大纲

(3)连续系统的输入输出模型、离散系统的输入输出模型、数学模型之间的等价变换、噪声模型及其分类。(2课时/课内)
(4)经典的系统辨识和建模方法,注重实用性,包括:频率响应法和实验测取过程的频率响应Levy法,频率响应的辨识和脉冲响应辨识的基本原理,用M序列作输入信号的离散算法,用M序列作输入信号的一次完成算法,用M序列作输入信号的递推算法,用M序列作输入信号时脉冲响应估计的统计性质,用M序列作输入信号辨识脉冲响应的步骤。3-5人分组设计课程仿真作业和研讨,内容:利用相关分析法辨识脉冲响应。(8课时/课内)
(5)最小二乘法参数辨识方法:最小二乘法的基本概念、最小二乘问题的提法、最小二乘问题的解、最小二乘参数估计的收敛性、最小二乘参数估计的几何解析、最小二乘参数估计的统计性质、最小二乘参数估计的递推算法、最小二乘递推算法的几种变形。(7课时/课内)
(6)模型阶次辨识:Hankel矩阵判秩法、F-Test定阶法等。(2课时/课内)
课程作业1——利用相关分析法辨识脉冲响应:过程仿真,白噪声生成,M序列生成,互相关函数的计算,计算脉冲响应估计值(课外);
课程作业2——递推最小二乘估计(RLS)及模型阶次辨识(F-Test):过程仿真,辨识模型,辨识算法,仿真数据,F-Test定阶法,计算性能指标。
(10)期末考试,注重考查系统辨识和建模的基本概念和基本理论。(课外)
后续课程
现代交流调速技术,实时优化与先进控制等
教材及参考书
萧德云. 系统辨识理论及应用. 清华大学出版社,2014年7月.
潘立登,潘仰东,系统辨识与建模,化工工业出版社,北京,2004.
理想白噪声和带限白噪声的产生与分析

理想白噪声和带限白噪声的产生与分析摘要 利用Matlab 仿真分析产生的高斯白噪声和均匀白噪声通过低通滤波器和带通滤波器后的时域及频域波形,以便更好地理解白噪声。
背景 在实际应用中,通信设备的各种电子器件、传输线、天线等都会产生噪声,伴随着信号的产生、传输和处理的全过程。
噪声也是一种随机过程,而白噪声具有均匀功率谱密度,在数学处理上具有方便、简单的优点。
电子设备中的起伏过程如电阻热噪声、散弹噪声等,在相当宽的频率范围内具有均匀的功率谱密度,可以当做白噪声处理,因而研究白噪声的特性显得非常重要。
实验特点与原理(1)随机信号的分析方法在信号系统中,把信号分为确知信号与随机信号两类。
在工程技术中,一般用概率密度、均值、均方值、方差、自相关函数、频谱、功率谱密度等描述随机过程的统计特性。
①均值均值E[x(t)](μ)表示集合平均值或数学期望值。
基于随机过程的各态历经性,可用时间间隔T 内的幅值平均值表示:∑-==10/)()]([N t N t x t x E均值表达了信号变化的中心趋势,或称之为直流分量。
②均方值均方值E[x 2(t)](2ϕ),或称为平均功率:N t x t x E N t /)()]([(1022∑-==均方值表达了信号的强度,其正平方根值,又称为有效值,也是信号的平均能量的一种表达。
③方差定义: N t x E t x N t /)]]([)([122∑-=-=σ可以证明,2ϕ=2σ+2μ。
其中:2σ描述了信号的波动量;2μ 描述了信号的静态量。
④自相关函数信号的相关性是指客观事物变化量之间的相依关系。
对于平稳随机过程x(t)和y(t)在两个不同时刻t 和t+τ的起伏值的关联程度,可以用相关函数表示。
在离散情况下,信号x(n)和y(n)的相关函数定义为:∑∑-=-+=101N t xy N /)t (y )t (x ),t (N R τττ τ,t=0,1,2,……N-1随机信号的自相关函数表示波形自身不同时刻的相似程度。
10 白噪声过程通过线性系统讲解

| H(j) |
C0
0 0
0
5、输出窄带噪声的总平均功率
输出窄带噪声的总平均功率为
RY
(0)
N 0 K 0 2 2
sin( /
/ 2) 2
cos 0
| 0
N 0 K 0 2 2
N 0 K 0 2 f
a(0)
输出窄带噪声总平均功率与系统带宽成正比
(0)
sin
相关时间0
sin d 1
0
2 4f
3、噪声通频带
由于输出噪声的功率谱为矩形,系统 的噪声通频带等于信号的通频带,即:
fe
f
2
,故有关系式
0fe 1/ 4,也即0与fe成反比。
若fe大,则
0
2
根据对称性:
Rh (
)
2
e| |
3、输出自相关函数
RY ( ) RX ( z)Rh (z)dz
N0
(
z)
e | z| dz
2
2
N0 ( z)e|z|dz 4
N0 e| |
4
4、相关系数和相关时间
0
cos cos0 sin sin 0 d
N0
K
2 0
2
0 0
e2 / 2
cos
cos0 d
N0
K
2 0
cos 0
0 e2 / 2 cos d
0
N0
《系统辨识》第1次课_第一章

参数 模型辨识
最小二乘法
极大似然法
26
1.4.2辨识的内容和步骤
(1)明确辨识目的。它将决定模型的类型、精度及辨识方法。 (2)掌握先验知识。对预选模型种类和辨识试验设计起指导作用 (3)选定系统模型种类,确定验前假定模型。 (4)试验设计。选择试验信号、采样间隔数据长度等。 (5)数据处理。
直流、低频数据:零均值化(差分法和平均法等)。 高频成分数据:低通滤波。
代替或部分代替对真实系统的试验。传统上大多采用第一
种方法,随着科学技术的发展,尽管第一种方法在某些情
况下仍然是必不可少的,但第二种方法日益成为人们更为
常用的方法,主要原因在于:
7
(1)系统还处于设计阶段,真实的系统尚未建立,人们需要更
准确地了解未来)在真实系统上进行试验可能会引起系统破坏或发生故障,
实体确定了系统的构成,也就确定了系统的边界; 属性也称为描述变量,描述每一实体的特征; 活动定义了系统内部实体之间的相互作用,从而确定了系统内部发生变化的过程。
6
1.1.2 模型
为了研究、分析、设计和实现一个系统,需要进行试
验。试验的方法基本上可分为两大类:一种是直接在真实
系统上进行,另一种是先构造模型,通过对模型的试验来
(6)模型结构辨识。确定模型的阶次和纯延时等。 (7)模型参数辨识。 (8)模型校验。
27
模型验证:
对辨识所取得的模型进行验证是系统辨识的重要环 节。验证的目的是为了确定该模型是否是模型集中针对 当前观测数据的最佳选择。验证的方法主要有:
(1)利用先验知识验证,即根据对系统已有的知识来判断模型 是否适用。 (2)利用数据检验。 当利用一组数据辨识得到一个模型后,通常希望用另一组未 参与辨识的数据检验模型的适用性。如果失败:说明原数据包含 的信息不足或所选的模型类不合适。 另外,也可以用一组数据对不同模型进行比较,以选用更适 合的模型。 (3)利用实际响应检验。比较实际系统和模型的阶跃响应、脉 冲响应是判别的重要手段。
白噪声序列模型形式

白噪声序列模型形式1.引言1.1 概述白噪声是一种随机信号,其在不同频率下具有均匀分布的能量,即在整个频谱范围内的每个频率上都具有相同的能量。
与其他信号相比,白噪声在时间和频率上都是均匀分布的,不受前后相关性的影响。
白噪声在许多领域都有应用,特别是在信号处理、通信系统和物理实验中。
因为它具有唯一的特性,即与其他信号不相关,因此可以用作信号处理算法和系统的基准。
此外,由于白噪声被认为是一种理想的随机信号,它也常常用作模型中的一个基本组成部分。
本文将重点介绍白噪声序列的模型形式。
为了更好地理解白噪声序列的特点和应用,首先将给出白噪声序列的定义和特点。
然后,将详细讨论白噪声序列的模型形式,包括常见的数学表达和统计特性。
通过深入研究白噪声序列的模型形式,可以更好地理解其在实际应用中的作用和意义。
在接下来的章节中,我们将探索白噪声序列的模型形式,并探讨其在信号处理和通信系统中的应用。
我们将重点关注白噪声序列的生成和分析方法,以及如何利用它们来模拟真实世界中的随机过程。
通过深入研究白噪声序列的模型形式,我们可以更好地理解其在现实世界中的应用,并为相关领域的研究和开发提供有益的指导。
本文的最后一部分将总结我们对白噪声序列模型形式的探讨,并展望未来的研究方向。
在总结部分,我们将回顾本文的主要观点和结论,并对我们对白噪声序列模型形式的理解进行总结。
在展望部分,我们将提出一些可能的研究方向和未来的发展趋势,以进一步深入研究白噪声序列的模型形式和应用。
通过本文的研究,我们期望能够增加对白噪声序列模型形式的理解,并为相关领域的研究和开发提供有益的指导。
同时,我们也希望能够促进对白噪声序列在实际应用中的运用,推动相关领域的发展和进步。
1.2文章结构文章结构部分的内容如下:1.2 文章结构本文按照以下结构组织和阐述白噪声序列模型形式的相关内容:引言部分将通过概述问题的背景和意义引入白噪声序列的定义和特点,为读者提供一个整体的认识。
《系统辨识》实验手册

《系统辨识》实验手册第二炮兵工程大学控制工程系2015年5月目录实验1 白噪声和M序列的产生---------------------------------------------------------- 2 实验2 相关分析法辨识脉冲响应------------------------------------------------------- 5 实验3 最小二乘法的实现--------------------------------------------------------------- 9 实验4 递推最小二乘法的实现---------------------------------------------------------- 12 附录实验报告模板---------------------------------------------------------------------- 16实验1 白噪声和M 序列的产生一、实验目的1、熟悉并掌握产生均匀分布随机序列方法以及进而产生高斯白噪声方法2、熟悉并掌握M 序列生成原理及仿真生成方法二、实验原理1、混合同余法混合同余法是加同余法和乘同余法的混合形式,其迭代式如下:111(*)mod /n n n n x a x b MR x M +++=+⎧⎨=⎩ 式中a 为乘子,0x 为种子,b 为常数,M 为模。
混合同余法是一种递归算法,即先提供一个种子0x ,逐次递归即得到一个不超过模M 的整数数列。
2、正态分布随机数产生方法由独立同分布中心极限定理有:设随机变量12,,....,,...n X X X 相互独立,服从同一分布,且具有数学期望和方差:2(),()0,(1,2,...)k k E X D X k μσ==>=则随机变量之和1nk i X =∑的标准化变量:()nnnkk kXE X Xn Y μ--==∑∑∑近似服从(0,1)N 分布。
系统建模与辨识快速掌握

《系统辨识》第1讲要点●引言课程名称:系统辨识(System identification)现代控制论:辨识、状态估计和控制理论什么是辨识(Identification)?System Identification系统辩识,又译为“系统识别”和“系统同定”,目前尚无公认的统一定义。
《中国大百科全书》中记述为:系统辩识是根据系统的输入/输出时间函数,确定系统行为的数学模型,是现代控制理论的一个分支(中国大百科自动控制卷486-488页)。
(1) 辨识是研究建立系统或生产过程数学模型的一种理论和方法。
(2) 辨识是种从含有噪声的测量数据(输入、输出数据)中提取被研究对象数学模型的一种统计方法。
(3) 辨识模型是对象输入输出特性在某种准则意义下的一种近似。
近似的程度取决于人们对系统先验知识的认识和对数据集性质的了解程度,以及所选用的辨识方法是否合理。
(4) 辨识技术帮助人们在表征被研究的对象、现象或系统、过程的复杂因果关系时,尽可能准确地确立它们之间的定量依存关系。
(5) 辨识是一种实验统计的建模方法。
通俗地说,系统辩识是研究怎样利用对未知系统的试验数据或在线运行数据(输入/输出数据)建立描述系统的数学模型的科学。
钱学森把系统广义概括为“依一定顺序相互联系着的一组事物”。
“系统辩识”是“系统分析”和“控制系统设计”的逆问题。
基于实际系统的复杂性,描述其特性的数学模型具有“近似性”和“非唯一性”;辩识方法亦有多样性。
没有绝对好的数学模型和绝对好的辩识方法。
什么是较好的模型?依据辩识的不同目的,有不同答案。
一般说,能够满足目的要求的,比较简单的模型,是较好的模型。
参考书:1.方崇智、萧德云编著,《过程辨识》,清华大学出版社,北京,19882.蔡季冰编著,《系统辨识》,北京理工大学出版社,北京,19893.Lennart Ljung,《系统辨识-使用者的理论》(第二版),清华大学出版社,北京,2002预修课程:线性系统理论、自动控制理论基础、概率统计与随机过程第1章系统辨识的一些基本概念1.1 过程和模型1.1.1 过程(Process)●过程的描述框图(“黑箱”模型)●过程的行为特性表现在过程的输入输出数据之中。
系统辨识白噪声及M序列产生

A=6; x0=1; M=255; f=2; N=100; %初始化;x0=1; M=255;for k=1: N %乘同余法递推100次;x2=A*x0; %分别用x2和x0表示xi+1和xi-1;x1=mod (x2,M); %取x2存储器的数除以M的余数放x1(xi)中;v1=x1/256; %将x1存储器中的数除以256得到小于1的随机数放v1中;if(v1>0.5)v(:,k)=v1;else v(:,k)=(v1-0.5 )*f; %将v1中的数()减去0.5再乘以存储器f中的系数,存放在矩阵存储器v的第k列中,v(:,k)表示行不变、列随递推循环次数变化;endx0=x1; % xi-1= xi;v0=v1;end %递推100次结束;v2=v %该语句后无‘;’,实现矩阵存储器v中随机数放在v2中,且可直接显示在MATLAB的window中;k1=k;%grapher %以下是绘图程序;k=1:k1;plot(k,v,k,v,'r');xlabel('k'), ylabel('v');tktle(' (-1,+1)均匀分布的白噪声')A=6;N=100;x0=1;M=255;w=0.5; v2=0;%初始化s=sqrt(1/12);for k=1:Nx2=A*x0;x1=mod(x2,M);v1=x1/256;v2=v2+v1;v(:,k)=v1;x0=x1;v0=v1;v3=(v2-k/2)/(sqrt(k/12));e(:,k)=w+s*v3;ende2=ek1=k;k=1:k1;plot(k,e,k,e,'rx');xlabel('k'),ylabel('e');title('(0,1)正态分布的随机信号')2e2 =Columns 1 through 60.0234 -0.0911 0.2158 0.0449 0.0895 0.3134 Columns 7 through 120.4350 0.5193 0.4766 0.4012 0.4211 0.3714 Columns 13 through 180.4881 0.4708 0.5000 0.5420 0.4252 0.3426 Columns 19 through 240.4256 0.3340 0.3363 0.4384 0.4992 0.5454 Columns 25 through 300.5195 0.4717 0.4820 0.4476 0.5232 0.5107 Columns 31 through 360.5302 0.5594 0.4755 0.4143 0.4736 0.4043 Columns 37 through 420.4043 0.4804 0.5263 0.5618 0.5415 0.5036 Columns 43 through 480.5113 0.4835 0.5437 0.5334 0.5490 0.5727 Columns 49 through 540.5039 0.4530 0.5016 0.4437 0.4431 0.5064 Columns 55 through 600.5448 0.5746 0.5574 0.5251 0.5315 0.5076 Columns 61 through 660.5590 0.5501 0.5635 0.5840 0.5242 0.4798 Columns 67 through 720.5220 0.4711 0.4704 0.5257 0.5593 0.5856 Columns 73 through 780.5704 0.5418 0.5474 0.5260 0.5717 0.5637 Columns 79 through 840.5756 0.5939 0.5404 0.5004 0.5382 0.4923 Columns 85 through 900.4915 0.5413 0.5716 0.5954 0.5816 0.5556Columns 91 through 960.5606 0.5411 0.5826 0.5753 0.5862 0.6029Columns 97 through 1000.5539 0.5174 0.5518 0.5098>>3 X1=1;X2=0;X3=1;X4=0;X5=1;X6=0; %移位寄存器输入Xi初T态(0101),Yi为移位寄存器各级输出m=60; %置M序列总长度for i=1:m %1#Y6=X6;Y5=X5;Y4=X4; Y3=X3; Y2=X2; Y1=X1;X6=Y5;X5=Y4,X4=Y3; X3=Y2; X2=Y1;X1=xor(Y5,Y6); %异或运算if Y6==0U(i)=-1;elseU(i)=Y6;endendM=U%绘图i1=ik=1:1:i1;plot(k,U,k,U,'rx')xlabel('k')ylabel('M序列')title('移位寄存器产生的M序列')M =Columns 1 through 10-1 1 -1 1 -1 1 1 1 1 1 Columns 11 through 201 -1 -1 -1 -1 -1 1 -1 -1 -1 Columns 21 through 30-1 1 1 -1 -1 -1 1 -1 1 -1 Columns 31 through 40-1 1 1 1 1 -1 1 -1 -1 -1Columns 41 through 501 1 1 -1 -1 1 -1 -1 1 -1 Columns 51 through 601 1 -1 1 1 1 -1 1 1 -1 i1 =60。
白噪声
0.8047 -0.1328 0.2188 0.3359 -0.9531 -0.7188
0.6875 -0.8359 -0.0156 0.9219 0.5703 0.4531
-0.2500 -0.4844 0.1016 -0.3672 0.8047 -0.1328
0.0234 0.1406 0.8438 0.0820 0.4922 0.9609
0.7852 0.7266 0.3750 0.2578 0.5508 0.3164
0.9023 0.4336 0.6094 0.6680 0.0234 0.1406
0.8438 0.0820 0.4922 0.9609 0.7852 0.7266
白噪声的用途:
1 作为系统输入时,有 ,τ=0,1,2,…,即为系统的单位脉冲响应。
2 作为被辨识系统输入时,可以激发系统的所有模态,可对系统充分激励;
3 作为被辨识系统输入时,可防止数据病态,保证辨识精度。
4 在辨识过程中,以输出估计误差是否具有白色性来判断辨识方法的优劣,也可用来判断模型的结构和参数是否合适。
白噪声
如果一个零均值、平稳随机过程的谱密度为常数,我们称之为白噪声(由白色光联想而得)。白噪声有以下特点:
1
2 ,频谱宽度无限。
∞,τ=0
0,τ≠0
3 ,其中, 为Dirac函数,即 =
且
4 无记忆性,即t时刻的数值与t时刻以前的过去值无关,也不影响t时刻以后的将来值。从另一意义上说,即不同时刻的随机信号互不相关。
0.3750 0.2578 0.5508 0.3164 0.9023 0.4336
系统辨识与建模智慧树知到课后章节答案2023年下湘潭大学

系统辨识与建模智慧树知到课后章节答案2023年下湘潭大学湘潭大学第一章测试1. A system is a unity composed of various parts that are interconnectedconstrained and interacted with each other and have certain overallfunctions and comprehensive behaviors.()A:对 B:错答案:对2.Which one is not belong to modern control theory system?().A:System identification B:Modern control theory C:State estimationD:Automatic control答案:Automatic control3.建立数学模型的方法可大体分为:().A:观测法 B:理论分析法 C:测试法 D:实验法答案:理论分析法;测试法4.下列哪些属于非参数模型?()A:权序列模型 B:输入输出模型 C:状态空间模型 D:脉冲响应模型答案:权序列模型;脉冲响应模型5.针对水箱进行机理建模时,我们应该凭借哪种关系建立公式?().A:水箱流入量和流出量之差为流入水流量的增量 B:水箱流入量和流出量之差为液位的增量 C:水箱流入量和流出量之差为液体存储量的变化率 D:水箱流入量和流出量之差为流出水流量的增量答案:水箱流入量和流出量之差为液体存储量的变化率第二章测试1.下面哪些内容不属于系统辨识的基本内容?()A:观测数据 B:模型结构辨识 C:模型验证 D:模型参数辨识答案:观测数据2.白噪声过程没有“记忆性”,也就是说t时刻的数值与t时刻以前的值无关,也不影响t时刻以后的将来值。
()A:对 B:错答案:对3.关于白噪声的均匀分布计算问题,将产生的(0,1)均匀分布的随机数通通减去0.5,然后乘以存储器f中预置的系数,这里取f=2,从而得到新的分布()。
白噪声模型分析复杂系统中的随机波动

白噪声模型分析复杂系统中的随机波动引言在复杂系统中,随机波动是一种常见且重要的现象。
这些波动可能由多个因素引起,包括内部和外部的各种因素。
为了更好地理解和分析这些随机波动,研究者们开发了白噪声模型,这种模型在许多领域中被广泛应用,包括金融、物理学、生态学等。
本文将介绍白噪声模型,并探讨其在复杂系统中应用的意义和局限性。
白噪声模型的概念和特点白噪声是一种具有均值为零且方差恒定的随机过程,其特点是在所有频率上具有相等的能量分布。
这意味着白噪声的频谱是平坦的,不受频率的影响。
在时间域上,白噪声模型是一种随机过程,其值在每个时间点上都是独立和服从正态分布的。
因此,白噪声模型是一种无记忆、随机且不可预测的模型。
白噪声模型在复杂系统中的应用1. 金融领域白噪声模型在金融领域中被广泛应用,特别是在股票市场的价格波动分析中。
股票价格的随机波动被认为是由许多随机因素引起的,包括市场心理、新闻事件、投资者行为等。
白噪声模型可以用来模拟这些随机因素对股票价格的影响,帮助预测、分析和控制风险。
2. 生态学领域生态学中的许多现象也具有随机性和不确定性。
例如,种群数量的波动、物种分布的变化等都可以使用白噪声模型来进行建模和分析。
通过对这些随机波动的模拟和预测,我们可以更好地了解生态系统中各个组成部分的相互作用和变化规律。
3. 物理学领域在物理学中,白噪声模型可以用来描述与随机力和热力学有关的现象。
例如,在布朗运动中,颗粒在液体中的随机运动可以通过白噪声模型来解释和预测。
此外,白噪声模型还可以应用于信号处理、通信等领域,用于降噪和信号恢复。
白噪声模型的局限性虽然白噪声模型在许多领域中都具有广泛的应用,但它也存在一些局限性。
1. 忽略系统的复杂性白噪声模型只关注随机波动的统计特性,而忽略了复杂系统内部的结构和相互作用。
在复杂系统中,各个组成部分之间存在着多种复杂的关系和时空异质性,这些因素对波动的产生和传播可能具有重要影响。
因此,白噪声模型难以完全模拟和解释复杂系统中的随机波动。
报告中注意的系统辨识与建模方法选择

报告中注意的系统辨识与建模方法选择一、引言系统辨识与建模是在工程领域中非常重要的一项任务。
通过对系统进行辨识与建模,我们可以更好地理解系统的行为和特性,为系统的设计和控制提供依据。
然而,在进行系统辨识与建模时,我们需要注意选择适当的方法,以确保结果的准确性和可靠性。
本文将针对系统辨识与建模的方法选择进行详细论述。
二、确定问题和目标在进行系统辨识与建模时,首先需要明确问题和目标。
问题可以是系统的动态特性、参数估计、信号滤波等。
目标则是我们希望通过系统辨识与建模来解决的问题,例如控制系统设计、故障诊断等。
明确问题和目标可以帮助我们选择合适的方法。
三、基于数据的方法1. 时域方法时域方法是最常用的系统辨识与建模方法之一。
其基本思想是根据系统的输入和输出数据,通过对信号进行处理和分析,估计系统的动态特性和参数。
时域方法适用于系统辨识和参数估计问题,如ARIMA模型、自回归模型等。
2. 频域方法频域方法则是通过将时域信号转化到频域进行分析,从而得到系统的频率响应和特性。
频域方法适用于对系统的频率特性进行建模和辨识,如傅里叶变换、系统频率响应曲线的识别等。
四、基于模型的方法1. 物理建模方法物理建模方法是根据系统的物理原理和方程进行建模。
这种方法适用于我们对系统的工作原理有一定了解的情况,可以通过建立数学模型来描述系统的行为。
例如,通过牛顿定律建立机械系统的模型,通过电路理论建立电气系统的模型。
2. 统计建模方法统计建模方法是基于统计学原理进行建模。
这种方法适用于我们对系统的工作原理不清楚的情况,可以通过对系统的输入输出数据进行统计分析,得到系统的统计模型。
例如,通过回归分析建立系统的线性模型,通过时间序列分析建立系统的自回归模型。
五、模型选择的考虑因素在选择系统辨识与建模方法时,我们需要考虑以下因素:1. 数据质量数据质量是影响系统辨识与建模结果的关键因素之一。
如果输入输出数据不准确或存在噪声,将会对辨识与建模的效果产生负面影响。
imu误差 白噪声 零偏 刻度系数 尺度因子

IMU误差白噪声零偏刻度系数尺度因子一、引言惯性测量单元(IMU)是测量物体三轴向的角速度和加速度的装置,广泛应用于导航、控制和姿态估计等领域。
然而,由于制造工艺、温度和老化等因素的影响,IMU会存在误差,包括白噪声、零偏、刻度系数和尺度因子等。
这些误差会影响IMU的测量精度和稳定性,进而影响整个系统的性能。
因此,研究IMU误差是十分必要的。
二、白噪声白噪声是指IMU测量结果中的随机误差,其特点是具有恒定的幅度和频率,且不具有相关性。
白噪声的存在会对IMU的测量结果产生一定的影响,降低其精度和稳定性。
为了减小白噪声的影响,可以采用滤波算法和数据处理技术,如卡尔曼滤波器和粒子滤波器等。
这些算法能够利用历史数据对当前数据进行平滑处理,减小随机误差的影响。
三、零偏零偏是指IMU测量结果中的偏差,即在无外力作用下的测量值与真实值之间的差异。
零偏产生的原因可能是传感器内部的物理效应、制造工艺和温度等因素的影响。
零偏的存在会对IMU的测量结果产生较大的影响,尤其是在低速和静止状态下。
为了减小零偏的影响,可以采用温度补偿和校准等方法。
温度补偿可以通过建立温度与零偏之间的关系模型,对零偏进行实时补偿;校准则可以通过标定实验得到零偏的数值,对测量结果进行修正。
四、刻度系数刻度系数是指IMU中加速度计和陀螺仪之间的比例因子,其值的大小和稳定性对IMU的测量精度和稳定性具有重要影响。
刻度系数的不稳定会导致IMU的输出结果出现较大的偏差,影响整个系统的性能。
为了减小刻度系数的影响,可以采用实时监测和校准等方法。
实时监测可以通过建立刻度系数与时间之间的关系模型,对刻度系数进行实时补偿;校准则可以通过标定实验得到刻度系数的数值,对测量结果进行修正。
五、尺度因子尺度因子是指IMU中加速度计和陀螺仪之间的偏置误差,其大小和稳定性对IMU的测量精度和稳定性具有重要影响。
尺度因子不稳定的会导致IMU的输出结果出现偏差,影响整个系统的性能。
《系统辨识与建模》

《系统辨识与建模》课时:40参考书:1 徐南荣、宋文忠、夏安邦系统辨识,东南大学出版社,19912 方崇智、萧德云过程辨识,清华大学出版社,19883 Ljung L. And Soderstrom T. Theory and Practics of Recursive Identification, MIT.Press, Cambridge4 [美]P.艾克霍夫系统辨识-参数和状态估计,潘科炎等译,科学出版社,19775 [美]夏天长系统辨识—最小二乘,熊光楞、李芳芸译,清华大学出版社,1983期刊:1Automatica2Proc. IFAC Identification and System Parameter Estimation3IEEE Trans. On Automatic Control4自动化学报5控制理论与应用学习要求1 培养独立学习一门新课程的能力,为今后学习和研究打下基础(要求大家尽量少依赖听课,多自学)。
2 掌握基本的辨识理论和辨识技术3 能独立设计辨识实验,并编程计算4 学习一些现代建模技术考核办法给出一个数据文件,通过编程对其进行辨识,并写出报告第一讲概论实体与模型实体:客观存在的事物及其运动状态,有时也称之为“系统”模型:实体的一种简化描述。
模型保持实体的一部分特征,而将其它特征忽略或者变化。
不同的简化方法得到不同的模型。
模型分类:直觉模型:地图、建筑模型、照片、软件演示文档等物理模型:风洞、水力学模型、传热学模型、电力系统动态模拟模型等。
(缩小的复制品)数学模型:描述实体中一些关系和特征的数据模型。
例如:投入/产出模型、热源与室温的关系模型等。
数学模型数学模型还可分为:图表模型:如阶跃响应、脉冲响应、频率响应、温度与热电偶输出关系表解析模型:代数方程、微分方程、差分方程、状态方程程序模型:神经网络仿真程序语言模型:模糊关系模型获得数学模型的方法有:经验总结法:模糊关系模型、静态线性关系模型机理分析法:解析模型实验法:图表模型数据拟合法:解析模型、程序模型用数据拟合法获得解析模型的过程即为系统辨识。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验一、Matlab/Simulink上机练习
一、实验内容
1、系统辨识信号的产生:
U=idinput(N,type,Band,levels,auxvar);
2、用simulink产生Noise,Sine,PRBS,用示波器观测波形;
3、产生白噪声信号,计算其平均值,方差(和功率谱);
4、选一模型对象,求其阶跃响应,然后再用白噪声作输入,计算某系统输出。
二、实验结果
1、idinput函数
产生系统辨识常用的典型信号。
格式u = idinput(N,'sine',band,levels,sinedata)
指定产生信号的类型,可选类型如下
%产生高斯随机信号
u1=idinput(500,'rgs')
stairs(u1)
title('高斯随机信号')
ylim([-5 5])
%产生二值随机信号
u2=idinput(500,'rbs')
stairs(u2)
title('二值随机信号')
ylim([-1.5 1.5])
%产生二值伪随机信号
u3=idinput(500,'prbs') stairs(u3)
title('二值伪随机信号') ylim([-1.5 1.5])
m=mean(u3)
2、
3、% 产生白噪声N=100 a=idinput(100,'prbs') stairs(a)
title('白噪声N=100') ylim([-1.5 1.5])
m1=mean(a)
v1=var(a)
结果
m1 =
-0.1200
v1 =
0.9956
4、。
