初四试卷数学
初四期末数学试卷

初四期末数学试卷一.选择题(共12小题)1.已知等腰三角形的腰和底的长分别是一元二次方程x2﹣4x+3=0的根,则该三角形的周长可以是()A.5 B.7 C.5或7 D.102.若关于x一元二次方程x2-2x+kb+1=0有两个不相等实数根,则一次函数y=kx+b大致图象可能是()A.B.C.D.3.已知关于x的方程x2﹣2x+3k=0有两个不相等的实数根,则k的取值范围是()A.k<B.k>C.k<且k≠0 D.k>且k≠04.二次函数y=ax2+bx+c的图象在平面直角坐标系中的位置如图所示,则一次函数y=ax+b与反比例函数y=在同一平面直角坐标系中的图象可能是()A.B. C. D.5.已知二次函数y=x2+(m﹣1)x+1,当x>1时,y随x的增大而增大,而m的取值范围是()A.m=﹣1 B.m=3 C.m≤﹣1 D.m≥﹣16.如图,将⊙O沿弦AB折叠,圆弧恰好经过圆心O,点P是优弧上一点,则∠APB的度数为()A.45°B.30°C.75°D.60°7.如图,已知经过原点的⊙P与x、y轴分别交于A、B两点,点C是劣弧OB上一点,则∠ACB=()A.80°B.90°C.100°D.无法确定8.△ABC为⊙O的内接三角形,若∠AOC=160°,则∠ABC的度数是()A.80°B.160°C.100°D.80°或100°9.在同一直角坐标系中,函数y=﹣与y=ax+1(a≠0)的图象可能是()A.B.C.D.10.如图,A、B是双曲线y=上的两点,过A点作AC⊥x轴,交OB于D点,垂足为C.若△ADO的面积为1,D为OB的中点,则k的值为()A.B.C.3 D.411.如图,点A为∠α边上的任意一点,作AC⊥BC于点C,CD⊥AB于点D,下列用线段比表示cosα的值,错误的是()A.B.C.D.6题图7题图10题图11题图12.在△ABC中,若角A,B满足|cosA﹣|+(1﹣tanB)2=0,则∠C的大小是()A.45°B.60°C.75°D.105°二.填空题(共8小题)13.如图在半径为3的⊙O中,直径AB与弦CD相交于点E,连接AC,BD,若AC=2,则cosD=14.规定sin(α﹣β)=sinα•cosβ﹣cosα•sinβ,则sin15°=.15.如图点A在双曲线上,点B在双曲线y=上,且AB∥x轴,C,D在x轴上,若四边形ABCD为矩形,则它的面积为.16.如图已知点A在反比例函数y=(x<0)上,作Rt△ABC,点D为斜边AC的中点,连DB并延长交y轴于点E.若△BCE的面积为8,则k=.17.关于m的一元二次方程nm2﹣n2m﹣2=0的一个根为2,则n2+n﹣2=.18.已知关于x的一元二次方程x2+x﹣1=0有两个不相等的实数根,则k的取值范围是.19.下列函数(其中n为常数,且n>1)①y=(x>0);②y=(n﹣1)x;③y=(x>0);④y=(1﹣n)x+1;⑤y=﹣x2+2nx(x<0)中,y的值随x的值增大而增大的函数有个20.如图,边长为1的小正方形构成的网格中,半径为1的⊙O在格点上,则∠AED的正切值为.13题图15题图16题图20题图三.解答题(共10小题)21.关于x的一元二次方程x2+(2k+1)x+k2+1=0有两个不等实根x1,x2.(1)求实数k的取值范围.(2)若方程两实根x1,x2满足|x1|+|x2|=x1•x2,求k的值.22.如图所示抛物线y=x2+bx+c经过A、B两点,A、B两点的坐标分别为(-1,0)、(0,-3).(1)求抛物线的函数解析式;(2)点E为抛物线的顶点,点C为抛物线与x轴的另一交点,点D为y轴上一点,且DC=DE,求出点D的坐标;(3)在直线DE上存在点P,使得以C、D、P为顶点的三角形与△DOC相似,请你直接写出所有满足条件的点P的坐标.23.已知抛物线y=(x﹣m)2﹣(x﹣m),其中m是常数.(1)求证:不论m为何值,该抛物线与x轴一定有两个公共点;(2)若该抛物线的对称轴为直线x=2.5.①求该抛物线的函数解析式;②把该抛物线沿y轴向上平移多少个单位长度后,得到的抛物线与x轴只有一个公共点.24.如图AB是⊙O的弦,D为半径OA的中点,过D作CD⊥OA交弦于点E,交⊙O于点F,且CE=CB.(1)求证BC是⊙O切线;(2)连接AF,BF,求∠ABF度数;(3)若CD=15,BE=10,sinA=,求⊙O半径.25.如图,AB是⊙O的直径,点D是上一点,且∠BDE=∠CBE,BD与AE交于点F.(1)求证:BC是⊙O的切线;(2)若BD平分∠ABE,求证:DE2=DF•DB;(3)在(2)的条件下,延长ED,BA交于点P,若PA=AO,DE=2,求PD的长和⊙O的半径.26.有三张卡片(形状,大小,颜色,质地都相等),正面分别写上整式x2+1,﹣x2﹣2,3.将这三张卡片背面向上洗匀.从中任意抽取一张卡片,记卡片上的整式为A,再从剩下的卡片中任意抽取一张,记卡片上的整式为B,于是得到代数式.(1)请用画树状图或列表方法,写出代数式所有可能结果;(2)求代数式恰好是分式概率.27.如图在平面直角坐标系中,O为原点,直线AB分别与x轴、y轴交于B和A,与反比例函数图象交于C,D,CE⊥x轴于点E,tan∠ABO=,OB=4,OE=2.(1)求出两个函数解析式;(2)求△OCD的面积.28.如图,台风中心位于点O处,并沿东北方向(北偏东45°),以40千米/小时的速度匀速移动,在距离台风中心50千米的区域内会受到台风的影响,在点O的正东方向,距离60千米的地方有一城市A.(1)问:A市是否会受到此台风的影响,为什么?(2)在点O的北偏东15°方向,距离80千米的地方还有一城市B,问:B市是否会受到此台风的影响?若受到影响,请求出受到影响的时间;若不受到影响,请说明理由.29.如图一艘海上巡逻船在A地巡航,测得A地在观测站B的南偏东45°方向上,在观测站C的南偏西60°方向上,观测站B在观测站C的正西方向,此时A地与观测站B的距离为20海里.(1)求A地与观测站C的距离是多少海里?(2)现收到故障船D的求救信号,要求巡逻船从A地马上前去救援(C,A,D共线).已知D船位于观测站B的南偏西15°方向上,巡逻船的速度是12海里/小时,求巡逻船从A地到达故障船D处需要多少时间?(结果保留小数点后一位,参考数据≈1.41,≈1.73,≈2.24)30.阅读与应用:阅读1:a、b为实数,且a>0,b>0,因为(﹣)2≥0,所以a﹣2+b≥0从而a+b≥2(当a=b时取等号).阅读2:若函数y=x+;(m>0,x>0,m为常数),由阅读1结论可知:x+≥2,所以当x=,即x=时,函数y=x+的最小值为2.阅读理解上述内容,解答下列问题:问题1:已知一个矩形的面积为4,其中一边长为x,则另一边长为,周长为2(x+),求当x=时,周长的最小值为;问题2:已知函数y1=x+1(x>﹣1)与函数y2=x2+2x+10(x>﹣1),当x=时,的最小值为;问题3:某民办学校每天的支出总费用包含以下三个部分:一是教职工工资4900元;二是学生生活费成本每人10元;三是其他费用.其中,其他费用与学生人数平方成正比,比例系数为0.01.当学校学生人数为多少时,该校每天生均投入最低?最低费用是多少元?(生均投入=支出总费用÷学生人数)参考答案一选择题1.B;2.B;3.A;4.C;5.D;6.D;7.B;8.D;9.B;10.B;11.C;12.D 二.填空题13.;14.;15.2;16.16;17.26;18.k≥1;19.3;20.;三.解答题21.解:(1)∵原方程有两个不相等的实数根,∴△=(2k+1)2-4(k2+1)=4k2+4k+1-4k2-4=4k-3>0,+x2=-(2k+1)<0,又∵x1•x2=k2+1>0,∴x1<0,x2<0,解得:k>3/4;(2)∵k>3/4,∴x1∴PD/PC=PA/PD ,设OA=x ,∴PA=x ,PO=2x ,∴4/2X=X/4,∴2x =16,x=22,∴OA=2226.解:(1)画树状图:列表: (2,第二次第一次x 2+1-x 2-23 x 2+11222+--x x 132+x -x 2-22122--+x x 232--x 3 312+x 322--x。
初四数学测试题及答案

初四数学测试题及答案测试题:1. 某商店以原价售卖商品,现在打8.5折出售。
如果一件商品原价100元,打折后的价格是多少?2. 小明用一根长度为12厘米的铁丝做了一个正方形,求这个正方形的面积。
3. 某班级共有30名同学,其中男生占总人数的40%。
女生人数是男生人数的3倍。
那么女生人数是多少?4. 一辆汽车以每小时80公里的速度行驶,如果行驶5小时,总共行驶了多少公里?5. 某书店共有480本书,其中2/5是故事书。
那么故事书的数量是多少?答案:1. 打折后价格 = 原价 ×折扣打折后价格 = 100元 × 0.85 = 85元所以,打折后的价格是85元。
2. 正方形的边长 = 铁丝总长度 ÷ 4正方形的边长 = 12厘米 ÷ 4 = 3厘米正方形的面积 = 边长 ×边长正方形的面积 = 3厘米 × 3厘米 = 9平方厘米所以,这个正方形的面积是9平方厘米。
3. 男生人数 = 总人数 ×男生比例男生人数 = 30人 × 0.4 = 12人女生人数 = 男生人数 × 3女生人数 = 12人 × 3 = 36人所以,女生人数是36人。
4. 总行驶公里数 = 速度 ×时间总行驶公里数 = 80公里/小时 × 5小时 = 400公里所以,总共行驶了400公里。
5. 故事书的数量 = 全部书的数量 ×故事书比例故事书的数量 = 480本 × 2/5 = 192本所以,故事书的数量是192本。
以上是初四数学测试题及答案,希望对你的学习有所帮助。
初四期末考试数学试卷

一、选择题(每题5分,共25分)1. 下列各数中,绝对值最小的是()A. -3B. 2C. -1.5D. 0.52. 已知a > b,下列不等式中正确的是()A. a - b > 0B. a + b > 0C. a - b < 0D. a + b < 03. 在△ABC中,若∠A = 60°,∠B = 45°,则∠C的度数是()A. 75°B. 105°C. 120°D. 135°4. 下列函数中,是反比例函数的是()A. y = 2x + 3B. y = 3/xC. y = x^2D. y = √x5. 下列图形中,是轴对称图形的是()A. 等腰三角形B. 平行四边形C. 梯形D. 长方形二、填空题(每题5分,共25分)6. 已知a = -3,b = 2,则a + b = ________。
7. 下列方程中,x = 2是它的解的是()A. 2x - 1 = 3B. 2x + 1 = 3C. 2x - 1 = 1D. 2x + 1 = 18. 若sinθ = 1/2,则cosθ的值是 ________。
9. 下列数中,有理数是 ________。
10. 若x^2 - 5x + 6 = 0,则x的值为 ________。
三、解答题(共50分)11. (15分)解下列方程组:\[\begin{cases}2x + 3y = 8 \\x - y = 1\end{cases}\]12. (15分)已知函数y = -2x + 5,求以下问题:(1)当x = 3时,y的值为多少?(2)当y = -1时,x的值为多少?13. (20分)已知直角三角形ABC中,∠A = 90°,∠B = 30°,∠C= 60°,AB = 6cm,求:(1)BC的长度;(2)AC的长度;(3)三角形ABC的面积。
初四数学试题

初四数学试题一、选择题1、-2017的倒数的相反数是()A.-2017 B.-1/2017 C.2017 D.1/20172、下列四个选项中,计算结果最大的是()A.(-6)0 B.|-6| C.-6 D.1/63、关于▱ABCD的叙述,正确的是()A.若AB⊥BC,则▱ABCD是矩形;B.若AC⊥BD,则▱ABCD是正方形;C.若AC=BD,则▱ABCD是矩形;D.若AB=AD,则▱ABCD是正方形;4、下列运算正确的是()A.3a+2b=5abB.5y-2y=3C.6xy2-2xy2=4xy2D.-(a+b)+(c+d)=-a-b-c+d5、下列说法正确的是()A.4是无理数B.16的平方根是±4C.0的相反数是0D.-0.5的倒数是26、某企业今年3月份产值为a万元,4月份比3月份减少了10%,5月份比4月份增加了15%,则5月份产值是()万元7A8、如图,四边形ABCD中,AB=CD,对角线AC,BD相交于点O,AE⊥BD 于点E,CF⊥BD于点F,连接AF,CE,若DE=BF,则下列结论:①CF=AE;②OE=OF;③四边形ABCD是平行四边形;④图中共有四对全等三角形.其中正确结论的个数是()A.4B.3C.2D.19、已知四边形ABCD是平行四边形,对角线AC、BD交于点O,E是BC的中点,以下说法错误的是()A.OE=0.5DCB.OA=OCC.∠BOE=∠OBAD.∠OBE=∠OCE10、在一条笔直的公路上,依次有A、C、B三地.小明从A地途经C地前往距A地20千米的B地,到B地休息一段时间后立即按原路返回到A地.小明出发4小时的时候距离A地12千米.小明去时从C地到B地,返回时再由B地到C 地(包括在B地休息的时间)共用2小时.他与A地的距离s(单位:千米)和所用的时间t(单位:小时)之间的函数关系如图所示.下列说法:①小明去时的速度为10千米/时;②小明在B地休息了2/3小时;③小明回来时的速度为6千米/时;④C地与A地的距离为15千米,其中正确的个数为()A.1个B.2个C.3个D.4个7题图8题图9题图10题图11、如图,正方形ABCD的边长为4,P为正方形边上一动点,运动路线是A→B→C→D→A,设P点经过的路程为x,以点A、P、B为顶点的三角形的面积是y,则下列图象能大致反映y与x的函数关系的是()A.B.C.D.12、如图△ABC 内接于⊙O, AD ⊥BC, OE ⊥BC, OE=0.5BC.将△ACD 沿AC 折叠为△ACF,将△ABD 沿AB 折叠为△ABG ,延长FC 和GB 相交于点H .①∠BAC=45o ; ②四边形AFHG是正方形;③BC=BG+CF ;④若BD=6,CD=4,则AD=10. 以上说法正确的有( )A .4个B .3个C .2个D .1个 二、填空题13、在Rt △ABC 中,∠C=90°,AC=53,AB=10,则∠A=_________14、已知抛物线y=ax 2+bx+c 过(-1,1)和(5,1)两点,那么抛物线的对称轴是_____15、已知关于x 的不等式组⎩⎨⎧+->+>+5)2(32)(324x x a x x 仅三个整数解,则a 取值范围是_____ 16、如图,在菱形ABCD 中,AB=4,线段AD 的垂直平分线交AC 于点N ,△CND 的周长是10,则AC 的长为_________17、如图,在△ABC 中,∠C=90°,AC=8,BC=6,D 是边AB 的中点,现有一点P 位于边AC 上,使得△ADP 与△ABC 相似,则线段AP 的长为 _______18、在▱ABCD 中,对角线AC 与BD 相交于点O ,若AC=8,BD=6,则边长AB 的取值范围是_______________________16题图17题图18题图19、若关于x 的一元二次方程kx 2+2x-1=0有两个实数根,则k 的取值范围_______20、中百超市推出如下优惠方案:(1)一次性购物不超过100元,不享受优惠;(2)一次性购物超过100元,但不超过300元一律9折;(3)一次性购物超过300元一律8折.某人两次购物分别付款80元、252元,如果他将这两次所购商品一次性购买,则应付款____________元21、在△ABC 中,AB=13cm,AC=20cm,BC 边上高为12cm,则△ABC 的面积是____22、已知点A(-4,0),B(2,0).若点C 在直线y=0.5x+2上,且△ABC 是直角三角形,则点C 的个数是_______三、23、(1)计算︒⋅-+︒︒+︒30tan 3160sin 230cos 45cos 2(2)先化简再求值112)12(22-+-÷+-a a a a a a 其中0232=+-a a 、24、已知a+b=3,ab=2,求代数式a 3b+2a 2b 2+ab 3的值25、已知关于x 的一元二次方程x 2-6x+(2m+1)=0有实数根.(1)求m 取值范围.(2)如果方程的两个实数根为x 1,x 2,求2x 1x 2+x 1+x 2≥20,求m 取值范围.26、如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函y=m/x(m≠0)的图象交于第二象限内的A、B两点,与x轴交于点C.已知OA=5,tan∠AOC=3/4,点B纵坐标为6.(1)求反比例函数和一次函数的解析式;(2)求△AOB的面积;(3)根据图象直接写出不等式kx+b>m/x解集.27、某家电销售商场电冰箱的销售价为每台1600元,空调的销售价为每台1400元,每台电冰箱的进价比每台空调的进价多300元,商场用10000元购进电冰箱的数量与用8000元购进空调的数量相等.(1)求每台电冰箱与空调的进价分别是多少?(2)现在商场准备一次购进这两种家电共100台,设购进电冰箱x台,这100台家电的销售总利润为y元,要求购进空调数量不超过电冰箱数量的2倍,总利润不低于16200元,请分析合理的方案共有多少种?(3)实际进货时,厂家对电冰箱出厂价下调k(0<k<150)元,若商店保持这两种家电的售价不变,请你根据以上信息及(2)中条件,设计出使这100台家电销售总利润最大的进货方案.28、已知:如图,△ABC内接于⊙O,AB为直径,∠CBA的平分线交AC于点F,交⊙O于点D,DE⊥AB于点E,且交AC于点P,连结AD.(1)求证:∠DAC=∠DBA;(2)求证:P是线段AF的中点;(3)连接CD,若CD﹦3,BD﹦4,求⊙O的半径和DE的长.时,从B测得小船在北偏西15°方向,求小船沿途考察的时间.30、如图已知抛物线y=-0.25x+bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知B点的坐标为B(8,0).(1)求抛物线的解析式及其对称轴方程;(2)连接AC、BC,试判断△AOC与△COB是否相似?并说明理由;(3)M为抛物线上BC之间的一点,N为线段BC上的一点,若MN∥y轴,求MN的最大值;(4)在抛物线的对称轴上是否存在点Q,使△ACQ为等腰三角形?若存在,求出符合条件的Q点坐标;若不存在,请说明理由.1. D2. B3. C4. C5. C6. C 7解:延长BA交x轴于点D,∵四边形OABC是菱形,且C(0,2),∴OA=OC=AB=2,BA⊥x轴,∵∠AOC=60°,∴∠AOD=30°,∴AD=0.5OA=1,∴OD=3,∴BD=AB+AD=3,∴点B(3,3),∵双曲线y=k/x经过B点,∴k=xy=33.故选B8解:∵DE=BF,∴DF=BE,在Rt△DCF 和Rt△BAE中,CD=AB,DF=BE,∴Rt△DCF≌Rt△BAE(HL),∴FC=EA,故①正确;∵AE⊥BD于点E,CF⊥BD于点F,∴AE∥FC,∵FC=EA,∴四边形CFAE是平行四边形,∴EO=FO,故②正确;∵Rt△DCF≌Rt△BAE,∴∠CDF=∠ABE,∴CD∥AB,∵CD=AB,∴四边形ABCD是平行四边形,故③正确;可得出△CDF≌△BAE,△CDO≌△BAO,△CDE≌△BAF,△CFO≌△AEO,△CEO≌△AFO,△ADF≌△CBE等.故④图中共有四对全等三角形错误.故正确的有3个.故选:B.(3)当厂家对电冰箱出厂价下调k(0<k<150)元,则Y=(1600-1500+k)x+(1400-1200)(100-x)=(k-100)x+20000,①当k-100>0时,即100<k<150时,Y随x的增大而增大;∴当x=38时,Y 最大,②当k-100<0时,即0<k<100时,Y随x的增大而减小;∴当x=34时,Y最大,∵DE×AB=AD×BD,∴5DE=3×4,∴DE=2.4.即DE的长为2.4282930解(1)如图过点P作PD⊥AB于点D.在Rt△PBD中,∠BDP=90°,∠PBD=90°-45°=45°,∴BD=PD=3千米.在Rt△PAD中,∠ADP=90°,∠PAD=90°-60°=30°,∴AD=3PD=33千米,PA=6千米.∴AB=BD+AD=3+33千米;(2)如图,过点B作BF⊥AC于点F.根据题意得:∠ABC=105°,在Rt△ABF中,∠AFB=90°,∠BAF=30°,∴BF=0.5AB=(3+33)/2千米,AF=3/2AB=3+3 千米.在△ABC中,∠C=180°-∠BAC-∠ABC=45°.在Rt△BCF中,∠BFC=90°,∠C=45°,∴CF=BF=(3+33)/2千米,∴PC=AF+CF-AP=33千米.故小船沿途考察的时间为:33÷3=3(小时).30解:(1)∵点B(8,0)在抛物线y=-0.25x2+bx+4上,∴-0.25×64+8b+4=0,解得b=1.5,∴抛物线的解析式为y=-0.25x2+1.5x+4,对称轴为直线x==3;(2)△AOC∽△COB.理由如下:令y=0,则-0.25x2+1.5x+4=0,即x2-6x-16=0,解得x1=-2,x2=8,∴点A的坐标为(-2,0),令x=0,则y=4,∴点C的坐标为(0,4),∴OA= 2,OB=8,OC=4,∵OC/OA=OB/OC=2,∠AOC=∠COB=90°,∴△AOC∽△COB;(3)设直线BC的解析式为y=kx+b,则8k+b=0,b=4,解得k=-0.5,被,∴直线BC的解析式为y=-0.5x+4,∵MN∥y轴,∴MN=-0.25x2+1.5x+4-(-0.5x+4)=-0.25x2+1.5x+4+0.5x-4=-0. 25x2+2x=-0.25(x-4)2+4,∴当x=4时,MN的值最大,最大值为4;(4)由勾股定理得,AC=25,过点C作CD⊥对称轴于D,则CD=3,①AC=CQ时,DQ= 11,点Q在点D的上方时,点Q到x轴的距离为4+11,此时点Q1(3,4+11),点Q 在点D的下方时,点Q到x轴的距离为4-11,此时点Q2(3,4-11),②点Q为对称轴与x轴的交点时,AQ=5,CQ=22+42=5,∴AQ=CQ,此时,点Q3(3,0),综上所述,点Q的坐标为(3,4+11)或(3,4-11)或(3,0)时,△ACQ为等腰三角形时.。
初四中考题数学试卷

考试时间:120分钟总分:150分一、选择题(本大题共20小题,每小题3分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
)1. 下列各组数中,成等差数列的是()A. 2, 4, 8, 16B. 1, 3, 5, 7C. 3, 6, 12, 24D. 5, 10, 20, 402. 已知函数y = kx + b(k ≠ 0),若k > 0,则函数图象()A. 从左到右上升B. 从左到右下降C. 上下波动D. 无固定方向3. 在直角坐标系中,点A(2,3)关于y轴的对称点是()A. (-2,3)B. (2,-3)C. (-2,-3)D. (2,3)4. 已知等边三角形ABC的边长为a,则其面积S为()A. a²/2B. √3a²/2C. 3a²/2D. 2√3a²/35. 若sinα = 1/2,且α在第二象限,则cosα的值为()A. √3/2B. -√3/2C. 1/2D. -1/26. 下列函数中,有最小值的是()A. y = x²B. y = -x²C. y = x³D. y = -x³7. 若方程2x² - 4x + 3 = 0的两根为a和b,则a + b的值为()A. 2B. 1C. 0D. -18. 在等腰三角形ABC中,底边BC = 6cm,腰AB = AC = 8cm,则顶角A的度数为()A. 30°B. 45°C. 60°D. 90°9. 下列命题中,正确的是()A. 等腰三角形的底角相等B. 所有直角三角形都是等腰三角形C. 等边三角形一定是等腰三角形D. 等腰三角形的腰长一定相等10. 已知数列{an}的通项公式为an = 2n - 1,则数列的第10项是()A. 19B. 20C. 21D. 2211. 在平面直角坐标系中,点P(-2,3)关于原点的对称点是()A. (-2,-3)B. (2,-3)C. (2,3)D. (-2,3)12. 已知等差数列{an}的前三项分别为1,4,7,则该数列的公差是()A. 1B. 2C. 3D. 413. 若sinα = 3/5,且α在第三象限,则cosα的值为()A. -4/5B. -3/5C. 4/5D. 3/514. 下列函数中,有最大值的是()A. y = x²B. y = -x²C. y = x³D. y = -x³15. 若方程x² - 6x + 9 = 0的两根为a和b,则a² + b²的值为()A. 12B. 18C. 24D. 3016. 在等腰三角形ABC中,底边BC = 8cm,腰AB = AC = 10cm,则顶角A的度数为()A. 30°B. 45°C. 60°D. 90°17. 下列命题中,正确的是()A. 等腰三角形的底角相等B. 所有直角三角形都是等腰三角形C. 等边三角形一定是等腰三角形D. 等腰三角形的腰长一定相等18. 已知数列{an}的通项公式为an = 3n - 2,则数列的第7项是()A. 19B. 20C. 21D. 2219. 在平面直角坐标系中,点P(2,-3)关于x轴的对称点是()A. (2,3)B. (-2,-3)C. (-2,3)D. (2,-3)20. 已知等差数列{an}的前三项分别为3,6,9,则该数列的公差是()A. 1B. 2C. 3D. 4二、填空题(本大题共10小题,每小题3分,共30分。
初四数学试题

初四数学期末试题选择题(本大题共10小题,每小题3分,共30分)1.与21互为倒数的是 ( ) A.-2 B .-21 C .21 D .2 2. 2010年5月27日,上海世博会参观人数达到37.7万人,37.7万用科学记数法表示应为( )A.0.377×106B.3.77×105C.3.77×104D.377×1033. 函数y=中自变量x 的取值范围是( ) A.x≥-3 B.x≥-3且x ≠1 C.x≠1 D.x≠-3且x≠14.下列运算结果正确的是( )A .2a aB .a 2•a 3=a 6C .a 2•a 3=a 5D .a 2+a 3=a 65. 已知关于x 的分式方程+=1的解是非负数,则m 的取值范围是( )A.m >2B.m≥2C.m≥2且m≠3D.m >2且m≠36. 正n 边形每个内角的大小都为108°,则n =( )A .5B .6C .7D .87. 一元一次不等式组的解集在数轴上表示正确的是( ) A. B. C. D.8.如图,已知AB 是⊙O 的直径,CD 是弦且CD⊥AB,BC=6,AC=8,则sin∠ABD的值是( )A. B. C. D.9.小丽早上从家出发骑车去上学,途中想起忘了带昨天晚上完成的数学作业,于是打电话让妈妈马上从家里送来,同时小丽也往回骑,遇到妈妈后停下说了几句话,接着继续骑车去学校.设小丽从家出发后所用时间为t ,小丽与学校的距离为S .下面能反映S 与t 的函数关系的大致图象是()A. B. C. D.10. 若不等式ax+x>1+a的解集是x<1,则a必须满足的条件是()A.a<-1B.a<1C.a>-1D.a>111.参加一次商品交易会的每两家公司之间都签订了一份合同,所有公司共签订了45份合同.设共有x家公司参加商品交易会,则x满足的关系式为()A.x(x+1)=45B.x(x-1)=45C.x(x+1)=45D.x(x-1)=4512如图所示,抛物线y=ax2+bx+c的顶点为B(-1,3),与x轴的交点A在点(-3,0)和(-2,0)之间,以下结论:①b2-4ac=0;②a+b+c>0;③2a-b=0;④c-a=3其中正确的有()个.A.1B.2C.3D.4填空题(本大题共6小题,每小题3分,共18分)13. 把多项式9a3-ab2分解因式的结果是______ .14.已知扇形的半径为4cm,圆心角为120°,则扇形的弧长为______cm.15.二次函数y=(x+2)2-1向左、下各平移2个单位,所得的函数解析式为______ .16.若a,b,c表示△ABC的三边,且(a-3)2++|c-5|=0,则△ABC是______三角形.17.如果实数x,y满足方程组,则x2-y2的值为______.18.如图,AB为半圆的直径,且AB=4,半圆绕点B顺时针旋转45°,点A旋转到A′的位置,则图中阴影部分的面积为______解答题(本大题共8小题,共66分)19.(5分)计算:2sin30°+(π-3.14)0+|1-|+(-1)2017.20.(5分)先化简,再求值(1—2x 1+)÷212x 2+++x x 其中x =1-321.(8分)已知关于x 的一元二次方程x 2+(2k+3)x+k 2=0有两个不相等的实数根x 1,x 2.(1)求k 的取值范围; (2)若+=﹣1,求k 的值.22.(6分)如图,哨兵在灯塔顶部A 处测得遇难船只所在地B 处的俯角为60°,然后下到灯塔的C 处,测得B 处的俯角为30°.已知AC=40米,若救援船只以5m/s 的速度从灯塔底部D 处出发,几秒钟后能到达遇难船只的位置?(结果精确到个位).23.(8分)如图,已知一次函数y=k 1x+b (k 1≠0)的图象分别与x轴,y 轴交于A ,B 两点,且与反比例函数y=(k 2≠0)的图象在第一象限的交点为C ,过点C 作x 轴的垂线,垂足为D ,若OA=OB=OD=2(1)求一次函数的解析式;(2)求反比例函数的解析式.24.(8分) 雅安地震灾情牵动全国人民的心.某厂计划加工1500顶帐篷支援灾区,加工了300顶帐篷后,由于救灾需要,将工作效率提高到原计划的2倍,结果提前4天完成了任务.求原计划每天加工多少顶帐篷?25.(本题8分)不透明的袋子中装有红色小球1个、绿色小球2个,除颜色外无其他差别.(1)随机摸出一个小球后,放回并摇匀,再随机摸出一个,用列表或画村状图的方法求出“两球都是绿色”的概率;(2)随机摸出两个小球,求两次都是绿球的概率.26.(8分)如图,在△ABC中,AB=AC,以AB为直径作⊙O,交BC于点D,过点D作DE⊥AC,垂足为E.(1)求证:DE是⊙O的切线;(2)如果BC=8,AB=5,求CE的长.27.(10分)如图,抛物线y=﹣x2+bx+c与直线y= x+3交x轴负半轴于点A,交y 轴于点C,交x轴正半轴于点B.(1)求抛物线的解析式;(2)点P为抛物线上任意一点,设点P的横坐标为x.①若点P在第二象限,过点P作PN⊥x轴于N,交直线AC于点M,求线段PM关于x 的函数解析式,并求出PM的最大值;②若点P是抛物线上任意一点,连接CP,以CP为边作正方形CPEF,当点E落在抛物线的对称轴上时,请直接写出此时点P的坐标.答案一选择(共30分)1.D2.B3. B4.C5. C6.A7. C8. D9. B 10. A 11. B 12. B二填空(共30分)13. 3 14 38 π 15y=(x+4)2-3 16.直角 17. - 18 2π 三解答题19. a (3a+b )(3a-b )20. 原式=1x 1 =33 21解:(1)∵关于x 的一元二次方程x 2+(2k+3)x+k 2=0有两个不相等的实数根, ∴△=(2k+3)2-4k 2>0,解得:k >-.(2)∵x 1、x 2是方程x 2+(2k+3)x+k 2=0的实数根,∴x 1+x 2=-2k-3,x 1x 2=k 2,∴+==-=-1,解得:k 1=3,k 2=-1,经检验,k 1=3,k 2=-1都是原分式方程的根.又∵k >-,∴k=3.22.解:在Rt △BCD 中∵∠BCD=90°-30°=60°,∴,则BD=.在Rt △ABD 中,∵∠ABD=60°,∴.即 解得:CD=20.∴t=s .故约7s 后能到达遇难船只的位置.23解:(1)∵OA=OB=2,∴A (﹣2,0),B (0,2),将A 与B 代入y=k 1x+b 得:,解得:,则一次函数解析式为y=x+2;(2)∵OD=2,∴D(2,0),∵点C在一次函数y=x+2上,且CD⊥x轴,∴将x=2代入一次函数解析式得:y=2+2=4,即点C坐标为(2,4),∵点C在反比例图象上,∴将C(2,4)代入反比例解析式得:k2=8,则反比例解析式为y=.24.解:设原计划每天加工x顶帐篷,提高效率后每天加工的帐篷是2x顶,由题意,得,解得:x=150.经检验,x=150是原方程的解,且符合题意.答:原计划每天加工150顶帐篷.25.26.解:(1)连接OD,∵OD=OB(⊙O的半径),∴∠B=∠ODB(等边对等角);∵AB=AC(已知),∴∠B=∠C(等边对等角);∴∠C=∠ODB(等量代换),∴OD∥AC(同位角相等,两直线平行),∴∠ODE=∠DEC(两直线平行,内错角相等);∵DE⊥AC(已知),∴∠DEC=90°,∴∠ODE=90°,即DE⊥OD,∴DE是⊙O的切线;(2)连接AD,∵AB是⊙O的直径,∴∠ADB=90°(直径所对的圆周角是直角);∴AD⊥CD;在Rt△ACD和Rt△DCE中,∠C=∠C(公共角),∠CED=∠CDA=90°,∴Rt△ACD∽Rt△DCE(AA),∴=;又由(1)知,OD∥AC,O是AB的中点,∴OD是三角形ABC的中位线,∴CD=BC;∵BC=8,AB=5,AB=AC,∴CE=.27.解:(1)当x=0时,y=x+3=3,则C(0,3);当y=0时,x+3=0,解得x=-4,则A(-4,0),把A(-4,0),C(0,3)代入y=-x2+bx+c得,解得,∴抛物线解析式为y=-x2-x+3;(2)①设P(x,-x2-x+3)(-4<x<0),则M(x,x+3),∴PM=-x2-x+3-(x+3)=-x2-x=-(x+2)2+当x=-2时,线段PM的长有最大值,最大值为;②作PK⊥y轴于K,交抛物线的对称轴于G,如图,∵四边形PEFC为正方形,∴PE=PC,∠EPC=90°∵∠PGE=∠PKC=90°,∴∠PEG=∠CPK,易得△PEG≌△CPK,∴CK=PG,设P(x,-x2-x+3),抛物线的对称轴为直线x=-1,则G(-1,-x2-x+3),K(0,-x2-x+3),∴PG=|-1-x|=|x+1|,CK=|-x2-x+3-3|=|-x2-x|,∴|x+1|=|-x2-x|,解方程x+1=-x2-x得x1=-4,x2=-;解方程x+1=x2+x得x1=2,x2=-;∴P点坐标为(-4,0)或(-,)或(2,0)或(-,).。
初四数学试题及答案

初四数学试题及答案一、选择题(每题2分,共20分)1. 下列哪个选项不是有理数?A. πB. -3C. 0.5D. √42. 如果一个数的平方等于它本身,那么这个数可能是:A. 1B. -1C. 0D. 以上都是3. 一个圆的直径是10厘米,那么它的半径是:A. 5厘米B. 10厘米C. 20厘米D. 15厘米4. 以下哪个表达式是正确的?A. (-2)^2 = -4B. √16 = 4C. (-3)^3 = -27D. √9 = -35. 如果a > b,且b > 0,那么下列哪个不等式是正确的?A. a + b < bB. a - b > 0C. a * b < 0D. a / b < 16. 下列哪个是二次根式?A. √2xB. 3x + 2C. 4x^2D. 5x^37. 一个三角形的三边长分别为3, 4, 5,这个三角形是:A. 等边三角形B. 等腰三角形C. 直角三角形D. 钝角三角形8. 一个数的绝对值是其本身,这个数可能是:A. 正数B. 负数C. 零D. 以上都是9. 以下哪个表达式是正确的?A. 2x + 3y = 5xB. 3x - 2y = 5x + 2yC. 4x^2 - 9y^2 = (2x + 3y)(2x - 3y)D. x^2 - y^2 = (x + y)(x - y)10. 一个数的倒数是1/4,这个数是:A. 4B. 1/4C. 1/2D. 4/1二、填空题(每题2分,共20分)11. 如果一个数的相反数是-5,那么这个数是________。
12. 一个数的立方等于它本身,这个数可能是________、________、________。
13. 一个数的平方根是4,那么这个数是________。
14. 如果a + b = 10,且a - b = 2,那么2a的值是________。
15. 一个圆的周长是2πr,其中r是圆的半径,如果周长是12.56厘米,那么半径是________。
初四数学试题

初四数学试卷一、相信你的选择(每小题4分,共48分)1. 计算:ο45cos 2+ο60tan •ο30cos 等于( ) A. 1 B. 2 C. 2 D. 32.二次函数221y ax x a =++-的图象可能是( )3. 在△ABC 中,∠C =90°,tanA =31,则sinB =( )A.1010 B. 32 C.43D.101034. 一周日,王浩从家沿北偏西60ο方向走了100m 到李明家,约他一起上正南方向200m 的王辉家做作业,那王浩和王辉家的距离是( ) A.150m B.503m C.100m D.1003m5. 已知二次函数2(0)y ax bx c a =++≠的最大值为0,则( )A.a >0,ac b 42-=0B.a <0,ac b 42->0C. a >0,ac b 42-<0D. a <0,ac b 42-=0 6. 如图1,△ABC 的顶点都是正方形网格中的格点,则sin ∠ABC 等于(A. 5B. 552C. 55D. 327. 如图2是二次函数c bx ax y ++=2图象的一部分,图象过点A (-3,0),对称轴为x =-1.给出四个结论:①2b >ac 4;②02=+b a ;③0=+-c b a ;④5a <b .其中正确结论是( ). (A )②④ (B )①④ (C )②③ (D )①③ 8. 若抛物线c x x y +-=22与y 轴的交点为(0,-3),则下列说法不正确的是( ). A. 抛物线开口向上 B. 抛物线的对称轴是1=x C. 当1=x 时,y 有最大值为-4 D. 抛物线与x 轴的交点为(-1,0),(3,0) 9 A 、B 为Rt△ABC 的两锐角,∠C=90°,则有( )。
(A )sinA =sinB (B )cosA =cosB (C )sinB =cosC (D )sinA =cosB10、准备在坡角为α的山坡上栽树,要求相邻两树之间的水平距离为5米,那么这两树在坡面上的距离AB 为( )A . αcos 5B . αcos 5C . αsin 5D . αsin 511. 抛物线(1)(3)(0)y a x x a =+-≠的对称轴是直线( ) A .1x = B .1x =- C .3x =- D .3x =12、二次函数2y a x b x c =++的图象如图所示,则一次函数24y bx b ac =+-与反比例函数a b c y x++=在同一坐标系内的图象大致为( )A B C D 图1 图2二、试试你的身手(每小题4分,共40分)11. 一段铁路路基横断面为一个等腰梯形,若腰的坡度为i =2∶3,顶宽是3米,路基高是4米,则路基的下底宽是 .12..在二次函数c bx ax y ++=2中,函数y 与自变量x 的部分对应值如下表:x 2- 1- 0 1 2 3 4y 7 2 1- 2- m 27 则m 的值为 .13. 在平面直角坐标系中,先将抛物线22y x x =+-关于x 轴作轴对称变换,再将所得的抛物线关于y 轴作轴对称变换,那么经两次变换后所得的新抛物线的解析式为 . 14. 已知△ABC 中,∠C =90ο,3cos B =2,AC =52,则AB = .15. 如图5为二次函数c bx ax y ++=2的图象,在下列说法中:①ac <0; ②方程02=++c bx ax 的根是11-=x ,32=x ;③c b a ++>0 ;④当x >1时,y 随x 的增大而增大.正确的说法有_____________.(把正确的答案的序号都填在横线上) 16. 计算tan60ο+2sin45ο-2cos30ο= .17. 小刚身高1.7m ,测得他站立在阳光下的影子长为0.85m ,紧接着他把手臂竖直举起,测得影子长为1.1m ,那么小刚举起的手臂超出头顶 .18.将抛物线2(0)y ax bx c a =++≠向下平移3个单位,再向左平移4个单位得到抛物线2245y x x =--+,则原抛物线的顶点坐标是 .19.如图6,一游人由山脚A 沿坡角为30ο的山坡AB 行走600m ,到达一个景点B , 再由B 沿山坡BC 行走200m 到达山顶C ,若在山顶C 处观测到景点B 的俯角为45ο,则山高CD等于(结果用根号表示)20. 在平面直角坐标系中,已知一次函数(0)y kx b k =+≠的图象过点P (1,1),与x 轴交于点A ,与y 轴交于点B,且tan ∠ABO =3,那么点A 的坐标是 . 三、解答题(本大题共62分)21.(本小题6分)如图7,在△ABC 中,∠C =90ο,点D 、E 分别在AC 、AB 上,BD 平分∠ABC ,DE ⊥AB ,AE =6,cos A =53. 求:(1)DE 、CD 的长;(2)tan ∠DBC 的值.A B C D 图6 图7xxxx22. (本小题8分)某超市经销一种绿茶,每千克成本为50元.市场调查发现,在一段时间内,销售量w (千克)随销售单价x (元/千克)的变化而变化,具体关系式为:2402+-=x w .设这种绿茶在这段时间内的销售利润为y (元),解答下列问题:(1)求y 与x 的关系式;(2)当销售单价为多少元时,公司在这段时间内获得的利润最大? (3)如果物价部门规定这种绿茶的销售单价不得高于90元/千克,公司想要在这段时间内获得2250元的销售利润,销售单价应定为多少元?23.(本小题6分)如图8,学习了《测量物体的高度》后,老师带领同学们测量教学楼的高度,现提供测角仪和皮尺两种测量工具,请你设计一种测量方案,测出教学楼顶端A 到水平地面的距离AB .要求:(1)画出测量示意图;(2)写出测量步骤(测量数据用字母表示); (3)根据(2)中的数据计算楼高AB .24.(本小题8分)王慧家要在一面墙上开凿一个矩形窗户,.现准备了9.5米长的铝合金条,制成如图9所示的窗框.设窗户的宽为x 米,窗户的透光面积为y 平方米. (铝合金条的宽度忽略不计) (1)求窗户的透光面积y 与窗户的宽x 之间的函数关系式;(2)如果墙面的高度为2.8米,设计的透光面积为3平方米,请你计算出窗户的宽和高.25. (本小题6分)如图10所示,点P 表示广场上的一盏照明灯.(1)请你在图中画出小敏在照明灯P 照射下的影子(用线段表示);(2)若小丽到灯柱MO 的距离为4.5米,照明灯P 到灯柱的距离为1.5米,小丽目测照明灯P 的仰角为55°,她的目高QB 为1.6米,试求照明灯P 到地面的距离(结果精确到0.1米).0.5 图9图8(参考数据:tan 55 1.428≈°,sin 550.819≈°,cos550.574≈°)26.(本小题8分)愚溪桥主桥拱为抛物线型,桥身横跨愚溪,面临潇水,桥下冬暖夏凉,常有渔船停泊桥下避晒纳凉.已知在正常水位下测得主拱宽24m ,最高点离水面8m.请你解决下列问题: (1)求此桥拱线所在抛物线的解析式;(2)桥边有一浮在水面部分高4m ,最宽处122m 的河鱼餐船,试探索此船能否开到桥下?说明理由.27.(10分)如图11,抛物线2y x bx c =+-经过直线3y x =-与坐标轴的两个交点A ,B ,此抛物线与x 轴的另一个交点为C ,抛物线的顶点为D . (1)求此抛物线的解析式;(2)若点P 为抛物线上的一个动点,问是否存在使:5:4APC ACD S S =△△的点P ?若存在, 求出P 点的坐标;若不存在,请说明原因.28.(10分)太阳光线与水平线的夹角在一年中的变化较大,夏至时夹角最大,冬至时夹角最小,最小夹角约为30ο.现有两幢居民住宅楼高为15米,两楼相距20米,如图12所示. (1)在冬至时,甲楼的影子在乙楼上有多高?(2)若在本小区内继续兴建同样高的住宅楼,楼距至少应该多少米,才不影响楼房的采光(前一幢楼房的影子不能落在后一幢楼房上)?(计算结果精确到0.1米)图12O B Q P M55 4.5米 李艳宋兵 图10A图11参考答案一、选择题:1~6 C B D D D C 7~12 B C D B A D 二、填空题11、15米 12、-1 13、y=-x ²+x-2 14、6 15、①②④ 16、2 17、0.5m 18、(3,10)19、(300+1002)m 20、(-2,0)或(4,0) 三、解答题21、(1)在Rt △ADE 中,由AE =6,cos A =53,得AD =10,由勾股定理得DE =8.由角平分线的性质得:DC =DE =8.(2)由(1)得AC =18,又cos A =53=AB AC ,所以AB =30,. 由勾股定理得BC =24,所以tan ∠DBC =31.22、(1)120003402)2402()50()50(2-+-=+-⨯-=⋅-=x x x x w x y .即y 与x 的 关系式为:1200034022-+-=x x y ;(2)2450)85(212000340222+--=-+-=x x x y ,所以当销售单价定为85元时,公司在这段时间内获得的利润最大;(3)当2250=y 时,22502450)85(22=+--x .解得,751=x ,952=x .根据题意952=x 不和题意应舍去. 所以当销售单价为75元时,可获得销售利润2250元. 23、(1)测量图案(示意图)如图所示: (2)测量步骤: 第一步:在地面上选择点C 安装测角仪,测得楼顶A 的仰角∠AHE=α, 第二步:沿CB 前进到点D ,用皮尺量出C ,D 之间的距离CD=m , 第三步:在点D 安装测角仪,测得此时楼顶A 的仰角∠AFE=β, 第四步:用皮尺测出测角仪的高h .(3)计算:设AE =x ,tan HE x =α,tan EF x =β,∴αtan x HE =,βtan xEF =.∵HE -EF =m ,∴m x x =-βαtan tan ,解得αββαtan tan tan tan -⋅=m x ,∴AB =h m +-⋅αββαtan tan tan tan24、(1)由题意知,窗户的高为25.035.9--x 米,则x x y ⋅-=239,即x x y 29232+-=(0<x <3). (2)当y =3时,329232=+-x x ,解得11=x ,22=x .当1=x 时,3239=-x,而墙面的高度为2.8米,故不和题意,舍去;当2=x 时,5.1239=-x.所以如果设计的透光面积为3平方米,窗户的宽和高各为2米、1.5米. 25、(1)如图,连结P 点与小敏的头顶,并延长交地面于点C ,则线段AC 就是小敏的影子.(2)过点Q 作QE ⊥MO 于E ,过点P 作 PF ⊥OB 于F ,交EQ 于点D , 则PF ⊥EQ .在Rt △PDQ 中,PD =QD ×tan55ο =3×1.428≈4.3(米).因为DF =QB =1.6米,所以PF =5.9(米),即照明灯到地面的距离为5.9米.A E F H C DBC O B QD E P M 55 4.5米 李艳 宋兵 FA26、(1)如图所示,以正常水位水平线AB 为x 轴,AB 的中点O 为原点建立坐标系.由题意可知,抛物线顶点的坐标为C (0,8),因而可设抛物线所对应的函数关系式为82+=ax y ,又抛物线过点B (12,0),所以有0= a ×144+8,故18-=a ,所以抛物线的关系式为y =81812+-x ;(2)把26=x 代y =81812+-x得,48)26(1812=+-=y (米),因此时船浮在水面部分的高度为4米,所以从理论上讲,河鱼餐船刚好能驶入桥拱下纳凉. 四、附加题27、(1)易得直线3y x =-与坐标轴的交点坐标为A (3,0),B (0,-3),代入.2y x bx c =+-得 9303.b c c +-=⎧⎨-=-⎩,解得23.b c =-⎧⎨=⎩,所以此抛物线的解析式223y x x =--;(2)抛物线的顶点D (1,-4),与x 轴的另一个交点C (-1,0).设2(23)P a a a --,,则4:5)4421(:)324212=⨯⨯--⨯⨯a a (,化简得2235a a --=.当2235a a --=时,解得4a =或2a =-.所以P (4,5)或(-2,5);当2230a a --<时,即2220a a --+=,此方程无解.综上所述,满足条件的点的坐标为P (4,5)或(-2,5). 28、(1)作DE ⊥AB 于E ,由题意知∠ADE =30ο,DE =BC =20.在Rt △ADE 中,tan ∠ADE =DE AE ,所以AE =DE ×tan30ο=20×33≈11.5.则DC =BE =AB -AE =15-11.5=3.5.即冬至时甲楼的影子在乙楼上约3.5米高.(2)若要不影响要房间的采光,在Rt △ABC 中,AB =15,∠C =30ο,所以BC=ο30tan 15tan =C AB ≈26.0.即楼距至少28.2米,才不影响楼房的采光。
张店期末考试初四数学试卷

一、选择题(本大题共10小题,每小题3分,共30分)1. 下列各数中,不是有理数的是()A. 2.5B. -3/4C. √2D. 02. 若a、b是实数,且a+b=0,则下列等式中正确的是()A. a^2 = b^2B. a^2 = -b^2C. a^2 = b^2/2D. a^2 = -b^2/23. 已知一元二次方程x^2 - 5x + 6 = 0的解为x1、x2,则x1+x2的值为()A. 5B. -5C. 6D. -64. 在△ABC中,∠A=45°,∠B=60°,则∠C的度数为()A. 45°B. 60°C. 75°D. 90°5. 下列函数中,是反比例函数的是()A. y = x^2B. y = 2xC. y = 1/xD. y = 3x^26. 若a、b是实数,且a^2 + b^2 = 0,则a、b的值为()A. a=0,b=0B. a=0,b≠0C. a≠0,b=0D. a≠0,b≠07. 下列各图中,函数图象为正比例函数的是()A. B. C. D.8. 若等差数列{an}的首项为a1,公差为d,则第n项an=()A. a1 + (n-1)dB. a1 - (n-1)dC. a1 + ndD. a1 - nd9. 在△ABC中,若a=3,b=4,c=5,则△ABC是()A. 直角三角形B. 等腰三角形C. 等边三角形D. 一般三角形10. 下列各式中,正确的是()A. a^2 ≥ 0B. (a+b)^2 = a^2 + b^2C. (a-b)^2 = a^2 - b^2D.(a+b)(a-b) = a^2 - b^2二、填空题(本大题共10小题,每小题3分,共30分)11. 已知等差数列{an}的首项为2,公差为3,则第10项an=______。
12. 若a、b是实数,且a+b=5,ab=12,则a^2 + b^2的值为______。
初四数学月考试题

初四数学月考试题一、认真选一选(36分) 1、三角形的外心是()A .三条中线的交点B .三个内角的角平分线的交点C .三条边的垂直平分线的交点D .三条高的交点2、如图,⊙O 1的弦AB 是⊙O 2的切线,且AB ∥O 1O 2,如果AB=12cm ,那么阴影部分的面积为( )A .36πcm 2B .12πcm 2C .8πcm 2D .6πcm 23、二次函数y=kx2-6x+3的图象与x 轴有交点,则k 的取值范围是( ) A .k <3 B .k <3且k ≠0 C .k ≤3 D .k ≤3且k ≠04、已知反比例函数y=x k的图象如图所示,则二次函数y=2kx 2-x+k 2的图象大致为( )5、把二次函数y=x 2-2x-1的解析式配成顶点式为( )A .y=(x-1)2B .y=(x-1)2-2C .y=(x+1)2+1D .y=(x+1)2-2 6、有一实物如图,那么它的主视图是( )7、根据下列表格中二次函数y=ax 2+bx+c 的自变量x 与函数值y 的对应值,判断方程ax 2+bx+c=0(a≠0,a ,b ,c 为常数)的一个解x 的范围是( ) A .6<x <6.17 B .6.17<x <6.18C .6.18<x <6.19D .6.19<x <6.208、如图,A 是半径为2的⊙O 外的一点,OA=4,AB 是⊙O 的切线,点B 是切点,弦BC ∥OA ,则 弧BC 的长为( )A 、32πB 、38πC 、πD 、32π+39、二次函数y=x 2+bx+c 的图象上有两点(3,-4和(-5,-4),则此拋物线的对称轴是( ) A .直线x=4 B .直线x=3 C .直线x=-5 D .直线x=-110、在同一时刻,两根长度不等的竿子置于阳光之下,但看到它们的影长相等, 那么这两根竿子的相对位置是( )A .两竿都垂直于地面B .两竿平行斜插在地上C .两根竿子不平行D .一根竿倒在地上 11、如图,扇形OAB 的圆心角为90°,分别以OA ,OB 为直径在扇形内作 半圆,P 和Q 分别表示两个阴影( )A .P=QB .P >QC .P <QD .无法确定12、由n 个相同的小正方体搭成的几何体的视图如图所示,则搭成这个 几何体的个数是( )A.、4 B 、5 C 、6 D 、7 二、仔细填一填(18分)13、如图一个等边三角形的边长与它的一边相外切的圆的周长相等,当这个圆按箭头方向从某一位置沿等边三角形的三边做无滑动旋转,直至回到原出发位置时,则这个圆共转了 圈14、如图,已知:边长为1的圆内接正方形ABCD 中,P 为边CD 的中点,直线AP 交圆于E 点.则弦DE 的长为15、Rt △ABC 中,∠C=90°,AC=4,BC=3,则以直线AB 为轴旋转一周所得的几何体的表面积为16、如图,边长为1的菱形ABCD 绕点A 旋转,当B ,C 两点恰好落在扇形AEF 的弧EF 上,弧EF 的长度等于x 6.17 6.18 6.19 6.20y=ax 2+bx+c -0.03 -0.01 0.02 0.04 学校 姓名 班级 考号AB C DAC D B17、如图小明想测量电线杆AB 的高度,发现电线杆的影子恰好落在土坡的坡面CD 和地面BC 上,量得CD=4 m ,BC=10 m ,CD 与地面成30°角,且此时测得1 m 杆的影子长为2 m ,则电线杆的高度约为 结果保留两位有效数字(2 ≈1.41, 3≈1.73)18、如图,已知⊙P 的半径为2,圆心P 在抛物线y= 1/2x 2-1上运动,当⊙P 与x 轴相切时,圆心P 的坐标为 三、耐心做一做:19、(1)(7分)计算:(-1)2009×(-21)-2+( 3-π)0+|1-2sin60°|(2)画出右面物体的三视图20、(7分)一艘小船从码头A 出发,沿北偏东53°方向航行,航行一段时间到达小岛B 处后,又沿着北偏西22°方向航行了10海里到达C 处,这时从码头测得小船在码头北偏东23°的方向上,求此时小船与码头之间的距离( 2 ≈1.41,3≈1.73,结果保留整数).21、(7分)某乡薄铁社厂的王师傅要在长25cm ,宽18cm 的薄铁板上截出一个最大的圆和两个尽可能大的小圆,他先画了草图,但他在求小圆的半径时遇到了困难,则两个小圆的半径为22、(9分)某超市经销一种销售成本为每件40元的商品.据市场调查分析, 如果按每件50元销售,一周能售出500件,若销售单价每涨1元,每周销售量 就减少10件.设销售单价为每件x 元(x≥50),一周的销售量为y 件. (1)写出y 与x 的函数关系式.(标明x 的取值范围)(2)设一周的销售利润为S ,写出S 与x 的函数关系式,并确定当单价在什么范围 内变化时,利润随着单价的增大而增大?(3)在超市对该种商品投入不超过10 000元的情况下,使得一周销售利润 达到8 000元,销售单价应定为多少?23、(12分)如图,在平面直角坐标系中,⊙M 与x 轴交于A ,B 两点,AC 是⊙M 的直径,过点C 的直线交x 轴于点D ,连接BC ,已知点M 的坐标为(0,3),直线 CD 的函数解析式为y= -3 x+53 (1)求点D 的坐标和BC 的长;(2)求点C 的坐标和⊙M 的半径;(3)求证:CD 是⊙M 的切线.24、(12分)如图所示,△ABC ,AB=AC ,二次函数y=-21x 2+4x 的图象经过点 A 、B 、C ,点E (1,0),F (7,0),将正方形EFKD 沿y 轴正方向进行移动,速度为每秒移动2个单位,移动时间为t (0<t≤4),设移动过程中正方形与三角形部分重叠的面积为S(1)求△ABC 的面积S △ABC ;(2)求重叠部分面积S 关于时间t 的函数关系式,并指出自变量t 的取值范围;(3)当正方形的点E 、F 移动到二次函数图象上,求重叠部分面积S ,并请判断点D 、K 是否在△ABC 外接圆上并说明理由;如不在,也请说明理由.25、(12分)如图所示,在平面直角坐标系中,矩形ABOC的边BO 在x 轴的负半轴上,边OC 在y 轴的正半轴上,且AB=1,OB=3,矩形ABOC 绕点O 按顺时针方向旋转60°后得到矩形EFOD .点A 的对应点为点E ,点B 的对应点为点F ,点C 的 对应点为点D ,抛物线y=ax 2+bx+c 过点A ,E ,D . (1)判断点E 是否在y 轴上,并说明理由;(2)求抛物线的函数表达式;(3)在x 轴的上方是否存在点P ,点Q ,使以点O ,B ,P ,Q 为顶点的平行四边形的面积是矩形ABOC 面积的2倍,且点P 在抛物线上?若存在,请求出点P ,点Q 的坐标;若不存在,请说明理由.。
初四期末数学试题及答案

初四期末数学试题及答案一、选择题(每题3分,共30分)1. 下列哪个数是最小的正整数?A. -1B. 0C. 1D. 2答案:C2. 计算下列表达式的结果:\[ \frac{2}{3} + \frac{1}{2} \]A. 1B. \(\frac{7}{6}\)C. \(\frac{5}{6}\)D. \(\frac{4}{3}\)答案:B3. 一个圆的半径是5厘米,那么它的面积是多少平方厘米?A. 25B. 50C. 100D. 200答案:C4. 一个等腰三角形的底角是45度,那么它的顶角是多少度?A. 45B. 90C. 135D. 180答案:B5. 下列哪个选项表示的是一次函数?A. \(y = 3x + 2\)B. \(y = 3x^2 + 2\)C. \(y = \frac{1}{x}\)D. \(y = x^2 + 3x + 2\)答案:A6. 一个数的平方根是4,那么这个数是多少?A. 16B. -16C. 4D. -4答案:A7. 一个长方体的长、宽、高分别是2厘米、3厘米、4厘米,那么它的体积是多少立方厘米?A. 24B. 12C. 8D. 6答案:A8. 一个数的绝对值是5,那么这个数可以是下列哪个?A. 5B. -5C. 5和-5D. 0答案:C9. 计算下列表达式的结果:\[ 3^2 - 2^3 \]A. 1B. 5C. 7D. 9答案:B10. 一个直角三角形的两条直角边分别是3厘米和4厘米,那么它的斜边是多少厘米?A. 5B. 6C. 7D. 8答案:A二、填空题(每题4分,共20分)1. 一个数的立方是-27,那么这个数是______。
答案:-32. 一个数的倒数是\(\frac{1}{4}\),那么这个数是______。
答案:43. 一个数的平方是25,那么这个数是______。
答案:±54. 一个数的绝对值是8,那么这个数可以是______。
答案:8或-85. 一个数的平方根是2.5,那么这个数是______。
初中初四数学试卷

1. 下列各数中,正数是()A. -3B. 0C. 3D. -2.52. 下列各数中,无理数是()A. √9B. √16C. √25D. √-43. 下列各式中,正确的是()A. a^2 = b^2 => a = bB. a^2 = b^2 => a = -bC. a^2 = b^2 => a = ±bD. a^2 = b^2 => a = 04. 若a、b是方程2x^2 - 5x + 2 = 0的两根,则a + b的值为()A. 2B. 5C. 10D. -25. 在直角坐标系中,点A(2,3)关于x轴的对称点为()A.(2,-3)B.(-2,3)C.(-2,-3)D.(2,-3)6. 若a、b、c是等差数列,且a + b + c = 9,则a^2 + b^2 + c^2的值为()A. 27B. 45C. 36D. 547. 下列各函数中,是奇函数的是()A. y = x^2B. y = x^3C. y = x^4D. y = x^58. 若sinα = 1/2,则cosα的值为()A. √3/2B. -√3/2C. 1/2D. -1/29. 下列各三角形中,是直角三角形的是()A. 三边长分别为3、4、5B. 三边长分别为5、12、13C. 三边长分别为6、8、10D. 三边长分别为7、24、2510. 下列各数中,是二次根式的是()A. √4B. √-4C. √-1D. √011. 若x^2 - 4x + 3 = 0,则x的值为______。
12. 若sinα = 3/5,且α为锐角,则cosα的值为______。
13. 在等差数列{an}中,若a1 = 3,公差d = 2,则第10项an =______。
14. 若a、b、c是等比数列,且a + b + c = 24,ab = 48,则c的值为______。
15. 在直角坐标系中,点P(-3,2)到直线x + 2y - 1 = 0的距离为______。
初中数学:初四数学

初四数学试题一、选择题,每小题3分1、如果反比例函数的图象经过点(1.-2),则它还一定经过()A.(2,-1)B.(,2)C.(-2,-1)D.(,2)2、对于反比例函数y=,下列说法不正确的是()A.点(﹣2,﹣1)在它的图象上B.它的图象在第一、三象限C.当x>0时,y随x的增大而增大D.当x<0时,y随x的增大而减小3、已知二次函数y=ax2+bx-1(a≠0)的图象经过点(1,1),则代数式1-a-b的值为()A.-3B.-1C.2D.54、将函数与函数的大致图像画在同一坐标系牟,正确的函数图像是()5、点A(x1,y1),B(x2,y2),C(x3,y3)都在反比例函数y=−3x的图象上,若x1<x2<0<x3,则y1,y2,y3的大小关系是()A.y3<y1<y2B.y1<y2<y3C.y3<y2<y1D.y2<y1<y36、在△ABC中,∠C=90°,∠A,∠B,∠C的对边分别是a,b,c,则下列各项中正确的是()A.a=c·sinB B.a=c·cosB C.a=c·tanB D.以上均不正确7、在△ABC中,∠C=90°,如果tanA=,那么sinB的值等于()A.B.C.D.8、如图,CD是Rt△ABC斜边上的高,AC=4,BC=3,则cos∠BCD=()A. B. C. D.7 8 99、如图所示,在平面直角坐标系中,将矩形OABC沿OB对折,使点A落在A1处,已知AO=,AB=1,则点A1的坐标是()A.()B.()C.()D.()10、如图,在下列网格中,小正方形的边长均为1,点A,B,O都在格点上,则∠AOB的正弦值是( )A. B. C. D.11、下列函数解析式中,一定为二次函数的是()A.y=3x-1B.y=a x2+bx+cC.s=2t2-2t+1D.y=x2+1/x12、如果函数的图象是双曲线,而且在第二、四象限,那么k=().A. B.-1 C. D.113、当时,下列函数中,函数值y 随自变量x 增大而增大的是____________(只填写序号) ①;②;③;④y=x 214、若点A(m ,-2)在反比例函数y=1/x 的图象上,则当函数值y ≥-2时,自变量x 的取值范围是 .15、如图,在△ABC 中,∠A=30°,∠B=45°,AC=2√3,则AB 的长为 .16、在Rt △ACB 中,若∠C =90°,sin A =,b +c =6,则b=.17、小明同学在东西方向的沿江大道A 处,测得江中灯塔P 在北偏东60°方向上,在A 处正东400米的B 处,测得江中灯塔P 在北偏东30°方向上,则灯塔P 到沿江大道的距离为______米 18、函数y=√1−x √2x−1有意义,则x 的取值范围 。
初四数学试题及答案

初四数学试题第Ⅰ卷(选择题 共36分)一、选择题(本大题共12小题,在每小题给出的四个选项中,只有一个是正确的,请把正确的选择出来,每小题选对得3分,选错、不选或选出的答案超过一个,均记零分) 1.|—5|的倒数是A .—5B .-51 C .5 D .51 2.计算323)(a a ⋅的结果是A .8aB .9aC .10aD .11a3.下列图形:其中,既是轴对称图形,又是中心对称图形的个数是 A .1个B .2个C .3个D .4个4.函数12+=x y 与函数x k y =的图象相交于点(2, m),则下列各点不在函数x ky =的图象上的是A .(-2,-5)B .(25,4) C .(-1,10) D .(5,2)5.如图l 1//l 2, l 3⊥l 4,∠1=42°,那么∠2的度数为A .48°B .42°C .38°D .21°6.如图,数轴上A 、B 两点对应的实数分别为a ,b , 则下列结论不正确...的是A .0>+b aB .0<abC .0<-b aD .|a |—|b|>07.如图是某几何体的三视图,则该几何体的全面积是A .36πB .60πC .96πD .120π8.下列函数:①x y 3-= ②12-=x y ③)0(1<-=x xy ④322++-=x x y ,其中y 的值随x 值的增大而增大的函数有A .4个B .3个C .2个D .1个9.如图,E 是ABCD 的边AD 的中点,CE 与BA 的延长线交于点F ,若∠FCD=∠D ,则下列结论不成立...的是A .AD=CFB .BF=CFC .AF=CDD .DE=EF10.如图所示的两个转盘,每个转盘均被分成四个相同的扇形,转动转盘时指针落在每一个扇形内的机会均等,同时转动两个转盘,则两个指针同时落在标有奇数扇形内的概率为A .21B .31 C .41 D .81 11.若关于x 的不等式⎩⎨⎧≤-<-1270x m x 的整数解共有4个,则m 的取值范围是A .76<<mB .76<≤mC .76≤≤mD .76≤<m12.如图,矩形ABCD 的两对角线AC 、BD 交于点O ,∠AOB=60°,设AB=x cm ,矩形ABCD 的面积为scm 2,则变量s 与x 之间的函数关系式为A .23x s =B .233x s =C .223x s =D .221x s =第Ⅱ卷(非选择题 共84分)二、填空题(本大题共7小题,满分21分。
初四数学测试题及答案

初四数学测试卷桓台县实验中学命题人:刘桂兰分)分,共48(每个一、选择题:47.四个命题:①三角形的一条中线能将三角形分成面积相等的两部分;②有两边和2 +3的结果是1.计算-2其中一边的对角对应相等的两个三角形全等;③点P(1,2)关于原点的对称点坐标为D.A.7 B.5 C.51??(-1,-2);④两圆的半径分别是3和4,圆心距为d,若两圆有公共点,则其中正确的是下面所给的交通标志图中是轴对称图形的是 2..7?d?1A. ①②B.①③C.②③D.③④8.如图,在△ABC中,∠C=90°,M是AB的中点,动点P从点A出发,沿AC方向匀速运动到终点C,动点Q从点C出发,沿CB方向匀速运动到终点B.已知P,Q两点同时出发,并同时到达终点.连结MP,MQ,PQ.在整个运动过8题第9-),用科学计数法表示这个病毒纳M=10M(病毒直径为H3.如图,7N930纳M1△MPQ的面积大小变化情况是()程中,正确的是直径的大小,A.一直增大B.一直减小C.先减小后增大D.先增大后减小89--M MB. 3.0×A.30×1010910--M MD. 0.3×C. 3.0×10109. 甲计划用若干个工作日完成某项工作,从第三个工作日起,乙加入此项工作,且下列计算正确的是4.甲、乙两人工效相同,结果提前3天完成任务,则甲计划完成此项工作的天数是22263 A. B.a22(?a)?a?aa?A.8 B.7C.6D.5人数10. 如图,在△ABC中,以BC为直径的圆分别交边AC、AB于D、E两点,连接111022 C. D.aaa??a2?21a2?(?)?9BD、DE.若BD平分∠ABC,则下列结论不一定成立的是26=2AB·ACAE A.BD⊥ACB.4下图是某学校全体教职工年龄的频数分布直方5.C.△ADE是等腰三角形 D. BC=2AD.的原则,如年龄图(统计中采用“”上限不在内2.二次函数1134 36 38 40 42 44 46 48年龄bax?y?bxax?y?的图象大致是的图象如图所示,那么一次函数<<x38x小组,而不在34≤36≤36为岁统计在().yyyyy的是()36小组),根据图形提供的信息,下列说法中错误..A人.该学校教职工总人数是50xxxxx00000小组的教职工人数占该学校全体教职工4240≤x.年龄在B<(D)20%总人数的题10第(C)(A)(B)y1142<.教职工年龄的中位数一定落在C40≤x这一组22.如图,在平面直角坐标系中,抛物线12?2xxxyy??,经过平移得到抛物线22 40<这一组38≤x.教职工年龄的众数一定在D其对称轴与两段抛物线弧所围成的阴影部分的面积为().816 D C BA....42x0的取值范围在数+6,x2(P.如果点6)在平面直角坐标系的第四象限内,那么4-xx 轴上可表示为()204:二、填空题(每个分,共分)1 / 4在东营市中小学标准化建设工程中,某学校计划购进一批电脑和电子白.、(8分)20x.13.要使式子的取值范围是有意义,则x2?台电脑3.5万元,购买2板,经过市场考察得知,购买1台电脑和2台电子白板需要32已知,则4m=_________.分解因式:m﹣14.6m?m?2.1____________2m??2m?.2.5万元和1台电子白板需要、某校对甲、乙两名跳高运动员的近期跳高成绩进行统计分析,结果如下:15?(1)求每台电脑、每台电子白板各多少万元22m69x?1.0315.s?0.0006s?0,则这两名运动员中的,,,m.69x?1万元,但不(2)根据学校实际,需购进电脑和电子白板共30台,总费用不超过30乙甲乙甲的成绩更稳定。
初四数学阶段测试

初四数学阶段测试一、选择题1.(2021•潍坊)下列各数的相反数中,最大的是()A.B.1C.﹣D.﹣22.(2021•潍坊)第七次全国人口普查数据显示,山东省常住人口约为10152.7万人,将101527000用科学记数法(精确到十万位)表示为()A.1.02×108B.0.102×109C.1.015×108D.0.1015×109 3.(2020•潍坊)若m2+2m=1,则4m2+8m﹣3的值是()A.4B.3C.2D.14.(2020•潍坊)下列运算正确的是()A.2a+3b=5ab B.a3•a2=a5C.(a+b)2=a2+b2D.(a2b)3=a6b5.(2020•烟台)4的平方根是()A.2B.﹣2C.±2D.6.(2021•潍坊)若菱形两条对角线的长度是方程x2﹣6x+8=0的两根,则该菱形的边长为()A.B.4C.2D.57.(2020•潍坊)关于x的一元二次方程x2+(k﹣3)x+1﹣k=0根的情况,下列说法正确的是()A.有两个不相等的实数根B.有两个相等的实数根C.无实数根D.无法确定8.(2021•潍坊)不等式组的解集在数轴上表示正确的是()A.B.C.D.9.(2020•潍坊)若关于x的不等式组有且只有3个整数解,则a的取值范围是()A.0≤a≤2B.0≤a<2C.0<a≤2D.0<a<210.(2022•潍坊)秦兵马俑的发现被誉为“世界第八大奇迹”,兵马俑的眼睛到下巴的距离与头顶到下巴的距离之比约为,下列估算正确的是()A.0<<B.<<C.<<1D.>1二.填空题11(2020•潍坊)因式分解:x2y﹣9y=.12(2022•潍坊)方程组的解为.13(2021•潍坊)若x<2,且+|x﹣2|+x﹣1=0,则x=.14(2020•潍坊)若关于x的分式方程+1有增根,则m=.15知等腰三角形三边分别为a、b、4,且a、b是关于x的一元二次方程的两个根,则m的值是____三、解答题16(2021•烟台)先化简,再求值:,从﹣2<x≤2中选出合适的x的整数值代入求值.17(2022•潍坊)(1)在计算时,小亮的计算过程如下:解:===﹣2小莹发现小亮的计算有误,帮助小亮找出了3个错误.请你找出其他错误,参照①~③的格式写在横线上,并依次标注序号:①﹣22=4;②(﹣1)10=﹣1;③|﹣6|=﹣6;.请写出正确的计算过程.18. (2021•烟台)求不等式组的解集,并把它的解集表示在数轴上.19.022•聊城)为了解决雨季时城市内涝的难题,我市决定对部分老街道的地下管网进行改造.在改造一段长3600米的街道地下管网时,每天的施工效率比原计划提高了20%,按这样的进度可以比原计划提前10天完成任务.(1)求实际施工时,每天改造管网的长度;(2)施工进行20天后,为了减少对交通的影响,施工单位决定再次加快施工进度,以确保总工期不超过40天,那么以后每天改造管网至少还要增加多少米?。
初四数学测试题及答案范本

初四数学测试题及答案范本题目一:简单加减法计算1. 45 + 23 = ?2. 87 - 32 = ?3. 56 + 78 = ?4. 99 - 64 = ?5. 36 + 19 = ?答案一:1. 45 + 23 = 682. 87 - 32 = 553. 56 + 78 = 1344. 99 - 64 = 355. 36 + 19 = 55题目二:乘法口诀表填空填空题:请根据乘法口诀表的规律填写下面的空格。
1 2 3 4 5 ?6 8 10 ? 15 187 ? 14 21 28 3532 ? ? ? 40 4845 54 ? ? ? ?答案二:1 2 3 4 5 66 8 10 12 15 187 9 14 21 28 3532 36 42 48 40 4845 54 63 72 81 90题目三:简单代数方程解方程:请计算下列方程中的未知数 x 的值。
1. 2x + 5 = 172. 4x - 8 = 123. 3x + 7 = 254. 5x - 10 = 205. 6x + 3 = 39答案三:1. 2x + 5 = 172x = 17 - 52x = 12x = 62. 4x - 8 = 124x = 12 + 84x = 20x = 53. 3x + 7 = 253x = 25 - 73x = 18x = 64. 5x - 10 = 205x = 20 + 105x = 30x = 65. 6x + 3 = 396x = 39 - 36x = 36x = 6题目四:几何图形计算计算下列几何图形的面积和周长。
1. 正方形:边长为8 cm2. 矩形:长为12 cm,宽为6 cm3. 圆形:半径为5 cm4. 三角形:底边长为10 cm,高为8 cm答案四:1. 正方形:边长为8 cm面积 = 边长 ×边长 = 8 cm × 8 cm = 64 cm²周长 = 4 ×边长 = 4 × 8 cm = 32 cm2. 矩形:长为12 cm,宽为6 cm面积 = 长 ×宽 = 12 cm × 6 cm = 72 cm²周长 = 2 × (长 + 宽) = 2 × (12 cm + 6 cm) = 2 × 18 cm = 36 cm 3. 圆形:半径为5 cm面积= π × 半径² = 3.14 × 5 cm × 5 cm ≈ 78.5 cm²周长= 2 × π × 半径= 2 × 3.14 × 5 cm ≈ 31.4 cm4. 三角形:底边长为10 cm,高为8 cm面积 = 1/2 ×底边长 ×高 = 1/2 × 10 cm × 8 cm = 40 cm²周长未提供足够信息,无法计算。
初四数学试题参考答案
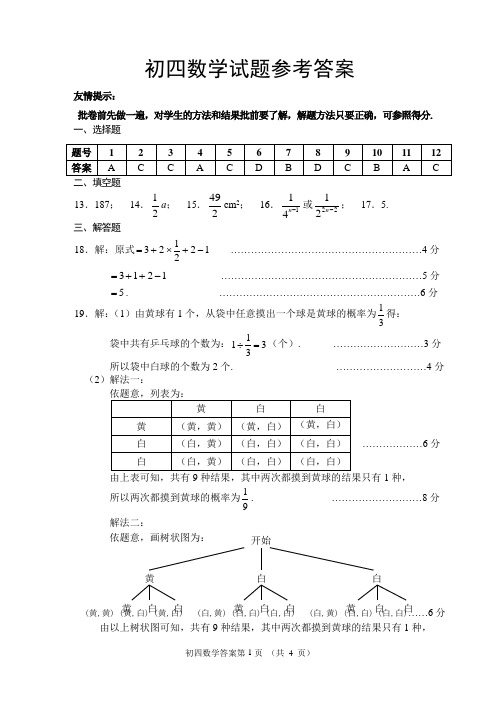
初四数学试题参考答案友情提示:批卷前先做一遍,对学生的方法和结果批前要了解,解题方法只要正确,可参照得分. 一、选择题13.187; 14.21a ; 15.492cm 2; 16.114n -或2221-n ; 17.5. 三、解答题18.解:原式122123-+⨯+= …………………………………………………4分 1213-++= ……………………………………………………5分 5=. ……………………………………………………6分19.解:(1)由黄球有1个,从袋中任意摸出一个球是黄球的概率为31得:袋中共有乒乓球的个数为:3311=÷(个). ………………………3分 所以袋中白球的个数为2个. ………………………4分 (2)解法一:1种,所以两次都摸到黄球的概率为91. ………………………8分解法二:依题意,画树状图为:(黄,黄) (黄,白) (黄,白) (白,黄) (白,白) (白,白) (白,黄) (白,白) (白,白)……6分由以上树状图可知,共有9种结果,其中两次都摸到黄球的结果只有1种,………………6分开始黄 白 白黄 白 白 黄 白 白 黄 白 白所以两次都摸到黄球的概率为91. ………………………8分 20.(1)解:∵二次函数12)31(2-+--=a x a ax y 的对称轴是x =-2∴22)31(-=---aa ………………………2分 解得a =-1 ………………………3分 经检验a =-1是原分式方程的解. ………………………4分 所以a =-1时,二次函数12)31(2-+--=a x a ax y 的对称轴是x =-2;…5分 (2)1)当a =0时,原方程变为-x -1=0,方程的解为x = -1; ……………7分 2)当a ≠0时,原方程为一元二次方程,012)31(2=-+--a x a ax ,当△≥0时,方程总有实数根, ∵△=)12(4)31(2---a a a=122+-a a ………………………8分 =2)1(-a ≥0 ………………………9分 所以a 取任何实数时,方程012)31(2=-+--a x a ax 总有实数根……10分21.(1)证明:在矩形ABCD 中,BC AD =,AD ∥BC ,︒=∠90B .∵AD ∥BC ,∴FAD BEA ∠=∠. ………………………1分 ∵DF ⊥AE ,∴︒=∠90DFA .∴DFA B ∠=∠. ………………………2分 ∵BC AE =,BC AD =,∴AD AE = ………………………3分 ∴△AEB ≌△DAF ………………………4分 ∴DF AB =. ………………………5分(2)解:由(1)可知:6==AB DF ,10==AD AE . …………………6分 在Rt △AFD 中,︒=∠90DFA ,∴86102222=-=-=DF AD AF . ………………………7分 ∴2810=-=-=AF AE EF , ………………………8分 在Rt △DFE 中,︒=∠90DFE ,∴3162tan ===∠DF EF EDF . ………………………10分22.(1)证明:连接FO 并延长交⊙O 于Q ,连接DQ . ………1分∵FQ 是⊙O 直径,∴∠FDQ =90°.∴∠QFD +∠Q =90°.∵CD ⊥AB ,∴∠P +∠C =90°.∵∠Q =∠C ,∴∠QFD =∠P .……………3分 ∵∠FOE =∠POF ,∴△FOE ∽△POF .…4分 ∴OE OFOF OP=.∴OE ·OP =OF 2=r 2. ………5分 (2)解:(1)中的结论成立. ……………6分理由:如图2,依题意画出图形,连接FO 并延长交⊙O 于M ,连接CM . ……………7分∵FM 是⊙O 直径,∴∠FCM =90°,∴∠M +∠CFM =90°. ∵CD ⊥AB ,∴∠E +∠D =90°.∵∠M =∠D ,∴∠CFM =∠E. ………8分 ∵∠POF =∠FOE ,∴△POF ∽△FOE .…9分∴OP OFOF OE=,∴OE ·OP =OF 2=r 2. ……10分 23.解:(1)设去年四月份每台A 型号彩电售价x 元,根据题意得:20004000050000=x . ………………2分 解得:2500=x .经检验,2500=x 是原方程的解. ∴2500=x .答:去年四月份每台A 型号彩电售价是2500元. ………………3分 (2)设电器城在此次进货中,购进A 型号彩电a 台,则B 型号彩电)20(a -台,依题意:⎩⎨⎧≤-+≥-+.33000)20(15001800,32000)20(15001800a a a a ………………5分解得:10320≤≤a . 由于a 只取非负整数,所以7=a ,8,9,10. ………………6分所以电器城在此次进货中,共有4种进货方案,分别是: 方案一:购进A 型号彩电7台、B 型号彩电13台; 方案二:购进A 型号彩电8台、B 型号彩电12台; 方案三:购进A 型号彩电9台、B 型号彩电11台;方案四:购进A 型号彩电10台、B 型号彩电10台. ………………7分 (3)设电器城获得的利润为y 元,则y 与a 的函数关系式为:6000100)20)(15001800()18002000(+-=--+-=a a a y . ……………9分 ∵6000100+-=a y ,y 随a 的增大而减小,且7=a ,8,9,10. ∴当7=a 时,y 可取得最大值,530060007100=+⨯-=最大y .第22题(图2)因此,当购进A 型号彩电7台、B 型号彩电13台时,电器城获得的利润最大,最大利润为5300元. ………………10分(注:其它解法可参照本解法给分)24. 解:(1)因为M (1,-4) 是二次函数k m x y ++=2)(的顶点坐标,所以324)1(22--=--=x x x y …………………………2分 令,0322=--x x 解之得3,121=-=x x .∴A ,B 两点的坐标分别为A (-1,0),B (3,0) …………………4分 (2)在二次函数的图象上存在点P ,使MAB PAB S S ∆∆=45设),,(y x p 则y y AB S PAB 221=⨯=∆,又8421=-⨯=∆AB S MAB , ∴.5,8452±=⨯=y y 即 ……5分 ∵二次函数的最小值为-4,∴5=y ……6分 当5=y 时,4,2=-=x x 或.故P 点坐标为(-2,5)或(4,5)……7分 (3)如图1,当直线)1(<+=b b x y 经过A 点时, 可得.1=b …8分 当直线)1(<+=b b x y 经过B 点时,可得.3-=b …9分 由图可知符合题意的b 的取值范围为13<<-b …10分第24题。
初四数学试题及答案

初四数学试题及答案一、选择题(每题3分,共30分)1. 下列哪个数是无理数?A. 3.14B. √2C. 0.33333...D. 2/3答案:B2. 一个数的平方等于它本身,这个数可能是:A. 0B. 1C. -1D. 以上都是答案:D3. 一个等腰三角形的两边长分别为3和4,那么它的周长可能是:A. 7B. 10C. 14D. 无法确定答案:B4. 如果一个二次方程的两个根的和为-5,那么这个二次方程可能是:A. x^2 - 5x + 6 = 0B. x^2 + 5x + 6 = 0C. x^2 - 5x - 6 = 0D. x^2 + 5x - 6 = 0答案:A5. 函数y = 2x + 3的图象经过的象限是:A. 第一、二、三象限B. 第一、二、四象限C. 第一、三、四象限D. 第二、三、四象限答案:C6. 一个圆的半径为5,那么它的面积是:A. 25πB. 50πC. 75πD. 100π答案:B7. 一个长方体的长、宽、高分别为2、3、4,那么它的体积是:A. 24B. 26C. 28D. 32答案:A8. 一个等差数列的前三项分别为2、5、8,那么它的第五项是:A. 11B. 14C. 17D. 20答案:B9. 函数y = x^2 - 6x + 8的最小值是:A. -1B. 0C. 1D. 8答案:A10. 一个三角形的三个内角的度数之和为:A. 90°B. 180°C. 360°D. 540°答案:B二、填空题(每题3分,共30分)11. 一个数的相反数是-5,那么这个数是_________。
答案:512. 一个数的绝对值是3,那么这个数可能是_________或_________。
答案:3或-313. 一个二次函数的顶点坐标为(2, -1),那么它的对称轴是_________。
答案:x=214. 一个直角三角形的两直角边长分别为3和4,那么它的斜边长是_________。
初四期末数学试题及答案

初四期末数学试题及答案一、选择题(每题3分,共30分)1. 下列哪个数是无理数?A. 3.14159B. 2.71828C. πD. √22. 如果一个二次方程的判别式小于0,那么这个方程:A. 有两个实数根B. 有一个实数根C. 没有实数根D. 无法确定3. 一个函数的图象是一条直线,那么这个函数:A. 一定是一次函数B. 可能是一次函数,也可能是正比例函数C. 一定是正比例函数D. 无法确定4. 下列哪个选项是正确的不等式?A. 5 > 3B. -3 ≥ 0C. -2 < 0D. 0 ≤ -15. 一个数的平方根是它本身,这个数是:A. 0C. -1D. 以上都不是6. 一个圆的半径是5,那么它的面积是:A. 25πB. 50πC. 100πD. 125π7. 一个数的绝对值是它本身,这个数:A. 一定是正数B. 一定是负数C. 可以是正数或0D. 无法确定8. 如果两个角的和是180°,那么这两个角:A. 是邻补角B. 是对顶角C. 是同位角D. 是补角9. 下列哪个选项是正确的比例关系?A. 3:6 = 1:2B. 4:8 = 2:1C. 5:10 = 1:2D. 6:12 = 2:310. 一个数列的前三项是1, 2, 3,如果这个数列是等差数列,那么第四项是:A. 4C. 6D. 7答案:1.C 2.C 3.B 4.C 5.A 6.B 7.C 8.D 9.C 10.A二、填空题(每题2分,共20分)11. 一个数的相反数是-5,那么这个数是______。
12. 如果一个三角形的三边长分别是3, 4, 5,那么这是一个______三角形。
13. 一个数的立方根是2,那么这个数是______。
14. 一个数的倒数是1/2,那么这个数是______。
15. 如果一个角的正弦值是1/2,那么这个角的度数是______。
16. 一个直角三角形的两条直角边分别是6和8,那么斜边长是______。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初四试卷数学
3.下列图形中,是中心对称图形,但不是轴对称图形的是()A.B.C.D.
为y,则能大致反映y与x函数关系的图象是()
A.B.C.D.
5题图7题图9题图10题图二、填空题11.分解因式:a3-4a2b+4ab2= ___________
其中正确的结论有_________(填正确序号)
13题图16题图17题图18题图
x
x
-x
1-
1
5
求出BE的长;若不能,请说明理由.
22.某学校要举办一次演讲比赛,每班只能选一人参加比赛.但八年级一班共有甲、乙两人的演
讲水平相不相上下,现要在他们两人中选一人去参加全校的演讲比赛,经班主任与全班同学协
商决定用摸小球的游戏来确定谁去参赛(胜者参赛).游戏规则如下:在两个不透明的盒子中,
一个盒子里放着两个红球,一个白球;另一个盒子里放着三个白球,一个红球,从两个盒子中各
摸一个球,若摸得的两个球都是红球,甲胜;摸得的两个球都是白球,乙胜,否则,视为平局.
若为平局,继续上述游戏,直至分出胜负为止.根据上述规则回答下列问题:(1)从两个盒子
各摸出一个球,一个球为白球,一个球为红球的概率是多少?(2)该游戏公平吗?请用列表或
树状图等方法说明理由.
23.为了解中考体育科目训练情况,某地从九年级学生中随机抽取了部分学生进行了
一次考前体育科目测试,把测试结果分为四个等级:A级:优秀;B级:良好;C级:及格;D级:不及格,并将测试结果绘成了如下两幅不完整的统计图.请根据统计图中的信息解答下列问题:(1)请将两幅不完整的统计图补充完整;
(2)如果该地参加中考学生将有4500名,根据测试情况请你估计不及格人数有多少?(3)从被抽测的学生中任选一名学生,则这名学生成绩是D级的概率是多少?
24.如图,一次函数y=kx+b的图象与反比例函数y=m/x的图象相交于点A(-2,1),
点B(1,n).(1)求此一次函数和反比例函数的解析式;
(2)请直接写出满足不等式kx+b-m/x<0的解集;
(3)在平面直角坐标系的第二象限内边长为1正方形EFDG边均平行于坐标轴,
若点E(-a,a),如图,当曲线y=m/x(x<0)与此正方形边有交点时,求a取值范围.
25.抛物线y1=x2+mx+n图象经过点P(-3,1),对称轴是经过(-1,0)且平行于y轴直线.(1)求m,n值. (2)如图一次函数y2=kx+b图象经过点P,与x轴相交于点A,与抛物线图象相交于另一点B,
点B在点P右侧,PA:PB=1:5,求一次函数表达式.(3)直接写出y1>y2时x的取值范围.
26.AB是⊙O直径,点P在线段AB延长线上,BP=OB=2,点Q在⊙O上,连接PQ.(1)如图①,线段PQ所在直线与⊙O相切,求线段PQ长;(2)如图②线段PQ与⊙O还有一个公共点C,且PC=CQ,连接OQ,AC交于点D.①判断OQ与AC位置关系,并说明理由;②求线段PQ长.
27.在△ABC中,∠A=90°,AB=8cm,AC=6cm,点M,点N同时从点A出发,点M沿边AB以4cm/s 速度向点B运动,点N从点A出发,沿边AC以3cm/s的速度向点C运动,(点M不与A,B重合,点N不与A,C重合),设运动时间为xs.(1)求证:△AMN∽△ABC;(2)当x为何值时,以MN为直径⊙O与直线BC相切?(3)把△AMN沿直线MN折叠得到△MNP,若△MNP与梯形BCNM重叠部分面积为y,试求y关于x的函数表达式,并求x为何值时,y的值最大,最大值是多少?
28.(1)如图1,在AB直线一侧C、D两点,在AB上找一点P,使C、D、P三点组成三角形周长最短,找出此点并说明理由.(2)如图2,在∠AOB内部有一点P,是否在OA、OB上分别存在点E、F,使得E、F、P三点组成的三角形的周长最短,找出E、F两点,并说明理由.(3)如图3,在∠AOB内部有两点M、N,是否在OA、OB上分别存在点E、F,使得E、F、M、N,四点组成的
四边形的周长最短,找出E、F两点,并说明理由.
19解:原式=1/(x-1),当x=3×3/3+1=3+1时,原式=3/3
20(1)证明:∵∠B+∠BCE=∠CEA=∠CEF+∠FEA,∵∠CEF=∠B,∴∠AEF=∠BCE;(2)解:如图1,设⊙C与BA切于点M,则CM=CF,CM⊥BA,∵CA=CB,CM⊥BA∴BM=AM=0.5AB=3,Rt△AMC 中,AC=5,AM=3,∴CF=CM=4,∴AF=1,∵CA=CB,∴∠B=∠C由(1)知∠AEF=∠BCE∴△AEF∽△BCE,∴EA/BC=AF/BE,设BE长为x,则EA长为6-x∴(6-x)/5=1/x,解得:x
1=1,x2=5,答:BE的长为1或5;(3)可能.如图2,①当CE=CF时,∠3=∠2=∠A,∴EF∥AB,此时E与B重合,与条件矛盾,不成立.②当CE=EF时,又∵△AEF∽△BCE,∴△AEF≌△BCE,∴AE=BC=5,∴BE=AB-5=1,③当CF=EF时,∠1=∠2=∠A=∠B,△FCE∽△CBA,∴EF/AC=CE/AB,∴EF/CE=AC/AB=5/6,∵△AEF∽△BCE,∴EA/BC=EF/CE=5/6,∴EA=5BC/6=5/6×5=25/6,∴EB=AB-
该游戏规则不公平
2223解:(1)总人数为:12÷30%=40(人),A级占:6/40×100%=15%,D级占:1-35%-30%-15%=20%;C级人数:40×35%=14(人),D级人数:40×20%=8(人),补全统计图得:(2)估计不及格的人数有:4500×20%=900(人);
(3)从被抽测的学生中任选一名学生,则这名学生成绩是D级的概率是:20%
m
2526解:∵对称轴是经过(-1,0)且平行于y轴的直线,∴-m/2=-1,∴m=2,∵二次函数y=x2+mx+n的图象经过点P(-3,1),∴9-3m+n=1,∴n=3m-8=-2;(2)∵m=2,n=-2,∴二次函数为y=x2+2x-2,作PC⊥x轴于C,BD⊥x轴于D,则PC∥BD,∴PC/BD=AP/AB,∵P(-3,1),∴PC=1,∵PA:PB=1:5,∴PA:AB=1:6,∴BD=6,∴B的纵坐标为6,代入二次函数为y=x2+2x-2得,6=x2+2x-2,解得x1=2,x2=-4(舍去),∴B (2,6),则−3k+b=1,2k+b=6,解得,k=1,b=4,∴一次函数的表达式为y
2=x+4;(3)由图象可知,当x<-3或x
>2时,y
1>y
2
y值最大,最大值是8
27.28解:(1)如图1,作C关于直线AB 的对称点C′,连接C′D交AB于点P.则点P就是所要求作的点.理由:在l上取不同于P的点P′,连接CP′、DP′.∵C 和C′关于直线l对称,∴PC=PC′,P′C=P′C′,而C′P+DP<C′P′+DP′,∴PC+DP<CP′+DP′∴CD+CP+DP<CD+CP′+DP′即△CDP周长小于△CDP′周长;(2)如图2,作P关于OA的对称点C,关于OB的对称点D,连接CD,交OA于E,OB于F,则点E,F就是所要求作的点.理由:在OA,OB上取不同于E,F的点E′,F′,连接CE′、E′P′,∵C和P 关于直线OA对称,∴PE=CE,CE′=PE′,PF=DF,PF′=DF′,∵PE+EF+PF=CE+EF+DF,PE′+PF′+E′F′=CE′+E′F′+DE′,∴CE+EF+DF<CE′+E′F′+DF′,′∴PE+EF+PF<PE′+PF′+E′F′;(3)如图3,作M关于OA的对称点C,关于OB的对称点D,连接CD,交OA于E,OB于F,则点E,F就是所要求作的点.理由:在OA,OB上取不同于E,F的点E′,F′,连接CE′、E′P′,∵C和P关于直线OA对称,∴PE=CE,CE′=PE′,PF=DF,PF′=DF′,由(2)得知MN+ME+EF+MF <ME′+E′F′+F′D。
