倍长中线法(经典例题)讲课讲稿
倍长中线法(经典例题)2资料讲解

倍长中线法(经典例题)2倍长中线法(加倍法)知识网络详解:中线是三角形中的重要线段之一,在利用中线解决几何问题时,常常采用“倍长中线法”添加辅助线.所谓倍长中线法,就是将三角形的中线延长一倍,以便构造出全等三角形,从而运用全等三角形的有关知识来解决问题的方法.倍长中线法的过程:延长某某到某点,使某某等于某某,使什么等于什么(延长的那一条),用SAS证全等(对顶角)倍长中线最重要的一点,延长中线一倍,完成SAS全等三角形模型的构造。
经典例题讲解:例1:△ABC中,AB=5,AC=3,求中线AD例2:已知在△ABC中,AB=AC,D在AB上,E在AC的延长线上,DE交BC于F,且DF=EF,求证:BD=CE例3:已知在△ABC 中,AD 是BC 边上的中线,E 是AD 上一点,且BE=AC ,延长BE 交AC 于F ,求证:AF=EF例4:如图,AD 为ABC ∆的中线,DE 平分BDA ∠交AB 于E ,DF 平分ADC ∠交AC 于F.求证:EF CF BE >+第 14 题图DF CBEAB例5:已知CD=AB ,∠BDA=∠BAD ,AE 是△ABD 的中线,求证:∠C=∠BAE自检自测:1、如图,△ABC 中,BD=DC=AC,E 是DC 的中点,求证,AD 平分∠BAE 。
2、在四边形ABCD 中,AB ∥DC ,E 为BC 边的中点,∠BAE=∠EAF ,AF 与DC 的延长线相交于点F 。
试探究线段AB 与AF 、CF 之间的数量关系,并证明你的结论.E DABCF EABCD3、已知:如图,在ABC∆中,ACAB≠,D、E在BC上,且DE=EC,过D作BADF//交AE于点F,DF=AC.求证:AE平分BAC∠4、如图,CB、CD分别是钝角△AEC和锐角△ABC的中线,且AC=AB.求证:①CE=2CD.②CB平分∠DCE.ABFD E C5、如图已知△ABC ,AD 是BC 边上的中线,分别以AB 边、AC 边为直角边各向形外作等腰直角三角形,求证EF =2AD.4、已知:如图,∆ABC 中,∠C=90︒,CM ⊥AB 于M ,AT 平分∠BAC 交CM 于D ,交BC 于T ,过D 作DE//AB 交BC 于E ,求证:CT=BE.DA BCMTE倍长中线法(加倍法)知识网络详解:中线是三角形中的重要线段之一,在利用中线解决几何问题时,常常采用“倍长中线法”添加辅助线.所谓倍长中线法,就是将三角形的中线延长一倍,以便构造出全等三角形,从而运用全等三角形的有关知识来解决问题的方法.倍长中线法的过程:延长某某到某点,使某某等于某某,使什么等于什么(延长的那一条),用SAS证全等(对顶角)倍长中线最重要的一点,延长中线一倍,完成SAS全等三角形模型的构造。
倍长中线法经典例题)

倍长中线法知识网络详解:中线是三角形中的重要线段之一,在利用中线解决几何问题时,常常采用“倍长中线法”添加辅助线.所谓倍长中线法,就是将三角形的中线延长一倍,以便构造出全等三角形,从而运用全等三角形的有关知识来解决问题的方法.倍长中线法的过程:延长某某到某点,使某某等于某某,使什么等于什么(延长的那一条),用SAS证全等(对顶角)倍长中线最重要的一点,延长中线一倍,完成SAS全等三角形模型的构造。
【方法精讲】常用辅助线添加方法——倍长中线△ABC中方式1:延长AD到E,AD是BC边中线使DE=AD,连接BE方式2:间接倍长作CF⊥AD于F,延长MD到作BE⊥AD的延长线于使DN=MD,连接BE 连接CN经典例题讲解:例1:△ABC中,AB=5,AC=3,求中线AD的取值范围例2:已知在△ABC 中,AB=AC ,D 在AB 上,E 在AC 的延长线上,DE 交BC 于F ,且DF=EF ,求证:BD=CE例3:已知在△ABC 中,AD 是BC 边上的中线,E 是AD 上一点,且BE=AC ,延长BE 交AC 于F ,求证:AF=EF例4:已知:如图,在ABC ∆中,AC AB ≠,D 、E 在BC 上,且DE=EC ,过D 作BA DF //交AE 于点F ,DF=AC. 求证:AE 平分BAC ∠BABFDEC例5:已知CD=AB ,∠BDA=∠BAD ,AE 是△ABD 的中线,求证:∠C=∠BAE自检自测:1、如图,△ABC 中,BD=DC=AC,E 是DC 的中点,求证,AD 平分∠BAE.2、在四边形ABCD 中,AB ∥DC ,E 为BC 边的中点,∠BAE=∠EAF ,AF 与DC 的延长线相交于点F 。
试探究线段AB 与AF 、CF 之间的数量关系,并证明你的结论.E DABFEABC3、如图,AD 为ABC ∆的中线,DE 平分BDA ∠交AB 于E ,DF 平分ADC ∠交AC 于F. 求证:EF CF BE >+4、已知:如图,∆ABC 中,∠C=90︒,CM ⊥AB 于M ,AT 平分∠BAC 交CM 于D ,交BC 于T ,过D 作DE//AB 交BC 于E ,求证:CT=BE.第 14 题图DF CBEADABCMTE。
倍长中线法(经典例题)

N作 BE! AD 的延长线于倍长中线法知识网络详解:中线是三角形中的重要线段之一,在利用中线解决几何问题时, 常常采用“倍长中线法”添加辅助线.所谓倍长中线法,就是将三角形的中线延长一倍,以便构造出全 等三角形,从而运用全等三角形的有关知识来解决问题的方法.倍长中线法的过程:延长某某到某点,使某某等于某某,使什么 等于什么(延长的那一条),用SAS 证全等(对顶角)倍长中线最重要的一点,延长中线一倍,完成SAS 全等三角形模 型的构造。
【方法精讲】常用辅助线添加方法倍长中线△ ABC 中式1:延长AD 到E,B --------------- ■ ------------- CDAD 是E BC使 DE=AD接BE方式2:间接倍长 AB 延长MD 到N, CE连接CN 经典例题讲解:例〔:△ ABC 中,AB=5 AC=3求中线 AD 的取值范围例2:已知在△ ABC 中,AB=AC D 在AB 上,E 在AC 的延长线上,DE 交 BC 于 F ,且 DF=EF 求证:BD=CE例3:已知在△ ABC 中 , AD 是 BC 边上的中线,E 是AD 上一点,且BE 二AC例4:已知:如图,在- ABC 中,AB = AC , DE 在 BC 上 ,且 DE 二EC 过 D 作 DF//BA 交 AE 于点 F , DF=AC.例 5:已知 CD=AB Z BDA M BAD AE 是A ABD 的中线,求证:/ C=Z BAE自检自测:1、如图,△ ABC 中 , BD=DC=AC,是 DC 的中点,求证,AD 平分/ BAE.使 DN=M ,BE延长BE 交AC 于F ,求证:AF=EF求证:AE 平分.BACDEAECCFAC2、在四边形ABCD K AB// DC E 为BC 边的中点,/ BAE K EAF AF与DC 的延长线相交于点F 。
试探究线段AB 与AF 、CF 之间的数量关 系,并证明你的结论.3、如图,AD 为 MBC 的中线,DE 平分.BDA 交AB 于E,DF 平分.AD 交 AC 于 F.求证:BE CF EF4、已知:如图, ABC 中, C=90,CM AB 于 M AT 平 分 BAC 交 CM 于 D,交 BC 于 T ,过 D 作 DE//AB 交 BC 于 E ,求证:CT=BE.ADBF。
倍长中线法(经典例题)2

倍长中线法〔加倍法〕知识网络详解:中线是三角形中的重要线段之一,在利用中线解决几何问题时,常常采用“倍长中线法〞添加辅助线.所谓倍长中线法,就是将三角形的中线延长一倍,以便构造出全等三角形,从而运用全等三角形的有关知识来解决问题的方法.倍长中线法的过程:延长某某到某点,使某某等于某某,使什么等于什么〔延长的那一条〕,用SAS证全等〔对顶角〕倍长中线最重要的一点,延长中线一倍,完成SAS全等三角形模型的构造。
经典例题讲解:例1:△ABC中,AB=5,AC=3,求中线AD的取值范围。
例2:在△ABC中,AB=AC,D在AB上,E在AC的延长线上,DE交BC于F,且DF=EF,求证:BD=CE例3:在△ABC 中,AD 是BC 边上的中线,E 是AD 上一点,且BE=AC ,延长BE 交AC 于F ,求证:AF=EF例4:如图,AD 为ABC ∆的中线,DE 平分BDA ∠交AB 于E ,DF 平分ADC ∠交AC 于F. 求证:EF CF BE >+例5:CD=AB ,∠BDA=∠BAD ,AE 是△ABD 的中线,求证:∠C=∠BAE第 14 题图DF CBEAB自检自测:1、如图,△ABC 中,BD=DC=AC,E 是DC 的中点,求证,AD 平分∠BAE 。
2、在四边形ABCD 中,AB ∥DC ,E 为BC 边的中点,∠BAE=∠EAF ,AF 与DC 的延长线相交于点F 。
试探究线段AB 与AF 、CF 之间的数量关系,并证明你的结论.3、:如图,在ABC ∆中,AC AB ≠,D 、E 在BC 上,且DE=EC ,过D 作BA DF //交AE 于点F ,DF=AC.求证:AE 平分BAC ∠F EAB C DABFDEC4、如图,CB、CD分别是钝角△AEC和锐角△ABC的中线,且AC=AB.求证:①CE=2CD.②CB平分∠DCE.5、如图△ABC,AD是BC边上的中线,分别以AB边、AC边为直角边各向形外作等腰直角三角形,求证EF=2AD.4、:如图,∆ABC 中,∠C=90︒,CM ⊥AB 于M ,AT 平分∠BAC 交CM 于D ,交BC 于T ,过D 作DE//AB 交BC 于E ,求证:CT=BE.倍长中线法〔加倍法〕知识网络详解:中线是三角形中的重要线段之一,在利用中线解决几何问题时,常常采用“倍长中线法〞添加辅助线.所谓倍长中线法,就是将三角形的中线延长一倍,以便构造出全等三角形,从而运用全等三角形的有关知识来解决问题的方法.倍长中线法的过程:延长某某到某点,使某某等于某某,使什么等于什么〔延长的那一条〕,用SAS 证全等〔对顶角〕倍长中线最重要的一点,延长中线一倍,完成SAS 全等三角形模型的构造。
中线倍长法及截长补短经典讲义

几何证明中常用辅助线(一)中线倍长法:例1 、求证:三角形一边上的中线小于其他两边和的一半。
已知:如图,△ABC中,AD是BC边上的中线,求证:AD ﹤21(AB+AC)小结:涉及三角形中线问题时,常采用延长中线一倍的办法,即中线倍长法。
它可以将分居中线两旁的两条边AB、AC和两个角∠BAD和∠CAD集中于同一个三角形中,以利于问题的获解。
例2、中线一倍辅助线作法△ABC中方式1:延长AD到E,AD是BC边中线使DE=AD,连接BE方式2:间接倍长AD于F,延长MD到N,作BE⊥AD的延长线于E 使DN=MD,连接BE 连接CD例3、△ABC中,AB=5,AC=3,求中线AD的取值范围例4、已知在△ABC中,AB=AC,D在AB上,E在AC的延长线上,DE交BC于F,且DF=EF,求证:BD=CE课堂练习:已知CD=AB,∠BDA=∠BAD,AE是△ABD的中线,求证:∠C=∠BAEC作业:1、在四边形ABCD 中,AB ∥DC ,E 为BC 边的中点,∠BAE=∠EAF ,AF 与DC 的延长线相交于点F 。
试探究线段AB 与AF 、CF 之间的数量关系,并证明你的结论2、已知:如图,∆ABC 中,∠C=90︒,CM ⊥AB 于M ,AT 平分∠BAC 交CM 于D ,交BC 于T ,过D 作DE//AB 交BC 于E ,求证:CT=BE.3:已知在△ABC 中,AD 是BC 边上的中线,E 是AD 上一点,且BE=AC ,延长BE 交AC 于F ,求证:AF=EF(二)截长补短法教八年级上册课本中,在全等三角形部分介绍了角的平分线的性质,这一性质在许多问题里都有着广泛的应用.而“截长补短法”又是解决这一类问题的一种特殊方法,在无法进行直接证明的情形下,利用此种方法常可使思路豁然开朗.请看几例.例1. 已知,如图1-1,在四边形ABCD 中,BC >AB ,AD =DC ,BD 平分∠ABC .求证:∠BAD +∠BCD =180°.分析:因为平角等于180°,因而应考虑把两个不在一起的通过全等转化成为平角,图中缺少全等的三角形,因而解题的关键在于构造直角三角形,可通过“截长补短法”来实现.证明:过点D 作DE 垂直BA 的延长线于点E ,作DF ⊥BC 于点F ,如图1-2∵BD 平分∠ABC ,∴DE =DF , 在Rt △ADE 与Rt △CDF 中,⎩⎨⎧==CD AD DFDE ∴Rt △ADE ≌Rt △CDF (HL ),∴∠DAE =∠DCF . 又∠BAD +∠DAE =180°,∴∠BAD +∠DCF =180°, 即∠BAD +∠BCD =180°.例2. 如图2-1,AD ∥BC ,点E 在线段AB 上,∠ADE =∠CDE ,∠DCE =∠ECB .DABCM TEABCD图1-1FEDCBA图1-2求证:CD =AD +BC .分析:结论是CD =AD +BC ,可考虑用“截长补短法”中的“截长”,即在CD 上截取CF =CB ,只要再证DF =DA 即可,这就转化为证明两线段相等的问题,从而达到简化问题的目的. 证明:在CD 上截取CF =BC ,如图2-2在△FCE 与△BCE 中,⎪⎩⎪⎨⎧=∠=∠=CE CE BCE FCE CB CF ∴△FCE ≌△BCE (SAS ),∴∠2=∠1.又∵AD ∥BC ,∴∠ADC +∠BCD =180°,∴∠DCE +∠CDE =90°, ∴∠2+∠3=90°,∠1+∠4=90°,∴∠3=∠4. 在△FDE 与△ADE 中,⎪⎩⎪⎨⎧∠=∠=∠=∠43DEDE ADE FDE ∴△FDE ≌△ADE (ASA ),∴DF =DA , ∵CD =DF +CF ,∴CD =AD +BC .例3. 已知,如图3-1,∠1=∠2,P 为BN 上一点,且PD ⊥BC 于点D ,AB +BC =2BD .求证:∠BAP +∠BCP =180°.分析:与例1相类似,证两个角的和是180°,可把它们移到一起,让它们是邻补角,即证明∠BCP =∠EAP ,因而此题适用“补短”进行全等三角形的构造. 证明:过点P 作PE 垂直BA 的延长线于点E ,如图3-2∵∠1=∠2,且PD ⊥BC ,∴PE =PD , 在Rt △BPE 与Rt △BPD 中,⎩⎨⎧==BP BP PDPE ∴Rt △BPE ≌Rt △BPD (HL ),∴BE =BD .∵AB +BC =2BD ,∴AB +BD +DC =BD +BE ,∴AB +DC =BE 即DC =BE -AB =AE .在Rt △APE 与Rt △CPD 中,⎪⎩⎪⎨⎧=∠=∠=DC AE PDC PEA PD PE ∴Rt △APE ≌Rt △CPD (SAS),∴∠PAE =∠PCD 又∵∠BAP +∠PAE =180°,∴∠BAP +∠BCP =180° 例4. 已知:如图4-1,在△ABC 中,∠C =2∠B ,∠1=∠2.求证:AB =AC +CD .分析:从结论分析,“截长”或“补短”都可实现问题的转化,即延长AC 至E 使CE =CD ,或在AB 上截取AF =AC .ADB CEF1234图2-2ABCDP12N图3-1P12NABCD E 图3-2DCB A12图4-1证明:方法一(补短法)延长AC 到E ,使DC =CE ,则∠CDE =∠CED ,如图4-2∴∠ACB =2∠E ,∵∠ACB =2∠B ,∴∠B =∠E , 在△ABD 与△AED 中,⎪⎩⎪⎨⎧=∠=∠∠=∠AD AD E B 21 ∴△ABD ≌△AED (AAS ),∴AB =AE . 又AE =AC+CE =AC +DC ,∴AB =AC +DC . 方法二(截长法)在AB 上截取AF =AC ,如图4-3 在△AFD 与△ACD 中,⎪⎩⎪⎨⎧=∠=∠=AD AD AC AF 21 ∴△AFD ≌△ACD (SAS ),∴DF =DC ,∠AFD =∠ACD .又∵∠ACB =2∠B ,∴∠FDB =∠B ,∴FD =FB . ∵AB =AF +FB =AC +FD ,∴AB =AC +CD .上述两种方法在实际应用中,时常是互为补充,但应结合具体题目恰当选择合适思路进行分析。
第一讲 倍长中线法

第一讲 倍长中线法索引1:ABC ∆中,AD 是BAC ∠的平分线,且BD=CD ,求证AB=AC方法1:作DE ⊥AB 于E ,作DF ⊥AC 于F ,证明二次全等 方法2:辅助线同上,利用面积方法3:倍长中线AD索引2:△ABC 中 ,AD 是BC 边中线方式1: 延长AD 到E, 使DE=AD ,连接BE 方式2:间接倍长,作CF ⊥AD 于F ,作BE ⊥AD 的延长线于E ,方式2:延长MD 到N , 使DN=MD ,连接CD例1:如图,△ABC 中,AB=5,AC=3,AD 为中线,则AD 的取值范围是_________.例2:已知在△ABC 中,AB=AC,D 在AB 上,E 在AC 的延长线上,DE 交BC 于F ,且DF=EF ,求证:BD=CED C B A例3:已知在△ABC 中,AD 是BC 边上的中线,E 是AD 上一点,且BE=AC ,延长BE 交AC 于F ,求证:AF=EF例4:已知:如图,在ABC ∆中,AC AB ≠,D 、E 在BC 上,且DE=EC ,过D 作BA DF //交AE 于点F , DF=AC. 求证:AE 平分BAC ∠例5:已知CD=AB ,∠BDA=∠BAD ,AE 是△ABD 的中线,求证:∠C=∠BAE例6.B A B F D EC能力检测 1.已知:如图,AD 是△ABC 的中线,求证:AB+AC>2AD.2.如图,在△ABC 中,AB >AC ,E 为BC 边的中点,AD 为∠BAC 的平分线,过E 作AD 的平行线,交AB 于F ,交CA 的延长线于G .求证:BF =CG .3、在四边形ABCD 中,AB ∥DC ,E 为BC 边的中点,∠BAE=∠EAF ,AF 与DC 的延长线相交于点F 。
试探究线段AB 与AF 、CF 之间的数量关系,并证明你的结论4.如图,AD 为ABC ∆的中线,DE 平分BDA ∠交AB 于E ,DF 平分ADC ∠交AC 于F.求证:EF CF BE >+第 14 题图 D F CB EA5.如图△ABD和△ACE是△ABC外两个等腰直角三角形,∠BAD=∠CAE=90∘.(1)判断CD与BE有怎样的数量关系;(2)探索DC与BE的夹角的大小;(3)求证:FA平分∠DFE;(4)取BC的中点M,连MA,探讨MA与DE的数量关系和位置关系。
倍长中线法(经典例题)

精品文档倍长中线法知识网络详解:中线是三角形中的重要线段之一,在利用中线解决几何问题时,常常采用“倍长中线法”添加辅助线.所谓倍长中线法,就是将三角形的中线延长一倍,以便构造出全等三角形,从而运用全等三角形的有关知识来解决问题的方法.倍长中线法的过程:延长某某到某点,使某某等于某某,使什么等于什么(延长的那一条),用SAS 证全等(对顶角)倍长中线最重要的一点,延长中线一倍,完成SAS 全等三角形模型的构造。
【方法精讲】常用辅助线添加方法——倍长中线△ABC中方式1: 延长AD 到E ,AD 是BC 边中线使DE=AD ,接BEDABCEDA BC精品文档方式2:间接倍长作CF ⊥AD 于F ,延长MD 到N ,作BE ⊥AD 的延长线于 E使DN=MD ,连接BE连接CN经典例题讲解:例1:△ABC 中,AB=5,AC=3,求中线AD 的取值范围FE DCBA NDCBAM精品文档例2:已知在△ABC 中,AB=AC ,D 在AB 上,E 在AC 的延长线上,DE 交BC 于F ,且DF=EF ,求证:BD=CE过D 作DG//AC例3:已知在△ABC 中,AD 是BC 边上的中线,E 是AD 上一点,且BE=AC ,延长BE 交AC 于F ,求证:AF=EFFEAFEC AB D精品文档例4:已知:如图,在ABC∆中,ACAB≠,D、E在BC上,且DE=EC,过D作BADF//交AE于点F,DF=AC.求证:AE平分BAC∠ABFD E C例5:已知CD=AB ,∠BDA=∠BAD ,AE 是△ABD 的中线,求证:∠C=∠BAE自检自测:1、如图,△ABC 中,BD=DC=AC,E 是DC 的中点,求证,AD 平分∠BAE.E DABC2、在四边形ABCD 中,AB ∥DC ,E 为BC 边的中点,∠BAE=∠EAF ,AF 与DC 的延长线相交于点F 。
试探究线段AB 与AF 、CF 之间的数量关系,并证明你的结论.3、如图,AD 为ABC ∆的中线,DE 平分BDA ∠交AB 于E ,DF 平分ADC ∠交AC 于F. 求证:EF CF BE >+FEABCD4、已知:如图,∆ABC 中,∠C=90︒,CM ⊥AB 于M ,AT 平分∠BAC 交CM 于D ,交BC 于T ,过D 作DE//AB 交BC 于E ,求证:CT=BE.第 14 题图DF CBEADABCMTE。
2辅助线作法--倍长中线讲义

、倍长中线(线段)造全等典例讲解倍长中线法例:ABC 中,人。
是・BAC 的平分线,且BD=CD ,求证AB=ACE 方式1涎长AD 到E,使DE=AD ,连接BE【经典例题】 例1:已知在△ ABC 中,AB=AC ,。
在AB 上,E 在AC 的延长线上,DE 交BC 于F,且ADF=EF ,求证:BD=CE 人【方法精讲】常用辅助线添加方法一一倍长中线AD 是BC 边中线D及时练习1 : ZXABC 中,AB=5 , AC=3,求中线AD 的取值范围例3:如图AD 为ABC 的中线DE 平分・BDA 交AB 于E ,DF 平分・ADC 交AC 于 F.求证:BE CF EF例2:已知在△ ABC 中,AD 是BC 边上的中线, E 是AD ± 一点,且 BE 二AC,延长BE及时练习2、已知:如图,在ABC 中,作 AB 式AC ,D 、E 在BC 上,且DE=EC 过D DF // BA 交 AE 于点 F ,DF=AC.课后作业1.( “希望杯”试题)已知'如图△ ABC 中,AB=10AC=8贝忡线AD 的取值范围是方式2 :间接倍长(不一定是中线,以中点为端点的线段即可)作CF 丄AD 于F,作BE 丄AD 的延长线于E连接BE 延长MD 到N, 使 DN=MD 连接CD求证:AE 平分・BACA2:如图, △ ABC 中,E 、F 分别在AB AC±^Z®LDF, D 是中点,试比较BE+CF 与EF 过矢训练1:如图, △ ABC 中,BD=DC=ACE 是DC 的中点,求证:AD 平分Z BAE.例 5:已知 CD=AB , ZBDA= /BAD, AE 是 AABD 的中线,求证:Z C= ZBAE 的大小.2. (09崇文二模)以ABC的两边AB AC为腰分别向外作等腰Rt砂和等腰Rt,・BAD二CAE =90旌接DE, M、N分别是BC DE的中点•探究:AMABC与DE的位置矢系及数量矢系.(1)如图①当为直角三角形时,AM与DE的位置矢系是 _______________ ,线段AM与DE的数量矢系是 __________(2)将图①中的等腰RLABD绕点A沿逆时针方向旋转二(0V二<90)后,如图②所示, (1 )问中得到的两个结论是否发生改变?并说明理由.0 C M £。
倍长中线法(经典例题)
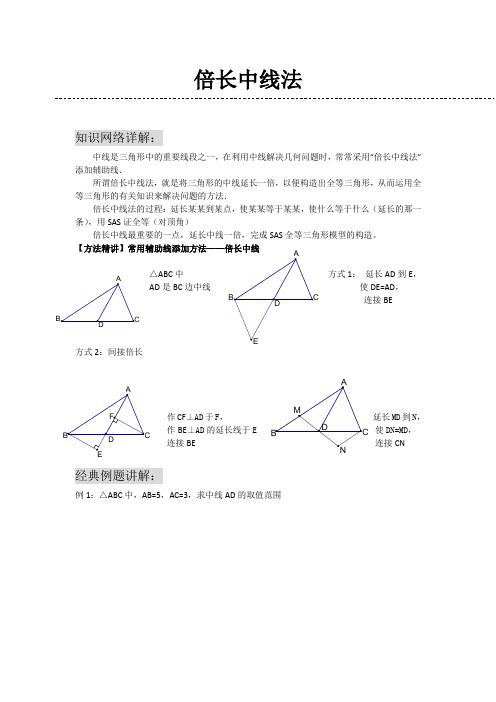
倍长中线法知识网络详解:中线是三角形中的重要线段之一,在利用中线解决几何问题时,常常采用“倍长中线法”添加辅助线.所谓倍长中线法,就是将三角形的中线延长一倍,以便构造出全等三角形,从而运用全等三角形的有关知识来解决问题的方法.倍长中线法的过程:延长某某到某点,使某某等于某某,使什么等于什么(延长的那一条),用SAS 证全等(对顶角)倍长中线最重要的一点,延长中线一倍,完成SAS 全等三角形模型的构造。
【方法精讲】常用辅助线添加方法——倍长中线△ABC 中 方式1: 延长AD 到E ,AD 是BC 边中线 使DE=AD ,连接BE方式2:间接倍长作CF ⊥AD 于F , 延长MD 到N ,作BE ⊥AD 的延长线于E 使DN=MD , 连接BE 连接CN经典例题讲解:例1:△ABC 中,AB=5,AC=3,求中线AD 的取值范围D ABCEDAB C F EDC B AN D C B AM例2:已知在△ABC 中,AB=AC ,D 在AB 上,E 在AC 的延长线上,DE 交BC 于F ,且DF=EF ,求证:BD=CE例3:已知在△ABC 中,AD 是BC 边上的中线,E 是AD 上一点,且BE=AC ,延长BE 交AC 于F ,求证:AF=EF例4:已知:如图,在ABC ∆中,AC AB ≠,D 、E 在BC 上,且DE=EC ,过D 作BA DF //交AE 于点F ,DF=AC.求证:AE 平分BAC ∠FE DA B CFEC ABD AB F D E C例5:已知CD=AB ,∠BDA=∠BAD ,AE 是△ABD 的中线,求证:∠C=∠BAE自检自测:1、如图,△ABC 中,BD=DC=AC,E 是DC 的中点,求证,AD 平分∠BAE.2、在四边形ABCD 中,AB ∥DC ,E 为BC 边的中点,∠BAE=∠EAF ,AF 与DC 的延长线相交于点F 。
试探究线段AB 与AF 、CF 之间的数量关系,并证明你的结论.E D ABCF EAB C D3、如图,AD 为ABC ∆的中线,DE 平分BDA ∠交AB 于E ,DF 平分ADC ∠交AC 于F. 求证:EF CF BE >+4、已知:如图,∆ABC 中,∠C=90︒,CM ⊥AB 于M ,AT 平分∠BAC 交CM 于D ,交BC 于T ,过D 作DE//AB 交BC 于E ,求证:CT=BE.第 14 题图DF CBEADABCMTE。
(完整版)倍长中线法(经典例题)0001

倍长中线法知识网络详解:中线是三角形中的重要线段之一,在利用中线解决几何问题时, 常常采用 倍长中线法 添加辅助线.所谓倍长中线法,就是将三角形的中线延长一倍,以便构造出全等三角形,从而运用全 等三角形的有关知识来解决问题的方法.倍长中线法的过程: 延长某某到某点,使某某等于某某,使什么等于什么(延长的那一 条),用SAS 证全等(对顶角)倍长中线最重要的一点,延长中线一倍,完成SAS 全等三角形模型的构造。
【方法精讲】常用辅助线添加方法一一倍长中线方式2:间接倍长作 CF 丄 AD 于 F ,作BE 丄AD 的延长线于E连接BE经典例题讲解:例ABC 中,AB=5, AC=3,求中线 AD 的取值范围△ ABC 中AD 是BC 边中线使 DE=AD, 连接BEA B 方式1 :延长AD 到E , D A DE A连接CNN例2:已知在△ ABC 中,AB=AC D 在AB 上,E 在AC 的延长线上,DE 交BC 于F ,且DF=EF , 求证:BD=CE例3:已知在△ ABC 中,AD 是BC 边上的中线,E 是AD 上一点,且 BE=AC 延长 BE 交AC 于F ,求证:AF=EFABC 中,AB AC ,D 、E 在 BC 上,且 DE=EC 过 D 作DF //BA 例4:已知:如图,在 交 AE 于点 F , DF=AC. 求证:AE 平分 BAC D例5:已知CD=AB / BDA=Z BAD, AE是厶ABD的中线,求证:/ C=Z BAE1、如图,△ ABC中,BD=DC=AC,E是DC的中点,求证,AD平分/ BAE.2、在四边形ABCD中,AB// DC, E为BC边的中点,/ BAE=Z EAF, AF与DC的延长线相交于点F。
试探究线段AB与AF、CF之间的数量关系,并证明你的结论•E3、如图,AD为ABC的中线,DE平分BDA交AB于E, DF平分ADC交AC于F.求证: BE CF EF第14题图4、已知:如图,ABC中,C=90 , CM AB于M , AT平分BAC交CM于D,交BC于T,过D作DE//AB交BC于E,求证:CT=BE.C。
倍长中线法(经典例题)2

倍长中线法(加倍法)知识网络详解:中线是三角形中的重要线段之一,在利用中线解决几何问题时,常常采用“倍长中线法”添加辅助线.所谓倍长中线法,就是将三角形的中线延长一倍,以便构造出全等三角形,从而运用全等三角形的有关知识来解决问题的方法.倍长中线法的过程:延长某某到某点,使某某等于某某,使什么等于什么(延长的那一条),用SAS证全等(对顶角)倍长中线最重要的一点,延长中线一倍,完成SAS全等三角形模型的构造。
经典例题讲解:例1:△ABC中,AB=5,AC=3,求中线AD的取值范围。
例2:已知在△ABC中,AB=AC,D在AB上,E在AC的延长线上,DE交BC于F,且DF=EF,求证:BD=CE例3:已知在△ABC 中,AD 是BC 边上的中线,E 是AD 上一点,且BE=AC ,延长BE 交AC 于F ,求证:AF=EF例4:如图,AD 为ABC ∆的中线,DE 平分BDA ∠交AB 于E ,DF 平分ADC ∠交AC 于F. 求证:EF CF BE >+例5:已知CD=AB ,∠BDA=∠BAD ,AE 是△ABD 的中线,求证:∠C=∠BAE第 14 题图DF CBEAB自检自测:1、如图,△ABC 中,BD=DC=AC,E 是DC 的中点,求证,AD 平分∠BAE 。
2、在四边形ABCD 中,AB ∥DC ,E 为BC 边的中点,∠BAE=∠EAF ,AF 与DC 的延长线相交于点F 。
试探究线段AB 与AF 、CF 之间的数量关系,并证明你的结论.3、已知:如图,在ABC ∆中,AC AB ≠,D 、E 在BC 上,且DE=EC ,过D 作BA DF //交AE 于点F ,DF=AC.求证:AE 平分BAC ∠F EAB C DABFDEC4、如图,CB、CD分别是钝角△AEC和锐角△ABC的中线,且AC=AB.求证:①CE=2CD.②CB平分∠DCE.5、如图已知△ABC,AD是BC边上的中线,分别以AB边、AC边为直角边各向形外作等腰直角三角形,求证EF=2AD.4、已知:如图,?ABC 中,?C=90?,CM?AB 于M ,AT 平分?BAC 交CM 于D ,交BC 于T ,过D 作DE//AB 交BC 于E ,求证:CT=BE.倍长中线法(加倍法)知识网络详解:中线是三角形中的重要线段之一,在利用中线解决几何问题时,常常采用“倍长中线法”添加辅助线.所谓倍长中线法,就是将三角形的中线延长一倍,以便构造出全等三角形,从而运用全等三角形的有关知识来解决问题的方法.倍长中线法的过程:延长某某到某点,使某某等于某某,使什么等于什么(延长的那一条),用SAS 证全等(对顶角)倍长中线最重要的一点,延长中线一倍,完成SAS 全等三角形模型的构造。
中线倍长法及截长补短经典讲义

几何证明中常用辅助线(一)中线倍长法:例1、求证:三角形一边上的中线小于其他两边和的一半。
已知:如图,△ABC 中,AD 是BC 边上的中线,求证:AD ﹤21(AB+AC)小结:涉及三角形中线问题时,常采用延长中线一倍的办法,即中线倍长法。
它可以将分居中线两旁的两条边AB 、AC 和两个角∠BAD 和∠CAD 集中于同一个三角形中,以利于问题的获解。
例2、中线一倍辅助线作法△ABC 中方式1:延长AD 到E , AD 是BC 边中线使连接BE方式2:间接倍长方式3:作CF ⊥AD 于F ,延长MD 到N 作BE ⊥AD 的延长线于E 使DN=MD ,连接BE连接CD例3、△ABC 中,AB=5,AC=3,求中线AD 的取值范围例4、已知在△ABC 中,AB=AC ,D 在AB 上,E 在AC 的延长线上,DE 交BC 于F ,且DF=EF ,求证:BD=CE 课堂练习:已知CD=AB ,∠BDA=∠BAD ,AE 是△ABD 的中线, 求证:∠C=∠BAE 作业:1、在四边形ABCD 中,AB ∥DC ,E 为BC 边的中点,∠BAE=∠EAF ,AF 与DC 的延长线相交于点F 。
试探究线段AB 与AF 、CF 之间的数量关系,并证明你的结论2、已知:如图,?ABC 中,?C=90?,CM ?AB 于M ,AT 平分?BAC 交CM 于D ,交BC 于T ,过D 作DE//AB 交BC 于E ,求证:CT=BE. 3:已知在△ABC 中,AD 是BC 边上的中线,E 是AD 上一点,且BE=AC ,延长BE 交AC 于F ,求证:AF=EF (二)截长补短法教八年级上册课本中,在全等三角形部分介绍了角的平分线的性质,这一性质在许多问题里都有着广泛的应用.而“截长补短法”又是解决这一类问题的一种特殊方法,在无法进行直接证明的情形下,利用此种方法常可使思路豁然开朗.请看几例. 例1.已知,如图1-1,在四边形ABCD 中,BC >AB ,AD =DC ,BDCBCABCD图1-1平分∠ABC .求证:∠BAD +∠BCD =180°.分析:因为平角等于180°,因而应考虑把两个不在一起的通过全等转化成为平角,图中缺少全等的三角形,因而解题的关键在于构造直角三角形,可通过“截长补短法”来实现. 证明:过点D 作DE 垂直BA 的延长线于点E ,作DF ⊥BC 于点F ,如图1-2∵BD 平分∠ABC ,∴DE =DF , 在Rt △ADE 与Rt △CDF 中,∴Rt △ADE ≌Rt △CDF (HL ),∴∠DAE =∠DCF . 又∠BAD +∠DAE =180°,∴∠BAD +∠DCF =180°, 即∠BAD +∠BCD =180°.例2. 如图2-1,AD ∥BC ,点E 在线段AB 上,∠ADE =∠CDE ,∠DCE =∠ECB .求证:CD =AD +BC .分析:结论是CD =AD +BC ,可考虑用“截长补短法”中的“截长”,即在CD 上截取CF =CB ,只要再证DF =DA 即可,这就转化为证明两线段相等的问题,从而达到简化问题的目的. 证明:在CD 上截取CF =BC ,如图2-2在△FCE 与△BCE 中,∴△FCE ≌△BCE (SAS ),∴∠2=∠1.又∵AD ∥BC ,∴∠ADC +∠BCD =180°,∴∠DCE +∠CDE =90°, ∴∠2+∠3=90°,∠1+∠4=90°,∴∠3=∠4. 在△FDE 与△ADE 中,∴△FDE ≌△ADE (ASA ),∴DF =DA , ∵CD =DF +CF ,∴CD =AD +BC .例3.已知,如图3-1,∠1=∠2,P 为BN 上一点,且PD ⊥BC 于点D ,AB +BC =2BD .求证:∠BAP +∠BCP =180°.分析:与例1相类似,证两个角的和是180°,可把它们移到一起,让它们是邻补角,即证明∠BCP =∠EAP ,因而此题适用“补短”进行全等三角形的构造. 证明:过点P 作PE 垂直BA 的延长线于点E ,如图3-2∵∠1=∠2,且PD ⊥BC ,∴PE =PD , 在Rt △BPE 与Rt △BPD 中,⎩⎨⎧==BP BP PDPE ∴Rt △BPE ≌Rt △BPD (HL ),∴BE =BD .∵AB +BC =2BD ,∴AB +BD +DC =BD +BE ,∴AB +DC =BE 即DC =BE -AB =AE .在Rt △APE 与Rt △CPD 中,⎪⎩⎪⎨⎧=∠=∠=DC AE PDC PEA PD PE FE DCBA图1-2ADB CE F1234图2-2ABCDP12N图3-1P12NABCDE 图3-2DCB A 12图4-1∴Rt △APE ≌Rt △CPD (SAS),∴∠PAE =∠PCD 又∵∠BAP +∠PAE =180°,∴∠BAP +∠BCP =180°例4. 已知:如图4-1,在△ABC 中,∠C =2∠B ,∠1=∠2.求证:AB =AC +CD .分析:从结论分析,“截长”或“补短”都可实现问题的转化,即延长AC 至E 使CE =CD ,或在AB 上截取AF =AC .证明:方法一(补短法)延长AC 到E ,使DC =CE ,则∠CDE =∠CED ,如图4-2 ∴∠ACB =2∠E ,∵∠ACB =2∠B ,∴∠B =∠E , 在△ABD 与△AED 中,∴△ABD ≌△AED (AAS ),∴AB =AE . 又AE =AC+CE =AC +DC ,∴AB =AC +DC . 方法二(截长法)在AB 上截取AF =AC ,如图4-3 在△AFD 与△ACD 中,∴△AFD ≌△ACD (SAS ),∴DF =DC ,∠AFD =∠ACD . 又∵∠ACB =2∠B ,∴∠FDB =∠B ,∴FD =FB . ∵AB =AF +FB =AC +FD ,∴AB =AC +CD .上述两种方法在实际应用中,时常是互为补充,但应结合具体题目恰当选择合适思路进行分析。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
倍长中线法(经典例题)
倍长中线法
知识网络详解:
中线是三角形中的重要线段之一,在利用中线解决几何问题时,常常采用“倍长中线法”添加辅助线.
所谓倍长中线法,就是将三角形的中线延长一倍,以便构造出全等三角形,从而运用全等三角形的有关知识来解决问题的方法.
倍长中线法的过程:延长某某到某点,使某某等于某某,使什么等于什么(延长的那一条),用SAS证全等(对顶角)
倍长中线最重要的一点,延长中线一倍,完成SAS全等三角形模型的构造。
【方法精讲】
△ABC中延长AD到E, AD是BC边中线使DE=AD,
连接BE
方式2:间接倍长
作CF⊥AD于F,延长MD 到N,
作BE⊥AD的延长线于E 使DN=MD,
连接BE 连接CN
经典例题讲解:
例1:△ABC中,AB=5,AC=3,求中线AD的取值范围
例2:已知在△ABC中,AB=AC,D在AB上,E在AC的延长线上,DE交BC于F,且DF=EF,求证:BD=CE
过D作DG//AC
例3:已知在△ABC 中,AD 是BC 边上的中线,E 是AD 上一点,且BE=AC ,延长BE 交AC 于F ,求证:AF=EF
例4:已知:如图,在ABC ∆中,AC AB ≠,D 、E 在
BC 上,且DE=EC ,过D 作BA DF //交AE 于点F ,DF=AC.
求证:AE 平分BAC ∠
例5:已知CD=AB ,∠BDA=∠BAD ,AE 是△ABD 的中线,求证:∠C=∠BAE
B
A
B
F
D
E
C
自检自测:
1、如图,△ABC中,BD=DC=AC,E是DC的中点,求证,AD平分∠BAE.
2、在四边形ABCD中,AB∥DC,E为BC边的中点,∠BAE=∠EAF,AF与DC的延长线相交于点F。
试探究线段AB与AF、CF之间的数量关系,并证明你的结论.
3、如图,AD为ABC
∆的中线,DE平分BDA
∠交AB于E,DF平分ADC
∠交AC于F. 求证:EF
CF
BE>
+
E
A
B C
4、已知:如图,∆ABC 中,∠C=90︒,CM ⊥AB 于M ,AT 平分∠BAC 交CM 于D ,交BC 于T ,过D 作DE//AB 交BC 于E ,求证:CT=BE.
第 14 题图 D
F C
B
E
A
D
A
B
C
M
T
E。
