复数的方根、乘幂与复变函数
复变函数第一章

z1 z1 z2 z2
Arg(
z1 z2
)
Arg
z1
Arg
z2
1、 幂函数
非零复数 z 的 n 次幂
zn rnein rn (cos n i sin n )
其中
zn z n , Arg zn nArg z.
令 r = 1,则得棣莫弗公式
(cos i sin )n cos n i sin n
21
•连续曲线 若实函数 x(t) 和 y(t) 在闭区间[, ]
上连续,则方程组
x x(t),
y
y(t),
( t )
或复数方程 z z(t) x(t) iy(t) ( t )
代表一条平面曲线,称为 z 平面上的连续曲线.
进一步地,若在 t 上,x '(t) 及 y '(t) 存在、
E(C)
线 C 把 z 平面唯一地分成
C、I(C) 及 E(C) 三个点集,
I(C)
它们具有如下性质:
(1)彼此不交;
O
C
x
(2)I(C) 是一个有界区域(称为 C 的内部);
(3)E(C) 是一个无界区域(称为 C 的外部).
25
•单连通区域 设 z 平面上的区域 D, 若在 D 内 无论怎样画简单闭曲线,其内部仍全含于 D, 则称 D 为单连通区域. 非单连通的区域称为多 连通区域.
y
z
v
w
2 O 2 x
4 O 4 u
31
•反函数 假设函数 w=f(z) 的定义域是 z 平面上的 集合 G,值域是 w 平面上的集合 G*. 对 G* 中 的每一个点 w,在 G 中有一个(或至少两个) 点与之相对应,则在 G* 上确定了一个单值(或
复数与复变函数的基本运算与性质

复数与复变函数的基本运算与性质复数是数学中的一种重要概念,可以用来描述平面上的点或向量。
复变函数则是一种将复数作为自变量和函数值的函数。
复数与复变函数都有其特定的基本运算与性质,本文将详细介绍。
一、复数的基本运算与性质1. 复数的表示复数可表示为 a + bi 的形式,其中 a 和 b 是实数,i 是虚数单位。
实部 a 表示复数在实轴上的投影,虚部 b 表示复数在虚轴上的投影。
2. 复数的加法和减法复数的加法和减法遵循实数的运算法则,即分别对实部和虚部进行相应的运算。
3. 复数的乘法复数的乘法按照分配律进行,即将每个部分相乘后再进行合并。
4. 复数的除法复数的除法可以通过乘以倒数的方式进行,即将除数的倒数乘以被除数。
5. 共轭复数共轭复数是指保持实部不变而虚部取负的两个复数。
共轭复数的乘积为实数,而共轭复数的和差仍为复数。
6. 模和辐角复数的模表示它与原点的距离,辐角表示其与实轴正向的夹角。
二、复变函数的基本运算与性质1. 复变函数的定义复变函数将复数作为自变量和函数值,可以表示为 f(z) = u(x, y) +iv(x, y),其中 u 和 v 分别是 x 和 y 的实函数,i 是虚数单位。
2. 复变函数的连续性复变函数 f(z) 连续的充要条件是 u 和 v 在 z 的实部和虚部上都连续。
3. 复变函数的导数对于复变函数 f(z),如果其在某一点 z 处存在导数,那么导数表示为 f'(z) = u_x(x, y) + iv_x(x, y),其中 u_x 和 v_x 分别是 u 和 v 对 x 的偏导数。
4. 柯西—黎曼方程柯西—黎曼方程是复变函数的一个重要性质,即 u_x = v_y 和 u_y = -v_x。
柯西—黎曼方程保证了复变函数可导的充分必要条件。
5. 复变函数的积分复变函数的积分可以用路径积分的方法进行,路径积分表示了函数在不同路径下的变化。
路径积分不依赖于具体的路径选择,而只取决于路径的起点和终点。
第一章3复数的乘幂与方根

第二节
复数的运算
一、复数的代数运算及共轭复数的运算法则
二、复数的代数运算的几何表示
三、复数的乘幂与方根
三、复数的乘幂与方根
1. 乘幂
设复数 ≠ 0, = (cos+sin),
则 = (cosn+sinn) ,为正整数.
规定 z
−n
1
= n.
z
), w3 = 2 (cos
+ i sin
),
16
16
16
16
1
8
1
8
这四个根是内接于以原点为圆心,半径为 2的圆的正方形的顶点
8
谢谢观看!
当 = , + 1, ⋯ 时,这些根又重复出现.
=
=
1
[cos
2 在几何上,
+ 2
+ 2
+ sin
], = 0,1,2, ⋯ , − 1
1
的个值是以原点为圆心, 为
半径的圆的内接正边形的个顶点.
例3.求 1 + .
4
解: 1 + = 2(cos + sin )
特别地,当 = 1时,得到棣莫弗公式
(cos+sin) = cosn+sinn.
2. 方根
z 称为的次方根.
设 z = r (cos + i sin ), w = (cos + i sin )
方程 wn = z 的根 w ,即 w =
n
n
有 (cos n + i sin n ) = r (cos + i sin )
复变函数1-3
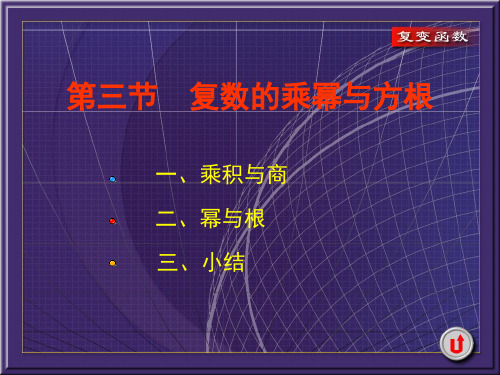
i,
z1 z2
cos
3
6
i
sin
3
6
3 1i. 22
7
二、幂与根
1. n次幂: n 个相同复数 z 的乘积称为z 的 n 次幂,
记作 zn , zn z z z .
n个
对于任何正整数n, 有 zn rn(cosn i sin n ).
如果我们定义
zn
1 zn
,
那么当
幂为负整数时,
求出z的幂.
8
2.棣莫佛公式
当 z 的模 r 1,即 z cos i sin ,
(cos i sin )n cosn i sin n .
棣莫佛公式
3. 方程 wn z 的根 w, 其中 z 为已知复数.
w
n
z
r
1 n
cos
2kπ n
i sin
2kπ n
(k 0,1,2, ,n 1)
w2
o
w0 x
w3
15
三、小结
应熟练掌握复数乘积与商,幂与根的运算. 在各种形式中以三角形式、指数形式最为方便:
z1
z2
r1
r ei(12 ) 2
z2 r e2 i(2 1 )
z1 r1
对于任何正整数n, 有 zn rn(cosn i sin n ).
w
n
z
r
1 n
cos
2kπ
i sin
2kπ
n
n
(k 0,1,2, ,n 1)
放映结束,按Esc退出.
16
i sin(1 2 n )]
r1 r2 rnei(12 n ) .
5
定理二 两个复数的商的模等于它们的模的商; 两 个复数的商的辐角等于被除数与除数的辐角之差.
1.2复数的运算及其几何意义

x1 ) y1 )
参数 t (, ),
上式可以借助复数合并为一个式子,即:
z x(t ) iy(t ) x1 t( x2 x1 ) + i [y1 t( y2 y1 )]. 过z1 , z2的直线方程是: z z(t ) z1 ), 0 t 1.
则将向量OZ1按逆时针方向
•z
y
旋转一个角 2 ,
r • z1
再伸长(缩短)到原来的 r2 倍,
所得向量OZ就表示乘积z1 z2.
1
o
r1
2
•
r2
z2
x
z1z2 r1r2[cos(1 2 ) i sin(1 2 )]
10
可将结论推广到 n 个复数相乘的情况:
设 zk rk (cosk i sink ) rkeik , (k 1,2,, n)
28
cos
π 4
2kπ 4
i sin
π 4
2kπ 4
w3
(k 0,1,2,3).
即 0
1
28
cos
π 16
i
sin
π 16
,
1
1
28
cos
9π 16
i
sin
9π 16
,
2
1
28
cos
17π 16
i
sin
17π 16
,
3
1
28
cos
25π 16
i sin
25π 16
.
15
;
(2) z z;
(3) z z z 2 ;
(4) z z 2 Re(z), z z 2i Im(z).
复数和、差、共轭的几何意义
复变函数的可导与解析

zz0
z z0
定义3
设复变函数 w f (z)在N (z0 )内有定义, 如 果 存 在 与 z无 关 的 复 常 数 L, 使 得 对 z z0 z N ( z0 ), 总有
w f ( z0 z) f ( z0 ) Lz o(| z |), 则称w f (z)在点z0处可微,并称 Lz为函数f (z)在点z0处的微分,记作
f(z)在 复 平 面 上 处 处处 处 解可 析导 ,, 且 f(z)ux ivx ex(coysisiny)f(z)
( 2 )f(z)xyixy
解 u(x, y) x y,v(x, y) xy,而
ux 1,uy 1, vx y,vy x ux,uy,vx,vy在复平面上处处但 连仅 续在 , x1, y 1时满足 CR条件
(7) f z 1w,其中与为两个互为反 数的单值函,且数w 0.
需要注意的是,复变数函的导数定义与一元 实函数的导数定义,然虽形式上一样,但在 本质上有很大的不同因。为一元实函数导数 定义中的极限是一元函实数的极限,而复变 函数导数定义中的极对限应于二元实函数的 极限。
设f(z)在z0可 导 , 即 极 限
f(z)在z 1i 处可导,在复平面上 处处不解析 .
( 3)f(z)x2iy
解 u(x, y) x2 ,v(x, y) y,而
ux 2x, uy 0, vx 0,vy 1 ux ,uy ,vx ,vy在复平面上处处连续, 但仅在直线x 1 上满足C R条件
f(z)在 直 线 x21上可 导 , 在 复 平 面 2
y
x y
y x
z在第一象限 z在第二象限 z在第三象限
x
arctan
y x
z在第四象限
复数的幂与根的运算

复数的幂与根的运算复数是由实部和虚部组成的数,可以表示为a + bi的形式,其中a为实部,b为虚部,i为虚数单位。
在复数运算中,我们经常会遇到复数的幂与根的运算,本文将详细讨论这两种运算及其特性。
一、复数的幂运算复数的幂运算是将一个复数自乘若干次。
设有一个复数z = a + bi,其中a为实部,b为虚部。
1. 复数的平方运算将复数z自乘一次,即z^2 = (a + bi)(a + bi)。
展开得到z^2 = a^2 + 2abi - b^2,整理后可得z^2 = (a^2 - b^2) + 2abi。
可以看出,复数的平方仍旧是一个复数,实部为a^2 - b^2,虚部为2ab。
2. 复数的立方运算将复数z自乘两次,即z^3 = z^2 * z = (a^2 - b^2 + 2abi)(a + bi)。
展开得到z^3 = (a^3 + 3a^2bi - 3ab^2 - b^3i),整理后可得z^3 = (a^3- 3ab^2) + (3a^2b - b^3)i。
同样地,复数的立方仍旧是一个复数,实部为a^3 - 3ab^2,虚部为3a^2b - b^3。
3. 复数的n次幂运算将复数z自乘n次,即z^n = z^(n-1) * z = ((a + bi)^(n-1))(a + bi)。
根据二项式定理展开后可得z^n = (a^n + na^(n-1)bi + C(n, 2)a^(n-2)b^2i^2 + ... + C(n, n-1)ab^(n-1)i^(n-1) + b^n * i^n)。
在上述展开式中,可以观察到幂次大于1的i项会相互抵消,因为i^2 = -1,而i^3 = -i,i^4 = 1,i^5 = i,以此类推。
因此,最终复数的n次幂展开式可简化为z^n = (a^n + C(n, 2)a^(n-2)b^2 - C(n, 4)a^(n-4)b^4 + ... + (-1)^(n/2)b^n) + (na^(n-1)b - C(n, 3)a^(n-3)b^3 + ... + (-1)^((n-1)/2)ab^(n-1))i。
复变函数的总结
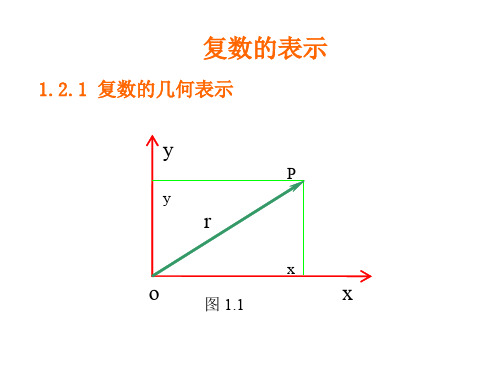
n0 n!
2!
n!
cos z (1)n1 z2n 1 1 z2 1 z4 (1)n1 z2n
n0 (2n)!
2! 4!
(2n)!
sin z (1)n z2n1 z 1 z3 1 z5 (1)n z2n1
n0 (2n 1)!
区域
z0的去心邻域 : 点集 z 0 z z0
简单闭曲线
称为z0的去心邻域
简
非简单
单
如果简单曲线的起点和终点重合,则称为简单闭曲线.
单连通与多连通
A l
l
B
(a)
l
A l
l B
(b) 图 1.6
ห้องสมุดไป่ตู้
A l
l
B
(c)
复变函数 f (z)
等价两个二元实函数 u u(x, y) v v(x, y)
考察复数项级数
k 0
wk
,如果 lim k
则当 l 1时,级数绝对收敛;当 l
wk1 l , w1k时,级数发
散;当 l 1,级数的敛散性需要进一步检验。
2、Gauss 判别法
中
对于
k 0
1且
wk
,
若有
wk wk 1
为复数。则当 Reμ
>
1
k
O
则称级数 fn (z) 在 B 内(或曲线 L 上)一致收敛。 n0
幂级数
定义 各项均为幂函数的复变函数项级数:
ak (z b)k a0 a1(z b) a2 (z b)2
复变函数第一章

1.1.4.复数四则运算的几何意义 .1.4.复数四则运算的几何意义 , θ θ 设有两个复数 z1 = r1(cos 1 + i sinθ1) z2 = r2 (cos 2 + i sinθ2)
则,z1 z 2 = r1 (cos θ 1 + i sin θ 1 )r2 (cos θ 2 + i sin θ 2 )
例1:下列复数化为三角表示式与指数表示式
2i ( 1 ) z = − 12 − 2i, ( 2 ) z = , ( 3 ) z = −3 + 4i −1+ i
例3:求下列方程所表示的曲线
(1) |z + i| = 2, ( 2) |z − 2i| = |z + 2|, ( 3 ) Im(i + z) = 4
________
7 1 z1 ∴ ( )=− + i z2 5 5
__ 1 3i 例2: z = - − 求 Re (z),Im (z)与z z i 1-i
− ( 1 − i) − 3i(i) − 1 + i + 3 2 + i ( 2 + i)( 1 − i) = = 解: z = = i( 1 − i) i +1 1+ i 2
x
(3)幅角主值的求法 (3)幅角主值的求法 y arctan x , ( x > 0 , y > 0 ) arctan y + π ( x < 0 , y > 0 ) , x arg z = arctan y − π , ( x < 0 , y < 0 ) x y arctan , ( x > 0, y < 0) x
复变函数8-17

第一章复数与复变函数1.1复数1.1.1复数及其代数运算1.复数概念,i虚数单位复数:z=x+iy(x,y),x,y分别称为实部与虚部,x=Re(z),y=Im(z)x=0,y,z=iy,纯虚数;y=0,z=x实数复数的相等,复数等于零,复数不可比较大小,只能说相等与否。
共轭复数:实部相等,虚部互为相反数,及x+iy与x-iy互为共轭复数,记。
2.复数的代数运算:加减乘除满足定理:(1)交换律(2)结合律(3)分配律注意:(1)z+0=z ,0*z=0 (2)z*1=z ,z*=1(3)若,则,中至少有一个为零,反之亦然;(4)(5)共轭复数运算性质:(1)(2)(3)(4)1.1.2复数的几何表示1.复平面:x轴定义为实轴,y轴虚轴;z=x+iy与一对有序实数(x,y)唯一确定。
xOy定义为复平面2.复数的模与辐角复数的向量表示;复数的模:向量z的长度为复数z的模,记(1)(2),z(3),,(4)(5)推论:(6)复数的辐角:Argz,无穷多个,相差2π的整数倍。
辐角主值:-π,称为辐角主值,记argz1.1.3复数四则运算的几何意义直角坐标与极坐标的关系:z=x+iy,z=r(),复数z的三角表达式。
讲解例题:复数乘除法的几何表达:(),()()()()定理1.1 两个非零复数乘积的模它们模的乘积,乘积的辐角等于它们辐角的和。
定理1.2 两个非零复数商的模它们模的商,商的辐角等于被除数与除数的辐角差。
复数的代数表达:z=x+iy复数的三角表达:z=r()欧拉公式:复数的指数表达:z=r()()习题讲解:1.1.4扩充复平面1.复数的球面表示(概念的理解)2. “无穷远点”的概念。
扩充复平面:包含无穷远点在内的复平面称为扩充复平面。
无穷远点是唯一的。
3.复数复数与扩充复平面上的无穷远点相对应。
复数的实部、虚部、辐角均无意义。
z=的运算规定(了解)1.2复数的乘幂与方根1.2.1复数的乘幂复数的指数表达:z=r,对于任何整数n,复数z的乘幂下列公式都成立:当r=1时,()欧拉公式:即可得出:()()1.2.2复数的方根(w,),复数w为复数z的n次根,记作w=,或者w=。
复变函数与积分变换重要知识点归纳

复变函数复习重点(一)复数的概念 1.复数的概念:zx iy =+,,x y 是实数, ()()Re ,Im x z y z ==.21i =-.注:一般两个复数不比较大小,但其模(为实数)有大小. 2.复数的表示1)模:22z x y =+;2)幅角:在0z ≠时,矢量与x 轴正向的夹角,记为()Arg z (多值函数);主值()arg z 是位于(,]ππ-中的幅角。
3)()argz 与arctanyx之间的关系如下: 当0,x > arg arctan yz x=;当0,arg arctan 0,0,arg arctan yy z x x y y z xππ⎧≥=+⎪⎪<⎨⎪<=-⎪⎩; 4)三角表示:()cos sin z z i θθ=+,其中arg z θ=;注:中间一定是“+”号。
5)指数表示:i zz e θ=,其中arg z θ=。
(二) 复数的运算 1.加减法:若111222,z x iy z x iy =+=+,则()()121212z z x x i y y ±=±+±2.乘除法: 1)若111222,z x iy z x iy =+=+,则()()1212122112z z x x y y i x y x y =-++;()()()()112211112121221222222222222222x iy x iy z x iy x x y y y x y x i z x iy x iy x iy x y x y +-++-===+++-++。
2)若121122,i i z z e z z e θθ==, 则()121212i z z z z e θθ+=;()121122i z z e z z θθ-= 3.乘幂与方根1) 若(cos sin )i z z i z e θθθ=+=,则(cos sin )n nn in z z n i n z e θθθ=+=。
复变函数论.

z
n
k
n
ze
i
arg z 2 k n
, k 0,1, 2,
n 1。
注意:从几何上看, n个顶点。
n
z 的 n 个值就是以原点为中心, r 为半径圆的内接正n边形的
1 n
例2:求 3 8 解:
3
8
8
3
8 e
3
i
2 k
3
, k 0,1, 2
3
0
8 e 3 2 cos i sin 1 3i 3 3
复数的四则运算定义为:设z1=x1+iy1和z2=x2+iy2
( z1 z2 ) ( x1 x2 ) i( y1 y2 )
z1z2 ( x1x2 y1 y2 ) i( x1 y2 x2 y1 )
z1 x1 x2 y1 y2 x2 y1 x1 y2 2 i z2 0 2 2 2 z2 x2 y2 x2 y2
N z0
P22
定义4:设有点 z0 ,点集 E
1) 若 0, s.t. N z0 E ,则 z0 为 E 的内点 2) 若 0, s.t. N z0 E ,则 z0 为 E 的外点 3) 若 0,
N z0 既有 E 中点也有非 E的点,
(1.9)
我们分别称(1.6)、(1.9)为非零复数的三角形式和指数形式. 利用 复数的三角表示,我们可以更简单的表示复数的乘法与除法: 设z1、z2是两个非零复数,则有
z1 | z1 | (cosArgz1 i sin Argz1 )
z2 | z2 | (cosArgz2 i sin Argz2 )
复数的乘幂与方根

Arg( z1z2 ) Argz1 Argz2.
3
几何意义
从几何上看, 两复数对应的向量分别为 z 先把 z1 按逆时针方向 y
z1 , z2 ,
旋转一个角 2 ,
再把它的模扩大到r2 倍, 所得向量 z 就表示积 z1 z2 .
r
o
1
z1
r1
2
r2
z2
n n 1 4 4 n w2 r (cos i sin ) n n
wn 1 r (cos
1 n
w1 r (cos
1 n
2
i sin
2
)
2(n 1)
n
i sin
2(n 1)
n
)
结论:在几何上 , n z的n个值就是以原点为中心 , n r为半径 的圆的内接正 n边形的n个顶点 .
x
复数相乘就是把模相乘, 辐角相加.
4
如果用指数形式表示复数:
z1 r1 e , z 2 r2 e z1 z 2 r1r2 ei (1 2 )
由此逐步可证, 如果
i 1
i 2
则定理一可简明地表示为
z k rk e
i k
rk (cos k i sin k ), (k 1,2, , n), i sin( 1 2 n )]
17 17 w2 2 cos i sin , 16 16 25 25 8 w3 2 cos i sin . 16 16
8
w1
y
1+i
2
8
2
复变函数复习提纲 (1)

1
1
i
2 k
n
, ,
i
k 0,1,
, n 1
如: z e
1 4
i 2 k
i
2 k
4
k 0,1, 2,3
2 k
2
二次根式:
z ei e
ln z
i 2 k
e
k 0,1
m z zk
1 d m1 m 计算: Re sf zk lim z zk f z z zk m 1 ! dz m 1
(3)本性奇点处的留数: 判断: f z 的洛朗级数展开中有无穷多负幂项,则 z =zk 为本性奇点。 计算:写出 f z 的洛朗级数,其 Resf zk a1 二、留数定理的应用 1、类型一:
2 2
2u 2u x 2 y 2 0 2 2 v v 0 2 2 x y
u x, y 为调和函数 v x, y 为调和函数
5、 给定实部(或虚部) ,求解析函数 f z 。 最常用的方法: (不定积分法,又叫偏微分法) ,大致步骤: 若已知实部 u u x, y ,利用 C R 条件,得
z 2 k 1 2k 1! z 2k 2k !
z z
cos z 1
k 0
k
收敛半径:由展开中心到最近奇点间的距离决定。 二、洛朗级数 1、 洛朗级数: 若 f z 在环形区域R2 z b R1内解析,
4
复变函数复习提纲
u 1 v 极坐标系下: 1 u v
复变函数与积分变换1.3复数的乘幂与方根

所以
z1 z 2 z 3 z1 z 2 z 2 z 3 z 3 z1 0 .
2 2 2
二、 乘方与开方运算(幂与根 ) 1)乘方
z r e
n n
in
r
n
co s n
i sin n
令|z|=1,则得到 德莫佛(De Moivre) 公式:
co s
3
i sin
n
co s n i sin n
2 )开方:
若满足 w
n
z
记为
则称w为z的n次方根, 于是
w
iArg z
n
z .
w e
n
inArg w
ze
推得
w n z a rg z 2 k A rg w n ( k 0,1, 2, , n 1)
例2 求
4
1 i.
2 co s i sin , 4 4
[解] 因为
1 i
所以
2 k 2 k 2 cos 4 i sin 4 4 4
, ( k 0,1, 2, 3)
4
1 i
8
w1
2
w0 x
w2
O
8
8
w3
四个根是内接于中心在原点半径为21/8的圆的正方形 的四个顶点.
例3 求
3
8.
解 因为 8 8 (cos i sin ), 所以
3
8
3
8 (cos
2 k
3
i sin i sin
2 k
复变函数教案第一章

复变函数教案课程性质《复变函数》是高等师范院校数学与应用数学专业的一门必修专业课,是数学分析的后续课程。
它在数学学科众多分支中都有着广泛的应用。
它的理论和方法,对于其它数学学科,对于物理、力学及工程技术中某些二维问题,都有广泛的应用.通过本课程的教学,使学生掌握复变函数论的基本理论和方法,提高分析问题和解决问题的能力,培养学生独立地分析和解决某些有关的理论和实际问题的能力.章节名称:第一章复数与复变函数学时安排:10学时教学要求:使学生掌握复数的概念,理解复数的几何意义及熟悉平面点集系列概念。
教学内容:复数及其代数运算;复数的乘幂与方根;平面点集;复变函数;复变函数的极限与连续教学重点:复数几何意义及复变函数的极限与连续。
教学难点:理解扩充复平面的相关概念。
教学手段:课堂讲授教学过程:一、引言复数的产生和复变函数理论的建立1,1545年,意大利数学家Cardan在解三次方程时,首先产生了负数开平方的思想。
后来,数学家引进了虚数,这在当时是不可接受的。
这种状况随着17、18世纪微积分的发明和给出了虚数的几何解析而逐渐好转。
2,1777年,瑞士数学家Euler建立了系统的复数理论,发现了复指数函数和三角函数之间的关系,创立了复变函数论的一些基本定理,并开始把它们应用到水力学和地图制图学上.用符号i表示虚数单位,也是Euler 首创的。
3,19世纪,法国数学家Cauchy 、德国数学家 Riemann 和Weierstrass 经过努力,建立了系统的复变函数理论,这些理论知直到今天都是比较完善的.4,20世纪以来,复变函数理论形成了很多分支,如整函数与亚纯函数理论、解析函数的边值问题、复变函数逼近论、黎曼曲面、单叶解析函数论等等,并广泛用于理论物理、弹性物理和天体力学、流体力学、电学等领域。
5,复变函数课程主要任务为研究复变数之间的相互依赖关系.其中许多概念、理论和方法是实变函数在复变函数领域内的推广和发展,在学习过程中要注意它们相似之处和不同之处的比较。
1复数概念2表示法3乘幂与方根4区域

把其中满足 0 的θ0称为辐角Argz的主值,
记作θ0=argz。 z=0时,辐角不确定。
计算 argz(z≠0)
arg
z
arctan 2
y x
x 0, y R
x 0, y 0
的公式
arctan
y x
x 0, y 0
3i 2
的模 ,辐角及辐.角主值
例 4 .求 (1 )e2 i(2 )3 e i(3 )e 2 的 ,辐 模 . 角
例5. 将zsinicos化为三角形式 式.与
5
5
§3 复数的乘幂与方根
1. 复数的乘积与商 2. 复数的乘幂 3.复数的方根
1. 乘积与商
定理1 两个复数乘积的模等于它们的模相乘, 两个复数乘积的辐角等于它们的辐角相加。
z n
1 zn
.
由定义 zn得 rnein
3.复数的方根(开方)——乘方的逆运算
问题 给定复数z=re i ,求所有的满足ωn=z 的
复数ω。
当z≠0时,有n个不同的ω值与 n 相z 对应,每一
个这样的ω值都称为z 的n次方根,记 n z
设ei,由 nz,有nein re i
•复数z 的实部 Re(z) = x ; 虚部 Im(z) = y . (real part) (imaginary part)
• 复数的模 |z| x2y2 0 • 判断复数相等 z 1 z 2 x 1 x 2 ,y 1 y 2 ,其 z 1 中 x 1 i1 y ,z 2 x 2 i2 y z 0 R z) eI(m z) 0(
1. 点的表示
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4、求出下列复变函数 的Leabharlann 部 和虚部 :(1) (2)
【解】令 ,则【解】令 ,则
. .
从而从而
………………………………………………………………………………………………………
2复数的幂与方根、区域、复变函数
1、求下列各式的值:
(1)
【解】因为
,
所以
.
………………………………………………………………………………………………………
(2)
【解】因为
,
所以
.
当 时, ;
当 时, .
………………………………………………………………………………………………………2、在复数范围内求解下列方程:
(1) (2)
【解】其图形如下所示【解】其图形如下所示
为无界、单连通、开区域.为无界、单连通、开区域.
(3) (4)
【解】其图形如下所示【解】其图形如下所示
为无界、多连通、开区域.为有界、多连通、闭区域.
(5) (6)
【解】其图形如下所示【解】其图形如下所示
为无界、多连通、闭区域.为无界、单连通、闭区域.
(1) (2)
【解】(1)原方程可化为
.
故
.
当 时, ;当 时, ;当 时, .
(2)由于
,
故
.
当 时, ;当 时, ;当 时, ;当 时, .
………………………………………………………………………………………………………
3、描出下列不等式所确定的区域或闭区域,并指明它是有界的还是无界的,单连通的还是多连通的:
