利用傅里叶频谱分析方法模拟各种衍射屏的衍射图样
实验报告之仿真(光的干涉与衍射)

大学物理创新性试验实验项目:单缝﹑双缝﹑多缝衍射现象仿真实验专业班级:材料成型及控制工程0903班姓名:曹惠敏学号:090201097目录1光的衍射2衍射分类3实验现象4仿真模拟5实验总结光的衍射光在传播路径中,遇到不透明或透明的障碍物,绕过障碍物,产生偏离直线传播的现象称为光的衍射。
光的衍射现象是光的波动性的重要表现之一.波动在传播过程中,只要其波面受到某种限制,如振幅或相位的突变等,就必然伴随着衍射的发生. 然而,只有当这种限制的空间几何线度与波长大小可以比拟时,其衍射现象才能显著地表现出来.所有光学系统,特别是成像光学系统,一般都将光波限制在一个特定的空间域内,这使得光波的传播过程实际上就是一种衍射过程.因此,研究各种形状的衍射屏在不同实验条件下的衍射特性,对于深刻理解衍射的实质,研究光波在不同光学系统中的传播规律分析复杂图像的空间频谱分布以及改进光学滤波器设计等具有非常重要的意义.随着计算机技术的飞速发展, 计算机仿真已深入各种领域。
光的干涉与衍射既是光学的主要内容 , 也是人们研究与仿真的热点。
由于光波波长较短,与此相应的复杂形状衍射屏的制作较困难,并且实验过程中对光学系统及环境条件的要求较高.因而在实际的实验操作和观察上存在诸多不便. 计算机仿真以其良好的可控性、无破坏、易观察及低成本等优点,为数字化模拟现代光学实验提供了一种极好的手段. 本次实验利用MATLAB软件实现对任意形状衍射屏的夫琅禾费衍射实验的计算机仿真。
衍射分类⒈菲涅尔衍射菲涅尔衍射:入射光与衍射光不都是平行光的衍射。
惠更斯提出,媒质上波阵面上的各点,都可以看成是发射子波的波源,其后任意时刻这些子波的包迹,就是该时刻新的波阵面。
菲涅尔充实了惠更斯原理,他提出波前上每个面元都可视为子波的波源,在空间某点P的振动是所有这些子波在该点产生的相干振动的叠加,称为惠更斯-菲涅尔原理。
惠更斯-菲涅尔原理能定性地描述衍射现象中光的传播问题,成为我们解释光的各类衍射现象的理论依据。
图像变换傅立叶频谱图ppt课件共31页文档

f(x,y) F (u,v)ej2(u x v)y dd uv
F ( u ,v ) R ( u ,v ) j( u I ,v )
频谱/模
F (u ,v )R 2 (u ,v ) I2 (u ,v )
能量谱/功率谱 P ( u ,v ) F ( u ,v ) 2 R 2 ( u ,v ) I 2 ( u ,v )
傅立叶逆变换
如何看频域图像
1、考虑到傅立叶变换具有对称性,为了便于显示,频率图像 往往以图像的中心为坐标原点,左上-右下、右上-左下对称。
2、图像中心为原始图像的平均亮度,频率为0.从图像中心向 外,频率增高。高亮度表明频率特征明显。
3、此外,频率域图像中心明显的频率变化方向与原图像中地 物方向垂直。也就是说如果原始图像中有多种水平分布的地物, 那么频率域图像中在垂直方向的频率变化比较明显。如果原始图 像中地物左下-右上分布,那么频率域图像中在左上-右下方向频率 变化比较明显,反之亦然。
主要贡献:在研究热的传播时创立了一套数学理论,1807年向巴黎 科学院呈交了《热的传播论文》,推导著名的热传导方程,并在求解该 方程时发现函数可由三角函数构成的级数形式表示,从而提出任意函数 可以展成三角函数的无穷级数。
• 数学与图像处理 • 空域与频域的桥梁
傅立叶变换
傅立叶变换是换域分析(空间域到频率域)是 一种广泛使用的工具,在图像处理中是一 种有效而重要的方法。在图像处理中,傅 立叶变换的应用十分广泛,如:图像特征 提取、频率域滤波、周期性噪声的去除、 图像恢复、纹理分析等。把傅立叶变换的 理论与遥感图像的物理解释相结合,有利 于解决大多数遥感图像处理问题。
相位角
(u,v)arctI(au,nv)
傅里叶红外光谱样品调制及图谱解析技巧

制备高聚物薄膜常用溶剂适合的溶剂高聚物苯 聚乙丁烯、聚丁二烯、聚苯乙烯等 甲》聚醋酸乙烯酯、乙基纤维董 二甲基甲酰胺 聚丙烯m氯仿或丙《 聚甲基丙烯酸甲酩 甲酸尼龙6 ;二氯乙烷聚碳酸ffii 丙n纤维素 四氯乙烷 涤纶 四氢咲响\聚氯乙烯二甲亚» 聚酰亚胺、聚甲醛(热》 甲苯、四氢蔡聚乙烯(热〉、聚丙烯(热》 1水_«乙烯静(热)、甲基纤维素常用的反射配件•固体样 品 -粉末样 晶 ・定性及 定*分析漫反射附件、7、-•a可用于,单层膜分析LB般镀膜■薄层分子取向研究黑色样品单次反射ATR3、液体样品的制备对于沸点较高且粘度较大的液体样品, 或一滴样品直接涂在KBr 窗片上进行测试对于沸点较低的样品及粘度小.流动性较大的 高沸点液体样品放在液体池中测试液体池是由两片KBr 窗片和能产生一定厚度的 垫片所组成切记不得有水-—•固体 •液体•不规则的 样品•非破坏性取 2ing气体池以及气体池架将气体池放在气体池架上即可,气体池的 两边由KBr 窗片或其它类型的盐片密封,要特 别注意防止盐片受潮。
.o®二、红外光谱解析技巧1、分子结构对基团吸收谱带位置的影响衽双原子分子中,其特征吸收谱带的位2由键力常数和原 子质fi 决定-在复杂的有机化合物分子中,某一基团的特征 吸收频率同时还要受到分子结构和外界条件的彭响。
同一种 基团由于其周围的化学环境不同,使其吸收频率会有所位移, 而不在同一位置出峰。
即基团的吸收不是固定在某一个频率 上,而在一定范围内波动. 如:C-H 的伸缩振动频率受到与这个碳原子邻接方式的影响C-C-H : C=C-H : C=C-H :外部条件对吸收的影响有!物态效应、晶体状态和溶剂效应• 主要讨论分子结构的影响因素有以下7个方面:3000—2850cm-1 3100-3000cm-1 3300 cm-1 附近-二元酸两个按基之间只有1一2个碳原子时,会出现两个UC=0相隔3个碳原子以上则没有这种偶合。
FFT计算衍射

1 快速傅里叶变换在衍射中的应用已知任意一个平面上光的复振幅分布,可以通过基尔霍夫衍射公式求出其他平面上的复振幅分布,基尔霍夫公式可表示为[1]:()()()exp 1,,cos ,12ikr U x y z U dSi rn r λ∑+⨯=⎰⎰(1.1)将0z =平面定义为衍射平面,0z =平面的坐标为00x y -,观察屏z d =平面的坐标为x y -,式中r 和()cos ,n r可以表示为:()cos ,r n r ⎧=⎪⎪⎨=⎪⎪⎩(1.2)带入(1.1)式可得:()()000001 2exp ,,U x y U x y dy dd x ∞∞-∞-∞⎛⎫⨯+⎝=⎰⎰(1.3)令:()12exp ,j h x y =⎛⎫ +⎝(1.4)由卷积的定义可知(1.3)可化为:()()()0,,,j U x y U x y h x y =⊗(1.5)其中⊗表示卷积。
对(1.5)式两边做傅里叶变换,并有傅里叶变换的性质得:(){}(){}(){}0,,,j F U x y F U x y F h x y =⋅(1.6)得到基尔霍夫传递函数:()(){}ex ,12p ,jxy j Hff F h x y F ⎧⎫⎪==⎬⎪⎛⎫ +⎝⎭式中,d 是不变量,它代表衍射平面到观察平面的距离,因此,给定光波长及衍射距离后,可通过FFT 求数值解。
所以,衍射场的表示式可以表示为:()(){}(){}{}1,,,j U x y FF Ux y F h x y -=⋅(1.7)式中的傅里叶变换和逆变换均可用FFT 求得数值解[2]。
理论上,只要满足基尔霍夫衍射的场均能利用(1.7)式采用FFT 求得数值解,而不必担心找不到傅里叶变换的解析表达式。
3 结论(一) 一方面,快速傅里叶变换通常只是傅里叶变换的一种快速近似计算方法,而且,数值计算中存在有限字长效应,存在截断误差。
因此利用快速傅里叶变换计算要得到完全无误的自在现场通常是不可能的。
实验四 傅立叶光学的空间频谱与空间滤波实验-10页精选文档

实验4 傅立叶光学的空间频谱与空间滤波实验一、实验目的1、了解透镜的傅里叶变换性质,加深对空间频率、空间频谱和空间滤波等概念的理解。
2、熟悉阿贝成像原理,从信息量的角度理解透镜孔径对分辨率的影响。
3、完成一维空间滤波、二维空间滤波及高通空间滤波。
二、实验原理1873年阿贝(E.Abbe )首先提出显微镜成像原理以及随后的阿贝—波特空间滤波实验,在傅里叶光学早期发展史上做出重要的贡献。
这些实验简单、形象,令人信服,对相干光成像的机理及频谱分析和综合原理做出深刻的解释,同时这种用简单的模板作滤波的方法一直延续至今,在图像处理技术中仍然有广泛的应用价值。
1、二维傅里叶变换和空间频谱在信息光学中常用傅里叶变换来表达和处理光的成像过程。
设在物屏X-Y 平面上光场的复振幅分布为g (x ,y ) ,根据傅里叶变换特性,可以将这样一个空间分布展开成一系列二维基元函数)](2exp[y f x f i y x +π的线性叠加,即⎰⎰+∞∞-+=y x y x y x df df y f x f i f f G y x g )](2exp[),(),(π (1)式中f x 、f y 为x 、y 方向的空间频率,即单位长度内振幅起伏的次数,G (f x ,f y )表示原函数g (x ,y )中相应于空间频率为f x 、f y 的基元函数的权重,亦即各种空间频率的成分占多大的比例,也称为光场(optical field )g (x ,y )的空间频谱。
G (f x 、f y )可由g (x ,y )的傅里叶变换求得⎰⎰+∞∞-+-=dxdy y f x f i y x g f f G y x y x )](2exp[),(),(π (2)g (x ,y )与G (f x ,f y )是一对傅里叶变换式,G (f x ,f y )称为g (x ,y )的傅里叶的变换,g (x ,y )是G (f x ,f y )的逆变换,它们分别描述了光场的空间分布及光场的频率分布,这两种描述是等效的。
夫琅和费光栅衍射的傅里叶频谱分析

§ 5.2 夫琅和费光栅衍射的傅里叶频谱分析一.屏函数的傅里叶变换1.周期性屏函数的傅里叶变换单缝、圆孔或者光栅,都是使入射波的波前改变,其作用可以用屏函数表示。
有一类应用广泛的衍射屏是衍射光栅,即具有周期性空间结构的衍射屏。
衍射屏具有空间的周期性,而波也具有空间的周期性,即衍射屏函数和复振幅都是空间的周期性函数,那么一定可以从数学上得到新的处理方法。
前面说过的反射、透射或闪耀光栅,可以认为是"黑白型"的。
即一部分使光全部透射或反射、另一部分全部不透光。
是典型的振幅型衍射屏,其屏函数表示为,X方向的透过率表示为其周期性表示为,d为最小的空间周期,即空间周期。
空间频率为。
如果透过率的变化是三角函数形式,即余弦或正弦型的,称为正弦光栅。
如果光栅刻线与y轴平行,则其透过率在X方向作周期性变化,周期为d,空间频率为f,f=1/d。
其屏函数可以写成。
平行光正入射,由于,则透射波的复振幅为。
而,所以,即,透射波实际上变为三列波关于波的方向,为平面波,其波矢在x方向的分量为,方向角为,其余两列波的方向角分别为,。
f为空间频率。
一列波,其空间频率越大,在X方向的波矢分量越大,即对于光轴的角度越大。
所以,对于有限大小的通光孔径,总是空间频率小的波可以通过,空间频率大的波不能通过。
这就是空间滤波的原理。
,0级波,方向,+1级波,方向,-1级波,方向对于一般的周期性的屏函数,可以用傅里叶级数将其展开为一系列正弦和余弦函数的和。
即,,其中,是基频。
或者,,,。
或者,傅里叶系数可以直接求出,的集合为傅里叶频谱,对于周期性的屏函数,的取值是分立的,非周期性的屏函数,的取值为连续的。
对于任何形式的衍射屏或物体,都可以将其看成是一系列空间频谱的叠加。
单色平面波照射到这些物体上,则分解成为一系列向不同方向出射的单色平面波,或者是分立的,或者是连续的。
每一个空间频谱代表一个衍射波。
如果用透镜将不同方向的衍射波汇聚到其像方焦平面的不同位置,得到一系列的衍射斑,则焦平面就是原图像的傅里叶频谱面。
工程光学下篇:第14.3节 光波衍射的傅里叶分析方法

如(x, y)点对应的平面波 在x方向的空间频率为:
u x sin cos f
L2
深圳大学光电工程学院
§14.3 光波衍射的傅里叶分析方法
夫琅和费衍射图样的特点
1. 衍射现象的扩散程度与孔径大小成反比: 依据:傅里叶变换的坐标缩放性质 FT{f (ax)} 1 F u a a 物理意义: 物函数坐标的收缩和展宽,使频谱函数坐标按同一比例 展宽或收缩,同时频谱的振幅相应降低或增加,但频谱 函数的形式不变 光的限制越严重,衍射现象越显著
y1) exp[
i2
(ux1
vy1 )]
dx1dy1
即:
衍射屏(x1, y1)
接收面(x, y)
E~(x, y) C FT{E~1(x1, y1)} 物面
频谱面(u, v)
除C 外,夫琅和费衍射的复振 幅分布是衍射屏复振幅分布的 傅里叶变换!
深圳大学光电工程学院
§14.3 光波衍射的傅里叶分析方法
接收面(x, y)
深圳大学光电工程学院
§14.3 光波衍射的傅里叶分析方法
夫琅和费衍射与傅里叶变换的关系
夫琅和费衍射公式:
E~(x, y) C
E~1
(
x1
,
令 :u x ,v y
y1
)
exp
ik
x f
x1
y f
y1 dx1dy1
f
f
E~(x, y) C
E~1 ( x1 ,
第十四章
傅里叶光学
本章内容
§14.1 平面波的复振幅分布和空间频率 §14.2 复杂复振幅分布及其分解 §14.3 光波衍射的傅里叶分析方法 §14.4 透镜的傅里叶变换性质和成像性质 §14.5 相干成像系统分析及相干传递函数 §14.6 非相干成像系统分析及光学传递函数 §14.7 阿贝成像理论与波特实验
利用傅里叶变换光谱分析的物理实验教程

利用傅里叶变换光谱分析的物理实验教程傅里叶变换在光谱分析中起着重要的作用。
通过傅里叶变换,我们可以将时域信号转换为频域信号,从而获得物质的光谱特征。
本教程将介绍如何利用傅里叶变换进行光谱分析的物理实验步骤。
一、实验目的本实验的目标是学习和掌握傅里叶变换在光谱分析中的应用。
具体而言,我们将通过实验探究如何通过傅里叶变换获取物质的光谱信息,了解不同频率分量对信号的影响,理解光谱分析的原理和意义。
二、实验器材和材料1. 光源:可以使用白炽灯、气体放电管等光源。
2. 光栅:具有一定刻线数的光栅,用于分散光束。
3. 准直系统:包括准直透镜、衍射光栅等。
4. 接收系统:接收器、滤光片等。
5. 数据采集设备:例如计算机、示波器等。
三、实验步骤1. 准备实验器材和材料,将光源、准直系统、接收器连接好。
2. 将光束通过准直透镜和衍射光栅进行准直和分散,使不同波长的光分别出射。
3. 调节接收系统,选择目标波长范围的光通过滤光片进入接收器。
注意调节滤光片的位置和角度,确保只有目标波长的光进入接收器。
4. 利用数据采集设备采集接收到的光信号,并记录下来。
5. 对采集到的光信号进行傅里叶变换,将时域信号转换为频域信号。
这一步可以使用计算机上的傅里叶变换软件完成。
6. 分析得到的频域信号,观察不同频率分量的幅度和相位信息。
根据频域信号的特征,可以推断出物质的光谱信息。
7. 重复上述步骤,可以采集不同波长范围的光信号,并进行光谱分析。
比较不同波长范围下的光谱特征差异。
8. 完成实验后,整理实验数据,总结并分析实验结果。
四、实验注意事项1. 在进行实验前,熟悉实验器材的操作方法和使用要求。
2. 操作时应注意光源的强度和稳定性,避免光强过大或过小导致实验结果的误差。
3. 在进行傅里叶变换时,应选择适当的参数设置,确保获得准确可靠的频域信号。
4. 针对不同的光谱分析目的,可以选择合适的滤光片和光栅,确保实验的有效性和可行性。
5. 实验数据的采集和处理过程中,应注意记录和保存数据的准确性和完整性。
《傅里叶分析》课件

通信系统
傅里叶分析可以用 于调制解调过程中 的频谱分析,以及 信道估计和均衡等 关键问题的解决, 提高通信系统的性 能。
图像处理
傅里叶分析可以用 于图像的频域滤波、 去噪和增强等操作, 以及图像压缩和特 征提取等应用,提 高图像处理的效果 和质量。
其他领域的 应用
除了信号处理、通 信系统和图像处理 外,傅里叶分析还 在许多其他领域中 有着广泛的应用, 如物理学、经济学 等。
《傅里叶分析》PPT课件
傅里叶分析是一种广泛应用于信号处理、通信系统、图像处理等领域的数学 工具。本课件将介绍傅里叶分析的定义、傅里叶级数和傅里叶变换,以及其 在各个领域中的实际应用。
傅里叶级数
傅里叶级数是用正弦和余弦函数将周期函数分解为一系列振幅和相位不同的谐波信号的方法。它可以表 示周期函数在频域上的相关信息。
总结
傅里叶分析是一种重要的数学工具,它可以用于分析和处理各种信号,并在信号处理、通信系统、图像 处理等领域中发挥作用。
1 傅里叶分析的重要性和应用
2 学习和研究傅里叶分析的意义
傅里叶分析在现代科学和工程中具有重要 地位,它为我们理解和处理信号提供了有 力的工具和方法。
学习和研究傅里叶分析不仅能够提高我们 的数学能力,还能够拓宽我们的科学视野, 培养我们的创新思维。
3 傅里叶变换的性质与应用
傅里叶变换具有平移性、尺度性和对称性等重要性质,它在信号处理、通信系统等领域 中有着广泛的应用。
傅里叶分析的实际应用
傅里叶分析在许多领域中发挥着重要作用,包括信号处理、通信系统、图像处理以及其他领域的实际应 用。
信号处理
傅里叶分析可以用 于分析和处理各种 信号,包括音频信 号、视频信号等, 以提取有用的信息 或实现信号压缩等 功能。
傅里叶光学 衍射

傅里叶光学衍射
傅里叶光学是一种基于傅里叶变换的光学分析方法,用于研究和描述光的传播、传输和干涉等现象。
衍射则是傅里叶光学中的一个重要概念,指的是光波在通过绕射物体或在光学衍射装置中遇到不同障碍物或孔径时发生的偏折、干涉和广泛分布的现象。
当光波通过一个物体或孔径时,由于光的波动性,光波在物体边缘处发生弯曲,并产生干涉、衍射效应。
这导致光波的幅度和相位在空间中发生变化,进而在接收屏幕上形成特定的光强和亮度分布。
衍射现象可以通过傅里叶光学的数学表达进行理解和描述。
根据傅里叶光学的原理,复杂的光波可以被分解成一系列具有不同频率的简单正弦波。
衍射可以被看作是这些不同频率的波在空间中互相干涉和综合的结果。
傅里叶光学提供了描述衍射现象的数学工具和方法,例如使用傅里叶变换分析光的传播和干涉,以及通过傅里叶光学的逆变换来重建或模拟复杂的光场。
衍射现象在许多光学应用中发挥着重要作用,例如在光学衍射实验中观察衍射图样,可用于分析和测量光源、物体的结构和特性。
此外,衍射也被广泛应用于光学显微镜、天文望远镜、激光技术等领域,为光学系统的设计和优化提供
重要参考。
基于FFT的傅里叶光谱Matlab仿真分析

第32卷第1期吉首大学学报(自然科学版)Vol.32No .12011年1月Journ al of Ji shou Universit y (Nat ural Science Edit ion)J an.2011文章编号:1007-2985(2011)01-0049-03基于FFT 的傅里叶光谱Matlab 仿真分析*叶伏秋(吉首大学物理科学与信息工程学院,湖南吉首416000)摘要:采用迈克尔逊干涉装置测定了钠光灯和汞灯的干涉图,利用傅里叶光谱中存在的干涉图和光谱图的变换关系,通过快速傅里叶变换(F FT)的方法分析了钠光灯和汞灯的辐射光谱.Matlab 仿真分析结果表明,采用傅里叶变换光谱可以清晰地展现辐射源的辐射光谱.关键词:傅里叶光谱;快速傅里叶变换;调制;解调中图分类号:O433.4文献标志码:A测量信号可以采用2种不同方法:时域测量和频域测量,时域测量用示波器来显示信号的波形,在示波器上可以直接读取脉冲的上升时间、脉冲宽度、相位差等信号信息.这种测量方式使用得最广泛,但这种方式对一些信号中的一些细节如很小的失真一般都很难观察得到.这时对于被测对象,也可以测量它在不同频率时的频率特性,这种测量方式称为频域测量.对在频域测量中得到的频谱进行分析,往往能够提供在时域测量中进行分析所观察不到的信息,甚至有些系统必须进行频谱分析.因此,在许多地方频谱分析显得更为重要,通常频谱分析是以快速傅里叶变换为基础.现代光学的一个重大进展是在光学中引入傅里叶变换概念,由此发展成为光学领域内的一个崭新分支傅里叶光学.傅里叶光学采用通信和信息理论中的傅里叶分析和线性系统理论方法,在二维空间域及其空间频率域讨论光学系统的特性[1].利用傅里叶光谱中存在的干涉图和光谱图的变换关系,可以通过傅里叶变换的方法测定并分析各种辐射光谱.Matlab 作为一种高效方便的科学计算软件被广泛的应用在各种计算领域[2],其将高性能的数值计算和可视化集成在一起,并内置了大量的函数库,特别是快速傅里叶变换F FT ,从而被广泛地应用于科学计算、控制系统、信息处理等领域的分析、仿真和设计工作.笔者通过利用迈克尔干涉装置测定钠光灯和汞灯的干涉图,然后采用Matlab 中的F FT 计算并分析出钠光灯和汞灯的辐射光谱.1快速傅里叶变换FFT傅立叶变换是信号分析和处理的重要工具,离散时间信号f (t)的连续傅立叶变换定义为[3]F (e j t )=N -1t=0f (t)e i t .(1)其中F (e j t )是一个连续函数,不能直接在计算机上做数值运算.为了在计算机上实现频谱分析,必须对f (t)的频谱作离散近似.有限长离散信号f (t)的离散傅立叶变换(DFT)定义为F (v)=N-1N-1t=0f (t)e -j2(v /N)t ,(2)其反变换定义为f (t)=N-1t=0F (v)e j2(v/N )t ,(3)其中t =0,1,2,,N - 1.1965年Cooley 和T ukey 巧妙地利用e -j2(v /N)t 因子的周期性和对称性,经过适当数学变换,提出了DFT 的快速算法,即*收稿日期6基金项目湖南省普通高等学校科学研究项目();湖南省普通高等学校教学改革研究资助项目作者简介叶伏秋(6),男,湖南益阳人,吉首大学物理科学与信息工程学院副教授,硕士,主要从事物理学研究:2010-10-1:10A100:197-.快速离散傅里叶变换.此后FFT 算法被广泛运用于各种计算领域.2傅里叶光谱分析傅里叶变换光谱技术[4]是利用迈克尔逊干涉仪对入射光进行干涉调制,采用探测器把干涉信号转换为电信号,经A/D 转换,成为数字化的时域干涉图,它与入射光的光谱图之间存在傅里叶变换关系,通过对干涉图实施傅里叶逆变换,就可获得入射光的光谱信息.傅里叶变换过程实际上就是对待测光进行调制与解调的过程,通过调制将待测光的高频率调制成可以掌控、接收的频率,然后将接收到的信号送到解调器中进行分解,得出待测光中的频率成分及各频率对应的强度值.这样就得到了待测光的光谱图.调制过程由迈克尔孙干涉仪实现,设一单色光进入干涉仪后,它将被分成2束后进行干涉,干涉后的光强值为I (x)=I 0cos 2x ,(4)其中:x 为光程差,它随动镜的移动而变化;为单色光的波数值.如果待测光为连续光谱,那么干涉后的光强为I (x)=+-I ()cos 2x d .(5)采集待测光的干涉强度信息的装置如图1,分别用钠光灯和汞灯作为待测光源,测得干涉图如图2,3所示.1-外置光源;2-内置光源(溴钨灯);3-可变光栏;4-准直镜;5-平面反射镜;6-精密平移台;7-电机;8-动镜;9-干涉板;-补偿板;11-定镜;12-接收器1;13-参考光源(H e Ne 激光器);14-分束器;15-平面反射镜;16-接收器2;17-光源转换镜(物镜)图1采集待测光的干涉强度信息的迈克尔逊干涉装置图2钠光灯干涉图从接收器上采集到的数据送入计算机中,利用Mat lab 中的F FT 进行数据处理得到傅里叶光谱即解调.傅里叶光谱满足的方程就是解调方程:I ()=+-I (x)cos 2x dx,(6)该方程就是傅里叶变换光谱学中干涉图-光谱图关系的基本方程.对于给定的波数,如果已知干涉图与光程差的关系式I (x),就可以用解调方程计算这波数处的光谱强度I ()为了获得整个工作波数范围的光谱图,只需对所希望的波段内的每一个波数反复按照解调方程进行傅里叶变换运算就行了图,5分别为用FF T 进行变换得到的钠光灯和汞灯的光谱图从图可以清楚地看到钠光灯辐射的波长大约在550吉首大学学报(自然科学版)第32卷..4.490图3汞灯干涉图nm 附近的双线光谱,而从图5也可以清楚地看到汞灯辐射的波长大约在550nm 附近的光谱.图4钠灯光谱图图5汞灯光谱图3结语FF T 是离散傅里叶变换的快速算法,可以将信号变换到频域,从而在频域中可以很清晰地展现信号在时域上很难看到的一些特征.同时F FT 也可以将一个信号的频谱提取出来以便于进行频谱分析.因此,FF T 在各种信号处理中得到了广泛使用.在本文中,笔者分别把钠光灯和汞灯的辐射光入射到迈克尔逊干涉装置中进行干涉调制,得到时域干涉图,然后使用FFT 对干涉图进行傅里叶变换,得到了2种光源的辐射光谱图,在光谱图中可以清楚地看到了2种光源辐射的光波波长.参考文献:[1]吕乃光.傅里叶光学[M].北京:机械工业出版社,2006:44.[2]宋兆基.MAT LAB 6.5在科学计算中的应用[M].北京:清华大学出版社,2005:2- 3.[3]殷勤业.傅里叶变换及其应用[M].张建国译.西安:西安交通大学出版社,2005:203-217.[4]沈学础.傅里叶变换光谱学引论和进展[J].物理学进展,1982(3):1- 5.(下转第62页)51第1期叶伏秋:基于FF T 的傅里叶光谱Matlab 仿真分析62吉首大学学报(自然科学版)第32卷[24]LI Xiao hua.Energy Efficient Wir eless Sensor Networ ks with Tr ansmission Diversit y[J].IEE Elect ronics Letter s,2003,39:1753-1755.[25]Zhanshan(Sam)MA.Insect Population Inspir ed Wireless Sensor Networ ks:A U nified Ar chit ecture with Survival Analysis,Evolut ionar y Game Theory,and Hybrid F ault Models[C]//International Conference on Bio Medical Engineer ing and Infor matics.China:H ainan,2008.[26]M A Yi zhong,CAO H ui,MA Jun.T he Intrusion Detect ion Method based on Game Theory in Wir eless Sensor Networ k[C]//Ubi Media Computing,2008Fir st IEEE Inter national Conference.China:Beijing,2008:326-331.[27]SANG SEON BYU N.Dynamic Spectr um Allocation in Wireless Cognitive Sensor Networ ks:Improving Fa irness andEner gy Efficiency[C]//T he68th IEEE Vehicular Technology Confer ence.Canada:Calgar y,2008:1- 5.Key Technologies and Evolution in Wireless Sensor Network Data GatheringLIANG Ping yuan1,2,CH EN Bing quan1,3,TAN Zi you1(1.College of P hysics Science and Infor mat ion Engineering,Jishou Univer sity,Jishou416000,China;2.School of I nformation Science and Technology,Sun Yat sen University,Guangzhou510006,China;3.College of Electricity and Information Engineer ing,Hunan University,Changsha410082,China)Abstr act:Because of the self organization network structur e,wir eless sensor networ k(WSN)data gath ering has enormous advantages compared with other networks.H owever,many key problems have not been resolved in wireless sensor networks yet because of limited resources.In this paper,the key technol ogy and main challenges in WSN data gathering are summarized,and the main per for mance index and re search methods of WSN network protocols in data gathering ar e introduced.At the same time,several new technology combined with WSN are analyzed and discussed.In the end,the research direction in the future is prospected.Key words:wireless sensor networks;summary;data gathering;MIMO(责任编辑陈炳权) (上接第51页)Matlab Simulation Analysis of Fourier Spectrum Based on FFTYE Fu qiu(College of Physics Science and Infor mation Engineer ing,Jishou University,Jishou416000,H unan China)Absttract:T he interference pattern of the sodium lamp light and the mercury lamp light is measur eed by Michael interference device,using the tr ansformation relations of the interference pattern and the spectra which exist in Four ier spectr um,the sodium lamp and mercury lamp radiation spectrum is analyzed by fast Fourier transform method.T he results show that the Fourier transfor m spectrum can clearly display the r adiation spectrum of the radiation source.Key words:Fourier spectrum;fast Fourier transform;modulation;demodulation(责任编辑陈炳权)。
MATLAB 傅立叶变换 和衍射积分 模拟光学

MATLAB编程用两种方法模拟光学实验摘要:利用MA TLAB软件编程实现了用衍射积分的方法对单缝衍射、杨氏双缝干涉、黑白光栅衍射的计算机模拟;以及用傅立叶变换方法对简单孔径衍射、黑白光栅及正弦光栅夫琅和费衍射的模拟。
关键词:MA TLAB;衍射积分;傅立叶变换;计算机模拟引言:美国Mathworks公司推出的MA TLAB,是一种集数值计算、符号预算、可视化建模、仿真和图形处理等多种功能于一体的优秀图形化软件。
本文介绍了通过MA TLAB软件编程实现用衍射积分和傅立叶变换实现夫琅和费衍射计算机模拟的方法。
计算机模拟为衍射实验的验证提供一条简捷、直观的途径。
从而加深了对物理原理、概念和图像的理解。
正文:大学教学课程中引入计算机模拟技术正日益受到重视,与Basic、C和Fortran相比,用MA TLAB软件做光学试验的模拟,只需要用数学方式表达和描述,省去了大量繁琐的编程过程。
下面来介绍利用MA TLAB进行光学模拟的两种方法。
(一)衍射积分方法:该方法首先是由衍射积分算出接收屏上的光强分布,然后根据该分布调制色彩作图,从而得到衍射图案。
1.单缝衍射。
把单缝看作是np个分立的相干光源,屏幕上任意一点复振幅为np个光源照射结果的合成,对每个光源,光程差Δ=ypsinΦ,sinΦ=ys/D,光强I=I0(Σcosα)2+(Σsinα)2,其中α=2Δ/λ=πypys/λ D编写程序如下,得到图1lam=500e-9;a=1e-3;D=1;ym=3*lam*D/a;ny=51;ys=linspace(-ym,ym,ny);np=51;yp=linspace(0,a,np);for i=1:nysinphi=ys(i)/D;alpha=2*pi*yp*sinphi/lam;图1 单缝衍射的光强分布 sumcos=sum(cos(alpha));sumsin=sum(sin(alpha));B(i,:)=(sumcos^2+sumsin^2)/np^2;endN=255;Br=(B/max(B))*N;subplot(1,2,1)image(ym,ys,Br); colormap(gray(N)); subplot(1,2,2) plot(B,ys); 2. 杨氏双缝干涉两相干光源到接收屏上P 点距离r 1=(D 2+(y-a/2)2)1/2, r 2=(D 2+(y+a/2)2)1/2,相位差Φ=2π(r 2-r 1)/λ,光强I=4I 0cos 2(Φ/2)编写程序如下,得到图2 clear lam=500e-9 a=2e-3;D=1;ym=5*lam*D/a;xs=ym;n=101;ys=linspace(-ym,ym,n); for i=1:nr1=sqrt((ys(i)-a/2).^2+D^2);r2=sqrt((ys(i)+a/2).^2+D^2); phi=2*pi*(r2-r1)./lam;B(i,:)=sum(4*cos(phi/2).^2); endN=255;Br=(B/4.0)*N subplot(1,2,1) image(xs,ys,Br); colormap(gray(N)); subplot(1,2,2) plot(B,ys) 3. 光栅衍射公式:I=I 0(sin α/α)2(sin(λβ)/sin β)2α=(πa/λ)sin Φ β=(πd/λ)sin Φ 编写程序如下:得到图3clearlam=500e-9;N=2; a=2e-4;D=5;d=5*a; ym=2*lam*D/a;xs=ym; n=1001;ys=linspace(-ym,ym,n); for i=1:nsinphi=ys(i)/D; alpha=pi*a*sinphi/lam; beta=pi*d*sinphi/lam;B(i,:)=(sin(alpha)./alpha).^2.*(sin(N*beta)./sin(beta)).^2; B1=B/max(B);end图2 杨氏双缝干涉的光强分布图3 黑白光栅衍射光强分布NC=255;Br=(B/max(B))*NC; subplot(1,2,1) image(xs,ys,Br); colormap(gray(NC)); subplot(1,2,2) plot(B1,ys);(二)傅立叶变换方法:在傅立叶变换光学中我们知道夫琅和费衍射场的强度分布就等于屏函数的功率谱。
傅立叶变换与频谱分析

x1 (k )[ x 2 (m)e jm e jk ]
m
k
x1 ( k ) e j k [ x 2 ( m ) e j m ]
m
2-29
X 1 ( e j ) X 2 ( e j )
因此, (2-26)式描述的卷积特性成立。 卷积特性对于理解滤波器的功能非常有帮助。对于一个图 2.3 所示的线性移不变系统, 其输入与输出之间的关系在时域是一个线性卷积关系,那么根据(2-26)式,其在频域的关 系就是乘积的关系。因此,输出信号的幅度谱与输入信号的幅度谱之间的关系以及相位谱之 间的关系如下:
2-3 2-4 2-5 2-6
X ( ) tan 1 {
X i ( e j ) X r ( e j )
}
(2-5)式的 | X (e j ) | 是信号 x(n) 的频率响应幅度谱,而(2-6)式的 X ( ) 为相位谱。幅度 谱的值随频率的变化不会小于零,相位谱的主值随频率可以在(-,+)之间变化。
X ( e j )
n
x(n)e jn
2-1
这里,称为角频率,其与普通频率 f 和采样频率 f s 的关系如下:
1
傅立叶变换与频谱分析
2f fs
2-2
通过离散时间傅立叶变换 DTFT,时域信号 x(n) 被转化为频域分布信号 X (e j ) 。一般,
X (e j ) 是一个随角频率变化的复数,并且分布在(-,+)之间。尽管 x(n) 在时域是离
ax1 (n) bx 2 (n) 的离散傅立叶变换如下:
5
傅立叶变换与频谱分析
n
用快速傅里叶变换对信号进行频谱分析

实验二 用快速傅里叶变换对信号进行频谱分析一、实验目的1.理解离散傅里叶变换的意义;2.掌握时域采样率的确定方法;3.掌握频域采样点数的确定方法;4.掌握离散频率与模拟频率之间的关系;5.掌握离散傅里叶变换进行频谱分析时,各参数的影响。
二、实验原理序列的傅里叶变换结果为序列的频率响应,但是序列的傅里叶变换是频率的连续函数,而且在采用计算机计算时,序列的长度不能无限长,为了便于计算机处理,作如下要求:序列x (n )为有限长,n 从0~N -1,再对频率ω在0~2π范围内等间隔采样,采样点数为N ,采样间隔为2π/N 。
第k 个采样点对应的频率值为2πk /N 。
可得离散傅里叶变换及其逆变换的定义为∑-=-=102)()(N n n N k j e n x k X π (1)∑-==102)(1)(N k k Nn j e k X N n x π (2) 如果把一个有限长序列看作是周期序列的一个周期,则离散傅里叶变换就是傅里叶级数。
离散傅里叶变换也是周期的,周期为N 。
数字频率与模拟频率之间的关系为s f f /2πω=,即ss T f f πωπω22==(3) 则第k 个频率点对应的模拟频率为 Nkf NT k T N k f s s s k ==⋅=ππ212 (4) 在用快速傅里叶变换进行频谱分析时,要确定两个重要参数:采样率和频域采样点数,采样率可按奈奎斯特采样定理来确定,采样点数可根据序列长度或频率分辨率△f 来确定f Nf s ∆≤,则f f N s ∆≥ (5) 用快速傅里叶变换分析连续信号的频谱其步骤可总结如下:(1)根据信号的最高频率,按照采样定理的要求确定合适的采样频率f s ;(2)根据频谱分辨率的要求确定频域采样点数N ,如没有明确要求频率分辨率,则根据实际需要确定频率分辨率;(3)进行N 点的快速傅里叶变换,最好将纵坐标根据帕塞瓦尔关系式用功率来表示,横坐标根据式(7-21)转换为模拟频率Hz;(4)根据所得结果进行分析。
傅里叶衍射投影定理

傅里叶衍射投影定理
傅里叶衍射投影定理是光学中的一个重要定理,它描述了在夫琅禾费衍射条件下,空间中任意一个物体的衍射图案可以通过对其傅里叶变换的投影来计算。
具体来说,该定理表明,对于一个在空间中具有非零光强度分布的物体,其夫琅禾费衍射图案可以通过将该物体的光强度分布进行傅里叶变换,并将得到的傅里叶谱在某个平面上进行投影来计算。
这个投影平面被称为衍射平面,它与物体的距离满足夫琅禾费衍射条件。
傅里叶衍射投影定理的意义在于,它提供了一种计算衍射图案的方法,使得我们可以通过对物体的光强度分布进行傅里叶变换来预测其衍射图案。
这对于许多光学应用,如光学成像、光学设计和光学信号处理等都非常重要。
需要注意的是,傅里叶衍射投影定理只适用于夫琅禾费衍射条件下,即光源和衍射平面距离无限远,并且衍射物体的尺寸远小于光源到衍射平面的距离。
在其他情况下,需要使用更复杂的衍射理论来计算衍射图案。
傅里叶红外光谱分析原理与方法110页PPT

31、别人笑我太疯癫,我笑他人看不 穿。(名 言网) 32、我不想听失意者的哭泣,抱怨者 的牢骚 ,这是 羊群中 的瘟疫 ,我不 能被它 传染。 我要尽 量避免 绝望, 辛勤耕 耘,忍 受苦楚 。我一 试再试 ,争取 每天的 成功, 避免以 失败收 常在别 人停滞 不前时 ,我继 续拼搏 。
谢谢你的阅读
❖ 知识就是财富 ❖ 丰富你的人生
71、既然我已经踏上这条道路,那么,任何东西都不应妨碍我沿着这条路走下去。——康德 72、家庭成为快乐的种子在外也不致成为障碍物但在旅行之际却是夜间的伴侣。——西塞罗 73、坚持意志伟大的事业需要始终不渝的精神。——伏尔泰 74、路漫漫其修道远,吾将上下而求索。——屈原 75、内外相应,言行相称。——韩非
33、如果惧怕前面跌宕的山岩,生命 就永远 只能是 死水一 潭。 34、当你眼泪忍不住要流出来的时候 ,睁大 眼睛, 千万别 眨眼!你会看到 世界由 清晰变 模糊的 全过程 ,心会 在你泪 水落下 的那一 刻变得 清澈明 晰。盐 。注定 要融化 的,也 许是用 眼泪的 方式。
35、不要以为自己成功一次就可以了 ,也不 要以为 过去的 光荣可 以被永
傅里叶红外光谱分析原理与方法PPT文档共110页

11、获得的成功越大,就越令人高兴 。野心 是使人 勤奋的 原因, 节制使 人枯萎 。 12、不问收获,只问耕耘。如同种树 ,先有 根茎, 再有枝 叶,尔 后花实 ,好好 劳动, 不要想 太多, 那样只 会使人 胆孝懒 惰,因 为不实 践,甚 至不接 触社会 ,难道 你是野 人。(名 言网) 13、不怕,不悔(虽然只有四个字,但 常看常 新。 14、我在心里默默地为每一个人祝福 。我爱 自己, 我用清 洁与节 制来珍 惜我的 身体, 我用智 慧和知 识充实 我的头 脑。 15、这世上的一切都借希望而完成。 农夫不 会播下 一粒玉 米,如 果他不 曾希望 它长成 种籽; 单身汉 不会娶 妻,如 果他不 曾希望 有小孩 ;商人 或手艺 人不会 工作, 如果他 不曾希 望因此 而适的,否则就不是奢侈 。——CocoCha nel 62、少而好学,如日出之阳;壮而好学 ,如日 中之光 ;志而 好学, 如炳烛 之光。 ——刘 向 63、三军可夺帅也,匹夫不可夺志也。 ——孔 丘 64、人生就是学校。在那里,与其说好 的教师 是幸福 ,不如 说好的 教师是 不幸。 ——海 贝尔 65、接受挑战,就可以享受胜利的喜悦 。——杰纳勒 尔·乔治·S·巴顿
傅里叶红外光谱分析PPT课件

2021/4/2
.
34
•3.3 气体样品 •直接注入气体池内测试。 •3.4 塑料、高聚物样品 •3.4.1 溶液涂膜 •把样品溶于适当的溶剂中,然后把溶液一滴一 滴的滴加在KBr晶片上,待溶剂挥发后把留在 晶片上的液膜进行测试。
(1)—O—H 3650 3200 cm-1 确定 醇、酚、酸 在非极性溶剂中,浓度较小(稀溶液)时,峰形尖锐,强
吸收;当浓度较大时,发生缔合作用,峰形较宽。 注意区分 —NH伸缩振动: 3500 3100 cm-1
2021/4/2
.
38
4.1、红外吸收光谱的特征性
group frequency in IR
与一定结构单元相联系的、在一定范围内出现的化学键 振动频率——基团特征频率(特征峰);
例: 2800 3000 cm-1 —CH3 特征峰; 1600 1850 cm1 —C=O 特征峰;
基团所处化学环境不同,特征峰出现位置变化:
应用:有机化合物的结构解析。 定性:基团的特征吸收频率; 定量:特征峰的强度;
2021/4/2
.
6
1.2、红外吸收光谱产生的条件
condition of Infrared absorption spectroscopy
满足两个条件: (1)辐射应具有能满足物质产生振动跃迁所需的能量; (2)辐射与物质间有相互偶合作用。
2021/4/2
.
31
溶剂
可用区域
通常容器长度
CS2 除2200~2100cm-1与1600~1400cm-1以外的区域 0.5mm
§62衍射理论中的傅里叶方法
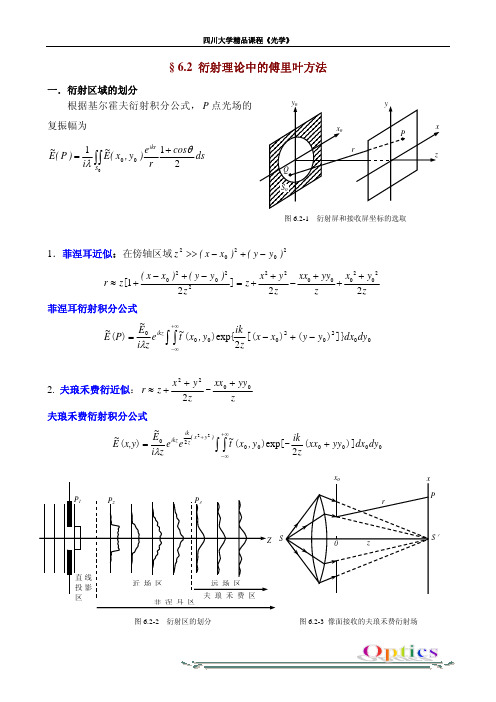
§ 6.2 衍射理论中的傅里叶方法一.衍射区域的划分图6.2-1 衍射屏和接收屏坐标的选取根据基尔霍夫衍射积分公式,点光场的复振幅为P ∫∫+=021100S ikr ds cos r e )y ,x (E ~i )P (E ~θλ1.菲涅耳近似:在傍轴区域20202)y y ()x x (z −+−>>][2202021z)y y ()x x (z r −+−+≈2222000022xx yy x y x y z z z z +++=+−+ 菲涅耳衍射积分公式∫∫+∞∞−−+−=00000002exp dy dx y y x x z ik y ,x t ~e z i E ~P E ~ikz ]})()[({)()(22λ2. 夫琅禾费衍近似:z yy xx z y x z r 00222+++≈-夫琅禾费衍射积分公式∫∫+∞∞−++=000000202exp 22dy dx yy xx z ik y ,x t ~e e zi E ~x,y E ~)y x (zik ikz )]([-)()(λPS ′图6.2-3 像面接收的夫琅禾费衍射场图6.2-2 衍射区的划分 菲涅耳区例 6.2-1 波长为5000的平行光垂直入射到半径为0.5mm 的圆孔衍射屏上。
问孔后多远以外属于夫琅禾费衍射区? Α例6.2-2 试证在点光源的共轭像面上接收到的是夫琅禾费衍射场。
二.夫琅禾费衍射实现屏函数的傅里叶变换∫∫+∞∞−++=0000002exp 22dy dx y f x f i y ,x t ~e z i e x,y E ~y x )y x (z ik ikz )]([-)()(λ)y x (z ikikz e z i e 222+=λℱ)}({0,0~y x t 夫琅禾费衍射场的强度分布==)y ,x (*E ~)y ,x (E ~)y ,x (I ℱ)}({00y x t ~,ℱ*)}({00y x t ~, 表明:夫琅禾费衍射的强度分布等于屏函数的功率谱。
6.5-6屏函数的傅里叶变换、阿贝成像、空间滤波

D 2 F
2F 的信息被截止,因此不 能分辨。 fM D
M对应的最大空间频率:
sin M f M f M sin M
D 2 F
显微镜的最小分辨率:
ym 0.61
N . A. 0.61
n sin M
F 0.61 1.22 D / 2F D
6.7、 阿贝成像原理与空间滤波 透镜成像有两个观点:
(1)
几何光学:自物点A,B,C发出的球 面波,经透镜折射后,各自会聚到它们的像 点A,B,C.
图中光线不同 的颜色表示发 自不同的物点.
像 面
A B
C
透 镜
C B AFra bibliotek(2)
阿贝成像原理: 物是一系列不同空间频率的集合.入 射光经物平面发生夫琅和费衍射,在透镜焦面(频谱面) 上形成一系列衍射光斑,各衍射光斑发出的球面次波在 相面上相干叠加,形成像.
1 D 0.8 ym F
阿贝成像真正意义:提供了一种新的频谱语言描述信息,启发 人们用改变频谱的手段来改造信息,即信息光学处理基础
•一个典型实验.
物平面
频谱面
像平面
F
A B C
C’ B’ A’
阿贝成像原理将成像过程分为两步:
第一步“分频”; 第二步“合成”.
空间滤波
频 谱 面
物 面 高频信息
由阿贝的观点来看,许多成像光学仪器就是一个低通滤波 器,物平面包含从低频到高频的信息,透镜口径限制了高频信 息通过,只许一定的低频通过,因此,丢失了高频信息的光束再 合成,图象的细节变模糊. 孔径越大,丢失的信息越少,图象 越清晰.
