全等三角形中考总复习PPT教学课件

合集下载

三角形全等判定复习ppt课件

N 明方法与前题基本相同,只
须证明⊿ABN≌⊿BCM
A
C
B
变式4:如图,⊿ABD,⊿ACE都是正三角形, 求证CD=BE
D
A
E
B
C
分析:此题实质上是把题目中的条件B,A,C三点改为不共线,证明方法与前题基本相同.
变式6:如图,分别以⊿ABC的边AB,AC为一边画正方形AEDB和正方形ACFG,连结CE,BG.
求证BG=CE
E
分析:此题是把两个三
角形改成两个正方形而
D
A
G 以,证法类同
FBBiblioteka C小结:1.证明两个三角形全等，要结合题目的条件和结论，选择恰当的判定方法
2.全等三角形，是证明两条线段或两个角相等的重要方法之一，证明时
①要观察待证的线段或角，在哪两个可能全等的三角形中。
②分析要证两个三角形全等，已有什么条件，还缺什么条件。
AB=CB
A
AD=CD
BD=BD
_
=
P
∴ △ABD≌△CBD(SSS)
B
D
∴∠ABD=∠CBD
_
=
在△ABP和△CBP中
C
AB=BC
∠ABP=∠CBP
BP=BP
∴ △ABP ≌ △CBP(SAS)
∴PA=PC
例4。已知:如图AB=AE,∠B=∠E，BC=ED AF⊥CD 求证：点F是CD的中点
分析：要证CF=DF可以考虑CF 、 DF所在的两个三角形全等，为此可添加辅助线构建三角形全等，如何添加辅助线呢?
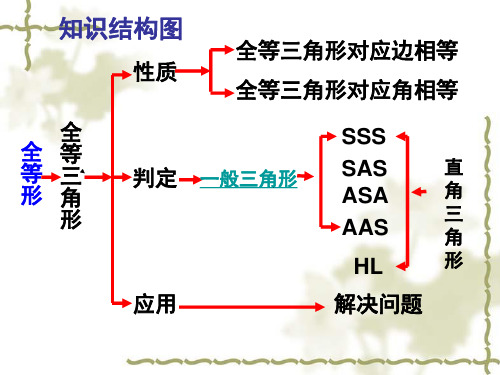
知识结构图
性质
全等三角形对应边相等全等三角形对应角相等
全全等等三形角
形

12-1 全等三角形课件(共26张PPT)

时，对应的顶点放在对应的位置上.
知识梳理
例题 1：如图所示，△ ≌△ ，指出所有的对应边和对应角.
AB与DC，AC与DB，BC与CB是对应边；
∠ABC与∠DCB，∠A与∠D，∠ACB与∠DBC是对应角。
【解答】（1）已知△ABC≌△DCB，故公共边BC和CB
是对应边，它们所对的∠A和∠D是对应角，最短边
【结论】本题考查了全等三角形的性质及
比较角的大小，解题的关键是找到两全等
三角形的对应角、对应边.
80°
.
知识梳理
例题4：如图，将长方形ABCD沿AE折叠，使D点落在BC边上的F点处，
如果∠BAF = 60°，那么∠DAE= 15°
角
例题5：如图，△ ABC ≌△ ADE，则AB = AD ，∠E =
知识梳理
把两个全等的三角形重合到一起，重合的顶点叫做对应顶点，重合
的边叫做对应边，重合的角叫做对应角。例如，图中的△ 和△
全等，记作△ ≌ ，其中点和点，点和点，点
和点是对应顶点；和，和，和是对应边；∠和
∠，∠和∠，∠和∠是对应角.
∠BAE = 130°，∠BAD = 50°，则∠BAC=
。
80°
∠C
，若
知识梳理
例题6：如图，已知△ ABC ≌△ EBF，AB ⊥ CE，ED ⊥ AC，∠A = 24°，
则：（1）AB =
EB ，BC = BF ，∠C = 66 °，∠EFB = 66 °；
（2）若AB = 5cm，BC = 3cm，则AF = 2cm 。
AB和DC是对应边，它们所对的∠ACB和∠DBC是对应
角，余下的一对边和一对角分别是对应边和对应角.
（2）根据书写规范可知点A和点D，点B和点C，点C

完整版-全等三角形总复习PPT教学课件

AC=BC
∠BCE=∠DCA
DC=EC
∴ △ACD≌△BCE (SAS)
∴ BE=AD
2024/3/9
29
6. 如图A、B、C在一直线上，△ABD，△BCE都是等边三角形，AE交BD于F，DC交BE于G，求证：BF＝BG。
AB
＝
DB
∠ABE ＝ ∠ DBC
BE＝BC ∴△ABE≌△DBC(SAS)
D
C
2
1
A
B
思路3：已知一边一角（边与角相邻）：
找夹这个角的另一边
AD=CB （SAS）
找夹这条边的另一角
∠ACD=∠CAB（ASA）
找边的对角
∠D=∠（B AAS）
15
如图，已知∠B= ∠E，要识别△ABC≌ △AED，需要添加的一个条件是--------------
A
D
C
E
思路4：
找夹边
AB=AE (ASA)
∴ △ADC ≌ △EDB
D
C
∴ AC = EB
在△ABE中，AE < AB+BE＝AB+AC
E
即 2AD < AB+AC
∴ AD 1 (AB AC) 2
2024/3/9
35
12.如图,已知AC∥BD，EA、EB分别平分∠CAB和∠DBA， CD过点E，则AB与AC+BD相等吗？请说明理由。
C A
∵ QD⊥OA，QE⊥OB，QD＝QE（已知）． ∴点Q在∠AOB的平分线上．（到角的两边的距
离相等的点在角的平分线上）
2024/3/9
10
2.如图, △ABC的角平分线BM,CN相交于点P, 求证：点P到三边AB、BC、CA的距离相等

人教版九年级数学中考总复习《全等三角形》 (共23张PPT)

等三角形的判定方法SAS即可得解. 证明：∵∠1=∠2，
∴∠1+∠FBE=∠2+∠FBE，即∠ABE=∠CBF.
∴△ABE≌△CBF（SAS）.
考题再现 1. （2014深圳）如图1-4-3-7，△ABC和△DEF中，AB=DE,∠B= ∠DEF，添加下列哪一个条件无法证明△ABC≌△DEF（ C ）
∴△AED≌△AEF（SAS）.
考点点拨：本考点的题型一般为解答题，难度中等. 解答本考点的有关题目，关键在于掌握全等三角形的判定方法与思路. 注意以下要点：判定两个三角形全等的一般方法有SSS、SAS、ASA、AAS、HL （相关要点详见“知识梳理”部分），同时要结合其他知识点如平行线、平行四边形的性质等来证明三角形全等. 另外，注意AAA、SSA不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，且若有两边一角对应相等时，角必须是两边的夹角.
3. 全等三角形的判定（1）边边边：三边对应相等的两个三角形全等（可简写成 “SSS”）. （2）边角边：两边和它们的夹角对应相等的两个三角形全等（可简写成“SAS”）. （3）角边角：两角和它们的夹边对应相等的两个三角形全等（可简写成“ASA”）. （4）角角边：两角和其中一角的对边对应相等的两个三角形全等（可简写成“AAS”）. （5）斜边直角边：斜边和一条直角边对应相等的两个直角三角形全等（可简写成“HL”）.
方法规律
中考考点精讲精练
考点1 全等三角形的概念和性质
考点精讲
【例1】（2016厦门）如图1-4-3-1，点
E，F在线段BC上，△ABF与△DCE全等，
点A与点D，点B与点C是对应顶点，AF与
DE交于点M，则∠DCE=
（）

全等三角形-中考数学总复习精品课件

三角形全等的条件
如何找边相等、角相等
1.找“角”相等的途径主要有:对顶角相等;两直线平行,同位角、内错角相等;余角等角代换;角平分线;平行四边形对角相等等.
2.找“边”相等主要借助中点、平行四边形对边相等来证明.
三角形全等的证明
如何找边相等、角相等
3．判定两个三角形全等的三个条件中，“边”是必不可少的．
垂足分别是点 D，E，AD＝3，BE＝1，则 DE 的长是( B )
3 A.2
B．2
C．2 2
D. 10
61．2如0° 图，△ABC≌△A′B′C′，其中∠A＝36°，∠C′＝24°，则∠B＝________.
7．如图，已知∠ABC＝∠DCB，添加下列条件中的一个：①∠A＝∠D，②AC＝DB， ③AB＝DC，其中不能确定△ABC≌△DCB的是_②_____(只填序号)．
A．∠A＝∠D B．AC＝DF C．AB＝ED D．BF＝EC
平移加翻折型
2．如图，在△ABC和△DEF中，AB＝DE，AC＝DF，BE＝CF，且 BC＝5，∠A＝70°，∠B＝75°，EC＝2，则下列结论中错误的是
( C)
A．BE＝3 B．∠F＝35° C．DF＝5 D．AB∥DE
平移型
3．如图，小强利用全等三角形的知识测量池塘两端M，N的距离，如果
对称型
解：(1)在△ABC 和△ADC 中，AABC＝＝AADC，，∴△ABC≌△ADC(SSS)， BC＝DC，
∴∠BAC＝∠DAC，即 AC 平分∠BAD (2) 由 (1) 得 ∠BAE ＝ ∠ DAE ，在 △BAE 和 △DAE 中，
BA＝DA， ∠BAE＝∠DAE，∴△BAE≌△DAE(SAS)，∴BE＝DE AE＝AE，

《全等三角形》数学教学PPT课件(6篇)

加深理解
E A
F
B
C
∆ABC ≌ ∆FDE
对应顶点对应顶点对应顶点对应角对应角对应角对应边对应边对应边
41
课堂测试 1.如果∆ABC≌ ∆ADC，AB=AD，∠B=70°, BC=3cm,那么∠D=___7_0,D°C=____3cm
D
课堂测试
2、若△AOC≌△BOD，对应边是应角是；
小组讨论完成
解：∵ △ABD ≌ △EBC，∴AB=EB，BD=BC, ∵BD=ED+EB ∴DE=BD-EB=BC-AB=5-3=2cm.
三、巩固练习
基础练习（教材第三十二页练习1-2题）
四、课堂小结，请大家回顾一下：
这节课你学到了什么？还有哪些疑惑？学生充分讨论回答。
点评梳理：
（1）全等三角形的概念及表示方法；（2）全等三角形的性质及应用。
思考
将两个全等三角形重合在一起，
重合的顶点叫对应顶点
A
D
重合的边叫对应边
重合的角叫对应角
根据动画效果，你能说出
这两个全等三角形的对应顶点、
B
CE
F 对应边、对应角各是什么吗？
36
全等三角形表示
如果两个三角形全等，那么该如何表示吗？
A
D
右图中的∆ABC和∆DEF全等
记作: ∆ABC ≌ ∆DEF
五、课后练习
1、教材第33-34页，1-6题。
第十二章全等三角形
12.1 全等三角形
人教版数学（初中）（八年级上）
Please Enter Your Detailed Text Here, The Content Should Be Concise And Clear, Concise And Concise Do Not Need Too Much Text

人教版九年级中考数学总复习课件第26课时全等三角形(共16张PPT)

第26课时全等三角形
考点1:全等三角形的概念及性质
全等图形
全等三角形
性质
能够完全重合的两个图形叫做全等形, 全等图形的形状和大小都相同.
能够完全重合的两个三角形叫做全等三角形.
(1)全等三角形的对应边 (2)全等三角形的对应角
相等；相等.
1.[教材原题]如图是两个全等三角形,图中的字母表
求证:AB∥CD.
D
C
证明:∵AE⊥BD,CF⊥BD
E
∴AEB CFD 90o
F
∵BF DE
A
B
∴ BF EF DE EF
即 BE DF 在 Rt△ABE 和 Rt△CDF 中
AB CD BE DF
∴∠B ∠D ∴AB∥CD.
∴ Rt△ABE ≌ Rt△CDF ( HL)
6.[变式]如图,已知 AB AD ,添加下列一个条件后,
You have to believe in yourself. That's the secret of success. 人必须相信自己，这是成功的秘诀。
4.[教材原题]如图,点 B,F,C,E 在一条直线上,
FB CE ,AB∥ED,AC∥FD.
求证: AB DE , AC DF .
A
∴ E ACF .
点悟:判断两个三角形全等,先挖掘题目中隐含的条件 (如公共边、公共角、对顶角等),再根据具体条件选择判定方法.
考点3:角的平分线的性质及判定
性质判定
角的平分线上的点到角的两边的
距离相等
.
角的内部到角的两边的距离相等
的点在角的平分线
上.
8.[教材原题]如图,△ABC 的 ABC 的外角的平分线 BD 与∠C 的外角的平分线 CE 相交于点 P. 求证:点 P 到三边 AB、BC、CA 所在直线的距离相等.

初三复习专题课件--全等三角形

所以AC＝BC且∠ACB＝90°，所以∠1＋∠2
＝90°，由BE⊥ l 得∠2＋∠3＝90°，所
以∠1＝∠3，在△ACD和△BCE中，∠ADC＝
∠BEC＝90°，所以△ACD≌△CBE。
（A.A.S.）
A
B
3
A
l
E
12
D
C
E
①
D
1
l
2
B
C
②
• （2）由△ACB是等腰直角三角形可知∠ACB＝90°，
即∠1＋∠2＝90°，AC＝BC，而由BE⊥ 得∠2l－
∠CBE＝90°，所以∠1＝∠CBE，于是
△ACD≌△CBE（AAS）
A
B
3
12
D
C
E
l
①
A
l
E
D
1
2
B
C
②
• 误点剖析：图②看上去较复杂，但只要针对问题的要求，把观察点置于△ACD和 △CBE中，然后研究它们的边与角之间的关系，就不致于混乱而感到复杂。
• 如果两个直角三角形有一条斜边和一条直角边对应相等，那么这两个直角三角
形全等，简称为（斜边，直角边或HL ）
• 3.全等三角形的性质 • 全等三角形的对应边相等，对应角相等。
• 三:典型例题
• 例1. 判断：都有两边长分别为3cm和5cm的两个等腰三角形全等。
• 分析：以3cm为腰或以5cm为腰画两个等腰三角形。
• 即∠APD＝∠BPC，所以△APD≌△CPB。
（SAS)，所以AD＝BC
D
• 误点剖析实际上，△PBC
• 可看作是△PDA绕着P点按顺
C • 时针方向旋转60°得到，

《三角形全等的判定》全等三角形PPT课件

好的△ ′′′剪下来，放到△ 上，它们全等吗？
画一个△ ′′′，使′′ = ，′’ =
，∠′ = ∠：
（1）画∠′ = ∠；
（2）在射线′上截取′′ = ，在
射线′上截取′′ = ；
（3）连接′′.
【结论】两边和它们的夹角分别相等的三角形全等。也就是说，三角形的两
⫽ .
∠4. 求证：∠5 = ∠6.
∵ ∠1 = ∠2，∠3 = ∠4， = ，
根据易证△ ≌△ ，
∴有 = ，
又∵ ∠3 = ∠4， = ，
则可根据判定△ ≌△ ，
故∠5 = ∠6.
知识梳理
例4：如图，、交于点，、为上两点， = ， =
就全等了.如果满足斜边和一条直角边分别相等，这两个直
角三角形全等吗？
教学新知
探索5：任意画出一个△，使∠=90°.再画一个 △ ′’’，使
∠′=90°，′′=，′′=.把画好的△′′′剪下来，放
到△上，它们全等吗？
画一个 △ ′′′ ，使 ∠′ = 90° ， ′′ =
求证 = .
∵⊥，⊥
∴∠与∠都是直角
在R △ 和Rt △ 中，
=
=
∴ △ ≌ △ （）
∴ = .
知识梳理
知识点1：“边边边”（或“SSS”）
1.三边分别相等的两个三角形全等（可以简写成“边边边”
两个三角形全等吗？上述六个条件中，有些条件是相关的.
能否在上述六个条件中选择部分条件，简捷地判定两个三角
形全等呢？
探索1：先任意画出一个△ ABC.再画一个△ A′B′C′，使△ ABC与
△ A′B′C′满足上述六个条件中的一个（一边或一角分别
相等）或两个（两边、一边一角或两角分别相等）.你

全等三角形中考复习PPT课件

高频考点
命题趋势
1.全等三角形的定义及性质 2.全等三角形的判定 3.全等三角形的综合应用
全等三角形是证明线段、
角的数量关系的有力工具，在中考中主要考查全等三角形的性质及判定的综合应用，大多数是以选择题、填空题或开放探索题的形式出现
第1页/共23页
1、能够完全重__合___ 的两个三角形叫做全等三角形. 2、全等三角形的对应边__相_等____，对应角__相__等___。全等三角形的对应线段（对应边上的中线、高，对应角的平分线）也__相_堂小结
1、全等三角形的概念—— 能够重合的三角形 2、全等三角形的性质—— 对应边相等、对应角相等 3、全等三角形的判定方法—— （SSS）（SAS）（ASA）（AAS）（ＨＬ）
第21页/共23页
作业:P77-78
第22页/共23页
感谢您的观看！
第23页/共23页
第16页/共23页
1.如图，AB∥DE，AC∥DF，AC=DF，下列条件中不能判断△ABC≌△DEF的是（ C）
A．AB=DE B．∠B=∠E
C．EF=BC
2.如图所示,已知在三角形纸片ABC中,BC=3,AB=6, ∠BCA=90°．在AC上取一点E,以BE为折痕,使AB的一部分与BC重合,A与BC延长线上的点D重合,则DE
找已知边的对角
∠B=∠D （AAS）
第7页/共23页
判定思路4
A
B
隐藏条件
——对顶角
要添防加止AC出=现BD或者 “ADS=SBAC”可的以错吗误？！
O
隐藏条件
——公共边
D
C
4.如图，已知∠A=∠B，要使△ADC≌△BCD，需要添
加的一个条件是__________。

全等三角形复习课件.说课课件

2023全等三角形复习课件.说课课件CATALOGUE目录•课程引入•全等三角形性质与判定•三角形全等的证明方法•全等三角形在实际生活中的应用•复习巩固与提高•说课内容展示与讲解01课程引入全等三角形是指能够完全重合的两个三角形，即形状相同且大小相等的三角形。

复习全等三角形基本概念定义全等三角形的对应边相等，对应角相等，周长相等，面积相等。

性质用全等符号“≌”表示两个三角形全等。

表示方法通过本次复习，使学生进一步熟悉全等三角形的性质和判定方法，掌握全等三角形的证明方法，提高运用全等三角形解决问题的能力。

复习目标采用讲解与练习相结合的方式，通过典型例题的分析和解题方法的指导，帮助学生巩固全等三角形的知识，提高解题能力和思维水平。

复习方法引入复习目标和方法02全等三角形性质与判定1全等三角形性质回顾23定义：两个三角形全等是指能够完全重合的两个三角形。

全等三角形的性质：全等三角形的对应边相等，对应角相等。

运用全等三角形的性质可以进行简单的几何证明。

全等三角形判定方法总结•定义：两个三角形全等是指能够完全重合的两个三角形。

•常用的判定方法有：SSS、SAS、ASA、AAS、HL。

•SSS：三边对应相等的两个三角形全等。

•SAS：两边及其夹角对应相等的两个三角形全等。

•ASA：两角及其夹边对应相等的两个三角形全等。

•AAS：两角及其中一个角的对边对应相等的两个三角形全等。

•HL：斜边和一条直角边对应相等的两个直角三角形全等。

经典例题解析在△ABC和△DEF中，AB=DE，AC=DF，∠B=∠E，求证：△ABC≌△DEF。

例题1解析例题2解析此题考查的是全等三角形的判定，根据ASA可以进行证明。

在Rt△ABC和Rt△DEF中，∠A=∠D=90°，BC=EF，求证：△ABC≌△DEF。

此题考查的是全等三角形的判定，根据HL可以进行证明。

03三角形全等的证明方法直接证明方法讲解根据全等三角形的定义，直接证明两个三角形全等的方法。