初二年级30道典型几何综合题
初二上册几何试题及答案

初二上册几何试题及答案一、选择题(每题3分,共30分)1. 下列哪个选项是线段的中点?A. 线段的两个端点B. 线段的两个端点的连线的交点C. 线段上距离两端点距离相等的点D. 线段的垂直平分线上的任意一点答案:C2. 一个角的度数是90°,那么这个角是:A. 锐角B. 直角C. 钝角D. 平角答案:B3. 如果两个角的和为180°,那么这两个角是:A. 互补角B. 互余角C. 相等角D. 同位角答案:A4. 一个三角形的三个内角之和是:A. 90°B. 180°C. 270°D. 360°答案:B5. 一个多边形的外角和是:A. 90°B. 180°C. 270°D. 360°答案:D6. 一个圆的周长是直径的多少倍?A. 2倍B. 3倍C. π倍D. 2π倍答案:C7. 一个圆的面积公式是:A. πr²B. 2πrC. πdD. πd²答案:A8. 一个正方形的对角线与边长的关系是:A. 相等B. 两倍C. 根号2倍D. 根号3倍答案:C9. 一个矩形的长和宽分别是a和b,那么它的面积是:A. a+bB. abC. a²D. b²答案:B10. 一个平行四边形的对角线互相:A. 平行B. 垂直C. 相等D. 相交答案:D二、填空题(每题3分,共30分)1. 一个等腰三角形的顶角是100°,那么它的两个底角分别是______。
答案:40°2. 如果一个角是30°的角,那么它的余角是______。
答案:60°3. 一个圆的半径是5cm,那么它的直径是______。
答案:10cm4. 一个正五边形的内角和是______。
答案:540°5. 一个梯形的上底和下底分别是3cm和7cm,高是4cm,那么它的面积是______。
八年级上册数学应用几何题30个

八年级上册数学应用几何题30个1、张大伯家有 940 千克水稻,每 50 千克装一袋,至少需要多少只袋子将这些水稻装起来?2、修一条长 960 米的水渠,原计划 24 天完成任务。
实际每天修 48 米,实际可提前几天完成任务?3、同学们排队做操,如果每行站 24 人,需要站 36 行;如果每行站 32 人,需要站多少行?4、一套服装,上衣 54 元,裤子 38 元。
①8 套这样的服装要多少元?②690 元最多可以买几这样的衣服?5、一瓶油,连瓶中 700 克,吃了油的一半后,连瓶还重450 克。
油重多少克?瓶子重多克?6、甲工程队每天修路 128 米,乙工程队每天修路 236 米,丙工程队每天修路 136 米,丁工程队每天修路 264 米。
现有一条 500 米的路,要求一天修完,选择哪几个工程队合修比较合适?7、学校新建了一幢教学楼,共 4 层,每层有 5 间教室,每间教室里安装了 12 盏日光灯。
这幢教学楼共安装了多少盏日光灯?8、 15 只青蛙 1 小时可以吃蚊子 480 只。
照这样计算,250只青蛙 1 小时可以吃多少只?如果 50 只蚊子重 1 克,这些蚊子工重多少克?9、春苗小学一年级和二年级组织小朋友一起去旅游。
一年级有 48 人,二年级有 44 人。
已知面包车每车坐 17 人,大巴每车坐 35 人。
请帮他们设计一个租车方案。
10、在公园门口,小李停放小汽车,第一小时需付款 4 元,以后每小时付款 2 元;小张停放面包车,第一小时需付款 5 元,以后每小时付款 3 元。
他们都付了 14 元,各停车几小时?13.( 1)水波小学每间教室有 3 个窗户,每个窗户安装 12 块玻璃, 9 间教室一共安装多少块玻璃?( 2)杨柳小学有 12 间教室,每间教室有 3 个窗户,一共安装 324 块玻璃。
平均每个窗户安装多少块玻璃?14.小红买了 2 盒绿豆糕,一共重 1 千克。
每盒装有 20 块,平均每块重多少克?15.一辆大巴车从张村出发,如果每小时行驶 60 千米, 4 小时就可以到达李庄。
初二数学几何题50道,要带答案带过程

初二数学几何题50道,要带答案带过程选择题:1. 若两角互为补角,则它们的差是()。
A.0°B.45°C.60°D.90°2. 在图中,如点S、T分别在边AB的延长线上,且∠ASP=60°,∠BAT=20°,则∠AST为()。
A.40°B.50°C.80°D.110°3. 已知正方形ABCD的边长为5cm,点E、F分别在边AD、AB上,且AE=BF,则三角形CEF的面积为()。
A.(5/8) cm²B.(9/8) cm²C.(13/8) cm²D.(15/8) cm²4. 如果一个圆心角的度数为30°,则它所对的弧度数是()。
A.π/6B.π/3C.π/4D.π/2填空题:1.如图,已知BC平分∠ABD,设∠BAC=a°,∠BCA=b°,则∠CBD=\_\_\_\_°。
2.如图,点A、B、C在同一条直线上,则对于ΔABC来说,以下说法正确的是:①AB=AC;②\angleBAC是钝角;③\angleABC+\angleACB =180^\circ,所以\angleABC=\_\_\_\_°,\angleACB=\_\_\_\_°。
3. 已知直角三角形ABC,其中\angleC=90°,BC=3,AC=4,则AB=\_\_\_\_。
4.如图,长方形ABCD中,点E、F分别为BC、CD上的点,若∠BAE=∠EFD,AB=10cm,则DF=\_\_\_\_cm。
解答题:1.如图,在\triangleABC中,垂足分别为D、E、F。
若AC=6,BD=8,DE=5,EF=9,则BC=()。
2.如图,已知\angleBAC=60°,AD平分\angleBAC,且BD=AD,点E为AD的延长线上的点,且\angleBEC=140°,则\angleACD=\_\_\_\_\_\_°。
【初中数学】几何综合题及答案,13道!

几何综合题复习几何综合题是中考试卷中常见的题型,大致可分为几何计算型与几何论证型综合题,它主要考查考生综合运用几何知识的能力。
一、几何论证型综合题例1、(盐城)如图,已知:⊙O 1与⊙O 2是等圆,它们相交于A 、B 两点,⊙O 2在⊙O 1上,AC 是⊙O 2的直径,直线CB 交⊙O 1于D ,E 为AB 延长线上一点,连接DE 。
(1)请你连结AD ,证明:AD 是⊙O 1的直径;(2)若∠E=60°,求证:DE 是⊙O 1的切线。
分析:解几何综合题,一要注意图形的直观提示,二要注意分析挖掘题目的隐含条件,不断地由已知想可知,发展条件,为解题创条件打好基础。
证明:(1)连接AD ,∵AC 是⊙O 2的直径,AB ⊥DC A∴∠ABD=90°,∴AD 是⊙O 1的直径O 1O 2(2)证法一:∵AD 是⊙O 1的直径,∴O 1为AD 中点CDB 连接O 1O 2,∵点O 2在⊙O 1上,⊙O 1与⊙O 2的半径相等,E∴O 1O 2=AO 1=AO 2∴△AO 1O 2是等边三角形,∴∠AO 1O 2=60°由三角形中位线定理得:O 1O 2∥DC ,∴∠ADB=∠AO 1O 2=60°∵AB ⊥DC ,∠E=60,∴∠BDE=30,∠ADE=∠ADB+∠BDE=60°+30°=90°又AD 是直径,∴DE 是⊙O 1的切线证法二:连接O 1O 2,∵点O 2在⊙O 1上,O 1与O 2的半径相等,∴点O 1在⊙O 2∴O 1O 2=AO 1=AO 2,∴∠O 1AO 2=60°∵AB 是公共弦,∴AB ⊥O 1O 2,∴∠O 1AB=30°∵∠E=60°∴∠ADE=180°-(60°+30°)=90°由(1)知:AD 是的⊙O 1直径,∴DE 是⊙O 1的切线.说明:本题考查了三角形的中位线定理、圆有关概念以及圆的切线的判定定理等。
【精品】初二年级30道典型几何综合题

30道典型几何综合题1、解答:解:(1)如图,作点D关于x轴的对称点D',连接CD'与x轴交于点E,连接DE.若在边OA上任取点E'与点E不重合,连接CE'、DE'、D'E'由DE'+CE'=D'E'+CE'>CD'=D'E+CE=DE+CE,可知△CDE的周长最小.∵在矩形OACB中,OA=3,OB=4,D为OB的中点,∴BC=3,D'O=DO=2,D'B=6,∵OE∥BC,∴Rt△D'OE∽Rt△D'BC,有∴∴点E的坐标为(1,0);(2)如图,作点D关于x轴的对称点D',在CB边上截取CG=2,连接D'G与x轴交于点E,在EA上截取EF=2,∵GC∥EF,GC=EF,∴四边形GEFC为平行四边形,有GE=CF,又GC、EF的长为定值,∴此时得到的点E、F使四边形CDEF的周长最小.∵OE∥BC,∴Rt△D'OE∽Rt△D'BG,有.∴∴∴点E的坐标为(,0),点F的坐标为(,0)(10分)2、解答:解:(1)设点B(4,﹣1)关于x轴的对称点是B',其坐标为(4,1),设直线AB'的解析式为y=kx+b,把A(2,﹣3),B'(4,1)代入得:,解得∴y=2x﹣7,令y=0得x=,即p=.(2)过A点作AE⊥x轴于点E,且延长AE,取A'E=AE.做点F(1,﹣1),连接A'F.那么A'(2,3).直线A'F的解析式为,即y=4x﹣5∵C点的坐标为(a,0),且在直线A'F上,∴a=.(3)存在使四边形ABMN周长最短的点M、N,作A关于y轴的对称点A′,作B关于x轴的对称点B′,连接A′B′,与x轴、y轴的交点即为点M、N,∴A′(﹣2,﹣3),B′(4,1),∴直线A′B′的解析式为:y=x﹣,∴M(,0),N(0,﹣).m=,n=﹣.3、解答:(1)证明:∵沿对角线BD对折,点C落在点C′的位置,∴∠A=∠C′,AB=C′D∴在△GAB与△GC′D中,∴△GAB≌△GC′D∴AG=C′G;(2)解:∵点D与点A重合,得折痕EN,∴DM=4cm,ND=5cm,∵EN⊥AD,∴MN==3(cm),由折叠的性质可知∠NDE=∠NDC,∵EN∥CD,∴∠END=∠NDC,∴∠END=∠NDC=∠NDE,∴EN=ED,设EM=x,则ED=EN=x+3,由勾股定理得ED2=EM2+DM2,即(x+3)2=x2+42,解得x=,即EM=.4、解答:解:(1)等腰.(2)如图①,连接BE,画BE的中垂线交BC与点F,连接EF,△BEF是矩形ABCD的一个折痕三角形.∵折痕垂直平分BE,AB=AE=2,∴点A在BE的中垂线上,即折痕经过点A.∴四边形ABFE为正方形.∴BF=AB=2,∴F(2,0).(3)矩形ABCD存在面积最大的折痕三角形BEF,其面积为4,理由如下:①当F在边BC上时,如图②所示.S△BEF≤S矩形ABCD,即当F与C重合时,面积最大为4.②当F在边CD上时,如图③所示,过F作FH∥BC交AB于点H,交BE于K.∵S△EKF=KF?AH≤HF?AH=S矩形AHFD,S△BKF=KF?BH≤HF?BH=S矩形BCFH,∴S△BEF≤S矩形ABCD=4.即当F为CD中点时,△BEF面积最大为4.下面求面积最大时,点E的坐标.①当F与点C重合时,如图④所示.由折叠可知CE=CB=4,在Rt△CDE中,ED===2.∴AE=4﹣2.∴E(4﹣2,2).②当F在边DC的中点时,点E与点A重合,如图⑤所示.此时E(0,2).综上所述,折痕△BEF的最大面积为4时,点E的坐标为E(0,2)或E(4﹣2,2).5、解答:解:(1)由折叠知BE=EM,∠B=∠EMP=90°.①△AEM的周长=AE+EM+AM=AE+EB+AM=AB+AM.∵AB=4,M是AD中点,∴△AEM的周长=4+2=6(cm);②现证明EP=AE+PD方法一:取EP的中点G,则在梯形AEPD中,MG为中位线,∴MG=(AE+PD),在Rt△EMP中,MG为斜边EP的中线,∴MG=EP,∴EP=AE+PD.方法二:延长EM交CD延长线于Q点.∵∠A=∠MDQ=90°,AM=DM,∠AME=∠DMQ,∴△AME≌△DMQ.∴AE=DQ,EM=MQ.又∵∠EMP=∠B=90°,∴PM垂直平分EQ,有EP=PQ.∵PQ=PD+DQ,∴EP=AE+PD.(2)△PDM的周长保持不变.设AM=x,则MD=4﹣x.由折叠性质可知,EM=4﹣AE,在Rt△AEM中,AE2+AM2=EM2,即AE2+x2=(4﹣AE)2,∴AE=(16﹣x2)又∵∠EMP=90°,∴∠AME+∠DMP=90°.∵∠AME+∠AEM=90°,∴∠AEM=∠DMP.又∠A=∠D,∴△PDM∽△MAE.∴∴C△PDM=C△MAE?=(4+x)?=8.∴△PDM的周长保持不变.6、解答:解:(1)∵A(﹣6,0),C(0,4)∴OA=6,OC=4设DE与y轴交于点M由DE∥AB可得△DMC∽△AOC又CD=AC∴∴CM=2,MD=3同理可得EM=3∴OM=6∴D点的坐标为(3,6);(2)由(1)可得点M的坐标为(0,6)由DE∥AB,EM=MD可得y轴所在直线是线段ED的垂直平分线∴点C关于直线DE的对称点F在y轴上∴ED与CF互相垂直平分∴CD=DF=FE=EC∴四边形CDFE为菱形,且点M为其对称中心作直线BM,设BM与CD、EF分别交于点S、点T可证△FTM≌△CSM∴FT=CS∵FE=CD∴TE=SD∵EC=DF∴TE+EC+CS+ST=SD+DF+FT+TS∴直线BM将四边形CDFE分成周长相等的两个四边形,由点B(6,0),点M(0,6)在直线y=kx+b上,可得直线BM的解析式为y=﹣x+6.(3)确定G点位置的方法:过A点作AH⊥BM于点H,则AH与y轴的交点为所求的G点由OB=6,OM=6可得∠OBM=60°∴∠BAH=30°在Rt△OAG中,OG=AO?tan∠BAH=2∴G点的坐标为.(或G点的位置为线段OC的中点)7、解答:解:(1)△A2B2C2的三个顶点的坐标分别是A2(4,0),B2(5,0),C2(5,2);(3分)(2)如果0<a≤3,那么点P1在线段OM上,PP2=PP1+P1P2=2OP1+2P1M=2(OP1+P1M)=2OM=6;(5分)如果a>3,那么点P1在点M的右边,PP2=PP1﹣P1P2=2OP1﹣2P1M=2(OP1﹣P1M)=2OM=6.所以PP2的长是6.(7分)8、解答:解:(1)Rt△CEF、Rt△ADE、Rt△AEF、Rt△AA1D1、Rt△ED1C1、Rt△C1B1F.(写出其中三个即可)(2)AF==5过E作EM⊥AF,垂足为M,交D1C1于N,则EM=2∵四边形A1B1C1D1是正方形∴D1C1∥AF∴△D1C1E∽△AFE∴设正方形A1B1C1D1的边长为x,则解得x=∴正方形A1B1C1D1的边长为.(3)∵D1C1=,EN=2﹣=∴S△D1EC1=××=∴=,C1B1=∴B1F=∴S△C1B1F1=××=∵∠1=∠2,∠1+∠4=90°,∠2+∠3=90°∴∠3=∠4∴E1点在C1F1上又∵S△正方形A1B1C1D=()2=∴S未被覆盖四边形=﹣﹣=.9、解答:解:(1)由题意可知:OA=2,∠AOB=30°,则根据直角三角形中30°所对的边是斜边的一半,则AB=1,根据勾股定理可以求得OB=;则点A的坐标为(1,),点B的坐标为(0,);(2)垂直.理由:连接DE,直角三角形ODE中,tan∠OED==,∴∠OED=60°.∵∠BAO=30°,∴OA⊥ED.(3)因为DE总是垂直于OA运动,因此可以看做直线DE沿OA方向进行运动.因此两者有公共点的取值范围就是O?A之间.当DE过O点时,t=0.当DE过A点时,直角三角形OAD中,OA=2,∠ODA=30°,因此OD=4,t=.因此t的取值范围是0≤t≤.(4)当0≤t≤时,S=t2;Smax=;当<t≤时,S=﹣t2﹣(﹣t)2=﹣(t﹣)2+,Smax=;当<t≤时,S=(2﹣t)2,S无最大值;综上所述S的最大值为.10、解答:解:(1)∵OA=OB=2,∴A(0,2)、B(2,0)、C(2,2).(3分)(2)△AOM∽△ONO’(4分)证明:∵四边形AOBC是正方形,∴∠AOM=90°.又O’N⊥OB,∴∠ONO'=90°.∴∠AOM=∠ONO’=90°.又根据对称性质可知:AM⊥OO’于D点,∴在Rt△ODM中,∠1+∠3=90°.在Rt△AOM中,∠2+∠3=90°,∴∠1=∠2.∴△AOM∽△ONO’(6分)(3)∵M是OB的中点,∴OM=?OB=1.∴在Rt△AOM中,AM=.又∵OD是Rt△AOM斜边上的高,∴.∴.(8分)又∵△AOM∽△ONO’,∴..∴.∴.(10分)11、解答:解:(1)∵A点第一次落在直线y=x上时停止旋转,∴OA旋转了45度.∴OA在旋转过程中所扫过的面积为.(2)∵MN∥AC,∴∠BMN=∠BAC=45°,∠BNM=∠BCA=45度.∴∠BMN=∠BNM.∴BM=BN.又∵BA=BC,∴AM=CN.又∵OA=OC,∠OAM=∠OCN,∴△OAM≌△OCN.∴∠AOM=∠CON.∴∠AOM=(90°﹣45°)=22.5度.∴旋转过程中,当MN和AC平行时,正方形OABC旋转的度数为45°﹣22.5°=22.5度.(3)在旋转正方形OABC的过程中,p值无变化.证明:延长BA交y轴于E点,则∠AOE=45°﹣∠AOM,∠CON=90°﹣45°﹣∠AOM=45°﹣∠AOM,∴∠AOE=∠CON.又∵OA=OC,∠OAE=180°﹣90°=90°=∠OCN.∴△OAE≌△OCN.∴OE=ON,AE=CN.又∵∠MOE=∠MON=45°,OM=OM,∴△OME≌△OMN.∴MN=ME=AM+AE.∴MN=AM+CN,∴p=MN+BN+BM=AM+CN+BN+BM=AB+BC=4.∴在旋转正方形OABC的过程中,p值无变化.12、解答:解:(1)图②中与△BCF全等的有△GDF、△GAH、△ECH.(2)D1F1=AH1,证明:∵,∴△AF1C≌△D1H1C.∴F1C=H1C,又CD1=CA,∴CD1﹣F1C=CA﹣H1C.即D1F1=AH1;(3)连接CG1.在△D1G1F1和△AG1H1中,∵,∴△D1G1F1≌△AG1H1.∴G1F1=G1H1,又∵H1C=F1C,G1C=G1C,∴△CG1F1≌△CG1H1.∴∠1=∠2.∵∠B=60°,∠BCF=30°,∴∠BFC=90°.又∵∠DCE=90°,∴∠BFC=∠DCE,∴BA∥CE,∴∠1=∠3,∴∠2=∠3,∴G1I=CI.13、解答:解:(1)BE=DF且BE⊥DF;(2)在△DFA和△BEA中,∵∠DAF=90°﹣∠FAB,∠BAE=90°﹣∠FAB,∴∠DAF=∠BAE,又AB=AD,AE=AF,∴△DFA≌△BEA,∴BE=DF;∠ADF=∠ABE,∴BE⊥DF;(3)AE=(﹣1)AD;(4)正方形.14、解答:解:(1)AB=AE,AB⊥AE;(2)将△BCG绕点C顺时针旋转90°后能与△ACE重合(或将△ACE绕点C逆时针旋转90°后能与△BCG重合),理由如下:∵AC⊥BC,DF⊥EF,B、F、C、E共线,∴∠ACB=∠ACE=∠DFE=90°,又∵AC=BC,DF=EF,∴∠DEF=∠D=45°,在△CEG中,∵∠ACE=90°,∴∠CGE+∠DEF=90°∴∠CGE=∠DEF=45°,∴CG=CE,在△BCG和△ACE中,∵,∴△BCG≌△ACE(SAS),∴将△BCG绕点C顺时针旋转90°后能与△ACE重合(或将△ACE绕点C逆时针旋转90°后能与△BCG重合).15、解答:解:(1)∠EBF=30°;(1分)∠QFC=60°;(2分)(2)∠QFC=60°.(1分)解法1:不妨设BP>AB,如图1所示.∵∠BAP=∠BAE﹣∠EAP=60°﹣∠EAP,∠EAQ=∠QAP﹣∠EAP=60°﹣∠EAP,∴∠BAP=∠EAQ.(2分)在△ABP和△AEQ中AB=AE,∠BAP=∠EAQ,AP=AQ,∴△ABP≌△AEQ.(SAS)(3分)∴∠AEQ=∠ABP=90°.(4分)∴∠BEF=180°﹣∠AEQ﹣∠AEB=180°﹣90°﹣60°=30°.∴∠QFC=∠EBF+∠BEF=30°+30°=60°.(5分)(事实上当BP≤AB时,如图2情形,不失一般性结论仍然成立,不分类讨论不扣分)解法2:设AP交QF于M∠QMP为△AMQ和△FMP共同的外角∴∠QMP=∠Q+∠PAQ=∠APB+∠QFC,由△ABP≌△AEQ得∠Q=∠APB,由旋转知∠PAQ=60°,∴∠QFC=∠PAQ=60°,(3)在图1中,过点F作FG⊥BE于点G.∵△ABE是等边三角形,∴BE=AB=2.由(1)得∠EBF=30°.在Rt△BGF中,BG==,∴BF==2.∴EF=2.(1分)∵△ABP≌△AEQ.∴QE=BP=x,∴QF=QE+EF=x+2.(2分)过点Q作QH⊥BC,垂足为H.在Rt△QHF中,y=QH=sin60°×QF=(x+2).(x>0)即y关于x的函数关系式是:y=x+.(3分)16、解答:解:(1)BG=AE,证明:易得BD=DC,GD=DE,∠GDB=∠EDA;故可得Rt△BDG≌Rt△EDA;故BG=AE;(2)成立:证明:连接AD,∵Rt△BAC中,D为斜边BC的中点,∴AD=BD,AD⊥BC,∴∠ADG+∠GDB=90°,∵EFGD为正方形,∴DE=DG,且∠GDE=90°,∴∠ADG+∠ADE=90°,∴∠BDG=∠ADE,在△BDG和△AED中,∴△BDG≌△AED(SAS),∴BG=AE;(3)由(2)可得BG=AE,当BG取得最大值时,AE取得最大值;分析可得:当旋转角度为270°时,BG=AE最大值为1+2=3,此时如图:AF=.17、解答:(1)证明:∵∠A=30°,∠ACB=90°,D是AB的中点.∴CD=AD=BD,又∠B=90°﹣∠A=60°,∴△BCD是等边三角形.又∵CN⊥DB,∴DN=DB.∵∠EDF=90°,△BCD是等边三角形,∴∠ADG=30°,而∠A=30°.∴GA=GD.∵GM⊥AB,∴AM=AD.又∵AD=DB,∴AM=DN.(2)解:(1)的结论依然成立.理由如下:∵DF∥AC,∴∠1=∠A=30°,∠AGD=∠GDH=90°,∴∠ADG=60°.∵∠B=60°,AD=DB,∴△ADG≌△DBH,∴AG=DH.又∵∠1=∠A,GM⊥AB,HN⊥AB,∴△AMG≌△DNH,∴AM=DN.18、解答:解:(1)∵点F在AD上,∴AF2=a2+a2,即AF=a,∴DF=b﹣a,∴S△DBF=DF×AB=×(b﹣a)×b=b2﹣ab;(2)连接AF,由题意易知AF∥BD,∴四边形AFDB是梯形,∴△DBF与△ABD等高同底,即BD为两三角形的底,由AF∥BD,得到平行线间的距离相等,即高相等,∴S△DBF=S△ABD=b2;(3)正方形AEFG在绕A点旋转的过程中,F点的轨迹是以点A为圆心,AF为半径的圆,第一种情况:当b>2a时,存在最大值及最小值,因为△BFD的边BD=b,故当F点到BD的距离取得最大、最小值时,S△BFD取得最大、最小值.如图②所示CF2⊥BD时,S△BFD的最大值=,S△BFD的最小值=,第二种情况:当b=2a时,存在最大值,不存在最小值.∴S△BFD的最大值=.(如果答案为4a2或b2也可).19、解答:(1)证明:证法一:在△ABP与△ADP中,∵AB=AD∠BAC=∠DAC,AP=AP,∴△ABP≌△ADP,∴BP=DP.(2分)证法二:利用正方形的轴对称性,可得BP=DP.(2分)(2)解:不是总成立.(3分)当四边形PECF的点P旋转到BC边上时,DP>DC>BP,此时BP=DP不成立,(5分)说明:未用举反例的方法说理的不得分.(3)解:连接BE、DF,则BE与DF始终相等,(6分)在图1中,由正方形ABCD可证:AC平分∠BCD,∵PE⊥BC,PF⊥BD,∴PE=PF,∠BCD=90°,∴四边形PECF为正方形.(7分)∴CE=CF,∵∠DCF=∠BCE,BC=CD,∴△BEC≌△DFC,∴BE=DF.(8分)20、解答:证明:(1)∵将菱形纸片AB(E)CD(F)沿对角线BD(EF)剪开,∴∠B=∠D,∵将△ECF的顶点F固定在△ABD的BD边上的中点处,△ECF绕点F在BD边上方左右旋转,∴BF=DF,∵∠HFG=∠B,又∵∠HFD=∠HFG+∠GFD=∠B+∠BHF∴∠GFD=∠BHF,∴△BFH∽△DGF,∴,∴BH?GD=BF2;(2)∵AG∥CE,∴∠FAG=∠C,∵∠CFE=∠CEF,∴∠AGF=∠CFE,∴AF=AG,∵∠BAD=∠C,∴∠BAF=∠DAG,∴△ABF≌△ADG,∴FB=DG,∴FD+DG=BD,故答案为:BD.21、解答:解:(1)相似(1分)由题意得:∠APA1=∠BPB1=α,AP=A1P,BP=B1P,则∠PAA1=∠PBB1=,(2分)∵∠PBB1=∠EBF,∴∠PAE=∠EBF,又∵∠BEF=∠AEP,∴△BEF∽△AEP;(3分)(2)存在,理由如下:(4分)易得:△BEF∽△AEP,若要使得△BEF≌△AEP,只需要满足BE=AE即可,(5分)∴∠BAE=∠ABE,∵∠BAC=60°,∴∠BAE=,∵∠ABE=β∠BAE=∠ABE,(6分)∴,;(7分)即α=2β+60°(3)连接BD,交A1B1于点G,过点A1作A1H⊥AC于点H.∵∠B1A1P=∠A1PA=60°,∴A1B1∥AC,由题意得:AP=A1P=2+x,∠A=60°,∴△PAA1是等边三角形,∴A1H=sin60°A1P=,(8分)在Rt△ABD中,BD=,∴BG=,(9分)∴(0≤x<2).(10分)22、解答:解:(1)∵点A(3,0),B(0,4),得OA=3,OB=4,∴在Rt△AOB中,由勾股定理,得AB==5,根据题意,有DA=OA=3.如图①,过点D作DM⊥x轴于点M,则MD∥OB,∴△ADM∽△ABO.有,得,∴OM=,∴,∴点D的坐标为(,).(2)如图②,由已知,得∠CAB=α,AC=AB,∴∠ABC=∠ACB,∴在△ABC中,∴α=180°﹣2∠ABC,∵BC∥x轴,得∠OBC=90°,∴∠ABC=90°﹣∠ABO=90°﹣β,∴α=2β;(3)若顺时针旋转,如图,过点D作DE⊥OA于E,过点C作CF⊥OA于F,∵∠AOD=∠ABO=β,∴tan∠AOD==,设DE=3x,OE=4x,则AE=3﹣4x,在Rt△ADE中,AD2=AE2+DE2,∴9=9x2+(3﹣4x)2,∴x=,∴D(,),∴直线AD的解析式为:y=x﹣,∵直线CD与直线AD垂直,且过点D,∴设y=﹣x+b,则b=4,∵互相垂直的两条直线的斜率的积等于﹣1,∴直线CD的解析式为y=﹣,若顺时针旋转,则可得直线CD的解析式为y=.∴直线CD的解析式为y=﹣或y=.23、解答:(1)证明:如图1,分别连接OE、0F,∵四边形ABCD是菱形,∴AC⊥BD,BD平分∠ADC.AO=DC=BC,∴∠COD=∠COB=∠AOD=90°.∠ADO=∠ADC=×60°=30°,又∵E、F分别为DC、CB中点,∴OE=CD,OF=BC,AO=AD,∴0E=OF=OA,∴点O即为△AEF的外心.(2)解:①猜想:外心P一定落在直线DB上.证明:如图2,分别连接PE、PA,过点P分别作PI⊥CD于I,PJ⊥AD于J,∴∠PIE=∠PJD=90°,∵∠ADC=60°,∴∠IPJ=360°﹣∠PIE﹣∠PJD﹣∠JDI=120°,∵点P是等边△AEF的外心,∴∠EPA=120°,PE=PA,∴∠IPJ=∠EPA,∴∠IPE=∠JPA,∴△PIE≌△PJA,∴PI=PJ,∴点P在∠ADC的平分线上,即点P落在直线DB上.②为定值2.当AE⊥DC时.△AEF面积最小,此时点E、F分别为DC、CB中点.连接BD、AC交于点P,由(1)可得点P即为△AEF的外心.如图3.设MN交BC于点G,设DM=x,DN=y(x≠0.y≠O),则CN=y﹣1,∵BC∥DA,∴△GBP≌△MDP.∴BG=DM=x.∴CG=1﹣x∵BC∥DA,∴△NCG∽△NDM,∴,∴,∴x+y=2xy,∴+=2,即=2.24、解答:解:(1)设AC=4x,BC=3x,在Rt△ABC中,AC2+BC2=AB2,即:(4x)2+(3x)2=102,解得:x=2,∴AC=8cm,BC=6cm;(2)①当点Q在边BC上运动时,过点Q作QH⊥AB于H,∵AP=x,∴BP=10﹣x,BQ=2x,∵△QHB∽△ACB,∴,∴QH=x,y=BP?QH=(10﹣x)?x=﹣x2+8x(0<x≤3),②当点Q在边CA上运动时,过点Q作QH′⊥AB于H′,∵AP=x,∴BP=10﹣x,AQ=14﹣2x,∵△AQH′∽△ABC,∴,即:=,解得:QH′=(14﹣2x),∴y=PB?QH′=(10﹣x)?(14﹣2x)=x2﹣x+42(3<x<7);∴y与x的函数关系式为:y=;(3)∵AP=x,AQ=14﹣2x,∵PQ⊥AB,∴△APQ∽△ACB,∴=,即:=,解得:x=,PQ=,∴PB=10﹣x=,∴≠,∴==≠,∴当点Q在CA上运动,使PQ⊥AB时,以点B、P、Q为定点的三角形与△ABC不相似;(4)存在.理由:∵AQ=14﹣2x=14﹣10=4,AP=x=5,∵AC=8,AB=10,∴PQ是△ABC的中位线,∴PQ∥BC,∴PQ⊥AC,∴PQ是AC的垂直平分线,∴PC=AP=5,∴当点M与P重合时,△BCM的周长最小,∴△BCM的周长为:MB+BC+MC=PB+BC+PC=5+6+5=16.∴△BCM的周长最小值为16.25、解答:解:(1)如图1,过点C作CN⊥x轴,垂足为N,则四边形DONC为矩形,∴ON=CD∵四边形ABCD是菱形,AB=10,∴AB=BC=CD=AD=10,∴ON=10,∵A(﹣6,0),∴OA=6,OD===8,∴点C的坐标为(10,8);(2)如图2,过点P作PH⊥BC,垂足为H,则∠PHC=∠AOD=90°,∵四边形ABCD是菱形,∴∠PCB=∠DAO,∴△PHC∽△DOA,∴==,∴==,∴PH=x,CH=x,∴BH=10﹣x,∵PE∥BC,BQ⊥PQ,∴∠PQB=∠QBC=∠PHB=90°,∴四边形PQBH为矩形,∴PQ=BH=10﹣x,∴y=10﹣x(0<x<10);(3)如图3,过点P作PH′⊥BC,垂足为H′,则四边形PQBH′是矩形,∴BQ=PH′=x,∵PE∥BC,∴∠PED=∠CBD,∵CD=CB,∴∠CBD=∠CDB,∴∠CDB=∠PED,∴PE=PD=10﹣x,QE=PQ﹣PE=x,过点D作DG⊥PQ于点G,过点A作AF⊥PQ交PQ的延长线于点F,∴∠DGF=∠AFG=90°,∵PQ∥BC,∴PQ∥AD,∴∠ADG=90°,∴四边形AFGD为矩形,∴AF=DG,∵PQ∥BC,∴∠DPG=∠C,∵∠DGP=∠PH′C=90°,∴△DGP∽△PH′C,∴=,∴AF=DG=(10﹣x)=8﹣x,∵S△BQE+S△AQE=EQ×BQ+EQ×AF,=×x×x+×x×(8﹣x)=x,S△DEP=PE×DG=(10﹣x)×(8﹣x),=x2﹣8x+40,∵S△BQE+S△AQE=S△DEP,∴x=(x2﹣8x+40),整理得,x2﹣25x+100=0,∴x1=5,x2=20,∵0<x<10,∴x2=20不符合题意,舍去,∴x1=5,∴x=5时,S△BQE+S△AQE=S△DEP,∵PH′=x=4<5,∴⊙P与直线BC相交.26、解答:(1)解:∵∠DBC=∠ACB=90°,∴△DBE∽△CAE,∴=,又∵BD=BC=2AC,∴DE=2CE;故答案为DE=2CE.(2)证明:如图2,∵∠DBC=∠ACB=120°,BD=BC,∴∠D=∠BCD=30°,∴∠ACD=90°,过点B作BM⊥DC于M,则DM=MC,BM=BC,∵AC=BC,∴BM=AC,又∵∠BMC=∠ACM=90°,∠MEB=∠CEA,∴△BME≌△ACE,∴ME=CE=CM,∴DE=3EC;(3)解:如图,过点B作BM′⊥DC于点M′,过点F作FN⊥DB交DB的延长线于点N,设BF=a,∵∠DBF=120°,∴∠FBN=60°,∴FN=a,BN=a,∵DB=BC=2BF=2a,∴DN=DB+BN=a,∴DF===a,∵AC=BC,BF=BC,∴BF=AC,∴△DBF≌△ACB,∴∠BDF=∠CBA,又∵∠BFG=∠DFB,∴△FBG∽△FDB,∴==,∴BF2=FG×FD,∴a2=a×FG,∴FG=a,∴DG=DF﹣FG=a,BG==a,∵△DKG和△DBG关于直线DG对称,∴∠GDH=∠BDF,∴∠ABC=∠GDH,又∵∠BGF=∠DGH,∴△BGF∽△DGH,∴=,∴GH==a,∵BH=BG+GH=a=10,∴a=2;∴BC=2a=4,CM′=BCcos30°=2,∴DC=2CM′=4,∵DE=3EC,∴EC=DC=.27、解答:(1)证明:①如图2:∵BM⊥直线a于点M,CN⊥直线a于点N,∴∠BMN=∠CNM=90°,∴BM∥CN,∴∠MBP=∠ECP,又∵P为BC边中点,∴BP=CP,又∵∠BPM=∠CPE,∴△BPM≌△CPE,(3分)②∵△BPM≌△CPE,∴PM=PE∴PM=ME,∴在Rt△MNE中,PN=ME,∴PM=PN.(5分)(2)解:成立,如图3.证明:延长MP与NC的延长线相交于点E,∵BM⊥直线a于点M,CN⊥直线a于点N,∴∠BMN=∠CNM=90°∴∠BMN+∠CNM=180°,∴BM∥CN∴∠MBP=∠ECP,(7分)又∵P为BC中点,∴BP=CP,又∵∠BPM=∠CPE,∴△BPM≌△CPE,∴PM=PE,∴PM=ME,则Rt△MNE中,PN=ME,∴PM=PN.(10分)(3)解:如图4,四边形M′BCN′是矩形,根据矩形的性质和P为BC边中点,得到△M′BP≌△N′CP,(11分)得PM′=PN′成立.即“四边形MBCN是矩形,则PM=PN成立”.(12分)28、解答:解:(1)EG=CG,EG⊥CG.(2分)(2)EG=CG,EG⊥CG.(2分)证明:延长FE交DC延长线于M,连MG.∵∠AEM=90°,∠EBC=90°,∠BCM=90°,∴四边形BEMC是矩形.∴BE=CM,∠EMC=90°,由图(3)可知,△BEF为等腰直角三角形,∴BE=EF,∴EF=CM.∵∠EMC=90°,FG=DG,∴MG=FD=FG.∵BC=EM,BC=CD,∴EM=CD.∵EF=CM,∴FM=DM,∴∠F=45°.又FG=DG,∠CMG=∠EMC=45°,∴∠F=∠GMC.∴△GFE≌△GMC.∴EG=CG,∠FGE=∠MGC.(2分)∵∠FMC=90°,MF=MD,FG=DG,∴MG⊥FD,∴∠FGE+∠EGM=90°,∴∠MGC+∠EGM=90°,即∠EGC=90°,∴EG⊥CG.(2分)29、解答:解:(1)证明:∵四边形OABC为正方形,∴OC=OA.∵三角板OEF是等腰直角三角形,∴OE1=OF1.又三角板OEF绕O点逆时针旋转至OE1F1的位置时,∠AOE1=∠COF1,∴△OAE1≌△OCF1.(3分)(2)存在.(4分)∵OE⊥OF,∴过点F与OE平行的直线有且只有一条,并与OF垂直,当三角板OEF绕O点逆时针旋转一周时,则点F在以O为圆心,以OF为半径的圆上.(5分)∴过点F与OF垂直的直线必是圆O的切线.又点C是圆O外一点,过点C与圆O相切的直线有且只有2条,不妨设为CF1和CF2,此时,E点分别在E1点和E2点,满足CF1∥OE1,CF2∥OE2.(7分)当切点F1在第二象限时,点E1在第一象限.在直角三角形CF1O中,OC=4,OF1=2,cos∠COF1==,∴∠COF1=60°,∴∠AOE1=60°.∴点E1的横坐标为:x E1=2cos60°=1,点E1的纵坐标为:y E1=2sin60°=,∴点E1的坐标为(1,);(9分)当切点F2在第一象限时,点E2在第四象限.同理可求:点E2的坐标为(1,﹣).(10分)综上所述,三角板OEF绕O点逆时针旋转一周,存在两个位置,使得OE∥CF,此时点E的坐标为E1(1,)或E2(1,﹣).(11分)30、解答:(1)证明:在△ABC和△AEP中,∵∠ABC=∠AEP,∠BAC=∠EAP,∴∠ACB=∠APE,在△ABC中,AB=BC,∴∠ACB=∠BAC,∴∠EPA=∠EAP.(2)解:?APCD是矩形.理由如下:∵四边形APCD是平行四边形,∴AC=2EA,PD=2EP,∵由(1)知∠EPA=∠EAP,∴EA=EP,则AC=PD,∴?APCD是矩形.(3)解:EM=EN.证明:∵EA=EP,∴∠EPA===90°﹣α,∴∠EAM=180°﹣∠EPA=180°﹣(90°﹣α)=90°+α,由(2)知∠CPB=90°,F是BC的中点,∴FP=FB,∴∠FPB=∠ABC=α,∴∠EPN=∠EPA+∠APN=∠EPA+∠FPB=90°﹣α+α=90°+α,∴∠EAM=∠EPN,∵∠AEP绕点E顺时针旋转适当的角度,得到∠MEN,∴∠AEP=∠MEN,∴∠AEP﹣∠AEN=∠MEN﹣∠AEN,即∠MEA=∠NEP,在△EAM和△EPN中,∴△EAM≌△EPN(AAS),∴EM=EN.26函数综合题1、解答:解:(1)取a=1,得抛物线y=x 2+2x+3,其顶点为P1(﹣1,2).取a=﹣1,得抛物线y=﹣x2+2x+3,其顶点为P2(1,4).由题意有P1、P2在直线l上,设直线l的解析式为y=kx+b,则解得:∴直线l的解析式为y=x+3.(2)∵抛物线y=ax2+2x+3的顶点P坐标为.显然P在直线y=x+3上.又能取到除0以外的所有实数,∴在y=x+3上仅有一点(0,3)不是该抛物线的顶点.(3)猜想:对于抛物线y=ax2+bx+c(a≠0),将其顶点的横坐标减少,纵坐标增加分别作为点A的横、纵坐标;把顶点的横坐标增加,纵坐标增加分别作为点B的横、纵坐标,则A,B两点也在抛物线y=ax2+bx+c(a≠0)上.证明如下:∵抛物线y=ax2+bx+c(a≠0)的顶点坐标为(),∴点A的坐标为,点B的坐标为.∵时,∴点A在抛物线y=ax2+bx+c(a≠0),同理有B也在抛物线上,故结论成立.2、解答:解:(1)∵抛物线y=ax2+bx+c与y轴交于点C(0,﹣2),代入得:c=﹣2,∴y=ax2+bx﹣2,把A(﹣2,﹣2),B(2,2)代入得:,解得:,∴y=x2+x﹣2,答:抛物线的解析式是y=x2+x﹣2.(2)∵MN=,点A,B都在直线y=x上,MN在直线AB上,MN在线段AB上,M的横坐标为m.如图1,过点M作x轴的平行线,过点N作y轴的平行线,它们相交于点H.∴△MHN是等腰直角三角形.∴MH=NH=1.∴点N的坐标为(m+1,m+1)①如图2,当m<0时,PM=﹣m,NQ=m+1﹣[(m+1)2+m+1﹣2]=﹣(m+1)2+2.当四边形PMQN为平行四边形时,PM=NQ.∴﹣m=﹣(m+1)2+2.解得:m=(不合题意舍去)或﹣,②如图3,当m>0,PM=m,NQ=m+1﹣[(m+1)2+m+1﹣2]=﹣(m+1)2+2.当四边形PMQN为平行四边形时,PM=NQ.∴m=﹣(m+1)2+2.解得:m=﹣2﹣(不合题意舍去)或﹣2,∴当m=﹣或m=﹣2时,以点P,M,Q,N为顶点的四边形能为平行四边形.3、解答:解:(1)∵抛物线y=mx 2﹣11mx+24m (m<0)与x轴交于B、C两点(点B在点C的左侧),∴抛物线与x轴的交点坐标为:0=mx2﹣11mx+24m,解得:x1=3,x2=8,∴OB=3,OC=8 (4分);(2)连接AD,交OC于点E,∵四边形OACD是菱形,∴AD⊥OC,OE=EC=×8=4,∴BE=4﹣3=1,又∵∠BAC=90°,∴△ACE ∽△BAE ,∴=,∴AE 2=BE?CE=1×4,∴AE=2,…(6分)∴点A 的坐标为(4,2)…(7分)把点A 的坐标(4,2)代入抛物线y=mx 2﹣11mx+24m ,得m=﹣,∴抛物线的解析式为y=﹣x 2+x ﹣12;…(9分)(3)∵直线x=n 与抛物线交于点M ,∴点M 的坐标为(n ,﹣n 2+n ﹣12),由(2)知,点D 的坐标为(4,﹣2),则C 、D 两点的坐标求直线CD 的解析式为y=x ﹣4,∴点N 的坐标为(n ,n ﹣4),∴MN=(﹣n 2+n ﹣12)﹣(n ﹣4)=﹣n 2+5n ﹣8,…(11分)∴S 四边形AMCN =S △AMN +S △CMN =MN?CE=(﹣n 2+5n ﹣8)×4 =﹣(n ﹣5)2+9 (13分)∴当n=5时,S 四边形AMCN =9.(14分)4、解答:(1)解:由A (﹣4,0)、B (﹣2,2)在抛物线y=ax 2+bx 图象上,得:(2分)解之得:a=﹣,b=﹣2,∴该函数解析式为:y=﹣x 2﹣2x .(4分)(2)证明:过点B 作BC 垂直于X 轴,垂足是点C .(6分)∵y=﹣x 2﹣2x=﹣(x+2)2+2,∴线段CO 、CA 、CB 的长度均为2,∴△ABC 和△OBC 为全等的等腰直角三角形,∴AB=OB且∠ABO=∠ABC+∠OBC=90°∴△OAB是等腰直角三角形(8分)(3)解:如图,将△OAB绕点O按逆时针方向旋转135°,得到△OA′B′其中点B′正好落在y轴上且B′A′∥x轴.又∵OB′和A′B′的长度为2,A′B′中点P的坐标为(,﹣2),显然不满足抛物线方程,∴点P不在此抛物线上(10分)(4)解:存在(11分)过点O,作OM∥AB交抛物线于点M易求出直线OM的解析式为:y=x联立抛物线解析式得:解之得点M(﹣6,﹣6),显然,点M(﹣6,﹣6)关于对称轴x=﹣2的对称点M′(2,﹣6)也满足要求,故满足条件的点M共有两个,坐标分别为(﹣6,﹣6)和(2,﹣6)∴s ABOM=S△ABO+s△AOM=×4×2+×4×6=16.(12分)(注:此题方法较多,只要合理均可给分)5、解答:解:(1)由题意得,解得:b=2,c=﹣3,则解析式为:y=x2+2x﹣3;(2)由题意结合图形则解析式为:y=x2+2x﹣3,解得x=1或x=﹣3,由题意点A(﹣3,0),∴AC=,CD=,AD=,由AC2+CD2=AD2,所以△ACD为直角三角形;(3)∵A(﹣3,0),B(1,0),∴AB=4,∵点E在抛物线的对称轴上,∴点E的横坐标为﹣1,当AB为平行四边形的一边时,EF=AB=4,∴F的横坐标为3或﹣5,把x=3或﹣5分别代入y=x2+2x﹣3,得到F的坐标为(3,12)或(﹣5,12);当AB为平行四边形的对角线时,由平行四边形的对角线互相平分,∴F点必在对称轴上,即F点与D点重合,∴F(﹣1,﹣4).∴所有满足条件的点F的坐标为(3,12),(﹣5,12),(﹣1,﹣4).6、解答:解:(1)由已知,得B(3,0),C(0,3),∴,解得,∴抛物线解析式为y=x2﹣4x+3;(2)∵y=x2﹣4x+3=(x﹣2)2﹣1,∴对称轴为x=2,顶点坐标为P(2,﹣1),∴满足条件的点M分别为M1(2,7),M2(2,2﹣1),M3(2,),M4(2,﹣2﹣1);(3)由(1),得A(1,0),连接BP,∵∠CBA=∠ABP=45°,∴当=时,△ABC∽△PBQ,∴BQ=3.∴Q1(0,0),∴当=时,△ABC∽△QBP,∴BQ=.∴Q ′(,0).(4)当0<x <3时,在此抛物线上任取一点E ,连接CE 、BE ,经过点E 作x 轴的垂线FE ,交直线BC 于点F ,设点F (x ,﹣x+3),点E (x ,x 2﹣4x+3),∴EF=﹣x 2+3x ,∴S △CBE =S △CEF +S △BEF =EF?OB ,=﹣x 2+x ,=﹣(x ﹣)2+,∵a=﹣<0,∴当x=时,S △CBE 有最大值,∴y=x 2﹣4x+3=﹣,∴E (,﹣).7、解答:解:(1)设二次函数的解析式为y=ax 2+bx+c由题意得,解得,∴二次函数的解析式为y=x 2﹣8x+12,(2分)点P 的坐标为(4,﹣4);(3分)(2)存在点D ,使四边形OPBD 为等腰梯形.理由如下:当y=0时,x 2﹣8x+12=0,∴x 1=2,x 2=6,∴点B的坐标为(6,0),设直线BP的解析式为y=kx+m则,解得∴直线BP的解析式为y=2x﹣12∴直线OD∥BP(4分)∵顶点坐标P(4,﹣4)∴OP=4设D(x,2x)则BD2=(2x)2+(6﹣x)2当BD=OP时,(2x)2+(6﹣x)2=32,解得:x1=,x2=2,(6分)当x2=2时,OD=BP=,四边形OPBD为平行四边形,舍去,∴当x=时四边形OPBD为等腰梯形,(7分)∴当D(,)时,四边形OPBD为等腰梯形;(8分)(3)①当0<t≤2时,∵运动速度为每秒个单位长度,运动时间为t秒,则MP=t,∴PH=t,MH=t,HN=t,∴MN=t,∴S=t?t?=t2(10分),②当2<t<4时,P1G=2t﹣4,P1H=t,∵MN∥OB∴△P1EF∽△P1MN,∴,∴,∴=3t2﹣12t+12,∴S=t2﹣(3t2﹣12t+12)=﹣t2+12t﹣12,∴当0<t≤2时,S=t2,当2<t<4时,S=﹣t2+12t﹣12.(12分)8、解答:解:(1)把点(0,﹣)代入抛物线,得:c=﹣;(2)把点(0,﹣)代入直线得:n=﹣.把点(m﹣b,m2﹣mb+n)代入抛物线,得:a(m﹣b)2+b(m﹣b)+c=m2﹣mb+n∵c=n=﹣,∴a(m﹣b)2+b(m﹣b)=m2﹣mb,am2﹣2abm+ab2+bm﹣b2﹣m2+mb=0(a﹣1)m2﹣(a﹣1)?2bm+(a﹣1)b2=0(a﹣1)(m2﹣2bm+b2)=0(a﹣1)(m﹣b)2=0∴a=1,当m﹣b=0时,抛物线与直线的两个交点就是一个点,所以m≠b.把a=1,c=﹣代入抛物线有:y=x2+bx﹣,当y=0时,x2+bx﹣=0,∴x1?x2=﹣;(3)y=x2+bx﹣,顶点(﹣,﹣﹣)当b≤0时,x=﹣1时,y=﹣b,比较﹣b与+的大小,得到:﹣4≤b≤0时,﹣b≥+,所以当b=0时,|y0|的最小值为.b≤﹣4时,﹣b≤+,所以当b=﹣4时,|y0|的最小值为.当b≥0时,x=1时,y=+b,比较+b与+的大小,得到:时,+b≥+,0≤b≤4所以当b=0时,|y0|的最小值为.b≥4时,+b≤+,所以当b=4时,|y0|的最小值为.故|y0|的最小值为或.9、解答:解:(1)设抛物线的解析式为y=kx2+a,∵经过点(2a,2a),4a 2k+a=2a,∴k=,(2)设抛物线上一点P(x,y),过P作PH⊥x轴,PG⊥y轴,在Rt△GDP中,由勾股定理得:PD2=DG2+PG2=(y﹣2a)2+x2=y2﹣4ay+4a2+x2,∵y=x2+a,∴x2=4a×(y﹣a)=4ay﹣4a2,∴PD2=y2﹣4ay+4a2+4ay﹣4a2=y2=PH2,∴PD=PH,(3)过B作BE⊥x,AF⊥x,由(2)的结论:BE=DB,AF=DA,∵DA=2DB,∴AF=2BE,∴AO=2OB,∴B是OA的中点,∵C是OD的中点,连接BC,∴BC===BE=DB,过B作BR⊥y,∵BR⊥CD,∴CR=DR,OR=a+=,∴=x2+a,∴x2=2a2,∵x>0,∴x=a,∴B(a,)AO=2OB,∴S△OBD=S△ABD=4,∴×2a×a=4,∴a2=4,∵a>0,∴a=2,10、解答:解:(1)∵y=x2+bx+c的顶点为(1,﹣2).∴y=(x﹣1)2﹣2,y=x2﹣2x﹣1;(2)设直线PE对应的函数关系式为y=kx+b,由题意四边形ABCD是菱形,故直线PE必过菱形ABCD的对称中心M.由P(0,﹣1),M(1,0),得从而得y=x﹣1,设E(x,x﹣1)代入y=x2﹣2x﹣1得x﹣1=x2﹣2x﹣1,解得x1=0,x2=3,根据题意得点E(3,2);(3)假设存在这样的点F,可设F(x,x2﹣2x﹣1),过点F做FG⊥y轴,垂足为G点.在Rt△POM和Rt△FGP中,∵∠OMP+∠OPM=90°,∠FPG+∠OPM=90°,∠OMP=∠FPG,又∠POMP=∠PGF,∴△POM∽△FGP∴∵OM=1,OP=1,∴GP=GF,即﹣1﹣(x2﹣2x﹣1)=x,解得x1=0,x2=1,根据题意得F(1,﹣2)以上各步均可逆,故点F(1,﹣2)即为所求,.S△PEF=S△MFP+S△MFE=2×1×2×2=311、解答:解:(1)∵四边形ABCD是矩形,∴AD=CB=10,AB=DC=8,∠D=∠DCB=∠ABC=90°,由折叠对称性:AF=AD=10,EF=DE,在Rt△ABF中,BF===6,∴CF=4,设EF=x,则EC=8﹣x,在Rt△ECF中,42+(8﹣x)2=x2,解得:x=5,∴CE=3,∵B(m,0),∴E(m+10,3),F(m+6,0);(2)分三种情况讨论:若AO=AF,∵AB⊥OF,∴BO=BF=6,∴m=6,若OF=FA,则m+6=10,解得:m=4,若AO=OF,在Rt△AOB中,AO2=OB2+AB2=m2+64,∴(m+6)2=m2+64,解得:m=,∴m=6或4或;(3)由(1)知:E(m+10,3),A(m,8).∴,得,∴M(m+6,﹣1),设对称轴交AD于G,∴G(m+6,8),∴AG=6,GM=8﹣(﹣1)=9,∵∠OAB+∠BAM=90°,∠BAM+∠MAG=90°,∴∠OAB=∠MAG,∵∠ABO=∠MGA=90°,∴△AOB∽△AMG,∴=,即:,∴m=12,12、解答:解:(1)令﹣x2﹣2x+3=0,(x+3)(x﹣1)=0,x1=﹣3,x2=1,A(﹣3,0)B.(1,0),C(0,3);(2)设直线AC的解析式为y=kx+b,由题意,得,解之得,故y=x+3;(3)设M点的坐标为(x,﹣x2﹣2x+3),AB=4,因为M在第二象限,所以﹣x2﹣2x+3>0,所以=6,解之,得x1=0,x2=﹣2,当x=0时,y=3,(不合题意)当x=﹣2时,y=3.所以M点的坐标为(﹣2,3);(4)由题意,得AB=4,PA=4﹣t,∵AO=3,CO=3,∴△AOC是等腰直角三角形,AQ=2t,所以Q点的纵坐标为t,S=(0<t<4)∵,∴当t=2时,△APQ最大,最大面积是.13、解答:解:(1)∵当x=0时,y=3,当y=0时,x=﹣1,∴A(﹣1,0),B(0,3),∵C(3,0),设抛物线的解析式为y=a(x+1)(x﹣3),∴3=a×1×(﹣3),∴a=﹣1,∴此抛物线的解析式为y=﹣(x+1)(x﹣3)=﹣x2+2x+3;(2)存在.①∵抛物线的对称轴为:x==1,∴如图对称轴与x轴的交点即为Q1,∵OA=OQ1,BO⊥AQ1,∴“当Q1B=AB时,设Q(1,q),∴1+(q﹣3)2=10,∴q=0,或q=6,∴Q(1,0)或Q(1,6)(在直线AB上,舍去).当Q2A=Q2B时,设Q2的坐标为(1,m),∴22+m2=12+(3﹣m)2,∴m=1,∴Q2(1,1);当Q3A=AB时,设Q3(1,n),∴22+n2=12+32,∴n=±,∴Q3(1,),Q4(1,﹣).∴符合条件的Q点坐标为Q1(1,0),Q2(1,1),Q3(1,),Q4(1,﹣).14、解答:解:(1)a=﹣1,b=﹣2,顶点C的坐标为(﹣1,4);(2)假设在y轴上存在满足条件的点D,过点C作CE⊥y轴于点E.由∠CDA=90°得,∠1+∠2=90°.又∠2+∠3=90°,∴∠3=∠1.又∵∠CED=∠DOA=90°,∴△CED∽△DOA,∴.设D(0,c),则.变形得c2﹣4c+3=0,解之得c1=3,c2=1.综合上述:在y轴上存在点D(0,3)或(0,1),使△ACD是以AC为斜边的直角三角形.(3)①若点P在对称轴右侧(如图①),只能是△PCQ∽△CAH,得∠QCP=∠CAH.延长CP交x轴于M,∴AM=CM,∴AM2=CM2.设M(m,0),则(m+3)2=42+(m+1)2,∴m=2,即M(2,0).设直线CM的解析式为y=k1x+b1,则,解之得,.∴直线CM的解析式.联立,解之得或(舍去).∴.②若点P在对称轴左侧(如图②),只能是△PCQ∽△ACH,得∠PCQ=∠ACH.过A作CA的垂线交PC于点F,作FN⊥x轴于点N.由△CFA∽△CAH得,由△FNA∽△AHC得.∴AN=2,FN=1,点F坐标为(﹣5,1).设直线CF的解析式为y=k2x+b2,则,解之得.∴直线CF的解析式.联立,解之得或(舍去).∴.∴满足条件的点P坐标为或.15、解答:解:(1)依题意得顶点A的坐标为(2,a),设P(1,n)据x=﹣,得A点的横坐标为m,即m=2,所以y=x2+4x﹣2,把P点的坐标代入得n=1,即P点的坐标为(1,1)(2)把抛物线化为顶点式:y=﹣(x﹣m)2+2,可知A(m,2),设C(n,2),把n代入y=﹣(x﹣m)2+2得y=﹣(n﹣m)2+2,所以P(n,﹣(n﹣m)2+2)∵AC=CP∴m﹣n=2+(m﹣n)2﹣2,即m﹣n=(m﹣n)2,∴m﹣n=0或m﹣n=1,又∵C点不与端点A、B重合∴m≠n,即m﹣n=1,则A(m,2),P(m﹣1,1)由AC=CP可得BE=AB∵OB=2∴OE=2﹣m,∴△OPE的面积S=(2﹣m)(m﹣1)=﹣(m﹣)2+(1<m<2),∴0<S<.16、解答:(1)证明:∵AC⊥BC,BD⊥CD,∴∠BDC=∠COA=90°,∠ACO+∠BCD=90°,∴∠BCD=∠OAC,∵△ABC为等腰直角三角形,∴BC=AC,∵在△BDC和△COA中∴△BDC≌△COA(AAS),(2)解:∵△BDC≌△COA,∴BD=CO,∵C点的坐标为(﹣1,0),∴BD=OC=1,∴B点的纵坐标为1,∵B点的横坐标为﹣3,∴B点的坐标为(﹣3,1),设BC所在直线的函数关系式为y=kx+b,∴,∴解方程组得,∴直线BC所在直线的解析式为:y=﹣x﹣,(3)解:存在,∵抛物线的解析式为:y=x2+x﹣2,∴y=x2+x﹣2=(x+)2﹣,∴二次函数的对称轴为x=﹣,①若以AC为直角边,C点为直角顶点,做CP1⊥AC,∵BC⊥AC,∴P1点为直线BC与对称轴直线x=﹣的交点,∵直线BC所在直线的解析式为:y=﹣x﹣,∴,∴解得,∴P1点的坐标为(﹣,﹣);②若以AC为直角边,A点为直角顶点,对称轴上有一点P2,使AP2⊥AC,∴过点A作AP2∥BC,交对称轴直线x=﹣于点P2,∵OD=3,OC=1,∴OA=CD=2,∴A点的坐标为(0,2),∴直线AP2的解析式为y=﹣x+2,∴,∴解得:,∴P2点的坐标为(﹣,),∴P点的坐标为P1(﹣,﹣)、P2(﹣,).17、解答:解:(1)抛物线y=ax2+bx+3经过点A(﹣3,0),B(﹣1,0)两点,∴,解得a=1,b=4,∴抛物线解析式为y=x2+4x+3;(2)由(1)配方得y=(x+2)2﹣1∴抛物线的顶点M(﹣2,﹣1),直线OD的解析式为y=x.于是设平移后的抛物线的顶点坐标为(h,h),∴平移后的抛物线解析式为y=(x﹣h)2+h,①当抛物线经过点C时,∵C(0,9),∴h2+h=9,解得h=,∴当≤h<时,平移的抛物线与射线CD(含端点C)只有一个公共点,②当抛物线与直线CD只有一个公共点时,由方程组,得x2+(﹣2h+2)x+h2+h﹣9=0,∴△=(﹣2h+2)2﹣4(h2+h﹣9)=0,解得h=4,此时抛物线y=(x﹣4)2+2与射线CD只有唯一一个公共点为(3,3),符合题意,综上所述,平移的抛物线与射线CD(含端点C)只有一个公共点时,顶点横坐标h的取值范围为h=4或≤h<;(3)设直线EF的解析式为y=kx+3(k≠0),点E、F的坐标分别为(m,m2),(n,n2),由得x2﹣kx﹣3=0,∴m+n=k,m?n=﹣3,作点E关于y轴的对称点R(﹣m,m2),作直线FR交y轴于点P,由对称性知∠EPQ=∠FPQ,此时△PEF的内心在y轴上,∴点P即为所求的点.由F,R的坐标可得直线FR的解析式为y=(n﹣m)x+mn记y=(n﹣m)x﹣3,当x=0时,y=﹣3,∴p(0,﹣3),∴y轴的负半轴上存在点P(0,﹣3)使△PEF的内心在y轴上.18、解答:解:(1)设抛物线的函数表达式为y=a(x﹣1)(x+3)∵抛物线交y轴于点E(0,﹣3),将该点坐标代入上式,得a=1∴所求函数表达式为y=(x﹣1)(x+3),即y=x2+2x﹣3;(2)∵点C是点A关于点B的对称点,点A坐标(﹣3,0),点B坐标(1,0),∴点C坐标(5,0),∴将点C坐标代入y=﹣x+m,得m=5,∴直线CD的函数表达式为y=﹣x+5,设K点的坐标为(t,0),则H点的坐标为(t,﹣t+5),G点的坐标为(t,t2+2t﹣3),∵点K为线段AB上一动点,∴﹣3≤t≤1,∴HG=(﹣t+5)﹣(t2+2t﹣3)=﹣t2﹣3t+8=﹣(t+)2+,∵﹣3<﹣<1,∴当t=﹣时,线段HG的长度有最大值;(3)∵点F是线段BC的中点,点B(1,0),点C(5,0),∴点F的坐标为(3,0),∵直线l过点F且与y轴平行,∴直线l的函数表达式为x=3,∵点M在直线l上,点N在抛物线上,∴设点M的坐标为(3,m),点N的坐标为(n,n2+2n﹣3),∵点A(﹣3,0),点C(5,0),∴AC=8,分情况讨论:①若线段AC是以点A、C,M、N为顶点的平行四边形的边,则需MN∥AC,且MN=AC=8.当点N在点M的左侧时,MN=3﹣n,∴3﹣n=8,解得n=﹣5,∴N点的坐标为(﹣5,12),当点N在点M的右侧时,MN=n﹣3,∴n﹣3=8,解得n=11,∴N点的坐标为(11,140),②若线段AC是以点A、C,M、N为顶点的平行四边形的对角线,由“点C与点A关于点B 中心对称”知:点M与点N关于点B中心对称,取点F关于点B的对称点P,则P点坐标为(﹣1,0)过P点作NP⊥x轴,交抛物线于点N,将x=﹣1代入y=x2+2x﹣3,得y=﹣4,过点N,B作直线NB交直线l于点M,在△BPN和△BFM中,∠NBP=∠MBF,BF=BP,∠BPN=∠BFM=90°,∴△BPN≌△BFM,∴NB=MB,∴四边形ANCM为平行四边形,∴坐标(﹣1,﹣4)的点N符合条件,∴当N的坐标为(﹣5,12),(11,140),(﹣1,﹣4)时,以点A、C、M、N为顶点的四边形为平行四边形.19、解答:解:(1)由已知得:A(﹣1,0),B(4,5),∵二次函数y=x2+bx+c的图象经过点A(﹣1,0),B(4,5),∴,解得:b=﹣2,c=﹣3;(2)如图:∵直线AB经过点A(﹣1,0),B(4,5),∴直线AB的解析式为:y=x+1,∵二次函数y=x2﹣2x﹣3,∴设点E(t,t+1),则F(t,t2﹣2t﹣3),∴EF=(t+1)﹣(t2﹣2t﹣3)=﹣(t﹣)2+,∴当t=时,EF的最大值为,∴点E的坐标为(,);(3)①如图:顺次连接点E、B、F、D得四边形EBFD.可求出点F的坐标(,),点D的坐标为(1,﹣4)S四边形EBFD=S△BEF+S△DEF=××(4﹣)+××(﹣1)=;②如图:。
八年级数学上册几何期末综合复习题1

八年级期末几何综合复习(一)1.如图,设△ABC和△CDE都是等边三角形,且∠EBD=65°,则∠AEB的度数是()A.115°B.120°C.125°D.130°2.如图,在四边形ABCD中,AB=AC,∠ABD=60°,∠ADB=78°,∠BDC=24°,则∠DBC=()A.18°B.20°C.25°D.15°3.如图,等腰Rt△ABC中,∠BAC=90°,AD⊥BC于点D,∠ABC的平分线分别交AC、AD于E、F两点,M为EF的中点,AM的延长线交BC于点N,连接DM,下列结论:①DF=DN;②△DMN为等腰三角形;③DM平分∠BMN;④AE=EC;⑤AE=NC,其中正确结论的个数是()A.2个B.3个C.4个D.5个4.如图,等腰Rt△ABC中,∠ABC=90°,AB=BC.点A、B分别在坐标轴上,且x轴恰好平分∠BAC,BC交x轴于点M,过C点作CD⊥x轴于点D,则的值为.5.已知Rt△ABC中,∠C=90°,AC=6,BC=8,将它的一个锐角翻折,使该锐角顶点落在其对边的中点D处,折痕交另一直角边于E,交斜边于F,则△CDE的周长为.6.如图,∠AOB=30°,点P为∠AOB内一点,OP=8.点M、N分别在OA、OB上,则△PMN周长的最小值为.7.如图,已知四边形ABCD中,对角线BD平分∠ABC,∠BAC=64°,∠BCD+∠DCA=180°,那么∠BDC为度.8如图,在直角坐标系中,点A(0,a2﹣a)和点B(0,﹣3a﹣5)在y轴上,点M在x轴负半轴上,S△ABM=6.当线段OM最长时,点M的坐标为.9.如图,△ABC中,AC=BC,∠ACB=90°,点D为BC的中点,点E与点C关于直线AD对称,CE与AD、AB分别交于点F、G,连接BE、BF、GD,求证:(1)△BEF为等腰直角三角形;(2)∠ADC=∠BDG.10.如图,等腰△ABC中,AB=CB,M为ABC内一点,∠MAC+∠MCB=∠MCA=30°(1)求证:△ABM为等腰三角形;(2)求∠BMC的度数.11.如图,直线AB交x轴于点A(a,0),交y轴于点B(0,b),且a、b满足|a+b|+(a ﹣5)2=0(1)点A的坐标为,点B的坐标为;(2)如图,若点C的坐标为(﹣3,﹣2),且BE⊥AC于点E,OD⊥OC交BE延长线于D,试求点D的坐标;(3)如图,M、N分别为OA、OB边上的点,OM=ON,OP⊥AN交AB于点P,过点P 作PG⊥BM交AN的延长线于点G,请写出线段AG、OP与PG之间的数列关系并证明你的结论.12.如图,在等边三角形△ABC中,AE=CD,AD、BE交于P点,BQ⊥AD于Q,(1)求证:BP=2PQ;(2)连PC,若BP⊥PC,求的值.13.在△ABC中,AD平分∠BAC交BC于D.(1)如图1,∠MDN的两边分别与AB、AC相交于M、N两点,过D作DF⊥AC于F,DM=DN,证明:AM+AN=2AF;(2)如图2,若∠C=90°,∠BAC=60°,AC=9,∠MDN=120°,ND∥AB,求四边形AMDN 的周长.14.如图1,在平面直角坐标系中,点A、B分别在x轴、y轴上.(1)如图1,点A与点C关于y轴对称,点E、F分别是线段AC、AB上的点(点E不与点A、C重合),且∠BEF=∠BAO.若∠BAO=2∠OBE,求证:AF=CE;(2)如图2,若OA=OB,在点A处有一等腰△AMN绕点A旋转,且AM=MN,∠AMN=90°.连接BN,点P为BN的中点,试猜想OP和MP的数量关系和位置关系,说明理由.15.已知点C为线段AB上一点,分别以AC、BC为边在线段AB同侧作△ACD和△BCE,且CA=CD,CB=CE,∠ACD=∠BCE,直线AE与BD交于点F.(1)如图1,若∠ACD=60°,则∠AFD=;(2)如图2,若∠ACD=α,连接CF,则∠AFC=(用含α的式子表示);(3)将图1中的△ACD绕点C顺时针旋转如图3,连接AE、AB、BD,∠ABD=80°,求∠EAB 的度数.16.等腰Rt△ACB,∠ACB=90°,AC=BC,点A、C分别在x轴、y轴的正半轴上.(1)如图1,求证:∠BCO=∠CAO(2)如图2,若OA=5,OC=2,求B点的坐标(3)如图3,点C(0,3),Q、A两点均在x轴上,且S△CQA=18.分别以AC、CQ为腰在第一、第二象限作等腰Rt△CAN、等腰Rt△QCM,连接MN交y轴于P点,OP的长度是否发生改变?若不变,求出OP的值;若变化,求OP的取值范围.17.如图,在平面直角坐标系中,已知A(0,a)、B(﹣b,0)且a、b满足+|a﹣2b+2|=0.(1)求证:∠OAB=∠OBA;(2)如图1,若BE⊥AE,求∠AEO的度数;(3)如图2,若D是AO的中点,DE∥BO,F在AB的延长线上,∠EOF=45°,连接EF,试探究OE和EF的数量和位置关系.19.如图①,平面直角坐标系XOY中,若A(0,a)、B(b,0)且(a﹣4)2+=0,以AB为直角边作等腰Rt△ABC,∠CAB=90°,AB=AC.(1)求C点坐标;(2)如图②过C点作CD⊥X轴于D,连接AD,求∠ADC的度数;(3)如图③在(1)中,点A在Y轴上运动,以OA为直角边作等腰Rt△OAE,连接EC,交Y轴于F,试问A点在运动过程中S△AOB:S△AEF的值是否会发生变化?如果没有变化,请直接写出它们的比值(不需要解答过程或说明理由).20.如图1,点A和点B分别在y轴正半轴和x轴负半轴上,且OA=OB,点C和点D分别在第四象限和第一象限,且OC⊥OD,OC=OD,点D的坐标为(m,n),且满足(m﹣2n)2+|n ﹣2|=0.(1)求点D的坐标;(2)求∠AKO的度数;(3)如图2,点P,Q分别在y轴正半轴和x轴负半轴上,且OP=OQ,直线ON⊥BP交AB 于点N,MN⊥AQ交BP的延长线于点M,判断ON,MN,BM的数量关系并证明.21.如图,△AOB和△ACD是等边三角形,其中AB⊥x轴于E点(1) 如图,若OC=5,求BD的长度(2) 设BD交x轴于点F,求证:∠OF A=∠DF A(3) 如图,若正△AOB的边长为4,点C为x轴上一动点,以AC为边在直线AC下方作正△ACD,连接ED,求ED的最小值八年级几何综合复习(二)1.如图,在△ABC中,∠C=90°,AC=3,BC=4,AB=5,角平分线AF和BG交于D,DE ⊥AB于E,则DE长为.2.已知AD为△ABC的内角平分线,AB=7cm,AC=8cm,BC=9cm,则CD的长为cm.如图,已知四边形ABCD中,AD∥BC,若∠DAB的平分线AE交CD于E,连结BE,且BE恰好平分∠ABC,判断AB的长与AD+BC的大小关系并证明.3.如图,△ABC中,∠ACB=90°,AC=BC,D在BC上,BM⊥AD于M,求∠CMA的度数.4.如图,BD是等腰直角△ABC的腰AC上的中线,AE⊥BD交BD、BC于E、F,求证:(1)∠ABD=∠CAF;(2)∠ADB=∠CDF.5.如图,平面直角坐标系中,A(2,0),△OAC为等边三角形.(1)如图1,若D(0,4),△ADE为等边三角形,∠DAC=10°,求∠AEC的度数.(2)如图2,若P为x轴正半轴上一点,且P在A的右侧,△PCM为等边三角形,MA的延长线交y轴于N,求AM﹣AP的值.(3)如图3,若P为x轴正半轴上一点,且P在A的右侧,△PAM为等边三角形,OM与PC交于F,求证:AF+MF=PF.6.已知△ABC中,∠ABC=90゜,AB=BC,点A、B分别是x轴和y轴上的一动点.(1)如图1,若点C的横坐标为﹣4,求点B的坐标;(2)如图2,BC交x轴于D,若点C的纵坐标为3,A(5,0),求点D的坐标.(3)如图3,分别以OB、AB为直角边在第三、四象限作等腰直角△OBF和等腰直角△ABE,EF交y轴于M,求S△BEM:S△ABO.7.如图,E是正方形ABCD中CD边上的任意一点,以点A为中心,把△ADE顺时针旋转90°得△ABE1,∠EAE1的平分线交BC边于点F,求证:△CFE的周长等于正方形ABCD 的周长的一半.8.如图,△ABC中,AC=BC,∠ACB=90°,点D为BC的中点,点E与点C关于直线AD 对称,CE与AD、AB分别交于点F、G,连接BE、BF、GD,求证:(1)△BEF为等腰直角三角形;(2)∠ADC=∠BDG.9.如图,等腰△ABC中,AB=CB,M为ABC内一点,∠MAC+∠MCB=∠MCA=30°(1)求证:△ABM为等腰三角形;(2)求∠BMC的度数.10.已知在△ABC中,AB=AC,射线BM、BN在∠ABC内部,分别交线段AC于点G、H.(1)如图1,若∠ABC=60°、∠MBN=30°,作AE⊥BN于点D,分别交BC、BM于点E、F.①求证:CE=AG;②若BF=2AF,连接CF,求∠CFE的度数;(2)如图2,点E为BC上一点,AE交BM于点F,连接CF,若∠BFE=∠BAC=2∠CFE,直接写出=.11.在平面直角坐标系中,点A(0,a)、B(b,0)且a>|b|.(1)若a、b满足a2+b2﹣4a﹣2b+5=0.①求a、b的值;②如图1,在①的条件下,将点B在x轴上平移,且b满足:0<b<2;在第一象限内以AB 为斜边作等腰Rt△ABC,请用b表示S四边形AOBC,并写出解答过程.(2)若将线段AB沿x轴向正方向移动a个单位得到线段DE(D对应A,E对应B)连接DO,作EF⊥DO于F,连接AF、BF.①如图2,判断AF与BF的关系并说明理由;②若BF=OA﹣OB,则∠OAF=(直接写出结果).12.已知点E在等边△ABC的边AB上,点P在射线CB上,AE=BP(1)如图1,求证:AP=CE;(2)如图2,求证:PE=EC;(3)如图3,若AE=2BE,延长AP至点M使PM=AP,连接CM,求证:CM=CE;13.CO是△ACE的高,点B在OE上,OB=OA,AC=BE(1)如图1,求证:∠A=2∠E;(2)如图2,CF是△ACE的角平分线.①求证:AC+AF=CE;②判断三条线段CE、EF、OF之间的数量关系,并给出证明.14.如图,在等腰Rt △ABC 中,∠ABC =90°,O 是AC 的中点,P ,Q 分别在AB ,BC 上(P ,Q 与A ,B ,C 都不重合),OP ⊥OQ ,OS ⊥AQ 交AB 于S .下列结论:①BQ =BS ;②P A =QB ;③S 是PB 的中点;④CQPS的值为定值.其中正确结论的个数是( )15.如图,AB ⊥BC ,AD ⊥DC ,∠BAD =130°,点M ,N 分别在BC ,CD 上,当△AMN 得周长最小时,∠MAN 的度数为_________.16.如图,在Rt △ABC 和Rt △BCD 中,∠BAC =∠BDC =90°,BC =8,AB =AC,∠CBD =45°,则△DMN 的周长为___________.17.如图1,在△ABC 中,AB =AC ,∠BAC =30°,点D 是△ABC 内一点,DB =DC ,∠DCB =30°,点E 是BD 延长线上一点,AE =AB . (1)直接写出∠ADE 的度数_______; (2)求证:DE =AD +DC ;(3)作BP 平分∠ABE ,EF ⊥BP ,垂足为F ,(如图2),若EF =3,求BP 的长.OBABC图2图1ABEBCF18.如图,在平面直角坐标系中,已知两点A (m ,0),B (0,n )(n >m >0),点C 在第一象限,AB ⊥BC ,BC =BA ,点P 在线段OB 上,OP =OA ,AP 的延长线与CB 的延长线交于点M ,AB 与CP 交于点N .(1)点C 的坐标为:__________(用含m ,n 的式子表示); (2)求证:BM =BN ;(3)设点C 关于直线AB 的对称点为D ,点C 关于直线AP 的对称点为G ,求证:D ,G 关于x 轴对称.19. 如图1,在平面直角坐标系中,△ABC 的顶点A (-3,0)、B (0,3),AD ⊥BC 于D 交BC 于D 点,交y 轴于点E (0,1) (1) 求C 点的坐标(2) 如图2,过点C 作CF ⊥CB ,且截取CF =CB ,连接BF ,求△BCF 的面积(3) 如图3,点P 为y 轴正半轴上一动点,点Q 在第三象限内,QP ⊥PC ,且QP =PC ,连接QO ,过点Q 作QR ⊥x 轴于R ,求OPQROC 的值。
初二几何试题及答案

初二几何试题及答案一、选择题(每题2分,共10分)1. 在直角三角形中,如果一个锐角为30°,那么另一个锐角的度数是多少?A. 30°B. 45°C. 60°D. 90°答案:C2. 一个矩形的长是10厘米,宽是5厘米,那么它的周长是多少厘米?A. 20厘米B. 25厘米C. 30厘米D. 50厘米答案:B3. 一个圆的半径是3厘米,那么它的直径是多少厘米?A. 6厘米B. 9厘米C. 12厘米D. 15厘米答案:A4. 在一个平行四边形中,如果对角线互相平分,那么这个平行四边形是:A. 正方形B. 长方形C. 菱形D. 梯形答案:B5. 如果一个三角形的三边长分别为3厘米、4厘米、5厘米,那么这个三角形是:A. 等边三角形B. 等腰三角形C. 直角三角形D. 钝角三角形答案:C二、填空题(每题2分,共10分)6. 一个三角形的内角和等于________度。
答案:1807. 如果一个圆的周长是12.56厘米,那么它的半径是________厘米。
答案:28. 在一个直角三角形中,斜边的长度是两直角边长度的________。
答案:平方和的平方根9. 一个矩形的对角线相等,那么这个矩形是________。
答案:正方形10. 一个平行四边形的对角线互相平分,那么这个平行四边形是________。
答案:矩形三、解答题(每题5分,共10分)11. 已知一个直角三角形的两条直角边分别为6厘米和8厘米,求斜边的长度。
答案:根据勾股定理,斜边长度为√(6² + 8²) = √(36 + 64) = √100 = 10厘米。
12. 一个圆的半径是4厘米,求其面积。
答案:圆的面积公式为A = πr²,所以面积为A = π × 4² = 16π ≈ 50.27平方厘米。
结束语:本试题涵盖了初二几何课程的基础知识和一些基本公式的应用,希望同学们通过练习能够加深对几何概念的理解和运用能力。
初二几何全等练习题

初二几何全等练习题题目一:在平面直角坐标系中,点A(0,0)、B(2,0)、C(2,3)、D(0,3)连成一个四边形ABCD。
求证:四边形ABCD是一个矩形。
解析:首先,我们可以通过计算四条边的长度来验证四边形ABCD是否是一个矩形。
AB = √[(2-0)²+(0-0)²] = √4 = 2,BC = √[(2-2)²+(3-0)²] = √9 = 3,CD = √[(0-2)²+(3-3)²] = √4 = 2,AD = √[(0-0)²+(3-0)²] = √9 = 3。
由此可知,AB = CD = 2,BC = AD = 3,即四边形ABCD的对边长度相等。
接下来,我们需要验证四边形的对角线相等。
AC = √[(2-0)²+(3-0)²] = √13,BD = √[(2-0)²+(0-3)²] = √13。
通过计算可知,AC = BD = √13,即四边形ABCD的对角线相等。
因此,根据矩形的定义,我们可以证明四边形ABCD是一个矩形。
题目二:在平面直角坐标系中,点A(0,0)、B(3,0)、C(3,4)连成一个三角形ABC。
若将三角形ABC绕原点顺时针旋转90°,求旋转后三角形的坐标。
解析:我们可通过旋转矩阵来求得旋转后三角形的坐标。
顺时针旋转90°的旋转矩阵为:旋转矩阵 R =(cos90°, sin90°)(-sin90°, cos90°)我们可以将点A(0,0)、B(3,0)、C(3,4)表示为矩阵的形式:A =(0, 0)B =(3, 0)C =(3, 4)将旋转矩阵与点A、B、C相乘,即可得到旋转后的三角形的坐标:R * A = (cos90°, sin90°)*(0, 0)=(0, 0)R * B = (cos90°, sin90°)*(3, 0) = (0, 3)R * C = (cos90°, sin90°)*(3, 4) =(-4, 3)因此,旋转后的三角形的坐标为:A'(0,0)、B'(0,3)、C'(-4,3)。
(完整版)初二数学几何类综合题及参考答案

初中几何综合测试题(时间120分满分100分)一.填空题(本题共22分,每空2分)1.一个三角形的两条边长分别为9和2,第三边长为奇数,则第三边长为 .2.△ABC三边长分别为3、4、5,与其相似的△A′B′C′的最大边长是 10,则△A′B′C′的面积是.4.弦AC,BD在圆内相交于E ,且,∠BEC=130°, 则∠ACD= .5.点O是平行四边形ABCD对角线的交点,若平行四边行ABCD的面 积为8cm,则△AOB的面积为 .6.直角三角形两直角边的长分别为5cm和12cm,则斜边上的中线长为 .7.梯形上底长为2,中位线长为5,则梯形的下底长为 .9.如图,分别延长四边形ABCD两组对边交于E、F,若DF=2DA,10.在Rt△ABC中,AD是斜边BC上的高,如果BC=a,∠B=30°, 那么AD等于 .二.选择题(本题共44分,每小题4分) 1.一个角的余角和它的补角互为补角,则这个角是 [ ]A.30°B.45°C.60°D.75° 2.依次连结等腰梯形的各边中点所得的四边形是 [ ]A.矩形B.正方形C.菱形D.梯形 3.如图,DF∥EG∥BC,AD=DE=EB,△ABC被分成三部分的 面积之比为 [ ]A.1∶2∶3B.1∶1∶1C.1∶4∶9D.1∶3∶5 4.如果两个圆的半径分别为4cm和5cm,圆心距为1cm,那么这两个圆 的位置关系是 [ ]A.相交B.内切C.外切D.外离 5.已知扇形的圆心角为120°,半径为3cm,那么扇形的面积为[ ] 6.已知Rt△ABC的斜边为10,内切圆的半径为2,则两条直角边的 长为 [ ] 7.和距离为2cm的两条平行线都相切的圆的圆心的轨迹是 [ ] A.和两条平行线都平行的一条直线。
B.在两条平行线之间且与两平行线都平行的一条直线。
C.和两平行线的距离都等于2cm的一条平行线。
立体几何经典大题(各个类型的典型题目)
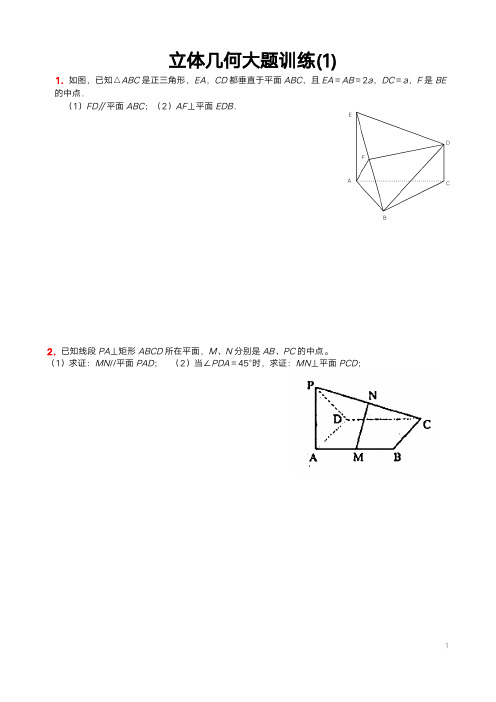
1.如图,已知△A B C是正三角形,E A,C D都垂直于平面A B C,且E A=A B=2a,D C=a,F是B E 的中点.(1)F D∥平面A B C;(2)A F⊥平面E D B.2.已知线段P A⊥矩形A B C D所在平面,M、N分别是A B、P C的中点。
(1)求证:MN//平面P A D;(2)当∠P D A=45°时,求证:MN⊥平面P C D;3.如图,在四面体A B C D中,C B=C D,,点E,F分别是A B,B D的中点.求证:(1)直线E F//面A C D;(2)平面面B C D.4.在斜三棱柱A1B1C1—A B C中,底面是等腰三角形,A B=A C,侧面B B1C1C⊥底面A B C (1)若D是B C的中点,求证A D⊥C C1;(2)过侧面B B1C1C的对角线B C1的平面交侧棱于M,若A M=MA1,求证截面MB C1⊥侧面B B1C1C;(3)A M=MA1是截面MB C1⊥平面B B1C1C的充要条件吗?请你叙述判断理由]ABC DE F5.如图,在正方体A B C D —A 1B 1C 1D 1中,M、N 、G分别是A 1A ,D 1C ,A D的中点.求证:(1)MN //平面A B CD ;(2)MN ⊥平面B 1B G .6.如图,在正方体A BCD -A 1B 1C 1D 1中,E 、F 为棱A D 、A B 的中点.(1)求证:E F ∥平面C B 1D 1;(2)求证:平面C A A 1C 1⊥平面C B 1D 1._G _M _D _1_C _1_B _1_A _1_N _D _C _B _A ABCDA 1B 1C 1D 1E F7、如图,在直四棱柱A B C D -A 1B 1C 1D 1中,底面A B C D为等腰梯形,A B ∥C D ,A B =4,B C =C D =2,A A 1=2,E 、E 1分别是棱A D 、A A 1的中点(1)设F 是棱A B的中点,证明:直线E E 1∥面F C C 1;(2)证明:平面D 1A C ⊥面B B 1C 1C 。
立体几何经典大题(各个类型的典型题目)

1.如图,已知△ABC 是正三角形,EA ,CD 都垂直于平面ABC ,且EA =AB =2a ,DC =a ,F 是BE 的中点.(1)FD ∥平面ABC ;(2)AF ⊥平面EDB .2.已知线段PA ⊥矩形ABCD 所在平面,M 、N 分别是AB 、PC 的中点。
(1)求证:MN //平面PAD ; (2)当∠PDA =45°时,求证:MN ⊥平面PCD ;F CBAEDA B C D EF 3.如图,在四面体ABCD 中,CB=CD,BD AD ⊥,点E ,F 分别是AB,BD 的中点.求证: (1)直线EF// 面ACD ; (2)平面⊥EFC 面BCD .4.在斜三棱柱A 1B 1C 1—ABC 中,底面是等腰三角形,AB =AC ,侧面BB 1C 1C ⊥底面ABC (1)若D 是BC 的中点,求证 AD ⊥CC 1;(2)过侧面BB 1C 1C 的对角线BC 1的平面交侧棱于M ,若AM =MA 1, 求证 截面MBC 1⊥侧面BB 1C 1C ;(3)AM =MA 1是截面MBC 1⊥平面BB 1C 1C 的充要条件吗?请你叙述判断理由]立体几何大题训练(3)C15. 如图,在正方体ABCD —A 1B 1C 1D 1中,M 、N 、G 分别是A 1A ,D 1C ,AD 的中点. 求证:(1)MN//平面ABCD ; (2)MN ⊥平面B 1BG .6. 如图,在正方体ABCD -A 1B 1C 1D 1中,E 、F 为棱AD 、AB 的中点. (1)求证:EF ∥平面CB 1D 1;(2)求证:平面CAA 1C 1⊥平面CB 1D 1.立体几何大题训练(4)7、如图,在直四棱柱ABCD-A 1B 1C 1D 1中,底面ABCD 为等腰梯形,AB ∥CD ,AB=4,BC=CD=2,AA 1=2,_ G_ M _ D_1_ C_1_ B_1_ A_1_ N_ D _ C_ B _ ABA 1FE、E1分别是棱AD、AA1的中点(1)设F是棱AB的中点,证明:直线EE1∥面FCC1;(2)证明:平面D1AC⊥面BB1C1C。
初二上册数学几何试题(附答案)
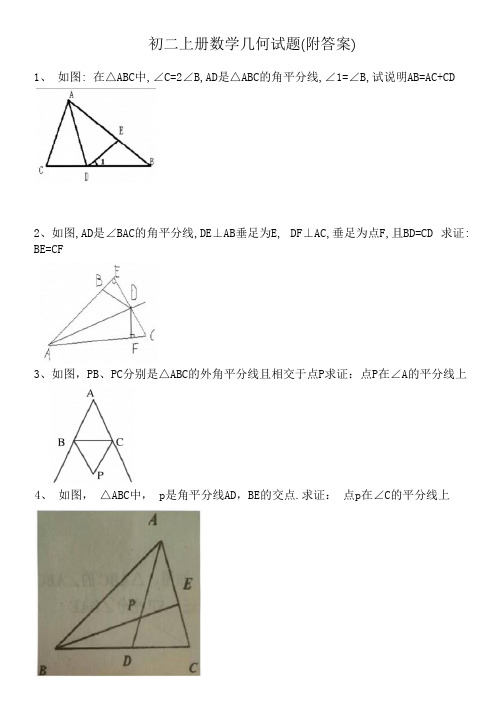
初二上册数学几何试题(附答案)1、如图: 在△ABC中,∠C=2∠B,AD是△ABC的角平分线,∠1=∠B,试说明AB=AC+CD2、如图,AD是∠BAC的角平分线,DE⊥AB垂足为E, DF⊥AC,垂足为点F,且BD=CD 求证: BE=CF3、如图,PB、PC分别是△ABC的外角平分线且相交于点P求证:点P在∠A的平分线上4、如图,△ABC中, p是角平分线AD,BE的交点.求证:点p在∠C的平分线上5、下列说法中,错误的是( )A. 三角形任意两个角的平分线的交点在三角形的内部B. 三角形两个角的平分线的交点到三边的距离相等C. 三角形两个角的平分线的交点在第三个角的平分线上D. 三角形任意两个角的平分线的交点到三个顶点的距离相等6、如图在三角形ABC 中BM=MC∠ABM=∠ACM 求证 AM平分∠BAC7、如图, AP、CP分别是△ABC外角∠MAC与∠NCA的平分线, 它们相交于点P, PD⊥BM 于点D, PF⊥BN于点F. 求证: BP为∠MBN的平分线。
8、如图,在∠AOB的两边OA, OB上分别取 OM=ON, OD=OE, DN 和EM 相交于点C. 求证: 点C在∠AOB的平分线上.9、如图, ∠B=∠C=90° , M是BC的中点, DM平分∠ADC.(1)若连接AM,则AM是否平分∠BAD?请你证明你的结论;(2)线段 DM与AM有怎样的位置关系?请说明理由.参考答案:1、因为∠1=∠B所以∠DEA=2∠B=∠C因为 AD是△ABC的角平分线所以∠CAD=∠EAD 因为 AD=AD所以△ADC 全等于△ADE 所以 AC=AE CD=DE 因为∠1=∠B 所以△EDB 为等腰三角形所以 EB=DE 因为 AB=AE+EB AC=AE CD=DE EB=DE所以 AB=AC+CD2、因为 ad是∠bac的角平分线, ,DE⊥AB, DF⊥AC, 所以DE=DF三角形DEB和三角形DFC均为直角三角形,又因为 BD=CD 所以BE=CF3、作PF⊥AD, PH⊥BC, PG⊥AE∵PB 平分∠DBC, PC平分∠ECB, PF⊥AD, PH⊥BC, PG⊥AE∴PF=PH,PG=PH(角平分线上的点到这个角的两边的距离相等)∴PF=PG∵PF⊥AD, PG⊥AE, PF=PG∴PA平分∠BAC(在一个角的内部,且到角的两边距离相等的点,在这个角的平分线上)4、作PG⊥BC,PH⊥AC,PQ⊥AB,垂足分别为G、H、Q,AD为∠A的平分线,PH=PQ;BE为∠B 的平分线, PQ=PG;所以PG=PH,又CP为RT△CGP和RT△CEP的公共斜边,所以△CGP≌△CHP,所以∠GCP=∠ECP,CP为∠的平分线,P点在∠C的平分线上5、 A6、∵BM=MC, ∴∠MBC=∠MCB, ∵∠ABM=∠ACM, ∴∠ABM+∠MBC=∠ACM+∠MCB, 即∠ABC=∠ACB,∴AB=AC, 在△AMB与△AMC中, AB=AC, ∠ABM=∠ACM, MB=MC, ∴△AMB≌△AMC(SAS),∴ ∠MAB=∠MAC, 即AM平分∠BAC。
几何图形综合题(10道)

题型四几何图形综合题类型一动态探究型1.如图, BD是正方形ABCD的对角线, BC=2,动点P从点B出发,以每秒1个单位长度的速度沿射线BC运动,同时动点Q从点C出发,以相同的速度沿射线BC运动,当点P出发后,过点Q 作QE⊥BD,交直线BD于点E,连接AP、AE、PE、QE,设运动时间为t(秒).(1)请直接写出动点P运动过程中,四边形APQD是什么四边形?(2)请判断AE, PE之间的数量关系和位置关系,并加以证明;(3)设△EPB的面积为y,求y与t之间的函数关系式;(4)请求出△EPQ的面积是△EDQ面积的2倍时t的值.第1题图解:(1)四边形APQD是平行四边形;【解法提示】∵四边形ABCD 是正方形,P 、Q 速度相同, ∴∠ABE =∠EBQ =45°,AD //BQ ,AD =BC =2,BP =CQ , ∴BC =AD =PQ ,∴四边形APQD 是平行四边形; (2)AE =PE , AE ⊥PE ; 证明如下: ∵QE ⊥BD ,∴∠PQE =90°-45°=45°, ∴∠ABE =∠EBQ =∠PQE =45°, ∴BE =QE ,在△AEB 和△PEQ 中,⎪⎩⎪⎨⎧=∠=∠=QE BE PQE ABE PQ AB , ∴△AEB ≌△PEQ (SAS ), ∴AE =PE ,∠AEB =∠PEQ , ∴∠AEP =∠BEQ =90°,∴AE ⊥PE ;(3)如解图①,过点E 作EF ⊥BC 于点F ,第1题解图①∵BC =2,CQ =t , ∴BQ =t +2,∵EF ⊥BC ,且∠EBC =∠EQB =45°, ∴EF =BF =FQ ,∴EF =21BQ =22+t , 又∵BP =QC =t ,∴y =21EF ·BP =21×22+t ×t , 即y =41t 2+21t ;(4)①当点P 在BC 的延长线上时,如解图②,作PM ⊥QE 于点M ,第1题解图②∵PQ =2,∠BQE =45°, ∴PM =22PQ =2,BE =QE =22BQ =22(t +2), ∴DE =BE -BD =22(t +2)-22=22t -2, ∵△EPQ 的面积是△EDQ 面积的2倍,∴EQ DE PM EQ ⋅⨯=⋅21221, ∴21×22(t +2)×2=2×21(22t -2)×22(t +2), 解得:t =3或t =-2(舍去), ∴t =3;②当P 在线段BC 上时,解法同①,此时DE =BD -BE =2-22t , ∵△EPQ 的面积是△EDQ 面积的2倍,∴EQ DE PM EQ ⋅⨯=⋅21221, ∴21×22(t +2)×2=2×21(2-22t )×22(t +2),解得:t =1或t =-2(舍去), ∴t =1;综上所述,当t =1或t =3时,△EPQ 的面积是△EDQ 面积的2倍.2.如图,在矩形ABCD 中,AB =6 cm ,BC =8 cm ,对角线AC ,BD 交于点O .点P 从点A 出发,沿AD 方向匀速运动,速度为 1 cm/s ;同时,点Q 从点D 出发,沿DC 方向匀速运动,速度为1 cm/s ;当一个点停止运动时,另一个点也停止运动.连接PO 并延长交BC 于点E ,过点Q 作QF ∥AC 交BD 于点F .设运动时间为t (s)(0<t <6),解答下列问题: (1)当t 为何值时,AP = PO ;(2)设五边形OECQF 的面积为S (cm 2),试确定S 与t 的函数关系式;(3)当t 为何值时,OD 平分∠COP ?第2题图解:(1)∵在矩形ABCD 中,AB =6 cm ,BC =8 cm ,∠ABC =90°, ∴AC =10 cm ,AO =12AC =5 cm , 如解图①,过点P 作PM ⊥AO 于点M ,第2题解图①当AP =PO =t 时,AM =12AO =52 cm , ∵∠PMA =∠ADC =90°,∠P AM =∠CAD , ∴△APM ∽△ACD ,∴AP AC =AM AD ,即t 10=528, 解得t =258,即t =258 s 时,AP =PO ;(2)如解图②,过点O 作OH ⊥BC 交BC 于点H ,则OH =12CD =12AB =3 cm .由矩形的性质可知∠PDO =∠EBO ,DO =BO , 在△DOP 和△BOE 中, ⎩⎪⎨⎪⎧∠PDO =∠EBO OD =OB∠DOP =∠BOE , ∴△DOP ≌△BOE (ASA), ∴BE =PD =(8-t )cm ,则S △BOE =12BE ·OH =12×(8-t )×3=12-32t . ∵FQ ∥AC ,第2题解图②∴△DFQ ∽△DOC ,相似比为DQ DC =t6,∴362t S S DOC DFQ △△, ∵S △DOC =14S 矩形ABCD =14×6×8=12 cm 2, ∴S △DFQ =12×t 236=t 23,∴S 五边形OECQF =S △DBC -S △BOE -S △DFQ =12×6×8-(12-32t )-t 23=-13t 2+32t +12,∴S 与t 的函数关系式为S =-13t 2+32t +12;(3)如解图③,过点D 作DM ⊥PE 于点M ,作DN ⊥AC 于点N , 易证△ADN ∽△ACD ,∴DN CD =AD AC ,即DN 6=810, ∴DN =245,第2题解图③∵∠POD =∠COD , ∴DM =DN =245,∴ON =OM =OD 2-DN 2=75, ∵S △POD =12OP ·DM =12×12PD ·DC , ∴OP ·DM =12PD ·DC , ∴OP =5-58t ,∴PM =OP - OM =185-58t , ∵PD 2=PM 2+DM 2, 即(8-t )2=(185-58t )2+(245)2, 解得t 1=16(不合题意,舍去),t 2=11239, ∴当t =11239 s 时,OD 平分∠COP .3.如图,已知△ABC 中,AB =10 cm ,AC =8 cm ,BC =6 cm .如果点P 由B 出发沿BA 向点A 匀速运动,同时点Q 由A 出发沿AC 向点C 匀速运动,它们的速度均为2 cm/s .连接PQ ,设运动的时间为t (单位:s)(0≤t ≤4).第3题图(1)当t 为何值时,PQ ∥BC ;(2)设△AQP 的面积为S (单位:cm 2),当t 为何值时,S 取得最大值,并求出最大值;(3)是否存在某时刻t ,使线段PQ 恰好把△ABC 的面积平分?若存在,求出此时t 的值;若不存在,请说明理由. 解:(1)由题意知BP =2t ,AP =10-2t ,AQ =2t , ∵PQ ∥BC , ∴△APQ ∽△ABC , ∴AP AB =AQ AC ,即10-2t 10=2t 8,解得t =209, 即当t 为209 s 时,PQ ∥BC ;(2)∵AB =10 cm ,AC =8 cm ,BC =6 cm , ∴AB 2=AC 2+BC 2, ∴△ABC 为直角三角形, ∴∠C =90°,如解图,过点P 作PD ⊥AC 于点D ,第3题解图则PD ∥BC , ∴△APD ∽△ABC , ∴AP AB =PD BC , ∴10-2t 10=PD 6, ∴PD =35(10-2t ),∴S =12AQ ·PD =12×2t ×35(10-2t )=-65t 2+6t =-65(t -52)2+7.5, ∵-65<0,抛物线开口向下,有最大值,且0≤t ≤4, ∴当t =2.5 s 时,S 有最大值,最大值是7.5 cm 2; (3)不存在.理由如下:假设存在某时刻t ,使线段PQ 恰好把△ABC 的面积平分,则S △AQP =12S △ABC ,即-65t 2+6t =12×12×8×6,整理得t 2-5t +10=0, ∵b 2-4ac =(-5)2-4×10=-15<0, ∴此方程无实数解,即不存在某时刻t ,使线段PQ 恰好把△ABC 的面积平分. 4.如图,在菱形ABCD 中,∠BAD =120°,边长AB =6,对角线AC 、BD 交于点 O ,线段AD 上有一动点P ,过点P 作PH ⊥BC 于点H ,交直线CD 于点Q ,连接OQ ,OP ,设线段PD =m . (1)求线段PH 的长度;(2)设△DPQ 的面积为S ,求S 与m 之间的关系式;(3)当△DPQ 的面积与△CQH 的面积相等时,m 的值是多少?第4题图解:(1)∵四边形ABCD是菱形,∴BC∥AD,AB=AD=CD=6,∵∠BAD=120°,∴∠ADC=60°,∴△ACD是等边三角形,如解图,过点C作CG⊥AD于G,在Rt△CDG中,∠CDG=60°,CD=6,∴DG=3,CG=33,∵BC∥AD, PH⊥BC,CG⊥AD,∴四边形CHPG是矩形,∴PH=CG=33,第4题解图(2)在Rt△PDQ中,∠PDQ=60°, DP=m,∴PQ3m,∴S=S△PDQ=12DP·PQ=12m×3m3m2(0<m≤6),(3)∵点Q在线段CD上,AD∥BC,∴△CHQ∽△DPQ,当△DPQ的面积与△CQH的面积相等时,有△CHQ≌△DPQ,∴CQ=DQ=1CD=3,2在Rt△PQD中,∠PDQ=60°, DQ=3,,∴DP=32时,△DPQ的面积与△CQH的面积相等.即m=325.如图,在平面直角坐标系中,长方形OABC的两边分别在x轴和y轴上,OA=12,OC=8,现有两动点P、Q分别从O、C同时出发,P在线段OA上沿OA方向以每秒1.5个单位长度的速度匀速运动,运动到点A停止,Q在线段CO上沿CO方向以每秒1个单位长度的速度匀速运动,运动到点O停止,设运动时间为t秒.(1)B点的坐标为,OQ=,AP=;(用含t 的代数式表示)(2)当t 为何值时,△BCQ 的面积不小于△BAP 的面积? (3)当t 为何值时,△OPQ 的面积与△BAP 的面积的和为36?请求出t 的值;连接AC ,试探究此时线段PQ 与AC 之间的数量关系并说明理由.第5题图 备用图解:(1)(12,8),8-t ,12-1.5t ; 【解法提示】∵四边形OABC 是矩形,且OA =12,OC =8,∴B (12,8),由题意得:OP =1.5t ,CQ =t ,∴AP =12-1.5t ,OQ =8-t .(2)∵S △BCQ ≥S △BAP , ∴21CQ ·BC ≥21AP ·AB , 12t ≥8(12-1.5t ), t ≥4,∵点P 在线段OA 上沿OA 方向以每秒1.5个单位长度的速度匀速运动,运动到点A 停止,点Q 在线段CO 上沿CO 方向以每秒1个单位长度的速度匀速运动,运动到点O 停止, ∴12÷1.5=8,8÷1=8, ∴0≤t ≤8,∴当4≤t ≤8时,△BCQ 的面积不小于△BAP 的面积; (3)由题意得:S △OPQ +S △BAP =36, ∴21OP ·OQ +21AP ·AB =36,21×1.5t ×(8-t )+()85.11221⋅-t =36, t =4或-4(舍),∴当t =4时,△OPQ 的面积与△BAP 的面积的和为36; 此时AC =2PQ ,理由如下: 如解图,第5题解图当t=4时,OP=1.5t=6,CQ=4,∴P和Q分别是OA和OC的中点,∴AC=2PQ.6.两个全等的三角形,△ABC,△DEF,按如图所示的位置摆放,点B与点D重合,边AB与边DE在同一条直线上(假设图形中所有的点,线都在同一平面内).其中,∠C=∠DEF=90°,∠ABC=∠F=30°,AC=DE=6 cm.现固定△DEF,将△ABC沿射线DE方向平移,当点C落在边EF上时停止运动.设△ABC平移的距离为x(cm),两个三角形重叠部分的面积为y(cm2).(1)当点C落在边EF上时,x=________ cm;(2)求y关于x的函数解析式,并写出自变量x的取值范围;(3)设边BC的中点为点M,边DF的中点为点N.直接写出在△ABC平移过程中,点M与点N之间距离的最小值.第6题图解:(1)15;【解法提示】如解图①,作CG⊥AB于点G,CH⊥FE于点H,第6题解图①在Rt△ABC中,由AC=6,∠ABC=30°,得BC=ACtan30°=6 3cm.在Rt△BCG中,BG=BC·cos30°=9 cm.∵四边形CGEH是矩形,∴CH=GE=BG+BE=9+6=15 cm.(2)①当0≤x<6时,如解图②,第6题解图②由∠GDB =60°,∠GBD =30°,DB =x ,得DG =12x ,BG =32x , 重叠部分的面积y =12DG ·BG =12×12x ×32x =38x 2; ②当6≤x <12时,如解图③,第6题解图③BD =x ,DG =12x ,BG =32x ,BE =x -6,EH =33(x -6), 重叠部分的面积y =S △BDG -S △BEH =12DG ·BG -12BE ·EH , 即y =12×12x ×32x -12(x -6)×33(x -6),化简得y =-324x 2+23x -63;③当12≤x ≤15时,如解图④,第6题解图④AC =6,BC =63,BD =x ,BE =x -6,EG =33(x -6),重叠部分的面积y =S △ABC -S △BEG =12AC ·BC -12BE ·EG ,即y =12×6×63-12(x -6)×33(x -6),化简得y =-36x 2+23x +123;综上所述,y =⎩⎪⎨⎪⎧38x 2(0≤x <6)-324x 2+23x -63(6≤x <12);-36x 2+23x +123(12≤x ≤15)(3)如解图⑤所示,作NG ⊥DE 于点G ,第6题解图⑤点M 在NG 上时MN 最短,NG 是△DEF 的中位线,NG =12EF =33,∵MB =12CB =33,∠B =30°,∴MG =12MB =332,则MN min =NG -MG =33-332=332.7.如图①,△ABC是等腰直角三角形,四边形ADEF是正方形,D、F分别在AB、AC边上,此时BD=CF,BD⊥CF成立.(1)当正方形ADEF绕点A逆时针旋转θ(0°<θ<90°)时,如图②,BD=CF成立吗?若成立,请证明;若不成立,请说明理由;(2)当正方形ADEF绕点A逆时针旋转45°时,如图③,延长BD 交CF于点G.①求证:BD⊥CF;②当AB=4,AD=2时,求线段BG的长.第7题图解:(1)BD=CF成立;证明:∵△ABC是等腰直角三角形,四边形ADEF是正方形,∴AB =AC , AD =AF ,∵∠BAD =∠CAF =θ,∴在△BAD 和△CAF 中,⎩⎪⎨⎪⎧AB =AC ,∠BAD =∠CAF ,AD =AF ,∴△BAD ≌△CAF (SAS),∴BD =CF ;(2)①证明:如解图,设BG 交AC 于点M ,由(1)可知△BAD ≌△CAF ,∴∠ABM =∠GCM ,∵∠BMA =∠CMG ,∴△BMA ∽△CMG ,∴∠BGC =∠BAC =90°,即BD ⊥CF ;②解:如解图,过点F 作FN ⊥AC 于点N ,第7题解图∵在正方形ADEF 中,AD =DE =2,∴AE =AD 2+DE 2=2,∴AN =FN =12AE =1,∵在等腰△ABC 中,AB =4,∴CN =AC -AN =3,BC =AB 2+AC 2=42,在Rt △FCN 中,tan ∠FCN =FN CN =13,∴tan ∠ABM =tan ∠FCN =13,∴AM =13AB =43,∴CM =AC -AM =4-43=83,BM =AB 2+AM 2=4103, 易证△BMA ∽△CMG ,∴BM BA =CM CG ,∴CG =4105,∴在Rt △BGC 中,BG =BC 2-CG 2=8105. 类型二 类比探究型8.已知△ABC 为等边三角形,点D 为直线BC 上的一动点(点D 不与B 、C 重合),以AD 为边作菱形ADEF (A 、D 、E 、F 按逆时针排列),使∠DAF =60°,连接CF .(1)如图①,当点D 在边BC 上时,求证:①BD =CF ; ②AC =CF +CD ;(2)如图②,当点D 在边BC 的延长线上且其他条件不变时,结论AC =CF +CD 是否成立?若不成立,请写出AC 、CF 、CD之间存在的数量关系,并说明理由;(3)如图③,当点D 在边CB 的延长线上且其他条件不变时,补全图形,并直接写出AC 、CF 、CD 之间存在的数量关系.第8题图(1)证明:∵四边形AFED 为菱形,∴AF =AD ,∵△ABC 是等边三角形,∴AB =AC =BC ,∠BAC =60°=∠DAF ,∴∠BAC -∠DAC =∠DAF -∠DAC ,即∠BAD =∠CAF ,在△BAD 和△CAF 中,⎪⎩⎪⎨⎧=∠=∠=AF AD CAF BAD AC AB ,∴△BAD ≌△CAF (SAS ),∴BD =CF ,∴CF +CD =BD +CD =BC =AC ;(2)解:不成立,AC 、CF 、CD 之间存在的数量关系是AC =CF -CD .理由如下:由(1)知:AB =AC =BC ,∠BAC =∠DAF =60°,∴∠BAC +∠DAC =∠DAF +∠DAC ,即∠BAD =∠CAF ,在△BAD 和△CAF 中,⎪⎩⎪⎨⎧=∠=∠=AF AD CAF BAD AC AB , ∴△BAD ≌△CAF (SAS ),∴BD =CF ,∴CF -CD =BD -CD =BC =AC ,即AC =CF -CD ;(3)解:补全图形如解图,AC =CD -CF .第8题解图【解法提示】∵∠BAC =∠DAF =60°,∴∠DAB =∠CAF ,在△BAD 和△CAF 中,⎪⎩⎪⎨⎧=∠=∠=AF AD CAF BAD AC AB , ∴△BAD ≌△CAF (SAS ),∴BD =CF ,∴CD -CF =CD -BD =BC =AC ,即AC =CD -CF .9.如图,已知∠AOB=120°,在∠AOB的平分线OM上有一点C,将一个60°角的顶点与点C重合,它的两条边分别与直线OA、OB相交于点D、E.第9题图(1)当∠DCE绕点C旋转到CD与OA垂直时(如图①),请猜想OE+OD与OC的数量关系,并说明理由;(2)当∠DCE绕点C旋转到CD与OA不垂直时,到达图②的位置,(1)中的结论是否成立?并说明理由;(3)当∠DCE绕点C旋转到CD与OA的反向延长线相交时,线段OD、OE与OC之间有怎样的数量关系?解:(1)∵OM是∠AOB的角平分线,1∠AOB=60°.∴∠AOC=∠BOC=2∵CD⊥OA,∴∠ODC =90°.∴∠OCD =30°.∴∠OCE =∠DCE -∠OCD =30°.在Rt △OCD 中,OD =21OC ,同理:OE =21OC .∴OD +OE =OC ;(2)(1)中结论仍然成立,理由如下:如解图①,过点C 作CF ⊥OA 于F ,CG ⊥OB 于G ,第9题解图①∴∠OFC =∠OGC =90°.∵∠AOB =120°,∴∠FCG =60°.同(1)的方法得,OF =21OC ,OG =21OC .∴OF +OG =OC .∵CF⊥OA,CG⊥OB,且点C是∠AOB的平分线OM上一点,∴CF=CG.∵∠DCE=60°,∠FCG=60°,∴∠DCF=∠ECG.∴△CFD≌△CGE(ASA),∴DF=EG.∴OF=OD-DF=OD-EG,OG=OE+EG.∴OF+OG=OD-EG+OE+EG=OD+OE.∴OD+OE=OC;(3)如解图②,过点C作CF⊥OA于F,CG⊥OB于G,第9题解图②∴∠OFC=∠OGC=90°,∵∠AOB=120°,∴∠FCG =60°.同(1)的方法得,OF =21OC ,OG =21OC ,∴OF +OG =OC .∵CF ⊥OA ,CG ⊥OB ,且点C 是∠AOB 的平分线OM 上一点, ∴CF =CG .∵∠DCE =60°,∠FCG =60°,∴∠DCF =∠ECG .∴△CFD ≌△CGE (ASA ).∴DF =EG .∴OF =DF -OD =EG -OD ,OG =OE -EG .∴OF +OG =EG -OD +OE -EG =OE -OD .∴OE -OD =OC .10.△ABC 为等边三角形,点M 是BC 中点,点P 在△ABC 所在平面内,连接P A ,PB ,PC ,PM ,直线PC 与直线AB 交于点D .(1)若点P 在△ABC 内,∠BPC =120°.①如图①,当点P 在AM 上时,求证:∠APD =∠BPM ;②如图②,当点P 不在AM 上时,∠APD =∠BPM 是否仍然成立?若成立,请证明;若不成立,请说明理由.(2)当点P 在△ABC 外,且点P 与点A 在直线BC 异侧时,若∠BPC =60°,∠APD 与∠BPM 有怎样的数量关系?第10题图解:(1)①证明:∵△ABC 是等边三角形,∴AB =AC ,∵点M 是BC 中点,∴BM =CM ,∴AM ⊥BC ,在△PMC 和△PMB 中,⎪⎩⎪⎨⎧=∠=∠=PM PM PMB PMC BM CM ,∴△PMC ≌△PMB (SAS ),1∠BPC=60°,∴∠MPC=∠MPB=2∵∠MPC=∠APD,∴∠APD=∠BPM;②∠APD=∠BPM仍然成立,如解图①,延长PM至K,使MK=PM,连接BK,延长PD至T,使PT=PB,连接TB、TA,第10题解图①由“倍长中线法”可证,△MCP≌△MBK(SAS),∴CP=BK,∠BCP=∠CBK,∴CP∥BK,∴∠PBK=∠PBC+∠CBK=∠PBC+∠BCP=180°-∠BPC=60°,∵∠BPT=180°-∠BPC=60°,∵PT =PB ,∴△PTB 是等边三角形,∴PB =BT ,∵∠PBT =∠ABC ,∴∠ABT =∠CBP ,在△ABT 和△CBP 中,⎪⎩⎪⎨⎧=∠=∠=BC AB CBP ABT BP BT , ∴△ABT ≌△CBP (SAS ),∴AT =PC ,∠ATB =∠CPB =120°,∵PC =BK ,∴AT =BK ,∴∠ATP =∠ATB -∠PTB =120°-60°=60°=∠PBK , 在△ATP 和△KBP 中,⎪⎩⎪⎨⎧=∠=∠=BP TP KBP ATP BK AT , ∴△ATP ≌△KBP (SAS ),∴∠APD =∠BPM ;(2)(Ⅰ)点D 在BA 延长线上时,如解图②,延长PM 至K ,使MK =PM ,连接BK ,在PD 上截取TB =TA ,连接PT 、PB ,第10题解图②同(1)②中的方法得,△MCP ≌△MBK (SAS ), ∴CP =BK ,CP ∥BK ,∴∠KBP =180°-∠BPC =120°.∵PT =PB ,∠BPC =60°,∴△PTB 是等边三角形,同(1)②的方法证得,△BAT≌△BCP(SAS),∴AT=CP=BK,∠ATB=∠CPB=60°=∠BTP,∴∠ATP=∠KBP=120°,∴△ATP≌△KBP(SAS),∴∠APT=∠KPB,∴∠APD=∠BPM;(Ⅱ)点D在AB延长线上时,如解图③,延长PM至K,使MK=MP,连接CK,第10题解图同(1)②的方法得,△MCK≌△MBP(SAS),∴CK=BP,∠CKP=∠BPK,∴CK∥BP,∴∠KCP=180°-∠BPC=120°,∵∠BPC=60°, PT=PC,∴△PTC是等边三角形,同(1)②的方法得,△CAT≌△CBP(SAS),∴AT=BP=CK,∠ATC=∠BPC=60°=∠CTP,∴∠ATP =∠KCP=120°,∴△KCP≌△ATP(SAS),∴∠CPK=∠APT,∵∠APD=120°+∠APT,∠BPM =60°-∠CPK,∴∠APD+∠BPM=180°.综上所述,∠APD=∠BPM或∠APD+∠BPM=180°.。
初二图形几何练习题

初二图形几何练习题1. 设直角三角形ABC中,∠ACB=90°,AC=8cm,BC=6cm。
求AB的长度。
解析:由勾股定理得:AB的长度为√(AC² + BC²) = √(8²+6²) =√(64+36) = √100 = 10cm。
2. 已知等边三角形ABC的周长为18cm,求三角形的边长。
解析:由题意可知,等边三角形的三条边相等,所以每条边的长度为18cm/3 = 6cm。
3. 在直角梯形ABCD中,AB∥CD,AB=5cm,BC=6cm,CD=8cm。
求梯形的面积。
解析:首先,找到梯形的高。
由于AB∥CD,所以梯形的高为BC的长度,即6cm。
接下来,根据梯形面积公式,面积S = 1/2 × (AB + CD) × BC = 1/2 × (5cm + 8cm) × 6cm = 1/2 × 13cm × 6cm = 39cm²。
4. 已知正方形ABCD的边长为10cm,求其对角线的长度。
解析:正方形的对角线长度可以通过勾股定理求得。
设对角线的长度为d,则根据勾股定理可得d² = 10² + 10² = 200。
解方程得d = √200 ≈ 14.14cm。
5. 平行四边形ABCD的边长分别为AB = 6cm,BC = 8cm,求平行四边形的面积。
解析:平行四边形的面积可以通过底边长度乘以高得到。
由于平行四边形的高无法直接确定,我们需要先找到平行四边形的高。
将平行四边形倾斜,使得AB和CD重合,如下图所示:A--------B| || || |D--------C此时,已知高为BC的长度,即8cm。
再利用底边AB的长度,可以求得平行四边形的面积为S = AB × BC = 6cm × 8cm = 48cm²。
6. 三角形ABC的三边分别为AB = 5cm,BC = 9cm,AC = 7cm。
初二几何练习题

初二几何练习题在初二数学学习中,几何是一个重要的内容部分,它涉及到图形的认识、性质和运用等方面。
为了帮助同学们更好地掌握几何知识,我整理了一些初二几何练习题,供大家练习和巩固知识。
1. 题目:已知直角三角形的直角边分别为3cm和4cm,求斜边的长度。
解析:根据毕达哥拉斯定理,直角三角形的斜边的长度等于直角边长度的平方和的平方根。
带入已知数据进行计算,斜边的长度为5cm。
2. 题目:在一个等边三角形中,每条边的长度为6cm,求它的高度和面积。
解析:在等边三角形中,高度是边长的正弦值乘以根号3的一半。
根据公式,计算得到高度为3√3 cm。
面积可以通过边长计算得到,即面积等于边长的平方乘以根号3的一半。
带入边长计算得到面积为9√3 cm²。
3. 题目:在一个正方形中,一条对角线的长度为8cm,求正方形的边长和面积。
解析:正方形的对角线等于边长的根号2倍。
根据公式,计算得到边长为8÷√2 cm。
面积等于边长的平方,带入边长计算得到面积为32 cm²。
4. 题目:一个等腰梯形的上底长为5cm,下底长为9cm,高度为6cm,求它的面积。
解析:等腰梯形的面积可以通过上底、下底和高度计算得到,即面积等于上底和下底和的一半乘以高度。
带入已知数据进行计算,面积为42 cm²。
5. 题目:在一个平行四边形中,一条对角线的长度为10cm,另一条对角线的长度为6cm,求平行四边形的面积。
解析:平行四边形的面积可以通过对角线的长度计算得到,即面积等于对角线之积的一半。
带入已知数据进行计算,面积为30 cm²。
6. 题目:在一个梯形中,上底长为8cm,下底长为12cm,高度为5cm,求梯形的面积。
解析:梯形的面积可以通过上底、下底和高度计算得到,即面积等于上底和下底和的一半乘以高度。
带入已知数据进行计算,面积为50 cm²。
通过以上的几何练习题,同学们可以巩固和运用几何知识,加深对几何图形的认识和理解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
30道典型几何综合题1、解答:解:(1)如图,作点D关于x轴的对称点D',连接CD'与x轴交于点E,连接DE.若在边OA上任取点E'与点E不重合,连接CE'、DE'、D'E'由DE'+CE'=D'E'+CE'>CD'=D'E+CE=DE+CE,可知△CDE的周长最小.∵在矩形OACB中,OA=3,OB=4,D为OB的中点,∴BC=3,D'O=DO=2,D'B=6,∵OE∥BC,∴Rt△D'OE∽Rt△D'BC,有∴∴点E的坐标为(1,0);(2)如图,作点D关于x轴的对称点D',在CB边上截取CG=2,连接D'G与x轴交于点E,在EA上截取EF=2,∵GC∥EF,GC=EF,∴四边形GEFC为平行四边形,有GE=CF,又GC、EF的长为定值,∴此时得到的点E、F使四边形CDEF的周长最小.∵OE∥BC,∴Rt△D'OE∽Rt△D'BG,有.∴∴∴点E的坐标为(,0),点F的坐标为(,0)(10分)2、解答:解:(1)设点B(4,﹣1)关于x轴的对称点是B',其坐标为(4,1),设直线AB'的解析式为y=kx+b,把A(2,﹣3),B'(4,1)代入得:,解得∴y=2x﹣7,令y=0得x=,即p=.(2)过A点作AE⊥x轴于点E,且延长AE,取A'E=AE.做点F(1,﹣1),连接A'F.那么A'(2,3).直线A'F的解析式为,即y=4x﹣5∵C点的坐标为(a,0),且在直线A'F上,∴a=.(3)存在使四边形ABMN周长最短的点M、N,作A关于y轴的对称点A′,作B关于x轴的对称点B′,连接A′B′,与x轴、y轴的交点即为点M、N,∴A′(﹣2,﹣3),B′(4,1),∴直线A′B′的解析式为:y=x﹣,∴M(,0),N(0,﹣).m=,n=﹣.3、解答:(1)证明:∵沿对角线BD对折,点C落在点C′的位置,∴∠A=∠C′,AB=C′D∴在△GAB与△GC′D中,∴△GAB≌△GC′D∴AG=C′G;(2)解:∵点D与点A重合,得折痕EN,∴DM=4cm,ND=5cm,∵EN⊥AD,∴MN==3(cm),由折叠的性质可知∠NDE=∠NDC,∵EN∥CD,∴∠END=∠NDC,∴∠END=∠NDC=∠NDE,∴EN=ED,设EM=x,则ED=EN=x+3,由勾股定理得ED2=EM2+DM2,即(x+3)2=x2+42,解得x=,即EM=.4、解答:解:(1)等腰.(2)如图①,连接BE,画BE的中垂线交BC与点F,连接EF,△BEF是矩形ABCD的一个折痕三角形.∵折痕垂直平分BE,AB=AE=2,∴点A在BE的中垂线上,即折痕经过点A.∴四边形ABFE为正方形.∴BF=AB=2,∴F(2,0).(3)矩形ABCD存在面积最大的折痕三角形BEF,其面积为4,理由如下:①当F在边BC上时,如图②所示.S△BEF≤S矩形ABCD,即当F与C重合时,面积最大为4.②当F在边CD上时,如图③所示,过F作FH∥BC交AB于点H,交BE于K.∵S△EKF=KF•AH≤HF•AH=S矩形AHFD,S△BKF=KF•BH≤HF•BH=S矩形BCFH,∴S△BEF≤S矩形ABCD=4.即当F为CD中点时,△BEF面积最大为4.下面求面积最大时,点E的坐标.①当F与点C重合时,如图④所示.由折叠可知CE=CB=4,在Rt△CDE中,ED===2.∴AE=4﹣2.∴E(4﹣2,2).②当F在边DC的中点时,点E与点A重合,如图⑤所示.此时E(0,2).综上所述,折痕△BEF的最大面积为4时,点E的坐标为E(0,2)或E(4﹣2,2).5、解答:解:(1)由折叠知BE=EM,∠B=∠EMP=90°.①△AEM的周长=AE+EM+AM=AE+EB+AM=AB+AM.∵AB=4,M是AD中点,∴△AEM的周长=4+2=6(cm);②现证明EP=AE+PD方法一:取EP的中点G,则在梯形AEPD中,MG为中位线,∴MG=(AE+PD),在Rt△EMP中,MG为斜边EP的中线,∴MG=EP,∴EP=AE+PD.方法二:延长EM交CD延长线于Q点.∵∠A=∠MDQ=90°,AM=DM,∠AME=∠DMQ,∴△AME≌△DMQ.∴AE=DQ,EM=MQ.又∵∠EMP=∠B=90°,∴PM垂直平分EQ,有EP=PQ.∵PQ=PD+DQ,∴EP=AE+PD.(2)△PDM的周长保持不变.设AM=x,则MD=4﹣x.由折叠性质可知,EM=4﹣AE,在Rt△AEM中,AE2+AM2=EM2,即AE2+x2=(4﹣AE)2,∴AE=(16﹣x2)又∵∠EMP=90°,∴∠AME+∠DMP=90°.∵∠AME+∠AEM=90°,∴∠AEM=∠DMP.又∠A=∠D,∴△PDM∽△MAE.∴∴C△PDM=C△MAE•=(4+x)•=8.∴△PDM的周长保持不变.6、解答:解:(1)∵A(﹣6,0),C(0,4)∴OA=6,OC=4设DE与y轴交于点M由DE∥AB可得△DMC∽△AOC又CD=AC∴∴CM=2,MD=3同理可得EM=3∴OM=6∴D点的坐标为(3,6);(2)由(1)可得点M的坐标为(0,6)由DE∥AB,EM=MD可得y轴所在直线是线段ED的垂直平分线∴点C关于直线DE的对称点F在y轴上∴ED与CF互相垂直平分∴CD=DF=FE=EC∴四边形CDFE为菱形,且点M为其对称中心作直线BM,设BM与CD、EF分别交于点S、点T可证△FTM≌△CSM∴FT=CS∵FE=CD∴TE=SD∵EC=DF∴TE+EC+CS+ST=SD+DF+FT+TS∴直线BM将四边形CDFE分成周长相等的两个四边形,由点B(6,0),点M(0,6)在直线y=kx+b上,可得直线BM的解析式为y=﹣x+6.(3)确定G点位置的方法:过A点作AH⊥BM于点H,则AH与y轴的交点为所求的G点由OB=6,OM=6可得∠OBM=60°∴∠BAH=30°在Rt△OAG中,OG=AO•tan∠BAH=2∴G点的坐标为.(或G点的位置为线段OC的中点)7、解答:解:(1)△A2B2C2的三个顶点的坐标分别是A2(4,0),B2(5,0),C2(5,2);(3分)(2)如果0<a≤3,那么点P1在线段OM上,PP2=PP1+P1P2=2OP1+2P1M=2(OP1+P1M)=2OM=6;(5分)如果a>3,那么点P1在点M的右边,PP2=PP1﹣P1P2=2OP1﹣2P1M=2(OP1﹣P1M)=2OM=6.所以PP2的长是6.(7分)8、解答:解:(1)Rt△CEF、Rt△ADE、Rt△AEF、Rt△AA1D1、Rt△ED1C1、Rt△C1B1F.(写出其中三个即可)(2)AF==5过E作EM⊥AF,垂足为M,交D1C1于N,则EM=2∵四边形A1B1C1D1是正方形∴D1C1∥AF∴△D1C1E∽△AFE∴设正方形A1B1C1D1的边长为x,则解得x=∴正方形A1B1C1D1的边长为.(3)∵D1C1=,EN=2﹣=∴S△D1EC1=××=∴=,C1B1=∴B1F=∴S△C1B1F1=××=∵∠1=∠2,∠1+∠4=90°,∠2+∠3=90°∴∠3=∠4∴E1点在C1F1上又∵S△正方形A1B1C1D=()2=∴S未被覆盖四边形=﹣﹣=.9、解答:解:(1)由题意可知:OA=2,∠AOB=30°,则根据直角三角形中30°所对的边是斜边的一半,则AB=1,根据勾股定理可以求得OB=;则点A的坐标为(1,),点B的坐标为(0,);(2)垂直.理由:连接DE,直角三角形ODE中,tan∠OED==,∴∠OED=60°.∵∠BAO=30°,∴OA⊥ED.(3)因为DE总是垂直于OA运动,因此可以看做直线DE沿OA方向进行运动.因此两者有公共点的取值范围就是O⇒A之间.当DE过O点时,t=0.当DE过A点时,直角三角形OAD中,OA=2,∠ODA=30°,因此OD=4,t=.因此t的取值范围是0≤t≤.(4)当0≤t≤时,S=t2;Smax=;当<t≤时,S=﹣t2﹣(﹣t)2=﹣(t﹣)2+,Smax=;当<t≤时,S=(2﹣t)2,S无最大值;综上所述S的最大值为.10、解答:解:(1)∵OA=OB=2,∴A(0,2)、B(2,0)、C(2,2).(3分)(2)△AOM∽△ONO’(4分)证明:∵四边形AOBC是正方形,∴∠AOM=90°.又O’N⊥OB,∴∠ONO'=90°.∴∠AOM=∠ONO’=90°.又根据对称性质可知:AM⊥OO’于D点,∴在Rt△ODM中,∠1+∠3=90°.在Rt△AOM中,∠2+∠3=90°,∴∠1=∠2.∴△AOM∽△ONO’(6分)(3)∵M是OB的中点,∴OM=•OB=1.∴在Rt△AOM中,AM=.又∵OD是Rt△AOM斜边上的高,∴.∴.(8分)又∵△AOM∽△ONO’,∴..∴.∴.(10分)11、解答:解:(1)∵A点第一次落在直线y=x上时停止旋转,∴OA旋转了45度.∴OA在旋转过程中所扫过的面积为.(2)∵MN∥AC,∴∠BMN=∠BAC=45°,∠BNM=∠BCA=45度.∴∠BMN=∠BNM.∴BM=BN.又∵BA=BC,∴AM=CN.又∵OA=OC,∠OAM=∠OCN,∴△OAM≌△OCN.∴∠AOM=∠CON.∴∠AOM=(90°﹣45°)=22.5度.∴旋转过程中,当MN和AC平行时,正方形OABC旋转的度数为45°﹣22.5°=22.5度.(3)在旋转正方形OABC的过程中,p值无变化.证明:延长BA交y轴于E点,则∠AOE=45°﹣∠AOM,∠CON=90°﹣45°﹣∠AOM=45°﹣∠AOM,∴∠AOE=∠CON.又∵OA=OC,∠OAE=180°﹣90°=90°=∠OCN.∴△OAE≌△OCN.∴OE=ON,AE=CN.又∵∠MOE=∠MON=45°,OM=OM,∴△OME≌△OMN.∴MN=ME=AM+AE.∴MN=AM+CN,∴p=MN+BN+BM=AM+CN+BN+BM=AB+BC=4.∴在旋转正方形OABC的过程中,p值无变化.12、解答:解:(1)图②中与△BCF全等的有△GDF、△GAH、△ECH.(2)D1F1=AH1,证明:∵,∴△AF1C≌△D1H1C.∴F1C=H1C,又CD1=CA,∴CD1﹣F1C=CA﹣H1C.即D1F1=AH1;(3)连接CG1.在△D1G1F1和△AG1H1中,∵,∴△D1G1F1≌△AG1H1.∴G1F1=G1H1,又∵H1C=F1C,G1C=G1C,∴△CG1F1≌△CG1H1.∴∠1=∠2.∵∠B=60°,∠BCF=30°,∴∠BFC=90°.又∵∠DCE=90°,∴∠BFC=∠DCE,∴BA∥CE,∴∠1=∠3,∴∠2=∠3,∴G1I=CI.13、解答:解:(1)BE=DF且BE⊥DF;(2)在△DFA和△BEA中,∵∠DAF=90°﹣∠FAB,∠BAE=90°﹣∠FAB,∴∠DAF=∠BAE,又AB=AD,AE=AF,∴△DFA≌△BEA,∴BE=DF;∠ADF=∠ABE,∴BE⊥DF;(3)AE=(﹣1)AD;(4)正方形.14、解答:解:(1)AB=AE,AB⊥AE;(2)将△BCG绕点C顺时针旋转90°后能与△ACE重合(或将△ACE绕点C逆时针旋转90°后能与△BCG重合),理由如下:∵AC⊥BC,DF⊥EF,B、F、C、E共线,∴∠ACB=∠ACE=∠DFE=90°,又∵AC=BC,DF=EF,∴∠DEF=∠D=45°,在△CEG中,∵∠ACE=90°,∴∠CGE+∠DEF=90°∴∠CGE=∠DEF=45°,∴CG=CE,在△BCG和△ACE中,∵,∴△BCG≌△ACE(SAS),∴将△BCG绕点C顺时针旋转90°后能与△ACE重合(或将△ACE绕点C逆时针旋转90°后能与△BCG重合).15、解答:解:(1)∠EBF=30°;(1分)∠QFC=60°;(2分)(2)∠QFC=60°.(1分)解法1:不妨设BP>AB,如图1所示.∵∠BAP=∠BAE﹣∠EAP=60°﹣∠EAP,∠EAQ=∠QAP﹣∠EAP=60°﹣∠EAP,∴∠BAP=∠EAQ.(2分)在△ABP和△AEQ中AB=AE,∠BAP=∠EAQ,AP=AQ,∴△ABP≌△AEQ.(SAS)(3分)∴∠AEQ=∠ABP=90°.(4分)∴∠BEF=180°﹣∠AEQ﹣∠AEB=180°﹣90°﹣60°=30°.∴∠QFC=∠EBF+∠BEF=30°+30°=60°.(5分)(事实上当BP≤AB时,如图2情形,不失一般性结论仍然成立,不分类讨论不扣分)解法2:设AP交QF于M∠QMP为△AMQ和△FMP共同的外角∴∠QMP=∠Q+∠PAQ=∠APB+∠QFC,由△ABP≌△AEQ得∠Q=∠APB,由旋转知∠PAQ=60°,∴∠QFC=∠PAQ=60°,(3)在图1中,过点F作FG⊥BE于点G.∵△ABE是等边三角形,∴BE=AB=2.由(1)得∠EBF=30°.在Rt△BGF中,BG==,∴BF==2.∴EF=2.(1分)∵△ABP≌△AEQ.∴QE=BP=x,∴QF=QE+EF=x+2.(2分)过点Q作QH⊥BC,垂足为H.在Rt△QHF中,y=QH=sin60°×QF=(x+2).(x>0)即y关于x的函数关系式是:y=x+.(3分)16、解答:解:(1)BG=AE,证明:易得BD=DC,GD=DE,∠GDB=∠EDA;故可得Rt△BDG≌Rt△EDA;故BG=AE;(2)成立:证明:连接AD,∵Rt△BAC中,D为斜边BC的中点,∴AD=BD,AD⊥BC,∴∠ADG+∠GDB=90°,∵EFGD为正方形,∴DE=DG,且∠GDE=90°,∴∠ADG+∠ADE=90°,∴∠BDG=∠ADE,在△BDG和△AED中,∴△BDG≌△AED(SAS),∴BG=AE;(3)由(2)可得BG=AE,当BG取得最大值时,AE取得最大值;分析可得:当旋转角度为270°时,BG=AE最大值为1+2=3,此时如图:AF=.17、解答:(1)证明:∵∠A=30°,∠ACB=90°,D是AB的中点.∴CD=AD=BD,又∠B=90°﹣∠A=60°,∴△BCD是等边三角形.又∵CN⊥DB,∴DN=DB.∵∠EDF=90°,△BCD是等边三角形,∴∠ADG=30°,而∠A=30°.∴GA=GD.∵GM⊥AB,∴AM=AD.又∵AD=DB,∴AM=DN.(2)解:(1)的结论依然成立.理由如下:∵DF∥AC,∴∠1=∠A=30°,∠AGD=∠GDH=90°,∴∠ADG=60°.∵∠B=60°,AD=DB,∴△ADG≌△DBH,∴AG=DH.又∵∠1=∠A,GM⊥AB,HN⊥AB,∴△AMG≌△DNH,∴AM=DN.18、解答:解:(1)∵点F在AD上,∴AF2=a2+a2,即AF=a,∴DF=b﹣a,∴S△DBF=DF×AB=×(b﹣a)×b=b2﹣ab;(2)连接AF,由题意易知AF∥BD,∴四边形AFDB是梯形,∴△DBF与△ABD等高同底,即BD为两三角形的底,由AF∥BD,得到平行线间的距离相等,即高相等,∴S△DBF=S△ABD=b2;(3)正方形AEFG在绕A点旋转的过程中,F点的轨迹是以点A为圆心,AF为半径的圆,第一种情况:当b>2a时,存在最大值及最小值,因为△BFD的边BD=b,故当F点到BD的距离取得最大、最小值时,S△BFD取得最大、最小值.如图②所示CF2⊥BD时,S△BFD的最大值=,S△BFD的最小值=,第二种情况:当b=2a时,存在最大值,不存在最小值.∴S△BFD的最大值=.(如果答案为4a2或b2也可).19、解答:(1)证明:证法一:在△ABP与△ADP中,∵AB=AD∠BAC=∠DAC,AP=AP,∴△ABP≌△ADP,∴BP=DP.(2分)证法二:利用正方形的轴对称性,可得BP=DP.(2分)(2)解:不是总成立.(3分)当四边形PECF的点P旋转到BC边上时,DP>DC>BP,此时BP=DP不成立,(5分)说明:未用举反例的方法说理的不得分.(3)解:连接BE、DF,则BE与DF始终相等,(6分)在图1中,由正方形ABCD可证:AC平分∠BCD,∵PE⊥BC,PF⊥BD,∴PE=PF,∠BCD=90°,∴四边形PECF为正方形.(7分)∴CE=CF,∵∠DCF=∠BCE,BC=CD,∴△BEC≌△DFC,∴BE=DF.(8分)20、解答:证明:(1)∵将菱形纸片AB(E)CD(F)沿对角线BD(EF)剪开,∴∠B=∠D,∵将△ECF的顶点F固定在△ABD的BD边上的中点处,△ECF绕点F在BD边上方左右旋转,∴BF=DF,∵∠HFG=∠B,又∵∠HFD=∠HFG+∠GFD=∠B+∠BHF∴∠GFD=∠BHF,∴△BFH∽△DGF,∴,∴BH•GD=BF2;(2)∵AG∥CE,∴∠FAG=∠C,∵∠CFE=∠CEF,∴∠AGF=∠CFE,∴AF=AG,∵∠BAD=∠C,∴∠BAF=∠DAG,∴△ABF≌△ADG,∴FB=DG,∴FD+DG=BD,故答案为:BD.21、解答:解:(1)相似(1分)由题意得:∠APA1=∠BPB1=α,AP=A1P,BP=B1P,则∠PAA1=∠PBB1=,(2分)∵∠PBB1=∠EBF,∴∠PAE=∠EBF,又∵∠BEF=∠AEP,∴△BEF∽△AEP;(3分)(2)存在,理由如下:(4分)易得:△BEF∽△AEP,若要使得△BEF≌△AEP,只需要满足BE=AE即可,(5分)∴∠BAE=∠ABE,∵∠BAC=60°,∴∠BAE=,∵∠ABE=β∠BAE=∠ABE,(6分)∴,即α=2β+60°;(7分)(3)连接BD,交A1B1于点G,过点A1作A1H⊥AC于点H.∵∠B1A1P=∠A1PA=60°,∴A1B1∥AC,由题意得:AP=A1P=2+x,∠A=60°,∴△PAA1是等边三角形,∴A1H=sin60°A1P=,(8分)在Rt△ABD中,BD=,∴BG=,(9分)∴(0≤x<2).(10分)22、解答:解:(1)∵点A(3,0),B(0,4),得OA=3,OB=4,∴在Rt△AOB中,由勾股定理,得AB==5,根据题意,有DA=OA=3.如图①,过点D作DM⊥x轴于点M,则MD∥OB,∴△ADM∽△ABO.有,得,∴OM=,∴,∴点D的坐标为(,).(2)如图②,由已知,得∠CAB=α,AC=AB,∴∠ABC=∠ACB,∴在△ABC中,∴α=180°﹣2∠ABC,∵BC∥x轴,得∠OBC=90°,∴∠ABC=90°﹣∠ABO=90°﹣β,∴α=2β;(3)若顺时针旋转,如图,过点D作DE⊥OA于E,过点C作CF⊥OA于F,∵∠AOD=∠ABO=β,∴tan∠AOD==,设DE=3x,OE=4x,则AE=3﹣4x,在Rt△ADE中,AD2=AE2+DE2,∴9=9x2+(3﹣4x)2,∴x=,∴D(,),∴直线AD的解析式为:y=x﹣,∵直线CD与直线AD垂直,且过点D,∴设y=﹣x+b,则b=4,∵互相垂直的两条直线的斜率的积等于﹣1,∴直线CD的解析式为y=﹣,若顺时针旋转,则可得直线CD的解析式为y=.∴直线CD的解析式为y=﹣或y=.23、解答:(1)证明:如图1,分别连接OE、0F,∵四边形ABCD是菱形,∴AC⊥BD,BD平分∠ADC.AO=DC=BC,∴∠COD=∠COB=∠AOD=90°.∠ADO=∠ADC=×60°=30°,又∵E、F分别为DC、CB中点,∴OE=CD,OF=BC,AO=AD,∴0E=OF=OA,∴点O即为△AEF的外心.(2)解:①猜想:外心P一定落在直线DB上.证明:如图2,分别连接PE、PA,过点P分别作PI⊥CD于I,PJ⊥AD于J,∴∠PIE=∠PJD=90°,∵∠ADC=60°,∴∠IPJ=360°﹣∠PIE﹣∠PJD﹣∠JDI=120°,∵点P是等边△AEF的外心,∴∠EPA=120°,PE=PA,∴∠IPJ=∠EPA,∴∠IPE=∠JPA,∴△PIE≌△PJA,∴PI=PJ,∴点P在∠ADC的平分线上,即点P落在直线DB上.②为定值2.当AE⊥DC时.△AEF面积最小,此时点E、F分别为DC、CB中点.连接BD、AC交于点P,由(1)可得点P即为△AEF的外心.如图3.设MN交BC于点G,设DM=x,DN=y(x≠0.y≠O),则CN=y﹣1,∵BC∥DA,∴△GBP≌△MDP.∴BG=DM=x.∴CG=1﹣x∵BC∥DA,∴△NCG∽△NDM,∴,∴,∴x+y=2xy,∴+=2,即=2.24、解答:解:(1)设AC=4x,BC=3x,在Rt△ABC中,AC2+BC2=AB2,即:(4x)2+(3x)2=102,解得:x=2,∴AC=8cm,BC=6cm;(2)①当点Q在边BC上运动时,过点Q作QH⊥AB于H,∵AP=x,∴BP=10﹣x,BQ=2x,∵△QHB∽△ACB,∴,∴QH=x,y=BP•QH=(10﹣x)•x=﹣x2+8x(0<x≤3),②当点Q在边CA上运动时,过点Q作QH′⊥AB于H′,∵AP=x,∴BP=10﹣x,AQ=14﹣2x,∵△AQH′∽△ABC,∴,即:=,解得:QH′=(14﹣2x),∴y=PB•QH′=(10﹣x)•(14﹣2x)=x2﹣x+42(3<x<7);∴y与x的函数关系式为:y=;(3)∵AP=x,AQ=14﹣2x,∵PQ⊥AB,∴△APQ∽△ACB,∴=,即:=,解得:x=,PQ=,∴PB=10﹣x=,∴≠,∴==≠,∴当点Q在CA上运动,使PQ⊥AB时,以点B、P、Q为定点的三角形与△ABC不相似;(4)存在.理由:∵AQ=14﹣2x=14﹣10=4,AP=x=5,∵AC=8,AB=10,∴PQ是△ABC的中位线,∴PQ∥BC,∴PQ⊥AC,∴PQ是AC的垂直平分线,∴PC=AP=5,∴当点M与P重合时,△BCM的周长最小,∴△BCM的周长为:MB+BC+MC=PB+BC+PC=5+6+5=16.∴△BCM的周长最小值为16.25、解答:解:(1)如图1,过点C作CN⊥x轴,垂足为N,则四边形DONC为矩形,∴ON=CD∵四边形ABCD是菱形,AB=10,∴AB=BC=CD=AD=10,∴ON=10,∵A(﹣6,0),∴OA=6,OD===8,∴点C的坐标为(10,8);(2)如图2,过点P作PH⊥BC,垂足为H,则∠PHC=∠AOD=90°,∵四边形ABCD是菱形,∴∠PCB=∠DAO,∴△PHC∽△DOA,∴==,∴==,∴PH=x,CH=x,∴BH=10﹣x,∵PE∥BC,BQ⊥PQ,∴∠PQB=∠QBC=∠PHB=90°,∴四边形PQBH为矩形,∴PQ=BH=10﹣x,∴y=10﹣x(0<x<10);(3)如图3,过点P作PH′⊥BC,垂足为H′,则四边形PQBH′是矩形,∴BQ=PH′=x,∵PE∥BC,∴∠PED=∠CBD,∵CD=CB,∴∠CBD=∠CDB,∴∠CDB=∠PED,∴PE=PD=10﹣x,QE=PQ﹣PE=x,过点D作DG⊥PQ于点G,过点A作AF⊥PQ交PQ的延长线于点F,∴∠DGF=∠AFG=90°,∵PQ∥BC,∴PQ∥AD,∴∠ADG=90°,∴四边形AFGD为矩形,∴AF=DG,∵PQ∥BC,∴∠DPG=∠C,∵∠DGP=∠PH′C=90°,∴△DGP∽△PH′C,∴=,∴AF=DG=(10﹣x)=8﹣x,∵S△BQE+S△AQE=EQ×BQ+EQ×AF,=×x×x+×x×(8﹣x)=x,S△DEP=PE×DG=(10﹣x)×(8﹣x),=x2﹣8x+40,∵S△BQE+S△AQE=S△DEP,∴x=(x2﹣8x+40),整理得,x2﹣25x+100=0,∴x1=5,x2=20,∵0<x<10,∴x2=20不符合题意,舍去,∴x1=5,∴x=5时,S△BQE+S△AQE=S△DEP,∵PH′=x=4<5,∴⊙P与直线BC相交.26、解答:(1)解:∵∠DBC=∠ACB=90°,∴△DBE∽△CAE,∴=,又∵BD=BC=2AC,∴DE=2CE;故答案为DE=2CE.(2)证明:如图2,∵∠DBC=∠ACB=120°,BD=BC,∴∠D=∠BCD=30°,∴∠ACD=90°,过点B作BM⊥DC于M,则DM=MC,BM=BC,∵AC=BC,∴BM=AC,又∵∠BMC=∠ACM=90°,∠MEB=∠CEA,∴△BME≌△ACE,∴ME=CE=CM,∴DE=3EC;(3)解:如图,过点B作BM′⊥DC于点M′,过点F作FN⊥DB交DB的延长线于点N,设BF=a,∵∠DBF=120°,∴∠FBN=60°,∴FN=a,BN=a,∵DB=BC=2BF=2a,∴DN=DB+BN=a,∴DF===a,∵AC=BC,BF=BC,∴BF=AC,∴△DBF≌△ACB,∴∠BDF=∠CBA,又∵∠BFG=∠DFB,∴△FBG∽△FDB,∴==,∴BF2=FG×FD,∴a2=a×FG,∴FG=a,∴DG=DF﹣FG=a,BG==a,∵△DKG和△DBG关于直线DG对称,∴∠GDH=∠BDF,∴∠ABC=∠GDH,又∵∠BGF=∠DGH,∴△BGF∽△DGH,∴=,∴GH==a,∵BH=BG+GH=a=10,∴a=2;∴BC=2a=4,CM′=BCcos30°=2,∴DC=2CM′=4,∵DE=3EC,∴EC=DC=.27、解答:(1)证明:①如图2:∵BM⊥直线a于点M,CN⊥直线a于点N,∴∠BMN=∠CNM=90°,∴BM∥CN,∴∠MBP=∠ECP,又∵P为BC边中点,∴BP=CP,又∵∠BPM=∠CPE,∴△BPM≌△CPE,(3分)②∵△BPM≌△CPE,∴PM=PE∴PM=ME,∴在Rt△MNE中,PN=ME,∴PM=PN.(5分)(2)解:成立,如图3.证明:延长MP与NC的延长线相交于点E,∵BM⊥直线a于点M,CN⊥直线a于点N,∴∠BMN=∠CNM=90°∴∠BMN+∠CNM=180°,∴BM∥CN∴∠MBP=∠ECP,(7分)又∵P为BC中点,∴BP=CP,又∵∠BPM=∠CPE,∴△BPM≌△CPE,∴PM=PE,∴PM=ME,则Rt△MNE中,PN=ME,∴PM=PN.(10分)(3)解:如图4,四边形M′BCN′是矩形,根据矩形的性质和P为BC边中点,得到△M′BP≌△N′CP,(11分)得PM′=PN′成立.即“四边形MBCN是矩形,则PM=PN成立”.(12分)28、解答:解:(1)EG=CG,EG⊥CG.(2分)(2)EG=CG,EG⊥CG.(2分)证明:延长FE交DC延长线于M,连MG.∵∠AEM=90°,∠EBC=90°,∠BCM=90°,∴四边形BEMC是矩形.∴BE=CM,∠EMC=90°,由图(3)可知,△BEF为等腰直角三角形,∴BE=EF,∴EF=CM.∵∠EMC=90°,FG=DG,∴MG=FD=FG.∵BC=EM,BC=CD,∴EM=CD.∵EF=CM,∴FM=DM,∴∠F=45°.又FG=DG,∠CMG=∠EMC=45°,∴∠F=∠GMC.∴△GFE≌△GMC.∴EG=CG,∠FGE=∠MGC.(2分)∵∠FMC=90°,MF=MD,FG=DG,∴MG⊥FD,∴∠FGE+∠EGM=90°,∴∠MGC+∠EGM=90°,即∠EGC=90°,∴EG⊥CG.(2分)29、解答:解:(1)证明:∵四边形OABC为正方形,∴OC=OA.∵三角板OEF是等腰直角三角形,∴OE1=OF1.又三角板OEF绕O点逆时针旋转至OE1F1的位置时,∠AOE1=∠COF1,∴△OAE1≌△OCF1.(3分)(2)存在.(4分)∵OE⊥OF,∴过点F与OE平行的直线有且只有一条,并与OF垂直,当三角板OEF绕O点逆时针旋转一周时,则点F在以O为圆心,以OF为半径的圆上.(5分)∴过点F与OF垂直的直线必是圆O的切线.又点C是圆O外一点,过点C与圆O相切的直线有且只有2条,不妨设为CF1和CF2,此时,E点分别在E1点和E2点,满足CF1∥OE1,CF2∥OE2.(7分)当切点F1在第二象限时,点E1在第一象限.在直角三角形CF1O中,OC=4,OF1=2,cos∠COF1==,∴∠COF1=60°,∴∠AOE1=60°.∴点E1的横坐标为:x E1=2cos60°=1,点E1的纵坐标为:y E1=2sin60°=,∴点E1的坐标为(1,);(9分)当切点F2在第一象限时,点E2在第四象限.同理可求:点E2的坐标为(1,﹣).(10分)综上所述,三角板OEF绕O点逆时针旋转一周,存在两个位置,使得OE∥CF,此时点E的坐标为E1(1,)或E2(1,﹣).(11分)30、解答:(1)证明:在△ABC和△AEP中,∵∠ABC=∠AEP,∠BAC=∠EAP,∴∠ACB=∠APE,在△ABC中,AB=BC,∴∠ACB=∠BAC,∴∠EPA=∠EAP.(2)解:▱APCD是矩形.理由如下:∵四边形APCD是平行四边形,∴AC=2EA,PD=2EP,∵由(1)知∠EPA=∠EAP,∴EA=EP,则AC=PD,∴▱APCD是矩形.(3)解:EM=EN.证明:∵EA=EP,∴∠EPA===90°﹣α,∴∠EAM=180°﹣∠EPA=180°﹣(90°﹣α)=90°+α,由(2)知∠CPB=90°,F是BC的中点,∴FP=FB,∴∠FPB=∠ABC=α,∴∠EPN=∠EPA+∠APN=∠EPA+∠FPB=90°﹣α+α=90°+α,∴∠EAM=∠EPN,∵∠AEP绕点E顺时针旋转适当的角度,得到∠MEN,∴∠AEP=∠MEN,∴∠AEP﹣∠AEN=∠MEN﹣∠AEN,即∠MEA=∠NEP,在△EAM和△EPN中,∴△EAM≌△EPN(AAS),∴EM=EN.26函数综合题1、解答:解:(1)取a=1,得抛物线y=x2+2x+3,其顶点为P1(﹣1,2).取a=﹣1,得抛物线y=﹣x2+2x+3,其顶点为P2(1,4).由题意有P1、P2在直线l上,设直线l的解析式为y=kx+b,则解得:∴直线l的解析式为y=x+3.(2)∵抛物线y=ax2+2x+3的顶点P坐标为.显然P在直线y=x+3上.又能取到除0以外的所有实数,∴在y=x+3上仅有一点(0,3)不是该抛物线的顶点.(3)猜想:对于抛物线y=ax2+bx+c(a≠0),将其顶点的横坐标减少,纵坐标增加分别作为点A的横、纵坐标;把顶点的横坐标增加,纵坐标增加分别作为点B的横、纵坐标,则A,B两点也在抛物线y=ax2+bx+c(a≠0)上.证明如下:∵抛物线y=ax2+bx+c(a≠0)的顶点坐标为(),∴点A的坐标为,点B的坐标为.∵时,∴点A在抛物线y=ax2+bx+c(a≠0),同理有B也在抛物线上,故结论成立.2、解答:解:(1)∵抛物线y=ax2+bx+c与y轴交于点C(0,﹣2),代入得:c=﹣2,∴y=ax2+bx﹣2,把A(﹣2,﹣2),B(2,2)代入得:,解得:,∴y=x2+x﹣2,答:抛物线的解析式是y=x2+x﹣2.(2)∵MN=,点A,B都在直线y=x上,MN在直线AB上,MN在线段AB上,M的横坐标为m.如图1,过点M作x轴的平行线,过点N作y轴的平行线,它们相交于点H.∴△MHN是等腰直角三角形.∴MH=NH=1.∴点N的坐标为(m+1,m+1)①如图2,当m<0时,PM=﹣m,NQ=m+1﹣[(m+1)2+m+1﹣2]=﹣(m+1)2+2.当四边形PMQN为平行四边形时,PM=NQ.∴﹣m=﹣(m+1)2+2.解得:m=(不合题意舍去)或﹣,②如图3,当m>0,PM=m,NQ=m+1﹣[(m+1)2+m+1﹣2]=﹣(m+1)2+2.当四边形PMQN为平行四边形时,PM=NQ.∴m=﹣(m+1)2+2.解得:m=﹣2﹣(不合题意舍去)或﹣2,∴当m=﹣或m=﹣2时,以点P,M,Q,N为顶点的四边形能为平行四边形.3、解答:解:(1)∵抛物线y=mx2﹣11mx+24m (m<0)与x轴交于B、C两点(点B在点C的左侧),∴抛物线与x轴的交点坐标为:0=mx2﹣11mx+24m,解得:x1=3,x2=8,∴OB=3,OC=8 (4分);(2)连接AD,交OC于点E,∵四边形OACD是菱形,∴AD⊥OC,OE=EC=×8=4,∴BE=4﹣3=1,又∵∠BAC=90°,∴△ACE∽△BAE,∴=,∴AE2=BE•CE=1×4,∴AE=2,…(6分)∴点A的坐标为(4,2)…(7分)把点A的坐标(4,2)代入抛物线y=mx2﹣11mx+24m,得m=﹣,∴抛物线的解析式为y=﹣x2+x﹣12;…(9分)(3)∵直线x=n与抛物线交于点M,∴点M的坐标为(n,﹣n2+n﹣12),由(2)知,点D的坐标为(4,﹣2),则C、D两点的坐标求直线CD的解析式为y=x﹣4,∴点N的坐标为(n,n﹣4),∴MN=(﹣n2+n﹣12)﹣(n﹣4)=﹣n2+5n﹣8,…(11分)∴S四边形AMCN=S△AMN+S△CMN=MN•CE=(﹣n2+5n﹣8)×4=﹣(n﹣5)2+9 (13分)∴当n=5时,S四边形AMCN=9.(14分)4、解答:(1)解:由A(﹣4,0)、B(﹣2,2)在抛物线y=ax2+bx图象上,得:(2分)解之得:a=﹣,b=﹣2,∴该函数解析式为:y=﹣x2﹣2x.(4分)(2)证明:过点B作BC垂直于X轴,垂足是点C.(6分)∵y=﹣x2﹣2x=﹣(x+2)2+2,∴线段CO、CA、CB的长度均为2,∴△ABC和△OBC为全等的等腰直角三角形,∴AB=OB且∠ABO=∠ABC+∠OBC=90°∴△OAB是等腰直角三角形(8分)(3)解:如图,将△OAB绕点O按逆时针方向旋转135°,得到△OA′B′其中点B′正好落在y轴上且B′A′∥x轴.又∵OB′和A′B′的长度为2,A′B′中点P的坐标为(,﹣2),显然不满足抛物线方程,∴点P不在此抛物线上(10分)(4)解:存在(11分)过点O,作OM∥AB交抛物线于点M易求出直线OM的解析式为:y=x联立抛物线解析式得:解之得点M(﹣6,﹣6),显然,点M(﹣6,﹣6)关于对称轴x=﹣2的对称点M′(2,﹣6)也满足要求,故满足条件的点M共有两个,坐标分别为(﹣6,﹣6)和(2,﹣6)∴s ABOM=S△ABO+s△AOM=×4×2+×4×6=16.(12分)(注:此题方法较多,只要合理均可给分)5、解答:解:(1)由题意得,解得:b=2,c=﹣3,则解析式为:y=x2+2x﹣3;(2)由题意结合图形则解析式为:y=x2+2x﹣3,解得x=1或x=﹣3,由题意点A(﹣3,0),∴AC=,CD=,AD=,由AC2+CD2=AD2,所以△ACD为直角三角形;(3)∵A(﹣3,0),B(1,0),∴AB=4,∵点E在抛物线的对称轴上,∴点E的横坐标为﹣1,当AB为平行四边形的一边时,EF=AB=4,∴F的横坐标为3或﹣5,把x=3或﹣5分别代入y=x2+2x﹣3,得到F的坐标为(3,12)或(﹣5,12);当AB为平行四边形的对角线时,由平行四边形的对角线互相平分,∴F点必在对称轴上,即F点与D点重合,∴F(﹣1,﹣4).∴所有满足条件的点F的坐标为(3,12),(﹣5,12),(﹣1,﹣4).6、解答:解:(1)由已知,得B(3,0),C(0,3),∴,解得,∴抛物线解析式为y=x2﹣4x+3;(2)∵y=x2﹣4x+3=(x﹣2)2﹣1,∴对称轴为x=2,顶点坐标为P(2,﹣1),∴满足条件的点M分别为M1(2,7),M2(2,2﹣1),M3(2,),M4(2,﹣2﹣1);(3)由(1),得A(1,0),连接BP,∵∠CBA=∠ABP=45°,∴当=时,△ABC∽△PBQ,∴BQ=3.∴Q1(0,0),∴当=时,△ABC∽△QBP,∴BQ=.∴Q′(,0).(4)当0<x<3时,在此抛物线上任取一点E,连接CE、BE,经过点E作x轴的垂线FE,交直线BC于点F,设点F(x,﹣x+3),点E(x,x2﹣4x+3),∴EF=﹣x2+3x,∴S△CBE=S△CEF+S△BEF=EF•OB,=﹣x2+x,=﹣(x﹣)2+,∵a=﹣<0,∴当x=时,S△CBE有最大值,∴y=x2﹣4x+3=﹣,∴E(,﹣).7、解答:解:(1)设二次函数的解析式为y=ax2+bx+c由题意得,解得,∴二次函数的解析式为y=x2﹣8x+12,(2分)点P的坐标为(4,﹣4);(3分)(2)存在点D,使四边形OPBD为等腰梯形.理由如下:当y=0时,x2﹣8x+12=0,∴x1=2,x2=6,∴点B的坐标为(6,0),设直线BP的解析式为y=kx+m则,解得∴直线BP的解析式为y=2x﹣12∴直线OD∥BP(4分)∵顶点坐标P(4,﹣4)∴OP=4设D(x,2x)则BD2=(2x)2+(6﹣x)2当BD=OP时,(2x)2+(6﹣x)2=32,解得:x1=,x2=2,(6分)当x2=2时,OD=BP=,四边形OPBD为平行四边形,舍去,∴当x=时四边形OPBD为等腰梯形,(7分)∴当D(,)时,四边形OPBD为等腰梯形;(8分)(3)①当0<t≤2时,∵运动速度为每秒个单位长度,运动时间为t秒,则MP=t,∴PH=t,MH=t,HN=t,∴MN=t,∴S=t•t•=t2(10分),②当2<t<4时,P1G=2t﹣4,P1H=t,∵MN∥OB∴△P1EF∽△P1MN,∴,∴,∴=3t2﹣12t+12,∴S=t2﹣(3t2﹣12t+12)=﹣t2+12t﹣12,∴当0<t≤2时,S=t2,当2<t<4时,S=﹣t2+12t﹣12.(12分)8、解答:解:(1)把点(0,﹣)代入抛物线,得:c=﹣;(2)把点(0,﹣)代入直线得:n=﹣.把点(m﹣b,m2﹣mb+n)代入抛物线,得:a(m﹣b)2+b(m﹣b)+c=m2﹣mb+n∵c=n=﹣,∴a(m﹣b)2+b(m﹣b)=m2﹣mb,am2﹣2abm+ab2+bm﹣b2﹣m2+mb=0(a﹣1)m2﹣(a﹣1)•2bm+(a﹣1)b2=0(a﹣1)(m2﹣2bm+b2)=0(a﹣1)(m﹣b)2=0∴a=1,当m﹣b=0时,抛物线与直线的两个交点就是一个点,所以m≠b.把a=1,c=﹣代入抛物线有:y=x2+bx﹣,当y=0时,x2+bx﹣=0,∴x1•x2=﹣;(3)y=x2+bx﹣,顶点(﹣,﹣﹣)当b≤0时,x=﹣1时,y=﹣b,比较﹣b与+的大小,得到:﹣4≤b≤0时,﹣b≥+,所以当b=0时,|y0|的最小值为.b≤﹣4时,﹣b≤+,所以当b=﹣4时,|y0|的最小值为.当b≥0时,x=1时,y=+b,比较+b与+的大小,得到:0≤b≤4时,+b≥+,所以当b=0时,|y0|的最小值为.b≥4时,+b≤+,所以当b=4时,|y0|的最小值为.故|y0|的最小值为或.9、解答:解:(1)设抛物线的解析式为y=kx2+a,∵经过点(2a,2a),4a2k+a=2a,∴k=,(2)设抛物线上一点P(x,y),过P作PH⊥x轴,PG⊥y轴,在Rt△GDP中,由勾股定理得:PD2=DG2+PG2=(y﹣2a)2+x2=y2﹣4ay+4a2+x2,∵y=x2+a,∴x2=4a×(y﹣a)=4ay﹣4a2,∴PD2=y2﹣4ay+4a2+4ay﹣4a2=y2=PH2,∴PD=PH,(3)过B作BE⊥x,AF⊥x,由(2)的结论:BE=DB,AF=DA,∵DA=2DB,∴AF=2BE,∴AO=2OB,∴B是OA的中点,∵C是OD的中点,连接BC,∴BC===BE=DB,过B作BR⊥y,∵BR⊥CD,∴CR=DR,OR=a+=,∴=x2+a,∴x2=2a2,∵x>0,∴x=a,∴B(a,)AO=2OB,∴S△OBD=S△ABD=4,∴×2a×a=4,∴a2=4,∵a>0,∴a=2,10、解答:解:(1)∵y=x2+bx+c的顶点为(1,﹣2).∴y=(x﹣1)2﹣2,y=x2﹣2x﹣1;(2)设直线PE对应的函数关系式为y=kx+b,由题意四边形ABCD是菱形,故直线PE必过菱形ABCD的对称中心M.由P(0,﹣1),M(1,0),得从而得y=x﹣1,设E(x,x﹣1)代入y=x2﹣2x﹣1得x﹣1=x2﹣2x﹣1,解得x1=0,x2=3,根据题意得点E(3,2);(3)假设存在这样的点F,可设F(x,x2﹣2x﹣1),过点F做FG⊥y轴,垂足为G点.在Rt△POM和Rt△FGP中,∵∠OMP+∠OPM=90°,∠FPG+∠OPM=90°,∠OMP=∠FPG,又∠POMP=∠PGF,∴△POM∽△FGP∴∵OM=1,OP=1,∴GP=GF,即﹣1﹣(x2﹣2x﹣1)=x,解得x1=0,x2=1,根据题意得F(1,﹣2)以上各步均可逆,故点F(1,﹣2)即为所求,S△PEF=S△MFP+S△MFE=2×1×2×2=3.11、解答:解:(1)∵四边形ABCD是矩形,∴AD=CB=10,AB=DC=8,∠D=∠DCB=∠ABC=90°,由折叠对称性:AF=AD=10,EF=DE,在Rt△ABF中,BF===6,∴CF=4,设EF=x,则EC=8﹣x,在Rt△ECF中,42+(8﹣x)2=x2,解得:x=5,∴CE=3,∵B(m,0),∴E(m+10,3),F(m+6,0);(2)分三种情况讨论:若AO=AF,∵AB⊥OF,∴BO=BF=6,∴m=6,若OF=FA,则m+6=10,解得:m=4,若AO=OF,在Rt△AOB中,AO2=OB2+AB2=m2+64,∴(m+6)2=m2+64,解得:m=,∴m=6或4或;(3)由(1)知:E(m+10,3),A(m,8).∴,得,∴M(m+6,﹣1),设对称轴交AD于G,∴G(m+6,8),∴AG=6,GM=8﹣(﹣1)=9,∵∠OAB+∠BAM=90°,∠BAM+∠MAG=90°,∴∠OAB=∠MAG,∵∠ABO=∠MGA=90°,∴△AOB∽△AMG,∴=,即:,∴m=12,12、解答:解:(1)令﹣x2﹣2x+3=0,(x+3)(x﹣1)=0,x1=﹣3,x2=1,A(﹣3,0)B.(1,0),C(0,3);(2)设直线AC的解析式为y=kx+b,由题意,得,解之得,故y=x+3;(3)设M点的坐标为(x,﹣x2﹣2x+3),AB=4,因为M在第二象限,所以﹣x2﹣2x+3>0,所以=6,解之,得x1=0,x2=﹣2,当x=0时,y=3,(不合题意)当x=﹣2时,y=3.所以M点的坐标为(﹣2,3);(4)由题意,得AB=4,PA=4﹣t,∵AO=3,CO=3,∴△AOC是等腰直角三角形,AQ=2t,所以Q点的纵坐标为t,S=(0<t<4)∵,∴当t=2时,△APQ最大,最大面积是.13、解答:解:(1)∵当x=0时,y=3,当y=0时,x=﹣1,∴A(﹣1,0),B(0,3),∵C(3,0),设抛物线的解析式为y=a(x+1)(x﹣3),∴3=a×1×(﹣3),∴a=﹣1,∴此抛物线的解析式为y=﹣(x+1)(x﹣3)=﹣x2+2x+3;(2)存在.①∵抛物线的对称轴为:x==1,∴如图对称轴与x轴的交点即为Q1,∵OA=OQ1,BO⊥AQ1,∴“当Q1B=AB时,设Q(1,q),∴1+(q﹣3)2=10,∴q=0,或q=6,∴Q(1,0)或Q(1,6)(在直线AB上,舍去).当Q2A=Q2B时,设Q2的坐标为(1,m),∴22+m2=12+(3﹣m)2,∴m=1,∴Q2(1,1);当Q3A=AB时,设Q3(1,n),∴22+n2=12+32,∴n=±,∴Q3(1,),Q4(1,﹣).∴符合条件的Q点坐标为Q1(1,0),Q2(1,1),Q3(1,),Q4(1,﹣).14、解答:解:(1)a=﹣1,b=﹣2,顶点C的坐标为(﹣1,4);(2)假设在y轴上存在满足条件的点D,过点C作CE⊥y轴于点E.由∠CDA=90°得,∠1+∠2=90°.又∠2+∠3=90°,∴∠3=∠1.又∵∠CED=∠DOA=90°,∴△CED∽△DOA,∴.设D(0,c),则.变形得c2﹣4c+3=0,解之得c1=3,c2=1.综合上述:在y轴上存在点D(0,3)或(0,1),使△ACD是以AC为斜边的直角三角形.(3)①若点P在对称轴右侧(如图①),只能是△PCQ∽△CAH,得∠QCP=∠CAH.延长CP交x轴于M,∴AM=CM,∴AM2=CM2.设M(m,0),则(m+3)2=42+(m+1)2,∴m=2,即M(2,0).设直线CM的解析式为y=k1x+b1,则,解之得,.∴直线CM的解析式.联立,解之得或(舍去).∴.②若点P在对称轴左侧(如图②),只能是△PCQ∽△ACH,得∠PCQ=∠ACH.过A作CA的垂线交PC于点F,作FN⊥x轴于点N.由△CFA∽△CAH得,由△FNA∽△AHC得.∴AN=2,FN=1,点F坐标为(﹣5,1).设直线CF的解析式为y=k2x+b2,则,解之得.∴直线CF的解析式.联立,解之得或(舍去).∴.∴满足条件的点P坐标为或.15、解答:解:(1)依题意得顶点A的坐标为(2,a),设P(1,n)据x=﹣,得A点的横坐标为m,即m=2,所以y=x2+4x﹣2,把P点的坐标代入得n=1,即P点的坐标为(1,1)(2)把抛物线化为顶点式:y=﹣(x﹣m)2+2,可知A(m,2),设C(n,2),把n代入y=﹣(x﹣m)2+2得y=﹣(n﹣m)2+2,所以P(n,﹣(n﹣m)2+2)∵AC=CP∴m﹣n=2+(m﹣n)2﹣2,即m﹣n=(m﹣n)2,∴m﹣n=0或m﹣n=1,又∵C点不与端点A、B重合∴m≠n,即m﹣n=1,则A(m,2),P(m﹣1,1)由AC=CP可得BE=AB∵OB=2∴OE=2﹣m,∴△OPE的面积S=(2﹣m)(m﹣1)=﹣(m﹣)2+(1<m<2),∴0<S<.16、解答:(1)证明:∵AC⊥BC,BD⊥CD,∴∠BDC=∠COA=90°,∠ACO+∠BCD=90°,∴∠BCD=∠OAC,∵△ABC为等腰直角三角形,∴BC=AC,∵在△BDC和△COA中∴△BDC≌△COA(AAS),(2)解:∵△BDC≌△COA,∴BD=CO,∵C点的坐标为(﹣1,0),∴BD=OC=1,∴B点的纵坐标为1,∵B点的横坐标为﹣3,∴B点的坐标为(﹣3,1),设BC所在直线的函数关系式为y=kx+b,∴,∴解方程组得,∴直线BC所在直线的解析式为:y=﹣x﹣,(3)解:存在,∵抛物线的解析式为:y=x2+x﹣2,∴y=x2+x﹣2=(x+)2﹣,∴二次函数的对称轴为x=﹣,①若以AC为直角边,C点为直角顶点,做CP1⊥AC,∵BC⊥AC,∴P1点为直线BC与对称轴直线x=﹣的交点,∵直线BC所在直线的解析式为:y=﹣x﹣,∴,∴解得,∴P1点的坐标为(﹣,﹣);②若以AC为直角边,A点为直角顶点,对称轴上有一点P2,使AP2⊥AC,∴过点A作AP2∥BC,交对称轴直线x=﹣于点P2,∵OD=3,OC=1,∴OA=CD=2,∴A点的坐标为(0,2),∴直线AP2的解析式为y=﹣x+2,∴,∴解得:,∴P2点的坐标为(﹣,),∴P点的坐标为P1(﹣,﹣)、P2(﹣,).17、解答:解:(1)抛物线y=ax2+bx+3经过点A(﹣3,0),B(﹣1,0)两点,∴,解得a=1,b=4,∴抛物线解析式为y=x2+4x+3;(2)由(1)配方得y=(x+2)2﹣1∴抛物线的顶点M(﹣2,﹣1),直线OD的解析式为y=x.于是设平移后的抛物线的顶点坐标为(h,h),∴平移后的抛物线解析式为y=(x﹣h)2+h,①当抛物线经过点C时,∵C(0,9),∴h2+h=9,解得h=,∴当≤h<时,平移的抛物线与射线CD(含端点C)只有一个公共点,②当抛物线与直线CD只有一个公共点时,由方程组,得x2+(﹣2h+2)x+h2+h﹣9=0,∴△=(﹣2h+2)2﹣4(h2+h﹣9)=0,解得h=4,此时抛物线y=(x﹣4)2+2与射线CD只有唯一一个公共点为(3,3),符合题意,综上所述,平移的抛物线与射线CD(含端点C)只有一个公共点时,顶点横坐标h的取值范围为h=4或≤h<;(3)设直线EF的解析式为y=kx+3(k≠0),点E、F的坐标分别为(m,m2),(n,n2),由得x2﹣kx﹣3=0,∴m+n=k,m•n=﹣3,作点E关于y轴的对称点R(﹣m,m2),作直线FR交y轴于点P,由对称性知∠EPQ=∠FPQ,此时△PEF的内心在y轴上,∴点P即为所求的点.由F,R的坐标可得直线FR的解析式为y=(n﹣m)x+mn记y=(n﹣m)x﹣3,当x=0时,y=﹣3,∴p(0,﹣3),∴y轴的负半轴上存在点P(0,﹣3)使△PEF的内心在y轴上.18、解答:解:(1)设抛物线的函数表达式为y=a(x﹣1)(x+3)∵抛物线交y轴于点E(0,﹣3),将该点坐标代入上式,得a=1∴所求函数表达式为y=(x﹣1)(x+3),即y=x2+2x﹣3;(2)∵点C是点A关于点B的对称点,点A坐标(﹣3,0),点B坐标(1,0),∴点C坐标(5,0),∴将点C坐标代入y=﹣x+m,得m=5,∴直线CD的函数表达式为y=﹣x+5,设K点的坐标为(t,0),则H点的坐标为(t,﹣t+5),G点的坐标为(t,t2+2t﹣3),∵点K为线段AB上一动点,∴﹣3≤t≤1,∴HG=(﹣t+5)﹣(t2+2t﹣3)=﹣t2﹣3t+8=﹣(t+)2+,∵﹣3<﹣<1,∴当t=﹣时,线段HG的长度有最大值;(3)∵点F是线段BC的中点,点B(1,0),点C(5,0),∴点F的坐标为(3,0),∵直线l过点F且与y轴平行,∴直线l的函数表达式为x=3,∵点M在直线l上,点N在抛物线上,∴设点M的坐标为(3,m),点N的坐标为(n,n2+2n﹣3),∵点A(﹣3,0),点C(5,0),∴AC=8,分情况讨论:①若线段AC是以点A、C,M、N为顶点的平行四边形的边,则需MN∥AC,且MN=AC=8.当点N在点M的左侧时,MN=3﹣n,∴3﹣n=8,解得n=﹣5,∴N点的坐标为(﹣5,12),当点N在点M的右侧时,MN=n﹣3,∴n﹣3=8,解得n=11,∴N点的坐标为(11,140),②若线段AC是以点A、C,M、N为顶点的平行四边形的对角线,由“点C与点A关于点B 中心对称”知:点M与点N关于点B中心对称,取点F关于点B的对称点P,则P点坐标为(﹣1,0)过P点作NP⊥x轴,交抛物线于点N,将x=﹣1代入y=x2+2x﹣3,得y=﹣4,过点N,B作直线NB交直线l于点M,在△BPN和△BFM中,∠NBP=∠MBF,BF=BP,∠BPN=∠BFM=90°,∴△BPN≌△BFM,∴NB=MB,∴四边形ANCM为平行四边形,∴坐标(﹣1,﹣4)的点N符合条件,∴当N的坐标为(﹣5,12),(11,140),(﹣1,﹣4)时,以点A、C、M、N为顶点的四边形为平行四边形.19、解答:解:(1)由已知得:A(﹣1,0),B(4,5),∵二次函数y=x2+bx+c的图象经过点A(﹣1,0),B(4,5),∴,解得:b=﹣2,c=﹣3;(2)如图:∵直线AB经过点A(﹣1,0),B(4,5),∴直线AB的解析式为:y=x+1,∵二次函数y=x2﹣2x﹣3,∴设点E(t,t+1),则F(t,t2﹣2t﹣3),∴EF=(t+1)﹣(t2﹣2t﹣3)=﹣(t﹣)2+,∴当t=时,EF的最大值为,∴点E的坐标为(,);(3)①如图:顺次连接点E、B、F、D得四边形EBFD.可求出点F的坐标(,),点D的坐标为(1,﹣4)S四边形EBFD=S△BEF+S△DEF=××(4﹣)+××(﹣1)=;②如图:。
