关于抛物线的十个最值问题-模板
高中数学抛物线最值问题精品

抛物线求最值问题(第一类)1.已知抛物线和一条直线,求抛物线上的一点到直线与(y 轴、准线、焦点)距离之和的最小值问题。
此类题常用方法转化为求焦点到直线的距离。
例题已知抛物线方程为x y 42=,直线l 的方程为04=+-y x ,在抛物线上有一动点P 到y 轴的距离为d1到直线l 的距离为d2,则d12的最小值为多少? 分析:如图点P 到y 轴的距离等于点P 到焦点F 的距离减1,过焦点F 作直线4=0的垂线,此时d12最小,依据抛物线方程求得F ,进而利用点到直线的距离公式求得d12的最小值.解:如图点P 到准线的距离等于点P 到焦点F 的距离,从而P 到y 轴的距离等于点P 到焦点F 的距离减1.过焦点F 作直线4=0的垂线,此时d122-1最小,∵F (1,0),则2,则d12的最小值为.抛物线求最值问题(其次类)2.已知抛物线和一个定点,①:定点在抛物线“内”,求抛物线上的一点到定点与(焦点、准线)距离之和的最值问题;②定点在抛物线“外”,求抛物线上的一点到定点与(焦点、准线)距离之差肯定值的最值问题。
此类题常用方法转化为三点共线或者顶点到直线问题。
例题已知点P在抛物线y2=4x上,则点P到点Q(2,-1)的距离与点P到抛物线焦点距离之和取得最小值时,点P的坐标为()A.⎪⎭⎫⎝⎛-1,41B.⎪⎭⎫⎝⎛1,41C.(1,2)D.(1,-2)分析:先推断点Q与抛物线的位置,即点Q在抛物线内,再由点P到抛物线焦点距离等于点P到抛物线准线距离,依据图象知最小值在M,P,Q三点共线时取得,可得到答案.解:点P到抛物线焦点距离等于点P到抛物线准线距离,如图,故最小值在M,P,Q三点共线时取得,此时P,Q的纵坐标都是-1,抛物线求最值问题(第三类)3.已知抛物线和一条直线,求抛物线上的一点到直线距离最小值问题。
此类题常用方法:①设点转化成二次函数问题;②求导数,让抛物线上点的切线斜率等于直线斜率。
抛物线专题(附答案)

抛物线专题考点1 抛物线的定义题型 利用定义,实现抛物线上的点到焦点的距离与到准线的距离之间的转换1.已知点P 在抛物线y 2 = 4x 上,那么点P 到点Q (2,-1)的距离与点P 到抛物线焦点距离之和的最小值为【[解析]过点P 作准线的垂线l 交准线于点R ,由抛物线的定义知,PR PQ PF PQ +=+,当P 点为抛物线与垂线l 的交点时,PR PQ +取得最小值,最小值为点Q 到准线的距离 ,因准线方程为x=-1,故最小值为32. 已知点),4,3(A F 是抛物线x y 82=的焦点,M 是抛物线上的动点,当MF MA +最小时, M 点坐标是 ( )A. )0,0(B. )62,3(C. )4,2(D. )62,3(-[解析] 设M 到准线的距离为MK ,则MK MA MF MA +=+|||,当MK MA +最小时,M 点坐标是)4,2(,选C考点2 抛物线的标准方程题型:求抛物线的标准方程3.求满足下列条件的抛物线的标准方程,并求对应抛物线的准线方程:(1)过点(-3,2) (2)焦点在直线上【解题思路】以方程的观点看待问题,并注意开口方向的讨论.[解析] (1)设所求的抛物线的方程为22y px =-或22(0)x py p =>, ∵过点(-3,2) ∴229)3(24⋅=--=p p 或 ∴2934p p ==或 ∴抛物线方程为243y x =-或292x y =,前者的准线方程是1,3x =后者的准线方程为98y =- (2)令0x =得2y =-,令0y =得4x =,∴抛物线的焦点为(4,0)或(0,-2),当焦点为(4,0)时,42p =, ∴8p =,此时抛物线方程216y x =;焦点为(0,-2)时22p = ∴4p =,此时抛物线方程28x y =-.∴所求抛物线方程为216y x =或28x y =-,对应的准线方程分别是4,2x y =-=.4.对于顶点在原点的抛物线,给出下列条件:①焦点在y 轴上;②焦点在x 轴上;③抛物线上横坐标为1的点到焦点的距离等于6;④抛物线的通径的长为5;⑤由原点向过焦点的某条直线作垂线,垂足坐标为(2,1).能使这抛物线方程为y 2=10x 的条件是____________.(要求填写合适条件的序号)[解析] 用排除法,由抛物线方程y 2=10x 可排除①③④,从而②⑤满足条件.5. 若抛物线的顶点在原点,开口向上,F 为焦点,M 为准线与Y 轴的交点,A 为抛物线上一点,且3||,17||==AF AM ,求此抛物线的方程[解析] 设点'A 是点A 在准线上的射影,则3|'|=AA ,由勾股定理知22|'|=MA ,点A 的横坐标为)23,22(p -,代入方程py x 22=得2=p 或4,抛物线的方程y x 42=或y x 82= 考点3 抛物线的几何性质题型:有关焦半径和焦点弦的计算与论证6.设A 、B 为抛物线px y22=上的点,且 90=∠AOB (O 为原点),则直线AB 必过的定点坐标为__________.【解题思路】由特殊入手,先探求定点位置 [解析]设直线OA 方程为kx y =,由⎩⎨⎧==px y kx y 22解出A 点坐标为)2,2(2k p k p ⎪⎩⎪⎨⎧=-=px y x k y 212解出B 点坐标为)2,2(2pk pk -,直线AB 方程为221)2(2k pk x k pk y ---=+,令0=y 得p x 2=,直线AB 必过的定点)0,2(p【指引】(1)由于是填空题,可取两特殊直线AB, 求交点即可;(2)B 点坐标可由A 点坐标用k1-换k 而得。
根据抛物线方程,给出10个别的题目。

根据抛物线方程,给出10个别的题目。
根据抛物线方程,给出10个别的题目
根据抛物线方程,我们可以基于不同的参数和情境创造多个题目。
以下是10个不同的题目的示例。
1. 抛物线线段的长度
根据给定的抛物线方程,计算抛物线线段的长度。
2. 抛物线的焦点和直线的交点
已知抛物线方程和直线方程,求抛物线焦点和直线的交点坐标。
3. 最高点的坐标
已知抛物线方程,求抛物线的最高点坐标。
4. 抛物线的对称轴
已知抛物线方程,求抛物线的对称轴方程。
5. 通过三个点确定抛物线
已知三个点的坐标,求通过这三个点的抛物线方程。
6. 抛物线的焦距和准线
已知抛物线方程,求抛物线的焦距和准线方程。
7. 包络方程
已知一组抛物线方程,求包络方程。
8. 两个抛物线的公共焦点
已知两个抛物线方程,求解这两个抛物线的公共焦点坐标。
9. 抛物线上的切线方程
已知抛物线方程,求抛物线上某点的切线方程。
10. 角度问题
已知抛物线方程及两个切线的方程,求两个切线的夹角。
这些题目仅是根据抛物线方程衍生出的一部分,通过这些题目的练习,可以加深对抛物线方程的理解和应用能力。
抛物线的最值汇总

1 此时 l AB : y x 4
利用弦长公式解题
题型二:抛物线的最值问题 练习: 已知抛物线y=x2,动弦AB的长为2,求AB中点纵坐标的最小值。 解法二: 设A( x1, y1 ), B( x2 y2 ), AB中点M ( x0 , y0 )
2 MN AD BC , MN
y1 y2 , kOB x1 x2
∴ x1x2+y1y2=0
∵ OA⊥OB ∴ kOAkOB=-1 ∵ y12=2px1,y22=2px2 ∴ y1y2=-4p2
y12 y2 2 y1 y2 0 2p 2p
∴ x1x2=4p2
∵ y1≠0,y2≠0
2 y A 、B 是抛物线 2 px ( p 0) 上的两点,满足 3、 OA OB (O 为坐标原点). 求证 : ⑴ A 、B 两点的横坐标之积 , 纵坐标之
题型三:抛物线的定值问题 2 A 、B 是抛物线 y 2 px ( p 0) 上的两点,满足 3、 OA OB (O 为坐标原点). 求证 : ⑴ A 、B 两点的横坐标之积 , 纵坐标之 积分别为定值; ⑵直线 AB 经过一个定点.
解:(1)设A(x1,y1),B(x2,y2),
kOA
抛物线的最值问题来表示试用两点且相交于与抛物线若直线的绝对值由轴的距离为该点纵坐标ob1ab过定点2p0
与抛物线有关的最值问题
题型二:抛物线最值问题
例1.在抛物线 y2=8x 上求一点P,使P到焦点F 的距离与到 Q(4 ,1)的距离的 和最小,并求最小值。 解:
p4 2p 8, 由 y2 8x 知:
∴ AB 过定点(2p,0).
变式3:定长为5的线段AB的两端点在抛物线y 2 4 x上移动, 试求线段AB中点M 到y轴的最短距离.
抛物线最值问题

2
= x2 - 2x + 9
= ( x - 1) 2 + 8
min
x³ 0
= 2 2, 此时M (1, 2)
变3
\ 当x = 1时,
2
变式训练:
已知点M 在抛物线y = 4 x上运动, 点Q在圆(x - 3) + y = 1上运动,则 MQ 的最小值是
.
2 2 2
小组讨论、交流:
只需求出动点M到圆心 A(3,0)距离最小值再 减去圆半径即可。
y
M
F
练习
A
Q .
x
所以 MQ min = 2 2 - 1
2
的最小值是多少?
小组讨论、交流:
y
M
F
x
l
已知点F为抛物线 y 2 = 4 x 的焦点,A(3,2) 为定点,点M 是抛物线上任意一点,则 MA + MF 的最小值是 ,此时点M的 坐标是
小组活动:
。
探究2
y
M A
讨论解决方案
F
x
探究3
已知抛物线y =4x和定点A(7,8), 抛物线上有一动点M,点M到点A 的距离为d1,点M到抛物线准线距离 为d 2,则d1+d 2的最小值是 .
2 2 最小值为AF =(7-1) +(8-0) =10
y M F
A
M
x
思考:已知点A30,点 ( , ) M在抛物线y2=4x 上运动,求 MA 的最小值,及此时点M的坐标.
解:设点M( x, y)是抛物线y 2=4x 上任一点,则y = 4 x
AM =
=
2
y M F Ax
抛物线难题集锦

抛物线难题集锦本文提供了一系列抛物线难题的解答,旨在帮助读者更好地理解抛物线的性质和特点。
以下是一些常见的抛物线难题及其解决方法。
问题1: 确定抛物线的顶点和焦点坐标解答:抛物线的标准方程为 $y = ax^2 + bx + c$。
1.要确定抛物线的顶点坐标,可以使用公式 $x = -\frac{b}{2a}$ 和 $y = c-\frac{b^2}{4a}$。
2.要确定抛物线的焦点坐标,可以使用公式 $x = -\frac{b}{2a}$ 和 $y = c-\frac{1}{4a}$。
问题2: 确定抛物线的对称轴方程解答:抛物线的标准方程为 $y = ax^2 + bx + c$。
1.要确定抛物线的对称轴方程,可以使用公式 $x = -\frac{b}{2a}$。
问题3: 计算抛物线与 x 轴的交点解答:抛物线与 x 轴的交点对应于方程 $y = 0$ 的解。
1.将抛物线方程 $y = ax^2 + bx + c$ 中的 y 替换为 0,可以得到一个关于 x 的二次方程 $ax^2 + bx + c = 0$。
2.可以使用求根公式或因式分解等方法求解该二次方程,从而得到抛物线与 x 轴的交点坐标。
问题4: 计算抛物线在某点的切线方程解答:1.首先,通过求导数可以得到抛物线的斜率方程,即 $y' = 2ax+ b$。
2.然后,将给定点的横坐标带入斜率方程,得到该点处的斜率。
3.最后,将斜率和给定点的坐标代入直线的点斜式方程中,即$y - y_0 = k(x - x_0)$,其中 $k$ 为斜率,$(x_0.y_0)$ 为给定点的坐标。
问题5: 求解已知两点的抛物线方程解答:1.已知两点的坐标为 $(x_1.y_1)$ 和 $(x_2.y_2)$。
2.使用已知点的坐标代入抛物线方程,可以得到一个二元一次方程组。
3.解二元一次方程组,求出抛物线的系数 $a$、$b$ 和 $c$,从而得到抛物线方程。
抛物线最值问题

抛物线最值问题最值训练一:例1.在抛物线y2=8x 上求一点P,使P到焦点F 的距离与到Q(4 ,1)的距离的和最小,并求最小值。
例2、在抛物线y2=64x上求一点,使它到直线L:4x+3y+46=0的距离最短,并求此距离。
跟踪训练练习1:在抛物线y2=64x上求一点,使它到直线L:4x+3y+46=0的距离最短,并求此距离。
练习2: 已知抛物线y=x2,动弦AB的长为2,求AB中点纵坐标的最小值。
练习3: 已知抛物线y=x2,动弦AB的长为2,求AB中点纵坐标的最小值。
练习4:若直线y=kx+b与抛物线x²=4y相较于A、B两点,且|AB|=4(1)试用k来表示b(2)求弦AB中点M离x轴的最短距离最值训练二:1、A、B是抛物线y²=2px (p>0)上的两点,满足OA⊥OB(O为坐标原点)。
求证:(1)A、B两点的横坐标之积,纵坐标之积分别为定值(2)直线AB经过一个定点跟踪训练:定长为5的线段AB的两端点在抛物线y²=4x上移动,试求线段AB中点M 到y轴的最短距离。
2.已知定点M(3,2),F是抛物线y²=2x的焦点,在此抛物线上求一点P,使|PM|+|PF|取得最小值,求点P的坐标。
跟踪训练1:设P是曲线y²=4(x-1)上一动点,则求点P到点(0,1)的距离和点P到y轴的距离之和的最小值。
跟踪训练2:设P为抛物线y=x²上一动点,求P到直线l:3x-4y-6=0的距离的最小值最值训练三1、已知抛物线y²=x,动弦AB长为2、求AB中点纵坐标的最小值。
跟踪训练1:点P在抛物线y²=x上,定点A(3,0),求|PA|的最小值跟踪训练2:若P为抛物线y²=x上一动点,Q为圆(x-3²+y²=1上一动点,求|PQ|的最小值。
抛物线典型例题12例(含标准答案)

《抛物线》典型例题12例典型例题一例1 指出抛物线的焦点坐标、准线方程. (1)y x 42= (2))0(2≠=a ay x分析:(1)先根据抛物线方程确定抛物线是四种中哪一种,求出p ,再写出焦点坐标和准线方程.(2)先把方程化为标准方程形式,再对a 进行讨论,确定是哪一种后,求p 及焦点坐标与准线方程.解:(1)2=p ,∴焦点坐标是(0,1),准线方程是:1-=y (2)原抛物线方程为:x a y 12=,ap 12=∴ ①当0>a 时,ap 412=,抛物线开口向右, ∴焦点坐标是)0,41(a ,准线方程是:a x 41-=. ②当0<a 时,a p 412-=,抛物线开口向左, ∴焦点坐标是)0,41(a ,准线方程是:ax 41-=. 综合上述,当0≠a 时,抛物线2ay x =的焦点坐标为)0,41(a ,准线方程是:ax 41-=. 典型例题二例2 若直线2-=kx y 与抛物线x y 82=交于A 、B 两点,且AB 中点的横坐标为2,求此直线方程.分析:由直线与抛物线相交利用韦达定理列出k 的方程求解.另由于已知与直线斜率及弦中点坐标有关,故也可利用“作差法”求k .解法一:设),(11y x A 、),(22y x B ,则由:⎩⎨⎧=-=xy kx y 822可得:04)84(22=++-x k x k .∵直线与抛物线相交,0≠∴k 且0>∆,则1->k . ∵AB 中点横坐标为:2842221=+=+∴kk x x , 解得:2=k 或1-=k (舍去). 故所求直线方程为:22-=x y .解法二:设),(11y x A 、),(22y x B ,则有22212188x y x y ==. 两式作差解:)(8))((212121x x y y y y -=+-,即2121218y y x x y y +=--. 421=+x x 444)(22212121-=-+=-+-=+∴k x x k kx kx y y ,448-=∴k k 故2=k 或1-=k (舍去). 则所求直线方程为:22-=x y .典型例题三例3 求证:以抛物线的焦点弦为直径的圆心与抛物线的准线相切. 分析:可设抛物线方程为)0(22>=p px y .如图所示,只须证明12MM AB =,则以AB 为直径的圆,必与抛物线准线相切. 证明:作l AA ⊥1于l BB A ⊥11,于1B .M 为AB 中点,作l MM ⊥1于1M ,则由抛物线的定义可知:BF BB AF AA ==11,在直角梯形A A BB 11中:AB BF AF BB AA MM 21)(21)(21111=+=+=AB MM 211=∴,故以AB 为直径的圆,必与抛物线的准线相切. 说明:类似有:以椭圆焦点弦为直径的圆与相对应的准线相离,以双曲线焦点弦为直径的圆与相应的准线相交.典型例题四例4(1)设抛物线x y 42=被直线k x y +=2截得的弦长为53,求k 值. (2)以(1)中的弦为底边,以x 轴上的点P 为顶点作三角形,当三角形的面积为9时,求P 点坐标.分析:(1)题可利用弦长公式求k ,(2)题可利用面积求高,再用点到直线距离求P 点坐标.解:(1)由⎩⎨⎧+==kx y x y 242得:0)44(422=+-+k x k x设直线与抛物线交于),(11y x A 与),(22y x B 两点.则有:4,122121k x x k x x =⋅-=+[][])21(5)1(54)(5))(21(22212212212k k k x x x x x x AB -=--=-+=-+=∴53)21(5,53=-∴=∴k AB ,即4-=k (2)9=∆S ,底边长为53,∴三角形高5565392=⨯=h ∵点P 在x 轴上,∴设P 点坐标是)0,(0x 则点P 到直线42-=x y 的距离就等于h ,即55612402220=+--x 10-=∴x 或50=x ,即所求P 点坐标是(-1,0)或(5,0). 典型例题五例5 已知定直线l 及定点A (A 不在l 上),n 为过A 且垂直于l 的直线,设N 为l 上任一点,AN 的垂直平分线交n 于B ,点B 关于AN 的对称点为P ,求证P 的轨迹为抛物线.分析:要证P 的轨迹为抛物线,有两个途径,一个证明P 点的轨迹符合抛物线的定义,二是证明P 的轨迹方程为抛物线的方程,可先用第一种方法,由A 为定点,l 为定直线,为我们提供了利用定义的信息,若能证明PN PA =且l PN ⊥即可.证明:如图所示,连结P A 、PN 、NB .由已知条件可知:PB 垂直平分NA ,且B 关于AN 的对称点为P . ∴AN 也垂直平分PB .则四边形P ABN 为菱形.即有PN PA =...l PN l AB ⊥∴⊥则P 点符合抛物线上点的条件:到定点A 的距离与到定直线的距离相等,所以P 点的轨迹为抛物线.典型例题六例6 若线段21P P 为抛物线)0(2:2>=p px y C 的一条焦点弦,F 为C 的焦点,求证:p F P FP 21121=+. 分析:此题证的是距离问题,如果把它们用两点间的距离表示出来,其计算量是很大的.我们可以用抛物线的定义,巧妙运用韦达定理,也可以用抛物线的定义与平面几何知识,把结论证明出来.证法一:)0,2(pF ,若过F 的直线即线段21P P 所在直线斜率不存在时, 则有p F P F P ==21,p p p F P FP 2111121=+=+∴. 若线段21P P 所在直线斜率存在时,设为k ,则此直线为:)0)(2(≠-=k px k y ,且设),(),,(222111y x P y x P .由⎪⎪⎩⎪⎪⎨⎧-=-=)2()2(p x k y px k y 得:04)2(22222=++-p k x k p x k 2221)2(kk p x x +=+∴ ① 4221p x x =⋅ ②根据抛物线定义有:p x x P P px F P p x F P ++=∴+=+=21211211,2,2 则F P F P F P F P F P F P 21212111⋅+=+4)(2)2)(2(22121212121p x x p x x p x x p x p x p x x +++++=++++= 请将①②代入并化简得:p F P FP 21121=+ 证法二:如图所示,设1P 、2P 、F 点在C 的准线l 上的射影分别是'1P 、'2P 、F ',且不妨设1122P P m n P P '=<=',又设2P点在F F '、11P P '上的射影分别是A 、B 点,由抛物线定义知,p F F m F P n F P ='==,,12又AF P 2∆∽12BP P ∆,1221P P F P BP AF =∴即nm nn m n p +=-- pn m m nn m p 2112)(=+∴=+∴ 故原命题成立.典型例题七例7 设抛物线方程为)0(22>=p px y ,过焦点F 的弦AB 的倾斜角为α,求证:焦点弦长为α2sin 2pAB =. 分析:此题做法跟上题类似,也可采用韦达定理与抛物线定义解决问题.证法一:抛物线)0(22>=p px y 的焦点为)0,2(p,过焦点的弦AB 所在的直线方程为:)2(tan px y -=α由方程组⎪⎩⎪⎨⎧=-=px y p x y 2)2(tan 2α消去y 得:0tan )(tan 4tan 422222=+-αααp p x设),(),,(2211y x B y x A ,则⎪⎪⎩⎪⎪⎨⎧=⋅+=+=+4)cot 21(tan )2(tan 22122221p x x p p x x ααα 又)(tan 2121x x y y -=α[]ααααααααα242222222222122122212sin 2sin 14)cot 1(cot 4sec 44)cot 1()tan 1(4)()tan 1())(tan 1(pp p p p x x x x x x AB =⋅=+⋅=⎥⎦⎤⎢⎣⎡⋅-++=-++=-+=∴即α2sin 2pAB =证法二:如图所示,分别作1AA 、1BB 垂直于准线l .由抛物线定义有:ααcos cos 11⋅-==+⋅==BF p BB BF p AF AA AF于是可得出:αcos 1-=p AF αcos 1+=pBFαααα22sin 2cos 12cos 1cos 1p pp p BFAF AB =-=++-=+=∴故原命题成立.典型例题八例8 已知圆锥曲线C 经过定点)32,3(P ,它的一个焦点为F (1,0),对应于该焦点的准线为1-=x ,过焦点F 任意作曲线C 的弦AB ,若弦AB 的长度不超过8,且直线AB 与椭圆22322=+y x 相交于不同的两点,求 (1)AB 的倾斜角θ的取值范围.(2)设直线AB 与椭圆相交于C 、D 两点,求CD 中点M 的轨迹方程. 分析:由已知条件可确定出圆锥曲线C 为抛物线,AB 为抛物线的焦点弦,设其斜率为k ,弦AB 与椭圆相交于不同的两点,可求出k 的取值范围,从而可得θ的取值范围,求CD 中点M 的轨迹方程时,可设出M 的坐标,利用韦达定理化简即可.解:(1)由已知得4=PF .故P 到1-=x 的距离4=d ,从而d PF = ∴曲线C 是抛物线,其方程为x y 42=.设直线AB 的斜率为k ,若k 不存在,则直线AB 与22322=+y x 无交点. ∴k 存在.设AB 的方程为)1(-=x k y由⎩⎨⎧-==)1(42x k y x y 可得:0442=--k y ky 设A 、B 坐标分别为),(11y x 、),(22y x ,则:442121-=⋅=+y y ky y222122122212)1(44)(1))(11(k k y y y y k k y y k AB +=-++=-+=∴∵弦AB 的长度不超过8,8)1(422≤+∴k k 即12≥k 由⎩⎨⎧=+-=223)1(22y x x k y 得:0)1(24)32(2222=-+-+k x k x k ∵AB 与椭圆相交于不同的两点,32<∴k 由12≥k 和32<k 可得:31<≤k 或13-≤<-k 故3tan 1≤≤θ或1tan 3-<<-θ 又πθ<≤0,∴所求θ的取值范围是:34πθπ<≤或4332πθπ≤< (2)设CD 中点),(y x M 、),(33y x C 、),(44y x D由⎩⎨⎧=+-=223)1(22y x x k y 得:0)1(24)32(2222=-+-+k x k x k 9325313231322232)1(2,324222224322132243<+≤∴<≤+-=∴+=+=+-=⋅+=+∴k k k x k k x x x k k x x k k x x则323211522<+-≤k 即3252<≤x . 3)1(2)1(23221222222+-⋅-⋅=+=∴-=x y x y k k x x y k 化简得:032322=-+x y x∴所求轨迹方程为:)3252(032322<≤=-+x x y x典型例题九例9 定长为3的线段AB 的端点A 、B 在抛物线x y =2上移动,求AB 的中点到y 轴的距离的最小值,并求出此时AB 中点的坐标.分析:线段AB 中点到y 轴距离的最小值,就是其横坐标的最小值.这是中点坐标问题,因此只要研究A 、B 两点的横坐标之和取什么最小值即可.解:如图,设F 是x y =2的焦点,A 、B 两点到准线的垂线分别是AC 、BD ,又M 到准线的垂线为MN ,C 、D 和N 是垂足,则2321)(21)(21=≥+=+=AB BF AF BD AC MN . 设M 点的横坐标为x ,纵坐标为y ,41+=x MN ,则454123=-≥x .等式成立的条件是AB 过点F . 当45=x 时,41221-=-=P y y ,故 22122)(212221221=-=++=+x y y y y y y , 221±=+y y ,22±=y . 所以)22,45(±M ,此时M 到y 轴的距离的最小值为45. 说明:本题从分析图形性质出发,把三角形的性质应用到解析几何中,解法较简.典型例题十例10 过抛物线px y 2=的焦点F 作倾斜角为θ的直线,交抛物线于A 、B 两点,求AB 的最小值. 分析:本题可分2πθ=和2πθ≠两种情况讨论.当2πθ≠时,先写出AB 的表达式,再求范围. 解:(1)若2πθ=,此时p AB 2=. (2)若2πθ≠,因有两交点,所以0≠θ. )2(tan p x y AB -=θ:,即2tan py x +=θ.代入抛物线方程,有0tan 222=--p y py θ. 故θθ22222212csc 44tan 4)(p p p y y =+=-, θθθ2222212212tan csc 4tan )()(p y y x x =-=-. 故θθθ422222csc 4)tan 11(csc 4p p AB =+=. 所以p p AB 2sin 22>=θ.因2πθ≠,所以这里不能取“=”.综合(1)(2),当2πθ=时,p AB 2=最小值. 说明:(1)此题须对θ分2πθ=和2πθ≠两种情况进行讨论; (2)从解题过程可知,抛物线点弦长公式为θ2sin 2pl =; (3)当2πθ=时,AB 叫做抛物线的通径.通径是最短的焦点弦.例11 过抛物线px y 22=)0(>p 的焦点F 作弦AB ,l 为准线,过A 、B 作l 的垂线,垂足分别为'A 、'B ,则①''FB A ∠为( ),②B AF '∠为( ).A .大于等于︒90B .小于等于︒90C .等于︒90D 不确定分析:本题考查抛物线的定义、直线与圆的位置关系等方面的知识,关键是求角的大小以及判定直线与圆是否相切.解:①点A 在抛物线上,由抛物线定义,则21'∠=∠⇒=AF AA , 又x AA //'轴31∠=∠⇒.∴32∠=∠,同理64∠=∠,而︒=∠+∠+∠+∠1804632,∴︒=∠+∠9063,∴︒=∠90''FB A .选C .②过AB 中点M 作l MM ⊥',垂中为'M , 则AB BF AF BB AA MM 21)(21)(21'''=+=+=.∴以AB 为直径的圆与直线l 相切,切点为'M .又'F 在圆的外部,∴︒<∠90'B AF .特别地,当x AB ⊥轴时,'M 与'F 重合,︒=∠90'B AF .即︒≤∠90'B AF ,选B .例12 已知点)2,3(M ,F 为抛物线x y 22=的焦点,点P 在该抛物线上移动,当PF PM +取最小值时,点P 的坐标为__________.分析:本题若建立目标函数来求PF PM +的最小值是困难的,若巧妙地利用抛物线定义,结合图形则问题不难解决.解:如图,由定义知PE PF =,故213=≥≥+=+MN ME PM PF PF PM .取等号时,M 、P 、E 三点共线,∴P 点纵坐标为2,代入方程,求出其横坐标为2,所以P 点坐标为)2,2(.。
高中数学抛物线最值问题讲课稿

抛物线求最值问题(第一类)1.已知抛物线和一条直线,求抛物线上的一点到直线与(y 轴、准线、焦点)距离之和的最小值问题。
此类题常用方法转化为求焦点到直线的距离。
例题已知抛物线方程为x y 42=,直线l 的方程为04=+-y x ,在抛物线上有一动点P 到y 轴的距离为d1,P 到直线l 的距离为d2,则d1+d2的最小值为多少?分析:如图点P 到y 轴的距离等于点P 到焦点F 的距离减1,过焦点F 作直线x-y+4=0的垂线,此时d1+d2最小,根据抛物线方程求得F ,进而利用点到直线的距离公式求得d1+d2的最小值.解:如图点P 到准线的距离等于点P 到焦点F 的距离,从而P 到y 轴的距离等于点P 到焦点F 的距离减1.过焦点F 作直线x-y+4=0的垂线,此时d1+d2=|PF|+d2-1最小, ∵F (1,0),则|PF|+d2==,则d1+d2的最小值为.抛物线求最值问题(第二类)2.已知抛物线和一个定点,①:定点在抛物线“内”,求抛物线上的一点到定点与(焦点、准线)距离之和的最值问题;②定点在抛物线“外”,求抛物线上的一点到定点与(焦点、准线)距离之差绝对值的最值问题。
此类题常用方法转化为三点共线或者顶点到直线问题。
例题已知点P在抛物线y2=4x上,那么点P到点Q(2,-1)的距离与点P到抛物线焦点距离之和取得最小值时,点P的坐标为()A.⎪⎭⎫⎝⎛-1,41B.⎪⎭⎫⎝⎛1,41C.(1,2)D.(1,-2)分析:先判断点Q与抛物线的位置,即点Q在抛物线内,再由点P 到抛物线焦点距离等于点P到抛物线准线距离,根据图象知最小值在M,P,Q三点共线时取得,可得到答案.解:点P到抛物线焦点距离等于点P到抛物线准线距离,如图PF+PQ=PM+PQ,故最小值在M,P,Q三点共线时取得,此时P,Q的纵坐标都是-1,抛物线求最值问题(第三类)3.已知抛物线和一条直线,求抛物线上的一点到直线距离最小值问题。
抛物线中的最值问题

8
16
5
当 x 3 时, d 有最小值为 8
87 。 精选80ppt
P(x,y)
o
x
5
法二、判别式法
解:当L平移到与抛物线y=x2只有一个公共点时,设此时的 直线为L1,其方程为3x-4y-b=0。则L与L1的距离即为所求。
3x-4y+b=0
①
y=x2
②
②代入①可得:4x2 -3x+b=0
∴ ⊿=(-3)2-4×4×b=0 可得
11 。
2
精选ppt
2
2
法二、判别式法
过A作同心圆,当圆与抛物线相 切时,P到A点的距离最小,设为r
则由 (y2x3x2)y2 r2
x 2 5 9 x r 2 0
可 得 :Δ( -25)41( 9r2)0
r
11 2
精选ppt
3
练习:
若P为抛物线y2=x上一动点,Q为圆(x-3)2+y2=1 上
b 9 16
L 与 L 1的距离是
d
6
(
9 16
)
32 (4)2
87 80
为所求 .
精选ppt
y o
y=x2
L1 L
x
6
练习:已知抛物线y2=4x,以抛物线上两点
A(4,4)、B(1,-2)的连线为底边△ABP,其顶点P
在抛物线的弧AB上运动,求: △ABP的最大面积
及此时点P的坐标。
分析1:动点在弧AB上运动,可以 设出点P的坐标,只要求出点P到线 段AB所在直线AB的最大距离即为 点P到线段AB的最大距离,也就求 出了△ABP的最大面积。
O
x
Q
精选ppt
2021年中考数学必刷压轴题专题:抛物线之最值问题(含解析)-个人用心整理
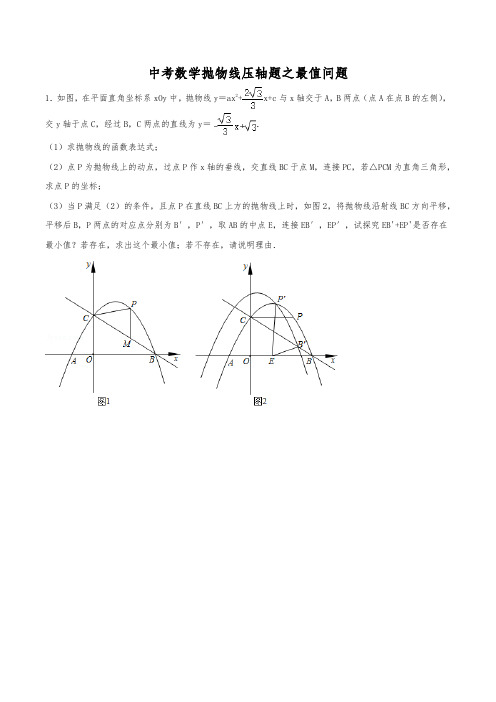
中考数学抛物线压轴题之最值问题1.如图,在平面直角坐标系xOy中,抛物线y=ax2+x+c与x轴交于A,B两点(点A在点B的左侧),交y轴于点C,经过B,C两点的直线为y=.(1)求抛物线的函数表达式;(2)点P为抛物线上的动点,过点P作x轴的垂线,交直线BC于点M,连接PC,若△PCM为直角三角形,求点P的坐标;(3)当P满足(2)的条件,且点P在直线BC上方的抛物线上时,如图2,将抛物线沿射线BC方向平移,平移后B,P两点的对应点分别为B′,P′,取AB的中点E,连接EB′,EP′,试探究EB'+EP'是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由.2.如图,抛物线y=ax2+bx+c与x轴相交于A(3,0)、B两点,与y轴交于点C(0,3),点B在x轴的负半轴上,且OA=3OB.(1)求抛物线的函数关系式;(2)若P是抛物线上且位于直线AC上方的一动点,求△ACP的面积的最大值及此时点P的坐标;(3)在线段OC上是否存在一点M,使BM+CM的值最小?若存在,请求出这个最小值及对应的M点的坐标;若不存在,请说明理由.3.在平面直角坐标系中,抛物线y=﹣x2+bx+c经过点A、B,C,已知A(﹣1,0),C(0,3).(1)求抛物线的解析式;(2)如图1,P为线段BC上一动点,过点P作y轴的平行线,交抛物线于点D,是否存在这样的P点,使线段PD的长有最大值?若存在,求出这个最大值;若不存在,请说明理由;(3)如图2,抛物线的顶点为E,EF⊥x轴于点F,N是直线EF上一动点,M(m,0)是x轴一个动点,请直接写出CN+MN+MB的最小值以及此时点M、N的坐标,直接写出结果不必说明理由.4.如图1,点A在x轴上,OA=4,将OA绕点O逆时针旋转120°至OB的位置.(1)求经过A、O、B三点的抛物线的函数解析式;(2)在此抛物线的对称轴上是否存在点P使得以P、O、B三点为顶点的三角形是等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由;(3 )如图2,OC=4,⊙A的半径为2,点M是⊙A上的一个动点,求MC+OM的最小值.5.如图,二次函数y=﹣x2+x+2的图象与x轴交于点A,B,与y轴交于点C.点P是该函数图象上的动点,且位于第一象限,设点P的横坐标为x.(1)写出线段AC,BC的长度:AC=,BC=;(2)记△BCP的面积为S,求S关于x的函数表达式;(3)过点P作PH⊥BC,垂足为H,连结AH,AP,设AP与BC交于点K,探究:是否存在四边形ACPH为平行四边形?若存在,请求出的值;若不存在,请说明理由,并求出的最大值.6.如图,直线y=x+2与抛物线y=x2﹣2mx+m2+m交于A、B两点(A在B的左侧),与y轴交于点C,抛物线的顶点为D,抛物线的对称轴与直线AB交于点M.(1)当四边形CODM是菱形时,求点D的坐标;(2)若点P为直线OD上一动点,求△APB的面积;′(3)作点B关于直线MD的对称点B',以点M为圆心,MD为半径作⊙M,点Q是⊙M上一动点,求QB'+ QB的最小值.7.如图,对称轴x=﹣1的抛物线y=ax2+bx+c与x轴交于A(2,0),B两点,与y轴交于点C(0,﹣2),(1)求抛物线的函数表达式;(2)若点P是直线BC下方的抛物线上的动点,求△BPC的面积的最大值;(3)若点P在抛物线对称轴的左侧运动,过点P作PD⊥x轴于点D,交直线BC于点E,且PE=OD,求点P的坐标;(4)在对称轴上是否存在一点M,使△AMC的周长最小.若存在,请求出M点的坐标和△AMC周长的最小值;若不存在,请说明理由.8.已知抛物线y=ax2+bx﹣4经过点M(﹣4,6)和点N(2,﹣6).(1)试确定该抛物线的函数表达式;(2)若该抛物线与x轴交于点A,B(点A在点B的左侧),与y轴交于点C①试判断△ABC的形状,并说明理由;②在该抛物线的对称轴上是否存在点P,使PM+PC的值最小?若存在,求出它的最小值;若不存在,请说明理由.9.如图,抛物线y=ax2﹣2ax+c的图象经过点C(0,﹣2),顶点D的坐标为(1,﹣),与x轴交于A、B 两点.(1)求抛物线的解析式.(2)连接AC,E为直线AC上一点,当△AOC∽△AEB时,求点E的坐标和的值.(3)点F(0,y)是y轴上一动点,当y为何值时,FC+BF的值最小.并求出这个最小值.(4)点C关于x轴的对称点为H,当FC+BF取最小值时,在抛物线的对称轴上是否存在点Q,使△QHF 是直角三角形?若存在,请求出点Q的坐标;若不存在,请说明理由.10.在平面直角坐标系中,抛物线y=﹣x2+bx+c经过点A、B、C,已知A(﹣1,0),C(0,3).(1)求抛物线的解析式;(2)如图1,P为线段BC上一点,过点P作y轴的平行线,交抛物线于点D,当△CDP为等腰三角形时,求点P的坐标;(3)如图2,抛物线的顶点为E,EF⊥x轴于点F,N是直线EF上一动点,M(m,0)是x轴一个动点,请直接写出CN+MN+MB的最小值以及此时点M、N的坐标.11.如图,抛物线y=ax2+bx+3与x轴交于A(﹣3,0),B(9,0)两点,与y轴交于点C,连接AC,BC.点P沿AC以每秒1个单位长度的速度由点A向点C运动,同时,点Q沿BO以每秒2个单位长度的速度由点B 向点O运动,当一个点停止运动时,另一个点也随之停止运动,连接PQ,过点Q作QD⊥x轴,与抛物线交于点D,连接PD与BC交于点E.设点P的运动时间为t秒(t>0)(1)求抛物线的表达式;(2)①直接写出P,D两点的坐标(用含t的代数式表示,结果需化简).②在点P,Q运动的过程中,当PQ=PD时,求t的值;(3)点M为线段BC上一点,在点P,Q运动的过程中,当点E为PD中点时,是否存在点M使得PM+BM 的值最小?若存在,请求出PM+BM的最小值;若不存在,请说明理由.12.已知抛物线y=ax2+bx+c(a≠0)过点A(1,0),B(3,0)两点,与y轴交于点C,OC=3.(1)求抛物线的解析式及顶点D的坐标;(2)过点A作AM⊥BC,垂足为M,求证:四边形ADBM为正方形;(3)点P为抛物线在直线BC下方图形上的一动点,当△PBC面积最大时,求点P的坐标;(4)若点Q为线段OC上的一动点,问:AQ+QC是否存在最小值?若存在,求岀这个最小值;若不存在,请说明理由.13.如图,已知二次函数y=ax2+bx+c(a≠0)的图象与直线AB相交,与x轴、y轴交于A(2,0)、B.(1)求点O关于AB的对称点P的坐标;(2)若点P在二次函数y=ax2+bx+c(a≠0)的图象上,求二次函数y=ax2+bx+c(a≠0)的关系式.(3)在(2)的条件下,在△ABP内存在点M,使得MA+MB+MP的值最小,则相应点M的坐标为.14.如图(1),二次函数y=ax2﹣bx(a≠0)的图象与x轴、直线y=x的交点分别为点A(4,0)、B(5,5).(1)a=,b=,∠AOB=°;(2)连接AB,点P是抛物线上一点(异于点A),且∠PBO=∠OBA,求点P的坐标;(3)如图(2),点C、D是线段OB上的动点,且CD=2.设点C的横坐标为m.①过点C、D分别作x轴的垂线,与抛物线相交于点F、E,连接EF.当CF+DE取得最大值时,求m的值并判断四边形CDEF的形状;②连接AC、AD,求m为何值时,AC+AD取得最小值,并求出这个最小值.15.如果一个三角形有一条边上的高等于这条边的一半,那么我们把这个三角形叫做“半高三角形”.如图1,对于△ABC,BC边上的高AD等于BC的一半,△ABC就是半高三角形,此时,称△ABC是BC类半高三角形;如图2,对于△EFG,EF边上的高GH等于EF的一半,△EFG就是半高三角形,此时,称△EFG是EF类半高三角形.(1)直接写出下列3个小题的答案.①若一个三角形既是等腰三角形又是半高三角形,则其底角度数的所有可能值为.②若一个三角形既是直角三角形又是半高三角形,则其最小角的正切值为.③如图3,正方形网格中,L,M是已知的两个格点,若格点N使得△LMN为半高三角形,且△LMN为等腰三角形或直角三角形,则这样的格点N共有个.(2)如图,平面直角坐标系内,直线y=x+2与抛物线y=x2交于R,S两点,点T坐标为(0,5),点P是抛物线y=x2上的一个动点,点Q是坐标系内一点,且使得△RSQ为RS类半高三角形.①当点P介于点R与点S之间(包括点R,S),且PQ取得最小值时,求点P的坐标.②当点P介于点R与点O之间(包括点R,O)时,求PQ+QT的最小值.16.如图1,抛物线y=ax2+(a+2)x+2(a≠0)与x轴交于点A(4,0),与y轴交于点B,在x轴上有一动点P(m,0)(0<m<4),过点P作x轴的垂线交直线AB于点N,交抛物线于点M.(1)求a的值;(2)若PN:MN=1:3,求m的值;(3)如图2,在(2)的条件下,设动点P对应的位置是P1,将线段OP1绕点O逆时针旋转得到OP2,旋转角为α(0°<α<90°),连接AP2、BP2,求AP2+BP2的最小值.17.如图1,抛物线y=ax2+bx+c经过点A(﹣2,0),点B(4,0),点D(2,4),与y轴交于点C,作直线BC,连接AC,CD.(1)求抛物线的函数表达式;(2)E是抛物线上的点,求满足∠ECD=∠ACO的点E的坐标;(3)点M在y轴上且位于点C上方,点N在直线BC上,点P为第一象限内抛物线上一点.若以点C,M,N,P为顶点的四边形是菱形,求菱形的边长.(4)如图2,E为OB的中点,将线段OE绕点O逆时针旋转得到OE′,旋转角为α(0°<α<90°),连接E′B、E′C,求E′B+E′C的最小值,请直接写出答案.18.如图1,抛物线y=ax2+(a+3)x+3(a≠0)与x轴交于点A(4,0),与y轴交于点B,在x轴上有一动点E(m,0)(0<m<4),过点E作x轴的垂线交直线AB于点N,交抛物线于点P,过点P作PM⊥AB于点M.(1)求a的值和直线AB的函数表达式;(2)设△PMN的周长为C1,△AEN的周长为C2,若=,求m的值;(3)如图2,在(2)条件下,将线段OE绕点O逆时针旋转得到OE′,旋转角为α(0°<α<90°),连接E′A、E′B,求E′A+E′B的最小值.19.在平面直角坐标系中,已知y=﹣x2+bx+c(b、c为常数)的顶点为P,等腰直角三角形ABC的顶点A 的坐标为(0,﹣1),点C的坐标为(4,3),直角顶点B在第四象限.(1)如图,若抛物线经过A、B两点,求抛物线的解析式.(2)平移(1)中的抛物线,使顶点P在直线AC上并沿AC方向滑动距离为时,试证明:平移后的抛物线与直线AC交于x轴上的同一点.(3)在(2)的情况下,若沿AC方向任意滑动时,设抛物线与直线AC的另一交点为Q,取BC的中点N,试探究NP+BQ是否存在最小值?若存在,求出该最小值;若不存在,请说明理由.20.如图,已知一条直线过点(0,4),且与抛物线y=x2交于A,B两点,其中点A的横坐标是﹣2.(1)求这条直线的函数关系式及点B的坐标.(2)在x轴上是否存在点C,使得△ABC是直角三角形?若存在,求出点C的坐标,若不存在,请说明理由.(3)过线段AB上一点P,作PM∥x轴,交抛物线于点M,点M在第一象限,点N(0,1),当点M的横坐标为何值时,MN+3MP的长度最大?最大值是多少?21.如图,抛物线y=x2﹣4x与x轴交于O,A两点,P为抛物线上一点,过点P的直线y=x+m与对称轴交于点Q.(1)这条抛物线的对称轴是,直线PQ与x轴所夹锐角的度数是;(2)若两个三角形面积满足S△POQ=S△PAQ,求m的值;(3)当点P在x轴下方的抛物线上时,过点C(2,2)的直线AC与直线PQ交于点D,求:①PD+DQ的最大值;②PD•DQ的最大值.22.如图,已知一次函数y1=x+b的图象l与二次函数y2=﹣x2+mx+b的图象C′都经过点B(0,1)和点C,且图象C′过点A(2﹣,0).(1)求二次函数的最大值;(2)设使y2>y1成立的x取值的所有整数和为s,若s是关于x的方程=0的根,求a的值;(3)若点F、G在图象C′上,长度为的线段DE在线段BC上移动,EF与DG始终平行于y轴,当四边形DEFG的面积最大时,在x轴上求点P,使PD+PE最小,求出点P的坐标.23.如图,抛物线y=(x+1)2+k与x轴交于A、B两点,与y轴交于点C(0,﹣3);(1)求抛物线的对称轴及k的值;(2)抛物线的对称轴上是否存在一点P,使得|PB﹣PC|的值最大?若存在,求出点P的坐标;(3)如果点M是抛物线在第三象限的一动点;当M点运动到何处时,M点到AC的距离最大?求出此时的最大距离及M的坐标.24.如图(1)抛物线y=ax2+bx+c(a≠o)的顶点为C(1,4),交x轴于A、B两点,交y轴于点D,其中点B的坐标为(3,0)(1)求抛物线的函数解析式;(2)如图(2)T是抛物线上的一点,过点T作x轴的垂线,垂足为点M,过点M作MN∥BD,交线段AD于点N,连接MD,若△DNM∽△BMD,求点T的坐标;(3)如图(3),过点A的直线与抛物线相交于E,且E点的横坐标为2,与y轴交于点F;直线PQ是抛物线的对称轴,G是直线PQ上的一动点,试探究在x轴上是否存在一点H,使D、G、H、F四点围成的四边形周长最小?若存在,求出这个最小值及点G、H的坐标;若不存在,请说明理由.25.如图,已知抛物线的顶点坐标为M(1,4),且经过点N(2,3),与x轴交于A、B两点(点A在点B 左侧),与y轴交于点C.(1)求抛物线的解析式及点A、B、C的坐标;(2)直线AN交y轴于点F,P是抛物线的对称轴x=1上动点,H是X轴上一动点,请探索:是否存在这样的P、H,使四边形CFHP的周长最短?若存在,请求出四边形CFHP的最短周长和点P、H的坐标;若不存在,请说明理由;(3)若点Q是∠MDB的角平分线上动点,点R是线段DB上的动点,Q、R在何位置时,BQ+QR的值最小.请直接写出BQ+QR的最小值和Q、R的坐标.26.在平面直角坐标系中,已知抛物线y=x2+bx+c(b,c为常数)的顶点为P,等腰直角三角形ABC的顶点A的坐标为(0,﹣1),C的坐标为(4,3),直角顶点B在第四象限.(1)如图,若该抛物线过A,B两点,求该抛物线的函数表达式;(2)平移(1)中的抛物线,使顶点P在直线AC上滑动,且与AC交于另一点Q.(i)若点M在直线AC下方,且为平移前(1)中的抛物线上的点,当以M、P、Q三点为顶点的三角形是等腰直角三角形时,求出所有符合条件的点M的坐标;(ii)取BC的中点N,连接NP,BQ.试探究是否存在最大值?若存在,求出该最大值;若不存在,请说明理由.27.如图,抛物线y=ax2+bx+c(a≠0)的图象过点C(0,1),顶点为Q(2,3),点D在x轴正半轴上,且OD=OC.(1)求直线CD的解析式;(2)求抛物线的解析式;(3)将直线CD绕点C逆时针方向旋转45°所得直线与抛物线相交于另一点E,求证:△CEQ∽△CDO;(4)在(3)的条件下,若点P是线段QE上的动点,点F是线段OD上的动点,问:在P点和F点移动过程中,△PCF的周长是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由.28.已知如图,二次函数y=ax2+2ax﹣3a(a≠0)图象的顶点为H,与x轴交于A、B两点(B在A点右侧),点H、B关于直线l:对称.(1)求A、B两点坐标,并证明点A在直线l上;(2)求二次函数解析式;(3)设点s是三角形ABH上的一动点,从点A沿着AHB方向以每秒1个单位长度移动,运动时间为t秒,到达点B时停止运动.当t为何值时,以点s为圆心的圆与两坐标轴都相切.(4)过点B作直线BK∥AH交直线l于K点,M、N分别为直线AH和直线l上的两个动点,连接HN、NM、MK,求HN+NM+MK和的最小值.1.【解答】解:(1)y=,过点B,C,则点B、C的坐标分别为:(3,0)、(0,),则c=,将点B的坐标代入抛物线表达式并解得:a=﹣,故抛物线的表达式为:y=﹣x2+x+;(2)①当∠PCM=90°时,由点A、B、C的坐标知,△ABC为直角三角形,故AC⊥BC,当△PCM为直角三角形时,点P与点A重合,∴点P(﹣1,0);②当∠CPM=90°时,则点C、P关于函数对称轴对称,此时点P(2,),故点P的坐标为(﹣1,0)或(2,);(3)存在,理由:点P(2,),设图象沿BC方向向左平移3m个单位,则向上平移m个单位,则平移后点B′、P′的坐标分别为:(3﹣3m,m)、(2﹣3m,m+),点E(1,0),分别过点A、E作直线BC的平行线n、m,过点B′作直线m的对称点B″,则EB′=EB″,当B″、E、P′三点共线时,EB'+EP'=EB″+EP′=B″P′最小;点E是AB的中点,则直线m与直线n、直线m与直线AC等距离,则点B″在直线n上,直线BC的倾斜角为30°,则直线B′B″的倾斜角为60°,则设直线B′B″的表达式为:y=x+b,将点B′的坐标代入上式并解得:直线B′B″表达式为:y=x+(4m﹣3)…①,设过点A的直线n的表达式为:y=﹣x+b′,将点A的坐标代入上式并解得:直线n的表达式为:y=﹣(x+1)…②,联立①②并解得:x=2﹣3m,故点B″(2﹣3m,m﹣),而P′(2﹣3m,m+),故EB'+EP'的最小值B″P′=2.2.【解答】解:(1)OA=3OB=3,则点B(﹣1,0),抛物线的表达式为:y=a(x+1)(x﹣3)=a(x2﹣2x﹣3),即﹣3a=3,解得:a=﹣1,故抛物线的表达式为:y=﹣x2+2x+3;(2)过点P作y轴的平行线交CA于点H,由点A、C的坐标得,直线AC的表达式为:y=﹣x+3△ACP的面积=PH×OA=3×(x2﹣2x+3+x﹣3)=(﹣x2+3x),当x=时,△ACP的面积的最大,最大值为:,此时点P(,);(3)过点M作MN⊥AC,则MN=CM,故当B、M、N三点共线时,BM+CM=BN最小,直线CA的倾斜角为45°,BN⊥AC,则∠NBA=45°,即BN=AB=2=AN,则点N(1,2),由点B、N的坐标得,直线BN的表达式为:y=x+1,故点M(0,1).3.【解答】解:(1)y=﹣x2+bx+c经过点C,则c=3,将点A的坐标代入抛物线表达式:y=﹣x2+bx+3并解得:b=2,抛物线的表达式为:y=﹣x2+2x+3;(2)存在,理由:令y=0,则x=﹣1或3,故点B(3,0),将点B、C的坐标代入一次函数表达式并解得:直线BC的表达式为:y=﹣x+3,设点D(x,﹣x2+2x+3),则点P(x,﹣x+3),则PD=(﹣x2+2x+3)﹣(﹣x+3)=﹣x2+3x,当x=时,PD最大值为:;(3)过点B作倾斜角为30°的直线BH,过点C作CH⊥BH交于点H,CH交对称轴于点N,交x轴于点M,则点M、N为所求,直线BH表达式中的k值为,则直线CH的表达式为:y=﹣x+3,当x=1时,y=3﹣,当y=0时,x=,故点N、M的坐标分别为:(1,3﹣)、(,0),CN+MN+MB的最小值=CH=CM+FH=.4.【解答】解:(1)如图1,过点B作BD⊥x轴于点D,∴∠BDO=90°,∵OA绕点O逆时针旋转120°至OB,∴OB=OA=4,∠AOB=120°,B在第二象限,∴∠BOD=60°,∴sin∠BOD=,cos∠BOD=,∴BD=OB=2,OD=OB=2,∴B(﹣2,2),设过点A(4,0),B(﹣2,2),O(0,0)的抛物线解析式为y=ax2+bx+c,∴,解得:,∴抛物线的函数解析式为y=x2﹣x;(2)存在△POB为等腰三角形,∵抛物线与x轴交点为A(4,0),O(0,0),∴对称轴为直线x=2,设点P坐标为(2,p),则OP2=22+p2=4+p2,BP2=(2+2)2+(p﹣2)2=p2﹣4p+28,①若OP=OB=4,则4+p2=42解得:p1=2,p2=﹣2,当p=﹣2时,∠POA=60°,即点P、O、B在同一直线上,∴p≠﹣2,∴P(2,2),②若BP=OB=4,则p2﹣4p+28=42解得:p1=p2=2,∴P(2,2);③若OP=BP,则4+p2=p2﹣4p+28,解得:p=2,∴P(2,2);综上所述,符合条件的点P只有一个,坐标为(2,2);(3)在OA上取点K,使AK=1,连接CK交圆与点M,连接OM、CM,此时,MC+OM=MC+KM=CK为最小值,理由:∵AK=1,MA=2,OA=4,∴AM2=AK•OA,而∠MAO=∠OAM,∴△AKM∽△AMO,∴=,即:MC+OM=MC+KM=CK,CK==5,即:MC+OM的最小值为CK=5.5.【解答】解:(1)二次函数y=﹣x2+x+2,当x=0时,y=2,∴C(0,2),∴OC=2,当y=0时,﹣x2+x+2=0,解得:x1=4,x2=﹣1,∴A(﹣1,0),B(4,0),∴OA=1,OB=4,由勾股定理得:AC==,BC==2;故答案为:,2;(4分)(2)∵B(4,0),C(0,2),∴直线BC的解析式为:y=﹣x+2,如图1,过P作PD∥y轴,交直线BC于D,设P(x,﹣x2+x+2),则D(x,﹣x+2),∴PD=(﹣x2+x+2)﹣(﹣x+2)=﹣x2+2x,有S=PD•OB=×4(﹣+2x)=﹣x2+4x(0<x<4);(6分)(3)不存在,如图2,∵AC2+BC2==25=AB2,∴△ABC为直角三角形,即AC⊥BC,∵PH⊥BC,∴AC∥PH,要使四边形ACPH为平行四边形,只需满足PH=AC=,(10分)∴S=BC•PH=×2×=5,∵而S=﹣x2﹣4x=﹣(x﹣2)2+4≤4,所以不存在四边形ACPH为平行四边形,∵AC∥PH,∴△AKC∽△PHK,∴===S≤;∴的最大值是.(12分)(说明:写出不存在给1分,其他说明过程酌情给分)6.【解答】解:(1)∵D(m,m),OD=m,四边形CODM为菱形,∴OD=OC=2=m,∴m=,∴D();(2)∵y=x+2与抛物线y=x2﹣2mx+m2+m交于A、B两点,∴联立,解得,,∵点A在点B的左侧,∴A(m﹣1,m+1),B(m+2,m+4),∴AB==3,∵直线OC的解析式为y=x,直线AB的解析式为y=x+2,∴AB∥OC,两直线AB、OC之间距离h=2×=,∴S△APB=AB•h=×3×=3;(3)∵A(m﹣1,m+1),B(m+2,m+4),∴AM=1×=,BM=2×=2,由M点坐标(m,m+2),D点坐标(m,m)可知以MC为半径的圆的半径为(m+2)﹣m=2,取MB的中点N,连接QB、QN、QB′,∴MN=BM=,∵,∠QMN=∠BMQ,∴△MNQ∽△MQB,∴,∴,由三角形三边关系,当Q、N、B′三点共线时QB′+QB最小,∵直线AB的解析式为y=x+2,∴直线AB与对称轴夹角为45°,∵点B、B′关于对称轴对称,∴∠BMB′=90°,由勾股定理得,QB′+QB最小值为B'N===.即QB'+QB的最小值是.7.【解答】解:(1)∵对称轴x=﹣1的抛物线y=ax2+bx+c与x轴交于A(2,0),B两点,∴B(﹣4,0).设抛物线解析式是:y=a(x+4)(x﹣2)(a≠0).把C(0,﹣2)代入,得a(0+4)(0﹣2)=﹣2.解得a=.故该抛物线解析式是:y=(x+4)(x﹣2)或y=x2+x﹣2;(2)设直线BC的解析式为y=mx+n,把B(﹣4,0),C(0,﹣2)代入得,解得,∴直线BC的解析式为y=﹣x﹣2;作PQ∥y轴交BC于Q,如图,设P(t,t2+t﹣2),则Q(t,﹣t﹣2),则PQ=﹣t﹣2﹣(t2+t﹣2)=﹣t2﹣t,S△PBC=S△PBQ+S△PCQ=•PQ•4=﹣t2﹣2t=﹣(t+2)2+2,当t=﹣2时,△PBC面积有最大值,最大值为2,此时P点坐标为(﹣2,﹣2);(3)设D(m,0),∵DP∥y轴,∴E(m,﹣m﹣2),P(m,m2+m﹣2),∵PE=OD,∴|﹣m|=4|﹣m﹣2﹣m2﹣m+2|,∴m2+3m=0或m2+5m=0,∴m=﹣3,m=0(舍去)或m=﹣5,m=0(舍去)∴P(﹣3,﹣)或P(﹣5,);(4)∵点A、B关于对称轴对称,∴点M为BC与对称轴的交点时,MA+MC的值最小,此时△AMC的周长最小.∵直线BC的解析式为y=﹣x﹣2.抛物线的对称轴为直线x=﹣1.∴当x=﹣1时,y=﹣.∴抛物线对称轴上存在点M(﹣1,﹣)符合题意,此时△AMC周长的最小值为AC+BC=2+2.8.【解答】解:(1)将点M、N的坐标代入抛物线表达式得:,解得:,故抛物线的表达式为:y=x2﹣x﹣4;(2)①y=x2﹣x﹣4,令y=0,则x=﹣2或8,x=0,则y=﹣4,故点A、B、C的坐标分别为:(﹣2,0)、(8,0)、(0,﹣4),则函数的对称轴为:x=3,则AB=10,BC=,AC=,则AB2=BC2+AC2,故△ABC为直角三角形;②作点M关于函数对称轴的对称点D(10,6),连接CD交函数对称轴于点P,则点P为所求,将点CD的坐标代入一次函数表达式:y=kx+b并解得:直线CD的表达式为:y=x﹣4,当x=3时,y=﹣1,故点P(3,﹣1),此时PM+PC的值最小为CD=10.9.【解答】解:(1)由题可列方程组:,解得:∴抛物线解析式为:y=x2﹣x﹣2;(2)如图1,∠AOC=90°,AC=,AB=4,设直线AC的解析式为:y=kx+b,则,解得:,∴直线AC的解析式为:y=﹣2x﹣2;当△AOC∽△AEB时=()2=()2=,∵S△AOC=1,∴S△AEB=,∴AB×|y E|=,AB=4,则y E=﹣,则点E(﹣,﹣);由△AOC∽△AEB得:∴;(3)如图2,连接BF,过点F作FG⊥AC于G,则FG=CFsin∠FCG=CF,∴CF+BF=GF+BF≥BE,当折线段BFG与BE重合时,取得最小值,由(2)可知∠ABE=∠ACO∴BE=ABcos∠ABE=ABcos∠ACO=4×=,|y|=OBtan∠ABE=OBtan∠ACO=3×=,∴当y=﹣时,即点F(0,﹣),CF+BF有最小值为;(4)①当点Q为直角顶点时(如图3):由(3)易得F(0,﹣),∵C(0,﹣2)∴H(0,2)设Q(1,m),过点Q作QM⊥y轴于点M.则Rt△QHM∽Rt△FQM∴QM2=HM•FM,∴12=(2﹣m)(m+),解得:m=,则点Q(1,)或(1,)当点H为直角顶点时:点H(0,2),则点Q(1,2);当点F为直角顶点时:同理可得:点Q(1,﹣);综上,点Q的坐标为:(1,)或(1,)或Q(1,2)或Q(1,﹣).10.【解答】解:(1)∵抛物线y=﹣x2+bx+c经过点A、B、C,把A(﹣1,0),C(0,3)代入解析式得,∴,解得b=2,c=3.故该抛物线解析式为:y=﹣x2+2x+3.(2)令﹣x2+2x+3=0,解得x1=﹣1,x2=3,即B(3,0),设直线BC的解析式为y=kx+b′,则,解得:,故直线BC的解析式为y=﹣x+3;∴设P(t,3﹣t),∴D(t,﹣t2+2t+3),∴PD=(﹣t2+2t+3)﹣(3﹣t)=﹣t2+3t,∵OB=OC=3,∴△BOC是等腰直角三角形,∴∠OCB=45°,当CD=PC时,则∠CPD=∠CDP,∵PD∥y轴,∴∠CPD=∠OCB=45°,∴∠CDP=45°,∴∠PCD=90°,∴直线CD的解析式为y=x+3,解得或,∴D(1,4),此时P(1,2);当CD=PD时,则∠DCP=∠CPD=45°,∴∠CDP=90°,∴CD∥x轴,∴D点的纵坐标为3,代入y=﹣x2+2x+3得,3=﹣x2+2x+3,解得x=0或x=2,此时P(2,1);当PC=PD时,∵PC=t,∴t=﹣t2+3t,解得t=0或t=3﹣,此时P(3﹣,);综上,当△CDP为等腰三角形时,点P的坐标为(1,2)或(2,1)或(3﹣,).(3)CN+MN+MB的最小值为,N坐标为(1,3﹣),M坐标为(,0).理由如下:如图,取G点坐标为(0,﹣),连接BG,∵B(3,0),∴直线BG解析式为:y=,∴tan∠GBO=,∴∠GBO=30°,过M点作MB′⊥BG,∴,∴CN+MN+MB=CN+MN+B′M,∴CN+MN+MB取最小值时,C、M、N、B′在同一条直线上,即CB′⊥BG,设直线CB′解析式为,∵C(0,3)故直线CB′解析式为为,∵抛物线的顶点为E坐标为(1,4),EF⊥x轴,N在EF、CB′上,∴N坐标为(1,3﹣),M(m,0)是x轴一个动点,也是CB′与x轴交点,∴M(,0).∵CG=3+,∠CGB=60°,∴CB′=CGsin∠CGB=(3+)×=,综上所述:CN+MN+MB的最小值为,N坐标为(1,3﹣),M坐标为(,0).11.【解答】解:(1)将A(﹣3,0),B(9,0)代入y=ax2+bx+3,得:,解得:,∴抛物线的表达式为y=﹣x2+x+3…①;(2)由题意得:∠ACO=∠OBC=30°,∠ACB=90°,将点B、C(0,3)的坐标代入一次函数表达式并解得:直线BC的表达式为:y=﹣x+3…②;①点P的坐标为(﹣3+t,t),点Q(9﹣2t,0),将点Q的坐标代入①式并整理得:点D[9﹣2t,(6t﹣t2)];②当PQ=PD时,则DQ中点的纵坐标=点P的纵坐标,即:[(6t﹣t2)]=t,解得:t=;(3)点P的坐标为(﹣3+t,t)、点D[9﹣2t,(6t﹣t2)],点E是PQ的中点,则点E[3﹣t,t+(6t﹣t2)],将点E的坐标代入②式并整理得:t2﹣6t+9=0,解得:t=3,即点P(﹣,)即点P是AC的中点,作点P关于直线BC的对称点P′,过点P′作P′H⊥x轴、BC于点H、M,过点P作PN⊥y轴于点N,则MH=MB,则此时,PM+BM=PM+MH=P′H为最小值,∵∠ACB=90°,PC=P′C,∠P′CM=∠NCP,∠P′MC=∠PNC=90°,∴△P′MC≌△PNC(AAS),∴MC=NC=OC,OM=OC==P′H,故PM+BM的最小值为.12.【解答】解:(1)函数的表达式为:y=a(x﹣1)(x﹣3)=a(x2﹣4x+3),即:3a=3,解得:a=1,故抛物线的表达式为:y=x2﹣4x+3,则顶点D(2,﹣1);(2)∵OB=OC=3,∴∠OBC=∠OCB=45°,AM=MB=ABsin45°==AD=BD,则四边形ADBM为菱形,而∠AMB=90°,∴四边形ADBM为正方形;(3)将点B、C的坐标代入一次函数表达式:y=mx+n并解得:直线BC的表达式为:y=﹣x+3,过点P作y轴的平行线交BC于点H,设点P(x,x2﹣4x+3),则点H(x,﹣x+3),则S△PBC=PH×OB=(﹣x+3﹣x2+4x﹣3)=(﹣x2+3x),∵﹣<0,故S△PBC有最大值,此时x=,故点P(,﹣);(4)存在,理由:如上图,过点C作与y轴夹角为30°的直线CH,作QH⊥CH,垂足为H,则HQ=CQ,AQ+QC最小值=AQ+HQ=AH,直线HC所在表达式中的k值为,直线HC的表达式为:y=x+3…①则直线AH所在表达式中的k值为﹣,则直线AH的表达式为:y=﹣x+s,将点A的坐标代入上式并解得:则直线AH的表达式为:y=﹣x+…②,联立①②并解得:x=,故点H(,),而点A(1,0),则AH=,即:AQ+QC的最小值为.13.【解答】解:(1)连接AB,过点O作OP⊥AB交AB于点G,过点P作PH⊥x轴于点H,∵点O关于AB的对称点P,∴OG=PG,tan∠BAO==,则∠BAO=60°,则∠GOA=∠GPA=30°,∠GAO=∠GAP=∠PAH=60°,则GA=OA=1,∵∠GAP=∠PAH,∴AH=AG=1,则PH=AHtan60°=,故点P(3,);(2)将点A,B,P的坐标代入二次函数表达式得:,解得:,故抛物线的表达式为:y=x2﹣x+2;(3)连接PB,由题意得:AB=4,AP=AO=2,BP=BO==2,则△ABP为直角三角形,△ABO、△ABP是两个全等的,均有一个角为30°的直角三角形,即AB=OB=2,AB=4,AP=OA=2,∠PBA=∠BAO=30°,∠BAO=∠BAP=60°,当∠BMA=∠BMC=∠AMC=120°时,MA+MB+MP的值最小(证明见备注),以BP边向上作等边三角形APA′,以AP边为基础向右作等边三角形APB′,连接AA′、BB′交于点M,则点M为所求点,BP=2,则∠A′BO=∠OBA+∠PBA+∠PBA′=30°+30°+60°=120°,则直线A′B的长度为2,倾斜角为30°,则x A′=A′Bcos30°=3,同理y A′=3,故点A′(3,3),由点AA′的坐标可得,直线AA′的表达式为:y=3(x﹣2)…①;同理可得:直线BB′的表达式为:y=x+2…②,联立①②并解得:x=,故点M(,),故答案为:(,).备注:已知三角形ABC,在其内部找一点P,使得PA+PB+PC为最小.如图,将三角形ABP逆时针旋转60度至三角形A'BP',连接PP',CA'.根据旋转变换,三角形P'BP为等边三角形,所以有PA+PB+PC=P'A'+PP'+PC.利用两点之间线段最短,当点P,P'在直线CA'上时,所求为最短,于是,转化为下图:则∠BPC=180°﹣∠BPP′=180°﹣60°=120°,∠BPA=∠BP′A′=180°﹣∠BP′P=120°,故∠APC=120°,故满足P的点,必须使∠APB=∠BPC=∠APB=120°.14.【解答】解:(1)将点A、B的坐标代入二次函数表达式得:,解得:,故二次函数表达式为:y=x2﹣4x,故:答案为:1,4,45°;(2)设直线BP交y轴于点H,∵∠HOB=∠AOB=45°,∠PBO=∠OBA,BO=BO,∴△HOB≌△AOB(AAS),∴OA=OH=4,即点H(0,4),则直线PB的表达式为:y=kx+4,将点B坐标代入上式并解得:直线PB的表达式为:y=x+4,将上式与二次函数表达式联立并解得:x=5或﹣(舍去正值),则点P(﹣,);(3)①由题意得:直线OB的表达式为:y=x,设点C(m,m),CD=2,直线OB的倾斜角为45度,则点D(m+2,m+2),则点F(m,m2﹣4m),点E[(m+2),(m+2)2﹣4(m+2)],则CF+DE=m﹣m2+4m+(m+2)﹣[(m+2)2﹣4(m+2)]=﹣2m2+6m+6,∵﹣2<0,故CF+DE有最大值,此时,m=,则点C、F、D、E的坐标分别为(,)、(,﹣)、(,)、(,﹣),则CF=DE=,CF∥ED,故四边形CDEF为平行四边形;②如图所示,过点A作CD的平行线,过点D作AC的平行线,交于点G,则四边形ACDG是平行四边形,。
抛物线的最值问题

O
.
F
x
y0 2 3 y0 46 y0 48y0 16 46 , ( y0 R ) d 16 80 5 此时P(9,24) 当y0 24时, d min 2
探究五:距离和的最小值。
例 在抛物线 y2=8x 上求一点P,使P到焦点F 的距离与到 Q(4 ,1)的距离的和 最小,并求最小值。 解:
解:直线与抛物线无交点,设抛物线上一点P( x0 . y0 )
例:在抛物线y2=64x上求一点,使它到直线L:4x+3y+46=0的距离最短,并求此距 离。 y
则y0 2 64x0 4 x0 3 y0 46 4 x0 3 y0 46 d | | 5 16 9
y0 2 将x0 代入得: 64 2
p4 2p 8, 由 y2 8x 知:
y
此抛物线的焦点坐标是:F (2 , 0)
准线l方程是:x 2 .
由定义知: PF dPl 即 | PF || PK | .
| PF | | PQ | | PK | | PQ |
K
P Q O 2 F 4
x
显然,当Q, P, K 三点共线时,
• 例:在抛物线y2 =64x上求一点,使它到 直线L:4x+3y+46=0的距离最短,并求 此距离。
例在抛物线y2=64x上求一点,使它到直线L: 4x+3y+46=0的距离最短,并求此距离。
y 解:设抛物线平行于L的切线方程为
4x 3 y m 0 x 联立 4 x 3 y m 0 2 P y 64x 2 消 x 得 y 48y 16m 0 L 48 48 4 16 m 0 m 36 y 24, x 9 46 36 2 P9,24 d min 有最小值.
关于抛物线的十个最值问题

关于抛物线的十个最值问题 本文用初等方法讨论了与抛物线有关的若干几何最值问题 ,得到了十 个有趣的结论为方便读者摘用,现用定理形式叙述如下定理 1 抛物线的所 有焦半径中,以过顶点的焦半径为最短证明不妨设抛物线的极坐标方程为 ρ=,则显然有 ρ≥,其中等号成立当且仅当 θ=2π+π∈即焦半径通过抛物线的 顶点时证毕定理 2 抛物线的过焦点的所有弦中,以抛物线的通径为最短证 明 设 抛 物 线 极 坐 标 方 程 为 ρ=, 焦 点 弦 为 , 且 设 ρ1,θ,ρ2,θ+π, 则 有 ││=ρ1+ρ2=+=≥2=通径长,其中等号成立当且仅当 θ=π+π2∈即弦为通径时证 毕定理 3 设,0 是抛物线 2=2>0 的对称轴上的定点,,是抛物线上的动点,则 ││= 证明由 ││2=-2+2=-2+2=2-2-+2=[--]2+2-, 并且注意到∈[0,+∞, 立知结论成 立证毕定理 4 设,是抛物线 2=2>0 内一定点,是焦点,是抛物线上的动点,则 ││+││=+2,证明如图 1 所示,作⊥准线=-2 于,则知││+││=││=--2=+2 证毕图 1 定理 5 设线段是抛物线 2=2>0 的过焦点的弦,分别以、为切点的抛物线的 两条切线相交于点,则三角形的面积的最小值为 2 证明设 1,1,2,2,则由、、 三点共线可得 12-21=2· 2-1……………1 于是利用 1 式由两切线方程 1=+1,2=+2, 易得的坐标,适合& ;∵· =-1,∴⊥,即││是△ 的边上的高图 2∵││≥││焦点到准线=-2 的距离=, 又由定理 2 知││≥2 通径长,∴△=12·││·││≥12·2·=2,因其中等号当且仅当⊥ 轴时成立,故三角形的最小值为 2 证毕定理 6 过抛物线 2=2 的顶点引两条互相垂直的动弦和,则三角形的面积的最小值为 42 证明设 1,1,2,2,则由⊥得 12+12=0……………………………………1 将 12=21,22=22 代入 1 立得 12=42…………2 于是△ 2=14·││2·││2& ;1-32+1-32=3-22+3-22…………2 图 4 将 1=122,2=222,3=322 及 1 代入 2 可 得 3=…………………………3 从 而 据 于 1 是 、 △ 3 的 可 面 得 积1-3=………………………………………………………4=12·││2=12·[1-32+1-32]=· · 1-32=22··2=22··≥22··=42 因当=1 且 3=0 时上式等号 成立,故等腰△ 面积的最小值为 42 证毕定理 8 设是抛物线的焦点弦,准线与 抛物线对称轴的交点为,则∠的最大值为 π2 证明如图 5 所示,设 1、1 分别 是、在准线上的射影,是焦点,连 1 和 1,则知 1 当⊥时,显然有∠=π2;2 当与 不垂直时,由│1│>│1│知 1∠1>∠1=π2-∠1,图 5∴∠1>π4;同理∠1>π4, 故有∠<π2 综合 1、 2,定理 8 获证定理 9 设是抛物线=2>0 的长为定长的 动弦,则Ⅰ当≥1 通径长时,的中点到轴的距离的最小值为 2-14;Ⅱ当<1 通径 长时,的中点到轴的距离的最小值为 24 证明设 0,0,将直线的参数方程其中 为参数,倾斜角 α≠π2 代入=2 并整理得 α2·2+20α-α·+02-0=0,故由韦达定理 和参数的几何意义以及││=立得 0& ;1+2=-20α-αα2=0………①图 612=02-0α2=-22……………②由①解 出 0 并代入②整理。
抛物线中的最值问题

抛物线中的最值问题作者:王荣李家洪来源:《高中生学习·高二理综版》2015年第03期圆锥曲线的最值是一类综合性强、涉及知识广的问题.破解这类问题常利用函数与方程、数形结合、转化与化归等数学思想与方法,将它转化为解不等式、求函数的值域或利用平面几何知识来解决.本文对抛物线中常见的几类最值分类探究.点与点、点与线之距离的最值问题例1 在抛物线[y2=2pxp>0]上求一点,使它到直线[l]:[Ax+By+C=0](其中[A≠0,pB2法1 由已知,直线[l]与抛物线相离,设直线[l1]:[Ax+By+m=0]与抛物线相切,联立[Ax+By+m=0,y2=2px]消去[x]得,[A2py2+By+m=0].由[Δ=B2-4∙A2p∙m=0]得,[m=pB22A].故直线[l1]的方程为:[Ax+By+pB22A=0].由两平行线间的距离公式得,[dmin=pB22A-CA2+B2=pB2-2AC2AA2+B2=2AC-pB22AA2+B2].进而得所求抛物线上的点为[pB22A2,-pBA].法2 由已知,直线[l]与抛物线相离,设抛物线上一点[Px0,y0],则[y02=2px0].点[P]到直线[l]的距离[d=Ax0+By0+CA2+B2=A∙y022p+By0+CA2+B2=A2p∙y0+pBA2+p2AC-pB2A2A2+B2.]又[pB2注意到[y0∈R],因此,当[y0=-pBA]时,[dmin=2AC-pB22AA2+B2],可得所求点的坐标为[pB22A2,-pBA].法3 由已知,直线[l]与抛物线相离,设抛物线上一点[Px0,y0]到直线[l]的距离最短.在抛物线[y2=2px]中,两边同时对[x]求导得[2y∙y=2p],即[y=py].故[y|y=y0=py0].由[py0=-AB]得,[y0=-pBA],即所求点[P]的坐标为[pB22A2,-pBA].根据点到直线的距离公式得[dmin=2AC-pB22AA2+B2].线段之和(或积)的最值问题例2 过抛物线[y2=2pxp>0]的焦点[F]作两条互相垂直的弦[AB],[CD],求[AB+CD]与[AB∙CD]的最小值.法1 由题意知,直线[AB],[CD]均不垂直于坐标轴.设直线[AB]的方程为[y=kx-p2],则直线[CD]的方程为[y=-1kx-p2].联立[y=kx-p2,y2=2px]消去[x]得,[ky2-2py-kp2=0].则[Δ=4p2k2+1>0]恒成立.记[Ax1,y1],[Bx2,y2],得[y1+y2=2pk],[y1y2=-p2].故[AB=1+1k2y1+y22-4y1y2=2p1+1k2],同理[CD=2p1+k2].[∴AB+CD=2p1+1k2+2p1+k2=2p2+k2+1k2,][AB∙CD=4p21+1k21+k2=4p22+k2+1k2],当[k2=1]即[k=±1]时,[AB+CDmin=8p],[AB∙CDmin=16p2].法2 由题意知,直线[AB],[CD]均不垂直于坐标轴.设[Ax1,y1],[Bx2,y2],直线[AB]的斜率为[k],则[y1-y2x1-x2=k].又[y12=2px1],[y22=2px2],两式相减得[y12-y22=2px1-x2],即[y1+y2=2p∙x1-x2y1-y2],故[y1+y2=2pk.]又直线[AB]的方程为[y=kx-p2],所以[y1+y2=kx1+x2-p],即[x1+x2=2pk2+p].由抛物线的定义得,[AB=AF+BF=x1+p2+x2+p2][=x1+x2+p][=2pk2+2p,]同理[CD=2p1+k2].以下略.点拨一般地,设[Ma,b]是不在抛物线的[y2=2pxp>0]上的定点,过点[M]作抛物线的两条互相垂直的弦[AB],[CD],求[AB+CD]与[AB∙CD]的最小值. (留与同学们解答)三角形、四边形等多边形之面积的最值问题例3 过抛物线[y2=2pxp>0]的顶点[O]引两条互相垂直的动弦[OA]和[OB],求三角形[AOB]的面积的最小值.法1 直线[OA]和[OB]的斜率均存在且不为零.设直线[OA]的方程为[y=kx],则直线[OB]的方程为[y=-1kx].联立[y=kx,y2=2px]得[A2pk2,2pk],同理得[B2pk2,-2pk].所以[SΔAOB=12OA∙OB][=124p2k4+4p2k2∙4p2k4+4p2k2=2p22+k2+1k2],当[k2=1]即[k=±1]时,[SΔAOBmin=4p2].法2 设[Ax1,y1],[Bx2,y2],由[OA⊥OB]得,[x1x2+y1y2][=0].又[y12=2px1],[y22=2px2],于是得[x1x2=4p2].[SΔAOB2=14OA2∙OB2=14x12+y12x22+y22=14x12+2px1x22+2px2][=14x1x22+2px1x2x1+x2+4p2x1x2][≥14x1x22+2px1x22x1x2+4p2x1x2][=144p22+2p∙4p224p2+4p2∙4p2=16p4].从而[SΔAOB≥4p2]. 当且仅当[x1=x2=2p]时取等号.因此[SΔAOBmin=4p2].点拨一般地,设[Pa,b]是抛物线上的一定点,过点[P]作抛物线[y2=2pxp>0]的两条互相垂直的动弦[PA]和[PB],求三角形[APB]的面积的最小值. (留与同学们解答)弦长为定值之动弦中点到准线距离的最值问题例4 定长为[l]([l>0])的线段[AB]的两端点在抛物线[y2=2pxp>0]上移动,求线段[AB]的中点[M]到[y]的最短距离.法1 由题意知,直线[AB]的斜率一定不为零.故可设直线[AB]的方程为[x=ty+m].联立[x=ty+m,y2=2px]消去[x]得,[y2-2pty-2pm=0].则[Δ=4ppt2+2m>0].记[Ax1,y1],[Bx2,y2],[∴y1+y2=2pt],[y1y2=-2pm].从而[x1+x2=ty1+y2+2m=2pt2+2m].[AB=1+t2y1+y22-4y1y2=4p1+t2pt2+2m,]又[AB=l].[∴4p1+t2pt2+2m=l2],即[m=l28p1+t2-12pt2].线段[AB]的中点[M]到[y]的距离[d=xM=x1+x22=pt2+m=l28p1+t2+12pt2].即[d=p2l2p2t2+1+t2].设[μ=t2+1],由[t∈R]知,[μ≥1].[∴d=p2l2p2μ+μ-1].若[l2p≥1]即[l≥2p]时,[dmin=l-p2].此时[t2=l2p-1].若[0综上可得[dmin=l-p2,l≥2p,l28p, 0法2 设线段[AB]的中点[Mx0,y0].直线[AB]的参数方程为[x=x0+tcosα,y=y0+tsinα](其中[t]为参数,直线的倾斜角[α∈0,π]).代入[y2=2px]整理得,[sin2αt2+][2y0sinα-pcosαt][+y02-2px0=0].记点[A],[B]对应的参数分别为[t1],[t2].由韦达定理与参数的几何意义知,[t1+t2=-2y0sinα-pcosαsin2α],[t1t2=y02-2px0sin2α].因为[M]是线段[AB]的中点,及[AB=l],所以[t1+t2=0],[t1t2=-l22].[∴y0=pcosαsinα,]且[y02-2px0=-14l2sin2α].线段[AB]的中点[M]到[y]的距离[d=x0=l28psin2α+y022p=l28psin2α+p2cos2αsin2α][=l28psin2α+p21sin2α-p2].令[μ=sin2α],由[α∈0,π]知,[0从而[d=l28pμ+2pl2μ-p2] .若[2pl≤1]即[l≥2p]时,[dmin=l-p2],此时[sin2α=2pl].若[2pl>1]即[0除上述几类最值问题,还有很多类型.解题中要灵活运用抛物线的定义、平面几何知识化为熟悉的类型运用常规方法求解.。
关于抛物线的十个最值问题

竭诚为您提供优质的服务,优质的文档,谢谢阅读/双击去除关于抛物线的十个最值问题本文用初等方法讨论了与抛物线有关的若干几何最值问题,得到了十个有趣的结论.为方便读者摘用,现用定理形式叙述如下:定理1.抛物线的所有焦半径中,以过顶点的焦半径为最短.证明:不妨设抛物线的极坐标方程为ρ= ,则显然有ρ≥ ,其中等号成立当且仅当θ=2kπ+π(k∈Z)即焦半径通过抛物线的顶点时.证毕.定理2.抛物线的过焦点的所有弦中,以抛物线的通径为最短.证明:设抛物线极坐标方程为ρ= ,焦点弦为Ab,且设A(ρ1,θ),b(ρ2,θ+π),则有│Ab│=ρ1+ρ2= + = ≥2p=通径长,其中等号成立当且仅当θ=kπ+π/2(k∈Z)即弦Ab为通径时.证毕.定理3.设A(a,0)是抛物线y2=2px(p>0)的对称轴上的定点,m(x,y)是抛物线上的动点,则│mA│min=证明:由│mA│2=(x-a)2+y2=(x-a)2+2px=x2-2(a-p)x+a2 =[x-(a-p)]2+p(2a-p),并且注意到x∈[0,+∞),立知结论成立.证毕.定理4.设A(a,b)是抛物线y2=2px(p>0)内一定点,F是焦点,m是抛物线上的动点,则(│mA│+│mF│)min=a+p/2.Q m A(a,b)证明:如图1所示,作AQ⊥准线L:x=-p/2于Q,则知o F x(│mA│+│mF│)min=│AQ│=a-(-p/2)=a+p/2.证毕. 图1定理5.设线段Ab是抛物线y2=2px(p>0)的过焦点的弦,分别以A、b 为切点的抛物线的两条切线相交于点m,则三角形Abm的面积的最小值为p2.证明:设A(x1,y1),b(x2,y2),则由A、F、b三点共线可得:x1y2-x2y1=p/2.(y2-y1) (1)于是利用(1)式由两切线方程yAm:y1y=p(x+x1),Abm:y2y=p(x+x2),m F x易得m的坐标(x,y)适合: b∵kmF·kAF=-1,∴mF⊥Ab,即│mF│是△mAb的Ab边上的高. 图2∵│mF│≥│FK│(焦点F到准线x=-p/2的距离)=p,又由定理2知│Ab│≥2p(通径长),∴s△mAb=1/2·│Ab│·│mF│≥1/2·2p·p=p2,因其中等号当且仅当Ab⊥x轴时成立,故三角形mAb的最小值为p2.证毕.定理6.过抛物线y2=2px的顶点o引两条互相垂直的动弦oA和ob,则三角形oAb的面积的最小值为4p2. y证明:设A(x1,y1),b(x2,y2),则由oA⊥ob得Ax1x2+y1y2=0 (1)o x将y12=2px1,y22=2px2代入(1)立得:x1x2=4p2 (2)于是b(s△oAb)2=1/4·│oA│2·│ob│2图3=1/4·(x12+y12)·(x22+y22)=1/4·(x12+2px1)·(x22+2px2)=1/4·[(x1x2)2+2px1x2(x1+x2)+4p2x1x2]≥1/4.[(x1x2)2+2px1x2(2√x1x2)+4p2x1x2] (3)将(2)式代入(3)则得(s△oAb)2≥16p4,从而s△oAb≥4p2,因其中等号当x1=x2=2p时取到,故三角形oAb的面积的最小值为4p2。
高考数学解题方法微专题(28)抛物线中的最值问题(含解析)

微专题(二十八) 抛物线中的最值问题求解与抛物线有关的最值问题方法较多,一般需要通过数形结合或利用函数思想来求最值,下面就抛物线最值问题的求法作一归纳.1.定义转换法[例1] 已知点P 是抛物线y 2=2x 上的动点,B (-1,1),点P 到直线l :x =-12的距离为d ,求d +|PB |的最小值.解析:由题意得抛物线y 2=2x 的焦点F ⎝ ⎛⎭⎪⎫12,0,直线l 是抛物线的准线,如图,连接BF ,PF ,所以d =|PF |,则d +|PB |=|PF |+|PB |≥|BF |=⎝ ⎛⎭⎪⎫-1-122+(1-0)2=132,当且仅当B ,P ,F 三点共线时取等号,所以d +|PB |的最小值为132. 名师点评 与抛物线上的点到准线距离有关的最值问题,一般都是利用抛物线的定义,将到准线的距离转化为到焦点的距离,然后通过数形结合直接判断出取得最值时所要满足的条件,这样就能避免烦琐的代数运算.[例2] 抛物线y =-x 2上的点到直线4x +3y -8=0距离的最小值是________.解析:解法一 如图,设与直线4x +3y -8=0平行且与抛物线y =-x 2相切的直线为4x+3y +b =0,切线方程与抛物线方程联立得⎩⎪⎨⎪⎧y =-x 2,4x +3y +b =0,消去y 整理得3x 2-4x -b =0,则Δ=16+12b =0,解得b =-43,所以切线方程为4x +3y -43=0,抛物线y =-x 2上的点到直线4x +3y -8=0距离的最小值是这两条平行线间的距离d =|8-43|5=43.解法二 由y =-x 2,得y ′=-2x .如图,设与直线4x +3y -8=0平行且与抛物线y =-x 2相切的直线与抛物线的切点是T (m ,-m 2),则切线斜率k =y ′|x =m =-2m =-43,所以m =23,即切点T ⎝ ⎛⎭⎪⎫23,-49,点T 到直线4x +3y -8=0的距离d =⎪⎪⎪⎪⎪⎪83-43-816+9=43,由图知抛物线y =-x 2上的点到直线4x +3y -8=0距离的最小值是43.答案:43名师点评 若抛物线上的点P 到直线l 的距离最小,则过点P 与l 平行的直线与抛物线相切,且最小距离为两平行直线间的距离,所以可将问题转化为求与抛物线相切的直线,然后求两平行直线间的距离.3.函数法针对上面的例2,我们给出第三种解决方法:解法三 设P (x ,-x 2),则点P 到直线4x +3y -8=0的距离d =|4x -3x 2-8|16+9=15⎪⎪⎪⎪⎪⎪3⎝ ⎛⎭⎪⎫x -232+203=35⎝ ⎛⎭⎪⎫x -232+43,在抛物线y =-x 2中,x ∈R ,所以当x =23时,d 取得最小值43,即抛物线y =-x 2上的点到直线4x +3y -8=0距离的最小值是43.[例3] 若点P 在抛物线y 2=x 上,点Q 在圆(x -3)2+y 2=1上,则|PQ |的最小值为________.解析:由题意得抛物线与圆不相交,且圆的圆心为A (3,0),则|PQ |≥|PA |-|AQ |=|PA |-1,当且仅当P ,Q ,A 三点共线时取等号,所以当|PA |取得最小值时,|PQ |最小.设P (x 0,y 0),则y 20=x 0,|PA |=(x 0-3)2+y 20=x 20-6x 0+9+x 0=⎝⎛⎭⎪⎫x 0-522+114,当且仅当x 0=52时,|PA |取得最小值112,此时|PQ |取得最小值112-1. 答案:112-1 名师点评 解与抛物线有关的最值问题可通过两点间距离公式或者点到直线的距离公式建立目标函数,再用求函数最值的方法求解.解题的关键是根据所给抛物线方程设出动点坐标.。
抛物线中的若干最值问题

抛物线中的若干最值问题
1.抛物线的最高点在哪里?
抛物线的最高点,即顶点,是x坐标为-b/2a的点,y坐标为f(-
b/2a)。
2.抛物线与x轴交点有几个?
抛物线与x轴交点有0个、1个或2个,具体取决于抛物线的开口方向和方程的根。
3.抛物线的对称轴方程是多少?
抛物线的对称轴方程是x=-b/2a,具有以下特点:
-对称轴垂直于x轴;
-顶点位于对称轴上。
4.抛物线的最小值在哪里?
当抛物线开口向上时,抛物线没有最小值,最小值为负无穷;当抛物线开口向下时,最小值为f(-b/2a)。
5.抛物线有没有最大值?
当抛物线开口向上时,最大值为f(-b/2a);当抛物线开口向下时,抛物线没有最大值,最大值为正无穷。
6.抛物线经过定点的条件是什么?
设定点为(x0,y0),则抛物线经过该点的条件是方程f(x0)=y0成立。
7.抛物线对于x轴的对称点是哪个?
抛物线上任意一点与x轴对称的点的纵坐标为该点纵坐标的相反数,横坐标不变。
8.抛物线的拐点在哪里?
当抛物线开口向上并且a>0时,抛物线不存在拐点;当抛物线开口向下并且a<0时,拐点的横坐标为-b/2a,纵坐标为f(-b/2a)-|a|/4。
9.抛物线的单调区间是什么?。
与抛物线有关的最值问题

与抛物线有关的最值问题一、定义法求最值例1:设P 是抛物线24y x =上的一个动点,F 是焦点.(1)求点P 到点(11)A -,的距离与点P 到直线1x =-的距离之和的最小值;(2)若B 点的坐标为(3,2),求|PB|+|PF|的最小值.分析:第(1)个问题可以转化为在曲线上求一点P ,使点P 到点(11)A -,的距离与点P 到(10)F ,的距离之和最小.第(2)个问题可以联想到平面上到两定点距离之和最短的点在两定点连线线段上的这一几何性质来解决.解:(1)如图1,易知抛物线的焦点为(10)F ,,准线是1x =-.由抛物线的定义知:点P 到直线1x =-的距离等于点P 到焦点F 的距离.于是,问题转化为:在曲线上求一点P ,使点P 到点(11)A -,的距离与点P 到(10)F ,的距离之和最小.显然,连结AF 交抛物线于P 点.故最小值为221+,即为5;(2)如图2,自B 作BQ 垂直准线于Q 交抛物线于1P ,此时,11PQ PF =,那么114PB PF PB PQ BQ ++==≥,即最小值为4. 点评:此题利用抛物线的定义,使抛物线上的点到准线的距离与点到焦点的距离相互转化.练习:若点A 的坐标为()2,3,F 为抛物线x y 22=的焦点,点P 在该抛物线上移动,为使得PF PA +取得最小值,求P 点坐标.解:由抛物线的定义,PF 等于P 到抛物线到准线的距离P P ',当且仅当在同一直线上时,有PF PA +=P P 'PA +最小,此时点P 的纵坐标等于A 点纵坐标,即2=y ,此时P 点坐标为()2,2. 二、函数法求最值例2:在抛物线24x y =上求一点,使它到直线y=4x-5的距离最短.分析:本题可以结合求一元二次函数的最值问题来解决,其最值总是在顶点或边界点达到,但要特别注意有的问题的顶点并不一定在给定的区间内。
如最值不在顶点,就要考虑边界点的函数值.解:设抛物线上的点)4,(2t t P ,点P到直线4x-y-5=0的距离174)21(41754422+-=+-=t t t d 当21=t 时,174min =d ,故所求点为)1,21(.点评:求最值问题也往往涉及到一元二次函数问题,这种问题在圆锥曲线的最值问题中也常常见到)1,21(.练习:已知一曲线x y 22=,(1)设点A 的坐标为)0,32(,求曲线上距点A 最近的点P 的坐标及相应的距离 |PA|;(2)设点A 的坐标为(a,0)a ∈R ,求曲线上点到点A 距离最小值d ,并写出d=f (a )的函数表达式.解:(1)设M (x,y )是曲线上任意一点,则x y 22= )0(≥x ,31)31(2)32()32(22222++=+-=+-=x x x y x MA ∵ x ≥0,94min 2=MA ∴ 所求P点的坐标是(0,0),相应的距离是32=AP .(2)设M (x,y )是曲线上任意一点,同理有x a x y a x MA 2)()(2222+-=+-=)12()]1([2-+--=a a x 0≥x ,综上所述,有⎪⎩⎪⎨⎧-=aa d 12)1a ()1a (时当时当<≥.三、判别式法求最值问题例3:抛物线y 2=2x 上点到直线x-y+3=0的最短距离是__________. 分析:将直线平移到与抛物线相切,联立直线与抛物线方程,消去y或x 得一个一元二次方程,利用△=0求出直线方程和切点,再求切点到已知直线的距离即可.解:设2l :x-y+c=0,又点 A 满足 ⎩⎨⎧==+-xy c y x 202消去x 得:y 2=2(y-c ) 即:y 2-2y+2c=0 ,由△=4-8c=0,得c=21,∴A (21,1),∴A 到直线 1l 的距离d= 113121++-= 245 即为所求.点评:结合判别式,求出抛物线y 2=2x 上点到直线x-y+3=0的最短距离,其实质是确定直线和抛物线的位置关系问题抛物线y 2=2x 上点到直线x-y+3=0的最短距离.练习:若点P 在y 2=x 上,点Q 在圆()23-x +y 2=1上,求PQ 的最小值.解:如图,要求PQ min ,只需以A 为圆心,r 为半径的圆与抛物线相切,再由r-1得.()⎪⎩⎪⎨⎧=+-=22223ry x xy , 消去y 得,x 2-5x+9-b 2=0 ,△=)9(4252r --= 0 , 解得 211411==r ∴ PQ1211-. 当然,如何求解与抛物线有关的最值,是一个综合性较强的问题,关键要灵活应用.。
抛物线最值问题

抛物线最值问题抛物线是二次函数的一种,其一般形式为f(x)=ax²+bx+c (a ≠0)。
在解决实际问题时,我们经常会遇到与抛物线最值相关的问题。
这类问题通常涉及到求函数的最大值或最小值,以及确定使函数取得最值的自变量的值。
下面我们来探讨一下抛物线最值问题的解决方法。
我们需要了解抛物线的开口方向和对称轴。
开口方向由a的正负决定,当a>0时,抛物线向上开口;当a<0时,抛物线向下开口。
对称轴是抛物线上的一条水平直线,使得抛物线上的点关于这条直线对称。
对称轴的方程为x=-b/2a。
我们可以根据抛物线的开口方向和对称轴来确定函数的最值。
1. 当a>0时,抛物线向上开口,函数在对称轴处取得最小值。
最小值为f(-b/2a)=4ac-b²/4a。
此时,自变量x=-b/2a使得函数取得最小值。
2. 当a<0时,抛物线向下开口,函数在对称轴处取得最大值。
最大值为f(-b/2a)=4ac-b²/4a。
此时,自变量x=-b/2a使得函数取得最大值。
3. 当a=0时,抛物线变为一次函数y=ax²+bx+c。
此时,函数在顶点处取得最大值或最小值。
顶点的横坐标为-b/2a,纵坐标为f(-b/2a)=4ac-b²/4a。
此时,自变量x=-b/2a使得函数取得最大值或最小值。
通过以上分析,我们可以总结出求解抛物线最值问题的一般步骤:1. 确定抛物线的开口方向和对称轴。
2. 根据开口方向和对称轴确定函数的最值及其对应的自变量的值。
3. 将最值代入实际问题中进行求解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
关于抛物线的十个最值问题
本文用初等方法讨论了与抛物线有关的若干几何最值问题,得到了十个有趣的结论.为方便读者摘用, 现用定理形式叙述如下: 定理 1.抛物线的所有焦半径中,以过顶点的焦半径为最短. 证明:不妨设抛物线的极坐标方程为ρ= ,则显然有ρ≥,其中等号成立当且仅当θ=2kπ+π(k∈Z)即焦半径通过抛物线的顶点时.证毕. 定理 2.抛物线的过焦点的所有弦中,以抛物线的通径为最短. 证明:设抛物线极坐标方程为ρ= ,焦点弦为AB,且设A(ρ1,θ),B(ρ2,θ+π),则有│AB│=ρ1+ρ2 = +
=
≥ 2p =通径长, 其中等号成立当且仅当θ=kπ+π/2 (k∈Z) 即弦AB为通径时.证毕. 定理 3.设A(a,0)是抛物线 y2=2px(p>0)的对称轴上的定点,M(x,y)是抛物线上的动点,则│MA│m in =
证明:由│MA│2= (x-a)2+y2=(x-a)2+2px = x2-2(a-p)x+a2 = [x-(a-p)]2+p(2a-p),并且注意到x∈[0,+∞),立知结论成立.证毕. 定理4.设A(a,b)是抛物线 y2=2px(p>0)内一定点, F是焦点,M 是抛物线上的动点,则
y (│MA│+│MF│)min
=a+p/2.
Q M
A(a,b) 证明:如图1所示,作AQ⊥准线L:x=-p/2于Q,则知O F
x (│MA│+│MF│)m in =│AQ│= a-(-p/2)=a+p/2.证毕.
图
1 定理5.设线段AB是抛物线y2=2px(p>0)的过焦点的弦,分别以A、B为切点的抛物线的两条切线相交于点M,则三角形ABM的面积的最小值为p2. 证明:设A(x1,y1),B(x2,y2),则由A、F、B三点共线可得:x1y2-x2y1=p/2·(y2-y1)……………(1)于是利用(1)式由两切线方程
y
AM:
y1y=p(x+x1),
A BM:
y2y=p(x+x2),
M F
x 易得M的坐标(x,y)适合:
B
∵ kMF·kAF=-1, ∴MF⊥AB,即│MF│是△MAB的AB边上的高. 图2 ∵ │MF│≥│FK│(焦点F到准线x=-p/2的距离)=p, 又由定理2知│AB│≥2p(通径长), ∴ S△MAB=1/2·│AB│·│MF│≥1/2·2p·p=p2,因其中等号当且仅当AB⊥x 轴时成立,故三角形MAB的最小值为p2.证毕. 定理6.过抛物线y2=2px的顶点O引两条互相垂直的动弦OA和OB,则三角形OAB的面积的最小值为4p2.
y 证明:设A(x1,y1),B(x2,y2),则由OA⊥OB 得
A x1x2+y1y2=0 ……………………………………
(1) O
x 将y12=2px1, y22=2px2代入(1)立得: x1x2=4p2 (2)
于是
B (S△OAB) 2
=1/4·│OA│2·│OB│2&nb
sp;
图3 =1/4·(x12+y12)·(x22+y22)
=1/4·(x12+2px1)·(x22+2px2)
=1/4·[(x1x2)2+2px1x2
(x1+x2)+4p2x1x2] ≥1/4·[(x1x2)2+2px 1x2 (2√x1x2)+4p2x1x2]………………………………………(3)将(2)式代入(3)则得(S△OAB)2≥16p4,从而S△OAB≥4p2,因其中等号当x1=x2=2p时取到,故三角形OAB的面积的最小值为4p2。
证毕. 定理7.抛物线 y2=2px的内接等腰直角三角形的面积的最小值为4p2. 证明:设Rt△ABC内接于抛物线 y2=2px,点C为直角顶点,设A(x1,y1),B(x2,y2),C(x3,y3),根据抛物线的对称性以及其开口方向,不妨设y1>0,y2<y3≤0,并记直线CA的斜率为k,则由y3-y1=k(x3-x1)=k(y32/2p -y12/2p) 及
y y3-y2=-1/k·(x3-x2)=-1/k·(y32/2p-y22/2p)
A 可得y1 =2p/k-y3 及y2=-2pk-y3 (1)
O
x 又由│AC│=│BC│有
C B
(x1-x3)2+(y1-y3)2=(x3-x2)2+(y3-y2)2 (2)
图4 将x1=y12/2p,x2=y22/2p,x3=y32/2p及(1)代入(2)可得y3= …………………………
(3) 从而据(1)、(3)可得y1-y3= ………………………………………………………(4) 于是△ABC的面积S=1/2·│AC│2 =1/2·[(x1-x3)2+(y1-y3)2]= ··(y1-y3)2
= 2p2 ··(
)2
=2p2··
≥2p2··
=4p2. 因当k=1且y3=0时上式等号成立,故等腰Rt△ABC面积的最小值为4p2.证毕. 定理8.设AB是抛物线的焦点弦, 准线与抛物线对称轴的交点为M, 则∠AMB的最大值为π/2. 证明:如图5所示, 设A1、B1分别是A、B在准线L上的y
射影, F是焦点, 连A1F和B1F, 则
知
A
A (1)当AB⊥MF时, 显然有∠AMB=π/2;
M F
X (2)当AB与MF不垂直时, 由│AA1│>│A1M│知B1
B ∠AMA1>∠A1AM=π/2-∠AMA1,
图 5 ∴∠AMA1>
π/4; 同理∠BMB1>π/4, 故有∠AMB<π/2. 综合(1)、(2), 定理8获证. 定理9.设AB是抛物线 y=a x2 (a>0) 的长为定长m的动弦, 则Ⅰ.当m≥1/a (通径长)时, AB的中点M到x轴的距离的最小值为(2ma-1)/4a ; Ⅱ.当m<1/a (通径长)时, AB 的中点M到x轴的距离的最小值为 am2/4. 证明:设M(x0,y0), 将直线AB的参数方程
y
(其中t为参数,倾斜角α≠π/2)
A 代入y=ax2 并整理得
M a(cosα)2·t2+(2ax0cosα-sinα)·t+(ax02-y 0)=0, B
故由韦达定理和参数 t的几何意义以及│AB│=m 立得0
X
t1+t2=-(2ax0cosα-sinα)/a(cosα)2 =0………①
图 6 t1t2=(ax02-y0)/a(cosα)2 =-(m/2)2 ……………②由①解出x0并代入②整理
得y0=(secα)2+(cosα)2-……③对③右边前两项利用基本不等式则得y0≥2·-=(2ma-1)/4a. 于是,令(secα)2 =(cosα)2, 得(cosα)2=. 因此, 当am≥1时,(y0)min=(2ma-1)/4a ; 当0<am<1时, 记
(cosα)2=x , 则③式化为关于x 的函数式y0=f(x)=·+·x-(0<x≤1).易证此函数是减函数, 故此时(y0)min=f(1)=.证毕. 定理10. 设AB是抛物线 y2=2px的焦点弦, O为坐标原点, 则三角形OAB的面积的最小值为p2/2 .
y 证明:(1)当AB⊥x轴时, 显然有SΔAOB=p2/2 ;
A (2)当AB不垂直x轴时, 设AB: y=k(x-p/2), 代O
F x 入 y2=2px并整理得k2x2-(pk2+2p)x+k2p2/4=0. 于是
B 设A(x1,y1),B(x2,y2),则由弦长公式和韦达定理得:
图7 │AB│=(1+k2 )[(x1+x2)2- 4x1x2]
=
=
. 又顶点O到弦AB的距离d =. 故此时SΔAOB =│AB│·d =··
=·>. 综合(1)、(2), 定理10获证 .。
