抛物线中的最值问题
抛物线上的点到直线的最大值

抛物线上的点到直线的最大值在二维平面几何中,我们经常会遇到抛物线与直线的关系。
本文将讨论一个有趣的问题:如何求解抛物线上的点到一条给定直线的距离的最大值。
问题描述设抛物线方程为y=ax2+bx+c,直线方程为y=mx+d,现在我们要找到在抛物线上的点(x,ax2+bx+c)到直线y=mx+d的距离的最大值。
求解方法为了求解这个问题,我们先要确定点到直线的距离公式。
点(x0,y0)到直线Ax+By+C=0的距离公式为:$$ \\frac{|Ax_0 + By_0 + C|}{\\sqrt{A^2 + B^2}} $$接下来,我们假设我们要求解的最大距离对应的点为(x1,ax12+bx1+c),那么点(x1,ax12+bx1+c)到直线y=mx+d的距离为:$$ \\frac{|m x_1 - ax_1^2 - bx_1 - d|}{\\sqrt{m^2 + 1}} $$为了找到最大距离,我们需要最大化上式。
我们可以通过微分来解决这个问题。
令 $f(x) = \\frac{|m x - ax^2 - bx - d|}{\\sqrt{m^2 + 1}}$,我们需要求解f(x)的极值点。
通过对f(x)求导并令导数为零,我们可以得到最大距离对应的x1的值。
接着,我们将x1的值代回到点的坐标中,即可以得到最大距离对应的点(x1,ax12+bx1+c)。
结论通过以上的求解过程,我们可以找到抛物线上的点到直线的最大距离。
这个问题涉及到了距离的计算和微分,通过适当的数学推导和分析,我们能够有效地解决这类问题。
在实际应用中,这个问题可能会有不同的变体或扩展,但基本的思路和方法仍然适用。
通过深入研究和灵活运用数学原理,我们可以解决更为复杂的几何问题,为实际问题的求解提供有力的支持。
以上是关于抛物线上的点到直线的最大值问题的基本介绍和解法,希望对读者有所启发。
感谢阅读!。
关于抛物线的十个最值问题-模板

关于抛物线的十个最值问题本文用初等方法讨论了与抛物线有关的若干几何最值问题,得到了十个有趣的结论.为方便读者摘用, 现用定理形式叙述如下: 定理 1.抛物线的所有焦半径中,以过顶点的焦半径为最短. 证明:不妨设抛物线的极坐标方程为ρ= ,则显然有ρ≥,其中等号成立当且仅当θ=2kπ+π(k∈Z)即焦半径通过抛物线的顶点时.证毕. 定理 2.抛物线的过焦点的所有弦中,以抛物线的通径为最短. 证明:设抛物线极坐标方程为ρ= ,焦点弦为AB,且设A(ρ1,θ),B(ρ2,θ+π),则有│AB│=ρ1+ρ2 = +=≥ 2p =通径长, 其中等号成立当且仅当θ=kπ+π/2 (k∈Z) 即弦AB为通径时.证毕. 定理 3.设A(a,0)是抛物线 y2=2px(p>0)的对称轴上的定点,M(x,y)是抛物线上的动点,则│MA│m in =证明:由│MA│2= (x-a)2+y2=(x-a)2+2px = x2-2(a-p)x+a2 = [x-(a-p)]2+p(2a-p),并且注意到x∈[0,+∞),立知结论成立.证毕. 定理4.设A(a,b)是抛物线 y2=2px(p>0)内一定点, F是焦点,M 是抛物线上的动点,则y (│MA│+│MF│)min=a+p/2.Q MA(a,b) 证明:如图1所示,作AQ⊥准线L:x=-p/2于Q,则知O Fx (│MA│+│MF│)m in =│AQ│= a-(-p/2)=a+p/2.证毕.图1 定理5.设线段AB是抛物线y2=2px(p>0)的过焦点的弦,分别以A、B为切点的抛物线的两条切线相交于点M,则三角形ABM的面积的最小值为p2. 证明:设A(x1,y1),B(x2,y2),则由A、F、B三点共线可得:x1y2-x2y1=p/2·(y2-y1)……………(1)于是利用(1)式由两切线方程yAM:y1y=p(x+x1),A BM:y2y=p(x+x2),M Fx 易得M的坐标(x,y)适合:B∵ kMF·kAF=-1, ∴MF⊥AB,即│MF│是△MAB的AB边上的高. 图2 ∵ │MF│≥│FK│(焦点F到准线x=-p/2的距离)=p, 又由定理2知│AB│≥2p(通径长), ∴ S△MAB=1/2·│AB│·│MF│≥1/2·2p·p=p2,因其中等号当且仅当AB⊥x 轴时成立,故三角形MAB的最小值为p2.证毕. 定理6.过抛物线y2=2px的顶点O引两条互相垂直的动弦OA和OB,则三角形OAB的面积的最小值为4p2.y 证明:设A(x1,y1),B(x2,y2),则由OA⊥OB 得A x1x2+y1y2=0 ……………………………………(1) Ox 将y12=2px1, y22=2px2代入(1)立得: x1x2=4p2 (2)于是B (S△OAB) 2=1/4·│OA│2·│OB│2 图3 =1/4·(x12+y12)·(x22+y22)=1/4·(x12+2px1)·(x22+2px2)=1/4·[(x1x2)2+2px1x2(x1+x2)+4p2x1x2] ≥1/4·[(x1x2)2+2px 1x2 (2√x1x2)+4p2x1x2]………………………………………(3)将(2)式代入(3)则得(S△OAB)2≥16p4,从而S△OAB≥4p2,因其中等号当x1=x2=2p时取到,故三角形OAB的面积的最小值为4p2。
抛物线的最大最小值怎么求

抛物线的最大最小值怎么求
概述
在数学中,我们经常要求解抛物线函数的最大值和最小值,这对于确定函数的
凹凸性和函数图像的特点都具有重要意义。
本文将介绍如何求解抛物线函数的最大值和最小值的方法。
抛物线函数的一般形式
抛物线函数通常表示为y=ax2+bx+c的形式,其中a eq0。
其中,a控制
了抛物线开口的方向,正值表示开口向上,负值表示开口向下;b控制了抛物线的
位置;c是y轴的截距。
最大最小值的求解
对于抛物线函数y=ax2+bx+c,它的最大值或最小值发生在顶点处。
因此,我们只需找到抛物线的顶点坐标即可求解最大最小值。
求解顶点坐标
抛物线的顶点坐标可以通过公式 $x = -\\frac{b}{2a}$ 求解得到。
将x的值代入
抛物线函数中即可得到对应的y值,从而确定顶点坐标。
确定最大最小值
通过观察a的正负性可以确定抛物线的开口方向,若a>0,则抛物线开口向上,顶点为最小值点;若a<0,则抛物线开口向下,顶点为最大值点。
示例
假设有抛物线函数y=2x2−4x+3,我们按照上述方法求解其最大最小值。
1. 求解顶点坐标: $x = -\\frac{-4}{2*2} = 1$,将x=1代入函数得到y=2∗12−
4∗1+3=1,所以顶点坐标为(1,1)。
2. 确定最大最小值:由于a=2>0,故
顶点为最小值点,最小值为1。
结论
通过以上方法,我们可以求解任意抛物线函数的最大最小值,进而帮助我们理
解函数的特性和性质。
抛物线函数的最大最小值计算在数学建模和实际问题求解中具有广泛的应用。
抛物线最值问题

2
= x2 - 2x + 9
= ( x - 1) 2 + 8
min
x³ 0
= 2 2, 此时M (1, 2)
变3
\ 当x = 1时,
2
变式训练:
已知点M 在抛物线y = 4 x上运动, 点Q在圆(x - 3) + y = 1上运动,则 MQ 的最小值是
.
2 2 2
小组讨论、交流:
只需求出动点M到圆心 A(3,0)距离最小值再 减去圆半径即可。
y
M
F
练习
A
Q .
x
所以 MQ min = 2 2 - 1
2
的最小值是多少?
小组讨论、交流:
y
M
F
x
l
已知点F为抛物线 y 2 = 4 x 的焦点,A(3,2) 为定点,点M 是抛物线上任意一点,则 MA + MF 的最小值是 ,此时点M的 坐标是
小组活动:
。
探究2
y
M A
讨论解决方案
F
x
探究3
已知抛物线y =4x和定点A(7,8), 抛物线上有一动点M,点M到点A 的距离为d1,点M到抛物线准线距离 为d 2,则d1+d 2的最小值是 .
2 2 最小值为AF =(7-1) +(8-0) =10
y M F
A
M
x
思考:已知点A30,点 ( , ) M在抛物线y2=4x 上运动,求 MA 的最小值,及此时点M的坐标.
解:设点M( x, y)是抛物线y 2=4x 上任一点,则y = 4 x
AM =
=
2
y M F Ax
抛物线的性质与定理应用

抛物线的性质与定理应用抛物线是数学中的一个重要概念,它具有许多独特的性质和定理。
作为一位初中数学特级教师,我将在本文中向大家介绍抛物线的性质与定理,并探讨它们在实际问题中的应用。
一、抛物线的基本性质抛物线是由一个定点(焦点)和一条定直线(准线)确定的曲线,具有以下基本性质:1. 对称性:抛物线关于准线对称,即准线是抛物线的对称轴。
这个性质使得我们在研究抛物线时可以利用对称性简化问题,节省计算时间。
2. 焦点与准线的关系:抛物线上的任意一点到焦点的距离等于该点到准线的距离。
这个性质被广泛应用于抛物线的测量和设计中,例如卫星天线的调整和太阳能聚光器的设计等。
3. 切线性质:抛物线上的切线与准线垂直。
这个性质使得我们可以通过求解切线斜率为零的方程来确定抛物线上的顶点,从而得到抛物线的标准方程。
二、抛物线的定理应用1. 焦半径定理:焦半径定理是抛物线的一个重要定理,它指出抛物线上任意一点到焦点的距离等于该点到准线的距离的两倍。
这个定理可以用来解决很多与焦点和准线有关的实际问题,例如抛物线反射器的设计和抛物面反射望远镜的原理等。
2. 焦点坐标定理:焦点坐标定理是抛物线的另一个重要定理,它指出抛物线的焦点坐标为(p,0),其中p是焦准距。
这个定理可以用来确定抛物线的焦点位置,从而进一步求解抛物线的标准方程。
3. 抛物线的最值问题:抛物线在一定范围内的最值问题是数学中常见的优化问题。
通过求解抛物线的最值,我们可以确定抛物线的最高点、最低点以及最值对应的自变量值。
这个问题在物理学、经济学和工程学等领域都有广泛的应用。
三、抛物线的实际应用举例1. 抛物线的轨迹问题:假设有一个人站在地面上,以一定的初速度和角度抛出一个物体。
我们可以利用抛物线的轨迹性质来计算物体的飞行距离、最大高度和落地点等。
这个问题在射击、投掷和运动等领域都有实际应用。
2. 抛物线的抛物面反射望远镜:抛物面反射望远镜是一种常见的望远镜设计,它利用抛物线的焦点和准线性质来聚集光线,从而实现远距离的观测。
抛物线中的最值问题探究

抛物线中的最值问题探究福建漳州市第一外国语学校(363000) 张芙蓉[摘 要]抛物线中的最值问题一直是中考数学的重难点,这类问题考查学生利用数学知识和思想方法解决问题的能力。
文章结合几道例题,从四个方面对抛物线中的最值问题进行分析探讨,以帮助学生突破难点,提升学生的思维品质,发展学生的核心素养。
[关键词]抛物线;最值问题;最大值;最小值[中图分类号] G 633.6 [文献标识码] A [文章编号] 1674-6058(2024)02-0031-03抛物线中的最值问题一直是中考数学的重难点,它包括抛物线中内接四边形面积的最大值或最小值、抛物线中线段和的最大值或最小值、抛物线中线段比的最大值或最小值、抛物线中面积的最大值或最小值等。
如何解答这类问题?下面笔者就此进行分类例析。
一、求抛物线内接四边形面积的最大值抛物线内接四边形是指四边形的四个顶点都在抛物线上,求抛物线内接四边形面积时,一般将其分割为两个三角形的面积,其中一个三角形的面积是固定的,另一个三角形的面积是可变的,只需求得它的最大值,即可求得内接四边形面积的最大值。
[例1]如图1所示,已知抛物线y =ax 2+bx +c (a ≠0)经过点M ()-2,92和N ()2,- 72两点,且抛物线与x 轴交于A 、B 两点(点A 在点B 的左侧),与y 轴交于点C 。
(1)若点M 是抛物线y =ax 2+bx +c 的顶点,求抛物线的解析式及A 、B 、C 的坐标;(2)在(1)的条件下,若点P 是A 、C 之间抛物线上的一点,求四边形APCN 面积的最大值及此时点P 的坐标。
分析:(1)设抛物线的顶点式为y =a(x +2)2+92,将点N 坐标代入即可求a 的值,从而确定抛物线的解析式。
(2)设P ()t ,-12t 2-2t +52,先求出直线AC 的解析式为y =12x +52,过点P 作PG ∥y 轴交AC 于点G ,则G ()t ,12t +52,得到S △PAC =-54()t +522+12516,当t =-52时,△PAC 的面积有最大值12516,此时P ()-52,358,求出直线CN 与x 轴的交点为()56,0,再求S △ACN =12×()56+5×()72+52=352,即可求四边形APCN 面积的最大值为40516。
初中数学专题分类突破:抛物线中几何图形的最值问题
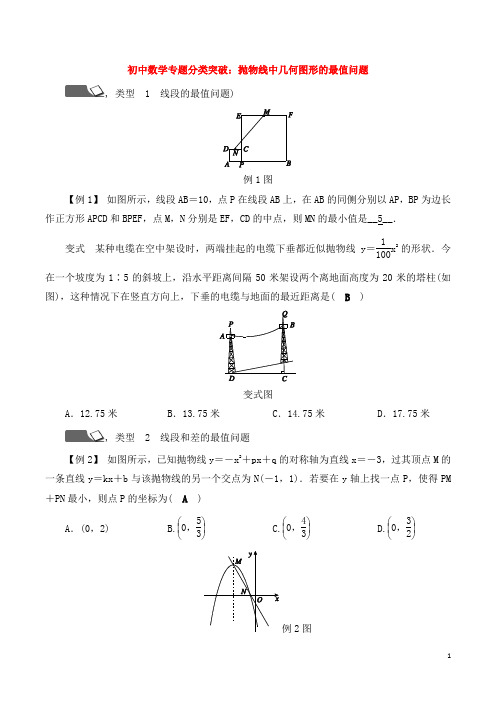
初中数学专题分类突破:抛物线中几何图形的最值问题 , 类型 1 线段的最值问题)例1图【例1】 如图所示,线段AB =10,点P 在线段AB 上,在AB 的同侧分别以AP ,BP 为边长作正方形APCD 和BPEF ,点M ,N 分别是EF ,CD 的中点,则MN 的最小值是__5__.变式 某种电缆在空中架设时,两端挂起的电缆下垂都近似抛物线y =1100x 2的形状.今在一个坡度为1∶5的斜坡上,沿水平距离间隔50米架设两个离地面高度为20米的塔柱(如图),这种情况下在竖直方向上,下垂的电缆与地面的最近距离是( B )变式图A .12.75米B .13.75米C .14.75米D .17.75米, 类型 2 线段和差的最值问题【例2】 如图所示,已知抛物线y =-x 2+px +q 的对称轴为直线x =-3,过其顶点M 的一条直线y =kx +b 与该抛物线的另一个交点为N(-1,1).若要在y 轴上找一点P ,使得PM +PN 最小,则点P 的坐标为( A )A .(0,2)B.⎝⎛⎭⎪⎫0,53C.⎝⎛⎭⎪⎫0,43D.⎝⎛⎭⎪⎫0,32例2图变式图变式 如图所示,二次函数y =-x 2-3x +4的图象交x 轴于A ,B ,交y 轴于点C.点P 是抛物线的对称轴上一动点,若|PA -PC|的值最大,则点P 的坐标为 ⎝ ⎛⎭⎪⎫-32,10 ., 类型 3 面积的最值问题【例3】 正方形OABC 的边长为4,对角线相交于点P ,抛物线l 经过O ,P ,A 三点,点E 是正方形内抛物线l 上的动点.则△OAE 与△OCE 面积之和的最大值是__9__.例3图变式图变式 如图所示,二次函数y =ax 2+bx 的图象经过点A(2,4)与B(6,0). (1)a =__-12__,b =__3__;(2)点C 是该二次函数图象上A ,B 两点之间的一动点,横坐标为x(2<x <6),写出四边形OACB 的面积S 关于点C 的横坐标x 的函数表达式,并求S 的最大值.解:(1)将A(2,4)与B(6,0)代入y =ax 2+bx , 得⎩⎨⎧4a +2b =4,36a +6b =0,解得⎩⎨⎧a =-12,b =3,变式答图(2)如图,过A作x轴的垂线,垂足为D(2,0),连结CD,CB,过C作CE⊥AD,CF⊥x轴,垂足分别为E,F,S△OAD =12OD·AD=12×2×4=4;S△ACD =12AD·CE=12×4×(x-2)=2x-4;S△BCD =12BD·CF=12×4×⎝⎛⎭⎪⎫-12x2+3x=-x2+6x,则S=S△OAD +S△ACD+S△BCD=4+2x-4-x2+6x=-x2+8x,∴S关于x的函数表达式为S=-x2+8x(2<x<6).∵S=-x2+8x=-(x-4)2+16,∴当x=4时,四边形OACB的面积S有最大值,最大值为16.1.(泸州中考)已知抛物线y=14x2+1具有如下性质:该抛物线上任意一点到定点F(0,2)的距离与到x轴第1题图的距离始终相等,如图,点M的坐标为(3,3),P是抛物线y=14x2+1上一动点,则△PMF周长的最小值是( C)A.3 B.4 C.5 D.6第2题图2.如图所示,抛物线y=-x2-2x+3 的图象与x轴交于A,B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.(1)写出A,B,C三点的坐标:A(__-3__,__0__),B(__1__,__0__),C(__0__,__3__).(2)点M为线段AB上一点(点M不与点A,B重合),过点M作x轴的垂线,与直线AC交于点E,与抛物线交于点P,过点P作PQ∥AB交抛物线于点Q,过点Q作QN⊥x轴于点N.若点P 在点Q左边,当矩形PMNQ的周长最大时,求△AEM的面积.解:(2)由抛物线y=-x2-2x+3=-(x+1)2+4可知,对称轴为直线x=-1,设点M的横坐标为m,则PM=-m2-2m+3,MN=(-m-1)×2=-2m-2,∴矩形PMNQ的周长=2(PM+MN)=2(-m2-2m+3-2m-2)=-2m2-8m+2=-2(m+2)2+10,∴当m =-2时矩形的周长最大.∵点A(-3,0),C(0,3),可求得直线AC 的函数表达式为y =x +3, 当x =-2时,y =-2+3=1,则点E(-2,1), ∴EM =1,AM =1,∴S =12AM ·EM =12.第3题图3.(东营中考)如图所示,直线y =-33x +3分别与x 轴、y 轴交于B ,C 两点,点A 在x 轴上,∠ACB =90°,抛物线y =ax 2+bx +3经过A ,B 两点.(1)求抛物线的解析式;(2)点M 是直线BC 上方抛物线上的一点,过点M 作MH⊥BC 于点H ,作MD∥y 轴交BC 于点D ,求△DMH 周长的最大值.解:(1)∵直线y =-33x +3分别与x 轴、y 轴交于B ,C 两点, ∴B(3,0),C(0,3), ∴OB =3,OC =3,∴BC =23, ∴∠CBO =30°,∠BCO =60°,∵∠ACB =90°,∴∠ACO =30°,∴AO =1,∴A(-1,0). ∵抛物线y =ax 2+bx +3经过A ,B 两点, ∴⎩⎪⎨⎪⎧a -b +3=0,9a +3b +3=0,解得⎩⎪⎨⎪⎧a =-33,b =233,∴抛物线解析式为y =-33x 2+233x + 3. (2)∵MD∥y 轴,MH ⊥BC ,∴∠MDH =∠BCO=60°,则∠DMH=30°, ∴DH =12DM ,MH =32DM ,∴△DMH 的周长=DM +DH +MH =DM +12DM +32DM =3+32DM ,∴当DM 有最大值时,其周长有最大值, ∵点M 是直线BC 上方抛物线上的一点,∴可设M ⎝ ⎛⎭⎪⎫t ,-33t 2+233t +3,则D ⎝ ⎛⎭⎪⎫t ,-33t +3,∴DM =-33t 2+233t +3-⎝ ⎛⎭⎪⎫-33t +3=-33t 2+3t =-33⎝ ⎛⎭⎪⎫t -322+334,∴当t =32时,DM 有最大值,最大值为334,此时3+32DM =3+32×334=93+98,即△DMH 周长的最大值为93+98.第4题图4.已知:抛物线l 1:y =-x 2+bx +3交x 轴于点A ,B(点A 在点B 的左侧),交y 轴于点C ,其对称轴为x =1,抛物线l 2经过点A ,与x 轴的另一个交点为E(5,0),交y 轴于点D ⎝⎛⎭⎪⎫0,-52. (1)求抛物线l 2的函数表达式;(2)M 为抛物线l 2上一动点,过点M 作直线MN ∥y 轴,交抛物线l 1于点N ,求点M 自点A运动至点E 的过程中,线段MN 长度的最大值.解:(1)∵抛物线l 1:y =-x 2+bx +3的对称轴为x =1,∴-b-2=1,解得b =2,∴抛物线l 1的解析式为y =-x 2+2x +3,令y =0,可得-x 2+2x +3=0,解得x =-1或x =3, ∴A 点坐标为(-1,0),∵抛物线l 2经过A ,E 两点, ∴可设抛物线l 2的解析式为y =a(x +1)(x -5), 又∵抛物线l 2交y 轴于点D ⎝⎛⎭⎪⎫0,-52, ∴-52=-5a ,解得a =12,∴y =12(x +1)(x -5)=12x 2-2x -52,∴抛物线l 2的函数表达式为y =12x 2-2x -52.(2)由题意可设M ⎝ ⎛⎭⎪⎫x ,12x 2-2x -52,∵MN ∥y 轴,∴N(x ,-x 2+2x +3),令-x 2+2x +3=12x 2-2x -52,解得x =-1或x =113.①当-1<x≤113时,MN =(-x 2+2x +3)-⎝ ⎛⎭⎪⎫12x 2-2x -52=-32x 2+4x +112=-32⎝ ⎛⎭⎪⎫x -432+496, 显然,-1<43≤113,∴当x =43时,MN 有最大值496;②当113<x≤5时,MN =⎝ ⎛⎭⎪⎫12x 2-2x -52-(-x 2+2x +3)=32x 2-4x -112=32⎝ ⎛⎭⎪⎫x -432-496,显然,当x >43时,MN 随x 的增大而增大,∴当x=5时,MN有最大值,32×⎝⎛⎭⎪⎫5-432-496=12.综上可知在点M自点A运动至点E的过程中,线段MN长度的最大值为12.。
高中数学抛物线最值问题讲课稿

抛物线求最值问题(第一类)1.已知抛物线和一条直线,求抛物线上的一点到直线与(y 轴、准线、焦点)距离之和的最小值问题。
此类题常用方法转化为求焦点到直线的距离。
例题已知抛物线方程为x y 42=,直线l 的方程为04=+-y x ,在抛物线上有一动点P 到y 轴的距离为d1,P 到直线l 的距离为d2,则d1+d2的最小值为多少?分析:如图点P 到y 轴的距离等于点P 到焦点F 的距离减1,过焦点F 作直线x-y+4=0的垂线,此时d1+d2最小,根据抛物线方程求得F ,进而利用点到直线的距离公式求得d1+d2的最小值.解:如图点P 到准线的距离等于点P 到焦点F 的距离,从而P 到y 轴的距离等于点P 到焦点F 的距离减1.过焦点F 作直线x-y+4=0的垂线,此时d1+d2=|PF|+d2-1最小, ∵F (1,0),则|PF|+d2==,则d1+d2的最小值为.抛物线求最值问题(第二类)2.已知抛物线和一个定点,①:定点在抛物线“内”,求抛物线上的一点到定点与(焦点、准线)距离之和的最值问题;②定点在抛物线“外”,求抛物线上的一点到定点与(焦点、准线)距离之差绝对值的最值问题。
此类题常用方法转化为三点共线或者顶点到直线问题。
例题已知点P在抛物线y2=4x上,那么点P到点Q(2,-1)的距离与点P到抛物线焦点距离之和取得最小值时,点P的坐标为()A.⎪⎭⎫⎝⎛-1,41B.⎪⎭⎫⎝⎛1,41C.(1,2)D.(1,-2)分析:先判断点Q与抛物线的位置,即点Q在抛物线内,再由点P 到抛物线焦点距离等于点P到抛物线准线距离,根据图象知最小值在M,P,Q三点共线时取得,可得到答案.解:点P到抛物线焦点距离等于点P到抛物线准线距离,如图PF+PQ=PM+PQ,故最小值在M,P,Q三点共线时取得,此时P,Q的纵坐标都是-1,抛物线求最值问题(第三类)3.已知抛物线和一条直线,求抛物线上的一点到直线距离最小值问题。
抛物线的最值问题

O
.
F
x
y0 2 3 y0 46 y0 48y0 16 46 , ( y0 R ) d 16 80 5 此时P(9,24) 当y0 24时, d min 2
探究五:距离和的最小值。
例 在抛物线 y2=8x 上求一点P,使P到焦点F 的距离与到 Q(4 ,1)的距离的和 最小,并求最小值。 解:
解:直线与抛物线无交点,设抛物线上一点P( x0 . y0 )
例:在抛物线y2=64x上求一点,使它到直线L:4x+3y+46=0的距离最短,并求此距 离。 y
则y0 2 64x0 4 x0 3 y0 46 4 x0 3 y0 46 d | | 5 16 9
y0 2 将x0 代入得: 64 2
p4 2p 8, 由 y2 8x 知:
y
此抛物线的焦点坐标是:F (2 , 0)
准线l方程是:x 2 .
由定义知: PF dPl 即 | PF || PK | .
| PF | | PQ | | PK | | PQ |
K
P Q O 2 F 4
x
显然,当Q, P, K 三点共线时,
• 例:在抛物线y2 =64x上求一点,使它到 直线L:4x+3y+46=0的距离最短,并求 此距离。
例在抛物线y2=64x上求一点,使它到直线L: 4x+3y+46=0的距离最短,并求此距离。
y 解:设抛物线平行于L的切线方程为
4x 3 y m 0 x 联立 4 x 3 y m 0 2 P y 64x 2 消 x 得 y 48y 16m 0 L 48 48 4 16 m 0 m 36 y 24, x 9 46 36 2 P9,24 d min 有最小值.
抛物线中的最值问题

抛物线中的最值问题作者:王荣李家洪来源:《高中生学习·高二理综版》2015年第03期圆锥曲线的最值是一类综合性强、涉及知识广的问题.破解这类问题常利用函数与方程、数形结合、转化与化归等数学思想与方法,将它转化为解不等式、求函数的值域或利用平面几何知识来解决.本文对抛物线中常见的几类最值分类探究.点与点、点与线之距离的最值问题例1 在抛物线[y2=2pxp>0]上求一点,使它到直线[l]:[Ax+By+C=0](其中[A≠0,pB2法1 由已知,直线[l]与抛物线相离,设直线[l1]:[Ax+By+m=0]与抛物线相切,联立[Ax+By+m=0,y2=2px]消去[x]得,[A2py2+By+m=0].由[Δ=B2-4∙A2p∙m=0]得,[m=pB22A].故直线[l1]的方程为:[Ax+By+pB22A=0].由两平行线间的距离公式得,[dmin=pB22A-CA2+B2=pB2-2AC2AA2+B2=2AC-pB22AA2+B2].进而得所求抛物线上的点为[pB22A2,-pBA].法2 由已知,直线[l]与抛物线相离,设抛物线上一点[Px0,y0],则[y02=2px0].点[P]到直线[l]的距离[d=Ax0+By0+CA2+B2=A∙y022p+By0+CA2+B2=A2p∙y0+pBA2+p2AC-pB2A2A2+B2.]又[pB2注意到[y0∈R],因此,当[y0=-pBA]时,[dmin=2AC-pB22AA2+B2],可得所求点的坐标为[pB22A2,-pBA].法3 由已知,直线[l]与抛物线相离,设抛物线上一点[Px0,y0]到直线[l]的距离最短.在抛物线[y2=2px]中,两边同时对[x]求导得[2y∙y=2p],即[y=py].故[y|y=y0=py0].由[py0=-AB]得,[y0=-pBA],即所求点[P]的坐标为[pB22A2,-pBA].根据点到直线的距离公式得[dmin=2AC-pB22AA2+B2].线段之和(或积)的最值问题例2 过抛物线[y2=2pxp>0]的焦点[F]作两条互相垂直的弦[AB],[CD],求[AB+CD]与[AB∙CD]的最小值.法1 由题意知,直线[AB],[CD]均不垂直于坐标轴.设直线[AB]的方程为[y=kx-p2],则直线[CD]的方程为[y=-1kx-p2].联立[y=kx-p2,y2=2px]消去[x]得,[ky2-2py-kp2=0].则[Δ=4p2k2+1>0]恒成立.记[Ax1,y1],[Bx2,y2],得[y1+y2=2pk],[y1y2=-p2].故[AB=1+1k2y1+y22-4y1y2=2p1+1k2],同理[CD=2p1+k2].[∴AB+CD=2p1+1k2+2p1+k2=2p2+k2+1k2,][AB∙CD=4p21+1k21+k2=4p22+k2+1k2],当[k2=1]即[k=±1]时,[AB+CDmin=8p],[AB∙CDmin=16p2].法2 由题意知,直线[AB],[CD]均不垂直于坐标轴.设[Ax1,y1],[Bx2,y2],直线[AB]的斜率为[k],则[y1-y2x1-x2=k].又[y12=2px1],[y22=2px2],两式相减得[y12-y22=2px1-x2],即[y1+y2=2p∙x1-x2y1-y2],故[y1+y2=2pk.]又直线[AB]的方程为[y=kx-p2],所以[y1+y2=kx1+x2-p],即[x1+x2=2pk2+p].由抛物线的定义得,[AB=AF+BF=x1+p2+x2+p2][=x1+x2+p][=2pk2+2p,]同理[CD=2p1+k2].以下略.点拨一般地,设[Ma,b]是不在抛物线的[y2=2pxp>0]上的定点,过点[M]作抛物线的两条互相垂直的弦[AB],[CD],求[AB+CD]与[AB∙CD]的最小值. (留与同学们解答)三角形、四边形等多边形之面积的最值问题例3 过抛物线[y2=2pxp>0]的顶点[O]引两条互相垂直的动弦[OA]和[OB],求三角形[AOB]的面积的最小值.法1 直线[OA]和[OB]的斜率均存在且不为零.设直线[OA]的方程为[y=kx],则直线[OB]的方程为[y=-1kx].联立[y=kx,y2=2px]得[A2pk2,2pk],同理得[B2pk2,-2pk].所以[SΔAOB=12OA∙OB][=124p2k4+4p2k2∙4p2k4+4p2k2=2p22+k2+1k2],当[k2=1]即[k=±1]时,[SΔAOBmin=4p2].法2 设[Ax1,y1],[Bx2,y2],由[OA⊥OB]得,[x1x2+y1y2][=0].又[y12=2px1],[y22=2px2],于是得[x1x2=4p2].[SΔAOB2=14OA2∙OB2=14x12+y12x22+y22=14x12+2px1x22+2px2][=14x1x22+2px1x2x1+x2+4p2x1x2][≥14x1x22+2px1x22x1x2+4p2x1x2][=144p22+2p∙4p224p2+4p2∙4p2=16p4].从而[SΔAOB≥4p2]. 当且仅当[x1=x2=2p]时取等号.因此[SΔAOBmin=4p2].点拨一般地,设[Pa,b]是抛物线上的一定点,过点[P]作抛物线[y2=2pxp>0]的两条互相垂直的动弦[PA]和[PB],求三角形[APB]的面积的最小值. (留与同学们解答)弦长为定值之动弦中点到准线距离的最值问题例4 定长为[l]([l>0])的线段[AB]的两端点在抛物线[y2=2pxp>0]上移动,求线段[AB]的中点[M]到[y]的最短距离.法1 由题意知,直线[AB]的斜率一定不为零.故可设直线[AB]的方程为[x=ty+m].联立[x=ty+m,y2=2px]消去[x]得,[y2-2pty-2pm=0].则[Δ=4ppt2+2m>0].记[Ax1,y1],[Bx2,y2],[∴y1+y2=2pt],[y1y2=-2pm].从而[x1+x2=ty1+y2+2m=2pt2+2m].[AB=1+t2y1+y22-4y1y2=4p1+t2pt2+2m,]又[AB=l].[∴4p1+t2pt2+2m=l2],即[m=l28p1+t2-12pt2].线段[AB]的中点[M]到[y]的距离[d=xM=x1+x22=pt2+m=l28p1+t2+12pt2].即[d=p2l2p2t2+1+t2].设[μ=t2+1],由[t∈R]知,[μ≥1].[∴d=p2l2p2μ+μ-1].若[l2p≥1]即[l≥2p]时,[dmin=l-p2].此时[t2=l2p-1].若[0综上可得[dmin=l-p2,l≥2p,l28p, 0法2 设线段[AB]的中点[Mx0,y0].直线[AB]的参数方程为[x=x0+tcosα,y=y0+tsinα](其中[t]为参数,直线的倾斜角[α∈0,π]).代入[y2=2px]整理得,[sin2αt2+][2y0sinα-pcosαt][+y02-2px0=0].记点[A],[B]对应的参数分别为[t1],[t2].由韦达定理与参数的几何意义知,[t1+t2=-2y0sinα-pcosαsin2α],[t1t2=y02-2px0sin2α].因为[M]是线段[AB]的中点,及[AB=l],所以[t1+t2=0],[t1t2=-l22].[∴y0=pcosαsinα,]且[y02-2px0=-14l2sin2α].线段[AB]的中点[M]到[y]的距离[d=x0=l28psin2α+y022p=l28psin2α+p2cos2αsin2α][=l28psin2α+p21sin2α-p2].令[μ=sin2α],由[α∈0,π]知,[0从而[d=l28pμ+2pl2μ-p2] .若[2pl≤1]即[l≥2p]时,[dmin=l-p2],此时[sin2α=2pl].若[2pl>1]即[0除上述几类最值问题,还有很多类型.解题中要灵活运用抛物线的定义、平面几何知识化为熟悉的类型运用常规方法求解.。
关于抛物线的十个最值问题

竭诚为您提供优质的服务,优质的文档,谢谢阅读/双击去除关于抛物线的十个最值问题本文用初等方法讨论了与抛物线有关的若干几何最值问题,得到了十个有趣的结论.为方便读者摘用,现用定理形式叙述如下:定理1.抛物线的所有焦半径中,以过顶点的焦半径为最短.证明:不妨设抛物线的极坐标方程为ρ= ,则显然有ρ≥ ,其中等号成立当且仅当θ=2kπ+π(k∈Z)即焦半径通过抛物线的顶点时.证毕.定理2.抛物线的过焦点的所有弦中,以抛物线的通径为最短.证明:设抛物线极坐标方程为ρ= ,焦点弦为Ab,且设A(ρ1,θ),b(ρ2,θ+π),则有│Ab│=ρ1+ρ2= + = ≥2p=通径长,其中等号成立当且仅当θ=kπ+π/2(k∈Z)即弦Ab为通径时.证毕.定理3.设A(a,0)是抛物线y2=2px(p>0)的对称轴上的定点,m(x,y)是抛物线上的动点,则│mA│min=证明:由│mA│2=(x-a)2+y2=(x-a)2+2px=x2-2(a-p)x+a2 =[x-(a-p)]2+p(2a-p),并且注意到x∈[0,+∞),立知结论成立.证毕.定理4.设A(a,b)是抛物线y2=2px(p>0)内一定点,F是焦点,m是抛物线上的动点,则(│mA│+│mF│)min=a+p/2.Q m A(a,b)证明:如图1所示,作AQ⊥准线L:x=-p/2于Q,则知o F x(│mA│+│mF│)min=│AQ│=a-(-p/2)=a+p/2.证毕. 图1定理5.设线段Ab是抛物线y2=2px(p>0)的过焦点的弦,分别以A、b 为切点的抛物线的两条切线相交于点m,则三角形Abm的面积的最小值为p2.证明:设A(x1,y1),b(x2,y2),则由A、F、b三点共线可得:x1y2-x2y1=p/2.(y2-y1) (1)于是利用(1)式由两切线方程yAm:y1y=p(x+x1),Abm:y2y=p(x+x2),m F x易得m的坐标(x,y)适合: b∵kmF·kAF=-1,∴mF⊥Ab,即│mF│是△mAb的Ab边上的高. 图2∵│mF│≥│FK│(焦点F到准线x=-p/2的距离)=p,又由定理2知│Ab│≥2p(通径长),∴s△mAb=1/2·│Ab│·│mF│≥1/2·2p·p=p2,因其中等号当且仅当Ab⊥x轴时成立,故三角形mAb的最小值为p2.证毕.定理6.过抛物线y2=2px的顶点o引两条互相垂直的动弦oA和ob,则三角形oAb的面积的最小值为4p2. y证明:设A(x1,y1),b(x2,y2),则由oA⊥ob得Ax1x2+y1y2=0 (1)o x将y12=2px1,y22=2px2代入(1)立得:x1x2=4p2 (2)于是b(s△oAb)2=1/4·│oA│2·│ob│2图3=1/4·(x12+y12)·(x22+y22)=1/4·(x12+2px1)·(x22+2px2)=1/4·[(x1x2)2+2px1x2(x1+x2)+4p2x1x2]≥1/4.[(x1x2)2+2px1x2(2√x1x2)+4p2x1x2] (3)将(2)式代入(3)则得(s△oAb)2≥16p4,从而s△oAb≥4p2,因其中等号当x1=x2=2p时取到,故三角形oAb的面积的最小值为4p2。
高考数学解题方法微专题(28)抛物线中的最值问题(含解析)

微专题(二十八) 抛物线中的最值问题求解与抛物线有关的最值问题方法较多,一般需要通过数形结合或利用函数思想来求最值,下面就抛物线最值问题的求法作一归纳.1.定义转换法[例1] 已知点P 是抛物线y 2=2x 上的动点,B (-1,1),点P 到直线l :x =-12的距离为d ,求d +|PB |的最小值.解析:由题意得抛物线y 2=2x 的焦点F ⎝ ⎛⎭⎪⎫12,0,直线l 是抛物线的准线,如图,连接BF ,PF ,所以d =|PF |,则d +|PB |=|PF |+|PB |≥|BF |=⎝ ⎛⎭⎪⎫-1-122+(1-0)2=132,当且仅当B ,P ,F 三点共线时取等号,所以d +|PB |的最小值为132. 名师点评 与抛物线上的点到准线距离有关的最值问题,一般都是利用抛物线的定义,将到准线的距离转化为到焦点的距离,然后通过数形结合直接判断出取得最值时所要满足的条件,这样就能避免烦琐的代数运算.[例2] 抛物线y =-x 2上的点到直线4x +3y -8=0距离的最小值是________.解析:解法一 如图,设与直线4x +3y -8=0平行且与抛物线y =-x 2相切的直线为4x+3y +b =0,切线方程与抛物线方程联立得⎩⎪⎨⎪⎧y =-x 2,4x +3y +b =0,消去y 整理得3x 2-4x -b =0,则Δ=16+12b =0,解得b =-43,所以切线方程为4x +3y -43=0,抛物线y =-x 2上的点到直线4x +3y -8=0距离的最小值是这两条平行线间的距离d =|8-43|5=43.解法二 由y =-x 2,得y ′=-2x .如图,设与直线4x +3y -8=0平行且与抛物线y =-x 2相切的直线与抛物线的切点是T (m ,-m 2),则切线斜率k =y ′|x =m =-2m =-43,所以m =23,即切点T ⎝ ⎛⎭⎪⎫23,-49,点T 到直线4x +3y -8=0的距离d =⎪⎪⎪⎪⎪⎪83-43-816+9=43,由图知抛物线y =-x 2上的点到直线4x +3y -8=0距离的最小值是43.答案:43名师点评 若抛物线上的点P 到直线l 的距离最小,则过点P 与l 平行的直线与抛物线相切,且最小距离为两平行直线间的距离,所以可将问题转化为求与抛物线相切的直线,然后求两平行直线间的距离.3.函数法针对上面的例2,我们给出第三种解决方法:解法三 设P (x ,-x 2),则点P 到直线4x +3y -8=0的距离d =|4x -3x 2-8|16+9=15⎪⎪⎪⎪⎪⎪3⎝ ⎛⎭⎪⎫x -232+203=35⎝ ⎛⎭⎪⎫x -232+43,在抛物线y =-x 2中,x ∈R ,所以当x =23时,d 取得最小值43,即抛物线y =-x 2上的点到直线4x +3y -8=0距离的最小值是43.[例3] 若点P 在抛物线y 2=x 上,点Q 在圆(x -3)2+y 2=1上,则|PQ |的最小值为________.解析:由题意得抛物线与圆不相交,且圆的圆心为A (3,0),则|PQ |≥|PA |-|AQ |=|PA |-1,当且仅当P ,Q ,A 三点共线时取等号,所以当|PA |取得最小值时,|PQ |最小.设P (x 0,y 0),则y 20=x 0,|PA |=(x 0-3)2+y 20=x 20-6x 0+9+x 0=⎝⎛⎭⎪⎫x 0-522+114,当且仅当x 0=52时,|PA |取得最小值112,此时|PQ |取得最小值112-1. 答案:112-1 名师点评 解与抛物线有关的最值问题可通过两点间距离公式或者点到直线的距离公式建立目标函数,再用求函数最值的方法求解.解题的关键是根据所给抛物线方程设出动点坐标.。
抛物线中的面积最值问题

抛物线中图形面积的最大(小)值问题解题思路:1. 坐标系内动点的坐标常常用解析式的代数式表示纵坐标;2. 表示坐标系中线段的长度一般用上减下(纵坐标),右减左(横坐标);3. 利用点的坐标代数式表示出相关线段的长度或图形的面积的函数关系式;4.用公式 21水平底×铅锤高求三角形面积5.求所列函数关系式的最大(小)值.6.用抛物线的切线性质求最大面积。
训练题:1.如图,抛物线y=-x 2+2x+3与X 轴相交于A 、B 两点(点A 在点B 的左侧),与y 轴相交于点C ,顶点为D.(1)直接写出A 、B 、C 三点的坐标和抛物线的对称轴;(2)连接BC ,与抛物线的对称轴交于点E ,点P 为线段BC 上的一个动点,过点P 作PF ∥DE 交抛物线于点F ,设点P 的横坐标为m ;①用含m 的代数式表示线段PF 的长,并求出当m 为何值时,四边形PEDF 为平行四边形? ②设△BCF 的面积为S ,求S 与m 的函数关系式.并求S 最大时的点P 的坐标.2.已知:抛物线y=ax2+bx+c (a ≠0)的对称轴为x=-1,与x 轴交于A ,B 两点,与y 轴交于点C ,其中A (-3,0),C (0,-2) (1)求这条抛物线的函数表达式;(2)已知在对称轴上存在一点P ,使得△PBC 的周长最小.请求出点P 的坐标; (3)若点D 是线段OC 上的一个动点(不与点O 、点C 重合).过点D 作DE ∥PC 交x 轴于点E .连接PD 、PE .设CD 的长为m ,△PDE 的面积为S .求S 与m 之间的函数关系式.试说明S 是否存在最大值?若存在,请求出最大值;若不存在,请说明理由.(1)由题意得129302baa b c c -=--+==-解得 23432a b c ===-∴此抛物线的解析式为y =32x 2+34x -2 (2)连结AC 、BC .因为BC 的长度一定,所以△PBC 周长最小,就是使PC+PB 最小.B 点关于对称轴的对称点是A 点,AC 与对称轴x =-1的交点即为所求的点P. 设直线AC的表达式为y=kx+b则⎩⎨⎧-==+-2b 0b k 3 解得⎪⎩⎪⎨⎧-=-=2b 32k ∴此直线的表达式为y =-32x -2 把x =-1代入得y =-34 ∴P 点的坐标为(-1,-34) 解法(二)连结AC 、BC .因为BC 的长度一定,所以△PBC 周长最小,就是使PC+PB 最小. B 点关于对称轴的对称点是A 点,AC 与对称轴x =-1的交点即为所求的点P. 设对称轴x =-1与x 轴的交点为F,由题意知OC=2,OA=3,OF=1, PF ∥OD∴∠APF=∠ACO,∠APF=∠AOC ∴∆APF ∽∆ACO ∴ PF AFOC OA=即3123PF -= ∴PF=43∴P 点的坐标为(-1,-34) (3)S 存在最大值 解法(一): ∵DE ∥PC 即DE ∥AC ∴∆OED ∽∆OAC ∴OD OE OC OA =即32m 2OE =- ∴OE =3-23m ,AE =3-OE =23m 方法一: 连结OPS =S 四边形PDOE -S △OED =S △POE +S △POD -S △OED=21⨯(3-23m )⨯34+21⨯(2-m)⨯1-21⨯(3-23m )⨯(2-m) =-43m 2+23m∵-43<0∴当m =1时,S 最大=-43+23=43方法二:S =S △OAC -S △OED -S △AEP -S △PCD=21⨯3⨯2-21⨯(3-23m )⨯(2-m )-21⨯23m ⨯34-21⨯m ⨯1 =-43m 2+23m =233(1)44m --+∵-43<0∴当m =1时,S 最大=43EDPxAyCOB 第24题图3.如图1,一条抛物线与轴交于A,B两点(点A在点B的左侧),与轴交于点C,且当x=-1和x=3时,的值相等.直线与抛物线有两个交点,其中一个交点的横坐标是6,另一个交点是这条抛物线的顶点M.(1)求这条抛物线的表达式.(2)动点P从原点O出发,在线段OB上以每秒1个单位长度的速度向点B运动,同时动点Q 从点B出发,在线段BC上以每秒2个单位长度的速度向点C运动,当一个点到达终点时,另一个点立即停止运动,设运动时间为秒.①若使△BPQ为直角三角形,请求出所有符合条件的值;②求为何值时,四边形ACQ P的面积有最小值,最小值是多少?(3)如图2,当动点P运动到OB的中点时,过点P作PD⊥轴,交抛物线于点D,连接OD,OM,MD得△ODM,将△OPD沿轴向左平移个单位长度(),将平移后的三角形与△ODM重叠部分的面积记为,求与的函数关系式.解:(1) ∵当和时,的值相等,∴抛物线的对称轴为直线,把和分别代入中,得顶点,另一个交点坐标为(6,6),则可设抛物线的表达式为,将(6,6)代入其中,解得,∴抛物线的表达式为,即.(2)如图1,当时,解得.由题意知,A(2,0),B(4,0),所以OA=2,OB=4;当时,,所以点C(0,-3),OC=3,由勾股定理知BC=5,OP=1×t=t,BQ=.①∵∠PBQ是锐角,∴有∠PQB=90º或∠BPQ=90º两种情况:当∠PQB=90º时,可得△PQB∽△COB,∴,∴,∴;·当∠BPQ=90º时,可得△BPQ∽△BOC,∴,∴,∴.由题意知,∴当或时,以B,P,Q为顶点的三角形是直角三角形.②如图1,过点Q作QG⊥AB于G,∴△BGQ∽△BOC,∴,∴,∴,·∴S四边形ACQP=S△ABC- S△BPQ====.∵>0,∴四边形ACQP的面积有最小值,又∵满足,∴当时,四边形ACQP的面积最小,最小值是.(3)如图2,由OB=4得OP=2,把代入中,得,所以D(2,-3),直线CD∥x轴,设直线OD的解析式为,则,所以,因为△P1O1D1是由△POD 沿x轴向左平移m个单位得到的,所以P1(2-m,0),D1(2-m,-3),E(2-m,).设直线OM的解析式为,则,所以.①当时,作FH⊥轴于点H,由题意O1(-m,0),又O1D1∥OD,所以直线O1D1的解析式为.联立方程组,解得,所以,所以FH=,S四边形OFD1E=S□OO1D1D-S△OO1F-S△DD1E===.②如图3,当时,设D1P1交OM于点F,直线OM的解析式为,所以,所以,∴S△OEF===综上所述,.4.如图,已知直角梯形OABC的边OA在y轴的正半轴上,OC在x轴的正半轴上,OA=AB=2,OC=3,过点B作BD⊥BC,交OA于点D.将∠DBC绕点B按顺时针方向旋转,角的两边分别交y轴的正半轴、x轴的正半轴于E和F.(1)求经过A、B、C三点的抛物线的解析式;(2)当BE经过(1)中抛物线的顶点时,求CF的长;(3)连接EF,设△BEF与△BFC的面积之差为S,问:当CF为何值时S最小,并求出这个最小值.解:(1)由题意可得A(0,2),B(2,2),C(3,0),设所求抛物线的解析式为y=ax2+bx+c,则解得∴抛物线的解析式为y=-x2+x+2.(2)设抛物线的顶点为G,则G(1,).如图,过点G作GH⊥AB,垂足为H,则AH=BH=1,GH=-2=.∵EA⊥AB,GH⊥AB,∴EA∥GH.∴GH是△BEA的中位线,∴EA=2GH=.过点B作BM⊥OC,垂足为M,则BM=OA=AB.∵∠EBF=∠ABM=90°,∴∠EBA=∠FBM=90°-∠ABF,∴Rt△EBA≌Rt△FBM,∴FM=EA=.∵CM=OC-OM=3-2=1,∴CF=FM+CM=.(3)设CF=a,则FM=a-1或1-a,同时0<a<3∴BF 2=FM 2+BM 2=(a -1)2+22=a 2-2a +5. ∵△EBA ≌△FBM ,∴BE =BF .则S △BEF =BE ×BF =BF 2=(a 2-2a +5),又∵S △BFC =FC ×BM =×a ×2=a ,∴S =(a 2-2a +5)-a =a 2-2a +,即S =(a -2)2+,∴当a =2(在0<a <3范围内)时,S 最小值=.5.(重庆市綦江县)如图,已知抛物线y =a (x -1)2+33(a ≠0)经过点A (-2,0),抛物线的顶点为D ,过O 作射线OM ∥AD .过顶点D 平行于x 轴的直线交射线OM 于点C ,B 在x 轴正半轴上,连结BC .(1)求该抛物线的解析式;(2)若动点P 从点O 出发,以每秒1个长度单位的速度沿射线OM 运动,设点P 运动的时间为t (s ).问:当t 为何值时,四边形DAOP 分别为平行四边形?直角梯形?等腰梯形?(3)若OC =OB ,动点P 和动点Q 分别从点O 和点B 同时出发,分别以每秒1个长度单位和2个长度单位的速度沿OC 和BO 运动,当其中一个点停止运动时另一个点也随之停止运动.设它们的运动的时间为t (s ),连接PQ ,当t 为何值时,四边形BCPQ 的面积最小?并求出最小值及此时PQ 的长.(4)在(3)中当t 为何值时,以O ,P ,Q 为顶点的三角形与△OAD 相似?(直接写出答案)DC M y P解:解:(1)把A(-2,0)代入y=a(x-1)2+,得0=a(-2-1)2+.∴a=-·································1分∴该抛物线的解析式为y=-(x-1)2+即y=-x2+x+.·······················3分(2)设点D的坐标为(x D,y D),由于D为抛物线的顶点∴x D=-=1,y D=-×12+×1+=.∴点D的坐标为(1,).如图,过点D作DN⊥x轴于N,则DN=,AN=3,∴AD==6.∴∠DAO=60°·······························4分∵OM∥AD①当AD=OP时,四边形DAOP为平行四边形.∴OP=6∴t=6(s)························5分②当DP⊥OM时,四边形DAOP为直角梯形.过点O作OE⊥AD轴于E.在Rt△AOE中,∵AO=2,∠EAO=60°,∴AE=1.(注:也可通过Rt△AOE∽Rt△AND求出AE=1)∵四边形DEOP为矩形,∴OP=DE=6-1=5.∴t=5(s)································6分③当PD=OA时,四边形DAOP为等腰梯形,此时OP=AD-2AE=6-2=4.∴t=4(s)综上所述,当t=6s、5s、4s时,四边形DAOP分别为平行四边形、直角梯形、等腰梯形.······································7分(3)∵∠DAO=60°,OM∥AD,∴∠COB=60°.又∵OC=OB,∴△COB是等边三角形,∴OB=OC=AD=6.∵BQ=2t,∴OQ=6-2t(0<t<3)过点P作PF⊥x轴于F,则PF=t.·······························8分∴S四边形BCPQ =S△COB -S△POQ=×6×-×(6-2t)×t=(t-)2+···························9分∴当t=(s)时,S四边形BCPQ的最小值为.················10分此时OQ=6-2t=6-2×=3,OP=,OF=,∴QF=3-=,PF=.∴PQ===·················12分6.(2014年四川巴中)如图,在平面直角坐标系xOy中,抛物线y=ax2+bx﹣4与x轴交于点A(﹣2,0)和点B,与y轴交于点C,直线x=1是该抛物线的对称轴.(1)求抛物线的解析式;(2)若两动点M,H分别从点A,B以每秒1个单位长度的速度沿x轴同时出发相向而行,当点M到达原点时,点H立刻掉头并以每秒个单位长度的速度向点B方向移动,当点M到达抛物线的对称轴时,两点停止运动,经过点M的直线l⊥x轴,交AC或BC 于点P,设点M的运动时间为t秒(t>0).求点M的运动时间t与△APH的面积S的函数关系式,并求出S的最大值.分析:(1)根据抛物线y=ax2+bx﹣4与x轴交于点A(﹣2,0),直线x=1是该抛物线的对称轴,得到方程组,解方程组即可求出抛物线的解析式;(2)由于点M到达抛物线的对称轴时需要3秒,所以t≤3,又当点M到达原点时需要2秒,且此时点H立刻掉头,所以可分两种情况进行讨论:①当0<t≤2时,由△AMP ∽△AOC,得出比例式,求出PM,AH,根据三角形的面积公式求出即可;②当2<t≤3时,过点P作PM⊥x轴于M,PF⊥y轴于点F,表示出三角形APH的面积,利用配方法求出最值即可.解:(1)∵抛物线y=ax2+bx﹣4与x轴交于点A(﹣2,0),直线x=1是该抛物线的对称轴,∴,解得:,∴抛物线的解析式是:y=x 2﹣x﹣4,(2)分两种情况:①当0<t≤2时,∵PM∥OC,∴△AMP∽△AOC,∴=,即=,∴PM=2t.解方程x2﹣x﹣4=0,得x1=﹣2,x2=4,∵A(﹣2,0),∴B(4,0),∴AB=4﹣(﹣2)=6.∵AH=AB﹣BH=6﹣t,∴S=PM•AH=×2t(6﹣t)=﹣t2+6t=﹣(t﹣3)2+9,当t=2时S的最大值为8;②当2<t≤3时,过点P作PM⊥x轴于M,作PF⊥y轴于点F,则△COB∽△CFP,又∵CO=OB,∴FP=FC=t﹣2,PM=4﹣(t﹣2)=6﹣t,AH=4+(t﹣2)=t+1,∴S=PM•AH=(6﹣t)(t+1)=﹣t2+4t+3=﹣(t﹣)2+,当t=时,S最大值为.综上所述,点M的运动时间t与△APQ面积S的函数关系式是S=,S的最大值为.7.如图1,已知直线12y x=-与抛物线2164y x=-+交于A B,两点.(1)求A B,两点的坐标;(2)求线段AB的垂直平分线的解析式;(3)如图2,取与线段AB等长的一根橡皮筋,端点分别固定在A B,两处.用铅笔拉着这根橡皮筋使笔尖P在直线AB上方的抛物线上移动,动点P将与A B,构成无数个三角形,这些三角形中是否存在一个面积最大的三角形?如果存在,求出最大面积,并指出此时P点的坐标;如果不存在,请简要说明理由.P8.如图,已知抛物线y=ax 2-2x+c 与x 轴交于A .B (3,0)两点,与y 轴的交点坐标为 (0,-3),直线l 与抛物线交于A .C 两点,其中C 点的横坐标为2. (1)求此抛物线的解析式以及抛物线的顶点坐标;(2)若点P 是线段AC 上的一个动点,过P 点作y 轴的平行线交抛物线于E 点,有人说当点E 处于抛物线的顶点时线段PE 的长度最大,你认为这种说法是否合理,若合理,请说明理由,若不合理,请求出线段PE 长度的最大值以及此时点E 的坐标;9.抛物线223y x x =-++与x 轴相交于A 、B 两点(点A 在点B 的左侧),y 轴相交于点C ,顶点为D .(1)直接写出A 、B 、C 三点的坐标和抛物线的对称轴;(2)连接BC ,与抛物线的对称轴交于点E ,点P 为线段BC 上的一个动点,过点P 作PF DE ∥ 交抛物线于点F ,设点P 的横坐标为m ;①用含m 的代数式表示线段PF 的长,并求出当m 为何值时,四边形PEDF 为平行四边形? ②设BCF △的面积为S ,求S 与m 的函数关系式,并求S 最大时的点P 的坐标.xy D C A O BAB C A xy FO D E 10.已知:抛物线的对称轴为x=-1,与x 轴交于A B ,两点,与y 轴交于点C ,其中()30A -,、()02C -,.(1)这条抛物线的函数表达式: .(2)已知在对称轴上存在一点P ,使得PBC △的周长最小.请求出点P 的坐标.(3)若点D 是线段OC 上的一个动点(不与点O 、点C 重合).过点D 作DE PC ∥交x 轴于点E .连接PD 、PE .设CD 的长为m ,PDE △的面积为S .求S 与m 之间的函数关系式.试说明S 是否存在最大值,若存在,请求出最大值;若不存在,请说明理由.11.如图,已知直角梯形OABC 的边OA 在y 轴的正半轴上,OC 在x 轴的正半轴上,OA =AB =2,OC =3,过点B 作BD ⊥BC ,交OA 于点D .将∠DBC 绕点B 按顺时针方向旋转,角的两边分别交y 轴的正半轴、x 轴的正半轴于E 和F .(1)经过A 、B 、C 三点的抛物线的解析式: ; (2)当BE 经过(1)中抛物线的顶点时,求CF 的长;(3)连结EF ,设△BEF 与△BFC 的面积之差为S ,问:当CF 为何值时S 最小,并求出这个最小值.A C x yB O。
抛物线中的若干最值问题

抛物线中的若干最值问题
1.抛物线的最高点在哪里?
抛物线的最高点,即顶点,是x坐标为-b/2a的点,y坐标为f(-
b/2a)。
2.抛物线与x轴交点有几个?
抛物线与x轴交点有0个、1个或2个,具体取决于抛物线的开口方向和方程的根。
3.抛物线的对称轴方程是多少?
抛物线的对称轴方程是x=-b/2a,具有以下特点:
-对称轴垂直于x轴;
-顶点位于对称轴上。
4.抛物线的最小值在哪里?
当抛物线开口向上时,抛物线没有最小值,最小值为负无穷;当抛物线开口向下时,最小值为f(-b/2a)。
5.抛物线有没有最大值?
当抛物线开口向上时,最大值为f(-b/2a);当抛物线开口向下时,抛物线没有最大值,最大值为正无穷。
6.抛物线经过定点的条件是什么?
设定点为(x0,y0),则抛物线经过该点的条件是方程f(x0)=y0成立。
7.抛物线对于x轴的对称点是哪个?
抛物线上任意一点与x轴对称的点的纵坐标为该点纵坐标的相反数,横坐标不变。
8.抛物线的拐点在哪里?
当抛物线开口向上并且a>0时,抛物线不存在拐点;当抛物线开口向下并且a<0时,拐点的横坐标为-b/2a,纵坐标为f(-b/2a)-|a|/4。
9.抛物线的单调区间是什么?。
初中知识 抛物线上一点到直线距离最大

初中知识:抛物线上一点到直线距离最大一、概述在初中数学学习中,抛物线和直线是常见的图形,在实际问题中,我们经常需要求解抛物线上某一点到直线的距离。
在这篇文章中,我们将探讨如何求解抛物线上一点到直线距离的最大值,这个问题涉及到数学分析知识中的极值问题。
通过本文的学习,读者将了解到如何运用基本的数学知识解决复杂的实际问题。
二、基本概念1. 抛物线:抛物线是二次函数图像的一种特殊情况。
其一般方程为y=ax^2 +bx+c,其中a、b、c为常数且a≠0。
抛物线开口方向由系数a的正负来决定,当a>0时,抛物线开口向上,当a<0时,抛物线开口向下。
2. 直线:直线是一种线性函数图像,其方程一般为y=kx+b,其中k 和b为常数。
3. 距离公式:点P(x,y)到直线Ax+By+C=0的距离可以利用公式d = |Ax+By+C| / √(A^2+B^2)来计算。
三、问题提出假设有一条抛物线y=ax^2+bx+c和一条直线y=kx+d,现在需要求解抛物线上一点到直线的距离的最大值。
四、问题分析为了求解这个问题,我们可以依次进行以下步骤:1. 我们需要确定抛物线上一点的坐标。
假设抛物线上一点的坐标为(x,ax^2+bx+c)。
2. 我们利用距离公式计算点(x,ax^2+bx+c)到直线y=kx+d的距离。
3. 我们需要对距离进行求导,找到距离函数的极值点。
4. 我们判断极值点是距离函数的最大值还是最小值,从而求得抛物线上一点到直线距离的最大值。
五、问题求解1. 确定抛物线上一点的坐标假设抛物线的方程为y=ax^2+bx+c,直线的方程为y=kx+d。
设抛物线上一点的坐标为(x,ax^2+bx+c)。
2. 计算点到直线的距离利用距离公式d = |Ax+By+C| / √(A^2+B^2),其中A、B、C分别为直线的系数,可以计算出抛物线上一点到直线的距离。
3. 对距离进行求导我们得到点到直线的距离函数为f(x) = |ax^2+bx+c-kx-d| /√(a^2+k^2)。
抛物线最值问题

抛物线最值问题抛物线是二次函数的一种,其一般形式为f(x)=ax²+bx+c (a ≠0)。
在解决实际问题时,我们经常会遇到与抛物线最值相关的问题。
这类问题通常涉及到求函数的最大值或最小值,以及确定使函数取得最值的自变量的值。
下面我们来探讨一下抛物线最值问题的解决方法。
我们需要了解抛物线的开口方向和对称轴。
开口方向由a的正负决定,当a>0时,抛物线向上开口;当a<0时,抛物线向下开口。
对称轴是抛物线上的一条水平直线,使得抛物线上的点关于这条直线对称。
对称轴的方程为x=-b/2a。
我们可以根据抛物线的开口方向和对称轴来确定函数的最值。
1. 当a>0时,抛物线向上开口,函数在对称轴处取得最小值。
最小值为f(-b/2a)=4ac-b²/4a。
此时,自变量x=-b/2a使得函数取得最小值。
2. 当a<0时,抛物线向下开口,函数在对称轴处取得最大值。
最大值为f(-b/2a)=4ac-b²/4a。
此时,自变量x=-b/2a使得函数取得最大值。
3. 当a=0时,抛物线变为一次函数y=ax²+bx+c。
此时,函数在顶点处取得最大值或最小值。
顶点的横坐标为-b/2a,纵坐标为f(-b/2a)=4ac-b²/4a。
此时,自变量x=-b/2a使得函数取得最大值或最小值。
通过以上分析,我们可以总结出求解抛物线最值问题的一般步骤:1. 确定抛物线的开口方向和对称轴。
2. 根据开口方向和对称轴确定函数的最值及其对应的自变量的值。
3. 将最值代入实际问题中进行求解。
抛物线中的定值、最值问题探究——以2017_年遵义市中考数学第27_题为例

抛物线中的定值、最值问题探究以2017年遵义市中考数学第27题为例包胜利(通渭县陇川学校ꎬ甘肃定西743319)摘㊀要:抛物线中的定值问题和最值问题是个难点ꎬ主要涉及动点及动点的路径问题ꎬ所利用的结论主要是两点之间线段最短以及垂线段最短.文章以2017年遵义市的一道中考题为例ꎬ先利用网络画板进行实验探究ꎬ然后给出试题的多种解法.关键词:定值ꎻ最值ꎻ动点ꎻ相似三角形中图分类号:G632㊀㊀㊀文献标识码:A㊀㊀㊀文章编号:1008-0333(2024)05-0002-03收稿日期:2023-11-15作者简介:包胜利(1975.10-)ꎬ男ꎬ甘肃省通渭人ꎬ本科ꎬ中小学一级教师ꎬ从事初中数学教学研究.㊀㊀初中最值问题大致分为几何最值和代数最值两类.几何最值是指在一定条件下ꎬ求几何图形中某个确定的几何量(如长度㊁角度㊁面积等)的最大值或最小值ꎬ而代数最值是指求一些简单的代数式或与实际问题相关(如用料最省㊁成本最低㊁能耗最少㊁产值最高㊁利润最高等)的问题.1几何最值问题的求解思路在初中阶段ꎬ解决几何最值问题的依据有两个ꎬ一是两点之间ꎬ线段最短ꎻ二是垂线段最短.由这两个依据延伸出以下常用的结论:三角形任意两边之和大于第三边ꎬ任意两边之差小于第三边ꎻ过圆内一点的所有弦中ꎬ垂直于过这点的直径的弦最短ꎻ直径是圆中最长的弦.因此ꎬ几何方法求最值的思路是:将几何图形中的最值转化成基本的几何模型 两点之间ꎬ线段最短 和 垂线段最短 .其关键是抓住运动变化中不变的相关量(长度㊁角度㊁面积)与变化的相关量比较大小.即通过平移㊁旋转㊁轴对称将多条线段首尾相连转化到两定点之间的线段上ꎬ实现 折 转 直 ꎬ利用 两点之间ꎬ线段最短 说明最小.或者将问题转化为一定点到一条定直线的距离ꎬ利用 垂线段最短 即可得出最小值.2几何最值案例分析2.1试题呈现如图1ꎬ抛物线y=ax2+bx-a-b(a<0ꎬaꎬb为常数)与x轴交于AꎬC两点ꎬ与y轴交于B点ꎬ直线AB的函数关系式为y=89x+163.(1)求该抛物线的解析式与C点坐标.(2)已知点M(mꎬ0)是线段OA上的一个动点ꎬ过点M作x轴的垂线l分别与直线AB和抛物线交于DꎬE两点ꎬ当m为何值时ꎬΔBDE恰好是以DE为底边的等腰三角形[1](3)在(2)问条件下ꎬ当ΔBDE恰好是以DE为底边的等腰三角形时ꎬ动点M相应位置记为点Mᶄꎬ将OMᶄ绕原点O顺时针旋转得到ON(旋转角在0ʎ到90ʎ之间).①探究:线段OB上是否存在定点P(P不与OꎬB重合)ꎬ无论ON如何旋转ꎬNPNB始终保持不变?若2存在ꎬ试求出P点坐标ꎻ若不存在ꎬ请说明理由[2].②试求出此旋转过程中ꎬNA+34NB的最小值[3].图1㊀中考题图2.2探究实验第(2)问:如图2ꎬ拖动点Mꎬ观察BE和BD测量值的变化ꎬ是否存在相等的情形ꎬ有几种情况?第(3)问:如图3所示ꎬ拖动点Nꎬ观察对应测量值ꎬ可以发现:当点P的坐标为(0ꎬ3)时ꎬNPNB=34(定值)ꎻ当ΔNOPʐΔBON时ꎬNA+34NB存在最小值ꎬ即求NA+NP的最小值.图2㊀探究等腰三角形图3㊀探究最小值问题2.3思路分析(1)根据已知条件求出AꎬB坐标ꎬ用待定系数法可求出抛物线解析式.(2)作BFʅlꎬ与l交于F点ꎬ根据等腰三角形的性质得到EF=FD=12DEꎬFM=OB=163ꎬ列方程即可得到结论.图4㊀探究定值问题(3)对于问题1ꎬ如图4所示ꎬ探究NPNB的定值是一个比值ꎬ可联想相似三角形或三角函数ꎬ寻找与固定点(点MᶄꎬOꎬB)有关的三角形ꎬ即探究以点OꎬPꎬBꎬN为顶点组成的某两个三角形是否相似ꎬ由此猜想NPNB可能的比值.若ΔNBPʐΔOBN时ꎬNBOB=NPONꎬ可得NPNB=ONOB=34ꎬ根据已知条件无法求出点P的坐标.若әNOPʐәBON时ꎬOPON=NPNB=ONOB=34ꎬNPNB不变ꎬ根据已知条件ON2=OP OBꎬ可以求出点P坐标是确定的.对于问题2ꎬ求两条线段和的最小值ꎬ首先想到 将军饮马 问题模型ꎬ即 PA+PB 型最短问题ꎬ但两条线段系数不为1.因此将34NB的系数转化为系数是1的线段ꎬ由问题1知NPNB=OPON=34ꎬ得到NP=34NBꎬ将NA+34NB转化为两个定点AꎬP间折线段和的最小值问题ꎬ即求NA+NP的最小值.2.4解法探究(1)因为直线l:y=89x+163与x轴交于A(-6ꎬ0)ꎬ与y轴交于B0ꎬ163æèçöø÷ꎬ将AꎬB坐标代人抛物线方程可得36a-6b-a-b=0ꎬ-a-b=163ꎬ{解得a=-89ꎬb=-409.ìîíïïïï所以该抛物线的解析式为y=-89x2-409x+163.由直线x=-b2a=-52可知点C坐标(1ꎬ0).(2)解法1㊀如图5所示ꎬEMʅx轴ꎬM(mꎬ0)ꎬ则Dmꎬ89m+163æèçöø÷ꎬEmꎬ-89m2-409m+163æèçöø÷.3ΔBDE是以DE为底边的等腰三角形ꎬ作BFʅlꎬ与l交于F点ꎬ所以DF=12DE.因为DE=-89m2-409m+163æèçöø÷-89m+163æèçöø÷=-89m2-489mꎬ由DF+DM=FM可得ꎬ12-89m2-489mæèçöø÷+89m+163æèçöø÷=163ꎬ整理得m2+4m=0ꎬ解得m1=-4ꎬm2=0(不合题意ꎬ舍去).图5㊀解法1图㊀㊀㊀㊀㊀㊀㊀㊀㊀图6㊀解法2图解法2㊀如图6所示ꎬ因为点M(mꎬ0)ꎬ且lʅx轴ꎬ所以Dmꎬ89m+163æèçöø÷.当DE为底时ꎬ作BGʅDE于Gꎬ则EG=GD=12EDꎬGM=OB=163ꎬ所以12-89m2-409m+163+89m+163æèçöø÷=163ꎬ解得m1=-4ꎬm2=0(不合题意ꎬ舍去).(3)解法1㊀对于问题1ꎬ存在点Pꎬ使NPNB始终保持不变.如图7所示ꎬ因为øNOP=øBONꎬ所以当øONP=øOBN时ꎬәONPʐәOBNꎬ此时NPNB=OPON=ONOB=4163=34ꎬ始终保持不变ꎬ所以OP=34ON=34ˑ4=3ꎬ存在点P(0ꎬ3).结论:无论ON如何旋转ꎬ总存在P(0ꎬ3)ꎬ使NPNB始终保持不变.对于问题2ꎬ由问题1知ꎬNP=34BNꎬ其中P(0ꎬ3)ꎬ所以NA+34NB=NA+NPꎬ所以当AꎬNꎬP共线ꎬ即图7㊀第(3)问图当N点旋转到AP上时ꎬNA+34NB的值最小ꎬ最小值即为AP=32+62=35.解法2㊀对于问题1ꎬ存在点Pꎬ使得NPNB始终保持不变.因为ON=4ꎬOB=163ꎬøNOP=øBONꎬ所以当ΔNOPʐΔBON时ꎬOPON=NPNB=ONOB=34ꎬ所以NPNB始终保持不变ꎬ即OP=3ꎬ所以P(0ꎬ3).对于问题2ꎬ由问题1知ꎬOPON=NPNB=34ꎬ所以NP=34NBꎬ所以NA+34NB=NA+NPꎬ所以此时NꎬAꎬP三点共线ꎬ如图7所示ꎬ所以NA+34NBæèçöø÷min=32+62=35.3结束语探求定值一般是先分清问题的不变量与变量ꎬ而定值往往与这些不变量中的某些量(或它们的代数式)有关ꎬ常将一般问题特殊化ꎬ运用特殊情形(即用特殊值㊁特殊位置㊁特殊图形等)探求定值.参考文献:[1]陆丽丽.巧构造妙转化:另类线段和的最值问题[J].上海中学数学ꎬ2019(10):19-21ꎬ43.[2]孙玉军ꎬ罗勇ꎬ李圣波.2017年中考 图形的变化 专题解题分析[J].中国数学教育ꎬ2018(Z1):115-123.[3]李玉荣.三类新型最值问题的解法探究:以近年中考试题为例[J].初中数学教与学ꎬ2019(21):31-34.[责任编辑:李㊀璟]4。
抛物线最大值最小值怎么求图片

抛物线最大值最小值求解方法
抛物线是一种常见的曲线形式,在数学和物理领域中经常遇到。
对于给定的抛物线函数,我们常常需要求解其最大值和最小值,这些值对于理解曲线形态和应用中具有重要意义。
下面将介绍抛物线最大值和最小值的求解方法。
抛物线方程
抛物线的一般方程形式为y=ax2+bx+c,其中a、b和c为常数,a eq0。
这种形式的抛物线开口方向由a的正负性决定,当a>0时,抛物线开口向上,当a<0时,抛物线开口向下。
求解最大值和最小值
最大值
抛物线的最大值出现在抛物线开口向下时,对应于抛物线顶点。
抛物线的顶点坐标可以通过以下公式求解:
$$ x = -\\frac{b}{2a} $$
将x的值带入抛物线方程,即可得到最大值的纵坐标。
最小值
同理,抛物线的最小值出现在抛物线开口向上时,也对应于抛物线顶点处。
最小值的求解方法与最大值相似,通过求解顶点即可确定最小值的坐标。
示例
假设有抛物线y=2x2+4x−3,通过以上方法可以求解其最大值和最小值:1. 求解顶点x坐标:
$$ x = -\\frac{4}{2 \\times 2} = -1 $$
2. 将x=−1带入抛物线方程,得到最大值或最小值的纵坐标。
结论
通过以上方法,可以比较简单地求解抛物线最大值和最小值。
这对于分析抛物线曲线形态、求解优化问题等具有一定的应用意义。
当遇到需要求解抛物线最大值和最小值的问题时,可以结合以上方法进行计算。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解:设 = P (x, y ) ∴ y
2 2
Q P 点在抛物线上, 点在抛物线上, PA = = = (x − 3)2 + y x 2 − 6x + 9 + x x 2 − 5x + 9 5 2 11 (x − ) + 2 4
例三、 例三、 已知定点M ),F是抛物线y =2x的焦点 的焦点, 已知定点M(3,2),F是抛物线y2=2x的焦点, 在此抛物线上求一点P |PM|+|PF|取得最小值 取得最小值, 在此抛物线上求一点P,使|PM|+|PF|取得最小值, 求点P 求点P的坐标
分析: ,由抛物线的定义: 如图, 分析: 如图 由抛物线的定义:
抛物线上的点到焦点的距离 与到准线的距离相等。 与到准线的距离相等。 即|PF| = |PN| ∴ |PM|+|PF|= |PM|+|PN| ∴当 M、P、N三点共 线时距离之和最小。 线时距离之和最小。
N F F
M
P M
解: 如图所示 在抛物线 y2 = 2x上任取一点 上任取一点 P’(x’,y’),作P’N’⊥准线 ,作MN 准线L, 作 交抛物线于P( , ) ⊥L ,MN交抛物线于 (x,y) 交抛物线于 由抛物线的定义得: 由抛物线的定义得: |P’F|= |P’N’|
练习: 练习:
1.已知M(a,0) 为抛物线y = 2px(p> 0)的对称轴
2
上的一个定点在抛物线上求一点N, 使得 MN 最小
2、求抛物线y2=64x上的点到直线 、求抛物线 上的点到直线 4x+3y+46=0 距离最小值,并求取得最小值 距离最小值, 时抛物线上的点的坐标
课堂小结: 课堂小结:
分析1 动点在弧AB上运动, 分析1:动点在弧AB上运动,可以设 AB上运动 出点P的坐标,只要求出点P 出点P的坐标,只要求出点P到线段 AB所在直线AB的最大距离即为点 所在直线AB的最大距离即为点P AB所在直线AB的最大距离即为点P到 线段AB的最大距离, AB的最大距离 线段AB的最大距离,也就求出了 ABP的最大面积 的最大面积。 △ABP的最大面积。 分析2:我们可以连接AB, 分析 :我们可以连接AB,作平行 AB AB的直线 与抛物线相切, 的直线L AB的直线L与抛物线相切,求出直 的方程,即可求出直线L 线L的方程,即可求出直线L与AB 间的距离,从而求出△ABP面积的 间的距离,从而求出△ABP面积的 最大值和点P的坐标。 最大值和点P的坐标。
练习、 练习、
P为抛物线 2=4y上的一动点,定点 (8,7),求 为抛物线x 上的一动点, 为抛物线 上的一动点 定点A( ) 求 P到x轴与到点 的距离之和的最小值 9 轴与到点A的距离之和的最小值 到 轴与到点
y P A
F O
y P A
所求p 所求p 点位置
F
x
O
x
Q
小结: 小结:
几何法,运用数形结合的思想, 几何法,运用数形结合的思想,利用抛物线的定 将到焦点的距离转化为到准线的距离, 义,将到焦点的距离转化为到准线的距离,将图 形局部进行转化, 形局部进行转化,使最值问题得以求解
2
y
y=x2
∴ y = x2
P(x,y)
o x
−6
87 。 80
法二、 法二、判别式法
解:当L平移到与抛物线y=x2只有一个公共点时,设此时的 平移到与抛物线y=x 只有一个公共点时, 直线为L1 其方程为3x 4y-b=0。 L1, 3xL1的距离即为所求 的距离即为所求。 直线为L1,其方程为3x-4y-b=0。则L与L1的距离即为所求。 3x-4y+b=0 ① y=x2 ② 代入①可得: ②代入①可得:4x2 -3x+b=0 ∴ ⊿=(-3)2-4×4×b=0 可 4 ⋅ 1 ⋅(9 − r 2 ) = 0 11 ∴ r= 2
练习: 练习: 为抛物线y 上一动点, 为圆 为圆( 上一动点 若P为抛物线 2=x上一动点,Q为圆(x-3)2+y2=1 上 为抛物线 一动点, 一动点,求|PQ|的最小值 的最小值 11
2 −1
例二、 例二、 为抛物线y= 上的一动点, 设P为抛物线y= x2上的一动点,求P点到直线 3x-4y-6=0的距离的最小值 的距离的最小值。 L: 3x-4y-6=0的距离的最小值。 法一、 法一、目标函数法
解:设 P ( x, y ) Q P 点在抛物线上, 点在抛物线上, 3x − 4y − 6 d = 5 5 3 2 87 4(x − ) + 8 16 = 5 3 当 x = 时, d 有最小值为 8 = 3x − 4x
在解析几何中, 在解析几何中,常见的最值问题的求解方法主要 有以下几种: 有以下几种: 函数法:选择恰当的变量,根据题意建立目标函数, 函数法:选择恰当的变量,根据题意建立目标函数, 再探求目标函数的最值方法。 再探求目标函数的最值方法。 判别式法: 判别式法: 利用已知条件构造一个含有某一变量的一 元二次方程, 元二次方程,通过判断方程的判别式寻求 题目的答案。 题目的答案。 几何法:利用数形结合的思想, 几何法:利用数形结合的思想,借助于几何图形中的 一些特点,将图形局部进行转化, 一些特点,将图形局部进行转化,使最值问 题得以求解。 题得以求解。
L y A(4,4)
P o B(1,-2) x
小结: 小结:
对于抛物线上一点到定点或者是定直线的最值 问题, 问题,可以由两点间距离公式或者点到直线的 距离公式建立目标函数, 距离公式建立目标函数,再用函数最值的方法 求解;也可以通过一些几何性质和已知条件构 求解;也可以通过一些几何性质和已知条件构 造一个含有某一变量的一元二次方程, 造一个含有某一变量的一元二次方程,通过判 断方程的判别式寻求题目的答案。 断方程的判别式寻求题目的答案。
N’ N
P’ M P F
即:|P’F|+|P’M|= |P’N’|+|P’M|
重合时, 三点共线, 当P’和P重合时,即PN⊥L,N、P、M三点共线, 和 重合时 ⊥ , 、 、 三点共线 ∴ |P’M|+ |P’N’| ≥ |PM|+|PN|= |PM|+|PF| 的纵坐标等于点M的纵坐标 又∵点P的纵坐标等于点 的纵坐标,即y=2 的纵坐标等于点 的纵坐标, 所以, 的坐标为( , ) 所以,点P的坐标为(2,2) 的坐标为
y
y=x2
L1 L
9 16 ∴ L 与 L 1 的距离是 b = −
o
x
d = 为所求
− 6 − (− 3
2
9 16
)
+ (− 4 )2
87 = 80
.
练习:已知抛物线y2=4x,以抛物线上两点 练习:已知抛物线y =4x, A(4,4)、B(1,-2)的连线为底边 ABP,其顶点P 的连线为底边△ A(4,4)、B(1,-2)的连线为底边△ABP,其顶点P 在抛物线的弧AB上运动, AB上运动 ABP的最大面积 在抛物线的弧AB上运动,求: △ABP的最大面积 及此时点P的坐标。 及此时点P的坐标。
= x
5 当 x = 时, PA 取最小值 2
11 。 2
法二、 法二、判别式法 过A作同心圆,当圆与抛物线相 作同心圆 当圆与抛物线相 切时,P 点的距离最小,设为 设为r 切时 P到A点的距离最小 设为
(x − 3)2 + y 2 = r 2 则由 2 y =x
⇒ x − 5x + 9 − r = 0
