椭圆双曲线方程知识汇总
高中数学有关圆-椭圆-双曲线-抛物线的详细知识点

<一>圆的方程(x-a)^2+(y-b)^2=r^2,圆心O(a,b),半径r。
(1)圆的一般式方程:x^2+y^2+Dx+Ey+F=0此方程可用于解决两圆的位置关系:配方化为标准方程:(x+D/2)^2.+(y+E/2)^2=(D^2+E^2-4F)/4其圆心坐标:(-D/2,-E/2)半径为r=√[(D^2+E^2-4F)]/2此方程满足为圆的方程的条件是:D^2+E^2-4F>0若不满足,则不可表示为圆的方程(2)点与圆的位置关系点P(X1,Y1) 与圆(x-a)^2+(y-b) ^2=r^2的位置关系:⑴当(x1-a)^2+(y1-b) ^2>r^2时,则点P在圆外。
⑵当(x1-a)^2+(y1-b) ^2=r^2时,则点P在圆上。
⑶当(x1-a)^2+(y1-b) ^2<r^2时,则点P在圆内。
圆与直线的位置关系判断平面内,直线Ax+By+C=0与圆x^2+y^2+Dx+Ey+F=0的位置关系判断一般方法是:1.由Ax+By+C=0,可得y=(-C-Ax)/B,(其中B不等于0),代入x^2+y^2+Dx+Ey+F=0,即成为一个关于x的一元二次方程f(x)=0。
利用判别式b^2-4ac的符号可确定圆与直线的位置关系如下:如果b^2-4ac>0,则圆与直线有2交点,即圆与直线相交。
如果b^2-4ac=0,则圆与直线有1交点,即圆与直线相切。
如果b^2-4ac<0,则圆与直线有0交点,即圆与直线相离。
2.如果B=0即直线为Ax+C=0,即x=-C/A,它平行于y轴(或垂直于x 轴),将x^2+y^2+Dx+Ey+F=0化为 (x-a)^2+(y-b) ^2=r^2。
令y=b,求出此时的两个x值x1、x2,并且规定x1<x2,那么:当x=-C/A<x1或x=-C/A>x2时,直线与圆相离;当x1<x=-C/A<x2时,直线与圆相交;半径r,直径d在直角坐标系中,圆的解析式为:(x-a)^2+(y-b)^2=r^2;x^2+y^2+Dx+Ey+F=0=> (x+D/2)^2+(y+E/2)^2=(D^2+E^2-4F)/4=> 圆心坐标为(-D/2,-E/2)其实只要保证X方Y方前系数都是1就可以直接判断出圆心坐标为(-D/2,-E/2)这可以作为一个结论运用的且r=根号(圆心坐标的平方和-F)<二>椭圆的标准方程椭圆的标准方程分两种情况:当焦点在x轴时,椭圆的标准方程是:x^2/a^2+y^2/b^2=1,(a>b>0);当焦点在y轴时,椭圆的标准方程是:y^2/a^2+x^2/b^2=1,(a>b>0);其中a>0,b>0。
高中数学【椭圆与双曲线】知识点总结

高中数学【椭圆与双曲线】知识点总结姓名:(一)椭圆1.椭圆的定义如果平面内一动点到两定点距离之和等于正的常数(大于两定点的距离),则动点的规迹是椭圆即|PF1|+|PF2|=2a其中P是动点,F1,F2是定点且|F1F2|=2C当a>c时表示当a=c时表示当a<c时第二定义:动点M与一个定点的距离和它到一条定直线的距离的比是常数e(0<e<1)时,这个点的规迹是椭圆。
定点是,定直是e是2.椭圆的标准方程参数方程(1)标准方程(2)参数方程3.椭圆的性质(1)焦点在x轴上的椭圆标准方程x,y的范围顶点焦点对称轴对称中心长半轴的长短半轴的长焦距离心率e=范围e越大椭圆越e越小椭圆越准线焦半径公式|PF1|=|PF2|=(F1,F2分别为椭圆的左右两焦点,P为椭圆上的一点)椭圆的通径(过椭圆的一个焦点F且垂直于它过焦点的对称轴的弦)|P1P2|=(2)焦点在y轴上的椭圆标准方程x,y的范围顶点焦点对称轴对称中心长半轴的长短半轴的长焦距离心率e=范围e越大椭圆越e越小椭圆越准线焦半径公式|PF1|=|PF2|=(F1,F2分别为椭圆的下上两焦点,P为椭圆上的一点)4.椭圆系(1)共焦点的椭圆系方程为2221x yk k c+=-(其中k>c2,c为半焦距)(2)具有相同离心率的标准椭圆系的方程2222(0) x ya bλλ+=>(二)双曲线1.双曲线的定义如果平面内一个动点到两定点距离之差的绝对值等于正的常数(小于两定点间的距离),那么动点的轨迹是双曲线若一个动点到两定点距离之差等于一个常数,常数的绝对值小于两定点间的距离,那么动点的轨迹是双曲线的一支F1,F2为两定点,P为一动点,(1)若||PF1|-|PF2||=2a①0<2a<|F1F2|则动点P的轨迹是②2a=|F1F2|则动点P的轨迹是③2a=0则动点P的轨迹是(2)若|P F1|-|PF2|=2a①0<2a<|F1F2|则动点P的轨迹是②2a=|F1F2|则动点P的轨迹是③2a=0则动点P的轨迹是2.双曲线的标准方程3.双曲线的性质(1)焦点在x轴上的双曲线标准方程x,y的范围顶点焦点对称轴对称中心实半轴的长虚半轴的长焦距离心率e=范围e越大双曲线的开口越e越小双曲线的开口越准线渐近线焦半径公式|PF1|=|PF2|= (F1,F2分别为双曲线的左右两焦点,P为椭圆上的一点)(3)焦点在y轴上的双曲线标准方程x,y的范围顶点焦点对称轴对称中心实半轴的长虚半轴的长焦距离心率e=范围e越大双曲线的开口越e越小双曲线的开口越准线渐近线焦半径公式|PF1|=|PF2|= (F1,F2分别为双曲线的下上两焦点,P为椭圆上的一点)4.等轴双曲线22(0)x yλλ=±③离心率为-=≠特点①实轴与虚轴长相等②渐近线互相垂直y x5.共轭双曲线以已知双曲线的虚轴为实轴,实轴为虚轴的双曲线叫原双曲线的共轭双曲线特点①有共同的渐近线②四焦点共圆双曲线22221x ya b+=的共轭双曲线是6.双曲线系(1)共焦点的双曲线的方程为2221x yk k c+=-(0<k<c2,c为半焦距)(2)共渐近线的双曲线的方程为2222(0) x ya bλλ-=≠。
椭圆双曲线知识点总结

椭圆知识点【知识点1】椭圆的概念:在平面内到两定点F 1、F 2的距离的和等于常数(大于|F 1F 2|)的点的轨迹叫椭圆.这两定点叫做椭圆的焦点,两焦点间的距离叫做焦距.当动点设为M 时,椭圆即为点集P ={}12|2M MF MF a += 注意:若)(2121F F PF PF =+,则动点P 的轨迹为线段21F F ;若)(2121F F PF PF <+,则动点P 的轨迹无图形。
【知识点2】椭圆的标准方程焦点在x 轴上椭圆的标准方程: ()222210x y a b a b += >>,焦点坐标为(c ,0),(-c ,0)焦点在y 轴上的椭圆的标准方程为:()222210x y a b b a+= >>焦点坐标为(0,c ,)(o ,-c )【知识点3】椭圆的几何性质:规律:(1)椭圆焦点位置与x 2,y 2系数间的关系:焦点在分母大的那个轴上.(2)椭圆上任意一点M 到焦点F 的所有距离中,长轴端点到焦点的距离分别为最大距离和最小距离,且最大距离为a +c ,最小距离为a -c .(3)在椭圆中,离心率22222221a b a b a a c a c e -=-===(4)椭圆的离心率e 越接近1椭圆越扁;e 越接近于0,椭圆就接近于圆; (5)离心率公式:在21PF F ∆中,α=∠21F PF ,β=∠12F PF ,()βαβαsin sin sin ++=e二、椭圆其他结论标准方程()222210x y a b a b += >> ()222210x y a b b a += >> 图形性质范围 a x a -≤≤b y b -≤≤对称性 对称轴:坐标轴 对称中心:原点顶点A 1(-a,0), A 2(a,0)B 1(0,-b ),B 2(0,b )A 1(0,-a ),A 2(0,a )B 1(-b,0),B 2(b,0)轴 长轴A 1A 2的长为2a ;短轴B 1B 2的长为2b焦距 ∣F 1F 2 |=2c离心率 e=ca∈(0,1) a ,b ,c 的关系c 2=a 2-b 21、若000(,)P x y 在椭圆22221x y a b +=上,则过0P 的椭圆的切线方程是00221x x y ya b+=若已知切线斜率K ,切线方程为222b k a kx y +±=2、若000(,)P x y 在椭圆22221x y a b +=外 ,则过Po 作椭圆的两条切线切点为P 1、P 2,则切点弦P 1P 2的直线方程是00221x x y ya b+= 3、椭圆22221x y a b+= (a >b >0)的左右焦点分别为F 1,F 2,点P 为椭圆上任意一点θ=∠21PF F ,则椭圆的焦点角形的面积为2tan221θb S PF F =∆4、以焦点半径PF 1为直径的圆必与以长轴为直径的圆内切.5、过焦点的弦中,通径(过焦点且与焦点所在坐标轴垂直的弦)最短ab 226、过椭圆一个焦点F 的直线与椭圆交于两点P 、Q, A 1、A 2为椭圆长轴上的顶点,A 1P 和A 2Q 交于点M ,A 2P 和A 1Q 交于点N ,则MF ⊥NF 。
椭圆双曲线抛物线知识点汇总

椭圆双曲线抛物线知识点汇总一、椭圆椭圆是平面内到定点 F1、F2 的距离之和等于常数(大于|F1F2|)的动点 P 的轨迹,F1、F2 称为椭圆的焦点,两焦点的距离|F1F2|称为椭圆的焦距。
1、椭圆的标准方程焦点在 x 轴上:\(\frac{x^2}{a^2} +\frac{y^2}{b^2} = 1\)(\(a > b > 0\)),其中\(a\)为长半轴长,\(b\)为短半轴长,\(c\)为半焦距,满足\(c^2 = a^2 b^2\)。
焦点在 y 轴上:\(\frac{y^2}{a^2} +\frac{x^2}{b^2} = 1\)(\(a > b > 0\))。
2、椭圆的性质范围:对于焦点在 x 轴上的椭圆,\(a \leq x \leq a\),\(b\leq y \leq b\);对于焦点在 y 轴上的椭圆,\(b \leq x \leq b\),\(a \leq y \leq a\)。
对称性:椭圆关于 x 轴、y 轴和原点对称。
顶点:焦点在 x 轴上时,顶点坐标为\((\pm a, 0)\),\((0, \pm b)\);焦点在 y 轴上时,顶点坐标为\((0, \pm a)\),\((\pm b, 0)\)。
离心率:椭圆的离心率\(e =\frac{c}{a}\)(\(0 < e <1\)),它反映了椭圆的扁平程度,\(e\)越接近0,椭圆越接近圆;\(e\)越接近 1,椭圆越扁。
3、椭圆的参数方程焦点在 x 轴上:\(\begin{cases}x = a\cos\theta \\ y =b\sin\theta\end{cases}\)(\(\theta\)为参数)焦点在 y 轴上:\(\begin{cases}x = b\cos\theta \\ y =a\sin\theta\end{cases}\)(\(\theta\)为参数)4、椭圆中的焦点三角形设 P 为椭圆上一点,F1、F2 为焦点,\(\angle F1PF2 =\theta\),则三角形 PF1F2 的面积为\(S = b^2\tan\frac{\theta}{2}\)。
双曲线和椭圆知识点汇总

椭圆知识点知识要点小结:知识点一:椭圆的定义平面内一个动点P 到两个定点1F 、2F 的距离之和等于常数)2(2121F F a PF PF >=+ ,这个动点P 的轨迹叫椭圆.这两个定点叫椭圆的焦点,两焦点的距离叫作椭圆的焦距. 注意:若)(2121F F PF PF =+,则动点P 的轨迹为线段21F F ; 若)(2121F F PF PF <+,则动点P 的轨迹无图形.知识点二:椭圆的标准方程1.当焦点在x 轴上时,椭圆的标准方程:12222=+by a x )0(>>b a ,其中222b a c -=2.当焦点在y 轴上时,椭圆的标准方程:12222=+bx a y )0(>>b a ,其中222b a c -=;注意:1.只有当椭圆的中心为坐标原点,对称轴为坐标轴建立直角坐标系时, 才能得到椭圆的标准方程;2.在椭圆的两种标准方程中,都有)0(>>b a 和222b a c -=; 3.椭圆的焦点总在长轴上.当焦点在x 轴上时,椭圆的焦点坐标为)0,(c ,)0,(c -; 当焦点在y 轴上时,椭圆的焦点坐标为),0(c ,),0(c - 知识点三:椭圆的简单几何性质椭圆:12222=+by a x )0(>>b a 的简单几何性质(1)对称性:对于椭圆标准方程12222=+by a x )0(>>b a :说明:把x 换成x -、或把y 换成y -、或把x 、y 同时换成x -、y -、原方程都不变,所以椭圆12222=+by a x 是以x 轴、y 轴为对称轴的轴对称图形,并且是以原点为对称中心的中心对称图形,这个对称中心称为椭圆的中心。
(2)范围:椭圆上所有的点都位于直线a x ±=和b y ±=所围成的矩形内,所以椭圆上点的坐标满足a x ≤,b y ≤。
(3)顶点:①椭圆的对称轴与椭圆的交点称为椭圆的顶点。
高中椭圆双曲线抛物线知识点汇总

高中椭圆双曲线抛物线知识点汇总一、椭圆的定义和基本特性1. 椭圆的定义:椭圆是平面上到两定点F1和F2的距离之和为常数2a (a>0)的点P的轨迹。
2. 椭圆的基本特性:椭圆有两条对称轴,长轴和短轴,焦点到中心的距离为c,满足c²=a²-b²,离心率e的定义为e=c/a。
3. 椭圆的标准方程:椭圆的标准方程为x²/a²+y²/b²=1(a>b>0),中心在原点,长轴与x轴平行。
二、双曲线的定义和基本特性1. 双曲线的定义:双曲线是平面上到两定点F1和F2的距离之差为常数2a的点P的轨迹。
2. 双曲线的基本特性:双曲线有两条对称轴,两个顶点,离心率e的定义为e=c/a。
3. 双曲线的标准方程:双曲线的标准方程为x²/a²-y²/b²=1(a>0,b>0),中心在原点,x²项系数为正。
三、抛物线的定义和基本特性1. 抛物线的定义:抛物线是平面上到定点F与直线l的距离相等的点P 的轨迹。
2. 抛物线的基本特性:抛物线有焦点F和直线l两个重要元素,焦点到顶点的距离为p,离心率e的定义为e=1。
3. 抛物线的标准方程:抛物线的标准方程为y²=2px(p>0),焦点在y轴上。
四、椭圆双曲线抛物线的性质比较1. 焦点、离心率和轴与方程的关系:椭圆的焦点在轴上,双曲线的焦点在中心轴的延长线上,抛物线的焦点在轴上。
2. 直线与曲线的关系:椭圆是对称轴与任意直线的交点个数有限,双曲线是对称轴与任意直线的交点有两个,抛物线是对称轴与任意直线的交点有且仅有一个。
3. 其他性质:椭圆和双曲线是封闭曲线,抛物线是开口向上或者向下的曲线。
五、高中数学中的应用1. 物理中的应用:椭圆、双曲线和抛物线在经典力学、电磁学等物理学科中有着重要的应用,比如行星轨道、抛物线运动等。
双曲线和椭圆的知识点

双曲线和椭圆的知识点一、双曲线的定义和基本性质双曲线是平面上的一种曲线,由两个相交的直线割成两个分支。
它的定义式为x^2/a^2-y^2/b^2=1或y^2/b^2-x^2/a^2=1,其中a和b为正实数。
双曲线有以下基本性质:1. 双曲线关于x轴、y轴对称;2. 双曲线有两条渐近线,即与x轴和y轴夹角趋近于0或π/2的直线;3. 双曲线在两条渐近线处无界;4. 双曲线分为左右两个分支,左分支开口向左,右分支开口向右;5. 双曲线在x=a和x=-a处有垂直渐近线。
二、椭圆的定义和基本性质椭圆是平面上一条封闭弧形,其所有点到两个定点之距离之和等于定长(即椭圆长轴),定义式为(x-h)^2/a^2+(y-k)^2/b^2=1或(x-h)^2/b^2+(y-k)^2/a^2=1,其中(h,k)为椭圆中心坐标,a和b为长短半轴长度。
椭圆有以下基本性质:1. 椭圆关于x轴、y轴对称;2. 椭圆有两条主轴,即长轴和短轴,交于椭圆中心;3. 椭圆的离心率为e=c/a,其中c为焦点到中心的距离;4. 椭圆上任意一点P(x,y)到焦点F1和F2的距离之和等于椭圆长轴长度;5. 椭圆在x=h处有垂直渐近线。
三、双曲线和椭圆的参数方程双曲线的参数方程为x=acosht,y=bsinht或x=asect,y=btant,其中t为参数。
这两种参数方程对应左右两个分支。
椭圆的参数方程为x=h+acosθ,y=k+bsinθ或x=h+bsinθ,y=k+acosθ,其中θ为参数。
四、双曲线和椭圆的焦点双曲线有两个焦点F1(ae,0)和F2(-ae,0),其中e为离心率。
椭圆也有两个焦点F1(h+ae,k)和F2(h-ae,k),其中a、b、h、k、e均已定义。
五、双曲线和椭圆的面积双曲线面积公式为S=abπ,其中a和b分别为左右两个分支的半轴长度。
椭圆面积公式为S=abπ,其中a和b分别为长轴和短轴长度。
六、双曲线和椭圆的应用1. 双曲线在物理学中有许多应用,如描述电磁波传播、天体运动等。
(完整版)椭圆,双曲线,抛物线知识点
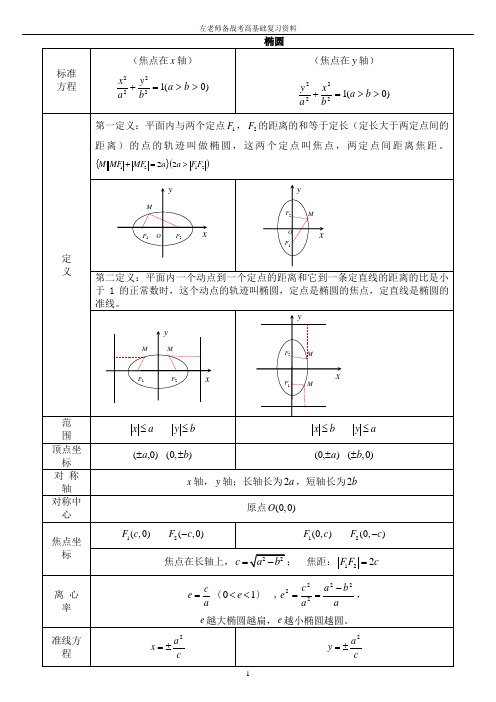
标准
方程
(焦点在 轴)
(焦点在 轴)
定 义
第一定义:平面内与两个定点 , 的距离的和等于定长(定长大于两定点间的距离)的点的轨迹叫做椭圆,这两个定点叫焦点,两定点间距离焦距。
第二定义:平面内一个动点到一个定点的距离和它到一条定直线的距离的比是小于1的正常数时,这个动点的轨迹叫椭圆,定点是椭圆的焦点,定直线是椭圆的准线。
顶点到准线的距离
焦点到准线的距离
焦点弦的几条性质
设直线过焦点F与抛物线 >0)交于 ,
则:(1) =
(2)
(3)通径长:
(4)焦点弦长
直线与抛物线的位置
抛物线 与直线 的位置关系:
利用 转化为一元二次方程用判别式确定。
切线
方程
焦点 ( )到准线 ( )的距离为
焦点 ( )到准线 ( )的距离为
椭圆上到焦点的最大(小)距离
最大距离为:
最小距离为:
相关应用题:远日距离
近日距离
椭圆的参数方程
( 为参数)
( 为参数)
椭圆上的点到给定直线的距离
利用参数方程简便:椭圆 ( 为参数)上一点到直线 的距离为:
直线和椭圆的位置
椭圆 与直线 的位置关系:
焦点 ( )到准线 ( )的距离为
焦点 ( )到准线 ( )的距离为
渐近线
方程
( )
( )
共渐近线的双曲线系方程
( )
( )
直线和双曲线的位置
双曲线 与直线 的位置关系:
利用 转化为一元二次方程用判别式确定。
二次方程二次项系数为零直线与渐近线平行。
相交弦AB的弦长
通径:
过双曲线上一点的切线
椭圆双曲线知识点的总结

椭圆知识点【知识点1】椭圆的概念:椭圆的第一定义 在平面内到两定点F 1、F 2的距离的和等于常数(大于|F 1F 2|)的点的轨迹叫椭圆.这两定点叫做椭圆的焦点,两焦点间的距离叫做焦距.当动点设为M 时,椭圆即为点集P ={}12|2M MF MF a += 注意:若)(2121F F PF PF =+,则动点P 的轨迹为线段21F F ;若)(2121F F PF PF <+,则动点P 的轨迹无图形。
椭圆的第二定义:在平面内,满足到定点的距离与到定直线的距离之比是等于一个常数的动点的轨迹叫做椭圆。
其中这个定点叫做椭圆的焦点,这条定直线叫做相应于该焦点的准线。
注:定义中的定点不在定直线上。
如果将椭圆的中心与坐标原点重合,焦点放在X 轴上,准线方程是: 焦点放在Y 轴上,准线方程是:【知识点2】椭圆的标准方程焦点在x 轴上椭圆的标准方程: ()222210x y a b a b += >>,焦点坐标为(c ,0),(-c ,0)焦点在y 轴上的椭圆的标准方程为:()222210x y a b b a+= >>焦点坐标为(0,c ,)(o ,-c )【知识点3】椭圆的几何性质:规律:(1)椭圆焦点位置与x 2,y 2系数间的关系:焦点在分母大的那个轴上.(2)椭圆上任意一点M 到焦点F 的所有距离中,长轴端点到焦点的距离分别为最大距离和最小距离,且最大距离标准方程()222210x y a b a b += >> ()222210x y a b b a += >> 图形性质范围 a x a -≤≤b y b -≤≤对称性 对称轴:坐标轴 对称中心:原点顶点A 1(-a,0), A 2(a,0)B 1(0,-b ),B 2(0,b )A 1(0,-a ),A 2(0,a )B 1(-b,0),B 2(b,0)轴 长轴A 1A 2的长为2a ;短轴B 1B 2的长为2b焦距 ∣F 1F 2 |=2c离心率 e=ca∈(0,1) a ,b ,c 的关系c 2=a 2-b 2为a +c ,最小距离为a -c .(3)在椭圆中,离心率22222221a b a b a a c a c e -=-===(4)椭圆的离心率e 越接近1椭圆越扁;e 越接近于0,椭圆就接近于圆;椭圆典型例题一、已知椭圆焦点的位置,求椭圆的标准方程。
椭圆与双曲线知识点总结

椭圆与双曲线知识点总结(一)椭圆1.椭圆的定义如果平面内一动点到两定点距离之和等于正的常数(大于两定点的距离),则动点的规迹是椭圆即|PF1|+|PF2|=2a 其中P是动点,F1,F2是定点且|F1F2|=2C当a>c时表示当a=c时表示当a<c时第二定义:动点M与一个定点的距离和它到一条定直线的距离的比是常数e(0<e<1)时,这个点的规迹是椭圆。
定点是,定直是e是2.椭圆的标准方程参数方程(1)标准方程(2)参数方程3.椭圆的性质(1)焦点在x标准方程x,y的范围顶点焦点对称轴对称中心长半轴的长短半轴的长焦距离心率e= 范围e越大椭圆越e越小椭圆越准线焦半径公式|PF1|= |PF2|= (F1,F2分别为椭圆的左右两焦点,P为椭圆上的一点) 椭圆的通径(过椭圆的一个焦点F且垂直于它过焦点的对称轴的弦)|P1P(2)焦点在y轴上的椭圆标准方程x,y的范围顶点焦点对称轴对称中心长半轴的长短半轴的长焦距离心率e= 范围e越大椭圆越e越小椭圆越准线焦半径公式|PF1|= |PF2|= (F1,F2分别为椭圆的下上两焦点,P为椭圆上的一点)4.椭圆系(1)共焦点的椭圆系方程为2221x yk k c+=-(其中k>c2,c为半焦距)(2 )具有相同离心率的标准椭圆系的方程2222(0) x ya bλλ+=>(二) 双曲线1.双曲线的定义如果平面内一个动点到两定点距离之差的绝对值等于正的常数(小于两定点间的距离),那么动点的轨迹是双曲线若一个动点到两定点距离之差等于一个常数,常数的绝对值小于两定点间的距离,那么动点的轨迹是双曲线的一支F1,F2为两定点,P为一动点,(1)若||PF1|-|PF2||=2a①0<2a<|F1F2|则动点P的轨迹是②2a=|F1F2|则动点P的轨迹是③2a=0则动点P的轨迹是(2) 若|P F1|-|PF2|=2a①0<2a<|F1F2|则动点P的轨迹是②2a=|F1F2|则动点P的轨迹是③2a=0则动点P的轨迹是2.双曲线的标准方程3.双曲线的性质(1)焦点在x轴上的双曲线标准方程x,y的范围顶点焦点对称轴对称中心实半轴的长虚半轴的长焦距离心率e= 范围e越大双曲线的开口越e越小双曲线的开口越准线渐近线焦半径公式|PF1|= |PF2|= (F1,F2分别为双曲线的左右两焦点,P为椭圆上的一点)(3)焦点在y轴上的双曲线标准方程x,y的范围顶点焦点对称轴对称中心实半轴的长虚半轴的长焦距离心率e= 范围e越大双曲线的开口越e越小双曲线的开口越准线渐近线焦半径公式|PF1|= |PF2|= (F1,F2分别为双曲线的下上两焦点,P为椭圆上的一点)4.等轴双曲线22(0)x yλλ-=≠特点①实轴与虚轴长相等②渐近线互相垂直y x=±③离心率为5.共轭双曲线以已知双曲线的虚轴为实轴,实轴为虚轴的双曲线叫原双曲线的共轭双曲线特点①有共同的渐近线②四焦点共圆双曲线22221x ya b+=的共轭双曲线是6.双曲线系(1)共焦点的双曲线的方程为2221x yk k c+=-(0<k<c2,c为半焦距)(2)共渐近线的双曲线的方程为2222(0) x ya bλλ-=≠。
中职教育数学《椭圆、双曲线、抛物线》知识点总结

椭圆、双曲线、抛物线相关知识点总结一、 椭圆的标准方程及其几何性质椭圆的定义:我们把平面内与两个定点12F F ,的距离的和等于常数()12F F 大于的点的轨迹叫做椭圆。
符号语言:()12222MF MF a a c +=>将定义中的常数记为a 2,则:①.当122a F F >时,点的轨迹是 椭圆②.当122a F F =时,点的轨迹是 线段 ③.当122a F F <时,点的轨迹 不存在焦点位置不确定的椭圆方程可设为:()2210,0,mx ny m n m n +=>>≠与椭圆12222=+by a x 共焦点的椭圆系方程可设为:()222221x y k b a k b k +=>-++ 与椭圆 12222=+by a x 共离心率的椭圆系方程可设为:)0,(2222≠=+λλb y a x双曲线的定义:我们把平面内与两个定点12F F ,的距离的差的绝对值等于常数()12F F 小于 的点的轨迹叫做双曲线。
符号语言:()12-222MF MF a a c =<将定义中的常数记为a 2,则:①.当122a F F <时,点的轨迹是 双曲线②.当122a F F =时,点的轨迹是 两条射线 ③.当122a F F >时,点的轨迹 不存在标准方程22221x y a b -= (0,0)a b >> 22221y x a b-= (0,0)a b >> 图 形性质焦点坐标 )0,(1c F -,)0,(2c F ),0(1c F -,),0(2c F焦 距 c F F 221=c F F 221= 范 围x a ≥,y R ∈y a ≥,x R ∈对 称 性 关于x 轴、y 轴和原点对称顶点坐标)0,(a ± ),0(a ±,实轴、虚轴 实轴长=a 2,虚轴长=b 2;实半轴长=a ,虚半轴长=ba b c 、、关系 222c a b =+离 心 率(e 1)ce a=>渐近线方程b y x a=± a y x b=±焦点位置不确定的双曲线方程可设为:()2210mx ny mn -=>与双曲线22221x y a b-=共焦点的双曲线系方程可设为:()2222221x y b k a a k b k -=-<<-+ 与双曲线22221x y a b -=共渐近线或离心率的双曲线系方程可设为:()22220x y a bλλ-=≠yoabxxy o a bx yao抛物线的定义:我们把平面内与一个定点F 和一条定直线l (l 不经过点F )距离相等 的点的轨迹叫做抛物线。
椭圆_双曲线_知识点

椭圆_双曲线_知识点
椭圆与双曲线是以二次曲线为基础的曲线,这两种曲线同属于双曲线族。
椭圆曲线的
二次方程如下:
$$\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$$
其中,a,b代表椭圆的两个半径;同时,双曲线的标准二次方程为:
$$\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1$$
可以看出,两者只有被除数和方向不同,同是都为常数。
从表面上看,椭圆是左右对称,而双曲线则形式各不相同,收放自如,具有左右对称性以及上下对称性。
这两种曲线均为二次曲线,但两者间仍有明显区别:对于同一点,椭圆曲线的切线是
弧形的,而双曲线的切线是折线的。
而且,椭圆的极点的横纵坐标都有实数值,而双曲线
的极点的横坐标为实数,纵坐标都是无穷小。
另外,椭圆、双曲线等二次曲线的性质有共同之处,比如可以到达任一点的过渡性、
经过原点的轨迹是完美的圆周、经过任一点的二阶导数值为0 。
椭圆曲线在数学中被广泛用于实际应用,比如加密技术中的椭圆曲线加密,常用于方
便快捷的现代加密算法;双曲线方程式是高等数学中重要的内容,可用于证明费马小定理。
椭圆与双曲线知识点总结

椭圆与双曲线知识点总结椭圆和双曲线是高中数学中重要的曲线类型,它们在几何、物理、工程等领域都有广泛的应用。
本文将对椭圆与双曲线的基本概念、性质以及相关公式进行总结。
一、椭圆1. 椭圆的定义:椭圆是平面上到两个定点F1、F2距离之和恒为常数2a的点P所构成的图形轨迹。
2. 椭圆的性质:- 两个焦点F1、F2与椭圆的中心O满足关系:OF1 + OF2 = 2a。
- 椭圆的半长轴为a,半短轴为b,有关系式a > b。
- 椭圆的离心率e满足关系e = c/a,其中c为焦点到中心的距离。
- 椭圆的离心率介于0到1之间,当离心率为0时,椭圆退化成一个圆。
3. 椭圆的方程:椭圆的标准方程为(x - h)²/a² + (y - k)²/b² = 1,其中(h, k)为中心坐标。
4. 椭圆的重要公式:- 椭圆的周长C = 4a(E(e)),其中E(e)为第二类椭圆积分。
- 椭圆的面积S = πab。
二、双曲线1. 双曲线的定义:双曲线是平面上到两个定点F1、F2距离之差恒为常数2a的点P所构成的图形轨迹。
2. 双曲线的性质:- 两个焦点F1、F2与双曲线的中心O满足关系:|OF1 - OF2| = 2a。
- 双曲线的半长轴为a,半短轴为b,有关系式a > b。
- 双曲线的离心率e满足关系e = c/a,其中c为焦点到中心的距离。
- 双曲线的离心率大于1。
- 对于双曲线的每个点P,其到焦点的距离之差等于常数。
3. 双曲线的方程:双曲线的标准方程为(x - h)²/a² - (y - k)²/b² = 1,其中(h, k)为中心坐标。
4. 双曲线的重要公式:- 双曲线的渐近线方程为y = ±b/a * x。
- 双曲线的面积S = πab。
总结:椭圆和双曲线是两种常见的曲线类型,具有各自的定义、性质和方程。
掌握椭圆和双曲线的知识,有助于我们理解和解决与这两类曲线相关的问题。
椭圆双曲线知识点梳理

c 离心率 e=a,e∈(1,+∞),其中 c= a2+b2 线段 A1A2 叫做双曲线的实轴,它的长 A1A2=2a; 实虚轴 线段 B1B2 叫做双曲线的虚轴,它的长 B1B2=2b;a 叫做双曲线的实半轴长,b 叫做双曲线的虚半轴长 a、b、的关系 c c2=a2+b2 (c>a>0,c>b>0)
(2)2a<F1F2. 这两点与椭圆的定义有本质的不同: ①当 MF1-MF2=2a 时,曲线仅表示焦点 F2 所对应的 一支; ②当 MF1-MF2=-2a 时,曲线仅表示焦点 F1 所对应 的一支; ③当 2a=F1F2 时,轨迹是一直线上以 F1、F2 为端点向 外的两条射线; ④当 2a>|F1F2|时,动点轨迹不存在.
图形
要点梳理
范围 对称性 顶点 渐近线 准线
忆一忆知识要点
x≥a 或 x≤-a,y∈R x∈R, y≤-a 或 y≥a 对称轴:坐标轴 对称中心:原点 A1(-a,0),A2(a,0) A1(0,-a),A2(0, a) b y=± x a a2 x=±c a y=± x b a2 y=±c
性 质
e c a
O
y
x
②e的含义: e是表示双曲线开口大小的一个量, e越大开口越大!
2 2 c a b 1 ( b )2 , e a a a
b e 2 1. a b 当e (1, )时, (0, ), 且e增大, b 也增大 a a e增大时,渐近线与实轴的夹角增大.
方法与技巧
1.椭圆上任意一点 M 到焦点 F 的所有距离中,长轴端点到 焦点的距离分别为最大距离和最小距离, 且最大距离为 a +c,最小距离为 a-c. 2.求椭圆离心率 e 时,只要求出 a,b,c 的一个齐次方程, 再结合 b2=a2-c2 就可求得 e (0<e<1). 3.求椭圆方程时,常用待定系数法,但首先要判断是否为 标准方程,判断的依据是:(1)中心是否在原点,(2)对称 轴是否为坐标轴.
圆锥曲线(椭圆,双曲线,抛物线)的定义、方程和性质知识总结

椭圆的定义、性质及标准方程1. 椭圆的定义:⑴第一定义:平面内与两个定点12F F 、的距离之和等于常数〔大于12F F 〕的点的轨迹叫做椭圆。
这两个定点叫做椭圆的焦点,两焦点的距离叫做椭圆的焦距。
⑵第二定义:动点M 到定点F 的距离和它到定直线l 的距离之比等于常数)10(<<e e ,那么动点M 的轨迹叫做椭圆。
定点F 是椭圆的焦点,定直线l 叫做椭圆的准线,常数e 叫做椭圆的离心率。
说明:①假设常数2a 等于2c ,那么动点轨迹是线段12F F 。
②假设常数2a 小于2c ,那么动点轨迹不存在。
2. 椭圆的标准方程、图形及几何性质:标准方程)0(12222>>=+b a by a x 中心在原点,焦点在x 轴上)0(12222>>=+b a b x a y 中心在原点,焦点在y 轴上图形范围 x a y b ≤≤,x b y a ≤≤,顶点()()()()12120000A a A a B b B b --,、,,、,()()()()12120000A a A a B b B b --,、,,、,对称轴 x 轴、y 轴;长轴长2a ,短轴长2b ; 焦点在长轴上x 轴、y 轴;长轴长2a ,短轴长2b ;焦点在长轴上焦点 ()()1200F c F c -,、, ()()1200F c F c -,、, 焦距 )0(221>=c c F F)0(221>=c c F F离心率 )10(<<=e ace )10(<<=e ace 准线2a x c=±2a y c=±参数方程与普通方程22221x y a b +=的参数方程为 ()cos sin x a y b θθθ=⎧⎨=⎩为参数 22221y x a b +=的参数方程为 ()cos sin y a x b θθθ=⎧⎨=⎩为参数3. 焦半径公式:椭圆上的任一点和焦点连结的线段长称为焦半径。
圆锥曲线(椭圆,双曲线,抛物线)的定义、方程和性质知识总结

圆锥曲线(椭圆,双曲线,抛物线)的定义、方程和性质知识总结-标准化文件发布号:(9556-EUATWK-MWUB-WUNN-INNUL-DDQTY-KII2椭圆的定义、性质及标准方程1. 椭圆的定义:⑴第一定义:平面内与两个定点12F F 、的距离之和等于常数(大于12F F )的点的轨迹叫做椭圆。
这两个定点叫做椭圆的焦点,两焦点的距离叫做椭圆的焦距。
⑵第二定义:动点M 到定点F 的距离和它到定直线l 的距离之比等于常数)10(<<e e ,则动点M 的轨迹叫做椭圆。
定点F 是椭圆的焦点,定直线l 叫做椭圆的准线,常数e 叫做椭圆的离心率。
说明:①若常数2a 等于2c ,则动点轨迹是线段12F F 。
②若常数2a 小于2c ,则动点轨迹不存在。
2. 椭圆的标准方程、图形及几何性质:标准方程)0(12222>>=+b a b y a x 中心在原点,焦点在x 轴上)0(12222>>=+b a b xa y 中心在原点,焦点在y 轴上图形范围 x a y b ≤≤,x b y a ≤≤,顶点()()()()12120000A a A a B b B b --,、,,、,()()()()12120000A a A a B b B b --,、,,、,对称轴 x 轴、y 轴; 长轴长2a ,短轴长2b ; 焦点在长轴上 x 轴、y 轴;长轴长2a ,短轴长2b ;焦点在长轴上焦点 ()()1200F c F c -,、, ()()1200F c F c -,、, 焦距 )0(221>=c c F F)0(221>=c c F F离心率)10(<<=e ace )10(<<=e ace33. 焦半径公式:椭圆上的任一点和焦点连结的线段长称为焦半径。
焦半径公式:椭圆焦点在x 轴上时,设12F F 、分别是椭圆的左、右焦点,()00P x y ,是椭圆上任一点,则10PF a ex =+,20PF a ex =-。
椭圆抛物线双曲线公式大全

椭圆抛物线双曲线公式大全一、椭圆。
(一)椭圆的标准方程。
1. 焦点在x轴上。
设椭圆的标准方程为frac{x^2}{a^2}+frac{y^2}{b^2} = 1(a>b>0),其中a为长半轴长,b为短半轴长,c为半焦距,且c^2=a^2-b^2,焦点坐标为(± c,0)。
2. 焦点在y轴上。
方程为frac{y^2}{a^2}+frac{x^2}{b^2}=1(a > b>0),焦点坐标为(0,± c),同样c^2=a^2-b^2。
(二)椭圆的离心率。
e=(c)/(a)(0 < e<1),离心率反映了椭圆的扁平程度。
(三)椭圆的参数方程。
<=ft{begin{array}{l}x = acosθ y=bsinθend{array}right.(θ为参数)二、抛物线。
(一)抛物线的标准方程。
1. 焦点在x轴正半轴上。
方程为y^2=2px(p>0),焦点坐标为((p)/(2),0),准线方程为x =-(p)/(2)。
2. 焦点在x轴负半轴上。
y^2=-2px(p > 0),焦点(-(p)/(2),0),准线x=(p)/(2)。
3. 焦点在y轴正半轴上。
x^2=2py(p>0),焦点(0,(p)/(2)),准线y =-(p)/(2)。
4. 焦点在y轴负半轴上。
x^2=-2py(p>0),焦点(0,-(p)/(2)),准线y=(p)/(2)。
(二)抛物线的离心率。
e = 1三、双曲线。
(一)双曲线的标准方程。
1. 焦点在x轴上。
方程为frac{x^2}{a^2}-frac{y^2}{b^2}=1(a>0,b>0),其中a为实半轴长,b为虚半轴长,c为半焦距,且c^2=a^2+b^2,焦点坐标为(± c,0)。
2. 焦点在y轴上。
frac{y^2}{a^2}-frac{x^2}{b^2} = 1(a>0,b>0),焦点坐标为(0,± c),c^2=a^2+b^2。
椭圆双曲线抛物线知识点汇总

椭圆双曲线抛物线知识点汇总一、椭圆1、定义平面内与两个定点$F_1$,$F_2$的距离之和等于常数(大于$|F_1F_2|$)的点的轨迹叫做椭圆。
这两个定点叫做椭圆的焦点,两焦点间的距离叫做椭圆的焦距。
2、标准方程(1)焦点在$x$轴上:$\frac{x^2}{a^2} +\frac{y^2}{b^2} = 1$($a > b > 0$),其中$a$为长半轴长,$b$为短半轴长,$c$为半焦距,满足$c^2 = a^2 b^2$。
(2)焦点在$y$轴上:$\frac{y^2}{a^2} +\frac{x^2}{b^2} = 1$($a > b > 0$)。
3、椭圆的性质(1)对称性:椭圆关于$x$轴、$y$轴和原点对称。
(2)范围:对于焦点在$x$轴上的椭圆,$a \leq x \leq a$,$b \leq y \leq b$;对于焦点在$y$轴上的椭圆,$b \leq x \leq b$,$a \leq y \leq a$。
(3)顶点:焦点在$x$轴上时,顶点坐标为$(\pm a, 0)$,$(0, \pm b)$;焦点在$y$轴上时,顶点坐标为$(0, \pm a)$,$(\pm b, 0)$。
(4)离心率:$e =\frac{c}{a}$($0 < e < 1$),反映了椭圆的扁平程度。
4、椭圆中的重要结论(1)过椭圆焦点的弦长:若弦过焦点$F_1$,则弦长$|AB| = 2a e(x_1 + x_2)$。
(2)椭圆上一点到焦点的距离:设椭圆上一点$P(x_0, y_0)$,两焦点为$F_1$,$F_2$,则$|PF_1| = a + ex_0$,$|PF_2| = aex_0$。
二、双曲线1、定义平面内与两个定点$F_1$,$F_2$的距离之差的绝对值等于常数(小于$|F_1F_2|$)的点的轨迹叫做双曲线。
这两个定点叫做双曲线的焦点,两焦点间的距离叫做双曲线的焦距。
2、标准方程(1)焦点在$x$轴上:$\frac{x^2}{a^2} \frac{y^2}{b^2} =1$($a > 0$,$b > 0$),其中$c^2 = a^2 + b^2$。
椭圆双曲线知识点总结

椭圆知识点【知识点1】椭圆的概念:在平面内到两定点F 1、F 2的距离的和等于常数(大于|F 1F 2|)的点的轨迹叫椭圆.这两定点叫做椭圆的焦点,两焦点间的距离叫做焦距.当动点设为M 时,椭圆即为点集P ={}12|2M MF MF a +=【知识点2】椭圆的标准方程焦点在x 轴上椭圆的标准方程:()222210x ya b a b+= >>,焦点坐标为(c ,0),(-c ,0) 焦点在y 轴上的椭圆的标准方程为:()222210x y a b b a+= >>焦点坐标为(0,c ,)(o ,-c )【知识点3】椭圆的几何性质:规律:(1)椭圆焦点位置与x 2,y 2系数间的关系:焦点在分母大的那个轴上.(2)椭圆上任意一点M 到焦点F 的所有距离中,长轴端点到焦点的距离分别为最大距离和最小距离,且最大距离为a +c ,最小距离为a -c .(3)在椭圆中,离心率22222221a b a b a a c a c e -=-===(4)椭圆的离心率e 越接近1椭圆越扁;e 越接近于0,椭圆就接近于圆;【知识点4】椭圆中的焦点三角形:定 义:∣PF 1∣+∣PF 2∣=2a ∣F 1F 2∣=2c余弦定理:∣F 1F 2∣2=∣PF 1∣2+∣PF 2∣2-2∣PF 1∣∣PF 2∣cosθ(∠F 1PF 2=θ)面积公式:在椭圆12222=+by a x (a >b >0)中,焦点分别为1F 、2F ,点P 是椭圆上任意一点,θ=∠21PF F ,则2tan 221θb S PF F =∆【知识点5】点(x 0,y 0)与椭圆22221x y a b+=(a >b >0)的位置关系:点P 在椭圆上⇔2200221x y a b+=点P 在椭圆内部⇔2200221x y a b +< 点P 在椭圆外部⇔2200221x y a b+>【知识点6】直线与椭圆位置关系的判断:① 直线斜率存在时221y kx bmx ny =+⎧⎨+=⎩⇒222()210m k n x kbnx b +++-=直线与椭圆相交0>∆⇔ 直线与椭圆相切0=∆⇔ 直线与椭圆相离0<∆⇔② 直线斜率不存在时22221x m x y ab =⎧⎪⎨+=⎪⎩判断y 有几个解标准方程()222210x y a b a b += >> ()222210x y a b b a+= >> 图形性质范围 a x a -≤≤b y b -≤≤对称性 对称轴:坐标轴 对称中心:原点顶点A 1(-a,0), A 2(a,0)B 1(0,-b ),B 2(0,b )A 1(0,-a ),A 2(0,a )B 1(-b,0),B 2(b,0)轴 长轴A 1A 2的长为2a ;短轴B 1B 2的长为2b焦距 ∣F 1F 2 |=2c离心率 e=ca∈(0,1) a ,b ,c 的关系c 2=a 2-b 2双曲线知识点【知识点1】双曲线的概念:在平面内到两定点F 1、F 2的距离的差的绝对值等于常数(小于|F 1F 2|)的点的轨迹叫双曲线.这两定点叫做椭圆的焦点,两焦点间的距离叫做焦距.当动点设为M 时,椭圆即为点集P ={}12|2M MF MF a -=【知识点2】双曲线的标准方程焦点在x 轴上双曲线的标准方程: ()222210,0x y a b a b-= >>,焦点坐标为(c ,0),(-c ,0)焦点在y 轴上的双曲线的标准方程为:()222210,0y x a b b a-= >>焦点坐标为(0,c ,)(o ,-c )【知识点3】双曲线的几何性质标准方程x 2a 2-y 2b 2=1(a >0,b >0) y 2a 2-x 2b 2=1(a >0,b >0) 图 形性 质范 围 x ≥a 或x ≤-a ,y ∈Rx ∈R ,y ≤-a 或y ≥a对称性 对称轴:坐标轴 对称中心:原点顶点A 1(-a,0),A 2(a,0) A 1(0,-a ),A 2(0,a )渐近线y =±b a x y =±a b x离心率e =ca,e ∈(1,+∞),其中c =a 2+b 2 实虚轴 线段A 1A 2叫做双曲线的实轴,它的长|A 1A 2|=2a ;线段B 1B 2叫做双曲线的虚轴,它的长|B 1B 2|=2b ;a 叫做双曲线的实半轴长,b 叫做双曲线的虚半轴长a 、b 、c 的关系 c 2=a 2+b 2(c >a >0,c >b >0)规律:1.双曲线为等轴双曲线⇔双曲线的离心率e =2⇔双曲线的两条渐近线互相垂直(位置关系).2.区分双曲线中的a ,b ,c 大小关系与椭圆a ,b ,c 关系,在椭圆中a 2=b 2+c 2,而在双曲线中c 2=a 2+b 2.(2)双曲线的离心率大于1,而椭圆的离心率e ∈(0,1). (3)在双曲线中,离心率22222221c c a b be a a a a+====+ (4)双曲线的离心率e 越接近大,开口越阔.【知识点4】双曲线中的焦点三角形:定 义:∣PF 1∣-∣PF 2∣=±2a ∣F 1F 2∣=2c余弦定理:∣F 1F 2∣2=∣PF 1∣2+∣PF 2∣2-2∣PF 1∣∣PF 2∣cosθ(∠F 1PF 2=θ)面积公式:在双曲线12222=+by a x (a >b >0)中,焦点分别为1F 、2F ,点P 是双曲线上任意一点,θ=∠21PF F ,则122tan2F PF b S θ∆=【知识点5】直线与双曲线的位置关系的判断:设直线)0(:≠+=m m kx y l ,双曲线)0,0(12222>>=-b a by a x 联立解得02)(222222222=----b a m a mkx a x k a b(1)若0222=-k a b 即a bk ±=,直线与双曲线渐近线平行,直线与双曲线相交于一点; (2)若0222≠-k a b 即ab k ±≠时,))((4)2(222222222b a m a k a b mk a -----=∆①0>∆⇒直线与双曲线相交,有两个交点; ②0=∆⇒直线与双曲线相切,有一个交点; ③0<∆⇒直线与双曲线相离,无交点;【知识点6】弦长公式:│AB │=2221212121||1()4k x x k x x x x +⋅-=+⋅+-⋅21ka∆=+, 12211AB y y k ==+-211k a∆=+ (其中k 为直线斜率) 【知识点7】中点弦问题(点差法):遇到弦中点,两式减一减。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高二上学期数学知识总结
必修五第一章:《解三角形》
1、解三角形(求边、角、面积)
2、判断三角形形状
3、解三角形的应用题
必修五第二章:《数列》
1、等差数列和等比数列的基本性质和综合应用
2、数列通项公式求解
3、数列的前n项和公式求解
4、数列的应用题
必修五第三章:《不等式》
1、求解未知数的取值范围
2、不等式的基本运算
3、不等式求解
4、均值不等式应用求最值
5、简单的线性规划问题
6、不等式表示平面区域选修2-1 第一章《简单逻辑用语》
1、命题的真假
2、两种量词(全称量词、存在性量词)
3、三个基本逻辑连接词
4、四种命题
5、四种条件
6、反证法证明命题
选修2-1 第二章《圆锥曲线》
1、求曲线的标准方程
2、判断曲线的类型
3、定义的应用
4、求曲线的离心率
5、中点弦问题
6、焦点三角形
7、弦长公式
8、最值问题
9、圆锥曲线应用题 10、圆锥曲线的位置关系 11、曲线的轨迹求解
选修2-1第三章:《空间向量和空间立体几何》
1、空间向量的基本公式
2、空间立体几何的距离和角度求解
3、空间线面关系证明
4、共面向量基本定理
必修五第二章《数列》
等差数列等比数列
函数概念定义特征
通项通项公式求解方法函数关系
前n 项和求和公式求解方法函数关系
二者关系
判定证明1 定义定义
2 函数关系函数关系
3 前n项和的函数关系
4
}
{
n
a是等差数列,公差为d,则
←→}
{
n
S
n是等差数列,公差为
}
{
n
a是等比数列,公比为q,则
Λ,
,
,
2
3
2k
k
k
k
k
S
S
S
S
S-
-为等比数列,公比为
5
}
{
n
a是等差数列,公差为d,则
Λ,
,
,
2
3
2k
k
k
k
k
S
S
S
S
S-
-为等差数列,公差为
}
{
n
a是等比数列,公比为q,
n
T为前n项积,
则Λ,
,
,
2
3
2k
k
k
k
k
T
T
T
T
T-
-为等比数列,公比为
6
}
{
n
a是等差数列,公差为d,则
}
{
n
ka是等差数列,公差为
}
{
kn
a是等差数列,公差为
}
{
n
a是等比数列,公比为q,则
}
{
n
ka是等比数列,公比为
}
{
kn
a是等比数列,公比为
7 若}
{
n
a是正项等比数列,则}
{log
n
m
a是等差数列若}
{log
n
m
a是等差数列,则}
{
n
a是正项等比数列8
}
{
n
a,}
{
n
b是等差数列,公差分别为
2
1
,d
d,
则}
{
n
n
lb
ka+是等差数列,公差为
}
{
n
a,}
{
n
b是等比数列,公比分别为
2
1
,q
q
则}
*
{
n
n
b
a是等比数列,公比为
等差数列等比数列
性质单
调
性
项
间
关
系
n
m
a
a,之间的关系:
n
m
a
a,之间的关系:
求公差:求公比:
如果q
p
n
m+
=
+,则
q
p
n
m
a
a
a
a,
,
,的关系:如果q
p
n
m+
=
+,则
q
p
n
m
a
a
a
a,
,
,的关系:
中
项
关
系
等差中项定义:等比中项定义:
1
1
,
,
+
-n
n
n
a
a
a之间的关系:
1
1
,
,
+
-n
n
n
a
a
a之间的关系:
如果m,n,p成等差数列,则p
n
m
a
a
a,
,的关系:如果m,n,p成等差数列,则
p
n
m
a
a
a,
,的关系:
首
尾
项
关
系
等距性:等距性:
n
S与中间项的关系:
n
S与中间项的关系:
常用的题目插
数
问
题
奇
数
项
偶
数
项
奇数项和
奇
S,偶数项和
偶
S,公差为d,则
1、若等差数列}
{
n
a有2n项,则
奇
S+
偶
S=
奇
S-
偶
S=
偶
奇
S
S=
2、若等差数列}
{
n
a有2n+1项,则
奇
S+
偶
S=
奇
S-
偶
S=
偶
奇
S
S=
奇数项和
奇
S,偶数项和
偶
S,公比为q,则
若等比数列}
{
n
a有2n项,则
奇
S+
偶
S=
奇
S-
偶
S=
偶
奇
S
S=
常用设法三项四项
选修2-1 椭圆、双曲线方程知识汇总
抛物线。
