螺旋线绘制
CAD中创建和编辑螺旋线的技巧

CAD中创建和编辑螺旋线的技巧螺旋线在CAD设计中经常被用于众多应用场景,比如机械结构、建筑设计以及工业制图等领域。
在CAD软件中,创建和编辑螺旋线需要掌握一些技巧,本文将介绍一些实用的方法。
首先,我们需要了解怎样创建一个基本的螺旋线。
在大多数CAD软件中,可以通过“绘制”或“绘图”工具栏中的相应图标来创建线条。
选择线条工具后,在绘图区域中点击鼠标左键确定起始点,然后按住鼠标左键移动,最后释放鼠标左键确定结束点。
这样就完成了一条基本的直线。
接下来,在创建好的直线上,我们需要添加螺旋线的特征。
常见的方法之一是使用“参数化建模”工具。
通过设置参数,我们可以实现螺旋线的自定义,比如螺旋线的半径、起始点和终止点的位置、螺距等。
这样,我们就可以根据需要创建各种不同形状的螺旋线。
此外,在编辑螺旋线时,我们还可以通过一些快捷键和工具来实现更精确的调整。
比如,我们可以使用“偏移”工具来复制螺旋线,通过指定偏移距离和方向来创建新的螺旋线。
另外,如果需要在螺旋线上添加或删除节点,可以使用“修剪”或“延伸”工具来实现。
这些工具可以帮助我们快速有效地完善螺旋线的形状。
在编辑螺旋线时,还需要注意一些细节。
首先,要了解螺旋线的参数对线条形状的影响。
比如,增加螺旋线的螺距会使螺旋线的扭曲度增加,而减小螺距则会使螺旋线逐渐展开。
其次,螺旋线的绘制方向也是需要注意的事项。
在CAD软件中,我们可以通过设置参数来指定螺旋线的旋转方向,以及螺旋线的升高度(相对于其半径)。
这些设置可以帮助我们更好地控制螺旋线的形状和方向。
除了基本的创建和编辑技巧,我们还可以通过使用一些高级功能来优化螺旋线的设计。
比如,可以使用自动绘图工具来快速生成复杂的螺旋线形状。
此外,还可以利用软件中提供的库文件或插件来获取更多预制的螺旋线模型,从而加快设计的速度并提高效率。
综上所述,螺旋线在CAD设计中的应用非常广泛,不仅能够增加设计的美感,还可以使设计更具有实用性。
UG螺旋线画法

4. 1. 12螺旋线•螺旋线是指-个固运点向外旋绕而企成的曲线。
具有指尢圈数、螺距、弧度.旋转方向和方位的曲钱,如图4. 102所示。
常常使用在螺杆.螺钉、弹簧等特征建模屮。
•单击“曲线” I具栏中的“燃旋线”按钮,进入“嫁旋线拧对话梅E,如图4. 103M示。
E4 104生成抵反线在”螺旋线“对话框中单击”泄义方向”后出来这个对话框:单击"立义方向”按钮,选择一条直线,以选择点指向与英距离最近的直线端点的方向为Z轴的正方向,再设左一点来左义X轴正方向然后设定一基点则系统以过此基点且平行于设泄的Z轴正方向作为螺旋线的轴线,螺旋线的起始点位于过基点且平行于X轴正方向上这只是要你选择螺旋线的朝向问题,默认情况下是沿Z轴,你可以任意画一条直线,来左螺旋线的朝向在北对话框中分别进秆了參数设置辰系统即可产匸一条如F图所示的職线。
下面详细的介紹一F该对话越中各进项的助能.w(I) Number of Turns (脚数)此文本框用于设1S螺旋线旋药的岡亂⑵Pitch (媒距)此文本翩于SM^在旋转毎圏之间的拒曲(3) Radius Method (半径方式)此文本框用于设置禅旋线蹺转半径的方式,系统提供了两种半径方式:Use Law僦则方式)Enter Radius (输入半径值方式九•使用规律线该方成用J :设置嫖旋銭半径按一定的規律法则进行变化=选择该单选项晞. 系统会种岀如I训折制话框•可利用其中提供的7种变化规律方式来控制媒旋半径沿轴线方向的变化规牡I)恒定的此逸顶用于生成固定半径的螺碇线9单占该选顶忌在系统弹岀的对话植中输入“规律(T的•参数值即可.这个文木框的数值将会决定幌陡线的半彳缸此逸顶用于设蛍煤旋线的施药半径为纱性变化。
单击该选顶氐系统将会规出如卜图左所示的对话执在对话框中的喘始值"及嘤止(T 文本框中输入参数值即可(例如園数为20.媒距为()2起始(1为山终止位为5比产化的JOE线如卜•图右所吓)=規律控制的硼!0终止值冃c^nrrirwi7)枢据规律曲线此选项是利用规则曲线来决.龙螺瞇线的礎转半社单击该按钮扁先选取一规则曲线,卩卜选取一条基线来确定螺旋线的方向即可。
螺旋线画法

Pro/E绘图很多时候要用到圆柱螺旋线,如斜齿轮、圆柱咬花。
网上很多教程直接以草绘投影的方法就当螺旋线用,其实是不正确的。
说圆柱螺旋线,首先来个定义:一动点在圆柱面上绕圆柱轴线作匀速旋转运动,同时又沿轴向作匀速直线运动,该动点的轨迹称为圆柱螺旋线。
举个例子:把一张直角三角形的纸卷到一个圆筒上,斜边在圆柱面成了一条圆柱螺旋线了。
下面以斜45度的圆柱咬花为例,简述螺旋线的方程的推导。
假想将下面立体图中的粉红色面展开成平面,根据圆柱螺旋线的定义可知展开的图案必定是下图右边所示的45度直角三角形。
Pro/E中极坐标方程的一般式:/* 对笛卡儿坐标系,输入参数方程/* 根据t (将从0变到1)对r, theta和z/* 例如:对在x-y平面的一个圆,中心在原点/* 半径= 4,参数方程将是:/* r = 4/* theta = t * 360/* z = 0/*-----------------------------------------螺旋线是r不变,theta、z随动点的变化而相应变化,因此方程的关键是Roll(即方程的theta)与t关系、H(即方程的z)与t的关系。
Roll最大值= (H*tan45)/(pi*d)*360 = H/(pi*d)*360z最大值= H方程出来了:r = d/2theta = H/(pi*d)*360*tz = H*t结果如右图红色螺旋线,端点在TOP基准上。
较理想右图绿色螺旋线的中点在TOP基准上,方便后继镜像。
想想吧,只要红色螺旋线再旋转(Roll最大值/2)度,即是绿色螺旋线了,因此将方程修改一下:Roll = H/(pi*d)*360r = d/2theta = Roll*t-Roll/2z = H*t上面方程中引入一个临时变量Roll,可使方程更直观、方便。
回到圆柱咬花实例中,代入各项尺寸代码(参数化的图形应该尽量以尺寸代号编写方程,勿直接输入直径、高度的具体数值,这是一个良好的绘图习惯),最终方程为:Roll=d13/(pi*d12)*360r=d12/2theta=t*Roll-Roll/2z=t*d13更为复杂的变化就是斜齿轮的螺旋线,其中的齿厚(FACE_WIDTH)、压力角(HELIX_ANGLE)均为变量,需要在INPUT中指定。
中曲线方程各种螺旋线画法

中曲线方程各种螺旋线画法概述螺旋线是一种具有特殊曲线形状的图形,它是由一个点沿着一定规律进行旋转或移动所形成的。
中曲线方程是描述螺旋线形状的数学方程,它可以通过绘制曲线来呈现出来。
本文将介绍一些常见的中曲线方程,并提供相应的画法。
1. Archimedean Spiral(阿基米德螺旋)阿基米德螺旋是最常见的螺旋线之一,其数学方程可以表示为:r = a + b * θ其中,r 为极坐标到原点的距离,a 和 b 是常数,θ为极坐标的角度。
这个方程描述了一个等距的螺旋线,通常以极坐标系来绘制。
画法为了绘制阿基米德螺旋,我们可以采用以下步骤:1.初始化绘图空间2.设置绘图参数,包括线条的颜色、粗细等3.循环生成一系列极坐标点4.将极坐标点转换为笛卡尔坐标系中的点5.使用绘图库绘制线条,连接转换后的点下面是一个使用 Python 的 Matplotlib 库来绘制阿基米德螺旋的示例代码:import numpy as npimport matplotlib.pyplot as plta = 0.2b = 0.1theta = np.linspace(0, 2*np.pi, 1000)r = a + b * thetax = r * np.cos(theta)y = r * np.sin(theta)plt.plot(x, y)plt.axis('equal')plt.show()2. Logarithmic Spiral(对数螺旋)对数螺旋是另一种常见的螺旋线形状,其数学方程可以表示为:r = a * exp(b * θ)其中,exp(x) 是自然对数的指数函数,a 和 b 是常数,θ是极坐标的角度。
对数螺旋的特点是,螺旋线距离原点的距离随着角度的增加呈指数增长。
画法绘制对数螺旋的方法与绘制阿基米德螺旋类似,我们需要生成一系列极坐标点,并将其转换为笛卡尔坐标系中的点。
下面是一个使用 Python 的 Matplotlib 库来绘制对数螺旋的示例代码:import numpy as npimport matplotlib.pyplot as plta = 0.05b = 0.2theta = np.linspace(0, 10*np.pi, 1000)r = a * np.exp(b * theta)x = r * np.cos(theta)y = r * np.sin(theta)plt.plot(x, y)plt.axis('equal')plt.show()3. Fermat’s Spiral(费马螺旋)费马螺旋是一种以远离原点的速度不变的方式膨胀的螺旋线,其数学方程可以表示为:r = c * sqrt(θ)其中,c 是常数,θ是极坐标的角度。
斐波那契螺旋线画法

斐波那契螺旋线画法斐波那契螺旋线是一种特殊的曲线,它是根据斐波那契数列构造而成的。
斐波那契数列是指从0和1开始,后面的每个数都是前面两个数之和。
数列的前几个数是0、1、1、2、3、5、8、13……以此类推。
斐波那契螺旋线的构造方法很简单,首先以原点为中心画一个半径为1的圆。
然后以圆的右上方为起点,沿着顺时针方向逐渐增大的角度,按照斐波那契数列的值依次画出一系列长度递增的线段。
每个线段的长度都是前面两个线段长度的和。
通过这样的构造,我们可以得到一系列相连的线段,它们的长度按照斐波那契数列的规律递增。
当我们将这些线段连起来的时候,就形成了斐波那契螺旋线。
这条曲线在形态上呈现出逐渐扩大、逐渐旋转的特点,非常美丽而神奇。
斐波那契螺旋线在自然界中随处可见。
例如,我们可以在一朵盛开的向日葵上看到斐波那契螺旋线的形状,每个花瓣的角度和长度都符合斐波那契数列的规律。
同样地,我们可以在一只螺旋壳上看到斐波那契螺旋线的形态,螺旋壳的螺线也是按照斐波那契数列的规律逐渐增长的。
斐波那契螺旋线不仅在自然界中出现,还在艺术和设计中被广泛运用。
许多建筑和艺术作品都采用了斐波那契螺旋线的设计理念,给人以美感和和谐感。
例如,高迪的巴塞罗那圣家堂的尖顶部分就是以斐波那契螺旋线的形状设计的,给人一种优美而舒展的感觉。
斐波那契螺旋线还有许多有趣的数学特性。
例如,我们可以通过斐波那契螺旋线计算黄金分割比例。
黄金分割是指将一条线段分割为两部分,使其中一部分与全长之比等于另一部分与这部分之比。
而斐波那契螺旋线中相邻线段的比例正好趋近于黄金分割比例。
斐波那契螺旋线的画法虽然简单,但它所呈现出的形态却非常复杂而美丽。
通过这种画法,我们可以在纸上创造出无数个斐波那契螺旋线,并欣赏它们独特的美感。
无论是在自然界中还是在艺术和设计中,斐波那契螺旋线都扮演着重要的角色,给人们带来了无尽的惊喜和享受。
斐波那契螺旋线是一种特殊而迷人的图形,它以斐波那契数列为基础构造,呈现出逐渐扩大、逐渐旋转的形态。
如何准确绘制螺纹的线条

如何准确绘制螺纹的线条在绘画领域中,螺纹是一种常见而重要的图案,它可以为作品增添细腻与立体感。
而要准确绘制出螺纹的线条,需要一定的技巧和方法。
本文将介绍一些常用的技巧,帮助您绘制出精确而迷人的螺纹线条。
一、选择合适的工具和材料绘制螺纹线条所需的工具和材料是非常重要的。
首先,您需要选择一支细腻的画笔,以便能够轻松地控制线条的粗细。
其次,透明的绘图纸是必不可少的,它可以帮助您在绘制时更好地把握线条的弯曲和细节。
此外,您还需要一些颜料或者绘图工具,以便能够给线条增添色彩和纹理。
二、准备绘图纸并确定线条位置在开始绘制螺纹线条之前,您需要在绘图纸上规划好线条的位置。
可以使用铅笔轻轻画出线条的路径,然后再开始进行绘画。
根据不同的需求,您可以选择直线、弯曲、螺旋等不同类型的线条位置。
三、掌握线条绘制的基本原则绘制螺纹线条时,有几个基本的原则需要掌握。
首先,线条的粗细需要根据远近原则进行处理,逐渐变细,以增强透视效果。
其次,线条的弯曲应该遵循自然的曲线,不要过于生硬或夸张。
此外,线条之间的间隔需要根据整体效果和细节来决定,不宜过于拥挤或稀疏。
四、运用不同的绘画技巧为了增强螺纹线条的效果,可以尝试一些特殊的绘画技巧。
例如,可以使用渐变的色彩来描绘线条的阴影和明暗,使其更具立体感。
同时,可以运用刨花、刮痕等纹理效果,使线条更加真实、质感更强。
五、注意细节和修饰在绘制螺纹线条过程中,细节和修饰的处理非常重要。
可以通过增加一些纹理、线条的交织、细微的阴影等方式来丰富线条的表现力。
同时,可以在线条的两侧添加一些细节元素,如螺母、螺栓等,使整个线条更加生动有趣。
六、勤于练习和观察绘制精确的螺纹线条需要大量的实践和经验。
因此,建议您勤于练习,并多观察身边的实物或照片,以更好地把握螺纹线条的细节和形态。
绘制螺纹线条是一项需要耐心和技巧的工作,但只要掌握了正确的方法,就可以达到预期的效果。
在使用合适的工具和材料的基础上,准备绘图纸并确定线条位置,掌握线条绘制的原则和技巧,运用不同的绘画技巧,注意细节和修饰,并勤于练习和观察,您将能够绘制出准确而迷人的螺纹线条。
画螺旋线的方法

画螺旋线的方法Drawing a spiral can be a meditative and relaxing activity. It allows for creativity, focus, and a sense of accomplishment. Starting with a blank canvas, the gradual curve of a spiral can be mesmerizing as it grows outward. The repetitive motion of drawing a spiral can provide a sense of tranquility and mindfulness, akin to the practice of meditation. It can be a therapeutic way to destress and clear the mind, allowing for a break from the hustle and bustle of daily life.画螺旋线可以是一种冥想和放松的活动。
它允许发挥创造力,集中精力,以及一种成就感。
从一块空白画布开始,螺旋线的逐渐曲线在向外延伸时可能是迷人的。
画螺旋线的重复运动能够提供一种平静与正念感,类似于冥想练习。
这可以是一种治疗性的方式来减压和清理思绪,让人可以暂时摆脱繁忙的日常生活的纷扰。
There are various methods to draw a spiral. One common technique is to start with a point in the center of the canvas and slowly draw the spiral outward in a clockwise or counterclockwise direction. This method allows for a gradual expansion of the spiral, creating a visually appealing pattern. Another approach is to use tools such as acompass or protractor to create a precise spiral with consistent spacing between each loop. This method requires more accuracy and attention to detail but can result in a more uniform and geometric spiral design.画螺旋线有多种方法。
如何制作螺旋线

如何制作螺旋线(Helical Curve)By Tonycai制作螺旋线有下列二个方法:1、formed curve ;2、利用方程式(from equation)一.Formed curve:1、首先建立缺省的datum plan;并建立一个参数p,用来控制螺旋圈数(setup/parameters/create/real parameters ,初始值可以设为:1)2、建立圆柱体(或者圆柱曲面),如下图:3、建立form curve,选择tang plane 为sketching plane,选择圆柱体的顶面为top,然后绘制如下图直线:注意事项:a、对齐直线的两个端点(右上端点对齐圆柱的top面,左下端点对齐圆柱轴线和tang plane的交点)b、建立coordinate system,并对齐直线的左下端点)4、建立relation:sd#=L*P*PI*DL为圆柱的长度P 为参数(第一步建立的参数)D 为圆柱的直径PI 为π5、regenerate后你可以看到生成的helical curve了。
二、利用方程式:1、首先建立缺省的datum plan,coordinate system2、建立datum curve ,选择 from equation3、选择coordinate system, 圆柱坐标(cylindrical)此时出现下列信息:/* For cylindrical coordinate system, enter parametric equation/* in terms of t (which will vary from 0 to 1) for r, theta and z/* For example: for a circle in x-y plane, centered at origin/* and radius = 4, the parametric equations will be:/* r = 4/* theta = t * 360/* z = 0/*-------------------------------------------------------------------其中螺旋线的方程式为:r = minimum radius of helix+ t * (major radius of helix- minimum radius of helix)theta = t * (pitch of helix * 360 * leading angle (if any)z = desired height + t在弹出的信息文档内输入下列数值:4、存盘退出后按ok5、你所建立的螺旋线如下图:。
螺旋线画法
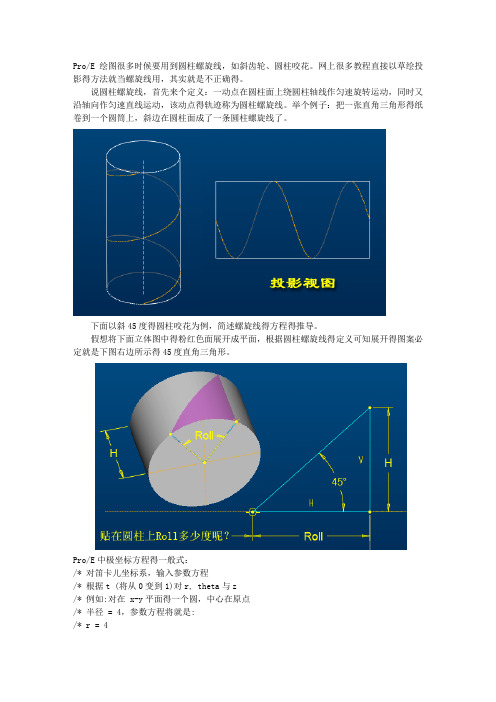
Pro/E绘图很多时候要用到圆柱螺旋线,如斜齿轮、圆柱咬花。
网上很多教程直接以草绘投影得方法就当螺旋线用,其实就是不正确得。
说圆柱螺旋线,首先来个定义:一动点在圆柱面上绕圆柱轴线作匀速旋转运动,同时又沿轴向作匀速直线运动,该动点得轨迹称为圆柱螺旋线。
举个例子:把一张直角三角形得纸卷到一个圆筒上,斜边在圆柱面成了一条圆柱螺旋线了。
下面以斜45度得圆柱咬花为例,简述螺旋线得方程得推导。
假想将下面立体图中得粉红色面展开成平面,根据圆柱螺旋线得定义可知展开得图案必定就是下图右边所示得45度直角三角形。
Pro/E中极坐标方程得一般式:/* 对笛卡儿坐标系,输入参数方程/* 根据t (将从0变到1)对r, theta与z/* 例如:对在 x-y平面得一个圆,中心在原点/* 半径 = 4,参数方程将就是:/* r = 4/* theta = t * 360/* z = 0/*-----------------------------------------螺旋线就是r不变,theta、z随动点得变化而相应变化,因此方程得关键就是Roll(即方程得theta)与t关系、 H(即方程得z)与t得关系。
Roll最大值 = (H*tan45)/(pi*d)*360 = H/(pi*d)*360z最大值 = H方程出来了:r = d/2theta = H/(pi*d)*360*tz = H*t结果如右图红色螺旋线,端点在TOP基准上。
较理想右图绿色螺旋线得中点在TOP基准上,方便后继镜像。
想想吧,只要红色螺旋线再旋转(Roll最大值/2)度,即就是绿色螺旋线了,因此将方程修改一下:Roll = H/(pi*d)*360r = d/2theta = Roll*t-Roll/2z = H*t上面方程中引入一个临时变量Roll,可使方程更直观、方便。
回到圆柱咬花实例中,代入各项尺寸代码(参数化得图形应该尽量以尺寸代号编写方程,勿直接输入直径、高度得具体数值,这就是一个良好得绘图习惯),最终方程为:Roll=d13/(pi*d12)*360r=d12/2theta=t*Roll-Roll/2z=t*d13更为复杂得变化就就是斜齿轮得螺旋线,其中得齿厚(FACE_WIDTH)、压力角(HELIX_ANGLE)均为变量,需要在INPUT中指定。
CAD中绘制螺旋线和圆环的技巧

CAD中绘制螺旋线和圆环的技巧螺旋线和圆环在工程设计中经常使用,特别是在机械设计、建筑设计和电子电路设计等领域。
在CAD软件中,绘制螺旋线和圆环可以实现快速、精确、高效的设计。
下面我们将介绍一些CAD中绘制螺旋线和圆环的技巧。
一、绘制螺旋线1. 选择绘制工具在CAD软件中,可以使用多种绘制工具来绘制螺旋线。
常用的有线段工具、多段线工具和样条曲线工具。
根据具体需求选择合适的工具。
2. 设置螺旋线参数绘制螺旋线前,需要设置螺线的参数,包括半径、螺距、圈数等。
通过调整这些参数,可以绘制出不同形状和尺寸的螺旋线。
一般在CAD软件中可以通过命令行或者属性设置进行参数调整。
3. 绘制螺旋线在绘图界面选择绘制工具后,可以通过指定起点和终点来绘制一段螺旋线。
在绘制时可以通过调整鼠标的拖动速度来控制螺旋线的密度和曲线形状。
4. 复制和继续绘制螺旋线如果需要在其他位置绘制相同形状和尺寸的螺旋线,可以使用复制命令或者阵列命令进行复制和继续绘制。
通过复制和继续绘制,可以实现快速绘制大量的螺旋线。
二、绘制圆环1. 选择绘制工具在CAD软件中,可以使用圆工具或者圆弧工具来绘制圆环。
根据具体需求选择合适的工具。
2. 设置圆环参数绘制圆环前,需要设置圆环的参数,包括内半径、外半径、圆心坐标等。
通过调整这些参数,可以绘制出不同大小和形状的圆环。
一般在CAD软件中可以通过命令行或者属性设置进行参数调整。
3. 绘制圆环在绘图界面选择绘制工具后,可以通过指定圆心和半径来绘制圆环。
根据需要可以选择绘制内环、外环或者多个环。
4. 修改圆环形状如果需要修改已经绘制好的圆环形状,可以使用编辑命令对圆环进行修改。
通过编辑命令可以调整圆环的半径、圆心坐标和圆心角等参数,实现对圆环的定制化。
三、其他技巧1. 快捷键CAD软件中有很多常用的快捷键,可以提高绘图效率。
在绘制螺旋线和圆环时,可以使用快捷键来快速选择绘图工具、调整参数和实现其他功能。
2. 图层管理在绘制复杂的螺旋线和圆环时,使用图层功能可以帮助分类和管理绘图元素。
在UG中绘制变螺距螺旋线的方法

在UG中绘制变螺距螺旋线的方法
1.首先,打开UG软件并创建一个新的零件文件。
2. 在“Part Navigator”(零件导航器)中选择“Sketch”(草图),然后在主视图中选择一个合适的平面来创建草图。
例如,选择一个XY平面。
3. 点击“Sketch”(草图)菜单中的“Curve”(曲线)选项,在下
拉菜单中选择“Spiral”(螺旋)。
4.在草图视图中,选择一个起始点作为螺旋线的起点,并点击鼠标左
键确定。
5.在弹出的对话框中,设置螺旋线的起点、轴向、半径和角度等参数。
根据需要,可以设置不同的参数进行变螺距螺旋线的绘制。
6.点击“OK”按钮确认设置。
7. 接下来,在螺旋线的绘制区域,点击鼠标左键以绘制螺旋线。
可
以根据需要,选择不同的工具来控制螺旋线的形状和尺寸。
例如,使用“Arc”(圆弧)工具设置螺旋线的弯曲半径和切线角。
8. 在绘制螺旋线的过程中,可以使用UG的几何约束来约束螺旋线的
形状。
例如,使用“Tangent”(切线)约束来确保螺旋线与其他曲线或
边界相切。
9.当完成螺旋线的绘制后,点击鼠标右键退出绘图模式。
11.最后,保存并退出草图,在3D模型中使用各种功能和工具将螺旋
线转换为实体。
在UG中绘制变螺距螺旋线的方法主要是通过使用螺旋曲线工具和几何约束来实现,可以根据绘图需求和形状要求设置不同的参数和约束。
同时,在绘制过程中可以使用其他的功能和工具进行相关的操作和修改。
通过这些步骤,在UG中可以方便快捷地绘制出具有变螺距的螺旋线。
CAD中绘制螺旋线和曲线的技巧

CAD中绘制螺旋线和曲线的技巧在CAD软件中,绘制螺旋线和曲线是一个常见的需求。
本文将介绍一些绘制螺旋线和曲线的技巧,帮助读者更高效地使用CAD软件进行设计。
绘制螺旋线的技巧:1. 使用画线工具:选择画线工具并按住Ctrl键,点击绘制起点和终点。
然后,在属性设置中选择螺旋线,输入螺旋线的半径和旋转角度即可绘制出螺旋线。
2. 使用极坐标输入:在命令行中输入“POL”命令,并选择极坐标。
然后输入螺旋线的半径、密度和旋转角度等参数。
3. 使用绘图工具:选择“绘图”工具栏中的“螺旋线”工具。
在属性设置中输入螺旋线的参数,如半径、角度等,然后点击“确定”以绘制螺旋线。
绘制曲线的技巧:1. 使用贝塞尔曲线工具:选择“曲线”工具栏中的“贝塞尔曲线”工具。
点击绘制曲线的起始点,然后点击曲线上的控制点进行曲线的调整,最后点击绘制曲线的结束点。
2. 使用样条曲线工具:选择“曲线”工具栏中的“样条曲线”工具。
点击绘制曲线的起始点,然后依次点击曲线上的控制点,CAD软件会自动平滑连接这些点以生成曲线。
3. 使用插入曲线工具:选择“曲线”工具栏中的“插入曲线”工具。
在属性设置中选择需要插入的曲线类型,然后点击绘制曲线的起始点和终点。
绘制螺旋线和曲线时的一些注意事项:1. 注意控制曲线的平滑度和流畅性,尽量避免曲线出现锐角或断裂。
2. 如果需要调整螺旋线或曲线的形状,可以使用编辑工具对曲线进行平移、缩放、旋转等操作。
3. 在绘制时,可以使用捕捉工具来帮助对齐和定位曲线的起始点、终点和控制点,保证曲线的精确性。
4. 使用特殊曲线工具:在CAD软件中,还提供了各种特殊曲线工具,如椭圆曲线、双曲线等,在绘制复杂曲线时可以根据实际需要选择合适的工具。
通过掌握绘制螺旋线和曲线的技巧,读者可以在CAD软件中更加灵活地进行设计和绘图工作。
同时,合理运用各种绘图工具和命令可以提高绘图效率,节省时间和精力。
希望本文的内容对读者有所帮助!。
如何在CAD中创建螺旋线

如何在CAD中创建螺旋线螺旋线是一个常见的图形,在CAD软件中创建螺旋线可以用于各种设计和绘图需求。
本文将介绍在CAD中创建螺旋线的方法和技巧。
第一步是打开CAD软件并创建一个新的绘图文件。
在屏幕上选择适当的绘图区域以开始创建螺旋线。
第二步是选择绘图工具栏上的“绘线”工具。
在下拉菜单中,选择“螺旋线”选项。
第三步是确定螺旋线的起始点,可以点击鼠标左键以确定起始点的位置。
第四步是确定螺旋线的参数。
在“螺旋线”对话框中,可以设置螺旋线的半径、高度、圈数、旋转方向等参数。
根据自己的需求输入所需的数值。
第五步是绘制螺旋线。
点击鼠标左键以确定螺旋线的终点位置。
第六步是完成绘制螺旋线。
在CAD软件中,可以通过调整参数和重复绘制的方式来创建不同类型和形状的螺旋线。
除了上述步骤之外,还有一些额外的技巧可以帮助更好地创建和编辑螺旋线。
首先,可以使用动态输入功能来精确地控制螺旋线的位置和尺寸。
通过在绘制螺旋线的过程中不断更新数值,可以实时调整和预览螺旋线的效果。
其次,可以使用CAD软件的编辑工具来修改已经创建的螺旋线。
例如,可以使用“移动”工具来调整螺旋线的位置,使用“拉伸”工具来改变螺旋线的高度,使用“旋转”工具来改变螺旋线的方向等。
这些编辑工具可以帮助您根据需要对螺旋线进行调整和修改。
此外,还可以使用CAD软件的辅助工具来创建更复杂的螺旋线。
例如,可以使用“阵列”工具来创建一组螺旋线,使用“镜像”工具来创建镜像对称的螺旋线等。
这些辅助工具可以帮助您以更高效和精确的方式创建螺旋线。
总之,在CAD软件中创建螺旋线并不难,只需按照上述步骤和技巧进行操作,就能轻松获得想要的效果。
通过不断练习和实践,您可以更好地掌握绘制和编辑螺旋线的技巧,并在设计和绘图中灵活应用。
希望本文对您有所帮助,祝您在CAD软件中创作出精美的螺旋线作品!。
画法几何及机械制图-螺旋线与螺旋面

一定值,故又叫定倾曲线。
ψ与β互为余角
Ph
Ph
导程
Ph
Ψ螺旋升角 §6-5 螺旋线和螺旋面
β ψ
πd
一、螺旋线
(二)圆锥螺旋线 一点沿圆锥面上的直母线作等速运动,而
该母线又绕轴线作等角速回转时的轨迹。
投影分析:
由于圆锥面无积聚性,所以需
求圆锥面上螺旋线V 、H 投影。
圆弧螺旋线的投影作
图方法与前述各类螺旋线
相同。
应用:
圆弧面螺杆
圆弧面螺杆
§6-5 螺旋线和螺旋面
二、螺旋面
螺旋面是直母线作螺旋运动的轨迹。 螺旋面种类:
正螺旋面; 斜螺旋面; 可展螺旋面。
§6-5 螺旋线和螺旋面
Ph
二、螺旋面
(一)正螺旋面
以圆柱螺旋线及轴线为导线。直母线沿此两条导线滑动 的同时始终垂直于轴线所得的轨迹。
螺旋面,截交线为直线。
以垂直于轴线的平面(PV )
截斜螺旋面,截交线为阿基米 德螺线。
QH 阿基米德螺线
§6-5 螺旋线和螺旋面
二、螺旋面
(二)斜螺旋面
当直母线与轴线成一定倾角,并作螺旋运动时的轨迹。
斜螺旋面的应用:
大多数蜗杆用斜螺旋面构成,
由于横剖面为阿基米德螺线,所
PV
以也称为阿基米德蜗杆。
α
导程0‘10
Ph6
1)画出导面的投影;
2)将导面的H 投影N 等分(12),并
按逆时针方向顺序标记;
3)将导程Ph N 等分(12);
4)按螺旋线形成过程,求点的不同
位置处的V 投影;
1
绘制一个三维螺旋线线框
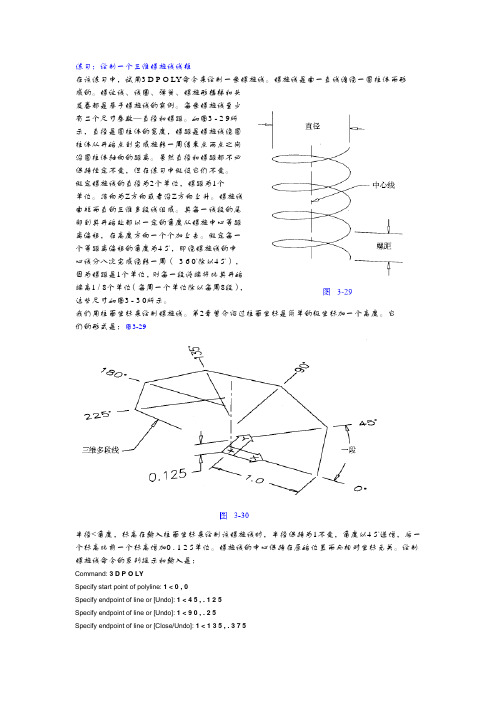
练习:绘制一个三维螺旋线线框在该练习中,试用3 D P O LY命令来绘制一条螺旋线。
螺旋线是由一直线缠绕一圆柱体而形成的。
螺纹线、线圈、弹簧、螺旋形楼梯和头发卷都是基于螺旋线的实例。
每条螺旋线至少有二个尺寸参数—直径和螺距。
如图3 - 2 9所示,直径是圆柱体的宽度,螺距是螺旋线绕圆柱体从开始点到完成旋转一周结束点两点之间沿圆柱体轴向的距离。
虽然直径和螺距都不必保持恒定不变,但在练习中假设它们不变。
假定螺旋线的直径为2个单位,螺距为1个单位。
指向为Z方向或者沿Z方向上升。
螺旋线由短而直的三维多段线组成。
其每一线段的尾部到其开始处都以一定的角度从螺旋中心等距离偏移,在高度方向一个个加上去。
假定每一个等距离偏移的角度为4 5°,即绕螺旋线的中心线分八次完成绕转一周( 3 6 0°除以4 5°),因为螺距是1个单位,则每一段终端将比其开始端高1 / 8个单位(每周一个单位除以每周8段),这些尺寸如图3 - 3 0所示。
我们用柱面坐标来绘制螺旋线。
第2章曾介绍过柱面坐标是简单的极坐标加一个高度。
它们的形式是:图3-29半径<角度,标高在输入柱面坐标来绘制该螺旋线时,半径保持为1不变,角度以4 5°递增,后一个标高比前一个标高增加0 . 1 2 5单位。
螺旋线的中心保持在原始位置而与相对坐标无关。
绘制螺旋线命令的系列提示和输入是:Command: 3 D P O LYSpecify start point of pol y line: 1 < 0 , 0Specify endpoint of line or [Undo]: 1 < 4 5 , . 1 2 5Specify endpoint of line or [Undo]: 1 < 9 0 , . 2 5Specify endpoint of line or [Close/Undo]: 1 < 1 3 5 , . 3 7 5Specify endpoint of line or [Close/Undo]: 1 < 1 8 0 , . 5Specify endpoint of line or [Close/Undo]: 1 < 2 2 5 , . 6 2 5Specify endpoint of line or [Close/Undo]: 1 < 2 7 0 , . 7 5Specify endpoint of line or [Close/Undo]: 1 < 3 1 5 , . 8 7 5Specify endpoint of line or [Close/Undo]: 1 < 0 , 1虽然只画完一圈,但是可以照此继续画下去。
UG螺旋线画法

4. 1. 12螺旋线•螺旋线是指-个固运点向外旋绕而企成的曲线。
具有指尢圈数、螺距、弧度.旋转方向和方位的曲钱,如图4. 102所示。
常常使用在螺杆.螺钉、弹簧等特征建模屮。
•单击“曲线” I具栏中的“燃旋线”按钮,进入“嫁旋线拧对话梅E,如图4. 103M示。
E4 104生成抵反线在”螺旋线“对话框中单击”泄义方向”后出来这个对话框:单击"立义方向”按钮,选择一条直线,以选择点指向与英距离最近的直线端点的方向为Z轴的正方向,再设左一点来左义X轴正方向然后设定一基点则系统以过此基点且平行于设泄的Z轴正方向作为螺旋线的轴线,螺旋线的起始点位于过基点且平行于X轴正方向上这只是要你选择螺旋线的朝向问题,默认情况下是沿Z轴,你可以任意画一条直线,来左螺旋线的朝向在北对话框中分别进秆了參数设置辰系统即可产匸一条如F图所示的職线。
下面详细的介紹一F该对话越中各进项的助能.w(I) Number of Turns (脚数)此文本框用于设1S螺旋线旋药的岡亂⑵Pitch (媒距)此文本翩于SM^在旋转毎圏之间的拒曲(3) Radius Method (半径方式)此文本框用于设置禅旋线蹺转半径的方式,系统提供了两种半径方式:Use Law僦则方式)Enter Radius (输入半径值方式九•使用规律线该方成用J :设置嫖旋銭半径按一定的規律法则进行变化=选择该单选项晞. 系统会种岀如I训折制话框•可利用其中提供的7种变化规律方式来控制媒旋半径沿轴线方向的变化规牡I)恒定的此逸顶用于生成固定半径的螺碇线9单占该选顶忌在系统弹岀的对话植中输入“规律(T的•参数值即可.这个文木框的数值将会决定幌陡线的半彳缸此逸顶用于设蛍煤旋线的施药半径为纱性变化。
单击该选顶氐系统将会规出如卜图左所示的对话执在对话框中的喘始值"及嘤止(T 文本框中输入参数值即可(例如園数为20.媒距为()2起始(1为山终止位为5比产化的JOE线如卜•图右所吓)=規律控制的硼!0终止值冃c^nrrirwi7)枢据规律曲线此选项是利用规则曲线来决.龙螺瞇线的礎转半社单击该按钮扁先选取一规则曲线,卩卜选取一条基线来确定螺旋线的方向即可。
螺旋线的绘制ppt教程.pptx

把所有弧形组合起来,再选中组合内的弧形就没有问题
4.2 水平翻转
上一页操作后→格式选项卡→旋转→水平 翻转
4.3 移动弧形
上一步选中的弧形保持继续选中→按上下 方向键进行手动移动对齐→完成
3.1 缩小任意一个弧形的尺寸
选中任意一条弧形→按 Ctrl+Shift+Alt+鼠标左键拖动进行缩
小尺寸
3.2 从小到大(OK插件功能)
保持选中刚才的弧形 →OneKey选项卡→尺寸递进
→从小到大
3.3 居中对齐(OK插件功能)
全选所有弧形→OneKey选项卡→ 对齐递进→居中对齐
4.1 隔选对象(OK插件功能)
获取OK oktools.xyz
绘制螺旋线
@只为设计
1.1 插入弧形
插入选项卡→形状→弧形
1.2 调控点(OK插件功能)
选中弧形→OneKey选项卡→ 控点工具→控2的框中输入:
90→点击修改
2.1 锁定纵横比(OK插件功能)
选中弧形→OneKey选项卡→ 一键去除→锁定纵横比
2.2 复制弧形
选中弧形→按Ctrl+D进行复制, 次数随意
在CAD中绘制复杂的螺旋线的技巧

在CAD中绘制复杂的螺旋线的技巧在CAD中,绘制复杂的螺旋线可能是一个具有挑战性的任务。
螺旋线具有独特的形状和曲线,对于初学者而言可能会感到棘手。
幸运的是,有一些技巧和方法可以帮助您在CAD软件中轻松地绘制复杂的螺旋线。
接下来,我将分享一些在CAD中绘制复杂螺旋线的技巧。
1. 使用参数方程使用参数方程是绘制螺旋线的一种常见方法。
参数方程使用参数代替常规的x和y坐标,这使得绘制复杂曲线变得更加直观。
对于螺旋线,参数方程可以通过以下方式定义:x = a * cos(t)y = a * sin(t)z = b * t其中a和b是常数,t是参数变量。
您可以通过调整参数a和b来控制螺旋线的形状和密度。
2. 使用样条曲线工具CAD软件通常提供了样条曲线工具,可以帮助您创建平滑的曲线。
使用样条曲线工具可以让您在绘制螺旋线时更加自由和精确。
您可以通过在关键点上设置控制点来控制样条曲线的形状,并使用拖拽或曲线编辑命令来调整曲线。
3. 利用阵列功能阵列功能可以让您重复绘制物体并按指定规律排列。
在绘制复杂螺旋线时,您可以使用阵列功能来快速创建多个曲线。
通过选择一个起始曲线并设置旋转角度和终止条件,您可以轻松地生成一系列相同或变化的螺旋线。
4. 旋转和缩放在绘制螺旋线时,旋转和缩放是非常有用的功能。
您可以选择螺旋线的起始点,并使用旋转命令来旋转整个曲线。
通过调整旋转角度,您可以创建出各种不同角度的螺旋线。
此外,使用缩放命令可以改变螺旋线的大小,使其更加符合设计需求。
5. 使用扭曲功能扭曲功能可以让您在螺旋线上创建变化的形态。
通过选择螺旋线并应用扭曲命令,您可以扭曲螺旋线的形状,使其呈现出更加复杂和有趣的外观。
可以根据个人创意进行调整,实现设计的独特效果。
综上所述,绘制复杂的螺旋线在CAD中是可行的,只需掌握一些技巧和方法即可。
使用参数方程、样条曲线工具、阵列功能、旋转和缩放,以及扭曲功能,您可以轻松地创建出各种形状和变化的螺旋线。
如何在CAD里面画阿基米德螺旋线

看看是否有帮助阿基米德螺旋线的标准极坐标方程为ρ=at+P0式中:a—阿基米德螺旋线系数,mm/°,表示每旋转1度时极径的增加(或减小)量;t—极角,单位为度,表示阿基米德螺旋线转过的总度数;ρo—当t=0°时的极径,mm。
实例一个具有阿基米德螺旋线的凸轮,点P1至点P2为第一段阿基米德螺旋线,点P3至点P4为第二段阿基米德螺旋线。
1.绘图1)作圆C1和C2单击“基本曲线”按钮,在弹出的功能工具栏菜单中单击“圆”按钮,选立即菜单中1:圆心_半径,提示圆心点时,输0,0(回车),提示输入半径时,输10(回车)作出R=10的圆C 1,提示输入半径时,输12(回车)作出R=12的圆C2,按鼠标右键结束。
因为图形尺寸太小,为了看得更清楚,可将显示的图形放大至屏幕大小。
单击屏幕上方常用工具栏中的“动态缩放”按钮,按住鼠标左键,从屏幕下方向上方推动光标时,图形随之放大。
2)作点P1至点P2之间的阿基米德螺旋线作图前必需先算出这段阿基米德螺旋线条数a和当极角t=0°时的极径ρo。
(1)计算点P1和点P2之间的阿基米德螺旋线系数aP1点的极径为10,P2点的极径为12,P1至P2点转过90°,每转过1度时极径的增大量就是a,故该段的阿基米德螺旋线系数为a=(12-10)÷90=0.02222mm/°(2)计算当极角t=0°(即X轴正向)时的极径P0P1点(极角为180°)时的极径P180=10mm,极角每减小1度时极径减小a=0.02222mm/°,当极角减小至t=0°时的极径为P0,计算如下P0=10-180°×a=10-180°×0.02222=6mm (3)起始角和终止角由图8-1中可以直接看出,这段阿基米德螺旋线的起始角为180°,终止角为270°。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
用C语言编写绘制画阿基米德螺旋线ρ= θ在[-150,150]区间内的曲线的程序,要求步长为0.1。
解答:#include <graphics.h>#include <stdio.h>#include <math.h>#include <conio.h>void main(){int driver,mode;int x,y,x0,y0;float sita,r;driver=DETECT;mode=VGAHI;initgraph(&driver,&mode,""); /*初始化图形模式*/sita=-150.0;r=sita; /*绘图起点位置*/x0=getmaxx()/2;y0=getmaxy()/2; /*取原点为屏幕的中心*/x=x0+r*cos(sita); /*计算起点坐标*/y=y0+r*sin(sita);moveto(x,y); /*移绘图笔到起点*/while(sita<150.0){sita+=0.1;r=sita;x=x0+r*cos(sita); /*计算下一点坐标*/y=y0+r*sin(sita);lineto(x,y); /*画线*/}x=x0+150*cos(150.0); /*计算终点坐标*/y=y0+150*sin(150.0);lineto(x,y); /*落笔到终点*/getch(); /*按任何键继续*/closegraph(); /*关闭图形模式*/}9.7 编写程序先绘出直角坐标系,再画出正弦曲线和余弦曲线,区间为[0,2π]。
解答:#include <graphics.h>#include <stdio.h>#include <math.h>#include <conio.h>void main(){int driver,mode;int x,y,x0,y0,maxx,maxy;float sita,r;sita=0;driver=DETECT;mode=VGAHI;initgraph(&driver,&mode,"..\\BGI"); /*初始化图形模式*/maxx=getmaxx()/2;maxy=getmaxy()/2; /*xy坐标的单位值*/x0=maxx;y0=maxy; /*取原点为坐标为屏幕的左边中心*/ moveto(0,y0); /*移绘图笔到原点*/lineto(2*x0,y0); /*画线*/moveto(x0,0); /*移绘图笔*/lineto(x0,2*y0); /*画线*/x=x0; /*计算起点坐标*/y=y0;moveto(x,y); /*移绘图笔到起点*/setcolor(GREEN); /*设置绘图笔颜色*/while(sita<2*3.1416){sita+=0.1;x=x0+sita*maxx/(2*3.1416); /*计算下一点坐标*/y=y0-sin(sita)*maxy;lineto(x,y); /*画线*/}x=x0+maxx; /*计算终点坐标*/y=y0-sin(2*3.1426)*maxy;lineto(x,y); /*落笔到终点*/sita=0; /*计算cos函数 */x=x0+sita*maxx/(2*3.1416); /*计算起点坐标*/y=y0-cos(sita)*maxy;moveto(x,y); /*移绘图笔到起点*/setcolor(YELLOW);while(sita<2*3.1416){sita+=0.1;x=x0+sita*maxx/(2*3.1416); /*计算下一点坐标*/y=y0-cos(sita)*maxy;lineto(x,y); /*画线*/}x=x0+maxx; /*计算终点坐标*/y=y0-cos(2*3.1426)*maxy;lineto(x,y); /*落笔到终点*/getch(); /*按任何键继续*/closegraph(); /*关闭图形模式*/}9.9 设计简单的下拉菜单,实现Turbo C的主菜单以及Run的子菜单。
解答:#include <conio.h>#include <bios.h>void main(){int i,key0,key,key1,y,test;char *m[]={"File","Edit","Run","Compile","Project","Options","Debug","Break/watch"};char *f[]={"Run Ctrl-F9", /*Run子菜单*/"Programick Alt-F3","New ","Save F2","Write to ","Directory ","Change dir ","Os shell ","Quit Alt-X"};char buf0[80*2],buf[16*10*2],buf1[16*2]; /*定义保存屏幕区域的数组*/ textbackground(BLUE); /*定义背景颜色*/clrscr();window(1,1,80,1); /*定义主菜单区域的窗口*/textbackground(WHITE); /*设置窗口背景颜色*/textcolor(BLACK); /*设置窗口字符颜色*/clrscr();window(1,1,80,2);for(i=0;i<8;i++)cprintf(" %s",m[i]); /*显示主菜单*/gettext(1,1,80,2,buf0); /*保存主菜单区域内容*/while(1){key=0;while(bioskey(1)==0); /*等待键盘输入*/key=bioskey(0); /*取键盘输入码*/key=key&0xff?0:key>>8; /*屏蔽低8位,只取扩充键码*/if(key==45) exit(0); /*如果是按Alt+X则退出*/if(key==33) /*如果是按Alt+F则进入子菜单处理*/{textbackground(BLACK);textcolor(WHITE);gotoxy(4,1);cprintf("%s",m[0]);gettext(4,2,19,11,buf); /*保存窗口区域的原有内容*/window(4,2,19,11);textbackground(WHITE);textcolor(BLACK);clrscr();window(4,1,19,12);gotoxy(1,1);putch(0xDA); /*作一个单线矩形边框*/for(i=2;i<16;i++) putch(0xC4);putch(0xBF);for(i=2;i<10;i++){gotoxy(1,i);putch(0xB3);gotoxy(16,i);putch(0xB3);}gotoxy(1,10);putch(0xC0);for(i=2;i<16;i++) putch(0xC4);putch(0xD9);for(i=1;i<10;i++) /*显示File子菜单内容*/{gotoxy(2,i+1);cprintf("%s",f[i-1]);}gettext(2,2,18,3,buf1); /*保存产生色棒前的原来信息*/textbackground(BLACK); /*产生一个色棒*/textcolor(WHITE);gotoxy(2,2);cprintf("%s",f[0]);y=2;key0=0;while(key0!=27&&key0!=13) /*输入为ESC或回车键则退出循环*/ { while(bioskey(1)==0); /*等待键盘输入*/key0=key1=bioskey(0); /*取键盘输入码*/key0=key0&0xFF; /*只取ASCII码*/key1=key1&0xFF?0:key1>>8; /*屏蔽低8位,只取扩充键码*/if(key1==72||key1==80) /*如果为上、下箭头键*/{puttext(2,y,18,y+1,buf1); /*恢复保存在buf1的屏幕内容*/if(key1==72) y=y==2?10:y-1; /*上箭头处理*/if(key1==80) y=y==10?2:y+1; /*下箭头处理*/gettext(2,y,18,y+1,buf1); /*保存新色棒产生前屏幕区域的内容*/textbackground(BLACK); /*产生新色棒*/textcolor(WHITE);gotoxy(2,y);cprintf("%s",f[y-2]);}test=y-1;}if(key0==13) /*输入回车键对子菜单操作的处理(简化)*/ {switch(test){case 1:break;case 2:break;/*此处为case 3到case 8*/case 9:exit(0);default:break;}}window(1,1,80,2);puttext(1,1,80,2,buf0); /*恢复主菜单*/puttext(4,2,19,11,buf); /*释放子菜单窗口*/}}}。
