点与圆的位置关系 课件
点和圆的位置关系(共32张PPT)

随堂练习
6.如图,⊿ABC中,∠C=90°, B
BC=3,AC=6,CD为中线,
以C为圆心,以 3 5 为半径作圆,
2
C
则点A、B、D与圆C的关系如何?
D A
7.画出由所有到已知点O的距离大于或 等于2CM并且小于或等于3CM的点组 成的图形。
OO
问:如图已知矩形ABCD的边AB=3厘米,AD=4厘米
(1)以点A为圆心,3厘米为半径作圆A ,则点B、C、D与圆A的位置关系如何?
(B在圆上,D在圆外,C在圆外)
A
D
(2)以点A为圆心,4厘米为半径作圆A,
则点B、C、D与圆A的位置关系如何?
B
C
(B在圆内,D在圆上,C在圆外)
(3)以点A为圆心,5厘米为半径作圆A,则点B、C、D 与圆A的位置关系如何?
∴经过点A,B,C三点可以作一个圆,并且只能作 一个圆.
A
O C
B
定理:
不在同一直线上的三点确定一个圆.
1.由定理可知:经过三角形三
个顶点可以作一个圆.并且只 能作一个圆.
2.经过三角形各顶点的圆叫做三 角形的外接圆。
3.三角形外接圆的圆心叫做三角 B
形的外心,这个三角形叫做
这个圆的内接三角形。
经过一个已知点A能确定一个圆吗?
形的外接圆的面积. 垂直平分线的交点
已知:不在同一直线上的三点 A、B、C
()
证明:∵点O在AB的垂直平分线上,
⊙O的半径6cm,当OP=6时,点P在
;
经过三角形各顶点的圆叫做三角形的外接圆。
圆的外部可以看成是
。
思考:过任意四个点是不是一定可以作一个圆?请举
例说明.
【点和圆的位置关系】PPT课件

9.用反证法证明“垂直于同一条直线的两条直线平行”, 第一步先假设( D ) A.相交 B.两条直线不垂直 C.两条直线不垂直于同一条直线 D.垂直于同一条直线的两条直线相交
10.【2018·舟山】用反证法证明时,假设结论“点在圆 外”不成立,那么点与圆的位置关系只能是( D )
1. 你虽然没有完整地回答问题,但你能大胆发言就是好样的!
此页为防盗标记页(下载后可删)
1、你的眼睛真亮,发现这么多问题! 2、能提出这么有价值的问题来,真了不起! 3、会提问的孩子,就是聪明的孩子! 4、这个问题很有价值,我们可以共同研究一下! 5、这种想法别具一格,令人耳目一新,请再说一遍好吗? 6、多么好的想法啊,你真是一个会想的孩子! 7、猜测是科学发现的前奏,你们已经迈出了精彩的一步! 8、没关系,大声地把自己的想法说出来,我知道你能行! 9、你真聪明!想出了这么妙的方法,真是个爱动脑筋的小朋友! 10、你又想出新方法了,真会动脑筋,能不能讲给大家听一听? 11、你的想法很独特,老师都佩服你! 12、你特别爱动脑筋,常常一鸣惊人,让大家禁不住要为你鼓掌喝彩! 13、你的发言给了我很大的启发,真谢谢你! 14、瞧瞧,谁是火眼金睛,发现得最多、最快? 15、你发现了这么重要的方法,老师为你感到骄傲! 16、你真爱动脑筋,老师就喜欢你思考的样子! 17、你的回答真是与众不同啊,很有创造性,老师特欣赏你这点! 18、××同学真聪明!想出了这么妙的方法,真是个爱动脑筋的同学! 19、你的思维很独特,你能具体说说自己的想法吗? 20、这么好的想法,为什么不大声地、自信地表达出来呢? 21、你有自己独特想法,真了不起! 22、你的办法真好!考虑的真全面! 23、你很会思考,真像一个小科学家! 24、老师很欣赏你实事求是的态度! 25、你的记录很有特色,可以获得“牛津奖”!
华师大版数学九年级下册同步课件:27. 点与圆的位置关系

(3)三角形的外心是三角形三条边的垂直平分线的交点, 它到三角形三个顶点的距离相等.
例题讲授
例1 如图,在△ABC中,∠C=90°,AB=5cm,
BC=4cm,以点A为圆心、3cm为半径画圆,并判断:
随堂演练
1.圆心为O的两个同心圆,半径分别为1和2,若OP= 3 ,则点P
在(D )
A.大圆内 B.小圆内
C.小圆外 D.大圆内,小圆外
o
2.三角形的外心具有的性质是( B )
A.到三边的距离相等. B.到三个顶点的距离相等. C.外心在三角形的外. D.外心在三角形内.
3.等腰三角形底边上的高与一腰的垂直平分线的交点是( C )
线段AB的垂直平分线l1上,又在线段BC的垂直 平分线l2上,即点P为l1与l2的交点,而l1⊥l,
C l2⊥l这与我们以前学过的“过一点有且只有一 条直线与已知直线垂直”相矛盾,所以过同一
条直线上的三点不能作圆.
定理:不在同一直线上的三个点确定一个圆.
位置关系
有且只有
已知:不在同一直线上的三点A、B、C. 求作: ⊙O,使它经过点A、B、C.
A.重心 B.垂心 C.外心 D.无法确定.
4.已知AB=4 cm,则过点A,B且半径为3 cm的圆有( B )
A.1个
B.2个
C.3个 D.4个
5.如图,在△ABC中,点O在边AB上,且点O为△ABC的外心,求 ∠ACB的度数. 解:∵点O为△ABC的外心, ∴OA=OB=OC, ∴∠OAC=∠OCA,∠OCB=∠OBC. ∵∠OAC+∠OCA+∠OCB+∠OBC=180°, ∴∠OCA+∠OCB=90°, 即∠ACB=90°.
圆与圆有关的位置关系点与圆的位置关系课件

两圆内切
总结词:两圆之间的距离等于两圆的半径之差 两圆有且仅有一个公共点
两圆心之间的距离等于两圆的半径之差 两圆的圆心距离减去两圆的半径之差等于零
两圆外切
总结词:两圆之间的距离大于两圆的半径之和 两圆有且仅有一个公共点
两圆心之间的距离大于两圆的半径之和 两圆的圆心距离减去两圆的半径之和大于零
利用平面几何知识,如三角形中 位线、圆心角和弧长等,计算两 圆心之间的距离,从而、计算方法 圆的面积公式为S=πr²,其中π取3.14。
计算方法为将半径分为小段,每段小扇形的面积为πr²/4,再相加得到圆的面积。
圆的周长计算
总结词:公式、计算方法
圆的周长公式为C=2πr,其中π取3.14。
02
圆的定义与性质
圆的定义
平面内,一个动点到一个定点( 圆心)的距离等于定长(半径)的
运动轨迹形成的图形叫圆。
圆心决定圆的位置,半径决定 圆的大小。
圆是轴对称图形,任何一条直 径所在的直线都是它的对称轴
。
圆的性质
圆的任意两条直径必定相交于圆心。 圆内两条不平行弦的垂直平分线必定通过圆心。
圆的半径是直径的一半,且直径是半径的两倍。
在圆上,点与圆心的距离等于半径。
详细描述
当一个点在圆上时,它与圆心的距离等于该圆的半径。这意味着该点位于圆 的边缘,与圆相切,并且在该点的切线与圆相切。
点在圆外
总结词
在圆外,点与圆心的距离大于半径。
详细描述
当一个点在圆外时,它与圆心的距离大于该圆的半径。这意味着该点位于圆的外 部,与圆不相交、不切也不相离。
性质2
在同一直线上,任意三点确定一个圆
性质3
点与圆的位置关系

试试看!
用反证法证明(填空):在三角形的内角中, 至少有一个角大于或等于60° 已知:如图, ∠A,∠B,∠C是△ABC的内角
求证: ∠A,∠B,∠C中至少有一个角大 于或等于60度
假设所求证的结论不成立,即 B 证明 ∠A__60°, ∠B__60°,∠C__60° < < < 则 ∠A+∠B+∠C < 180度
圆外的点
圆上的点
圆内的点
平面上的一个圆,把平面上的点分成三类:圆上的 点,圆内的点和圆外的点。 圆的内部可以看成是到圆心的距离小于半径的的点的集 合 ; 圆 的 外 部 可 以 看 成 是 到圆心的距离大于半径的点的集合 。
典型例题
例:如图已知矩形ABCD的边AB=3厘米,AD=4厘 米
(1)以点A为圆心,3厘米为半径作 圆A,则点B、C、D与圆A的位置关系 如何? (B在圆上,D在圆外,C在圆外)
问:⊙O的半径6cm,当OP=6时, 点P在圆上 ;当OP <6 时点P 在圆内;当OP ≤6 时,点P不在 圆外。
画出由所有到已知点O的距离大于 或等于2CM并且小于或等于3CM的 点组成的图形。
O
O
问题:多少个点可以确定一个圆呢? 解决: 步骤1:过一点,可以画多少个圆?
步骤2:过两点,可以画多少个圆? 步骤3:过三个点,可以做多少个圆?
A
D
(2)以点A为圆心,4厘米为半径作圆A, 则点B、C、D与圆A的位置关系如何?
(B在圆内,D在圆上,C在圆外)
B
C
(3)以点A为圆心,5厘米为半径作圆A,则点B、C、 D与圆A的位置关系如何? (B在圆内,D在圆内,C在圆上)
问1:⊙O的半径10cm,A、B、C三点 到圆心的距离分别为8cm、10cm、 12cm,则点A、B、C与⊙O的位置关 系是: 点A在 圆内 ∵OA=8<10 ∴点A在圆内 点B在 圆上 ∵OB=10=10 ∴点B在圆上 点C在 圆外 ∵OC=12>10 ∴点C在圆外
点与圆、直线与圆位置关系
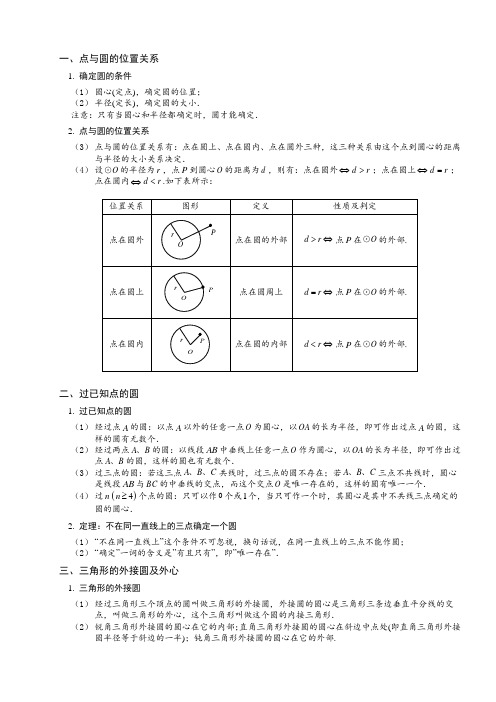
一、点与圆的位置关系1.确定圆的条件(1)圆心(定点),确定圆的位置;(2)半径(定长),确定圆的大小.注意:只有当圆心和半径都确定时,圆才能确定.2.点与圆的位置关系(3)点与圆的位置关系有:点在圆上、点在圆内、点在圆外三种,这三种关系由这个点到圆心的距离与半径的大小关系决定.(4)设O=;⊙的半径为r,点P到圆心O的距离为d,则有:点在圆外⇔d r>;点在圆上⇔d r 点在圆内⇔d r<.如下表所示:二、过已知点的圆1.过已知点的圆(1)经过点A的圆:以点A以外的任意一点O为圆心,以OA的长为半径,即可作出过点A的圆,这样的圆有无数个.(2)经过两点A B、的圆:以线段AB中垂线上任意一点O作为圆心,以OA的长为半径,即可作出过点A B、的圆,这样的圆也有无数个.(3)过三点的圆:若这三点A B C、、三点不共线时,圆心、、共线时,过三点的圆不存在;若A B C是线段AB与BC的中垂线的交点,而这个交点O是唯一存在的,这样的圆有唯一一个.(4)过n()4n≥个点的圆:只可以作0个或1个,当只可作一个时,其圆心是其中不共线三点确定的圆的圆心.2.定理:不在同一直线上的三点确定一个圆(1)“不在同一直线上”这个条件不可忽视,换句话说,在同一直线上的三点不能作圆;(2)“确定”一词的含义是”有且只有”,即”唯一存在”.三、三角形的外接圆及外心1.三角形的外接圆(1)经过三角形三个顶点的圆叫做三角形的外接圆,外接圆的圆心是三角形三条边垂直平分线的交点,叫做三角形的外心,这个三角形叫做这个圆的内接三角形.(2)锐角三角形外接圆的圆心在它的内部;直角三角形外接圆的圆心在斜边中点处(即直角三角形外接圆半径等于斜边的一半);钝角三角形外接圆的圆心在它的外部.2. 三角形外心的性质(1) 三角形的外心是指外接圆的圆心,它是三角形三边垂直平分线的交点,它到三角形各顶点的距离相等; (2) 三角形的外接圆有且只有一个,即对于给定的三角形,其外心是唯一的,但一个圆的内接三角形却有无数个,这些三角形的外心重合.一、点与圆的位置关系【例1】 已知圆内一点到圆周上的点的最大距离是7,最小距离是5,则该圆的半径是( )A .2B .6C .12D .7【巩固】1、一个已知点到圆周上的点的最大距离为5cm ,最小距离为1cm ,则此圆的半径为______.2、若⊙O 所在平面内一点P 到⊙O 上的点的最大距离为a ,最小距离为b (a>b ),则此圆的半径为( )DA .2b a + B .2ba - C .22ba b a -+或 D .b a b a -+或3、定义:定点A 与O ⊙上的任意一点之间的距离的最小值称为点A 与O ⊙之间的距离.现有一矩形ABCD如图,14cm 12cm AB BC ==,,K ⊙与矩形的边AB BC CD 、、分别相切于点E F G 、、,则点A 与K ⊙的距离为______________.【例2】 已知ABC ∆中,90C ∠=︒,2AC =,3BC =,AB 的中点为M ,⑴以C 为圆心,2为半径作C ⊙,则点A ,B ,M 与C ⊙的位置关系如何? ⑵若以C 为圆心作C ⊙,使A ,B ,M 三点至少有一点在C ⊙内,且至少有一点在C ⊙外,求C⊙半径r 的取值范围.M CBA【巩固】1、Rt ABC ∆的两条直角边3BC =,4AC =,斜边AB 上的高为CD ,若以C 为圆心,分别以12r =,2 2.4r =,33r =为半径作圆,试判断D 点与这三个圆的位置关系.DCBA2、在ABC ∆中,90C ∠=︒,4AC =,5AB =,以点C 为圆心,以r 为半径作圆,请回答下列问题,并说明理由.⑴当r 取何值时,点A 在C ⊙上,且点B 在C ⊙内部?⑵当r 在什么范围内取值时,点A 在C ⊙外部,且点B 在C ⊙的内部? ⑶是否存在这样的实数r ,使得点B 在C ⊙上,且点A 在C ⊙内部?CBA二、过三点的圆【例3】 如图,四边形ABCD 中,AB AC AD ==,若7613CAD BDC ∠=︒∠=︒,,则CBD ∠=_________,BAC ∠=__________.DCBA【例4】 如图,在平面直角坐标系中,O '与两坐标轴分别交于A B C D ,,,四点,已知:()60A ,,()03B -,,()20C -,,则点D 的坐标是( ) A .()02,B .()03,C .()04,D .()05,三、三角形的外接圆及外心【例5】 如图,ABC ∆内接于O ⊙,120BAC ∠=︒,AB AC =,BD 为O ⊙的直径,6AD =,则BC =.【巩固】等边三角形的外接圆的半径等于边长的( )倍.ABCD .12【例6】 设Rt ABC ∆的两条直角边长分别为3,4,则此直角三角形的内切圆半径为 ,外接圆半径为 .【巩固】1、如图,直角坐标系中一条圆弧经过网格点A B C ,,,其中B 点的坐标为()44,,则该圆弧所在圆的圆心的坐标为 .2、ABC ∆中,10AB AC ==,12BC =,求其外接圆的半径.【例7】 在等腰ABC ∆中,AB BC =,BH 是高,点M 是边AB 的中点,而经过点B ,M 于C 的圆同BH的交点是K ,求证32BK R =,其中R 是ABC ∆的外接圆半径.【巩固】1、已知∆ABC 中,=AB AC ,D 是∆ABC 外接圆劣弧AC 上的点(不与点A C ,重合),延长BD 至E .⑴求证:AD的延长线平分∠CDE;⑵若30∠=︒BAC,∆ABC中BC边上的高为2∆ABC外接圆的面积.AB CD E2、已知如图,ACD∆的外角平分线CB交其外接圆于B,连接BA、BD,求证:BA BD=.N一、直线与圆的位置关系设O⊙的半径为r,圆心O到直线l的距离为d,则直线和圆的位置关系如下表:切线的性质定理:圆的切线垂直于过切点的半径.推论1:经过圆心且垂直于切线的直线必经过切点.推论2:经过切点且垂直于切线的直线必经过圆心.注意:这个定理共有三个条件,即一条直线满足:①垂直于切线②过切点③过圆心①过圆心,过切点⇒垂直于切线.AB过圆心,AB过切点M,则AB l⊥.②过圆心,垂直于切线⇒过切点.AB过圆心,AB l⊥,则AB过切点M.③过切点,垂直于切线⇒过圆心.AB l⊥,AB过切点M,则AB过圆心.l3.切线的判定(1)定义法:和圆只有一个公共点的直线是圆的切线;(2)距离法:和圆心距离等于半径的直线是圆的切线;(3)定理:经过半径的外端并且垂直于这条半径的直线是圆的切线.注意:定理的题设是①“经过半径外端”,②“垂直于半径”,两个条件缺一不可;定理的结论是“直线是圆的切线”.因此,证明一条直线是圆的切线有两个思路:①连接半径,证直线与此半径垂直;②作垂直,证垂直在圆上.l4.切线长和切线长定理(1)切线长:在经过圆外一点的圆的切线上,这点和切点之间的线段的长,叫做这点到圆的切线长.(2)切线长定理:从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角.三、三角形的内切圆1.三角形的内切圆:和三角形各边都相切的圆叫做三角形的内切圆,内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形.2. 多边形的内切圆:和多边形的各边都相切的圆叫做多边形的内切圆,这个多边形叫做圆的外切多边形.3. 直角三角形内切圆的半径与三边的关系cb acbaO F ED CACBAC B A设a 、b 、c 分别为ABC △中A ∠、B ∠、C ∠的对边,面积为S ,则内切圆半径为sr p=,其中()12p a b c =++.若90C ∠=︒,则()12r a b c =+-. 一、直线与圆位置关系的确定【例1】 如图,已知⊙O 是以数轴的原点O 为圆心,半径为1的圆,45AOB ∠=︒,点P 在数轴上运动,若过点P 且与OA 平行的直线与⊙O 有公共点,设OP x =,则x 的取值范围是A .0≤x B.≤x C .-1≤x ≤1D .x【例2】 Rt ABC ∆中,90C ∠=︒,3cm AC =,4cm BC =,给出下列三个结论: ①以点C 为圆心,3 cm长为半径的圆与AB 相离;②以点C 为圆心,4cm 长为半径的圆与AB 相切;③以点C 为圆心,5cm 长为半径的圆与AB 相交.上述结论中正确的个数是( ) A .0个 B .l 个 C .2个 D .3个【巩固】在Rt ABC ∆中,90C ∠=︒,12cm AC =,16cm BC =,以点C 为圆心,r 为半径的圆和AB 有怎样的位置关系?为什么?⑴ 9cm r =;⑵10cm r =;⑶9.6cm r =.DCBA【例3】 如下左图,在直角梯形ABCD 中,AD BC ∥,90C =︒∠,且AB AD BC >+,AB 是O 的直径,则直线CD 与O 的位置关系为( ) A .相离 B .相切 C .相交 D .无法确定【巩固】如图,BC是半圆O的直径,点D是半圆上的一点,过点D作O的切线AD,BA DA⊥,10BC=,4AD=,那么直线CE与以点O为圆心,52为半径的圆的位置关系是.二、切线的性质及判定【例4】已知:O为BAC∠平分线上一点,OD AB⊥于D,以O为圆心.以OD为半径作圆O.求证:O⊙与AC相切.【巩固】如图,ABC∆为等腰三角形,AB AC=,O是底边BC的中点,O⊙与腰AB相切于点D,求证AC 与O⊙相切.【例5】已知:如图,ABC∆内接于O,AD是过A的一条射线,且B CAD∠=∠.求证:AD是O的切线.【巩固】已知:如图,AB是O⊙的直径,C为O⊙上一点,MN过C点,AD MN⊥于D,AC平分DAB∠.求证:MN为O⊙的切线.【例6】如图,已知OA是O⊙的半径,B是OA中点,BC OA⊥,P是OA延长线上一点,且PA AC=.求证:PC是O⊙的切线.【巩固】如图,AB是O⊙的直径,C点在圆上,CD AB⊥于D.P在BA延长线上,且PCA ACD∠=∠.求证:PC是O⊙的切线.BP【例7】如图,O⊙是Rt ABC∆的外接圆,90ABC∠=︒,点P是圆外一点,PA切O⊙于点A,且PA PB=.(1)求证:PB是O⊙的切线.(2)已知1PA BC=,求O⊙的半径.【巩固】1、如图,AB 为O ⊙的直径,D 是BC 的中点,DE AC ⊥交AC 的延长线于E ,O ⊙的切线BF 交AD 的延长线于点F .求证:DE 是O ⊙的切线;FAB2、如图,已知O 是正方形ABCD 对角线上一点,以O 为圆心、OA 长为半径的O ⊙与BC 相切于M ,与AB 、AD 分别相交于E 、F .(1)求证:CD 与O ⊙相切.(2)若正方形ABCD 的边长为1,求O ⊙的半径.【例8】 如图,AB BC =,以AB 为直径的O ⊙交AC 于点D ,过D 作DE BC ⊥,垂足为E .(1)求证:DE 是O ⊙的切线;(2)作DG AB ⊥交O ⊙于G ,垂足为F ,若308A AB ∠=︒=,,求弦DG 的长.【巩固】如图,AC 为O ⊙的直径,B 是O ⊙外一点,AB 交O ⊙于E 点,过E 点作O ⊙的切线,交BC 于D 点,DE DC =,作EF AC ⊥于F 点,交AD 于M 点.求证:BC 是O ⊙的切线;D CB A【例9】 如图,AB 是O 的直径,30BAC ∠=︒,M 是OA 上一点,过M 作AB 的垂线交AC 于点N ,交BC 的延长线于点E ,直线CF 交EN 于点F ,且ECF E ∠=∠. (1)证明CF 是O 的切线;(2)设O 的半径为1,且AC CE =,求MO 的长.A1. 已知60ABC ∠=︒,点O 在ABC ∠的平分线上,5cm OB =,以O 为圆心3cm 为半径作圆,则O 与BC 的位置关系是________.2.如图,半径为3cm 的O ⊙切直线AC 于B ,3cm AB BC =,,则AOC ∠的度数是 .3.如图所示在Rt ABC ∆中,90B ∠=︒,A ∠的平分线交BC 于D ,E 为AB 上一点,DE DC =,以D 为圆心,以DB 的长为半径画圆.求证:(1)AC 是D ⊙的切线;(2)AB EB AC +=.E B4.如图,四边形ABCD 内接于O ,BD 是O 的直径,AE CD ⊥,垂足为E ,DA 平分BDE ∠.(1)求证:AE 是O 的切线;(2)若301cm DBC DE ∠==,,求BD 的长.5.如图,在以O 为圆心的两个同心圆中,AB 经过圆心O ,且与小圆相交于点A 、与大圆相交于点B .小圆的切线AC 与大圆相交于点D ,且CO 平分ACB ∠. ⑴ 试判断BC 所在直线与小圆的位置关系,并说明理由; ⑵ 试判断线段AC AD BC 、、之间的数量关系,并说明理由;⑶ 若8cm 10cm AB BC ==,,求大圆与小圆围成的圆环的面积.。
《点和圆的位置关系》圆PPT课件

C l2⊥l,这与我们以前学过的“过一点有且只有 一条直线与已知直线垂直”相矛盾,所以过同
一条直线上的三点不能作圆.
24.2.1 点和圆的位置关系
反证法的定义
要点归纳
先假设命题的结论不成立,然后由此经过推理得出矛盾(常 与公理、定理、定义或已知条件相矛盾),由矛盾判定假设 不正确,从而得到原命题成立,这种方法叫做反证法.
F
C M
24.2.1 点和圆的位置关系
位置关系
归纳总结
定理: 不在同一直线上的三个点确定一个圆.
有且只有
F
A
B
●
o
C
G
24.2.1 点和圆的位置关系
试一试:
已知△ABC,用直尺与圆规作出过A、B、C三点的圆.
A
O C
B
24.2.1 点和圆的位置关系
概念认知
经过三角形三个顶点的圆叫做三角形的外接圆,
BC=4cm,以点A为圆心、3cm为半径画圆,并判断:
B
(1)点C与⊙A的位置关系;
D●
(2)点B与⊙A的位置关系;
(3)AB的中点D与⊙A的位置关系.
A
C
解:已知⊙A的半径r=3 cm. (1) 因为AC AB2 BC2 52 42 3(cm) r ,所以点C在⊙A上. (2) 因为AB=5 cm>3 cm=r, 所以点B在⊙A外. (3)因为 DA 1 AB 2.5cm3cm r,所以点D在⊙A内.
解:(1)当0<r<3时,点A,B在⊙C外. (2)当3<r<4时,点A在⊙C内,点B在⊙C外.
24.2.1 点和圆的位置关系
课堂小结
点与圆的 位置关系
位置关系数量化
点和圆的位置关系ppt课件

2cm O·
判一判: 下列说法是否正确
(1)任意的一个三角形一定有一个外接圆( √ ) (2)任意一个圆有且只有一个内接三角形( × ) (3)经过三点一定可以确定一个圆( × ) (4)三角形的外心到三角形各顶点的距离相等( √ )
课随堂堂演小练结
注意:同一直线上的三个点不能作圆
第二十四章 圆
24.2.1 点和圆的位置关系(1)
新课导入
问题 我国射击运动员在伦敦奥运会上获金牌,为我国赢得 荣誉.如图是射击靶的示意图,它是由许多同心圆(圆心相同, 半径不相同)构成的,你知道击中靶上不同位置的成绩是如何 计算的吗?
探究新课
问题1:观察下图中点和圆的位置关系有哪几种? 点与圆的位置关系有三种: 点在圆内,如点B. 点在圆上,如点C. 点在圆外,如点A.
问题2 :设点到圆心的距离为d,圆的半径为r,量一量 在点和圆三种不同位置关系时,d与r有怎样的数量关系?
反过来,由d与r的数量关系,怎样判定点与圆的位置关系 呢?
点P在⊙O内 点P在⊙O上 点P在⊙O外
要点归纳 点和圆的位置关系
点P在⊙O内 点P在⊙O上
点P在⊙O外
点P在圆环内 数形结合:
位置关系
问题2 :过两个点能不能确定一个圆? 能画出无数个圆,圆心都在线段AB的垂直平分线上.
问题3:过不在同一直线上的三点能不能确定一个圆?
经过A,B两点的圆的圆心在线段AB的 垂直平分线上.
经过B,C两点的圆的圆心在线段BC的 垂直平分线上.
经过A,B,C三点的圆的圆心应该在这两条 垂直平分线的交点O的位置.
典例解析 例:如图所示,已知在△ABC中,AB=13,
试判断A、D、B三点与⊙C的位置关系. 解:在Rt△ABC中,AC=12,AB=13, 由勾股定理,得
24.2.1 点和圆的位置关系(优秀经典公开课比赛课件)

5.在平面直角坐标系中,作以原点 为圆心,半径为 4 的⊙O,试确定点(-2,-3),(4,
-2), C(2 3, 2) 与⊙O 的位置关系.
四.中考链接
1.下列说法不正确的是( ).
A.任何一个三角形都有外接圆
B.等边三角形的外心是这个三角形的中心
C.直角三角形的外心是其斜边的中点 D.一个三角形的外心不可能在三角形的外部
2.已知⊙ O 的半径为 1,点到圆心的距离为 d,若关于的方程 x2-2x+d=0 有实根,
则点 在⊙ O 的
。
三、课堂练习 1. 已知⊙ O 的半径为 10 厘米,根据下列点 P 到圆心的距离,判定点 P 与圆的位置 关系,并说明理由.
(1)8 厘米;(2)10 厘米;(3)12 厘米.
2.在△ ABC 中,∠ C=90°,AB=5cm,BC=4 cm,以点 A 为圆心,以 3 cm 为半径作圆,
请判断:(1)C、B、AB 的中点 D 与⊙A 的位置关系.
3.判断下列说法是否正确
(1)任意的一个三角形一定有一个外接圆( ).
(2)任意一个圆有且只有一个内接三角形( )
(3)经过三点一定可以确定一个圆( )
(4)三角形的外心到三角形各顶点的距离相等( )
4.经过一 P 点可以做
个圆;经过两点 P、Q 可以作
个圆,圆心在
上;
经过不在同一直线上的三个点可以作
(3)作圆,使该圆经过已知点 A、B、C 三点 ①当 A、B、C 三点不在同一直线上时,你是如何做的?如何确定圆心?你能作出几个
这样的圆?(如图 1)
② 当 A、B、C 三点在同一直线上时又如何?
点与圆的位置关系PPT教学课件

(2)若以点 C 为圆心作⊙C,使 A,B,M 三点中至少有一点在⊙
C 内,且至少有一点在⊙C 外,求⊙C 的半径 r 的取值范围.
解:∵ 241<4<5,∴以点 C 为圆心作⊙C,A,B,M 三点中至少
有一点在⊙C 内时,r>
41 2.
当至少有一点在⊙C 外时,r<5.
故⊙C 的半径 r 的取值范围为
设⊙O 的半径为 R cm,则RR+-OOPP==150,, 解得RO=P=7.25.,5.即⊙O 的半径为 7.5 cm. 当点 P 在圆外时,同理可得⊙O 的半径为 2.5 cm. 故⊙O 的半径为 7.5 cm 或 2.5 cm.
• 长江三角洲的位置及其优越性 • 长江三角洲的范围,地形和气候特点 • 长江三角洲的农业发展现状
EG
沪杭线
-------
9.(2020·河北沧州新华区月考)如图,在网格图中(每个小正方形
的边长均为 1)选取 9 个格点(格线的交点称为格点).如果以 A
为圆心,r 为半径画圆,选取的格点中除点 A 外恰好有 3 个
在圆内,则 r 的取值范围为( )
A.2 2<r< 17 B. 17<r<3 2
C. 17<r<5
D.5<r< 29
当第一次点 P 在⊙O 上时,(2+1)x=7-1,解得 x=2. 当第二次点 P 在⊙O 上时,(2+1)x=7+1,解得 x=83.
11.(教材改编题)如图,在矩形 ABCD 中,AB=3,AD=4. (1)以点 A 为圆心,4 为半径画⊙A,并说出点 B,C,D 与⊙A
的位置关系;
解:点B在⊙A内,点C在⊙A外,点D在⊙A上.画图略.
冀教版 九年级下
第二十九章 点与圆的位置关系
中学公开课教学优质课件推选点与圆的位置关系

()
3、任意一个圆有一个内接三角形,并且只有一个内接三角形
()
错 4、三角形的外心就是这个三角形任意两边垂直平分线的交点 ()
5、三角形的外心到三边的距离相等 ( )
对
错
思考: 如图,CD所在的直线垂直平分线
段AB,怎样用这样的工具找到圆形工件的
圆心.
∵A、B两点在圆上,所以
圆心必与A、B两点的距离
过两点能作几个圆?
过A、B两点的圆的圆心有何特点?
A
●O
●O
B
经过两点A,B的圆的圆心在线段AB的垂直平分线上.
以线段AB的垂直平分线上的任意一点为圆心,这点 到A或B的距离为半径作圆.
1、三点不共线
已知:不在同一直线上的三点
F
A、B、C
A
求作:⊙O,使它经过A、B、C
B
作法:
O
1、连结AB,作线段AB的
过三点
AB
1、若三点共线,则过这三点只能 作一条直线.
2、若三点不共线,则过这三点不 能作直线,但过任意其中两点一共 可作三条直线.
A
C
B
C
直线公理:两点确定一条直线
对于一个圆来说,过几 个点能作一个圆,并且 只能作一个圆?
过一点能作几个圆?
A
无数个 过A点的圆的圆心有何特点? 平面上除A点外的任意一点
OA < r, OB = r, OC > r.
问题3:反过来,已知点到圆心的距离和圆的半径, 能否 判断点和圆的位置关系?
设⊙O的半径为r,点P到圆心的距离OP = d,则有:
点P在圆内
d<r;
点P在圆上 d = r;
点P在圆外
d>r .
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
l1⊥l,l2⊥l,这与我们以前学过的
“过一点有且只有一条直线与已知
直线垂直”相矛盾,所以过同一条
直线上的三点不能作圆.
什么叫反证法?
先假设命题的结论不成立,然后由此经过推理得出 矛盾(常与公理、定理、定义或已知条件相矛盾), 由矛盾判定假设不正确,从而得到原命题成立,这 种方法叫做反证法.
一个三角形的外接圆有几个? 一个圆的内接三角形有几个?
分别画一个锐角三角形、直角三角形和钝角三
角形,再画出它们的外接圆,观察并叙述各三角形
与它的外心的位置关系.
A
A
A
●O
●O
B
┐
CB
C
●O
B
C
锐角三角形的外心位于三角形内, 直角三角形的外心位于直角三角形斜边中点, 钝角三角形的外心位于三角形外.
1、判断下列说法是否正确
我国射击运动员在奥运 会上屡获金牌,为我国赢得 荣誉,右图是射击靶的示意 图,它是由许多同心圆(圆 心相同,半径不等的圆)构 成的,你知道击中靶上不同 位置的成绩是如何计算的吗?
学习目标
• 1、了解点与圆的三种位置关心,会根据 圆心距和半径的大小关系来判断改点在 圆的什么位置;
• 2、理解三角形外心和外接圆的意义。 • 3、明确反证法是证明题的一种方法,了
(1)任意的一个三角形一定有一个外接圆( √ ). (2)任意一个圆有且只有一个内接三角形( × ) (3)经过三点一定可以确定一个圆( × ) (4)三角形的外心到三角形各顶点的距离相等( √ )
2、若一个三角形的外心在一边上,则此三角形的
形状为( B )
A、锐角三角形
B、直角三角形
C、钝角三角形 D、等腰三角形
2、已知AB为⊙O的直径,P为⊙O 上任意一点,则
点关于AB的对称点P′与⊙O的位置为( c )
(A)在⊙O内 (B)在⊙O 外 (C)在⊙O 上 (D)不能确定
典型例题
例:如图已知矩形ABCD的边AB=3厘米,AD=4厘米
(1)以点A为圆心,3厘米为半径作
圆A,则点B、C、D与圆A的位置关系
如何?(B在圆上,D在圆外,C在圆外)
A
D
(2)以点A为圆心,4厘米为半径作圆A,
则点B、C、D与圆A的位置关系如何?
B
C
(B在圆内,D在圆上,C在圆外)
(3)以点A为圆心,5厘米为半径作圆A,则点B、C、 D与圆A的位置关系如何?
(B在圆内,D在圆内,C在圆上)
1、平面上有一点A,经过已知A点的圆有几 个?圆心在哪里?
●
●O
● ●A O O
(1)经过不在同一条直线上的三点作一个圆, 如何确定这个圆的圆心?
3、平面上有三点A、B、C,经过A、B、C 三点的圆有几个?圆心在哪里?
经过A,B两点的圆的圆心在线段AB的垂直平分线上.
●A
经过B,C两点的圆的圆心在线段AB
的垂直平分线上.
经过A,B,C三点的圆的圆心应该这两 ●B ┏●O
●C
条垂直平分线的交点O的位置.
求证:在一个三角形中,至少有一 个内角小于或等于60度。
反证法常用于解决用直接证法不易证明或不能证明 的命题,主要有:
(1)命题的结论是否定型的; (2)命题的结论是无限型的; (3)命题的结论是“至多”或“至少”型的.
爆破时,导火索燃烧的速度是每秒0.9cm, 点导火索的人需要跑到离爆破点120m以外的 的安全区域,已知这个导火索的长度为18cm, 如果点导火索的人以每秒6.5m的速度撤离, 那么是否安全?为什么?
●O
●
O
无数个,圆心为点A以外任意一点,半径为这 点与点A的距离
●O ●O ●O
2、平面上有两点A、B,经过已知点A、B 的圆有几个?它们的圆心分布有什么特点?
无数个。它们的圆心都在线段AB的垂直平分线上。 以线段AB的垂直平分线上的任意一点为圆心,以这点 到A或B的距离为半径作圆.
经过已知的三点作圆,这样的圆能作出多少个?
点P在圆上 d = r;
点P在圆外 d > r .
P
P
符号 读
作“等价于”,它
表示从符号
的左端可以得到右
P
O
r
端从右端也可以得
A
到左端.
练一练
1、⊙O的半径10cm,A、B、C三点到圆心的距离分别为 8cm、10cm、12cm,则点A、B、C与⊙O的位置关系是:
点A在 圆内 ;点B在 圆上 ;点C在 圆外 。
归纳结论:
不在同一条直线上的三个点确定一个圆。
经过三角形三个顶点可以画一个圆,并且只能画一个.
经过三角形三个顶点的圆叫做三
A
角形的外接圆。
三角形外接圆的圆心叫做这个
三角形的外心。
这个三角形叫做这个圆的 B 内接三角形。
●O C
三角形的外心就是三角形三条边的垂直平分 线的交点,它到三角形三个顶点的距离相等。
B
C
D
小结与归纳
◆用数量关系判断点和圆的位置关系。 ◆不在同一直线上的三点确定一个圆。 ◆求解特殊三角形直角三角形、等边三角形、 等腰三角形的外接圆半径。 ◆在求解等腰三角形外接圆半径时,运用了 方程的思想。
(2)经过同一条直线三个点能作出一个圆吗?
P
l1
l2
A
B
C
如图,假设过同一条直线l上三点A、 B、C可以作一个圆,设这个圆的圆
解其证明的方式和步骤,会用反证法证 明较简单的题。
自学指导
• 认真看课本ቤተ መጻሕፍቲ ባይዱ0-92页练习以上的内容 • 1、通过“问题”的分析总结出点与圆的
位置关系的性质和判定 • 2、通过“探究”学习,确定一个圆的条
件以及三角形外心的定义 • 3、通过P92页的“思考”明确反证法的
思路和证明格式。 • 8分钟后,比一比看谁能正确做出检测题。
典型例题
如图,已知等边三角形ABC中,边长为
6cm,求它的外接圆半径。
A
E
O
B
DC
1、如图,已知 Rt⊿ABC 中 ,C 90
若 AC=12cm,BC=5cm,
C
求它的外接圆半径。
B
O
A
如图,等腰⊿ABC中, AB AC 13c,m
BC 10cm ,求⊿ABC外接圆的半径。
A
O
问题探究
问题1:观察图中点A,点B,点C与圆的位置关系?
点A在圆内,
点B在圆上, 点C在圆外.
A
O
C
r B
问题2:设⊙O半径为 r , 说出来点A,点B, 点C与圆心O的距离与半径的关系:
OA < r, OB = r, OC > r.
设⊙O的半径为r,点P到圆心的距离OP = d,
则有:
点P在圆内 d < r ;
