弹塑性力学讲义屈服条件

合集下载

第六章屈服条件

第六章屈服条件§6.1应力空间与屈服条件弹性力学只研究物体在弹性范围内的变形规律；塑性力学的研究范围扩展到塑性变形阶段，研究材料在塑性变形情况下力与变形之间的关系。

材料在塑性变形时其内力应该满足一定的条件—屈服条件。

屈服条件是求解塑性力学问题所必需的补充方程。

屈服条件是塑性力学中的重要概念之一。

正确理解屈服条件的有关概念，对于分析和解决塑性力学问题是至关重要的。

在单向拉伸时，标志材料进入塑性状态的是应力达到材料的屈服极限s σ。

对于具有明显屈服极限的材料，s σ可以在拉伸曲线上找到。

而对于没有明显屈服极限的材料，则按规定用取对应于残余应变2.0=ε％时的应力作为材料的s σ。

但对于复杂应力状态，问题就复杂多了，因为一点的应力状态是由六个应力分量确定的，显然不应选取海六个应力分量中的某一个作为判断材料是否进入塑性状态的判据。

因此，在分析中需要引进应力空间和应变空间的概念。

所谓应力空间或应变空间就起以应力分量或应变分量为坐标轴所确定的空间。

任一点的应力状态或应变状态，可以通过变换用主应力或主应变来表示，由于其几何图形和数学表达式都比较简单，使用起来也非常方便，一般都采用主应力或主应变坐标系。

由主应力1σ、2σ和3σ所确定的应力状态，可以用应力空间中的一个点来表示。

在应力空间或应变空间中，每一个点都代表一个应力状态或一个应变状态。

应力或应变状态的变化，可以在相应空间中绘出一条相应的曲线，这样的曲线称为应力路径或应变路径。

根据不同路径所进行的实验，可以确定从弹性阶段进入塑性阶段的界限，即确定屈服点，这些屈服点连结起来后形成一个曲面，这样的曲面称为屈服面。

屈服面的数学表达式称为屈服函数。

对于理想塑性材料，这个曲面称为极限曲面，应力状态只能在这个曲面之内或在曲面之上。

在屈服面内的应力状态为弹性应力状态(弹塑性材料)或刚性状态(刚塑性材科)，而在屈服面上的应力状态则为塑性状态，即一旦应力状态到达屈服面之上，则认为材料已进入塑性状态了。

弹性与塑性力学基础-第五章屈服准则与塑性应力应变关系

i
1 2
( 1 2 ) 2 ( 2 3 ) 2 ( 3 1 ) 2 s
(5-3)
在塑性状态下等效应力总是等于流动应力
注意：
此时已不能将s理解为屈服极限而是单向应力状态下的对应于一定温度、一定变形程度及一定应变速率的流动应力。
该应力不是以名义应力来表示而是用真实应力来表示，是把开始
第五章屈服准则与塑性应力应变关系
§5-1 屈服准则的概念
5.1.2 屈服准则(塑性条件)的表示方法拉压性能相同的材料屈服准则不应因应力偏量第三不变量J3的符号变化而变化

1、2及3都为正，J3>0；
1、2及3都为负，J3<0;
屈服准则或者与J3无关或者是J3的偶函数。
弹性与塑性力学基础
f ( 1 , 2 , 3 ) C
可用应力张量不变量来表示(与坐标系选择无关)
(5-1)
f ( I1 , I 2 , I 3 ) C
可用应力偏量不变量J2、J3表示 (由于静液应力不影响屈服)
f (2 3 1 3 ) 其中 J 2 ( 1
弹性与塑性力学基础
第五章
屈服准则与塑性应力应变关系
弹性与塑性力学基础
第五章屈服准则与塑性应力应变关系
§5-1 屈服准则的概念
5.1.1 屈服准则的概念 5.1.2 屈服准则(塑性条件)的表示方法
5.1.3 屈服准则
§5-2 米塞斯屈服准则
5.2.1 米塞斯屈服准则 5.2.2 米塞斯屈服准的物理意义
性状态的依据
(5-9)
塑性变形时单位形状变化弹性位能Uf它可以作为判断是否进入塑

塑性力学第三章-屈服条件讲课稿

后继屈服条件
进入塑性后，屈服面的变化规律
后继屈服函数：对于理想塑性材料：
f
对于强化材料，后继屈服函数可写成
(ij,ha)0
（1）等向强化（各向同性）模型
f (ij) K 0
K K(ha)
_____
K( dp),
_____
dp
32dipjdipj
K( dWp), dWp ijdipj
T:maxsk
M: 3s Tresca 六边形外切于Mises 圆
2
y
0
2k 2
3
3
s
s
2
:T
s
s
3
:
M
1
x
屈服条件的实验验证
薄壁管轴向拉伸和内压作用下的实验比较薄壁管轴向拉伸和扭转作用下的实验比较
薄壁管轴向拉伸和内压作用下的实验(Lode,1926)
qR h,z2P R,h r0 P
令
1 ,2 z,3 r 0
x , y, z 0 ,x,yy z zx 0
x y 2 y z 2 z x 2 6 x 2 2 y y z 2 z 2 x s 2
x2y 2x y3x 2y s 2
两种屈服条件的比较
（1）单向拉伸时重合：
Tres:cmaa x2s k
Mis:ess Tresca 六边形内接于Mises 圆（2）纯剪切时重合：
2 2k
2
2 2k
122k
1 2k
12k 0
2 2k
1
122k
2、Mises 屈服条件
Mises条件的常用形式：（1）应力偏张量第二不变量形式：
J2 k22
1 6 x y 2 y z 2 z x 2 6 x 2 y y 2 z z 2x k 2 2

弹塑性力学-15 屈服理论

S
等倾线
L P
2
一点的应力矢量 OP 1e1 2e2 3e3
15.1 屈服理论分析
2. 屈服条件的一般形式
3 QL
OP 1e1 2e2 3e3
P
n
1 3
e1
1 3
e2
1 3 e3
平面 o S
2
1
OQ OP n
1 3
(1
2
3
)
15.1 屈服理论分析
3. 屈服条件的一般形式
ij
0
ABCA
对整个循环，附加应力
( ij
0 ij
)d
p ij
0
在弹性变形上做功为零 ABCA
AB ( ij
0 ij
)d
p ij
BC
( ij
0 ij
)d
p ij
CA ( ij
0 ij
)d
p ij
0
15.1 屈服理论分析
6. Drucker公设
AB ( ij
0 ij
)d
p ij
BC ( ij
4
xy s
2
1
均为
x s
2
3
xy s
2
1
椭圆
15.2 经典屈服准则
3. 屈服准则的验证 M
P
薄壁圆筒承受拉扭
M P
Mises准则更好！
xy / s
0.6
Mises准则
0.4 铜 0.2 软钢 Tresca准则
铝
0 0.2 0.4 0.6 0.8 x / s
塑性屈服理论
15.1 屈服理论分析 15.2 经典屈服准则 15.3 后继屈服与硬化

塑力 3、屈服条件

故，k 1 s / 2
纯剪切试验：
1 s , 2 0, 3 s
故，k 1 s
若材料满足Tresca屈服条件，则：
s
2
s
二、 Mises屈服条件
Tresca屈服条件有以下问题：没考虑中间主应力的影响；当应力处在屈服面的棱线上时，处理会遇到数学上的困难；主应力大小未知时，屈服条件十分复杂。因此， Mises(1913) 提出了另一个屈服条件：
（3）弹性形变比能形式：（Hencky）根据弹性理论，形状改变比能：
Mises条件的常用形式([( 1 2 ) 2 ( 2 3 ) 2 ( 3 1 ) 2 ]
6E (1 ) 1 1 4 2 2k 2 J2 ' J2 ' k2 E 2G 2G 3 3G
②、屈服面的形状 1 4 2 2 2 2 J 2 ' [( 1 2 ) ( 2 3 ) ( 3 1 ) ] k 2 6 3
4k 2 8 r 2 J 2 ' 2 k 2 const 3 3
2
Mises屈服条件在平面上的一个圆，在应
2
1 2 2 k
1 2 k
2 2k
1 2k
0
1 2 2k
1
2 2k
Tresca屈服柱被得到的图形。
3＝ 0
平面所截后
k的试验确定：
简单拉伸试验： 1 s , 2 3 0, 1 3 s
力空间是一个圆柱体。
③、 k的试验确定：简单拉伸试验： J ' 2
4 2 1 k2 k2 s 3 3 2 纯剪切试验： J ' 2 4 k 2 k 3 2 s 2 2 s 3 2

弹塑性力学-屈服条件

不会出现反向屈服。恢复掉的弹性应变是：
e
=1 E
1 s
因此，C点的应变是 C=Be=9s
（3） = 01 当= (1)s，材料产生反向屈服，当从D点到E点时，产生压缩塑
性应变是
p=
1 D h
18 s
而从C点到E点产生的弹性应变是e = (1+)s，最后的应变是
E= (1+)s18s+9s= (1+10)s
• 背应力增量应平行于塑性应变增量 dij=c dipj
式中c是材料常数，由试验确定。 • 对于Mises屈服条件，该模型可写成
ij
c
p ij
3 2
sij
c
p ij
sij
c
p ij
s
单轴加载（拉伸或压缩）时
s11=
2 3
s22=s33=
1 3
1p1 p
p 22
p 33
1 2
p
强化模型式简化为：
中性变载?d
n
d 加载
卸载?d
ij
加载面
任何一种应力状态都不能位于加载面之外
• 增量前 f (ij，) = 0， • 增量后 f (ij+dij，+d) = 0
• 一致性条件：
f ij
dij
f
d
0
f (ijdij , d f (ij,
内变量的性质
• 随加载过程，内变量不断地增加 • 中性变载或者卸载时，则内变量保持不变
hp=s
（1） = 0 1 当=s时，材料屈服，当s<<1即从A到B点，产生塑性变形，
B点的总应变为
(p)B
1
s h

弹塑性力学讲义屈服条件

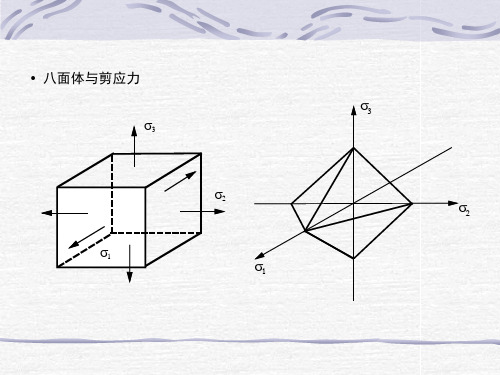
还有,由于拉压屈服应力相等,因而可得到σ1-σ2空间中的另外六个应力屈服点 A3:(σ1,σ2,σ3) = (3t,t,0) A4:(σ1,σ2,σ3) = (t,3t,0) B3:(σ1,σ2,σ3) = (3t,2t,0) B4:(σ1,σ2,σ3) = (2t,3t,0) C3:(σ1,σ2,σ3) = (2t,t,0) C4:(σ1,σ2,σ3) = (t,2t,0) 因此,根据这些点的数据,可以作出在σ1-σ2空间中的屈服面.容易证
e3 '
e1 '
σ3
σ1
J2 的物理意义
J2与弹性状态的形状改变能成正比
1 sijeij= 1 sijsij= 1 J2 2 4G 2G
J2也与材料八面体上的剪应力成比例
材料常数k2由简单实验确定 (1)单轴拉伸:屈服时 σ1 =σs,σ2 =σ3 =0,代入屈服条件
σ2 J 2 = s = k 22 3
k2 =
1 3
σs
(2)剪切:屈服时τ =τs σ1= τs,σ2=0,σ3= τs,,屈服条件 J2= τ2 =k2 s k2 = τs. 因此,如果材料服从Mises屈服条件,则 σs= 3τs
两种屈服条件比较
e2'
如假定单轴拉伸时两个屈服面重合,则Tresca六边形内接于Mises圆;
s1 = 1 2 x 1 6 y= 2 2π rσ sin(θ σ + ) 3 3
s2 =
2 y= 3
1 2
2 rσ sin θБайду номын сангаасσ 3
1 6 2 2π rσ sin(θ σ ) 3 3
s3 =
x
y=
屈服面的一般形状

塑性力学课件第三章屈服条件

理想塑性材料：进入塑性阶段以后，在应力空间中代表应力状态的点均位于屈服曲面 f（σij）= C上。由于没有强化现象，应力状态变化时，尽管塑性变形还可以不断增长，而屈服函数的值却不再增长。即不可能有df＞0的情况出现。代表应力状态的点只能在屈服面上移动，这时有df = 0，属于加载；当代表应力状态的点移向屈服面以内时，df＜0，属于卸载。即 df＜0，卸载（3—34） df = 0，加载由实验结果得知，加载及中性变载时产生新的塑性变形，卸载及时不产生新的塑性变形，其各应力分量与各应变分量的改变服从弹性规律。
§3.5 Mises屈服条件
Tresca屈服条件完全忽视了居于中间大小的主应力对材料屈服的影响，这是和实际有出入的。 Mises用Tresca屈服条件的屈服轨迹正六边形ABCDEF的外接园作为屈服轨迹。 2 由（3—23）式知圆的半径为 σs，
3
2 2 圆的方程为： R2 = s 3
（3—25）
简单加载定理：对小变形的受力物体，满足下列三个条件即可保证物体内所有各点都处于简单加载（充分条件）：（1）物体上所有外加荷载（包括表面力和体积力）成比例增长。如有位移边界条件，只能是零位移边界条件；（2）应力强度和应变强度呈幂关系 i A in ; 1 （3）材料不可压缩，即泊松比μ= 。
S
s
2
二、各主应力不按大小顺序排列时的 Tresca屈服条件（3—16）可改写为： σmax－σmin =σs （3—19）（3—19）等价于下式中至少有一个式子成立： 1 3 s 0 0 3 s 1 1 2 s 0 （3—20） 1 2 s 0 2 3 s 0 2 3 s 0

弹塑性力学第七章屈服条件

其他领域中的屈服条件应用
生物医学
在生物医学领域，如人体骨骼、牙齿等组织的力学性能分析中，需要考虑材料的屈服条件。
能源工程
在核能、太阳能等能源工程领域，相关设备的材料选择和设计需要考虑其屈服条件。
环境工程
在环境工程领域，如土压力、岩石压力等问题的分析中，需要利用屈服条件来评估结构的稳定性和安全性。
20世纪初，德国科学家R.Von Mises 提出Von Mises屈服条件，成为弹塑性力学中最为广泛应用的屈服条件之一。
现代屈服条件的进展
随着计算机技术和数值计算方法的不断发展，现代屈服条件的研究更加深入和广泛。
目前，研究者们正在探索更加精确和实用的屈服条件，以适应各种复杂材料和工程应用的需求。
弹塑性力学的重要性在于，许多工程结构和材料在承受外力时，其变形行为既不是完全弹性也不是完全塑性，而是介于两者之间。因此，理解弹塑性行为对于准确预测结构的响应和保证工程安全至关重要。
屈服条件的概述
屈服条件是弹塑性力学中的一个基本概念，它描述了材料在应力达到某一特定值时开始发生屈服（即塑性变形）的条件。
07 总结与展望
总结
屈服条件的定义与分类
总结了屈服条件的定义，以及按不同标准分类的屈服条件类型，如按材料性质、应力状态等。
屈服条件的物理意义
解释了屈服条件在材料力学行为中的物理意义，包括材料内部的微观结构变化、应力分布等。
屈服条件的应用场景
列举了屈服条件在不同工程领域中的应用，如结构稳定性分析、材料强度设计等。
混合阶段中，应力-应变关系表现为非线性，材料同时具有弹性和塑性行为。
加载和卸载路径的影响
在混合阶段，材料的响应不仅取决于当前的应力状态，还受到之前加载和卸载路径的影响。

塑性力学-屈服条件

第二章屈服条件第二节初始屈服条件和初始屈服曲面初始屈服条件的应力表示形式：简单应力状态=−s σσ0=−s ττ单拉纯剪()0ij f σ=与应力状态的各分量有关；一般应力状态),,(321=I I I f 与坐标选取无关：屈服与静水应力无关：),(32=J J f 屈服函数在应力空间表示一个曲面代表材料屈服各种可能的应力状态(4)讨论和评价屈服条件的常数：s s στ5.0=Tresca:Mises:ss στ577.0=实际工程材料：ss στ)6.0~56.0(= 中间主应力和平均应力Tresca:Mises:2σm σ不包含未考虑未考虑包含使用方便Mises:光滑曲线或曲面，数学上运用方便Tresca:能预先判明主应力的代数值大小时，方程简单结论Tresca和Mises条件主要适用于韧性金属材料，材料性质对静水压力不敏感这两个条件差别不大，使用各有方便之处，在实际工程问题广泛应用后继屈服条件的一般形式后继屈服面是以为参数的一族曲面K 硬化材料：随着塑性变形的发展不断变化。

后继屈服面不仅与应力有关，而且与变形历史有关(),0ij f K σ=K 称为硬化参数，表示塑性变形的大小及历史后继屈服函数、硬化函数确定后继屈服面的形状以及随塑性变形发展的变化规律重要任务，一大难题是后继弹性阶段的界限，是判断材料处于后继弹性还是塑性状态的准则在应力空间中，材料的应力不可能位于屈服面外2. 加、卸载准则材料进入塑性以后，加、卸载适用不同的变形规律单向应力状态，通过应力本身的大小变化复杂应力状态，六个应力分量可独立变化(1)理想塑性材料的加载、卸载准则fσ=无硬化，初始屈服面和后继屈服面重合()0ij9基本概念（定义）：载荷变化过程中加载：应力点保持在屈服面上，产生新的塑性变形卸载：应力点退回屈服面内，不产生新的塑性变形(2)硬化材料的加、卸载准则后继屈服面和初始屈服面不重合, 与塑性变形的大小和历史有关.(),0ij f K σ=9基本概念（定义）：载荷变化过程中加载：应力点过渡到相邻的屈服面上，产生新的塑性变形，硬化参数变化卸载：应力点退回屈服面内，不产生新的塑性变形，硬化参数不变化中性变载：应力点沿着屈服面滑动，不产生新的塑性变形，硬化参数不变化2. 等向硬化模型没有考虑静水应力、Bauschinger 效应后继屈服面形状、中心位置不变，等向相似扩大初始屈服Mises 条件，同心圆；Tresca 条件，同心正六边形0)(=−k K i σ 后继屈服函数形式简单，包含内变量平面图形由函数决定，半径由含内变量的函数确定i σ)(k K πsk K σ=)(初始屈服条件：后继屈服条件：?)(=k K 内变量的演化对于复杂加载（非简单加载）的情况，如何寻找材料硬化条件？内变量－－单位体积的塑性功)(p i W F =σ∫∫==pijij p p d dW W εσ3. 随动硬化模型一个方向硬化，相反方向同等软化屈服面大小、形状不变，整体平移4. 混合硬化模型随动硬化和等向硬化模型结合屈服面大小、形状、位置变化。

塑性成形原理-屈服准则

2
1 3
2 2
1 3
上式中分子是三向应力莫尔圆中σ 2 到大圆圆心的距离，分母为大圆半径。当σ2在σ1与σ3之间变化时，μσ则在-1~1之间变化。因此，μσ实际上表示了在三向应力莫尔圆中的相对位置变化。
由罗德应力参数可推出
带入米塞斯准则整理可得
1 3
令
应力，它是金属塑性加工变形抗力的指标。
二、屈雷斯加屈服准则
1864年由法国工程师屈雷斯加(Tresca)提出。
表述：当受力物体中的最大切应力达到某一定值时，物
体就发生屈服。或者说，材料处于塑性状态时，其最大切应力是一不变的定值。
该定值只取决于材料在变形条件下的性质，而与应力状
态无关。所以该屈服准则又称最大切应力不变条件。该准则可以写成：
各向同性硬化假说的要点：
（1）材料在硬化后仍然保持各向同性；（2）硬化后屈服轨迹的中心位置和形状都不变，它们在π平面上仍然是以原点
为中心的对称封闭曲线，但
其大小则随变形的进行而不断的扩大。 Mises屈服准则和Tresca屈服准则等强化模型的后续屈服轨迹在π平面上是一系列扩大且同心的圆和正六边形。
max C
三、米塞斯屈服准则
德国力学家米塞斯(Mises)于1913年提出了另一个屈服准则，
并称之为米塞斯屈服准则。
表述：在一定的变形条件下，当受力物体内一点的应力偏张量的
第二不变量J2'达到某一定值时，该点就开始进入塑性状态。
更方便的表述形式是：当点应力状态的等效应力达到某一与应力状态无关的定
弹性变形时应力与应变完全成线性关系的材料；
理想塑性材料：塑性变形时不产生硬化的材料；

【弹塑性力学】5-屈服准则

(3Rt a 1) (3Rt a 1)
• 其中 R t 为单轴抗拉强度,a为系数
2
a 1
mm1
1 Rt
mRc /Rt
R c 为单轴抗压强度
32
双剪应力屈服准则（俞茂鋐,1961）
f
(13,12 )
13
12
1
1 2
( 2
3) kb
0
当12
23或 2
1 2
( 1
3 )时
f
(13, 23)
p 3st/R
对于Tresca屈服条件: 13 =k=2s p = 2st/R
39
（2）管段的两端是封闭的:
应力状态为,z= pR/2t， = pR/t，r=0， zr=r=z=0
1 J2 = +66([(2zrzr2r)2+(2rz)]=)162+23((pR/tz))22
13 = = pR/t
（1）单轴拉伸:屈服时 1 =s,2 =3 =0，代入屈服条件
J23s2 k2,
ks
3
（2）剪切：屈服时 =s 1= s，2=0，3= s,，屈服条件
J2s2k2, ks
12
两种屈服条件比较
• 如假定单轴拉伸时
两个屈服面重合,则
Tresca六边形内接于
MisesБайду номын сангаас;
外切 T resca六边形
• （1）圆外接于六边形
32 3ssin in ,k
6cco s 33sin
• （2）圆内接于六边形
32 3ssin in ,k
6cco s 33sin
29
Zienkiewicz-Pande条件:

塑性力学讲义-屈服条件

（4）由于拉压屈服极限相等，曲线C对称于原点O。由上面的分析可知屈服曲线C可分成形状相同的12个部分，只需考虑C的1/12即可。实验时，采用Lode应力参数 0 1 这样一个取值范围内的应力组合就能确定屈服曲线的具体形状。
屈服曲线
2
C
B
O
A
30
B
当应力分量满足某一关系时，材料将重新进入塑性状态而产生新的塑性变形，这种现象叫强化。在复杂应力状态下，由于会有各种应力状态的组合能达到初始屈服或后继屈服，在应力空间中这些应力点的集合而成的面就是初始屈服面或后继屈服面。如果是理想塑性材料，后继屈服面和初始屈服面是重合的。但对强化材料，两者不重合。随着塑性变形的发展，后继屈服面是不断变化的，故后继屈服面又称为加载面。材料在初始屈服以后再进入塑性状态时应力分量间所必须满足的函数关系叫做强化
2 2 2 2 2 2
2
6 xy yz zx 2 s
Mises条件：当应力强度达到一定数值时，材料开始屈服，进入塑性状态。
i 2k s
Mises条件可看成为当形状改变比能达到一定数值时开始屈服。或认为只要应力偏张量的第二不变量达到某一数值时，或八面体剪应力达到一定数值时开始屈服，进入塑性状态。
屈服线上有角点，给数学处理带来了困难，没有考虑平均应力对屈服的影响。二、Von.Mises屈服条件 Mises指出Trecsa屈服条件在偏量平面上的六个角点虽然由试验得出，但是六边形则是直线连接假设的结果，且数学上使用起来不方便。于1913年提出以外接圆柱代替六棱柱似乎更合理，且避免了因曲线不光滑在数学上引起的困难。屈服曲线就是Tresca 六边形的外接圆。方程为

塑性力学02-屈服条件学习资料

3
y p4
2
它对应平面的A点. 在纯剪切屈服时
1 s ,2 0 ,3 s , 0 , 0 它对应平面的B点.
这样AB之间的屈服曲线可以通过双向应力实验来决定.例如可以通过薄壁圆筒同时受拉和扭作用来得到. 于是通过对称性就得到整个屈服曲线.
2-3 Tresca条件和Mises条件. 这是两个常用的屈服条件.
第二章屈服条件
• 第一章介绍的是应力和应变的概念, 接下来就应该介绍应力应变的关系. 在弹性力学中, 应力应变是线性关系,是一一对应的比较简单关系, 但在塑性力学中, 没有这种简单的关系. 第一章曾经指出材料在屈服以后要有不能恢复的塑性变形. 问题就出在这个地方, 那么材料在什么时候屈服, 屈服以后又服从什么规则.这就是这一章和下一章要解决的问题.
f 0
f 的梯度方向
屈服面 f ij 0
(2)硬化材料的加,卸载准则.
对于硬化材料,后继屈服面和初始屈服面不同, 与塑性变形的大小和历史有关.
f ij,K 0
加,卸载准则为:
f
0,
df
f ij
d ij
0
f
0,
df
f ij
d ij
0
f
0,
df
f ij
d ij
0
加载; 中性变载; 卸载.
o
y
主应力排序为 r
x
最大剪应力为
r
max 12 r
代入Tresca和Mises条件发
现它们有一样的屈服条件:
r s
2-4 Tresca条件和Mises条件的实验验证
前面已经提到这两个屈服条件是建立在假设基础上的, 需要通过实验来验证. 这里介绍两个有名的实验.

塑性力学之屈服条件与破坏条件

理想线性强化刚塑性力学模型，其应力应变关系的数学表达式为：
s E1
(当 0 时)
◆ 幂强化力学模型
为了避免在 s 处的变化，有时可以采用幂强化力学模型。当表达式中幂强化系数 n 分别取 0 或 1 时，就代表理想弹塑性模型和理想刚塑性模型。其应力应变关系表达式为：
图3.8 子午平面二次式屈服曲线的三种形式
3.1 基本概念小结
屈服
应力(应变) 满足条件
屈服条件
以应力(应变) 函数形式表达在应力空间内的表示
在π平面或子午面上的投影
屈服函数
弹性到塑性的过渡
屈服曲面
屈服曲线
3.2 描述屈服条件的坐标体系
(σ1,σ2,σ3) ：力学(土力学)
1 m ( 1 2 3 ) 3 1 r ( 1 2 ) 2 ( 2 3 ) 2 ( 3 1 ) 2 3 1 1 2 2 1 3 tan ( ) 3 1 3
d －构件危险点的形状改变比能
0 d
－形状改变比能的极限值，由单拉实验测得
屈服条件
强度条件
实验表明：对塑性材料，此理论比第三强度理论更符合试验结
果，在工程中得到了广泛应用。
强度理论的统一表达式： r [ ]
r ,1 1 [ ]
r ,3 1 3 [ ]
(p, q, θσ)：土力学
1 p ( 1 2 3 ) 3 1 q ( 1 2 ) 2 ( 2 3 ) 2 ( 3 1 ) 2 2 1 1 2 2 1 3 tan ( ) 3 1 3

塑性力学第三章-屈服条件

第三章
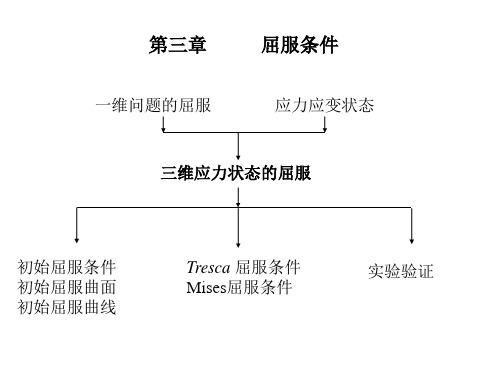
一维问题的屈服
屈服条件
应力应变状态
三维应力状态的屈服
初始屈服条件初始屈服曲面初始屈服曲线
Tresca 屈服条件 Mises屈服条件
实验验证
初始屈服条件
初始弹性状态的界限为初始屈服条件
ɺ φ (σ ij , ε ij , ε ij , t , T ) = 0
影响因数：应力影响因数： 1应力、2应变、3应变率、4时间、5温度应力、应变应变、应变率应变率、时间时间、温度
_____ p
_____ p
2 p p dε ij dε ij 3
K = ϕ ( ∫ dW p ) , dW p = σ ij dε ijp
采用Mises屈服条件，线性强化屈服条件，采用屈服条件
f = σ −σ s = 0
φ =σ −K = 0
简单拉伸时，简单拉伸时，
σ = σ s + E pε p
σ z + 4τ zθ = σ s
2 2
(σ 1 − σ 2 )2 + (σ 2 − σ 3 )2 2 + (σ 3 − σ 1 ) = 2σ s2
σ z 2 + 3τ zθ 2 = σ s2
σz σ s τ + 3 zθ = 1 σ s
2 2
σ z 2 + 4τ zθ 2 = σ s2
P = 0,
µσ = −1
µσ = 0
(θ = −300 )
(θ = 00 )
P = πR 2 q ,
P = 2πR 2 q ,
µσ = 1
(θ = 300 )
σ1 − σ 3 Tresca : =1 σs

塑性理论第六章屈服准则

2
……(a)

（在外表面）
p
2r
z
t

P

p （在内表面） 0
当外表面屈服时：
pr 1 t
2 z
pr 2t
3 0
……(b)
1）由米塞斯屈服准则
( 1 2 ) 2 3 3 1 2 s2
1 s 2 3 0
Mises屈服准则： 1 2 2 2 1 2 2 3 3 1 s 2
Mises屈服准则在纯剪切应力状态时：
σ2
O
σ1 σ
xy 1 3 k
2
得：
Mises屈服准则又可以表示为：
3 0 对于Mises 2 2 ( 1 2 ) 2 2 3 3 1 2 s2 6 K 2
σ2
1 s 2
2 s
D
1 2
2 1 2 2
2 s
' 2
E
P F
1'
C
1 s
将坐标轴旋转45度:
6.2 Tresca屈服准则
1864年，法国工程师屈雷斯加: 当材料中的最大切应力达到某一定值时，材料就屈服。即材料处于塑性状态时，其最大切应力是一不变的定值， ——又称为最大切应力不变条件:
max
max min
2
C
C为材料性能常数，可通过单拉求得 :
材料单向拉伸时的应力 : K为材料屈服时的最大切应力值，即剪切屈服强度
当主应力不知时，上述Tresca准则不便使用
对于平面变形及主应力为异号的平面应力问题：

弹塑性力学讲义屈服条件

第六章屈服条件

弹性与塑性力学基础-第五章屈服准则与塑性应力应变关系

塑性力学第三章-屈服条件讲课稿

弹塑性力学-15 屈服理论

塑力 3、屈服条件

弹塑性力学-屈服条件

弹塑性力学讲义屈服条件

塑性力学课件 第三章 屈服条件

弹塑性力学第七章屈服条件

塑性力学-屈服条件

塑性成形原理-屈服准则

【弹塑性力学】5-屈服准则

塑性力学讲义-屈服条件

塑性力学02-屈服条件学习资料

塑性力学之屈服条件与破坏条件

塑性力学第三章-屈服条件

塑性理论 第六章 屈服准则

塑性力学课件第三章屈服条件

塑性理论第六章屈服准则