现代测试技术--8 误差分析32页PPT
合集下载
试验误差分析ppt课件

1 误差的基本概念
误差
误差:在试验过程中由于实验仪器精度的限制,实验方法的不完善,科 研人员认识能力的不足和科研水平的限制等方面的原因,在试验中获得 的试验值与它的真值并不一致,这种矛盾在数值上表现为误差。
绝对误差 算术平均误差
相对误差 标准误差
绝对误差
误差
试验值与真值之差称为绝对误差,即
绝对误差=试验值-真值
试验误差分析
汇报提纲
1 误差的基本概念 2 文献阅读
1 误差的基本概念
真值
真值:是指在某一时刻和某一状态下,某量的客观值或实际值。
1)理论真值:例如,三角形三内角之和恒为180°,同一量值自身 之差恒为零,自身之比恒为1,等等。 2)约定真值:国际计量大会中所规定的共七种单位的量值,都可认 为是约定真值。 3)相对真值:用高一级仪器检定低一级仪器时,更具体说,当高一 级与低一级仪器的误差之比为(1/3~1/120)时,则可认为前者是后 者的相对真值。
拉伸速率可能对薄膜的力学性能测试结果带来影响;同时 ,若拉伸试验装置上下夹具不在一个平面上,或者样品拉伸方 向有一定的倾斜角度等,都会对力学性能的拉伸带来误差。
误差评估
1.薄膜各向异性带来的误差
由于轧制方向不同,微观上聚合物的分子链排列延伸的方向 不同,沿各方向上的力学性能也可能会有不同。
对未辐照的PI薄膜进行平行拉伸(y方向)和垂直拉伸(x方
绝对误差反映了试验值偏离真值的大小, 这个偏差可正可负。通常所说的误差一般指 绝对误差。
误差
相对误差
绝对误差虽然在一定条件下能反映试验值的准确 程度,但还不全面。所以为了判断试验值的准确性 ,还必须考虑试验值本身的大小,故引出了相对误 差。
误差
误差分析ppt

5
4.真值 任何测量都存在误差,真值不可能得到,只能尽
量接近 (1) 约定真值 由国际计量大会定义的单位(国际
单位)及我国法定的计量单位 七个基本单位:
长度、质量、时间、电流强度、热力学温度 发光强度、物质的量 例如:1米是光在真空中在 1/299792458 秒的时间 间隔内行程的长度.
6
(2)标准值(相对真值) 通过高精密度测量到获得的更 接近真值的值。 获得标准值的试样为标准试样(标准参考物质) 经有权威机构认定并提供
(2) 产生的原因 偶然因素、不确定因素
13
3. 过失
分析过程中的过失造成的误差不同于前两类误差。 它是由于分析工作者粗心大意或违反操作规程所产生的错误,
如溶液溅失、沉淀穿滤、读数记错等,都会使结果有较大的 “误差”。在处理所得数据时,如发现由于过失引起的“误差”,
应该把该次测定结果弃去不用。
14
(1) 准确度──分析结果与真实值的接近程度 (2) 精密度──几次平行测定结果相互接近程度 (3) 两者的关系
精密度是保证准确度的先决条件; 精密度高准确度不一定高; 准确度高精密度一定高。
9
精密度好, 准确度不好
精密度、 准确度都很好
精密度、 准确度都不好 10
二、系统误差和偶然误差
1. 系统误差 (可定误差)
滴定管,容量瓶未校正。
c.试剂误差——所用试剂有杂质
例:去离子水不合格;
试剂纯度不够
(含待测组份或干扰离子)。
d.操作误差——操作人员主观因素造成
例:对指示剂颜色辨别偏深或偏浅;
滴定管读数不准。
12
2. 偶然误差(随机误差,不可定误差):
由不确定原因引起
(1) 特点 a.不恒定不具单向性(大小、正负不定) b.难以校正,不可消除(原因不定) c.服从统计规律 (正态分布)
4.真值 任何测量都存在误差,真值不可能得到,只能尽
量接近 (1) 约定真值 由国际计量大会定义的单位(国际
单位)及我国法定的计量单位 七个基本单位:
长度、质量、时间、电流强度、热力学温度 发光强度、物质的量 例如:1米是光在真空中在 1/299792458 秒的时间 间隔内行程的长度.
6
(2)标准值(相对真值) 通过高精密度测量到获得的更 接近真值的值。 获得标准值的试样为标准试样(标准参考物质) 经有权威机构认定并提供
(2) 产生的原因 偶然因素、不确定因素
13
3. 过失
分析过程中的过失造成的误差不同于前两类误差。 它是由于分析工作者粗心大意或违反操作规程所产生的错误,
如溶液溅失、沉淀穿滤、读数记错等,都会使结果有较大的 “误差”。在处理所得数据时,如发现由于过失引起的“误差”,
应该把该次测定结果弃去不用。
14
(1) 准确度──分析结果与真实值的接近程度 (2) 精密度──几次平行测定结果相互接近程度 (3) 两者的关系
精密度是保证准确度的先决条件; 精密度高准确度不一定高; 准确度高精密度一定高。
9
精密度好, 准确度不好
精密度、 准确度都很好
精密度、 准确度都不好 10
二、系统误差和偶然误差
1. 系统误差 (可定误差)
滴定管,容量瓶未校正。
c.试剂误差——所用试剂有杂质
例:去离子水不合格;
试剂纯度不够
(含待测组份或干扰离子)。
d.操作误差——操作人员主观因素造成
例:对指示剂颜色辨别偏深或偏浅;
滴定管读数不准。
12
2. 偶然误差(随机误差,不可定误差):
由不确定原因引起
(1) 特点 a.不恒定不具单向性(大小、正负不定) b.难以校正,不可消除(原因不定) c.服从统计规律 (正态分布)
测量误差分析(精品课件)

n
xi X0 2
i 1
n
因为真值X0为未知,所以必须用残差vi 来表示,即
n
vi2
i 1
n 1
n
2
xi x
i 1
n 1
此式称贝塞尔公式。
欢迎下载 可修改
20
三、测量结果的置信度
假设用 对x μ进行估计的误差为
,那 x
么 x 。对于某一指定的区间[-λ, λ], x
落在该 区间内的概率为 x
对于同一测量结果,置信区间不同,其 置信概率是不同的。
置信区间越宽,置信概率越大;反之亦 然。
欢迎下载 可修改
24
一列等精度测量的结果可以表达为在一定 的置信概率之下,以测定值子样平均值为 中心,以置信区间半长为误差限的量
测量结果=子样平均值±置信区间半长(置 信概率P=?)
欢迎下载 可修改
n
n
欢迎下载 可修改
16
算术平均值的性质 用算术平均值代替被测量的真值,则有
vi xi x
式中 vi —— xi的剩余误差; xi —— 第i个测量值,i=1,2,…,n。
欢迎下载 可修改
17
(1)剩余误差的代数和等于零,即
n
vi 0
i 1
(2)剩余误差的平方和为最小,即
n
vi2 最小
25
例题1:
在等精度测量条件下对某透平机械的 转速进行了20次测量,获得如下的一列测 定值(单位:r/min)
x
1 n
n i1
xi
子样方差:描述子样在其平均值附近散布
程度
s2
1 n
n i 1
(xi
x)2
欢迎下载 可修改
现代分析测试技术PPT课件

气相色谱分析法 高效液相色谱分析
分子质谱分析 原子质谱分析
现代分析测试技术
热分析法 放射化学分析法
14
概
述
按仪器的用途可分为:
1.成分分析类(原子、离子、分子、基团) 如:原子吸收光谱、
红外光谱、X射线衍射等。
2.结构分析类(原子结构、分子结构、晶体结构、微观结构)如:
红外光谱、X射线衍射、透射电镜等。
现代分析测试技术
19
概述部分的要求
1. 了解现代物质分析、仪器分析的概念 2. 掌握现代物质分析有哪几大类分析方法 3. 掌握物相、元素、微观分析的区别 4. 了解现代物质分析的特点、应用范围
现代分析测试技术
20
课堂复习
1. 现代物质分析常用方法(按照原理)有_________、 __________、
• 《仪器分析原理》何金兰等,21教材,科学出版社(2002)
现代分析测试技术
3
其它参考书
物相、元素分析与微观分析的区别
重要
劣质食盐
NaCl KCl Na2SO4 K2SO4
物相
NaCl、KCl、Na2SO4、K2SO4
元素
Na、K、 Cl、 S、O
微观
现代分析测试技术
4
元素分析结果的表征形式:
10
概
述
重要
2. 现代分析测试技术的分析方法
按仪器的工作 原理可分为:
分析方法 (工作原理)
光学分析法 电化学分析法 色谱分析法 质谱分析法 其现代它分分析测析试技方术法 (如:热分析法) 11
光学分析法----按原理分类
重要
光谱法:测量的信号是物质内部能级跃迁所产生的发射、吸收、散
测量误差分析与处理措施ppt课件

测量误差的分类
01
02
03
系统误差
在一定条件下,测量误差 具有确定的规律性。
随机误差
由于偶然因素引起的测量 误差,无规律可循。
粗大误差
明显超出正常范围,与实 际情况明显不符的测量误 差。
测量误差的来源
测量设备误差
设备本身精度不足或老 化等引起的误差。
环境因素
温度、湿度、气压等环 境条件变化引起的误差
函数建模法
函数建模法是一种基于数学模型的误差分析方法,通过建立 测量值与真实值之间的数学模型,分析误差产生的原因和规 律。
函数建模法适用于需要对误差进行深入分析和预测的情况。 通过建立测量值与真实值之间的函数关系,可以分析误差产 生的原因和规律,进而对测量过程进行优化和改进。这种方 法精度较高,但需要较深的数学基础和建模技巧。
统计分析法
统计分析法是一种基于数学统计原理的误差分析方法,通过对大量测量数据进行统计分析,计算误差 的分布和规律。
统计分析法适用于需要对大量测量数据进行误差分析的情况。通过统计学的手段,如平均值、方差、 置信区间等,可以全面了解误差的分布和规律,进而对测量过程进行优化和控制。这种方法精度较高 ,但需要较复杂的数学处理和较多的数据支持。
04
误差控制与预防
误差控制策略
制定测量标准
建立完善的测量标准体系 ,确保测量数据的准确性 和可靠性。
定期校准设备
对测量设备进行定期校准 ,确保设备性能稳定,减 少误差产生。
培训测量人员
提高测量人员的技能水平 ,确保他们能够正确、规 范地进行测量操作。
误差预防措施
优化测量方法
采用先进的测量方法和技术,提高测 量精度和准确性。
测量数据的准确性和可靠性。
误差分析ppt课件

对于15V、±2.5级电压表
x
x x
100%
xm x
s
100%
15 2.5% 100% 3.75% 10
从结果可以看出,用15V、±2.5级的电压表测量较为合适。
17
结论:在进行仪表选择时,我们应注意, 同样量程的仪表,仪表等级数越小,测量 越准确;而对于不同量程、不同等级的仪 表,我们应该根据被测量的大小,兼顾仪 表级别和量程上限,合理选择仪表。
2
2
d 2 2
1
随机误差在-δ至+δ范围内概率为:
P( ) 1
2
2
e d 2 2
2
2
2
e d 2 2
0
经变换,(1.3.22)式为
P( )
2
t
t2
e 2 dt 2(t)
2 0
若某随机误差在±t 范围内出现的概率为2Φ(t), 则超出该误差范围的概率为
x
1 n
n i 1
xi
x1
x2
4
x3
x6
8.00mm
1 2
3
4
5
6
xi / mm 8.04 8.02 7.96 5.99 9.33 7.9827
2、随机误差的计算方法
1)算术平均值
x
1 n
n i 1
xi
x1
x2
x3 n
...
xn
28
返回
上一页
下一页
(2) 标准差
测量误差分析及处PPT课件

12
• 安装误差
p3 (hg) (0.05m 1000kg/m 3 9.8m/s 2 )
490N/m 2 0.49kPa • 读数误差
p4 2kPa
13
• 总系统误差为: • 1)若按算术综合法
n
p pi (3 1.2 0.490 2)kPa 6.690kPa i 1
p
p p
6.690 300
2.23%
14
• 2)若按几何综合法
n
p pi i1
32 1.22 0.4902 22
3.831kPa
p
p p
3.831 300
1.27%
15
随机误差
• 随机误差可分正态分布与非正态分布两大 类。其中非正态分布又有均匀分布随机误 差与反正弦分布随机误差之分。但就大多 数测量而言,其随机误差都服从正态分布 规律,因而以下讨论只限于正态分布随机 误差。
• n 时,i 0,即由于正负误差的互相抵消,
一列等精度测量中各个误差的代数和趋于零。
17
• 高斯(C. F. Gauss)于1795年提出随机误差 分布规律的函数表达式,亦称为误差方程 或称或然率方程
2
y
1
e 2 2
2
• 标准误差(或称均方根误差) 2i
n
18
• | k | 0.6745(即| | 0.6745 ) 概率为50%
测量误差分析及处理
1
误差的来源与分类
• 人们的观察能力、测量仪器、测量方法、 环境条件等
• 测量值与真值之差称为误差 • 绝对误差=测量值-真值; • 相对误差= 绝对误差/真值(测量值) • 绝对误差和相对误差均可为正值或负值
2
1、系统误差 在测量过程中,出现某些规律性的以及影 响程度由确定的因素所引起的误差。
• 安装误差
p3 (hg) (0.05m 1000kg/m 3 9.8m/s 2 )
490N/m 2 0.49kPa • 读数误差
p4 2kPa
13
• 总系统误差为: • 1)若按算术综合法
n
p pi (3 1.2 0.490 2)kPa 6.690kPa i 1
p
p p
6.690 300
2.23%
14
• 2)若按几何综合法
n
p pi i1
32 1.22 0.4902 22
3.831kPa
p
p p
3.831 300
1.27%
15
随机误差
• 随机误差可分正态分布与非正态分布两大 类。其中非正态分布又有均匀分布随机误 差与反正弦分布随机误差之分。但就大多 数测量而言,其随机误差都服从正态分布 规律,因而以下讨论只限于正态分布随机 误差。
• n 时,i 0,即由于正负误差的互相抵消,
一列等精度测量中各个误差的代数和趋于零。
17
• 高斯(C. F. Gauss)于1795年提出随机误差 分布规律的函数表达式,亦称为误差方程 或称或然率方程
2
y
1
e 2 2
2
• 标准误差(或称均方根误差) 2i
n
18
• | k | 0.6745(即| | 0.6745 ) 概率为50%
测量误差分析及处理
1
误差的来源与分类
• 人们的观察能力、测量仪器、测量方法、 环境条件等
• 测量值与真值之差称为误差 • 绝对误差=测量值-真值; • 相对误差= 绝对误差/真值(测量值) • 绝对误差和相对误差均可为正值或负值
2
1、系统误差 在测量过程中,出现某些规律性的以及影 响程度由确定的因素所引起的误差。
误差分析与数据处理ppt课件.ppt
(4)缓变误差: 是指数值上随时间缓慢变化的误差,一般它是由零部件的
老化、机械零件内应力变化引起的。由于它有不平稳随机 过程的特点,误差值在单调缓慢变化,因此不能象对系统 误差那样引进一次修正量即能校正,又不能象对一般随机 误差那样按平稳随机过程的特点来处理,因而常需不断进 行校正,测量准确度与对仪器仪表的校正周期有关。
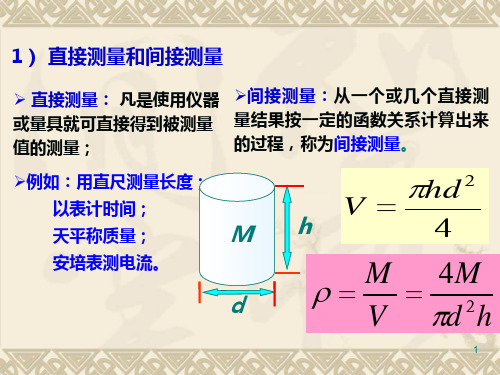
1) 直间接测量:从一个或几个直接测
或量具就可直接得到被测量 量结果按一定的函数关系计算出来
值的测量;
的过程,称为间接测量。
➢例如:用直尺测量长度;
以表计时间;
天平称质量;
M
安培表测电流。
d
V hd 2
h
4
M V
4M
d 2h
1
2)等精度测量和非等精度测量
2
1.2真值、代表值与误差
1.2.1真值
指在某一时刻和某一位置的某个物理量客观存在的真实值。严 格地讲,真值是无法测得的,只能测得真值的近似值。实际应 用中真值是指测量次数无限多时的平均值作为真值。
➢理论真值:理论上证明过的某些已知的固定量值,如三角 形之和为180º。
➢约定真值:国际计量组织通过决议规定的某些计量单位的 量值,如规定铂铱合金的国际千克原器为1kg的质量单位。 光在真空中1s时间内传播距离的1/299792485为1米。
仪器
天平不等臂
6
➢系统误差的分类
1)按系统误差产生的原因分 ➢设备误差:由于测量仪器、工具的不准确或安装不正确造成的,如 仪器的零位不准,空行程、不水平、不垂直、导线的影响等。 ➢环境误差:由于测量环境条件变化的影响,如温度、压力、外电磁 场的影响。 ➢人员误差:由测量人员自身造成的,如读数的偏大、偏小、测量的 超前或滞后等。 ➢方法误差:由于测量方法不完善,计算公式的近似简化引起的。
老化、机械零件内应力变化引起的。由于它有不平稳随机 过程的特点,误差值在单调缓慢变化,因此不能象对系统 误差那样引进一次修正量即能校正,又不能象对一般随机 误差那样按平稳随机过程的特点来处理,因而常需不断进 行校正,测量准确度与对仪器仪表的校正周期有关。
1) 直间接测量:从一个或几个直接测
或量具就可直接得到被测量 量结果按一定的函数关系计算出来
值的测量;
的过程,称为间接测量。
➢例如:用直尺测量长度;
以表计时间;
天平称质量;
M
安培表测电流。
d
V hd 2
h
4
M V
4M
d 2h
1
2)等精度测量和非等精度测量
2
1.2真值、代表值与误差
1.2.1真值
指在某一时刻和某一位置的某个物理量客观存在的真实值。严 格地讲,真值是无法测得的,只能测得真值的近似值。实际应 用中真值是指测量次数无限多时的平均值作为真值。
➢理论真值:理论上证明过的某些已知的固定量值,如三角 形之和为180º。
➢约定真值:国际计量组织通过决议规定的某些计量单位的 量值,如规定铂铱合金的国际千克原器为1kg的质量单位。 光在真空中1s时间内传播距离的1/299792485为1米。
仪器
天平不等臂
6
➢系统误差的分类
1)按系统误差产生的原因分 ➢设备误差:由于测量仪器、工具的不准确或安装不正确造成的,如 仪器的零位不准,空行程、不水平、不垂直、导线的影响等。 ➢环境误差:由于测量环境条件变化的影响,如温度、压力、外电磁 场的影响。 ➢人员误差:由测量人员自身造成的,如读数的偏大、偏小、测量的 超前或滞后等。 ➢方法误差:由于测量方法不完善,计算公式的近似简化引起的。
测量误差分析与处理措施ppt课件

滑动平均滤波
对连续采样的数据进行滑 动平均处理,以减小随机 误差的影响,平滑数据波 动。
中值滤波
对采样数据进行排序处理 ,取其中位数作为滤波结 果,以消除异常值的干扰 。
测量结果的评估与决策
不确定度评估:通过对测量结果的不确定度进行分析,可以了解测量结 果的可靠程度,为后续决策提供依据。
基于测量结果的决策:根据测量结果的评估,制定相应的决策方案。例 如,在产品质量控制中,根据测量结果判断是否合格,并采取相应的处
人员培训与技能提升
提高测量人员的专业水平
通过定期培训和考核,提高测量人员的专业知识和技能水平,确保他们能够正确 、准确地进行测量操作。
增强测量人员的质量意识
加强质量教育,使测量人员充分认识到测量误差对产品质量和客户满意度的影响 ,增强他们的质量意识和责任心。
0进行设备校准
测量设备在使用过程中会出现漂移或 磨损,定期进行设备校准可以确保测 量结果的准确性和可靠性。
测量过程的控制与优化
控制环境条件
测量过程中的环境条件(如温度、湿度、压力等)会影响测量结果的准确性, 需要严格控制环境条件以减少误差。
优化测量流程
对测量流程进行优化,减少不必要的环节和操作,可以降低误差产生的可能性 。
本课程采用了讲解、案例分析、 讨论等多种教学方法,有效地激 发了同学们的学习兴趣和参与度
,取得了良好的教学效果。
学习收获与体会
知识层面
通过对误差理论的系统学习,同 学们对测量数据的处理和分析有
了更为全面和准确的认识。
能力提升
通过课程中的实例分析和实践操作 ,同学们初步具备了运用所学知识 解决实际问题的能力。
测量误差的来源
01
02
误差分析与数据处理PPT课件

用标准差估值 :
n
(xi x)2
i1
n 1
(6—10)
式中: n 为有限次, x 为算式平均值,代替真值 T ,
x
n
xi n
i 1
2021
( sj )
T
100%
( bc )
x
100%
(6—3) (6—4)
之所以要采用相对误差来评价被测值的精度,是因为对不同的被测 值,绝对误差难以评定测量精度的高低。
2021
13
例如,采用两种方法来测量h1 100mm的尺寸,分别获得测量误
差为 L1 10m和 L2 8m,很明显后一种方法测量结果的
冲击或振动)等所造成的误差。
2021
9
过失误差的数值远远大于系统误差,已经不属于误差范围,必须 剔除掉。过失误差无规律可循,只要多加警惕,细心操作,一般都可 以避免。应当指出,上述误差可以在一定条件下相互转化。对于某一 具体误差,在一条件下是系统误差,在另一条件下可能是随机误差, 反之亦然。例如:按一定公称尺寸制造的量块,存在着制造误差,其 中就某一块量块制造的误差的数值来说,若用以进行标定或测量,所 造成的误差是系统误差;但是,就此量块整批而言,则该量块的制造
x T 测量某一参数所得的测量值 与该参数的真值 之差 为绝对误
差。即:
xT
它与被测参数有相同的单位。
测量的真值是一个理想的概念,一般是不知道的。然而在某些特定
的情况下,其真值是可知的。例如:三角形的内角和为 1 8 0 ,一个整 的圆周角为 3 6 0 。为了使用上的方便和要求,在有些情况下,可以采用
四、随机误差的评定指标
任何测试与观察总是不可避免的存在误差,这种误差具有随机性。
n
(xi x)2
i1
n 1
(6—10)
式中: n 为有限次, x 为算式平均值,代替真值 T ,
x
n
xi n
i 1
2021
( sj )
T
100%
( bc )
x
100%
(6—3) (6—4)
之所以要采用相对误差来评价被测值的精度,是因为对不同的被测 值,绝对误差难以评定测量精度的高低。
2021
13
例如,采用两种方法来测量h1 100mm的尺寸,分别获得测量误
差为 L1 10m和 L2 8m,很明显后一种方法测量结果的
冲击或振动)等所造成的误差。
2021
9
过失误差的数值远远大于系统误差,已经不属于误差范围,必须 剔除掉。过失误差无规律可循,只要多加警惕,细心操作,一般都可 以避免。应当指出,上述误差可以在一定条件下相互转化。对于某一 具体误差,在一条件下是系统误差,在另一条件下可能是随机误差, 反之亦然。例如:按一定公称尺寸制造的量块,存在着制造误差,其 中就某一块量块制造的误差的数值来说,若用以进行标定或测量,所 造成的误差是系统误差;但是,就此量块整批而言,则该量块的制造
x T 测量某一参数所得的测量值 与该参数的真值 之差 为绝对误
差。即:
xT
它与被测参数有相同的单位。
测量的真值是一个理想的概念,一般是不知道的。然而在某些特定
的情况下,其真值是可知的。例如:三角形的内角和为 1 8 0 ,一个整 的圆周角为 3 6 0 。为了使用上的方便和要求,在有些情况下,可以采用
四、随机误差的评定指标
任何测试与观察总是不可避免的存在误差,这种误差具有随机性。
现代测试技术--8 误差分析共32页

现代测试技术--8 误差分析
41、实际上,我们想要的不是针对犯 罪的法 律,而 是针对 疯狂的 法律。 ——马 克·吐温 42、法律的力量应当跟随着公民,就 像影子 跟随着 身体一 样。— —贝卡 利亚 43、法律和制度必须跟上人类思想进 步。— —杰弗 逊 44、人类受制于法律,法律受制于情 理。— —托·富 勒
45、法律的制定是为了保证每一个人 自由发 尔
31、只有永远躺在泥坑里的人,才不会再掉进坑里。——黑格尔 32、希望的灯一旦熄灭,生活刹那间变成了一片黑暗。——普列姆昌德 33、希望是人生的乳母。——科策布 34、形成天才的决定因素应该是勤奋。——郭沫若 35、学到很多东西的诀窍,就是一下子不要学很多。——洛克
41、实际上,我们想要的不是针对犯 罪的法 律,而 是针对 疯狂的 法律。 ——马 克·吐温 42、法律的力量应当跟随着公民,就 像影子 跟随着 身体一 样。— —贝卡 利亚 43、法律和制度必须跟上人类思想进 步。— —杰弗 逊 44、人类受制于法律,法律受制于情 理。— —托·富 勒
45、法律的制定是为了保证每一个人 自由发 尔
31、只有永远躺在泥坑里的人,才不会再掉进坑里。——黑格尔 32、希望的灯一旦熄灭,生活刹那间变成了一片黑暗。——普列姆昌德 33、希望是人生的乳母。——科策布 34、形成天才的决定因素应该是勤奋。——郭沫若 35、学到很多东西的诀窍,就是一下子不要学很多。——洛克
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
现代测试技术--8 误差分析
•
46、寓形宇内复几时,曷不委心任去 留。
•
47、采菊东篱下,悠然见南山。
•
48、啸傲东轩下,聊复得此生。
ห้องสมุดไป่ตู้
•
49、勤学如春起之苗,不见其增,日 有所长 。
•
50、环堵萧然,不蔽风日;短褐穿结 ,箪瓢 屡空, 晏如也 。
56、书不仅是生活,而且是现在、过 去和未 来文化 生活的 源泉。 ——库 法耶夫 57、生命不可能有两次,但许多人连一 次也不 善于度 过。— —吕凯 特 58、问渠哪得清如许,为有源头活水来 。—— 朱熹 59、我的努力求学没有得到别的好处, 只不过 是愈来 愈发觉 自己的 无知。 ——笛 卡儿
拉
60、生活的道路一旦选定,就要勇敢地 走到底 ,决不 回头。 ——左
•
46、寓形宇内复几时,曷不委心任去 留。
•
47、采菊东篱下,悠然见南山。
•
48、啸傲东轩下,聊复得此生。
ห้องสมุดไป่ตู้
•
49、勤学如春起之苗,不见其增,日 有所长 。
•
50、环堵萧然,不蔽风日;短褐穿结 ,箪瓢 屡空, 晏如也 。
56、书不仅是生活,而且是现在、过 去和未 来文化 生活的 源泉。 ——库 法耶夫 57、生命不可能有两次,但许多人连一 次也不 善于度 过。— —吕凯 特 58、问渠哪得清如许,为有源头活水来 。—— 朱熹 59、我的努力求学没有得到别的好处, 只不过 是愈来 愈发觉 自己的 无知。 ——笛 卡儿
拉
60、生活的道路一旦选定,就要勇敢地 走到底 ,决不 回头。 ——左
