14从三个方向看物体的形状级优质课

合集下载

1.4 从三个方向看物体的形状精品教案(大赛一等奖作品)

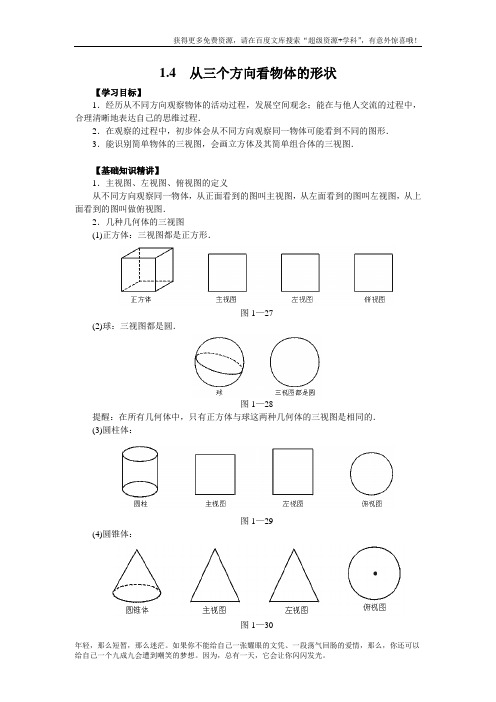
1.4 从三个方向看物体的形状【学习目标】1．经历从不同方向观察物体的活动过程，发展空间观念；能在与他人交流的过程中，合理清晰地表达自己的思维过程．2．在观察的过程中，初步体会从不同方向观察同一物体可能看到不同的图形．3．能识别简单物体的三视图，会画立方体及其简单组合体的三视图．【基础知识精讲】1．主视图、左视图、俯视图的定义从不同方向观察同一物体，从正面看到的图叫主视图，从左面看到的图叫左视图，从上面看到的图叫做俯视图．2．几种几何体的三视图(1)正方体：三视图都是正方形．图1—27(2)球：三视图都是圆．图1—28提醒：在所有几何体中，只有正方体与球这两种几何体的三视图是相同的．(3)圆柱体：图1—29(4)圆锥体：图1—30圆锥的主视图、左视图都是三角形，而俯视图的图中有一个点表示圆锥的顶点，因为从上往下看圆锥时先看到圆锥的顶点，再看到底面的圆．3．如何画三视图当用若干个小正方体搭成新的几何体，如何画这个新的几何体的三视图？(1)由照片画三视图．由照片可以清楚地看到每个小正方体的位置，这样画三视图比较直观．画三视图，都要注意从这个方向看时几何体有几列，每列有几个正方体(即有几层)，根据看到的列数、层数，画出相应的图．注意：主视图与左视图中每列的正方形都是从下往上排，底层整齐，不能出现悬空．而俯视图则有可能出现中空的现象．如右图：从正面看，2列，每列一层；从左面看，2列，每列一层；从上面看，2列，左列2层，右列一层．则三视图是：图1—31注意：照片中的几何体为了使大家看清前后情况，因此照片中的物体一般朝左偏的位置是正面．(2)由俯视图画主视图、左视图．解法一：根据俯视图摆出几何体，按照(1)的方法画主视图、左视图．解法二：直接由俯视图确定主视图、左视图的列数、层数，并画出图．①主视图与俯视图列数相同，俯视图中每列的方框内的最大数字即为主视图本列的层数．②左视图的列数与俯视图的行数相同，俯视图每一横行的方框内的最大数字，就是这一横行逆时针转90°所成的左视图中的列的层数．如：俯视图俯视图2列，则主视图也有两列，左列中的三个方框中最大的是3，右列是1，所以主视图左列三层，右列一层；俯视图三行，则左视图有三列，俯视图从上至下三行最大数字分别为1，2，3，则左视图三列从左至右分别有1，2，3层．画图如下．(3)其他几何体的三视图：从某方向看时，这个几何体最大边缘的形状及能够看到的顶点及棱．【学习方法指导】［例1］根据每组三视图，判断几何体形状：(1)先看什么比较明显呢？图1—33(2)图1—34点拨：(1)中俯视图是六边形，说明是柱或是锥，而主视图、左视图都是矩形，说明是柱即六棱柱．(2)中由主视图、左视图是三角形说明是锥体，而底面是四边形，说明不是圆锥，而是棱锥，是四棱锥．俯视图中的点是锥点，四条线段是锥的四条棱．解答：(1)六棱柱(2)四棱锥［例2］用长∶宽∶高＝3∶1∶1的两个长方体如图1—35摆放，画出三视图．图1—35点拨：只要把较长的长方体看作由三个正方体排起来的即可，主视图左部分三份，右部分一份，都只有一层；左视图两列，左列1份，右列两份(挡住一份)；俯视图是两个长3份的长方形交叉放．三视图如下：［例3］用小立方体搭成一个几何体，使它的主视图和俯视图如图所示．搭建这样的几何体，最多要几个小立方体？最少要几个小立方体？图1—37点拨：①由于主视图每列的层数即是俯视图中该列的最大数字，因此，用的方块数最多的情况是每个方框都用该列的最大数字．即如图1—36所示；此种情况共用小立方体17块．图1—36图1—37②而搭建这样的几何体，每列只要有一个最大数字即可满足条件，其他方框内的数字可减少到最少的1，即如图1—37所示；这样的摆法只需立方体11块．解：摆这样的几何体，最多用17块立方体，最少用11块立方体．【拓展训练】某几何体左视图是长方形，说出这个几何体的两种可能性．点拨：对于棱柱，长方体的左视图可以是长方形；而圆柱，也可以符合条件．说明：考虑这类问题，可先从柱、锥、球开始，再往下细分，逐步排除不可能的，缩小思考范围．专题14 相交线与平行线、三角形及尺规作图学校：___________姓名：___________班级：___________一、选择题：（共4个小题）1．【2015凉山州】如图，将一块三角板的直角顶点放在直尺的一边上，当∠2=38°时，∠1=（）A．52° B．38° C．42° D．60°【答案】A．【解析】试题分析：如图：∵∠3=∠2=38°（两直线平行同位角相等），∴∠1=90°﹣∠3=52°，故选A．【考点定位】平行线的性质．2．【2015德阳】如图，在五边形ABCDE中，AB=AC=AD=AE，且AB∥ED，∠EAB=120°，则∠D CB=（）A．150° B．160° C．130° D．60°【答案】A．【解析】【考点定位】1．等腰三角形的性质；2．平行线的性质；3．多边形内角与外角．3．【2015德阳】如图，在Rt △ABC 中，∠ACB =90°，CD 为AB 边上的高，若点A 关于CD 所在直线的对称点E 恰好为AB 的中点，则∠B 的度数是（）A．60° B．45° C．30° D．75°【答案】C．【解析】试题分析：∵在Rt △ABC 中，∠ACB =90°，CD 为AB 边上的高，点A 关于CD 所在直线的对称点E 恰好为AB 的中点，∴∠CED =∠A ，CE =BE =AE ，∴∠ECA =∠A ，∠B =∠BCE ，∴△ACE 是等边三角形，∴∠CED =60°，∴∠B =12∠CED =30°．故选C．【考点定位】1．直角三角形斜边上的中线；2．轴对称的性质． 4．【2015眉山】如图，在Rt △ABC 中，∠B =900，∠A =300，DE 垂直平分斜边AC ，交AB 于D ，E 是垂足，连接CD ．若BD =l ，则AC 的长是（）A ．32B ．2C ．34D ．4【答案】A．【解析】【考点定位】1．含30度角的直角三角形；2．线段垂直平分线的性质；3．勾股定理．二、填空题：（共4个小题）5．【2015绵阳】如图，AB∥CD，∠CDE=119°，GF交∠DEB的平分线EF于点F，∠AGF=130°，则∠F= ．【答案】9.5°．【解析】试题分析：∵AB∥CD，∠CDE=119°，∴∠AED=180°﹣119°=61°，∠DEB=119°．∵GF交∠DEB的平分线EF于点F，∴∠GEF=12×119°=59.5°，∴∠GEF=61°+59.5°=120.5°．∵∠AGF=130°，∴∠F=∠AGF﹣∠GEF=130°﹣120.5°=9.5°．故答案为：9.5°．【考点定位】平行线的性质．6．【2015乐山】如图，在等腰三角形ABC中，AB=AC，DE垂直平分AB，已知∠ADE=40°，则∠DBC= °．【答案】15．【解析】试题分析：∵DE垂直平分AB，∴AD=BD，∠AED=90°，∴∠A=∠ABD，∵∠ADE=40°，∴∠A=90°﹣40°=50°，∴∠ABD=∠A=50°，∵AB=AC，∴∠ABC=∠C=12（180°﹣∠A）=65°，∴∠DBC=∠ABC﹣∠ABD=65°﹣50°=15°，故答案为：15．【考点定位】1．线段垂直平分线的性质；2．等腰三角形的性质．7．【2015巴中】如图，在△ABC中，AB=5，AC=3，AD、AE分别为△ABC的中线和角平分线，过点C作CH⊥AE于点H，并延长交AB于点F，连结DH，则线段DH的长为．【答案】1．【解析】【考点定位】1．三角形中位线定理；2．等腰三角形的判定与性质．8．【2015攀枝花】如图，在边长为2的等边△ABC中，D为BC的中点，E是AC边上一点，则BE +DE的最小值为．．【解析】试题分析：作B关于AC的对称点B′，连接BB′、B′D，交AC于E，此时BE+ED=B′E+ED=B′D ，根据两点之间线段最短可知B′D就是BE+ED的最小值，∵B、B′关于AC的对称，∴AC、BB ′互相垂直平分，∴四边形ABCB′是平行四边形，∵三角形ABC是边长为2，∵D为BC的中点，∴AD⊥BC，∴AD=，BD=CD=1，BB′=2AD=B′G⊥BC的延长线于G，∴B′G=AD在Rt△B′BG中，BG DG=BG﹣BD=3﹣1=2，在Rt△B′DG中，BD．故BE+ED．【考点定位】1．轴对称-最短路线问题；2．等边三角形的性质；3．最值问题；4．综合题．三、解答题：（共2个小题）9．【2015广安】手工课上，老师要求同学们将边长为4cm的正方形纸片恰好剪成六个等腰直角三角形，聪明的你请在下列四个正方形中画出不同的剪裁线，并直接写出每种不同分割后得到的最小等腰直角三角形面积（注：不同的分法，面积可以相等）【答案】答案见试题解析．【解析】（2）正方形A BCD中，E、F分别是AB、BC的中点，O是AC、BD的交点，连接OE、OF，即可把正方形纸片恰好剪成六个等腰直角三角形；然后根据三角形的面积公式，求出分割后得到的最小等腰直角三角形面积即可；（3）正方形ABCD中，F、H分别是BC、DA的中点，O是AC、BD的交点，连接HF，即可把正方形纸片恰好剪成六个等腰直角三角形；然后根据三角形的面积公式，求出分割后得到的最小等腰直角三角形面积即可；试题解析：根据分析，可得：．（1）第一种情况下，分割后得到的最小等腰直角三角形是△AEH、△BEF、△CFG、△DHG，每个最小的等腰直角三角形的面积是：（4÷2）×（4÷2）÷2=2×2÷2=2（cm2）；（2）第二种情况下，分割后得到的最小等腰直角三角形是△AEO、△BEO、△BFO、△CFO，每个最小的等腰直角三角形的面积是：（4÷2）×（4÷2）÷2=2×2÷2=2（cm2）；（3）第三种情况下，分割后得到的最小等腰直角三角形是△AHO、△DHO、△BFO、△CFO ，每个最小的等腰直角三角形的面积是：（4÷2）×（4÷2）÷2=2×2÷2=2（cm2）；（4）第四种情况下，分割后得到的最小等腰直角三角形是△AEI、△OEI，每个最小的等腰直角三角形的面积是：（4÷2）×（4÷2）÷2÷2=2×2÷2÷2=1（cm2）．【考点定位】1．作图—应用与设计作图；2．操作型．10．【2015重庆市】如图1，在△ABC中，∠ACB=90°，∠BAC=60°，点E是∠BAC角平分线上一点，过点E作AE的垂线，过点A作AB的垂线，两垂线交于点D，连接DB，点F是BD的中点，DH⊥AC，垂足为H，连接EF，HF．（1）如图1，若点H是AC的中点，AC=AB，BD的长；（2）如图1，求证：HF=EF；（3）如图2，连接CF，CE．猜想：△CEF是否是等边三角形？若是，请证明；若不是，说明理由．【答案】（1）AB =BD =【解析】试题解析：（1）∵∠ACB =90°，∠BAC =60°，∴∠ABC =30°，∴AB =2AC =2×∵AD ⊥AB ，∠CAB =60°，∴∠DAC =30°，∵AH =12AC =，∴AD =cos30AH=2，∴BD =（2）如图1，连接AF ，∵AE 是∠BAC 角平分线，∴∠HAE =30°，∴∠ADE =∠DAH =30°，在△DAE 与△ADH 中，∵∠AHD =∠DEA =90°，∠ADE =∠DAH ，AD =A D ，∴△DAE ≌△ADH ，∴DH =AE ，∵点F 是BD 的中点，∴DF =AF ，∵∠EAF =∠EAB ﹣∠FAB =30°﹣∠FAB ，∠FDH =∠FDA ﹣∠HD A =∠FDA ﹣60°=（90°﹣∠FBA ）﹣60°=30°﹣∠FBA ，∴∠EAF =∠FDH ，在△DHF 与△AEF 中，∵DH =AE ，∠HDF =∠EAH ，DF =AF ，∴△DHF ≌△AEF ，∴HF =EF ；（3）如图2，取A B 的中点M ，连接CM ，FM ，在R t △ADE 中，AD =2AE ，∵DF =BF ，AM =BM ，∴AD =2FM ，∴FM =AE ，∵∠ABC =30°，∴AC =CM =12AB =AM ，∵∠CAE =12∠CAB =30°∠CMF =∠AMF ﹣∠AMC =30°，在△ACE 与△MCF 中，∵AC =CM ，∠CAE =∠CMF ，AE =MF ，∴△ACE ≌△MCF ，∴CE =CF ，∠ACE =∠MCF ，∵∠ACM =60°，∴∠ECF =60°，∴△CEF 是等边三角形．【考点定位】1．全等三角形的判定与性质；2．等边三角形的判定与性质；3．三角形中位线定理；4．探究型．。

从三个方向看物体的形状优秀教案

从三个方向看物体的形状【教学目标】1．经历从不同方向观察物体的活动过程，体会出从不同方向看同一物体，可能看到不同的结果；能识别从不同方向看几何体得到相应的平面图形。

2．通过观察能画出不同角度看到的平面图形（三视图）。

【教学重难点】1．重点：学会从不同方向看实物的方法，画出三视图。

2．难点：画出三视图，由三视图判断几何体。

【教学准备】正方体模型。

【教学过程】一、定向示标：教师演示庐山景观，请学生背诵苏东坡《题西林壁》，并说说诗中意境。

并出现：横看成岭侧成峰，远近高低各不同。

不识庐山真面目，只缘身在此山中。

生：观赏美景，思考“岭”与“峰”的区别。

导入语：多美的山，多美的诗！诗情画意来自作者苏东坡从多个角度对庐山的仔细观察。

从哪些角度呢？生：横看，侧看，远看，近看，在山中看。

师：回答得非常好！可能有些同学会纳闷，今天老师上数学课怎么会念起古诗来？其实，苏东坡通过作这首诗，教给了我们观察祖国大好山河的方法：从多个角度仔细观察，才能发现庐山奇妙、壮观的美丽景色。

这就是我们这节课将要学习的内容——《从三个方向看物体的形状》。

看什么呢？看生活中熟悉的物体和数学中熟悉的简单几何体。

然后教师板书课题并出示学习目标二、自学指导：下面请同学们认真看课本内容，能否通过观察和抽象思维来回答完成问题：（一）看课本的图1~21，你能分别说出A、B、C、D每台摄像机拍到的是哪一张照片吗？你是如何得出这个结论的？（二）看课本的图1~22，你能画出从正面、左面、上面看到的几何体的形状图吗？（要给予充分的活动时间，以便学生进行尝试和交流体验，通过小组活动，培养学生团结协作精神。

）探究二：如图是由几个小立方体块所搭几何体的从上面看几何体的形状图，小正方形中的数字表示在该位置小立块的个数，请画出从正面、左面看到的这个几何体的形状图。

师：你对小正方形中的数字如何理解？你是怎样画出的？学生学习小组活动，用小立方体搭几何模型，然后根据几何模型画出几何体的形状图。

1.4 从三个方向看物体的形状(市级优质课)(共54张PPT)

棱柱
圆锥
棱锥
·
2019/7/15
试举出正视图是圆的立体图形。
答：圆柱、球、圆锥。
注意：（1）单一视图可能有多种形状的立体图形。
（2）由视图描述物体形状须齐备三种视图。
2019/7/15
下面一个物体的三视图，请说出该物体形状的名称．
直三棱柱三视图中有两个是长方形的几何体
圆柱体柱体
2019/7/15
A．三棱锥 B．五棱柱 C．五棱锥 D．三棱柱
2019/7/15
4．如图所示是由几个相同的小正方形搭成的几何体的三视图，则搭成这个几何体的小正方体的个数是（）
A．2个 B． 3个 C． 4个 D． 5个
主视图
2019/7/15
左视图
俯视图
2
2019/7/15
球体圆柱
原图
主视图
俯视图
左视图
一个几何体由几个大小相同的小立方块搭成。
这个几何体的三视图如图所示。请你搭出满足条件的几何体。你搭的几何体由几个小立方块构成的？与同伴进行交流。
2019/7/15
主视图
21 11
俯视图
左视图
一个几何体由几个大小相同的小立方体块搭成。这个几何体的俯视图和左视图如图所示。 1、你能搭出满足条件的几何体吗？
主视图
左视图
俯视图
B
A
2019/7/15
展开
立体图形
平面图形
围成
2019/7/15
请你试一试。
俯视图
2、这样的几何体至少需要 5
左视图
个小立方体。
这样的几何体最多需要 6 个小立方体。
2019/7/15
2、下列几何体中，同一个几何体的主视图与俯视图不同的是（）

1.4从三个方向看物体的形状(省优质课)讲解

每一个物体都有三视图。
从正面看到的图形从左面看到的图形从上面看到的图形
叫主视图，叫左视图，叫俯视图。
思考
当知道某物体的几何体时，你能否画出该几何体的三视图？
30.09.2020
四棱锥
主视图
30.09.2020
左视图
俯视图
30.09.2020
30.09.2020
主视图
三视左视图图俯视图
1.4从三个方向看物体的形状
30.09.2020
教学目标
能画出从不方向观察几何体的平面图形(三视图).
由三视图想象出立体图形经历立体图形与平面图形互相转
化的过程.
30.09.2020
30.09.2020
你认识吗？
30.09.2020
30.09.2020
他们为什么会出现争执？
30.09.2020
漫画 “6”与“9”
本课预习要点：
1、现在我们学习了从不同方向看同一物体。并得知 “从不同方向观察同一物体时，可能看到不同的图形 ”
。 2、观察三种形状时，我们应站在观察者的角度想象，画出从三个方向看到的_____平_图面形，而不能站在自己的角
度。 3、数学中我们只从三个不同方向看同一物体，所以，
从上面看
30.09.2020
主视图左视图
俯视图
30.09.2020
主视图
左视图
俯视图
30.09.2020
三视图的对应规律
主视图和俯视图长对正主视图和左视图高平齐俯视图和左视图宽相等
30.09.2020
考考你
主视图（ A ）左视图（ A ）俯视图（ B ）
A
30.09.2020

北师大版七年级数学上册1.4 从三个方向看物体的形状公开课优质教案(7)

1.4从不同的方向看【学习目标】课标要求：1、能识别简单物体的三视图，会画立方体及其简单组合的三视图，能根据三视图描述基本几何体或实物原形。

2、、经历“从不同方向观察物体”的活动过程，发展学生的空间概念和合理的想象；在观察过程中，初步体会从不同方向观察同一物体得到的结果是不一样的；让学生学会用自己的语言、合理清晰地向别人表述自己的思维过程，能画出简单组合物体的三视图。

3、培养学生重视实践、善于观察的习惯,在与他人合作、交流时和谐、友好地相处。

目标达成：能识别简单物体的三视图，会画立方体及其简单组合的三视图，能根据三视图描述基本几何体或实物原形学习流程：【课前展示】书中引例【创境激趣】观看《盲人摸象》的故事，提请学生思考：为什么不同的盲人得出不同的大象形状？认识物体，当然一个十分重要的方法是看、观察，那么不同的角度观察是否也会得到不同的感受呢？【自学导航】教师在展示台上放置三样物体（球、水瓶、水杯），使它们在一条直线上，水瓶在中间，要求学生坐在自己的位置上观察，并说说你实际看到了什么？并在学生回答的基础上，请学生思考：同样的三样物体，为什么看到的不是一样的呢？从而引出课题“从不同方向看”。

【合作探究】辨别活动：小华、小彬也和我们一样在观察，你知道四幅图中哪幅图是小华看到的？哪幅图是小彬看到的吗（媒体展示图片）？学生口述结论，并说出判断的理由。

并适时地提出新的问题，如“要同时看到兵乓球、水杯、水瓶，那么我们应该站在什么位置呢？”【展示提升】典例分析知识迁移教师在展示台上出示正方体、长方体和锥体的几何模型，要求学生思考：（1）在自己的位置上能看到什么，把看到的结果和同学交流一下，你们看到的是否一样？（2）五幅图分别是从什么方向上观察到的结果？【强化训练】汽车从小明身边经过，小明最先看到什么，然后呢？按先后顺序给这几幅图标上序号。

（多媒体展示汽车行驶的画面）【归纳总结】通过本节课的学习，你有哪些收获?【板书设计】①② ③ ④ ⑤。

《从三个方向看物体的形状》教案 (公开课)2022年2

1.4 从三个方向看物体的形状一、学习方式1．学习方法〔1〕通过教师设置的问题情境〔转动的小人玩具、由远而近的汽车、三人从不同方向观察同一生活用品〕引起对“从不同方向观察同一物体得到不同结果〞这一问题的关注。

〔2〕通过从不同方向观察三个几何体，交流、讨论、师生问答，进一步分析“从不同方向看〞的不同结果。

〔3〕通过小组活动，观察相同的几个正方体摆出的几何图形，逐步升华到识别简单的三视图以及用简单的三视图表示其结果。

2．学习倾向通过自己观察、动手摆放、自由改变角度、小组成员的相互交流，自然融入学习气氛当中，形成对“从不同方向看〞这一问题的正确认识。

二、学习任务分析1．学生的认知起点〔1〕已有的生活体验。

〔2〕对常见的较为规那么的几何图形的认识。

从不同方向观察物体进一步从正、左、右、前、后五个方向观察几何体、正方体、四棱锥、长方体。

〔3〕简单的画图能力。

2．学习任务三、教学目标1．认识从不同方向观察物体，会有不同的结果。

2．学会从正面、左面、上面观察几何体并会识别简单的三视图。

3．初步学会画简单的三视图。

4．在探索、思考的过程中培养学生辩证法思想，学会多侧面观察事物。

四、教学重点和难点重点：经历观察、探索、思考的过程，认识从不同方向看到不同结果，会识别并绘制简单三视图。

难点：建立“多侧面观察事物〞的思维习惯，在分析数学问题和处理生活中的事情时，做到不以偏概全。

五、教学过程表12.4有理数的加法〔1〕二、教学目标1．使学生掌握有理数加法法那么，并能运用法那么进行计算；2．在有理数加法法那么的教学过程中，注意培养学生的观察、比较、归纳及运算能力．三、教学重点和难点重点：有理数加法法那么．难点：异号两数相加的法那么．四、教学手段现代课堂教学手段五、教学方法启发式教学六、教学过程〔一〕、师生共同研究有理数加法法那么前面我们学习了有关有理数的一些根底知识，从今天起开始学习有理数的运算．这节课我们来研究两个有理数的加法．两个有理数相加，有多少种不同的情形？为此，我们来看一个大家熟悉的实际问题：足球比赛中赢球个数与输球个数是相反意义的量．假设我们规定赢球为“正〞，输球为“负〞．比方，赢3球记为+3，输2球记为-2．学校足球队在一场比赛中的胜负可能有以下各种不同的情形：(1)上半场赢了3球，下半场赢了2球，那么全场共赢了5球．也就是(+3)+(+2)=+5．①(2)上半场输了2球，下半场输了1球，那么全场共输了3球．也就是(-2)+(-1)=-3．②现在，请同学们说出其他可能的情形．答：上半场赢了3球，下半场输了2球，全场赢了1球，也就是(+3)+(-2)=+1；③上半场输了3球，下半场赢了2球，全场输了1球，也就是(-3)+(+2)=-1；④上半场赢了3球下半场不输不赢，全场仍赢3球，也就是(+3)+0=+3；⑤上半场输了2球，下半场两队都没有进球，全场仍输2球，也就是(-2)+0=-2；上半场打平，下半场也打平，全场仍是平局，也就是0+0=0．⑥上面我们列出了两个有理数相加的7种不同情形，并根据它们的具体意义得出了它们相加的和．但是，要计算两个有理数相加所得的和，我们总不能一直用这种方法．现在我们大家仔细观察比较这7个算式，看能不能从这些算式中得到启发，想方法归纳出进行有理数加法的法那么？也就是结果的符号怎么定？绝对值怎么算？这里，先让学生思考2～3分钟，再由学生自己归纳出有理数加法法那么：1．同号两数相加，取相同的符号，并把绝对值相加；2．绝对值不相等的异号两数相加，取绝对值较大的加数符号，并用较大的绝对值减去较小的绝对值，互为相反数的两个数相加得0；3．一个数同0相加，仍得这个数．〔二〕、应用举例变式练习例1 计算以下算式的结果，并说明理由：(1)(+4)+(+7)； (2)(-4)+(-7)； (3)(+4)+(-7)；(4)(+9)+(-4)；(5)(+4)+(-4)； (6)(+9)+(-2)； (7)(-9)+(+2)；(8)(-9)+0；(9)0+(+2)； (10)0+0．学生逐题口答后，教师小结：进行有理数加法，先要判断两个加数是同号还是异号，有一个加数是否为零；再根据两个加数符号的具体情况，选用某一条加法法那么．进行计算时，通常应该先确定“和〞的符号，再计算“和〞的绝对值．解：(1) (-3)+(-9) (两个加数同号，用加法法那么的第2条计算)=-(3+9) (和取负号，把绝对值相加)=-12．下面请同学们计算以下各题：(1)(-0.9)+(+1.5)； (2)(+2.7)+(-3)； (3)(-1.1)+(-2.9)；全班学生书面练习，四位学生板演，教师对学生板演进行讲评．〔三〕、小结这节课我们从实例出发，经过比较、归纳，得出了有理数加法的法那么．今后我们经常要用类似的思想方法研究其他问题．应用有理数加法法那么进行计算时，要同时注意确定“和〞的符号，计算“和〞的绝对值两件事．七、练习设计1．计算：(1)(-10)+(+6)； (2)(+12)+(-4)； (3)(-5)+(-7)； (4) (+6)+(+9)；(5)67+(-73)； (6)(-84)+(-59)； (7)33+48；(8)(-56)+37．2．计算：(1)(-0.9)+(-2.7)； (2)3.8+(-8.4)；(3)(-0.5)+3；(4)3.29+1.78； (5)7+(-3.04)；(6)(-2.9)+(-0.31)；(7)(-9.18)+6.18； (8)4.23+(-6.77)；(9)(-0.78)+0．4*．用“＞〞或“＜〞号填空：(1)如果a＞0，b＞0，那么a+b ______0；(2)如果a＜0，b＜0，那么a+b ______0；(3)如果a＞0，b＜0，|a|＞|b|，那么a+b ______0；(4)如果a＜0，b＞0，|a|＞|b|，那么a+b ______0．5*．分别根据以下条件，利用|a|与|b|表示a与b的和：(1)a＞0，b＞0； (2) a＜0，b＜0；(3)a＞0，b＜0，|a|＞|b|； (4)a＞0，b＜0，|a|＜|b|．八、板书设计九、教学后记“有理数加法法那么〞的教学，可以有多种不同的设计方案．大体上可以分为两类：一类是较快地由教师给出法那么，用较多的时间(30分钟以上)组织学生练习，以求熟练地掌握法那么；另一类是适当加强法那么的形成过程，从而在此过程中着力培养学生的观察、比较、归纳能力，相应地适当压缩应用法那么的练习，如本教学设计．现在，试比较这两类教学设计的得失利弊．第一种方案，教学的重点偏重于让学生通过练习，熟悉法那么的应用，这种教法近期效果较好．第二种方案，注重引导学生参与探索、归纳有理数加法法那么的过程，主动获取知识．这样，学生在这节课上不仅学懂了法那么，而且能感知到研究数学问题的一些根本方法．这种方案减少了应用法那么进行计算的练习，所以学生掌握法那么的熟练程度可能稍差，这是教学中应当注意的问题．但是，在后续的教学中学生将千万次应用“有理数加法法那么〞进行计算，故这种缺陷是可以得到弥补的．第一种方案削弱了得出结论的“过程〞，失去了培养学生观察、比较、归纳能力的一次时机．权衡利弊，我们主张采用第二种教学方。

14从三个方向看物体的形状 ppt课件

2020/12/12
只不远横题
缘识近看身庐高成
西林壁
在山低岭
——
此真各侧
山面不成
中。
目，
同峰，苏。轼
1
1.为什么同是这几个娃娃，拍出来的照片会不同？
2.你知道每张照片分别是站在哪个方向拍的吗？
2020/12/12
2
精品资料
• 你怎么称呼老师？
• 如果老师最后没有总结一节课的重点的难点，你是否会认为老师的教学方法需要改进？
从正面看
从左面看
2020/12/12
21
课堂小结
通过本节的学习, 我们学会了哪些知识？
2020/12/12
22
习题1.6知识技能:1,2,3,4.
2020/12/12
23
1、如右图所示的礼品盒，你
哦知道下面的三幅图分别是从左面
，礼品
哪个方向看到的吗？你能说出这三幅视图的名称吗？
盒
，
2020/12/12
9
从左面看
2020/12/12
从
上从正面看
面看
从左面看
从上面看
当我们从不同方向观察同一物体
时，通常可以看到不同的平面图
形。
10
从正面看高
长
从上面看
2020/12/12
从左面看
思路点拨
1、从正面看反映原
宽
图的长和高
2、从左面看反映原图的高和宽
3、从上面看反映原图的长和高
19
归纳：
13 21
从上面看
看列，取大数，左右相对应左画两个，右画三个
从正面看

从三个方向看物体的形状初中数学经典课件

)
正面
A.
B.
C.
D.
随堂练习
A 2.从左面看如图所示的几何体,得到的平面图形是(
)
随堂练习
D 3.如图是从三个方向看某几何体的平面图形，则这个几何体是（）
A.三棱柱
B.三棱锥
C.圆柱
D.圆锥
从正面看
从左面看
从上面看
随堂练习
4.如下图是由几个小立方块所搭几何体，从上面看的平面图形如下图，小正
第4课
从三个方向看物体的形状
学习目标
1.初步体会从不同方向观察物体可能看到不同的图形,发展空间观念 2.能识别从三个方向看到的物体的形状图,会画立方体及其简单组合体从三个方向看到的形状图. 3.能在与他人交流的过程中,合理清晰地表达自己的思维过程
重难点
重点：会画正方体及其简单组合体从三个不同方向看到的形状图难点：能根据三种从三个不同方向看到的形状图描述基本几何体或实物原形
随堂练习
解：（1）10块；（2）
（3）6+6+6+5+5+6+3+3=40(cm2).
本课小结
从三个方向看物体的形状
从不同的方向观察立体图形
由从不同方向看到的物体形状图确定实物形状
从正面看从左面看从上面看
根据从前面看到的图形、从上面看到的图形和从左边看到的图形想象立体图形的前面、上面和左侧面的局部形状，然后再综合起来考虑整体图形．
学以致用
由几个相同的小立方块搭成一个几何体，它的三个形状图如下所示，求这个几何体是由多少个小立方块搭成的，并在从它上面看到的形状图上体现小立方块的个数.
从正面看
从左面看

《从三个方向看物体的形状》word教案 (公开课获奖)2022北师版 (9)

1.4 从三个方向看物体的形状教学目标1、知识技能：能识别简单物体的三视图，会画立方体及其简单组合的三视图，能根据三视图描述基本几何体或实物原形。

2、过程目标：经历“从不同方向观察物体”的活动过程，发展学生的空间概念和合理的想象；在观察过程中，初步体会从不同方向观察同一物体得到的结果是不一样的；能画出简单组合物体的三视图。

3、情感目标：培养学生重视实践、善于观察的习惯,在与他人合作、交流时和谐、友好地相处。

学情分析学生刚从小学升到中学，思维以形象思维为主，抽象水平较低。

从不同的方向看，也正是立足于此，主要是引导学生从不同的角度观察几何体，因而多为直观的操作、感受，当然也需要进行一定的抽象，如将从某个角度正视的结果抽象成视图，因而具有一定的抽象要求，但这样的抽象水平相对较低，学生应该已经具备这样的认知基础了。

重难点重点：会画立方体及其简单组合的三种图形难点：根据从上面看的形状图及其相应位置的立方体的数量，画出从正面看与从左面看的形状图。

教法启发式教学学法自主、合作学习教学程序及内容一、创设情景、激发兴趣利用多媒体演示，使学生切身感受从不同的方向看到的物体时不同的。

横看成岭侧成峰，远近高低各不同，不识庐山真面目，只缘身在此山中这一首苏东坡的诗表现了观察庐山的几种方式：横看、侧看、远看、近看、身处山中看，也说明了观察物体是有讲究的，《从不同方向看》这节课就是学习和研究观察物体的数学方法。

第二环节：观察实物、探究新知活动1：让学生观察这五张图片，回答分别是从哪个方位看到的？并在学生回答的基础上，请学生思考：同样的物体，为什么看到的不是一样的呢？揭示课题《从不同方向看》。

我们从不同的方向观察同一物体时，通常可以看到不同的图形。

第三环节：想想练练、巩固提高活动1：画出下面几何体的从正面看、左面看、上面看所看到的图。

个人修订意见由学生分组，每人摆出一个立方体，所有人都画出这个立体图形的三视图，比较谁画的又快又对。

《从三个方向看物体的形状》PPT课件 (公开课获奖)2022年北师大版 (6)

解去括号，得 3x2-3x=2x-4-4
移项，合并同类项，得方程的一般形式：
3x2-5x+8=0 它的二次项系数是3，一次项系数是-5，常数项是8
1、填空：
方程
一般式
x2-4x-3=0 x2-4x-3=0
0.5x2= 5
0.5x2-√5 =0
2 y-4y2=0 -4y2 +√2y =0
(2x)2=(x+1)2 3x2-2x-1=0
从上面看
从前面看
从左面看
从上面看
从前面看
从你所在的位置看这组几何体，看到的是什么样子？能否把你所看到的样子画下来？
1 正看三条边，侧看三条边，上看圆圈圈，就是没直边（打一几何体）________． 2 我是一个几何体，从前面看和左面看我都是长方形，猜猜我是谁？ ________．
从上面看
认识一元二次方程
问题1
5x-15=0
这是一个什么样的方程？
只含有一个未知数（元），并且未知数的次数是1的整式方程叫一元一次方程（linear equation with one unknown）
问题2 大明休闲中心有一个长为10m，宽为6m的游泳池，
现想将游泳池的面积改造成35m2，若长宽同时减少相同的长度，问减少多少米？
解：设减少x米，则长为(10-x)米，宽为(6-x)米
(10-x)(6-x)=35
10 x
X2-16x+25=0
想一想
10-x
6
6-x
x
这个方程与以前所学的一元一次方程有什么异同？
5x-15=0
①
X2-16x+25=0
②
相同点：方程两边都是整式;都含有一个未知数

《从三个方向看物体的形状》教案 (公开课)2022年 (2)

从三个方向看物体的形状教学实录课前准备：教具：多媒体课件、照片〔校园运动场一角〕四张、水瓶1、乒乓球1、圆住体1、自制长方体1、正方体5学具：〔按学习小组准备〕玩具汽车1、自制长方体1、正方体5、圆锥体1等。

教学过程：师：同学们，我们一起来看四张照片〔电脑投影照片〕，请说说照片上拍的是哪个地方的景物？生：是我们学校篮球场。

师：看看这几张照片是一样的吗？生：不是，是因为老师拍摄时选择的地点不同，是从不同的方向拍下来的。

师：very good！这节课让我们一起来研究从不同方向观察物体的问题。

〔板书：从不同方向看〕[摆出一组物体：乒乓球、小瓶、水杯，并站在不同角度观察]师：说说老师应该看到什么样的图形。

生：〔纷纷举手，发表自己的见解〕师：同学们说得很好。

通过刚刚的观察和说明，我们可以看出从不同方向观察物体可以看到不同的图形。

师：下面请各小组同学利用现有的物体摆放不同的组合，并讨论从不同方向看到的图形。

生：摆物体，积极活动，剧烈讨论，交流。

师：通过刚刚的实际操作，谈谈你有什么体会？生：真正理解了老师说的“从不同方向观察物体可以看到不同的图形〞。

师：Good!Good!下面请同学们看老师给出的五幅图片，再观察老师摆出的一组物体组合，请大家讨论一下，这五幅图片分别是从什么方向看到的。

生：〔小组讨论，交流〕师：请各小组派代表发表小组意见。

生：五幅图分别是从方向看到的。

师：答复非常正确，各小组分别加10分，这说明有了物体组合和图片就能判断出观测方向，下面老师摆出一个组合体，请同学们试试说明你从上、左、前三个方向观察分别能看到什么样的图形，可以下位观察验证。

〔用五个正方体摆〕生：〔小组讨论，说明从三个方向看到的图形，也有的下位验证，然后分组发言〕。

师：非常好，从不同方向观察物体可能看到不同的图形，我们把从正面看到的图形称为主视图；从左面看到的图形称为左视图；从上面看到的图形称为俯视图。

下面请同学们画出老师摆出的物体的主视图、左视图、俯视图。