易错点:对随机事件、必然事件和不可能事件判断不清
新人教版九年级上册数学[随机事件和概率--知识点整理及重点题型梳理]
![新人教版九年级上册数学[随机事件和概率--知识点整理及重点题型梳理]](https://img.taocdn.com/s3/m/721dc7c9f61fb7360a4c6512.png)
新人教版九年级上册初中数学重难点有效突破知识点梳理及重点题型巩固练习随机事件和概率--知识讲解【学习目标】1、通过对生活中各种事件的判断,归纳出必然事件、不可能事件和随机事件的特点,并根据这些特点对有关事件作出准确判断;2、初步理解概率定义,通过具体情境了解概率意义.【要点梳理】要点一、必然事件、不可能事件和随机事件【 391875 名称:随机事件与概率初步:随机事件】1.定义:(1)必然事件在一定条件下重复进行试验时,在每次试验中必然会发生的事件,叫做必然事件.(2)不可能事件在每次试验中都不会发生的事件叫做不可能事件.(3)随机事件在一定条件下,可能发生也可能不发生的事件,称为随机事件.要点诠释:1.必然发生的事件和不可能发生的事件均为“确定事件”,随机事件又称为“不确定事件”;2.要知道事件发生的可能性大小首先要确定事件是什么类型.一般地,必然发生的事件发生的可能性最大,不可能发生的事件发生的可能性最小,随机事件发生的可能性有大有小,不同的随机事件发生的可能性的大小有可能不同.要点二、概率的意义概率是从数量上刻画了一个随机事件发生的可能性的大小.一般地,在大量重复试验中,如果事件A发生的频率会稳定在某个常数附近,那么这个常数就叫做事件A的概率(probability),记为.要点诠释:(1)概率是频率的稳定值,而频率是概率的近似值;(2)概率反映了随机事件发生的可能性的大小;(3) 事件A的概率是一个大于等于0,且小于等于1的数,,即,其中P(必然事件)=1,P(不可能事件)=0,0<P(随机事件)<1.【典型例题】类型一、随机事件1.(1)指出下列事件中,哪些是不可能事件?哪些是必然事件?哪些是随机事件?①若 a、b、c都是实数,则a(bc)=(ab)c;②没有空气,动物也能生存下去;③在标准大气压下,水在 90℃时沸腾;④直线 y=k(x+1)过定点(-1,0);⑤某一天内电话收到的呼叫次数为 0;⑥一个袋内装有形状大小完全相同的一个白球和一个黑球,从中任意摸出 1个球则为白球.【答案与解析】①④是必然事件;②③是不可能事件;⑤⑥是随机事件.【总结升华】准确掌握定义,依据定义判别.【 391875 名称:随机事件与概率初步:经典例题1】举一反三【变式1】下列事件是必然事件的是( ).A.明天要下雨;B.打开电视机,正在直播足球比赛;C.抛掷一枚正方体骰子,掷得的点数不会小于1;D.买一张彩票,一定会中一等奖.【答案】C.【变式2】下列说法中,正确的是( ).A.生活中,如果一个事件不是不可能事件,那么它就必然发生;B.生活中,如果一个事件可能发生,那么它就是必然事件;C.生活中,如果一个事件发生的可能性很大,那么它也可能不发生;D.生活中,如果一个事件不是必然事件,那么它就不可能发生.【答案】C.2. 在一个不透明的口袋中,装有10个除颜色外其它完全相同的球,其中5个红球,3个蓝球,2个白球,它们已经在口袋中搅匀了.下列事件中,哪些是必然发生的?哪些是不可能发生的?哪些是可能发生的?(1)从口袋中任取出一个球,它恰是红球;(2)从口袋中一次性任意取出2个球,它们恰好全是白球;(3)从口袋中一次性任意取出5个球,它们恰好是1个红球,1个蓝球,3个白球. 【答案与解析】(1)可能发生,因为袋中有红球;(2)可能发生,因为袋中刚好有2个白球;(3)不可能发生,因为袋中只有2个白球,取不出3个白球.【总结升华】了解并掌握三种事件的区别和联系.举一反三【变式】甲、乙两人做掷六面体骰子的游戏,双方规定,若掷出的骰子的点数大于3,则甲胜,若掷出的点数小于3,则乙胜,游戏公平吗?若不公平,请你设计出一种对于双方都公平的游戏.【答案】不公平,小于3的点数有1、2,大于3的点数有4、5、6,因此,它们的可能性是不同的,所以不公平.可设计掷出的点数为偶数时甲胜,掷出的点数为奇数时乙胜.类型二、概率3.(2015春•山亭区期末)一只口袋里放着4个红球、8个黑球和若干个白球,这三种球除颜色外没有任何区别,并搅匀.(1)取出红球的概率为,白球有多少个?(2)取出黑球的概率是多少?(3)再在原来的袋中放进多少个红球,能使取出红球的概率达到?【答案与解析】解:(1)设袋中有白球x个.由题意得:4+8+x=4×5,解得:x=8,答:白球有8个;(2)取出黑球的概率为:,答:取出黑球的概率是,(3)设再在原来的袋中放入y个红球.由题意得:3(4+y)=20+y,或2(4+y)=8+8,解得:y=4,答:再在原来的袋中放进4个红球,能使取出红球的概率达到.【总结升华】此题考查了概率公式的应用.用到的知识点为:概率=所求情况数与总情况数之比.举一反三【变式】(2014•宁波模拟)中央电视台“非常6+1”栏目中有个互动环节,在电视直播现场有三个“金蛋”三个“银蛋”其中只有一个“金蛋”内有礼物,银蛋也是如此.有一个打进电话的观众,选择并打开后得到礼物的可能性是()A.B.C.D.【答案】D.【 391875 名称:随机事件与概率初步:例6及思考题】投篮次数n8 10 12 9 16 10进球次数m 6 8 9 7 12 7进球频率nm(1)计算表中各场次比赛进球的频率;(2)这位运动员每次投篮,进球的概率约为多少? 【答案与解析】 (1)投篮次数n 8 10 12 9 16 10 进球次数m 6897127进球频率nm0.75 0.8 0.75 0.78 0.75 0.7 (2)P(进球)≈0.75.【总结升华】频率和概率的关系:当大量重复试验时,频率会稳定在概率附近. 举一反三【变式】某射手在同一条件下进行射击,结果如下表所示:射击次数(n) 10 20 50 100 200 500 击中靶心次数(m)9 19 44 91 178 451 击中靶心频率()(1)计算表中击中靶心的各个频率(精确到0.01);(2)这个射手射击一次,击中靶心的概率约是多少(精确到0.1)?【答案】 (1)击中靶心的各个频率依次是:0.90,0.95,0.88,0.91,0.89,0.90. (2)这个射手击中靶心的概率约为0.9.。
概率初步知识点

概率初步知识点归纳1、概率的有关概念1.概率的定义:某种事件在某一条件下可能发生,也可能不发生,但可以知道它发生的可能性的大小,我们把刻划(描述)事件发生的可能性的大小的量叫做概率.2、事件类型:○1必然事件:有些事情我们事先肯定它一定发生,这些事情称为必然事件.○2不可能事件:有些事情我们事先肯定它一定不会发生,这些事情称为不可能事件.○3不确定事件:许多事情我们无法确定它会不会发生,这些事情称为不确定事件.必然事件、不可能事件都是在事先能肯定它们会发生,或事先能肯定它们不会发生的事件,因此它们也可以称为确定性事件.不确定事件都是事先我们不能肯定它们会不会发生,我们把这类事件称为随机事件。
练习:1.足球比赛前,裁判通常要掷一枚硬币来决定比赛双方的场地与首先发球者,其主要原因是( ).A.让比赛更富有情趣B.让比赛更具有神秘色彩C.体现比赛的公平性D.让比赛更有挑战性2.小张掷一枚硬币,结果是一连9次掷出正面向上,那么他第10次掷硬币时,出现正面向上的概率是( ).A.0 B.1 C.0.5 D.不能确定3.关于频率与概率的关系,下列说法正确的是( ).A.频率等于概率B.当试验次数很多时,频率会稳定在概率附近C.当试验次数很多时,概率会稳定在频率附近D.试验得到的频率与概率不可能相等4.下列说法正确的是( ).A.一颗质地均匀的骰子已连续抛掷了2000次,其中,抛掷出5点的次数最少,则第2001次一定抛掷出5点B.某种彩票中奖的概率是1%,因此买100张该种彩票一定会中奖C.天气预报说明天下雨的概率是50%.所以明天将有一半时间在下雨D.抛掷一枚图钉,钉尖触地和钉尖朝上的概率不相等5.下列说法正确的是( ).A.抛掷一枚硬币5次,5次都出现正面,所以投掷一枚硬币出现正面的概率为1B.“从我们班上查找一名未完成作业的学生的概率为0”表示我们班上所有的学生都完成了作业C.一个口袋里装有99个白球和一个红球,从中任取一个球,得到红球的概率为1%,所以从袋中取至少100次后必定可以取到红球(每次取后放回,并搅匀) D.抛一枚硬币,出现正面向上的概率为50%,所以投掷硬币两次,那么一次出现正面,一次出现反面6.在一个不透明的袋子中装有4个除颜色外完全相同的小球,其中白球1个,黄球1个,红球2个,摸出一个球不放回,再摸出一个球,两次都摸到红球的概率是( ).A .21 B .31 C .61 D .81 7.在今年的中考中,市区学生体育测试分成了三类,耐力类、速度类和力量类.其中必测项目为耐力类,抽测项目为:速度类有50m 、100m 、50m × 2往返跑三项,力量类有原地掷实心球、立定跳远、引体向上(男)或仰卧起坐(女)三项.市中考领导小组要从速度类和力量类中各随机抽取一项进行测试,请问同时抽中50m × 2往返跑、引体向上(男)或仰卧起坐(女)两项的概率是( ). A .31B .32C .61D .918.元旦游园晚会上,有一个闯关活动:将20个大小、重量完全一样的乒乓球放入一个袋中,其中8个白色的,5个黄色的,5个绿色的,2个红色的.如果任意摸出一个乒乓球是红色,就可以过关,那么一次过关的概率为( ). A .32 B .41 C .51 D .101 9.下面4个说法中,正确的个数为( ). (1)“从袋中取出一只红球的概率是99%”,这句话的意思是肯定会取出一只红球,因为概率已经很大(2)袋中有红、黄、白三种颜色的小球,这些小球除颜色外没有其他差别,因为小张对取出一只红球没有把握,所以小张说:“从袋中取出一只红球的概率是50%” (3)小李说,这次考试我得90分以上的概率是200% (4)“从盒中取出一只红球的概率是0”,这句话是说取出一只红球的可能性很小 A .3 B .2 C .1 D .0 10.下列说法正确的是( ).A .可能性很小的事件在一次试验中一定不会发生B .可能性很小的事件在一次试验中一定发生C .可能性很小的事件在一次试验中有可能发生D .不可能事件在一次试验中也可能发生 3、(重点)概率的计算1、概率的计算方式:概率的计算有理论计算和实验计算两种方式,根据概率获得的方式不同,它的计算方法也不同.2、如何求具有上述特点的随机事件的概率呢? 如果一次试验中共有n 种可能出现的结果,而且这些结果出现的可能性都相同,其中事件A 包含的结果有m 种,那么事件A 发生的概率P(A)=n m 。
第23章 概率初步章节易错题型分析(解析版)初中数学

第23章概率初步章节易错题型分析易错点1:事件的分类1.抛掷两枚分别标有1,2,3,4的四面体骰子,写出这个实验中的一个随机事件是____________________;写出这个实验中的一个必然事件是____________________.【难度】★【答案】随机事件:一枚骰子4朝上,一枚骰子3朝上;必然事件:任意两个骰子面朝上的数字和不小于2.【解析】随机事件是有时会发生,有时不会发生;必然事件是每次一定发生,不可能不发生.2.下列三个事件:①明天,上海会下雨;②将汽油滴入水中,汽油会浮在水面上;③任意投掷一枚质地均匀的硬币,硬币停止后,正面朝上;④方程2340-+=有两个不相等的实数x x根,其中必然事件是()A.②④ B.①③④ C.④ D.②【难度】★【答案】D【解析】(1)错,上海明天不一定下雨;(2)水的密度大,油都飘在水面上;(3)错,可能反面朝上;(4)错,方程没有实数根.【解析】考察等可能事件,以及方程的根,生活常识等问题.3.从一副没有大、小王的扑克牌中任意抽取牌,请判断以下事件是必然事件、不可能事件还是随机事件.(1)任意抽取5张牌,其中有一张是大王.(2)任意抽取5张牌,四种花色都有.(3)任意抽取5张牌,都是K.(4)任意抽取13张牌,至少有4张是同一花色.(5)任意抽取13张牌,其中有4张是黑桃.【难度】★【答案】(1)不可能事件;(2)随机事件;(3)不可能事件;(4)必然事件;(5)随机事件.【解析】(1)没有大小王,所以是不可能事件;(2)可能发生;(3)总共有4张K;(4)必然发生;(5)有可能发生.【总结】考察学生对随机事件,必然事件和不可能事件的理解和掌握.4.下列事件中,是不可能发生的是()A.随意掷一枚均匀的硬币两次,至少有一次反面朝上B.随意掷两个均匀的骰子,朝上面的点数之和为1C.今年冬天黑龙江会下雪D.一个转盘被分成6个扇形,按红、白、白、红、红、白排列,指针停在红色区域【难度】★【答案】B【解析】B.朝上面的点数和必定大于等于2;A.随机事件;C.随机事件;D.随机事件【总结】考察学生对随机事件,必然事件和不可能事件的理解和掌握.5.下列事件必然发生的是()A.明天会下雨B.任意买一张电影票,座位号是奇数C.下课铃响了,同学们都走出教室D.在只装有6个白球和4个红球的口袋中,摸不到黑球【难度】★【答案】D【解析】A.随机事件;B.随机事件;C.随机事件;D.必然事件.【总结】考察学生对随机事件,必然事件和不可能事件的理解和掌握.易错点2:事件的概率1.现有2008年奥运会福娃卡片20张,其中贝贝6张,京京5张,欢欢4张,迎迎3张,妮妮2张,每张卡片大小、质地均匀相同,将画有福娃的一面朝下反扣在桌子上,从中随机抽取一张,抽到京京的概率是()A.110B.310C.14D.15【难度】★★【答案】C【解析】51204p==.【总结】考察学生对事件可能性的大小的掌握情况.2.袋子里装有红、黄、蓝三种小球,其形状、大小、质量、质地等完全相同,每种颜色的小球各5个,且分别标有数字1,2,3,4,5.现从中摸出一球:(1)摸出的球是蓝色球的概率是________.(2)摸出的球是红色1号球的概率是________.(3)摸出的球是5号球的概率是________.【难度】★【答案】(1)13p=;(2)115p=;(3)15p=.【解析】(3)31155p==.【总结】考察学生对等可能事件的理解和掌握.3.两个装有乒乓球的盒子,其中一个装有2个白球1个黄球,另一个装有1个白球2个黄球.现从这两个盒中随机各取出一个球,则取出的两个球一个是白球一个是黄球的概率为__________.【难度】★【答案】59.【解析】22115 33339+=.【总结】注意分情况,第一个盒子摸出的是白球或者是黄球两种情况.4.一个袋中装有2个黄球和两个红球,任意摸出一个球后放回,再任意摸出一个球,则两次都找到红球的概率为__________.【难度】★★【答案】14.【解析】111224p==.【总结】考察学生对概率的理解和掌握,可用树状图或列表法进行计算.5.某家庭电话,打进的电话响第一声时被接的概率为0.1,响第二声被接的概率为0.15,响第三声或第四声被接的概率都是0.2,则电话在响第五声之前被接的概率为____________.【难度】★【答案】0.65.【解析】0.1+0.15+0.2+0.2=0.65.【总结】考察学生对概率的理解.6.一个不透明的袋中装有除颜色外均相同的5个红球和3个黄球,从中随机摸出一个,摸到黄球的概率是()A.18B.13C.38D.35【难度】★★【答案】C【解析】随机摸出一个球,总共有8种情况,摸到黄球的可能性是3种,故38p=.【总结】考察学生对等可能事件的理解和掌握.7.用1、2、3三个数字组成没有重复数字的三位数,其中排出偶数的概率是__________.【难度】★★【答案】13.【解析】组成的三位数有:123,132,213,231,312,321,故偶数概率为:2163p==.【总结】考查学生对枚举法的掌握.8.袋中有红黑蓝3球,从中摸出一个放回,共摸3次,摸到二红一蓝的机会是_________.【难度】★★【答案】31279p==.【解析】三次摸得的颜色共有如下情况:红红红,红红黑,红红蓝,红黑红,红黑黑,红黑蓝,红蓝红,红蓝黑,红蓝蓝,黑红红,黑红黑,黑红蓝,黑黑红,黑黑蓝,黑黑黑,黑蓝红,黑蓝黑,黑蓝蓝,蓝红红,蓝红黑,蓝红蓝,蓝黑黑,蓝黑红,蓝黑蓝,蓝蓝红,蓝蓝黑,蓝蓝蓝,故摸到二红一蓝的机会是31279p==.【总结】考察学生对等可能事件的理解和掌握,注意对所有可能性的分析.9.有四张背面相同的纸牌A,B,C,D,其正面分别画有四个不同的几何图形(如图).小华将这4张纸牌背面朝上洗匀后摸出一张,放回洗匀后再摸出一张.(1)用树状图(或列表法)表示两次摸牌所有可能出现的结果,(纸牌可用A,B,C,D表示).(2)求摸出两张牌面图形都是中心对称图形的纸牌的概率.【难度】★★【答案】(1)如图;(2)14.【解析】(1)树状图如图所示;(2)圆与平行四边形是中心对称图形,故概率为:41164p==.【总结】考察学生树状图的理解与掌握,注意分析中心对称图形.10.在一个不透明的口袋中有除了颜色外,大小、形状都一样的5个红球、3个黄球和2个绿球,把它们在口袋中搅匀,请判断以下事件是必然事件、不可能事件,还是随机事件.(1)从口袋中任意取出1个球,是一个绿球.(2)从口袋中一次任意取出5个球,全是黄球.(3)从口袋中一次任意取出5个球,只有黄球和绿球,没有红球.(4)从口袋中一次任意取出6个球,恰好红、黄、绿三种颜色的球都齐了.(5)从口袋中一次任意取出9个球,恰好红、黄、绿三种颜色的球都齐了.【难度】★★【答案】(1)随机事件;(2)不可能事件;(3)随机事件;(4)随机事件;(5)必然事件.【解析】(1)21105p==;(2)不可能,总共只有3个黄球;(3)110p=;(4)有6种可能,1黄1绿4红,1黄2绿3红,2黄1绿3红,2黄2绿2红,3黄1绿2红,3黄2绿1红;(5)必然事件,不管剩哪个颜色的球,最后三个颜色肯定都是全的.【总结】考察学生结合实际情况对不可能事件、随机事件以及必然事件的理解和掌握,注意分情况讨论.11.口袋中有5张完全相同的卡片,分别写有1厘米、2厘米、3厘米、4厘米和5厘米,口袋外有2张卡片分别写有4厘米和5厘米.现随机从袋中取出一张卡片,与袋外两张卡片放在一起,以卡片上的数量分别作为三条线段的长度,回答下列问题:(1)求这三条线段能构成三角形的概率.(2)求这三条线段能构成直角三角形的概率.【难度】★★【答案】(1)45p=;(2)15p=.【解析】(1)设第三边长为x,5454x-<<+,即19x<<,符合条件的有4种,故概率为:45p=;(2)构成直角三角形只有一种情况:3、4、5,所以概率为:15p=.【总结】考察三角形的三边关系,注意利用概率问题来解答.12.在围棋盒中有x颗黑色棋子和y颗白色棋子,从盒中随机地取出一个棋子,如果它是黑色棋子的概率是38.(1)试写出y与x的函数关系式.(2)若往盒中再放进10颗黑色棋子,则取得黑色棋子的概率变为12,求x和y的值.【难度】★★【答案】(1)53y x=;(2)15x=,25y=.【解析】(1)由题意,可得38xx y=+,故53y x=;(2)由题意,可得:101102xx y+=++,又53y x=,故解得:15x=,25y=.【总结】考察对概率公式的准确理解及运用.13.将正面分别标有数字2、3、4背面花色相同的三张卡片洗匀后.背面朝上放在桌面上.(1)随机地抽取一张,求抽得偶数的概率.(2)随机地抽取一张作为个位上的数字(不放回)再抽取一张作为十位上的数字,请你画出树形图,并根据树形图求恰好取到“24”的概率是多少?【难度】★★【答案】(1)23p=,(2)16p=.【解析】(1)抽得的偶数为2或4,故概率为23p=;(2)树形图如图所示,故恰好取到“24”的概率是16p =. 【总结】考察学生对事件可能性的大小的掌握情况.14.某校有A 、B 两个阅览室,甲、乙、丙三名学生各自随机选择其中的一个阅览室自习.(1)求甲、乙、丙三名学生在同一个阅览室自习的概率.(2)求甲、乙、丙三名学生中至少有一人在B 阅览室自习的概率.【难度】★★【答案】(1)14p =;(2)17188p =-=. 【解析】(1)经分析可知,共有八种可能性,故甲、乙、丙三名学生在同一个阅览室自习的 概率为:2184p ==; (2)甲、乙、丙三名学生中至少有一人在B 阅览室自习的概率为17188p =-=. 【总结】考察学生对事件可能性的大小的掌握情况,注意进行分析.15.如图,电路图上有四个开关A 、B 、C 、D 和一个小灯泡,闭合开关D 或同时闭合开关A ,B ,C 都可使小灯泡发光.(1)任意闭合其中一个开关,则小灯泡发光的概率是多少?(2)任意闭合两个开关,请用画树状图或列表法的方法求出小灯泡发光的概率.【难度】★★【答案】(1)14p =;(2)12p =. 【解析】(1)共有4种情况,故任意闭合其中一个开关,则小灯泡发光的概率是14p =; (2)如图所示,任意闭合两个开关共有12种情况,只要闭合D 开关,则小灯泡一定发光,DCBA故概率是61122p==.【总结】考察学生对事件可能性的大小的掌握情况,注意进行分析.16.妞妞和她的爸爸玩“锤子、剪刀、布”游戏.每次用一只手可以出锤子、剪刀、布三种手势之一,规则是锤子赢剪刀、剪刀赢布、布赢锤子,若两人出现相同手势,则算打平.(1)你帮妞妞算算爸爸出“锤子”手势的概率是多少?(2)妞妞决定这次出“布”手势,妞妞赢的概率有多大?(3)妞妞和爸爸出相同手势的概率是多少?【难度】★★【答案】(1)13p=;(2)13p=;(3)3193p==.【解析】(1)爸爸可以出三种手势,出“锤子”是其中一种,故概率为13p=;(2)妞妞赢的话,爸爸只能出锤子,故概率为13p=;(3)两人都出锤子,或者都出布,或者都出剪刀,这样有三种情况,总共有9种情况:布剪刀,布锤子,布布,或者剪刀剪刀,剪刀锤子,剪刀布,或者锤子剪刀,锤子锤子,锤子布,故相同手势的概率为3193p==.【总结】考察学生对事件可能性的大小的掌握情况,注意对所有情况的分析.。
《随机事件》知识全解

《随机事件》知识全解课标要求:了解必然事件、不可能事件、随机事件的特点.知识结构:⎧⎧⎨⎪⎨⎩⎪⎩必然事件确定事件事件不可能事件随机事件内容解析:知识点1:必然事件、不可能事件、随机事件的定义在一定条件下,有些事件必然会发生,这样的事件称为必然事件。
相反地,有些事件必然不会发生,这样的事件称为不可能事件. 必然事件与不可能事件统称确定事件。
在一定条件下,可能发生也可能不发生的事件称为随机事件.注意:在叙述必然事件、不可能事件和随机事件时,一定要强调在一定条件下。
这是因为必然事件、不可能事件和随机事件都必须受到一定条件的制约.知识点2:事件发生的可能性的大小要知道事件发生的可能性的大小,首先要确定这个事件是什么事件。
必然事件一定发生;不可能事件一定不会发生;随机事件发生的可能性有大有小,不同的随机事件发生的可能性的大小有可能相同.注意:不大可能发生的事件是指事件发生的可能性很小,但还是有可能发生,因此必是随机事件.不可能发生事件是可以预知、确定的事件.两者不能混为一谈.重点难点本节重点是随机事件的特点数学重点的解决方法:通过大量丰富多彩的案例,激发学生的学习热情,调动学生的学习兴趣,使学生对随机事件有比较充分的感知,从不同的侧面,不同的视角进一步对随机事件的理解与认识.本节的难点是判断生活中哪些事件是随机事件相对于学生以前学习过的传统的数学知识,作为概率的第一节课,对随机事件的提法与描述,学生是会感到陌生而且困难的. 因此,多举一些例子加深学生对随机事件及其特点的理解与认识.教法引导心理学认为:认知从感知开始,感知是认知的门户,是一切知识的来源。
在课堂中,通过案例及演示实验,小组讨论,大组交流,逐步形成对随机事件的特点及定义的理性认识,注意调动学生的积极性. 引导学生积极参与教学活动.学法建议学生通过活动、细心观察、阅读、思考、同学之间的交流,讨论、探究、总结随机事件的定义,为本章的学习打下坚实的基础.。
八年级数学下册8.1确定事件与随机事件什么叫必然事件?什么叫不可能事件?素材

什么叫必然事件?什么叫不可能事件?
【问题】一、什么叫必然事件?什么叫不可能事件?
难易度:★★★★
关键词:可能性
答案:
事先能肯定它一定会发生的事件称为必然事件,事先能肯定它一定不会发生的事件称为不可能事件,必然事件和不可能事件统称为确定事件.
【举一反三】
典题:袋子中装有4个黑球和2个白球,这些球的形状、大小、质地等完全相同,在看不到球的条件下,随机地从袋子中摸出三个球,下列事件是必然事件的是()
A.摸出的三个球中至少有一个球是黑球
B.摸出的三个球中至少有一个球是白球
C.摸出的三个球中至少有两个球是黑球
D.摸出的三个球中至少有两个球是白球
思路导引:必然事件就是一定发生的事件,依据定义即可作出判断.
标准答案:
解:A、是必然事件;
B、是随机事件,选项错误;
C、是随机事件,选项错误;
D、是随机事件,选项错误.
故选A.
1。
八年级数学下册 8.1 确定事件与随机事件 什么是随机事件、必然事件、不可能事件?素材 (新版)苏科版

什么是随机事件、必然事件、不可能事件?
难易度:★★★
关键词:可能性
答案:
随机事件:在一定条件下,可能发生也可能不发生的事件.
必然事件:在每一次试验中都一定会发生的事件为必然事件。
不可能事件:在每一次试验中都一定不会发生的事件为“不可能事件”.
【举一反三】
典题:下列事件中,是必然事件的是()
A.掷一枚均匀的普通正方体骰子,骰子停止后朝上的点数是1
B.中秋节晚上能看到月亮
C.打开电视,正在播广告
D.抛掷一枚硬币,掷得的结果不是正面就是反面。
思路导引:A、B、C为随机事件,D为必然事件.
标准答案:解:D
1。
【期末复习】2019年 九年级数学上册 期末复习 概率初步 知识点+易错题精选(含答案)

2019年九年级数学上册期末复习概率初步知识点+易错题精选概率的概念某种事件在某一条件下可能发生,也可能不发生,但可以知道它发生的可能性的大小,我们把刻划(描述)事件发生的可能性的大小的量叫做概率.事件类型:①必然事件:有些事情我们事先肯定它一定发生,这些事情称为必然事件.②不可能事件:有些事情我们事先肯定它一定不会发生,这些事情称为不可能事件.③不确定事件:许多事情我们无法确定它会不会发生,这些事情称为不确定事件.概率的计算一般地,如果在一次试验中,有n种可能的结果,并且它们发生的可能性都相等,事件A包含其中的m中结果,那么事件A发生的概率为(1)列表法求概率当一次试验要设计两个因素,并且可能出现的结果数目较多时,为不重不漏地列出所有可能的结果,通常采用列表法。
(2)树状图法求概率当一次试验要设计三个或更多的因素时,用列表法就不方便了,为了不重不漏地列出所有可能的结果,通常采用树状图法求概率。
利用频率估计概率①利用频率估计概率:在同样条件下,做大量的重复试验,利用一个随机事件发生的频率逐渐稳定到某个常数,可以估计这个事件发生的概率。
②在统计学中,常用较为简单的试验方法代替实际操作中复杂的试验来完成概率估计,这样的试验称为模拟实验。
③随机数:在随机事件中,需要用大量重复试验产生一串随机的数据来开展统计工作。
把这些随机产生的数据称为随机数。
概率初步 易错题精选一、选择题1.下列成语中描述的事件必然发生的是( )A .水中捞月B .瓮中捉鳖C .守株待兔D .拔苗助长2.一只不透明的袋子中装有4个黑球、2个白球,每个球除颜色外都相同,从中任意摸出3个球,下列事件为必然事件的是( )A .至少有1个球是黑球B .至少有1个球是白球C.至少有2个球是黑球 D .至少有2个球是白球3.如图是一个转盘,转盘分成8个相同的扇形,颜色分为红、绿、黄三种颜色,指针的位置固定,转动转盘后任其自由停止,其中的某个扇形会恰好停在指针所指的位置(指针指向两个扇形的交线时,当作指向指针右边的扇形),则指针指向红色的概率是( )A .41B .83C .85D .214.如图的四个转盘中,C ,D 转盘分成8等分,若让转盘自由转动一次,停止后,指针落在阴影区域内的概率最大的转盘是( )5.市举办了首届中学生汉字听写大会.从甲、乙、丙、丁4套题中随机抽取一套训练,抽中甲的概率是( )A .23B .31C .41 D .1 6.有6张写有数字的卡片,它们的背面都相同,现将它们背面朝上(如图所示),从中任意一张是数字3的概率是( )A .61B .31C .21D .32 7.小明同时向上掷两枚质地均匀、同样大小的正方体骰子,骰子的六个面上分别刻有1到6的点数,掷得面朝上的点数之和是3的倍数的概率是( ) A .13 B .16 C .518 D .56 8.盒子里有3支红色笔芯,2支黑色笔芯,每支笔芯除颜色外均相同.从中任意拿出一支笔芯,则拿出黑色笔芯的概率是( )A .23B .15C .0.4D .359.向一个图案如下图所示的正六边形靶子上随意抛一枚飞镖,则飞镖插在阴影区域的概率为( )A 1-B .16C .1-.1510.一个质地均匀的正四面体的四个面上依次标有数字-2、0、1、2,连续抛掷两次,朝下一面的数字分别是a 、b ,将其作为M 点的横、纵坐标,则点M(a ,b)落在以A(-2,0)、B(2,0)、C(0,2)为顶点的三角形内(包含边界)的概率是( )A .B .C .D .11.甲、乙、丙三位同学参加一次节日活动,很幸运的是,他们都得到了一件精美的礼物。
随机事件与概率重难点解析版
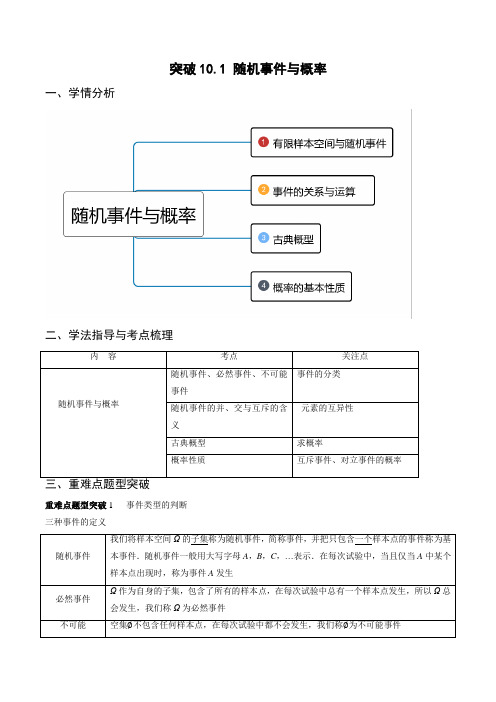
突破10.1 随机事件与概率一、学情分析二、学法指导与考点梳理内容考点关注点随机事件与概率随机事件、必然事件、不可能事件事件的分类随机事件的并、交与互斥的含义元素的互异性古典概型求概率概率性质互斥事件、对立事件的概率重难点题型突破1 事件类型的判断三种事件的定义随机事件我们将样本空间Ω的子集称为随机事件,简称事件,并把只包含一个样本点的事件称为基本事件.随机事件一般用大写字母A,B,C,…表示.在每次试验中,当且仅当A中某个样本点出现时,称为事件A发生必然事件Ω作为自身的子集,包含了所有的样本点,在每次试验中总有一个样本点发生,所以Ω总会发生,我们称Ω为必然事件不可能空集∅不包含任何样本点,在每次试验中都不会发生,我们称∅为不可能事件事件例1.(1)、(2022·全国·高二课时练习)以下现象中不是随机现象的是( ). A .在相同的条件下投掷一枚均匀的硬币两次,正反两面都出现 B .明天下雨C .连续两次抛掷同一骰子,两次都出现2点D .平面四边形的内角和是360° 【答案】D 【解析】 【分析】根据随机现象的定义进行判断即可. 【详解】因为平面四边形的内角和是360°是一个确定的事实,而其他三个现象都是随机出现的, 所以选项D 不符合题意, 故选:D(2)、(2022·全国·高二课时练习)(多选题)下列说法正确的是( ) A .必然事件的概率为0 B .事件∅是一个基本事件C .随机事件A 的概率满足()01P A ≤≤D .每一个随机事件都是样本空间的一个子集 【答案】CD 【解析】 【分析】根据随机事件、必然事件及不可能事件的定义与性质,逐一分析各选项即可求解. 【详解】解:对A :必然事件的概率为1,故选项A 错误;对B :事件∅中不包含任何样本点,故事件∅不是一个基本事件,故选项B 错误; 对C :随机事件A 的概率满足()01P A ≤≤,故选项C 正确; 对D :每一个随机事件都是样本空间的一个子集,故选项D 正确. 故选:CD.【变式训练1-1】、(2022·全国·高二课时练习)在下列现象中,随机现象是______.(选填序号) ①汽车排放尾气会污染环境; ②实数a 、b 都不为0,则220a b +=;③任取一个正方体的4个顶点,这4个顶点不共面;④将一枚硬币连掷三次,结果出现三次正面;⑤函数log a y x =(01a <<)在定义域内为严格增函数; ⑥三个小球全部放入两个盒子中,其中一个盒子里有三个球. 【答案】③④⑥ 【解析】 【分析】根据给定条件,利用随机事件、不可能事件、必然事件的定义逐一判断各个命题作答. 【详解】对于①,汽车排放的尾气一定会污染环境,①是必然事件;对于②,因实数a 、b 都不为0,则220,0a b >>,220a b +>,②是不可能事件; 对于③,正方体的4个顶点可能在一个平面内,也可能不在同一平面内,③是随机事件;对于④,一枚硬币连掷三次,出现的结果有3次反面、2次反面1次正面、1次反面2次正面,3次正面,④是随机事件;对于⑤,函数log a y x =(01a <<)在定义域内为严格减函数,⑤是不可能事件;对于⑥,三个小球全部放入两个盒子中,某个盒子中可能有0个球、1个球、2个球、3个球,⑥是随机事件.所以随机现象是③④⑥. 故答案为:③④⑥【变式训练1-2】、((2022·全国·高二课时练习)期末考试结束,高二(1)班班主任张老师从班里的40名学生中,随机抽取10名学生的语文和数学成绩进行抽样分析,研究学生偏科现象.将10名学生编号为1、2、3、…、10,再将他们的两科成绩(单位:分)绘成如图所示的折线图.从两科成绩均超过70分的学生中随机抽取2人进行访谈,则这2人中恰有1人是语文成绩高于数学成绩的概率为______.【答案】35##0.6【解析】 【分析】依据古典概型去求这2人中恰有1人是语文成绩高于数学成绩的概率. 【详解】设“抽取的这2人中恰有1人是语文成绩高于数学成绩”为事件B .因为两科成绩均超过70分的学生编号分别是1、3、4、9、10,其中语文成绩高于数学成绩的学生编号分别是1、4、10.则从这5位学生中随机抽取2人构成的样本空间为()()()()()()()()()(){}1,3,1,4,1,9,1,10,3,4,3,9,3,10,4,9,4,10,9,10Ω=,10个样本点 事件B 包含()()()()()(){}13193431049910,,,,,,,,,,,,共6个样本点. 所以这2人中恰有1人是语文成绩高于数学成绩的概率()63105P B ==. 故答案为:35重难点题型突破2 事件关系的判断1.互斥(互不相容)定义 一般地,如果事件A 与事件B 不能同时发生,也就是说A ∩B 是一个不可能事件,即A ∩B =∅,则称事件A 与事件B 互斥(或互不相容)含义 A 与B 不能同时发生符号表示A ∩B =∅图形表示2、互为对立定义 一般地,如果事件A 与事件B 在任何一次试验中有且仅有一个发生,即A ∪B =Ω,且A ∩B=∅,那么称事件A 与事件B 互为对立.事件A 的对立事件记为A -含义 A 与B 有且仅有一个发生 符号表示A ∩B =∅,A ∪B =Ω图形表示元件故障”,则表示电路故障的事件为( )A.E F B.E F C.E F D.E F⋃【答案】B【解析】【分析】根据并联电路可得答案.【详解】因为甲、乙两个元件构成一并联电路,所以只有当甲、乙两个元件都故障时,才造成电路故障,所以表示电路故障的事件为E F.故选:B(2)、(2022·河北·邢台市南和区第一中学高一阶段练习)小赵同学准备了四个游戏,四个游戏中的不透明的盒子中均装有3个白球和2个红球(小球除颜色外都相同),游戏规则如下表所示:游戏1 游戏2 游戏3 游戏4取球规则一次性取一个,取一次一次性取两个,取一次一次性取一个,不放回地取两次一次性取一个,有放回地取两次获胜规则取到红球→小赵胜取到白球→小赵败两个球不同色→小赵胜两个球同色→小赵败两个球不同色→小赵胜两个球同色→小赵败两个球不同色→小赵胜两个球同色→小赵败若你和小赵同学玩这四个游戏中的一个,你想获胜,则应该选()A.游戏1 B.游戏2 C.游戏3 D.游戏4【答案】A【解析】【分析】分别求出游戏1、游戏2、游戏3、游戏4试验的样本空间,设事件A=“取到白球”,事件B=“取到的两个球同色”,事件C=“取到的两个球同色” ,事件D“取到的两个球同色”,求出事件A B C D、、、包含的样本个数,由古典概型的概率公式代入即可得出答案.【详解】设3个白球分别为a,b,c,2个红球分别为1,2.游戏1:这个试验的样本空间可记为{},,,1,2a b c Ω=,共包含5个样本点.设事件A =“取到白球”,则{},,A a b c =,包含3个样本点,所以()35P A =. 游戏2:这个试验的样本空间可记为()()()()()()()()()(){},,,,,1,,2,,,,1,,2,,1,,2,1,2a b a c a a b c b b c c Ω=,共包含10个样本点.设事件B =“取到的两个球同色”,则()()()(){},,,,,,1,2B a b a c b c =,包含4个样本点.所以()25P B =. 游戏3:这个试验的样本空间可记为()()()()()()()()()(){Ω,,,,,1,,2,,,,,,1,,2,,,,,a b a c a a b a b c b b c a c b =()()()()()()()()()()},1,,2,1,,1,,1,,1,2,2,,2,,2,,2,1c c a b c a b c ,共包含20个样本点.设事件C =“取到的两个球同色”,则()()()()()()()(){},,,,,,,,,,,,1,2,2,1C a b b a a c c a b c c b =,包含8个样本点,所以()25P C =.游戏4:这个试验的样本空间可记为()()()()()()()()()()()()(){Ω,,,,,,,1,,2,,,,,,,,1,,2,,,,,,,a a a b a c a a b a b b b c b b c a c b c c =()()()()()()()()()()()()},1,,2,1,,1,,1,,1,1,1,2,2,,2,,2,,2,1,2,2c c a b c a b c ,共包含25个样本点.设事件D“取到的两个球同色”,则()()()()()(){(),,,,,,,,,,,,,,D a a a b a c b c b b b a c c =()()()()()()},,,,1,1,1,2,2,1,2,2c a c b ,包含13个样本点,所以()1325P D =. 故选:A.【变式训练2-1】、(2022·四川·宜宾市教科所三模(文))一批产品共7件,其中5件正品,2件次品,从中随机抽取2件,下列两个事件互斥的是( ) A .“恰有2件次品”和“恰有1件次品” B .“恰有1件次品”和“至少1件次品” C .“至多1件次品”和“恰有1件次品” D .“恰有1件正品”和“恰有1件次品”【答案】A 【解析】 【分析】本题考查互斥事件的概念:事件A 与事件B 不会同时发生. 【详解】5件正品,2件次品,从中随机抽取2件共有如下可能性结果: “两件次品”,“一件正品一件次品”,“两件正品”根据互斥事件可知:A正确;“至少1件次品”包含“两件次品”和“一件正品一件次品”,B不正确;“至多1件次品”包含“一件正品一件次品”,“两件正品”,C不正确;“恰有1件正品”和“恰有1件次品”是同一事件,D不正确;故选:A.重难点题型突破3 事件的运算1、包含关系定义一般地,若事件A发生,则事件B一定发生,我们就称事件B包含事件A(或事件A包含于事件B)含义A发生导致B发生符号表示B⊇A(或A⊆B)图形表示特殊情形如果事件B包含事件A,事件A也包含事件B,即B⊇A且A⊆B,则称事件A与事件B 相等,记作A=B2、并事件(和事件)定义一般地,事件A与事件B至少有一个发生,这样的一个事件中的样本点或者在事件A中,或者在事件B中,我们称这个事件为事件A与事件B的并事件(或和事件)含义A与B至少一个发生符号表示A∪B(或A+B)图形表示3、交事件(积事件)定义一般地,事件A与事件B同时发生,这样的一个事件中的样本点既在事件A中,也在事件B中,我们称这样的一个事件为事件A与事件B的交事件(或积事件)含义A与B同时发生符号表示A∩B(或AB)图形表示例3.(1)、(2022·河北·邢台市南和区第一中学高二阶段练习)已知()(),若A B⊆,则()P A B=________.【答案】0.7##710【解析】 【分析】由事件的包含关系可得()()P A B P B =,即可求出答案. 【详解】如果A B ⊆,那么()()P A P B ≤,所以()()0.7P A B P B ==. 故答案为:0.7.(2)、(2022·全国·高三专题练习)(多选题)下列说法不.正确的是( ) A .若A ,B 为两个事件,则“A 与B 互斥”是“A 与B 相互对立”的必要不充分条件 B .若A ,B 为两个事件,则()()()P A B P A P B +=+ C .若事件A ,B ,C 两两互斥,则()()()1P A P B P C ++= D .若事件A ,B 满足()()1P A P B +=,则A 与B 相互对立 【答案】BCD 【解析】 【分析】A. “A 与B 互斥”是“A 与B 相互对立”的必要不充分条件,所以该选项正确;B. ()()()()P A B P A P B P A B +=+-,所以该选项错误;C. 举反例说明()()()1P A P B P C ++=不一定成立,所以该选项错误;D. 举反例说明A 与B 不对立,所以该选项错误. 【详解】解:A. 若A ,B 为两个事件,“A 与B 互斥”则“A 与B 不一定相互对立”; “A 与B 相互对立”则“A 与B 互斥”,则“A 与B 互斥”是“A 与B 相互对立”的必要不充分条件,所以该选项正确;B. 若A ,B 为两个事件,则()()()()P A B P A P B P A B +=+-,所以该选项错误;C. 若事件A ,B ,C 两两互斥,则()()()1P A P B P C ++=不一定成立,如:掷骰子一次,记A =向上的点数为1,B =向上的点数为2,C =向上的点数为3,事件A ,B ,C 两两互斥,则()()()1111++=6662P A P B P C ++=.所以该选项错误;D. 抛掷一枚均匀的骰子,所得的点数为偶数的概率是12,掷一枚硬币,正面向上的概率是12,满足()()1P A P B +=,但是A 与B 不对立,所以该选项错误.故选:BCD【变式训练3-1】、(2022·全国·高三专题练习)(多选题)从2名男同学和3名女同学中任选2人参加社区服务,记事件“选中的2人都是女同学”的概率为1P ;事件“选中2人都是男同学”的概率为2P ;事件“选中1名男同学1名女同学”的概率3P .则下列选项正确的是( ) A .123P P P += B .132=P P C .122P P >D .2123=P P P【答案】BC 【解析】 【分析】根据题意列出基本事件,根据古典概型概率公式分别求出1P ,2P ,3P ,然后结合选项逐项分析即可求出结果. 【详解】将2名男同学分别记为x ,y ,3名女同学分别记为a ,b ,c ,则从5名同学中任选2人参加社区服务的所有可能情况有(,)x y ,(,)x a ,(,)x b ,(,)x c ,(),y a ,(),y b ,(),y c ,(,)a b ,(,)a c ,(,)b c 共10种,则1310P =,2110P =,363105P ==, 因此132=P P ,122P P >,123P P P +≠,2123P P P ≠,故选:BC.重难点题型突破4 古典概型 1、古典概型的定义 试验具有如下共同特征:(1)有限性:样本空间的样本点只有有限个; (2)等可能性:每个样本点发生的可能性相等.我们将具有以上两个特征的试验称为古典概型试验,其数学模型称为古典概率模型,简称古典概型. 2、古典概型的概率计算公式一般地,设试验E 是古典概型,样本空间Ω包含n 个样本点,事件A 包含其中k 个样本点,则定义事件A 的概率P (A )=k n =n (A )n (Ω),其中n (A )和n (Ω)分别表示事件A 和样本空间Ω包含的样本点个数.知识点七 互斥事件、对立事件的概率公式及应用概率的基本性质性质1 对任意的事件A ,都有P (A )≥0.性质2 必然事件的概率为1,不可能事件的概率为0,即P (Ω)=1,P (∅)=0. 性质3 如果事件A 与事件B 互斥,那么P (A ∪B )=P (A )+P (B ).性质4 如果事件A 与事件B 互为对立事件,那么P (B )=1-P (A ),P (A )=1-P (B ).性质5如果A⊆B,那么P(A) ≤P(B).性质6设A,B是一个随机试验中的两个事件,我们有P(A∪B)=P(A)+P(B)-P(A∩B).例4.(1)、(2022·广东·模拟预测)甲、乙、丙三人是某商场的安保人员,根据值班需要甲连续工作2天后休息一天,乙连续工作3天后休息一天,丙连续工作4天后休息一天,已知3月31日这一天三人均休息,则4月份三人在同一天工作的概率为()A.13B.25C.1130D.310【答案】B【解析】【分析】由条件确定三人在同一天工作的天数,利用古典概型概率公式求事件的概率.【详解】4月份日期为1号,2号,3号,⋅⋅⋅,30号,甲工作的日期为1,2,4,5,7,8,10,11,…,28,29,乙工作的日期为1,2,3,5,6,7,9,10,11,⋅⋅⋅,29,30,丙工作的日期为1,2,3,4,6,7,8,9,⋅⋅⋅,28,29,在同一天工作的日期为1,2,7,11,13,14,17,19,22,23,26,29,所以三人在同一天工作的概率为122305P==.故选:B.(2)、(2022·河南·模拟预测(文))齐国的大将田忌很喜欢赛马,他与齐威王进行赛马比赛,他们都各有上、中、下等马各一匹,每次各出一匹马比一场,比赛完三场(每个人的三匹马都出场一次)后至少赢两场的获胜.已知同等次的马,齐威王的要强于田忌的,但是不同等次的马,都是上等强于中等,中等强于下等,如果两人随机出马,比赛结束田忌获胜的概率为()A.12B.13C.14D.16【答案】D【解析】【分析】列举出各种对应情况,由概率公式即可得到答案.【详解】将齐威王的上、中、下等马分别记为A,B,C,田忌的上、中、下等马分别记为a,b,c,则他们比赛的情况如下:齐威王的马A B C胜者田忌的马a b c齐威王田忌的马 a c b齐威王 田忌的马 b ac齐威王 田忌的马 bc a齐威王 田忌的马 c ab田忌 田忌的马cba齐威王由上表可知,只有齐威王的马(),,A B C 对田忌的马(),,c a b 这种情况,田忌获胜,所以田忌获胜的概率16P =. 故选:D【变式训练4-1】、(2022·全国·高一专题练习)(多选题)甲、乙两人在5次体育测试中的成绩(成绩为整数,满分为100分)如下表,其中乙的第5次成绩的个位数被污损,用x 代替,则第1次 第2次 第3次 第4次 第5次 甲 91 86 88 92 93乙878586999xB .从甲的5次成绩中任取2次成绩,均大于甲的平均成绩的概率是310C .当3x =时,甲、乙两人的平均成绩相等D .乙的平均成绩低于甲的平均成绩的概率是310【答案】BCD 【解析】 【分析】直接求出甲的平均成绩,可判断A 选项;列举出从甲的5次成绩中任取2次成绩样本空间,从而得出均大于甲的平均成绩的样本点,再根据古典概型求出概率,即可判断B 选项;当3x =时,求出乙的平均成绩,即可判断C 选项;列举出乙的第5次成绩的所有可能情况,从而得出低于甲的平均成绩的情况,从而求出概率,即可判断D 选项. 【详解】解:对于A ,甲的平均成绩为9186889293905++++=分,故A 错误;对于B ,从甲的5次成绩中任取2次成绩样本空间有()()()()(){91,86,91,88,91,92,91,93,86,88,Ω=()()()()()}86,92,86,93,88,92,88,93,92,93,共10个样本点,其中均大于甲的平均成绩的样本点有3个,为()91,92,()91,93,()92,93,故所求概率为310,故B 正确; 对于C ,由于甲的平均成绩为9186889293905++++=分,当3x =时,则乙的平均成绩为8785869993905++++=分,此时甲、乙两人的平均成绩相等,故C 正确;对于D ,乙的第5次成绩可能是90,91,92,93,94,95,96,97,98,99,共10种可能, 可知当3x =时,甲、乙两人的平均成绩相等,所以当乙的第5次成绩为90,91,92时,乙的平均成绩低于甲的平均成绩, 所以乙的平均成绩低于甲的平均成绩的概率是310,故D 正确. 故选:BCD.【变式训练4-2】、(2021·全国·高一单元测试)(多选题)下面有三个游戏,则( ) 取球方式结果游戏1 有3个黑球和1个白球游戏时,不放回地依次取2个球取出的2个球同色→甲胜,取出的2个球不同色→乙胜游戏2 有2个黑球和2个白球游戏时,有放回地依次取2个球取出的2个球同色→甲胜,取出的2个球不同色→乙胜游戏3有2个黑球和2个白球,游戏时,不放回地依次取2个球取出的2个球同色→甲胜,取出的2个球不同色→乙胜【答案】AB 【解析】 【分析】分别判断每个游戏甲胜、乙胜的概率是否相等即可. 【详解】对于游戏1,样本空间中的样本点共有12个,取出的2个球同色对应的样本点有6个,其概率是12,取出的2个球不同色的概率也是12,故游戏1公平;对于游戏2,样本空间中的样本点共有16个,分析易知,取出的2个球同色和取出的2个球不同色的概率都是12,故游戏2公平;对于游戏3,样本空间中的样本点共有12个,取出的2个球同色的概率是13,取出的2个球不同色的概率是23,故游戏3不公平,乙胜的概率大.故选:AB例5、(2022·安徽·合肥一六八中学模拟预测(文))一场马拉松,不仅是一次身体的长途跋涉,更是对城市文化的寻找与认同.在某市举行的马拉松“半马精英赛”的赛事中,25名参赛选手的成绩(单位:分钟)的茎叶图如图所示:(1)已知选手甲的成绩为85分钟,若从成绩不超过85分钟的选手中随机抽取3人接受电视台采访,求甲被选中的概率;(2)若从总体中选取一个样本,使得该样本的平均水平与总体相同,且样本的方差不大于7,则称选取的样本具有集中代表性,试从总体(25名参赛选手的成绩)选取一个具有集中代表性且样本容量为5的样本,并求该样本的方差.【答案】(1)3 5(2)样本为:88、90、93、94、95;方差为6.8,答案不唯一.【解析】【分析】(1)根据古典概率的求法,求出总事件数,求出目标事件数即可;(2)先计算平均数,然后选择一个符合要求的样本,再求方差.(1)成绩不超过85分的参赛选手共5人,设为甲,乙,丙,丁,戊,随机选取3人的基本事件有:甲乙丙,甲乙丁,甲乙戊,甲丙丁,甲丙戊,甲丁戊,乙丙丁,乙丙戊,乙丁戊,丙丁戊,总数有10种,甲在其中有6种,记被选中的概率为3 (),()5 P A P A=.(2)因为25名参赛选手的成绩的总分为2300,所以总体的平均数为230092 25=.具有集中代表性且样本容量为5的一个样本为:88、90、93、94、95,该样本的方差为222222(8892)(9092)(9392)(9492)(9592)346.855s-+-+-+-+-===.答案不唯一,符合题意即可.【变式训练5-1】、(2022·江苏省响水中学高二阶段练习)有编号分别为1,2,3,4的四个不同的盒子和四个不同的小球,现把四个小球都逐个随机放入盒子里.(用数字作答)(1)求恰有一个盒子没放球的概率;(2)若四个盒子都有球,且编号为1的小球不能放入编号为1的盒子中,有多少种不同的放法?【答案】(1)9 16(2)18【解析】【分析】(1)根据题意,求得每个球都有4种放法有256种,进而求得恰有一个盒子没放球的放法,结合古典摡型的概率计算公式,即可求解;(2)先放1号球,有3种放法,其余三个球在三个位置全排列,即可求解.(1)解:每个球都有4种放法,故有4444256⨯⨯⨯=种不同的放法,选出一个盒子为空,再从4个小球中选两个作为一个元素,同另外两个元素在三个位置全排列,则共有123 443144C C A=种不同的放法,故所求概率为144925616=.(2)解:先放1号球,有3种放法,其余三个球在三个位置全排列,共有133318C A=种不同的放法.四、课堂定时训练(45分钟)1.(2022·安徽师范大学附属中学模拟预测(文))由于发现新冠阳性感染者,2022年4月17日-23日芜湖市主城区实施静态管理,最终控制了疫情.初三、高三学生于27日返校复课,返校前需提供48小时核酸检测阴性证明.为配合核酸检测,我市从3名护士和2名医生中随机选取两位派往某社区检测点工作,则恰好选取一名医生和一名护士的概率为()A.15B.14C.25D.35【答案】D【解析】【分析】枚举所有情况求解即可【详解】记3名护士为cde,2名医生为AB,两个检测点分别为:AB,Ac,Ad,Ae,Bc,Bd,Be,cd,ce,de共10个基本事件,其中恰好选取一名医生和一名护士有Ac,Ad,Ae,Bc,Bd,Be共6种,所以概率为63 105=故选:D2.(2022·全国·高一单元测试)不透明的袋中装有大小相同的四个球,四个球上分别标有数字“2”、“ 3”、“ 4”、“ 6”,现从中随机选取三个球,则所选的三个球上的数字中一个数字的两倍等于其余两个数字之和的概率为()A.14B.13C.12D.23【答案】C【解析】【分析】根据给定条件,利用列举法结合古典概型计算作答.【详解】由于4个球上的数字分别为2、3、4、6,则从4个球中随机选出3个的基本事件空间为:()()()()2,3,4,2,4,6,2,3,6,3,4,6,共4种,其中满足中间数的两倍等于其余两个数字之和的基本事件为()()2,3,4,2,4,6,共2种,所以所求概率2142 P==.故选:C3.(2022·全国·高一单元测试)从2022年北京冬奥会、冬残奥会志愿者的28730人中随机抽取20人,测得他们的身高分别为(单位:cm):162、153、148、154、165、168、172、171、170、150、151、152、160、165、164、179、149、158、159、175,根据样本频率分布估计总体分布的原理,在所有志愿者中任抽取一人身高在155.5cm 170.5cm -之间的概率为( ) A .25B .920C .12D .1120【答案】B 【解析】 【分析】根据题意,分析20人的数据可得,身高在155.5cm 170.5cm -之间的人数,由等可能事件概率的计算可得答案. 【详解】根据题意,分析20人的数据可得,身高在155.5cm 170.5cm -之间的有9人, 则在志愿者中任抽取一人身高在155.5cm 170.5cm -之间的概率为920. 故选:B.4.(2022·河北邯郸·二模)甲、乙两人玩一个传纸牌的游戏,每个回合,两人同时随机从自己的纸牌中选一张给对方.游戏开始时,甲手中的两张纸牌数字分别为1,3,乙手中的两张纸牌数字分别为2,4.则一个回合之后,甲手中的纸牌数字之和大于乙手中的纸牌数字之和的概率为( ) A .12B .14C .34D .38【答案】B 【解析】 【分析】用列举法,结合古典概型计算公式进行求解即可. 【详解】甲手中的两张纸牌数字用{}1,3表示,乙手中的两张纸牌数字用{}2,4表示,一个回合之后,甲、乙两人手中的两张纸牌数字分别为:(1){}{}2,314、,; (2){}{}4,321、,;(3){}{}1,234、,:(4){}{}1,423、,共4种情况, 其中甲手中的纸牌数字之和大于乙手中的纸牌数字之和共有一种情况,所以甲手中的纸牌数字之和大于乙手中的纸牌数字之和的概率为14,故选:B5.(2022·广东湛江·二模)某学校组建了合唱、朗诵、脱口秀、舞蹈、太极拳五个社团,该校共有2000名同学,每名同学依据自己兴趣爱好最多可参加其中一个,各个社团的人数比例的饼状图如图所示,其中参加朗诵社团的同学有8名,参加太极拳社团的有12名,则( )A .这五个社团的总人数为100B .脱口秀社团的人数占五个社团总人数的20%C .这五个社团总人数占该校学生人数的4%D .从这五个社团中任选一人,其来自脱口秀社团或舞蹈社团的概率为40% 【答案】BC 【解析】 【分析】计算出五个社团的总人数,可判断A,C;计算出脱口秀社团的人数,判断B;计算脱口秀社团或舞蹈社团的人数占五个社团总人数的比例,可判断D. 【详解】由于参加朗诵社团的同学有8名,该社团人数占比为10% , 故社团总人数为80人,故A 错误;合唱团人数为8030%24⨯= ,舞蹈社团人数为8025%20⨯=人, 故脱口秀社团的人数为80241220816----= , 故脱口秀社团的人数占五个社团总人数的1620%80=,故B 正确; 五个社团总人数占该校学生人数的804%2000= ,故C 正确; 脱口秀社团人数占五个社团总人数的20%,,舞蹈社团的人数占五个社团总人数的25% ,因此这两个社团人数占五个社团总人数的45%, 故从这五个社团中任选一人,其来自脱口秀社团或舞蹈社团的概率为45%,D 错误, 故选:BC6.(2022·湖南·临澧县第一中学高一阶段练习)“新冠肺炎”席卷全球,我国医务工作者为了打好这次疫情阻击战,充分发挥优势,很快抑制了病毒,据统计老年患者治愈率为70%,中年患者治愈率为86%,青年患者治愈率为95%.某医院共有300名老年患者,400名中年患者,500名青年患者,则( ) A .若从该医院所有患者中抽取容量为20的样本,老年患者应抽取5人B.该医院中年患者所占的频率为1 3C.估计该医院的平均治愈率大约是86%D.估计该医院的平均治愈率大约是84%【答案】ABC【解析】【分析】利用分层抽样可判断A选项;利用频率公式可判断B选项;计算出该医院的平均治愈率,可判断CD选项. 【详解】对于A选项,若从该医院所有患者中抽取容量为20的样本,老年患者应抽取的人数为3002051200⨯=,A对;对于B选项,该医院中年患者所占的频率为400112003=,B对;对于CD选项,估计该医院的平均治愈率大约是3000.74000.865000.950.857586%1200⨯+⨯+⨯=≈,C对D错.故选:ABC.7.(2022·黑龙江·哈尔滨三中高二期中)某校举行篮球比赛,甲、乙两班各出5名运动员(3男2女)进行比赛,为增加趣味性,下半场从两班各抽取两人交换队伍后进行比赛,则下半场从乙班抽取一名运动员为女生的概率是_________.【答案】25##0.4【解析】【分析】根据古典概型的计算公式即可求解. 【详解】解:乙班共5名运动员,其中2名女生,故抽取一名女生的概率25 P=.故答案为:2 58.(2022·四川·泸县五中高二期中(理))算盘是中国传统的计算工具,其形长方,周为木框,内贯直柱,俗称“档”,档中横以梁,梁上两珠,每珠作数五,梁下五珠,每珠作数一.算珠梁上部分叫上珠,梁下部分叫下珠.例如,在十位档拨上一颗上珠和两颗下珠,个位档拨上四颗下珠,则表示数字74.若在个、十、百、千位档中随机选择一档拨一颗下.珠,再从四个档中随机选择两个不同档位各拨一颗上.珠,则所表示的数字小于400的概率为__________。
高中数学例题:必然事件、随机事件、不可能事件的判定

高中数学例题:必然事件、随机事件、不可能事件的判定例1.指出下列事件是必然事件、不可能事件,还是随机事件.(1)“天上有云朵,下雨”;(2)“在标准大气压下且温度高于0℃时,冰融化”;(3)“某人射击一次,不中靶”;(4)“如果a>6,那么a-b>0”;(5)“掷一枚硬币,出现反面朝上”;(6)“从3个次品、1个正品共4个产品中抽取2个产品,抽到的都是正品”;(7)“从分别标有1,2,3,4,5的5张标签中任取一张,得到4号签”;(8)“某电话机在1分钟内收到2次呼叫”;(9)“没有水分,种子发芽”;(10)“同时抛掷两枚硬币一次,都出现正面向上”.【解析】(2)、(4)是必然事件,(6)、(9)是不可能事件,(1)、(3)、(5)、(7)、(8)、(10)是随机事件.【总结升华】判断一个事件是哪类事件要看两点:一是看条件,二是看结果发生与否,在条件S下事件发生与否是对应于条件S而言的.特别需要指出的是:对于一个事件,如果叙述不明确,则容易导致不同的理解.举一反三:【变式1】下列事件中,不可能事件是( )A.三角形内角和为180°B.在同一个三角形中大边对大角C.锐角三角形中两个内角的和小于90°D.三角形中任意两边的和大于第三边【答案】 C.【解析】“三角形内角和为180°”、“在同一个三角形中大边对大角”、“三角形中任意两边的和大于第三边”都为为必然事件,锐角三角形中两个内角的和大于90°,小于90°为不可能事件.【变式2】下列说法中不正确的是().A.不可能事件的概率为0,必然事件的概率为1B.某人射击9次,击中靶3次,则他击中靶的概率为13 C.“直线y=k(x+1)过定点(-1,0)”是必然事件D.“将一个骰子抛掷两次,所得点数之和大于7”是随机事件【答案】B。
正确区分三种“事件”

正确区分三种“事件”吴育弟日常生活中我们遇到的事件可分为三类:不可能事件、必然事件和不确定事件(或随机事件).不可能事件是我们事先能肯定它一定不会发生的事情,即发生的机会为0.例如抛掷1个均匀的正方体骰子,8点朝上;“石油工人一声吼,地球也要抖三抖”;5-3<0,都是不可能发生的,是不可能事件.不确定事件(也叫随机事件)是我们事先无法肯定它会不会发生的事情,即有时会发生,有时不会发生,发生的机会有大有小,介于0和1之间.例如2元钱买一张体育彩票中了500万;班级里有同年同月同日生的同学;明日有大风;直角三角形是轴对称图形,都是随机事件(或不确定事件).必然事件是我们事先能肯定它一定发生的事情,即不可能不发生,发生的机会为1.例如同一地区冬天比夏天的平均气温低;3个人分成两组,其中有一组为2人;等腰三角形的两底角相等,都是必然事件.必然事件和不可能事件都是确定事件,发生的机会分别为1和0;随机事件的发生是不确定的,发生的机会有大有小,其大小介于0和1之间.例题(2014年梅州)下列事件中是必然事件的是()A.明天太阳从西边升起B.篮球队员在罚球线上投篮一次,未投中C.实心铁球投入水中会沉入水底D.抛出一枚硬币,落地后正面朝上分析:太阳都是东升西落,所以太阳不会从西边升起,A是不可能事件;篮球队员在罚球线上投篮一次可能投中,可能投不中,所以选项B是不确定事件;根据生活常识可知实心铁球投入水中肯定会沉入水底,所以选项C是必然事件;硬币有正反两面,所以抛出去的硬币落地后可能正面朝上,也可能反面朝上,所以选项D是不确定事件.故选C.小试身手:下列事件:①随意翻到一本书的某页,这页的页码是奇数;②测得某天的最高气温是100℃;③掷一次骰子,向上一面的数字是2;④度量三角形的内角和,结果是180°.其中是随机事件的是.(填序号)答案:①③.。
2023年沪科版数学重难点易错点

2023年沪科版数学重难点易错点1相似三角形(7个考点)考点1:相似三角形的概念、相似比的意义、画图形的放大和缩小考核要求:(1)理解相似形的概念;(2)掌握相似图形的特点以及相似比的意义,能将已知图形按照要求放大和缩小。
考点2:平行线分线段成比例定理、三角形一边的平行线的有关定理考核要求:理解并利用平行线分线段成比例定理解决一些几何证明和几何计算。
注意:被判定平行的一边不可以作为条件中的对应线段成比例使用。
考点3:相似三角形的概念考核要求:以相似三角形的概念为基础,抓住相似三角形的特征,理解相似三角形的定义。
考点4:相似三角形的判定和性质及其应用考核要求:熟练掌握相似三角形的判定定理(包括预备定理、三个判定定理、直角三角形相似的判定定理)和性质,并能较好地应用。
考点5:三角形的重心考核要求:知道重心的定义并初步应用。
2锐角三角比(2个考点)考点6:锐角三角比(锐角的正弦、余弦、正切、余切)的概念,30度、45度、60度角的三角比值。
考点7:解直角三角形及其应用考核要求:(1)理解解直角三角形的意义;(2)会用锐角互余、锐角三角比和勾股定理等解直角三角形和解决一些简单的实际问题,尤其应当熟练运用特殊锐角的三角比的值解直角三角形。
3二次函数(4个考点)考点8:函数以及函数的定义域、函数值等有关概念,函数的表示法,常值函数考核要求:(1)通过实例认识变量、自变量、因变量,知道函数以及函数的定义域、函数值等概念;(2)知道常值函数;(3)知道函数的表示方法,知道符号的意义。
考点9:用待定系数法求二次函数的解析式考核要求:(1)掌握求函数解析式的方法;(2)在求函数解析式中熟练运用待定系数法。
注意求函数解析式的步骤:一设、二代、三列、四还原。
考点10:画二次函数的图像考核要求:(1)知道函数图像的意义,会在平面直角坐标系中用描点法画函数图像(2)理解二次函数的图像,体会数形结合思想;(3)会画二次函数的大致图像。
随机事件必然事件不可能事件关系频率的稳定性频率和概率的区别与联系

一、频率的稳定性即大量重复试验时,任何结果(事件)出现的频率尽管是随机的,却“稳定”在某一个常数附近,试验的次数越多,频率与这个常数的偏差大的可能性越小,这一常数就成为该事件的概率;二、“频率”和“概率”这两个概念的区别是频率具有随机性,它反映的是某一随机事件出现的频繁程度,它反映的是随机事件出现的可能性;概率是一个客观常数,它反映了随机事件的属性。
三、随机事件的定义:在随机试验中,可能出现也可能不出现,而在大量重复试验中具有某种规律性的事件叫做随机事件,随机事件通常用大写英文字母A、B、C等表示。
必然事件的定义:必然会发生的事件叫做必然事件;不可能事件:肯定不会发生的事件叫做不可能事件;概率的定义:1.在大量进行重复试验时,事件A发生的频率总是接近于某个常数,在它附近摆动。
这时就把这个常数叫做事件A的概率,记作P(A)。
2.m,n的意义:事件A在n次试验中发生了m次。
3.因0≤m≤n,所以,0≤P(A)≤1,必然事件的概率为1,不可能发生的事件的概率0。
四、随机事件概率的定义:对于给定的随机事件A,随着试验次数的增加,事件A发生的频率总是接近于区间[0,1]中的某个常数,我们就把这个常数叫做事件A的概率,记作P(A)。
五、必然事件包括不可能事件吗必然事件不包括不可能事件。
必然事件,在一定的条件下重复进行试验时,有的事件在每次试验中必然会发生,这样的事件叫必然发生的事件,简称必然事件。
必然事件发生的概率为1,但概率为1的事件不一定为必然事件。
不可能事件:概率论中把在一定条件下不可能发生的事件叫不可能事件。
必然事件和不可能事件统称为确定事件。
概率论术语:表示在一定条件下,必然出现的事情。
如从混有四件次品的产品中任意抽取五件,那么“其中必有一件是正品”就是一个必然事件。
是随机事件的一种极端情形。
必然事件发生的概率为1,但概率为1的事件不一定为必然事件连续型随机变量X,取值为样本空间中任意有限个点的概率为0,从整个样本空间剔除这有限个点,取到'非该有限个点'概率依然为1。
高中数学知识点题库 100必然事件、不可能事件、随机事件

1.命题甲:事件A与B是互斥事件;命题乙:事件A¯+B¯是必然事件,则命题乙是命题甲的()A、充分非必要条件B、必要不充分条件C、充要条件D、非充分也非必要条件答案:B解析:命题甲:事件A与B是互斥事件,则事件A与B不能同时发生,即A与B只能发生一件,则A¯与B¯也只能发生一件所以事件A¯+B¯是必然事件,所以命题甲可以推出命题乙.命题乙:事件A¯+B¯是必然事件,即事件A¯与B¯可能同时发生,则事件则事件A与B 也能同时发生,则事件A与B不是互斥事件,所以命题乙不能推出命题甲.所以命题乙是命题甲的必要不充分条件.题干评注:必然事件、不可能事件、随机事件问题评注:在一定的条件下重复进行试验时,有的事件在每次试验中必然会发生,这样的事件叫必然发生的事件,简称必然事件。
2.从12个同类产品(其中10个是正品,2个是次品)中任意抽取3个的是()A、3个都是正品B、至少有1个是次品C、3个都是次品D、至少有1个是正品答案:D解析:任意抽取3个一定会发生的事:最少含有一个正品题干评注:必然事件、不可能事件、随机事件问题评注:在一定的条件下重复进行试验时,有的事件在每次试验中必然会发生,这样的事件叫必然发生的事件,简称必然事件。
3.以下结论错误的有()①如果一件事发生的机会只有十万分之一,那么它就不可能发生;②如果一件事发生的机会达到99.5%,那么它就必然发生;③如果一件事不是不可能发生的,那么它就必然发生;④如果一件事不是必然发生的,那么它就不可能发生.A、1个B、2个C、3个D、4个答案:C解析:①如果一件事发生的机会只有十万分之一,那么它是一个小概率事件,它就不可能发生,故①正确.②如果一件事发生的机会达到99.5%,那么它有可能发生,也有可能不发生,故②不正确,③如果一件事不是不可能发生的,那么它是一个随机事件,可能发生也可能不发生,故③不正确,④如果一件事不是必然发生的,那么它是一个随机事件,可能发生也可能不发生.故④不正确.总上可知有3个结论是错误的.题干评注:必然事件、不可能事件、随机事件问题评注:在一定的条件下重复进行试验时,有的事件在每次试验中必然会发生,这样的事件叫必然发生的事件,简称必然事件。
1、什么是必然事件什么是不可能事件什么是随机事件.ppt

等可能性事件的概率可以用列举法而求得。
列举法就是把要数的对象一一列举出来分析求解 的方法.
概率的定义是什么?
一般的,在大量重复试验中,如果事件A 发生的频率m/n会稳定在某个常数p附近, 那么这个常数p就叫做事件A的概率 (probability),记为P(A)=p
0≤P(A) ≤1. 必然事件的概率是1,不可能事件的 概率是0.
由于3/8大于7/72, 所以第二步应踩B区
遇到地雷的概率为7/72,
例3:如图:计
算机扫雷游戏,在 9×9个小方格中, 随机埋藏着10个地 雷,每个小方格只 有1个地雷,,小王 开始随机踩一个小 方格,标号为3,在 3的周围的正方形中 有3个地雷,我们把 他的去域记为A区, A区外记为B区,, 下一步小王应该踩 在A区还是B区?
解:一共有7中等可能的结果。 (1)指向红色有3种结果,
P(红色)=__3_/7__ (2)指向红色或黄色一共有5种 等可能的结果,P( 红或黄)=__5_/_7___ (3)不指向红色有4种等可能的结果解:A区有8格3个雷,
遇雷的概率为3/8, B区有9×9-9=72个小方格, 还有10-3=7个地雷,
1.出现的结果有限多个;
2.各结果发生的可能性相等; 在P(A)=m/n中,分子m
等可能性事件的概率可以用列和目举分,两母法者n有而都何表求区示得别结,。它果们的之数
归纳:
间有怎样的数量关
一般的,如果在一次实验中,系能有大?Pn于(种A1)吗可可?能能小的于吗?可
结果,并且它们发生的可能性都相等,事件包
1、什么是必然事件?什么是不可能事件? 什么是随机事件?
2、随机事件应注意什么?
(1) 试验应在相同条件下; (2)可以重复大量试验;
正确区分三种“事件”

正确区分三种“事件”吴育弟日常生活中我们遇到的事件可分为三类:不可能事件、必然事件和不确定事件(或随机事件).不可能事件是我们事先能肯定它一定不会发生的事情,即发生的机会为0.例如抛掷1个均匀的正方体骰子,8点朝上;“石油工人一声吼,地球也要抖三抖”;5-3<0,都是不可能发生的,是不可能事件.不确定事件(也叫随机事件)是我们事先无法肯定它会不会发生的事情,即有时会发生,有时不会发生,发生的机会有大有小,介于0和1之间.例如2元钱买一张体育彩票中了500万;班级里有同年同月同日生的同学;明日有大风;直角三角形是轴对称图形,都是随机事件(或不确定事件).必然事件是我们事先能肯定它一定发生的事情,即不可能不发生,发生的机会为1.例如同一地区冬天比夏天的平均气温低;3个人分成两组,其中有一组为2人;等腰三角形的两底角相等,都是必然事件.必然事件和不可能事件都是确定事件,发生的机会分别为1和0;随机事件的发生是不确定的,发生的机会有大有小,其大小介于0和1之间.例题下列事件中是必然事件的是()A.明天太阳从西边升起B.篮球队员在罚球线上投篮一次,未投中C.实心铁球投入水中会沉入水底D.抛出一枚硬币,落地后正面朝上分析:太阳都是东升西落,所以太阳不会从西边升起,A是不可能事件;篮球队员在罚球线上投篮一次可能投中,可能投不中,所以选项B是不确定事件;根据生活常识可知实心铁球投入水中肯定会沉入水底,所以选项C是必然事件;硬币有正反两面,所以抛出去的硬币落地后可能正面朝上,也可能反面朝上,所以选项D 是不确定事件.故选C.小试身手:下列事件:①随意翻到一本书的某页,这页的页码是奇数;②测得某天的最高气温是100℃;③掷一次骰子,向上一面的数字是2;④度量三角形的内角和,结果是180°.其中是随机事件的是.(填序号)参考答案:①③.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
对随机事件、必然事件和不可能事件判断不清
判断下列事件哪些是确定事件, 哪些是不确定事件(随机事件)?.
1 有4名同学,其中有一班的,有二班的,也有三班的,
例
则他们中间有2名同学是同一个班的.
2 从有理数中任取一个数,平方之后比0大.
1 有4名同学,其中有一班的,有二班的,也有三班的,
则他们中间有2名同学是同一个班级的.
2 从有理数中任取一个数,平方之后比0大.
解:
正确解答
1 是不确定事件 随机事件; 2 是确定事件.
解:Biblioteka 1 是确定事件; 2 是不确定事件 随机事件 .
回顾反思
错解没有准确把握确定事件与 不确定事件(随机事件)的概念,对事 件作出了错误的判断.
神龙教育
神龙教育
制作
同行 配套课件
《同行》学案 教师用书课件 数学(青岛版)9年级下册
易错点
必然事件和不可能事件都为确定事件. 必然事件是一定会发生的事件. 不可能事件是一定不会发生的事件. 随机事件(不确定事件)是不一定发生的事件. 对这些概念理解不深,容易在判断时产生混淆,特 别是不可能事件和不确定事件. 所以要准确理解概念的内涵,注意区分它们之 间的不同.
