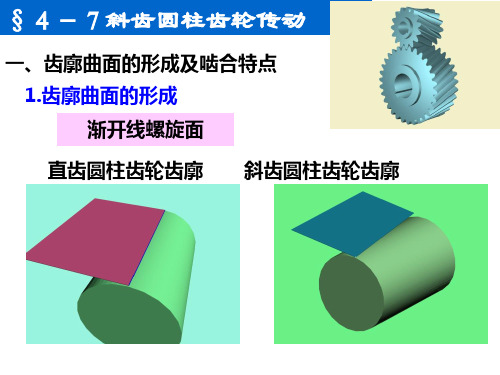
齿廓曲面的形成
斜齿圆柱齿轮齿廓曲面

斜齿圆柱齿轮齿廓曲面
斜齿圆柱齿轮齿廓曲面是一种在机械工程中广泛应用的曲面。
它由两个相交的螺旋线组成,其中一个螺旋线是凸轮螺旋线,另一个是凹槽螺旋线。
斜齿圆柱齿轮齿廓曲面的形成过程比较复杂。
首先,我们需要对齿轮的齿廓进行设计。
在设计时,我们需要考虑齿轮的模数、齿数、压力角、齿高、螺旋角等参数。
这些参数将决定齿轮的形状、大小和功能。
接下来,我们通过计算机辅助设计软件(CAD)进行建模。
在建模过程中,我们需要使用各种数学公式和计算机软件技术来创建斜齿圆柱齿轮齿廓曲面。
这些曲面由凸轮螺旋线和凹槽螺旋线组成,它们在齿轮的两侧交替出现,形成了独特的齿形。
最后,我们通过计算机辅助制造(CAM)软件进行加工。
在加工过程中,我们需要使用数控机床等设备,按照设计好的模型进行切削加工。
切削完成后,我们还需要进行精加工和检验等工序,以确保齿轮的精度和质量符合要求。
总之,斜齿圆柱齿轮齿廓曲面是一种在机械工程中具有重要应用价值的曲面。
它的形成需要经过多个步骤和复杂的计算过程。
通过科学合理的设计和精确的制造加工,我们可以得到高质量的斜齿圆柱齿轮,为机械设备的运行提供稳定、可靠的传动装置。
《机械基础》(教程全集)8章

模数
压力角 螺旋角 齿顶高系数 顶隙系数 全齿高
α β
齿顶高
齿根高 分度圆直径 齿顶圆直径 齿根圆直径 中心距 a d
==
=(+)=1.25 d=z=z/cosβ =d+2=(z/cosβ+2) =d-2=(z/cosβ-2.5) a=(+)/2=(+)/2cosβ
8.5.3斜齿圆柱齿轮传动的正确啮合条件 一对外啮合斜齿轮的正确啮合条件是:两轮的法向模数和法向压 力角必须分别相等,且两轮的螺旋角必须大小相等、旋向相反 (内啮合时旋向相同),即式中,“-”表示旋向相反。
轮即将脱离接触,故B1为轮齿的终止啮合点。
根据分析,齿轮连续传动的条件是:两齿轮的实际啮合线B1B2应大于 或等于齿轮的基圆齿距pb。通常把B1B2与pb的比值ε 称为重合度,只 要重合度ε ≥1齿轮就可连续传动。 齿轮传动的重合度越大,则同时参与啮合的轮齿越多,不仅传动平稳 性好,每对轮齿所分担的载荷亦小,相对地提高了齿轮的承载能力。
8.5.4斜齿圆柱齿轮传动的重合度 图8-11所示为斜齿圆柱齿轮传动啮合线图。由于螺旋齿面的原因,从 啮合始点A到啮合终点A′比直齿轮传动的B至B′要长,f=btanβ ,b为 齿宽。分析表明,斜齿圆柱齿轮传动的重合度可表达为 ε =ε α +ε β (8-14) 式中,ε α 为端面重合度,其大小与同齿数的直齿圆柱齿轮传动相同; ε β 为纵向重合度,ε β =btanβ /pt。总重合度ε 随着β 的增大而增 加。 总重合度β 可用公式计算或查线图求得(详见《机械零件设计手册》)。
由于斜齿轮的螺旋形轮齿使一对轮齿的啮合过程延长、重合度增大,因此斜齿轮较
直齿圆柱齿轮传动平稳、承载能力大。但斜齿轮在传动中有轴向力Fa,为了克服这一 缺点,可采用人字齿轮,使两边产生的轴向力Fa相互抵消。人字齿轮制造比较困难, 精度较低,主要用于重型机械。
斜齿圆柱齿轮齿廓曲面的形成

斜齿圆柱齿轮齿廓曲面的形成
斜齿圆柱齿轮齿廓曲面的形成是通过两个齿轮之间的啮合过程。
其中一个齿轮被称为驱动齿轮,另一个齿轮被称为从动齿轮。
首先,确定齿轮的基本参数,包括齿数、模数、压力角等。
然后,根据这些参数计算出齿轮的尺寸和齿廓曲线的形状。
齿廓曲线的形状是通过齿轮的插齿切削来制造的。
插齿切削是一种将切削刀具沿着齿轮齿廓的方向进行切削的方法。
切削刀具的形状和尺寸与所需的齿廓曲线形状相对应。
插齿切削的过程中,切削刀具的齿形会逐渐将齿轮齿廓形成,而切削刀具和齿轮之间的相对运动会导致材料的去除。
最终,通过连续的切削动作,将齿轮的齿廓逐渐形成。
需要注意的是,斜齿圆柱齿轮的齿廓曲面是斜的,而不是垂直于齿轮轴线的。
这是为了使齿轮的啮合更加平稳。
总的来说,斜齿圆柱齿轮齿廓曲面的形成是通过插齿切削将切削刀具沿着齿轮齿廓的方向进行切削,使齿轮的齿廓逐渐形成。
齿轮的齿廓曲线
该比值称为模数
m=p/π
于是有: d=mz, r = mz/2
模数的单位:mm,它是决定齿轮尺寸的一个基本参 数。齿数相同的齿轮,模数大,尺寸也大。
Z=18 不同模数的齿轮
为了便于制造、检验和互换使用,国标GB1357 -87规定了标准模数系列。
Tab 10-1 modules of Involute Cylindrical Gears
First series
0.12, 0.15, 0.2, 0.25, 0.3, 0.4, 0.5, 0.6, 0.8, 1, 1.25, 1.5, 2, 2.5, 3, 4, 5, 6, 8, 10, 12, 16, 20, 25
Second series
0.35, 0.7, 0.9, 1.75, 2.25, 2.75, (3.25), 3.5, (3.75), 4.5, 5.5, (6.5), 7, 9, (11), 14, 18, 22, 28, (30)
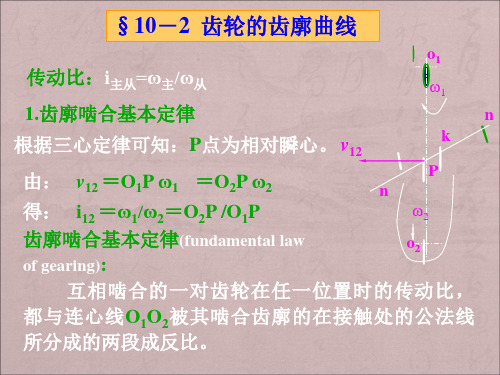
互相啮合的一对齿轮在任一位置时的传动比,
都与连心线O1O2被其啮合齿廓的在接触处的公法线 所分成的两段成反比。
如果要求传动比为常数,则应使O2P/O1P为常数。
由于O2 、O1为定点,故P必为一个定点,称为节点
(the pitch point) 。
o1
节圆(the pitch circle):
r’1
一、外齿轮(external gear)
1.名称与符号
分度圆(d 和 r)
齿距pk 齿厚sk 齿槽宽ek 分度圆 齿顶圆
齿顶圆(da 和 ra)
齿根圆(df 和 rf) 齿顶高ha
基圆 齿根圆
基圆(db 和 rb)
齿数 厚sk
z齿齿距槽pk宽ek齿
齿轮机构

齿轮机构(Gears)是现代机械中应用最广泛的一种传动机构,与其它传动机构相比,齿轮机构的优点是:结构紧凑,工作可靠,效率高,寿命长,能保证恒定的传动比,适用的范围广。
齿轮机构可以分为定传动比齿轮机构和变传动比齿轮机构。
本章仅讨论定传动比的齿轮机构。
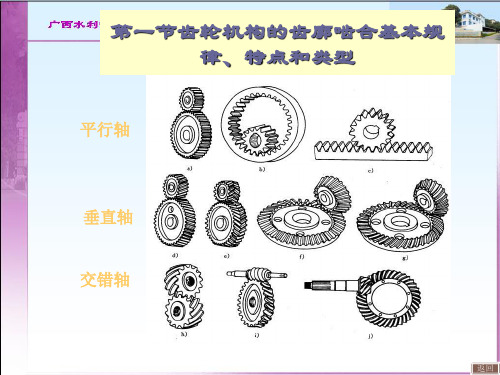
齿轮机构的类型很多,根据其传动轴线的相对位置,它可分为三类:1、平行轴齿轮机构(Gears with Parallel Axes)两齿轮的传动轴线平行,这是一种平面齿轮机构,如表5-1所示。
它可分为:外啮合齿轮机构(有直齿轮、斜齿轮和人字齿轮传动三类)内啮合齿轮机构(有直齿轮和斜齿轮传动两类)齿轮齿条机构(有直齿条和斜齿条传动两类)点击表中图形,观察各类齿轮传动的运动特点和齿形。
表5-1 平行轴齿轮机构2、相交轴齿轮机构(Gears with Intersecting Axes)两齿轮的传动轴线相交于一点,这是一种空间齿轮机构,如表5-2所示。
它有直齿圆锥齿轮传动、斜齿圆锥齿轮传动和曲线齿圆锥齿轮传动。
表5-2 相交轴齿轮机构ff3、交错轴齿轮机构(Gears with Skew Axes)两齿轮的传动轴线为空间任意交错位置,它也是空间齿轮机构,如表5-3所示。
表5-3 交错轴齿轮机构此外,还有实现变传动比运动的非圆齿轮机构(Non-circular Gear),如下图所示。
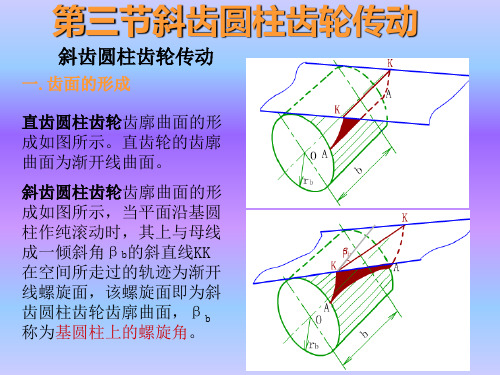
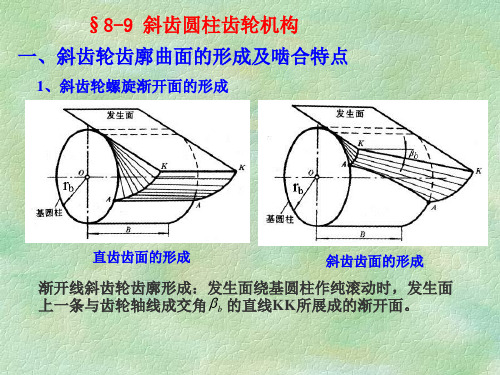
图5-2一、斜齿圆柱齿轮齿廓曲面的形成渐开线直齿齿廓曲面的生成原理如图5-33a 所示,发生面S在基圆柱上作纯滚动时,其上与基圆柱母线平行的直线KK所展成的渐开面即为直齿轮的齿面。
(a) (b) (c)图5-33斜齿轮的齿面形成原理如图5-34a所示,发生面S 沿基圆柱纯滚动时,其上一条与基圆柱母线呈βb角的直线KK所展成的渐开螺旋面就是斜齿轮的齿廓曲面。
(a) (b) (c)图5-34一对直齿轮啮合时,齿面的接触线与齿轮的轴线平行(图5-33b),而一对斜齿轮啮合时,齿面接触线是斜直线(图5-34b),接触线先由短变长,而后又由长变短,直至脱离啮合。
齿轮机构的齿廓啮合基本规律特点和类型
第八节 直齿圆锥齿轮传动
圆锥齿轮传动用来传递相交 两轴的运动和动力。
分直齿圆锥齿轮和曲 齿圆锥齿轮
返回
一、传动比和几何尺寸计算
1)分度圆:d1=mz1, d2=mz2 2)齿顶高:ha=m, 齿根高:hf=1.2m
3)传动比:i12= d2/d1 = z2/z1
=ctg δ1=tg δ2
1 2 2 d1 d 2 2 注意:分度圆锥角:δ1=arcctg i12, δ2= 900-δ1 齿顶角:θa1= θa2=arctg ha/R, 齿根角: θf1= θf2=arctg hf/R 锥距: R
图5-20 背锥及当量齿数
平行轴
垂直轴
交错轴
返回
一、齿轮机构的特点和类型
(一)平行轴线齿轮传动
返回
(二)空间齿轮传动
5
返回
齿轮传动的基本要求
传动准确和平稳(任意瞬时传动比恒定)------由齿
轮轮廓和制造精度决定。
传动比
1 i12 2
承载能力强(足够强度、刚度、耐磨)--------由齿
轮尺寸、材料和工艺决定。
返回
三、正确啮合条件
mn1= mn2 =m αn1= αn2=200 β1= -β2外啮合 (mt1= mt2 ) (αt1= αt2) ( β1=β2内啮合 )
返回
四、当量齿数
图5-18 斜齿圆柱齿轮的当量齿数
zmt 2 d z zv 2 3 pn pn cos pt cos cos3
5、分度圆---圆周上的 P/ π =m(模数)为标准值 GB1357-87,压力角α亦为标准值的圆。 d=m Z,α=200,标准齿轮 P=s+e,s=e= π m/2
第三节斜齿圆柱齿轮传动
轴向力Fa的方向用左、右手定则来判断:主动轮为右旋 齿轮时,用右手握轴,四指弯曲方向为主动轴的旋转方 向,伸直的大拇指指向为主动轮的轴向力Fa的方向;主 动轮为左旋齿轮时,左手握轴,判断方法相同。从动轮 的轴向力Fa的方向,与主动轮的相反。
斜齿轮受力分析例题:
分析斜齿轮1轮齿的旋向及齿轮1、2的受力
第三节斜齿圆柱齿轮传动
斜齿圆柱齿轮传动
一.齿面的形成
直齿圆柱齿轮齿廓曲面的形 成如图所示。直齿轮的齿廓 曲面为渐开线曲面。
斜齿圆柱齿轮齿廓曲面的形 成如图所示,当平面沿基圆 柱作纯滚动时,其上与母线 成一倾斜角βb的斜直线KK 在空间所走过的轨迹为渐开 线螺旋面,该螺旋面即为斜 齿圆柱齿轮齿廓曲面,βb 称为基圆柱上的螺旋角。
数称为当量齿数,用 z v表示。铣刀 刀号应z v 按照选取
图 6-40
为确定当量齿数 z v ,如图4-30
所示。过斜齿轮分度圆上C点,作 斜齿轮法面剖面,得到一椭圆。 该剖面上C点附近的齿型可以视为 斜齿轮的法面齿型。以椭圆上点C
的曲率半径 作为虚拟直齿轮的
分度圆半径,并设该虚拟直齿轮 的模数和压力角分别等于斜齿轮 的法面模数和压力角,该虚拟直 齿轮即为当量齿轮,其齿数即为 当量齿数。
图a所示为一直齿条的情况,其上法面 和端面是同一个平面,所以有:
n t
对于斜齿条来说,因为轮齿倾斜了一个角 ,
于是就有端面与法面之分,如图b所示的斜齿条。
abc平面为端面,a'b'c为法面。 abc 即为端 面压力角,a 'b ' c为法面压力角。
由于 abc 和 a'b'c 这两个直角三角形等高,
所以
mn mt cos
斜齿和蜗杆传动
2、蜗杆的特性系数
q=d1/ma1
则:d1=qma1=qmt2
规定q与ma1取一系列标准的对应值,如ma1=10时, 只能 取q=8。
3、标准中心距
a=r1+r2=ma1q+ mt2z2= mt2(q+z2)
4、其它尺寸参照齿轮与齿条的啮合来计算
主剖面相当于齿条,则蜗轮在主剖面内相当于渐开线齿轮。
2、在主剖面内,蜗杆蜗轮的啮合相当于齿条与齿轮的啮合。
3、正确啮合条件
2 +1= 90º ma1=mt2 a1=t2
四、蜗杆蜗轮的几何尺寸
设蜗杆的头数为Z1,升角为,导程为l
1、分度圆直径
蜗杆:d1=l/tg=z1pa1/ tg=z1ma1/ tg
直线形刀刃,刀刃与蜗杆轴线在同一水平面内。
蜗杆齿呈螺旋形,分为左旋和右旋,其螺旋升角为 ,螺旋角为 1 ,
存在如下关系:
1 90o
蜗轮是用蜗杆状的刀具,采用范成法加工。
2、蜗杆的齿形 蜗杆齿形
轴剖面:齿形为直线 法面:齿形为曲线
3、啮合状态
端面:齿形为阿基米德螺旋线
对于两轴的交错角=90º的传动
=1+2=90º =2
蜗轮的圆柱面作成内凹弧形, 部分地包柱蜗杆。一般蜗杆 为主动件。
4、传动特点
传动比大,传动平稳,传动效
率低,一般 =0.7~0.8,自锁 蜗杆 <0.5
通常蜗杆的头数即齿数Z1=1~4
三、蜗杆蜗轮的正确啮合条件
主剖面
1、主剖面:过蜗杆的轴线作垂直与蜗轮轴线的剖面。 蜗轮是用与蜗杆类似的滚刀按啮合关系加工的。蜗杆在
4、斜齿轮传动会产生轴向力。
§8-10 蜗杆蜗轮机构
(完整版)齿轮的齿廓曲线

Fn rk
NB rb k k KA0
力方向与速度方向所夹锐角
O
为渐开线上该点之压力角
αk(pressure angle)。
基圆
rb=rk cosαk
离中心越远,渐开线上的压力角
越大。基圆上的压力角为0。
(4)渐开线形状取决于基圆 基圆越大,渐开线越平直,
当rb→∞,变成直线。
Σ3 Σ1
Σ2
互相啮合的一对齿轮在任一位置时的传动比,
都与连心线O1O2被其啮合齿廓的在接触处的公法线 所分成的两段成反比。
如果要求传动比为常数,则应使O2P/O1P为常数。
由于O2 、O1为定点,故P必为一个定点,称为节点
(the pitch point) 。
o1
节圆(the pitch circle):
r’1
发生线
K
当直线沿一圆周作相切纯滚 动时,直线上任一点的轨迹 AK,称为该圆的渐开线。
B
rb
定直线
基圆
A
k
O
二、渐开线的性质
发生线
(1)BK = A B
(2) BK为渐开线在K点的法 线,又因发生线恒切于基 圆,故知渐开线上任意点 的法线切于基圆。
(3)渐开线上点K的压力角 定义:啮合时K点正压
Vk
(5)基圆内无渐开线。
B2
B1
rb1
思考:10-20
K
KO2
o2 KO1 o1
三、渐开线方程式及渐开线函数
αk
k
rk是渐开线在任意点K的向径。当渐开线与 vk
r r cos 其共轭齿廓在K点啮合时,在三角形BOK
中
A
θk
b
K
《机械设计基础》第6章 齿轮传动(2)

斜齿轮传动的重合 度比直齿轮大
五、斜齿圆柱齿轮的当量齿数
用仿形法加工斜齿轮时,为便于选择刀号,应了 用仿形法加工斜齿轮时,为便于选择刀号, 解斜齿轮的法面齿形。 解斜齿轮的法面齿形。 一法平面与斜齿轮分度圆柱的交线为一椭圆, 一法平面与斜齿轮分度圆柱的交线为一椭圆, 如图,其长半轴a和短半轴b分别为: 如图,其长半轴a和短半轴b分别为:
⑵斜齿轮齿廓曲面的形成 发生面上与基圆柱母线成一角度β 的直线KK KK, 发生面上与基圆柱母线成一角度βb的直线KK, 在基圆柱上纯滚动时,直线KK KK在空间所展出的轨迹 在基圆柱上纯滚动时,直线KK在空间所展出的轨迹 为一渐开螺旋面,此曲面即为斜齿轮的齿廓曲面 斜齿轮的齿廓曲面。 为一渐开螺旋面,此曲面即为斜齿轮的齿廓曲面。
tan β =
πd
ps
, tan βb =
πdb
ps
所以: 所以:
tanβb=tanβcos αt β β
模数(m ⑵ 模数 n和mt) 由图可得, 由图可得, pn=ptcosβ pn=mnπ, pt=mtπ 因为 mn=mtcosβ 所以有 ⑶压力角(αn和αt) 压力角 由图可得, 由图可得,
五、斜齿圆柱齿轮的受力分析(如图) 斜齿圆柱齿轮的受力分析(如图)
由力矩平衡条件可得: 由力矩平衡条件可得: 圆周力: 圆周力: 径向力: 径向力: 轴向力: 轴向力:
2 T1 Ft = d1
Ft tanαn Fr = Fn′ tanαn = cosβ
Fa = Ft tanβ
的方向: 圆周力 Ft 的方向:在主动轮上 F t 对其轴之矩与转动 方向相反; 对其轴之矩与转向相同。 方向相反;在从动轮上 Ft 对其轴之矩与转向相同。 的方向:对两轮都是指向各自的轮心。 径向力 Fr 的方向:对两轮都是指向各自的轮心。
第三节渐开线齿廓的形成及特点

N1
C
N
K
O2
二、渐开线齿廓的啮合特点 ——满足齿廓啮合基本定律
渐开线齿轮的传动比
基圆的公切线是一 条定直线,与连心线只 能交于固定点C,因此 能实现传动比恒定的传 动。
O1
N1
C
N
i
O2 C O1C
K
N
r '2 r '1 rb 2 rb 1
N2
O2
二、渐开线齿廓的啮合特点 ——满足齿廓啮合基本定律
二、渐开线齿廓的啮合特点 ——中心距可分性
当齿轮制成后,基 圆半径rb已确定,传动 比i=rb2 /rb1, 即使有制 造、安装的误差或轴承 磨损导致中心距变更时, 其传动比仍保持不变, 这一特性称为中心距可 分性。它给齿轮的制造 和安装带来了很大的方 便。 由于上述特性,工 程上广泛采用渐开线齿 廓曲线。
i
O2C O1C
r '2 r '1
rb 2 rb1
渐开线齿轮的传动比等于节圆半径的反 比,也等于基圆半径的反比。啮合点一定在 公切线 N1N2 上移动, N1N2 称为啮合线。 过节点作的圆称为节圆,一对齿轮啮合时 才出现节圆,单个齿轮没有节圆,也就不存在 节点。 一对齿轮传动时,相当于它的一对节圆 作纯滚动。
二、渐开线齿廓的啮合特点 ——中心距可分性
齿轮工、车工和铣工配换交 换齿轮时,都凭目测安装,安装 中心距与设计中心距可能会有误 差,这对齿轮传动质量会有影响 吗?
1 r rb 2 i12 2 r rb1
' 2 ' 1
齿轮制成后,基圆半径已 定,即使中心距稍有变动, 传动比仍不变。
二、渐开线齿廓的啮合特点
斜齿圆柱齿轮齿廓曲面 -回复

斜齿圆柱齿轮齿廓曲面-回复
什么是斜齿圆柱齿轮齿廓曲面?如何计算和绘制斜齿圆柱齿轮的齿廓曲面?本文将一步一步地回答这些问题。
第一步:理解斜齿圆柱齿轮齿廓曲面的概念。
斜齿圆柱齿轮是一种常见的齿轮类型,其特点是齿廓不是圆弧形状,而是呈扭曲的曲线形状。
齿廓曲面是指齿轮上的每个齿的侧面形状。
第二步:了解斜齿圆柱齿轮齿廓曲面的计算方法。
斜齿圆柱齿轮的齿廓曲线由以下几个参数确定:齿数、模数、齿轮厚度、螺旋角和齿廓曲线形状。
第三步:计算斜齿圆柱齿轮齿廓曲面的具体步骤。
首先,确定齿廓曲线的形状。
常见的曲线形状有渐开线、圆滚线和正弦曲线。
其次,根据齿数和模数计算每个齿的基圆半径和压力角。
然后,根据基圆半径和螺旋角计算每个齿的齿廓角度。
最后,根据齿廓曲线的形状和齿廓角度,计算出齿廓曲线的具体坐标点。
第四步:绘制斜齿圆柱齿轮齿廓曲面。
在计算出齿廓曲线的坐标点后,可以使用计算机辅助设计软件或CAD软件绘制齿廓曲线。
将齿廓曲线绘制在齿轮的侧面上,就可以得到斜齿圆柱齿轮的齿廓曲面。
总结起来,斜齿圆柱齿轮齿廓曲面是指齿轮上的齿的侧面形状,它的计算
和绘制需要考虑参数如齿数、模数、齿轮厚度、螺旋角和齿廓曲线形状等。
通过一系列的计算和绘制步骤,可以得到斜齿圆柱齿轮的齿廓曲面。
机械设计基础第五章下
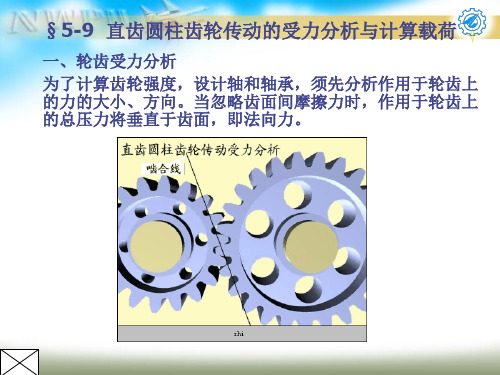
斜齿圆柱齿轮传动的设计特点
当量齿轮的形成示意
长半轴 a =d / 2cosβ 短半轴 b = d / 2 则椭圆在C点曲率半径为 a2 d b 2 cos2
以为半径,以法向模数mn、标准压力角αn作出的假想 直齿圆柱齿轮的齿形,与斜齿轮的法向齿廓十分接近。 该假想的直齿圆柱齿轮称为该斜齿圆柱齿轮的当量齿轮, 其齿数Zv称为当量齿数。 mn Z 2 d Z Zv 2 3 mn mn cos mn cos cos3 Zv>Z,故Zmin<17例:β=15°Zmin=15 β=30° Zmin=11
1) 端面模数mt和法向模数mn 见斜齿轮展开图:Pn为法向齿距, Pt为端面齿距。mn为法向模数, mt为端面模数。 Pn=Pt · cosβ mn=mt · cosβ
斜齿圆柱齿轮传动的设计特点
2) 端面压力角αt和法向压力角αn 以齿条为例,可推导出:
tg t
tg n
cos
法面参数为标准值 3、重合度 由于斜齿轮接触线是倾斜的, 它的实际啮合线比直齿有所 增加。 直齿 = L / pb 斜齿 = + = +btgb/pb b↑ β↑ ε↑ 直齿<1.98 斜齿可达10
斜齿圆柱齿轮传动的设计特点
二、基本参数和尺寸计算 1、螺旋角β β是反映斜齿轮特征的一个重要参数,不同圆上的螺旋角 不同,若不特别注明,β是指分度圆柱面上的螺旋角。 β↑ ε↑ 平稳↑ 但Fa↑ 推荐:β=10°~25° 有特殊噪声要求 β可更高。 2、端面参数和法面参数关系(见图5-36 5-37)
一、选择题 1、开式齿轮传动的主要失效是( ) (a)齿面胶合 (b)齿面点蚀 (c)齿面磨损 2、渐开线齿轮传动,齿形系数YFS只与齿轮的( )有关。 (a)模数m (b)齿数Z (c)基圆直径 3、复合齿形系数YFS与Z的关系是( )。 (a)随Z的增大而增大 (b)随Z的增大而减小 (c)与Z无关 4、齿轮的齿面接触应力是( )。 (a)按对称循环变化的 (b)按脉动循环变化的 (c)不变化 5、正变位齿轮与标准齿轮相比,分度圆上的齿距( )。 (a)变大 (b)变小 (c)不变
A第四章齿轮 - 03
2.背锥及当量齿轮
r
δ
R1z 当量齿数: 源自v cose e’p
f δ f’
1
zv用途: ①选择盘状铣刀的刀号; ②计算弯曲强度时,按zv查齿形系数; ③不发生根切的最少齿数
zmin = zvmin cosδ =17 cosδ
rv
O1
rv
二、正确啮合条件
规定:大端参数为标准值.
m1=m2=m
轴面重合度εβ:
B1
B2
B
B1 B1 B2 B2
B sin
mn
β
B↑,β↑→εβ↑,ε↑
β
b
b
B
B2
△L
B1
L
1 端面重合度εα: [ z1 (tg at1 tg t ) z 2 (tg at 2 tg t )] 2
六、当量齿轮和当量齿数zv
β β
b
右旋
β β β l
左旋
tg d 1 tg b d b cos t
d
tgβ b = tgβ cosαt
αt为端面压力角
π db β
πd
2.法面模数mn和端面模数mt
Pn = Pt cosβ
πmn =πmt cosβ 法面
mn = mtcosβ
pt
端面
3.法面压力角αn和端面压力角αt ab =a′b′
∑
同时指向啮合点
或同时背离啮合点
分类: 按齿形分:直齿、斜齿、曲齿
直齿
斜齿
曲齿
按啮合方式分:
外啮合、内啮合、平面啮合
外啮合
内啮合
平面啮合
一、齿廓的形成
1.理论齿廓:
一个圆平面在一圆锥上作纯滚动时,平面上任一点的轨迹,到 锥顶距离相等,形成一条球面渐开线。 发生面 O2
平行轴斜齿圆柱齿轮传动

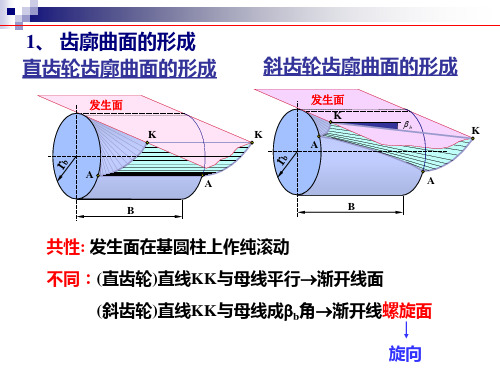
平行轴斜齿圆柱齿轮传动一、斜齿圆柱齿轮齿廓曲面的形成、啮合特点及应用1、斜齿圆柱齿轮齿廓曲面的形成和特点由于圆柱齿轮是有一定宽度的,因此轮齿的齿廓沿轴线方向形成一曲面。
直齿轮轮齿渐开线曲面的形成如图所示。
平面与基圆柱相切于母线,当平面沿基圆柱作纯滚动时,其上与母线平行的直线KK在空间所走过的轨迹即为渐开线曲面,平面称为发生面,形成的曲面即为直齿轮的齿廓曲面。
斜齿圆柱齿轮齿廓曲面的形成如图所示,当平面沿基圆柱作纯滚动时,其上与母线成一倾斜角βb的斜直线KK在空间所走过的轨迹为渐开线螺旋面,该螺旋面即为斜齿圆柱齿轮齿廓曲面,βb称为基圆柱上的螺旋角。
直齿圆柱齿轮啮合时,齿面的接触线均平行于齿轮轴线。
因此轮齿是沿整个齿宽同时进入啮合、同时脱离啮合的,载荷沿齿宽突然加上及卸下。
因此直齿轮传动的平稳性较差,容易产生冲击和噪声,不适合用于高速和重载的传动中。
一对平行轴斜齿圆柱齿轮啮合时,斜齿轮的齿廓是逐渐进入啮合、逐渐脱离啮合的。
如图所示,斜齿轮齿廓接触线的长度由零逐渐增加,又逐渐缩短,直至脱离接触,载荷也不是突然加上或卸下的,因此斜齿轮传动工作较平稳。
2、应用由于斜齿轮传动有上述这些特点,因而不论从受力或传动来说都要比直齿轮传动好,所以在高速大功率的传动中,斜齿轮传动应用广泛。
但是,由于斜齿轮的轮齿是螺旋形的,因而比直齿轮传动要多一个轴向分力。
必要时可采用人字齿以消除轴向力。
二、渐开线斜齿圆柱齿轮的基本参数及几何尺寸计算螺旋角分度圆柱面上的螺旋线的切线与与齿轮轴线之间所夹的锐角(或展开图上斜直线与直母线之间所夹的锐角)称为齿轮的螺旋角,以β表示,为使斜齿轮传动时不产生过大的轴向推力,设计时一般取=8~12度。
2)法面参数(下标为n):在垂直于轮齿方向截面内定义的参数,法面齿形为端面齿形的投影。
由于在切制轮齿时,刀具进刀的方向一般是垂直于法面的,帮其参数与法面参数相同,所以规定法面参数取标准值。
法面摸数mn符合国家规定的标准摸数系列表(GB/T1357-87).法面压力角法面齿顶高系数法面顶隙系数端面参数(下标为t):垂直于齿轮回转轴线的截面内定义的参数,主要用于几何尺寸计算。
α'啮合角与α压力角的关系
2、相互啮合的一对斜齿轮 齿廓曲面的形成
特点1: 一个左旋、另一个右旋
齿面接触线
1
线为斜线 逐渐进入/脱离啮合(加载/卸载) 传动平稳,冲击,振动,噪音小
斜齿圆柱齿轮
直齿圆柱齿轮
直齿轮: 齿面接触线与齿向(轴线)平行 突然进入/脱离啮合(加载/卸载) 传动平稳性差,冲击,振动,噪 音大
a' c tana n a' b'
ab ab'
ac tana t a' b'
a
at
a’
an c
ac' ac cos
tanat=
tanan/cos
3、 正确啮合条件
mn1 mn 2 a n1 a n 2 2 1
1、 齿廓曲面的形成 直齿轮齿廓曲面的形成
发生面 K K
斜齿轮齿廓曲面的形成
发生面 发生面 K A
b
K
A B
A B
A
共性: 发生面在基圆柱上作纯滚动 不同:(直齿轮)直线KK与母线平行渐开线面 (斜齿轮)直线KK与母线成b角渐开线螺旋面 旋向
螺旋线旋向判别: 将齿轮轴线垂直,前表面的螺旋线走向: 右边高——右旋 左边高——左旋
1 、法面模数 mn与端面模数 mt
分度圆柱
pt
B
展 开 d
d
端面(t-t)、法面(n-n) 端面齿距pt与法面齿距pn关系:
pn pt cos
mn mt cos
mn = mt cos
2、 法面压力角an与端面压力角at
端面压力角at与法面压力角an关系
b’ b
§10—2齿轮的齿廓曲线
以O1为圆心,O1P为半径作圆;以O2为圆心,O2P为 半径作圆。这两个圆分别称为齿轮 、2的节圆 齿轮1、 的节圆 的节圆,节圆半径 齿轮 用r1′、r2′(节圆上的参数用带′的字母)来表示。 节圆特征: 节圆特征 ① r1′+r2′=a′:说明一对齿轮传动时, 两节圆必相切; ② 两节圆作纯滚动,因为节点是速度 瞬心,此点具有相同的绝对速度。 ∴ 定传动比传动时,两齿轮的节圆相 切作纯滚动。 ③ i12=ω1 /ω2= O2P/ O1P= r2′/ r1′,传动比 等于两节圆半径的反比。
圆盘1上的已知曲线C1就会走出一 1 C 系列的轨迹,作这些轨迹的包络 线,则得到所求的齿廓曲线C2。
三、齿廓曲线的选择 理论上,只要给出一齿廓C1 ,就可以求出另一条满足 定传动比的共轭齿廓C2。但生产实际上,选择齿廓曲线时, 不仅要满足传动比要求,还必须从设计、制造、安装和使 用等方面予以考虑。 目前对定传动比传动的齿轮来说,最常用的齿廓是渐 开线(Involute) ,其次是摆线(Cycloid) 和变态摆线,近年 来出现了圆弧(Arc) 、抛物线(Parabola) 等。 由于渐开线齿廓具有良好的传动性能,便于制造、安 装、测量和互换性好等优点,所有目前绝大部分齿轮都采 用渐开线齿廓。 本章只讨论渐开线齿轮。
二、共轭齿廓曲线(Conjugate Profiles) 共轭齿廓是指能满足啮合基本定律(即能实现预定传 共轭齿廓 动比传动)的一对齿廓。共轭齿廓在啮合时,两齿廓接触 点(啮合点)的公法线通过节点P。 理论上,只要给定一齿轮的齿廓曲线C1,并给定中心 距O1O2和传动比i12,就可以求出与之共轭的另一齿轮的齿 廓曲线C2。这一点对于齿轮的加工是很有意义的,齿轮加 工的刀具→已知的齿廓曲线,待加工齿廓的齿轮→未知曲 线。 共轭齿廓曲线的求法,有:包络线法、鲁罗图解法、 共轭齿廓曲线的求法 齿廓法线法等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
发生面 基圆柱 (base cylinder) rb K K (generating plane)
B
平行基圆柱母 线的KK线
rb
K
K
B
rb
K A
K A
B
rb
K A A
K
B
rb
K A A
K
B
K rb A A
K
B
K rb A A
K
ቤተ መጻሕፍቲ ባይዱ
B
沿齿宽同时进入与退出啮合。
K rb A A
K
B
渐开面
AA平行于基圆柱母线
与轴线垂直的平面—端面 (transverse plane)
K rb A
K
A
B
K rb A
K
A
B
K rb A
K
A
B
K rb A A
K
A
端面为渐开线。
B
K
rb
K
βb——基圆柱螺旋角 B
K rb K A
B
K rb A K
B
K K A K rb A
B
K A rb A K
B
端面为渐开线。
K K
观察与另一齿轮的啮合
按顶圆作出轮齿
K
K
前端面一点 进入啮合
接触线由 短到长
接触线由 长到短
后端面一点 退出啮合
斜齿圆柱齿轮的传动特点
(与直齿轮比较)
*1.两种齿轮的端面齿廓均为精 确的渐开线;
K K rb A B A B 精确的渐开线 K A A K
斜齿轮齿面的啮合情况
接触由点到线逐渐进入、退出啮合。
*3,接触情况:
直齿轮---同时进入、同时分离;( 直齿轮---同时进入、同时分离;( ε< 2 ) ---同时进入 斜齿轮----逐渐进入、脱离啮合( 斜齿轮----逐渐进入、脱离啮合( ε ----逐渐进入 ↑↑) ↑↑)
*斜齿轮传动平稳,减少了 冲击,振动和噪音。
B
K A K rb A
B
K A rb A K
B
K A rb A K
B
齿面与基圆柱的交线AA ——螺旋线
K A rb A K
B
K A rb A K
KK线形成齿面的轨迹——渐开螺旋面 B (involute helicoid)
K A rb A K
B
K A rb A K
B
K A rb A K
*1.两种齿轮的端面齿廓均为精确的渐开线;
平行轴线的直线
*2.齿廓与基圆柱的交线: 直齿轮----直线; ----直线 直齿轮----直线; 斜齿轮-----螺旋线. -----螺旋线 斜齿轮-----螺旋线
螺旋线
K K rb A B A B K A A K
直齿轮齿面的啮合情况
沿齿宽同时进入与退出啮合。
