函数中点的存在性问题(解析版)

合集下载

难点7-双变量的“任意性”“存在性”问题

难点7-双变量的“任意性”“存在性”问题本页仅作为文档页封面，使用时可以删除This document is for reference only-rar21year.March难点7 双变量的“任意性”与“存在性”问题1.“存在=存在”型∃x1∈D1,∃x2∈D2,使得f(x1)=g(x2),等价于函数f(x)在D1上的值域A与函数g(x)在D2上的值域B 的交集不为空集,即A∩B≠⌀.其等价转化的基本思想:两个函数有相等的函数值,即它们的值域有公共部分.典例1已知函数f(x)=x2-ax3,a>0,x∈R.g(x)=.若∃x1∈(-∞,-1],∃x2∈,使得f(x1)=g(x2),求实数a的取值范围.解析∵f(x)=x2-ax3,∴f '(x)=2x-2ax2=2x(1-ax).令f '(x)=0,得x=0或x=.∵a>0,∴>0,∴当x∈(-∞,0)时, f '(x)<0,∴f(x)在(-∞,-1]上单调递减, f(x)在(-∞,-1]上的值域为.∵g(x)=,∴g'(x)==.∵当x<-时,g'(x)>0,∴g(x)在上单调递增,∴g(x)<g=,∴g(x)在上的值域为.若∃x1∈(-∞,-1],∃x2∈,使得f(x1)=g(x2),则1+<,a<.故实数a的取值范围是.对点练已知函数f(x)=和函数g(x)=a·sin x-a+1(a>0),若存在x1,x2∈[0,1],使得f(x1)=g(x2)成立,则实数a的取值范围是( )A. B.[1,2)C. D.答案 C 设函数f(x),g(x)在[0,1]上的值域分别为A,B,则“存在x1,x2∈[0,1],使得f(x1)=g(x2)成立”等价于“A∩B≠⌀”.当0≤x≤时, f(x)=-x+单调递减,所以0≤f(x)≤;当<x≤1时, f '(x)=>0,所以f(x)=单调递增,<f(x)≤,故f(x)在[0,1]上的值域A=.当x∈[0,1]时,x∈,y=sin x在[0,1]上单调递增.又a>0,所以g(x)=asin x-a+1在[0,1]上单调递增,其值域B=.由A∩B≠⌀,得0≤1-a≤或0≤1-≤,解得≤a≤2.故选C.2.“任意=存在”型∀x1∈D1,∃x2∈D2,使得f(x1)=g(x2),等价于函数f(x)在D1上的值域A是函数g(x)在D2上的值域B的子集,即A⊆B.其等价转化的基本思想:函数f(x)的任意一个函数值都与函数g(x)的某一个函数值相等,即f(x)的函数值都在g(x)的值域之中.典例2 已知函数f(x)=,x∈[0,1].(1)求f(x)的单调区间和值域;(2)设a≥1,函数g(x)=x3-3a2x-2a,x∈[0,1].若对于任意的x1∈[0,1],总存在x∈[0,1],使得g(x0)=f(x1)成立,求a的取值范围.解析(1)f '(x)==-,x∈[0,1].令f '(x)=0,解得x=或x=(舍去).当x变化时, f '(x), f(x)的变化情况如下表所示:x01f '(x)-0+f(x)-↘-4↗-3所以f(x)的递减区间是,递增区间是.f(x)min =f=-4,又f(0)=-, f(1)=-3,所以f(x)max=f(1)=-3.故当x∈[0,1]时, f(x)的值域为[-4,-3].(2)“对于任意的x1∈[0,1],总存在x∈[0,1],使得g(x)=f(x1)成立”等价于“在x∈[0,1]上,函数f(x)的值域B是函数g(x)的值域A的子集,即B⊆A”.因为a≥1,且g'(x)=3(x2-a2)<0,所以当x∈[0,1]时,g(x)为减函数,所以g(x)的值域A=[1-2a-3a2,-2a].由B⊆A,得1-2a-3a2≤-4且-2a≥-3,又a≥1,故1≤a≤.对点练已知函数f(x)=x2-ax3(a>0),x∈R.(1)求f(x)的单调区间和极值;(2)若对于任意的x1∈(2,+∞),都存在x2∈(1,+∞),使得f(x1)·f(x2)=1.求a的取值范围.解析(1)由已知,有f '(x)=2x-2ax2(a>0).令f '(x)=0,解得x=0或x=.当x变化时, f '(x), f(x)的变化情况如下表:x(-∞,0)f '(x)-0+0-f(x)↘0↗↘所以, f(x)的单调递增区间是;单调递减区间是(-∞,0),.当x=0时, f(x)有极小值,且极小值f(0)=0;当x=时,f(x)有极大值,且极大值f=.(2)由f(0)=f=0及(1)知,当x∈时, f(x)>0;当x∈时, f(x)<0.设集合A={f(x)|x∈(2,+∞)},集合B=,则“对于任意的x 1∈(2,+∞),都存在x2∈(1,+∞),使得f(x1)·f(x2)=1”等价于A⊆B.显然,0∉B.下面分三种情况讨论:①当>2,即0<a<时,由f=0可知,0∈A,而0∉B,所以A不是B的子集.②当1≤≤2,即≤a≤时,有f(2)≤0,且此时f(x)在(2,+∞)上单调递减,故A=(-∞,f(2)),因而A⊆(-∞,0);由f(1)≥0,有f(x)在(1,+∞)上的取值范围包含(-∞,0),即(-∞,0)⊆B.所以,A⊆B.③当<1,即a>时,有f(1)<0,且此时f(x)在(1,+∞)上单调递减,故B=,A=(-∞,f(2)),所以A不是B的子集.综上,a的取值范围是.3.“任意≥(≤、>、<)任意”型∀x1∈D1,∀x2∈D2,f(x1)>g(x2)恒成立,等价于f(x)min>g(x)max,或等价于f(x)>g(x)max恒成立,或等价于f(x)min>g(x)恒成立.其等价转化的基本思想是函数f(x)的任何一个函数值均大于函数g(x)的任何一个函数值.∀x1∈D1,∀x2∈D2,f(x1)<g(x2)恒成立,等价于f(x)max<g(x)min,或等价于f(x)<g(x)min恒成立,或等价于f(x)max<g(x)恒成立.其等价转化的基本思想是函数f(x)的任何一个函数值均小于函数g(x)的任何一个函数值.∀x1∈D1,∀x2∈D2,f(x1)-g(x2)>k恒成立,等价于[f(x1)-g(x2)]min>k恒成立,也等价于f(x)min-g(x)max>k.∀x1∈D1,∀x2∈D2,f(x1)-g(x2)<k恒成立,等价于[f(x1)-g(x2)]max<k恒成立,也等价于f(x)max-g(x)min<k.典例3 设函数f(x)=x3-x2-3.(1)求f(x)的单调区间;(2)设函数g(x)=+xln x,如果对任意的x1,x2∈,都有f(x1)≤g(x2)成立,求实数a的取值范围.解析(1)f '(x)=3x2-2x.f '(x)>0时,x<0或x>,f '(x)<0时,0<x<.所以, f(x)的递增区间是(-∞,0),;递减区间是.(2)由(1)知,函数f(x)在上单调递减,在上单调递增,而f=-, f(2)=1,故f(x)在区间上的最大值f(x)max=f(2)=1.“对任意的x1,x2∈,都有f(x1)≤g(x2)成立”等价于“对任意的x∈,g(x)≥f(x)max恒成立”,即当x∈时,g(x)=+xln x≥1恒成立,即a≥x-x2lnx恒成立,记u(x)=x-x2ln x,则有a≥u(x)max.u'(x)=1-x-2xln x,可知u'(1)=0.当x∈时,1-x>0,2xln x<0,则u'(x)>0, 所以u(x)在上递增;当x∈(1,2)时,1-x<0,2xln x>0,则u'(x)<0,所以u(x)在(1,2)上递减.故u(x)在区间上的最大值u(x)max=u(1)=1,所以实数a的取值范围是[1,+∞).点拨 (1)∀x 1∈D 1,∀x 2∈D 2,f(x 1)>g(x 2)恒成立,通常等价转化为f(x)min >g(x)max .这是两个独立变量——双变量问题,不等式两边f(x 1),g(x 2)中自变量x 1,x 2可能相等,也可能不相等; (2)对任意的x∈[m,n],不等式f(x)>g(x)恒成立,通常等价转化为[f(x)-g(x)]min >0.这是单变量问题,不等式两边f(x),g(x)的自变量x 相等. 对点练函数f(x)=+1(m≠0),g (x)=x 2e ax (a∈R).(1)直接写出函数f(x)的单调区间;(2)当m>0时,若对于任意的x 1,x 2∈[0,2], f(x 1)≥g(x 2)恒成立,求a 的取值范围. 解析 (1)当m>0时,f(x)的递增区间是(-1,1);递减区间是(-∞,-1),(1,+∞). 当m<0时,f(x)的递增区间是(-∞,-1),(1,+∞);递减区间是(-1,1).(2)当m>0时,“对于任意的x 1,x 2∈[0,2],f(x 1)≥g(x 2)恒成立”等价于“对于任意的x∈[0,2],f(x)min ≥g(x)max 成立”.当m>0时,由(1)知,函数f(x)在[0,1]上单调递增,在[1,2]上单调递减,因为f(0)=1,f(2)=+1>1,所以f(x)min =f(0)=1,故应满足1≥g(x)max .因为g(x)=x 2e ax ,所以g'(x)=(ax 2+2x)e ax .①当a=0时,g(x)=x 2,此时g(x)max =g(2)=4,不满足1≥g(x)max .②当a≠0时,令g'(x)=0,得x=0或x=-.(i)当-≥2,即-1≤a<0时,在[0,2]上,g'(x)≥0,g(x)在[0,2]上单调递增,g(x)max =g(2)=4e 2a .由1≥4e 2a,得a≤-ln 2,所以-1≤a≤-ln 2.(ii)当0<-<2,即a<-1时,在上,g'(x)≥0,g(x)递增;在上,g'(x)<0,g(x)递减.g(x)max =g =,由1≥,得a≤-,所以a<-1.(iii)当-<0,即a>0时,显然在[0,2]上,g'(x)≥0,g(x)单调递增,于是g(x)max =g(2)=4e 2a >4,此时不满足1≥g(x)max .综上,a的取值范围是(-∞,-ln 2].4.“任意≥(≤、>、<)存在”型∀x1∈D1,∃x2∈D2,使得f(x1)>g(x2)成立,等价于f(x)min>g(x)min.其等价转化的基本思想是函数f(x)的任意一个函数值大于函数g(x)的某一个函数值,但并不要求大于函数g(x)的所有函数值.∀x1∈D1,∃x2∈D2,使得f(x1)<g(x2)成立,等价于f(x)max<g(x)max.其等价转化的基本思想是函数f(x)的任意一个函数值小于函数g(x)的某一个函数值,但并不要求小于函数g(x)的所有函数值.∀x1∈D1,∃x2∈D2,使得f(x1)-g(x2)>k成立,等价于f(x)min-g(x)min>k.∀x1∈D1,∃x2∈D2,使得f(x1)-g(x2)<k成立,等价于f(x)max-g(x)max<k.典例4 函数f(x)=ln x-x+-1,g(x)=x2-2bx+4,若对任意的x1∈(0,2),存在x2∈[1,2],使得f(x1)≥g(x2)成立,求实数b的取值范围.解析“对任意的x1∈(0,2),存在x2∈[1,2],使得f(x1)≥g(x2)成立”等价于“f(x)在(0,2)上的最小值不小于g(x)在[1,2]上的最小值,即f(x)min ≥g(x)min(*)”.f '(x)=--=,当x∈(0,1)时, f '(x)<0, f(x)单调递减;当x∈(1,2)时, f '(x)>0, f(x)单调递增.故当x∈(0,2)时, f(x)min=f(1)=-.又g(x)=(x-b)2+4-b2,x∈[1,2],①当b<1时,g(x)min=g(1)=5-2b>3,此时与(*)矛盾;②当b∈[1,2]时,g(x)min=g(b)=4-b2≥0,同样与(*)矛盾;③当b∈(2,+∞)时,g(x)min=g(2)=8-4b,由8-4b≤-,得b≥.综上,实数b的取值范围是.对点练已知函数f(x)=x3+x2+ax.(1)若f(x)在区间[1,+∞)上单调递增,求a的最小值;(2)若g(x)=,∀x1∈,∃x2∈,使得f '(x1)≤g(x2)成立,求a的取值范围.解析(1)由题设知f '(x)=x2+2x+a≥0,即a≥-(x+1)2+1在[1,+∞)上恒成立,而y=-(x+1)2+1在[1,+∞)上单调递减,则ymax =-3,∴a≥-3,∴amin=-3.(2)“∀x1∈,∃x2∈,使f '(x1)≤g(x2)成立”等价于“x∈时,f'(x)max ≤g(x)max恒成立”.∵f '(x)=x2+2x+a=(x+1)2+a-1在上递增,∴f '(x)max=f '(2)=8+a,又g'(x)==,∴g(x)在(-∞,1)上递增,在(1,+∞)上递减.∴当x∈时,g(x)max=g(1)=,由8+a≤得,a≤-8,所以a的取值范围是.5.“存在≥(≤、>、<)存在”型若∃x1∈D1,∃x2∈D2,使得f(x1)>g(x2)成立,等价于f(x)max≥g(x)min.其等价转化的基本思想是函数f(x)的某一个函数值大于函数g(x)的某一个函数值,即只要有这样的函数值即可.若∃x1∈D1,∃x2∈D2,使得f(x1)<g(x2)成立,等价于f(x)min<g(x)max.其等价转化的基本思想是函数f(x)的某一个函数值小于函数g(x)的某一个函数值,即只要有这样的函数值即可.若∃x1∈D1,∃x2∈D2,使得f(x1)-g(x2)>k成立,等价于[f(x1)-g(x2)]max>k,也等价于f(x)max-g(x)min>k.若∃x1∈D1,∃x2∈D2,使得f(x1)-g(x2)<k成立,等价于[f(x1)-g(x2)]min<k,也等价于f(x)min-g(x)max<k.典例5 已知函数f(x)=4ln x-ax+(a≥0).(1)直接写出函数f(x)的单调区间;(2)当a≥1时,设g(x)=2e x-4x+2a,若存在x1,x2∈,使f(x1)>g(x2),求实数a的取值范围.解析(1)当a=0时,函数f(x)的递减区间为,递增区间为.当0<a<1时,函数f(x)的递减区间为,,递增区间为.当a≥1时, f(x)的递减区间为(0,+∞).（2)“存在x1,x2∈,使f(x1)>g(x2)”等价于“ 当x∈时, f(x)max>g(x)min”.由(1)知,当x∈时, f(x)max=f=-4ln 2+a+6, 由g'(x)=2e x-4>0,得x>ln 2,所以g(x)在(0,ln 2)上单调递减,在(ln 2,+∞)上单调递增,故当x∈时,g(x)min=g(ln 2)=4-4ln 2+2a,由f(x)max >g(x)min,得-4ln 2+a+6>4-4ln 2+2a,又a≥1,所以1≤a<4.对点练设函数f(x)=-ax.(1)若函数f(x)在(1,+∞)上为减函数,求实数a的最小值;(2)若存在x1,x2∈[e,e2],使f(x1)≤f '(x2)+a成立,求实数a的取值范围.解析(1)由题设知f '(x)=-a≤0在(1,+∞)上恒成立,则只需f '(x)max≤0.又f '(x)=-a=-+-a,所以当=,即x=e2时, f '(x)max=-a,由-a≤0得a≥,故a的最小值为.11 (2)“存在x 1,x 2∈[e,e 2],使f(x 1)≤f '(x 2)+a 成立”等价于“当x 1,x 2∈[e,e 2]时,f(x 1)min ≤f '(x 2)max +a”.由(1)知,当x∈[e,e 2]时, f '(x)max =f '(e 2)=-a,所以f '(x)max +a=. 则问题等价于“当x∈[e,e 2]时, f(x)min ≤”.①当a≥时,由(1)得f '(x)max =-a≤0, f(x)在[e,e 2]上为减函数,则f(x)min =f(e 2)=-ae 2,由f(x)min ≤,得a≥-.②当a<时, f '(x)=-+-a 在[e,e 2]上的值域为. (i)当-a≥0,即a≤0时, f '(x)≥0在[e,e 2]恒成立,故f(x)在[e,e 2]上为增函数,于是f(x)min =f(e)=e-ae≥e>,与f(x)min ≤矛盾.(ii)当-a<0,即0<a<时,由f '(x)的单调性和值域知,存在唯一的x 0∈(e,e 2),使f '(x)=0,且满足:当x∈(e,x 0)时, f '(x)<0, f(x)为减函数;当x∈(x 0,e 2)时, f '(x)>0, f(x)为增函数,所以f(x)min =f(x 0)=-ax 0≤,x 0∈(e,e 2).所以a≥->->-=,与0<a<矛盾.综上,a 的取值范围是a≥-.。

专题10 函数中点的存在性问题(解析版)

决战2020年中考典型压轴题大突破模块三中考压轴题函数综合题专题考向导航函数综合题是初中数学中覆盖面最广、综合性最强的题型。

近几年的中考压轴题多以数学综合题的形式出现。

解数学综合题一般可分为认真审题、理解题意，探求解题思路，正确解答三个步骤。

解数学综合题必须要有科学分析问题的方法。

数学思想是解数学综合题的灵魂，要善于总结数学综合题中所隐含的转化思想、数形结合思想、分类讨论的思想、方程的思想等，更要结合实际问题加以领会与掌握，这是学习解综合题的关键。

函数是初中数学的重点，也是难点，更是中考命题的主要考查对象,由于这类题型能较好地考查学生的函数思想、数形结合思想、分类讨论思想、转化思想，能较全面地反映学生的综合能力,因此是各地中考的热点题型，并且长盛不衰，年年有新花样。

专题10 函数“存在性”问题方法点拨这类问题的知识覆盖面较广，综合性较强，题意构思非常精巧，解题方法灵活，对学生分析问题和解决问题的能力要求较高，是近几年来各地中考的“热点”。

这类题目解法的一般思路是:假设存在→推理论证→得出结论。

若能导出合理的结果，就做出“存在”的判断，导出矛盾，就做出不存在的判断. 由于“存在性”问题的结论有两种可能，所以具有开放的特征。

在假设存在性以后进行的推理或计算，对基础知识、基本技能提出了较高要求,并具备较强的探索性，正确、完整地解答这类问题，是对我们知识能力的一次全面的考验。

精典例题(2019·白银)如图，抛物线y＝ax2+bx+4交x轴于A（﹣3，0），B（4，0）两点，与y轴交于点C，连接AC，BC．点P是第一象限内抛物线上的一个动点，点P的横坐标为m．（1）求此抛物线的表达式；（2）过点P作PM⊥x轴，垂足为点M，PM交BC于点Q．试探究点P在运动过程中，是否存在这样的点Q，使得以A，C，Q为顶点的三角形是等腰三角形．若存在，请求出此时点Q的坐标，若不存在，请说明理由；（3）过点P作PN⊥BC，垂足为点N．请用含m的代数式表示线段PN的长，并求出当m为何值时PN 有最大值，最大值是多少？【点睛】（1）由二次函数交点式表达式，即可求解；（2）分AC ＝AQ 、AC ＝CQ 、CQ ＝AQ 三种情况，分别求解即可；（3）由PN ＝PQ sin ∠PQN =√22（−13m 2+13m +4+m ﹣4）即可求解．【详解】解：（1）由二次函数交点式表达式得：y ＝a （x +3）（x ﹣4）＝a （x 2﹣x ﹣12）＝ax 2﹣ax ﹣12a ，即：﹣12a ＝4，解得：a =−13，则抛物线的表达式为y =−13x 2+13x +4；（2）存在，理由：点A 、B 、C 的坐标分别为（﹣3，0）、（4，0）、（0，4），则AC ＝5，AB ＝7，BC ＝4√2，∠OBC ＝∠OCB ＝45°，将点B 、C 的坐标代入一次函数表达式：y ＝kx +b 并解得：y ＝﹣x +4…①，同理可得直线AC 的表达式为：y =43x +4，设直线AC 的中点为K （−32，2），过点M 与CA 垂直直线的表达式中的k 值为−34，同理可得过点K 与直线AC 垂直直线的表达式为：y =−34x +78⋯②， ①当AC ＝AQ 时，如图1，则AC ＝AQ ＝5，设：QM ＝MB ＝n ，则AM ＝7﹣n ，由勾股定理得：（7﹣n ）2+n 2＝25，解得：n ＝3或4（舍去4），故点Q （1，3）；②当AC ＝CQ 时，如图1，CQ ＝5，则BQ ＝BC ﹣CQ ＝4√2−5，则QM ＝MB =8−5√22，故点Q （5√22，8−5√22）； ③当CQ ＝AQ 时，联立①②并解得：x =252（舍去）；故点Q 的坐标为：Q （1，3）或（5√22，8−5√22）；（3）设点P （m ，−13m 2+13m +4），则点Q （m ，﹣m +4）， ∵OB ＝OC ，∴∠ABC ＝∠OCB ＝45°＝∠PQN ， PN ＝PQ sin ∠PQN =√22（−13m 2+13m +4+m ﹣4）=−√26（m ﹣2）2+2√23， ∵−√26＜0，∴PN 有最大值，当m ＝2时，PN 的最大值为：2√23．巩固突破1．(2020·青白江区模拟)如图，抛物线y ＝ax 2+bx +c 与x 轴相交于A （3，0）、B 两点，与y 轴交于点C （0，3），点B 在x 轴的负半轴上，且OA ＝3OB ．（1）求抛物线的函数关系式；（2）若P 是抛物线上且位于直线AC 上方的一动点，求△ACP 的面积的最大值及此时点P 的坐标；（3）在线段OC 上是否存在一点M ，使BM +√22CM 的值最小？若存在，请求出这个最小值及对应的M点的坐标；若不存在，请说明理由．【点睛】（1）OA＝3OB＝3，则点B（﹣1，0），抛物线的表达式为：y＝a（x+1）（x﹣3）＝a（x2﹣2x﹣3），即可求解；（2）△ACP的面积=12PH×OA=12×3×（x2﹣2x+3+x﹣3）=32（﹣x2+3x），即可求解；（3）故当B、M、N三点共线时，BM+√22CM＝BN最小，即可求解．【详解】解：（1）OA＝3OB＝3，则点B（﹣1，0），抛物线的表达式为：y＝a（x+1）（x﹣3）＝a（x2﹣2x﹣3），即﹣3a＝3，解得：a＝﹣1，故抛物线的表达式为：y＝﹣x2+2x+3；（2）过点P作y轴的平行线交CA于点H，由点A、C的坐标得，直线AC的表达式为：y＝﹣x+3△ACP的面积=12PH×OA=12×3×（x2﹣2x+3+x﹣3）=32（﹣x2+3x），当x=32时，△ACP的面积的最大，最大值为：278，此时点P（32，154）；（3）过点M作MN⊥AC，则MN=√22CM，故当B、M、N三点共线时，BM+√22CM＝BN最小，直线CA的倾斜角为45°，BN⊥AC，则∠NBA＝45°，即BN=√22AB＝2√2=AN，则点N（1，2），由点B、N的坐标得，直线BN的表达式为：y＝x+1，故点M（0，1）．2．(2019·青海)如图1（注：与图2完全相同），在直角坐标系中，抛物线经过点A（1，0）、B（5，0）、C（0，4）三点．（1）求抛物线的解析式和对称轴；（2）P是抛物线对称轴上的一点，求满足P A+PC的值为最小的点P坐标（请在图1中探索）；（3）在第四象限的抛物线上是否存在点E，使四边形OEBF是以OB为对角线且面积为12的平行四边形？若存在，请求出点E坐标，若不存在请说明理由（请在图2中探索）【点睛】（1）将点A、B的坐标代入二次函数表达式得：y＝a（x﹣1）（x﹣5）＝a（x2﹣6x+5），即可求解；（2）连接B、C交对称轴于点P，此时P A+PC的值为最小，即可求解；（3）S四边形OEBF＝OB×y E＝5×y E＝12，则y E=125，将该坐标代入二次函数表达式即可求解．【详解】解：（1）将点A、B的坐标代入二次函数表达式得：y＝a（x﹣1）（x﹣5）＝a（x2﹣6x+5），则5a＝4，解得：a=4 5，抛物线的表达式为：y=45（x2﹣6x+5）=45x2−245x+4，函数的对称轴为：x＝3，顶点坐标为（3，−165）；（2）连接B 、C 交对称轴于点P ，此时P A +PC 的值为最小，将点B 、C 的坐标代入一次函数表达式：y ＝kx +b 得：{0=5k +bb =4，解得：{k =−45b =4，直线BC 的表达式为：y =−45x +4，当x ＝3时，y =85，故点P （3，85）；（3）存在，理由：四边形OEBF 是以OB 为对角线且面积为12的平行四边形，则S 四边形OEBF ＝OB ×|y E |＝5×|y E |＝12，点E 在第四象限，故：则y E =−125，将该坐标代入二次函数表达式得： y =45（x 2﹣6x +5）=−125，解得：x ＝2或4，故点E 的坐标为（2，−125）或（4，−125）． 3．(2020·锦江区模拟)如图，在平面直角坐标系中，抛物线y ＝ax 2+bx +c 的图象与x 轴交于A （4，0），B 两点，与y 轴交于点C （0，2），对称轴x =32与x 轴交于点H ．（1）求抛物线的函数表达式；（2）直线y ＝kx +1（k ≠0）与y 轴交于点E ，与抛物线交于点 P ，Q （点P 在y 轴左侧，点Q 在y 轴右侧），连接CP ，CQ ，若△CPQ 的面积为√172，求点P ，Q 的坐标；（3）在（2）的条件下，连接AC 交PQ 于G ，在对称轴上是否存在一点K ，连接GK ，将线段GK 绕点G 逆时针旋转90°，使点K 恰好落在抛物线上，若存在，请直接写出点K 的坐标；若不存在，请说明理由．【点睛】（1）对称轴x =32，则点B （﹣1，0），则抛物线的表达式为：y ＝a （x +1）（x ﹣4）＝a （x 2﹣3x ﹣4），即可求解；（2）△CPQ 的面积=12×CE ×（n ﹣m ）=√172，即n ﹣m =√17，联立抛物线于直线PQ 的表达式并整理得：−12x 2+（32−k ）x +1＝0…①，m +n ＝3﹣2k ，mn ＝﹣2，n ﹣m =√17=√(m +n)2−4mn =√(3−2k)2+8，即可求解；（3）证明△GNK ≌△K ′MG （AAS ），NK =32−27=1714=MG ，NG =137−m ，则点K ′（157−m ，4314），将该坐标代入抛物线表达式，即可求解．【详解】解：（1）对称轴x =32，则点B （﹣1，0），则抛物线的表达式为：y ＝a （x +1）（x ﹣4）＝a （x 2﹣3x ﹣4），即﹣4a ＝2，解得：a =−12，故抛物线的表达式为：y =−12x 2+32x +2；（2）设直线PQ 交y 轴于点E （0，1），点P 、Q 横坐标分别为m ，n ，△CPQ 的面积=12×CE ×（n ﹣m ）=√172，即n ﹣m =√17，联立抛物线于直线PQ 的表达式并整理得：−12x 2+（32−k ）x +1＝0…①，m +n ＝3﹣2k ，mn ＝﹣2，n ﹣m =√17=√(m +n)2−4mn =√(2k −3)2+9 解得：k ＝0（舍去）或3；故y ＝3x +1，则−12x 2+32x +2＝3x +1，解得：x =−3±√172，故点P 、Q 的坐标分别为：（−3−√172，−7−3√172）、（−3+√172，−7+3√172）；（3）设点K （32，m ），联立PQ 和AC 的表达式并解得：x =27，故点G （27，137），过点G 作y 轴的平行线交过点K ′与x 轴的平行线于点M ，交过点K 与x 轴的平行线于点N ，则△GNK ≌△K ′MG （AAS ）， NK =32−27=1714=MG ，NG =137−m ，则点K ′（157−m ，4314）将该坐标代入抛物线表达式并解得：m =9±√2114，故点K （32，9+√2114）或（32，9−√2114）．4．(2020·下陆区模拟)如图，在矩形OABC 中，点O 为原点，点A 的坐标为（0，8），点C 的坐标为（6，0）．抛物线y =−49x 2+bx +c 经过点A 、C ，与AB 交于点D ．（1）求抛物线的函数解析式；（2）点P 为线段BC 上一个动点（不与点C 重合），点Q 为线段AC 上一个动点，AQ ＝CP ，连接PQ ，设CP ＝m ，△CPQ 的面积为S ． ①求S 关于m 的函数表达式；②当S 最大时，在抛物线y =−49x 2+bx +c 的对称轴l 上，若存在点F ，使△DFQ 为直角三角形，请直接写出所有符合条件的点F 的坐标；若不存在，请说明理由．【点睛】（1）将A 、C 两点坐标代入抛物线y =−49x 2+bx +c ，即可求得抛物线的解析式；（2）①先用m 表示出QE 的长度，进而求出三角形的面积S 关于m 的函数； ②直接写出满足条件的F 点的坐标即可，注意不要漏写．【详解】解：（1）将A 、C 两点坐标代入抛物线，得 {c =8−49×36+6b +c =0，解得：{b =43c =8，∴抛物线的解析式为y =−49x 2+43x +8；（2）①∵OA ＝8，OC ＝6， ∴AC =√OA 2+OC 2=10，过点Q 作QE ⊥BC 与E 点，则sin ∠ACB =QE QC =AB AC =35， ∴QE 10−m=35，∴QE =35（10﹣m ），∴S =12•CP •QE =12m ×35（10﹣m ）=−310m 2+3m ；②∵S =12•CP •QE =12m ×35（10﹣m ）=−310m 2+3m =−310（m ﹣5）2+152， ∴当m ＝5时，S 取最大值；在抛物线对称轴l 上存在点F ，使△FDQ 为直角三角形， ∵抛物线的解析式为y =−49x 2+43x +8的对称轴为x =32， D 的坐标为（3，8），Q （3，4），当∠FDQ ＝90°时，F 1（32，8），当∠FQD ＝90°时，则F 2（32，4），当∠DFQ ＝90°时，设F （32，n ），则FD 2+FQ 2＝DQ 2，即94+（8﹣n ）2+94+（n ﹣4）2＝16，解得：n ＝6±√72， ∴F 3（32，6+√72），F 4（32，6−√72），满足条件的点F 共有四个，坐标分别为 F 1（32，8），F 2（32，4），F 3（32，6+√72），F 4（32，6−√72）．5．(2019·临朐二模)如图，在平面直角坐标系中，抛物线y ＝ax 2+bx +1交y 轴于点A ，交x 轴正半轴于点B（4，0），与过A 点的直线相交于另一点D （3，52），过点D 作DC ⊥x 轴，垂足为C ．（1）求抛物线的表达式；（2）点P 在线段OC 上（不与点O ，C 重合），过P 作PN ⊥x 轴，交直线AD 于M ，交抛物线于点N ，NE ⊥AD 于点E ，求NE 的最大值；（3）若P 是x 轴正半轴上的一动点，设OP 的长为t ．是否存在t ，使以点M ，C ，D ，N 为顶点的四边形是平行四边形？若存在，求出t 的值；若不存在，请说明理由．【点睛】（1）将点B 、D 的坐标代入二次函数表达式，即可求解；（2）利用NE ＝MN cos ∠ENP =2√55（−34m 2+114m +1−12m ﹣1），即可求解；（3）设：OP ＝t ，则点M （t ，12t +1）、N （t ，−34t 2+114t +1），由|MN |＝CD ，即可求解．【详解】解：（1）将点B 、D 的坐标代入二次函数表达式得：{16a +4b +1=09a +3b +1=52，解得：{a =−34b =114，则函数的表达式为：y =−34x 2+114x +1；（2）将点A （0，1）、D 的坐标代入一次函数表达式：y ＝mx +n 并解得：直线AD 的表达式为：y =12x +1，即直线AD 的倾斜角的正切值为12，则tan ∠ENP =12，则cos ∠ENP =2√55，设点N （m ，−34m 2+114m +1）、点M （12m +1），则NE ＝MN cos ∠ENP =2√55（−34m 2+114m +1−12m ﹣1）=−3√510（m −32）2+27√540，故当m =32时，则NE 的最大值为27√540；（3）设：OP ＝t ，则点M （t ，12t +1）、N （t ，−34t 2+114t +1），点M 可能在CD 得左侧也可能在CD 得右侧，由题意得：|MN |＝CD ， ±52=−34t 2+114t +1−12t ﹣1，解得：t =9±√2016（舍去负值），故t =9+√2016时，以点M ，C ，D ，N 为顶点的四边形是平行四边形． 6．(2019·恩施州)如图，抛物线y ＝ax 2﹣2ax +c 的图象经过点C （0，﹣2），顶点D 的坐标为（1，−83），与x 轴交于A 、B 两点．（1）求抛物线的解析式．（2）连接AC ，E 为直线AC 上一点，当△AOC ∽△AEB 时，求点E 的坐标和AEAB 的值．（3）点F （0，y ）是y 轴上一动点，当y 为何值时，√55FC +BF 的值最小．并求出这个最小值．（4）点C 关于x 轴的对称点为H ，当√55FC +BF 取最小值时，在抛物线的对称轴上是否存在点Q ，使△QHF 是直角三角形？若存在，请求出点Q 的坐标；若不存在，请说明理由．【点睛】（1）将点C 、D 的坐标代入抛物线表达式，即可求解；（2）当△AOC ∽△AEB 时，S △AOC S △AEB=（AC AB ）2＝（√54）2=516，求出y E =−85，由△AOC ∽△AEB 得：AO AC=AE AB=√5，即可求解；（3）如图2，连接BF ，过点F 作FG ⊥AC 于G ，当折线段BFG 与BE 重合时，取得最小值，即可求解；（4）①当点Q 为直角顶点时，由Rt △QHM ∽Rt △FQM 得：QM 2＝HM •FM ；②当点H 为直角顶点时，点H （0，2），则点Q （1，2）；③当点F 为直角顶点时，同理可得：点Q （1，−32）．【详解】解：（1）由题可列方程组：{c =−2a −2a +c =−83，解得：{a =23c =−2∴抛物线解析式为：y =23x 2−43x ﹣2；（2）如图1，∠AOC ＝90°，AC =√5，AB ＝4，设直线AC 的解析式为：y ＝kx +b ，则{−k +b =0b =−2，解得：{k =−2b =−2，∴直线AC 的解析式为：y ＝﹣2x ﹣2；当△AOC ∽△AEB 时S △AOC S △AEB=（AC AB）2＝（√54）2=516，∵S △AOC ＝1，∴S △AEB =165， ∴12AB ×|y E |=165，AB ＝4，则y E =−85，则点E （−15，−85）；由△AOC ∽△AEB 得：AO AC=AE AB=√5∴AE AB=√55；（3）如图2，连接BF ，过点F 作FG ⊥AC 于G ，则FG ＝CF sin ∠FCG =√55CF ，∴√55CF +BF ＝GF +BF ≥BE ，当折线段BFG 与BE 重合时，取得最小值，由（2）可知∠ABE ＝∠ACO∴BE ＝AB cos ∠ABE ＝AB cos ∠ACO ＝45=8√55，|y |＝OB tan ∠ABE ＝OB tan ∠ACO ＝3×12=32，∴当y =−32时，即点F （0，−32），√55CF +BF 有最小值为8√55；（4）①当点Q 为直角顶点时（如图3）：由（3）易得F （0，−32），∵C （0，﹣2）∴H （0，2）设Q （1，m ），过点Q 作QM ⊥y 轴于点M ．则Rt △QHM ∽Rt △FQM ∴QM 2＝HM •FM ， ∴12＝（2﹣m ）（m +32），解得：m =1±√334，则点Q （1，1+√334）或（1，1−√334）当点H 为直角顶点时：点H （0，2），则点Q （1，2）；当点F 为直角顶点时：同理可得：点Q （1，−32）；综上，点Q 的坐标为：（1，1+√334）或（1，1−√334）或Q （1，2）或Q （1，−32）．7．(2019·阜新)如图，抛物线y ＝ax 2+bx +2交x 轴于点A （﹣3，0）和点B （1，0），交y 轴于点C ．（1）求这个抛物线的函数表达式．（2）点D 的坐标为（﹣1，0），点P 为第二象限内抛物线上的一个动点，求四边形ADCP 面积的最大值．（3）点M 为抛物线对称轴上的点，问：在抛物线上是否存在点N ，使△MNO 为等腰直角三角形，且∠MNO 为直角？若存在，请直接写出点N 的坐标；若不存在，请说明理由．【点睛】（1）抛物线的表达式为：y ＝a （x +3）（x ﹣1）＝a （x 2+2x ﹣3）＝ax 2+2ax ﹣3a ，即﹣3a ＝2，即可求解；（2）S 四边形ADCP ＝S △APO +S △CPO ﹣S △ODC ，即可求解；（3）分点N 在x 轴上方、点N 在x 轴下方两种情况，分别求解．【详解】解：（1）抛物线的表达式为：y ＝a （x +3）（x ﹣1）＝a （x 2+2x ﹣3）＝ax 2+2ax ﹣3a ，即﹣3a＝2，解得：a=−2 3，故抛物线的表达式为：y=−23x2−43x+2，则点C（0，2），函数的对称轴为：x＝﹣1；（2）连接OP，设点P（x，−23x2−43x+2），则S＝S四边形ADCP＝S△APO+S△CPO﹣S△ODC=12×AO×y P+12×OC×|x P|−12×CO×OD=12×3×（−23x2−43x+2）+12×2×（﹣x）−12×2×1=−x2﹣3x+2，∵﹣1＜0，故S有最大值，当x=−32时，S的最大值为174；（3）存在，理由：△MNO为等腰直角三角形，且∠MNO为直角时，点N的位置如下图所示：①当点N在x轴上方时，点N的位置为N1、N2，N1的情况（△M1N1O）：设点N1的坐标为（x，−23x2−43x+2），则M1E＝x+1，过点N1作x轴的垂线交x轴于点F，过点M1作x轴的平行线交N1F于点E，∵∠FN 1O +∠M 1N 1E ＝90°，∠M 1N 1E +∠EM 1N 1＝90°，∴∠EM 1N 1＝∠FN 1O ， ∠M 1EN 1＝∠N 1FO ＝90°，ON 1＝M 1N 1， ∴△M 1N 1E ≌△N 1OF （AAS ），∴M 1E ＝N 1F ，即：x +1=−23x 2−43x +2，解得：x =−7±√734（舍去负值），则点N 1（−7+√734，−3+√734）； N 2的情况（△M 2N 2O ）：同理可得：点N 2（−1−√734，−3+√734）； ②当点N 在x 轴下方时，点N 的位置为N 3、N 4，同理可得：点N 3、N 4的坐标分别为：（−7−√734，−3−√734）、（−1+√734，−3−√734）；综上，点N 的坐标为：（−7+√734，−3+√734）或（−1−√734，−3+√734）或（−7−√734，−3−√734）或（−1+√734，−3−√734）． 8．(2019·通辽)已知，如图，抛物线y ＝ax 2+bx +c （a ≠0）的顶点为M （1，9），经过抛物线上的两点A （﹣3，﹣7）和B （3，m ）的直线交抛物线的对称轴于点C ．（1）求抛物线的解析式和直线AB 的解析式．（2）在抛物线上A 、M 两点之间的部分（不包含A 、M 两点），是否存在点D ，使得S △DAC ＝2S △DCM ？若存在，求出点D 的坐标；若不存在，请说明理由．（3）若点P 在抛物线上，点Q 在x 轴上，当以点A ，M ，P ，Q 为顶点的四边形是平行四边形时，直接写出满足条件的点P 的坐标．【点睛】（1）二次函数表达式为：y＝a（x﹣1）2+9，即可求解；（2）S△DAC＝2S△DCM，则S△DAC=12DH（x C﹣x A）=12（﹣x2+2x+8﹣2x+1）（1+3）=12（9﹣1）（1﹣x）×2，即可求解；（3）分AM是平行四边形的一条边、AM是平行四边形的对角线两种情况，分别求解即可．【详解】解：（1）二次函数表达式为：y＝a（x﹣1）2+9，将点A的坐标代入上式并解得：a＝﹣1，故抛物线的表达式为：y＝﹣x2+2x+8…①，则点B（3，5），将点A、B的坐标代入一次函数表达式并解得：直线AB的表达式为：y＝2x﹣1；（2）存在，理由：二次函数对称轴为：x＝1，则点C（1，1），过点D作y轴的平行线交AB于点H，设点D（x，﹣x2+2x+8），点H（x，2x﹣1），∵S△DAC＝2S△DCM，则S△DAC=12DH（x C﹣x A）=12（﹣x2+2x+8﹣2x+1）（1+3）=12（9﹣1）（1﹣x）×2，解得：x＝﹣1或5（舍去5），故点D（﹣1，5）；（3）设点Q（m，0）、点P（s，t），t＝﹣s2+2s+8，①当AM是平行四边形的一条边时，点M向左平移4个单位向下平移16个单位得到A，同理，点Q（m，0）向左平移4个单位向下平移16个单位为（m﹣4，﹣16），即为点P，即：m﹣4＝s，﹣16＝t，而t＝﹣s2+2s+8，解得：s＝6或﹣4，故点P（6，﹣16）或（﹣4，﹣16）；②当AM是平行四边形的对角线时，由中点公式得：m+s＝﹣2，t＝2，而t＝﹣s2+2s+8，解得：s＝1±√7，故点P（1+√7，2）或（1−√7，2）；综上，点P（6，﹣16）或（﹣4，﹣16）或（1+√7，2）或（1−√7，2）．9．(2019·长沙模拟)如图，在平面直角坐标系中，直线y=12x﹣1与抛物线y=−512x2+bx+c相交于A，B两点，点A在x轴上，点B的横坐标为﹣6，点P是抛物线上位于直线AB上方的一动点（不与点A，B重合）．（1）求该抛物线的解析式；（2）连接P A，PB，在点P运动的过程中，是否存在某一位置，使得△P AB恰好是一个以点P为直角顶点的等腰直角三角形？若存在，求出点P的坐标；若不存在，请说明理由；（3）过点P作PD∥y轴交直线AB于点D，以PD为直径的⊙E与直线AB相交于点G，求DG的最大值．【点睛】（1）在函数y=12x﹣1中，求出A（2，0）、B（﹣6，﹣4），将A（2，0），B（﹣6，﹣4）代入y=−512x2+bx+c中，即可求解；（2）存在，理由：由A、B点坐标得：则点E（﹣2，﹣2），则AE=√(−2−2)2+(−2)2=2√5，tan∠OAC=AOAE=ACAF，即：2√5=√5AF，则AF＝5，可得直线EF的表达式为：y＝﹣2x﹣6…②，联立①②即可求解；（3）GD ＝PD sin ∠DPG =5（−512x 2−76x +4−12x +1），即可求解．【详解】解：（1）在函数y =12x ﹣1中，当y ＝0时，x ＝2，∴A （2，0），当x ＝﹣6时，y ＝﹣4，∴B （﹣6，﹣4），将A （2，0），B （﹣6，﹣4）代入y =−512x 2+bx +c 中，得{−512×22+2b +c =0−512×(−6)2−6b +c =−4，解得{b =−76c =4，∴该抛物线得解析式为y =−512x 2−76x +4…①；（2）存在，理由：设直线AB 交y 轴于点C ，则点C （0，﹣1），如图所示，作线段AB 的垂直平分线交x 轴于点F 、交y 轴于点E ，由A 、B 点坐标得：则点E （﹣2，﹣2），则AE =√(−2−2)2+(−2)2=2√5， tan ∠OAC =AO AE =ACAF ，即：2√5=√5AF，则AF ＝5，故点F （﹣3，0），由点E （﹣2，﹣2）、F （﹣3，0）得直线EF 的表达式为：y ＝﹣2x ﹣6…②，联立①②并解得：x ＝﹣4或6（舍去x ＝6），故点P 的坐标为（﹣4，2）， PE =√(−4+2)2+(2+2)2=2√5；（3）如下图所示，PD 为直径，则∠PGD ＝90°，即：PG ⊥AC∠OAC ＝90°﹣∠PDC ＝∠DPG ，在Rt △AOC 中，sin ∠OAC =15=sin ∠DPG ，则GD ＝PD sin ∠DPG ，设点P 坐标为（x ，−512x 2−76x +4），则点D （x ，12x ﹣1）， GD ＝PD sin ∠DPG =1√5（−512x 2−76x +4−12x +1），当x =−b 2a =−2时，GD 最大，最大值为：4√53． 10．(2019·硚口区区模拟)抛物线y =ax 2−12x +54经过点E （5，5），其顶点为C 点．（1）求抛物线的解析式，并直接写出C 点坐标．（2）将直线y =12x 沿y 轴向上平移b 个单位长度交抛物线于A 、B 两点．若∠ACB ＝90°，求b 的值．（3）是否存在点D （1，a ），使抛物线上任意一点P 到x 轴的距离等于P 点到点D 的距离？若存在，请求点D 的坐标；若不存在，请说明理由．【点睛】（1）将点E 坐标代入解析式，求出系数a ，获得解析式，并求出顶点C 坐标；（2）平移直线y =12x ，获得平移后的解析式y =12x +b ，直线与抛物线交于两点A 、B ，设A （x 1，y 1）、B （x 2，y 2），因为∠ACB ＝90°，利用A 、B 、C 三点构造相似，得到1−x 1y 2−1=y 1−1x 2−1，将直线与抛物线联立获得方程，根据韦达定理，获得x 1+x 2，x 1•x 2，从而获得关于b 的方程，求出b 值；（3）过点P 作PQ ⊥x 轴，设点P （m ，14m 2−12m +54）因为PQ ＝PD ，所以PQ 2＝PD 2，整理可得(a −2)m 2+2(a −2)m +2(a −2)(a −12)=0，所以当a ＝2时，存在点D （1，2）．【详解】解：（1）将点E （5，5）代入y ＝ax 2−12x +545＝25a −52+54a =14∴y =14x 2−12x +54，顶点（1，1）（2）直线y =12x 平移后获得解析式y =12x +b交抛物线于A （x 1，y 1）、B （x 2，y 2）y 1=12x 1+b ，y 2=12x 2+b联立{y =12x +by =14x 2−12x +54x 2﹣4x +5﹣4b ＝0∴x 1+x 2＝4，x 1•x 2＝5﹣4b如图，过点A 、B 作y 轴的平行线与过点C 平行于x 轴的线交于点E ，F可证△ACE ∽△BCF∴1−x 1y 2−1=y 1−1x 2−1∴（x 1+x 2）﹣（x 1•x 2）﹣1＝y 1•y 2﹣（y 1+y 2）+1∴b 2﹣5b +94=0，解，b 1=92，b 2=12（舍）∴b =92．（3）设P（m，n），作PQ⊥x轴于Q若PQ＝PD，则PQ2＝PD2（m﹣1）2+（n﹣a）2＝n2整理得m2﹣2m+1+a2﹣2an＝0将n=14m2−12m+54代入整理得(a−2)m2+2(a−2)m+2(a−2)(a−12)=0当a＝2时，方程成立∴D（1，2）11．(2020·云南模拟)如图，抛物线y＝ax2+bx+3经过点B（﹣1，0），C（2，3），抛物线与y轴的交点A，与x轴的另一个交点为D，点M为线段AD上的一动点，设点M的横坐标为t．（1）求抛物线的表达式；（2）过点M作y轴的平行线，交抛物线于点P，设线段PM的长为1，当t为何值时，1的长最大，并求最大值；（先根据题目画图，再计算）（3）在（2）的条件下，当t为何值时，△P AD的面积最大？并求最大值；（4）在（2）的条件下，是否存在点P，使△P AD为直角三角形？若存在，直接写出t的值；若不存在，说明理由．【点睛】（1）利用待定系数法即可解决问题；（2）易知直线AD 解析式为y ＝﹣x +3，设M 点横坐标为m ，则P （t ，﹣t 2+2t +3），M （t ，﹣t +3），可得l ＝﹣t 2+2t +3﹣（﹣t +3）＝﹣t 2+3t ＝﹣（t −32）2+94，利用二次函数的性质即可解决问题；（3）由S △P AD =12×PM ×（x D ﹣x A ）=32PM ，推出PM 的值最大时，△P AD 的面积最大；（4）如图设AD 的中点为K ，设P （t ，﹣t 2+2t +3）．由△P AD 是直角三角形，推出PK =12AD ，可得（t −32）2+（﹣t 2+2t +3−32）2=14×18，解方程即可解决问题；【详解】解：（1）把点 B （﹣1，0），C （2，3）代入y ＝ax 2+bx +3，则有{a −b +3=04a +2b +3=3，解得{a =−1b =2，∴抛物线的解析式为y ＝﹣x 2+2x +3．（2）在y ＝﹣x 2+2x +3中，令y ＝0可得0＝﹣x 2+2x +3，解得x ＝﹣1或x ＝3，∴D （3，0），且A （0，3），∴直线AD 解析式为y ＝﹣x +3，设M 点横坐标为m ，则P （t ，﹣t 2+2t +3），M （t ，﹣t +3），∵0＜t ＜3，∴点M 在第一象限内，∴l ＝﹣t 2+2t +3﹣（﹣t +3）＝﹣t 2+3t ＝﹣（t −32）2+94，∴当t =32时，l 有最大值，l 最大=94；（3）∵S △P AD =12×PM ×（x D ﹣x A ）=32PM ，∴PM 的值最大时，△P AD 的面积中点，最大值=32×94=278． ∴t =32时，△P AD 的面积的最大值为278．（4）如图设AD 的中点为K ，设P （t ，﹣t 2+2t +3）．∵△P AD 是直角三角形，∴PK =12AD ，∴（t −32）2+（﹣t 2+2t +3−32）2=14×18，整理得t （t ﹣3）（t 2﹣t ﹣1）＝0，解得t ＝0或3或1±√52， ∵点P 在第一象限，∴t =1+√52． 12．(2019·大渡口区模拟)如图，抛物线y =−35x 2+125x +3与x 轴交于点A 和点B （点A 在点B 的左侧），与y 轴交于点C ，连结BC ．（1）如图1，点N 为抛物线上的一动点，且位于直线BC 上方，连接CN 、BN ．点P 是直线AB 上的动点．当△NBC 面积取得最大值时，求出点N 的坐标及△NBC 面积的最大值，并求此时PN +CP 的最小值；（2）如图2，点M 、P 分别为线段BC 和线段OB 上的动点，连接PM 、PC ，是否存在这样的点P ，使△PCM 为等腰三角形，△PMB 为直角三角形同时成立？若存在，求出点P 的坐标；若不存在，请说明理由．【点睛】（1）S△NBC=12HN×OB=52（−35x2+125x+3+35x﹣3）=−32x2+152x，求出N的坐标是(52，214)，点C关于直线AB的对称点C'（0，﹣3），PN+PC的最小值为NC′即可求解；（2）利用△BMP～△BOC，即可求解．【详解】解：（1）过点N作y轴的平行线交直线BC与点H，y=−35x2+125x+3，令x＝0，则y＝3，令y＝0，则x＝5或﹣1，即点A、B、C的坐标分别为（﹣1，0）、（5，0）、（0，3），则直线BC的表达式为：y＝kx+3，将点B坐标代入上式并解得：k=−3 5，则直线BC的表达式为：y=−35x+3，设点N（x，−35x2+125x+3），点H（x，−35x+3），S△NBC=12HN×OB=52（−35x2+125x+3+35x﹣3）=−32x2+152x，∵−32＜0，则S△NBC有最大值，当x=52时，△NBC面积最大，最大值为758；此时点N的坐标是(52，214)，如图，点C 关于直线AB 的对称点C '（0，﹣3），PN +PC 的最小值NC′=√(214+3)2+(52)2=√11894；（2）存在，∵B （5，0），C （0，3），∴BC =√32+52=√34，①当∠PMB ＝90°，则∠PMC ＝90°，△PMC 为等腰直角三角形，MP ＝MC ，设PM ＝t ，则CM =t ，MB =√34−t ，∵∠MBP ＝∠OBC ，∴△BMP ～△BOC ，∴PM OC =BM OB =BP BC ，即t 3=√34−t 5=√34，解得t =3√348，BP =174， ∴OP =OB −BP =5−174=34，当∠PMB ＝90°，CM ＝PM 时，同理可得：点P （3√34−95，0）；此时P 点坐标为(34，0)或（3√34−95，0）． 13．(2019·崇安区一模)已知二次函数y ＝ax 2﹣9ax +18a 的图象与x 轴交于A ，B 两点（A 在B 的左侧），图象的顶点为C ，直线AC 交y 轴于点D ．（1）连接BD ，若∠BDO ＝∠CAB ，求这个二次函数的表达式；（2）是否存在以原点O 为对称中心的矩形CDEF ？若存在，求出这个二次函数的表达式，若不存在，请说明理由．【点睛】（1）利用配方法求出抛物线y ＝ax 2﹣9ax +18a 的顶点C 的坐标为（92，−94a ）．作CM ⊥x 轴于M ，则OM =92，CM ＝|−94a |．求出A （3，0），B （6，0）．再证明△ODA ∽△OBD ，根据相似三角形对应边成比例求出OD ＝3√2．根据平行线分线段成比例定理得出OD CM =OA AM ，求得CM =3√22，那么|−94a |=3√22，求出a ，即可得到二次函数的解析式；（2）连接OC ，根据矩形的性质得出OC ＝OD ，那么∠ODC ＝∠OCD ．再证明∠OCD ＝∠DCM ．作AN ⊥OC 于N ，根据角平分线的性质得出AN ＝AM =32．由sin ∠AON =AN OA =12，得出∠AON ＝30°，求出CM ＝OM •tan30°=3√32，那么|−94a |=3√32，求出a ，即可得到二次函数的解析式．【详解】解：（1）∵y ＝ax 2﹣9ax +18a ＝a （x −92）2−94a ，∴顶点C （92，−94a ）．作CM ⊥x 轴于M ，则OM =92，CM ＝|−94a |．当y ＝0时，ax 2﹣9ax +18a ＝0，解得x 1＝3，x 2＝6，∴A （3，0），B （6，0）．∵∠BDO ＝∠CAB ，∠CAB ＝∠DAO ，∴∠DAO ＝∠BDO ．在△ODA 与△OBD 中，{∠DAO =∠BDO ∠AOD =∠DOB =90°，∴△ODA ∽△OBD ，∴OD OB =OA OD ，即OD 6=3OD ，∴OD ＝3√2．∵CM ∥OD ，∴OD CM =OA AM ，即3√2CM =392−3，∴CM =3√22，∴|−94a |=3√22，∴a ＝±2√23，∴二次函数的解析式为y =2√23x 2﹣6√2x +12√2或y =−2√23x 2+6√2x ﹣12√2；（2）存在．连接OC ，则OC ＝OD ．∴∠ODC ＝∠OCD ．∵CM ∥OD ，∴∠ODC ＝∠DCM ，∴∠OCD ＝∠DCM ．作AN ⊥OC 于N ，AN ＝AM =32．∵sin ∠AON =AN OA =323=12， ∴∠AON ＝30°，∴CM ＝OM •tan30°=92×√33=3√32， ∴|−94a |=3√32， ∴a ＝±2√33， ∴二次函数的解析式为y =2√33x 2﹣6√3x +12√3或y =−2√33x 2+6√3x ﹣12√3．14．(2019·长沙一模)如图，已知直线y ＝kx ﹣6与抛物线y ＝ax 2+bx +c 相交于A ，B 两点，且点A （1，﹣4）为抛物线的顶点，点B 在x 轴上．（1）求抛物线的解析式；（2）在（1）中抛物线的第二象限图象上是否存在一点P ，使△POB 与△POC 全等？若存在，求出点P 的坐标；若不存在，请说明理由；（3）若点Q 是y 轴上一点，且△ABQ 为直角三角形，求点Q 的坐标．【点睛】（1）已知点A 坐标可确定直线AB 的解析式，进一步能求出点B 的坐标．点A 是抛物线的顶点，那么可以将抛物线的解析式设为顶点式，再代入点B 的坐标，依据待定系数法可解．（2）首先由抛物线的解析式求出点C 的坐标，在△POB 和△POC 中，已知的条件是公共边OP ，若OB与OC 不相等，那么这两个三角形不能构成全等三角形；若OB 等于OC ，那么还要满足的条件为：∠POC ＝∠POB ，各自去掉一个直角后容易发现，点P 正好在第二象限的角平分线上，联立直线y ＝﹣x 与抛物线的解析式，直接求交点坐标即可，同时还要注意点P 在第二象限的限定条件．（3）分别以A 、B 、Q 为直角顶点，分类进行讨论．找出相关的相似三角形，依据对应线段成比例进行求解即可．【详解】解：（1）把A （1，﹣4）代入y ＝kx ﹣6，得k ＝2，∴y ＝2x ﹣6，令y ＝0，解得：x ＝3，∴B 的坐标是（3，0）．∵A 为顶点，∴设抛物线的解析为y ＝a （x ﹣1）2﹣4，把B （3，0）代入得：4a ﹣4＝0，解得a ＝1，∴y ＝（x ﹣1）2﹣4＝x 2﹣2x ﹣3．（2）存在．∵OB ＝OC ＝3，OP ＝OP ，∴当∠POB ＝∠POC 时，△POB ≌△POC ，此时PO 平分第二象限，即PO 的解析式为y ＝﹣x ．设P （m ，﹣m ），则﹣m ＝m 2﹣2m ﹣3，解得m =1−√132（m =1+√132＞0，舍），∴P （1−√132，√13−12）．（3）①如图，当∠Q 1AB ＝90°时，△DAQ 1∽△DOB ，∴AD OD =DQ 1DB ，即√56=13√5，∴DQ 1=52， ∴OQ 1=72，即Q 1（0，−72）；②如图，当∠Q 2BA ＝90°时，△BOQ 2∽△DOB ，∴OB OD =OQ 2OB ，即36=OQ 23， ∴OQ 2=32，即Q 2（0，32）；③如图，当∠AQ 3B ＝90°时，作AE ⊥y 轴于E ，则△BOQ 3∽△Q 3EA ，∴OBQ 3E =OQ 3AE ，即34−OQ 3=OQ 31，∴OQ 32﹣4OQ 3+3＝0，∴OQ 3＝1或3，即Q 3（0，﹣1），Q 4（0，﹣3）．综上，Q 点坐标为（0，−72）或（0，32）或（0，﹣1）或（0，﹣3）．15．(2019·海南)如图，已知抛物线y ＝ax 2+bx +5经过A （﹣5，0），B （﹣4，﹣3）两点，与x 轴的另一个交点为C ，顶点为D ，连结CD ．（1）求该抛物线的表达式；（2）点P 为该抛物线上一动点（与点B 、C 不重合），设点P 的横坐标为t ．①当点P 在直线BC 的下方运动时，求△PBC 的面积的最大值；②该抛物线上是否存在点P ，使得∠PBC ＝∠BCD ？若存在，求出所有点P 的坐标；若不存在，请说明理由．【点睛】（1）将点A 、B 坐标代入二次函数表达式，即可求解；（2）①S △PBC =12PG （x C ﹣x B ），即可求解；②分点P 在直线BC 下方、上方两种情况，分别求解即可．【详解】解：（1）将点A 、B 坐标代入二次函数表达式得：{25a −5b +5=016a −4b +5=−3，解得：{a =1b =6，故抛物线的表达式为：y＝x2+6x+5…①，令y＝0，则x＝﹣1或﹣5，即点C（﹣1，0）；（2）①如图1，过点P作y轴的平行线交BC于点G，将点B、C的坐标代入一次函数表达式并解得：直线BC的表达式为：y＝x+1…②，设点G（t，t+1），则点P（t，t2+6t+5），S△PBC=12PG（x C﹣x B）=32（t+1﹣t2﹣6t﹣5）=−32t2−152t﹣6，∵−32＜0，∴S△PBC有最大值，当t=−52时，其最大值为278；②设直线BP与CD交于点H，当点P在直线BC下方时，∵∠PBC ＝∠BCD ，∴点H 在BC 的中垂线上，线段BC 的中点坐标为（−52，−32），过该点与BC 垂直的直线的k 值为﹣1，设BC 中垂线的表达式为：y ＝﹣x +m ，将点（−52，−32）代入上式并解得：直线BC 中垂线的表达式为：y ＝﹣x ﹣4…③，同理直线CD 的表达式为：y ＝2x +2…④，联立③④并解得：x ＝﹣2，即点H （﹣2，﹣2），同理可得直线BH 的表达式为：y =12x ﹣1…⑤，联立①⑤并解得：x =−32或﹣4（舍去﹣4），故点P （−32，−74）；当点P （P ′）在直线BC 上方时，∵∠PBC ＝∠BCD ，∴BP ′∥CD ，则直线BP ′的表达式为：y ＝2x +s ，将点B 坐标代入上式并解得：s ＝5，即直线BP ′的表达式为：y ＝2x +5…⑥，联立①⑥并解得：x ＝0或﹣4（舍去﹣4），故点P （0，5）；故点P 的坐标为P （−32，−74）或（0，5）．16．(2019·山西)综合与探究如图，抛物线y ＝ax 2+bx +6经过点A （﹣2，0），B （4，0）两点，与y 轴交于点C ，点D 是抛物线上一个动点，设点D 的横坐标为m （1＜m ＜4）．连接AC ，BC ，DB ，DC ．（1）求抛物线的函数表达式；（2）△BCD 的面积等于△AOC 的面积的34时，求m 的值；（3）在（2）的条件下，若点M 是x 轴上一动点，点N 是抛物线上一动点，试判断是否存在这样的点M ，使得以点B ，D ，M ，N 为顶点的四边形是平行四边形？若存在，请直接写出点M 的坐标；若不存在，请说明理由．【点睛】（1）由抛物线交点式表达，即可求解；（2）利用S △BDC =12HD ×OB ，即可求解；（3）分BD 是平行四边形的一条边、BD 是平行四边形的对角线两种情况，分别求解即可．【详解】解：（1）由抛物线交点式表达式得：y ＝a （x +2）（x ﹣4）＝a （x 2﹣2x ﹣8）＝ax 2﹣2ax ﹣8a ，即﹣8a ＝6，解得：a =−34，故抛物线的表达式为：y =−34x 2+32x +6；（2）点C （0，6），将点B 、C 的坐标代入一次函数表达式并解得：直线BC 的表达式为：y =−32x +6，如图所示，过点D 作y 轴的平行线交直线BC 与点H ，设点D （m ，−34m 2+32m +6），则点H （m ，−32m +6）S △BDC =12HD ×OB ＝2（−34m 2+32m +6+32m ﹣6）＝2（−34m 2+3m ），34S △ACO =34×12×6×2=92，即：2（−34m 2+3m ）=92，解得：m ＝1或3（舍去1），故m ＝3；（3）当m ＝3时，点D （3，154），①当BD 是平行四边形的一条边时，如图所示：M 、N 分别有三个点，设点N （n ，−34n 2+32n +6）则点N 的纵坐标为绝对值为154，即|−34n 2+32n +6|=154，解得：n ＝﹣1或3（舍去）或1±√14，故点N （N ′、N ″）的坐标为（﹣1，154）或（1+√14，−154）或（1−√14，−154），当点N （﹣1，154）时，由图象可得：点M （0，0），当N ′的坐标为（1+√14，−154），由中点坐标公式得：点M ′（√14，0），同理可得：点M ″坐标为（−√14，0），故点M 坐标为：（0，0）或（√14，0）或（−√14，0）；②当BD 是平行四边形的对角线时，点B 、D 的坐标分别为（4，0）、（3，154）设点M （m ，0），点N （s ，t ），由中点坐标公式得：{4+3=m +s 154+0=t +0，而t =−34s 2+32s +6，解得：t =154，s ＝﹣1，m ＝8，故点M 坐标为（8，0）；故点M 的坐标为：（0，0）或（√14，0）或（−√14，0）或（8，0）．17．(2019·眉山)如图1，在平面直角坐标系中，抛物线y =−49x 2+bx +c 经过点A （﹣5，0）和点B （1，0）．（1）求抛物线的解析式及顶点D 的坐标；（2）点P是抛物线上A、D之间的一点，过点P作PE⊥x轴于点E，PG⊥y轴，交抛物线于点G，过点G作GF⊥x轴于点F，当矩形PEFG的周长最大时，求点P的横坐标；（3）如图2，连接AD、BD，点M在线段AB上（不与A、B重合），作∠DMN＝∠DBA，MN交线段AD于点N，是否存在这样点M，使得△DMN为等腰三角形？若存在，求出AN的长；若不存在，请说明理由．【点睛】（1）抛物线的表达式为：y=−49（x+5）（x﹣1），即可求解；（2）PE=−49m2−169m+209，PG＝2（﹣2﹣m）＝﹣4﹣2m，矩形PEFG的周长＝2（PE+PG），即可求解；（3）分MN＝DM、NM＝DN、DN＝DM，三种情况分别求解．【详解】解：（1）抛物线的表达式为：y=−49（x+5）（x﹣1）=−49x2−169x+209，则点D（﹣2，4）；（2）设点P（m，−49m2−169m+209），则PE=−49m2−169m+209，PG＝2（﹣2﹣m）＝﹣4﹣2m，矩形PEFG的周长＝2（PE+PG）＝2（−49m2−169m+209−4﹣2m）=−89（m+174）2+252，∵−89＜0，故当m=−174时，矩形PEFG周长最大，此时，点P的横坐标为−17 4；（3）∵∠DMN＝∠DBA，∠BMD+∠BDM＝180°﹣∠ADB，∠NMA+∠DMB＝180°﹣∠DMN，∴∠NMA＝∠MDB，∴△BDM ∽△AMN ，AN BM =AM BD ，而AB ＝6，AD ＝BD ＝5，①当MN ＝DM 时，∴△BDM ≌△AMN ，即：AM ＝BD ＝5，则AN ＝MB ＝1； ②当NM ＝DN 时，则∠NDM ＝∠NMD ，∴△AMD ∽△ADB ，∴AD 2＝AB ×AM ，即：25＝6×AM ，则AM =256，而AN BM =AM BD ，即AN 6−256=2565，解得：AN =5536；③当DN ＝DM 时，∵∠DNM ＞∠DAB ，而∠DAB ＝∠DMN ， ∴∠DNM ＞∠DMN ，∴DN ≠DM ；故AN ＝1或5536．。

(完整版)二次函数与三角形的存在性问题的解法

二次函数与三角形的存在性问题一、预备知识1、坐标系中或抛物线上有两个点为P （x1，y ），Q （x2，y ）(1)线段对称轴是直线2x 21x x +=(2)AB 两点之间距离公式：221221)()(y y x x PQ -+-=中点公式：已知两点()()2211y ,x Q ,y ,x P ，则线段PQ 的中点M 为⎪⎭⎫ ⎝⎛++222121y y ,x x 。

2、两直线的解析式为11b x k y +=与 22b x k y +=如果这两天两直线互相垂直，则有121-=⋅k k3、平面内两直线之间的位置关系：两直线分别为：L1：y=k1x+b1 L2：y=k2x+b2（1）当k1=k2，b1≠b2 ，L1∥L2（2）当k1≠k2，，L1与L2相交（3）K1×k2= -1时， L1与L2垂直二、三角形的存在性问题探究：三角形的存在性问题主要涉及到的是等腰三角形，等边三角形，直角三角形（一）三角形的性质和判定：1、等腰三角形性质：两腰相等，两底角相等，三线合一（中线、高线、角平分线）。

判定：两腰相等，两底角相等，三线合一（中线、高线、角平分线）的三角形是等腰三角形。

2、直角三角形性质：满足勾股定理的三边关系，斜边上的中线等于斜边的一半。

判定：有一个角是直角的三角形是直角三角形。

3、等腰直角三角形性质：具有等腰三角形和等边三角形的所以性质，两底角相等且等于45°。

判定：具有等腰三角形和等边三角形的所以性质的三角形是等腰直角三角形4、等边三角形性质：三边相等，三个角相等且等于60°，三线合一，具有等腰三角形的一切性质。

判定：三边相等，抛物线或坐标轴或对称轴上三个角相等，有一个角是60°的等腰三角形是等边三角形。

总结：（1）已知A 、B 两点，通过“两圆一线”可以找到所有满足条件的等腰三角形，要求的点（不与A 、B 点重合）即在两圆上以及两圆的公共弦上（2）已知A 、B 两点，通过“两线一圆”可以找到所有满足条件的直角三角形，要求的点（不与A 、B 点重合）即在圆上以及在两条与直径AB 垂直的直线上。

一次函数综合—线段和差、存在性问题解析

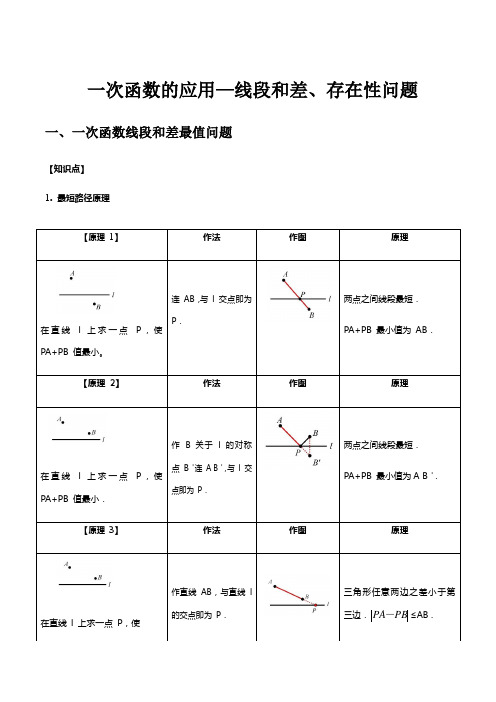
一次函数的应用—线段和差、存在性问题一、一次函数线段和差最值问题【知识点】1. 最短路径原理【原理1】作法作图原理在直线l 上求一点P，使PA+PB 值最小。

连AB，与l 交点即为P．两点之间线段最短．PA+PB 最小值为AB．【原理2】作法作图原理在直线l 上求一点P，使PA+PB 值最小．作 B 关于l 的对称点B＇连A B＇，与l 交点即为P．两点之间线段最短．PA+PB 最小值为A B＇．【原理3】作法作图原理在直线l 上求一点P，使作直线AB，与直线l的交点即为P．三角形任意两边之差小于第三边．≤AB .PBPA－（1）求线段和最小时动点坐标或直线解析式；（2）求三角形周长最小值；（3）求线段差最大时点的坐标或直线解析式。

3. 口诀：“和小异，差大同”（一）一次函数线段和最小值问题【例题讲解】★★☆例题1．在平面直角坐标系xOy 中，y 轴上有一点P ，它到点(4,3)A ，(3,1)B 的距离之和最小，则点P 的坐标是( ) A ．(0,0)B ．4(0,)7C ．5(0,)7D ．4(0,)5【答案】C的值最大 .【原理 4】作法作图原理在直线 l 上求一点 P ，使的值最大 .作 B 关于 l 的对称点 B ＇作直线 A B ＇，与 l 交点即为 P ．三角形任意两边之差小于第三边．≤A B ＇ .PB PA －PB PA －PB PA －【解析】解：作A 关于y 轴的对称点C ，连接BC 交y 轴于P ，则此时AP PB +最小，即此时点P 到点A 和点B 的距离之和最小，(4,3)A ，(4,3)C ∴-，设直线CB 的解析式是y kx b =+，把C 、B 的坐标代入得：3413k bk b =-+⎧⎨-=+⎩，解得：47k =-，57b =，4577y x ∴=-+，把0x =代入得：57y =，即P 的坐标是5(0,)7，故选：C ．【备注】本题考查了轴对称-最短路线问题，一次函数的解析式，坐标与图形性质等知识点，关键是能画出P 的位置，题目比较典型，是一道比较好的题目．★★☆练习1．如图，在平面直角坐标系中，已知点(2,3)A ，点(2,1)B -，在x 轴上存在点P 到A ，B 两点的距离之和最小，则P 点的坐标是．【答案】(1,0)-【解析】解：作A 关于x 轴的对称点C ，连接BC 交x 轴于P ，则此时AP BP +最小，A 点的坐标为(2,3)，B 点的坐标为(2,1)-，(2,3)C ∴-，设直线BC 的解析式是：y kx b =+，把B 、C 的坐标代入得：2123k b k b -+=⎧⎨+=-⎩解得11k b =-⎧⎨=-⎩．即直线BC 的解析式是1y x =--，当0y =时，10x --=，解得：1x =-，P ∴点的坐标是(1,0)-．故答案为：(1,0)-．【备注】本题考查了一次函数图象上点的坐标特征，用待定系数法求一次函数的解析式，轴对称-最短路线问题的应用，关键是能找出P 点，题目具有一定的代表性，难度适中．★★☆练习2．如图，直线34120x y +-=与x 轴、y 轴分别交于点B 、A 两点，以线段AB 为边在第一象限内作正方形ABCD ．若点P 为x 轴上的一个动点，求当PC PD +的长最小时点P 的坐标．【答案】详见解析【解析】解：直线34120x y +-=与x 轴、y 轴分别交于点B 、A 两点，则点A 、B 的坐标分别为：(0,3)，(4,0)，如图所示，过点C 作CH x ⊥轴交于点H ，90ABO BAO ∠+∠=︒，90ABO CBH ∠+∠=︒，CBH BAO ∴∠=∠，又90AOB CHB ∠=∠=︒，AB BC =，()AOB BHC AAS ∴∆≅∆，4CH OB ∴==，3HB OA ==，故点(7,4)C ，同理可得点(3,7)D ，确定点C 关于x 轴的对称点(7,4)C '-，连接C D '交x 轴于点P ，则此时PC PD +的长最小，将点C '、D 的坐标代入一次函数表达式并解得：直线CD 的表达式为：116144y x =-+，当0y =时，6111x =，故点61P，0)．(11【备注】本题考查的是一次函数上坐标点的特征，涉及到点的对称性、正方形性质等，本题的难点在于：通过证明三角形全等，确定点C、D的坐标．★★☆例题2．在平面直角坐标系中，矩形OACB的顶点O在坐标原点，顶点A、B分别在x轴、y轴的正半轴上，3OB=，D为边OB的中点，若E为x轴上的一个动点，当CDE∆的周长最小时，求点E OA=，4的坐标()A．(3,0)-B．(1,0)C．(0,0)D．(3,0)【答案】B【解析】解：如图，作点D关于x轴的对称点D'，连接CD'与x轴交于点E，连接DE．若在边OA上任取点E'与点E不重合，连接CE'、DE'、D E''由DE CE D E CE CD D E CE DE CE'+'=''+'>'='+=+，可知CDE∆的周长最小．OB=，D为边OB的中点，42∴=，OD∴，(0,2)D在矩形OACB 中，3OA =，4OB =，D 为OB 的中点，3BC ∴=，2D O DO '==，6D B '=，//OE BC ，Rt ∴△D OE Rt '∽△D BC '，∴OE D OBC D B '=' 即236OE = 1OE =，∴点E 的坐标为(1,0)故选：B ．【备注】此题主要考查轴对称--最短路线问题，解决此类问题，一般都是运用轴对称的性质，将求折线问题转化为求线段问题，其说明最短的依据是三角形两边之和大于第三边．★★☆练习1．如图，在平面直角坐标系中，点A 、B 的坐标分别为(1,4)和(3,0)，点C 是y 轴上的一个动点，连接AC 、BC ，当ABC ∆的周长最小值时，ABC ∆的面积为．【答案】3【解析】解：如图，作点A 关于y 轴的对称点A '，连接A B '交y 轴于点C '，此时ABC ∆'的周长最小，设直线A B ' 的解析式为y kx b =+，(1,4)A '-，(3,0)B ，∴430k b k b -+=⎧⎨+=⎩，1k ∴=-，3b =，∴直线A B ' 的解析式为3y x =-+，当0x =时，3y =，(0,3)C ∴'，ABC AA BAA C S SS∆'''∴=-11242122=⨯⨯-⨯⨯ 413=-=．所以ABC ∆'的面积为3．故答案为：3．【备注】本题考查了轴对称、最短路线问题、坐标与图形性质、三角形的面积，解决本题的关键是掌握轴对称的性质．★★☆练习2．如图，在平面直角坐标系中，直线122y x =+与x 轴、y 轴分别交于A 、B 两点，以AB 为边在第二象限内作正方形ABCD ．（1）求点A 、B 的坐标，并求边AB 的长；（2）求点C 和点D 的坐标；（3）在x 轴上找一点M ，使MDB ∆的周长最小，请求出M 点的坐标，并直接写出MDB ∆的周长最小值．【答案】详见解析【解析】解：（1）对于直线122y x =+，令0x =，得到2y =；令0y =，得到4x =-，(4,0)A ∴-，(0,2)B ，即4OA =，2OB =，则224225AB =+=；（2）过D 作DE x ⊥轴，过C 作CF y ⊥轴，四边形ABCD 为正方形，AB BC AD ∴==，90ABC BAD BFC DEA AOB ∠=∠=∠=∠=∠=︒，90FBC ABO ∠+∠=︒，90ABO BAO ∠+∠=︒，90DAE BAO ∠+∠=︒，FBC OAB EDA ∴∠=∠=∠，()DEA AOB BFC AAS ∴∆≅∆≅∆，2AE OB CF ∴===，4DE OA FB ===，即426OE OA AE =+=+=，246OF OB BF =+=+=，则(6,4)D -，(2,6)C -；（3）如图所示，连接BD ，找出B 关于y 轴的对称点B '，连接DB '，交x 轴于点M ，此时BM MD DM MB DB +=+'='最小，即BDM ∆周长最小，(0,2)B ，(0,2)B ∴'-，设直线DB '解析式为y kx b =+，把(6,4)D -，(0,2)B '-代入得：642k b b -+=⎧⎨=-⎩，解得：1k =-，2b =-，∴直线DB '解析式为2y x =--，令0y =，得到2x =-，则M 坐标为(2,0)-，此时MDB ∆的周长为21062+．【备注】本题属于一次函数综合题，涉及的知识有：待定系数法求一次函数解析式，坐标与图形性质，勾股定理，全等三角形的判定与性质，正方形的性质，对称性质，以及一次函数与坐标轴的交点，熟练掌握性质及定理是解本题的关键（二）一次函数线段差最大值问题【例题讲解】★★☆例题1．已知，如图点(1,1)A ，(2,3)B -，点P 为x 轴上一点，当||PA PB -最大时，点P的坐标为( )A ．1(,0)2B ．5(,0)4C ．1(,0)2-D ．(1,0)【答案】A【解析】解：作A 关于x 轴对称点C ，连接BC 并延长交x 轴于点P ， (1,1)A ，C ∴的坐标为(1,1)-，连接BC ，设直线BC 的解析式为：y kx b =+，∴123k b k b +=-⎧⎨+=-⎩，解得：21k b =-⎧⎨=⎩， ∴直线BC 的解析式为：21y x =-+，当0y =时，12x =， ∴点P 的坐标为：1(2，0)，当B ，C ，P 不共线时，根据三角形三边的关系可得：||||PA PB PC PB BC -=-<，∴此时||||PA PB PC PB BC -=-=取得最大值．故选：A ．【备注】此题考查了轴对称、待定系数法求一次函数的解析式以及点与一次函数的关系．此题难度较大，解题的关键是找到P 点，注意数形结合思想与方程思想的应用．★★☆练习1．平面直角坐标系中，已知(4,3)A 、(2,1)B ，x 轴上有一点P ，要使PA PB -最大，则P 点坐标为【答案】(1,0)【解析】解：(4,3)A 、(2,1)B ，x 轴上有一点P ，||PA PB AB ∴-，∴当A ，B ，P 三点共线时，PA PB -最大值等于AB 长，此时，设直线AB 的解析式为y kx b =+，把(4,3)A 、(2,1)B 代入，可得3412k b k b =+⎧⎨=+⎩，解得11k b =⎧⎨=-⎩， ∴直线AB 的解析式为1y x =-，令0y =，则1x =，P ∴点坐标为(1,0)，故答案为：(1,0)．【备注】本题主要考查了坐标与图形性质，利用待定系数法求得直线AB 的解析式是解决问题的关键． ★★☆练习2．如图，在平面直角坐标系中，点A 的坐标为(0,4)，点B 的坐标为(6,0)，点P 在一次函数1322y x =+的图象上运动，则PB PA -的最大值为( )A ．2B ．233C ．4D ．143【答案】C【解析】解：如图，作点A 关于直线1322y x =+的对称点K ，连接AK 交直线于H ，连接PK ．AK PH ⊥，(0,4)A ，∴直线AK 的解析式为24y x =-+，由132224y x y x ⎧=+⎪⎨⎪=-+⎩，解得12x y =⎧⎨=⎩， (1H ∴，20，AH KH =，(2,0)K ∴．PB PA PB PK KB ∴-=-，∴当点P 在BK 的延长线上时，P B P K BK '-'=的值最大，最大值为624-=，故选：C ．【备注】本题考查一次函数图象上的点的特征、轴对称等知识，解题的关键是学会利用对称解决最值问题属于中考常考题型．【题型知识点总结】一次函数最短路径问题注意事项：1. 根据“和小异，差大同”判断是否需要作对称；2. 作对称时注意要选取动点运动的直线为对称轴作某一定点的对称点。

二次函数与几何的动点及最值、存在性问题(解析版)-2024中考数学

二次函数与几何的动点及最值、存在性问题目录题型01平行y轴动线段最大值与最小值问题题型02抛物线上的点到某一直线的距离问题题型03已知点关于直线对称点问题题型04特殊角度存在性问题题型05将军饮马模型解决存在性问题题型06二次函数中面积存在性问题题型07二次函数中等腰三角形存在性问题题型08二次函数中直角三角形存在性问题题型09二次函数中全等三角形存在性问题题型10二次函数中相似三角形存在性问题题型11二次函数中平行四边形存在性问题题型12二次函数中矩形存在性问题题型13二次函数中菱形存在性问题题型14二次函数中正方形存在性问题二次函数常见存在性问题：(1)等线段问题：将动点坐标用函数解析式以“一母式”的结构表示出来，再利用点到点或点到直线的距离公式列出方程或方程组，然后解出参数的值，即可以将线段表示出来.【说明】在平面直角坐标系中该点在某一函数图像上，设该点的横坐标为m，则可用含m字母的函数解析式来表示该点的纵坐标，简称“设横表纵”或“一母式”.(2)平行y轴动线段最大值与最小值问题：将动点坐标用函数解析式以“一母式”的结构表示出来，再用纵坐标的较大值减去较小值，再利用二次函数的性质求出动线段的最大值或最小值.(3)求已知点关于直线对称点问题：先求出直线解析式，再利用两直线垂直的性质(两直线垂直，斜率之积等于-1)求出已知点所在直线的斜率及解析式，最后用中点坐标公式即可求出对称点的坐标.(4)“抛物线上是否存在一点，使其到某一直线的距离为最值”的问题：常常利用直线方程与二次函数解析式联立方程组，求出切点坐标，运用点到直线的距离公式进行求解.(5)二次函数与一次函数、特殊图形、旋转及特殊角度综合：图形或一次函数与x 轴的角度特殊化，利用与角度有关知识点求解函数图像上的点，结合动点的活动范围，求已知点与动点是否构成新的特殊图形.2.二次函数与三角形综合(1)将军饮马问题:本考点主要分为两类：①在定直线上是否存在点到两定点的距离之和最小;②三角形周长最小或最大的问题，主要运用的就是二次函数具有对称性.(2)不规则三角形面积最大或最小值问题:利用割补法将不规则三角形分割成两个或以上的三角形或四边形，在利用“一母式”将动点坐标表示出来，作线段差，用线段差来表示三角形的底或高，用面积公式求出各部分面积，各部分面积之和就是所求三角形的面积.将三角形的面积用二次函数的结构表示出来，再利用二次函数的性质求出面积的最值及动点坐标.(3)与等腰三角形、直角三角形的综合问题:对于此类问题，我们可以利用两圆一线或两线一圆的基本模型来进行计算.问题分情况找点画图解法等腰三角形已知点A ，B 和直线l ，在l 上求点P ，使△PAB 为等腰三角形以AB为腰分别以点A ，B 为圆心，以AB 长为半径画圆，与已知直线的交点P 1，P 2，P 4，P 5即为所求分别表示出点A ，B ，P 的坐标，再表示出线段AB ，BP ，AP 的长度，由①AB =AP ；②AB =BP ；③BP =AP 列方程解出坐标以AB 为底作线段AB 的垂直平分线，与已知直线的交点P 3即为所求分别表示出点A ，B ，P 的坐标，再表示出线段AB ，BP ，AP 的长度，由①AB =AP ；②AB =BP ；③BP =AP 列方程解出坐标问题分情况找点画图解法直角三角形已知点A ，B 和直线l ，在l 上求点P ，使△PAB 为直角三角形以AB为直角边分别过点A ，B 作AB 的垂线，与已知直线的交点P 1，P 4即为所求分别表示出点A ，B ，P 的坐标，再表示出线段AB ，BP ，AP 的长度，由①AB 2=BP 2+AP 2；②BP 2=AB 2+AP 2；③AP 2=AB 2+BP 2列方程解出坐标以AB 为斜边以AB 的中点Q 为圆心，QA 为半径作圆，与已知直线的交点P 2，P 3即为所求注：其他常见解题思路有：①作垂直，构造“三垂直”模型，利用相似列比例关系得方程求解；②平移垂线法：若以AB 为直角边，且AB 的一条垂线的解析式易求(通常为过原点O 与AB 垂直的直线)，可将这条直线分别平移至过点A 或点B 得到相应解析式，再联立方程求解．(4)与全等三角形、相似三角形的综合问题:在没有指定对应点的情况下，理论上有六种情况需要讨论，但在实际情况中，通常不会超过四种，要注意边角关系，积极分类讨论来进行计算.情况一探究三角形相似的存在性问题的一般思路：解答三角形相似的存在性问题时，要具备分类讨论思想及数形结合思想，要先找出三角形相似的分类标准，一般涉及动态问题要以静制动，动中求静，具体如下：①假设结论成立，分情况讨论．探究三角形相似时，往往没有明确指出两个三角形的对应点(尤其是以文字形式出现求证两个三角形相似的题目)，或者涉及动点问题，因动点问题中点的位置的不确定，此时应考虑不同的对应关系，分情况讨论；②确定分类标准．在分类时，先要找出分类的标准，看两个相似三角形是否有对应相等的角，若有，找出对应相等的角后，再根据其他角进行分类讨论来确定相似三角形成立的条件；若没有，则分别按三种角对应来分类讨论；③建立关系式，并计算．由相似三角形列出相应的比例式，将比例式中的线段用所设点的坐标表示出来(其长度多借助勾股定理运算)，整理可得一元一次方程或者一元二次方程，解方程可得字母的值，再通过计算得出相应的点的坐标．情况二探究全等三角形的存在性问题的思路与探究相似三角形的存在性问题类似，但是除了要找角相等外，还至少要找一组对应边相等．3.二次函数与四边形的综合问题特殊四边形的探究问题解题步骤如下：①先假设结论成立；②设出点坐标，求边长；③建立关系式，并计算．若四边形的四个顶点位置已确定，则直接利用四边形边的性质进行计算；若四边形的四个顶点位置不确定，需分情况讨论：a.探究平行四边形：①以已知边为平行四边形的某条边，画出所有的符合条件的图形后，利用平行四边形的对边相等进行计算；②以已知边为平行四边形的对角线，画出所有的符合条件的图形后，利用平行四边形对角线互相平分的性质进行计算；③若平行四边形的各顶点位置不确定，需分情况讨论，常以已知的一边作为一边或对角线分情况讨论．b.探究菱形：①已知三个定点去求未知点坐标；②已知两个定点去求未知点坐标，一般会用到菱形的对角线互相垂直平分、四边相等的性质列关系式．c.探究正方形：利用正方形对角线互相垂直平分且相等的性质进行计算，一般是分别计算出两条对角线的长度，令其相等，得到方程再求解．d.探究矩形：利用矩形对边相等、对角线相等列等量关系式求解；或根据邻边垂直，利用勾股定理列关系式求解.题型01平行y轴动线段最大值与最小值问题1(2023·广东东莞·一模)如图，抛物线y=x2+bx+c与x轴交于A、B两点，与y轴交于点C，OA=OC =3，顶点为D．(1)求此函数的关系式；(2)在AC 下方的抛物线上有一点N ，过点N 作直线l ∥y 轴，交AC 与点M ，当点N 坐标为多少时，线段MN 的长度最大？最大是多少？(3)在对称轴上有一点K ，在抛物线上有一点L ，若使A ，B ，K ，L 为顶点形成平行四边形，求出K ，L 点的坐标．(4)在y 轴上是否存在一点E ，使△ADE 为直角三角形，若存在，直接写出点E 的坐标；若不存在，说明理由．【答案】(1)y =x 2+2x -3(2)当N 的坐标为-32,-154 ，MN 有最大值94(3)K -1，4 ，L -1，-4 或K -1，12 ，L -5，12 或K -1，12 ，L 3，12(4)存在，点E 的坐标为0,32 或0,-72或0,-1 或0,-3【分析】(1)由OA =OC =3求得A -3,0 ,C 0，-3 ,再分别代入抛物线解析式y =x 2+bx +c ，得到以b ，c 为未知数的二元一次方程组，求出b ，c 的值即可；(2)求出直线AC 的解析式，再设出M 、N 的坐标，把MN 表示成二次函数，配方即可；(3)根据平行四边形的性质，以AB 为边，以AB 为对角线，分类讨论即可；(4)设出E 的坐标，分别表示出△ADE 的平分，再分每一条都可能为斜边，分类讨论即可．【详解】(1)∵抛物线y =x 2+bx +c 经过点A ，点C ，且OA =OC =3,∴A -3,0 ,C 0，-3 ,∴将其分别代入抛物线解析式，得c =-39-3b +c =0，解得b =2c =-3 ．故此抛物线的函数表达式为：y =x 2+2x -3；(2)设直线AC 的解析式为y =kx +t ，将A -3,0 ,C 0，-3 代入，得t =-3-3k +t =0 ，解得k =-1t =-3 ，∴直线AC 的解析式为y =-x -3，设N 的坐标为n ，n 2+2n -3 ，则M n ，-n -3 ，∴MN =-n -3-n 2+2n -3 =-n 2-3n =-n +32 +94，∵-1<0，∴当n =-32时，MN 有最大值，为94，把n =-32代入抛物线得，N 的坐标为-32,-154，当N 的坐标为-32,-154 ，MN 有最大值94；(3)①当以AB 为对角线时，根据平行四边形对角线互相平分，∴KL 必过-1,0 ，∴L 必在抛物线上的顶点D 处，∵y =x 2+2x -3=x +1 2-4，∴K -1，4 ，L -1，-4②当以AB 为边时，AB =KL =4，∵K 在对称轴上x =-1，∴L 的横坐标为3或-5，代入抛物线得L -5,12 或L 3,12 ，此时K 都为-1，12 ，综上，K -1，4 ，L -1，-4 或K -1，12 ，L -5，12 或K -1，12 ，L 3，12 ；(4)存在，由y =x 2+2x -3=x +1 2-4，得抛物线顶点坐标为D -1,-4 ∵A -3，0 ，∴AD 2=-3+1 2+0+4 2=20，设E 0，m ，则AE 2=-3-0 2+0-m 2=9+m 2，DE 2=-1-0 2+-4-m 2=17+m 2+8m ，①AE 为斜边，由AE 2=AD 2+DE 2得：9+m 2=20+17+m 2+8m ，解得：m =-72，②DE 为斜边，由DE 2=AD 2+AE 2得：9+m 2+20=17+m 2+8m ，解得：m =32，③AD 为斜边，由AD 2=ED 2+AE 2得：20=17+m 2+8m +9+m 2，解得：m =-1或-3，∴点E 的坐标为0,32 或0,-72或0,-1 或0,-3 ．【点睛】本题主要考查待定系数法求二次函数解析式，二次函数图象与性质，平行四边形的判定与性质以及勾股定理等知识，会运用待定系数法列方程组，两点间距离公式求MN 的长，由平行四边形的性质判定边相等，运用勾股定理列方程．2(2023·河南南阳·统考一模)如图，抛物线与x 轴相交于点A 、B (点A 在点B 的左侧)，与y 轴的交于点C 0，-4 ，点P 是第三象限内抛物线上的一个动点，设点P 的横坐标为m ，过点P 作直线PD ⊥x 轴于点D ，作直线AC 交PD 于点E ．已知抛物线的顶点P 坐标为-3，-254．(1)求抛物线的解析式；(2)求点A 、B 的坐标和直线AC 的解析式；(3)求当线段CP =CE 时m 的值；(4)连接BC ，过点P 作直线l ∥BC 交y 轴于点F ，试探究：在点P 运动过程中是否存在m ，使得CE =DF ，若存在直接写出m 的值；若不存在，请说明理由．【答案】(1)y =14x 2+32x -4(2)A -8，0 ，B 2，0 ，y =-12x -4(3)-4(4)存在，m =2-25或m =-4【分析】(1)运用待定系数法即可求得抛物线的解析式；(2)令y =0，解方程即可求得点A 、B 的坐标，再运用待定系数法即可求得直线AC 的解析式；(3)过点C 作CF ⊥PE 于点F ，根据等腰三角形的性质可得点F 是PE 的中点，设P m ,14m 2+32m -4 ，则E m ，-12m -4 ，可得F m ，18m 2+12m -4 ，再由点F 与点C 的纵坐标相同建立方程求解即可；(4)过C 作CH ⊥PD 于H ，设P m ,14m 2+32m -4 ，由PF ∥BC ，可得直线PF 解析式为y =2x +14m 2-12m -4，进而可得OF =14m 2-12m -4 ，再证得Rt △CHE ≅Rt △DOF HL ，得出∠HCE =∠FDO ，进而推出∠FDO =∠CAO ，即tan ∠FDO =tan ∠CAO ，据此建立方程求解即可．【详解】(1)解：∵抛物线的顶点坐标为-3，-254∴设抛物线的解析式为y =a x +3 2-254，把点C 0，-4 代入，得：-4=9a -254，解得：a =14，∴y =14x +3 2-254=14x 2+32x -4，∴该抛物线的解析式为y =14x 2+32x -4．(2)解：令y =0，得14x 2+32x -4=0，解得：x 1=-8，x 2=2，∴A -8，0 ，B 2，0 ，，设直线AC 的解析式为y =kx +b ，则-8k +b =0b =-4 ，解得：k =-12b =-4 ，∴直线AC 的解析式为y =-12x -4．(3)解：如图，过点C 作CF ⊥PE 于点F ，∵CP =CE ，∴EF =PF ，即点F 是PE 的中点，设P m ,14m 2+32m -4 ，则E m ，-12m -4 ，∴F m ，18m 2+12m -4 ，∵PE ∥y 轴，CF ⊥PE ，∴CF ∥x 轴，∴18m 2+12m -4=-4，解得：m =-4或m =0(不符合题意，舍去)，∴m =-4．(4)解：存在m ，使得CE =DF ，理由如下：如图：过C 作CH ⊥PD 于H ，设P m,14m2+32m-4，由B2，0，C0，-4，由待定系数法可得直线BC解析式为y=2x-4，根据PF∥BC，设直线PF解析式为y=2x+c，将P m,14m2+32m-4代入得：1 4m2+32m-4=2m+c，∴c=14m2-12m-4，∴直线PF解析式为y=2x+14m2-12m-4，令x=0得y=14m2-12m-4，∴F0,14m2-12m-4，∴OF=14m2-12m-4，∵∠CHD=∠PDO=∠COD=90°，∴四边形CODH是矩形，∴CH=OD，∵CE=DF，∴Rt△CHE≅Rt△DOF HL，∴∠HCE=∠FDO，∵∠HCE=∠CAO，∴∠FDO=∠CAO，∴tan∠FDO=tan∠CAO，∴OF OD =OCOA，即14m2-12m-4-m=48=12，∴1 4m2-12m-4=-12m或14m2-12m-4=12m，解得：m=-4或m=4或m=2-25或m=2+25，∵P在第三象限，∴m=2-25或m=-4．【点睛】本题属于二次函数综合题，主要考查了待定系数法求函数解析式、二次函数综合应用、等腰三角形性质、矩形判定及性质、相似三角形判定及性质、解直角三角形等知识点，解题的关键是用含m的代数式表示相关点坐标和相关线段的长度．3(2023·山东聊城·统考三模)抛物线y=-x2+bx+c与x轴交于点A3,0，与y轴交于点C0,3，点P 为抛物线上的动点．(2)若P 为直线AC 上方抛物线上的动点，作PH ∥x 轴交直线AC 于点H ，求PH 的最大值；(3)点N 为抛物线对称轴上的动点，是否存在点N ，使直线AC 垂直平分线段PN ？若存在，请直接写出点N 的纵坐标；若不存在，请说明理由．【答案】(1)b =2，c =3(2)PH 取得最大值为94(3)存在，2-2或2+2【分析】(1)将坐标代入解析式，构建方程求解；(2)设PH 交y 轴于点M ，P m ,-m 2+2m +3 ，则PM =m ；待定系数法确定直线AC 的解析式为y =-x +3，从而确定PH =m -m 2-2m =-m 2+3m =-m -32 2+94，解得PH 最大值为94；(3)如图，设PN 与AC 交于点G ，可设直线PN 的解析式为y =x +p ，设点N (1,n )，求得y =x +(n -1)；联立y =-x +3y =x +(n -1) ，解得x =-n 2+2y =n 2+1，所以点P 的横坐标为2×-n 2+2 -1=-n +3，纵坐标为2×n2+1 -n =2，由二次函数解析式构建方程-(-n +3)2+2(-n +3)+3=2，解得n =2±2；【详解】(1)∵抛物线y =-x 2+bx +c 与x 轴交于点A 3,0 ，与y 轴交于点C 0,3 ，∴-9+3b +c =0c =3，解得：b =2c =3 ，∴b =2，c =3；(2)设PH 交y 轴于点M ，P m ,-m 2+2m +3 ，∴PM =m ，∵PH ∥x 轴，∴点H 的纵坐标为-m 2+2m +3，设直线AC 的解析式为y =kx +n ，∴3k +n =0n =3 ，解得：k =-1n =3 ，∴直线AC 的解析式为y =-x +3．∴-m 2+2m +3=-x +3，∴x =m 2-2m ，∴H m 2-2m ,-m 2+2m +3 ，∴PH =m -m 2-2m =-m 2+3m =-m -322+94，∴当m =32时，PH 取得最大值为94(3)存在点N ，使直线AC 垂直平分线段PN ，点N 的纵坐标为2-2或2+2如图，设PN 与AC 交于点G ，∵AC 垂直平分PN ，直线AC 的解析式为y =-x +3∴可设直线PN 的解析式为y =x +p 设点N (1,n )，则n =1+p ∴p =n -1，∴y =x +(n -1)联立y =-x +3y =x +(n -1) ，解得x =-n 2+2y =n 2+1∴点P 的横坐标为2×-n 2+2 -1=-n +3，纵坐标为2×n 2+1 -n =2∴-(-n +3)2+2(-n +3)+3=2，解得n =2±2∴点N 的纵坐标为2-2或2+2．【点睛】本题考查利用二次函数解析式及点坐标求待定参数、待定系数法确定函数解析式、二次函数极值及其它二次函数综合问题，利用直线间的位置关系、点线间的位置关系，融合方程的知识求解坐标是解题的关键．题型02抛物线上的点到某一直线的距离问题1(2023·广东梅州·统考二模)探究求新：已知抛物线G 1:y =14x 2+3x -2，将抛物线G 1平移可得到抛物线G 2:y =14x 2．(1)求抛物线G 1平移得到抛物线G 2的平移路径；(2)设T 0,t ，直线l ：y =-t ，是否存在这样的t ，使得抛物线G 2上任意一点到T 的距离等于到直线l 的距离？若存在，求出t 的值；若不存在，试说明理由；(3)设H 0,1 ，Q 1,8 ，M 为抛物线G 2上一动点，试求QM +MH 的最小值．参考公式：若点M x 1,y 1 ，N x 2,y 2 为平面上两点，则有MN =x 1-x 22+y 1-y 2 2．【答案】(1)将G 1向左平移-6个单位，向上平移11个单位(2)存在，1(3)9【分析】(1)设G 1向左平移a 个单位，向上平移b 个单位得到函数G 2，列方程组即可求解；(2)设P x 0,x 204为抛物线G 2上的一点，根据题意列方程即可；(3)点H 坐标与(2)中t =1时的T 点重合，过点M 作MA ⊥l ，垂足为A ，如图所示，则有MH =MA ，当且仅当Q ,M ,A 三点共线时QM +MA 取得最小值．【详解】(1).解：设G 1向左平移a 个单位，向上平移b 个单位得到函数G 2，由平移法则可知14(x +a )2+3(x +a )-2+b =14x 2，整理可得14x 2+3+12a x +14a 2+3a -2+b =14x 2，可得方程组3+12a =014a 2+3a -2+b =0，解得a =-6b =11 ；∴平移路径为将G 1向左平移-6个单位，向上平移11个单位；(2)解：存在这样的t ，且t =1时满足条件，设P x 0,x 204为抛物线G 2上的一点，则点P 到直线l 的距离为x 204+t ，点P 到点T 距离为(x 0-0)2+x 204-t2，联立可得：x 204+t =(x 0-0)2+x 204-t2，两边同时平方合并同类项后可得x 20-x 20t =0解得：t =1；(3)解：点H 坐标与(2)中t =1时的T 点重合，作直线l ：y =-1，过点M 作MA ⊥直线l ，垂足为A ，如图所示，则有MH =MA ，此时QM +MH =QM +MA ，当且仅当Q ,M ,A 三点共线时QM +MA 取得最小值即QM +MA =QA =8-(-1)=9∴QM +MH 的最小值为9；【点睛】本题考查二次函数综合题，涉及到线段最小值、平移性质等，灵活运用所学知识是关键．2(2023·湖北宜昌·统考一模)如图，已知：点P 是直线l ：y =x -2上的一动点，其横坐标为m (m 是常数)，点M 是抛物线C ：y =x 2+2mx -2m +2的顶点．(1)求点M 的坐标；(用含m 的式子表示)(2)当点P 在直线l 运动时，抛物线C 始终经过一个定点N ，求点N 的坐标，并判断点N 是否是点M 的最高位置？(3)当点P 在直线l 运动时，点M 也随之运动，此时直线l 与抛物线C 有两个交点A ，B (A ，B 可以重合)，A ，B 两点到y 轴的距离之和为d ．①求m 的取值范围；②求d 的最小值．【答案】(1)M -m ,-m 2-2m +2(2)N (1,3)，点N 是点M 的最高位置(3)①m ≤-52或m ≥32；②d 取得最小值为2【分析】(1)将抛物线解析式写成顶点式即可求解；(2)根据解析式含有m 项的系数为0，得出当x =1时，y =3，即N (1,3)，根据二次函数的性质得出-m 2-2m +2=-m +1 2+3的最大值为3，即可得出点N 是点M 的最高位置；(3)①根据直线与抛物线有交点，联立方程，根据一元二次方程根的判别式大于等于0，求得m 的范围，即可求解；②设A ,B 的坐标分别为x 1,y 1 ,x 2,y 2 ，其中x 1<x 2，由①可知x 1,x 2是方程x 2+2mx -x -2m +4=0的两根，根据x 1+x 2=-2m +1，分情况讨论，求得d 是m 的一次函数，进而根据一次函数的性质即可求解．【详解】(1)解：y =x 2+2mx -2m +2=x +m 2-m 2-2m +2，∴顶点M -m ,-m 2-2m +2 ，(2)解：∵y =x 2+2mx -2m +2=x 2+2+2m x -1 ，∴当x =1时，y =3，抛物线C 始终经过一个定点1,3 ，即N (1,3)；∵M -m ,-m 2-2m +2 ，-m 2-2m +2=-m +1 2+3，∴M 的纵坐标最大值为3，∴点N 是点M 的最高位置；(3)解：①联立y =x -2y =x 2+2mx -2m +2 ，得x 2+2mx -x -2m +4=0，∵直线l 与抛物线C 有两个交点A ，B (A ，B 可以重合)，∴Δ=b 2-4ac =2m -1 2-4-2m +4 ，=4m 2+4m -15≥0，∵4m 2+4m -15=0，解得m 1=-52,m 2=32，∴当4m 2+4m -15≥0时，m ≤-52或m ≥32，②设A ,B 的坐标分别为x 1,y 1 ,x 2,y 2 ，其中x 1<x 2，由①可知x 1,x 2是方程x 2+2mx -x -2m +4=0的两根，∴x1+x 2=-2m +1，当m =-3时，如图所示，y A =0，当-3≤m ≤-52时，y 1≥0,y 2≥0，则d =x 1+x 2 =-2m +1 ，∵-2<0，∴当m =-52时，d 取得最小值为-2×-52 +1=5+1=6，当m ≥32时，d =-x 1+x 2 =--2m +1 =2m -1，∴当m =32时，d 取得最小值为2×32-1=2，综上所述，d 取得最小值为2．【点睛】本题考查了二次函数的性质，一元二次方程与二次函数的关系，熟练掌握二次函数的性质是解题的关键．3(2023·云南楚雄·统考一模)抛物线y =x 2-2x -3交x 轴于A ，B 两点(A 在B 的左边)，C 是第一象限抛物线上一点，直线AC 交y 轴于点P ．(1)直接写出A ，B 两点的坐标；(2)如图①，当OP =OA 时，在抛物线上存在点D (异于点B )，使B ，D 两点到AC 的距离相等，求出所有满足条件的点D 的横坐标；(3)如图②，直线BP 交抛物线于另一点E ，连接CE 交y 轴于点F ，点C 的横坐标为m ，求FP OP 的值(用含m 的式子表示)．【答案】(1)A (-1,0)，B (3,0)(2)0或3-41或3+41(3)13m 【分析】(1)令y =0，解方程可得结论；(2)分两种情形：①若点D 在AC 的下方时，过点B 作AC 的平行线与抛物线交点即为D 1．②若点D 在AC 的上方时，点D 1关于点P 的对称点G (0,5)，过点G 作AC 的平行线交抛物线于点D 2，D 3，D 2，D 3符合条件．构建方程组分别求解即可；(3)设E 点的横坐标为n ，过点P 的直线的解析式为y =kx +b ，由y =kx +b y =x 2-2x -3 ，可得x 2-(2+k )x -3-b =0，设x 1，x 2是方程x 2-(2+k )x -3-b =0的两根，则x 1x 2=-3-b ，推出x A ⋅x C =x B ⋅x E =-3-b 可得n =-1-b 3，设直线CE 的解析式为y =px +q ，同法可得mn =-3-q 推出q =-mn -3，推出q =-(3+b )-1-b 3 -3=13b 2+2b ，推出OF =13b 2+b ，可得结论．【详解】(1)解：令y =0，得x 2-2x -3=0，解得：x =3或-1，∴A (-1,0)，B (3,0)；(2)∵OP =OA =1，∴P (0,1)，∴直线AC 的解析式为y =x +1．①若点D 在AC 的下方时，过点B 作AC 的平行线与抛物线交点即为D 1．∵B (3,0)，BD 1∥AC ，∴直线BD 1的解析式为y =x -3，由y =x -3y =x 2-2x -3，解得x =3y =0 或x =0y =-3 ，∴D 1(0,-3)，∴D 1的横坐标为0．②若点D 在AC 的上方时，点D 1关于点P 的对称点G (0,5)，过点G 作AC 的平行线l 交抛物线于点D 2，D 3，D 2，D 3符合条件．直线l 的解析式为y =x +5，由y =x +5y =x 2-2x -3 ，可得x 2-3x -8=0，解得：x =3-412或3+412，∴D 2，D 3的横坐标为3-412，3+412，综上所述，满足条件的点D 的横坐标为0，3-412，3+412．(3)设E 点的横坐标为n ，过点P 的直线的解析式为y =kx +b ，由y =kx +b y =x 2-2x -3，可得x 2-(2+k )x -3-b =0，设x 1，x 2是方程x 2-(2+k )x -3-b =0的两根，则x 1x 2=-3-b ，∴x A ⋅x C =x B ⋅x E =-3-b∵x A =-1，∴x C =3+b ，∴m =3+b ，∵x B =3，∴x E =-1-b 3，∴n =-1-b 3，设直线CE 的解析式为y =px +q ，同法可得mn =-3-q∴q =-mn -3，∴q =-(3+b )-1-b 3 -3=13b 2+2b ，∴OF =13b 2+2b ，∴FP OP=13b +1=13(m -3)+1=13m ．【点睛】本题属于二次函数综合题，考查了二次函数的性质，一次函数的性质，一元二次方程的根与系数的关系等知识，解题的关键是学会构建一次函数，构建方程组确定交点坐标，学会利用参数解决问题，属于中考压轴题．题型03已知点关于直线对称点问题1(2023·辽宁阜新·统考中考真题)如图，在平面直角坐标系中，二次函数y =-x 2+bx -c 的图象与x 轴交于点A (-3,0)和点B (1,0)，与y 轴交于点C ．(1)求这个二次函数的表达式．(2)如图1，二次函数图象的对称轴与直线AC :y =x +3交于点D ，若点M 是直线AC 上方抛物线上的一个动点，求△MCD 面积的最大值．(3)如图2，点P 是直线AC 上的一个动点，过点P 的直线l 与BC 平行，则在直线l 上是否存在点Q ，使点B 与点P 关于直线CQ 对称？若存在，请直接写出点Q 的坐标；若不存在，请说明理由．【答案】(1)y =-x 2-2x +3；(2)S △MCD 最大=98；(3)Q 1-5，-5 或1+5，5 ．【分析】(1)根据抛物线的交点式直接得出结果；(2)作MQ ⊥AC 于Q ，作ME ⊥AB 于F ，交AC 于E ，先求出抛物线的对称轴，进而求得C ，D 坐标及CD 的长，从而得出过M 的直线y =x +m 与抛物线相切时，△MCD 的面积最大，根据x +m =-x 2-2x +3的△=0求得m 的值，进而求得M 的坐标，进一步求得CD 上的高MQ 的值，进一步得出结果；(3)分两种情形：当点P 在线段AC 上时，连接BP ，交CQ 于R ，设P (t ，t +3)，根据CP =CB 求得t 的值，可推出四边形BCPQ 是平行四边形，进而求得Q 点坐标；当点P 在AC 的延长线上时，同样方法得出结果．【详解】(1)解：由题意得，y =-(x +3)(x -1)=-x 2-2x +3；(2)解：如图1，作MQ ⊥AC 于Q ，作ME ⊥AB 于F ，交AC 于E ，∵OA =OC =3，∠AOC =90°，∴∠CAO =∠ACO =45°，∴∠MEQ =∠AEF =90°-∠CAO =45°，抛物线的对称轴是直线：x =-3+12=-1，∴y =x +3=-1+3=2，∴D (1,2)，∵C (0,3)，∴CD =2，故只需△MCD 的边CD 上的高最大时，△MCD 的面积最大，设过点M 与AC 平行的直线的解析式为：y =x +m ，当直线y =x +m 与抛物线相切时，△MCD 的面积最大，由x +m =-x 2-2x +3得，x 2+3x +(m -3)=0，由△=0得，32-4(m -3)=0得，m -3=94，∴x 2+3x +94=0，∴x 1=x 2=-32，∴y =--32 2-2×-32 +3=154，y =x +3=-32+3=32，∴ME =154-32=94，∴MQ =ME ⋅sin ∠MEQ =ME ⋅sin45°=94×22=928，∴S △MCD 最大=12×2×928=98；(3)解：如图2，当点P 在线段AC 上时，连接BP ，交CQ 于R ，∵点B 和点Q 关于CQ 对称，∴CP =CB ，设P (t ，t +3)，由CP 2=CB 2得，2t 2=10，∴t 1=-5，t 2=5(舍去)，∴P -5，3-5 ，∵PQ ∥BC ，∴CR =BR =1，∴CR =QR ，∴四边形BCPQ 是平行四边形，∵1+(-5)-0=1-5，0+(3-5)-3=-5，∴Q 1-5，-5 ；如图3，当点P 在AC 的延长线上时，由上可知：P 5，3+5 ，同理可得：Q 1+5，5 ，综上所述：Q 1-5，-5 或1+5，5 ．【点睛】本题考查了二次函数及其图象的性质，一元二次方程的解法，平行四边形的判定和性质，轴对称的性质等知识，解决问题的关键是分类讨论．2(2023·四川甘孜·统考中考真题)已知抛物线y =x 2+bx +c 与x 轴相交于A -1，0 ，B 两点，与y 轴相交于点C 0，-3 ．(1)求b ，c 的值；(2)P 为第一象限抛物线上一点，△PBC 的面积与△ABC 的面积相等，求直线AP 的解析式；(3)在(2)的条件下，设E 是直线BC 上一点，点P 关于AE 的对称点为点P ，试探究，是否存在满足条件的点E ，使得点P 恰好落在直线BC 上，如果存在，求出点P 的坐标；如果不存在，请说明理由．【答案】(1)b =-2,c =-3.(2)y =x +1(3)存在，点P 的坐标为1+21,-2+21 或1-21,-2-21【分析】(1)由待定系数法即可求解；(2)S △PBC =S △ABC 得到AP ∥BC ，即可求解；(3)由题意的：∠AEP =∠AEP ,P E =PE ，即可求解．【详解】(1)由题意，得1-b +c =0,c =-3.∴b =-2,c =-3.(2)由(1)得抛物线的解析式为y =x 2-2x -3．令y =0，则x 2-2x -3=0，得x 1=-1，x 2=3．∴B 点的坐标为3，0 ．∵S △PBC =S △ABC ，∴AP ∥BC ．∵B 3，0，C 0，-3 ，∵AP∥BC，∴可设直线AP的解析式为y=x+m．∵A(-1，0)在直线AP上，∴0=-1+m．∴m=1．∴直线AP的解析式为y=x+1．(3)设P点坐标为m，n．∵点P在直线y=x+1和抛物线y=x2-2x-3上，∴n=m+1，n=m2-2m-3．∴m+1=m2-2m-3．解得m1=4，m2=-1(舍去)．∴点P的坐标为4，5．由翻折，得∠AEP=∠AEP ,P E=PE．∵AP∥BC，∴∠PAE=∠AEP '．∴∠PAE=∠PEA．∴PE=PA=4+12=52．2+5-0设点E的坐标为t，t-3，则PE2=t-42．2+t-3-52=52∴t=6±21．当t=6+21时，点E的坐标为6+21,3+21．设P (s,s-3),由P E=AP，P E=PE=52得：s-6-212，2=522+s-3-3-21解得：s=1+21，则点P 的坐标为1+21,-2+21．当t=6-21时，同理可得，点P 的坐标为1-21,-2-21．综上所述，点P 的坐标为1+21,-2+21．或1-21,-2-21【点睛】本题是二次函数的综合题，主要考查了用待定系数法求一次函数、二次函数的解析式，二次函数的性质，此题题型较好，综合性比较强，用的数学思想是分类讨论和数形结合的思想．3(2023·江苏连云港·连云港市新海实验中学校考二模)如图，“爱心”图案是由抛物线y=-x2+m的一部分及其关于直线y=-x的对称图形组成，点E、F是“爱心”图案与其对称轴的两个交点，点A、B、C、D是该图案与坐标轴的交点，且点D的坐标为6,0．(1)求m 的值及AC 的长；(2)求EF 的长；(3)若点P 是该图案上的一动点，点P 、点Q 关于直线y =-x 对称，连接PQ ，求PQ 的最大值及此时Q 点的坐标．【答案】(1)m =6，AC =6+6(2)52(3)2542，Q -234,-12【分析】(1)用待定系数法求得m 与抛物线的解析式，再求出抛物线与坐标轴的交点坐标，进而求得A 的坐标，根据对称性质求得B ，C 的坐标，即可求得结果；(2)将抛物线的解析式与直线EF 的解析式联立方程组进行求解，得到E ，F 的坐标，即可求得结果；(3)设P (m ,-m 2+6)，则Q (m 2-6,-m )，可得PQ =2×m -12 2-252 ，即求m -12 2-252的最值，根据二次函数的最值，即可得到m 的值，即可求得．【详解】(1)把D 6,0 代入y =-x 2+m 得0=-6+m解得m =6∴抛物线的解析式为：y =-x 2+6∴A 0,6根据对称性可得B -6,0 ，C 0,-6∴AC =AO +OC =6+6(2)联立y =-x y =-x 2+6解得x =3y =-3 或x =-2y =2 ∴E -2,2 ，F 3,-3∴EF =-2-3 2+2+3 2=52(3)设P (m ,-m 2+6)，则Q (m 2-6,-m )∴PQ =m -m 2-6 2+-m 2+6--m 2整理得PQ =2×m -12 2-254 ∵m -12 2≥0∴当m -12 2=0时，即m =12时，m -12 2-254 有最大值为254∴PQ 的最大值为2542∴12 2-6=-234故Q -234,-12【点睛】本题考查二次函数综合应用，涉及待定系数法求函数解析式，两点间的距离公式，求抛物线与一次函数的交点坐标，二次函数的最值等知识，解题的关键是掌握关于直线y =-x 对称的点坐标的关系．题型04特殊角度存在性问题1(2023·山西忻州·统考模拟预测)如图，抛物线y =18x 2+34x -2与x 轴交于A ，B 两点，与y 轴交于点C ．P 是直线AC 下方抛物线上一个动点，过点P 作直线l ∥BC ，交AC 于点D ，过点P 作PE ⊥x 轴，垂足为E ，PE 交AC 于点F ．(1)直接写出A ，B ，C 三点的坐标，并求出直线AC 的函数表达式；(2)当线段PF 取最大值时，求△DPF 的面积；(3)试探究在拋物线的对称轴上是否存在点Q ，使得∠CAQ =45°？若存在，请直接写出点Q 的坐标；若不存在，请说明理由．【答案】(1)A -8,0 ，B 2,0 ，C 0,-2 ．y =-14x -2(2)85(3)存在，-3,3 或-3,-253【分析】(1)对于直线y =18x 2+34x -2，当x =0时，y =-2，即点C 0,-2 ，令18x 2+34x -2=0，则x =2或-8，则点A ，B 的坐标分别为-8,0 ，2,0 即求出三个点的坐标，设直线AC 的表达式为y =kx +b ，利用待定系数法求解即可；(2)设点P 的横坐标为m ，则P m ,18m 2+34m -2 ，F m ,-14m -2 ，表示出PF =-18m 2-m ，求出PF max =2，再表示出点D 到直线PF 的距离d =85，利用S △DPF =12⋅PF ⋅d 进行求解即可；(3)由抛物线的表达式知，其对称轴为x =-3，当点Q 在x 轴上方时，设抛物线的对称轴交x 轴于点N ，交AC 于H ，故点Q 作QT ⊥AC 于点T ，在△AQH 中,∠CAQ =45°，tan ∠QHA =4，用解直角三角形的方法求出QH =174，即可求出Q 点坐标，当点Q Q 在x 轴上方时，直线AQ 的表达式为y =35x +8 ，当∠CAQ =45°时，AQ ⊥AQ ，即可求解．【详解】(1)解：对于抛物线y =18x 2+34x -2，当x =0时，y =-2，即点C 0,-2 ，令18x 2+34x -2=0，则x =2或-8，则点A ，B 的坐标分别为-8,0 ，2,0 ，即点A ，B ，C 三点的坐标分别为-8,0 ，2,0 ，0,-2 ，设直线AC 的表达式为y =kx +b ，则-8k +b =0b =-2 ，解得k =-14b =-2 ，∴直线AC 的函数表达式为y =-14x -2；(2)设点P 的横坐标为m ，则P m ,18m 2+34m -2 ，F m ,-14m -2 ，PF =-14m -2 -18m 2+34m -2 =-18m 2-m ，当m =--12×-18 =-4时，PF 最大，PF max =-18×(-4)2--4 =2，此时，P -4,-3 ，由B 2,0 ，C 0,-2 ，可得直线BC 的函数表达式为y =x -2，设直线l 的函数表达式为y =x +p ，将P -4,-3 代入可得p =1，∴直线l 的函数表达式为y =x +1，由y =-14x -2y =x +1 ，解得x =-125y =-75，∴D -125,-75 ，点D 到直线PF 的距离d =-125--4 =85，∴S △DPF =12⋅PF ⋅d =12×2×85=85．(3)存在，理由：由抛物线的表达式知，其对称轴为x =-3，当点Q 在x 轴上方时，如下图：设抛物线的对称轴交x 轴于点N ，交AC 于H ，故点Q 作QT ⊥AC 于点T ，则∠ACO =∠QHA ，则tan ∠ACO =tan ∠QHA =4，当x =3时，y =-14x -2=-54，则点H -3,-54 ，由点A ，H 的坐标得，AH =5174，在△AQH 中，∠CAQ =45°，tan ∠QHA =4，设TH =x ，则QT =4x ，则QH =17x ，则AH =AT +TH =5x =5174，则x =174，则QH =17x =174，则174-54=3，则点Q -3,3 ；当点Q Q 在x 轴上方时，直线AQ 的表达式为y =35x +8 ，当∠CAQ =45°时，AQ ⊥AQ ，则直线AQ 的表达式为y =-53x +8 ，当x =-3时，y =-5x +8 =-25，。

函数恒成立存在性与有解问题

函数恒成立存在性问题知识点梳理1、恒成立问题的转化：()a f x >恒成立⇒()max a f x >；()()min a f x a f x ≤⇒≤恒成立2、能成立问题的转化：()a f x >能成立⇒()min a f x >；()()max a f x a f x ≤⇒≤能成立3、恰成立问题的转化：()a f x >在M 上恰成立⇔()a f x >的解集为M ()()R a f x M a f x C M ⎧>⎪⇔⎨≤⎪⎩在上恒成立在上恒成立另一转化方法：若A x f D x ≥∈)(,在D 上恰成立，等价于)(x f 在D 上的最小值A x f =)(min ，若,D x ∈Bx f ≤)(在D 上恰成立，则等价于)(x f 在D 上的最大值B x f =)(max .4、设函数()x f 、()x g ，对任意的[]b a x ,1∈，存在[]d c x ,2∈，使得()()21x g x f ≥，则()()x g x f min min ≥5、设函数()x f 、()x g ，对任意的[]b a x ,1∈，存在[]d c x ,2∈，使得()()21x g x f ≤，则()()x g x f max max ≤6、设函数()x f 、()x g ，存在[]b a x ,1∈，存在[]d c x ,2∈，使得()()21x g x f ≥，则()()x g x f min max ≥7、设函数()x f 、()x g ，存在[]b a x ,1∈，存在[]d c x ,2∈，使得()()21x g x f ≤，则()()x g x f max min ≤8、若不等式()()f x g x >在区间D 上恒成立，则等价于在区间D 上函数()y f x =和图象在函数()y g x =图象上方；9、若不等式()()f x g x <在区间D 上恒成立，则等价于在区间D 上函数()y f x =和图象在函数()y g x =图象下方；例题讲解：题型一、常见方法1、已知函数12)(2+-=ax x x f ，xax g =)(，其中0>a ，0≠x ． 1）对任意]2,1[∈x ，都有)()(x g x f >恒成立，求实数a 的取值范围；2）对任意]4,2[],2,1[21∈∈x x ，都有)()(21x g x f >恒成立，求实数a 的取值范围；2、设函数b x x a x h ++=)(，对任意]2,21[∈a ，都有10)(≤x h 在]1,41[∈x 恒成立，求实数b 的取值范围．3、已知两函数2)(x x f =，m x g x-⎪⎭⎫ ⎝⎛=21)(，对任意[]2,01∈x ，存在[]2,12∈x ，使得()21)(x g x f ≥，则实数m 的取值范围为题型二、主参换位法(已知某个参数的范围，整理成关于这个参数的函数)1、对于满足2p ≤的所有实数p,求使不等式212x px p x ++>+恒成立的x 的取值范围。

人教版九年级下册反比例函数存在性问题解析版(综合复习)

反比例函数存在性问题解析版一．相似1．Rt△ABC在直角坐标系内的位置如图所示，反比例函数y＝（k≠0）在第一象限内的图象与BC边交于点D（4，1），与AB边交于点E（2，n）．（1）求反比例函数的解析式和n值；（2）当＝时，求直线AB的解析式；（3）设P是线段AB边上的点，在（2）的条件下，是否存在点P，以B、C、P为顶点的三角形与△EDB相似？若存在，请直接写出此时点P的坐标；若不存在，请说明理由．【解答】解：（1）∵D（4，1）、E（2，n）在反比例函数y＝的图象上，∴4＝k，2n＝k，∴k＝4，n＝2，∴反比例函数的解析式为y＝；（2）如图1，过点E作EH⊥BC，垂足为H．第1页（共49页）在Rt△BEH中，tan∠BEH＝tan∠A＝，EH＝2，所以BH＝1．∴D（4，1），E（2，2），B（4，5）．设直线AB的解析式为y＝kx+b，代入B（4，3）、E（2，2），得，解得：，因此直线AB的函数解析式为：y＝x+1；（3）存在，如图2，作EF⊥BC于F，PH⊥BC于H，当△BED∽△BPC时，，∴＝，∵BF＝1，∴BH＝，第2页（共49页）∴CH＝，可得＝x+1，x＝1，点P的坐标为（1，）；如图3，当△BED∽△BCP时，＝，∵EF＝2，BF＝1，由勾股定理，BE＝，∴＝，∴BP＝，∴，BF＝1，BH＝，∴CH＝，可得＝x+1，x＝，点P的坐标为（，），点P的坐标为（1，）；（，）．二．直角三角形1．如图，已知直线OA与反比例函数y＝（m≠0）的图象在第一象限交于点A．若OA＝4，直线OA与x轴的夹角为60°．（1）求点A的坐标；（2）求反比例函数的解析式；第3页（共49页）（3）若点P是坐标轴上的一点，当△AOP是直角三角形时，直接写出点P的坐标．【解答】解：（1）如图1，过点A作AE⊥x轴于E，∵∠AOE＝60°，AE⊥OE，∴∠OAE＝30°，∴OE＝OA＝2，AE＝OE＝2，∴点A（2，2）；（2）∵反比例函数y＝的图象过点A，∴m＝2×2＝4，∴反比例函数解析式为y＝；（3）如图，第4页（共49页）当点P1在y轴上时，且∠AP1O＝90°，又∵∠AOP1＝30°，∴AP1＝2，OP1＝AP1＝2，∴点P1（0，2）；当点P2在x轴上，且∠AP2O＝90°，又∵∠OAP2＝30°，∴OP2＝2，∴点P2（2，0）；当点P3在y轴上，且∠P3AO＝90°，又∵∠AOP3＝30°，∴OP3＝2AP3，AO＝AP3＝4，∴OP3＝，∴点P3（0，）；当点P4在x轴上，且∠P4AO＝90°，∵∠AOP4＝60°，第5页（共49页）∴∠AP4O＝30°，∴OP4＝2OA＝8，∴点P4（8，0）；综上所述：点P的坐标为（0，2）或（2，0）或（0，）或（8，0）．2．如图，一次函数y＝kx+b（k≠0）与反比例函数的图象在第一象限交于A、B两点，A点的坐标为（m，4），B点的坐标为（3，2），连接OA、OB，过B作BD⊥y轴，垂足为D，交OA于C．若OC＝CA，（1）求一次函数和反比例函数的表达式；（2）求△AOB的面积；（3）在直线BD上是否存在一点E，使得△AOE是以AO为直角边的直角三角形，直接写出所有可能的E点坐标．【解答】解：（1）∵点B（3，2）在反比例函数y＝的图象上，∴a＝3×2＝6，∴反比例函数的表达式为y＝，∵点A的纵坐标为4，∵点A在反比例函数y＝图象上，第6页（共49页）∴A（，4），∴，∴，∴一次函数的表达式为y＝﹣x+6；（2）如图1，过点A作AF⊥x轴于F交OB于G，∵B（3，2），∴直线OB的解析式为y＝x，∴G（，1），A（，4），∴AG＝4﹣1＝3，∴S△AOB＝S△AOG+S△ABG＝×3×3＝．（3）如图2中，第7页（共49页）①当∠AOE1＝90°时，∵点A（，4），∴直线AC的解析式为y＝x，∴直线OE1的解析式为y＝﹣x，当y＝2时，x＝﹣，∴E1（﹣，2）；②当∠OAE2＝90°时，可得直线AE2的解析式为y＝﹣x+，当y＝2时，x＝，∴E2（，2）．综上所述，满足条件的点E坐标为（﹣，2）或（，2）．3．已知：如图，一次函数y＝﹣2x+10的图象与反比例函数y＝的图象相交于A、B两点（A在B的右侧），点A横坐标为4．（1）求反比例函数解析式及点B的坐标；（2）观察图象，直接写出关于x的不等式﹣2x+10﹣＞0的解集；第8页（共49页）（3）反比例函数图象的另一支上是否存在一点P，使△P AB是以AB为直角边的直角三角形？若存在，求出所有符合条件的点P的坐标；若不存在，请说明理由．【解答】解：（1）把x＝4代入y＝﹣2x+10得y＝2，∴A（4，2），把A（4，2）代入y＝，得k＝4×2＝8．∴反比例函数的解析式为y＝，解方程组，得，或，∴点B的坐标为（1，8）；（2）观察图象得，关于x的不等式﹣2x+10﹣＞0的解集为：1＜x＜4或x＜0；（3）存在，理由：①若∠BAP＝90°，过点A作AH⊥OE于H，设AP与x轴的交点为M，如图1，第9页（共49页）对于y＝﹣2x+10，当y＝0时，﹣2x+10＝0，解得x＝5，∴点E（5，0），OE＝5．∵A（4，2），∴OH＝4，AH＝2，∴HE＝5﹣4＝1．∵AH⊥OE，∴∠AHM＝∠AHE＝90°．又∵∠BAP＝90°，∴∠AME+∠AEM＝90°，∠AME+∠MAH＝90°，∴∠MAH＝∠AEM，∴△AHM∽△EHA，∴，即，∴MH＝4，∴M（0，0），第10页（共49页）可设直线AP的解析式为y＝mx，则有4m＝2，解得m＝，∴直线AP的解析式为y＝x，解方程组，得，，∴点P的坐标为（﹣4，﹣2）．②若∠ABP＝90°，同理可得：点P的坐标为（﹣16，﹣）．综上所述：符合条件的点P的坐标为（﹣4，﹣2）、（﹣16，﹣）．4．已知：一次函数y＝﹣2x+10的图象与反比例函数y＝（k＞0）的图象相交于A，B两点（A在B的右侧）．（1）当A（4，2）时，求反比例函数的解析式及B点的坐标；（2）在（1）的条件下，反比例函数图象的另一支上是否存在一点P，使△P AB是以AB 为直角边的直角三角形？若存在，求出所有符合条件的点P的坐标；若不存在，请说明理由．第11页（共49页）【解答】解：（1）把A（4，2）代入y＝，得k＝4×2＝8．∴反比例函数的解析式为y＝．解方程组，得，∴点B的坐标为（1，8）；（2）存在，理由：①若∠BAP＝90°，过点A作AH⊥OE于H，设AP与x轴的交点为M，如图1，对于y＝﹣2x+10，当y＝0时，﹣2x+10＝0，解得x＝5，∴点E（5，0），OE＝5．∵A（4，2），∴OH＝4，AH＝2，∴HE＝5﹣4＝1．第12页（共49页）∵AH⊥OE，∴∠AHM＝∠AHE＝90°．又∵∠BAP＝90°，∴∠AME+∠AEM＝90°，∠AME+∠MAH＝90°，∴∠MAH＝∠AEM，∴△AHM∽△EHA，∴，即，∴MH＝4，∴M（0，0），可设直线AP的解析式为y＝mx，则有4m＝2，解得m＝，∴直线AP的解析式为y＝x，解方程组，得，∴点P的坐标为（﹣4，﹣2）．②若∠ABP＝90°，同理可得：点P的坐标为（﹣16，﹣）．综上所述：符合条件的点P的坐标为（﹣4，﹣2）、（﹣16，﹣）．第13页（共49页）三．平行四边形1．如图，一次函数y1＝kx+b的图象与反比例函数y2＝的图象交于A（2，m），B（n，1）两点，连接OA，OB．（1）求这个一次函数的表达式；（2）求△OAB的面积；（3）问：在直角坐标系中，是否存在一点P，使以O，A，B，P为顶点的四边形是平行四边形？若存在，直接写出点P的坐标；若不存在，请说明理由．【解答】解：（1）∵点A（2，m），B（n，1）在反比例函数y2＝上，∴2m＝6，n＝6，∴m＝3，∴A（2，3），B（6，1），∵点A（2，3），B（6，1）在一次函数y1＝kx+b上，∴，∴，∴一次函数的表达式为y1＝﹣x+4；第14页（共49页）（2）如图1，记一次函数y1＝﹣x+4的图象与x，y轴的交点为点D，C，针对于y1＝﹣x+4，令x＝0，则y1＝4，∴C（0，4），∴OC＝6，令y1＝0，则﹣x+4＝0，∴x＝8，∴D（8，0），∴OD＝8，过点A作AE⊥y轴于E，过点B作BF⊥x轴于F，∵A（2，3），B（6，1），∴AE＝2，BF＝1，∴S△AOB＝S△COD﹣S△AOC﹣S△BOD＝OC•OD﹣OC•AE﹣OD•BF＝×4×8﹣×4×2﹣×8×1＝8；（3）存在，如图2，当AB和OB为邻边时，点B（6，1）先向左平移6个单位再向下平移1个单位到点O（0，第15页（共49页）0），则点A也先向左平移6个单位再向下平移1个单位到点P（2﹣6，3﹣1），即P（﹣4，2）；当OA和OB为邻边时，点O（0，0）先向右平移2个单位再向上平移3个单位到点A（2，3），则点B也先向右平移2个单位再向上平移3个单位到点P'（6+2，1+3），即P'（8，4）；当AB和OA为邻边时，点A（2，3）先向右平移4个单位再向下平移2个单位到点B（6，1），则点O也先向右平移4个单位再向下平移2个单位到点P''（0+4，0﹣2），即P'（4，﹣2）；点P的坐标为（﹣4，2）或（4，﹣2）或（8，4）．2．如图，在平面直角坐标系xOy中，一次函数y＝x+b的图象经过点A（﹣2，0），与反比例函数y＝的图象交于点B（a，4）和点C．（1）求一次函数和反比例函数的表达式；第16页（共49页）（2）若点P在y轴上，且△PBC的面积等于6，求点P的坐标；（3）设M是直线AB上一点，过点M作MN∥x轴，交反比例函数y＝的图象于点N，若A，O，M，N为顶点的四边形为平行四边形，求点M的坐标．【解答】解：（1）∵一次函数y＝x+b的图象经过点A（﹣2，0），∴b＝2，∴直线解析式为y＝x+2，∵点B（a，4）在直线y＝x+2上，∴4＝a+2，∴a＝2，∴点B（2，4），∵反比例函数y＝的图象过点B（2，4），∴k＝2×4＝8，∴反比例函数解析式为y＝；（2）如图1，设直线AB与y轴交于点D，点P坐标为（0，p），第17页（共49页）∵直线AB与y轴交于点D，∴点D（0，2），联立方程得：，解得：，或，∴C（﹣4，﹣2），∴S△PBC＝S△BPD+S△PDC＝，∴p＝0或4，∴P（0，0）或（0，4）；（3）如图2，设M（m﹣2，m），则N（），第18页（共49页）∵以A，O，M，N为顶点的四边形为平行四边形，MN∥OA，OA＝2，∴MN＝OA＝2，∴，∴或，∴点M坐标为（2﹣2，）或（﹣2，﹣2）或（2，）或（﹣2，）．3．如图，在平面直角坐标系xOy中，一次函数y＝x+b的图象经过点C（0，2），与反比例函数y＝（x＞0）的图象交于点A（1，a）．（1）求一次函数和反比例函数的表达式；（2）设M是反比例函数y＝（x＞0）图象上一点，N是直线AB上一点，若以点O、M、C、N为顶点的四边形是平行四边形，求点N的坐标．第19页（共49页）【解答】解：（1）∵点C（0，2）在直线y＝x+b上，∴b＝2，∴一次函数的表达式为y＝x+2；∵点A（1，a）在直线y＝x+2上，∴a＝3，∴点A（1，3），∵点A（1，3）在反比例函数y＝（x＞0）的图象上，∴k＝1×3＝3，∴反比例函数的表达式为y＝；（2）由（1）知，直线AB的表达式为y＝x+2，反比例函数的表达式为y＝，设点M（m，），N（n，n+2），若以点O、M、C、N为顶点的四边形是平行四边形，则①以OC和MN为对角线时，第20页（共49页）∴＝0，，∴m＝，n＝﹣或m＝﹣（此时，点M不在第一象限，舍去），n＝，∴N（﹣，﹣+2），②以CN和OM为对角线时，∴＝，＝，∴m＝n＝﹣2+或m＝n＝﹣2﹣（此时，点M不在第一象限，舍去），∴N（﹣2+，），③以CM和ON为对角线时，∴＝，＝，∴m＝n＝或m＝n＝﹣（此时，点M不在第一象限，舍去），∴N（，2+），即满足条件的点N的坐标为（﹣，﹣+2）或（﹣2+，）或（，2+）．4．阅读理解：已知：对于实数a≥0，b≥0，满足a+b≥2，当且仅当a＝b时，等号成立，此时取得代数式a+b的最小值．根据以上结论，解决以下问题：（1）拓展：若a＞0，当且仅当a ＝1时，a+有最小值，最小值为2；（2）应用：①如图1，已知点P为双曲线y＝（x＞0）上的任意一点，过点P作P A⊥x轴，PB⊥y第21页（共49页）轴，四边形OAPB的周长取得最小值时，求出点P的坐标以及周长最小值；②如图2，已知点Q是双曲线y＝（x＞0）上一点，且PQ∥x轴，连接OP、OQ，当线段OP取得最小值时，在平面内取一点C，使得以O、P、Q、C为顶点的四边形是平行四边形，求出点C的坐标．【解答】解：（1）由题意得：a+≥2＝2，故a+有最小值为2；此时a＝，解得a＝±1（舍去负值），故答案为1，2；（2）设点P（x，），则四边形OAPB的周长＝2PB+2AP＝2（x+）≥2（2）＝8，此时x＝，解得x＝±2（舍去负值），则点P（2，2），故答案为：P（2，2），周长最小8；（3）设点P（x，），第22页（共49页）则由题意得：OP2＝x2+（）2≥2x＝8，当OP最小时，x＝，解得x＝±2（舍去负值），故点P（2，2），当y＝2时，y＝＝2，解得x＝4，即点Q（4，2），则PQ＝4﹣2＝2，①当PQ是边时，∵PQ∥x轴，∴四边形OPQC为平行四边形时，点C在x轴上，即OC＝PQ＝2，则点C（2，0）或（﹣2，0）；②当PQ是对角线时，设点C的坐标为（x，y），由中点的性质得：（2+4）＝（x+0）且（2+2）＝（0+y），解得，故点C（6，4）．故答案为：（﹣2，0）、（2，0）或（6，4）．四．菱形1．如图，在同一平面直角坐标系中，直线y＝x+2和双曲线y＝相交于A、B两点．第23页（共49页）（1）连结AO、BO，求出△AOB的面积．（2）已知点E在双曲线y＝上且横坐标为1，作EF垂直于x轴垂足为F，点H是x 轴上一点，连结EH交双曲线于点I，连结IF并延长交y轴于点G，若点G坐标为（0，﹣），请求出H点的坐标．（3）已知点M在x轴上，点N是平面内一点，以点O、E、M、N为顶点的四边形是菱形，请你直接写出N点的坐标．【解答】解：（1）如图1中，设AB交y轴于C．由，解得或，∴A（2，4），B（﹣4，﹣2），第24页（共49页）∵直线AB交y轴于C（0，2），∴S△AOB＝S△AOC+S△OCB＝×2×2+×2×4＝6．（2）如图2中，由题意E（1，8），F（1，0），∵G（0，﹣），∴直线FG的解析式为y＝x﹣，由，解得或，∴I（，），∴直线EH的解析式为y＝x+令y＝0，解得x＝，∴H（，0）．第25页（共49页）（3）如图3中，∵E（1，8），∴OE＝＝，当OM1是菱形的对角线时，E，N1关于x轴对称，可得N1（1，﹣8）．当OM为菱形的边时，可得N2（1+，8），N4（1﹣，8）．当OE为菱形的对角线时，连接M3N3交OE于T，EN3交y轴于P．∵M3N3⊥OE，∴∠OTM3＝90°，∵∠POE＝∠TM3O，∴sin∠POE＝sin∠OM3T，∴＝，∴OM3＝，第26页（共49页）∴M3（，0），∵TN3＝TM3，T（，4），∴可得N3（﹣，8），综上所述，满足条件的点N的坐标为（1，﹣8）或（1+，8）或（1﹣，8）或（﹣，8）．2．如图，已知直线y＝kx+b与反比例函数y＝（x＞0）的图象分别交于点A（m，3）和点B（6，n），与坐标轴分别交于点C和点D．（1）求直线AB的解析式；（2）若点P是反比例函数第一象限内，直线CD上方一动点，当△ABP面积为5时，求点P的坐标．（3）若M是平面直角坐标系内一动点，在y轴上是否存在一动点Q，使以A、C、Q、M为顶点的四边形为菱形？若存在，请直接写出Q点的坐标；否则，说明理由．【解答】解：（1）把点A（m，3）、B（6，n）分别代入y＝①得3m＝6，6n＝6，解得m＝2，n＝1，∴A（2，3），B（6，1），把A（2，3），B（6，1）代入y＝kx+b得，第27页（共49页）解得，∴直线AB的解析式为y＝﹣x+4；（2）将直线AB向右平移h个单位得到直线l，直线l与反比例函数的交点即为所求点P，过点D作DH⊥l交于点H，设直线l交x轴于点M，由直线AB的表达式知，tan∠HMD＝，则sin∠HMD＝，则HD＝DM sin∠HMD＝h×＝h，由点A、B的坐标知，AB＝＝2，则△ABP面积＝×AB×h＝×2h＝5，解得h＝，则DM＝h＝5，即直线AB向右平移5个单位得到直线l，则直线l的表达式为y＝﹣（x﹣5）+4②，联立①②并解得：，故点P的坐标为（1，6）或（12，）；第28页（共49页）（3）存在，理由：设点P（a，b），点Q（0，t），由A、C的坐标知，AC2＝5，①当AC是边时，点C向右平移2个单位向下平移1个单位得到点A，同样点P（Q）向右平移2个单位向下平移1个单位得到点点Q（P），则a+2＝0且b﹣1＝t且AC＝PC或a﹣2＝0且b+1＝t且AC＝QC，即a+2＝0且b﹣1＝t且a2+（b﹣4）2＝5或a﹣2＝0且b+1＝t且（t﹣4）2＝5，解得t＝4（舍去）或2或4±，②当AC是对角线时，由中点公式得：（2+0）＝（3+4）＝（b+t）且CP＝CQ，即a2+（b﹣4）2＝（t ﹣4）2，解得t＝1.5；故点Q的坐标为（0，2）或（0，4+）或（0，4﹣）或（0，1.5）．3．如图1，在平面直角坐标系中，直线y＝x+12与双曲线y＝﹣交于A、B两点（点A 在点B左边），过A、O两点作直线，与双曲线的另一交点为D，过B作直线AO的平行线交双曲线于点C．（1）则点A坐标为（﹣6，4），点B坐标为（﹣3，8），并求直线BC的解析式；（2）如图2，点P在y轴负半轴上，连接PB，交直线AO于点E，连接CE、P A，且S△P AB＝S△BCE，将线段PO在y轴上移动，得到线段P′O′（如图3），请求出|P′B ﹣O′D|的最大值；（3）如图4，点M在x轴上，在平面内是否存在一点N，使以点C、D、M、N 为顶点第29页（共49页）的四边形是菱形？若存在，请直接写出符合条件的N点坐标；若不存在，请说明理由．【解答】解：（1）联立方程组，解得，，∴A（﹣6，4），B（﹣3，8），设直线OA的解析式为y＝kx（k≠0），则4＝﹣6k，解得，k＝﹣，第30页（共49页）∴直线OA的解析式为：y＝x，∵BC∥OA，∴设直线BC的解析式为y＝x+b，则8＝﹣+b，解得b＝6，∴直线BC的解析式为y＝x+6，故答案为：（﹣6，4），（﹣3，8）．（2）∵A、D关于原点对称，A（﹣6，4），∴D（6，﹣4），设P（0，a），∴，∵S△BCE＝S△BCA＝[28﹣（﹣2）]•|（﹣3）﹣（﹣6）|＝45，∴S△P AB＝24＝9﹣a，∴a＝﹣4，∴P（0，﹣4），将B向上平移4个单位，得到B1（﹣3，12），设B1，B2关于Y轴对称，则B2（3，12），连接DB2并延长交y轴于O′，∴|P′B﹣O′D|的最大值＝DB2＝＝．第31页（共49页）第32页（共49页）（3）联立方程组，解得，，∴C （12，﹣2），若CD 为对角线，则M （8，0），N （10，﹣6）．若CD 为边，且CD ＝MD ，则M （6+2，0），N （12+2，2）或M （6﹣2，0）．N（12﹣2，2）若CD 为边，且CD ＝MC ，则M （6，0），N （0，﹣2）．综上所述，满足条件的点N 的坐标为（10，﹣6）或（12+2，2）或（12﹣2，2）或（0，﹣2）．4．如图，在平面直角坐标系中，四边形ABCD 的顶点A 、B 在函数y ＝（x ＞0）的图象上，顶点C 、D 在函数y ＝（x ＞0）的图象上，其中0＜m ＜n ，对角线BD ∥y 轴，且BD⊥AC于点P．已知点B的横坐标为4．（1）当m＝4，n＝20时，①点B的坐标为（4，1），点D的坐标为（4，5），BD的长为5．②若点P的纵坐标为2，求四边形ABCD的面积．③若点P是BD的中点，请说明四边形ABCD是菱形．（2）当四边形ABCD为正方形时，直接写出m、n之间的数量关系．【解答】解：（1）①当x＝4时，y＝＝1，∴点B的坐标为（4，1）；当y＝2时，2＝，解得：x＝2，∴点A的坐标为（2，2）；当n＝20时，y＝，当x＝4时，y＝5，故点D（4，5），BD＝5﹣1＝4，故答案为（4，1）；（4，5）；4；②∵BD∥y轴，BD⊥AC，点P的纵坐标为2，第33页（共49页）∴A（2，2），C（10，2）．∴AC＝8，∴四边形ABCD的面积＝AC×BD＝×8×4＝16；③四边形ABCD为菱形，理由如下：由①得：点B的坐标为（4，1），点D的坐标为（4，5），∵点P为线段BD的中点，∴点P的坐标为（4，3）．当y＝3时，3＝，解得：x＝，∴点A的坐标为（，3）；当y＝3时，3＝，解得：x＝，∴点C的坐标为（，3）．∴P A＝4﹣＝，PC＝﹣4＝，∴P A＝PC．∵PB＝PD，∴四边形ABCD为平行四边形．又∵BD⊥AC，∴四边形ABCD为菱形；（2）四边形ABCD能成为正方形．第34页（共49页）当四边形ABCD为正方形时，设P A＝PB＝PC＝PD＝t（t≠0）．当x＝4时，y＝＝，∴点B的坐标为（4，），∴点A的坐标为（4﹣t，+t）．∵点A在反比例函数y＝的图象上，∴（4﹣t）（+t）＝m，化简得：t＝4﹣，∴点D的纵坐标为+2t＝+2（4﹣）＝8﹣，∴点D的坐标为（4，8﹣），∴4×（8﹣）＝n，整理，得：m+n＝32．即四边形ABCD能成为正方形，此时m+n＝32．5．已知：如图，正比例函数y1＝kx（k＞0）的图象与反比例函数y2＝的图象相交于点A 和点C，设点C的坐标为（2，n）．（1）求k与n的值；（2）点B是x轴上的一个动点，连结AB、BC，作点A关于直线BC的对称点Q，在点B的移动过程中，是否存在点B，使得四边形ABQC为菱形？若存在，求出点B的坐标；若不存在请说明理由．第35页（共49页）【解答】解：（1）把点C的坐标（2，n）代入y2＝，解得：n＝3，∴点C的坐标为（2，3），把点C（2，3）代入y1＝kx得：3＝2k，解得：k＝；（2）存在，理由：①如图1，当点B在x轴的正半轴且AB＝AC时，四边形ABQC为菱形．第36页（共49页）∵点A与点Q关于直线BC对称，∴AC＝QC，AB＝QB，∴AC＝QC＝AB＝QB．∴四边形ABQC为菱形．由（1）中点C的坐标（2，3），可求得：OC＝，∵点A与点C关于原点对称，∴点A的坐标为（﹣2，﹣3），∴OA＝OC＝，AC＝2，∴AC＝AB＝2．过点A作AH⊥x轴于点H，则AH＝3．在Rt△AHB中，由勾股定理得：BH＝＝，又∵OH＝2，∴OB＝BH﹣OH＝﹣2，∴点B的坐标为（﹣2，0）；②如图2，当点B在x轴的负半轴且AB＝AC时，四边形ABQC为菱形．过点A作AT⊥x轴于点T，第37页（共49页）同理可求得：BT＝＝，又∵OT＝2，∴OB＝BT+OT＝+2，∴点B的坐标为（﹣﹣2，0），综上，当点B的坐标为（﹣2，0）或（﹣﹣2，0）时，四边形ABQC为菱形．五．等腰三角形1．如图，一次函数y＝﹣x+1的图象与两坐标轴分别交于A，B两点，与反比例函数的图象交于点C（﹣2，m）．（1）求反比例函数的解析式；（2）若点P在y轴正半轴上，且与点B，C构成以BC为腰的等腰三角形，请直接写出所有符合条件的P点坐标．第38页（共49页）【解答】解：（1）∵点C（﹣2，m）在一次函数y＝﹣x+1的图象上，把C点坐标代入y＝﹣x+1，得m＝﹣（﹣2）+1＝3，∴点C的坐标是（﹣2，3），设反比例函数的解析式为，把点C的坐标（﹣2，3）代入得，，解得k＝﹣6，∴反比例函数的解析式为；（2）在直线y＝﹣x+1中，令x＝0，则y＝1，∴B（0，1），由（1）知，C（﹣2，3），∴BC＝＝2，当BC＝BP时，BP＝2，∴OP＝2+1，∴P（0，2+1），当BC＝PC时，点C在BP的垂直平分线，∴P（0，5），即满足条件的点P的坐标为（0，5）或（0，）．2．如图，在平面直角坐标系中，点A（2，m）在正比例函数y＝x（x＞0）的图象上，反第39页（共49页）比例函数y＝（x＞0）的图象经过点A，点P是x轴正半轴上一动点，过点P作x轴的垂线，与正比例函数y＝x（x＞0）的图象交于点C，点B是线段CP与反比例函数的交点，连接AP、AB．（1）求该反比例函数的表达式；（2）观察图象，请直接写出当x＞0时，x≤的解集；（3）若S△ABP＝1，求B点坐标；（4）点Q是A点右侧双曲线上一动点，是否存在△APQ为以P为直角顶点的等腰直角三角形？若存在，求出点Q坐标；若不存在，请说明理由．【解答】解：（1）当x＝2时，y＝x＝3，故点A（2，3），将点A的坐标代入反比例函数表达式得：3＝，解得k＝6，故反比例函数表达式为y＝；（2）观察图象，请直接写出当x＞0时，x≤的解集为0＜x≤2；第40页（共49页）（3）设点B（m，），则S△ABP＝×BP×（x B﹣x A）＝××|（m﹣2）|＝1，解得m＝3或1.5，故点B的坐标为（3，2）或（1.5，4）；（4）存在，理由：设点Q的坐标为（t，），点P（n，0），∵△APQ为以P为直角顶点的等腰直角三角形，故AP＝QP，∠APQ＝90°，过点A、Q分别作x轴的垂线，垂足分别为M、N，∵∠APM+∠QPN＝90°，∠QPN+∠PQN＝90°，∴∠APM＝∠PQN，∵∠AMP＝∠PNQ＝90°，AP＝QP，∵△AMP≌△PNQ（AAS），∴AM＝PN，PM＝QN，即n﹣2＝且t﹣n＝3，第41页（共49页）解得t＝6，故点Q（6，1）．3．已知一次函数y＝kx+b与反比例函数y＝的图象交于A（﹣3，2）、B（1，n）两点（1）求一次函数和反比例函数的表达式；（2）△AOB的面积为8；（3）直接写出不等式kx+b＞的解集0＜x ＜1或x＜﹣3；（4）点P在x的负半轴上，当△P AO为等腰三角形时，直接写出点P的坐标．【解答】解：（1）∵反比例函数y＝经过点A（﹣3，2），∴m＝﹣6，∵点B（1，n）在反比例函数图象上，∴n＝﹣6．∴B（1，﹣6），把A，B的坐标代入y＝kx+b，则，解得，∴一次函数的解析式为y＝﹣2x﹣4，反比例函数的解析式为y＝﹣；第42页（共49页）（2）如图设直线AB交y轴于C，则C（0，﹣4），∴S△AOB＝S△OCA+S△OCB＝×4×3+×4×1＝8，故答案为8；（3）观察函数图象知，kx+b＞的解集为0＜x＜1或x＜﹣3，故答案为0＜x＜1或x＜﹣3；（4）由题意OA＝＝，当AO＝AP时，可得P1（﹣6，0），当OA＝OP时，可得P2（﹣，0），P4（，0）（舍去），当P A＝PO时，过点A作AJ⊥x轴于J．设OP3＝P3A＝x，在Rt△AJP3中，则有x2＝22+（3﹣x）2，解得x＝，第43页（共49页）∴P3（﹣，0），综上所述，满足条件的点P的坐标为（﹣，0）或（﹣，0）或（﹣6，0）．六．其他1．定义：如图1，点P为∠AOB平分线上一点，∠MPN的两边分别与射线OA，OB交于M，N两点，若∠MPN绕点P旋转时始终满足OM•ON＝OP2，则称∠MPN是∠AOB的“相关角”．（1）如图1，已知∠AOB＝60°，点P为∠AOB平分线上一点，∠MPN的两边分别与射线OA，OB交于M，N两点，且∠MPN＝150°．求证：∠MPN是∠AOB的“相关角”；（2）如图2，如果∠MON＝60°，OP＝2，∠APB是∠MON的关联角，连接AB，求△MON的面积和∠MPN的度数；（3）如图3，C是函数y＝（x＞0）图象上的一个动点，过点C的直线CD分别交x 轴和y轴于点A，B两点，且满足BC＝3CA，∠AOB的“相关角”为∠APB，求出OP 的长及相应点P的坐标．【解答】解：（1）∵∠AOB＝60°，P为∠AOB的平分线上一点，第44页（共49页）∴∠AOP＝∠BOP＝∠AOB＝30°，∵∠MOP+∠OMP+∠MPO＝180°，∴∠OMP+∠MPO＝150°，∵∠MPN＝150°，∴∠MPO+∠OPN＝150°，∴∠OMP＝∠OPN，∴△MOP∽△PON，∴，∴OP2＝OM•ON，∴∠MPN是∠AOB的“相关角”；（2）设∠MON＝60°＝α，如图1，过点A作AH⊥OB于点H，连接AB．∵∠APB是∠MON的智慧角，∴OP2＝OA•OB，∵点P为∠MON的平分线上一点，第45页（共49页）∴∠AOP＝∠BOP＝＝30°，∴△AOP∽△POB，∴∠OAP＝∠OPB，∴∠APB＝∠OPB+∠OP A＝∠OAP+∠OP A＝180°﹣30°＝150°，∴S△AOB＝•OB•AH＝•OB•OA•sinα＝OP2•sinα，∵OP＝2，∴S△AOB＝2sinα＝，故△AOB的面积为，∠APB的度数为150°；（3）设点C（a，b），则ab＝4，过点C作CH⊥OA于H；分两种情况：①当点B在y轴正半轴上时；Ⅰ、当点A在x轴的负半轴上，如图2所示：BC＝3CA不可能，第46页（共49页）Ⅱ、当点A在x轴的正半轴上时，如图3所示：∵BC＝3CA，∴，∵CH∥OB，∴△ACH∽△ABO，∴，∴，∴OB＝4b，OA＝a，∴OA•OB＝a•4b＝ab＝，∵∠APB是∠AOB的“相关角”，∴OP2＝OA•OB，∴OP＝＝＝，∵∠AOB＝90°，OP平分∠AOB，第47页（共49页）∴点P的坐标为：（，）；②当点B在y轴的负半轴上时，如图4所示：∵BC＝3CA，∴AB＝2CA，∴，∵CH∥OB，∴△ACH∽△ABO，∴，∴，∴OB＝2b，OA＝a，∴OA•OB＝a•2b＝ab＝，∵∠APB是∠AOB的“相关角”，∴OP2＝OA•OB，第48页（共49页）∴OP＝＝＝，∵∠AOB＝90°，OP平分∠AOB，∴点P的坐标为：（，﹣）；综上所述：点P的坐标为：（，）或（，﹣）．第49页（共49页）。

一次函数中的(特殊图形)存在性问题(解析版)八年级数学上册同步考点归类培优题库

专题十五一次函数中的（特殊图形）存在性问题考点一直角三角形存在性问题【方法点拨】分类讨论哪个角为直角，一般分三种情况，简称“两垂线+一圆”1．如图1，在平面直角坐标系中，点A 坐标为（﹣4，4），点B 的坐标为（4，0）．（1）求直线AB 的解析式；（2）点M 是坐标轴上的一个点，若AB 为直角边构造直角三角形△ABM ，请求出满足条件的所有点M 的坐标；（3）如图2，以点A 为直角顶点作∠CAD ＝90°，射线AC 交x 轴的负半轴与点C ，射线AD 交y 轴的负半轴与点D ，当∠CAD 绕点A 旋转时，OC ﹣OD 的值是否发生变化？若不变，直接写出它的值；若变化，直接写出它的变化范围（不要解题过程）．【思路点拨】（1）由A 、B 两点的坐标利用待定系数法可求得直线AB 的解析式；（2）分别过A 、B 两点作AB 的垂线，与坐标轴的交点即为所求的M 点，再结合相似三角形的性质求得OM 的长即可求得点M 的坐标；（3）过A 分别作x 轴和y 轴的垂线，垂足分别为E 、F ，可证明△AEC ≌△AFD ，可得到EC ＝FD ，从而可把OC ﹣OD 转化为FD ﹣OD ，再利用线段的和差可求得OC ﹣OD ＝OE +OF ＝8；【解析】解：（1）设直线AB 的解析式为：y ＝kx +b （k ≠0）．∵点A （﹣4，4），点B （0，2）在直线AB 上，∴{−4k +b =4b =2，解得{k =−12b =2， ∴直线AB 的解析式为：y =−12x +2；（2）∵△ABM 是以AB 为直角边的直角三角形，∴有∠BAM ＝90°或∠ABM ＝90°，①当∠BAM ＝90°时，如图1，过A 作AB 的垂线，交x 轴于点M 1，交y 轴于点M 2，则可知△AEM 1∽△BEA ，∴M 1E AE =AE BE ，由（1）可知OE ＝OB ＝AE ＝4，∴M 1E 4=48，解得M 1E ＝2， ∴OM 1＝2+4＝6，∴M 1（﹣6，0），∵AE ∥y 轴，∴M 1EM 1O =AEOM 2，即26=4OM 2，解得OM 2＝12，∴M 2（0，12）；②当∠ABM ＝90°时，如图2，过B 作AB 的垂线，交y 轴于点M 3，设直线AB交y轴于点E，则由（1）可知E（0，2），∴OE＝2，OB＝4，由题意可知△BOE∽△M3OB，∴OEOB =OBOM3，即24=4OM3，解得OM3＝8，∴M3（0，﹣8），综上可知点M的坐标为（﹣6，0）或（0，12）或（0，﹣8）；（3）不变．理由如下：过点A分别作x轴、y轴的垂线，垂足分别为G、H，如图3．则∠AGC＝∠AHD＝90°，又∵∠HOC＝90°，∴∠GAH＝90°，∴∠DAG+∠DAH＝90°，∵∠CAD＝90°，∴∠DAG+∠CAG＝90°，∴∠CAG＝∠DAH．∵A （﹣4，4），∴OG ＝AH ＝AG ＝OH ＝4．在△AGC 和△AHD 中{∠AGC =∠AHD AG =AH ∠CAG =∠DAH∴△AGC ≌△AHD （ASA ），∴GC ＝HD ．∴OC ﹣OD ＝（OG +GC ）﹣（HD ﹣OH ）＝OG +OH ＝8．故OC ﹣OD 的值不发生变化，值为8．【点睛】本题为一次函数的综合应用，涉及知识点有待定系数法、全等三角形的判定和性质、相似三角形的判定和性质及分类讨论思想等．在（1）中注意待定系数法的应用步骤，在（2）中确定出M 点的位置是解题的关键，在（3）中构造三角形全等是解题的关键．本题考查知识点较多，综合性较强，难度适中．2．已知，如图1，在平面直角坐标系xOy 中，矩形OABC 的边OA 在y 轴的正半轴上，OC 在x 轴的正半轴上，OA ＝2，OC ＝3，过原点O 作∠AOC 的平分线交AB 于点D ，连接DC ，过点D 作DE ⊥DC ，交OA 于点E ．（1）求经过点E 、D 的直线解析式；（2）将∠EDC 绕点D 按顺时针方向旋转后，角的一边与y 轴的正半轴交于点F ，另一边与线段OC 交于点G ，使得EF ＝2GO ，请求出此时OG 的长度．（3）对于（2）中的点G ，在直线ED 上是否存点P ，使得点P 与点D 、G 构成的△DPG 是直角三角形？若存在，请求出点P 的坐标；若不存在，请说明理由．【思路点拨】（1）只要证明△ADE ∽△BCD ，可得AD BC =AE DB ，求出AE 即可解决问题；（2）由△ADE ≌△RDG ，可得AF ＝RG ，设OG ＝m ，则AF ＝GR ＝2﹣m ，构建方程即可解决问题；（3）分两种情形①作GP ⊥BE 于P ，则△PDG 是直角三角形．②作P ′G ⊥DG 交直线DE 于P ′，则△DGP ′是直角三角形．分别根据一次函数利用方程组确定交点坐标即可；【解析】解：（1）如图1中，∵四边形ABCO 是矩形，∴∠OAB ＝∠B ＝90°，∵∠AOD ＝∠DOC ＝45°，∴OA ＝AD ＝2，DB ＝1，∵DE ⊥DC ，∴∠EDC ＝90°，∴∠ADE +∠BDC ＝90°，∵∠BDC +∠BCD ＝90°，∴∠ADE ＝∠DCB ，∴△ADE ∽△BCD ，∴AD BC =AE DB ，∴AE ＝1，∴E （0，1），设直线DE 的解析式为y ＝kx +b ，则有{b =12k +b =2，解得{k =12b =1∴直线DE 的解析式为y =12x +1（2）如图2中，作DR ⊥OC 于R ．易知△ADE≌△RDG，∴AF＝RG，设OG＝m，则AF＝GR＝2﹣m，∴EF＝1+2﹣m＝3﹣m，∵EF＝2OG，∴3﹣m＝2m，∴m＝1，∴OG＝1．（3）如图3中，①作GP⊥BE于P，则△PDG是直角三角形．∵G（1，0），GP⊥BE，∴直线PG的解析式为y＝﹣2x+2，由{y =12x +1y =−2x +2，解得{x =25y =65， ∴P （25，65）． ②作P ′G ⊥DG 交直线DE 于P ′，则△DGP ′是直角三角形，∵直线DG 的解析式为y ＝2x ﹣2，∴直线GP ′的解析式为y =−12x +12，由{y =−12x +12y =12x +1，解得{x =−12y =34， ∴P ′（−12，34），综上所述，满足条件的点P 坐标为（25，65）或（−12，34）．【点睛】本题考查一次函数综合题、旋转变换、全等三角形的判定和性质．相似三角形的判定和性质、直角三角形的性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形和相似三角形解决问题，学会用分类讨论的思想思考问题，属于中考压轴题．考点二等腰三角形存在性问题【方法点拨】分类讨论哪两条边相等，一般分三种情况，简称“两圆+一中垂线”1．如图1，在平面直角坐标系中，O 是坐标原点，长方形OACB 的顶点A 、B 分别在x 轴与y 轴上，已知OA ＝6，OB ＝10．点D 为y 轴上一点，其坐标为（0，2），点P 从点A 出发以每秒2个单位的速度沿线段AC ﹣CB 的方向运动，当点P 与点B 重合时停止运动，运动时间为t 秒．（1）当点P 经过点C 时，求直线DP 的函数解析式；（2）①求△OPD 的面积S 关于t 的函数解析式；②如图②，把长方形沿着OP 折叠，点B 的对应点B ′恰好落在AC 边上，求点P 的坐标．（3）点P 在运动过程中是否存在使△BDP 为等腰三角形？若存在，请求出点P 的坐标；若不存在，请说明理由．【思路点拨】（1）设直线DP 解析式为y ＝kx +b ，将D 与C 坐标代入求出k 与b 的值，即可确定出解析式；（2）①当P 在AC 段时，三角形ODP 底OD 与高为固定值，求出此时面积；当P 在BC 段时，底边OD 为固定值，表示出高，即可列出S 与t 的关系式；②当点B 的对应点B ′恰好落在AC 边上时，关键勾股定理即可求出此时P 坐标；（3）存在，分别以BD ，DP ，BP 为底边三种情况考虑，利用勾股定理及图形与坐标性质求出P 坐标即可．【解析】解：（1）∵OA ＝6，OB ＝10，四边形OACB 为长方形，∴C （6，10）．设此时直线DP 解析式为y ＝kx +b ，把（0，2），C （6，10）分别代入，得{b =26k +b =10，解得{k =43b =2则此时直线DP 解析式为y =43x +2；（2）①当点P 在线段AC 上时，OD ＝2，高为6，S ＝6；当点P 在线段BC 上时，OD ＝2，高为6+10﹣2t ＝16﹣2t ，S =12×2×（16﹣2t ）＝﹣2t +16；②设P （m ，10），则PB ＝PB ′＝m ，如图2，∵OB ′＝OB ＝10，OA ＝6，∴AB ′=√OB′2−OA 2=8，∴B ′C ＝10﹣8＝2，∵PC ＝6﹣m ，∴m 2＝22+（6﹣m ）2，解得m =103 则此时点P 的坐标是（103，10）；（3）存在，理由为：若△BDP 为等腰三角形，分三种情况考虑：如图3，①当BD ＝BP 1＝OB ﹣OD ＝10﹣2＝8，在Rt △BCP 1中，BP 1＝8，BC ＝6，根据勾股定理得：CP 1=√82−62=2√7，∴AP 1＝10﹣2√7，即P 1（6，10﹣2√7）；②当BP 2＝DP 2时，此时P 2（6，6）；③当DB ＝DP 3＝8时，在Rt △DEP 3中，DE ＝6，根据勾股定理得：P 3E =√82−62=2√7，∴AP 3＝AE +EP 3＝2√7+2，即P 3（6，2√7+2），综上，满足题意的P 坐标为（6，6）或（6，2√7+2）或（6，10﹣2√7）．【点睛】此题属于一次函数综合题，涉及的知识有：待定系数法确定一次函数解析式，坐标与图形性质，等腰三角形的性质，勾股定理，利用了分类讨论的思想，熟练掌握待定系数法是解本题第一问的关键．2．如图①，在平面直角坐标系中，△AOB的边OA在x轴上，点A坐标为（14，0），点B在第一象限，∠BAO＝45°，AB＝8√2．D为射线OB上一点，过D作直线l∥y轴交OA于E，交射线AB于G．（1）求B点坐标；（2）当D为线段OB中点时，在直线l上找点P，当△PBD为等腰三角形，请直接写出P点坐标；（3）如图②，F为AO中点，当S△BDF＝2S△BDG时，求D点坐标．【思路点拨】（1）先求出BH＝AH＝8，进而求出OH＝6，即可得出结论；（2）先设出点P坐标，进而表示出DP，BP，BD，再分三种情况讨论建立方程求解即可得出结论；（3）先求出OF，直线OB，AB的解析式，进而设出点D的坐标，表示出S△BDG=12|m﹣14|×|6﹣m|，S△BDF ＝|143m﹣28|，最后用面积关系建立方程求解即可得出结论．【解析】解：（1）如图①，过点B作BH⊥OA于H，∵∠BAO＝45°，AB＝8√2，∴BH＝AH=1√2AB＝8，∵A（14，0），∴OA＝14，∴OH＝OA﹣AH＝6，∴B（6，8）；（2）∵DE ⊥OA ，∴DE ∥BH ，∵点D 是OB 中点，∴DE =12BH ＝4，OE =12OH ＝3，∴D （3，4），设P （3，m ），∵B （6，8），∴DP ＝|m ﹣4|，BD ＝5，BP 2＝（m ﹣8）2+9，∵△PBD 为等腰三角形，∴①DP ＝BD ，∴|m ﹣4|＝5，∴m ＝9或m ＝﹣1，∴P （3，9）或（3，﹣1），②DP ＝BP ，∴（m ﹣4）2＝（m ﹣8）2+9，∴m =578， ∴P （3，578）③BD ＝BP ，∴25＝（m ﹣8）2+9，∴m ＝4（舍）或m ＝12，∴P （3，12），即：满足条件的点P （3，9）或（3，﹣1）或（3，578）或（3，12）；（3）如图由（1）知，B （6，8），∴直线OB 的解析式为y =43x ，∵A （14，0），∴直线AB 的解析式为y ＝﹣x +14，∵点F 是OA 中点，∴OF =12OA ＝7，设点D （m ，43m ），∴G （m ，﹣m +14）， ∴S △BDG =12|﹣m +14−43m |×|6﹣m |=12|m ﹣14|×|6﹣m |， S △BDF ＝|S △BOF ﹣S △DOF |＝|12×7×8−12×7×43m |＝|143m ﹣28|，∵S △BDF ＝2S △BDG ，∴|143m ﹣28|＝212|m ﹣14|×|6﹣m |， ∴m ＝4或m ＝8， ∴D （4，163）或（8，323）．【点睛】此题是三角形综合题，主要考查了勾股定理，等腰三角形的性质，三角形的面积公式，分类讨论的思想，解本题的关键是用方程的思想解决问题．考点三等腰直角三角形存在性问题【方法点拨】分类讨论哪个角为直角且哪两条边相等1．正方形OABC 的边长为1，把它放在如图所示的直角坐标系中，点M （t ，0）是x 轴上一个动点（t ≥1），连接BM ，在BM 的右侧作正方形BMNP ；直线DE 的解析式为y ＝2x +b ，与x 轴交于点D ，与y 轴交于点E ，当△PDE 为等腰直角三角形时，点P 的坐标是（2，4）或（2，1）．【思路点拨】过点P 作PF ⊥BC 交CB 的延长线于点F ，根据同角的余角相等可得∠ABM ＝∠FBP ，然后利用“角角边”证明△ABM 和△FBP 全等，根据全等三角形对应边相等可得BF ＝AB ，PF ＝AM ，然后根据正方形OABC 的边长为2以及点M （t ，0）表示出点P 的坐标，再利用直线DE 的解析式求出点D 、E 的坐标，然后分①DE 是斜边时，利用勾股定理以及两点间的距离公式分别表示出PD 、PE 、DE 的平方，再根据等腰直角三角形的三边关系，②PD 是斜边时，过点P 作PF ⊥y 轴于点F ，然后利用“角角边”证明△EDO 和△PEF 全等，根据全等三角形对应边相等可得EF ＝DO ，PC ＝EO ，然后用b 、t 表示并求解即可得到点P 的坐标．【解析】解：如图，过点P 作PF ⊥BC 交CB 的延长线于点F ，∵四边形OABC 与四边形BMNP 都是正方形，∴∠ABM +∠MBF ＝90°，∠FBP +∠MBF ＝90°，∴∠ABM ＝∠FBP ，在△ABM 和△FBP 中，{∠ABM =∠FBP∠BAM =∠F =90°BM =BP，∴△ABM ≌△FBP （AAS ），∴BF ＝AB ，PF ＝AM ，∵正方形OABC 的边长为1，点M （t ，0），∴BF ＝1，PF ＝t ﹣1，点P 到x 轴的距离为t ﹣1+1＝t ，∴点P 的坐标为（2，t ），又∵当y ＝0时，2x +b ＝0，解得x =−b 2，当x ＝0时，y ＝b ，∴点D （−b 2，0），E （0，b ），①DE 是斜边时，PD 2＝（b 2+2）2+t 2，PE 2＝（b ﹣t ）2+22，DE 2＝（b 2）2+b 2， ∵△PDE 是等腰直角三角形，∴PD 2＝PE 2，且PD 2+PE 2＝DE 2，即（b 2+2）2+t 2＝（b ﹣t ）2+22，且（b 2+2）2+t 2+（b ﹣t ）2+22＝（b 2）2+b 2， 14b 2+2b +4+t 2＝b 2﹣2bt +t 2+4，且14b 2+2b +4+t 2+b 2﹣2bt +t 2+4=14b 2+b 2，整理得，b =83（t +1）且t 2﹣b （t ﹣1）+4＝0，∴t 2−83（t +1）（t ﹣1）+4＝0，整理得，t 2＝4，解得t 1＝2，t 2＝﹣2（舍去），∴点P 的坐标是（2，2）；②PD 是斜边时，∵△PDE 是等腰直角三角形，∴PE ⊥DE ，且PE ＝DE ，过点P 作PF ⊥y 轴于点F∵∠DEO +∠PEO ＝90°，∠DEO +∠EDO ＝90°，∴∠PEO ＝∠EDO ，在△EDO 和△PEF 中，{∠PEO =∠EDO ∠DOE =∠EFP =90°PE =DE，∴△EDO ≌△PEF （AAS ），∴EF ＝DO =b 2，PC ＝EO ＝b ，又∵点P （2，t ），∴b ＝2，b ﹣t =b 2，解得t=b2=12×2＝1，∴点P坐标为（2，1），此时点C、F重合，点M、A重合，综上所述，点P的坐标为（2，4）或（2，1）．故答案为：（2，2）或（2，1）．【点睛】本题是一次函数的综合题型，主要利用了全等三角形的判定与性质，等腰三角形的性质，直线与坐标轴的交点的求解，勾股定理的应用，综合题但难度不大，要注意分情况讨论．2．如图，在平面直角坐标系中，直线l1的解析式为y＝﹣x，直线l2与l1交于点A（a，﹣a），与y轴交于点B（0，b），其中a，b满足（a+2）2+√b−3=0．（1）求直线l2的解析式；（2）在平面直角坐标系中第二象限有一点P（m，5），使得S△AOP＝S△AOB，请求出点P的坐标；（3）已知平行于y轴且位于y轴左侧有一动直线，分别与l1，l2交于点M、N，且点M在点N的下方，点Q为y轴上一动点，且△MNQ为等腰直角三角形，请直接写出满足条件的点Q的坐标．【思路点拨】（1）由偶次方及被开方数非负，可求出a 、b 的值，进而可得出点A 、B 的坐标，由点A 、B 的坐标，利用待定系数法即可求出直线l 2的解析式；（2）由△AOP 和△AOB 等底及S △AOP ＝S △AOB ，可得出点P 到AO 的距离与点B 到AO 的距离相等，分点P 在l 1的右侧及点P 在l 1的左侧两种情况考虑：①当点P 在l 1的右侧时，设点P 为P 1，则P 1B ∥l 1，根据平行线的性质结合点B 的坐标可得出直线P 1B 的解析式，再利用一次函数图象上点的坐标特征可求出点P 1的坐标；②当点P 在l 1的左侧时，设点P 为P 2，设直线y ＝5与直线l 1交于点E ，利用一次函数图象上点的坐标特征可求出点E 的坐标，再由点E 为P 1P 2中点，可求出点P 2的坐标；（3）设动直线为x ＝t ，由题可得﹣2＜t ＜0，则点M 的坐标为（t ，﹣t ），点N 的坐标为（t ，12t +3），进而可得出MN 的长度．分∠NMQ ＝90°、∠MNQ ＝90°及∠MQN ＝90°三种情况，利用等腰直角三角形的性质可求出点M 、N 、Q 的坐标，此题得解．【解析】解：（1）∵a 、b 满足（a +2）2+√b −3=0，∴a +2＝0，b ﹣3＝0，∴a ＝﹣2，b ＝3，∴点A 的坐标为（﹣2，2），点B 的坐标为（0，3）．设直线l 2的解析式为y ＝kx +c （k ≠0），将A （﹣2，2）、B （0，3）代入y ＝kx +c ，得：{−2k +c =2c =3，解得：{k =12c =3， ∴直线l 2的解析式为y =12x +3．（2）∵S △AOP ＝S △AOB ，∴点P 到AO 的距离与点B 到AO 的距离相等，且点P 位于l 1两侧（如图1）．①当点P 在l 1的右侧时，设点P 为P 1，则P 1B ∥l 1，∴直线P 1B 的解析式为：y ＝﹣x +3，当y ＝5时，有﹣x +3＝5，解得：x ＝﹣2，∴点P 1的坐标为（﹣2，5）；②当点P 在l 1的左侧时，设点P 为P 2，设直线y ＝5与直线l 1交于点E ，则点E 的坐标为（﹣5，5），∵点E 为P 1P 2中点，∴点P 2的坐标为（﹣8，5）．综上所述：点P 的坐标为（﹣2，5）或（﹣8，5）．（3）设动直线为x ＝t ，由题可得﹣2＜t ＜0，则点M 的坐标为（t ，﹣t ），点N 的坐标为（t ，12t +3）， ∴MN =32t +3（如图2）．①当∠NMQ ＝90°时，有MN ＝MQ ，即32t +3＝﹣t ，解得：t =−65，∴点M 的坐标为（−65，65）． ∵MQ ∥x 轴，∴点Q 的坐标为（0，65）； ②当∠MNQ ＝90°时，有MN ＝NQ ，即32t +3＝﹣t ，解得：t =−65，∴点N 的坐标为（−65，125）． ∵NQ ∥x 轴，∴点Q 的坐标为（0，125）；③当∠MQN ＝90°时，点Q 到MN 的距离=12MN ，即﹣t =12×（32t +3），解得：t =−67，∴点M 的坐标为（−67，67），点N 的坐标为（−67，187）．∵△MNQ 为等腰直角三角形，∴点Q 的坐标为（0，127）．综上所述：点Q 的坐标为（0，65）或（0，125）或（0，127）．【点睛】本题考查了待定系数法求一次函数解析式、偶次方及被开方数的非负性、三角形的面积、一次函数图象上点的坐标特征以及等腰直角三角形，解题的关键是：（1）根据点的坐标，利用待定系数法求出一次函数解析式；（2）分点P 在l 1的右侧及点P 在l 1的左侧两种情况求出点P 的坐标；（3）分∠NMQ ＝90°、∠MNQ ＝90°及∠MQN ＝90°三种情况，利用等腰直角三角形的性质求出点Q 的坐标．3．在平面直角坐标系xOy 中，直线l 1：y ＝k 1x +2√3与x 轴、y 轴分别交于点A 、B 两点，OA =√3OB ，直线l 2：y ＝k 2x +b 经过点C （1，−√3），与x 轴、y 轴和线段AB 分别交于点E 、F 、D 三点．（1）求直线l 1的解析式；（2）如图①：若EC ＝ED ，求点D 的坐标和△BFD 的面积；（3）如图②：在坐标轴上是否存在点P ，使△PCD 是以CD 为底边的等腰直角三角形，若存在，请直接写出点P 的坐标；若不存在，请说明理由．【思路点拨】（1）求出点A的坐标，利用待定系数法即可解决问题；（2）如图1中，作CM⊥OA于M，DN⊥CA于N．由△CME≌△DNE（AAS），推出CM＝DN由C（1，−√3），可得CM＝DN=√3，再利用待定系数法即可解决问题；（3）分点P在y轴或x轴两种情形分别求解即可解决问题；【解析】解：（1）∵直线y＝k1x+2√3与y轴B点，∴B（0，2√3），∴OB＝2√3，∵OA=√3OB＝6，∴A（6，0），把A（6，0）代入y＝k1x+2√3得到，k1=−√33，∴直线l1的解析式为y=−√33x+2√3．（2）如图1中，作CM⊥OA于M，DN⊥CA于N．∵∠CME＝∠DNE＝90°，∠MEC＝∠NED，EC＝DE，∴△CME≌△DNE（AAS），∴CM＝DN∵C （1，−√3），∴CM ＝DN =√3，当y =√3时，√3=−√33x +2√3，解得x ＝3，∴D （3，√3），把C （1，−√3），D （3，√3）代入y ＝k 2x +b ，得到{k 2+b =−√33k 2+b =√3，解得{k 2=√3b =−2√3， ∴直线CD 的解析式为y =√3x ﹣2√3，∴F （0，﹣2√3），∴S △BFD =12×4√3×3＝6√3．（3）①如图③﹣1中，当PC ＝PD ，∠CPD ＝90°时，作DM ⊥OB 于M ，CN ⊥y 轴于N ．设P （0，m ）．∵∠DMP ＝∠CNP ＝∠CPD ＝90°，∴∠CPN +∠PCN ＝90°，∠CPN +∠DPM ＝90°，∴∠PCN ＝∠DPM ，∵PD ＝PC ，∴△DMP ≌△NPC （AAS ），∴CN ＝PM ＝1，PN ＝DM ＝m +√3，∴D （m +√3，m +1），把D 点坐标代入y =−√33x +2√3，得到：m +1=−√33（m +√3）+2√3，解得m ＝4√3−6，∴P （0，4√3−6）．②如图③﹣2中，当PC＝PC，∠CPD＝90时，作DM⊥OA于M，CN⊥OA于N．设P（n，0）．同法可证：△DMP≌△PNC，∴PM＝CN=√3，DM＝PN＝n﹣1，∴D（n−√3，n﹣1），把D点坐标代入y=−√33x+2√3，得到：n﹣1=−√33（n−√3）+2√3，解得n＝2√3∴P（2√3，0）．综上所述，满足条件的点P坐标为（0，4√3−6）或（2√3，0）【点睛】本题属于一次函数综合题，考查了待定系数法，全等三角形的判定和性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，学会利用参数解决问题，属于中考压轴题．4．如图1，在平面直角坐标系中，A（a，0），B（0，b），且a，b满足b=√a2−4+√4−a2+16a+2（1）求直线AB的解析式；（2）第一象限内是否存在一点M，使△ABM是等腰直角三角形，若存在，求出点M的坐标；若不存在，请说明理由；（3）如图2过点A的直线y＝kx﹣2k交y轴负半轴于点P，N点的横坐标为﹣1，过点N的直线y=k2x−k2交AP于点M，交x轴于点C，求证：NC＝MC．【思路点拨】（1）由二次根式的被开方数是非负数可以求得a 、b 的值．则易求点A 、B 的坐标．设直线AB 的方程为y ＝kx +b （k ≠0），将其分别代入该解析式列出关于k 、b 的方程组，通过解方程组即可求得它们的值；（2）需要分类讨论：当AB 为底和当AB 为腰时，分别求得点M 的坐标；（3）将y ＝kx ﹣2k 与y =k 2x −k 2联立求出M 的坐标为（3，k ），由条件可求得N 的坐标为（﹣1，﹣k ），C 的坐标为（1，0），作CG ⊥x 轴于G 点，MH ⊥x 轴于H 点，可证△NGC ≌△MHC ，得NC ＝MC ．【解析】解：（1）依题意，得：{a 2−4≥04−a 2≥0a +2≠0，解得a ＝2；则b ＝4．所以A （2，0），B （0，4），设直线AB 解析式为y ＝kx +b （k ≠0），将A 与B 坐标代入得：{2k +b =0b =4，解得：{k =−2b =4，则直线AB 的解析式为y ＝﹣2x +4；（2）如图1，分三种情况：①如图1，当BM ⊥BA ，且BM ＝BA 时，过M 作MN ⊥y 轴于N ，∵BM ⊥BA ，MN ⊥y 轴，OB ⊥OA ，∴∠MBA ＝∠MNB ＝∠BOA ＝90°，∴∠NBM +∠NMB ＝90°，∠ABO +∠NBM ＝90°，∴∠ABO ＝∠NMB ，在△BMN 和△ABO 中{∠MNB =∠BOA ∠NMB =∠ABO BM =AB，∴△BMN ≌△ABO （AAS ），MN ＝OB ＝4，BN ＝OA ＝2，∴ON ＝2+4＝6，∴M 的坐标为（4，6 ）；②如图2当AM ⊥BA ，且AM ＝BA 时，过M 作MN ⊥x 轴于N ，△BOA ≌△ANM （AAS ），同理求出M 的坐标为（6，2）；③如图4，当AM⊥BM，且AM＝BM时，过M作MN⊥X轴于N，MH⊥Y轴于H，则△BHM≌△AMN，∴MN＝MH，设M（x，x），由勾股定理得，（x﹣2）2+x2＝（4﹣x）2+x2，解得，x＝3；∴M点的坐标为（3，3）综上所知M点的坐标为（4，6）（6，2）（3，3）；（3）将y＝kx﹣2k与y=k2x−k2联立求出M的坐标为（3，k），由条件可求得N的坐标为（﹣1，﹣k），C的坐标为（1，0），作CG⊥x轴于G点，MH⊥x轴于H点，可证△NGC≌△MHC，得NC＝MC．【点睛】本题主要考查对一次函数图象上点的坐标特征，等腰直角三角形性质，用待定系数法求正比例函数的解析式，全等三角形的性质和判定，二次根式的性质等知识点的理解和掌握，综合运用这些性质进行推理和计算是解此题的关键．。

专题02 二次函数中的存在性问题之等腰三角形(19眉山)(解析版)

专题02 二次函数中的存在性问题之等腰三角形【典例1】（2019•眉山）如图1，在平面直角坐标系中，抛物线y=−49x2+bx+c经过点A（﹣5，0）和点B（1，0）．（1）求抛物线的解析式及顶点D的坐标；（2）点P是抛物线上A、D之间的一点，过点P作PE⊥x轴于点E，PG⊥y轴，交抛物线于点G，过点G作GF⊥x轴于点F，当矩形PEFG的周长最大时，求点P的横坐标；（3）如图2，连接AD、BD，点M在线段AB上（不与A、B重合），作∠DMN＝∠DBA，MN交线段AD于点N，是否存在这样点M，使得△DMN为等腰三角形？若存在，求出AN的长；若不存在，请说明理由．【点拨】（1）抛物线的表达式为：y=−49（x+5）（x﹣1），即可求解；（2）PE=−49m2−169m+209，PG＝2（﹣2﹣m）＝﹣4﹣2m，矩形PEFG的周长＝2（PE+PG），即可求解；（3）分MN＝DM、NM＝DN、DN＝DM，三种情况分别求解．【解答】解：（1）抛物线的表达式为：y=−49（x+5）（x﹣1）=−49x2−169x+209，则点D（﹣2，4）；（2）设点P（m，−49m2−169m+209），则PE=−49m2−169m+209，PG＝2（﹣2﹣m）＝﹣4﹣2m，矩形PEFG的周长＝2（PE+PG）＝2（−49m2−169m+209−4﹣2m）=−89（m+174）2+252，∵−89＜0，故当m=−174时，矩形PEFG周长最大，此时，点P 的横坐标为−174；（3）∵∠DMN ＝∠DBA ， ∠BMD +∠BDM ＝180°﹣∠ADB ， ∠NMA +∠DMB ＝180°﹣∠DMN ， ∴∠NMA ＝∠MDB ， ∴△BDM ∽△AMN ，AN BM=AM BD，而AB ＝6，AD ＝BD ＝5， ①当MN ＝DM 时， ∴△BDM ≌△AMN ，即：AM ＝BD ＝5，则AN ＝MB ＝1； ②当NM ＝DN 时，则∠NDM ＝∠NMD ， ∴△AMD ∽△ADB ，∴AD 2＝AB ×AM ，即：25＝6×AM ，则AM =256，而AN BM=AM BD，即AN6−256=2565，解得：AN =5536； ③当DN ＝DM 时，∵∠DNM ＞∠DAB ，而∠DAB ＝∠DMN ， ∴∠DNM ＞∠DMN ， ∴DN ≠DM ；故AN ＝1或5536．【点睛】本题考查的是二次函数综合运用，涉及到一次函数、三角形相似和全等、等腰三角形性质等知识点，其中（3），要注意分类求解，避免遗漏．【精练1】抛物线y =−29x 2+bx +c 与x 轴交于A （﹣1，0），B （5，0）两点，顶点为C ，对称轴交x 轴于点D ，点P 为抛物线对称轴CD 上的一动点（点P 不与C ，D 重合）．过点C 作直线PB 的垂线交PB 于点E ，交x轴于点F．（1）求抛物线的解析式；（2）当△PCF的面积为5时，求点P的坐标；（3）当△PCF为等腰三角形时，请直接写出点P的坐标．【点拨】（1）函数的表达式为：y=29（x+1）（x﹣5），即可求解；（2）确定PB、CE的表达式，联立求得点F（2−2m3，0），S△PCF=12×PC×DF=12（2﹣m）（2−2m3−2）＝5，即可求解；（3）分当CP＝CF、CP＝PF、CP＝PF三种情况，分别求解即可．【解答】解：（1）函数的表达式为：y=29（x+1）（x﹣5）=−29x2+89x+109；（2）抛物线的对称轴为x＝2，则点C（2，2），设点P（2，m），将点P、B的坐标代入一次函数表达式：y＝sx+t并解得：函数PB的表达式为：y=−13mx+5m3，∵CE⊥PE，故直线CE表达式中的k值为3m，将点C的坐标代入一次函数表达式，同理可得直线CE的表达式为：y=3mx+(2−6m)，解得：x＝2−2m 3，故点F（2−2m3，0），S △PCF =12×PC ×DF =12（|2﹣m |）（|2−2m 3−2|）＝5，解得：m ＝5或﹣3，故点P （2，﹣3）或（2，5）；（3）由（2）确定的点F 的坐标得： CP 2＝（2﹣m ）2，CF 2＝（2m 3）2+4，PF 2＝（2m 3）2+m 2，①当CP ＝CF 时，即：（2﹣m ）2＝（2m 3）2+4，解得：m ＝0或365（0舍去），②当CP ＝PF 时，同理可得：m =−9±3√132， ③当CF ＝PF 时，同理可得：m ＝±2（舍去2），故点P （2，365）或（2，﹣2）或（2，−9−3√132）或（2，−9+3√132）【点睛】本题考查的是二次函数综合运用，涉及到一次函数、等腰三角形性质、图形的面积计算等，其中（3），要注意分类求解，避免遗漏．【精练2】如图，直线y ＝﹣x +3与x 轴、y 轴分别交于B 、C 两点，抛物线y ＝﹣x 2+bx +c 经过点B 、C ，与x 轴另一交点为A ，顶点为D ．（1）求抛物线的解析式；（2）在x 轴上找一点E ，使EC +ED 的值最小，求EC +ED 的最小值；（3）在抛物线的对称轴上是否存在一点P ，使得∠APB ＝∠OCB ？若存在，求出P 点坐标；若不存在，请说明理由．【点拨】（1）直线y ＝﹣x +3与x 轴、y 轴分别交于B 、C 两点，则点B 、C 的坐标分别为（3，0）、（0，3），将点B 、C 的坐标代入二次函数表达式，即可求解；（2）如图1，作点C 关于x 轴的对称点C ′，连接CD ′交x 轴于点E ，则此时EC +ED 为最小，即可求解；（3）分点P 在x 轴上方、点P 在x 轴下方两种情况，分别求解．【解答】解：（1）直线y ＝﹣x +3与x 轴、y 轴分别交于B 、C 两点，则点B 、C 的坐标分别为（3，0）、（0，3），将点B 、C 的坐标代入二次函数表达式得：{−9+3b +c =0c =3，解得：{b =2c =3，故函数的表达式为：y ＝﹣x 2+2x +3，令y ＝0，则x ＝﹣1或3，故点A （﹣1，0）；（2）如图1，作点C 关于x 轴的对称点C ′，连接CD ′交x 轴于点E ，则此时EC +ED 为最小，函数顶点D 坐标为（1，4），点C ′（0，﹣3），将CD 的坐标代入一次函数表达式并解得：直线CD 的表达式为：y ＝7x ﹣3，当y ＝0时，x =37，故点E （37，0），则EC +ED 的最小值为DC ′=√1+(4+3)2=5√2；（3）①当点P 在x 轴上方时，如下图2，∵OB ＝OC ＝3，则∠OCB ＝45°＝∠APB ，过点B作BH⊥AP于点H，设PH＝BH＝m，则PB＝P A=√2m，由勾股定理得：AB2＝AH2+BH2，16＝m2+（√2m﹣m）2，解得：m2＝8+4√2，则PB2＝2m2＝16+8√2则y P=√PB2−22=2+2√2；②当点P在x轴下方时，则y P＝﹣（2+2√2）；故点P的坐标为（1，2+2√2）或（1，﹣2﹣2√2）．【点睛】本题考查的是二次函数综合运用，涉及到一次函数、等腰三角形性质、点的对称性等，其中（3），要注意分类求解，避免遗漏．【精练3】如图，抛物线与x轴交于A，B两点，与y轴交于点C（0，﹣2），点A的坐标是（2，0），P为抛物线上的一个动点，过点P作PD⊥x轴于点D，交直线BC于点E，抛物线的对称轴是直线x＝﹣1．（1）求抛物线的函数表达式；（2）若点P在第二象限内，且PE=14OD，求△PBE的面积．（3）在（2）的条件下，若M为直线BC上一点，在x轴的上方，是否存在点M，使△BDM是以BD为腰的等腰三角形？若存在，求出点M的坐标；若不存在，请说明理由．【点拨】（1）点A（2，0）、点B（﹣4，0），则函数的表达式为：y＝a（x﹣2）（x+4）＝a（x2+2x﹣8），即可求解；（2）PE=14OD，则PE＝（14x2+12x﹣2−12x+2）=14（﹣x），求得：点D（﹣5，0），利用S△PBE=12PE×BD=12（14x2+12x﹣2−12x+2）（﹣4﹣x），即可求解；（3）BD ＝1＝BM ，则y M ＝﹣BM sin ∠ABC ＝﹣11√5=−√55，即可求解．【解答】解：（1）点A 的坐标是（2，0），抛物线的对称轴是直线x ＝﹣1，则点B （﹣4，0），则函数的表达式为：y ＝a （x ﹣2）（x +4）＝a （x 2+2x ﹣8），即：﹣8a ＝﹣2，解得：a =14，故抛物线的表达式为：y =14x 2+12x ﹣2；（2）将点B 、C 的坐标代入一次函数表达式：y ＝mx +n 并解得：直线BC 的表达式为：y =−12x ﹣2，则tan ∠ABC =12，则sin ∠ABC =15，设点D （x ，0），则点P （x ，14x 2+12x ﹣2），点E （x ，−12x ﹣2），∵PE =14OD ，∴PE ＝（14x 2+12x ﹣2+12x +2）=14（﹣x ），解得：x ＝0或﹣5（舍去x ＝0），即点D （﹣5，0） S △PBE =12×PE ×BD =12（14x 2+12x ﹣2+12x +2）（﹣4﹣x ）=58；（3）由题意得：△BDM 是以BD 为腰的等腰三角形，①当BD ＝BM 时，过点M 作MH ⊥x 轴于点H ， BD ＝1＝BM ，则MH ＝y M ＝BM sin ∠ABC ＝1×5=√55，则x M =20+2√55，故点M （−20+2√55，√55）；②如图，当BD＝DM时，过点D作DH⊥BC于H，∴BM＝2BH，在Rt△BHD中，BH＝BD cos∠ABC=2√5 5，∴BM=4√5 5，过点M作MG⊥x轴于G，MG＝BM•sin∠ABC=4 5，BG＝BM•cos∠ABC=8 5，点M（−285，45）；故点M坐标为（−20+2√55，√55）或（−285，45）．【点睛】主要考查了二次函数的解析式的求法和与几何图形结合的综合能力的培养．要会利用数形结合的思想把代数和几何图形结合起来，利用点的坐标的意义表示线段的长度，从而求出线段之间的关系．【精练4】如图1，在平面直角坐标系中，抛物线y=−49x2+bx+c经过点A（﹣5，0）和点B（1，0）．（1）求抛物线的解析式及顶点D的坐标；（2）点P是抛物线上A、D之间的一点，过点P作PE⊥x轴于点E，PG⊥y轴，交抛物线于点G，过点G作GF⊥x轴于点F，当矩形PEFG的周长最大时，求点P的横坐标；（3）如图2，连接AD、BD，点M在线段AB上（不与A、B重合），作∠DMN＝∠DBA，MN交线段AD于点N，是否存在这样点M，使得△DMN为等腰三角形？若存在，求出AN的长；若不存在，请说明理由．【点拨】（1）抛物线的表达式为：y=−49（x+5）（x﹣1），即可求解；（2）PE=−49m2−169m+209，PG＝2（﹣2﹣m）＝﹣4﹣2m，矩形PEFG的周长＝2（PE+PG），即可求解；（3）分MN＝DM、NM＝DN、DN＝DM，三种情况分别求解．【解答】解：（1）抛物线的表达式为：y=−49（x+5）（x﹣1）=−49x2−169x+209，则点D（﹣2，4）；（2）设点P（m，−49m2−169m+209），则PE=−49m2−169m+209，PG＝2（﹣2﹣m）＝﹣4﹣2m，矩形PEFG的周长＝2（PE+PG）＝2（−49m2−169m+209−4﹣2m）=−89（m+174）2+252，∵−89＜0，故当m=−174时，矩形PEFG周长最大，此时，点P的横坐标为−17 4；（3）∵∠DMN＝∠DBA，∠BMD+∠BDM＝180°﹣∠ADB，∠NMA+∠DMB＝180°﹣∠DMN，∴∠NMA＝∠MDB，∴△BDM∽△AMN，ANBM =AMBD，而AB＝6，AD＝BD＝5，①当MN＝DM时，∴△BDM≌△AMN，即：AM＝BD＝5，则AN＝MB＝1；②当NM ＝DN 时，则∠NDM ＝∠NMD ， ∴△AMD ∽△ADB ，∴AD 2＝AB ×AM ，即：25＝6×AM ，则AM =256，而AN BM=AM BD，即AN6−256=2565，解得：AN =5536； ③当DN ＝DM 时，∵∠DNM ＞∠DAB ，而∠DAB ＝∠DMN ， ∴∠DNM ＞∠DMN ， ∴DN ≠DM ；故AN ＝1或5536．【点睛】本题考查的是二次函数综合运用，涉及到一次函数、三角形相似和全等、等腰三角形性质等知识点，其中（3），要注意分类求解，避免遗漏．【精练5】如图1，在平面直角坐标系中，抛物线y =13x 2−13x ﹣4交x 轴于A 、B 两点，交y 轴于点C ．（1）点P 为线段BC 下方抛物线上的任意一点，一动点G 从点P 出发沿适当路径以每秒1个单位长度运动到y 轴上一点M ，再沿适当路径以每秒1个单位长度运动到x 轴上的点N ，再沿x 轴以每秒√2个单位长度运动到点B ．当四边形ACPB 面积最大时，求运动时间t 的最小值；（2）过点C 作AC 的垂线交x 轴于点D ，将△AOC 绕点O 旋转，旋转后点A 、C 的对应点分别为A 1、C 1，在旋转过程中直线A 1C 1与x 轴交于点Q ．与线段CD 交于点I ．当△DQI 是等腰三角形时，直接写出DQ 的长度．【点拨】（1）过点B 作BK ⊥BC 交y 轴于点K ，作P ′H ⊥BK 交BK 于点H 、交y 轴于点M 、交x 轴于点N ，则此时运动的时间最小，即可求解；（2）将△AOC 绕点O 旋转，相当于存在一个半径为OR 圆O ，在整个旋转过程中，AC 始终为垂直于OR 的切线，确定圆的半径OR 后，分OR 靠近x 轴、y 轴两种大情况，分别在四个象限逐次求解即可．【解答】解：（1）y =13x 2−13x ﹣4，令x ＝0，则y ＝﹣4，令y ＝0，则x ＝3或﹣4，故点A 、B 、C 的坐标分别为（﹣3，0）、（4，0）、（0，﹣4），则直线BC 的表达式为：y ＝x ﹣4， S 四边形ACPB ＝S △ABC +S △PBC ，∵S △ABC 为常数，∴只要S △PBC 取得最大值，四边形ACPB 面积即为最大，设点P （x ，13x 2−13x ﹣4），则点S （x ，x ﹣4），S △PBC =12×PS ×OB =12×4×（x ﹣4−13x 2+13x +4）=−23x 2+43x ， ∵−23＜0，则S △PBC 有最大值，即四边形ACPB 面积有最大值，此时，x ＝2，故点P （2，−103）；作点P 关于y 轴的对称点P ′（﹣2，−103），过点B 作BK ⊥BC 交y 轴于点K ，作P ′H ⊥BK 交BK 于点H 、交y 轴于点M 、交x 轴于点N ，则此时运动的时间最小， t ＝P ′M +MN +√22BN ＝PM +MN +HN ，直线BK ⊥BC ，则直线BK 的表达式为：y ＝﹣x +b ，将点B 的坐标代入上式并解得：直线BK 的表达式为：y ＝﹣x +4…①，同理可得直线P ′H 的表达式为：y ＝x −43⋯②，联立①②并解得：x =83，故点H （83，43），则t ＝P ′H =√(−2−83)2+(−103−43)2=14√23，故运动时间t 的最小值为14√23；（2）∵AC ⊥AD ，则直线CD 的表达式为：y =34x ﹣4，故点D （163，0）；如图2，过点O 作OR ⊥AC 于点R ，由面积公式得：12OR ×AC =12OA ×OC ，即：OR =3×45=125，设∠ACD ＝α，则tan α=34，sin α=35，则tan2α=247，tan 12α=12（证明见备注），情况一：当OR 靠近y 轴时，①当OR 在一、三象限时，如图3，4：在图3中，IQ＝ID，则OQ=ORsinα=12535=4，故QD=163+4=283；在图4中，IQ＝ID，同理QD=163−4=43；②当OR在二、四象限时，如图5，6：在图5中，DI＝DQ，则∠DQI＝∠DIQ=12∠ODC=12α，OQ=ORsin12α=12√55，则DQ=12√55−163，在图6中，同理可得：DQ=12√55+163；情况二：当OR靠近x轴时，如下图：当点R在二、四象限时，如图7，见左侧图，同理可得：DQ=163+52=476；见右侧图，同理可得：DQ=163−52=176；当点R 在一、三象限时，如图8，同理可得：DQ =163−6√53（左侧图）或163+6√53（右侧图）；综上，DQ 的长度为283或43或12√55−163或12√55+163或476或176或163−6√53或163+6√53．备注：已知tan α=34，求tan2α和tan 12α．如图△ABD 是以BD 为底的等腰三角形，AC ⊥BD ，过点D 作DH ⊥AB ，则设：∠DAC ＝∠BAC ＝α，tan α=34，设BC ＝CD ＝3a ，则AC ＝4a ，由三角形的面积公式得：12AH ×AB =12×DB ×AC ，解得：AH =6a×4a 5a=245，则sin2α＝sin ∠BAD =DHAD =2425，tan2α=247，同理可得：tan 12α=12．【点睛】本题考查的是二次函数综合运用，涉及到一次函数、圆的基本知识、图形的面积计算等，其中（2），要注意分类求解，通过画图确定图象的位置，避免遗漏．【精练6】如图，已知抛物线y ＝﹣x 2+bx +c 与x 轴交于A 、B 两点，AB ＝4，交y 轴于点C ，对称轴是直线x ＝1．（1）求抛物线的解析式及点C 的坐标；（2）连接BC ，E 是线段OC 上一点，E 关于直线x ＝1的对称点F 正好落在BC 上，求点F 的坐标；（3）动点M 从点O 出发，以每秒2个单位长度的速度向点B 运动，过M 作x 轴的垂线交抛物线于点N ，交线段BC 于点Q ．设运动时间为t （t ＞0）秒． ①若△AOC 与△BMN 相似，请直接写出t 的值；②△BOQ 能否为等腰三角形？若能，求出t 的值；若不能，请说明理由．【点拨】（1）将A 、B 关坐标代入y ＝﹣x 2+bx +c 中，即可求解；（2）确定直线BC 的解析式为y ＝﹣x +3，根据点E 、F 关于直线x ＝1对称，即可求解；（3）①△AOC 与△BMN 相似，则MB MN=OA OC或OC OA，即可求解；②分OQ ＝BQ 、BO ＝BQ 、OQ ＝OB 三种情况，分别求解即可．【解答】解：（1））∵点A 、B 关于直线x ＝1对称，AB ＝4， ∴A （﹣1，0），B （3，0），代入y ＝﹣x 2+bx +c 中，得：{−9+3b +c =0−1−b +c =0，解得{b =2c =3，∴抛物线的解析式为y ＝﹣x 2+2x +3， ∴C 点坐标为（0，3）；（2）设直线BC 的解析式为y ＝mx +n ，则有：{n =33m +n =0，解得{m =−1n =3，∴直线BC 的解析式为y ＝﹣x +3， ∵点E 、F 关于直线x ＝1对称，又E 到对称轴的距离为1， ∴EF ＝2，∴F 点的横坐标为2，将x ＝2代入y ＝﹣x +3中，得：y＝﹣2+3＝1，∴F（2，1）；（3）①如下图，连接BC交MN于Q，MN＝﹣4t2+4t+3，MB＝3﹣2t，△AOC与△BMN相似，则MBMN =OAOC或OCOA，即：3−2t−4t+4t+3=3或13，解得：t=32或−13或1（舍去32、−13），故：t＝1；②∵M（2t，0），MN⊥x轴，∴Q（2t，3﹣2t），∵△BOQ为等腰三角形，∴分三种情况讨论，第一种，当OQ＝BQ时，∵QM⊥OB∴OM＝MB∴2t＝3﹣2t∴t=3 4；第二种，当BO＝BQ时，在Rt△BMQ中∵∠OBQ＝45°，∴BQ=√2BM，∴BO=√2BM，即3=√2(3−2t)，∴t=6−3√24；第三种，当OQ＝OB时，则点Q、C重合，此时t＝0 而t＞0，故不符合题意综上述，当t=34秒或6−3√24秒时，△BOQ为等腰三角形．【点睛】主要考查了二次函数的解析式的求法和与几何图形结合的综合能力的培养．要会利用数形结合的思想把代数和几何图形结合起来，利用点的坐标的意义表示线段的长度，从而求出线段之间的关系．。

问题2.2 函数中存在性与恒成立问题-2016届高三数学跨越一本线(解析版)

2016届高三数学跨越一本线精品问题二函数中存在性与恒成立问题函数内容作为高中数学知识体系的核心,也是历年高考的一个热点.在新课标下的高考越来越注重对学生的综合素质的考察,恒成立问题便是一个考察学生综合素质的很好途径,它主要涉及到一次函数、二次函数、三角函数、指数函数和对数函数等常见函数的图象和性质,渗透着换元、化归、数形结合、函数与方程等思想方法,在培养思维的灵活性、创造性等方面起到了积极的作用.近几年的数学高考和各地的模考联考中频频出现存在性与恒成立问题,其形式逐渐多样化,但它们大都与函数、导数知识密不可分.解决高中数学函数的存在性与恒成立问题常用以下几种方法：①函数性质法；②分离参数法；③主参换位法；④数形结合法等. 一、函数性质法【例1】（1）已知函数12)(2+-=ax x x f ,xax g =)(,其中0>a ,0≠x ．若对任意]2,1[∈x ,都有)()(x g x f >恒成立,求实数a 的取值范围；（2）已知两函数2)(x x f =,m x g x-⎪⎭⎫ ⎝⎛=21)(,若对任意[]2,01∈x ,存在[]2,12∈x ,使得()21)(x g x f ≥,求实数m 的取值范围.【分析】（1）根据题意条件中的x 是同一值,故不难想到将问题等价转化为函数0)()(>-x g x f 恒成立,在通过分离变量,从而可创设出新函数,再求出此函数的最值来解决问题．（2）根据题意在本题所给条件中不等式的两边它们的自变量不一定是同一数值,故可分别对在两个不同区间内的函数)(x f 和)(x g 分别求出它们的最值,再根据只需满足()()min minf xg x ≥即可求解．【解析】（1）由12012232++<⇒>-+-x xx a x a ax x 成立, 只需满足12)(23++=x xx x ϕ的最小值大于a 即可．对12)(23++=x x x x ϕ求导,0)12(12)(2224>+++='x x x x ϕ,故)(x ϕ在]2,1[∈x 是增函数,32)1()(min ==ϕϕx ,所以a 的取值范围是320<<a ．【点评】在解决函数存在性与恒成立问题时,一种最重要的思想方法就是构造适当的函数,即构造函数法,然后利用相关函数的图象和性质解决问题,同时注意在一个含多个变量的数学问题中,需要确定合适的变量和参数,从而揭示函数关系,使问题更加面目更加清晰明了,一般来说,已知存在范围的量视为变量,而待求范围的量视为参数.此法关键在函数的构造上,常见于两种----一分为二或和而为一,另一点充分利用函数的图象来分析,即体现数形结合思想. 【牛刀小试】已知=)(x f x x +221,=)(x g a x -+)1ln(,若对任意123,,[0,2]x x x ∈,恒有()()()123f x f x g x +>,求实数a 的取值范围.【解析】()(),f x g x 在[]0,2上都是增函数,所以()f x 的值域，，]40[=A ()g x 的值域]3ln ,[a a B --=.若对任意123,,[0,2]x x x ∈,恒有()()()123f x f x g x +>,则2max min )()(x g x f >,即a ->3ln 0,所以3ln >a .二、分离参数法【例2】已知函数()ln f x ax x x =+的图象在点e x =（e 为自然对数的底数）处的切线的斜率为3．（1）求实数a 的值；（2）若2()f x kx ≤对任意0x >成立,求实数k 的取值范围.【分析】（1）由'()ln 1f x a x =++结合条件函数()ln f x ax x x =+的图象在点e x =处的切线的斜率为3,可知'(e)3f =,可建立关于a 的方程：ln e 13a ++=,从而解得1a =；（2）要使2()f x kx ≤对任意0x >恒成立,只需max 2()[]f x k x ≥即可,而由（1）可知()ln f x x x x =+,∴问题即等价于求函数1ln ()xg x x+=的最大值,可以通过导数研究函数()g x 的单调性,从而求得其最值：221(1ln )ln '()x x x x g x x x⋅-+==-,令'()0g x =,解得1x =,当01x <<时,'()0g x >,∴()g x 在(0,1)上是增函数；当1x >时,'()0g x <,∴()g x 在(1,)+∞上是减函数,因此()g x 在1x =处取得最大值(1)1g =,∴1k ≥即为所求.【点评】在函数存在性与恒成立问题中求含参数范围过程中,当其中的参数（或关于参数的代数式）能够与其它变量完全分离出来并,且分离后不等式其中一边的函数（或代数式）的最值或范围可求时,常用分离参数法.此类问题可把要求的参变量分离出来,单独放在不等式的一侧,将另一侧看成新函数,于是将问题转化成新函数的最值问题：若对于取值范围内的任一个数都有恒成立,则；若对于取值范围内的任一个数都有恒成立,则.常见的有一个口诀：大就大其最大,小就小其最小,即最终转换为求函数最值. 利用分离参数法来确定不等式(),0f x λ≥,（ D x ∈,λ为实参数）恒成立中参数λ的取值范围的基本步骤:（1）将参数与变量分离,即化为()()g f x λ≥（或()()g f x λ≤）恒成立的形式；（2）求()f x 在x D ∈上的最大（或最小）值；（3）解不等式()max()g f x λ≥(或()()ming f x λ≤) ,得λ的取值范围.【牛刀小试】若10,2x ⎛⎤∈ ⎥⎝⎦时220x ax ++>恒成立,求实数a 的取值范围.【答案】9.2a >-三、主参换位法【例3】已知函数()ln()(x f x e a a =+为常数）是实数集R 上的奇函数,函数()()sin g x f x x λ=+是区间[]1,1-上的减函数,(Ⅰ)求a 的值；(Ⅱ)若[]2()11,1g x t t x λ≤++∈-在上恒成立,求t的取值范围.【分析】在第二小题所给条件中出现了两个字母：λ及t ,那么解题的关键恰恰就在于该把其中哪个字母看成是一个变量,另一个作为常数.而根据本题中的条件特征显然可将λ视作自变量,则上述问题即可转化为在(],1-∞-内关于λ的一次函数大于等于0恒成立的问题,问题即可求解.【解析】（Ⅰ）1a =(Ⅱ)由(Ⅰ)知：()f x x =,()sin g x x x λ∴=+,()g x 在[]11-，上单调递减, ()cos 0g x x λ'∴=+≤cos x λ∴≤-在[]11-，上恒成立,1λ∴≤-，[]max ()(1)sin1g x g λ=-=--, ∴只需2sin11t t λλ--≤++,2(1)sin110t t λ∴++++≥（其中1λ≤-）恒成立,由上述②结论：可令()2(1)sin110(1f t t λλλ=++++≥≤-）,则2t 101sin110t t +≤⎧⎨--+++≥⎩,21sin10t t t ≤-⎧∴⎨-+≥⎩,而2sin10t t -+≥恒成立, 1t ∴≤-.【点评】某些函数存在性与恒成立问题中,当分离参数会遇到讨论的麻烦或者即使能容易分离出参数与变量,但函数的最值却难以求出时,可考虑变换思维角度.即把主元与参数换个位置,再结合其它知识,往往会取得出奇制胜的效果.此类问题的难点常常因为学生的思维定势,易把它看成关于的不等式讨论,从而因计算繁琐出错或者中途夭折；若转换一下思路,把待求的x 为参数,以为变量,构造新的关于参数的函数,再来求解参数应满足的条件这样问题就轻而易举的得到解决了.【牛刀小试】若不等式()2211x m x ->-对任意[]1,1m ∈-恒成立,求实数x 的取值范围.12x -<<四、数形结合法【例4】已知函数()222f x x kx =-+,在1x ≥-恒有()f x k≥,求实数k 的取值范围.【分析】为了使题中的条件()f x k ≥在[)1,x ∈-+∞恒成立,应能想到构造出一个新的函数()()F x f x k=-,则可把原题转化成所构造新的函数在区间[)1,-+∞时恒大于等于0的问题,再利用二次函数的图象性质进行分类讨论,即可使问题得到圆满解决. 【解析】令()()222F x f x k x kx k=-=-+-,则()0F x ≥对[)1,x ∈-+∞恒成立,而()F x 是开口向上的抛物线. 当图象与x 轴无交点满足0∆<,即()24220k k ∆=--<,解得21k -<<.当图象与x 轴有交点,且在[)1,x ∈-+∞时()0F x ≥,则由二次函数根与系数的分布知识及图象可得：()010212F k ⎧⎪∆≥⎪⎪-≥⎨⎪-⎪-≤-⎪⎩解得32k -≤≤-, 故由①②知31k -≤<.【点评】如果题中所涉及的函数对应的图象、图形较易画出时,往往可通过图象、图形的位置关系建立不等式从而求得参数范围. 解决此类问题经常要结合函数的图象,选择适当的两个函数,利用函数图像的上、下位置关系来确定参数的范围.利用数形结合解决不等式问题关键是构造函数,准确做出函数的图象.常见的有两类函数：若二次函数()20y ax bx c a =++≠大于0恒成立,则有00a >⎧⎨∆<⎩,同理,若二次函数()20y ax bx c a =++≠小于0恒成立,则有00a <⎧⎨∆<⎩.若是二次函数在指定区间上的恒成立问题,还可以利用韦达定理以及根与系数的分布知识求解.其它函数：()0f x >恒成立⇔min ()0f x >（注：若()f x 的最小值不存在,则()0f x >恒成立⇔()f x 的下界大于0）；()0f x <恒成立⇔max ()0f x <（注：若()f x 的最大值不存在,则()0f x <恒成立⇔()f x 的上界小于0）.（对于()()f xg x ≥型问题,利用数形结合思想转化为函数图象的关系再处理）,这种方法尤其对于选择题、填空题这种方法更显方便、快捷.【牛刀小试】设1a ≥,()32f x x x a =-+,若()f x a ≥对任意[]1,2x ∈恒成立,求实数a 的取值范围.【解析】当312a ≤≤时32x x a a -+≥显然成立,当32a >时不等式可转化为32,a x a x--≥ 作y x a=-的图像,使其图像在()3212a y x x -=≤≤图像上方,可得13222312a a a a ⎧⎛⎫-≥- ⎪⎪⎪⎝⎭⎨⎪-≥-⎪⎩,解得52a ≥ 五、存在性之常用模型及方法【例5】设函数()21ln 2a f x a x x bx -=+-,a R ∈且1a ≠.曲线()y f x =在点()()1,1f 处的切线的斜率为0.（1）求b 的值；（2）若存在[)1,x ∈+∞,使得()1af x a <-,求a 的取值范围. 【分析】（1）根据条件曲线()y f x =在点()()1,1f 处的切线的斜率为0,可以将其转化为关于a ,b 的方程,进而求得b 的值：()()1af x a x b x'=+--,()10f '=⇒()101a a b b +--=⇒=；（2）根据题意分析可得若存在[1,)x ∈+∞,使得不等式()1af x a <-成立,只需min ()1a f x a >-即可,因此可通过探求()f x 的单调性进而求得()f x 的最小值,进而得到关于a 的不等式即可,而由（1）可知()21ln 2a f x a x x x -=+-,则()()()11x a x a f x x---⎡⎤⎣⎦'=,因此需对a 的取值范围进行分类讨论并判断()f x 的单调性,从而可以解得a的取值范围是()()11,-+∞ .②当112a <<时,11a a>-,()()()2minln 112111a a a a a f x f a a a a a a ⎛⎫==++> ⎪-----⎝⎭, 不合题意,无解,10分③当1a >时,显然有()0f x <,01a a >-,∴不等式()1af x a <-恒成立,符合题意,综上,a 的取值范围是()()11,-+∞ .【点评】解决函数中存在性问题常见方法有两种：一是直接法同上面所讲恒成立；二是间接法,先求其否定（恒成立）,再求其否定补集即可解决.它的逻辑背景：原命题为",()"x M P x ∀∈的否定为",()"x M P x ∃∈⌝；原命题为",()"x M P x ∃∈的否定为“,()"x M P x ∀∈⌝.处理的原则就是：不熟系问题转化为熟悉问题.【牛刀小试】已知=)(x f x x +221,=)(x g a x -+)1ln(, (1)若存在]2,0[,21∈x x ,使得)()(21x g x f >,求实数a 的取值范围； (2)若存在]2,0[,21∈x x ,使得)()(21x g x f =,求实数a 的取值范围.巩固强化1. 已知函数)1(1)(>-=a a a x f x x ,当⎥⎦⎤⎢⎣⎡∈2,0πθ变化时,0)1()sin (≥-+m f m f θ 恒成立,则实数m 的取值范围是___________．【答案】1≤m【解析】由11()()x x x x f x a a f x a a ---=-=-=-,则函数1()xxf x a a =-为奇函数,又因1a >则函数1()x xf x a a =-在R 上单调增,又由0)1()sin (≥-+m f m f θ化简得(sin )(1)(sin )(1)f m f m f m f m θθ≥--≥-，,故sin 1m m θ≥-,当2πθ=时,sin 1m m θ≥-恒成立,当0,)2πθ∈[时,即11sin m θ<-,令函数11sin y θ=-可得1y ≥,即min 1()11sin θ=-,所以1≤m ．2. 已知函数2(),([2,2])f x x x ∈-=,2()sin(2)3,[0,]62g x a x a x ππ=++∈,1[2,2]x ∀∈-,001[0,],()()2x g x f x π∃∈=总使得成立,则实数a 的取值范围是．【答案】(,4][6,)-∞-+∞3.设函数f (x )＝ax ＋sin x ＋cos x ．若函数f (x )的图象上存在不同的两点A ,B ,使得曲线y ＝f (x )在点A ,B 处的切线互相垂直,则实数a 的取值范围为．【答案】]1,1[-【解析】因为),4cos(2sin cos )(π++=-+='x a x x a x f则存在实数2,1x x ,使得1))4cos(2))(4cos(2(21-=++++ππx a x a 成立.不妨设11)(0,4k a x a π=++∈+则22)[4k a x a π=++∈因此222120()2,12,1,1 1.k k a a a a <-≤-≤-≤-≤≤ 4.已知函数e ()ln ,()e xxf x mx a x mg x =--=,其中m ,a 均为实数．（1）求()g x 的极值；（2）设1,0m a =<,若对任意的12,[3,4]x x ∈12()x x ≠,212111()()()()f x f xg x g x -<-恒成立,求a 的最小值；（3）设2a =,若对任意给定的0(0,e]x ∈,在区间(0,e]上总存在1212,()t t t t ≠,使得120()()()f t f t g x == 成立,求m 的取值范围．【答案】(1)极大值为1,无极小值；(2) 3 -22e 3；(3)3[,)e 1+∞-．（2）当1,0m a =<时,()ln 1f x x a x =--,(0,)x ∈+∞． ∵()0x af x x-'=>在[3,4]恒成立,∴()f x 在[3,4]上为增函数． …………………4分设1e ()()e xh x g x x ==,∵12e (1)()x x h x x --'=> 0在[3,4]恒成立, ∴()h x 在[3,4]上为增函数． …………………5分设21x x >,则212111()()()()f x f xg x g x -<-等价于2121()()()()f x f x h x h x -<-, 即2211()()()()f x h x f x h x -<-．设1e ()()()ln 1e xu x f x h x x a x x=-=---⋅,则u (x )在[3,4]为减函数．∴21e (1)()10e x a x u x x x -'=--⋅≤在（3,4）上恒成立． …………………6分 ∴11e ex x a x x---+≥恒成立．设11e ()ex x v x x x --=-+,∵112e (1)()1e x x x v x x ---'=-+=121131e [()]24x x ---+,x ∈[3,4], ∴1221133e [()]e 1244x x --+>>,∴()v x '< 0,()v x 为减函数．∴()v x 在[3,4]上的最大值为v (3) = 3 -22e 3． ………………… 8分∴a ≥3 -22e 3,∴a 的最小值为3 -22e 3． …………………9分（3）由（1）知()g x 在(0,e]上的值域为(0,1]． …………………10分 ∵()2ln f x mx x m =--,(0,)x ∈+∞,当0m =时,()2ln f x x =-在(0,e]为减函数,不合题意． ………………… 11分当0m ≠时,2()()m x m f x x -'=,由题意知()f x 在(0,e]不单调, 所以20e m <<,即2em >．① …………………12分此时()f x 在2(0,)m 上递减,在2(,e)m 上递增, ∴(e)1f ≥,即(e)e 21f m m =--≥,解得3e 1m -≥．② 由①②,得3e 1m -≥． …………………13分 ∵1(0,e]∈,∴2()(1)0f f m=≤成立． …………………14分下证存在2(0,]t m∈,使得()f t ≥1．取e m t -=,先证e 2m m-<,即证2e 0m m ->．③ 设()2e x w x x =-,则()2e 10x w x '=->在3[,)e 1+∞-时恒成立． ∴()w x 在3[,)e 1+∞-时为增函数．∴3e ))01((w x w ->≥,∴③成立．再证()e m f -≥1． ∵e e 3()1e 1m m f m m m --+=>>-≥,∴3e 1m -≥时,命题成立．综上所述,m 的取值范围为3[,)e 1+∞-． …………………16分 5.（2015福建高考理20）已知函数()()ln 1f x x =+,()()g x kx k =∈R ． (1)求证：当0x >时,()f x x <；(2)求证：当1k <时,存在00x >,使得对任意的()00,x x ∈,恒有()()f x g x >.【解析】（1）令()()()ln 1F x f x x x x =-=+-,[)0,x ∈+∞,则有()1111x F x x x -'=-=++．当()0,x ∈+∞时,()0F x '<,所以()F x 在[)0,+∞上单调递减,故当0x >时,()()00F x F <=,即当0x >时,()f x x <．6.（2015天津高考理20（2））已知函数(),n f x nx x x =-∈R ,其中*n ∈N ,2n …. 设曲线()y f x =与x 轴正半轴的交点为P ,曲线在点P 处的切线方程为()y g x =,求证：对于任意的正实数x ,都有()()f x g x ….【证明】设点P 的坐标为0(,0)x ,则110n x n -=,又()1n f x n nx -=-,则20()f x n n '=-,曲线()y f x =在点P 处的切线方程为()00()y f x x x '=-,即()00()()g x f x x x '=-,令()()()F x f x g x =-,即()00()()()F x f x f x x x '=--,则0()()()F x f x f x '''=-, 由于1()n f x nx n -'=-+在()0,+∞上单调递减,故()F x '在()0,+∞上单调递减,又因为0()0F x '=, 所以当0(0,)x x ∈时,0()0F x '>,当0(,)x x ∈+∞时,0()0F x '<,所以()F x 在0(0,)x 内单调递增,在0(,)x +∞内单调递减,所以对任意的正实数x 都有0()()0F x F x =…,即对任意的正实数x ,都有()()f x g x ….7（2015北京高考理18（3））已知函数()1ln 1x f x x +=-.设实数k 使得()33x f x k x ⎛⎫>+ ⎪⎝⎭对()0,1x ∈恒成立,求k 的最大值.【解析】构造函数()()31ln ,0,113x x P x k x x x ⎛⎫+=-+∈ ⎪-⎝⎭,又()00P =,若()0P x >对()0,1x ∀∈恒成立,则()00P '…,又()()()4222212111k x P x k x x x --'=-+=--, 即()020P k '=-…,得2k …,又当2k =时,()323x f x x ⎛⎫>+ ⎪⎝⎭对()0,1x ∈恒成立, 因此k 的最大值为2.8.（2015福建高考理20(3)）已知函数()()ln 1f x x =+,()()g x kx k =∈R ．确定k 的所有可能取值,使得存在0t >,对任意的()0,x t ∈恒有()()2f x g x x -<．当1k <时,由（2）知,存在00x >,使得当()00,x x ∈时,()()f x g x >, 此时()()()()f x g x f x g x -=-=()ln 1x kx +-．令()()2ln 1N x x kx x =+--,[)0,x ∈+∞, 则有()()22211211x k x k N x k x x x --++-'=--=++,当x ⎛ ∈ ⎝时,()0N x '>,()N x 在⎡⎢⎢⎣上单调递增,故()()00N x N >=, 即()()2f x g x x ->．记0x 1x ,则当()10,x x ∈时,恒有()()2f x g x x ->,故满足题意的t 不存在．当1k =时,由（1）知,当0x >时,()()()()()ln 1f x g x g x f x x x -=-=-+．令()()2ln 1H x x x x =-+-,[)0,x ∈+∞,则有()2121211x x H x x x x --'=--=++．当0x >时,()0H x '<,所以()H x 在[)0,+∞上单调递减,故()()00H x H <=．故当0x >时,恒有()()2f x g x x -<,此时,任意正实数t 均满足题意．综上所述,1k =．记0x 与12k -的较小者为1x ,当()10,x x ∈时,恒有()()2f x g x x ->,故满足题意的t 不存在．当1k =时,由（1）知,0x >,()()f x g x -=()()()ln 1f x g x x x -=-+．令()()2ln 1M x x x x =-+-,[)0,x ∈+∞,则有()2121211x x M x x x x --'=--=++．当0x >时,()0M x '<,所以()M x 在[)0,+∞上单调递减,故()()00M x M <=,故当0x >时,恒有()()2f x g x x -<,此时,任意正实数t 均满足题意．综上所述,1k =．9.（2015全国2高考理21（2））设函数()2e mx f x x mx =+-.若对于任意[]12,1,1x x ∈-,都有()()121e f x f x --…,求m 的取值范围.综上所述,m 的取值范围是[]1,1-.10.（2015四川高考理21（2））已知函数()()222ln 22f x x a x x ax a a =-++--+,其中0a >. 求证：存在()0,1a ∈,使得()0f x …在区间()1,+∞内恒成立,且()0f x =在区间()1,+∞ 内有唯一解.令000101ln 1x x a x ---=+,()()1ln 1u x x x x =--≥ 由()110u x x '=-…知,函数()u x 在区间()1,+∞上单调递增. 所以()()()0011101e e 2011111e 1eu u x u a x ----=<=<=<++++,即()00,1a ∈. 当0a a =时,有()00f x '=,()()000f x x ϕ==.再由（Ⅰ）可知,()f x '在区间()1,+∞上单调递增.故当()01,x x ∈时,有()00f x '<,从而()()00f x f x '>=；当()0,x x ∈+∞时,有()00f x '>,从而()()00f x f x >=；所以当()1,x ∈+∞时,()0f x ?.综上所述,存在()0,1a ∈,使得()0f x ?在区间()1,+∞内恒成立, 且()0f x =在()1,+∞内有唯一解.：。

二次函数中点的存在性问题

二次函数中的存在性问题1．已知抛物线y=﹣x2+x﹣3与x轴交于A，B两点，与y轴交于点C．在直线CA上方的抛物线上是否存在一点D，使得△ACD的面积最大？若存在，求出点D的坐标；若不存在，请说明理由．2．已知y=ax2+bx+c（a≠0）图象与直线y=kx+4相交于A（1，m），B（4，8）两点，与x轴交于原点及点C．（1）求直线和抛物线解析式；（2）在x轴上方的抛物线上是否存在点D，使S△OCD=2S△OAB？如果存在，求出点D坐标，如果不存在，说明理由．3．已知直线y=x﹣3与x轴交于点A，与y轴交于点C，抛物线y=﹣x2+mx+n经过点A和点C．（1）求此抛物线的解析式；（2）在直线CA上方的抛物线上是否存在点D，使得△ACD的面积最大？若存在，求出点D的坐标；若不存在，说明理由．4．在平面直角坐标系xOy中，抛物线y=﹣x2+bx+c与x轴交于A、B两点（点A在点B的左侧），过点A的直线y=kx+1交抛物线于点C（2，3）．（1）求直线AC及抛物线的解析式；（2）若直线y=kx+1与抛物线的对称轴交于点E，以点E为中心将直线y=kx+1顺时针旋转90°得到直线l，设直线l与y轴的交点为P，求△APE的面积；（3）若G为抛物线上一点，是否存在x轴上的点F，使以B、E、F、G为顶点的四边形为平行四边形？若存在，直接写出点F的坐标；若不存在，请说明理由．5．如图，在平面直角坐标系中，抛物线交x轴于A，B两点（A在B的左侧），交y轴于点C．（1）求直线BC的解析式；（2）求抛物线的顶点及对称轴；（3）若点Q是抛物线对称轴上的一动点，线段AQ+CQ是否存在最小值？若存在，求出点Q的坐标；若不存在，说明理由；（4）若点P是直线BC上方的一个动点，△PBC的面积是否存在最大值？若存在，求出点P的坐标及此时△PBC 的面积；若不存在，说明理由．1．已知抛物线y=﹣x2+x﹣3与x轴交于A，B两点，2．与y轴交于点C．在直线CA上方的抛物线上是否存在3．一点D，使得△ACD的面积最大？若存在，求出点D4．的坐标；若不存在，请说明理由．解答：解：对于抛物线y=﹣x2+x﹣3，令y=0，得到﹣x2+x﹣3=0，解得：x=1或x=4，∴B（1，0），A（4，0），令x=0，得到y=﹣3，即C（0，﹣3），设直线AC解析式为y=kx+b，将A与C坐标代入得：，解得：k=，b=﹣3，∴直线AC解析式为y=x﹣3，设平行于直线AC，且与抛物线只有一个交点的直线方程为y=x+m，此时直线与抛物线交于点D，使得△ACD的面积最大，与二次函数解析式联立消去y得：﹣x2+x﹣3=x+m，整理得：3x2﹣12x+4m+12=0，∴△=144﹣12（4m+12）=0，解得：m=0，∴此时直线方程为y=x，点D坐标为（2，）．2．（2008•宁波校级自主招生）已知y=ax2+bx+c（a≠0）图象与直线y=kx+4相交于A（1，m），B（4，8）两点，与x轴交于原点及点C．（1）求直线和抛物线解析式；（2）在x轴上方的抛物线上是否存在点D，使S△OCD=2S△OAB？如果存在，求出点D坐标，如果不存在，说明理由．解答：解：（1）∵直线y=kx+4过A（1，m），B（4，8）两点，∴，解得，∴y=x+4，把O、A、B三点坐标代入抛物线解析式，得，，∴y=﹣x2+6x；∴S△OCD=2S△OAB=12，×6×h=12，解得h=4，由﹣x2+6x=4，得x=3±，∴D（3+，4）或（3﹣，4）．3．（2014春•昌平区期末）已知直线y=x﹣3与x轴交于点A，与y轴交于点C，抛物线y=﹣x2+mx+n经过点A和点C．（1）求此抛物线的解析式；（2）在直线CA上方的抛物线上是否存在点D，使得△ACD的面积最大？若存在，求出点D的坐标；若不存在，说明理由．解答：解：（1）把x=0代入y=x﹣3得y=﹣3，则C点坐标为（0，﹣3），把y=0代入y=x﹣3得x﹣3=0，解得x=4，则A点坐标为（4，0），把A（4，0），C（0，﹣3）代入y=﹣x2+mx+n得，解得，所以二次函数解析式为y=﹣x2+x﹣3；（2）存在．过D点作直线AC的平行线y=kx+b，当直线y=kx+b与抛物线只有一个公共点时，点D到AC的距离最大，此时△ACD的面积最大，∵直线AC的解析式为y=x﹣3，∴k=，即y=x+b，由直线y=x+b和抛物线y=﹣x2+x﹣3组成方程组得，消去y得到3x2﹣12x+4b+12=0，∴△=122﹣4×3×（4b+12）=0，解得b=0，∴3x2﹣12x+12=0，解得x1=x2=2，把x=2，b=0代入y=x+b得y=，∴D点坐标为（2，）．4．（2010•孝感模拟）在平面直角坐标系xOy中，抛物线y=﹣x2+bx+c与x轴交于A、B两点（点A在点B的左侧），过点A的直线y=kx+1交抛物线于点C（2，3）．（1）求直线AC及抛物线的解析式；（3）若G为抛物线上一点，是否存在x轴上的点F，使以B、E、F、G为顶点的四边形为平行四边形？若存在，直接写出点F的坐标；若不存在，请说明理由．解答：解：（1）∵点C（2，3）在直线y=kx+1上，∴2k+1=3．解得k=1．∴直线AC的解析式为y=x+1．∵点A在x轴上，∴A（﹣1，0）．∵抛物线y=﹣x2+bx+c过点A、C，∴解得∴抛物线的解析式为y=﹣x2+2x+3．（2）由y=﹣x2+2x+3=﹣（x﹣1）2+4，可得抛物线的对称轴为x=1，B（3，0）．∴E（1，2）．根据题意，知点A旋转到点B处，直线l过点B、E．设直线l的解析式为y=mx+n．将B、E的坐标代入y=mx+n中，联立可得m=﹣1，n=3．∴直线l的解析式为y=﹣x+3．∴P（0，3）．过点E作ED⊥x轴于点D．∴S△PAE=S△PAB﹣S△EAB=AB•PO﹣AB•ED=×4×（3﹣2）=2．（3）存在，点F的坐标分别为（3﹣，0），（3+，0），（﹣1﹣，0）（﹣1+，0）．5．（2013秋•红安县校级月考）如图，在平面直角坐标系中，抛物线交x轴于A，B两点（A在B的左侧），交y轴于点C．（1）求直线BC的解析式；（3）若点Q是抛物线对称轴上的一动点，线段AQ+CQ是否存在最小值？若存在，求出点Q的坐标；若不存在，说明理由；（4）若点P是直线BC上方的一个动点，△PBC的面积是否存在最大值？若存在，求出点P的坐标及此时△PBC 的面积；若不存在，说明理由．考点：二次函数综合题．专题：压轴题．分析：（1）令y=0，解关于x的一元二次方程求出点B的坐标，令x=0求出点C的坐标，设直线BC的解析式为y=kx+b，然后利用待定系数法求一次函数解析式解答即可；（2）把二次函数解析式整理成顶点式形式，然后写出顶点坐标与对称轴即可；（3）根据轴对称确定最短路线问题，直线BC与对称轴的交点即为使线段AQ+CQ最小的点Q，然后利用直线解析式求解即可；（4）过点P作PD∥y轴与BC相交于点D，根据抛物线解析式与直线BC的解析式表示出PD，再根据S△PBC=S△PCD+S△PBD列式整理，然后利用二次函数最值问题解答．解答：解：（1）令y=0，则﹣x2+x+2=0，整理得，x2﹣2x﹣3=0，解得x1=﹣1，x2=3，所以，点B的坐标为（3，0），令x=0，则y=2，所以，点C的坐标为（0，2），设直线BC的解析式为y=kx+b，则，解得，所以，直线BC的解析式为y=﹣x+2；（2）∵y=﹣x2+x+2，=﹣（x2﹣2x+1）+2+，=﹣（x﹣1）2+，∴顶点坐标为（1，），（3）由轴对称确定最短路线问题，直线BC与对称轴的交点即为使线段AQ+CQ最小的点，x=1时，y=﹣×1+2=，所以，存在Q（1，），使线段AQ+CQ最小；（4）如图，过点P作PD∥y轴与BC相交于点D，则PD=（﹣x2+x+2）﹣（﹣x+2）=﹣x2+2x，所以，S△PBC=S△PCD+S△PBD，=×（﹣x2+2x）×3，=﹣x2+3x，=﹣（x﹣）2+，所以，当x=时，△PBC的面积最大为，此时，y=﹣×（）2+×+2=，所以，存在P（，），使S△PBC最大=．点评：本题是二次函数综合题型，主要利用了抛物线与x轴的交点坐标的求解，待定系数法求一次函数解析式，二次函数的顶点坐标与对称轴的求法，轴对称确定最短路线问题，二次函数的最值问题．。

函数的存在性问题和零点问题

函数的存在性问题和零点问题【知识梳理】1．函数的零点：使函数y ＝f (x )的值为0的实数x 称为函数y ＝f (x )的零点．(1)函数的零点⇔方程的根；(2)零点存在理论：在区间[a ，b ]上连续；f (a )·f (b )<0.2．常见求解方法(1)直接解方程，如一元二次方程；(2)用二分法求方程的近似解；(3)一元二次方程实根分布规律；(4)用数形结合法将方程的根转化为函数零点．画出y ＝f (x )图象可用到以下方法：①用图象变换法则画复杂函数图象；②用求导得出较复杂函数的单调性，然后再画图象，如y ＝ln x x ；③可以将原函数进行分离为两个较为简单的函数如方程e x ln x ＝1，转化为y ＝ln x ，y ＝⎝ ⎛⎭⎪⎫1e x ； ④如果是带有参数的方程，可以进行参数分离变为m ＝g (x )，再画y ＝g (x )与y ＝m (常数函数)的图象．【热点探究】► 探究点一用零点存在定理判断函数零点零点存在定理是间接判断方程的根或函数零点的间接方法．只能大致判断零点所在区间以及区间中零点的个数，不能够准确求解零点的值．【例1】已知函数f (x )＝1＋x －x 22＋x 33－x 44＋…＋x 20112011，g (x )＝1－x ＋x 22－x 33＋x 44－…－x 20112011，设F (x )＝f (x ＋3)·g (x －3)，且函数F (x )的零点均在区间[a ，b ](a <b ，a ，b ∈Z)内，则b －a 的最小值为________．► 探究点二用图象判定方程的根由于函数的零点⇔方程的根，所以当方程的根不能够直接求出时，可以通过图象来判断对应方程的根的个数．【例2】 (1)已知函数f (x )＝2x ＋x ，g (x )＝x ＋log 2x ，h (x )＝x 3＋x 的零点依次为a ，b ，c ，则a ，b ，c 的大小顺序为________．(2)设定义在R 上的函数f (x )＝⎩⎪⎨⎪⎧1|x －3|，x ≠3，1，x ＝3，若关于x 的方程f 2(x )＋af (x )＋b ＝0有5个不同实数解，则实数a 的取值范围是________．►探究点三不定方程的根的判断所谓不定方程，是指未知数的个数多于方程个数，且未知数受到某些限制(如要求是有理数、整数或正整数等等)的方程或方程组．常见问题有：(1)求不定方程的解；(2)判定不定方程是否有解；(3)判定不定方程的解的个数．【例3】设m∈N，若函数f(x)＝2x－m10－x－m＋10存在整数零点，则m的取值集合为________．►探究点四含参数的方程根的问题含有参数的方程根的问题，随着参数取值不同，方程根的个数不同，所以需要借助于数形结合和分类讨论的思想来解决．【例4】已知函数f(x)＝12x2－a ln x(a∈R)．(1)若函数f(x)在x＝2处的切线方程为y＝x＋b，求a，b的值；(2)讨论方程f(x)＝0的解的个数，并说明理由．【例5】已知定义在（0，+∞）上的三个函数f（x）=lnx，g（x）=x2-af（x），h(x)=x-a x且g（x）在x=1处取得极值．（1）求函数g（x）在x=2处的切线方程；（2）求函数h（x）的单调区间；（3）把h（x）对应的曲线C1向上平移6个单位后得到曲线C2，求C2与g（x）对应曲线C3的交点个数，并说明理由．【巩固训练】（全国II 理）已知函数()x x x f -=3。

二次函数中等腰三角形点的存在性问题(共15张PPT)

1. 如图，已知点A (-2，1)，B (4，3)，则线段AB的长是________.
C
练习：如图，已知点A (-2，3)，B (4，-1)，则线段AB的长是________.
y
(-2，3) A.
x o
B. (4，-1)
例题精讲
1. 如图，抛物线y=ax2+bx﹣3（a≠0）的顶点为E，该抛物线与x轴交于A、B两点，与y轴交于点C，且BO=OC=3AO．（1）求抛物线的解析式；（2）在抛物线的对称轴上是否存在点P，使△PBC是等腰三角形？若存在，请写出符合条件的P点坐标，若不存在，请说明理由．
四.问题应用
①注意分类方式，要做到不重、不漏； ②操作分三步进行；
P1(0, 2), P2 (0, 2), P3(0, 2
3),
P4
(0,
2 3
3)
一、回顾两点间距离公式
1.两点间距离公式
平面直角坐标系中，点A坐标为(x1，y1)，点B坐标为(x2，y2)，
则两点间距离公式
AB
(x2 x1)2 ( y2 y1)2 .
一.问题的提出
如图，点A、B为两定点，在直线m上是否存在一点P，使得 △PAB是等腰三角形？
二.问题分析
演示
三.问题解决——几何作图法
分类： ①以P为顶点,PA=PB ②以A为顶点,AP=AB ③以B为A为圆心AB为半径 ③以B为圆心BA为半径
【方法小结】
1. 若一个三角形是等腰三角形，没有明确给出底边和腰，则需要进行分类讨论. 2. 以线段AB为边的等腰三角形构造方法如上图所示（基本图形）. 等腰三角形的另一个顶点在线段AB的垂直平分线上，或以点A、点B为圆心，AB长为半径的圆周上（不与线段AB共线）.（两圆一线法找点）

反比例函数与特殊三角形存在性问题(解析版)(人教版) -九年级数学下册

专题02反比例函数与特殊三角形存在性问题类型一、等腰三角形存在性问题(1)求双曲线的解析式；(2)求点E B F ，，的坐标：(3)若点P 为x 轴上一动点，使得标【答案】(1)()20=>y x x∴(,0)A a ，(0,)C b ，OA =∵F E 、分别是AB BC 、边中点，∴11,22AF b CE a ==，F ⎛ ⎝∴1124AOF S AF OA ab == △∵(1,2)E ，5OE =，∴点G 的横坐标为10122+=在Rt ,Rt OGM OCE △△中，∵GOM COE ∠=∠，OGM ∠∴OGM OCE △∽△，OG OC∴(2,1)E ，11,2G ⎛⎫ ⎪⎝⎭，OE 在Rt ,Rt OGM OCE △△中，∵GOM COE ∠=∠，OGM ∠∴OGM OCE △∽△，∴OG OC OM OE =，1OC =，OE(1)试说明反比例函数ky x=的图象也经过点B ；(2)如图2，正方形ABCD 向下平移得到正方形MNPQ ，边MN 在x 轴上，反比例函数图象分别交正方形MNPQ 的边PQ 、PN 于点E 、F ．①求MEF 的面积；②在x 轴上是否存在一点G ，使得GEF △是等腰三角形，若存在，直接写出点G②点F 、E 的坐标分别为：()3,1、3,22⎛⎫⎪⎝⎭，设点(),0G m ，则222313(3)(21)24EF =-+-=，2(FG m =当EF EG =时，即213(3)14m =-+，解得：92m =或32，当9m =时，点E 、F 、G 三点共线，故舍去，3m ∴=(1)求k 的值．(2)将正方形OABC 分别沿直线AB BC ，翻折，得到正方形【点睛】本题考查正方形的性质，轴对称的性质，待定系数法求解析式，等腰三角形性质，两点距离求解；坐标系内灵活运用轴对称性质求解点坐标是解题的关键．【变式训练3】．如图，一次函数y ax b =+的图象与反比例函数点，与x 轴交于点C ，与y 轴交于点D ，已知点A 坐标为(1)求反比例函数的解析式和一次函数的解析式；(2)连接OA 、OB ，求AOB 的面积；(3)观察图象直接写出kax b x+>时x 的取值范围是；(4)直接写出：P 为x 轴上一动点，当三角形OAP 为等腰三角形时点【答案】(1)3y x=，1122y x =-；(2)54AOB S =(1,0)C ∴，111122AOB AOC BOC S S S ∴=+=⨯⨯+ （3）解：由图象得：kax b x+>（4）解：当AOP ∆是等腰三角形时，存在以下三种情况：①当OA OP =时，如图2，(3,1)A ，10OA ∴=，1(10P ∴-②当OA AP =时，如图3，(6,0)P ∴；③当OP AP =时，如图4，过A 作AE 设OP x =，则AP x =，3PE x =-，AP ∴2221(3)x x ∴+-=，53x =，5(3P ∴，0)综上，P 的坐标为()10,0或()10,0-，【点睛】本题考查了反比例函数与一次函数的综合问题，数与一次函数的解析式，等腰三角形的判定，三角形面积公式，本题难度适中，并运用了分类讨论的思想解决问题．类型二、直角三角形存在性问题(1)求m和k的值；(2)x轴上是否存在一点请说明理由．m=，【答案】(1)2(2)存在，()50，或(5(1)求反比例函数的解析式；(2)连接EF、OE、OF，求OEF的面积；(3)是否存在x轴上的一点P，使得EFP△是不以点P为直角顶点的直角三角形？若存在，请求出符合题意的点P的坐标；若不存在，请说明理由．【答案】(1)12yx=；(2)452(3)155,0 8P⎛⎫⎪，25,0 2P⎛⎫- ⎪8OA =Q ，8x ∴=时，32y =，38,2F ⎛⎫∴ ⎪⎝⎭，即，32AF =，39622BF =-=，设所求点P 坐标为(,0)a ，38,2F ⎛⎫⎪⎝⎭，(2,6)E ，()222322582624EF ⎛⎫∴-+- ⎪⎝⎭==()()22222064EP a a a -+--==(1)若4BC=，求点E的坐标；(2)连接AE，OE．①若AOE△的面积为24，求k的值；②是否存在某一位置使得AE OA⊥【答案】(1)4 6,3 E⎛⎫ ⎪⎝⎭(2)①18；②不存在，理由见解析(1)求a ，b 的值及反比例函数的解析式；(2)若1OD =，求点C 的坐标，判断四边形ABCD 的形状并说明理由；(3)若点M 是反比例函数(0)k y x x=>图象上的一个动点，当（3）①当90MAD ∠=︒∴56n =，则 1.2n =，()5,1.2M ∴，②当90AMD ∠= 时，由图得()3,M n n +∴()(36n n +=，解得：12333333,22n n -+--==(舍去)(M ∴3332+，3332-+)333333设点3,2Q a a ⎛⎫- ⎪⎝⎭，则2PQ a =+∵45PAQ ∠=︒∴AQ 平分PAO ∠．∴322a a +=-，解得45a =-3346a ⎛⎫-=-⨯-=∵AQ 平分PAO ∠，∴322a a -=+，∴45a =-∴33462255a ⎛⎫-=-⨯-=⎪⎝⎭∴361222PA a ⎛⎫=⨯-=⨯=⎪∴2AQ AP ==，∴2PA =，∴()2,2P -，综上所述，存在点P 使得APQ △【点睛】本题主要考查了待定系数法求反比例函数的解析式，的性质，解题的关键是分三种情况求出点(1)求反比例函数ky x=的表达式及E 点坐标；(2)如图2，连接DE ，AC ，试判断DE 与AC 的数量和位置关系，并说明理由；(3)如图3，连接AE ，在反比例函数ky x=的图象上是否存在点F ，使得AEF ∠=在，请求出点F 的坐标；若不存在，说明理由．【答案】(1)反比例函数的表达式为12y x=，点E 坐标为()6,2作AG AE ⊥，且使AG AE =点E 作EN y ⊥轴于点N ，易得∴6AM NE AB ===，MG ∴点G 坐标为()1,9将()6,2E 和()1,9G 代入直线7k ⎧=-(1)=a，b=；设点()0N m ，（其中0m >），则90MCN ∠=︒Q ，90MCF NCE ∴∠+∠=︒．NE l ⊥ 于点E ，90CMN ∠=︒ ，90CME NMG ∴∠+∠=︒ME l ⊥ 于点E ，。

点的存在性问题

二次函数中存在点的问题1、如图，在平面直角坐标系xOy 中，AB ⊥x 轴于点B ，AB=3，tan ∠AOB=3/4。

将△OAB 绕着原点O 逆时针旋转90o ，得到△OA 1B 1；再将△OA 1B 1绕着线段OB 1的中点旋转180o ，得到△OA 2B 1，抛物线y=ax 2+bx+c （a ≠0）经过点B 、B 1、A 2。

（1）求抛物线的解析式；（2）在第三象限内，抛物线上的点P 在什么位置时，△PBB 1的面积最大？求出这时点P 的坐标；（3）在第三象限内，抛物线上是否存在点Q ，使点Q 到线段BB 1的距离为22？若存在，求出点Q 的坐标；若不存在，请说明理由。

2、如图，经过原点的抛物线y=﹣x 2+2mx （m ＞0）与x 轴的另一个交点为A ．过点P （1，m ）作直线PM ⊥x 轴于点M ，交抛物线于点B ．记点B 关于抛物线对称轴的对称点为C （B 、C 不重合）．连接CB ，CP ．（1）当m=3时，求点A 的坐标及BC 的长；（2）当m ＞1时，连接CA ，问m 为何值时CA ⊥CP ？（3）过点P 作PE ⊥PC 且PE=PC ，问是否存在m ，使得点E 落在坐标轴上？若存在，求出所有满足要求的m 的值，并定出相对应的点E 坐标；若不存在，请说明理由．3、如图，矩形OABC的两边在坐标轴上，连接AC，抛物线y=x2 经过A，B两点。

（1）求A点坐标及线段AB的长；（2）若点P由点A出发以每秒1个单位的速度沿AB边向点B 移动，1秒后点Q也由点A出发以每秒7个单位的速度沿AO，OC，CB边向点B移动，当其中一个点到达终点时另一个点也停止移动，点P的移动时间为t秒。

①当PQ⊥AC时，求t的值；②当PQ∥AC时，对于抛物线对称轴上一点H，∠HOQ＞∠POQ，求点H的纵坐标的取值范围。

4、如图，抛物线y=ax2+bx+2交x轴于A（﹣1，0），B（4，0）两点，交y轴于点C，与过点C且平行于x轴的直线交于另一点D，点P是抛物线上一动点．（1）求抛物线解析式及点D坐标；（2）点E在x轴上，若以A，E，D，P为顶点的四边形是平行四边形，求此时点P的坐标；（3）过点P作直线CD的垂线，垂足为Q，若将△CPQ沿CP翻折，点Q的对应点为Q′．是否存在点P，使Q′恰好落在x轴上？若存在，求出此时点P的坐标；若不存在，说明理由．。

专题22.9 二次函数中的存在性问题-重难点题型(举一反三)(人教版)(解析版)

专题22.9 二次函数中的存在性问题-重难点题型【人教版】【题型1 二次函数中直角三角形存在性问题】【例1】（2021•罗湖区校级模拟）如图，已知抛物线y＝﹣x2+2x+3与x轴交于点A、B，与y轴交于点C，点P是抛物线上一动点，连接PB，PC．（1）点A的坐标为（﹣1，0），点B的坐标为（3，0）；（2）如图1，当点P在直线BC上方时，过点P作PD上x轴于点D，交直线BC于点E．若PE＝2ED，求△PBC的面积；（3）抛物线上存在一点P，使△PBC是以BC为直角边的直角三角形，求点P的坐标．【解题思路】（1）根据抛物线解析式令y＝0求出A，B的坐标即可；（2）先求得点C的坐标，再用待定系数法求得直线BC的解析式；由PE＝2ED可得PD＝3ED，设P（m，﹣m2+2m+3），则E（m，﹣m+3），用含m的式子表示出PD和DE，根据PD＝3ED得出关于m的方程，解得m的值，则可得PE的长，然后按照三角形的面积公式计算即可；（3）分两种情况：①点C为直角顶点；②点B为直角顶点．过点C作直线P1C⊥BC，交抛物线于点P1，连接P 1B ，交x 轴于点D ；过点B 作直线BP 2⊥BC ，交抛物线于点P 2，交y 轴于点E ，连接P 2C ，分别求得直线P 1C 和直线BP 2的解析式，将它们分别与抛物线的解析式联立，分别解方程组，即可求得点P 的坐标．【解答过程】解：（1）令抛物线y ＝0，则﹣x 2+2x +3＝0，解得：x 1＝﹣1，x 2＝3， ∴A （﹣1，0），B （3，0）；故答案为：（﹣1，0），（3，0）；（2）在y ＝﹣x 2+2x +3中，当x ＝0时，y ＝3， ∴C （0，3）．设直线BC 的解析式为y ＝kx +b ，将B （3，0），C （0，3）代入，得： {b =33k +b =0，解得{k =−1b =3，∴直线BC 的解析式为y ＝﹣x +3，若PE ＝2ED ，则PD ＝3ED ，设P （m ，﹣m 2+2m +3）， ∵PD ⊥x 轴于点D ， ∴E （m ，﹣m +3），∴﹣m 2+2m +3＝3（﹣m +3）， ∴m 2﹣5m +6＝0，解得m 1＝2，m 2＝3（舍）， ∴m ＝2，此时P （2，3），E （2，1）， ∴PE ＝2，∴S △PBC =12PE •OB =12×2×3＝3． ∴△PBC 的面积为3；（3）∵△PBC 是以BC 为直角边的直角三角形，∴有两种情况：①点C 为直角顶点，如图，过点C 作直线P 1C ⊥BC ，交抛物线于点P 1，连接P 1B ，交x 轴于点D ，∵B （3，0），C （0，3）， ∴OB ＝OC ＝3，∴∠BCO ＝∠OBC ＝45°． ∵P 1C ⊥BC ， ∴∠DCB ＝90°， ∴∠DCO ＝45°，又∵∠DOC ＝90°， ∴∠ODC ＝45°＝∠DCO ， ∴OD ＝OC ＝3， ∴D （﹣3，0），∴直线P 1C 的解析式为y ＝x +3，联立{y =−x 2+2x +3y =x +3，解得{x =1y =4或{x =0y =3（舍）；∴P 1（1，4）； ②点B 为直角顶点，如图，过点B 作直线BP 2⊥BC ，交抛物线于点P 2，交y 轴于点E ，连接P 2C ，∵P 1C ⊥BC ，BP 2⊥BC ， ∴P 1C ∥BP 2，∴设直线BP 2的解析式为y ＝x +b ，将B （3，0）代入，得0＝3+b ， ∴b ＝﹣3，∴直线BP 2的解析式为y ＝x ﹣3，联立{y =−x 2+2x +3y =x −3，解得{x =−2y =−5或{x =3y =0（舍），∴P 2（﹣2，﹣5）．综上，点P 的坐标为（1，4）或（﹣2，﹣5）．【变式1-1】（2021春•望城区校级月考）如图，在平面直角坐标系xOy 中，已知抛物线y ＝ax 2+bx +c 与x 轴交于A （﹣3，0），B （1，0）两点，与y 轴交于点C （0，3），连接AC ，点P 为第二象限抛物线上的动点．（1）求a 、b 、c 的值；（2）连接P A 、PC 、AC ，求△P AC 面积的最大值；（3）在抛物线的对称轴上是否存在一点Q ，使得△QAC 为直角三角形，若存在，请求出所有符合条件的点Q 的坐标；若不存在，请说明理由．【解题思路】（1）根据抛物线与x 轴的交点坐标，设成抛物线解析式，再将点C 坐标代入求解，即可得出结论；（2）先求出直线AC 的解析式，设出点P 坐标，表示出点Q 坐标，再用三角形的面积公式，得出函数关系式，即可得出结论；（3）运用配方法求出抛物线对称轴，设点Q （﹣1，n ），根据A （﹣3，0），C （0，3），可运用勾股定理分别求出：AC 2，CQ 2，AQ 2，由于△QAC 为直角三角形，可以分三种情况：∠CAQ ＝90°或∠ACQ ＝90°或∠AQC ＝90°，对每种情况运用勾股定理列方程求解即可．【解答过程】解：（1）∵抛物线y ＝ax 2+bx +c 经过A （﹣3，0），B （1，0），C （0，3）三点 ∴{9a −3b +c =0a +b +c =0c =3，解得：{a =−1b =−2c =3∴a ＝﹣1，b ＝﹣2，c ＝3；（2）如图1，过点P 作PE ∥y 轴，交AC 于E ， ∵A （﹣3，0），C （0，3）， ∴直线AC 的解析式为y ＝x +3，由（1）知，抛物线的解析式为y ＝﹣x 2﹣2x +3，设点P （m ，﹣m 2﹣2m +3），则E （m ，m +3），∴S △ACP =12PE •（x C ﹣x A ）=12×[﹣m 2﹣2m +3﹣（m +3）]×（0+3）=−32（m 2﹣3m ）=−32（m +32）2+278， ∴当m =−32时，S △P AC 最大=278；（3）存在，点Q 的坐标为：（﹣1，﹣2）或（﹣1，4）或（﹣1，3+√172）或（﹣1，3−√172）．如图2，∵A （﹣3，0），C （0，3）， ∴OA ＝OC ＝3，∴AC 2＝OA 2+OC 2＝32+32＝18， ∵y ＝﹣x 2﹣2x +3＝﹣（x +1）2+4， ∴抛物线对称轴为x ＝﹣1，设点Q （﹣1，n ），则AQ 2＝[﹣1﹣（﹣3）]2+n 2＝n 2+4，CQ 2＝[0﹣（﹣1）]2+（n ﹣3）2＝n 2﹣6n +10， ∵△QAC 为直角三角形，∴∠CAQ ＝90°或∠ACQ ＝90°或∠AQC ＝90°，①当∠CAQ ＝90°时，根据勾股定理，得：AQ 2+AC 2＝CQ 2， ∴n 2+4+18＝n 2﹣6n +10，解得：n ＝﹣2， ∴Q 1（﹣1，﹣2）；②当∠ACQ ＝90°时，根据勾股定理，得：CQ 2+AC 2＝AQ 2， ∴n 2﹣6n +10+18＝n 2+4，解得：n ＝4， ∴Q 2（﹣1，4）；③当∠AQC ＝90°时，根据勾股定理，得：CQ 2+AQ 2＝AC 2， ∴n 2﹣6n +10+n 2+4＝18，解得：n 1=3+√172，n 2=3−√172， ∴Q 3（﹣1，3+√172），Q 4（﹣1，3−√172）；综上所述，点Q 的坐标为：（﹣1，﹣2）或（﹣1，4）或（﹣1，3+√172）或（﹣1，3−√172）．【变式1-2】（2021•长沙模拟）如图，抛物线y ＝﹣x 2+bx +c 与x 轴相交于A 、B 两点，与y 轴相交于点C ，且点B 与点C 的坐标分别为B （3，0）．C （0，3），点M 是抛物线的顶点．点P 为线段MB 上一个动点，过点P 作PD ⊥x 轴于点D ，若OD ＝m ．（1）求二次函数解析式；（2）设△PCD 的面积为S ，试判断S 有最大值或最小值？若有，求出其最值，若没有，请说明理由；（3）在MB 上是否存在点P ，使△PCD 为直角三角形？若存在，请写出点P 的坐标；若不存在，请说明理由．【解题思路】（1）将B （3，0）、C （0，3）代入y ＝﹣x 2+bx +c ，列方程组求出b 、c 的值即可；（2）先求BM 所在直线的解析式，用含m 的代数式表示点P 的坐标及△PCD 的面积，求出S 关于m 的函数关系式，用函数的性质判断并求出S 的最值；（3）存在符合条件的点P ，分三种情况根据点P 的位置或勾股定理列方程求出m 的值及点P 的坐标．【解答过程】解：（1）把B （3，0）、C （0，3）代入y ＝﹣x 2+bx +c ，得{−9+3b +c =0c =3，解得{b =2c =3， ∴二次函数的解析式为y ＝﹣x 2+2x +3．（2）S 有最大值．如图1，设直线BM 的解析式为y ＝kx +a ， ∵y ＝﹣x 2+2x +3＝﹣（x ﹣1）2+4， ∴该抛物的顶点坐标为M （1，4），把M （1，4）、B （3，0）代入y ＝kx +a ，得{k +a =43k +a =0，解得{k =−2a =6，∴y ＝﹣2x +6， ∵D （m ，0）， ∴P （m ，﹣2m +6）；由S △PCD =12PD •OD ，得S =12m （﹣2m +6）＝﹣m 2+3m ；∵当点P 与点B 重合时，不存在以P 、C 、D 为顶点的三角形，∴1≤m ＜3， ∴S 不存在最小值；∵S ＝﹣m 2+3m ＝﹣（m −32）2+94， ∴当m =32时，S 最大=94， ∴S 的最大值为94．（3）存在．若∠DPC ＝90°，如图2，则PC ∥x 轴， ∴P （m ，3），且在直线y ＝﹣2x +6上， ∴﹣2m +6＝3，解得m =32， ∴P （32，3）；若∠PCD ＝90°，如图3，则PC 2+CD 2＝PD 2， ∴m 2+（﹣2m +6﹣3）2+m 2+32＝（﹣2m +6）2，整理得m 2+6m ﹣9＝0，解得m 1＝（3√2−3，m 2=−3√2−3（不符合题意，舍去）； ∴P （3√2−3，12−6√2）；若∠PDC ＝90°，则CD 2+PD 2＝PC 2， ∴m 2+32+（﹣2m +6）2＝m 2+（﹣2m +6﹣3）2，整理得12m ＝36，解得m ＝3，此时不存在以P ，C ，D 为顶点的三角形， ∴m ＝3舍去．综上所述，点P 的坐标为（32，3）或（3√2−3，12−6√2）．【变式1-3】（2021•长沙模拟）如图，抛物线y＝ax2+bx过A（4，0），B（1，3）两点，点C、B关于抛物线的对称轴对称，过点B作直线BH⊥x轴，交x轴于点H．（1）求抛物线的表达式；（2）直接写出点C 的坐标，并求出△ABC 的面积；（3）点P 是抛物线上一动点，且位于第四象限，当△ABP 的面积为6时，求出点P 的坐标；（4）若点M 在直线BH 上运动，点N 在x 轴上运动，是否存在以点C 、M 、N 为顶点的三角形为等腰直角三角形？若存在，请直接写出此时点M 的坐标，若不存在，请说明理由．【解题思路】（1）利用待定系数法解决问题即可；（2）求出抛物线的对称轴，再根据对称性求出点C 的坐标即可解决问题；（3）设点P （m ，﹣m 2+4m ），根据S △ABP ＝S △ABH +S 梯形AHDP ﹣S △PBD ，建立方程求解即可；（4）分别以点C 、M 、N 为直角顶点分三类进行讨论，利用全等三角形和勾股定理ON 的长即可．【解答过程】解：（1）∵抛物线y ＝ax 2+bx 过A （4，0），B （1，3）两点， ∴{16a +4b =0a +b =3，解得：{a =−1b =4，∴抛物线的解析式为y ＝﹣x 2+4x ．（2）如图1，∵y ＝﹣x 2+4x ＝﹣（x ﹣2）2+4， ∴对称轴为直线x ＝2，∵B ，C 关于对称轴对称，B （1，3）， ∴C （3，3）， ∴BC ＝2，∴S△ABC=12×2×3＝3．（3）如图1，设点P（m，﹣m2+4m），根据题意，得：BH＝AH＝3，HD＝m2﹣4m，PD＝m﹣1，∴S△ABP＝S△ABH+S梯形AHDP﹣S△PBD，∴6=12×3×3+12×（3+m﹣1）×（m2﹣4m）−12×（m﹣1）×（3+m2﹣4m），解得：m1＝0，m2＝5，∵点P是抛物线上一动点，且位于第四象限，∴m＞0，∴m＝5，﹣m2+4m＝﹣52+4×5＝﹣5，∴P（5，﹣5）；（4）点M在直线BH上，点N在x轴上，△CMN为等腰直角三角形时，分三类情况讨论：①以点M为直角顶点且M在x轴上方时，如图2，CM＝MN，∠CMN＝90°，∵∠CBM＝∠MHN＝90°，∴∠CMB+∠NMH＝∠NMH+∠MNH＝90°，∴∠CMB＝∠MNH，∴△CBM≌△MHN（AAS），∴BC＝MH＝2，BM＝HN＝3﹣2＝1，∴M（1，2）；②以点M为直角顶点且M在x轴下方时，如图3，过点C作CD∥y轴，过点N作NE∥y轴，过点M作DE∥x轴交CD于点D，交NE于E，∵∠CMN＝∠CDM＝∠MEN＝90°，CM＝MN，∴∠CMD+∠NME＝∠NME+∠MNE＝90°，∴∠CMD＝∠MNE，∴△NEM≌△MDC（AAS），∴NE＝MD＝BC＝2，EM＝CD＝5，∵∠ENH＝∠NEM＝∠NHM＝90°，∴四边形EMHN是矩形，∴HM＝NE＝2，∴M（1，﹣2）；③以点N为直角顶点且N在y轴左侧时，如图4，CN＝MN，∠MNC＝90°，过点M作ME∥x轴，过点N作EN∥y轴交CB的延长线于D，同理可得：△NEM≌△CDN（AAS），∴ME＝DN＝3，NE＝CD＝HM＝5，∴M（1，﹣5）；④以点N为直角顶点且N在y轴右侧时，如图5，过点M作ME∥x轴，过点N作NE∥y轴交BC延长线于D，同理可得：△NEM≌△CDN（AAS），∴ME＝DN＝NH＝3，NE＝CD＝3﹣2＝1，∴HM＝NE＝1，∴M（1，﹣1）；⑤以C为直角顶点时，不能构成满足条件的等腰直角三角形；综上所述，当△CMN为等腰直角三角形时，M点坐标为（1，2）或（1，﹣2）或（1，﹣5）或（1，﹣1）．【题型2 二次函数中等腰三角形存在性问题】【例2】（2020秋•曾都区期末）如图，抛物线y＝ax2+4x+c经过A（﹣3，﹣4），B（0，﹣1）两点，点P 是y轴左侧且位于x轴下方抛物线上一动点，设其横坐标为m．（1）直接写出抛物线的解析式；（2）将线段AB绕点B顺时针旋转90°得线段BD（点D是点A的对应点），求点D的坐标，并判断点D是否在抛物线上；（3）过点P作PM⊥x轴交直线BD于点M，试探究是否存在点P，使△PBM是等腰三角形？若存在，求出点m的值；若不存在，说明理由．【解题思路】（1）根据待定系数法即可求出抛物线的解析式；（2）作辅助线构造一线三垂直模型，在证明三角形全等即可求出点D的坐标，把点D的坐标带入解析式即可判断点D是否在抛物线上；（3）先写出点P，M，B的坐标，由（2）得出∠BMP＝45°，分∠BMP是顶角和底角两种情况讨论即可．【解答过程】解：（1）把点A（﹣3，﹣4），B（0，﹣1）带入解析式y＝ax2+4x+c，得{−4=9a −12+c −1=c，解得{a =1c =−1， ∴y ＝x 2+4x ﹣1；（2）如图，作AC ⊥y 轴于点C ，作DH ⊥y 轴于点H ，∵∠CAB +∠ABC ＝90°，∠HBD +∠ABC ＝90°，∴∠CAB ＝∠HBD ，在△ABC 和△DBH 中，{∠DHB =∠BCA ∠CAB =∠HBD DB =BA，∴△ABC ≌△DBH （AAS ），∴HB ＝AC ＝3，DH ＝BC ＝3，∴OH ＝2，∴D （﹣3，2），把D （﹣3，2）代入y ＝x 2+4x ﹣1中，得（﹣3）2+4×（﹣3）﹣1＝﹣4≠2，∴点D 不在抛物线上；（3）存在点P ，∵D （﹣3，2），B （0，﹣1），∴直线BD 的解析式为y ＝﹣x ﹣1，设P （m ，m 2+4m ﹣1），则M （m ，﹣m ﹣1），由（2）知：∠BMP ＝45°，当△PBM 是等腰三角形，且45°为底角时，有∠MBP＝90°或∠MPB＝90°，若∠MBP＝90°，则P与A重合，即m＝﹣3，若∠MPB＝90°，则PB∥x轴，即P的纵坐标为﹣1，∴m2+4m﹣1＝﹣1，解得m＝0（舍）或m＝﹣4，∴m＝﹣4，若45°为顶角，即MP＝MB，∵MP＝﹣m﹣1﹣m2﹣4m+1＝﹣m2﹣5m，MB=−√m2+m2=−√2m，∴﹣m2﹣5m=−√2m，解得m＝﹣5−√2（舍）或m＝﹣5+√2，∴m的值为﹣3，﹣4，﹣5+√2．【变式2-1】（2020秋•云南期末）如图，直线y=−12x+2与x轴交于点B，与y轴交于点C，已知二次函数的图象经过点B，C和点A（﹣1，0）．（1）求B，C两点的坐标．（2）求该二次函数的解析式．（3）若抛物线的对称轴与x轴的交点为点D，则在抛物线的对称轴上是否存在点P，使△PCD是以CD 为腰的等腰三角形？如果存在，直接写出点P的坐标；如果不存在，请说明理由．【解题思路】（1）令直线y=−12x+2的x＝0，y＝0，求出对应的y和x的值，得到点C、B的坐标；（2）用待定系数法设二次函数解析式，代入点A、B、C的坐标求出解析式；（3）利用“两圆一中垂”找到对应的等腰三角形，结合勾股定理和等腰三角形的性质求点P的坐标．【解答过程】解：（1）对直线y=−12x+2，当x＝0时，y＝2，y＝0时，x＝4，∴B（4，0），C（0，2）．（2）设二次函数为y ＝a （x ﹣m ）（x ﹣n ）（a ≠0），∵二次函数图象经过B （4，0），A （﹣1，0），∴y ＝a （x ﹣4）（x +1），把点C （0，2）代入y ＝a （x ﹣4）（x +1）得：a （0﹣4）（0+1）＝2，解得：a =−12，∴y =−12（x ﹣4）（x +1）=−12x 2+32x +2．（3）∵二次函数图象经过B （4，0），A （﹣1，0），∴对称轴为x =4−12=32， ∴D （32，0），∵C （0，2），∴CD =√22+(32)2=52，①如图1，当CD ＝PD 时，PD =52，∴P 1（32，52），P 2（32，−52）， ②如图2，当CD ＝CP 3时，过点C 作CH ⊥DP 3于点H ，∵CD ＝CP 3，CH ⊥DP 3，∴DH ＝P 3H ，∵C （0，2），∴DH ＝2，∴P 3H ＝2，∴P 3D ＝4，∴P 3（32，4），综上所述：存在P 1（32，52），P 2（32，−52），P 3（32，4），使△PCD 是以CD 为腰的等腰三角形．【变式2-2】（2021•南充）如图，已知抛物线y＝ax2+bx+4（a≠0）与x轴交于点A（1，0）和B，与y轴交于点C，对称轴为直线x=5 2．（1）求抛物线的解析式；（2）如图1，若点P是线段BC上的一个动点（不与点B，C重合），过点P作y轴的平行线交抛物线于点Q，连接OQ，当线段PQ长度最大时，判断四边形OCPQ的形状并说明理由；（3）如图2，在（2）的条件下，D是OC的中点，过点Q的直线与抛物线交于点E，且∠DQE＝2∠ODQ．在y轴上是否存在点F，得△BEF为等腰三角形？若存在，求点F的坐标；若不存在，请说明理由．【解题思路】（1）用待定系数法即可求解；（2）设点P的坐标为（x，﹣x+4），则点Q的坐标为（x，x2﹣5x+4），则PQ＝（﹣x+4）﹣（x2﹣5x+4）＝﹣x 2+4x ，进而求解；（3）当∠DQE ＝2∠ODQ ，则∠HQA ＝∠HQE ，则直线AQ 和直线QE 关于直线QH 对称，进而求出点E 的坐标为（5,4），再分BE ＝BF 、BE ＝EF 、BF ＝EF 三种情况，分别求解即可．【解答过程】解：（1）由题意得：{a +b +4=0−b 2a =52，解得{a =1b =−5，故抛物线的表达式为y ＝x 2﹣5x +4①；（2）对于y ＝x 2﹣5x +4，令y ＝x 2﹣5x +4＝0，解得x ＝1或4，令x ＝0，则y ＝4，故点B 的坐标为（4,0），点C （0,4），设直线BC 的表达式为y ＝kx +t ，则{t =44k +t =0，解得{k =−1t =4，故直线BC 的表达式为y ＝﹣x +4，设点P 的坐标为（x ，﹣x +4），则点Q 的坐标为（x ，x 2﹣5x +4），则PQ ＝（﹣x +4）﹣（x 2﹣5x +4）＝﹣x 2+4x ，∵﹣1＜0，故PQ 有最大值，当x ＝2时，PQ 的最大值为4＝CO ，此时点Q 的坐标为（2，﹣2）；∵PQ ＝CO ，PQ ∥OC ，故四边形OCPQ 为平行四边形；（3）∵D 是OC 的中点，则点D （0,2），由点D 、Q 的坐标，同理可得，直线DQ 的表达式为y ＝﹣2x ﹣2，过点Q 作QH ⊥x 轴于点H ，则QH ∥CO ，故∠AQH ＝∠ODA ，而∠DQE ＝2∠ODQ ．∴∠HQA ＝∠HQE ，则直线AQ 和直线QE 关于直线QH 对称，故设直线QE 的表达式为y ＝2x +r ，将点Q 的坐标代入上式并解得r ＝﹣6，故直线QE 的表达式为y ＝2x ﹣6②，联立①②并解得{x =5y =4（不合题意的值已舍去），故点E 的坐标为（5,4），设点F 的坐标为（0，m ），由点B 、E 的坐标得：BE 2＝（5﹣4）2+（4﹣0）2＝17，同理可得，当BE ＝BF 时，即16+m 2＝17，解得m ＝±1；当BE ＝EF 时，即25+（m ﹣4）2＝17，方程无解；当BF ＝EF 时，即16+m 2＝25+（m ﹣4）2，解得m =258；故点F 的坐标为（0,1）或（0，﹣1）或（0，258）．【变式2-3】（2021•建华区二模）综合与探究如图，在平面直角坐标系中，直线y ＝﹣3x ﹣3与x 轴交于点A ，与y 轴交于点C ．抛物线y ＝x 2+bx +c 经过A 、C 两点，且与x 轴交于另一点B （点B 在点A 右侧）．（1）求抛物线的解析式及点B 坐标；（2）设该抛物线的顶点为点H ，则S △BCH ＝ 3 ；（3）若点M 是线段BC 上一动点，过点M 的直线ED 平行y 轴交x 轴于点D ，交抛物线于点E ，求ME 长的最大值及点M 的坐标；（4）在（3）的条件下：当ME 取得最大值时，在x 轴上是否存在这样的点P ，使得以点M 、点B 、点P 为顶点的三角形是等腰三角形？若存在，请直接写出所有点P 的坐标；若不存在，请说明理由．【解题思路】（1）由直线y ＝﹣3x ﹣3与x 轴交于点A ，与y 轴交于点C ，得A （﹣1，0）、C （0，﹣3），将A （﹣1，0）、C （0，﹣3）代入y ＝x 2+bx +c ，列方程组求b 、c 的值及点B 的坐标；（2）设抛物线的对称轴交BC 于点F ，求直线BC 的解析式及抛物线的顶点坐标，再求出点F 的坐标，推导出S △BCH =12FH •OB ，可求出△BCH 的面积；（3）设点E 的横坐标为x ，用含x 的代数式表示点E 、点M 的坐标及线段ME 的长，再根据二次函数的性质求出线段ME 的最大值及点M 的坐标；（4）在x 轴上存在点P ，使以点M 、B 、P 为顶点的三角形是等腰三角形．由（3）得D （32，0），M （32，−32），由勾股定理求出OM ＝BM =3√22，由等腰三角形PBM 的腰长为32或3√22求出OP 的长即可得到点P 的坐标．【解答过程】解：（1）∵直线y ＝﹣3x ﹣3与x 轴、y 轴分别交于点A 、C ， ∴A （﹣1，0），C （0，﹣3），∵抛物线y ＝x 2+bx +c 经过点A （﹣1，0），C （0，﹣3）， ∴{1−b +c =0c =−3，解得{b =−2c =−3，∴抛物线的解析式为y ＝x 2﹣2x ﹣3．当y ＝0时，由x 2﹣2x ﹣3＝0，得x 1＝﹣1，x 2＝3， ∴B （3，0）．（2）设抛物线的对称轴交BC 于点F ，交x 轴于点G ．设直线BC 的解析式为y ＝kx ﹣3，则3k ﹣3＝0，解得k ＝1， ∴y ＝x ﹣3；∵y ＝x 2﹣2x ﹣3＝（x ﹣1）2﹣4， ∴抛物线的顶点H （1，﹣4），当x ＝1时，y ＝1﹣3＝﹣2， ∴F （1，﹣2），∴FH ＝﹣2﹣（﹣4）＝2，∴S △BCH =12FH •OG +12FH •BG =12FH •OB =12×2×3＝3．故答案为：3．（3）设E （x ，x 2﹣2x ﹣3）（0＜x ＜3），则M （x ，x ﹣3）， ∴ME ＝x ﹣3﹣（x 2﹣2x ﹣3）＝﹣x 2+3x ＝﹣（x −32）2+94， ∴当x =32时，ME 最大=94，此时M （32，−32）．（4）存在．如图3，由（2）得，当ME 最大时，则D （32，0），M （32，−32），∴DO ＝DB ＝DM =32； ∵∠BDM ＝90°，∴OM ＝BM =√(32)2+(32)2=3√22．点P 1、P 2、P 3、P 4在x 轴上，当点P 1与原点O 重合时，则P 1M ＝BM =3√22，P 1（0，0）；当BP 2＝BM =3√22时，则OP 2＝3−3√22=6−3√22， ∴P 2（6−3√22，0）；当点P 3与点D 重合时，则P 3M ＝P 3B =32，P 3（32，0）；当BP 4＝BM =3√22时，则OP 4＝3+3√22=6+3√22， ∴P 4（6+3√22，0）．综上所述，P 1（0，0），P 2（6−3√22，0），P 3（32，0），P 4（6+3√22，0）．【题型3 二次函数中平行四边形存在性问题】【例3】（2020秋•元阳县期末）如图，直线y=−12x+c与x轴交于点A（﹣3，0），与y轴交于点C，抛物线y =12x 2+bx +c 经过点A ，C ，与x 轴的另一个交点为B （1，0），连接BC ．（1）求抛物线的函数解析式．（2）M 为x 轴的下方的抛物线上一动点，求△ABM 的面积的最大值．（3）P 为抛物线上一动点，Q 为x 轴上一动点，当以B ，C ，Q ，P 为顶点的四边形为平行四边形时，求点P 的坐标．【解题思路】（1）将A （﹣3，0），B （1，0）代入抛物线y =12x 2+bx +c ，即可求解析式；（2）由题意可知，当点M 为抛物线的顶点，即可求面积；（3）分两种情况：①当以BC 为边时，PQ ＝BC ，则点B 到点C 的竖直距离＝点P 到点Q 的竖直距离，即|12x 2+x −32|=32，当点P 在x 轴上方时，12x 2+x −32=32，求得P (−√7−1，32)或P (√7−1，32)，当点P 在x 轴下方时，12x 2+x −32=−32，求得P (−2，−32)；②当以BC 为对角线时，点P 与点Q 不能同时在抛物线上和x 轴上，故此种情况不成立．【解答过程】解：（1）将A （﹣3，0），B （1，0）代入抛物线y =12x 2+bx +c ，∴{12+b +c =0，12×(−3)2−3b +c =0，解得{b =1c =−32，∴抛物线的函数解析式为y =12x 2+x −32；（2）∵M 是x 轴的下方的抛物线上一动点，且△ABM 的面积最大， ∴点M 为抛物线的顶点， ∴M （﹣1，﹣2），∴△ABM 的面积的最大值=12×(3+1)×2=4；（3）分两种情况：①当以BC 为边时，由平行四边形的性质可知，PQ ＝BC ，∴点B 到点C 的竖直距离＝点P 到点Q 的竖直距离，即|12x 2+x −32|=32，当点P 在x 轴上方时，12x 2+x −32=32，解得x 1=−√7−1，x 2=√7−1， ∴P (−√7−1，32)或P (√7−1，32)，当点P 在x 轴下方时，12x 2+x −32=−32，解得x 1＝﹣2，x 2＝0（舍去）， ∴P (−2，−32)；②当以BC 为对角线时，点P 与点Q 不能同时在抛物线上和x 轴上，故此种情况不成立，综上可知，点P 的坐标为(−√7−1，32)或（(√7−1，32)或(−2，−32)．【变式3-1】（2020秋•泰山区期末）如图，抛物线y =12x 2+bx +c 经过点A （﹣4，0），点M 为抛物线的顶点，点B 在y 轴上，且OA ＝OB ，直线AB 与抛物线在第一象限交于点C （2，6），如图．（1）求直线AB 和抛物线的表达式；（2）在y 轴上找一点Q ，使得△AMQ 的周长最小，在备用图中画出图形并求出点Q 的坐标；（3）在坐标平面内是否存在点N ，使以点A 、O 、C 、N 为顶点且AC 为一边的四边形是平行四边形？若存在，请直接写出点N 的坐标；若不存在，请说明理由．【解题思路】（1）抛物线y =12x 2+bx +c 经过A （﹣4，0），C （2，6），代入即可得抛物线表达式为y =12x 2+2x ，由OA ＝OB ，得B （0，4），用待定系数法即可得直线AB 表达式为y ＝x +4；（2）作A 关于y 轴的对称点A '，连接A 'M 交y 轴于Q ，连接AM ，此时△AQM 的周长最小，由A '（4，0），M （（﹣2，﹣2），可得直线A 'M 表达式为y =13x −43，从而可得Q （0，−43）；（3）分两种情况：①以AC 、AO 为边，此时A （﹣4，0）平移到C （2，6）时，O （0，0）即平移到N ，即得N （6，6）；②以AC 、AN 为边，同理可得N （﹣6，﹣6）．【解答过程】解：（1）抛物线y =12x 2+bx +c 经过A （﹣4，0），C （2，6），∴{12×16−4b +c =012×4+2b +c =6，解得{b =2c =0， ∴抛物线表达式为y =12x 2+2x ， ∵A （﹣4，0），OA ＝OB ， ∴B （0，4），设直线AB 表达式为y ＝mx +n ， ∴{0=−4m +n 4=n ，解得{m =1n =4， ∴直线AB 表达式为y ＝x +4；（2）作A 关于y 轴的对称点A '，连接A 'M 交y 轴于Q ，如图：连接AM ，此时△AQM 的周长最小， ∵A （﹣4，0），A 、A '关于y 轴对称， ∴A '（4，0），∵y =12x 2+2x =12（x +2）2﹣2， ∴M （（﹣2，﹣2），设直线A 'M 表达式为y ＝sx +t ，则{4s +t =0−2s +t =−2，解得{s =13t =−43， ∴直线A 'M 表达式为y =13x −43，令x ＝0得y =−43， ∴Q （0，−43）；（3）存在，理由如下： ①以AC 、AO 为边，如图：∵四边形AONC 是平行四边形，∴A （﹣4，0）平移到C （2，6）时，O （0，0）即平移到N ， ∴N （6，6）；②以AC 、AN 为边，如图：∵四边形ANOC 是平行四边形，∴C （2，6）平移到O （0，0）时，A （﹣4，0）即平移到N ，∴N（﹣6，﹣6）；综上述所：以点A、O、C、N为顶点且AC为一边的四边形是平行四边形，则N的坐标为（6，6）或（﹣6，﹣6）．【变式3-2】（2021春•雨花区期末）如图，已知抛物线y＝ax2+bx+c的对称轴为直线x＝﹣1，且抛物线经过A（1，0），C（0，3）两点，与x轴交于点B．（1）求抛物线的解析式；（2）若点P从点B出发，沿着射线BC运动，速度每秒√2个单位长度，过点P作直线PM∥y轴，交抛物线于点M．设运动时间为t秒．①在运动过程中，当t为何值时，使（MA+MC）（MA﹣MC）的值最大？并求出此时点P的坐标．②若点N同时从点B出发，向x轴正方向运动，速度每秒v个单位长度，问：是否存在t使点B，C，M，N构成平行四边形？若存在，求出t，v的值；若不存在，说明理由．【解题思路】（1）先根据对称轴求出点B的坐标，再根据待定系数法即可求出抛物线的解析式；（2）①根据题意表示出BA和BC的值，再利用平方差公式表示出（MA+MC）（MA﹣MC）的值，求出最值即可；②根据对角线的情况分三种情况讨论即可．【解答过程】解：（1）∵抛物线的对称轴为x＝﹣1，∴B（﹣3，0），设抛物线的解析式为y＝a（x+3）（x﹣1），代入C（0，3），得3＝a×3×（﹣1），解得a＝﹣1，∴y＝﹣（x+3）（x﹣1）＝﹣x2﹣2x+3；（2）①∵B（﹣3，0），C（0，3），∴直线BC 的解析式为y ＝x +3，设P （m ，m +3），则点M 为（m ，﹣m 2﹣2m +3）， ∴（MA +MC ）（MA ﹣MC ）＝MA 2﹣MC 2＝（1﹣m ）2﹣（﹣m 2﹣2m +3）2﹣（﹣m ）2﹣（﹣m 2﹣2m +3﹣3）2 ＝﹣6m 2﹣14m +10 =−6(m +76)2+1096，当m =−76时，（MA +MC ）（MA ﹣MC ）最大，此时PB =116√2，所以此时t =√2=116， ∴当t =116时，使（MA +MC ）（MA ﹣MC ）的值最大，此时点P 的坐标为（−76，116）；②存在t 的值，由题意得B （﹣3，0），C （0，3），M （t ﹣3，﹣t 2+4t ），N （v ﹣3，0），若BC 为对角线，则： {−3+0=t −3+v −30+3=−t 2+4t +0，解得：{t =1v =2或{t =3v =0（舍），∴t ＝1，v ＝2，若BM 为对角线，则： {−3+t −3=0+v −30−t 2+4t =3+0，解得：{t =1v =−2（舍）或者{t =3v =0（舍），∴此种情况无满足的t ，v ，若BN 为对角线，则： {−3+v −3=0+t −30+0=3−t 2+4t，解得：{t =2−√7v =5−√7（舍）或者{t =2+√7v =5+√7，∴t ＝2+√7，v ＝5+√7，综上，t ＝1，v ＝2，或者t ＝2+√7，v ＝5+√7．【变式3-3】（2021•北碚区校级模拟）如图1，在平面直角坐标系中，抛物线y ＝ax 2+bx ﹣6与x 轴交于A ，C （﹣6，0）两点（点A 在点C 右侧），交y 轴于点B ，连接BC ，且AC ＝4．（1）求抛物线的解析式．（2）若P 是BC 上方抛物线上不同于点A 的一动点，连接P A ，PB ，PC ，求当S △PBC −12S △P AC 有最大值时点P 的坐标，并求出此时的最大值．（3）如图2，将原抛物线向右平移，使得点A 刚好落在原点O ，M 是平移后的抛物线上一动点，Q 是直线BC 上一动点．当A ，M ，B ，Q 组成的四边形是平行四边形时，请直接写出此时点Q 的坐标．【解题思路】（1）由点C 的坐标，即AC ＝4，可求出点A 的坐标，把点A 和点C 的坐标代入抛物线中，即可求得抛物线的解析式；（2）过点P 作x 轴的垂线，交x 轴于点D ，交BC 于点E ，设出点P 的坐标，分别表达点D 和点E 的坐标，进而表达S △PBC −12S △P AC ，根据二次函数的性质求得最大值及点P 的坐标；（3）先求出平移后的抛物线的解析式，再分别讨论AB 为边，AB 为对角线两种情况讨论；根据平行四边形的性质可求出点Q 的坐标．【解答过程】解：（1）∵C （﹣6，0）， ∴OC ＝6， ∵AC ＝4，∴OA ＝2，即A （﹣2，0），∵点A （﹣2，0），C （﹣6，0）在抛物线y ＝ax 2+bx ﹣6上，∴{4a −2b −6=036a −6b −6=0，解得，{a =−12b =−4， ∴抛物线的解析式为：y =−12x 2﹣4x ﹣6；（2）过点P 作x 轴的垂线，交x 轴于点D ，交BC 于点E ，如图，由（1）中抛物线的解析式可得B （0，﹣6）， ∴直线BC 的解析式为：y ＝﹣x ﹣6，设点P 的横坐标为m ，则P （m ，−12m 2﹣4m ﹣6）（﹣6＜m ＜0，且m ≠0）， ∴D （m ，0），E （m ，﹣m ﹣6），∴PE =−12m 2﹣4m ﹣6﹣（﹣m ﹣6）=−12m 2﹣3m ， |PD |＝|−12m 2﹣4m ﹣6|， ∴S △PBC −12S △P AC=12•PE •（x B ﹣x C ）−12×12|PD |•AC=12•（−12m 2﹣3m ）×6−12×12|−12m 2﹣4m ﹣6|×4 =−32m 2﹣9m ﹣|−12m 2﹣4m ﹣6|，当﹣6＜m ＜﹣2时，−12m 2﹣4m ﹣6＞0S △PBC −12S △P AC =−32m 2﹣9m ﹣（−12m 2﹣4m ﹣6）＝﹣m 2﹣5m +6＝﹣（m +52）2+494，当m =−52时，S △PBC −12S △P AC 的最大值为494，P （−52，78）；当﹣2＜m ＜0时，S △PBC −12S △P AC =−32m 2﹣9m ﹣（12m 2+4m +6）＝﹣2m 2﹣13m ﹣6＝﹣2（m +134）2+1218＜968，∵968＜494，综上，当P （−52，78）时，S △PBC −12S △P AC 的最大值为494；（3）将原抛物线向右平移，使得点A 刚好落在原点O ，则平移后的抛物线为：y =−12x 2﹣2x ， ①当AB 为边时，分两种情况：a ．当四边形ABQM 是平行四边形时，由平行四边形的性质可知，AB ∥MQ ，AM ∥BQ ，如图，过点A 作AM ∥BC ，与平移后的抛物线交于点M ， ∵直线BC 的解析式为：y ＝﹣x ﹣6，则直线AM 的解析式为：y ＝﹣x ﹣2，联立{y =−x −2y =−12x 2−2x ，解得，{x =−1−√5y =−1+√5，或{x =−1+√5y =−1−√5， ∴M 1（﹣1−√5，﹣1+√5），M 2（﹣1+√5，﹣1−√5）， ∴Q 1（1−√5，﹣7+√5），Q 2（1+√5，﹣7−√5）； b ．当四边形ABMQ 是平行四边形时，如图，设点M5的横坐标为t，则M5（t，−12t2﹣2t），由平移的性质可得，Q5（t﹣2，−12t2﹣2t+6），∵点Q5在直线BC上，∴−12t2﹣2t+6＝﹣（t﹣2）﹣6，解得t＝﹣1+√21或t＝﹣1−√21．∴Q5（﹣3−√21，﹣3+√21），Q6（﹣3+√21，﹣3−√21）；②当AB为对角线时，由平行四边形的性质可知，AM∥BQ，如图，∵A（﹣2，0），B（0，﹣6），∴AB的中点为（﹣1，﹣3），由①可知，M3（﹣1+√5，﹣1−√5），M4（﹣1−√5，﹣1+√5）；∴Q3（﹣1−√5，﹣5+√5），Q4（﹣1+√5，﹣5−√5）；∴符合题意的点Q的坐标为：（1+√5，﹣7−√5），（1−√5，﹣7+√5），（﹣3−√21，﹣3+√21），（﹣3+√21，﹣3−√21），（﹣1−√5，﹣5+√5），（﹣1+√5，﹣5−√5）．【题型4 二次函数中菱形存在性问题】【例4】（2020秋•巴南区期末）如图，抛物线y ＝﹣x 2+bx +c 与x 轴交于点A （1，0）和点B （﹣3，0），与y 轴交于点C ．（1）求b ，c 的值；（2）如图1，点P 为直线BC 上方抛物线上的一个动点，设点P 的横坐标m ．当m 为何值时，△PBC 的面积最大？并求出这个面积的最大值．（3）如图2，将该抛物线向左平移2个单位长度得到新的抛物线y ＝a 1x 2+b 1x +c 1（a 1≠0），平移后的抛物线与原抛物线相交于点D ，点M 为直线BC 上的一点，点N 是平面坐标系内一点，是否存在点M ，N ，使以点B ，D ，M ，N 为顶点的四边形为菱形，若存在，请直接写出点M 的坐标；若不存在，请说明理由．【解题思路】（1）将点A （1，0）和点B （﹣3，0）代入y ＝﹣x 2+bx +c ，即可求解析式；（2）求出直线BC 的解析式y ＝x +3，过P 点作PQ ⊥x 轴交BC 于Q ，由已知可得P （m ，﹣m 2﹣2m +3），则Q （m ，m +3），则S △PBC =−32（m +32）2+278，当m =−32时，S △PBC 有最大值278，此时P （−32，154）；（3）平移后抛物线解析式为y ＝﹣x 2﹣6x ﹣5，联立﹣x 2﹣2x +3＝﹣x 2﹣6x ﹣5，求出D （﹣2，3），则BD =√10，设M （t ，t +3），分三种情况：当四边形BDMN 为菱形时，由DB ＝DM ，得10＝（t +2）2+t 2，求出M （1，4）；当四边形BDNM 为菱形时，由BD ＝BM ，得10＝（t +3）2+（t +3）2，求出M （√5−3，√5）或M （−√5−3，−√5）；当四边形BMDN 为菱形时，设BD 的中点为G ，则G （−52，32），由勾股定理得BM 2＝BG 2+GM 2，即2（t +3）2＝（√102）2+（t +52）2+（t +32）2，求出M （−74，54）．【解答过程】解：（1）将点A （1，0）和点B （﹣3，0）代入y ＝﹣x 2+bx +c ，得{−1+b +c =0−9−3b +c =0，解得{b =−2c =3，∴y ＝﹣x 2﹣2x +3；（2）令x ＝0，则y ＝3， ∴C （0，3），设直线BC 的解析式为y ＝kx +b ，则有{b =3−3k +b =0，解得{k =1b =3，∴y ＝x +3，过P 点作PQ ⊥x 轴交BC 于Q ，由已知可得P （m ，﹣m 2﹣2m +3），则Q （m ，m +3），∴S △PBC =12×3×（﹣m 2﹣2m +3﹣m ﹣3）=32（﹣m 2﹣3m ）=−32（m +32）2+278， ∴当m =−32时，S △PBC 有最大值278，此时P （−32，154）；（3）∵y ＝﹣x 2﹣2x +3＝﹣（x +1）2+4，将抛物线向左平移2个单位长度，则y ＝﹣（x +3）2+4＝﹣x 2﹣6x ﹣5，联立﹣x 2﹣2x +3＝﹣x 2﹣6x ﹣5， ∴x ＝﹣2， ∴D （﹣2，3）， ∵B （﹣3，0）， ∴BD =√10， ∵M 点在直线BC 上，设M （t ，t +3），当四边形BDMN 为菱形时，如图1， ∴DB ＝DM ， ∴10＝（t +2）2+t 2， ∴t ＝1或t ＝﹣3（舍）， ∴M （1，4）；当四边形BDNM 为菱形时，如图2，∴BD ＝BM ，∴10＝（t +3）2+（t +3）2， ∴t =√5−3或t =−√5−3，∴M （√5−3，√5）或M （−√5−3，−√5）；当四边形BMDN 为菱形时，如图3，设BD 的中点为G ，则G （−52，32），∵GM ⊥BD ， ∴BM 2＝BG 2+GM 2， ∴2（t +3）2＝（√102）2+（t +52）2+（t +32）2， ∴t =−74， ∴M （−74，54）；综上所述：M 点的坐标为（1，4）或（√5−3，√5）或（−√5−3，−√5）或（−74，54）．【变式4-1】（2021•湘潭）如图，一次函数y=√33x−√3图象与坐标轴交于点A、B，二次函数y=√33x2+bx+c图象过A、B两点．（1）求二次函数解析式；（2）点B关于抛物线对称轴的对称点为点C，点P是对称轴上一动点，在抛物线上是否存在点Q，使得以B、C、P、Q为顶点的四边形是菱形？若存在，求出Q点坐标；若不存在，请说明理由．【解题思路】（1）由y =√33x −√3可求出A （3，0），B （0，−√3），代入二次函数y =√33x 2+bx +c 即得二次函数解析式为y =√33x 2−2√33x −√3；（2）由二次函数y =√33x 2−2√33x −√3可得其对称轴为直线x =2√332×√33=1，设P （1，m ），Q （n ，√33n 2−2√33n −√3），而C 与B 关于直线x ＝1对称，可得C （2，−√3）， ①当BC 、PQ 为对角线时，{0+22=1+n2−√3−√32=m+√33n 2−2√33n−√32，可得{m =−2√33n =1，此时四边形BQCP 是平行四边形，根据P （1，−2√33），B （0，−√3），C （2，−√3）可得PB ＝PC ，即得此时Q （1，−4√33）；②BP 、CQ 为对角线时，同理可得Q （﹣1，0）；③以BQ 、CP 为对角线，同理可得Q （3，0）．【解答过程】解：（1）在y =√33x −√3中，令x ＝0得y =−√3，令y ＝0得x ＝3，∴A （3，0），B （0，−√3），∵二次函数y =√33x 2+bx +c 图象过A 、B 两点， ∴{0=3√3+3b +c−√3=c ，解得{b =−2√33c =−√3， ∴二次函数解析式为y =√33x 2−2√33x −√3；（2）存在，理由如下：由二次函数y =√33x 2−2√33x −√3可得其对称轴为直线x =2√332×√33=1，设P （1，m ），Q （n ，√33n 2−2√33n −√3），而B （0，−√3），∵C 与B 关于直线x ＝1对称， ∴C （2，−√3），①当BC 、PQ 为对角线时，如图：此时BC 的中点即是PQ 的中点，即{0+22=1+n2−√3−√32=m+√33n 2−2√33n−√32，解得{m =−2√33n =1，∴当P （1，−2√33），Q （1，−4√33）时，四边形BQCP 是平行四边形，由P （1，−2√33），B （0，−√3），C （2，−√3）可得PB 2=43=PC 2， ∴PB ＝PC ，∴四边形BQCP 是菱形， ∴此时Q （1，−4√33）； ②BP 、CQ 为对角线时，如图：同理BP 、CQ 中点重合，可得{0+12=2+n2−√3+m 2=−√3+√33n 2−2√33n−√32，解得{m =0n =−1，∴当P （1，0），Q （﹣1，0）时，四边形BCPQ 是平行四边形，由P （1，0），B （0，−√3），C （2，−√3）可得BC 2＝4＝PC 2， ∴四边形BCPQ 是菱形， ∴此时Q （﹣1，0）；③以BQ 、CP 为对角线，如图：BQ 、CP 中点重合，可得{0+n 2=2+12−√3+√33n 2−2√33n−√32=−√3+m2，解得{m =0n =3，∴P （1，0），Q （3，0）时，四边形BCQP 是平行四边形，由P （1，0），B （0，−√3），C （2，−√3）可得BC 2＝4＝PC 2， ∴四边形BCQP 是菱形， ∴此时Q （3，0）；综上所述，Q 的坐标为：（1，−4√33）或（﹣1，0）或（3，0）．【变式4-2】（2021春•无棣县月考）如图，在平面直角坐标系中，二次函数y ＝x 2+bx +c 的图象与x 轴交于A 、B 两点，B 点的坐标为（3，0），与y 轴交于点C （0，﹣3），点P 是直线BC 下方抛物线上的一个动点．（1）求二次函数解析式；（2）连接PO ，PC ，并将△POC 沿y 轴对折，得到四边形POP 'C ．是否存在点P ，使四边形POP 'C 为菱形？若存在，求出此时点P 的坐标；若不存在，请说明理由；（3）当点P 运动到什么位置时，四边形ABPC 的面积最大？求出此时P 点的坐标和四边形ABPC 的最大面积．【解题思路】（1）先根据点C坐标求出c＝﹣3，再将点B坐标代入二次函数解析式中求出b，即可得出结论；（2）连接PP'交y轴于E，根据菱形的性质判断出点E是OC的中点，进而求出点P的纵坐标，最后代入二次函数解析式中求解，即可得出结论；（3）设出点P的坐标，进而利用梯形的面积+三角形的面积得出S四边形ABPC=−32（m−12）2+398，即可得出结论．【解答过程】解：（1）∵二次函数y＝x2+bx+c与y轴的交点C（0，﹣3），∴c＝﹣3，∴二次函数的解析式为y＝x2+bx﹣3，∵点B（3，0）在二次函数图象上，∴9+3b﹣3＝0，∴b＝﹣2，∴二次函数的解析式为y＝x2﹣2x﹣3；（2）存在，理由：如图1，连接PP'交y轴于E，∵四边形POP'C为菱形，∴PP'⊥OC，OE＝CE=12OC，∵点C（0，﹣3），∴OC＝3，∴OE=3 2，∴E（0，−3 2），∴点P 的纵坐标为−32，由（1）知，二次函数的解析式为y ＝x 2﹣2x ﹣3，∴x 2﹣2x ﹣3=−32，∴x =2−√102或x =2+√102， ∵点P 在直线BC 下方的抛物线上，∴0＜x ＜3，∴点P （2+√102，−32）；（3）如图2，过点P 作PF ⊥x 轴于F ，则PF ∥OC ，由（1）知，二次函数的解析式为y ＝x 2﹣2x ﹣3，令y ＝0，则x 2﹣2x ﹣3＝0，∴x ＝﹣1或x ＝3，∴A （﹣1，0），∴设P （m ，m 2﹣2m ﹣3）（0＜m ＜3），∴F （m ，0），∴S 四边形ABPC ＝S △AOC +S 梯形OCPF +S △PFB =12OA •OC +12（OC +PF ）•OF +12PF •BF=12×1×3+12（3﹣m 2+2m +3）•m +12（﹣m 2+2m +3）•（3﹣m ）=−32（m −32）2+758，∴当m =32时，四边形ABPC 的面积最大，最大值为758，此时，P （32，−154），即点P 运动到点（32，−154）时，四边形ABPC 的面积最大，其最大值为758．【变式4-3】（2020秋•南岸区期末）如图，在平面直角坐标系xOy中，二次函数y＝x2+bx+c的图象与x轴交于点A（4，0）和B（﹣1，0），交y轴于点C．（1）求二次函数y＝x2+bx+c的表达式；（2）将点C向右平移n个单位得到点D，点D在该二次函数图象上．点P是直线BD下方该二次函数图象上一点，求△PBD面积的最大值以及此时点P的坐标；（3）在（2）中，当△PBD面积取得最大值时，点E是过点P且垂直于x轴直线上的一点．在该直角坐标平面内，是否存在点Q，使得以点P，D，E，Q四点为顶点的四边形是菱形？若存在，直接写出满足条件的点Q的坐标；若不存在，请说明理由．【解题思路】（1）用待定系数法即可求解；（2）由s =12PF （x D ﹣x B ）=12×PF ×（3+1），即可求解；（3）①当PE 为对角线时，如图2，则PE ⊥DQ ，且D 、Q 关于直线PE 对称，即可求解；②当DE 为对角线时，证明△DNP ≌△EMQ （AAS ），进而求解；③当PD 为对角线时，由DG 2+EG 2＝DG 2，即可求解．【解答过程】解：（1）根据题意得：{16+4b +c =01−b +c =0，解得：{b =−3c =−4， ∴这个二次函数的表达式为y ＝x 2﹣3x ﹣4；（2）∵y ＝x 2﹣3x ﹣4与y 轴交点为（0，﹣4），∵将点C 向右平移后得到点D ，则点D 的纵坐标为﹣4．令y ＝﹣4，即x 2﹣3x ﹣4＝﹣4，得x 1＝0，x 2＝3．∴D （3，﹣4）．设直线BD 的表达式为y ＝mx +n ，则{0=−m +n −4=3m +n ，解得{m =−1n =−1， ∴经过B （﹣1，0），D （3，﹣4）的直线为y ＝﹣x ﹣1．∵P 是函数y ＝x 2﹣3x ﹣4图象上一点，则设P （t ，t 2﹣3t ﹣4）．如图1，过点P 作PF ⊥x 轴，交BD 于点F ，则F （t ，﹣t ﹣1）．设△PBD的面积为s，则s=12PF（x D﹣x B）=12×PF×（3+1）＝2PF＝2[（﹣t﹣1）﹣（t2﹣3t﹣4）]＝﹣2（t﹣1）2+8，∴t＝1时，△PBD的面积最大，最大为8．此时，点P（1，﹣6）；（3）存在以点P，D，E，Q四点为顶点的四边形是菱形，分三种情况：①当PE为对角线时，如图2，∵PE⊥x轴，CD//x轴，∴PE⊥DQ，且D、Q关于直线PE对称，因为D（3，﹣4），P（1，﹣6），∴Q（﹣1，﹣4）；②当DE为对角线时，设Q（3，k），如图3、图4，则DQ//PE，DQ＝PE，作DN⊥PE于E，EM⊥DQ于M，∵∠P＝∠Q，DP＝EQ，.∴△DNP≌△EMQ（AAS），∴QM＝PN＝﹣4﹣（﹣6）＝2，∵EM＝3﹣1＝2，QE＝DQ＝k+4，∴（k+4）2＝22+22，解得k＝﹣4±2√2，∴点Q的坐标有（3，﹣4+2√2），（3，﹣4﹣2√2）；③当PD为对角线时，如图5，设点Q坐标为（3，a），。

导数系列——零点存在性问题

导数系列——零点存在问题例1.设f(x)是定义在R 且周期为1的函数，在区间)0,1⎡⎣上，()2,,x x Df x x x D ⎧∈=⎨∉⎩其中集合D=1,n x x n N n +⎧⎫-=∈⎨⎬⎩⎭，则方程f(x)-lgx=0的解的个数是 __________ .例2．已知函数f （x ）=﹣kx 2（k ∈R ）有四个不同的零点，则实数k 的取值范围是（）A ．k ＜0B ．k ＜1C ．0＜k ＜1D ．k ＞1例4.例5.已知函数f （x ）= {函数g （x ）=f ²（x ）+f （x ）+t （t ∈R ）关于g （x ）的零点，下列判断不正确的是（）A.t=1/4时，有一个零点B.1/4＞t ＞-2时，有2个零点C.t=-2时，有3个零点D.t ＜-2时，有4个零点log 3（-x ）（x ＜0）3 x(x ≥0)例6.已知函数f(x)=若关于x 的函数y=f 2（x ）-bf （x ）+1有8个不同的零点，则实数b 的取值范围是_______例7、设函数f(x)满足f(x)=f(3x),且当x ∈[1,3)时,f(x)=lnx.若在区间[1,9)内，存在3个不同的实数x1,x2,x3，使得f(x1)/x1=f(x2)/x2=f(x3)/x3=t ，则实数t 的取值范围为_______例8．f(x)=x³+ax²+bx+c 有极值点x ₁,x ₂ 且f(x ₁)= x ₁,则关于x 的方程3[f(x)]²+2a f(x)+b=0的不同实根个数为例9.设函数f(x)满足f(x)=f(-x),f(x)=f(2-x)；且当x ∈[0,1]时f(x)=x³；又有g(x)=｜xcos(πx)｜则h(x)=f(x)－g(x)在[－1/2，3/2]上的零点个数为例10.已知函数f （x ）=x-1+a/e x（a ∈R ，e 为自然对数的底数）．（Ⅰ）若曲线y=f （x ）在点（1，f （1））处的切线平行于x 轴，求a 的值；（Ⅱ）求函数f （x ）的极值；（Ⅲ）当a=1时，若直线l ：y=kx-1与曲线y=f （x ）没有公共点，求k 的最大值．|lg(-x)|，x ＜0 x 3-6x+4，x≥0例11.函数f （x ）的导函数为f ’（x ）=3x^2-8x-60,求f （x ）零点个数。

恒成立和存在性问题

恒成⽴和存在性问题⾼⼀函数专题同步拔⾼，难度4颗星！模块导图知识剖析恒成⽴和存在性问题类型(1) 单变量的恒成⽴问题①∀x ∈D ，f (x )<a 恒成⽴，则f (x )max <a②∀x ∈D ，f (x )>a 恒成⽴，则f (x )min >a③∀x ∈D ，f (x )<g (x )恒成⽴，则F (x )=f (x )−g (x )<0，∴f (x )max <0④∀x ∈D ，f (x )>g (x )恒成⽴，则F (x )=f (x )−g (x )>0，∴f (x )min >0(2) 单变量的存在性问题①∃x 0∈D ，使得f (x 0)<a 成⽴，则f (x )min <a②∃x 0∈D ，使得f (x 0)>a 成⽴，则f (x )max >a③∃x 0∈D ，使得f (x 0)<g (x 0)恒成⽴，则F (x )=f (x )−g (x )<0，∴f (x )min <0④∃x 0∈D ，使得f (x 0)>g (x 0)恒成⽴，则F (x )=f (x )−g (x )>0，∴f (x )max >0(3) 双变量的恒成⽴与存在性问题①∀x 1∈D ,∃x 2∈E ，使得f (x 1)<g (x 2)恒成⽴，则f (x )max <g (x )max ;②∀x 1∈D ,∃x 2∈E ，使得f (x 1)>g (x 2)恒成⽴，则f (x )min >g (x )min ;③∀x 1∈D ,∀x 2∈E ,f (x 1)<g (x 2)恒成⽴，则f (x )max <g (x )min ;④∃x 1∈D ，∃x 2∈E , 使得f (x 1)<g (x 2)恒成⽴，则f (x )min <g (x )max ;(4) 相等问题①∃x 1∈D ,∃x 2∈E ，使得f (x 1)=g (x 2)，则两个函数的值域的交集不为空集；②∀x 1∈D ,∃x 2∈E ，使得f (x 1)=g (x 2)，则f (x )的值域⊆g (x )的值域解题⽅法恒成⽴和存在性问题最终可转化为最值问题，具体的⽅法有直接最值法分类参数法变换主元法数形结合法经典例题【题型⼀】恒成⽴和存在性问题的解题⽅法直接构造函数最值法【典题1】设函数f (x )=3|x |x 2+9的最⼤值是a ，若对于任意的x ∈[0,2)，a >x 2−x +b 恒成⽴，则b 的取值范围是_.【解析】当x =0时，f (x )=0；当x ≠0时，f (x )=3|x |x 2+9=3|x |+9|x |≤32√9=12，则f (x )max=12，即a =12．由题意知x 2−x+b <12在x ∈[0,2)上恒成⽴，即x 2−x +b −12<0在x ∈[0,2)上恒成⽴(∗)，(把不等式中移到右边，使得右边为，从⽽构造函数y =g (x )求最值)令g (x )=x 2−x +b −12，则问题(∗)等价于在x ∈[0,2)上g (x )<0恒成⽴，在x ∈[0,2)上，g (x )<g (2)=4−2+b −12=32+b∴32+b ≤0即b ≤−32．【点拨】① 直接构造函数最值法：遇到类似不等式f (x )<g (x )恒成⽴问题，可把不等式变形为f (x )−g (x )<0，从⽽构造函数h (x )=f (x )−g (x )求其最值解决恒成⽴问题；② 在求函数的最值时，⼀定要优先考虑函数的定义域;③ 题⽬中y =g (x )在x ∈[0,2)上是取不到最⼤值，g (x )<g (2)=32+b ，⽽要使得g (x )<0恒成⽴，32+b 可等于0，即32+b ≤0，⽽不是32+b <0分离参数法【典题1】已知函数f (x )=3x +8x +a 关于点(0,−12)对称，若对任意的x ∈[−1,1]，k ⋅2x −f (2x )≥0恒成⽴，则实数k 的取值范围为_.【解析】由y =3x +8x 为奇函数，可得其图象关于(0,0)对称，可得f (x )的图象关于(0,a )对称，函数f (x )=3x +8x +a 关于点(0,−12)对称，可得a =−12，对任意的x ∈[−1,1]，k ⋅2x −f (2x )≥0恒成⽴，⇔∀x ∈[−1,1]，k ⋅2x −3⋅2x +82x −12≥0恒成⽴，【思考：此时若利⽤直接构造函数最值法，求函数f (x )=k ⋅2x −3⋅2x +82x −12，x ∈[−1,1]的最⼩值，第⼀函数较复杂，第⼆函数含参要分即k ⋅2x ≥3⋅2x +82x −12在x ∈[−1,1]恒成⽴，所以k ≥82x 2−122x +3，(使得不等式⼀边是参数k ，另⼀边不含k 关于x 的式⼦，达到分离参数的⽬的)令t =12x ，由x ∈[−1,1]，可得t ∈12,2，设h (t )=8t 2−12t +3=8t −342−32，当t =2时，h (t )取得最⼤值11，则k 的取值范围是k ≥11.【点拨】①分离参数法：遇到类似k ⋅f (x )≥g (x )或k +f (x )≥g (x )等不等式恒成⽴问题，可把不等式化简为k >h (x )或k <h (x )的形式，达到分离参数的⽬的，再求解y =h (x )的最值处理恒成⽴问题；② 恒成⽴问题最终转化为最值问题，⽽分离参数法，最好之处就是转化后的函数不含参，避免了⿇烦的分离讨论.【典题2】已知f (x )=log 21−a ⋅2x +4x ，其中a 为常数(1)当f (1)−f (0)=2时，求a 的值；(2)当x ∈[1,+∞)时，关于x 的不等式f (x )≥x −1恒成⽴，试求a 的取值范围；【解析】 (1)f (1)−f (0)=2⇒log 2(1−2a +4)−log 2(1−a +1)=log 24⇒log 2(5−2a )=log 24(2−a )⇒5−2a =8−4a ⇒a =32；(2)log 21−a ⋅2x +4x ≥x −1=log 22x −1⇒1−a ⋅2x +4x ≥2x −1⇒a ≤2x +12x −12，令t =2x ，∵x ∈[1,+∞)∴t ∈[2,+∞)，设h (t )=t +1t −12，则a ≤h (t )min ,∵h (t )在[2,+∞)上为增函数⇒t =2时，h (t )=t +1t −12有最⼩值为2，∴a ≤2.【点拨】在整个解题的过程中不断的利⽤等价转化，把问题慢慢变得更简单些.变换主元法【典题1】对任意a ∈[−1,1]，不等式x 2+(a −4)x −2a >0恒成⽴，求x 的取值范围.思考痕迹见到本题中“x 2+(a −4)x −2a >0恒成⽴”潜意识中认为x 是变量，a 是参数，这样会构造函数f (x )=x 2+(a −4)x −2a ，⽽已知条件是a ∈[−1,1]，觉得怪怪的做不下去;此时若把a 看成变量，x 看成参数呢？【解析】因为不等式x 2+(a −4)x −2a >0恒成⽴⇔不等式(x −2)a +x 2−4x >0恒成⽴...①，令f (a )=(x −2)a +x 2−4x ,若要使得①成⽴，只需要f (−1)>0f (1)>0⇔x 2−5x +2>0x 2−3x −2>0解得x >5+√172或x <3−√172,故x 的取值范围x ∣x >5+√172 或 x <3−√172.【点拨】变换主元法，就是要分辨好谁做函数的⾃变量，谁做参数，⽅法是以已知范围的字母为⾃变量.数形结合法【典题1】已知a >0,f (x )=x 2−a x , 当x∈(−1,1)时，有f (x )<12恒成⽴，求a 的取值范围.思考痕迹本题若⽤直接最值法，求函数f (x )=x 2−a x ,x ∈(−1,1)的最⼤值，就算⽤⾼⼆学到的导数求解也是难度很⼤的事情；⽤分离参数法呢？试试也觉得⼀个硬⾻头.看看简单些的想法吧！【解析】不等式x 2−a x <12(x ∈(−1,1))恒成⽴等价于x 2−12<a x (x ∈(−1,1))恒成⽴...①，令f (x )=x 2−12,g (x )=a x ，若①成⽴，则当x ∈(−1,1)时，f (x )=x 2−12的图像恒在g (x )=a x 图像的下⽅，则需要g (1)>f (1)g (−1)>f (−1)⇔a >121a >12或a =1(不要漏了a =1，因为a >0，g (x )=a x 不⼀定是指数函数)⼜a >0，所以12<a <2,即实数a 的取值范围为12,2.【点拨】① 数形结合法：∀x ∈D ,f (x )<g (x )恒成⽴⇒在x ∈D 上，函数y =f (x )的图像在函数y =g (x )图像的下⽅.② 遇到h (x )<0不等式恒成⽴，可以把不等式化为f (x )<g (x )⽤数形结合法，⽽函数y =f (x )与y =g (x )最好是熟悉的函数类型，⽐如本题中构造出f (x )=x 2−12,g (x )=a x 两个常见的基本初级函数.【题型⼆】恒成⽴与存在性问题混合题型【典题1】已知函数f (x )=x 3+1,g (x )=2−x −m +1．(1)若对任意x 1∈[−1,3]，任意x_2∈[0 ,2]都有f(x_1)≥g(x_2)成⽴，求实数m 的取值范围．()[]()()(){{{}{{[](2)若对任意x_2∈[0 ,2]，总存在x_1∈[-1 ,3]使得f(x_1)≥g(x_2)成⽴，求实数m的取值范围．【解析】(1)由题设函数f(x)=x^3+1，g(x)=2^{-x}-m+1．对任意x_1∈[-1 ,3]，任意x_2∈[0 ,2]都有f(x_1)≥g(x_2)成⽴，知：f\left(x_{1}\right)_{\min } \geq g\left(x_{2}\right)_{\max }，∵f(x)在[-1 ,3]上递增，\therefore f\left(x_{1}\right)_{\min }=f(-1)=0⼜∵g(x)在[0 ,2]上递减，\therefore g\left(x_{2}\right)_{\max }=g(0)=2-m∴有0≥2-m，∴m的范围为[2 ,+∞)(2)由题设函数f(x)=x^3+1，g(x)=2^{-x}-m+1．对任意x_2∈[0 ,2]，总存在x_1∈[-1 ,3]使得f(x_1)≥g(x_2)成⽴，知f\left(x_{1}\right)_{\max } \geq g\left(x_{2}\right)_{\max }，∴有f(3)≥g(0)，即28≥2-m，∴M的范围为[-26 ,+∞)．【点拨】对于双变量的恒成⽴--存在性问题，⽐如第⼆问中怎么确定f\left(x_{1}\right)_{\max } \geq g\left(x_{2}\right)_{\max }，即到底是函数最⼤值还是最⼩值呢？具体如下思考如下，⼀先把g\left(x_{2}\right)看成定值m，那\exists x_{1} \in[-1,3]，都有f\left(x_{1}\right) \geq m，当然是要f(x)_{\max } \geq m；⼆再把f\left(x_{1}\right)看成定值n，那\forall x_{2} \in[0,2]，都有n \geq g\left(x_{2}\right)，当然是n \geq g(x)_{\max }；故问题转化为f\left(x_{1}\right)_{\max } \geq g\left(x_{2}\right)_{\max }.其他形式的双变量成⽴问题同理，要理解切记不要死背.【典题2】设f(x)=\dfrac{x^{2}}{x+1}，g(x)=ax+3-2a(a>0)，若对于任意x_1∈[0 ,1]，总存在x_0∈[0 ,1]，使得g(x_0)=f(x_1)成⽴，则a的取值范围是\underline{\quad \quad }．【解析】\because f(x)=\dfrac{x^{2}}{x+1}，当x=0时，f(x)=0，当x≠0时，f(x)=\dfrac{1}{\dfrac{1}{x^{2}}+\dfrac{1}{x}}=\dfrac{1}{\left(\dfrac{1}{x}+\dfrac{1}{2}\right)^{2}-\dfrac{1}{4}}，由0<x≤1，即\dfrac{1}{x} \geq 1，\left(\dfrac{1}{x}+\dfrac{1}{2}\right)^{2}-\dfrac{1}{4} \geq 2，\therefore 0<f(x) \leq \dfrac{1}{2}，故0 \leq f(x) \leq \dfrac{1}{2}，⼜因为g(x)=ax+3-2a(a>0)，且g(0)=3-2a,g(1)=3-a．由g(x)递增，可得3－2a≤g(x)≤3-a，对于任意x_1∈[0 ,1]，总存在x_0∈[0 ,1]，使得g(x_0)=f(x_1)成⽴，可得\left[0, \dfrac{1}{2}\right] \subseteq[3-2 a, 3-a]，可得\left\{\begin{array}{l} 3-2 a \leq 0 \\ 3-a \geq \dfrac{1}{2} \end{array}\right.，\therefore \dfrac{3}{2} \leq a \leq \dfrac{5}{2}．巩固练习1(★★) 已知1+2^x+a\cdot 4^x>0对⼀切x∈(-∞ ,1]上恒成⽴，则实数a的取值范围是\underline{\quad \quad }．2 (★★) 若不等式2x-1>m(x^2-1)对满⾜|m|≤2的所有m都成⽴，求x的取值范围.3 (★★) 若不等式3x^2-\log_a x<0在x\in\left(0, \dfrac{1}{3}\right)内恒成⽴，实数a的取值范围．4 (★★★) 已知函数f(x)=x^2-3x，g(x)=x^2-2mx+m，若对任意x_1∈[-1 ,1]，总存在x_2∈[-1 ,1]使得f(x_1)≥g(x_2 )，则实数m的取值范围．5 (★★★) 已知a>0且a≠1，函数f(x)=a^x+a^{-x}(x∈[－1 ,1])，g(x)=ax^2-2ax+4-a(x∈[-1 ,1])．(1)求f(x)的单调区间和值域；(2)若对于任意x_1∈[-1 ,1]，总存在x_0∈[-1 ,1]，使得g(x_0)=f(x_1)成⽴，求a的取值范围；(3)若对于任意x_0∈[-1 ,1]，任意x_1∈[-1 ,1]，都有g(x_0)≥f(x_1)恒成⽴，求a的取值范围．答案1.\left(-\dfrac{3}{4},+\infty\right)2.\dfrac{\sqrt{7}-1}{2}<x<\dfrac{\sqrt{3}+1}{2}3.\dfrac{1}{27} \leq a<14.m≤-1或m≥3Processing math: 64%5.(1) \left[2, a+\dfrac{1}{a}\right](2) a>1(3) \left[\dfrac{1}{3}, 1\right)。

中考数学第二轮专题复习第41课存在性问题、定值问题(含答案)

∴MC的解析式为：y＝－x－3，令y＝0，则x＝－3，
∴E点坐标为(－3，0)，
∴OE＝OB＝3，且OC⊥BE，
∴CE＝CB，∴∠B＝∠E，设P(x，－x－3)，
(1)证明：如图1中， ∵AE∥DF，AD∥EF，∴四边形ABCD是平行四边形， ∵四边形ABOC是正方形， ∴AC＝AB＝OC＝OB，∠ACE＝∠ABD＝90°， ∵E，D分别是OC，OB的中点， ∴CE＝BD， ∴△CAE≌△ABD(SAS)， ∴AE＝AD， ∴四边形AEFD是菱形．
(2)解：如图1中，连接DE. ∵S△SE△ODA＝DB＝12 S×△4A×CE＝4＝12 8×，8×4＝16， ∴S△AED＝S正方形ABOC－2S△ABD－S△EOD＝64－2×16－8＝24， ∴S菱形AEFD＝2S△AED＝48.
y y
2x 2 2x2 8x
6
，
解得：
x1 y1
10，
x2 y2
4 6
，
∴S△ABD＝
1 2
×2×6＝6，
设点E(m，2m－2)，
∵直线BE将△ABD的面积分为1∶2两部分，
∴ ∴S1△×ABE2＝×(132mS△－AB2D)＝＝22或或S1△×ABE2＝×23(2mS△－AB2D)＝＝44，，
(2)∵y＝2x2－8x＋6＝2(x－2)2－2，
∴顶点M的坐标为(2，－2)，
∵抛物线的顶点M与对称轴l上的点N关于x轴对称，
∴点N(2，2)，
设直线AN解析式为：y＝kx＋b，
由题意可得
0 2
k b 2k b
，解得：bk
2 2
，
∴直线AN解析式为：y＝2x－2，
联立方程组得：点D(4，6)，

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

决战2020年中考典型压轴题大突破模块三中考压轴题函数综合题专题考向导航函数综合题是初中数学中覆盖面最广、综合性最强的题型。

近几年的中考压轴题多以数学综合题的形式出现。

解数学综合题一般可分为认真审题、理解题意，探求解题思路，正确解答三个步骤。

解数学综合题必须要有科学分析问题的方法。

这类题目解法的一般思路是:假设存在→推理论证→得出结论。

若能导出合理的结果，就做出“存在”的判断，导出矛盾，就做出不存在的判断. 由于“存在性”问题的结论有两种可能，所以具有开放的特征。

精典例题(2019·白银)如图，抛物线y＝ax2+bx+4交x轴于A（﹣3，0），B（4，0）两点，与y轴交于点C，连接AC，BC．点P是第一象限内抛物线上的一个动点，点P的横坐标为m．（1）求此抛物线的表达式；（2）过点P作PM⊥x轴，垂足为点M，PM交BC于点Q．试探究点P在运动过程中，是否存在这样的点Q，使得以A，C，Q为顶点的三角形是等腰三角形．若存在，请求出此时点Q的坐标，若不存在，请说明理由；（3）过点P作PN⊥BC，垂足为点N．请用含m的代数式表示线段PN的长，并求出当m为何值时PN 有最大值，最大值是多少？【点睛】（1）由二次函数交点式表达式，即可求解；（2）分AC ＝AQ 、AC ＝CQ 、CQ ＝AQ 三种情况，分别求解即可；（3）由PN ＝PQ sin ∠PQN =√22（−13m 2+13m +4+m ﹣4）即可求解．【详解】解：（1）由二次函数交点式表达式得：y ＝a （x +3）（x ﹣4）＝a （x 2﹣x ﹣12）＝ax 2﹣ax ﹣12a ，即：﹣12a ＝4，解得：a =−13，则抛物线的表达式为y =−13x 2+13x +4；（2）存在，理由：点A 、B 、C 的坐标分别为（﹣3，0）、（4，0）、（0，4），则AC ＝5，AB ＝7，BC ＝4√2，∠OBC ＝∠OCB ＝45°，将点B 、C 的坐标代入一次函数表达式：y ＝kx +b 并解得：y ＝﹣x +4…①，同理可得直线AC 的表达式为：y =43x +4，设直线AC 的中点为K （−32，2），过点M 与CA 垂直直线的表达式中的k 值为−34，同理可得过点K 与直线AC 垂直直线的表达式为：y =−34x +78⋯②， ①当AC ＝AQ 时，如图1，则AC ＝AQ ＝5，设：QM ＝MB ＝n ，则AM ＝7﹣n ，由勾股定理得：（7﹣n ）2+n 2＝25，解得：n ＝3或4（舍去4），故点Q （1，3）；②当AC ＝CQ 时，如图1，CQ ＝5，则BQ ＝BC ﹣CQ ＝4√2−5，则QM ＝MB =8−5√22，故点Q （5√22，8−5√22）； ③当CQ ＝AQ 时，联立①②并解得：x =252（舍去）；故点Q 的坐标为：Q （1，3）或（5√22，8−5√22）；（3）设点P （m ，−13m 2+13m +4），则点Q （m ，﹣m +4）， ∵OB ＝OC ，∴∠ABC ＝∠OCB ＝45°＝∠PQN ， PN ＝PQ sin ∠PQN =√22（−13m 2+13m +4+m ﹣4）=−√26（m ﹣2）2+2√23， ∵−√26＜0，∴PN 有最大值，当m ＝2时，PN 的最大值为：2√23．巩固突破1．(2020·青白江区模拟)如图，抛物线y ＝ax 2+bx +c 与x 轴相交于A （3，0）、B 两点，与y 轴交于点C （0，3），点B 在x 轴的负半轴上，且OA ＝3OB ．（1）求抛物线的函数关系式；（2）若P 是抛物线上且位于直线AC 上方的一动点，求△ACP 的面积的最大值及此时点P 的坐标；（3）在线段OC 上是否存在一点M ，使BM +√22CM 的值最小？若存在，请求出这个最小值及对应的M点的坐标；若不存在，请说明理由．【点睛】（1）OA＝3OB＝3，则点B（﹣1，0），抛物线的表达式为：y＝a（x+1）（x﹣3）＝a（x2﹣2x﹣3），即可求解；（2）△ACP的面积=12PH×OA=12×3×（x2﹣2x+3+x﹣3）=32（﹣x2+3x），即可求解；（3）故当B、M、N三点共线时，BM+√22CM＝BN最小，即可求解．【详解】解：（1）OA＝3OB＝3，则点B（﹣1，0），抛物线的表达式为：y＝a（x+1）（x﹣3）＝a（x2﹣2x﹣3），即﹣3a＝3，解得：a＝﹣1，故抛物线的表达式为：y＝﹣x2+2x+3；（2）过点P作y轴的平行线交CA于点H，由点A、C的坐标得，直线AC的表达式为：y＝﹣x+3△ACP的面积=12PH×OA=12×3×（x2﹣2x+3+x﹣3）=32（﹣x2+3x），当x=32时，△ACP的面积的最大，最大值为：278，此时点P（32，154）；（3）过点M作MN⊥AC，则MN=√22CM，故当B、M、N三点共线时，BM+√22CM＝BN最小，直线CA的倾斜角为45°，BN⊥AC，则∠NBA＝45°，即BN=√22AB＝2√2=AN，则点N（1，2），由点B、N的坐标得，直线BN的表达式为：y＝x+1，故点M（0，1）．2．(2019·青海)如图1（注：与图2完全相同），在直角坐标系中，抛物线经过点A（1，0）、B（5，0）、C（0，4）三点．（1）求抛物线的解析式和对称轴；（2）P是抛物线对称轴上的一点，求满足P A+PC的值为最小的点P坐标（请在图1中探索）；（3）在第四象限的抛物线上是否存在点E，使四边形OEBF是以OB为对角线且面积为12的平行四边形？若存在，请求出点E坐标，若不存在请说明理由（请在图2中探索）【点睛】（1）将点A、B的坐标代入二次函数表达式得：y＝a（x﹣1）（x﹣5）＝a（x2﹣6x+5），即可求解；（2）连接B、C交对称轴于点P，此时P A+PC的值为最小，即可求解；（3）S四边形OEBF＝OB×y E＝5×y E＝12，则y E=125，将该坐标代入二次函数表达式即可求解．【详解】解：（1）将点A、B的坐标代入二次函数表达式得：y＝a（x﹣1）（x﹣5）＝a（x2﹣6x+5），则5a＝4，解得：a=4 5，抛物线的表达式为：y=45（x2﹣6x+5）=45x2−245x+4，函数的对称轴为：x＝3，顶点坐标为（3，−165）；（2）连接B 、C 交对称轴于点P ，此时P A +PC 的值为最小，将点B 、C 的坐标代入一次函数表达式：y ＝kx +b 得：{0=5k +bb =4，解得：{k =−45b =4，直线BC 的表达式为：y =−45x +4，当x ＝3时，y =85，故点P （3，85）；（3）存在，理由：四边形OEBF 是以OB 为对角线且面积为12的平行四边形，则S 四边形OEBF ＝OB ×|y E |＝5×|y E |＝12，点E 在第四象限，故：则y E =−125，将该坐标代入二次函数表达式得： y =45（x 2﹣6x +5）=−125，解得：x ＝2或4，故点E 的坐标为（2，−125）或（4，−125）． 3．(2020·锦江区模拟)如图，在平面直角坐标系中，抛物线y ＝ax 2+bx +c 的图象与x 轴交于A （4，0），B 两点，与y 轴交于点C （0，2），对称轴x =32与x 轴交于点H ．（1）求抛物线的函数表达式；（2）直线y ＝kx +1（k ≠0）与y 轴交于点E ，与抛物线交于点 P ，Q （点P 在y 轴左侧，点Q 在y 轴右侧），连接CP ，CQ ，若△CPQ 的面积为√172，求点P ，Q 的坐标；（3）在（2）的条件下，连接AC 交PQ 于G ，在对称轴上是否存在一点K ，连接GK ，将线段GK 绕点G 逆时针旋转90°，使点K 恰好落在抛物线上，若存在，请直接写出点K 的坐标；若不存在，请说明理由．【点睛】（1）对称轴x =32，则点B （﹣1，0），则抛物线的表达式为：y ＝a （x +1）（x ﹣4）＝a （x 2﹣3x ﹣4），即可求解；（2）△CPQ 的面积=12×CE ×（n ﹣m ）=√172，即n ﹣m =√17，联立抛物线于直线PQ 的表达式并整理得：−12x 2+（32−k ）x +1＝0…①，m +n ＝3﹣2k ，mn ＝﹣2，n ﹣m =√17=√(m +n)2−4mn =√(3−2k)2+8，即可求解；（3）证明△GNK ≌△K ′MG （AAS ），NK =32−27=1714=MG ，NG =137−m ，则点K ′（157−m ，4314），将该坐标代入抛物线表达式，即可求解．【详解】解：（1）对称轴x =32，则点B （﹣1，0），则抛物线的表达式为：y ＝a （x +1）（x ﹣4）＝a （x 2﹣3x ﹣4），即﹣4a ＝2，解得：a =−12，故抛物线的表达式为：y =−12x 2+32x +2；（2）设直线PQ 交y 轴于点E （0，1），点P 、Q 横坐标分别为m ，n ，△CPQ 的面积=12×CE ×（n ﹣m ）=√172，即n ﹣m =√17，联立抛物线于直线PQ 的表达式并整理得：−12x 2+（32−k ）x +1＝0…①，m +n ＝3﹣2k ，mn ＝﹣2，n ﹣m =√17=√(m +n)2−4mn =√(2k −3)2+9 解得：k ＝0（舍去）或3；故y ＝3x +1，则−12x 2+32x +2＝3x +1，解得：x =−3±√172，故点P 、Q 的坐标分别为：（−3−√172，−7−3√172）、（−3+√172，−7+3√172）；（3）设点K （32，m ），联立PQ 和AC 的表达式并解得：x =27，故点G （27，137），过点G 作y 轴的平行线交过点K ′与x 轴的平行线于点M ，交过点K 与x 轴的平行线于点N ，则△GNK ≌△K ′MG （AAS ）， NK =32−27=1714=MG ，NG =137−m ，则点K ′（157−m ，4314）将该坐标代入抛物线表达式并解得：m =9±√2114，故点K （32，9+√2114）或（32，9−√2114）．4．(2020·下陆区模拟)如图，在矩形OABC 中，点O 为原点，点A 的坐标为（0，8），点C 的坐标为（6，0）．抛物线y =−49x 2+bx +c 经过点A 、C ，与AB 交于点D ．（1）求抛物线的函数解析式；（2）点P 为线段BC 上一个动点（不与点C 重合），点Q 为线段AC 上一个动点，AQ ＝CP ，连接PQ ，设CP ＝m ，△CPQ 的面积为S ． ①求S 关于m 的函数表达式；②当S 最大时，在抛物线y =−49x 2+bx +c 的对称轴l 上，若存在点F ，使△DFQ 为直角三角形，请直接写出所有符合条件的点F 的坐标；若不存在，请说明理由．【点睛】（1）将A 、C 两点坐标代入抛物线y =−49x 2+bx +c ，即可求得抛物线的解析式；（2）①先用m 表示出QE 的长度，进而求出三角形的面积S 关于m 的函数； ②直接写出满足条件的F 点的坐标即可，注意不要漏写．【详解】解：（1）将A 、C 两点坐标代入抛物线，得 {c =8−49×36+6b +c =0，解得：{b =43c =8，∴抛物线的解析式为y =−49x 2+43x +8；（2）①∵OA ＝8，OC ＝6， ∴AC =√OA 2+OC 2=10，过点Q 作QE ⊥BC 与E 点，则sin ∠ACB =QE QC =AB AC =35， ∴QE 10−m=35，∴QE =35（10﹣m ），∴S =12•CP •QE =12m ×35（10﹣m ）=−310m 2+3m ；②∵S =12•CP •QE =12m ×35（10﹣m ）=−310m 2+3m =−310（m ﹣5）2+152， ∴当m ＝5时，S 取最大值；在抛物线对称轴l 上存在点F ，使△FDQ 为直角三角形， ∵抛物线的解析式为y =−49x 2+43x +8的对称轴为x =32， D 的坐标为（3，8），Q （3，4），当∠FDQ ＝90°时，F 1（32，8），当∠FQD ＝90°时，则F 2（32，4），当∠DFQ ＝90°时，设F （32，n ），则FD 2+FQ 2＝DQ 2，即94+（8﹣n ）2+94+（n ﹣4）2＝16，解得：n ＝6±√72， ∴F 3（32，6+√72），F 4（32，6−√72），满足条件的点F 共有四个，坐标分别为 F 1（32，8），F 2（32，4），F 3（32，6+√72），F 4（32，6−√72）．5．(2019·临朐二模)如图，在平面直角坐标系中，抛物线y ＝ax 2+bx +1交y 轴于点A ，交x 轴正半轴于点B（4，0），与过A 点的直线相交于另一点D （3，52），过点D 作DC ⊥x 轴，垂足为C ．（1）求抛物线的表达式；（2）点P 在线段OC 上（不与点O ，C 重合），过P 作PN ⊥x 轴，交直线AD 于M ，交抛物线于点N ，NE ⊥AD 于点E ，求NE 的最大值；（3）若P 是x 轴正半轴上的一动点，设OP 的长为t ．是否存在t ，使以点M ，C ，D ，N 为顶点的四边形是平行四边形？若存在，求出t 的值；若不存在，请说明理由．【点睛】（1）将点B 、D 的坐标代入二次函数表达式，即可求解；（2）利用NE ＝MN cos ∠ENP =2√55（−34m 2+114m +1−12m ﹣1），即可求解；（3）设：OP ＝t ，则点M （t ，12t +1）、N （t ，−34t 2+114t +1），由|MN |＝CD ，即可求解．【详解】解：（1）将点B 、D 的坐标代入二次函数表达式得：{16a +4b +1=09a +3b +1=52，解得：{a =−34b =114，则函数的表达式为：y =−34x 2+114x +1；（2）将点A （0，1）、D 的坐标代入一次函数表达式：y ＝mx +n 并解得：直线AD 的表达式为：y =12x +1，即直线AD 的倾斜角的正切值为12，则tan ∠ENP =12，则cos ∠ENP =2√55，设点N （m ，−34m 2+114m +1）、点M （12m +1），则NE ＝MN cos ∠ENP =2√55（−34m 2+114m +1−12m ﹣1）=−3√510（m −32）2+27√540，故当m =32时，则NE 的最大值为27√540；（3）设：OP ＝t ，则点M （t ，12t +1）、N （t ，−34t 2+114t +1），点M 可能在CD 得左侧也可能在CD 得右侧，由题意得：|MN |＝CD ， ±52=−34t 2+114t +1−12t ﹣1，解得：t =9±√2016（舍去负值），故t =9+√2016时，以点M ，C ，D ，N 为顶点的四边形是平行四边形． 6．(2019·恩施州)如图，抛物线y ＝ax 2﹣2ax +c 的图象经过点C （0，﹣2），顶点D 的坐标为（1，−83），与x 轴交于A 、B 两点．（1）求抛物线的解析式．（2）连接AC ，E 为直线AC 上一点，当△AOC ∽△AEB 时，求点E 的坐标和AEAB 的值．（3）点F （0，y ）是y 轴上一动点，当y 为何值时，√55FC +BF 的值最小．并求出这个最小值．（4）点C 关于x 轴的对称点为H ，当√55FC +BF 取最小值时，在抛物线的对称轴上是否存在点Q ，使△QHF 是直角三角形？若存在，请求出点Q 的坐标；若不存在，请说明理由．【点睛】（1）将点C 、D 的坐标代入抛物线表达式，即可求解；（2）当△AOC ∽△AEB 时，S △AOC S △AEB=（AC AB ）2＝（√54）2=516，求出y E =−85，由△AOC ∽△AEB 得：AO AC=AE AB=√5，即可求解；（3）如图2，连接BF ，过点F 作FG ⊥AC 于G ，当折线段BFG 与BE 重合时，取得最小值，即可求解；（4）①当点Q 为直角顶点时，由Rt △QHM ∽Rt △FQM 得：QM 2＝HM •FM ；②当点H 为直角顶点时，点H （0，2），则点Q （1，2）；③当点F 为直角顶点时，同理可得：点Q （1，−32）．【详解】解：（1）由题可列方程组：{c =−2a −2a +c =−83，解得：{a =23c =−2∴抛物线解析式为：y =23x 2−43x ﹣2；（2）如图1，∠AOC ＝90°，AC =√5，AB ＝4，设直线AC 的解析式为：y ＝kx +b ，则{−k +b =0b =−2，解得：{k =−2b =−2，∴直线AC 的解析式为：y ＝﹣2x ﹣2；当△AOC ∽△AEB 时S △AOC S △AEB=（AC AB）2＝（√54）2=516，∵S △AOC ＝1，∴S △AEB =165， ∴12AB ×|y E |=165，AB ＝4，则y E =−85，则点E （−15，−85）；由△AOC ∽△AEB 得：AO AC=AE AB=√5∴AE AB=√55；（3）如图2，连接BF ，过点F 作FG ⊥AC 于G ，则FG ＝CF sin ∠FCG =√55CF ，∴√55CF +BF ＝GF +BF ≥BE ，当折线段BFG 与BE 重合时，取得最小值，由（2）可知∠ABE ＝∠ACO∴BE ＝AB cos ∠ABE ＝AB cos ∠ACO ＝45=8√55，|y |＝OB tan ∠ABE ＝OB tan ∠ACO ＝3×12=32，∴当y =−32时，即点F （0，−32），√55CF +BF 有最小值为8√55；（4）①当点Q 为直角顶点时（如图3）：由（3）易得F （0，−32），∵C （0，﹣2）∴H （0，2）设Q （1，m ），过点Q 作QM ⊥y 轴于点M ．则Rt △QHM ∽Rt △FQM ∴QM 2＝HM •FM ， ∴12＝（2﹣m ）（m +32），解得：m =1±√334，则点Q （1，1+√334）或（1，1−√334）当点H 为直角顶点时：点H （0，2），则点Q （1，2）；当点F 为直角顶点时：同理可得：点Q （1，−32）；综上，点Q 的坐标为：（1，1+√334）或（1，1−√334）或Q （1，2）或Q （1，−32）．7．(2019·阜新)如图，抛物线y ＝ax 2+bx +2交x 轴于点A （﹣3，0）和点B （1，0），交y 轴于点C ．（1）求这个抛物线的函数表达式．（2）点D 的坐标为（﹣1，0），点P 为第二象限内抛物线上的一个动点，求四边形ADCP 面积的最大值．（3）点M 为抛物线对称轴上的点，问：在抛物线上是否存在点N ，使△MNO 为等腰直角三角形，且∠MNO 为直角？若存在，请直接写出点N 的坐标；若不存在，请说明理由．【点睛】（1）抛物线的表达式为：y ＝a （x +3）（x ﹣1）＝a （x 2+2x ﹣3）＝ax 2+2ax ﹣3a ，即﹣3a ＝2，即可求解；（2）S 四边形ADCP ＝S △APO +S △CPO ﹣S △ODC ，即可求解；（3）分点N 在x 轴上方、点N 在x 轴下方两种情况，分别求解．【详解】解：（1）抛物线的表达式为：y ＝a （x +3）（x ﹣1）＝a （x 2+2x ﹣3）＝ax 2+2ax ﹣3a ，即﹣3a＝2，解得：a=−2 3，故抛物线的表达式为：y=−23x2−43x+2，则点C（0，2），函数的对称轴为：x＝﹣1；（2）连接OP，设点P（x，−23x2−43x+2），则S＝S四边形ADCP＝S△APO+S△CPO﹣S△ODC=12×AO×y P+12×OC×|x P|−12×CO×OD=12×3×（−23x2−43x+2）+12×2×（﹣x）−12×2×1=−x2﹣3x+2，∵﹣1＜0，故S有最大值，当x=−32时，S的最大值为174；（3）存在，理由：△MNO为等腰直角三角形，且∠MNO为直角时，点N的位置如下图所示：①当点N在x轴上方时，点N的位置为N1、N2，N1的情况（△M1N1O）：设点N1的坐标为（x，−23x2−43x+2），则M1E＝x+1，过点N1作x轴的垂线交x轴于点F，过点M1作x轴的平行线交N1F于点E，∵∠FN 1O +∠M 1N 1E ＝90°，∠M 1N 1E +∠EM 1N 1＝90°，∴∠EM 1N 1＝∠FN 1O ， ∠M 1EN 1＝∠N 1FO ＝90°，ON 1＝M 1N 1， ∴△M 1N 1E ≌△N 1OF （AAS ），∴M 1E ＝N 1F ，即：x +1=−23x 2−43x +2，解得：x =−7±√734（舍去负值），则点N 1（−7+√734，−3+√734）； N 2的情况（△M 2N 2O ）：同理可得：点N 2（−1−√734，−3+√734）； ②当点N 在x 轴下方时，点N 的位置为N 3、N 4，同理可得：点N 3、N 4的坐标分别为：（−7−√734，−3−√734）、（−1+√734，−3−√734）；综上，点N 的坐标为：（−7+√734，−3+√734）或（−1−√734，−3+√734）或（−7−√734，−3−√734）或（−1+√734，−3−√734）． 8．(2019·通辽)已知，如图，抛物线y ＝ax 2+bx +c （a ≠0）的顶点为M （1，9），经过抛物线上的两点A （﹣3，﹣7）和B （3，m ）的直线交抛物线的对称轴于点C ．（1）求抛物线的解析式和直线AB 的解析式．（2）在抛物线上A 、M 两点之间的部分（不包含A 、M 两点），是否存在点D ，使得S △DAC ＝2S △DCM ？若存在，求出点D 的坐标；若不存在，请说明理由．（3）若点P 在抛物线上，点Q 在x 轴上，当以点A ，M ，P ，Q 为顶点的四边形是平行四边形时，直接写出满足条件的点P 的坐标．【点睛】（1）二次函数表达式为：y＝a（x﹣1）2+9，即可求解；（2）S△DAC＝2S△DCM，则S△DAC=12DH（x C﹣x A）=12（﹣x2+2x+8﹣2x+1）（1+3）=12（9﹣1）（1﹣x）×2，即可求解；（3）分AM是平行四边形的一条边、AM是平行四边形的对角线两种情况，分别求解即可．【详解】解：（1）二次函数表达式为：y＝a（x﹣1）2+9，将点A的坐标代入上式并解得：a＝﹣1，故抛物线的表达式为：y＝﹣x2+2x+8…①，则点B（3，5），将点A、B的坐标代入一次函数表达式并解得：直线AB的表达式为：y＝2x﹣1；（2）存在，理由：二次函数对称轴为：x＝1，则点C（1，1），过点D作y轴的平行线交AB于点H，设点D（x，﹣x2+2x+8），点H（x，2x﹣1），∵S△DAC＝2S△DCM，则S△DAC=12DH（x C﹣x A）=12（﹣x2+2x+8﹣2x+1）（1+3）=12（9﹣1）（1﹣x）×2，解得：x＝﹣1或5（舍去5），故点D（﹣1，5）；（3）设点Q（m，0）、点P（s，t），t＝﹣s2+2s+8，①当AM是平行四边形的一条边时，点M向左平移4个单位向下平移16个单位得到A，同理，点Q（m，0）向左平移4个单位向下平移16个单位为（m﹣4，﹣16），即为点P，即：m﹣4＝s，﹣16＝t，而t＝﹣s2+2s+8，解得：s＝6或﹣4，故点P（6，﹣16）或（﹣4，﹣16）；②当AM是平行四边形的对角线时，由中点公式得：m+s＝﹣2，t＝2，而t＝﹣s2+2s+8，解得：s＝1±√7，故点P（1+√7，2）或（1−√7，2）；综上，点P（6，﹣16）或（﹣4，﹣16）或（1+√7，2）或（1−√7，2）．9．(2019·长沙模拟)如图，在平面直角坐标系中，直线y=12x﹣1与抛物线y=−512x2+bx+c相交于A，B两点，点A在x轴上，点B的横坐标为﹣6，点P是抛物线上位于直线AB上方的一动点（不与点A，B重合）．（1）求该抛物线的解析式；（2）连接P A，PB，在点P运动的过程中，是否存在某一位置，使得△P AB恰好是一个以点P为直角顶点的等腰直角三角形？若存在，求出点P的坐标；若不存在，请说明理由；（3）过点P作PD∥y轴交直线AB于点D，以PD为直径的⊙E与直线AB相交于点G，求DG的最大值．【点睛】（1）在函数y=12x﹣1中，求出A（2，0）、B（﹣6，﹣4），将A（2，0），B（﹣6，﹣4）代入y=−512x2+bx+c中，即可求解；（2）存在，理由：由A、B点坐标得：则点E（﹣2，﹣2），则AE=√(−2−2)2+(−2)2=2√5，tan∠OAC=AOAE=ACAF，即：2√5=√5AF，则AF＝5，可得直线EF的表达式为：y＝﹣2x﹣6…②，联立①②即可求解；（3）GD ＝PD sin ∠DPG =5（−512x 2−76x +4−12x +1），即可求解．【详解】解：（1）在函数y =12x ﹣1中，当y ＝0时，x ＝2，∴A （2，0），当x ＝﹣6时，y ＝﹣4，∴B （﹣6，﹣4），将A （2，0），B （﹣6，﹣4）代入y =−512x 2+bx +c 中，得{−512×22+2b +c =0−512×(−6)2−6b +c =−4，解得{b =−76c =4，∴该抛物线得解析式为y =−512x 2−76x +4…①；（2）存在，理由：设直线AB 交y 轴于点C ，则点C （0，﹣1），如图所示，作线段AB 的垂直平分线交x 轴于点F 、交y 轴于点E ，由A 、B 点坐标得：则点E （﹣2，﹣2），则AE =√(−2−2)2+(−2)2=2√5， tan ∠OAC =AO AE =ACAF ，即：2√5=√5AF，则AF ＝5，故点F （﹣3，0），由点E （﹣2，﹣2）、F （﹣3，0）得直线EF 的表达式为：y ＝﹣2x ﹣6…②，联立①②并解得：x ＝﹣4或6（舍去x ＝6），故点P 的坐标为（﹣4，2）， PE =√(−4+2)2+(2+2)2=2√5；（3）如下图所示，PD 为直径，则∠PGD ＝90°，即：PG ⊥AC∠OAC ＝90°﹣∠PDC ＝∠DPG ，在Rt △AOC 中，sin ∠OAC =15=sin ∠DPG ，则GD ＝PD sin ∠DPG ，设点P 坐标为（x ，−512x 2−76x +4），则点D （x ，12x ﹣1），GD ＝PD sin ∠DPG =1√5（−512x 2−76x +4−12x +1），当x =−b2a =−2时，GD 最大，最大值为：4√53．10．(2019·硚口区区模拟)抛物线y =ax 2−12x +54经过点E （5，5），其顶点为C 点．（1）求抛物线的解析式，并直接写出C 点坐标．（2）将直线y =12x 沿y 轴向上平移b 个单位长度交抛物线于A 、B 两点．若∠ACB ＝90°，求b 的值．（3）是否存在点D （1，a ），使抛物线上任意一点P 到x 轴的距离等于P 点到点D 的距离？若存在，请求点D 的坐标；若不存在，请说明理由．【点睛】（1）将点E 坐标代入解析式，求出系数a ，获得解析式，并求出顶点C 坐标；（2）平移直线y =12x ，获得平移后的解析式y =12x +b ，直线与抛物线交于两点A 、B ，设A （x 1，y 1）、B （x 2，y 2），因为∠ACB ＝90°，利用A 、B 、C 三点构造相似，得到1−x 1y 2−1=y 1−1x 2−1，将直线与抛物线联立获得方程，根据韦达定理，获得x 1+x 2，x 1•x 2，从而获得关于b 的方程，求出b 值；（3）过点P 作PQ ⊥x 轴，设点P （m ，14m 2−12m +54）因为PQ ＝PD ，所以PQ 2＝PD 2，整理可得(a −2)m 2+2(a −2)m +2(a −2)(a −12)=0，所以当a ＝2时，存在点D （1，2）．【详解】解：（1）将点E （5，5）代入y ＝ax 2−12x +54 5＝25a −52+54 a =14∴y =14x 2−12x +54，顶点（1，1）（2）直线y =12x 平移后获得解析式y =12x +b 交抛物线于A （x 1，y 1）、B （x 2，y 2） y 1=12x 1+b ，y 2=12x 2+b 联立{y =12x +by =14x 2−12x +54x 2﹣4x +5﹣4b ＝0 ∴x 1+x 2＝4，x 1•x 2＝5﹣4b如图，过点A 、B 作y 轴的平行线与过点C 平行于x 轴的线交于点E ，F可证△ACE ∽△BCF ∴1−x 1y 2−1=y 1−1x 2−1∴（x 1+x 2）﹣（x 1•x 2）﹣1＝y 1•y 2﹣（y 1+y 2）+1 ∴b 2﹣5b +94=0，解，b 1=92，b 2=12（舍） ∴b =92．（3）设P（m，n），作PQ⊥x轴于Q若PQ＝PD，则PQ2＝PD2（m﹣1）2+（n﹣a）2＝n2整理得m2﹣2m+1+a2﹣2an＝0将n=14m2−12m+54代入整理得(a−2)m2+2(a−2)m+2(a−2)(a−12)=0当a＝2时，方程成立∴D（1，2）11．(2020·云南模拟)如图，抛物线y＝ax2+bx+3经过点B（﹣1，0），C（2，3），抛物线与y轴的交点A，与x轴的另一个交点为D，点M为线段AD上的一动点，设点M的横坐标为t．（1）求抛物线的表达式；（2）过点M作y轴的平行线，交抛物线于点P，设线段PM的长为1，当t为何值时，1的长最大，并求最大值；（先根据题目画图，再计算）（3）在（2）的条件下，当t为何值时，△P AD的面积最大？并求最大值；（4）在（2）的条件下，是否存在点P，使△P AD为直角三角形？若存在，直接写出t的值；若不存在，说明理由．【点睛】（1）利用待定系数法即可解决问题；（2）易知直线AD 解析式为y ＝﹣x +3，设M 点横坐标为m ，则P （t ，﹣t 2+2t +3），M （t ，﹣t +3），可得l ＝﹣t 2+2t +3﹣（﹣t +3）＝﹣t 2+3t ＝﹣（t −32）2+94，利用二次函数的性质即可解决问题；（3）由S △P AD =12×PM ×（x D ﹣x A ）=32PM ，推出PM 的值最大时，△P AD 的面积最大；（4）如图设AD 的中点为K ，设P （t ，﹣t 2+2t +3）．由△P AD 是直角三角形，推出PK =12AD ，可得（t −32）2+（﹣t 2+2t +3−32）2=14×18，解方程即可解决问题；【详解】解：（1）把点 B （﹣1，0），C （2，3）代入y ＝ax 2+bx +3，则有{a −b +3=04a +2b +3=3，解得{a =−1b =2，∴抛物线的解析式为y ＝﹣x 2+2x +3．（2）在y ＝﹣x 2+2x +3中，令y ＝0可得0＝﹣x 2+2x +3，解得x ＝﹣1或x ＝3， ∴D （3，0），且A （0，3）， ∴直线AD 解析式为y ＝﹣x +3，设M 点横坐标为m ，则P （t ，﹣t 2+2t +3），M （t ，﹣t +3）， ∵0＜t ＜3，∴点M 在第一象限内，∴l ＝﹣t 2+2t +3﹣（﹣t +3）＝﹣t 2+3t ＝﹣（t −32）2+94， ∴当t =32时，l 有最大值，l 最大=94；（3）∵S △P AD =12×PM ×（x D ﹣x A ）=32PM ，∴PM 的值最大时，△P AD 的面积中点，最大值=32×94=278． ∴t =32时，△P AD 的面积的最大值为278．（4）如图设AD 的中点为K ，设P （t ，﹣t 2+2t +3）．∵△P AD 是直角三角形， ∴PK =12AD ，∴（t −32）2+（﹣t 2+2t +3−32）2=14×18，整理得t （t ﹣3）（t 2﹣t ﹣1）＝0，解得t ＝0或3或1±√52，∵点P 在第一象限， ∴t =1+√52． 12．(2019·大渡口区模拟)如图，抛物线y =−35x 2+125x +3与x 轴交于点A 和点B （点A 在点B 的左侧），与y 轴交于点C ，连结BC ．（1）如图1，点N 为抛物线上的一动点，且位于直线BC 上方，连接CN 、BN ．点P 是直线AB 上的动点．当△NBC 面积取得最大值时，求出点N 的坐标及△NBC 面积的最大值，并求此时PN +CP 的最小值；（2）如图2，点M 、P 分别为线段BC 和线段OB 上的动点，连接PM 、PC ，是否存在这样的点P ，使△PCM 为等腰三角形，△PMB 为直角三角形同时成立？若存在，求出点P 的坐标；若不存在，请说明理由．【点睛】（1）S△NBC=12HN×OB=52（−35x2+125x+3+35x﹣3）=−32x2+152x，求出N的坐标是(52，214)，点C关于直线AB的对称点C'（0，﹣3），PN+PC的最小值为NC′即可求解；（2）利用△BMP～△BOC，即可求解．【详解】解：（1）过点N作y轴的平行线交直线BC与点H，y=−35x2+125x+3，令x＝0，则y＝3，令y＝0，则x＝5或﹣1，即点A、B、C的坐标分别为（﹣1，0）、（5，0）、（0，3），则直线BC的表达式为：y＝kx+3，将点B坐标代入上式并解得：k=−3 5，则直线BC的表达式为：y=−35x+3，设点N（x，−35x2+125x+3），点H（x，−35x+3），S△NBC=12HN×OB=52（−35x2+125x+3+35x﹣3）=−32x2+152x，∵−32＜0，则S△NBC有最大值，当x=52时，△NBC面积最大，最大值为758；此时点N的坐标是(52，214)，如图，点C 关于直线AB 的对称点C '（0，﹣3）， PN +PC 的最小值NC′=√(214+3)2+(52)2=√11894；（2）存在，∵B （5，0），C （0，3）， ∴BC =√32+52=√34，①当∠PMB ＝90°，则∠PMC ＝90°，△PMC 为等腰直角三角形，MP ＝MC ，设PM ＝t ，则CM =t ，MB =√34−t ， ∵∠MBP ＝∠OBC ， ∴△BMP ～△BOC ， ∴PM OC=BM OB=BP BC，即t3=√34−t5=√34，解得t =3√348，BP =174， ∴OP =OB −BP =5−174=34，当∠PMB ＝90°，CM ＝PM 时，同理可得：点P （3√34−95，0）；此时P 点坐标为(34，0)或（3√34−95，0）．13．(2019·崇安区一模)已知二次函数y ＝ax 2﹣9ax +18a 的图象与x 轴交于A ，B 两点（A 在B 的左侧），图象的顶点为C ，直线AC 交y 轴于点D ．（1）连接BD ，若∠BDO ＝∠CAB ，求这个二次函数的表达式；（2）是否存在以原点O 为对称中心的矩形CDEF ？若存在，求出这个二次函数的表达式，若不存在，请说明理由．【点睛】（1）利用配方法求出抛物线y ＝ax 2﹣9ax +18a 的顶点C 的坐标为（92，−94a ）．作CM ⊥x 轴于M ，则OM =92，CM ＝|−94a |．求出A （3，0），B （6，0）．再证明△ODA ∽△OBD ，根据相似三角形对应边成比例求出OD ＝3√2．根据平行线分线段成比例定理得出ODCM=OAAM，求得CM =3√22，那么|−94a |=3√22，求出a ，即可得到二次函数的解析式；（2）连接OC ，根据矩形的性质得出OC ＝OD ，那么∠ODC ＝∠OCD ．再证明∠OCD ＝∠DCM ．作AN ⊥OC 于N ，根据角平分线的性质得出AN ＝AM =32．由sin ∠AON =AN OA =12，得出∠AON ＝30°，求出CM ＝OM •tan30°=3√32，那么|−94a |=3√32，求出a ，即可得到二次函数的解析式．【详解】解：（1）∵y ＝ax 2﹣9ax +18a ＝a （x −92）2−94a ， ∴顶点C （92，−94a ）．作CM ⊥x 轴于M ，则OM =92，CM ＝|−94a |．当y ＝0时，ax 2﹣9ax +18a ＝0，解得x 1＝3，x 2＝6， ∴A （3，0），B （6，0）．∵∠BDO ＝∠CAB ，∠CAB ＝∠DAO ， ∴∠DAO ＝∠BDO ．在△ODA 与△OBD 中， {∠DAO =∠BDO ∠AOD =∠DOB =90°， ∴△ODA ∽△OBD ， ∴OD OB=OA OD，即OD 6=3OD，∴OD ＝3√2． ∵CM ∥OD ， ∴OD CM=OA AM，即3√2CM =392−3， ∴CM =3√22， ∴|−94a |=3√22， ∴a ＝±2√23， ∴二次函数的解析式为y =2√23x 2﹣6√2x +12√2或y =−2√23x 2+6√2x ﹣12√2；（2）存在．连接OC ，则OC ＝OD ．∴∠ODC ＝∠OCD ． ∵CM ∥OD ， ∴∠ODC ＝∠DCM ， ∴∠OCD ＝∠DCM ．作AN ⊥OC 于N ，AN ＝AM =32．∵sin ∠AON =AN OA =323=12，∴∠AON ＝30°， ∴CM ＝OM •tan30°=92×√33=3√32， ∴|−94a |=3√32， ∴a ＝±2√33， ∴二次函数的解析式为y =2√33x 2﹣6√3x +12√3或y =−2√33x 2+6√3x ﹣12√3．14．(2019·长沙一模)如图，已知直线y ＝kx ﹣6与抛物线y ＝ax 2+bx +c 相交于A ，B 两点，且点A （1，﹣4）为抛物线的顶点，点B 在x 轴上．（1）求抛物线的解析式；（2）在（1）中抛物线的第二象限图象上是否存在一点P ，使△POB 与△POC 全等？若存在，求出点P 的坐标；若不存在，请说明理由；（3）若点Q 是y 轴上一点，且△ABQ 为直角三角形，求点Q 的坐标．【点睛】（1）已知点A 坐标可确定直线AB 的解析式，进一步能求出点B 的坐标．点A 是抛物线的顶点，那么可以将抛物线的解析式设为顶点式，再代入点B 的坐标，依据待定系数法可解．（2）首先由抛物线的解析式求出点C 的坐标，在△POB 和△POC 中，已知的条件是公共边OP ，若OB与OC 不相等，那么这两个三角形不能构成全等三角形；若OB 等于OC ，那么还要满足的条件为：∠POC ＝∠POB ，各自去掉一个直角后容易发现，点P 正好在第二象限的角平分线上，联立直线y ＝﹣x 与抛物线的解析式，直接求交点坐标即可，同时还要注意点P 在第二象限的限定条件．（3）分别以A 、B 、Q 为直角顶点，分类进行讨论．找出相关的相似三角形，依据对应线段成比例进行求解即可．【详解】解：（1）把A （1，﹣4）代入y ＝kx ﹣6，得k ＝2， ∴y ＝2x ﹣6，令y ＝0，解得：x ＝3， ∴B 的坐标是（3，0）． ∵A 为顶点，∴设抛物线的解析为y ＝a （x ﹣1）2﹣4，把B （3，0）代入得：4a ﹣4＝0，解得a ＝1，∴y ＝（x ﹣1）2﹣4＝x 2﹣2x ﹣3．（2）存在．∵OB ＝OC ＝3，OP ＝OP ，∴当∠POB ＝∠POC 时，△POB ≌△POC ，此时PO 平分第二象限，即PO 的解析式为y ＝﹣x ．设P （m ，﹣m ），则﹣m ＝m 2﹣2m ﹣3，解得m =1−√132（m =1+√132＞0，舍）， ∴P （1−√132，√13−12）．（3）①如图，当∠Q 1AB ＝90°时，△DAQ 1∽△DOB ， ∴AD OD=DQ 1DB ，即√56=13√5，∴DQ 1=52， ∴OQ 1=72，即Q 1（0，−72）；②如图，当∠Q 2BA ＝90°时，△BOQ 2∽△DOB ， ∴OB OD=OQ 2OB ，即36=OQ 23，∴OQ 2=32，即Q 2（0，32）；③如图，当∠AQ 3B ＝90°时，作AE ⊥y 轴于E ，则△BOQ 3∽△Q 3EA ，∴OBQ 3E =OQ 3AE ，即34−OQ 3=OQ 31，∴OQ 32﹣4OQ 3+3＝0，∴OQ 3＝1或3，即Q 3（0，﹣1），Q 4（0，﹣3）．综上，Q 点坐标为（0，−72）或（0，32）或（0，﹣1）或（0，﹣3）．15．(2019·海南)如图，已知抛物线y ＝ax 2+bx +5经过A （﹣5，0），B （﹣4，﹣3）两点，与x 轴的另一个交点为C ，顶点为D ，连结CD ．（1）求该抛物线的表达式；（2）点P 为该抛物线上一动点（与点B 、C 不重合），设点P 的横坐标为t ．①当点P 在直线BC 的下方运动时，求△PBC 的面积的最大值；②该抛物线上是否存在点P ，使得∠PBC ＝∠BCD ？若存在，求出所有点P 的坐标；若不存在，请说明理由．【点睛】（1）将点A 、B 坐标代入二次函数表达式，即可求解；（2）①S △PBC =12PG （x C ﹣x B ），即可求解；②分点P 在直线BC 下方、上方两种情况，分别求解即可．【详解】解：（1）将点A 、B 坐标代入二次函数表达式得：{25a −5b +5=016a −4b +5=−3，解得：{a =1b =6，故抛物线的表达式为：y＝x2+6x+5…①，令y＝0，则x＝﹣1或﹣5，即点C（﹣1，0）；（2）①如图1，过点P作y轴的平行线交BC于点G，将点B、C的坐标代入一次函数表达式并解得：直线BC的表达式为：y＝x+1…②，设点G（t，t+1），则点P（t，t2+6t+5），S△PBC=12PG（x C﹣x B）=32（t+1﹣t2﹣6t﹣5）=−32t2−152t﹣6，∵−32＜0，∴S△PBC有最大值，当t=−52时，其最大值为278；②设直线BP与CD交于点H，当点P在直线BC下方时，∵∠PBC ＝∠BCD ，∴点H 在BC 的中垂线上，线段BC 的中点坐标为（−52，−32），过该点与BC 垂直的直线的k 值为﹣1，设BC 中垂线的表达式为：y ＝﹣x +m ，将点（−52，−32）代入上式并解得：直线BC 中垂线的表达式为：y ＝﹣x ﹣4…③，同理直线CD 的表达式为：y ＝2x +2…④，联立③④并解得：x ＝﹣2，即点H （﹣2，﹣2），同理可得直线BH 的表达式为：y =12x ﹣1…⑤，联立①⑤并解得：x =−32或﹣4（舍去﹣4），故点P （−32，−74）；当点P （P ′）在直线BC 上方时，∵∠PBC ＝∠BCD ，∴BP ′∥CD ，则直线BP ′的表达式为：y ＝2x +s ，将点B 坐标代入上式并解得：s ＝5，即直线BP ′的表达式为：y ＝2x +5…⑥，联立①⑥并解得：x ＝0或﹣4（舍去﹣4），故点P （0，5）；故点P 的坐标为P （−32，−74）或（0，5）．16．(2019·山西)综合与探究如图，抛物线y ＝ax 2+bx +6经过点A （﹣2，0），B （4，0）两点，与y 轴交于点C ，点D 是抛物线上一个动点，设点D 的横坐标为m （1＜m ＜4）．连接AC ，BC ，DB ，DC ．（1）求抛物线的函数表达式；（2）△BCD 的面积等于△AOC 的面积的34时，求m 的值；（3）在（2）的条件下，若点M 是x 轴上一动点，点N 是抛物线上一动点，试判断是否存在这样的点M ，使得以点B ，D ，M ，N 为顶点的四边形是平行四边形？若存在，请直接写出点M 的坐标；若不存在，请说明理由．【点睛】（1）由抛物线交点式表达，即可求解；（2）利用S △BDC =12HD ×OB ，即可求解；（3）分BD 是平行四边形的一条边、BD 是平行四边形的对角线两种情况，分别求解即可．【详解】解：（1）由抛物线交点式表达式得：y ＝a （x +2）（x ﹣4）＝a （x 2﹣2x ﹣8）＝ax 2﹣2ax ﹣8a ，即﹣8a ＝6，解得：a =−34，故抛物线的表达式为：y =−34x 2+32x +6；（2）点C （0，6），将点B 、C 的坐标代入一次函数表达式并解得：直线BC 的表达式为：y =−32x +6，如图所示，过点D 作y 轴的平行线交直线BC 与点H ，设点D （m ，−34m 2+32m +6），则点H （m ，−32m +6）S △BDC =12HD ×OB ＝2（−34m 2+32m +6+32m ﹣6）＝2（−34m 2+3m ），34S △ACO =34×12×6×2=92，即：2（−34m 2+3m ）=92，解得：m ＝1或3（舍去1），故m ＝3；（3）当m ＝3时，点D （3，154），①当BD 是平行四边形的一条边时，如图所示：M 、N 分别有三个点，设点N （n ，−34n 2+32n +6）则点N 的纵坐标为绝对值为154，即|−34n 2+32n +6|=154，解得：n ＝﹣1或3（舍去）或1±√14，故点N （N ′、N ″）的坐标为（﹣1，154）或（1+√14，−154）或（1−√14，−154），当点N （﹣1，154）时，由图象可得：点M （0，0），当N ′的坐标为（1+√14，−154），由中点坐标公式得：点M ′（√14，0），同理可得：点M ″坐标为（−√14，0），故点M 坐标为：（0，0）或（√14，0）或（−√14，0）；②当BD 是平行四边形的对角线时，点B 、D 的坐标分别为（4，0）、（3，154）设点M （m ，0），点N （s ，t ），由中点坐标公式得：{4+3=m +s 154+0=t +0，而t =−34s 2+32s +6，解得：t =154，s ＝﹣1，m ＝8，故点M 坐标为（8，0）；故点M 的坐标为：（0，0）或（√14，0）或（−√14，0）或（8，0）．17．(2019·眉山)如图1，在平面直角坐标系中，抛物线y =−49x 2+bx +c 经过点A （﹣5，0）和点B （1，0）．（1）求抛物线的解析式及顶点D 的坐标；（2）点P是抛物线上A、D之间的一点，过点P作PE⊥x轴于点E，PG⊥y轴，交抛物线于点G，过点G作GF⊥x轴于点F，当矩形PEFG的周长最大时，求点P的横坐标；（3）如图2，连接AD、BD，点M在线段AB上（不与A、B重合），作∠DMN＝∠DBA，MN交线段AD于点N，是否存在这样点M，使得△DMN为等腰三角形？若存在，求出AN的长；若不存在，请说明理由．【点睛】（1）抛物线的表达式为：y=−49（x+5）（x﹣1），即可求解；（2）PE=−49m2−169m+209，PG＝2（﹣2﹣m）＝﹣4﹣2m，矩形PEFG的周长＝2（PE+PG），即可求解；（3）分MN＝DM、NM＝DN、DN＝DM，三种情况分别求解．【详解】解：（1）抛物线的表达式为：y=−49（x+5）（x﹣1）=−49x2−169x+209，则点D（﹣2，4）；（2）设点P（m，−49m2−169m+209），则PE=−49m2−169m+209，PG＝2（﹣2﹣m）＝﹣4﹣2m，矩形PEFG的周长＝2（PE+PG）＝2（−49m2−169m+209−4﹣2m）=−89（m+174）2+252，∵−89＜0，故当m=−174时，矩形PEFG周长最大，此时，点P的横坐标为−17 4；（3）∵∠DMN＝∠DBA，∠BMD+∠BDM＝180°﹣∠ADB，∠NMA+∠DMB＝180°﹣∠DMN，∴∠NMA＝∠MDB，∴△BDM ∽△AMN ，AN BM =AM BD ，而AB ＝6，AD ＝BD ＝5，①当MN ＝DM 时，∴△BDM ≌△AMN ，即：AM ＝BD ＝5，则AN ＝MB ＝1； ②当NM ＝DN 时，则∠NDM ＝∠NMD ，∴△AMD ∽△ADB ，∴AD 2＝AB ×AM ，即：25＝6×AM ，则AM =256，而AN BM =AM BD ，即AN 6−256=2565，解得：AN =5536； ③当DN ＝DM 时，∵∠DNM ＞∠DAB ，而∠DAB ＝∠DMN ， ∴∠DNM ＞∠DMN ，∴DN ≠DM ；故AN ＝1或5536．。

函数中点的存在性问题(解析版)

难点7-双变量的“任意性”“存在性”问题

专题10 函数中点的存在性问题(解析版)

(完整版)二次函数与三角形的存在性问题的解法

一次函数综合—线段和差、存在性问题解析

二次函数与几何的动点及最值、存在性问题(解析版)-2024中考数学

函数恒成立存在性与有解问题

人教版九年级下册 反比例函数存在性问题解析版(综合复习)

一次函数中的(特殊图形)存在性问题(解析版)八年级数学上册同步考点归类培优题库

专题02 二次函数中的存在性问题之等腰三角形(19眉山)(解析版)

问题2.2 函数中存在性与恒成立问题-2016届高三数学跨越一本线(解析版)

二次函数中点的存在性问题

函数的存在性问题和零点问题

二次函数中等腰三角形点的存在性问题(共15张PPT)

反比例函数与特殊三角形存在性问题(解析版)(人教版) -九年级数学下册

点的存在性问题

专题22.9 二次函数中的存在性问题-重难点题型(举一反三)(人教版)(解析版)

导数系列——零点存在性问题

恒成立和存在性问题

中考数学第二轮专题复习第41课存在性问题、定值问题(含答案)

人教版九年级下册反比例函数存在性问题解析版(综合复习)