基于剑桥模型的砂土剪胀模型
H = dH =
d(
p v
)
= 0=
d R(
p v
)
=
M
4
M
4 p
( M 4-
4) (
M
4 p
-
4) d
p v
( 6)
2 砂土的本构模型
在推导过程中采用的平均应力
p=
1 3
(
1+
2+
3)
为有效平均应力, 剪应力为
q = 1 ( 1 - 2) 2 + ( 2 - 3) 2 + ( 3 - 1) 2. 2
p v
)
= 0,
其中: d
p v
为总塑性体应变增量;
(
d
p v
)
= 0为平均应
力引起的塑性体应变; 应力比 为偏应力与有效平
均应力之比; R ( ) 为应力路径修正函数.
构造应力路径修正函数为
R(
)=
(M4-
4)
(
M
4 p
-
M
4
M
4 p
4) =
d
p v
(d
p v
)
=0
( 5)
根据剪胀性岩土材料的特点, 平均应力只能引
界状态理论, 在已有的弹塑性模型基础上引入与相 变点相关的状态参量, 提出一个能够较好反应岩土 材料剪胀性的弹塑性本构模型.
1 状态参量及硬化参数的确定
1 1 砂土临界状态线 Roscoe 等人的试验研究表明, 重塑黏土的临界
状态线在 e lg p ( 孔隙比 有效应力) 平面上为直线, 然而对于砂土等无黏性土, 由于材料成分以及组构 与黏性土不同, 必然影响应力 应变曲线. 研究者早 就发现临界状态线在 e lg p 平面上并非直线[ 11 13] . L i 等人( 1998) 在对早期文献研究的基础上, 认为砂
性, 但却无法恰当的描述中密及密实砂土相变后的 剪胀特性[ 6 9] . 对于剪胀性材料, 其应力 应变曲线上 都会出现一个特征点, 即体积由剪缩向剪胀过渡的 点, 该点处体应变增量为零, 是土体变形过程中最密 实的状态, 即相变点[ 10] , 利用相变点能够反映密实 砂土初始阶段和以后的体变特性. 本文作者基于临
第1期
迟明杰等: 基于剑桥模型的砂土剪胀模型
51
起塑性体缩, 即( d
p v
)
=0
0. 相变时, 即 = M p 时,
d
p v
=
0,
R(
) = 0; 临界状态时, 即
=
M
时, d
p v
=
0, R (
)=
0; 各 向等 压 加 载 时 d
p v
=
(d
p v
)
= 0,
R ( ) = 1. 可得硬化参数
( 15)
1+ e0 pa
pa
可以看出弹性模量随平均压力而变化.
2 2 塑性变形
在相变状态时塑性体应变增量为零, 采用相变
状态时的能量耗散方程, 可得塑性势函数为
g=
q2 +
M
2 p
p
2-
M
2 p
pxp
=
0
( 16)
由式( 11) 和式( 16) 可得
p pa
1+
q2
M
2 p
p
2
=
1+ -
e0
p v
( 19)
由一致性条件得
df =
f p
dp
+
f q
d
q
+
f H
dH
=
f p
dp
+
f q
d
q
-
1 R(
)d
p v
=
f p
dp
+
f q
d
q
-
1 R( )
f p
=
0
( 20)
式中:
=
dp
+
M
2 p
2qp p 2-
q 2dq
R(
).
52
北京交通大学学报
第 32 卷
塑性应变增量与塑性势面正交, 并采用相关联
由式( 7) , p 0 p x 等向固结, 则体应变为
v=
e v
+
p v
=
1+
e0
px pa
-
p0 pa
( 9)
式中:
v,
e v
,
p v
分别为总体应变、弹性体应变分量、
塑性体应变分量.
由式( 8) , p x p 0 回弹, 则体应变为
e v
=
1+
e0
px pa
-
p0 pa
( 10)
由式( 9) 和式( 10) 可得
图 2 相变线与稳态线的关系[ 16]
F ig. 2 Relationship betw een PT L and CSL
由图 2 也可以看出, 砂土的临界状态线和相变 线 PT L 在对数坐标下已经不再是直线, 根据相变点 的特点建议相变线采用公式
p ep = e0- p p a
( 2)
式中: e0 为初始孔隙比; p 为参数. 对于剪胀性砂土存在一个临界剪胀围压 p min,
其中: 1, 2, 3 为 3 个主应力. 2 1 弹性体应变及弹性模量
由图 4, 设比体积 v = 1+ e. 对于砂土正常固结 线有
e= a-
p pa
( 7)
回弹线有
p e = b - pa
( 8)
式中: a, b , , , 均为材料参数; p 为固结围压.
图 4 砂土固结线与回弹线
Fig. 4 N CL and SL
当围压超过临界剪胀围压时, 砂土不再发生剪胀现 象[ 5] , 可认为此时 ep= ec, 由式( 1) 和式( 2) 得
图 3 相变线与临界状态线
Fig . 3 PT L and CSL
当初始孔隙比 e0< ec 时, ep < ec; 当 e0 ec 时, ep= ec. 可以看出, 在初始孔隙比由密实状态向临界状态
议采用如下的基本形式作为砂土的临界孔隙比计算 公式[ 14]
p ec = e - c pa
( 1)
式中: e , c, 为材料常数; p a 为单位大气压, 通常 取 101 kP a; p 表示有效平均应力. 1 2 砂土相变线
文献[ 15] 对丰浦砂( T oyoura sand) 的研究结果
表明, 初始围压一定, 相变孔隙比 ep 与相变有效平 均应力 p p 成线性关系, 见图 1.
则退化为原弹塑性模型. 模型包含 9 个材料参数, 参数比较容易确定. 数值模拟结果能较好的描述
砂土的主要特性.
关键词: 岩土工程; 砂土; 本构模型; 硬化参数; 相变线; 状态参量
中图分类号: T U 411 3
文献标志码: A
Dilatant Model of Sand Based on the Cam Clay Model
第 32 卷 第 1 期 2008 年 2 月
北京交通大学学 报 JOU RN AL O F BEIJIN G JIAOT O NG U N IV ERSI T Y
文章编号: 1673 0291( 2008) 01 0049 05
基于剑桥模型的砂土剪胀模型
V ol. 32 N o. 1 Feb. 2008
剪胀性是岩土材料的基本特性之一[ 1] . 英国剑 桥大学的 Roscoe 等人基于饱和正常固结土 和重塑 土试验[ 2] , 提出了 Cam clay 弹塑性模型[ 3] 和修正剑 桥模型[ 4 5] , 该模型是反映压硬性和剪缩性最简单、 物理意义最明确的弹塑性模型之一. 剑桥弹塑性模 型能够比较成功的描述正常固 结土的一些重 要特
迟明杰, 赵成刚
( 北京交通大学 土木建筑工程学院, 北京 100044)
摘 要: 对于中密砂和密砂, 剪胀现象是一个比较显著的特征, 相变线是描述剪胀现象的一条特征
线, 相变线比较容易确定. 本文在已有弹塑性模型基础上, 对硬化参数进行修正, 并引入与相变线相
关的状态参量, 建立了一个新的剪胀性砂土本构模型. 该模型尤其适合于中密砂和密砂, 对于松砂
关系, 见图 3. 鉴于以往的状态参数的定义形式, 这
里状态参量定义为
= e p - ec
( 3)
图 1 相变时孔隙比与有效应力的关系[ 15] F ig. 1 Relationship betw een e and p p
Verdugo 对丰浦砂的研究结果表明[ 16] , 对于初 始孔隙比相同的砂土, 施加初始有效围压越大, 相变 点的有效平均压力就越大, 相变点就越逼近稳态线 CSL( 最终破坏线或临界状态线) , 见图 2.
1, ( i = j ) .
0, ( i j )
由式( 12) 可得弹性体应变增量为
d
e v
=
d
e 1
1
+
d
e 22
+
d
e 33
=
3( 1 - 2 E
) dp ( 13)
式( 10) 两边微分得
d
e v
=
1+
e0
p pa
-
1
1 pa
d
p
( 14)
由式( 13) 和式( 14) 得到弹性模量
E=
3( 1 - 2 ) p -1 1
+
p0 pa
21743341
ｊ ７
（） １
式中： 叩＝ｑｐ ， ／ ｇ为剪切 应力 ， Ｐ为有 效体 积 应力 ； 为 临界 状态 应力 比。 Ｍ
收稿 日期 ：０ ５０ ． ２０ ． １ ６０
基金项 目ｔ 国家 自 然科学基金资助项 目（ ４９５ ） ５ ７０ ７ ０ 作者简介 ： 寨理曼 （ ７ 一） 女， １ ７ ， 河南三门峡人 ， 士生 ， 从事本构关系模 型研究 。Ｅ ｍ ｉ ｑ ｌ ａ ＠１ ． ｍ ９ 博 主要 － ａ ：ｉ ｉ ｎ ６ ｔ ｌ ｎ ｍ ３ ｏ
－ － — —
４ ０３ －— － —
维普资讯
这 三种 剪胀 函 数具有 一定 的相似 性 ， 都是 在 刁和 ｄ＝ｄ ｄ ： 间定义 一 个 唯一 的关 系式 。 实践 证 ｅ／ｅ 之 明 ， 种形式 的剪胀 仅适 用于 模 拟重 塑黏 土及 松 砂等 硬化 型 土体 的变 形 。 这 在 相 同的 孙 相 同 的剪 切 荷载 增 量作 用 下 ， 砂 和 密砂 在 ｇ—Ｐ空 间 的不 排 水 应 力路 径 明 显 不 同 ， 松 如 图 １ 示 。如果 ｄ是 与 刁唯一 相关 的 函数 ， 无论 是松 砂还 是 密砂 ， 所 则 塑性 流 动方 向 和不排 水应 力 路径 的方 向将 由 刁唯 一确定 ， 种假 定 明显 和上 述 的试 验结果 相 矛盾 。 这 为了分别 描述 松 砂 和密砂 的 不 同剪 切 特 性 ， 首先 需 要 选 择 一 个 量 ， 松 砂 和 密 砂 的分 类 作 适 当判 对
经典 的 临界状 态模 型在模 拟 砂土 的受 剪特 性 时有 一定 的 局 在 剪缩 、 密砂 剪胀 ， 排水 条件 下松 砂 和密砂 的有 效 应力 路径 也 不 相 同 。在 三轴 应 力 条 件 下 ， 胀 定 义 为 不 剪 塑 性剪切 应 变增量 与 塑性体 积应 变增 量之 比 （ ＝ ｄ ： ｅ ） 剪 胀 函数 与砂 土 的应 力 、 变及 强 度 特 性 ｄ ￡／ 。 ｄ 应 密切 相关 。Ｔ ｙ ｒ 早研 究 了剪胀 问题 ， ａｌ 最 ｏ 随后 Ｒ ｗ 提 出 了一 种 剪 胀 关 系 ， 后 来 建 立 的 砂 土 本 构 模 型 ｏｅ 在
剑桥模型
1.剑桥模型（Cam-clay Model ）剑桥模型是由英国剑桥大学Roscoe 等于1963年提出的，这个模型基于正常固结土和超固结土试样的排水和不排水三轴实验基础上，提出了土体临界状态的概念，并在实验基础上，再引入加工硬化原理和能量方程，提出剑桥模型。
这个模型从试验和理论上较好的阐明了土体弹塑性变形特征，尤其考虑了土的塑性体积变形，因而一般认为，剑桥模型的问世，标志着土本构理论发展的新阶段的开始。
（1） 剑桥模型。
剑桥模型基于传统塑性位势理论，采用单屈服面和关联流动法则屈服面形式也不是基于大量的实验而提出的假设，而是依据能量理论提出的。
依据能量方程，外力做功dW 一部分转化为弹性能e dW ，另一部分转化为耗散能（或称塑性能）p dW ,因而有dW =e dW +p dW（1-154） e dW =e eV qd d p γε+' （1-155）p pV p qd d p dW γε+'= （1-156）剑桥模型中，由各向等压固结实验中回弹曲线确定弹性体积变形p p d e k d eV ''+=1ε （1-157）式中，k 为膨胀指数，即 p In e '-回弹曲线的斜率。
同时，假设弹性剪切变形为零，即0=e d γ （1-158）则弹性能 p d ekp p d k dW e '+=''=1υ （1-159）剑桥模型中还建立如下的能量方程，即塑性能等于由于摩擦产生的能量耗散，则有 p p p V d p qd d p γνγε'=+'- （1-160）式中第一项改用负号，是因为p V d ε取以压为正。
代入式（1-161）⎪⎭⎪⎬⎫==ij pij p d s d d λεεθθσ （1-161） 并考虑式（1-158），则有γγγνd p M d p M d p dW p p p '='='= （1-162） 式中，M 为q p '-'平面上的破坏线的斜率，即ϕϕ'-'=sin 3sin 6M （1-163） 式中ϕ'为土体有效摩擦角。
土的剑桥模型发展综述
土的剑桥模型发展综述----97dbe56c-6ead-11ec-b680-7cb59b590d7d土体本构理论是岩土工程学科的重要基础理论。
随着对土体力学特性的不断深入,塑性理论逐渐被应用于土体本构关系的研究中来。
roscoe[1]于1963年提出著名的剑桥粘土模型,是应用塑性理论的代表,被看做现代土力学的开端。
在本构理论的研究和发展过程中，各种建模思想层出不穷，各种形式的土体本构模型层出不穷，但唯一公认的弹塑性模型是剑桥模型。
目前，国际岩土本构法的一个主要发展趋势是回归剑桥模型，并在剑桥模型的基础上对其进行改进和修正。
本文简要介绍了剑桥模式，并对剑桥模式的发展进行了系统评述。
1.关于剑桥模型及修正剑桥模型1958年至1963年，英国剑桥大学的Roscoe等人[1]在正常固结粘土和弱超固结粘土三轴试验的基础上，提出了剑桥粘土的本构模型，标志着人们对土壤力学性质的理解出现了第一次飞跃。
他们系统地将“帽”屈服准则、正交流动准则和加工硬化定律应用于cam模型，提出了临界状态线、状态边界界面和弹性壁等一系列物理概念，形成了第一个相对完整的土塑性模型。
Roscoc和Burland[2]进一步修正了剑桥模型，认为剑桥模型的屈服面轨迹应为椭圆，并给出了著名的修正剑桥模型。
可以说，剑桥模型开创了土壤力学的临界状态理论。
试验证明,对于正常固结粘土和弱固结的饱和重塑粘土,孔隙比e与外力p,q之间存在有唯一的关系,且不随应力路径而发生变化。
该模型本文试图描述在实验室试验中观察到的现象，即从初始状态加载到保持塑性恒定体积变形的临界状态。
其基本组成如下：(1)在(e,p)平面中,存在一条曲线,在正常固结粘性土中的所有应力遵循此路径,这被称为正常固结线(ncl)。
这条线提供了体积硬化规则,可以被广义化为一般应力条件。
（2）（E，P，q）空间中有一条直线，所有剩余态都遵循这条路径，这与实验类别和初始条件无关。
这条线平行于（E，P）平面上的正常固结线，在该平面上发生剪切变形而不发生体积变形。
土的弹塑性模型
土的弹塑性模型近年来，根据弹塑性理论建立的土的弹塑性模型发展很快，各国学者提出的弹塑性本构模型很多。
下面几节分别介绍剑桥模型，修正剑桥模型，Lade-Duncan 模型，以及清华模型的基本概念。
一．剑桥模型英国剑桥大学Roscoc 和他的同事（1958 ~ 1963 ）在正常固结粘土和超固结粘土试样的排水和不排水三轴试验的基础上，发展了Rendulic （1937）提出的饱和粘土有效应力和孔隙比成唯一关系的概念，提出完全状态边界面的思想。
他们假定土体是加工硬化材料，服从相关联流动规则，根据能量方程，建立剑桥模型。
剑桥模型从理论上阐明了土体弹塑性的变形特性，标志着土的本构理论发展新阶段的开始。
1.临界状态线和Roscoe 面各向等压固结过程中，孔隙比e 或比容()1e υυ=+与有效应力的关系可用下式表示： ln N p υλ'=- （1） 式中 N —— 当 1.0p '=时的比容。
因此exp N p υλ-⎛⎫'= ⎪⎝⎭（2）（a ）,p q ''平面（b ）,ln p υ'平面图1 临界状态线正常固结粘土排水和不排水三轴试验表明：它们有条共同的破坏轨迹，与排水条件无关。
破坏轨迹在,p q ''平面上是一条过原点的直线，在,ln p υ'平面上也是直线，目与正常固结线平行，分别如图（a ）和（b 〕 所示。
破坏轨迹线可用下式表示：cs csq Mp '= （3）ln cs csp υλ'=Γ- （4） 式中 CS ——表示临界状态；M——,p q''平面上临界状态线斜率；Γ—— 1.0p'=时土体的比容；csυ'平面上临界状态线斜率。
λ——,ln p一旦土体的应力路径到达这条线，土体就会发生塑性流动。
这时土体被认为处于临界状态，破坏轨迹被称为临界状态线。
临界状态线在,,''空间为一条空间曲线，如下图2所示。
基于剑桥模型的砂土剪胀模型
关键词： 岩土工程 ； 土； 砂 本构模型； 硬化参数 ； 变线； 态参量 相 状 中 图分类 号 ： Ｕ １ ． Ｔ ４ １３ 文献标 志 码 ： Ａ
Ｄｉａ ａ ｔ Ｍ ｏ ｅ ｆＳ ｎ ｓ ｄ ｏ ｈｅ Ｃａ － ａ ｏ ｅ ｌｔ ｎ ｄ ｌｏ ａ ｄ Ｂａ ｅ ｎ ｔ ｍ Ｃｌ ｙ Ｍ ｄ ｌ Ｃ ｎｊｅ Ｈ ｈ ｎ ｇ ｎ ＨＩＭｉｇ ｉ；Ｚ Ａ０ Ｃ ｅｇ ａ ｇ
界状态 理论 ， 已有 的 弹 塑性 模 型 基 础 上 引入 与相 在 变点相 关 的状态 参 量 ， 出一 个 能 够 较 好 反应 岩土 提
材料 剪胀 性 的弹 塑性本 构模 型 ．
桥模 型［５， ４ 该模 型是 反 映 压 硬性 和剪 缩 性 最 简 单 、 － Ｊ
物理意 义最 明确 的弹 塑性 模 型之 一 ． 桥 弹 塑性 模 剑
关 的状 态参量 ， 立 了一个新 的 剪胀性 砂 土本 构模 型 ． 建 该模 型 尤其 适合 于 中密砂 和 密砂 ， 于松 砂 对
则退 化 为原 弹塑性模 型 ． 型 包含 ９个材料 参数 ， 模 参数 比较 容 易确 定 ． 值 模 拟 结 果 能较 好 的描 述 数
砂 土的主要 特 性 ．
（ｃ ｏｌ ｆ ｉｌ ｎ ｉｅｒ ｇａ ｄＡｃ ｉｃｕｅ Ｂｉｎ ａｔｎ ｎｖｒ ｔ， ｅｉｇ１０ ４ ， ｈｎ ） Ｓｈ ｏ ｏ ｖ ｇ ｅｉ ｎ ｒ ｔ ｔｒ， ｅ ｉｇＪ ｏｏ ｇＵ ｉ ｓｙ Ｂ ｉｎ ０ ０ ４ Ｃ ｉ Ｃ ｉＥ ｎ ｎ ｈｅ ． ｊ ｉ ｅｉ ｊ ａ
ｈ ｖｏ ｓｏ ｄｉ ａ ｉｒ ｆｍｅ ｕｍ ｅ ｓ ａ ｄ ａ ｅ ｅ ｓ ｎ ａ ｅ ｂ ｅ ｒ ｃｓ ｌ ｅ ｅ ｅ ｅ ｄ ｎ ｅ ｓ ｎ ｎｄ ｄ ｎｓ ａ ｄ ｈ ｖ ｅ ｎ ｐ ｅ ｉｅｙ ｒ ｐｒ ｓ ｎｔｄ． Ｋｅ ｒ ｓ： ｅ ｔ ｃ ｉａ ｎｇ ｎ ｅ ｉ ｙ ｗｏ ｄ ｇ ｏ ｅ ｈｎ ｃ ｅ ｉ ｅ ｒｎｇ；ｓ ｎ ｌ ａ ｄ；ｃ ｎｓｉｕｔｖ ｄｅ ；ｈａ ｄ ｎ ｎｇ ｐ ｒ ｍｅ ｅ ；ｐ ａ ｅ ｔａ ｉｉ ｎ ｏ ｔｔ ｉ ｅ ｍｏ ｌ ｒ ｅ ｉ ａ ａ ｔ ｒ ｈ ｓ ｒ ｎｓｔｏ
基于ABAQUS二次开发状态相关砂土本构模型的研究
基于ABAQUS二次开发状态相关砂土本构模型的研究司海宝;杨为民;黄伟【摘要】剪胀性是砂土最重要的特性之一,其变形主要取决砂土的当前状态,而基于状态相关砂土本构模型能较好反映砂土剪胀性.ABAQUS作为有限元计算平台,具有强大的非线性计算和前后处理功能,标准ABAQUS程序仅包含一些通用土体本构模型,缺少状态相关砂土本构模型,因而有必要针对土木工程具体问题进行二次开发.利用二次开发工具和UMAT数据接口程序,采用隐式积分算法将基于状态相关砂土本构模型嵌入到标准ABAQUS程序中,并将有限元数值计算结果与实验数据及理论计算值比较,进行单元敏感性分析.计算结果表明子程序运行稳定可靠,不仅充分利用ABAQUS方便、快捷的前后处理和强大的非线性求解平台,还可以完成更复杂,且切合实际土体应力应变关系的有限元数值计算,拓展ABAQUS在土木工程领域应用能力.【期刊名称】《安徽工业大学学报（自然科学版）》【年(卷),期】2013(030)003【总页数】7页(P301-307)【关键词】状态相关砂土模型;ABAQUS;隐式积分算法;二次开发【作者】司海宝;杨为民;黄伟【作者单位】安徽工业大学建筑工程学院,安徽马鞍山 243032;港口航道重点实验室南京水利科学研究院,江苏南京 210045;中国地质科学院地质力学研究所,北京100081;安徽工业大学建筑工程学院,安徽马鞍山 243032【正文语种】中文【中图分类】TU476剪胀性是砂土最重要的特性之一，砂土在剪切条件下除了发生剪切变形外，还会产生体积变形，砂土的体积变形可能是膨胀，也可能是压缩，主要取决于砂土的当前状态[1]。
Li和Dafalias在三轴压缩空间内建立弹塑性本构模型，进一步拓展了状态相关剪胀理论，较好模拟了砂土在各种状态下变形特征[2-3]。
ABAQUS是目前土木工程中应用较为广泛的非线性有限元分析软件，具有很强的非线性计算功能和前、后处理能力，同时其强大的二次开发功能使得其在工程领域具有良好的开放性。
岩土塑性力学剑桥模型
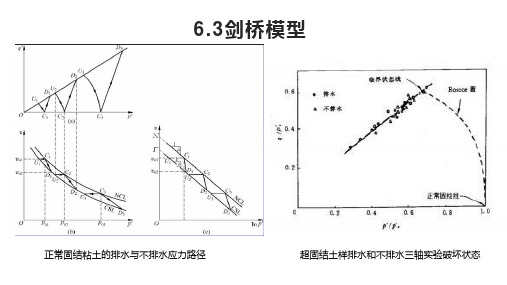
图 6 - 1 6 表 示 土 样 在 单 剪 时 的 变 形 情 况 。 土 样 高 为 H ， 水 平 截 面 积 为 A . 剪 切 变 形 后 ， 水 平 位 移 为 d u ， 竖 向 位 移 为 d v， 如 图 6 - 1 6
中 所 示 。 在 剪 切 变 形 过 程 中 ， 正 应 力 ’ 和 剪 应 力 所 做 的 功 等 于 - ’ 。假 设 由 于 摩 擦 所 产 生 的 能 量 消 耗 与 摩 擦 系
间中。正常固结土应力路径都在Roscoe面上，超固结状态用位于该面下面的点表示，在该面以上是不可能有点来表示
应力状态的。Roscoe面成为一个边界，在该面的面上或以下是可能的状态，在该面以上是不可能的状态， Roscoe面
称为状态边界面。超固结上样的应力路径在土样破坏时到达Hvorslev面，在土样破坏后应变增大时趋向临界状态。
有关，为了适用更一般的情况，采用等效的符号改写式6.3.17，得
(6.3.18)
式中负号是由于一 代表膨胀引起，这也是剑桥模型的假设之一 。
将 式 6 . 3 . 1 8 代 入 式 6 . 3 . 1 2 ， 并 考 虑 = 0 ， 得
(6.3.19)
结 合 式 6 . 3 . 9 ， 式 6 . 3 .1 0 ， 式 6 . 3 . 1 5 和 式 6 . 3 . 1 9 ， 得 到 能 量 方 程
6.3剑桥模型
正常固结粘土的排水与不排水应力路径
超固结土样排水和不排水三轴实验破坏状态
各向等压加 载 与卸 载 试 验
超固结比对不 排 水 应 力路 径 的 影 响
6.3.3 完全的状态边界面
在p'，q，v空间中，正常固结和超固结土样的应力路径不能超过 Roscoe面和Hvorslev面，处在这两个面包围的空
10分钟认识剑桥模型
10分钟认识剑桥模型王川第一节：认识“临界状态”首先，大家一定接受以下两张图（无数实验已经证明过）：图1 摩尔库伦强度理论图2 土的压实曲线（e为孔隙比，p’为有效应力）那么，如果把τ换成偏应力q（其中q=σ1-σ3），把σ换成平均主应力p（其中p=(σ1+2σ3)/3，p’表示其有效应力），就得到三轴实验中的p-q曲线：图3 p-q曲线土样的体积由固体颗粒和空隙组成，由于固体颗粒不可压缩，故土样体积的变化完全取决于空隙的变化，即土样体积v和孔隙率e描述的物理意义等价。
那么，将图2中e替换为v，就得到v-logp曲线：图4 v-logp曲线与图1和图2一样，图3和图4同样经历了无数实验的验证，属于“事实”。
基于图3和图4的定量分析以及实验观察，可以得出一个结论，这个结论就是临界状态（critical state）：无论土样的初始状态和经历的应力路径如何，在剪切的最终阶段，只有剪应变在持续增加，而土样所受的有效应力和体积趋于不变。
临界状态由图3和图4同时确定，因此图3和图4中的曲线也叫临界状态线CSL （Critical State Line）。
将临界状态现象翻译成数学语言：（1）体积不变对应于，为p’引起的体积的改变；（2）剪应变在变对应于，为q引起的剪应变；（3）有效应力不变等价于q与p’的比值为常量。
若令在一般情况下，有（被叫做应力比），则可以定义临界状态下的应力比：（被叫做临界状态应力比）。
从图3中能看出，M为常量，即“有效应力不变”。
◆第二节：剑桥模型假设（1）所有的剪应变都不可恢复，即（为弹性剪应变），（为塑性剪应变）。
（2）假定塑性变性能增量可表示为：（这一假设看不懂没关系，继续往后看）。
（3）相关联流动法则：（与塑性力学中关联流动一致）。
◆第三节：剑桥模型推导从能量角度推导屈服函数：应变能的增量等于主应力p’和偏应力q所做的功，即（式1）因为：（此处用了假设1）所以：（式2）（此处用了假设2）由式1和式2得：（式3）根据（假设1），整理式3得：d为剪胀系数，表示塑性应变的方向（因为d体现了与的相对大小，与塑性力学中流动法则表达得意义一致）；为剪胀方程。
第12讲part1 Camclay(Cam-clay model剑桥模型)
Original (1963)(原始) Modified (1968)(修正)
Theory of plasticity
1 e0
ln
px p0
C D
p3 ln p
e v
1 e0
ln
px p0
p v
v
e v
1 e0
ln
px p0
ln
px
1 e0
p v
ln
p0
lnp
gure 2.8 Results of isotropic compression and swelling tests
ln
px
1 e0
b) Determinations of the plastic potential and yield function
Plastic potential defines direction of plastic strain increment. Yield function specifies whether plastic strain increments occur when subjected to a new loading increment
q
f=0
0
p0
px p
Figure 2.9 The meaning of yield locus in Cam-clay model
应变确定 dij diej dipj e e0
Elastic strain
第八章 本构-修正剑桥模型
7.5.1 Elastic properties
常用对数
自然对数
The elastic stiffness is nonlinear and depends on the current stress level.
剑桥模型
7.5.2 Yield criterion
Cam Clay Model Modified Cam Clay Model
(i) Influence of intermediate principal stress on deformation and strength (1)
Stress ratio – strain increment ratio relation Direction of strain increments on octahedral plane
(i) Influence of intermediate principal stress (ii) Stress path dependency of plastic flow (iii) Positive dilatancy during strain hardening (iv) Anisotropy and non-coaxiality (v) Behavior under cyclic loading (vi) Influence of density and confining pressure (vii) Structured soil (viii) Time effect and age effect
' po
pf
qf
M
破坏时
1 p / p 2
' f ' 0
1 k
f