流体动力学基础
合集下载
热工流体动力学基础
精品课件
【例】 如图所示，水泵汲入 管的外径为114mm，壁厚为4mm， 压出管的外径为88.5mm，壁厚 为4mm。在汲入管中水的流速 为1.5m/s。求在压出管中水的
流速。
【解】 已知，汲入管的内经D1=114-2×4=106mm，w1=1.5m/s，
D2=88.5-2×4=80.5mm，设在汲入管与压出管之间没有渗漏，
z1pg1 w 2g 12 z2pg2 w 2g22
伯努力方程
不可压缩的理想液体在等温流动过程中， 在管道的任一截面上，流体的静压能、 位能及动能之和是不变的。 三者之间可以相互转化
精品课件
(2)实际情况下的伯努力方程 实际流体有粘性，流动过程中有能量损失，能量方程：
z 1g p 1 1 21 2 z 2g p 2 1 2 2 2h L
输入机械能 H e15 (0 10)5 1 2 01 0 .24 (2 7.3 025 3.1 62 7 )50 11.9 7(P 1 7)3 a
精品课件
2.压头间的转换 （1）几何压头和静压头之间的转变
1-1和2-2的伯努力方程:
hg1hs1hg2hs2
因为 hg2(在下)＞hg1(在上)
则 hs2＜hs1
【解】 1000℃时烟气的密度为： 0(pp0)(T T1 0)
1.399994102 2730.27(k4g/m3) 1013225731000
1000℃时烟气的粘度为：
02T7C 3C2T7332
1.587105(1227 7311377)331 (2277 )32 334.9105(Pas)
精品课件
吸风管内风速
w 1 3 V F 6 1 3 0 4 V 6 0 d 1 2 0 30 4 6 3 9 .1 0 2 0 4 .3 0 2 0 3 .1 0 6 ( m 7 /s ) w 2 3 V F 6 2 3 0 4 V 6 0 d 2 2 0 30 4 6 3 9 .1 0 0 2 4 .4 0 2 0 2 .3 0 0 ( m 5 /s )
【例】 如图所示，水泵汲入 管的外径为114mm，壁厚为4mm， 压出管的外径为88.5mm，壁厚 为4mm。在汲入管中水的流速 为1.5m/s。求在压出管中水的
流速。
【解】 已知，汲入管的内经D1=114-2×4=106mm，w1=1.5m/s，
D2=88.5-2×4=80.5mm，设在汲入管与压出管之间没有渗漏，
z1pg1 w 2g 12 z2pg2 w 2g22
伯努力方程
不可压缩的理想液体在等温流动过程中， 在管道的任一截面上，流体的静压能、 位能及动能之和是不变的。 三者之间可以相互转化
精品课件
(2)实际情况下的伯努力方程 实际流体有粘性，流动过程中有能量损失，能量方程：
z 1g p 1 1 21 2 z 2g p 2 1 2 2 2h L
输入机械能 H e15 (0 10)5 1 2 01 0 .24 (2 7.3 025 3.1 62 7 )50 11.9 7(P 1 7)3 a
精品课件
2.压头间的转换 （1）几何压头和静压头之间的转变
1-1和2-2的伯努力方程:
hg1hs1hg2hs2
因为 hg2(在下)＞hg1(在上)
则 hs2＜hs1
【解】 1000℃时烟气的密度为： 0(pp0)(T T1 0)
1.399994102 2730.27(k4g/m3) 1013225731000
1000℃时烟气的粘度为：
02T7C 3C2T7332
1.587105(1227 7311377)331 (2277 )32 334.9105(Pas)
精品课件
吸风管内风速
w 1 3 V F 6 1 3 0 4 V 6 0 d 1 2 0 30 4 6 3 9 .1 0 2 0 4 .3 0 2 0 3 .1 0 6 ( m 7 /s ) w 2 3 V F 6 2 3 0 4 V 6 0 d 2 2 0 30 4 6 3 9 .1 0 0 2 4 .4 0 2 0 2 .3 0 0 ( m 5 /s )
4工程流体力学 第四章流体动力学基础
因为 F 沿 y 轴正向，所以 Fy 取正值
Fy F V•n dS = -V0 dS
= =
=
ρ vV n dS ρ vV n dS ρ vV n dS ρ vV n dS
CS
S0
S1
S2
v = -V0 sin
0
0
§4-2 对控制体的流体力学积分方程（续18）
由于V1，V2在y方向上无分量，
忽略粘性摩擦力，控制体所受表面力包括两
端面及流管侧表面所受的压力，沿流线方向总压
力为：
FSl
pS p δpS δS
p
δp 2
δS
Sδ p 1 δpδS 2
流管侧表面所受压力在流 线方向分量，平均压强
§4-2 对控制体的流体力学积分方程（续27z）
控制体所受质量力只有重力，沿流线方向分
Q2
Q0 2
1 cosθ
注意：同一个问题，控制体可以有不同的取法，
合理恰当的选取控制体可以简化解题过程。
§4-2 对控制体的流体力学积分方程（续23）
微元控制体的连续 方程和动量方程
从流场中取一段长度为l 的流管元，因
为流管侧面由流线组成，因此无流体穿过；流 体只能从流管一端流入，从另一端流出。
CS
定义在系统上 的变量N对时 间的变化率
定义在固定控制 体上的变量N对 时间的变化率
N变量流出控制 体的净流率
——雷诺输运定理的数学表达式，它提供了对
于系统的物质导数和定义在控制体上的物理量
变化之间的联系。
§4-2 对控制体的流体力学积分方程 一、连续方程
在流场内取一系统其体积为 ，则系统内
的流体质量为：
根据物质导数的定义，有：
Fy F V•n dS = -V0 dS
= =
=
ρ vV n dS ρ vV n dS ρ vV n dS ρ vV n dS
CS
S0
S1
S2
v = -V0 sin
0
0
§4-2 对控制体的流体力学积分方程（续18）
由于V1，V2在y方向上无分量，
忽略粘性摩擦力，控制体所受表面力包括两
端面及流管侧表面所受的压力，沿流线方向总压
力为：
FSl
pS p δpS δS
p
δp 2
δS
Sδ p 1 δpδS 2
流管侧表面所受压力在流 线方向分量，平均压强
§4-2 对控制体的流体力学积分方程（续27z）
控制体所受质量力只有重力，沿流线方向分
Q2
Q0 2
1 cosθ
注意：同一个问题，控制体可以有不同的取法，
合理恰当的选取控制体可以简化解题过程。
§4-2 对控制体的流体力学积分方程（续23）
微元控制体的连续 方程和动量方程
从流场中取一段长度为l 的流管元，因
为流管侧面由流线组成，因此无流体穿过；流 体只能从流管一端流入，从另一端流出。
CS
定义在系统上 的变量N对时 间的变化率
定义在固定控制 体上的变量N对 时间的变化率
N变量流出控制 体的净流率
——雷诺输运定理的数学表达式，它提供了对
于系统的物质导数和定义在控制体上的物理量
变化之间的联系。
§4-2 对控制体的流体力学积分方程 一、连续方程
在流场内取一系统其体积为 ，则系统内
的流体质量为：
根据物质导数的定义，有：
流体动力学基础
流体动力学基础流体动力学是研究流体的运动规律和性质的科学，它是流体力学的分支之一，广泛应用于航空、航天、水力、能源等领域。
本文将介绍流体动力学的基础概念、基本方程以及常用方法。
一、流体动力学的基本概念1. 流体力学与流体静力学的区别流体力学研究流体在运动中的行为，包括流体的流动速度、压力、密度等参数的分布规律；而流体静力学则研究流体在静止状态下的平衡规律，主要关注流体的静压力和浮力等性质。
2. 流体的本构关系流体的本构关系描述了流体的应力与变形速率之间的关系。
常见的本构关系有牛顿黏性流体、非牛顿流体以及理想流体等。
3. 流体的运动描述流体的运动可以通过流体速度场来描述，流体速度场是空间中的矢量函数，它描述了流体的速度分布。
流体速度场的描述可以使用欧拉描述方法或者拉格朗日描述方法。
二、流体动力学的基本方程1. 连续性方程连续性方程描述了质量守恒的原理，即单位时间内通过某一截面的质量是恒定的。
对于稳定流动的不可压缩流体来说，连续性方程可表示为流体密度与速度之积在空间中的量级是恒定的。
2. 动量方程动量方程是描述质点运动定律的基本方程，对流体来说，动量方程体现了运动流体的动力学行为。
对于稳定流动的不可压缩流体来说，动量方程可表示为流体的密度乘以速度与压力梯度的叠加等于外力的结果。
3. 能量方程能量方程描述了热力学系统的能量守恒原则，对于流体来说，能量方程考虑了流体的流动对能量转移的影响，以及热源、做功所导致的能量变化。
三、流体动力学的常用方法1. 数值模拟方法数值模拟是流体动力学研究的重要工具，通过在计算机上建立流体动力学方程的数值解，可以模拟复杂流动现象，如湍流、多相流等。
2. 实验方法实验方法是流体动力学研究的另一重要手段，通过搭建实验平台，测量流体的压力、速度等参数，从而验证理论和数值模拟结果的准确性。
3. 理论分析方法理论分析方法是流体动力学研究中的基础，通过建立假设和推导数学表达式，可以得到流体动力学问题的解析解，为实验和数值模拟提供参考。
流体动力学基础
四. 流管和流束
流管——在流场中作一不是流线的封闭周线C，过该周线上 的所有流线组成的管状表面。 流体不能穿过流管，流管就像真正的管子一样将其内外的流 体分开。 稳定流动中，流管的形状和位置不随时间发生变化。
流束——充满流管的一束流体。 微元流束——截面积无穷小的流束。微元流束的极限是 流线。 微元流束和流线的差别： 流束是一个物理概念，涉及流速、压强、动量、能量、 流量等等； 流线是一个数学概念，只是某一瞬时流场中的一条光滑 曲线。
三、.迹线与流线
1.迹线 流体质点在空间运动时描绘的轨迹。它给 出了同一流体质点在不同时刻的空间位置。 2.流线 指某一瞬时流场中一组假想的曲线，曲线 上每一点的切线都与速度矢量相重合。
流线的几个性质：
在稳定流动中，流线不随时间改变其位置和形状，流线 和迹线重合。在非稳定流动中，由于各空间点上速度随时间 变化，流线的形状和位置是在不停地变化的。 流线不能彼此相交和折转，只能平滑过渡。 流线密集的地方流体流动的速度大，流线稀疏的地方流动 速度小。
管径的估算
一般化工管道为圆形，若以d表示管道的内 径，则式 u = V s 可写成
A
u =
Vs d
2
d=
4
4Vs u
此式是设计管道或塔器直径的基本公式。
例 : 某厂要求安装一根输水量为 45m3/h 的管道， 取自来水在管内的流速为 1.5m/s, 试选择一合 适的管子。 解： 4Vs 4 45/ 3600 d= = = 0.103m = 103mm u 3.141.5 算出的管径往往不能和管子规格中所列的 标准管径相符，此时可在规格中选用和计算直 径相近的标准管子。
参考教材附录二十三，本题用 Ø114×4mm 热轧无 缝钢管合适。其管子外径为114mm，壁厚为4mm， 管径确定后，还应重新核定流速。 水在管中的实际流速为
流体动力学基础(医学课件)
结果分析与解读方法
结果分析方法
根据实验目的和数据特点，选择 合适的结果分析方法，如统计分 析、流场可视化、量纲分析等。
结果解读
理解实验结果所反映的流体动力 学现象和规律，如流动特性、阻 力特性、流场分布等，为医学研
究提供理论依据和指导。
结果应用
将实验结果应用于医学领域，如 疾病诊断、药物研发、医疗器械 设计等，推动医学技术的进步和
肺部微循环流体力学
肺部微循环流体力学问题主要涉及肺毛细血管、肺泡等微观结构的血 流动力学特性，对肺功能和疾病发生发展有重要影响。
其他相关临床问题
药物输送流体力学
药物输送过程中的流体力学问题，如 药物颗粒在血液中的流动和分布特性 ，对药物疗效和副作用有重要影响。
生物材料流体力学
生物材料在临床应用中的流体力学问 题，如人工器官、血管替代物等的血 流动力学特性，对移植手术的成功率 和患者康复有关键作用。
泌尿系统流体动力学
尿液流动特性
研究尿液在泌尿系统内的流动特性，包括流动速度、流量等现象 及其对泌尿系统功能的影响。
尿道阻力与排尿过程
分析尿道阻力、排尿过程及其与膀胱收缩力、括约肌张力等的关系 ，揭示排尿过程的调控机制。
尿流动力学指标
介绍尿流动力学指标如尿流速度、尿量等在泌尿系统疾病诊断与治 疗中的应用价值。
呼吸系统流体动力学
空气流动特性
气流速度与压力
研究空气在呼吸道内的流动特性，包 括层流、湍流等现象及其对呼吸过程 的影响。
探讨气流速度、压力及其在呼吸系统 疾病如慢性阻塞性肺疾病等的发生发 展中的作用。
呼吸道阻力与通气量
分析呼吸道阻力、通气量及其与呼吸 频率、潮气量等的关系，揭示呼吸过 程的调控机制。
1.3、流体动力学
热加工炉工作系统示意简图
物料
预
热
装
燃料
置
热加工炉
烟 囱
管 路
送风机
排风机
1
§1.3、流体动力学基础
质
量
守
三
恒
大 守
能 量
恒
守
定
恒
律
动
量
守
恒
连
流体运动
续
微分方程组
性
方 程
恒
定
如何应用连续
能 量 方 程
总 方程、能量方程、
流
三 大
动量方程求解流 体动力学问题
动
方
量 方
程 定解条件
程
2
§1.3、流体动力学基础
动能增量ΔE：
E E22 E11
dQdt
g
u22 2
u12 2
dA1
dQdt
u22 2g
u12 2g
(3)
上三式代入功能原理：
p1 Z1
dA2 p2 Z2
WP WG E22 E11
0
dQdt Z1
Z2
p1
p2 dQdt
dQdt
u22 2g
u12 2g
0
28
各项除以γdQdt，按断面分别列于等式两端得：
（2）按欧拉自变量（即描述流动所需的空间坐标数目）分类 一元流动：只有一个坐标自变量 B(x,τ) 二元流动：有两个坐标自变量 B(x,y,τ) 三元流动：三个坐标自变量 B(x,y,z,τ)
11
3、流体流动是如何分类的？
（３）按运动要素是否随时间变化 稳定流动（恒定流）：欧拉法所描述的流场中每一空间点上的所有 运动参数均不随时间变化的流动。 非稳定流动（非恒定流）：欧拉法所描述的流场规律与时间有关的 流动。
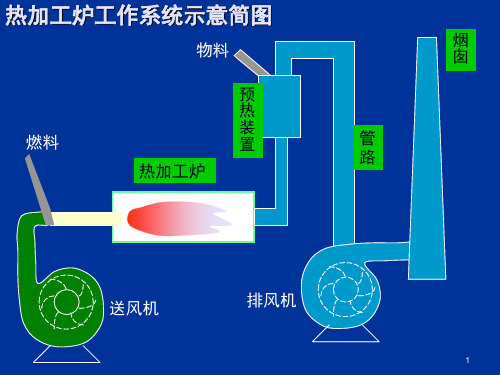
物料
预
热
装
燃料
置
热加工炉
烟 囱
管 路
送风机
排风机
1
§1.3、流体动力学基础
质
量
守
三
恒
大 守
能 量
恒
守
定
恒
律
动
量
守
恒
连
流体运动
续
微分方程组
性
方 程
恒
定
如何应用连续
能 量 方 程
总 方程、能量方程、
流
三 大
动量方程求解流 体动力学问题
动
方
量 方
程 定解条件
程
2
§1.3、流体动力学基础
动能增量ΔE：
E E22 E11
dQdt
g
u22 2
u12 2
dA1
dQdt
u22 2g
u12 2g
(3)
上三式代入功能原理：
p1 Z1
dA2 p2 Z2
WP WG E22 E11
0
dQdt Z1
Z2
p1
p2 dQdt
dQdt
u22 2g
u12 2g
0
28
各项除以γdQdt，按断面分别列于等式两端得：
（2）按欧拉自变量（即描述流动所需的空间坐标数目）分类 一元流动：只有一个坐标自变量 B(x,τ) 二元流动：有两个坐标自变量 B(x,y,τ) 三元流动：三个坐标自变量 B(x,y,z,τ)
11
3、流体流动是如何分类的？
（３）按运动要素是否随时间变化 稳定流动（恒定流）：欧拉法所描述的流场中每一空间点上的所有 运动参数均不随时间变化的流动。 非稳定流动（非恒定流）：欧拉法所描述的流场规律与时间有关的 流动。
流体动力学基础理论
流体动力学基础理论流体动力学是研究流体运动规律及其物理现象的学科，其基础理论包括流体静力学和流体动力学两个部分。
本文将围绕流体动力学的基础理论展开论述，包括主要概念、基本方程和典型应用等内容。
一、流体动力学概述流体动力学是研究流体在受力作用下的运动规律的学科。
在研究流体动力学时，通常将流体视为连续分布的介质，分析其运动状态和受力情况。
流体动力学的研究对象包括气体、液体和等离子体等。
流体动力学的基本假设有两个，即连续介质假设和边界层假设。
连续介质假设认为流体可以被看作是连续分布的介质，从而可以用连续函数来描述其物理量。
边界层假设认为流体与物体表面之间存在一层边界层，该层内的流体性质发生较大变化，而在该层外的流体相对稳定。
二、基本方程流体动力学的基本方程包括质量守恒方程、动量守恒方程和能量守恒方程三个方程。
这三个方程构成了描述流体运动规律的基本框架。
1. 质量守恒方程质量守恒方程描述了流体质量的变化情况，其数学表达式为：∂ρ/∂t + ∇·(ρv) = 0其中，ρ表示流体的密度，t表示时间，v表示流体的速度，∇·表示散度运算符。
质量守恒方程表明在流体中，质量的增减与流体的速度有关，通过质量守恒方程可以研究流体的质量流动和密度分布情况。
2. 动量守恒方程动量守恒方程描述了流体运动的动力学规律，其数学表达式为：ρ(∂v/∂t + v·∇v) = -∇p + ∇·τ + ρg其中，p表示流体的压力，τ表示流体的黏性应力，g表示重力加速度。
动量守恒方程表明流体的运动受到压力、黏性应力和重力的综合作用，通过动量守恒方程可以研究流体的速度场和受力情况。
3. 能量守恒方程能量守恒方程描述了流体能量的变化情况，其数学表达式为：ρCv(∂T/∂t + v·∇T) = ∇·(κ∇T) + Q其中，Cv表示流体的定压比热容，T表示流体的温度，κ表示流体的热导率，Q表示流体受到的热源项。
流体动力学基础
市政工程中的雨水排放系统需要考虑 流体动力学原理，以确保在暴雨等极 端天气条件下，雨水能够快速、顺畅 地排出城市区域，防止内涝现象的发 生。
03
污水处理
污水处理厂的设计和运行中，流体动 力学知识有助于优化处理工艺流程， 提高污水处理的效率和效果，减少对 环境的不良影响。
THANKS
感谢观看
规律2
在同一水平面上，流体的 静压力相等，与深度成正 比。
规律3
在垂直方向上，流体静压 力随深度线性增加，即符 合帕斯卡定律。
压力的测定及表示方法
测定方法1
液柱法，通过测量液柱的高度 来计算压力。
测定方法2
弹性法，利用弹性元件的变形 来测量压力。
表示方法1
绝对压力，以绝对真空为基准 表示的压力。
表示方法2
一维、二维与三维流动
根据流动的空间维度，流动可分为一维（如管道流动）、 二维（如平板间的流动）和三维（如绕物体的流动）流动 。高维流动通常更难以分析和计算。
恒定流连续性方程
质量守恒
恒定流连续性方程基于质量守恒 原理，即单位时间内流入和流出
控制体的流体质量相等。
方程的表述
在不可压缩流体中，恒定流的连续 性方程可表述为流速的散度为零（ 即流入和流出某点的流体体积流量 相等）。
应用场景
恒定流连续性方程在管道流动、水 坝设计、风洞实验等方面有广泛应 用，可用于分析流体在复杂几何形 状中的流动行为。
恒定流能量方程及其应用
伯努利定理
恒定流能量方程，又称伯努利定理，描述了不可压缩流体在恒定流动过程中压力、位能和 动能之间的关系。
方程表述
在不可压缩、无粘性流体的恒定流动中，单位体积流体的压力能、位能和动能之和保持不 变。
液压流体力学第五章流体动力学基础
液压流体力学
南京工程学院
夏庆章
20150720
第五章 流体动力学基础
• • • • • • 流体动力学概述 5.1理想流体的运动微分方程式 5.3理想流体的伯努利方程式 5.4实际流体总流的伯努利方程式 5.7伯努利方程的应用 5.8动量、动量矩定理及其应用
流体动力学概述
流体动力学是研究流体在外力作用下的运
动规律即研究流体动力学物理量和运动学 物理量之间的关系的科学。 流体动力学主要研究内容就是要建立流体 运动的动量平衡定律、动量矩平衡定律和 能量守恒定律（热力学第一定律）。
5.1 理想流体的运动微分方程式
1、选取控制体：在所研究的运动流体中，任取一 微小平行六面体，如图5-1所示。六面体边长分别 为dx、dy、dz，平均密度为 ，顶点A 处的压强 为 p。 2、受力分析 质量力：fxdxdydz , fydxdydz , fzdxdydz 表面力：设A点压强为p时，则与其相邻的ABCD 、 ADEH、ABGH三个面上的压强均为p，而与这三个 面相对应的EFGH、 BCFG、 CDEF 面上的压强可 由泰勒级数展开略去二阶以上无穷小量而得到，分 p p p p dz p dx p dy 别为 z x y
p V p V z1 1 1 z 2 2 2 h w g 2 g g 2 g
2 2
式（5-1）的几何解释如图5-1所示，实际总水头线沿微元流 束下降，而静水头线则随流束的形状上升或下降。
图5-1 伯努利方程的几何解释
二、黏性流体总流的伯努利方程 流体的实际流动都是由无数微元流束所组成的有效截面为 有限值的总流流动，例如流体在管道中和渠道中的流动等。 微元流束的有效截面是微量，因而在同一截面上流体质点 的位置高度 z 、压强 p 和流速 V 都可认为是相同的。而 总流的同一有效截面上，流体质点的位置高度 z 、压强 p 和流速 V 是不同的。总流是由无数微元流束所组成的。 因此，由黏性流体微元流束的伯努利方程来推导总流的伯 努利方程，对总流有效截面进行积分时，将遇到一定的困 难，这就需要对实际流动作某些必要的限制。为了便于积 分，首先考虑在什么条件下总流有效截面上各点的 p z 常数？这只有在有效截面附近处有缓变流动时 g 才能符合这个要求。
南京工程学院
夏庆章
20150720
第五章 流体动力学基础
• • • • • • 流体动力学概述 5.1理想流体的运动微分方程式 5.3理想流体的伯努利方程式 5.4实际流体总流的伯努利方程式 5.7伯努利方程的应用 5.8动量、动量矩定理及其应用
流体动力学概述
流体动力学是研究流体在外力作用下的运
动规律即研究流体动力学物理量和运动学 物理量之间的关系的科学。 流体动力学主要研究内容就是要建立流体 运动的动量平衡定律、动量矩平衡定律和 能量守恒定律（热力学第一定律）。
5.1 理想流体的运动微分方程式
1、选取控制体：在所研究的运动流体中，任取一 微小平行六面体，如图5-1所示。六面体边长分别 为dx、dy、dz，平均密度为 ，顶点A 处的压强 为 p。 2、受力分析 质量力：fxdxdydz , fydxdydz , fzdxdydz 表面力：设A点压强为p时，则与其相邻的ABCD 、 ADEH、ABGH三个面上的压强均为p，而与这三个 面相对应的EFGH、 BCFG、 CDEF 面上的压强可 由泰勒级数展开略去二阶以上无穷小量而得到，分 p p p p dz p dx p dy 别为 z x y
p V p V z1 1 1 z 2 2 2 h w g 2 g g 2 g
2 2
式（5-1）的几何解释如图5-1所示，实际总水头线沿微元流 束下降，而静水头线则随流束的形状上升或下降。
图5-1 伯努利方程的几何解释
二、黏性流体总流的伯努利方程 流体的实际流动都是由无数微元流束所组成的有效截面为 有限值的总流流动，例如流体在管道中和渠道中的流动等。 微元流束的有效截面是微量，因而在同一截面上流体质点 的位置高度 z 、压强 p 和流速 V 都可认为是相同的。而 总流的同一有效截面上，流体质点的位置高度 z 、压强 p 和流速 V 是不同的。总流是由无数微元流束所组成的。 因此，由黏性流体微元流束的伯努利方程来推导总流的伯 努利方程，对总流有效截面进行积分时，将遇到一定的困 难，这就需要对实际流动作某些必要的限制。为了便于积 分，首先考虑在什么条件下总流有效截面上各点的 p z 常数？这只有在有效截面附近处有缓变流动时 g 才能符合这个要求。
流体动力学基础
例3、如图所示，有一上方开口截面积很大的水槽，槽内水深h = 40 cm ，接到槽外水平管的截面积依次是1.0 cm2, 0.5 cm2 , 0.25 cm2 。 试求： 1）体积流量 QV 。 2）各段水平管中水流速度 vc ,vd ,ve 。 3）与水平管相连的各压强计中水柱高度 hc , hd , he 。
第二章 流体动力学基础
1、理解理想流体和定常流动（稳定流动）的概念 2、掌握运用连续性方程和伯努利方程 3、了解黏滞定律、泊肃叶定律、斯托克斯定律 4、了解测量液体黏度的实验方法。
第一节、理想流体的定常流动 第二节、伯努利方程 第三节、伯努利方程的应用 第四节、黏性流体的流动 第五节、泊肃叶定律和斯托克斯定律
a
h
c
hd :
d
1 2 1 2 Pd v d Pb v b , 其中Pb =P0 2 2 1 2 1 2 gh d P0 v d P0 v b 2 2 2 v b2 v d hc = 30cm 2g
e
b
例3、如图所示，有一上方开口截面积很大的水槽，槽内水深h = 40 cm ，接到槽外水平管的截面积依次是1.0 cm2, 0.5 cm2 , 0.25 cm2 。 试求： 3）与水平管相连的各压强计中水柱高度 hc , hd , he 。
a
h c
d e
b
例3、如图所示，有一上方开口截面积很大的水槽，槽内水深h = 40 cm ，接 到槽外水平管的截面积依次是1.0 cm2, 0.5 cm2 , 0.25 cm2 。 试求： 1）体积流量 QV 。
a h c d e
解（1）
b
QV Sb vb， 其中S b =Se，vb = 2gh
流体力学-第四章 流体动力学基础
Dt t CV
CS
单位质量流体的能量 e (u V 2 gz) 流体系统的总能量
2
DE ed eV ndS
Dt t CV
CS
E ed
初始时刻系统与控制体重合
Q WSYS Q WCV
ed eV ndS Q W
t CV
CS
§4.2 对控制体的流体力学积分方程
§4.1 系统和控制体，雷诺输运定理
雷诺输运定理：
举例：动量定理运用于流体系统
F Dk Dt
F 是外界作用系统的合力，K 是系统的动量，
k Vd
由于系统不断改变位置、形状大小，组成系统的流体质点的密度和速度随
时间也是变化的，所以系统的动量也是变化的，求其对时间的变化率，即
求该流体系统体积分的物质导数。
取 N M 单位体积的质量
DM 0 Dt
d V ndS 0
t CV
CS
d V ndS 0
t CV
CS
积分形式的连续性方程
§4.2 对控制体的流体力学积分方程
非定常流动情况下：
d V ndS 0
t CV
CS
即单位时间内控制体内流体质量的增加或减少等于同时间内通过控制面流入 或流出的净流体质量。如果控制体内的流体质量不变，则必然同一时间内流 入与流出控制体的流体质量相等。
左端第一项——是控制体内流体动量随时间变化而产生的力，它反映流体运动的非定常性
左端第二项——是单位时间内流体流入和流出控制体的动量之差，它表示流入动量与流出动量
不等所产生的力。
§4.2 对控制体的流体力学积分方程
定常流动条件：
F
FB FS
VV ndS
CS
VV ndS
流体动力学基础
（4-7） ）
r ur 1 r ∂u r r 2 f − ∇p + ν ∇ u = + (u ∇)u （4-8） ） ρ ∂t 粘性流体运动微分方程，又称纳维 斯托克斯方程（ 纳维-斯托克斯方程 方程） 粘性流体运动微分方程，又称纳维 斯托克斯方程（N-S方程） 方程
用矢量表示
§4.2
4.2.1
元流的伯努利方程
1 ∂p du z Z− = ρ ∂z dt
（1）物理意义：作用在单位质量流体上的质量力与 物理意义： 表面力之代数和等于其加速度。 表面力之代数和等于其加速度。 （2）适用条件：理想流体。 适用条件：理想流体。
4.1.2
粘性流体运动微分方程
∂u x ∂u x ∂u x ∂u x 1 ∂p 2 X− + ν∇ u x = + ux + uy + uz ρ ∂x ∂t ∂x ∂y ∂z ∂u y ∂u y ∂u y ∂u y 1 ∂p 2 Y− + ν∇ u y = + ux + uy + uz ρ ∂y ∂t ∂x ∂y ∂z ∂u z ∂u z ∂u z ∂u z 1 ∂p 2 Z− + ν∇ u z = + ux + uy + uz ∂t ∂x ∂y ∂z ρ ∂z
理想流体运动微分方程的伯努利积分 理想流体运动微分方程的伯努利积分
Euler方程三式分别乘以流线上两邻点坐标增量 、dy、 方程三式分别乘以流线上两邻点坐标增量dx、 、 方程三式分别乘以流线上两邻点坐标增量 dz，然后相加得： ，然后相加得：
1 ∂p ∂p ∂p ( Xdx + Ydy + Zdz ) − ( dx + dy + dz ) ρ ∂x ∂y ∂z du y du x du z = dx + dy + dz dt dt dt 引入限定条件： 引入限定条件：
流体动力学基础
（2－64）
②.偏心环状缝隙流 当两圆柱不同心，而偏心时，设偏心距为e， 两圆柱同心时的缝隙为δ，如图2－31。
则偏心环缝的流量为（详见P45页推导）：
d 3 p d q (1 1.5 2 ) 12l 2
式中，ε＝e/δ为偏心比。 所以，当v=0时，是压差流；
q C g A0 2p /
式中，Cg为流量系数，它是实际流量qr与理想流量qt之比 值。即：
Cg＝qr / qt ＝Cc•Cυ
Cc为孔口收缩系数（Cc=A2/A0）。
不同的孔口有不同的Cg值。 1）薄壁孔（孔口的长径比）： 图2－25a，此时，可定无沿程损失，只有
进口处的局部损失，
弯曲、管道截面积变化、液压元件等）而产生的 阻力损失，称为局部压力损失，其计算公式为：
p m
2
2
式中，ξ为局部损失系数（查表2-5、2-6、2-7 可得，P35~36），υ为液体过流断面上平均速度， ρ为液体密度。
（4）管道系统总压力损失Δp总和：
Δp总＝∑Δpl＋∑Δpm ＝∑λ(L/d)（ρυ2/2）＋∑ξ（ρυ2/2） （举例，例2－7，P37~38） （习题3：练习2-5、2-6、2-7、2-8）
压差流的流量计算公式为（详细推导见42－43页）：
q1
b 3 p 1 2l
（2－57）
②.剪切流（图2－28） 缝隙两端无压差，设上平板以速度 沿正向运动，下平板不动。缝隙中 流体在上平板带动下层层移动，称 这种流动为剪切流。 剪切流的流量计算公式为（详细推 导见43页）：
当δ/d<<1时，可将环状缝隙展开成平面计算， 流量的计算为（此时，b=πd，由式（2－57）得）：
第三讲 流体动力学基础
流体静压力矢量： F= -∫ApdAn
三、 流体静压力的两个重要特性。 1、流体静压力的方向总是沿受作用面法线方向。
2、平衡流体内任一点处的静压强的数值与其作用 面的方向无关，它只是该点空间坐标的函数。
10
§2-2 流体的平衡微分方程（欧拉平衡微分方程）
1 p f z
1、流量 单位时间内通过某一过流断面的流体量。体积流量qv或Q表示，质量流量 qm 。 qv vdA v A 体积流量（m3/s）： A
质量流量（kg/s）：
qm ρ vdA ρv A
A
2、净通量 在流场中取整个封闭曲面作为控制面，封闭曲面内的空间称为控制体。 流过全部封闭控制面A的流量称为净流量，或净通量。
动量修正系数是无量纲数，它的大小取决于总流过水断面的流速分布， 分布越均匀，β 值越小，越接近于1.0。
41
层流流速分布
湍流流速分布
断面流速分布 圆管层流 圆管紊流 旋转抛物面 对数规律
动能修正系数
动量修正系数 β =4/3 β =1.02~1.05
=2.0 =1.05~1.1
42
§3-3 连续方程式（一元流动）
绝对真空 p=0
15
第三章
流体动力学基础
16
3-1描述流体运动的两种方法
流体运动实际上就是大量流体质点运动的总和。
描述流体的运动参数在流场中各个不同空间位置上随时 间 连续变化的规律。
拉格朗日法（Lagrange）：流体质点 着眼点不同
跟踪追迹法
欧拉法（ Euler）：空间 设立观察站法
17
一、 拉格朗日法与质点系
32
流线的性质：
1. 在某一时刻，过某一空间点只有一条流线。流线不能 相交，不能突然转折。三种例外： 驻点 相切点
流体动力学基础
1.3 流体动力学基础 教案目录 电子课件【掌握内容】（1）基本概念：流量、流速、压头等（2）质量流量、体积流量之间关系（3）流态判断（4）连续性方程的表达式、物理意义及计算（5）伯努利方程的表达式、物理意义及计算（6）流体阻力的种类及产生的原因【理解内容】（1）管道截面上的速度分布（2）阻力计算（3）简单管路、串联管路、并联管路计算【了解内容】（1）伯努利方程的应用（2）动量方程1.3.1基本概念1.3.1.1流量与流速(1)流量：单位时间内流过管道任一截面的流体量，称为流量。
①体积流量：单位时间内流过管道任一截面的流体体积，以符号V 表示，单位为m 3/s ②质量流量：单位时间内流过管道任一截面的流体质量，以符号M 表示，单位为kg/s(2)流速：单位时间内流体的质点在流动方向上流过的距离称为流速.FV w = （m/s ） (3)质量流量与体积流量和平均流速间的关系。
wF V =（m 3/s ）ρρwF V M == （kg/s ）对于气体： 222111T V p T V p = 122112T T p p V V = （m 3/s ） 122111221122T T p p w T T p p F V F V w === （m/s ） [例题1-4] 某硅酸盐窑炉煅烧后产生的烟气量为10万m 3/h ，该处压强为负100Pa ，气温为800℃,经冷却后进入排风机，这时的风压为负1000Pa ，气温为200℃，求这时的排风量（不计漏风等影响）。
解： 1p =101325-100=101225Pa ， 2p =101325-1000=100325Pa1T =273+800=1073K 2T =273+200=473K1V =1.0×105m 3/h 2V =1073473100325101225100.15⨯⨯⨯ =4.44×104 (m 3/h)硅酸盐窑炉系统中，可近似认为1p =2p =0p （大气压），1211212273273t t V T T V V ++== （m 3/s ） 1.3.1.2稳定流与非稳定流运动流体全部质点所占的空间称为流场。
相关主题
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
刻的流体运动状况和形态，通常用流线谱表示 （1）流线：指瞬时流动的方向线（是描述流场中各点流动方 向的曲线），即速度场的矢量线。
（2）流线的性质 不同的流线，不能相交； 流线不能是同一时刻折线，而是一条光滑的曲线； 恒定流时，流线的形状和位置不随时间而变。
8
（3）流线和迹线有什么区别？
迹线和流线最基本的差别是： 迹线是同一流体质点在不同时刻的位移曲线，与
拉格朗日观点对应； 流线是同一时刻、不同流体质点速度矢量与之相
切的曲线，与欧拉观点相对应。 即使是在恒定流中，迹线与流线重合，两者仍是
完全不同的概念。
9
3、流体流动是如何分类的？
（1）根据流体不同的性质分类： 按照连续性分…按照粘性分…按照粘性规律分…按照压缩性分… （2）按欧拉自变量（即描述流动所需的空间坐标数目）分类
将物质运动的普遍原理（质量守恒、牛顿第二定律、机械能守恒、 能量守恒、动量矩定理等）运用到流体运动上，即可得到流体运动过 程中各种物理量之间的确定关系式，这些关系式即构成了流体动力学 基本原理（基本方程）。
本章主要讨论一元稳定流动时，这些关系式的具体表达形式。 ➢ 建立方法
通常采用欧拉法来建立流体动力学的基本原理，也就是在流场中 任取一确定的空间作为研究对象，此空间称为控制体，控制体的边界 称为控制面，不属于控制体的空间称为外界。考察该控制体各种守恒 关系即可得到流体动力学的基本方程
在工程流体力学中很少采用
5
1、描述流体运动的方法有哪几种?
（2）欧拉法 （euler method） 基本思想：欧拉法是以流场中每一空间位置作为描述 对象，描述这些位置上流体物理参数对于时间的分布 规律即以流场作为描述对象研究流动的方法。—流场法
空间位置的标志—欧拉自变量 识别空间位置的办法是采用空间坐标系，空间坐标系 的坐标变量称为欧拉自变量，此时空间上任一位置的 物理参数可表示为时间的函数
例：空间位置速度 任意时刻任意空间点的速度，可表示为
6
1、描述流体运动的方法有哪几种?
（3）两种方法的区别
欧拉法把流场的运动要素和物理量都用场的形式表达，为在 分析流体力学问题时直接运用场论的数学知识创造了便利条件
欧拉法是描述流体运动常用的一种方法。
7
有关流场的几个基本概念
2、什么是流线、迹线？有何区别? 在欧拉法中，为了观察描述流场中各个空间位置在任意时
10
均匀流
（5）按流线是否为彼此平行分：非均匀流 渐变流
急变流
均匀流：是指各运动要素不随空间变化而变化，流线是平行直 线的流动。 均匀流与恒定流（稳定流）的区别？
均匀流
渐变流 非均匀流
均匀流
急变流 非均匀流 均匀流
均
流线图
匀 流
11
4. 什么是流管、流束、总流、过流断面？
（1）流管——由流线组成。 流体不能穿过流管 稳定流动中，流管的形状和位置不随时间发生变化。
4
1、描述流体运动的方法有哪几种?
（1）拉格朗日方法（lagrangian method） 基本思想：跟踪每个流体质点的运动全过程，记录它们在运动过 程中的各物理量及其变化规律—质点系法（“质点标志”的方 法）。用于研究流体的波动和震荡等
质点标志—拉格朗日自变量 质点位置—迹线
质点运动的轨迹称为迹线，迹线方程可表示为
流体动力学基础
1
§1.3、流体动力学基础
本节目标
通过本单元的学习，应达到下述目标 熟悉理解有关术语、基本原理及其应用 主要术语： 流量、质量流量、体积流量、平均流速、流线、流管、 微元流管、过流断面、驻点、位置水头、静压水头、动 压水头、测压管水头、总水头、动能修正系数、动量修 正系数、均匀管流、非均匀管流 主要原理 连续性方程、伯努利方程、动量方程 工程应用 具备应用连续性方程、伯努利方程、动量方程分析解决 问题的能力
返 2回
教学内容
§1.3.1、流体流动的基本概念 §1.3.2、连续性方程 §1.3.3、伯努利方程及其应用 §1.3.4、动量方程及其应用
3
§1.3.1、流体流动的基本概念
主要内容：
❖ 1、描述流体运动的方法有哪几种？ ❖ 2、什么是流线？与迹线有何区别？ ❖ 3、流体流动是如何分类的？
注意稳定流动、均匀流动 ❖4、什么是流管、流束、总流和过水断面？ ❖5、什么是流量？ ❖6、什么是流体动力学？
返回 14
ቤተ መጻሕፍቲ ባይዱ
§1.3.2、连续性方程
要求： 掌握连续性方程的表达式； 了解连续性方程的证明过程； 理解连续性方程的依据； 掌握连续性方程的应用
（2）流束——充满流管的一束流体。 （3）微元流束——截面积无穷小的流束。 微元流束的极限是流线。 （4）微元流束和流线的差别：
流束是一个物理概念 流线是一个数学概念，只是某一瞬时流场中的一条光滑曲线。 （5）总流——截面积有限大的流束。 如管中的水流及气流都是总流。 （6）过流断面：指垂直于流线的断面。
一元流动：需要一个坐标自变量B(x，t)就能描述的流动，如管内气 体流动 二元流动： 三元流动： （３）按运动要素是否随时间变化 恒定流（稳定流动）：欧拉法所描述的流场中每一空间点上的所有 运动参数均不随时间变化的流动。 非恒定流：欧拉法所描述的流场规律与时间有关的流动。 （4）按流体与固体边界的相对位置关系分: 内部流动：固体边界包围流体的流动。 外部流动（绕流）：流体包围固体边界的流动。
12
5、什么是流量?有哪两种表示方法？
（1）流量定义：指单位时间通过某断面的流体量。
（2）表示方法：
体积流量：指单位时间通过某断面的体积量，以Q 表示，
单位为m3/s或m3/h。
dQ udA
Q udA Q vA A
v——某断面流体的平均流速m/s。
质量流量：指单位时间通过某断面的体积量， 以m表示， 单位为kg/s或kg/h。
体积流量与质量流量的关系为： m Q vA
（3）平均流速： v Q 1 udA AA
13
6、什么是流体动力学？（ fluid dynamics）
主要研究流体在力作用下的运动规律及其与边界的相互作用的科学。 本章所讨论的流体动力学限于一元稳定流动问题
流体动力学基本原理（basic theory of fluid dynamics） ➢ 概念
（2）流线的性质 不同的流线，不能相交； 流线不能是同一时刻折线，而是一条光滑的曲线； 恒定流时，流线的形状和位置不随时间而变。
8
（3）流线和迹线有什么区别？
迹线和流线最基本的差别是： 迹线是同一流体质点在不同时刻的位移曲线，与
拉格朗日观点对应； 流线是同一时刻、不同流体质点速度矢量与之相
切的曲线，与欧拉观点相对应。 即使是在恒定流中，迹线与流线重合，两者仍是
完全不同的概念。
9
3、流体流动是如何分类的？
（1）根据流体不同的性质分类： 按照连续性分…按照粘性分…按照粘性规律分…按照压缩性分… （2）按欧拉自变量（即描述流动所需的空间坐标数目）分类
将物质运动的普遍原理（质量守恒、牛顿第二定律、机械能守恒、 能量守恒、动量矩定理等）运用到流体运动上，即可得到流体运动过 程中各种物理量之间的确定关系式，这些关系式即构成了流体动力学 基本原理（基本方程）。
本章主要讨论一元稳定流动时，这些关系式的具体表达形式。 ➢ 建立方法
通常采用欧拉法来建立流体动力学的基本原理，也就是在流场中 任取一确定的空间作为研究对象，此空间称为控制体，控制体的边界 称为控制面，不属于控制体的空间称为外界。考察该控制体各种守恒 关系即可得到流体动力学的基本方程
在工程流体力学中很少采用
5
1、描述流体运动的方法有哪几种?
（2）欧拉法 （euler method） 基本思想：欧拉法是以流场中每一空间位置作为描述 对象，描述这些位置上流体物理参数对于时间的分布 规律即以流场作为描述对象研究流动的方法。—流场法
空间位置的标志—欧拉自变量 识别空间位置的办法是采用空间坐标系，空间坐标系 的坐标变量称为欧拉自变量，此时空间上任一位置的 物理参数可表示为时间的函数
例：空间位置速度 任意时刻任意空间点的速度，可表示为
6
1、描述流体运动的方法有哪几种?
（3）两种方法的区别
欧拉法把流场的运动要素和物理量都用场的形式表达，为在 分析流体力学问题时直接运用场论的数学知识创造了便利条件
欧拉法是描述流体运动常用的一种方法。
7
有关流场的几个基本概念
2、什么是流线、迹线？有何区别? 在欧拉法中，为了观察描述流场中各个空间位置在任意时
10
均匀流
（5）按流线是否为彼此平行分：非均匀流 渐变流
急变流
均匀流：是指各运动要素不随空间变化而变化，流线是平行直 线的流动。 均匀流与恒定流（稳定流）的区别？
均匀流
渐变流 非均匀流
均匀流
急变流 非均匀流 均匀流
均
流线图
匀 流
11
4. 什么是流管、流束、总流、过流断面？
（1）流管——由流线组成。 流体不能穿过流管 稳定流动中，流管的形状和位置不随时间发生变化。
4
1、描述流体运动的方法有哪几种?
（1）拉格朗日方法（lagrangian method） 基本思想：跟踪每个流体质点的运动全过程，记录它们在运动过 程中的各物理量及其变化规律—质点系法（“质点标志”的方 法）。用于研究流体的波动和震荡等
质点标志—拉格朗日自变量 质点位置—迹线
质点运动的轨迹称为迹线，迹线方程可表示为
流体动力学基础
1
§1.3、流体动力学基础
本节目标
通过本单元的学习，应达到下述目标 熟悉理解有关术语、基本原理及其应用 主要术语： 流量、质量流量、体积流量、平均流速、流线、流管、 微元流管、过流断面、驻点、位置水头、静压水头、动 压水头、测压管水头、总水头、动能修正系数、动量修 正系数、均匀管流、非均匀管流 主要原理 连续性方程、伯努利方程、动量方程 工程应用 具备应用连续性方程、伯努利方程、动量方程分析解决 问题的能力
返 2回
教学内容
§1.3.1、流体流动的基本概念 §1.3.2、连续性方程 §1.3.3、伯努利方程及其应用 §1.3.4、动量方程及其应用
3
§1.3.1、流体流动的基本概念
主要内容：
❖ 1、描述流体运动的方法有哪几种？ ❖ 2、什么是流线？与迹线有何区别？ ❖ 3、流体流动是如何分类的？
注意稳定流动、均匀流动 ❖4、什么是流管、流束、总流和过水断面？ ❖5、什么是流量？ ❖6、什么是流体动力学？
返回 14
ቤተ መጻሕፍቲ ባይዱ
§1.3.2、连续性方程
要求： 掌握连续性方程的表达式； 了解连续性方程的证明过程； 理解连续性方程的依据； 掌握连续性方程的应用
（2）流束——充满流管的一束流体。 （3）微元流束——截面积无穷小的流束。 微元流束的极限是流线。 （4）微元流束和流线的差别：
流束是一个物理概念 流线是一个数学概念，只是某一瞬时流场中的一条光滑曲线。 （5）总流——截面积有限大的流束。 如管中的水流及气流都是总流。 （6）过流断面：指垂直于流线的断面。
一元流动：需要一个坐标自变量B(x，t)就能描述的流动，如管内气 体流动 二元流动： 三元流动： （３）按运动要素是否随时间变化 恒定流（稳定流动）：欧拉法所描述的流场中每一空间点上的所有 运动参数均不随时间变化的流动。 非恒定流：欧拉法所描述的流场规律与时间有关的流动。 （4）按流体与固体边界的相对位置关系分: 内部流动：固体边界包围流体的流动。 外部流动（绕流）：流体包围固体边界的流动。
12
5、什么是流量?有哪两种表示方法？
（1）流量定义：指单位时间通过某断面的流体量。
（2）表示方法：
体积流量：指单位时间通过某断面的体积量，以Q 表示，
单位为m3/s或m3/h。
dQ udA
Q udA Q vA A
v——某断面流体的平均流速m/s。
质量流量：指单位时间通过某断面的体积量， 以m表示， 单位为kg/s或kg/h。
体积流量与质量流量的关系为： m Q vA
（3）平均流速： v Q 1 udA AA
13
6、什么是流体动力学？（ fluid dynamics）
主要研究流体在力作用下的运动规律及其与边界的相互作用的科学。 本章所讨论的流体动力学限于一元稳定流动问题
流体动力学基本原理（basic theory of fluid dynamics） ➢ 概念