经典正弦定理、余弦定理知识点总结及证明

合集下载

(经典)正弦定理、余弦定理知识点总结及最全证明(最新整理)

3．(1)正弦 (2)正弦一解、两解或无解
π
①一解 ②二解 ③一解 ④一解
所对的边分别为 a，b，c.若 a＝2，B＝，c＝2 6
(3)余弦 (4)余弦
3，则 b＝________．
1
1
1
abc
4． (1) absinC bcsinA acsinB
解：由余弦定理知 b2＝a2＋c2－2accosB＝22
2
2
2
2
22
1 . 3
则解此三角形的结果有( )
A．无解
B．一解
C．两解
D．一解或两解
c·sinB 5
解：由正弦定理知 sinC＝
＝，又由
b6
c>b>csinB 知，C 有两解．也可依已知条件，画
【自查自纠】
出△ABC，由图知有两解．故选 C.
abc 1．(1) ＝＝＝2R
sinA sinB sinC
时，只有一解．
(4)已知两边及夹角，用____________定理，
必有一解．
4．三角形中的常用公式或变式
(1)三角形面积公式 S△＝
＝
＝
____________＝
____________＝
____________．其中 R，r 分别为三角形外接圆、
内切圆半径．
(2)A＋B＋C＝π，则 A＝__________，
A ＝ __________，从而 sinA＝ 2
____________，
cosA＝
____________，
tanA＝
____________；
A
A
sin ＝__________，cos ＝__________，

正余弦定理重要知识点(经典)

正余弦定理重要知识点本张武林秘籍，乃武林之精髓所在，得此天书者，细细研习，来日方长，必成大器。

下星期一需要全部背住，不然你不知道我要出哪一招。

1、正弦定理：在C ∆AB 中，a 、b 、c 分别为角A 、B 、C 的对边，R 为C∆AB 的外接圆的半径，则有2sin sin sin a b c R C===A B （R 是三角形外接圆半径）． 2、正弦定理的变形公式：①2sin a R =A ，2sin b R =B ，2sin c R C =； ②sin 2a R A =，sin 2b R B =，sin 2c C R=； ③::sin :sin :sin a b c C =A B3、余弦定理：在C ∆AB 中，有2222cos a b c bc =+-A ，2222cos b a c ac =+-B ，2222cos c a b ab C =+-4、余弦定理的推论：222cos 2b c a bc +-A =，222cos 2a c b ac+-B =，222cos 2a b c C ab +-=． 5、三角形面积公式：111sin sin sin 222C S bc ab C ac ∆AB =A ==B 两边夹角的正弦值两边之积⨯⨯=∆21ABC S 高底⨯=∆21ABC S 6、①如果一个三角形两边的平方和等于第三边，那么第三边所对的角为直角； ②如果小于第三边的平方，那么第三边所对的角为钝角；③如果大于第三边的平方，那么第三边所对角为锐角。

（课本第6页右下角）例如a 、b 、c 是C ∆AB 的角A 、B 、C 的对边，则：①若①222a b c +=，则90C =；②若222a b c +<，则．︒︒<<18090C ，C 为钝角③若222a b c +>，则︒︒<<900C ；C 为锐角7、在三角形中一些重要的知识点；1.2.π=++C B A ,)0(,,π，∈C B A3.4.任意两边之和大于第三边，任意两边之差小于第三边。

高中数学知识点总结正弦定理与余弦定理

高中数学知识点总结正弦定理与余弦定理正弦定理与余弦定理是高中数学中的重要知识点，用于求解不规则三角形的边长和角度。

本文将对这两个定理进行详细总结与讲解。

一、正弦定理1.1 定义正弦定理是指在任意三角形中，三条边与其对应的角的正弦值之间的关系。

设三角形的三边分别为a、b、c，对应的角度为A、B、C，则正弦定理的表达式为：a/sinA = b/sinB = c/sinC1.2 推导我们通过利用三角形的面积公式S=1/2 * a * b * sinC，并将其转换为对角线的形式，可以得到正弦定理的推导过程。

1.3 应用正弦定理可以用于求解不规则三角形的边长和角度。

当我们已知三条边或者两条边和夹角时，可以利用正弦定理求解未知的边长或者角度。

二、余弦定理2.1 定义余弦定理是指在任意三角形中，三条边和它们对应的角之间的关系。

设三角形的三边分别为a、b、c，对应的角度为A、B、C，则余弦定理的表达式为：c^2 = a^2 + b^2 - 2ab * cosC2.2 推导我们可以通过利用向量的几何关系，将余弦定理的表达式推导出来。

这个过程较为繁琐，这里就不做详细讲解。

2.3 应用余弦定理可以用于求解不规则三角形的边长和角度。

当我们已知三条边或者两条边和夹角时，可以利用余弦定理求解未知的边长或者角度。

三、正弦定理与余弦定理的比较3.1 适用范围正弦定理适用于任意三角形，而余弦定理只适用于任意三角形，不能用于直角三角形。

3.2 计算难度正弦定理的计算相对简单，只需要记住一个公式，而余弦定理的计算稍复杂，需要使用开方和乘法等运算。

3.3 精度误差由于余弦定理中涉及到平方运算，可能会带来一定的误差，而正弦定理中没有涉及到平方运算，计算结果更加准确。

3.4 应用场景正弦定理在计算不规则三角形的边长和角度时较为常用，尤其适用于已知两边和夹角的情况。

而余弦定理在计算不规则三角形的边长和角度时同样常用，特别适用于已知三边的情况。

1.1 正弦定理和余弦定理

1.1 正弦定理和余弦定理知识点归纳：一.正弦定理：R CcB b A a 2sin sin sin ===（R 为△ABC 外接圆的半径）（1）变形公式：1.化边为角：2sin 2sin 2sin a R A b R B c R C ===，，；2.化角为边：Rc C R b B R a A 2sin ,2sin ,2sin === 3.::sin :sin :sin a b c A B C = 4.三角形的内切圆半径cb a S r ABC++=∆2二.余弦定理：A bc c b a cos 2222-+=；变形：（1）bc a c b A 2cos 222-+=；B ac c a b cos 2222-+=； ac b c a B 2cos 222-+=；C ab b a c cos 2222-+=. abc b a C 2cos 222-+=变形：（2）A C B C B A cos sin sin 2sin sin sin 222-+=B C A C A B cos sin sin 2sin sin sin 222-+= C B A B A C cos sin sin 2sin sin sin 222-+=三.三角形中的边角关系和性质：（1）π=++C B A2222π=++C B A 在Rt △中，222c b a =+，C=A+B=900.（2）-tanC B)+(A tan -cosC, B)+cos(A sinC,=B)+sin(A ==（3）2cos 2sinC B A =+ 2sin 2cos CB A =+ 2c o t 2t a nC B A =+ （4）tanA+tanB+tanC= tanA ·tanB ·tanC（5）b a >⇔B A >⇔B A sin sin >.⇔cosA<cosB （6）21sin 21==C ab S ×底×高Rabc 4=.)(2c b a r ++=（三角形的内切圆半径r ，外接圆半径R ）（7）ma+nb=kc ⇔msinA+nsinB=ksinC （8）ma=nb ⇔ msinA=nsinB(9)若A 、B 、C 成等差数列，则B 060=.(10)若三角形中三内角成等差数列，三边成等比数列⇔三角形为正三角形（11）余弦定理是勾股定理的推广：判断C ∠为锐角222c b a >+⇔，C ∠为直角222c b a =+⇔， C ∠为钝角222c b a <+⇔．课堂训练一、选择题1．已知△ABC 中，a ＝4，b ＝43，∠A ＝30°，则∠B 等于……………………....( ) A ．30° B ．30°或150° C ．60° D ．60°或120°2．已知△ABC 中，AB ＝6，∠A ＝30°，∠B ＝120°，则△ABC 的面积为…………..( ) A ．9B ．18C ．93D ．1833．已知△ABC 中，a ∶b ∶c ＝1∶3∶2，则A ∶B ∶C 等于………………………..( )A ．1∶2∶3B ．2∶3∶1C ．1∶3∶2D ．3∶1∶2 4．已知△ABC 中，sin A ∶sin B ∶sin C ＝k ∶(k ＋1)∶2k (k≠0)，则k 的取值范围为…..( ) A ．(2，＋∞) ] B ．(-∞，0) C ．(-21，0)D ．(21，＋∞)5．在△ABC 中，根据下列条件解三角形，其中有一解的是………………………..( ) A ．b ＝7，c ＝3，C ＝30° B ．b ＝5，c ＝42，B ＝45° C ．a ＝6，b ＝63，B ＝60° D ．a ＝20，b ＝30，A ＝30° * 6．在△ABC 中，A ＝60°，b ＝1，其面积为3，则sin sin sin a b cA B C++++等于….( )A ．33B ．3392C ．338D ．239二、填空题7．在△ABC 中，若∠B ＝30°，AB ＝23，AC ＝2，则△ABC 的面积是________． 8．设△ABC 的外接圆半径为R ，且已知AB ＝4，∠C ＝45°，则R ＝________．9．已知△ABC 的面积为23，且b ＝2，c ＝3，则∠A ＝________．10*．若三角形中有一个角为60°，夹这个角的两边的边长分别是8和5，则它的内切圆半径等于________，外接圆半径等于________．三、解答题11．在△ABC 中，∠C ＝60°，BC ＝a ，AC ＝b ，a ＋b ＝16． (1)试写出△ABC 的面积S 与边长a 的函数关系式．(2)当a 等于多少时，S 有最大值？并求出这个最大值．12．在△ABC 中，已知a 2-a ＝2(b ＋c )，a ＋2b ＝2c -3，若sin C ∶sin A ＝4∶13，求a ，b ，c ．13．在△ABC 中，求证2tan 2tanBA b a b a -=+-．14*．在一个三角形中，若有一个内角不小于120°，求证：最长边与最短边之比不小于3．同步提升一、选择题：1、在△ABC 中，已知b ＝4 ，c ＝2 ，∠A＝120°，则a 等于( )A ．2B ．6C ．2 或6D ．272、在△ABC 中，已知三边a 、b 、c 满足(a ＋b ＋c)(a ＋b －c)＝3ab ，则∠C 等于 ( ) A ．15° B ．30° C ．45° D ．60°3、已知在△ABC 中:，sinA: sinB: sinC ＝3: 5 :7，那么这个三角形的最大角是 ( )A ．135°B ．90°C ．120°D ．150°4、在△ABC 中，若c 4－2(a 2＋b 2)c 2＋a 4＋a 2b 2＋b 4＝0，则C 等于 ( )A ．90°B ．120°C ．60°D ．120°或60° 二、填空题：5、已知△ABC 中,A ＝60°,最大边和最小边是方程x 2－9x ＋8＝0的两个正实数根,那么BC 边长______．6、△ABC 中，a 、b 分别是角A 和角B 所对的边，a ＝3,b ＝1,B 为30°，则角A 的值为______.7、在△ABC 中，cos A ＝135,sin B ＝53,则cos C 的值为______. 8、在△ABC 中，若sin A sin B ＝cos 22C ，则△ABC 为______.9、若三角形中有一个角为60°，夹这个角的两边的边长分别是8和5，外接圆半径等于_______．三、解答题：10、在ABC ∆中，,15,8,2==+=+ac c a B C A 求b 的值。

正弦定理余弦定理知识点

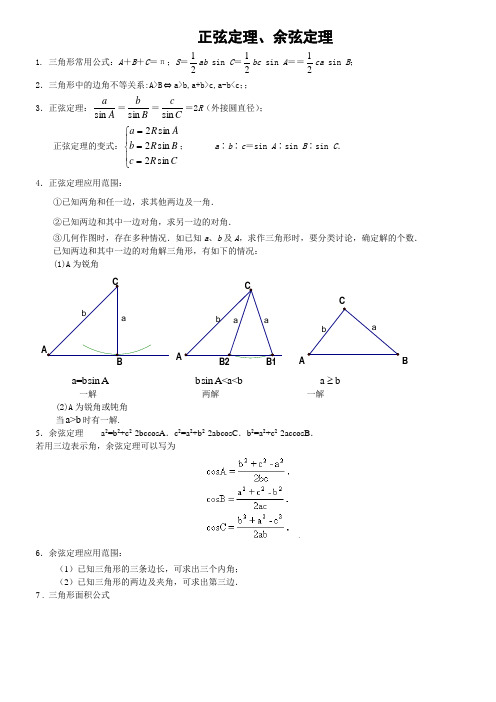
正弦定理、余弦定理1. 三角形常用公式：A ＋B ＋C ＝π；S ＝21ab sin C ＝21bc sin A ＝＝21ca sin B ； 2．三角形中的边角不等关系:A>B ⇔a>b,a+b>c,a-b<c ；； 3．正弦定理：A a sin ＝B b sin ＝Ccsin ＝2R （外接圆直径）；正弦定理的变式：⎪⎩⎪⎨⎧===C R c B R b A R a sin 2sin 2sin 2； a ∶b ∶c ＝sin A ∶sin B ∶sin C ．4．正弦定理应用范围：①已知两角和任一边，求其他两边及一角． ②已知两边和其中一边对角，求另一边的对角．③几何作图时，存在多种情况．如已知a 、b 及A ，求作三角形时，要分类讨论，确定解的个数．已知两边和其中一边的对角解三角形，有如下的情况： (1)A 为锐角babaabaB1BACACA BCB2a=bsin A bsin A<a<b a b ≥ 一解两解一解(2)A 为锐角或钝角当a>b 时有一解.5．余弦定理 a 2=b 2+c 2-2bccosA ．c 2=a 2+b 2-2abcosC ．b 2=a 2+c 2-2accosB ．若用三边表示角，余弦定理可以写为、6．余弦定理应用范围：（1）已知三角形的三条边长，可求出三个内角；（2）已知三角形的两边及夹角，可求出第三边． 7 . 三角形面积公式课堂互动知识点1 运用判断三角形形状例题1在△ABC 中已知acosB=bcosA,试判断△ABC 的形状.【分析】利用正弦定理或余弦定理判断三角形形状,可以将三角形中的边用角表示,也可将角用边来表示．从中找到三角形中的边角关系，判断出三角形的形状. 【答案】解法1：由扩充的正弦定理：代入已知式 2RsinAcosB=2RsinBcosAsinAcosB-cosAsinB=0 ， sin(A-B)=0A-B=0 ∴A=B 即△ABC 为等腰三角形解法2:由余弦定理: 22222222bca cb b ac b c a a -+⋅=-+⋅ 22b a = ∴ b a = 即△ABC 为等腰三角形. 巩固练习1．在∆ABC 中，若2222sin sin 2cos cos b C c B b B C +=，试判断三角形的形状．2．在ABC ∆中,已知a 2tanB=b 2tanA,试判断这个三角形的形状. 3．已知ABC ∆中，有cos 2cos sin cos 2cos sin A C BA B C+=+，判断三角形形状.知识点2 运用正、余弦定理解三角形解三角形问题中正、余弦定理的选择:(1)在下述情况下应首先使用余弦定理:①已知三条边(边边边),求三个角;②已知两边和它们的夹角(边角边),求其它一边和两角;(2)在下述情况下应首先使用正弦定理:①已知两边和一边的对角(边边角),求其它一边和两角;②已知两角和任一边(角角边、角边角),求其它两边和一角. 例题2 在△ABC 中，已知3=a ，2=b ，B=45︒ 求A 、C 及c .【分析】在解斜三角形应用过程中，注意要灵活地选择正弦定和余弦定理，解得其它的边和角【答案】解法1：由正弦定理得：23245sin 3sin sin === b B a A ∵B=45︒<90︒ 即b <a ∴A=60︒或120︒当A=60︒时C=75︒ 22645sin 75sin 2sin sin +===BC b c 当A=120︒时C=15︒ 22645sin 15sin 2sin sin -===B C b c 解法2：设c =x 由余弦定理 B ac c a b cos 2222-+=将已知条件代入，整理：0162=+-x x 解之：226±=x 当226+=c 时2)13(231226223)226(22cos 22221=++=+⋅⋅-++=-+=bc a c b A 从而A=60︒ ，C=75︒ 当226-=c 时同理可求得：A=120︒ C=15︒. 巩固练习1．已知在ABC ∆中，,6,45=︒=∠BC AB A 在ABC ∆中，213,2tan tan +=-=c b bb c B A3．在ABC ∆中，已知A 、B 、C 成等差数列，且sin 求三边a 、b 、c ．4．在ABC ∆中，已知B C A 2=+，tan tan ⋅C A 又知顶点C 的对边C 上的高等于34知识点3 例题3 已知A 、B 、C 为锐角，tanA=1，tanB=2 角的范围确定角．本题应先求出A+B 和C 式求出A+B+C ．【答案】 A B C 、、为锐角 ∴<0°A tan()tan tan tan tan A B A B A B +=+-⋅=+-=-112123[]tan()tan ()A B C A B C ++=++ =所以A+B+C=πsin sin sin sin cos 22222ααββα-++-221336-+=(cos cos sin sin )αβαβ --=-25936cos()αβ∴-=cos()αβ5972巩固练习1．在∆ABC 中,a 、b 、c 分别是角A 、B 、C 的对边,设a+c=2b,A-C=3π,求sinB 的值. 2．在∆ABC 中，a ，b ，c 分别是∠∠∠A B C ，，的对边长，已知a ，b ，c 成等比数列，且a c ac bc 22-=-，求∠A 的大小及b Bcsin 的值． 3．在ABC ∆中，若4,5==b a且3231)cos(=-B A ，求这个三角形的面积．例题4 在ABC ∆中,角A 、B 、C 的对边分别为a 、b 、c,证明:C B A cb a sin )sin(222-=-.【分析】在用三角式的恒等变形证明三角形中的三角等式时，其解题的一般规律是：二项化积、倍角公式，提取公因式，再化积.遇有三角式的平方项，则利用半角公式降次. 【答案】证法一:由正弦定理得C A B C B A c b a 2222222sin 22cos 2cos sin sin sin -=-=-=C A B A B 2sin 2)sin()sin(2-+-=CB AC 2sin )sin(sin -=C B A sin )sin(-.证法二:由余弦定理得a 2=b 2+c 2-2bccosA,则222c b a -=22cos 2cA bc c -=1-c b 2∙cosA,又由正弦定理得c b =C Bsin sin ,∴222c b a -=1-C B sin sin 2∙cosA=C A B C sin cos sin 2sin -=C A B B A sin cos sin 2)sin(-+=C A B B A sin cos sin cos sin -=C B A sin )sin(-. 证法三:C B A sin )sin(-=CAB B A sin cos sin cos sin -. 由正弦定理得cbC B c a C A ==sin sin ,sin sin ,∴CB A sin )sin(-=cAb B a cos cos -,又由余弦定理得CB A sin )sin(-=cbc a c b b ac b c a a 22222222-+⋅--+⋅=22222222)()(c a c b b c a -+--+=222c b a -.巩固练习1．已知锐角三角形ABC 中，3sin()5A B +=，1sin()5A B -=. （1）求证tan 2tan A B =；（2）设3AB =，求AB 边上的高．【考题再现】1．（04年全国Ⅲ）在ABC ∆中，3AB =，BC =4AC =，则边AC 上的高（A （B （C ）32（D ）2．（05年湖南卷）已知在△ABC 中，sinA （sinB ＋cosB ）－sinC ＝0，sinB ＋cos2C ＝0，求角A 、B 、C 的大小.3.（春季北京）在△ABC 中，sin A +cos A =22，AC =2，AB =3，求tan A 的值和△ABC 的面积. 4. （05年江苏卷）ABC ∆中，3A π=，3BC =，则ABC ∆的周长为（A ）33B π⎛⎫++ ⎪⎝⎭ （B ）36B π⎛⎫++ ⎪⎝⎭ （C ）6sin 33B π⎛⎫++ ⎪⎝⎭ （D ）6sin 36B π⎛⎫++ ⎪⎝⎭5．（06年湖北卷）若ABC ∆的内角A 满足2sin 23A =，则sin cos A A +=A.3 B ．3- C ．53 D ．53- 6. （安徽卷）如果111A B C ∆的三个内角的余弦值分别等于222A B C ∆的三个内角的正弦值，则（）A ．111ABC ∆和222A B C ∆都是锐角三角形 B ．111A B C ∆和222A B C ∆都是钝角三角形 C ．111A B C ∆是钝角三角形，222A B C ∆是锐角三角形D ．111A B C ∆是锐角三角形，222A B C ∆是钝角三角形【模拟训练】1．（北京市朝阳区二模题）在∆ABC 中，cos2cos2B A >是A B >的（）（A ）充分而不必要条件（B ）必要而不充分条件（C ）充要条件（D ）既不充分也不必要条件2．（04年南京市二模题）在∆ABC 中，A ，B ，C 为三角形的三个内角，且A B C <<，4sin 5B =4cos(2)5A C +=-，求cos2A 的值3．（04年华南师大附中）在∆ABC 中，,,a b c 分别为角,,A B C 的对边，且274sin cos 222B C A +-= （1）求A ∠的度数（2）若a =3b c +=，求b 和c 的值4．（05年南通市基地学校联考）在∆ABC 中，边AB为最长边，且sin sin A B ⋅=，则cos cos A B ⋅的最大值是5.（06年湖北八校第二次联考）已知关于x 的方程22cos cos 2sin02Cx x A B -⋅+=的两根之和等于两根之积的一半，则ABC ∆一定是（A ）直角三角形（B ）钝角三角形（C ）等腰三角形（D ）等边三角形.6.(06年黄岗市荆州市高三年级模拟)已知ABC ∆的三个内角为A 、B 、C 所对的三边为a 、b 、c ，若ABC ∆的面积为222()S a b c =--，则tan2A=__________．教考链接在证明三角形问题或者三角恒等式时，要注意正弦定理、余弦定理的适用题型与所证结论的联系，并注意特殊正、余弦关系的应用，比如互补角的正弦值相等，互补角的余弦值互为相反数等；另外，在三角恒等式的证明或者三角形形状的判断，关键是正、余弦定理的边角互换．运用正、余弦定理求解三角形的有关问题，要非常熟悉了三角函数公式及三角形的有关性质，如三角函数的定义、勾股定理、正弦定理、余弦定理是常用的工具，同时注意三角形面积公式ah S 21=，C ab S sin 21=，还要注意三角形内角和π=++C B A 的制约关系，此外，要对常见解题方法与解题技巧的总结，这样才能不断提高三角形问题的求解能力．参考答案课堂互动例题1 巩固练习1．【答案】[解法1]：由正弦定理2sin sin sin a b cR A B C===，R 为∆ABC 外接圆的半径，将原式化为22228sin sin 8sin sin cos cos R B C R B C B C =，sin sin 0B C ≠，sin sin cos cos B C B C ∴=. 即cos()0B C +=,90B C ∴+=，90A =. 故∆ABC 为直角三角形[解法2]：将已知等式变为2222(1cos )(1cos )2cos cos b C c B b B C -+-=，由余弦定理可得22222222222222a b c a c b b c b c ab ac ⎛⎫⎛⎫+-+-+-⋅-⋅ ⎪ ⎪⎝⎭⎝⎭222222222a c b a b c bc ac ab+-+-=⋅⋅，即22b c +22222222()()4a b c a c b a⎡⎤+-++-⎣⎦= 也即222b c a +=，故∆ABC 为直角三角形．2．【答案】解法1:由已知得A A bB B a cos sin cos sin 22=,由正弦定理得AAB B B A cos sin sin cos sin sin 22=,∵sinAsinB ≠0,∴sinAcosA=sinBcosB,即sin2A=sin2B,∴2A=2B 或2A=1800-2B,即A=B 或A+B=900.∴ABC ∆是等腰三角形或直角三角形.解法2: 由已知得A A bB B a cos sin cos sin 22=,由正弦定理得A a b b a cos cosB 22=,即Aba cos cosB =,又由余弦定理得bcac b b a 22ac b -c a 222222-+=+,整理得(a 2-b 2)(a 2+b 2-c 2)=0,∴a=b,或a 2+b 2=c 2, ∴ABC ∆是等腰三角形或直角三角形. 3．解：由已知得例题2 巩固练习1．【答案】解法1：由正弦定理，得2345sin 26sin =︒=C 因3226sin =⨯=⋅A AB 6,2==AB BC 由623<<，则有二解，即︒=∠60C 或︒=∠120C︒=︒-︒-︒=∠754560180B 或︒=︒-︒-︒=∠1545120180B故13sin sin +=⇒⋅=AC B ABC AC 或13-=AC ，︒=∠︒=∠15,120B C ︒=∠︒=∠75,60B C 解法2：令AC=b ，则由余弦定理222245cos 62)6(=︒-+b b 1302322±=⇒=+-b b b又C b b cos 222)6(222⋅-+=︒=∠±=⇒60,21cos C C 或︒=∠120C ︒=︒+︒-︒=∠⇒75)6045(180B 或︒=︒+︒-︒=∠15)12045(180B . 2【答案】由已知有bc B A 21tan tan =+，化简并利用正弦定理：B C B A B A B A sin sin 2sin cos sin cos cos sin =+ BCB A B A sin sin 2sin cos )sin(=+0cos sin 2sin =-A C C由0sin ≠，故︒=⇒=6021cos A A 由213+=cb，可设k c k b 2,)13(=+=，由余弦定理，得 k a k k k a 6)13(24)13(22222=⇒+-++=由正弦定理Cc A a sin sin =得 226232sin sin =⋅==kk a A c C 由b c <则C 是锐角，故︒=--︒=︒=75180,45C A B C3．【答案】由已知，得2C A B +=，又由︒=++180C B A ︒=⇒60B 故4160cos sin sin 2=︒=C A ①又由B c a S ABC sin 2134⋅⋅==∆164334=⇒=⇒ac ac ② 故64)sin ()sin (sin sin 22===C c A a C A ac 8sin sin ==⇒Cc A a由3460sin 8sin 8sin sin =︒⋅=⋅==B AB a b 则21260cos cos 222=-+=︒=ac b c a B即964848)(3)(222=+=+⇒=-+c a ac b c a 64=+⇒c a ③ 把③与②联立，得)26(2),26(2-=+=c a 或)26(2),26(2+=-=c a4．【答案】由已知B C A 2=+，及︒=+︒=⇒︒=++120,60180C A B C B A由CA C A C A tan tan 1tan tan )tan(-+=+及32tan tan ,3)tan(+=⋅-=+C A C A得33tan tan +=+C A ，以C A tan ,tan 为一元二次方程032)33(2=+++-x x 的两个根，解方程，得⎩⎨⎧+==32tan 1tan C A 或⎩⎨⎧=+=1tan 32tan C A ⎩⎨⎧︒=︒=⇒7545C A 或⎩⎨⎧︒=︒=4575C A 若︒=︒=75,45C A ，则860sin 34=︒=a ，6445sin 34=︒=b ，)13(445sin 75sin 8sin sin +=︒︒==A C a c若︒=︒=45,75C A ，则︒=60sin 34a ︒==75sin 34,8b )13(64-=)623(4-=)13(8sin sin -==B C b c 例题3 巩固练习1．【答案】由正弦定理和已知条件a+c=2b,得sinA+sinC=2sinB.由和差化积公式,得2sin 2C A +cos 2C A -=2sinB. 由A+B+C=π得sin 2C A +=cos 2B .又A-C=3π,得2cos 23B =sinB.∴2cos 23B=2sin 2B cos 2B ,∵0<2B <2π,∴cos 2B ≠0,∴sin2B =43.∴cos 2B =2sin 12B -=413,∴sinB=2sin 2B cos 2B =2∙43∙413=839. 2．【答案】（I ） a b c ，，成等比数列 ∴=b ac 2又a c ac bc 22-=- ∴+-=b c a bc 222 在∆ABC 中，由余弦定理得cos A b c a bc bc bc =+-==2222212∴∠=︒A 60 （II ）在∆ABC 中，由正弦定理得sin sin B b Aa= ∴=︒=︒=b B c b ca sin sin sin 2606032． 3．【答案】解法1：由余弦定理得c c bc a c b A 892cos 2222-=-+= cc ac b c a B 1092cos 2222+=-+= 由正弦定理得：B A B A sin 45sin sin 4sin 5=⇒= 3231)cos 1(4510989222=-++⋅-⇒B c c c c 3231])109(1[4580812224=+-+-c c c c 63632318016282222=⇒=⇒=-⇒c c cc 故1694893689cos 2=-=-=c c A7165sin =A 4715sin 21=⋅⋅=∆A c b S ABC解法2：如图，作B A CAD -=∠，AD 交BC 于D ，令x CD = 则由5=a 知，x AD x BD -=-=5,5，在CAD ∆中由余弦定理3231)5(84)5()cos(222=--+-=-x x x B A化简得199=⇒=x x ，在CAD ∆中由正弦定理)sin(4)sin(sin )sin(sin B A B A CD ADC B A CD C AD -=-⋅=⇒-=783)(cos 142=--=B A 74158735421sin 21=⨯⨯⨯=⋅⋅=∆C BC AC S ABC例题4 巩固练习1．【答案】（1）证明：因为3sin()5A B +=，1sin()5A B -=，所以3sin cos cos sin 51sin cos cos sin 5A B A B A B A B ⎧+=⎪⎪⎨⎪-=⎪⎩，2sin cos 51cos sin 5A B A B ⎧=⎪⎪⇒⎨⎪=⎪⎩，tan 2tan A B ⇒=.所以tan 2tan A B =（2）因为2A B ππ<+<，3sin()5A B +=，所以3tan()4A B +=-，即tan tan 31tan tan 4A B A B +=--，将tan 2tan A B =代入上式并整理得 22tan 4tan 10B B --=.解得tan B =tan B =tan 2tan 2A B ==. 设AB 边上的高为CD.则tan tan CD CD AB AD DB A B =+=+=AB=3，得CD= 2AB边上的高等于2考题再现1．【答案】由余弦定理，得1cos 2A =，60A ︒=，所以AC边上的高sin 2BD AB A =⋅=选B.2．【答案】解法1：由0sin )cos (sin sin =-+C B B A 得.0)sin(cos sin sin sin =+-+B A B A B A所以.0sin cos cos sin cos sin sin sin =--+B A B A B A B A 即.0)cos (sin sin =-A A B因为),,0(π∈B 所以0sin ≠B ，从而.sin cos A A = 由),,0(π∈A 知.4π=A 从而π43=+C B . 由.0)43(2cos sin 02cos sin =-+=+B B C B π得即.0cos sin 2sin .02sin sin =-=-B B B B B 亦即由此得.125,3,21cos ππ===C B B 所以,4π=A .125,3ππ==C B 解法2：由).223sin(2cos sin 02cos sin C C B C B -=-==+π得由B <0、π<c ，所以.22223ππ-=-=C B C B 或即.22232ππ=-=+B C C B 或由0sin )cos (sin sin =-+C B B A 得 .0)sin(cos sin sin sin =+-+B A B A B A 所以.0sin cos cos sin cos sin sin sin =--+B A B A B A B A 即.0)cos (sin sin =-A A B 因为0sin ≠B ，所以.sin cos A A =由.4),,0(ππ=∈A A 知从而π43=+C B ，知B+2C=23π不合要求.再由π212=-B C ，得.125,3ππ==C B 所以,4π=A .125,3ππ==C B .3．【答案】解法1：∵sin A +cos A =2cos （A －45°）=22，∴cos （A －45°）=21. 又0°＜A ＜180°，∴A －45°=60°，A =105°. ∴tan A =tan （45°+60°）=3131-+=－2－3.∴sin A =sin105°=sin （45°+60°）=sin45°cos60°+cos45°sin60°=462+. ∴S △ABC =21AC ·AB sin A =21·2·3·462+=43（2+6）.4．【答案】在ABC ∆内，由正弦定理得3sin sin sin sin 3AC AB BC B C A π====∴(),3AC B AB C A B B ππ⎛⎫===-+=+⎡⎤ ⎪⎣⎦⎝⎭ ∴周长为AB AC BC ++sin sin 33B B π⎤⎛⎫=+++ ⎪⎥⎝⎭⎦3sin 32B B ⎫=+⎪⎪⎭6sin 36B π⎛⎫=++ ⎪⎝⎭ 5．【答案】由sin2A ＝2sinAcosA >0，可知A 这锐角，所以sinA ＋cosA >0，又25(sin cos )1sin 23A A A +=+=，故选A.6．【答案】111A B C ∆的三个内角的余弦值均大于0，则111A B C ∆是锐角三角形，若222A B C ∆是锐角三角形，由211211211sin cos sin()2sin cos sin()2sin cos sin()2A A A B B B C C C πππ⎧==-⎪⎪⎪==-⎨⎪⎪==-⎪⎩，得212121222A A B B C C πππ⎧=-⎪⎪⎪=-⎨⎪⎪=-⎪⎩，那么，2222A B C π++=，所以222A B C ∆是钝角三角形．故选D ．模拟训练1．【答案】2222cos 2cos 212sin 12sin sin sin B A B A B A >⇔->-⇔<⇔sin sin A B A B >⇔> 2．【答案】∵A B C <<，A B C π++=，∴0,022B AC ππ<<<+<，由4sin 5B =得3cos 5B =，∴4sin()5A C +=，()3cos 5A C +=- 又由4cos(2)5A C +=-得3sin(2)5A C += ∴()33447sin sin 2()555525A A C A C ⎛⎫⎛⎫=+--=⨯---⨯=⎡⎤ ⎪ ⎪⎣⎦⎝⎭⎝⎭2527cos 212sin 625A A =-=. 3．【答案】由题意得[]2721cos()2cos 12B C A -+-+= ()2721cos 2cos 12A θ+-+= ∴1cos 2A = 03A π<<2221cos 22b c a A bc +-==()223b c a bc +-=将3a b c =+=代入得2,bc =由3b c +=及2bc =，得1,2b c ==或2,1b c ==.4．【答案】因为cos cos sin sin cos()1A B A B A B ⋅+⋅=-≤，易得cos cos A B ⋅的最大值为24+. 5．【答案】由题意可知：211cos cos cos 2sin 222C CA B -=⋅⋅=，从而2cos cos 1cos()1cos cos sin sin A B A B A B A B =++=+-cos cos sin sin 1A B A B +=，cos()1A B -=又因为A B ππ-<-<所以0A B -=，所以ABC ∆一定是等腰三角形选C6．【答案】1sin 2S bc A =，222()S a b c =--，2222cos a b c bc A =+-， ∴1sin 22cos 2bc A bc bc A =-，∴22sin 11cos 2tan 4sin 22sin cos 22A A A A A A -===。

(经典)正弦定理、余弦定理知识点总结及最全证明

正弦定理、余弦定理知识点总结及证明方法1.掌握正弦定理、余弦定理，并能解决一些简单的三角形度量问题.2.能够运用正弦定理、余弦定理等知识和方法解决一些与测量和几何计算有关的实际问题.主要考查有关定理的应用、三角包等变换的能力、运算能力及转化的数学思想.解三角形常常作为解题工具用丁立体几何中的计算或证明，或与三角函数联系在一起求距离、高度以及角度等问题，且多以应用题的形式出现.1.正弦定理(1)正弦定理：在一个三角形中，各边和它所对角的正弦的比相等，即.其中R是三角形外接圆的半径.(2)正弦定理的其他形式：① a = 2RsinA , b =, csinO；③ a : b ： c= _______________________________2.余弦定理(1)余弦定理：三角形中任何一边的平■方等——王彦文宵铜峡一中丁其他两边的平■方的和减去这两边与它们的火角的余弦的积的两倍.即a2=, b2=,c?=.若令C= 90°, WJ c2=,即为勾股定理.(2)余弦定理的变形：cosA =, cosB=, cosC^.若C为锐角，则cosC>0,即a2 + b2 ; 若C为钝角，贝U cosC<0,即a2+ b2.故由a2+ b2与c2值的大小比较，可以判断C为锐角、钝角或直角.(3)正、余弦定理的一个重要作用是实现边角,余弦定理亦可以写成sin2A= sin2B+ sin2C—2sinBsinCcosA，类似地，sin2B= ________________ ; sin2C= _________ _S 意式中隐含条件A+ B+ C= TT .3.解斜三角形的类型(1)已知三角形的任意两个角与一边，用理.只有一解.(2)已知三角形的任意两边与其中一边的对角，用定理，可能有L如在△ ABC中，已知a, b和A时，解的情况如表：②sin A=2R' sinB=A为锐角A为钝角或直角图形关系式a= bsinA bsinA<a< b a为a>b解的个数①②③④(3)已知三边，用理.有解时，只有一解.(4)已知两边及火角，用理, 必有一解.4.三角形中的常用公式或变式⑴三角形面积公式& =:其中R, r分别为三角形外接圆、内切圆半径.(2)A+ B+ C=兀，WJ A=,A5 = , 从而sinA = tanAtanBtanC (3)a+ c sinA+ sinCcosA = , tanA =<(3)互化sin2C+ sin2A—2sinCsinAcosB sin2A+sin2B— 2sinAsinBcosC3. (1)正弦(2)正弦一解、两解或无解①一解②二解③一解④一解⑶余弦⑷余弦1 1 1 abc 14. (1)2absinC 2bcsinA 2acsinB 4R 2 (a+ b+ c)r在△ ABC中，A>B 是sinA>sinB 的( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件解：因为在同一三角形中，角大则边大，边大则正弦大，反之也成立，故是充要条件.故选C.兀B+ C (2)代(B+ Q 2— Fsin(B+ C) — cos(B+ C)2 (1)b* 1 2+ c2— 2bccosA c2 + a2— 2cacosB a2 + b2—2abcosC a2 + b2b2+ c2—a2c2+ a2—b2a2+ b2—c2(2)2bc2ca2ab—tan(B+ C) co岩si号«C tan 2在△ ABC中，已知b= 6, c= 10, B= 30°,则解此三角形的结果有（）A.无解B. 一解C.两解D. 一解或两解解：由正弦定理知sinC=半=5, 乂由b 6c>b>csinB知，C有两解.也可依已知条件，画出△ ABC,由图知有两解.故选 C.（2012陕西）在^ABC中，角A, B, C所对的边…一…Tt i—一，分力U为a, b, c.右a= 2, B= c= 2寸3,贝U b =.解：由余弦定理知b2= a2 + c2—2accoSB=22 + （2^3）2— 2X 2X^/3X c%= 4, b= 2.故填2.（2013陕西）®AABC的内角A, B, C所对的边分别为a, b, c,若bcosC+ ccosB= asinA,则^ABC 的形状为（）A.锐角三角形B.直角三角形C.钝角三角形D.不确定解：由已知和正弦定理可得sinBcosC+ sinCcosB= sinA sinA,即sin（B+ Q= sinAsinA, 亦即sinA= sinAsinA.因为0<A<TT,所以sinA= 1, 所以A=2.所以三角形为直角三角形.故选B.在^ABC中，角A, B, C所对的边分别为a, b, c,若 a =寸2, b=2, sinB+ cosB=寸2,则角 A解：sinB+ cosB= ^2,,•寸2sin B+4 =寸2,即sin B+4 = 1._____ __ _兀兀_兀乂.. B€ （0,冗）... B+； = ；, B=~.4 2 4a b asinBsinA= b根据正弦正理、皿=sinB，可侍12'. a<b, . . Av B... A=g.故填&类型一正弦定理的应用△ ABC的内角A, B, C的对边分别为a, b, c,已知A— C= 90 , a+ c=寸2b,求C.解：由a+ c=寸2b及正弦定理可得sinA+sinO 2sinB乂由丁A— C= 90 , B= 180 — (A+C),故cosC + sinC = sinA + sinC=戒sin(A + Q =戒sin(90 + 2Q =匝sin2(45 + Q.,•哀sin(45 + C) = 2 戒sin(45 + C)cos(45 + C),* 一1即cos(45 + C) = 2.乂 .。

正弦定理和余弦定理考点与提醒归纳

正弦定理和余弦定理考点与提醒归纳一、基础知识1．正弦定理a sin A ＝b sin B ＝c sin C＝2R (R 为△ABC 外接圆的半径)．正弦定理的常见变形(1)a ＝2R sin A ，b ＝2R sin B ，c ＝2R sin C ；(2)sin A ＝a 2R ，sin B ＝b 2R ，sin C ＝c 2R； (3)a ∶b ∶c ＝sin A ∶sin B ∶sin C ； (4)a ＋b ＋c sin A ＋sin B ＋sin C ＝a sin A. 2．余弦定理a 2＝b 2＋c 2－2bc cos A ； b 2＝c 2＋a 2－2ca cos B ； c 2＝a 2＋b 2－2ab cos C . 3．三角形的面积公式(1)S △ABC ＝12ah a (h a 为边a 上的高)；(2)S △ABC ＝12ab sin C ＝12bc sin A ＝12ac sin B ；(3)S ＝12r (a ＋b ＋c )(r 为三角形的内切圆半径)．二、常用结论汇总——规律多一点 1．三角形内角和定理在△ABC 中，A ＋B ＋C ＝π；变形：A ＋B 2＝π2－C2.2．三角形中的三角函数关系(1)sin(A ＋B )＝sin C ；(2)cos(A ＋B )＝－cos C ； (3)sin A ＋B 2＝cos C 2；(4)cos A ＋B 2＝sin C2.3．三角形中的射影定理在△ABC 中，a ＝b cos C ＋c cos B ；b ＝a cos C ＋c cos A ；c ＝b cos A ＋a cos B . 4．用余弦定理判断三角形的形状在△ABC 中，a ，b ，c 分别为角A ，B ，C 的对边，当b 2＋c 2－a 2>0时，可知A 为锐角；当b 2＋c 2－a 2＝0时，可知A 为直角；当b 2＋c 2－a 2<0时，可知A 为钝角．第一课时正弦定理和余弦定理(一) 考点一利用正、余弦定理解三角形考法(一) 正弦定理解三角形[典例] (1)(2019·江西重点中学联考)在△ABC 中，a ＝3，b ＝2，A ＝30°，则cos B ＝________.(2)设△ABC 的内角A ，B ，C 的对边分别为a ，b ，c .若a ＝3，sin B ＝12，C ＝π6，则b ＝________.[解析] (1)由正弦定理可得sin B ＝b sin A a ＝2×sin 30°3＝13，∵a ＝3>b ＝2，∴B <A ，即B 为锐角，∴cos B ＝1－sin 2B ＝223. (2)∵sin B ＝12且B ∈(0，π)，∴B ＝π6或B ＝5π6，又∵C ＝π6，∴B ＝π6，A ＝π－B －C ＝2π3.又a ＝3，由正弦定理得a sin A ＝bsin B ，即3sin 2π3＝b sinπ6，解得b ＝1. [答案] (1)223 (2)1考法(二) 余弦定理解三角形[典例] (1)(2019·山西五校联考)在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，若b cos A ＋a cos B ＝c 2，a ＝b ＝2，则△ABC 的周长为( )A ．7.5B ．7C ．6D ．5(2)(2018·泰安二模)在△ABC 中，内角A ，B ，C 的对边分别为a ，b ，c ，且c －b2c －a＝sin Asin B ＋sin C，则角B ＝________.[解析] (1)∵b cos A ＋a cos B ＝c 2，∴由余弦定理可得b ·b 2＋c 2－a 22bc ＋a ·a 2＋c 2－b 22ac ＝c 2，整理可得2c 2＝2c 3，解得c ＝1，则△ABC 的周长为a ＋b ＋c ＝2＋2＋1＝5.(2)由正弦定理可得c －b2c －a ＝sin A sin B ＋sin C ＝a b ＋c， ∴c 2－b 2＝2ac －a 2，∴c 2＋a 2－b 2＝2ac ， ∴cos B ＝a 2＋c 2－b 22ac ＝22，∵0<B <π，∴B ＝π4.[答案] (1)D (2)π4[题组训练]1.△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，若b 2＝ac ，c ＝2a ，则cos C ＝( ) A.24B ．－24C.34D ．－34解析：选B 由题意得，b 2＝ac ＝2a 2，即b ＝2a ，∴cos C ＝a 2＋b 2－c 22ab ＝a 2＋2a 2－4a 22a ×2a＝－24.2.△ABC 的内角A ，B ，C 的对边分别为a ，b ，c .已知sin B ＋sin A (sin C －cos C )＝0，a ＝2，c ＝2，则C ＝( )A.π12 B.π6C.π4D.π3解析：选B 因为sin B ＋sin A (sin C －cos C )＝0，所以sin(A ＋C )＋sin A sin C －sin A cos C ＝0，所以sin A cos C ＋cos A sin C ＋sin A sin C －sin A cos C ＝0，整理得sin C (sin A ＋cos A )＝0.因为sin C ≠0，所以sin A ＋cos A ＝0，所以t a n A ＝－1，因为A ∈(0，π)，所以A ＝3π4，由正弦定理得sin C ＝c ·sin Aa ＝2×222＝12，又0＜C ＜π4，所以C ＝π6.3.在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，已知sin 2B ＋sin 2C ＝sin 2A ＋sin B sin C .(1)求角A 的大小；(2)若cos B ＝13，a ＝3，求c 的值．解：(1)由正弦定理可得b 2＋c 2＝a 2＋bc ，由余弦定理得cos A ＝b 2＋c 2－a 22bc ＝12，因为A ∈(0，π)，所以A ＝π3.(2)由(1)可知sin A ＝32，因为cos B ＝13，B 为△ABC 的内角，所以sin B ＝223，故sin C ＝sin(A ＋B )＝sin A cos B ＋cos A sin B ＝32×13＋12×223＝3＋226. 由正弦定理a sin A ＝c sin C得c ＝a sin C sin A ＝3×(3＋22)32×6＝1＋263.考点二判定三角形的形状[典例] (1)设△ABC 的内角A ，B ，C 所对的边分别为a ，b ，c ，若b cos C ＋c cos B ＝a sin A ，则△ABC 的形状为( )A ．锐角三角形B ．直角三角形C ．钝角三角形D ．不确定(2)在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，若sin A sin B ＝ac ，(b ＋c ＋a )(b ＋c －a )＝3bc ，则△ABC 的形状为( )A ．直角三角形B ．等腰非等边三角形C ．等边三角形D ．钝角三角形[解析] (1)法一：因为b cos C ＋c cos B ＝a sin A ，由正弦定理知sin B cos C ＋sin C cos B ＝sin A sin A ，得sin(B ＋C )＝sin A sin A .又sin(B ＋C )＝sin A ，得sin A ＝1，即A ＝π2，因此△ABC 是直角三角形．法二：因为b cos C ＋c cos B ＝b ·a 2＋b 2－c 22ab ＋c ·a 2＋c 2－b 22ac ＝2a 22a ＝a ，所以a sin A ＝a ，即sin A ＝1，故A ＝π2，因此△ABC 是直角三角形．(2)因为sin A sin B ＝a c ，所以a b ＝ac，所以b ＝c .又(b ＋c ＋a )(b ＋c －a )＝3bc ，所以b 2＋c 2－a 2＝bc ，所以cos A ＝b 2＋c 2－a 22bc ＝bc 2bc ＝12.因为A ∈(0，π)，所以A ＝π3，所以△ABC 是等边三角形．[答案] (1)B (2)C[变透练清]1.(变条件)若本例(1)条件改为“a sin A ＋b sin B <c sin C ”，那么△ABC 的形状为________．解析：根据正弦定理可得a 2＋b 2<c 2，由余弦定理得cos C ＝a 2＋b 2－c 22ab <0，故C 是钝角，所以△ABC 是钝角三角形．答案：钝角三角形2.(变条件)若本例(1)条件改为“c －a cos B ＝(2a －b )cos A ”，那么△ABC 的形状为________．解析：因为c －a cos B ＝(2a －b )cos A ， C ＝π－(A ＋B )，所以由正弦定理得sin C －sin A cos B ＝2sin A cos A －sin B ·cos A ，所以sin A cos B ＋cos A sin B －sin A cos B ＝2sin A cos A －sin B cos A ，所以cos A (sin B －sin A )＝0，所以cos A ＝0或sin B ＝sin A ，所以A ＝π2或B ＝A 或B ＝π－A (舍去)，所以△ABC 为等腰或直角三角形．答案：等腰或直角三角形3.(变条件)若本例(2)条件改为“cos A cos B ＝ba ＝2”，那么△ABC 的形状为________．解析：因为cos A cos B ＝b a ，由正弦定理得cos A cos B ＝sin B sin A ，所以sin 2A ＝sin 2B .由ba ＝2，可知a ≠b ，所以A ≠B .又因为A ，B ∈(0，π)，所以2A ＝π－2B ，即A ＋B ＝π2，所以C ＝π2，于是△ABC 是直角三角形．答案：直角三角形[课时跟踪检测]A 级1．在△ABC 中，内角A ，B ，C 的对边分别为a ，b ，c .若sin A a ＝cos Bb ，则B 的大小为( )A ．30°B ．45°C ．60°D ．90°解析：选B 由正弦定理知，sin A sin A ＝cos Bsin B ，∴sin B ＝cos B ，∴B ＝45°.2．在△ABC 中，内角A ，B ，C 的对边分别为a ，b ，c .已知b ＝40，c ＝20，C ＝60°，则此三角形的解的情况是( )A ．有一解B ．有两解C ．无解D ．有解但解的个数不确定解析：选C 由正弦定理得b sin B ＝c sin C， ∴sin B ＝b sin Cc＝40×3220＝3>1.∴角B 不存在，即满足条件的三角形不存在．3．(2018·重庆六校联考)在△ABC 中，cos B ＝ac (a ，b ，c 分别为角A ，B ，C 的对边)，则△ABC 的形状为( )A ．直角三角形B ．等边三角形C ．等腰三角形D ．等腰三角形或直角三角形解析：选A 因为cos B ＝ac ，由余弦定理得a 2＋c 2－b 22ac ＝a c ，整理得b 2＋a 2＝c 2，即C 为直角，则△ABC 为直角三角形．4．在△ABC 中，a ，b ，c 分别是内角A ，B ，C 的对边．若b sin A ＝3c sin B ，a ＝3， cos B ＝23，则b ＝( )A ．14B ．6 C.14D.6解析：选D ∵b sin A ＝3c sin B ⇒ab ＝3bc ⇒a ＝3c ⇒c ＝1，∴b 2＝a 2＋c 2－2ac cos B ＝9＋1－2×3×1×23＝6，∴b ＝ 6.5．(2019·莆田调研)在△ABC 中，内角A ，B ，C 的对边分别为a ，b ，c ，若a sin B cos C ＋c sin B cos A ＝12b ，且a >b ，则B ＝( )A.π6B.π3C.2π3D.5π6解析：选A ∵a sin B cos C ＋c sin B cos A ＝12b ，∴根据正弦定理可得sin A sin B cos C ＋sinC sin B cos A ＝12sin B ，即sin B (sin A cos C ＋sin C cos A )＝12sin B ．∵sin B ≠0，∴sin(A ＋C )＝12，即sin B ＝12.∵a >b ，∴A >B ，即B 为锐角，∴B ＝π6.6．(2019·山西大同联考)在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，若2(b cos A ＋a cos B )＝c 2，b ＝3,3cos A ＝1，则a ＝( )A.5 B ．3 C.10D ．4解析：选B 由正弦定理可得2(sin B cos A ＋sin A cos B )＝c sin C ， ∵2(sin B cos A ＋sin A cos B )＝2sin(A ＋B )＝2sin C ，∴2sin C ＝c sin C ，∵sin C >0，∴c ＝2，由余弦定理得a 2＝b 2＋c 2－2bc cos A ＝32＋22－2×3×2×13＝9，∴a ＝3.7．在△ABC 中，AB ＝6，A ＝75°，B ＝45°，则AC ＝________. 解析：C ＝180°－75°－45°＝60°，由正弦定理得AB sin C ＝ACsin B ，即6sin 60°＝AC sin 45°，解得AC ＝2. 答案：28．设△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，且a ＝2，cos C ＝－14，3sin A ＝2sin B ，则c ＝________.解析：∵3sin A ＝2sin B ，∴3a ＝2b . 又∵a ＝2，∴b ＝3.由余弦定理可知c 2＝a 2＋b 2－2ab cos C ， ∴c 2＝22＋32－2×2×3×⎝⎛⎭⎫－14＝16，∴c ＝4. 答案：49．(2018·浙江高考)在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c .若a ＝7，b ＝2，A ＝60°，则sin B ＝________，c ＝________.解析：由正弦定理a sin A ＝bsin B ，得sin B ＝b a ·sin A ＝27×32＝217.由余弦定理a 2＝b 2＋c 2－2bc cos A ，得7＝4＋c 2－4c ×cos 60°，即c 2－2c －3＝0，解得c ＝3或c ＝－1(舍去)．答案：2173 10．在△ABC 中，a ，b ，c 分别为角A ，B ，C 所对的边，sin A ，sin B ，sin C 成等差数列，且a ＝2c ，则cos A ＝________.解析：因为sin A ，sin B ，sin C 成等差数列，所以2sin B ＝sin A ＋sin C ．由正弦定理得a ＋c ＝2b ，又因为a ＝2c ，可得b ＝32c ，所以cos A ＝b 2＋c 2－a 22bc ＝94c 2＋c 2－4c 22×32c 2＝－14.答案：－1411．在△ABC 中，内角A ，B ，C 的对边分别为a ，b ，c ，且A ＝2B . (1)求证：a ＝2b cos B ； (2)若b ＝2，c ＝4，求B 的值．解：(1)证明：因为A ＝2B ，所以由正弦定理a sin A ＝b sin B ，得a sin 2B ＝bsin B ，所以a ＝2b cos B .(2)由余弦定理，a 2＝b 2＋c 2－2bc cos A ，因为b ＝2，c ＝4，A ＝2B ，所以16c os 2B ＝4＋16－16cos 2B ，所以c os 2B ＝34，因为A ＋B ＝2B ＋B <π，所以B <π3，所以cos B ＝32，所以B ＝π6.12．(2019·绵阳模拟)在△ABC 中，a ，b ，c 分别为内角A ，B ，C 的对边，且2a sin A ＝(2b ＋c )sin B ＋(2c ＋b )sin C .(1)求A 的大小；(2)若sin B ＋sin C ＝1，试判断△ABC 的形状．解：(1)由已知，结合正弦定理，得2a 2＝(2b ＋c )b ＋(2c ＋b )c ，即a 2＝b 2＋c 2＋bc . 又由余弦定理，得a 2＝b 2＋c 2－2bc cos A ，所以bc ＝－2bc cos A ，即cos A ＝－12.由于A 为△ABC 的内角，所以A ＝2π3.(2)由已知2a sin A ＝(2b ＋c )sin B ＋(2c ＋b )sin C ，结合正弦定理，得2sin 2A ＝(2sin B ＋sin C )sin B ＋(2sin C ＋sin B )sin C ，即sin 2A ＝sin 2B ＋sin 2C ＋sin B sin C ＝sin 22π3＝34.又由sin B ＋sin C ＝1，得sin 2B ＋sin 2C ＋2sin B sin C ＝1，所以sin B sin C ＝14，结合sin B ＋sin C ＝1，解得sin B ＝sin C ＝12.因为B ＋C ＝π－A ＝π3，所以B ＝C ＝π6，所以△ABC 是等腰三角形．B 级1．(2019·郑州质量预测)在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c .若2c os 2A ＋B2－cos 2C ＝1,4sin B ＝3sin A ，a －b ＝1，则c 的值为( )A.13B.7C.37D ．6解析：选A 由2c os 2A ＋B2－cos 2C ＝1，得1＋c os(A ＋B )－(2c os 2C －1)＝2－2c os 2C －cos C ＝1，即2c os 2C ＋cos C －1＝0，解得cos C ＝12或cos C ＝－1(舍去)．由4sin B ＝3sin A及正弦定理，得4b ＝3a ，结合a －b ＝1，得a ＝4，b ＝3.由余弦定理，知c 2＝a 2＋b 2－2ab cos C ＝42＋32－2×4×3×12＝13，所以c ＝13.2．(2019·长春模拟)在△ABC 中，内角A ，B ，C 所对的边分别为a ，b ，c ，且c ＝3，2sin A a ＝t a n Cc，若sin(A －B )＋sin C ＝2sin 2B ，则a ＋b ＝________. 解析：∵2sin A a ＝t a n C c ＝sin C c cos C ，且由正弦定理可得a ＝2R sin A ，c ＝2R sin C (R 为△ABC的外接圆的半径)，∴cos C ＝12.∵C ∈(0，π)，∴C ＝π3.∵sin(A －B )＋sin C ＝2sin 2B ，sin C ＝sin(A＋B )，∴2sin A cos B ＝4sin B cos B ．当cos B ＝0时，B ＝π2，则A ＝π6，∵c ＝3， ∴a ＝1，b ＝2，则a ＋b ＝3.当cos B ≠0时，sin A ＝2sin B ，即a ＝2b .∵cos C ＝a 2＋b 2－c 22ab ＝12，∴b 2＝1，即b ＝1，∴a ＝2，则a ＋b ＝3.综上，a ＋b ＝3.答案：33．在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，且2a cos C －c ＝2b .(1)求角A 的大小；(2)若c ＝2，角B 的平分线BD ＝3，求a .解：(1)2a cos C －c ＝2b ⇒2sin A cos C －sin C ＝2sin B ⇒2sin A cos C －sin C ＝2sin(A ＋C )＝2sin A cos C ＋2cos A sin C ，∴－sin C ＝2cos A sin C ，∵sin C ≠0，∴cos A ＝－12，又A ∈(0，π)，∴A ＝2π3. (2)在△ABD 中，由正弦定理得，AB sin ∠ADB ＝BD sin A， ∴sin ∠ADB ＝AB sin A BD ＝22. 又∠ADB ∈(0，π)，A ＝2π3， ∴∠ADB ＝π4，∴∠ABC ＝π6，∠ACB ＝π6，b ＝c ＝2，由余弦定理，得a 2＝c 2＋b 2－2c ·b ·cos A ＝(2)2＋(2)2－2×2×2c os 2π3＝6，∴a ＝ 6.。

正弦定理和余弦定理笔记

正弦定理和余弦定理笔记一、正弦定理。

（一）定理内容。

在一个三角形中，各边和它所对角的正弦值的比相等，即(a)/(sin A)=(b)/(sinB)=(c)/(sin C) = 2R（R为三角形外接圆半径）。

（二）证明方法。

1. 外接圆法。

- 设ABC的外接圆半径为R。

- 连接圆心O与三角形的三个顶点A、B、C。

- 对于∠ A，根据同弧所对的圆周角是圆心角的一半，可知∠ A=(1)/(2)∠BOC。

- 由正弦定义，在BOC中，a = 2Rsin A，同理可得b = 2Rsin B，c = 2Rsin C，所以(a)/(sin A)=(b)/(sin B)=(c)/(sin C)=2R。

2. 向量法（略提）- 利用向量的数量积公式→AB·→AC=|→AB||→AC|cos A，通过一系列向量运算也可证明正弦定理，但相对外接圆法较复杂。

（三）应用。

1. 已知两角和一边，求其他边和角。

- 例如，已知A = 30^∘，B = 45^∘，a = 10。

- 根据三角形内角和C=180^∘-A - B = 105^∘。

- 由正弦定理(a)/(sin A)=(b)/(sin B)，可得b=(asin B)/(sin A)。

- 先求出sin 45^∘=(√(2))/(2)，sin 30^∘=(1)/(2)，则b=(10×frac{√(2))/(2)}{(1)/(2)} = 10√(2)。

- 再根据(a)/(sin A)=(c)/(sin C)求出c的值，sin105^∘=sin(60^∘+45^∘)=sin60^∘cos45^∘+cos60^∘sin45^∘=(√(6)+√(2))/(4)，c=(asin C)/(sin A)=(10×frac{√(6)+√(2))/(4)}{(1)/(2)} = 5(√(6)+√(2))。

2. 已知两边和其中一边的对角，求其他边和角（可能有一解、两解或无解情况）- 例如，已知a = 10，b = 20，A = 30^∘。

解三角形之：正弦定理和余弦定理

三角之：正弦定理，余弦定理 2011-7-23一．基础知识（1）正弦定理：Cc Bb Aa sin sin sin ==(2)余弦定理： cos 2222ab c b a -+= AB ac c a b cos 2222-+=C ab b a c cos 2222-+= 注意：正弦定理和余弦定理都是“知三求一”,但应注意区别：正弦定理是“知两角一边可以求一边”或“知两边一角可以求一角”；余弦定理是“知三边可以求一角”或“知两边一角可以求一边”。

正弦定理推论:（1）a=2RsinA,b=2RsinB,c=2RsinC (2)C Rc B Rb A Ra sin 2,sin 2,sin 2===(3) a :b :c=sinA:sinB:sinC(4)C B A c b a C B A sin sin sin >>⇔>>⇔>> 余弦定理推论：abcb a C acbc a B bcac b A 2cos ,2cos ,2cos 222222222-+=-+=-+=（2）三角形面积公式：,sin 21C ab S ABC =∆,sin 21A bc S ABC =∆B ca S ABC sin 21=∆二.基础题型题型一：解三角形（在各种情况下能熟练解三角形,只需说明做法即可）例1: 解此三角形中，oo C B a ABC 75,60,8===∆（已知两角一边）例2：解此三角形中，oo C A c 75,45,3ABC ===∆（已知两角一边）例3：解此三角形中，oB c a ABC 150,3,1===∆（已知一角两边）例4：解此三角形中，045,1,2===∆B c b ABC （已知一角两边）例5：解此三角形中，oB b a ABC 45,2,3===∆（已知一角两边）例6：解此三角形中，,30,2,34o C c b ABC ===∆（已知一角两边）例7：ABC ∆中，若8:7:5::=c b a ，解此三角形小结：（1）三角形中必须已知三个条件时（其中必须有边和角），才可解三角形。

高中数学必修五-正弦定理与余弦定理

正弦定理与余弦定理知识集结知识元正弦定理公式知识讲解1．正弦定理【知识点的知识】1．正弦定理和余弦定理定理正弦定理余弦定理内容＝2R（R是△ABC外接圆半径）a2＝b2+c2﹣2bc cos A，b2＝a2+c2﹣2ac cos B，c2＝a2+b2﹣2ab cos C变形形式①a＝2R sin A，b＝2R sin B，c＝2R sin C；②sin A＝，sin B＝，sin C＝；③a：b：c＝sin A：sin B：sin C；④a sin B＝b sin A，b sin C＝c sin B，a sin C＝c sin A cos A＝，cos B＝，cos C＝解决三角形的问题①已知两角和任一边，求另一角和其他两条边；②已知两边和其中一边的对角，求另一边和其他两角①已知三边，求各角；②已知两边和它们的夹角，求第三边和其他两角在△ABC中，已知a，b和角A时，解的情况A为锐角A为钝角或直角图形关系式a＝b sin A b sin A＜a＜b a≥b a＞b一解两解一解一解解的个数由上表可知，当A为锐角时，a＜b sin A，无解．当A为钝角或直角时，a≤b，无解．2、三角形常用面积公式1．S＝a•h a（h a表示边a上的高）；2．S＝ab sin C＝ac sin B＝bc sin A．3．S＝r（a+b+c）（r为内切圆半径）．【正余弦定理的应用】1、解直角三角形的基本元素．2、判断三角形的形状．3、解决与面积有关的问题．4、利用正余弦定理解斜三角形，在实际应用中有着广泛的应用，如测量、航海、几何等方面都要用到解三角形的知识（1）测距离问题：测量一个可到达的点到一个不可到达的点之间的距离问题，用正弦定理就可解决．解题关键在于明确：①测量从一个可到达的点到一个不可到达的点之间的距离问题，一般可转化为已知三角形两个角和一边解三角形的问题，再运用正弦定理解决；②测量两个不可到达的点之间的距离问题，首先把求不可到达的两点之间的距离转化为应用正弦定理求三角形的边长问题，然后再把未知的边长问题转化为测量可到达的一点与不可到达的一点之间的距离问题．（2）测量高度问题：解题思路：①测量底部不可到达的建筑物的高度问题，由于底部不可到达，因此不能直接用解直角三角形的方法解决，但常用正弦定理计算出建筑物顶部或底部到一个可到达的点之间的距离，然后转化为解直角三角形的问题．②对于顶部不可到达的建筑物高度的测量问题，我们可选择另一建筑物作为研究的桥梁，然后找到可测建筑物的相关长度和仰、俯角等构成三角形，在此三角形中利用正弦定理或余弦定理求解即可．点拨：在测量高度时，要理解仰角、俯角的概念．仰角和俯角都是在同一铅锤面内，视线与水平线的夹角．当视线在水平线之上时，成为仰角；当视线在水平线之下时，称为俯角．例题精讲正弦定理公式例1.已知△ABC中，角A，B，C所对的边分别是a，b，c．若A=45°，B=30°，a=，则b=（）A．B．1 C．2 D．例2.在△ABC中，角A，B，C的对边分别为a，b，c，若，则B=（）A．B．C．D．或例3.在△ABC中，已知三个内角为A，B，C满足sin A：sin B：sin C=3：5：7，则C=（）A．90°B．120°C．135°D．150°利用正弦定理解三角形知识讲解【正余弦定理的应用】1、解直角三角形的基本元素．2、判断三角形的形状．3、解决与面积有关的问题．4、利用正余弦定理解斜三角形，在实际应用中有着广泛的应用，如测量、航海、几何等方面都要用到解三角形的知识例题精讲利用正弦定理解三角形例1.在△ABC中，a，b，c是内角A，B，C所对的边．若a>b，则下列结论不一定成立的（）A．A>B B．sin A>sin BC．cos A<cos B D．sin2A>sin2B例2.在△ABC中，角A，B，C的对边分别是a，b，c，且，则角A的大小为（）A．B．C．D．例3.在△ABC中，三内角A，B，C的对边分别为a，b，c，若sin B =b sin A，则a=（）A ．B ．C．1 D．三角形面积公式的简单应用知识讲解1．余弦定理【知识点的知识】1．正弦定理和余弦定理定理正弦定理余弦定理内容＝2R（R是△ABC外接圆半径）a2＝b2+c2﹣2bc cos A，b2＝a2+c2﹣2ac cos B，c2＝a2+b2﹣2ab cos C变形形式①a＝2R sin A，b＝2R sin B，c＝2R sin C；②sin A＝，sin B＝，sin C＝；③a：b：c＝sin A：sin B：sin C；④a sin B＝b sin A，b sin C＝c sin B，a sin C＝c sin A cos A＝，cos B＝，cos C＝解决三角形的问题①已知两角和任一边，求另一角和其他两条边；②已知两边和其中一边的对角，求另一边和其他两角①已知三边，求各角；②已知两边和它们的夹角，求第三边和其他两角A为锐角A为钝角或直角图形关系式a＝b sin A b sin A＜a＜b a≥b a＞b 解的个数一解两解一解一解由上表可知，当A为锐角时，a＜b sin A，无解．当A为钝角或直角时，a≤b，无解．例题精讲三角形面积公式的简单应用例1.已知△ABC的内角A，B，C的对边分别为a，b，c，且（a+b）2=c2+ab，B=30°，a=4，则△ABC的面积为（）A．4 B．3C．4D．6例2.设△ABC的三个内角A，B，C成等差数列，其外接圆半径为2，且有，则三角形的面积为（）A．B．C．或D．或例3.在△ABC中角ABC的对边分别为a、b、c，cos C=，且a cos B+b cos A=2，则△ABC面积的最大值为（）A．B．C．D．利用余弦定理解三角形当堂练习填空题练习1.如图，O在△ABC的内部，且++3=，则△ABC的面积与△AOC的面积的比值为_____．练习2.锐角△ABC的内角A，B，C的对边分别为a，b，c，已知c2-8=（a-b）2，a=2c sin A，则△ABC的面积为____．练习3.在△ABC中，内角A，B，C的对边分别为a，b，c，已知，则的最大值是____．解答题练习1.'在△ABC中，角A，B，C所对的边分别为a，b，c，且满足．（1）求角B的大小；（2）若D为AC的中点，且BD=1，求S△ABC的最大值．'练习2.'在△ABC中，角A、B、C的对边分别是a、b、c，若（a+c）sin B-b sin C=b cos A．（1）求角A；（2）若△ABC的面积为4，a=6，求△ABC的周长．'练习3.'△ABC内角A，B，C所对的边分别为a，b，c．若。

正弦定理余弦定理知识点总结及最全证明

正弦定理余弦定理知识点总结及最全证明正弦定理概述：正弦定理是三角形的一个重要定理，它描述了三角形中各边与其相对的正弦值之间的关系。

正弦定理可以用于求解任意三角形的边长或角度。

正弦定理表达式：在一个三角形ABC中，有以下正弦定理的表达式：a/sin(A) = b/sin(B) = c/sin(C)其中，a、b、c分别表示三角形的边长，A、B、C表示三角形的角度。

正弦定理表明，三角形的任意一边的长度与这条边相对的角的正弦值成正比。

正弦定理的证明：可以使用数学推导来证明正弦定理。

这里给出一种较为详细的证明方法。

证明：1. 通过三角形的边长关系：a = b * sin(A) / sin(B)和c = b *sin(C) / sin(B)，可得到以下关系式：a * sin(B) = b * sin(A)和c * sin(B) = b * sin(C)2.利用向量叉积原理知识，假设D为线段BC上的一点，则由向量的垂直性知：向量BD与向量AD是垂直的，向量CD与向量AD是垂直的。

3. 记向量AD为向量a，向量BD为向量b，向量CD为向量c，由向量b与向量a的垂直性可得：向量b·向量a = ，b， * ，a， *sin(∠BA) = b * AD * sin(∠BA)。

4. 同理，由向量c与向量a的垂直性可得：向量c·向量a = ，c，* ，a，* sin(∠CA) = c * AD * sin(∠CA)。

5. 因为∠C + ∠A = ∠BA，即∠CA + ∠BA = 180°，所以sin(∠BA) = sin(∠CA)。

所以有b * AD * sin(∠BA) = c * AD *sin(∠CA)。

6. 即有b * AD * sin(∠BA) = c * AD * sin(∠BA)，那么b = c，所以定理得证。

余弦定理概述：余弦定理是三角形的另一个重要定理，它描述了三角形中各边与其相对的角之间的关系。

正余弦定理知识点权威总结

正余弦定理知识点权威总结：一、正弦定理和余弦定理1、定理正弦定理余弦定理2、内容1、正弦定理：在C∆AB中，a、b、c分别为角A、B、C的对边，R为C∆AB的外接圆的半径，则有2sin sin sina b cRC===A B．2222222222cos,2cos,2cos.a b c bc Ab c a ac Bc a b ab C=+-=+-=+-3、推论①a=2RsinA,b=2RsinB,c=2RsinC;②sinA=2aR,sinB=2bR,sinC=2cR;③a:b:c=sinA: sinB: sinC;④sin sin sin sina b c aA B C A++=++222222222cos;2cos;2cos.2b c aAbca c bBcaa b cCab+-=+-=+-=4、注意（1）在△ABC中，已知A,a,b，讨论三角形解的情况.先由aAbBsinsin=可进一步求出B；则 C=180°-(A+B),从而ACacsinsin=.（2）在ΔABC中，sinA>sinB是A>B的充要条件。

（∵sinA>sinB⇔22a bR R>⇔a>b⇔A>B）由余弦定理判断三角形的形状a2=b2+c2⇔A是直角⇔△ABC是直角三角形，a2＞b2+c2⇔A是钝角⇔△ABC是钝角三角形，a2＜b2+c⇔A是锐角/△ABC是锐角三角形。

（注意：A是锐角/ △ABC是锐角三角形，必须说明每个角都是锐角）5、三角形面积公式三角形面积公式：①111sin sin sin222CS bc ab C ac∆AB=A==B；②prcpbpappSABC=---=∆))()((，其中2cbap++=，r为内切圆半径；③RabcSABC4=∆，R为外接圆半径．6、已知两边和其中1.当A为钝角或直角时，必须a＞b才能有且只有一解；否则无解．2.当A为锐角时，如果a≥b，那么只有一解；如果a＜b，那么可以分下面三种情况来讨论：一边的对角解三角形，有两解、一解、无解三种情况（1）若a＞b sin A，则有两解；（2）若a=b sin A，则只有一解；（3）若a＜b sin A，则无解．注意在已知三角形的两边及其中一边的对角解三角形时，只有当A为锐角且b sin A ＜a＜b时，有两解；其他情况时则只有一解或无解．（1）A为直角或钝角（2）A为锐角7、解三角形的一般思路：（1）已知两角及一边，利用正弦定理求解；（2）已知两边及其中一边的对角，利用正弦定理或余弦定理求解，解的情况可能不唯一；（3）已知两边及其夹角，利用余弦定理求解；（4）已知三边，利用余弦定理求解.8、方法与技巧总结1、已知两角A、B，一边a,由A+B+C=π及sin sin sina b cA B C==，可求角C，再求b、c；2、已知两边b、c与其夹角A，由a2=b2+c2-2b c cosA，求出a，再由余弦定理，求出角B、C；3、已知三边a、b、c，由余弦定理可求出角A、B、C；4、已知两边a、b及其中一边的对角A，由正弦定理sin sina bA B=，求出另一边b的对角B，由C=π-(A+B)，求出c，再由sin sina cA C=求出C，而通过sin sina bA B=求B时，可能出一解，两解或无解。

(整理版)第十七讲正弦定理与余弦定理

第十七讲正弦定理与余弦定理1、正弦定理：在三角形ABC 中，a,b,c 分别为角A ，B ，C 的对边，R 为三角形ABC 的外接圆的半径，那么有2sin sin sin sin sin sin a b c a b c R A B C A B C++====++，注意以下一些变式： ()()()1sin sin sin ,2sin ,sin ,sin 22232sin ,2sin ,2sin .a b c a b c A B C A B C R R R a R A b R B b R C ::=::======2、余弦定理：在三角形ABC 中，有222222222222222222cos 22cos ,2cos ,cos 22cos cos 2b c a A bc a b c bc A a c b b a c ac B B ac c a b ab C a b c C ab ⎧+-=⎪⎧=+-⎪⎪+-⎪=+-=⎨⎨⎪⎪=+-⎩⎪+-=⎪⎩3、其它公式：（1）射影公式：cos cos ,cos cos ,cos cos a b C c B b a C c A c a B b A =+=+=+()()()()()()()()()()()()()()()()2122122211221112sin 32241142sin sin sin 56221,,,,72282a abc S ah S ab C S RS R A B C S a b c r S x y x y AB x y AC x y S AB AC AB AC a b c S P ∆∆∆∆∆∆∆∆=====++-===•-•++⎫==⎪⎭2七个三角形面积公式：，，，，＝由及向量的数量积公式可得这叫海伦公式()，一般不用其中r 为三角形ABC 内切圆半径，R 为外接圆的半径，()12p a b c =++ 4、正弦定理在解三角形中的应用：〔1〕两角和一边解三角形，只有一解。

正、余弦定理总结

正余弦定理知识点总结：一、正弦定理和余弦定理1、正弦定理和余弦定理注：在ΔABC中，sinA>sinB是A>B的充要条件。

（∵sinA>sinB ⇔22a bR R>⇔a>b ⇔A>B ）二、应用举例1、实际问题中的常用角（1）仰角和俯角在视线和水平线所成的角中，视线在水平线上方的角叫仰角，在水平线下文的叫俯角（如图①）（2）方位角从指北方向顺时针转到目标方向线的水平角，如B 点的方位角为α（如图②）注：仰角、俯角、方位角的区别是：三者的参照不同。

仰角与俯角是相对于水平线而言的，而方位角是相对于正北方向而言的。

（3）方向角：相对于某一正方向的水平角（如图③）①北偏东α即由指北方向顺时针旋转α到达目标方向； ②北偏本α即由指北方向逆时针旋转α到达目标方向；③南偏本等其他方向角类似。

（4）坡度：坡面与水平面所成的二面角的度数（如图④，角θ为坡角）坡比：坡面的铅直高度与水平长度之比（如图④，i 为坡比） 2、ΔABC 的面积公式（1）1()2a a S a h h a =表示边上的高；（2）111sin sin sin ()2224abcS ab C ac B bc A R R ====为外接圆半径；（3）1()()2S r a b c r =++为内切圆半径。

〖例1〗（11浙江文）在ABC ∆中，角,,A B C 所对的边分,,a b c .若cos sin a A b B =，则2sin cos cos A A B +=（）A ．12 B ．12C ． -1D ． 1 答案：D1.在△ABC 中，222sin sin sin sin sin A B C B C ≤+-，则A 的取值范围是（A ）(0,]6π（B ）[,)6ππ（C ）(0,]3π（D ）[,)3ππ答案：C 解析：由222sin sin sin sin sin A B C B C ≤+-得222a b c bc ≤+-，即222122b c a bc +-≥，∴1cos 2A ≥，∵0A π<<，故03A π<≤，选C ．2.在△ABC 中，角A 、B 、C 的对边分别是a 、b 、c ，若A ∶B ∶C ＝1∶2∶3，则a ∶b ∶c 等于( )A．1∶2∶3 B．2∶3∶4 C．3∶4∶5 D．1∶3∶2答案 D3．在△ABC 中，若tan A ＝13，C ＝150°，BC ＝1，则AB ＝________.答案 102解析 ∵tan A ＝13，A ∈(0,180°)，∴sin A ＝1010.由正弦定理知BC sin A ＝AB sin C ，∴AB ＝BC ·sin C sin A ＝1×sin 150°1010＝102.4．在△ABC 中，A ＝60°，a ＝63，b ＝12，S △ABC ＝183，则a ＋b ＋csin A ＋sin B ＋sin C＝________，c ＝________.答案 12 6解析 a ＋b ＋c sin A ＋sin B ＋sin C ＝a sin A ＝6332＝12.∵S △ABC ＝12ab sin C ＝12×63×12sin C ＝18 3.∴sin C ＝12，∴c sin C ＝asin A＝12，∴c ＝6.〖例2〗（1）（10上海文）若△ABC 的三个内角满足sin :sin :sin 5:11:13A B C =则△ABCA ．一定是锐角三角形.B ．一定是直角三角形.C ．一定是钝角三角形.D ．可能是锐角三角形，也可能是钝角三角形. 解析：由sin :sin :sin 5:11:13A B C =及正弦定理得a:b:c=5:11:13由余弦定理得0115213115cos 222<⨯⨯-+=c ，所以角C 为钝角（2）在锐角△ABC 中，BC ＝1，B ＝2A ，则ACcos A 的值等于______，AC 的取值范围为________．解析：由正弦定理得AC sin2A ＝BC sin A . 即AC 2sin A cos A ＝1sin A .∴ACcos A＝2.∵△ABC 是锐角三角形，∴0＜A ＜π2，0＜2A ＜π2，0＜π－3A ＜π2，解得π6＜A ＜π4.由AC ＝2cos A 得AC 的取值范围为(2，3)．答案：2 (2，3)1．在△ABC 中，若a cos A ＝b cos B ＝ccos C，则△ABC 是( ) A．直角三角形 B．等边三角形 C．钝角三角形 D．等腰直角三角形答案 B解析由正弦定理知：sin A cos A ＝sin B cos B ＝sin Ccos C ，∴tan A ＝tan B ＝tan C ，∴A ＝B ＝C .2．在△ABC 中，sin A ＝34，a ＝10，则边长c 的取值范围是( )A.⎝ ⎛⎭⎪⎫152，＋∞ B．(10，＋∞) C．(0,10) D.⎝⎛⎦⎥⎤0，403答案 D解析 ∵c sin C ＝a sin A ＝403，∴c ＝403sin C ．∴0<c ≤403.3．在△ABC 中，a ＝2b cos C ，则这个三角形一定是( )A．等腰三角形 B．直角三角形 C．等腰直角三角形 D．等腰或直角三角形答案 A解析由正弦定理：sin A ＝2sin B cos C ，∴sin(B ＋C )＝2sin B cos C ∴sin B cos C ＋cos B sin C ＝2sin B cos C ，∴sin(B －C )＝0，∴B ＝C .4、在△ABC 中，cos 2B 2＝a ＋c2c ，(a ，b ，c 分别为角A ，B ，C 的对边)，则△ABC 的形状为( )A ．正三角形 B ．直角三角形C ．等腰三角形或直角三角形D ．等腰直角三角形解析：∵cos 2B2＝a ＋c 2c ，∴cos B ＋12＝a ＋c 2c ，∴cos B ＝ac ，∴a 2＋c 2－b 22ac ＝a c， ∴a 2＋c 2－b 2＝2a 2，即a 2＋b 2＝c 2，∴△ABC 为直角三角形．答案：B〖例3〗（2009浙江文）在ABC ∆中，角,,AB C 所对的边分别为,,a b c ，且满足cos 25A =，3AB AC ⋅=．（I ）求ABC ∆的面积；（II ）若1c =，求a 的值．解析：（Ⅰ）531)552(212cos2cos 22=-⨯=-=A A 又),0(π∈A ，54cos1sin2=-=A A ，而353cos .===bc A ，所以5=bc ，所以ABC ∆（Ⅱ）由（Ⅰ）知5=bc ，而1=c ，所以5=b ，所以5232125cos 222=⨯-+=-+=Abc c b a1、在ABC ∆中，角,,A B C 所对的边分别为,,a b c ，且满足cos 25A =，3AB AC ⋅=．（I ）求ABC∆的面积；（II ）若6b c +=，求a 的值．解（1）因为cos 25A =，234cos 2cos 1,sin 255A A A ∴=-==，又由3AB AC ⋅=得cos 3,bc A =5bc ∴=，1sin 22ABC S bc A ∆∴==（2）对于5bc =，又6b c +=，5,1b c ∴==或1,5b c ==，由余弦定理得2222cos 20a b c bc A =+-=，a ∴=2、在∆ABC 中，sin(C-A)=1, sinB=13。

(完整版)(经典)正弦定理、余弦定理知识点总结及最全证明(最新整理)

正弦定理、余弦定理知识点总结及证明方法——王彦文青铜峡一中1．掌握正弦定理、余弦定理，并能解决一些简单的三角形度量问题．2．能够运用正弦定理、余弦定理等知识和方法解决一些与测量和几何计算有关的实际问题．主要考查有关定理的应用、三角恒等变换的能力、运算能力及转化的数学思想．解三角形常常作为解题工具用于立体几何中的计算或证明，或与三角函数联系在一起求距离、高度以及角度等问题，且多以应用题的形式出现．1．正弦定理(1)正弦定理：在一个三角形中，各边和它所对角的正弦的比相等，即．其中R 是三角形外接圆的半径．(2)正弦定理的其他形式：①a ＝2R sin A ，b ＝，c ＝；②sin A ＝，sin B ＝，a2Rsin C ＝；③a ∶b ∶c ＝______________________.2．余弦定理(1)余弦定理：三角形中任何一边的平方等于其他两边的平方的和减去这两边与它们的夹角的余弦的积的两倍．即a 2＝，b 2＝，c 2＝ .若令C ＝90°，则c 2＝，即为勾股定理．(2)余弦定理的变形：cos A＝，cos B ＝，cos C ＝ .若C 为锐角，则cos C >0，即a 2＋b 2______c 2；若C 为钝角，则cos C <0，即a 2＋b 2______c 2.故由a 2＋b 2与c 2值的大小比较，可以判断C 为锐角、钝角或直角．(3)正、余弦定理的一个重要作用是实现边角____________，余弦定理亦可以写成sin 2A ＝sin 2B ＋sin 2C －2sin B sin C cos A ，类似地，sin 2B ＝____________；sin 2C ＝__________________.注意式中隐含条件A ＋B ＋C ＝π.3．解斜三角形的类型(1)已知三角形的任意两个角与一边，用____________定理．只有一解．(2)已知三角形的任意两边与其中一边的对角，用____________定理，可能有___________________．如在△ABC 中，已知a ，b和A 时，解的情况如表：A 为锐角A 为钝角或直角图形关系式a ＝b sin A b sin A <a <b a ≥b a >b解的个数① ② ③ ④ (3)已知三边，用____________定理．有解时，只有一解．(4)已知两边及夹角，用____________定理，必有一解．4．三角形中的常用公式或变式(1)三角形面积公式S △＝＝＝____________＝____________＝____________．其中R ，r 分别为三角形外接圆、内切圆半径．(2)A ＋B ＋C ＝π，则A ＝__________，＝__________，从而sin A ＝A 2____________，cos A ＝____________，tan A ＝____________；sin ＝__________，cos ＝__________，A 2A2tan ＝________.tan A ＋tan B ＋tan C ＝A 2__________.(3)若三角形三边a ，b ，c 成等差数列，则2b ＝____________⇔2sin B ＝____________⇔2sin ＝cos ⇔2cos ＝cos ⇔tan tan ＝B 2A －C 2A ＋C 2A －C 2A 2C 2.13【自查自纠】1．(1)＝＝＝2R a sin A b sin B c sin C (2)①2R sin B 2R sin C ②　b 2R c 2R ③sin A ∶sin B ∶sin C 2．(1)b 2＋c 2－2bc cos A c 2＋a 2－2ca cos B a 2＋b 2－2ab cos C a 2＋b 2(2) >　b 2＋c 2－a 22bc c 2＋a 2－b 22ca a 2＋b 2－c 22ab <(3)互化　sin 2C ＋sin 2A －2sin C sin A cos B sin 2A ＋sin 2B －2sin A sin B cos C 3．(1)正弦　(2)正弦　一解、两解或无解　①一解②二解　③一解　④一解　(3)余弦　(4)余弦4．(1)ab sin C bc sin A ac sin B 121212abc 4R (a ＋b ＋c )r 12(2)π－(B ＋C )　－　π2B ＋C 2sin(B ＋C )　－cos(B ＋C )－tan(B ＋C )　cos sin B ＋C 2B ＋C21tan B ＋C 2tan A tan B tan C (3)a ＋c sin A ＋sin C 在△ABC 中，A >B 是sin A >sin B 的( )A ．充分不必要条件 B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件解：因为在同一三角形中，角大则边大，边大则正弦大，反之也成立，故是充要条件．故选C .　在△ABC 中，已知b ＝6，c ＝10，B ＝30°，则解此三角形的结果有( )A ．无解 B ．一解C ．两解 D ．一解或两解解：由正弦定理知sin C ＝＝，又由c ·sin B b 56c >b >c sin B 知，C 有两解．也可依已知条件，画出△ABC ，由图知有两解．故选C .　()设△ABC 的内角A, B, C 所2013·陕西对的边分别为a, b, c, 若b cos C ＋c cos B ＝a sin A, 则△ABC 的形状为( )A ．锐角三角形B ．直角三角形C ．钝角三角形D ．不确定解：由已知和正弦定理可得sin B cos C ＋sin C cos B ＝sin A ·sin A ，即sin(B ＋C )＝sin A sin A ，亦即sin A ＝sin A sin A .因为0<A <π，所以sin A ＝1，所以A ＝.所以三角形为直角三π2角形．故选B .　()在△ABC 中，角A ，B ，C 2012·陕西所对的边分别为a ，b ，c .若a ＝2，B ＝，c ＝2π6，则b ＝________．3解：由余弦定理知b 2＝a 2＋c 2－2ac cos B ＝22＋2－2×2×2×cos ＝4，b ＝2.故填2.(23)3π6　在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，若a ＝，b ＝2，sin B ＋cos B ＝，22则角A 的大小为________．解：∵sin B ＋cos B ＝，2∴sin ＝，即sin ＝1.2(B ＋π4)2(B ＋π4)又∵B ∈(0，π)，∴B ＋＝，B ＝.π4π2π4根据正弦定理＝，可得sin A ＝a sin A bsin B＝.a sin B b 12∵a ＜b ，∴A ＜B .∴A ＝.故填.π6π6类型一　正弦定理的应用　△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，已知A －C ＝90°，a ＋c ＝b ，求C .2解：由a ＋c ＝b 及正弦定理可得sin A ＋2sin C ＝sin B .2又由于A －C ＝90°，B ＝180°－(A ＋C )，故cos C ＋sin C ＝sin A ＋sin C ＝sin(A ＋C )＝2sin(90°＋2C )＝sin2(45°＋C )．22∴sin(45°＋C )＝2sin(45°＋22C )cos(45°＋C )，即cos(45°＋C )＝.12又∵0°＜C ＜90°，∴45°＋C ＝60°，C ＝15°.【评析】利用正弦定理将边边关系转化为角角关系，这是解此题的关键．　()在△ABC 中，角A ，B ，2012·江西C 的对边分别为a ，b ，c .已知A ＝，b sin π4(π4＋C)－c sin＝a .(π4＋B )(1)求证：B －C ＝；π2(2)若a ＝，求△ABC 的面积．2解：(1)证明：对b sin－c sin (π4＋C )(π4＋B )＝a 应用正弦定理得sin B sin－sin C sin (π4＋C )＝sin A ，(π4＋B )即sin B －sin C(22sin C ＋22cos C )＝，整理得sin B cos C －(22sin B ＋22cos B)22sin C cos B ＝1，即sin ＝1.(B －C )由于B ，C ∈，∴B －C ＝.(0，3π4)π2(2)∵B ＋C ＝π－A ＝，又由(1)知B －C ＝3π4，π2∴B ＝，C ＝.5π8π8∵a ＝，A ＝，∴由正弦定理知b ＝2π4a sin Bsin A＝2sin ，c ＝＝2sin .5π8a sin C sin A π8∴S △ABC ＝bc sin A ＝×2sin ×2sin12125π8π8×22＝sin sin ＝cos sin ＝sin25π8π82π8π822＝.π412类型二　余弦定理的应用　在△ABC 中，a ，b ，c 分别是角A ，B ，C的对边，且＝－.cos B cos C b2a ＋c (1)求B 的大小；(2)若b ＝，a ＋c ＝4，求△ABC 的面积．13解：(1)由余弦定理知，cos B ＝，a 2＋c 2－b 22accos C ＝，将上式代入＝－得a 2＋b 2－c 22ab cos B cos C b 2a ＋c ·＝－，a 2＋c 2－b 22ac 2ab a 2＋b 2－c 2b2a ＋c整理得a 2＋c 2－b 2＝－ac .∴cos B ＝＝＝－.a 2＋c 2－b 22ac －ac 2ac 12∵B 为三角形的内角，∴B ＝π.23(2)将b ＝，a ＋c ＝4，B ＝π代入b 2＝a 21323＋c 2－2ac cos B ，得13＝42－2ac －2ac cos π，23解得ac ＝3.∴S △ABC ＝ac sin B ＝.12334【评析】①根据所给等式的结构特点利用余弦定理将角化边进行变形是迅速解答本题的关键．②熟练运用余弦定理及其推论，同时还要注意整体思想、方程思想在解题过程中的运用．　若△ABC 的内角A ，B ，C 所对的边a ，b ，c 满足(a ＋b )2－c 2＝4，且C ＝60°，则ab的值为( )A. B ．8－4 C ．1 D.43323解：由余弦定理得c 2＝a 2＋b 2－2ab cos C ＝a 2＋b 2－ab ，代入(a ＋b )2－c 2＝4中得(a ＋b )2－(a 2＋b 2－ab )＝4，即3ab ＝4，∴ab ＝.故选A .43类型三　正、余弦定理的综合应用　()△ABC 的内2013·全国新课标Ⅱ角A 、B 、C 的对边分别为a ，b ，c ，已知a ＝b cos C ＋c sin B .(1)求B ；(2)若b ＝2，求△ABC 面积的最大值．解：(1)由已知及正弦定理得sin A ＝sin B cos C ＋sin C sin B .①又A ＝π－(B ＋C )，故sin A ＝sin(B ＋C )＝sin B cos C ＋cos B sin C .②由①，②和C ∈(0，π)得sin B ＝cos B .又B ∈(0，π)，所以B ＝.π4(2)△ABC 的面积S ＝ac sin B ＝ac .1224由已知及余弦定理得4＝a 2＋c 2－2ac cos .π4又a 2＋c 2≥2ac ，故ac ≤，42－2当且仅当a ＝c 时，等号成立．因此△ABC 面积的最大值为＋1.2【评析】(1)化边为角与和角或差角公式的正向或反向多次联用是常用的技巧；(2)已知边及其对角求三角形面积最值是高考中考过多次的问题，既可用三角函数求最值，也可以用余弦定理化边后用不等式求最值．　()设△ABC 的内角A ，B ，2013·山东C 所对的边分别为a ，b ，c ，且a ＋c ＝6，b ＝2，cos B＝.79(1)求a ，c 的值；(2)求sin(A －B )的值．解：(1)由余弦定理b 2＝a 2＋c 2－2ac cos B ，得b 2＝(a ＋c )2－2ac (1＋cos B )，又a ＋c ＝6，b ＝2，cos B ＝，所以ac ＝9，解得a ＝3，c ＝3.79(2)在△ABC 中，sin B ＝＝，1－cos 2B 429由正弦定理得sin A ＝＝.a sin B b 223因为a ＝c ，所以A 为锐角，所以cos A ＝＝.1－sin 2A 13因此sin(A －B )＝sin A cos B －cos A sin B ＝.10227类型四　判断三角形的形状在三角形ABC 中，若tan A ∶tan B ＝a 2∶b 2，试判断三角形ABC 的形状．解法一：由正弦定理，得＝，a 2b 2sin 2Asin 2B所以＝，tan A tan B sin 2Asin 2B所以＝，即sin2A ＝sin2B .sin A cos B cos A sin B sin 2A sin 2B所以2A ＝2B ，或2A ＋2B ＝π，因此A ＝B或A ＋B ＝，从而△ABC 是等腰三角形或直角三π2角形．解法二：由正弦定理，得＝，所以a 2b 2sin 2Asin 2B＝，所以＝，再由正、余弦tan A tan B sin 2A sin 2B cos B cos A sin A sin B定理，得＝，化简得(a 2－b 2)(c 2－a 2a 2＋c 2－b 22ac b 2＋c 2－a 22bca b －b 2)＝0，即a 2＝b 2或c 2＝a 2＋b 2.从而△ABC 是等腰三角形或直角三角形．【评析】由已知条件，可先将切化弦，再结合正弦定理，将该恒等式的边都化为角，然后进行三角函数式的恒等变形，找出角之间的关系；或将角都化成边，然后进行代数恒等变形，可一题多解，多角度思考问题，从而达到对知识的熟练掌握．　()在△ABC 中，若sin 2A2012·上海＋sin 2B <sin 2C ，则△ABC 的形状是( )A ．锐角三角形B ．直角三角形C ．钝角三角形D ．不能确定解：在△ABC 中，∵sin 2A ＋sin 2B <sin 2C ，∴由正弦定理知a 2＋b 2<c 2.∴cos C ＝a 2＋b 2－c 22ab<0，即∠C 为钝角，△ABC 为钝角三角形．故选C .类型五　解三角形应用举例　某港口O 要将一件重要物品用小艇送到一艘正在航行的轮船上．在小艇出发时，轮船位于港口O 北偏西30°且与该港口相距20 n mile 的A 处，并以30 n mile/h 的航行速度沿正东方向匀速行驶．假设该小艇沿直线方向以v n mile/h 的航行速度匀速行驶，经过t h 与轮船相遇．(1)若希望相遇时小艇的航行距离最小，则小艇航行速度的大小应为多少？(2)假设小艇的最高航行速度只能达到30 n mile/h ，试设计航行方案(即确定航行方向和航行速度的大小)，使得小艇能以最短时间与轮船相遇，并说明理由．解法一：(1)设相遇时小艇航行的距离为S n mile ，则S ＝900t 2＋400－2·30t ·20·cos （90°－30°）＝＝900t 2－600t ＋400900(t －13)2＋300，故当t ＝时，S min ＝10，此时v ＝＝3013310313.3即小艇以30 n mile/h 的速度航行，相遇3时小艇的航行距离最小．(2)设小艇与轮船在B 处相遇，则v 2t 2＝400＋900t 2－2·20·30t ·cos(90°－30°)，故v 2＝900－＋.600t 400t 2∵0<v ≤30，∴900－＋≤900，即－600t 400t 22t 2≤0，3t解得t ≥.又t ＝时，v ＝30.故v ＝30时，t2323取得最小值，且最小值等于.23此时，在△OAB 中，有OA ＝OB ＝AB ＝20，故可设计航行方案如下：航行方向为北偏东30°，航行速度为30 n mile/h ，小艇能以最短时间与轮船相遇．解法二：(1)若相遇时小艇的航行距离最小，又轮船沿正东方向匀速行驶，则小艇航行方向为正北方向．设小艇与轮船在C 处相遇．在Rt△OAC 中，OC ＝20cos30°＝10，AC ＝320sin30°＝10.又AC ＝30t ，OC ＝vt ，此时，轮船航行时间t ＝＝，v ＝＝1030131031330.3即小艇以30 n mile/h 的速度航行，相遇3时小艇的航行距离最小．(2)假设v ＝30时，小艇能以最短时间与轮船在D 处相遇，此时AD ＝DO ＝30t .又∠OAD ＝60°，所以AD ＝DO ＝OA ＝20，解得t ＝.23据此可设计航行方案如下：航行方向为北偏东30°，航行速度的大小为30 n mile/h.这样，小艇能以最短时间与轮船相遇．证明如下：如图，由(1)得OC ＝10，AC ＝10，3故OC >AC ，且对于线段AC 上任意点P ，有OP ≥OC >AC .而小艇的最高航行速度只能达到30 n mile/h ，故小艇与轮船不可能在A ，C 之间(包含C )的任意位置相遇．设∠COD ＝θ(0°<θ<90°)，则在Rt△COD 中，CD ＝10tan θ，OD ＝.3103cos θ由于从出发到相遇，轮船与小艇所需要的时间分别为t ＝和t ＝，所以10＋103tan θ30103v cos θ＝.10＋103tan θ30103v cos θ由此可得，v ＝.153sin （θ＋30°）又v ≤30，故sin(θ＋30°)≥，从而，3230°≤θ<90°.由于θ＝30°时，tan θ取得最小值，且最小值为.33于是，当θ＝30°时，t ＝10＋103tan θ30取得最小值，且最小值为.23【评析】①这是一道有关解三角形的实际应用题，解题的关键是把实际问题抽象成纯数学问题，根据题目提供的信息，找出三角形中的数量关系，然后利用正、余弦定理求解．②解三角形的方法在实际问题中，有广泛的应用．在物理学中，有关向量的计算也要用到解三角形的方法．近年的高考中我们发现以解三角形为背景的应用题开始成为热点问题之一．③不管是什么类型的三角应用问题，解决的关键都是充分理解题意，将问题中的语言叙述弄明白，画出帮助分析问题的草图，再将其归结为属于哪类可解的三角形．④本题用几何方法求解也较简便．　()如图，渔船2012·武汉5月模拟甲位于岛屿A 的南偏西60°方向的B 处，且与岛屿A 相距12海里，渔船乙以10海里/小时的速度从岛屿A 出发沿正北方向航行，若渔船甲同时从B 处出发沿北偏东α的方向追赶渔船乙，刚好用2小时追上．(1)求渔船甲的速度；(2)求sin α的值．解：(1)依题意，∠BAC ＝120°，AB ＝12，AC ＝10×2＝20，在△ABC 中，由余弦定理知BC 2＝AB 2＋AC 2－2AB ·AC ·cos∠BAC ＝122＋202－2×12×20×cos120°＝784，BC ＝28.所以渔船甲的速度为v ＝＝14(海里/小282时)．(2)在△ABC 中，AB ＝12，∠BAC ＝120°，BC ＝28，∠BCA ＝α，由正弦定理得＝AB sin αBCsin ∠BAC，即＝，从而sin α＝12sin α28sin120°12sin120°28＝.33141．已知两边及其中一边的对角解三角形时，要注意解的情况，谨防漏解．2．在判断三角形的形状时，一般将已知条件中的边角关系利用正弦定理或余弦定理转化为角角关系(注意应用A ＋B ＋C ＝π这个结论)或边边关系，再用三角变换或代数式的恒等变形(如因式分解、配方等)求解，注意等式两边的公因式不要约掉，要移项提取公因式，否则有可能漏掉一种形状．3．要熟记一些常见结论，如三内角成等差数列，则必有一角为60°；若三内角的正弦值成等差数列，则三边也成等差数列；内角和定理与诱导公式结合产生的结论：sin A ＝sin(B ＋C )，cos A ＝－cos(B ＋C )，sin ＝cos ，sin2A ＝－A 2B ＋C2sin2(B ＋C )，cos2A ＝cos2(B ＋C )等．4．应用正、余弦定理解斜三角形应用题的一般步骤：(1)分析：理解题意，分清已知与未知，画出示意图；(2)建模：根据已知条件与求解目标，把已知量与求解量尽量集中到一个三角形中，建立一个解斜三角形的模型；(3)求解：利用正、余弦定理有序地解出三角形，求得数学模型的解；(4)检验：检验上述所求得的解是否符合实际意义，从而得出实际问题的解．5．正、余弦定理是应用极为广泛的两个定理，它将三角形的边和角有机地联系起来，从而使三角与几何产生联系，为求与三角形有关的量(如面积、外接圆、内切圆半径和面积等)提供了理论依据，也是判断三角形形状、证明三角形中有关等式的重要依据．主要方法有：化角法，化边法，面积法，运用初等几何法．注意体会其中蕴涵的函数与方程思想、等价转化思想及分类讨论思想．。

第一节正弦定理和余弦定理(知识梳理)

第一节正弦定理和余弦定理复习目标学法指导1.会证明正弦定理、余弦定理.2.理解正弦定理、余弦定理在讨论三角形边角关系时的作用.3.能用正弦定理、余弦定理解斜三角形.4.会用正弦定理、余弦定理讨论三角形解的情形.5.了解正弦定理与三角形外接圆半径的关系.1.正弦定理和余弦定理是解三角形的基础,熟记定理内容及变形公式,在解决问题时注重数形结合.2.在给定方程的化简和变形上要注重“统一”“消元”思想的运用.统一:统一角度或边长.消元:多个角度利用A+B+C=π进行消元.一、正弦定理正弦定理内容:sin a A =sin b B =sin c C=2R(R 为△ABC 外接圆半径). 变形形式:①a=2Rsin A,b=2Rsin B,c=2Rsin C. ②sin A=2a R ,sin B=2b R ,sin C=2c R . ③a ∶b ∶c=sin A ∶sin B ∶sin C.④sin a A =sin sin a b A B ++=sin sin sin a b c A B C++++.1.概念理解(1)正弦定理主要解决两类三角形问题:①知两角和一边;②知两边和其中一边所对应的角.在第②类中要注意会出现两组解的特殊情况. (2)正弦定理中边角互化公式:a=2Rsin A 和sin A=2a R 是表达式变形中常用公式,在统一角度或统一长度上发挥作用. 2.与正弦定理有关的结论(1)三角形中:A+B+C=π,sin(A+B)=sin C, cos(A+B)=-cos C.(2)在△ABC 中,已知a,b 和A 时,解的情况如下:A 为锐角A 为钝角或直角图形关系式 a=bsin Absin A<a<ba ≥ba>b解的个数一解两解一解一解二、余弦定理余弦定理内容:a 2=b 2+c 2-2bc ·cos A, b 2=a 2+c 2-2ac ·cos B, c 2=a 2+b 2-2ab ·cos C.变形形式:cos A=2222bc a bc+-,cos B=2222ac b ac+-,cos C=2222a b c ab+-.1.概念理解(1)余弦定理解决两类三角形问题:一是知两边及其夹角的三角形,二是知三边的三角形.(2)利用余弦定理来解决三角形问题时,要注意角的取值范围.通常求解三角形的内角度数时,不是解该角的正弦,而是解该角的余弦. 2.与余弦定理有关的结论由cos A=2222b c a bc+-(设A 为最大内角)若b 2+c 2>a 2,则该三角形为锐角三角形. b 2+c 2=a 2,则该三角形为直角三角形. b 2+c 2<a 2,则该三角形为钝角三角形.1.在△ABC 中,内角A,B,C 的对边分别为a,b,c.若asin Bcos C+csin Bcos A=12b,且a>b,则∠B 等于( A ) (A)π6 (B)π3(C)2π3 (D)5π6 解析:由正弦定理得sin Asin Bcos C+sin Csin Bcos A=12sin B, 所以sin Bsin(A+C)=12sin B. 因为sin B ≠0, 所以sin(A+C)=12,即sin B=12,所以B=π6或5π6.又因为a>b, 所以A>B, 所以B=π6.故选A.2.在△ABC 中,已知b=40,c=20,C=60°,则此三角形的解的情况是( C ) (A)有一解 (B)有两解 (C)无解(D)有解但解的个数不确定解析:由正弦定理得sin b B =sin cC,所以sin B=sin b Cc=40220>1.所以角B 不存在,即满足条件的三角形不存在.故选C. 3.在△ABC 中,A=60°则△ABC 的面积等于 .解析:=4sin B, 所以sin B=1, 所以B=90°, 所以AB=2,所以S △ABC =12×2×23=23.答案:234.(2019·临海高三检测)设△ABC 的内角A,B,C 所对边的长分别为a,b,c.若b+c=2a,3sin A=5sin B,则角C= . 解析:由3sin A=5sin B,得3a=5b.又因为b+c=2a, 所以a=53b,c=73b,所以cos C=2222a b c ab +-=22257()()33523b b b b b +-⨯⨯=-12. 因为C ∈(0,π), 所以C=2π3. 答案:2π3考点一利用正弦定理解三角形 [例1] (1)在△ABC 中32°,求角A,C 和边c;(2)已知a,b,c 分别是△ABC 的三个内角A,B,C 所对的边,若3求角A 的大小.解:(1)由正弦定理sin a A =sin bB , 得sin A=sin a B b3,所以A=60°或120°. ①当A=60°时,C=75°,由sin a A =sin c C ,得c=sin sin a C A⋅=2·sin 75°62+②当A=120°时,C=15°,c=2·sin 15°62-解:(2)由A+C=2B,A+C+B=180°得B=60°.所以由正弦定理得3=1sin A, 所以sin A=12.所以A=30°或150°. 又因为b>a, 所以B>A. 所以A=30°.利用正弦定理解三角形(1)注重条件和图形的结合;(2)知两边及一边对应的角时,要区分三角形解的情况,通常情况下先利用正弦定理求角,再利用“大边对大角”的条件排除; (3)正弦定理的变形公式.1.(2019·浙江卷)在△ABC 中,∠ABC=90°,AB=4,BC=3,点D 在线段AC 上.若∠BDC=45°,则BD= ,cos ∠ABD= .解析:如图,易知sin C=45, cos C=35.在△BDC 中,由正弦定理可得sin BD C=sin BC BDC∠, 所以BD=sin sin BC C BDC⋅∠4352⨯122.由∠ABC=∠ABD+∠CBD=90°,可得cos ∠ABD=cos(90°-∠CBD)=sin ∠CBD=sin[π-(∠C+∠BDC)] =sin(∠C+∠BDC)=sin C ·cos ∠BDC+cos C ·sin ∠BDC=45×2+35×2=72.答案122722.在△ABC 中,B=60°3则AB+2BC 的最大值为 .解析:在△ABC 中,由正弦定理得sin AB C =sin BCA 3所以AB+2BC=2sin C+4sin A =2sin(120°-A)+4sin A 7ϕ),其中,tan ϕ3,又因为A ∈(0°,120°), 所以最大值为7答案7考点二利用余弦定理解三角形[例2] 若△ABC 的内角A,B,C 所对的边a,b,c 满足(a+b)2-c 2=4,且C=60°,则ab 的值为( ) (A)433(C)1 (D)23解析:由已知得a 2+b 2-c 2+2ab=4, 由于C=60°,所以cos C=2222a b c ab+-=12, 即a 2+b 2-c 2=ab,因此ab+2ab=4,ab=43,故选A.利用余弦定理解三角形:一般地,如果式子中含有角的余弦或边的二次关系时,考虑使用余弦定理.△ABC 中,角A,B,C 的对边分别是a,b,c,已知b=c,a 2=2b 2(1-sin A),则A 等于( C )(A)3π4 (B)π3 (C)π4 (D)π6解析:在△ABC 中,由余弦定理得a 2=b 2+c 2-2bccos A, 因为b=c,所以a 2=2b 2(1-cos A), 又因为a 2=2b 2(1-sin A), 所以cos A=sin A,所以tan A=1, 因为A ∈(0,π),所以A=π4,故选C. 考点三正、余弦定理的综合应用[例3] 设△ABC 的内角A,B,C 所对应的边分别为a,b,c, 已知()sin a bA B ++=sin sin a c AB --.(1)求角B; (2)若6,求△ABC 的面积.解:(1)因为()sin a bA B ++=sin sin a c AB --,所以a b c+=a ca b --, 所以a 2-b 2=ac-c 2, 所以cos B=2222a c b ac+-=2ac ac =12, 又因为0<B<π,所以B=π3.解:(2)由cos A=63可得sin A=33,由sin a A =sin b B可得a=2, 而sin C=sin(A+B) =sin Acos B+cos Asin B =3326+,所以△ABC 的面积S=12absin C=3322+.(1)利用正、余弦定理解三角形的关键是根据已知条件及所求结论确定三角形及所需应用的定理.(2)对于面积公式S=12absin C=12acsin B=12bcsin A,一般是已知哪一个角就选用哪一个公式.(2017·全国Ⅰ卷)△ABC 的内角A,B,C 的对边分别为a,b,c,已知△ABC的面积为23sin a A .(1)求sin Bsin C;(2)若6cos Bcos C=1,a=3,求△ABC 的周长. 解:(1)由题设得12acsin B=23sin a A ,即12csin B=3sin aA . 由正弦定理得12sin Csin B=sin 3sin A A ,故sin Bsin C=23.解:(2)由题设及(1)得cos Bcos C-sin Bsin C=-12,即cos(B+C)=- 12.所以B+C=2π3,故A=π3.由题设得12bcsin A=23sinaA,即bc=8,由余弦定理得b2+c2-bc=9,即(b+c)2-3bc=9,得b+c=33.故△ABC的周长为3+33.类型一利用正弦定理解三角形1.在△ABC中,角A,B,C所对的边分别是a,b,c.已知8b=5c,C=2B,则cos C等于( A )(A)725 (B)-725(C)±725(D)2425解析:因为8b=5c,所以由正弦定理,得8sin B=5sin C.又因为C=2B,所以8sin B=5sin 2B,所以8sin B=10sin Bcos B.因为sin B≠0,所以cos B=45,所以cos C=cos 2B=2cos2B-1=725.故选A.2.在△ABC中,a,b,c分别是内角A,B,C的对边,向量p=(1,-∥q,且bcos C+ccos B=2asin A,则C等于( A )(A)30°(B)60°(C)120° (D)150°解析:因为p∥q,cos B=sin B,所以即得所以B=120°.又因为bcos C+ccos B=2asin A,所以由正弦定理得sin Bcos C+sin Ccos B=2sin2A,即sin A=sin(B+C)=2sin2A,,又由sin A≠0,得sin A=12所以A=30°,C=180°-A-B=30°.故选A.类型二利用余弦定理解三角形3.已知锐角△ABC的内角A,B,C的对边分别为a,b,c,23cos2A+ cos 2A=0,a=7,c=6,则b等于( D )(A)10 (B)9 (C)8 (D)5解析:由23cos2A+cos 2A=0,得25cos2A=1,因为A为锐角,所以cos A=1.5b,又由a2=b2+c2-2bccos A,得49=b2+36-125整理得5b2-12b-65=0,解得b=-135(舍)或b=5.即b=5. 故选D.4.若锐角△ABC 的面积为,且AB=5,AC=8,则BC 等于 .解析:设内角A,B,C 所对的边分别为a,b,c.由已知及12得因为A 为锐角,所以A=60°,cos A=12.由余弦定理得a 2=b 2+c 2-2bccos A =64+25-2×40×12 =49,故a=7,即BC=7. 答案:7类型三正弦定理和余弦定理的综合应用 5.在△ABC 中,∠B=120°∠BAC的平分线则AC 等于( D )(C)2解析:如图,在△ABD 中,由正弦定理,得sin ∠ADB=sin AB BAD .由题意知0°<∠ADB<60°, 所以∠ADB=45°,则∠BAD=180°-∠B-∠ADB=15°, 所以∠BAC=2∠BAD=30°, 所以∠C=180°-∠BAC-∠B=30°, 所以于是由余弦定理,得AC=222cos120AB BC AB BC ︒+-⨯=()()221222222⎛⎫+-⨯⨯- ⎪⎝⎭=6.故选D.。

正弦定理和余弦定理_知识点及典型例题精编版

⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯最新料介绍⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯正弦定理和余弦定理重点梳理1．正弦定理abcsin A sin B2 Rsin C此中 R 是三角形外接圆的半径．由正弦定理能够变形为：(1)a ∶ b ∶ c ＝ sin A ∶ sin B ∶ sin C ；(2)a ＝ 2Rsin A ， b ＝ 2Rsin B ， c ＝ 2Rsin C ；abc(3)sin A ＝ 2R ， sin B ＝2R ， sin C ＝ 2R 等形式，以解决不一样的三角形问题．2．三角形面积公式1 1 1 abc 1(a ＋ b ＋ c) ·r(r 是三角形内切圆的半径 )，并可由此计算 R 、 r.S △ABC ＝ absin C ＝ bcsin A ＝ acsin B ＝ 4R ＝22223．余弦定理：a 2＝b 2＋c 2－2bccos A ，b 2＝a 2＋c 2－2accos B ，c 2＝a 2＋b 2－2abcos C .余弦定理能够变形为：b2c2a2a2c2b2a 2b 2c 2cos A ＝2bc， cos B ＝2ac， cos C ＝2ab .4．在解三角形时，正弦定理可解决两类问题：(1) 已知两角及任一边，求其余边或角；(2)已知两边及一边的对角，求其余边或角．状况 (2) 中结果可能有一解、二解、无解，应注意划分．余弦定理可解决两类问题：(1) 已知两边及夹角或两边及一边对角的问题； (2)已知三边问题．基础自测2π.1．在 △ ABC 中，若 b ＝1， c ＝，则 a ＝3，C ＝ 32．已知 △ ABC 的内角 A ， B ， C 的对边分别为 a ， b ， c ，若 c ＝ 2， b ＝ 6， B ＝ 120 °，则 a ＝ ________.93．在 △ ABC 中，若 AB ＝ 5， AC ＝ 5，且 cos C ＝ 10，则 BC ＝ ________ . 4．已知圆的半径为 4， a 、 b 、 c 为该圆的内接三角形的三边，若 abc ＝ 16 2，则三角形的面积为 ()2 A ．2 2 B ．8 2 C. 2D. 2题型分类深度解析题型一利用正弦定理求解三角形例 1 在△中，＝ 3，＝ 2，＝45°. 求角、和边c .ABC a b B A C1⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯最新料介绍⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯变式训练 1 已知 a ， b ， c 分别是△ ABC 的三个内角A ，B ，C 所对的边，若 a ＝ 1， b ＝ 3， A ＋ C ＝ 2B ，则 A＝题型二利用余弦定理求解三角形例 2 在△ ABC 中， a 、 b 、 c 分别是角 A 、 B 、 C 的对边，且cos B＝ cos Cb2a c.（ 1）求角 B 的大小；(2)若 b ＝ 13， a ＋ c ＝ 4，求△ ABC 的面积．变式训练 2 已知 A 、 B 、 C 为△ ABC 的三个内角，其所对的边分别为a 、b 、c ，且 2cos 2A+cos A=0 .2(1)求角 A 的值；(2) 若 a ＝ 2 3， b ＋ c ＝ 4，求△ ABC 的面积．题型三正、余弦定理的综合应用例 3. 在 △ABC 中， a 、b 、c 分别是角 A 、B 、 C 的对边已知 22(sin 2 A sin 2 C ) (a b)sin B ,△ABC 外接圆半径为2 .（ 1）求角 C 的大小；（ 2）求 △ABC 面积的最大值.变式训练 3 在△ ABC 中，内角 A ， B ， C 所对的边长分别是a ，b ， c.π(1) ，且△ ABC 的面积为 3，求 a ， b 的值；若 c ＝ 2， C ＝ 3 (2)若 sin C ＋ sin(B － A)＝ sin 2A ，试判断△ ABC 的形状．例 4 设△ ABC 的内角 A 、 B 、 C 所对的边分别为 a 、 b 、 c ，且 acosC ＋ 1 c ＝ b.2(1)求角 A 的大小； (2)若 a ＝ 1，求△ ABC 的周长 l 的取值范围．2。

(完整版)正弦定理、余弦定理知识点

正弦定理、余弦定理讲师：王光明【基础知识点】1. 三角形常用公式：A ＋B ＋C ＝π；S ＝ab sin C ＝bc sin A ＝＝ca sin B ；2121212．三角形中的边角不等关系: A>B a>b,a+b>c,a-b<c ；；⇔3．【正弦定理】：＝＝＝2R （外接圆直径）；A a sin B b sin Ccsin 正弦定理的变式：； a ∶b ∶c ＝sin A ∶sin B ∶sin C ．⎪⎩⎪⎨⎧===C R c B R b AR a sin 2sin 2sin 24．正弦定理应用范围： ①已知两角和任一边，求其他两边及一角． ②已知两边和其中一边对角，求另一边的对角．③几何作图时，存在多种情况．如已知a 、b 及A ，求作三角形时，要分类讨论，确定解的个数．已知两边和其中一边的对角解三角形，有如下的情况：(1)A 为锐角AABa=bsin A bsin A<a<b a b ≥ 一解两解一解(2)A 为锐角或钝角当时有一解.a>b 5．【余弦定理】　a 2=b 2+c 2-2bccosA ．c 2=a 2+b 2-2abcosC ．b 2=a 2+c 2-2accosB ．若用三边表示角，余弦定理可以写为、6．余弦定理应用范围：（1）已知三角形的三条边长，可求出三个内角；（2）已知三角形的两边及夹角，可求出第三边．【习题知识点】知识点1　运用判断三角形形状例题1在△ABC 中已知acosB=bcosA,试判断△ABC 的形状.【分析】利用正弦定理或余弦定理判断三角形形状,可以将三角形中的边用角表示,也可将角用边来表示．从中找到三角形中的边角关系，判断出三角形的形状.【解析】解法1：由扩充的正弦定理：代入已知式2RsinAcosB=2RsinBcosAsinAcosB-cosAsinB=0 ， sin(A-B)=0A-B=0 ∴A=B 即△ABC 为等腰三角形解法2:由余弦定理: 22222222bc a c b b ac b c a a -+⋅=-+⋅ 22b a = ∴ b a =即△ABC 为等腰三角形.知识点2 运用正、余弦定理解三角形解三角形问题中正、余弦定理的选择:(1)在下述情况下应首先使用余弦定理: ①已知三条边(边边边),求三个角;②已知两边和它们的夹角(边角边),求其它一边和两角;(2)在下述情况下应首先使用正弦定理:①已知两边和一边的对角(边边角),求其它一边和两角;②已知两角和任一边(角角边、角边角),求其它两边和一角.例题2　在△ABC 中，已知，，B=45︒ 求A 、C 及c .3=a 2=b 【分析】在解斜三角形应用过程中，注意要灵活地选择正弦定和余弦定理，解得其它的边和角【解析】解法1：由正弦定理得：23245sin 3sin sin === b B a A ∵B=45︒<90︒ 即b <a ∴A=60︒或120︒当A=60︒时C=75︒ 22645sin 75sin 2sin sin +===BCb c当A=120︒时C=15︒ 22645sin 15sin 2sin sin -===B C b c 解法2：设c =x 由余弦定理将已知条件代入，整理：解之：B ac c a b cos 2222-+=0162=+-x x 226±=x 当时从而A=60︒ ，C=75︒226+=c 2)13(231226223)226(22cos 22221=++=+⋅⋅-++=-+=bc a c b A 当时同理可求得：A=120︒ C=15︒.226-=c 知识点3 解决与三角形在关的证明、计算问题例题3 已知A 、B 、C 为锐角，tanA=1，tanB=2，tanC=3，求A+B+C 的值．　【分析】本题是要求角，要求角先要求出这个角的某一个三角函数值，再根据角的范围确定角．本题应先求出A+B 和C 的正切值，再一次运用两角和的正切公式求出A+B+C ．【解析】 A B C 、、为锐角∴<++<0270°°A B C 又，，由公式可得tan tan A B ==12tan()tan tan tan tan A B A B A B +=+-⋅=+-=-112123[]tan()tan ()A B C A B C ++=++=++-+⋅tan()tan tan()tan A B C A B C 1 =-+--⨯33133() =0所以A+B+C=π知识点4 求三角形的面积例题4 △ABC 中，D 在边BC 上，且BD ＝2，DC ＝1，∠B ＝60o ，∠ADC ＝150o ，求AC 的长及△ABC 的面积．【解析】在△ABC 中，∠BAD ＝150o －60o ＝90o ，∴AD ＝2sin60o ＝3．A在△ACD 中，AD 2＝(3)2＋12－2×3×1×cos150o ＝7，∴AC ＝7． ∴AB ＝2cos60o ＝1．S △ABC ＝21×1×3×sin60o ＝343．知识点4 解决实际为题例题4 如图，海中有一小岛，周围3.8海里内有暗礁。

正弦定理余弦定理

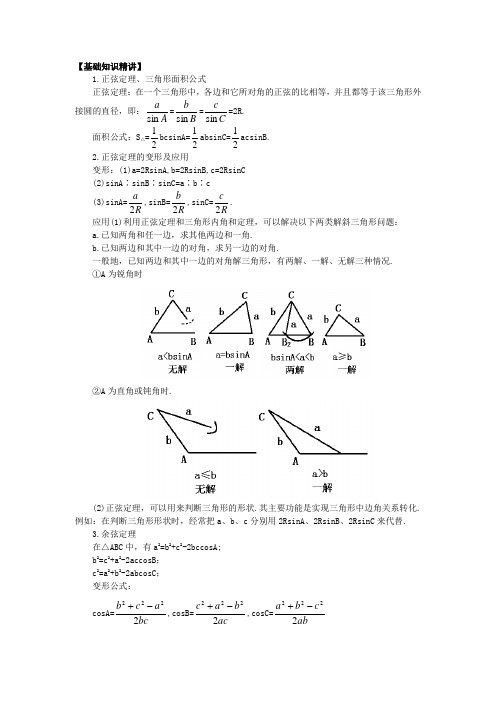
【基础知识精讲】1.正弦定理、三角形面积公式正弦定理：在一个三角形中，各边和它所对角的正弦的比相等，并且都等于该三角形外接圆的直径，即：A a sin =B b sin =C csin =2R. 面积公式：S △=21bcsinA=21absinC=21acsinB.2.正弦定理的变形及应用变形：(1)a=2RsinA,b=2RsinB,c=2RsinC (2)sinA ∶sinB ∶sinC=a ∶b ∶c (3)sinA=R a 2,sinB=R b 2,sinC=Rc 2. 应用(1)利用正弦定理和三角形内角和定理，可以解决以下两类解斜三角形问题：a.已知两角和任一边，求其他两边和一角.b.已知两边和其中一边的对角，求另一边的对角.一般地，已知两边和其中一边的对角解三角形，有两解、一解、无解三种情况. ①A 为锐角时②A 为直角或钝角时.(2)正弦定理，可以用来判断三角形的形状.其主要功能是实现三角形中边角关系转化.例如：在判断三角形形状时，经常把a 、b 、c 分别用2RsinA 、2RsinB 、2RsinC 来代替.3.余弦定理在△ABC 中，有a 2=b 2+c 2-2bccosA; b 2=c 2+a 2-2accosB ； c 2=a 2+b 2-2abcosC ；变形公式：cosA=bc a c b 2222-+,cosB=ac b a c 2222-+,cosC=abc b a 2222-+在三角形中，我们把三条边(a 、b 、c)和三个内角(A 、B 、C)称为六个基本元素，只要已知其中的三个元素(至少一个是边)，便可以求出其余的三个未知元素(可能有两解、一解、无解)，这个过程叫做解三角形，余弦定理的主要作用是解斜三角形.4.解三角形问题时，须注意的三角关系式：A+B+C=π 0＜A ，B ，C ＜πsin2B A +=sin 2C -π=cos 2Csin(A+B)=sinC特别地，在锐角三角形中，sinA ＜cosB,sinB ＜cosC,sinC ＜cosA.【重点难点解析】掌握正、余弦定理，并学会用其余弦定理解三角形.例1 在△ABC 中，已知A ＞B ＞C ，且A=2C,b=4,a+c=8，求a 、c 的长.解：由正弦定理A a sin =C c sin 及A=2C 得C a 2sin =C c sin ,即C C a cos sin 2=Ccsin , ∴cosC=ca 2. 由已知a+c=8=2b 及余弦定理，得cosC=abcb a 2222-+=)()2(222c a a c c a a +-++ =)(4))(35(c a a c a c a ++-=a ca 435-.∴ca 2=a ca 435-，整理得(2a-3c)(a-c)=0∴a ≠c,∴2a=3c. ∵a+c=8,∴a=524,c=516. 例2 在△ABC 中，如果lga-lgc=lgsinB=-lg 2，且B 为锐角，试判断此三角形的形状.解：∵lga-lgc=lgsinB=-lg 2,∴sinB=22 又∵0°＜B ＜90°，∴B=45° 由lga-lgc=-lg 2,得c a = 22. 由正弦定理得c A sin sin = 22.即2sin(135°-C)= 2sinC即2［sin135°cosC-cos135°sinC ］=2sinC.∴cosC=0,得C=90° 又∵A=45°,∴B=45°从而△ABC 是等腰直角三角形.例3 如图已知：平行四边形两邻边长为a 和b(a ＜b)，两对角线的一个交角为θ(0°＜θ＜90°)，求该平行四边形的面积.分析：由于已知了平行四边形相邻两边长和对角线的一个交角，再考虑到平行四边形的面积是△AOB 的四倍，因此只要求OA ·OB ·sin θ即可.解：设平行四边形ABCD 的对角线AC 与BD 相交于O.AB=a,BC=b,∠AOB=θ，又设OA=x,OB=y.在△AOB 中，应用余弦定理可得： a 2=x 2+y 2-2xycos θ ① 在△BOC 中，应用余弦定理可得： b 2=x 2+y 2-2xycos(180°-θ) ② 由②-①得： b 2-a 2=4xycos θ∵0°＜θ＜90°，∴xy=θcos 422a b - (b ＞a)∴S □=4S △AOB =2xysin θ=222b a -tan θ例4 在△ABC 中，已知4sinBsinC=1,b 2+c 2-a 2=bc,且B ＞C ，求A 、B 、C.分析：由于题设条件b 2+c 2-a 2=bc 十分特殊，将它与余弦定理对照可得A=60°,这样B+C=120°，于是再利用条件4sinBsinC=1，可求得B 与C.解：由余弦定理cosA=bca c a 2222-+=bc bc 2=21.又∵0°＜A ＜180°∴A=60°∴B+C=120°,又由于4sinBsinC=1 ∴4sinBsin(120°-B)=1 ∴4sinB(23cosB+21sinB)=1∴3sin2B+2sin 2B=1 ∴3sin2B=cos2B∴tan2B=33,∴2B=30°或2B=210°由于B+C=120°,且B ＞C ，60°＜B ＜120° ∴2B=210°,∴B=105°,从而C=15° ∴A=60°,B=105°,C=15°例5 已知△ABC 中，a ，b ，c 为角A ，B ，C 的对边，且a+c=2b ，A-C=3π,求sinB 的值. 解法一：由正弦定理和已知条件a+c=2b ，得sinA+sinC=2sinB ，由和差化积公式得 2sin2C A +·cos 2CA -=2sinB 由A+B+C=π，得 sin2C A +=cos 2B 又A-C=3π,得 23cos 2B =sinB∴23cos 2B =2sin 2B ·cos 2B又∵0＜2B ＜2π,cos 2B≠0 ∴sin2B =43 从而cos2B =2sin 12B -=413 ∴sinB=23·413 =839. 解法二：由正弦定理和已知条件a+c=2b ，得sinA+sinC=2sinB∵A-C=3π,A+B+C=π 两式相减可得B=32π-2C∴sin(3π+C)+sinC=2sinB 得sin 3πcosC+cos 3πsinC+sinC=2sinB∴23cosC+23sinC=2sinB即3cos(3π-C)=2sinB ∴3cos 2B =4sin 2B ·cos 2B∵0＜B ＜π,∴cos 2B≠0∴sin2B =43 cos2B =2sin 12B -=413 ∴sinB=23·cosB=839【难题巧解点拔】例1 △ABC 中，若a=5,b=4,cos(A-B)=3231，求AB. 分析：很明显，只要求cosC 的值，应用余弦定理即可求出AB. 解法一：由已知条件a=5,b=4b a b a -+=B A B A sin sin sin sin -+=2sin2cos 2cos2sinB A B A BA B A -+-+=9，①由已知cos(A-B)= 3231,根据半角公式有sin2B A +=2)cos(1B A --=81,cos 2B A -=2)cos(1B A -+=863代入①式得tg2B A +=639∵tg 2B A +=ctg 2C , ∴tg2C = 963,根据万能公式cosC=81∴c 2=a 2+b 2-2abcosC=36,AB=c=6解法二：∵A ＞B ，如图，作∠BAD=∠B,∴AD=BD∠CAD=∠A-∠B 令AD=BD=y,CD=x,由余弦定理cos(A-B)=boyx y b 2222-+= 3231,x=a-y,∴yy 8910-= 3231,y=4,x=1 △CAD 中再由余弦定理cosC=81,∴c=6 评析：上述解法反映边向角的转化，也可由角向边转化直接求出边.例2 半圆O 的直径为2，A 为直径延长线上的一点，且OA=2，B 为半圆周上任意一点以AB 为边向形外作等边三角形ABC(如图)，问B 点在什么位置时，边形OACB 的面积最大，并求出这个最大面积.解：设∠AOB=x ，则 S △AOB =21·2·1·sinx=sinx, AB 2=OA 2+OB 2-2·OA ·OB ·cosx=5-4cosx. S △ABC =43AB 2=43 (5-4cosx)= 45-3cosx ∴S OACB =S △AOB +S △ABC=sinx-3cosx+435 =2sin(x-3π)+435 ∵0＜x ＜π,-3π＜x-3π＜32π ∴x-3π=2π时，∴即x=65π时,S OACB 有最大值2+435(平方单位) 例3 已知△ABC 中，AB=AC=a,∠BAC=φ，等边三角形PQR 的三边分别通过A ，B ，C 三点.试求△PQR 的面积的最大值.分析：先依题意画出图形(如图).因为变动三角形PQR 为正三角形，它的面积S=43PQ 2，问题可转化为求边长PQ 的最大值.为此需要建立PQ 的函数式，这又必须选取适当的量作为自变量.观察图形可以发现，PQ 的位置是随着∠PAB 的大小变化而变化的.不妨就以∠PAB 为自变量.以下的程序就是应用三角形的边角关系，求出以∠PAB 的三角函数表示PQ 的解析式，最后求它的最大值.解：设∠PAB=x,那么∠PBA=120°-x,∠QAC=180°-x-φ，∠QCA=x+φ-60°.在△PAB 中，∵)120sin(x PA-︒=︒60sin AB ，∴PA=32a sin(120°-x),在△AQC 中，)60sin(︒-Φ+x AQ=︒60sin AC∴AQ=32a sin(x+φ-60°)∴PQ=PA+AQ=32a ［sin(120°-x)+sin(x+φ-60°)=34a sin(2Φ+30°)cos(90°-2Φ-x). 因为其中a,2Φ+30°都是常量，所以当90°-2Φ-x=0即x=90°-2Φ时，取得 (PQ)max =34a sin(2Φ+30°) 同时也就取得了 (S △)max =43 (PQ)2max=334a 2sin 2(2Φ+30°)例4 在△ABC 中，已知A=2C ，求证：3b ＜c-a ＜2b.证明：在△ABC 中，由A=2C ，得C=2A ，∴B=π-3A,∴0＜A ＜3πb ac - =B A C sin sin sin -=)sin(sin sin C A A C +-=2cos2sin 2sin2cos 2C A C A A C A C ++-+ =23sin 2sin A =2sin 2cos 2sin 42sin2A A A A -=12cos 412-A =1cos 21+A .∵0＜A ＜3π，∴21＜cosA ＜1，即2＜2cosA+1＜3∴31＜b a c -＜21,故3b ＜c-a ＜2b.评析：解本题的关键是利用正弦定理及三角公式将b a c -转化为1cos 21+A ，结合角A的取值范围推得结论.【课本难题解答】课本第132页，习题5.9第8题：｜F ｜≈132N ，β≈38° 第9题两条对角线的长分别是415cm 和43cm,面积是48cm 2.【命题趋势分析】本节主要考查：1.根据已知条件，求三角形的末知元素，或判断三角形的形状. 2.运用正、余弦定理及关系式A+B+C=π解决三角形中的计算和证明问题. 3.利用所学的三角知识解决与三角形有关的三角函数问题和简单的实际问题. 根据考试的方向，可以预见，利用正、余弦定理解斜三角形问题将会与三角函数、数列、方程、向量等知识相结合，尤其是与生活、生产、科学实验实际相结合，考查综合运用数学知识的能力.【典型热点考题】例1 在△ABC 中，a ，b ，c 分别是角A 、B 、C 的对边，设a+c=b ，A-C=3π，求sinB 的值.解：根据正弦定理和已知可得：sinA+sinC=2sinB,A+B+C=π 则2sin2C A +·cos 2CA -=2sinB.又A-C=3π,sin 2C A -=cos 2B∴2cos 2B cos 6π=2sinB=4sin 2B cos 2B又∵0＜2B ＜2π∴sin2B =43 cos2B =2sin 12B -= 413 ∴sinB=2·413·43=839例2 若△ABC 的三个内角A 、B 、C 成等差数列，且最大边为最小边的2倍，则三内角之比为 .解：设三角形三内角从小到大依次为B-d,B,B+d, 则B-d+B+B+d=180°∴B=60° 设最小边为x ，则最大边为2x,从而)60sin(d x -︒=)60sin(2d x +︒⇒tand=33,d=30° 所以三内角分别为A=30°,B=60°,C=90°,得三内角之比为1∶2∶3. ∴应填1∶2∶3.例3 在△ABC 中，A 、B 、C 三顶点所对边分别为a,b,c ，试证明b 2=c 2+a 2-2accosB.证明：因为=+则有：2=·=(+)·(+)=2+2+2·=AB 2+BC 2+2｜AB ｜·｜BC ｜cos(180°-B)=c 2+a 2-2accosB 所以b 2=c 2+a 2-2ac ·cosB例4 求sin 220°+cos 280°+3sin20cos80°的值.解：设△ABC 中的A=10°,B=20°,C=150°对应边分别为a,b,c. △ABC 的外接圆半径为2R ，则由正弦定理得： a=2Rsin10°,b=2Rsin20°,c=2Rsin150° 由余弦定理，得：(2Rsin150°)2=(2Rsin10°)2+(2Rsin20°)2-2(2Rsin10°)(2Rsin20°)cos150°即：sin 2150°=sin 210°+sin 220°+3sin10°sin20°则：cos 280°+sin 220°+3sin20°cos80°=41 说明：本题采用了构造法，题中余弦变正弦之后，注意到3=-2cos(180°-10°-20°).【同步达纲练习】一、选择题1.在△ABC 中，已知a=52,c=10,A=30°，则B 等于( ) A.105°B.60°C.15°D.105°或15°2.在△ABC 中，若b=22,a=2，且三角形有解，则A 的取值范围是( ) A.0°＜A ＜30° B.0°＜A ≤45° A.0°＜A ＜90°D.30°＜A ＜60° 3.在△ABC 中，若2cos A a =2cos B b =2cosC c，则△ABC 的形状是( )A.等腰三角形B.等边三角形C.直角三角形D.等腰直角三角形4.在△ABC 中，若a=2,b=22,c=6+2，则∠A 的度数是( )A.30°B.45°C.60°D.75°5.设m 、m+1、m+2是钝角三角形的三边长，则实数m 的取值范围是( ) A.0＜m ＜3 B.1＜m ＜3 C.3＜m ＜4 D.4＜m ＜66.在△ABC 中，已知sinA ∶sinB ∶sinC=3∶5∶7,则此三角形的最大内角的度数等于( )A.75°B.120°C.135°D.150°7.△ABC 中，若c=ab b a ++22，则角C 的度数是( ) A.60°B.120°C.60°或120°D.45°8.在△ABC 中，若A=60°,b=16,且此三角形的面积S=2203，则a 的值是( ) A. 2400B.25C.55D.499.在△ABC 中，若acosA=bcosB,则△ABC 是( )A.等腰三角形B.直角三角形C.等腰直角三角形D.等腰三角形或直角三角10.在钝角三角形ABC 中，三边长是连续自然数，则这样的三角形( ) A.不存在 B.有无数多个 C.仅有一个 D.仅有两个二、填空题1.在△ABC 中，A=120°,B=30°,a=8,则c= .2.在△ABC 中，已知a=32,cosC=31,S △ABC =43，则b= . 3.已知锐角三角形边长分别为2、3、x ，则x 的取值范围是 . 4.在△ABC 中，A=60°,b ∶c=8∶5,其内切圆关径r=23,则a= ，b= ,c= .5.在△ABC 中，A=60°,b=1,面积为3，则CB A cb a sin sin sin ++++= .6.在△ABC 中，已知A 、B 、C 成等差数列，且边b=2，则外接圆半径R= .三、解答题1.设三角形三边长分别为15，19，23，现将三边长各缩短x 后，围成一个钝角三角形，求x 的取值范围.2.在△ABC 中，已知它的三边a ，b ，c 成等比数列，试证明：tan 2A tan 2C ≥31.3.已知在△ABC 中，c=22,a ＞b,C=4π,tanA ·tanB=6,试求a,b 以及此三角形的面积.【素质优化训练】1.在△ABC 中，已知a-b=4,a+c=2b ，且最大角为120°，求△ABC 的三边长.2.如图，在60°的∠XAY 内部有一点P ，P 到边AX 的距离是PC=2，P 到边AY 的距离是PB=11，求点P 到顶点A 的距离.3.在△ABC 中，若C=3B ，求bc的取值范围.4.已知△ABC 是钝角三角形，∠B ＞90°,a=2x-5,b=x+1,c=4,求x 的取值范围.5.在△ABC 中，已知cos 2B+cos 2C=1+cos 2A,且sinA=2sinBcosC,cosC=sinB ，求证：b=c 且A=90°.6.在△ABC 中，a,b,c 分别是角A 、B 、C 的对边，若a 2+c 2=2001c 2,求BA Ccot cot cot +的值.【生活实际运用】某人在塔的正东方沿南60°西的道路前进40米后，望见塔在东北方向上，若沿途测得塔的最大仰角为30°，求塔高.解：如图，由题设条件知： ∠CAB=∠1=90°-60°=30°∠ABC=45°-∠1=45°-30°=15° ∴∠ACB=180°-∠BAC-∠ABC =180°-30°-15°=135° 又∵AB=40米.在△ABC 中，由正弦定理知：︒15sin AC =︒135sin 40∴AC=︒︒135sin 15sin 40=402sin(45°-30°)=402 (sin45°cos30°-cos45°sin30°) =402 (22·23-22·21)=20(3-1)在图中，过C 作AB 的垂线，设垂足为E ，则沿AB 测得塔的最大仰角就是∠CED ，∴∠CED=30°.在Rt △ACE 中，EC=AC ·sinBAC=AC ·sin30°=20·(3-1)·21=10(3-1) 在Rt △DCE 中，塔高CD=CE ·tan ∠CED=10(3-1)·tan30°=3)33(10- (米).【知识验证实验】外国船只除特许者外，不得进入离我国海岸线d 海里以内的海域.设B 和C 是我国的两个设在海边的观测站，B 与C 之间的距离为m 海里，海岸线是过B 、C 的直线.一外国船在A 点处，现测得∠ABC=α、∠ACB=β.试求α、β满足什么关系时，就应向示经特许的外国船只A 发出警告?解：如图所示，作AD ⊥BC ，垂足为D ，在△ABC 中，∠BAC=180°-(α+β)∴sin ∠BAC=sin(α+β).由正弦定理得：βsin AB =)sin(βα+BC ,αsin AC =)sin(βα+BC. ∵BC=m ，故有： AB=)sin(sin βαβ+m ,AC=)sin(sin βαα+m由于S △ABC =21BC ·AD=21 m ·AD 且S △ABC =21AB ·AC ·sin(α+β). 所以21)sin(sin βαα+m ·)sin(sin βαβ+m ·sin(α+β)= 21mAD.从而有：AD=)sin(sin sin βαβα+m因此，当AD ≤d,即)sin(sin sin βαβα+m ≤d 时，就应向外国船只A 发出警发.【知识探究学习】如图，在四边形ABCD 中，BC=m,DC=2m,四个内角A 、B 、C 、D 之比为3∶7∶4∶10,试求△ABD 的面积.解：由于四个内角A 、B 、C 、D 比为3∶7∶4∶10，所以可设它们的大小依次为：3x 、7x 、4x 、10x.由四边形的内角和为360°，所以有：3x+7x+4x+10x=360°，可求得：x=15°. 在△BCD 中，由余弦定理得； BD 2 =BC 2+DC 2-2BC ·DC ·cosC.=m 2+(2m)2-2·m ·(2m)cos60° =3m 2∴BD=3m.这时，在△BCD 中，BD 2+BC 2=DC 2,所以△BCD 是直角三角形，DC 是斜边. ∴∠CDB=30°,∠ADB=120°. 在△ABD 中，由正弦定理得：AB=A ADB BD sin sin ∠∙=︒︒45sin 120sin 3m =223m,另外∠ABD=105°-90°=15°,BD=3m.所以S △ADB =21AB ·BD ·sin15°=21·223m ·3m ·sin15° =8239-m 2.参考答案【同步达纲练习】一、1.D 2.B 3.B 4.A 5.B 6.B 7.B 8.C 9.D 10.C二、1.338 2.213 3.(5，13) 4.14，10，16 5. 338 6. 332 三、1.3＜x ＜112.提示可证：a+c ≥2b ，再得sinA+sinC ≥2sinB ，和差化积可得结论3.a=5106,b=558,S △=524【素质优化训练】1.a=14,b=10,c=62.143.1＜b c＜3 4. 310＜x ＜4 5.可求出B=C=45° 6.1000。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。