集合论(习题课)
集合论第一二章习题课

例6 已知m个整数a1,a2,…,am,试证:存在两个 整数k,l,0 k j m,使得ak+1+ak+2+…+al能被m整 除。
例7证明:对任意正整数N,存在N的一个倍数,使得 它仅由数字0和7组成。(例如N=3,有259×3=777; N=4,有1925×4=7700;N=5,有14×5=70;N=6, 有1295×6=7770等)。
W且S⊆W。
习题课(2) 例1在1000名大学生的调查中,有804人掌握
了英语,205 人掌握了日语,190人掌握了俄语,125人既 掌握了英语又掌握了日语,57人既掌握了日 语又掌握了俄语,85人既掌握了英语又掌握 了俄语。试求这1000名大学生中,英语、日
语、俄语全掌握的有多少人? (23人)
习题课(3) 例1 设A,B,C是三个任意集合,证明:
A (B C)=(A B) C。 [左边
=(A⋂BC⋂CC)∪(B⋂AC⋂CC)∪(C⋂BC⋂AC)∪(A⋂B⋂C)]
(ABC )(A C BC )(AB CC )(ABC C )
(A C B 例C 2设C )A,(A B,CB 是C三C C 个)任(A 意C集B 合C ,C )化简
例2 某班30名学生中学英语有7人,学日语 有5人,这两科都选有3人,问两科都不选
的有多少人?
例3 某校学生数学、物理、英语三科竞赛,某班30人, 学生中有15人参加了数学竞赛,8人参加了物理竞赛, 6人参加了英语竞赛,并且其中3人三科竞赛都参加了, 问至少有多少人一科竞赛都没有参加。 (7人) 例4 甲每5秒放一个爆竹,乙每6秒放一个,丙每7秒 放一个,每人都放21个爆竹,共能听见多少声响。 (54响)
集合习题课

集合习题课一、集合三要素:确定性、互异性、无序性。
1、若集合A 是由23,,02+-m m m 三个元素组成的集合,且,2A ∈则实数m 为( ) 2.A 3.B 30.或C 均可3,2,0.C二、集合的表示方法:列举法、描述法、图像法.三、集合的关系:元素与集合的关系用””或““∉∈;集合与集合的关系用”或“⊆“”。
2.下列各式中,正确的是( )A .23∈{x |x ≤3}B .23∉{x |x ≤3}C .23⊆{x |x ≤3}D .{23}⊄{x |x ≤3}3.已知集合A ={x ∈N *|-5≤x ≤5},则必有( )A .-1∈AB .0∈A C.3∈A D .1∈A1、 一般地,对于两个集合A 、B ,如果集合A 中任意一个元素都是集合B 中的元素,则 称 集合A 是集合B 的子集。
记作B A ⊆.4.满足M a ⊆}{的集合},,,{d c b a M 共有 ( )5.6个 B.7个 C.8个 D.15个6.已知集{}}{a x x B x x A <=<<=,21,满足A B ,则 ( )A.2≥aB. 1≤aC.1≥aD. 2≤a7.已知集合}{41>-<=x x x A 或,=B }{32+≤≤a x a x ,若A B ⊆,求实数a 的取值范围.2、 如果集合B A ⊆,但存在元素B x ∈,且A x ∉,则称集合A 是集合B 的真子集.记作:A B.3、 把不含任何元素的集合叫做空集.记作:∅.并规定:空集合是任何集合的子集.4、 如果集合A 中含有n 个元素,则集合A 有n 2个子集。
8.集合}{Z x x x A ∈<≤=且30的真子集的个数为 ( )A.5B.6C.7D.8四、集合运算1、 集合A 与B 的并集.记作:B A2、 A 与B 的交集.记作:B A .3、全集、补集?{|,}U C A x x U x U =∈∉且9.设集合A ={x|2≤x <4},B ={x|3x -7≥8-2x},则A ∪B 等于( )A .{x|x ≥3}B .{x|x ≥2}C .{x|2≤x <3}D .{x|x ≥4}10.集合A ={0,2,a},B ={1,2a }.若A ∪B ={0,1,2,4,16},则a 的值为( )A .0B .1C .2D .411.满足M ⊆{4321,,a a a a },且M ∩{321,,a a a }={21,a a }的集合M 的个数是( )A .1B .2C .3D .412.已知全集U=R ,集合A={x ︱-2≤x ≤3},B={x ︱x <-1或x >4},那么集合A ∩(CUB )等于( ).A.{x ︱-2≤x <4}B.{x ︱x ≤3或x ≥4}C .{x ︱-2≤x <-1} D.{-1︱-1≤x ≤3}13.(12分)已知全集{}6,5,4,3,2,1,0=U ,集合{}41≤<∈=x N x A ,(1)用列举法表示集合A 与B ;(2)求B A ⋂及)(B A C U ⋃。
大学集合论试题及答案

大学集合论试题及答案一、选择题(每题3分,共30分)1. 集合论的创始人是()。
A. 康托尔B. 罗素C. 希尔伯特D. 哥德尔2. 集合A和集合B的并集表示为()。
A. A∩BB. A∪BC. A-BD. A∩B'3. 若集合A是集合B的子集,则表示为()。
A. A⊆BB. A⊇BC. A⊂BD. A⊃B4. 空集是所有集合的()。
A. 子集B. 真子集C. 并集D. 交集5. 集合A和集合B的交集表示为()。
A. A∩BB. A∪BC. A-BD. A∩B'6. 若集合A和集合B的交集为空集,则A和B是()。
A. 子集B. 真子集C. 互斥的D. 相等的7. 集合的幂集是指()。
A. 集合的所有子集的集合B. 集合的所有元素的集合C. 集合的所有真子集的集合D. 集合的所有非空子集的集合8. 集合A和集合B的差集表示为()。
A. A∩BB. A∪BC. A-BD. A∩B'9. 集合的元素个数称为集合的()。
A. 基数B. 序数C. 秩D. 维数10. 集合论中,无限集合的基数可以是()。
A. 有限的B. 可数的C. 不可数的D. 以上都是二、填空题(每题2分,共20分)1. 集合{1, 2, 3}的幂集有个元素。
2. 集合{a, b, c}和集合{a, b}的交集是。
3. 集合{1, 2, 3}和集合{2, 3, 4}的并集是。
4. 集合{1, 2, 3}和集合{2, 3, 4}的差集是。
5. 集合{1, 2, 3}的补集在全集U={1, 2, 3, 4, 5}中是。
6. 若集合A={1, 2, 3},集合B={2, 3, 4},则A∪B= 。
7. 集合{1, 2, 3}的子集个数是。
8. 集合{1, 2, 3}的真子集个数是。
9. 集合{1, 2, 3}的非空真子集个数是。
10. 若集合A={1, 2, 3},集合B={2, 3, 4},则A∩B= 。
三、解答题(每题10分,共50分)1. 证明:若集合A是集合B的子集,且集合B是集合C的子集,则集合A是集合C的子集。
哈工大集合论习题课-第三章 关系习题课(学生)

习 题 课例1设{,,}A a b c =,给出A 上的一个二元关系,使其同时不满足自反性、反自反性、对称性、反对称和传递性的二元关系,并画出R 的关系图。
解:{(,),(,),(,),(,)}R a a b c c b a c =,关系图如图所示。
例2 设X 是一个集合,X =n ,求:1.X 上的二元关系有多少?()22n 2. X 上的自反的二元关系有多少? 3. X 上的反自反的二元关系有多少?解:因为把所有的反自反的二元关系的每个都加上对角线上的序对,就变成了自反的关系,因此,自反的与反自反的个数一样多。
即22nn-4. X 上的对称的二元关系有多少?2222n n n nn -++=,故共有222n n+个对称的关系。
5. X 上的反对称的二元关系有多少?22(32)n n n -∙6. X 上既是自反的也是反自反的二元关系的个数;(0)个7.X 上既不是自反的也不是反自反的二元关系有多少?2(2(22))n nn --解:解:可用容斥原理来计算设B 表示所有自反关系构成的集合,C 表示所有反自反关系构成的集合,则22nnB C -==。
而B C φ=,故B C B C =+,从而CC B C S B C S B C =-=--2222222222222(22)n n n n n n n n n n n ----=--=-=-于是,既不是自反的,也不是反自反关系共有22(22)n nn --个。
8.自反的且对称的关系有多少?[此结果与“反自反的且对称的关系有多少?”是一样多]即有222n n -(对角线上全去掉)9.自反的或对称的关系有多少?解:设B 表示自反关系的集合,C 表示对称关系的集合,则自反或对称关系的集合为:22222222n n n n nnB C B C B C +--=+-=+-。
10.X 上既是反自反的也是反对称的二元关系的个数为:223n n -;11.X 上既是对称的也是反对称的关系个数;解:X 上既是对称的也是反对称的关系X R I ⊆,故有2n 。
集合论作业

§3 关系的特性
1. 设 A={1, 2, 3}, 定义 A 上的二元关系如下: R={1, 1, 2, 2}, S={1, 1, 1, 2, 2, 1}, T={1, 2, 1, 3}, U={1, 3, 1, 2, 2, 1}.
试说明 R, S, T, U 是否是 A 上的对称关系和反对称关系.
2. 在 R2 平面上画出下述关系的关系图, 判断每一关系成立哪些性质. (1) R1={x, y | x=y}. (2) R3={x, y | | x |≤1 且| y |≥1}.
3. 设 A={1, 2, 3, 4}, 确定下列关系是否是自反的, 反自反的, 对称的, 反对称的或 传递的.
.
5
单元测试题(一)
一、单项选择题
1. 若集合 A={a, b, c}, 为空集合, 则下列表示正确的是( )
(A) {a}A
(B) {a}A
2. 对任意集合 S, S∪=S, 满足(
(C) aA )
(D) A
(A) 幂等律
(B) 零一律
(C) 同一律
(D) 互补律
3. 设 S1=, S2={}, S3=P({}), S4=P(), 以下命题为假的是( )
3. 找出由关系图所确定的关系并且给出它的关系矩阵.
f d e
b
c
a
7
§2 关系的运算
1. 设 A={1, 2, 3, 4}, R={1, 2, 2, 4, 3, 4, 4, 4}, S={1, 3, 2, 4, 4, 2, 4, 3}. (1) 求出 R∪S, R∩S, R-S, R1. (2) 求出 dom (R), ran (R), dom (R∩S), ran (R∩S).
集合论习题

课程作业——集合论部分•填空题1、集合有两种表示方法,分别为法和法。
2、“使有意义的所有的集合。
”可表示为:。
“大于3而小于或等于7的整数组成的集合”表示为。
3、写出A={a,b,c,d}}的全部子集,真子集为。
4、设A,B是两个集合,A={1,2,3,4},B={2,3,5},则A-B= ,r(B)-r(A)= ,r(A)的元素个数为。
5、设,则A-B= ,B-A= ,~A= ,~B= 。
6、全集E={a,b,c,d,e},A={a,d},B={a,b,e},C={b,d},求(AÇB)È~C= ,r(A)Çr(B)= 。
7、集合运算的基本定律:1)AÇA=A,满足律;2)AÇE=A,满足律;3)~(AÈB)=~AÇ~B,满足律。
8、A和B是任意两个集合,若有序对的第一个元素是A的一个元素,第二个元素是B的一个元素,则所有这样的有序对集合称为集合A和B 的,记作A´B,即A´B= 。
9、设A、B是两个集合,其中A={1,2},B={a,b,c},则A×B= ,B×A= ,所以笛卡尔积不满足律。
10、设A、B为两个有限集合,则根据包含排斥定理知:|A∪B|= 。
11、有序对(a,b)=(x,y)的充分条件是。
•单项选择题1、由集合运算定义,下列各式正确的有()。
•XÍXÈY B.XÊXÈY C.XÍXÇY D.YÍXÇY2、下列命题正确的是()。
A.fÇ{f}=f B.fÈ{f}=f C.{a}Î{a,b,c} D.fÎ{a,b,c}3、设集合,则()。
4、下列式子中正确的有()。
5、设为任意集合,下列命题正确的有()A、若,则;B、若,则;C、若则;D、若,则6、对于任意集合S,,满足()A、等幂律B、同一律C、零一律D、互补律7、某个集合的元数为10,可以构成()个子集。
集合论习题答案

P3 习题1.11.1.1 解:⑴ {2,3,5,7,11,13,17,19}; ⑵ {e,v,n,i,g}; ⑶ {-3,2};⑷ {-1}; ⑸ {2,271i +-,271i --}; ⑹ Φ ⑺ 共14项,前四项为极小因式:不能再分解为其它因式的因式:{①x+1,②x -1,③x 2+x+1,④x 2-x+1,①②x 2-1,①③x 3+2x 2+2x+1,①④x 3+1, ②③x 3-1,②④x 3-2x 2+2x -1,③④x 4+x 2+1,①②③x 4+x 3-x+1,①②④x 4-x 3+x -1,①③④x 5+x 4+x 3+x 2+x+1,②③④x 5-x 4+x 3-x 2+x -1)}1.1.2 解 ⑴ {x | x ∈I + , x<80}; ⑵ {x | x ∈I 且∃n ∈I 使x=2n+1}; ⑶ {x | x ∈I 且∃n ∈I 使x=5n};⑷ {(x,y)| x,y ∈R , x 2+y 2<1}; ⑸ {(ρ,θ)| ρ,θ∈R , ρ>1}; ⑹ {ax+b=0| a,b ∈R 且a ≠0}。
P5 习题1.21.2.1 答:为真的有:⑵、⑷、⑻、⑽,其余为假。
1.2.2 答:为真的有:⑴、⑷,其余为假。
1.2.3 解:A=Φ,B={0},C={…,-4,-2,0,2,4…},D={2,4},E={…,-4,-2,0,2,4…},F={2,4}, G=Φ,H={…,-4,-2,0,2,4…}。
∴ C=E=H ,D=F ,A=G 。
1.2.4 答:四个全为真。
证明:⑴ 例 A={a} , B={a,A}⑵ 例 B={A} , C={A , B}⑶ 例 A={Φ}⑷ 例 A={a} , B={a,A} , ∴ 2B ={Φ , {a} , {A} , B} ※1.2.5 解 ⑴ 幂集 {Φ} ;幂集的幂集 {Φ,{Φ}}⑵ 幂集 {Φ,{Φ},{a},{Φ,a}};幂集的幂集 零元素子集 {Φ,单元素子集 {Φ} , {{Φ}} , {{a}} , {{Φ,a}},双元素子集 {Φ,{Φ}} , {Φ,{a}} , {Φ,{Φ,a}} , {{Φ},{a}} , {{Φ},{Φ,a}} , {{a},{Φ,a}} , 三元素子集 {Φ,{Φ},{a}} , {Φ,{Φ},{Φ,a}} , {Φ,{a},{Φ,a}} , {{Φ},{a},{Φ,a}}}, 四元素子集 {Φ,{Φ},{a},{Φ,a}} 。
哈工大集合论习题课-第五章 图的基本概念习题课(学生)

第五章 图的基本概念习 题 课 11. 画出具有 6、8、10、…、2n 个顶点的三次图;是否有7个顶点的三次图?2. 无向图G 有21条边,12个3度数顶点,其余顶点的度数均为2,求G 的顶点数p 。
解:设图的顶点为p ,根据握手定理:1deg()2pi i v q ==∑,有212)12(2312⨯=-⨯+⨯p ,得15302==p p ,。
3. 下列各无向图中有几个顶点?(1)16条边,每个顶点的度为2;(2)21条边,3个4度顶点,其余的都为3度数顶点;(3)24条边,各顶点的度数相同。
解: 设图的顶点为p ,根据握手定理:(1)1deg()2p i i v q ==∑,即2221632p q ==⨯=;所以16p =,即有16个顶点。
(2)1deg()2p i i v q ==∑,即433(3)222142p q ⨯+⨯-==⨯=,所以13p =。
(3)各点的度数为k ,则1deg()2i pi v q ==∑,即222448k p q ⨯==⨯=,于是① 若1k =,48p =; ② 若2k =,24p =;③ 若3k =,16p =; ④ 若4k =,12p =;⑤ 若6k =,8p =;⑥ 若8k =,16p =; ⑦ 若12k =,4p =;⑧ 若16k =,3p =; ⑨ 若24k =,2p =; ⑩ 若48k =,1p =。
4.设图G 中9个顶点,每个顶点的度不是5就是6。
证明G 中至少有5个6度顶点或至少有6个5度顶点。
证:由握手定理的推论可知,G 中5度顶点数只能是0,2,6,8五种情况,此时6度顶点数分别为9,7,5,3,1个。
以上五种情况都满足至少5个6度顶点或至少6个5度顶点的情况。
5.有n 个药箱,若每两个药箱里有一种相同的药,而每种药恰好放在两个药箱中,问药箱里共有多少种药?[就是求一个完全图n K 的边数(1)(2)/2q p p =--g ]6.设G 是有p 个顶点,q 条边的无向图,各顶点的度数均为3。
哈工大集合论习题课-第六章 树及割集 习题课(学生)
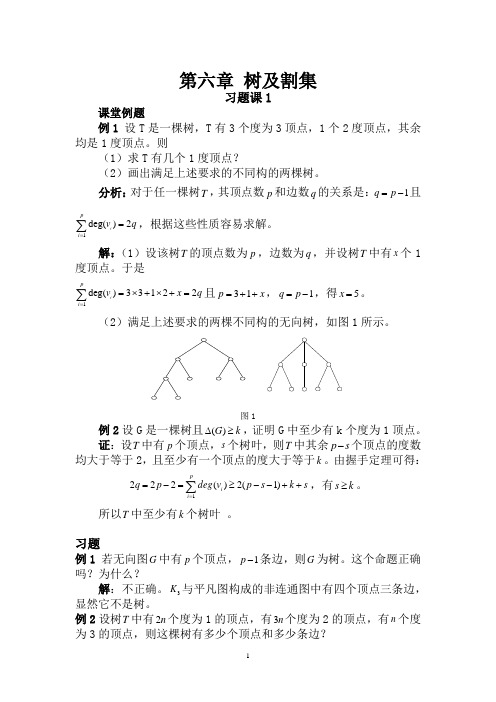
第六章 树及割集习题课1课堂例题例1 设T 是一棵树,T 有3个度为3顶点,1个2度顶点,其余均是1度顶点。
则(1)求T 有几个1度顶点?(2)画出满足上述要求的不同构的两棵树。
分析:对于任一棵树T ,其顶点数p 和边数q 的关系是:1q p =-且1deg()2ipi v q ==∑,根据这些性质容易求解。
解:(1)设该树T 的顶点数为p ,边数为q ,并设树T 中有x 个1度顶点。
于是1deg()33122ipi v x q ==⨯+⨯+=∑且31p x =++,1q p =-,得5x =。
(2)满足上述要求的两棵不同构的无向树,如图1所示。
图1例2设G 是一棵树且()G k ∆≥,证明G 中至少有k 个度为1顶点。
证:设T 中有p 个顶点,s 个树叶,则T 中其余p s -个顶点的度数均大于等于2,且至少有一个顶点的度大于等于k 。
由握手定理可得:1222()2(1)pi i q p deg v p s k s ==-=≥--++∑,有s k ≥。
所以T 中至少有k 个树叶 。
习题例1 若无向图G 中有p 个顶点,1p -条边,则G 为树。
这个命题正确吗?为什么?解:不正确。
3K 与平凡图构成的非连通图中有四个顶点三条边,显然它不是树。
例2设树T 中有2n 个度为1的顶点,有3n 个度为2的顶点,有n 个度为3的顶点,则这棵树有多少个顶点和多少条边?解:设T 有p 个顶点,q 条边,则123161q p n n n n =-=++-=-。
由deg()2v Vv q ∈=∑有:1223322(61)122n n n q n n ⨯+⨯+⨯==-=-,解得:n =2。
故11,12q p ==。
例3证明恰有两个顶点度数为1的树必为一条通路。
证:设T 是一棵具有两个顶点度数为1的(,)p q 树,则1q p =-且1deg()2pii v q ==∑2(1)p =-。
又T 除两个顶点度数为1外,其他顶点度均大于等于2,故211deg()2deg()2(1)p p iii i v v p -===+=-∑∑,即21deg()2(2)p ii v p -==-∑。
集合论-第三四章习题

例7 是否存在一个偏序关系≤,使得(X,≤)中有唯一 的极大元素,但没有最大元素?若有请给出一个具体 例子;若没有,请证明之。 例8 设R是X上的偏序关系,证明:
R是X上的全序关系X×X=R∪R-1。
例9设(A,≤)是偏序集,a∈A,f(a)={x|x∈A,x≤a},
证明:f:A→2A是一个单射,且当a≤b时,有
二、性质 定理1 设A,B,C是三个任意的集合,则 (1)若A⊆B,则|A|≤|B| ; (2)若|A|≤|B|,|B|≤|C|,则|A|≤|C| ; 推论:设A是无穷集合,则|N|≤|A|。 前面介绍了要证明两个集合基数相等必须在两个集 合之间建立起一个一一对应,但这往往是比较困难的。 下面介绍证明两个集合基数相等的一个比较简单的方 法,表示成下面的两个定理形式,这两个定理的证明 是冗长和复杂的,故略去。 定理2 (Zermelo)设A,B是两个任意集合,则|A|=|B|, |A|>|B|, |A|<|B|,三者中恰有一个成立。 这种性质称为三歧性,故这个定理称为三歧性定理。
习题课(2)
例1 设R是A上的二元关系,下面的结论是否正确?并 证明你的结论. (1)R是自反的,则R· R也是自反的 (2)R是对称的,则R· R也是对称的。 (3)R是反自反和传递的,则R是反对称的。 (正确\正确\正确) 例2 设R是集合A上的反对称关系,则t(R)一定是反对 称的吗? 例3 是否可以定义二元关系的反自反闭包与二元关系 的反对称闭包?为什么? 例4 是否存在X(|X|=n)上的一个二元关系R,使得 R1,R2,…,Rn两两不相等。 例5 证明:如果R是对称的,则R+也是对称的。
例3 设集合A={a,b,c,d,e}上关系R定义如下: R={(a,a),(a,b),(a,c),(a,d),(a,e),(b,b),(b,c),(b,e), (c,c),(c,e),(d,d),(d,e),(e,e)}。 1.写出R的关系矩阵; 2.验证(A,R)是偏序集; 3.画出Hasse图; 4.若A上的关系如下: R={(a,a),(a,b),(a,c),(a,d),(a,e),(b,b),(b,c),(b,e), (c,c), (c,d),(c,e),(d,d),(d,e),(e,e)},则有如何? 例4 证明:每个由n2+1个实数组成的数列中必有一个 长至少为n+1的不减子序列,或有一个长至少为n+1 的不增子序列。
集合论部分习题离散数学

二元关系和函数习题1.设集合,A上的二元关系,则关系()(A) (B) (C) (D)2.设集合,A上的二元关系,则关系()(A)(B) (C) (D)3.设,,从R到S不同的二元关系共有()个。
A) 6 (B) 7 (C) 32 (D) 644.设集合上的二元关系,则R具有()(A) 自反性(B) 传递性(C) 对称性(D) 非自反性5.设集合上的二元关系,则关系R不具有()(A) 自反性(B) 传递性(C) 对称性(D) 反对称性6.设集合上的二元关系R的关系矩阵如下,则R具有的性质是()。
(A)非自反性(B)反对称性(C)传递性(D)以上都不对7.设集合上的二元关系,则S是R的()(A) 自反(B) 传递(C) 对称(D) 以上都不对8.设集合上的二元关系则R()。
(A) 是等价关系但不是偏序关系(B) 是偏序关系但不是等价关系(C) 既是等价关系又是偏序关系(D) 既不是等价关系也不是偏序关系9.设集合,偏序关系是A上的整除关系,则偏序集上元素10是集合A的()。
(A)最大元(B) 最小元(C)极大元(D)极小元10.判断下述结论的正确性(1) 存在这样的关系,它可以既满足自反性,又满足非自反性。
()(2)存在这样的关系,它可以既不满足自反性,又不满足非自反性。
()(3)存在这样的关系,它可以既满足对称性,又满足反对称性。
()(4)存在这样的关系,它可以既不满足对称性,又不满足反对称性。
()11.写出三个特殊的关系不具备五个重要性质(自反、非自反、对称、反对称、传递)中的哪几个。
(1)恒等关系不具备()(2)全域关系不具备()(3)空关系不具备()12.设,则S上可以定义()个不同的二元关系,其中有()个等价关系,()个偏序关系,(A)1 (B)2 (C)3 (D)4 (E)5 (F)16是();是()。
(A) 等价关系但不是偏序关系(B) 偏序关系但不是等价关系(C) 等价关系和偏序关系(D) 既不是等价关系也不是偏序关系13.如果A={0,1} B={1,2} 则A2×B= 。
集合习题课 课件

跟踪训练 4 学校举办了排球赛,某班 45 名同学中有 12 名 同学参赛,后来又举办了田径赛,这个班有 20 名同学参赛, 已知两项都参赛的有 6 名同学,两项比赛中,这个班共有多 少名同学没有参加过比赛? 解 设 A={x|x 为参加排球赛的同学},B= {x|x 为参加田径赛的同学},则 A∩B={x|x 为 参加两项比赛的同学}.画出 Venn 图(如图), 可知没有参加过比赛的同学有:45-(12+20-6)=19(名). 答 这个班共有 19 名同学没有参加过比赛.
跟踪训练 2 设集合 A={x|x2-3x+2=0},集合 B={x|x2-4x+a =0,a 为常数},若 B A,求实数 a 的取值范围.
解 由已知得 A={1,2}.假设 B⊆A,故集合 B 有两种情况, B=∅或 B≠∅. 当 B=∅时,方程 x2-4x+a=0 无实根,
∴Δ=16-4a<0,∴a>4. 当 B≠∅时,若 Δ=0,则有 a=4,B={2}⊆A 满足条件;若 Δ>0, 则 1,2 是方程 x2-4x+a=0 的根,但由根与系数的关系知矛盾, 故 Δ>0 不成立.∴当 B≠∅时,a=4. 综上所述,满足 B⊆A 时,a 的取值范围是 a≥4. ∴满足 B⊆A 的 a 的取值范围是 a<4.
∴(∁IM)∩(∁IN)={d,e}∩{a,c}=∅.
5.已知全集 U=R,集合 A={1,2,3,4,5},B={x∈R|x≥3},下图
中阴影部分所表示的集合为
(B )
A.{1}
B.{1,2}
C.{1,2,3}
D.{0,1,2}
解析 由题意得,A∩B={3,4,5},阴影部分所表示的集合
为集合 A 去掉集合 A∩B 中的元素所组成的集合,所以为
求由 a 的可能取值组成的集合. 解 由题意得,P={-3,2}. 当 a=0 时,S=∅,满足 S⊆P; a≠0 时,方程 ax+1=0 的解为 x=-1a, 为满足 S⊆P,可使-1a=-3,或-1a=2, 即 a=13,或 a=-12. 故所求集合为0,13,-12.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解 (1)和 S5 不交的子集不含有 3 和 5,因此 X=S2. (2)S4 的子集只能是 S4 和 S5. 由于与 S2 不交,不能含有偶
数,因此 X=S5. (3)S1, S2, S3, S4 和 S5 都是 S1 的子集,不包含在 S3 的子集
含有偶数,因此 X=S1, S2 或 S4. (4)XS3=意味着 X 是 S3 的子集,因此 X=S3 或 S5. (5)由于 S3 是 S1 的子集,因此这样的 X 不存在.
4.证明 AB = AC AB = AC B = C
解题思路
分析命题:含有 3 个命题:
AB = AC AB = AC
①
②
B=C
③
证明要求
前提:命题①和②
结论:命题③
证明方法:
恒等式代入
反证法
利用已知等式通过运算得到新的等式
证 方法一:恒等变形法
B = B(BA) = B(AB) = B(AC) = (BA)(BC) = (AC)(BC) = (AB)C = (AC)C = C 方法二:反证法. 假设 B C,则存在 x (xB 且 xC), 或存在 x (xC 且 xB). 不妨设为前者. 若 x 属于 A,则 x 属于 AB 但是 x 不属于 AC,与已知矛盾;若 x 不属于 A,则 x 属于 AB 但 x 不属于 AC,也与已知矛盾.
“如果 P 则 Q”意味着 AB,“P 当且仅当 Q”意味着A=B.
通过集合运算判断 AB,即 AB = B, AB = A, AB = 三个等式 中有一个为真,则 AB. 可以通过文氏图判断集合的包含(注意这里是判断,而不是证明)
2.设
S1={1, 2, … , 8, 9},
S2={2, 4, 6, 8}
关系的闭包
也是一种运算 自反闭包、对称闭包、传递闭包
内容复习
偏序关系
自反、反对称、传递
通常用“≤”表示偏序
全序(线性次序):偏序且任意x,y∈X, 必有xRy或yRx
集合X={a,b}的幂集上的“”关系??
字典序:
有限字母表上的“≤”关系是全序关系 构造出的字的集合上的关系也是全序关系
分析 (1)判断元素 a 与集合 A 的隶属关系是否成立的基本方法如下:
把 a 作为一个整体,检查它在 A 中是否出现,注意这里的 a 可能 是集合表达式. (2)判断 AB 的四种方法: 若 A,B 是用枚举方式定义的,依次检查 A 的每个元素是否在 B 中 出现. 若 A,B 是谓词法定义的,且 A, B 中元素性质分别为 P 和 Q, 那么
内容复习
最大(小)元素、极大(小)元素、上下界、 上下确界
偏序关系上的性质
哈斯图
偏序关系的图形化表示
内容复习
等价关系
自反、对称、传递 等价类:[x]R={y|y∈X且xRy} X关于R的商集(X/R):等价类的集合
集合的划分 商集X/R是X的一个划分 任一划分均可构造一个等价关系
3. 判断以下命题的真假,并说明理由. (1)AB = A B= (2)A(BC) = (AB)(AC) (3)AA = A (4)如果 AB = B,则 A = E. (5)A = {x}x,则 xA 且 x A.
解题思路: 先将等式化简或恒等变形. 查找集合运算的相关的算律,如果与算律相符,结果为真. 注意以下两个重要的充要条件 AB = A AB = AB = AB AB = B AB = A 如果与条件相符,则命题为真. 如果不符合算律,也不符合上述条件,可以用文氏图表示 集合,看看命题是否成立.如果成立,再给出证明. 试着举出反例,证明命题为假.
方法三:利用已知等式通过运算得到新的等式. 由已知等式①和②可以得到 (AB) (AB) = (AC) (AC),即 AB = AC. 从而有 A(AB) =A(AC) 根据结合律得 (AA)B = (AA) C 由于 AA = , 化简上式得 B = C.
5.设 A,B 为集合,试确定下列各式成立的充分必要条件: (1)AB=B (2)AB=BA (3)AB=AB (4)AB=A
S3={1, 3, 5, 7, 9}
S4={3, 4, 5}
S5={3, 5} 确定在以下条件下 X 是否与 S1,…,S5 中某个集合相等? 如果是,又与哪个集合相等?
(1)若 XS5= (2)若 XS4 但 XS2= (3)若 XS1 且 X⋢S3 (4)若 XS3= (5)若 XS3 且 X⋢S1
解
(1)B=是 AB=A 的充分条件,但不是必要条件. 当 B 不 空但是与 A 不交时也有 AB=A.
(2)这是 DM 律,命题为真. (3)不符合算律,反例如下:
A={1},AA=,但是 A. (4)命题不为真. AB=B 的充分必要条件是 BA,不是
A=E. (5)命题为真,因为 x 既是 A 的元素,也是 A 的子集.
二、练习题 1.判断下列命题是否为真。 (1) (2) (3){} (4){} (5){a,b}{a,b,c,{a,b,c}} (6){a,b}{a,b,c,{a,b}} (7){a,b}{a,b,{{a,b}}} (8){a,b}{a,b,{{a,b}}} 解 (1)、(3)、(4)、(5)、(6)、(7)为真,其余为假.
内容复习
幂集 有序偶/n元集合
内容复习
关系的概念
笛卡尔乘积的子集
关系的表示
集合表示法/图形表示法/矩阵表示法 注意顺序或方向
关系的运算
交、并、补、差、对称差 复合(结合律) 逆关系
内容复习
关系的性质
研究集合X上的二元关系 自反、反自反、对称、反对称、传递 在关系图和关系矩阵上的表现
集合论(习题课)
湖南大学信息科学与工程学院 廖波
内容
内容复习 例题讲解 复习作业
内容复习
集合的概念
确定性、顺序无关性、唯一性
集合的表示
列举法、描述法
集合的关系
相等、包含 文氏图
内容复习
集合的运算
交、并、补、差、对称差 运算的性质
证明集合相等
A⊆B且B⊆A 运算性质的运用 定义
解题思路: 求解集合等式成立的充分必要条件可能用到集合的算律、 不同集合之间的包含关系、以及文氏图等. 具体求解过程 说明如下:
